Word problems for division and multiplication

Reading & Math for K-5

• Math
  • 2. Numbers

       1. Learning numbers
       2. Counting
       3. Comparing numbers
       4. Place Value
       5. Rounding
       6. Roman numerals
       7. Fractions & Decimals
          1. Fractions
          2. Decimals

    3. 4 Operations

       1. Addition
       2. Subtraction
       3. Multiplication
       4. Division
       5. Order of operations
       6. Flashcards
       7. Drills & practice
       8. Measurement
          1. Measurement
          2. Money
          3. Time

    4. Advanced

       1. Factoring & prime factors
       2. Exponents
       3. Proportions
       4. Percents
       5. Integers
       6. Algebra
       7. More
          1. Shape & geometry
          2. Data & graphing
          3. Word problems
• Reading
• Kindergarten
• Vocabulary
• Spelling
• Grammar & Writing
• Science
• Cursive
• |
• Bookstore

• Math
• Reading
• Kindergarten
• Vocabulary
• Spelling
• Grammar & Writing
• More
  • Science
  • Cursive
  • Bookstore

• Math
• Reading
• Kindergarten
• More
  • Vocabulary
  • Spelling
  • Grammar & Writing
  • Science
  • Cursive
  • Bookstore

Download & Print
Only $5.60

Word problem worksheets: Mixed multiplication & division

Below are six versions of our grade 4 math worksheet with mixed multiplication and division word problems.  All numbers are whole numbers with 1 to 4 digits.  Division questions may have remainders which need to be interpreted (e.g. «how many left over»).  In the last question of each worksheet, students are asked to write an equation with a variable for the unknown quantity.  These worksheets are pdf files.

We will learn how to solve step-by-step the word problems on
multiplication and division of whole numbers. We know, we need to do multiplication
and division in our daily life. Let us solve some word problem examples.

Word problems on multiplying and dividing of large numbers:

1. The cost of a chair is $980.50. Find the cost of such 2035 chairs.

Solution:

Cost of a chair =                             980.50

Number of chairs =                         × 2035

                                                     490250

                                                    2991500

                                                    0000000

                                             +  196100000

Cost of 2035 chairs =                  1995317.50

Therefore, cost of 2035 chairs is $1995317.50.

2. A tyre factory produces 6348 tyres a day. How many tyres
will the factory produce in 460 days?

Solution:

Number of tyres a tyre factory produces in one day =            6348

Number of day =                                                               × 460

                                                                                         0000

                                                                                     380880

                                                                               +  2539200

Total number of tyres produces in 460 days =                 2920080

Therefore, the tyre factory will produce 2920080 tyres in
460 days.

3. The cost of a flat is $4218000. If there are 36 similar
flats in a building, how much money will be collected by selling all the flats?

Solution:

Cost of one flat = $4218000

Number of similar flats = 36

Cost of 36 flats = $4218000 × 36

Hence, the money collected = $151848000

4. 470988 books are to be arranged equally in shelves. If 378 books are arranged in each shelf, how many shelves will be needed?

Solution:

Total number of books = 470988

Number of books arranged in each shelf = 378

Number of shelves needed = 470988 ÷ 378

Therefore, 1246 shelves needed to arrange 470988 books
equally.

5. The cost of 534 train tickets was $457104. Find the cost
of one ticket?

Solution:

Number of train tickets = 534

Cost of 534 train tickets = $457104

Cost of 1 train ticket = 457104 ÷ 534

Therefore, cost of one train ticket is $856.

6. 36 families went on trip which cost them $1216152. If each
family share the cost equally, how much did each family pay?

Solution:

Total number of families = 36

Total cost paid by 36 families = $1216152

Cost paid by each family = $1216152 ÷ 36

Hence, cost paid by each family = $33782

● Operations On Whole Numbers

• Addition Of Whole Numbers.
• Word Problems on Addition and Subtraction of Whole Numbers
• Subtraction Of Whole Numbers.
• Multiplication Of Whole Numbers.
• Properties Of Multiplication.
• Division Of Whole Numbers.
• Properties Of Division.
• Word Problems on Multiplication and Division of Whole Numbers
• Worksheet on Addition and Subtraction of Large Numbers
• Worksheet on Multiplication and Division of Large Numbers
• Worksheet on Operations On Whole Numbers

Multiplication and Division are a part of the primary school Mathematics curriculum. These are universal mathematical operations that lay down the foundation for the Quantitative Aptitude of an individual. They are the fundamentals of nearly all mathematical concepts, ingrained into basic Arithmetic, Geometry, Algebra, and Calculus. Thus it is essential for all the students to ace the Multiplication and Division word problems. Let’s understand more about multiplication and division word problems in this blog!

Multiplication and Division word problems are comprehensive mathematical questions designed to help students learn these skills by giving them real-life scenarios. These word problems help young children to relate to the problems on a personal level, activating their cognition in a better way. However, some of them may face a slight difficulty in understanding these questions. So, let’s try and understand how to progress with such questions.

Try solving these word problems using the BODMAS concept.
To know more about it, read our blog on BODMAS questions!

Multiplication Word Problems

Multiplication word problems generally include keywords like calculating the “total” number of objects, goods or production. Here are some examples of multiplication word problems:

Q1: There are 4 rows of seats in a class. Each row has 12 benches. How many students can sit in the class?

Ans:
In such questions, we take the following steps:

Note the number of benches in one row= 12
No. of rows = 4
Multiply the number with the number of rows = 12×4

Total number of seats available for students= 48

Therefore, 48 students can sit in the class!

Q2: A bottle factory produces 684 bottles a day. How many bottles will the factory produce in 46 days?

Ans:
Number of tyres a tyre factory produces in one day = 684
Number of days = 46

Total number of bottles produced = 684 x 46 = 31464

Therefore, the company will produce 31464 bottles in 46 days. 

Division Word Problems

Division word problems on the other hand, generally are the harder ones among Multiplication and Division word problems. They have questions that deal with segregating/putting/sorting objects into different sections. Here are some examples to help you understand better:

Q1: There are 140 peanuts in a bowl. A worker has to put them equally in 4 packets. How many peanuts will be there in one packet?
Ans:

For division word problems, we always start with identifying the dividend and the divisor. 

The total number of peanuts will be taken as a dividend. This is because we have to sort them into smaller groups i.e. divide the total number of peanuts

The number of packets will be the divisor because we have to divide the peanuts in the number of packets we have. 

Total number of peanuts, i.e. dividend= 140
No. of packets, i.e. divisor = 4
No. of packets = 140 / 4
After division, the quotient comes out to be 35.

Therefore, the total number of peanuts in a packet will be 35.

Practice Problems

The illustrations must have helped you understand how to solve multiplication and division word problems. Here are some questions based on the same concept for you to practice. The questions are mixed, so that you also work on identifying whether a question requires you to multiply or divide.

Q1: Alex has 150 tickets for a concert. He has to put them in 10 boxes. How many tickets will be there in a single box?

Q2: There are 10 candies in a packet. A shopkeeper buys 124 packets of these candies. How many candies does he have in total?

Q3: There are 5240 fish in a pond. The number of fish doubles in a month. How many fish will be there in the pond after two months?

Q4: A worker has 4500 loose sheets. He has to make notebooks with 120 pages. How many notebooks can he make?

Q5: It takes 15 minutes to make a card. A worker works for 6 hours in a day. How many cards will he be able to make?

Q6: A student is collecting leaves for a science experiment. He collects 6 new types of leaves in a day. How many leaves will he have in a week?

Q7: A shopkeeper earns 10$ on making a sale. If he makes 123 sales, how much money will he be able to earn?

Q8: Ron is taking his students out on a school trip. There are 2420 students in the school. A bus can only seat 45 students. How many buses will he need to take all the students on a trip?

Q9: A company makes 12 bulbs in a day. They work for 6 days a week. How many bulbs will they be able to make at the end of 8 weeks?

Q10: Samyak makes pen boxes in his workshop. If he works for 3 hours, he is able to make 1 box. He works for 8 hours a day. How many boxes will he be able to make in 12 days?

FAQs

So, by the end of this blog, we have given you all that was required to know about multiplication and division word problems. Hope you had no difficulty in grasping the concepts. Keep on practicing and you’ll be able to progress through the topic in no time. To help you with such topics, we have many informative blogs waiting for you. For more entertaining and informative content, follow Leverage Edu on Facebook, Instagram, and LinkedIn.

Word problems are fun and challenging to solve because they represent actual situations that happen in our world. As students, we are always wondering why we should learn one skill or another, and word problems help us see the practical value of what we are learning.

Read the tips and guidance and then work through the multiplication and division word problems in this lesson with your children. Try the three worksheets that are listed within the lesson (you will also find them at the bottom of the page.)

What is multiplication?

The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product. Suppose, you bought 6 pens on one day and 6 pens on the next day. Total pens you bought are now 2 times 6 or 6 + 6 = 12.

This can also be written as 2 x 6 = 12

Not the symbol used for multiplication. The symbol (x) is generally used to represent multiplication. Other common symbols that are used for multiplication are the asterisk (*) and dot (.)  

Important terms in the multiplication

Some important terms used in multiplication are – 

Multiplicand – The number to be multiplied is called the multiplicand. 

Multiplier – The number with which we multiply is called the multiplier.

Product – The result obtained after multiplying the multiplier and the multiplicand is called the product.

The relation between the multiplier, multiplicand and the product can be expressed as – 

Multiplier × Multiplicand = Product

Let us understand this using an example.

Suppose we have two numbers 9 and 5. We wish to multiply 9 by 5.

So, we express it as 9 x 5 which gives us 45.

Therefore, 9 x 5 = 45

Here, 9 is the multiplicand, 5 is the multiplier and 45 is the product.

What is division?

Division is the equal sharing of a given quantity.

For example, Alice wants to share 6 bananas equally with her friend Rose. So, she gives 3 of her bananas to Rose and she is also left with 3 bananas. This means that when we divide 6 by 2 we get 3.

Mathematically, we can write this as 

6 ÷ 2 = 3

Symbol for Division

In mathematics, there is a symbol for every operation. The symbol for division is (÷). Other than the forward-slash (/) is also used to denote the division of two numbers, where, the dividend comes before the slash and the divisor after it. For instance, if we wish to write 15 is being divided by 3, we can write it as 15 ÷ 3 or 15 / 3. Both mean the same.

Important terms in Division

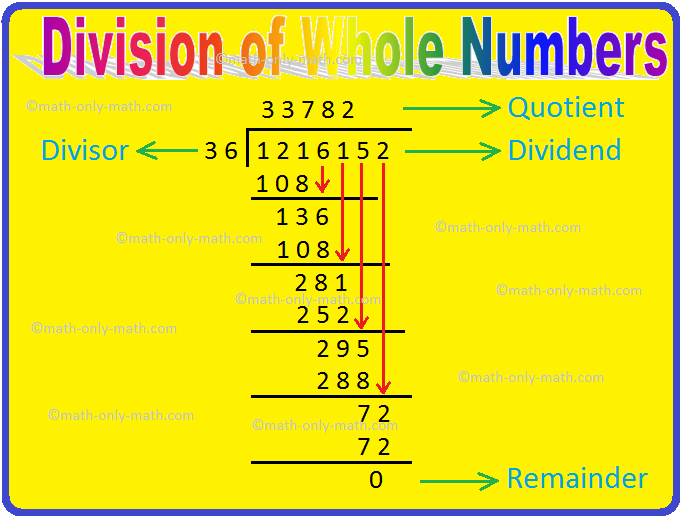
The number that is to be divided is called the Dividend.  Here, 6 is the dividend.

The number by which the dividend is being divided is called the Divisor. 

The result obtained by the process of division is called the Quotient.

The number that is left over after finding the quotient is called the Remainder.

Let us understand these by an example. 

Suppose, we have a pack of 65 chocolates and we want to divide them equally among 7 children while keeping the remaining chocolates with us. How many chocolates does each child get and how many chocolates are we left with after dividing these chocolates?

Using multiplication tables, we have 7 x 9 = 63

Therefore, 7 x 9 + 2 = 65

This means that the quotient when 65 is divided by 7 will be 9 and the remainder will be 2.

As per the definition of the four terms of division, we have

Divisor = 7

Dividend = 65

Quotient = 9

Remainder = 2

Remember: The remainder is always smaller than the divisor.

Formula for Division

There are four important terms in the division, namely, divisor, dividend, quotient, and the remainder. The formula for divisor constitutes all of these four terms. In fact, it is the relationship of these four terms among each that defines the formula for division. If we multiply the divisor with the quotient and add the result to the remainder, the result that we get is the dividend. This means,

Dividend = Divisor x Quotient + Remainder

What are word problems?

A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation. In other words, word problems describe a realistic problem and ask you to imagine how you would solve it using math. Word problems are fun and challenging to solve because they represent actual situations that happen in our world.

How to Solve Word Problems involving multiplication and division?

The following steps are involved in the process of solving word problems involving multiplication and division of numbers – 

1. Read through the problem carefully, and figure out what it is about. This is the most important step as it helps to understand two things – what is given in the question and what is required to be found out.
2. The next step is to represent unknown numbers using variables. Usually, these unknown numbers are the values that are required to be solved for.
3. Once the numbers have been represented as variables, the next step is to translate the rest of the problem in the form of a mathematical expression.
4. Once this expression has been formed, the last step is to solve this expression for the variable and obtain the desired result. 

Let us understand it through an example.

Example

A hawker delivers 148 newspapers every day. How many newspapers will he deliver in a non-leap year?

Solution

We have been given that a hawker delivers 148 newspapers every day. We need to find out the total number of newspapers that he will deliver in a non-leap year. Let us summarise the given information as

Number of newspapers delivered by the hawker in a day = 148

Number of newspapers that he will deliver in a non-leap year = ?

Now, we know that a non-leap year consists of 365 days. This means that we need to find out the total number of newspapers that the hawker will deliver in 365 days. Therefore,

Total number of days on which hawker delivers the newspapers = 365

Now, to find the total number of newspapers delivered by the hawker in 365 days we will have to multiply the Number of newspapers delivered by the hawker in a day by the total number of days in a year. So, we have,

Number of newspapers that he will deliver in a non-leap year = (Number of newspapers delivered by the hawker in a day ) x (total number of days in a year ) ……….. ( 1 )

Substituting the given values in the above equation, we have

Number of newspapers that he will deliver in a non-leap year = 148 x 365

Now, 148 x 365 = 54020 

Hence, the number of newspapers that he will deliver in a non-leap year = 54020

Let us consider another example.

Example 

In a school, a fee of £ 345 is collected per student. If there are 240 students in the school, how much fee is collected by the school?

Solution

We have been given that in a school a fee of £ 345 is collected per student. Also, there are 240 students in the school. We need to find out the total fee collected by the school from all students. Let us first summarise this information

Amount of fee collected by the school from each student = £ 345

Number of students in the school = 240

Total amount of fee collected by the school = ?

This can be calculated by multiplying the fee collected for each student by the number of students in the school. Therefore we have,

Total amount of fee collected by the school = (Amount of fee collected by the school from each student ) x (Number of students in the school ) …….. ( 1 )

Substituting the given information in the above equation, we get

Total amount of fee collected by the school = £ ( 345 x 240 )

Now, 345 x 240 = 82800

Hence, Total amount of fee collected by the school = £ 82800

Solving Multiplicative Comparison Word Problems

Multiplication as Comparing

In multiplicative comparison problems, there are two different sets being compared. The first set contains a certain number of items. The second set contains multiple copies of the first set.

Any two factors and their product can be read as a comparison. Let’s look at a basic multiplication equation:  4 x 2 = 8.

8 is the same as 4 sets of 2 or 2 sets of 4.
8 is 4 times as many as 2, and 2 times as many as 4.

What Operation to Use: Multiply? Divide? Add? Subtract?

The hardest part of any word problem is deciding which operation to use. There can be so many details included in a word problem that the question being asked gets lost in the whole situation. Taking time to identify what is important, and what is not, is essential.

Use a highlighter on written problems to identify words that tell you what you are solving, and give you clues about which operations to choose. Make notes in the margins by these words to help you clarify your understanding of the problem.

Remember: If you don’t know what’s being asked, it will be very difficult to know if you have a reasonable answer.

Different Types of Problem

There are three kinds of multiplicative comparison word problems (see list below). Knowing which kind of problem you have in front of you will help you know how to solve it.

• Product Unknown Comparisons
• Set Size Unknown Comparisons
• Multiplier Unknown Comparisons

The rest of this lesson will show how these three types of math problems can be solved.

Multiplication Problems: Product Unknown

In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the “multiplier” amount. The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed.

These problems in which you know both the number in one set, and the multiplier are called “Product Unknown” comparisons, because the total is the part that is unknown.

In order to answer the question you are being asked, you need to multiply the number in the set by the multiplier to find the product.

Product Unknown Comparisons

In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the “multiplier” amount. The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed. These problems in which you know both the number in one set, and the multiplier are called “Product Unknown” comparisons, because the total is the part that is unknown.

Let us understand it through an example.

Example

Mary is saving up money to go on a trip. This month, she saved three times as much as money as she saved last month. Last month, she saved £ 24.00. How much money did Mary save this month?

Solution

We have been given that Mary is saving up money to go on a trip. This month, she saved three times as much as money as she saved last month. Last month, she saved £24.00. we need to find out how much money did Mary save this month?

Now, as much as tells you that you have a comparison. Three times is the multiplier. 24 is the amount in the first set. The question being asked is how much money did Mary save this month? To find the answer, we multiply 24 by 3. Therefore, we have 24.00 x 3 = 72.

It is important to clearly show that you understand what your answer means. Instead of writing just 72, we will write it as Mary saved £ 72 this month.

Note that whenever we finish a math problem of any kind, we always go back to the original problem. Think: “What is the question we are being asked?” 

Make sure that our final answer is a reasonable answer for the question we are being asked.

We were asked, “How much money did Mary save this month?” 

Our answer is: Mary saved $72.00 this month. Our answer is reasonable because it tells how much money Mary saved this month. We multiplied a whole number by a whole number, so the amount of money Mary saved this month should be more than she saved last month. Seventy-Two is more than 24 . Our answer makes sense.

Multiplication Problems: Set Size Unknown

In some multiplicative comparison word problems, the part that is unknown is the number of items in one set. You are given the amount of the second set, which is a multiple of the unknown first set, and the “multiplier” amount, which tells you how many times bigger (or more) the second set is than the first. Remember, “bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed.

These problems in which you know both the number in the second set, and the multiplier are called “Set Size Unknown” comparisons, because the number in one set is the part that is unknown.

In order to answer the question you are being asked, you need to use the inverse operation of multiplication: division. This kind of division is “partition” or “sharing” division. Dividing the number in the second set by the multiplier will tell you the number in one set, which is the question you are being asked in this kind of problem.

Set Size Unknown Comparisons

In some multiplicative comparison word problems, the part that is unknown is the number of items in one set. You are given the amount of the second set, which is a multiple of the unknown first set, and the “multiplier” amount, which tells you how many times bigger (or more) the second set is than the first. Remember, “bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed. These problems in which you know both the number in the second set and the multiplier are called “Set Size Unknown” comparisons because the number in one set is the part that is unknown.

Let us understand it through an example.

Example

Jeff read 12 books during the month of August. He read four times as many books as Paul. How many books did Paul read?

Solution

We have been given that Jeff read 12 books during the month of August. He read four times as many books as Paul. We need to find out how many books did Paul read?

“As many as “ tells you that we have a comparison. Four times is the multiplier. 12 books is the amount in the second set. How many books did Paul read? This is the question we are being asked. To solve, divide 12 by 4. Now 12 ÷ 4 = 3. It is important to clearly show that we understand what our answer means. Instead of just writing 3, we write complete sentence that Paul read three books.

Note that whenever we finish a math word problem, always go back to the original problem. Think: “What is the question we are being asked?”  Make sure that our final answer is a reasonable answer for the question you are being asked. We were asked, “How many books did Paul read?”  Our answer is: Paul read three books. Our answer is reasonable because it tells how many books Paul read. We divided a whole number by a whole number, so the number of Paul’s books should be less than the number of Jeff’s books. Three is smaller than 12. My answer makes sense.

Multiplicative Comparison Problems: Multiplier Unknown

In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the number of items in the second set, which is a multiple of the first set. The “multiplier” amount is the part that is unknown.

The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed.

These problems in which you know both the number in one set, and the number in the second set are called “Multiplier Unknown” comparisons, because the multiplier is the part that is unknown.

In order to answer the question you are being asked, you need to use the inverse operation of multiplication: division. This kind of division is called “measurement” division.

Multiplier Unknown Comparisons

In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the number of items in the second set, which is a multiple of the first set. The “multiplier” amount is the part that is unknown. The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed. These problems in which you know both the number in one set and the number in the second set are called “Multiplier Unknown” comparisons because the multiplier is the part that is unknown. In order to answer the question you are being asked, you need to use the inverse operation of multiplication: division. This kind of division is called “measurement” division.

Let us understand it through an example.

Example

The gorilla in the Los Angeles Zoo is six feet tall. The giraffe is 18 feet tall. How many times taller than the gorilla is the giraffe?

Solution

We have been given that the gorilla in the Los Angeles Zoo is six feet tall. The giraffe is 18 feet tall. We need to find out how many times taller than the gorilla is the giraffe?

Taller than tells us that we have a comparison. Six feet is the amount in the first set. 18 feet is the amount in the second set. How many times taller than the gorilla is the giraffe? This is the question we are being asked. To solve this we divide18 feet by six feet. Now, 18 ÷ 6 = 3. It is important to clearly show that we understand what our answer means. Instead of just writing 3, we write the complete sentence that the giraffe is three times taller than the gorilla.

Note that whenever we finish a math word problem, always go back to the original problem. Think: “What is the question we are being asked?”  Make sure that your final answer is a reasonable answer for the question you are being asked. We were asked, “How much taller than the gorilla is the giraffe?”  Our answer is: The giraffe is three times taller than the gorilla. Our answer is reasonable because it tells how much taller the giraffe is, compared to the gorilla. We divided a whole number by a whole number, so our quotient should be less than my dividend. Three is less than 18, so our answer makes sense.

Solved Examples

Example 1 There are 287 rows in a stadium. How many students can be seated in this stadium if each row has 165 seats to be occupied?

Solution We are given that,

Number of rows in a stadium = 287

Number of seats in each row = 165

Total number of students that can be seated in the stadium = 287 x 165 = 47335.

Example 2 Henry bought 15 packets of cookies. Each packet contains 35 cookies. How many cookies in all does Henry have?

Solution We are given that

Number of packets of cookies bought by Henry = 15

Number of cookies in each packet = 35

Total number of cookies that Henry has = 15 x 35 = 525

Key Facts and Summary

1. The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product.
2. Division is the equal sharing of a given quantity.
3. A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation.

Recommended Worksheets

Fact Families for Multiplication and Division (Summer Themed) Math Worksheets
Multiplication and Division of Fractions (Veterans’ Day Themed) Math Worksheets
Multiplication and Division Problem Solving (Halloween Themed) Math Worksheets