10000+ результатов для ‘problems and solutions’
Discuss problems and solutions (Oxford Word Skills)
Случайное колесо
от Mgalitskiy
Oxford Word Skills Advanced unit 54
Problems and Solutions
Speaking Problems and solutions
Случайное колесо
от Enest13
Environmental problems, effects and solutions
Групповая сортировка
от Annalar030185
Environmental problems and solutions
Групповая сортировка
от Elenabasharina1
Problems and solutions 2
Сопоставить
от Annalele
Problems and solutions
Викторина
от Azapart
Habitat. Problems and Solutions
Сопоставить
от Gamper
Problems and solutions
Сопоставить
от Languageguru
Problems and solutions
Сопоставить
от Kristinastrikha
Problems and solutions 1
Пропущенное слово
от Annalele
Problems and solutions
Случайные карты
от Azapart
Environmental problems and solutions
Диаграмма с метками
от Olefir150295
problems and solutions IELTS
Упорядочивание
от Anna35
Environmental problems and solutions
Групповая сортировка
от Tstarobinets
Problems and solutions
Сопоставить
от Polinadereza
U5 Problems and solutions
Диаграмма с метками
от Hustyna24
Problems and Solutions
Случайные карты
от Thebarsiks
Problems and solutions
Кроссворд
от Evgcool97
GWB1_Unit4_health problems and solutions
Сопоставить
от Inyaz
Environment problems and solutions Unit6
Групповая сортировка
от Puzyrevasn
6.4 Speaking — problems and solutions
Привести в порядок
от Novorossiysk
Health problems and their solutions
Случайное колесо
от Evgenia24
Unit 14 IELTS (problems and solutions)
Случайное колесо
от Valolma09121996
ENGLISH
IELTS
Hobbies (Elementary Solutions) Unit 2A
Сопоставить
от Merelymercy
English
Activities and sport
Hobbies
Solutions Elementary
Speculating and discussing problems and solutions
Групповая сортировка
от Hop
EGE Orlova problems and solutions Hobby
Случайные карты
от Karolinka1
Car Problems and Solutions Innovations UI
Сопоставить
от Yulyaabrr
Health problems (Solutions Int Un 4)
Викторина с изображением
от Demmary
Solutions Intermediate
Week 1 Day 1. Problems and Solutions
Групповая сортировка
от Ssneglaw
* Problems and solutions (SO Inter 5.3)
Случайное колесо
от Hop
intermediate I
Speakout
Unit 3B. Vocabulary. Problems and solutions
Викторина
от Volokat
Problems and solutions, ESSAY FOR STATE EXAM
Случайное колесо
от Goncharovals196
Outcomes Advanced Unit 3 problems and solutions
Групповая сортировка
от Zauers
Speak Out Int Problems and Solutions
Пропущенное слово
от Wordwallstudent
Intermediate
English
Speakout
EGE Orlova problems and solutions Health
Случайные карты
от Karolinka1
Problems and Solutions Voc Speaking Practice (Business)
Случайные карты
от Blissnata
Business Benchmark
Healthy life style. Problems and solutions. ЕГЭ
Групповая сортировка
от Knowallteacher
11 класс
English
Problems — Solutions
Откройте поле
от Maryys
Problems & Solutions
Викторина
от Navigatoriya
Solutions elementary.Expressing likes and dislikes.
Откройте поле
от Gulgal2705
Likes and dislikes.
Solutions elementary.
CELT_P Protfolio Task MFP and Problems and Solutions
Сопоставить
от Altigrinova
Solutions Elementary 4A Countable and Uncountable
Групповая сортировка
от 4upikova
teens
Elementary
English
Solutions Elementary
Solutions Interm, Unit 4 Health problems
Сопоставить
от Demmary
Solutions Intermediate
EGE Orlova problems and solutions Nature Travelling Foreign lang
Случайные карты
от Karolinka1
Problems that lead to global warming and their solutions
Сопоставить
от Krolikmolikshu
Solutions Interm Un 8 Travel problems — complaining
Групповая сортировка
от Demmary
Solutions Intermediate
EGE Orlova IT and Modern Tech problems & Solutions
Случайные карты
от Karolinka1
INTER U5.3 Fill in the gaps ( problems and solutions)
Сопоставить
от Ovshaneva
English
SpeakOut
Forward 5, part 2, p 5, problems and solutions (could)
Сопоставить
от Beawesome3
Forward 5
Solutions PI 2G Sports clothing and equipment
Найди пару
от Natalsamarina
Solutions Pre Int
Solutions Pre-Int Accidents and injuries
Найди пару
от Natalsamarina
Solutions Pre Int
Solutions Interm 6F Verbs and Prepositions
Найди пару
от Marsla
Solutions Interm 3rd
2 Talking about problems Solutions A1
Случайные карты
от Zhenyashch
Teens
Solutions A2
Solutions Pre 1G Reacting and showing interest
Случайные карты
от 4upikova
teens
English
Solutions Pre-Intermediate
Environment (problems, consequences, solutions)
Групповая сортировка
от Gamper
problems or solutions
Групповая сортировка
от Volokat
Problems- solutions Travel
Случайные карты
от Wordwallstudent
Solutions Elementary Unit 7a Where are they from?_Nationalities
Сопоставить
от Juliadron1987
Elemetary — Intermadiate
Adults
English
Countries and Nationalities
Solutions
Focus 4 Problems Solutions Unit 8
Групповая сортировка
от Krolikmolikshu
Средняя школа
English
Focus 4
What’s happened? Problems & solutions
Случайные карты
от Englishchinese
Related Pages
More Math Word Problems
Algebra Word Problems
How to write algebra word problems into systems of linear equations and solve systems of linear equations
using elimination and substitution methods?
Grade 8 Algebra Word Problems
How to solve algebra word problems using systems of linear equations?
Example:
Devon is going to make 3 shelves for her father. He has a piece of lumber 12 feet long.
She wants the top shelf to be half a foot shorter than the middle shelf, and the bottom
shelf to be half a foot shorter than twice the length of the top shelf. How long will
each shelf be if she uses the entire 12 feet of wood?
- Show Video Lesson
Grade 8 Algebra Word Problems — Line Segments
Example:
If JK = 7x + 9, JL = 114 and KL = 9x + 9. Find KL.
- Show Video Lesson
Grade 8 number word problems — common core
How to write word problems into systems of linear equations and solve systems of linear equations
using elimination and substitution methods?
Example 1:
The sum of two numbers is 361 and the difference between the two numbers is 173. What are the
two numbers?
Example 2:
There are 356 Grade 8 students at Euclid’s Middle School. Thirty-four more than four times the
number of girls is equal to half the number of boys. How many boys are in Grade 8 at Euclid’s
Middle School? How many girls?
Example 3:
A family member has some five-dollar bills and one-dollar bills in their wallet. Altogether
she has 18 bills and a total of $62. How many of each bill does she have?
Example 1:
A friend bought 2 boxes of pencils and 8 notebooks for school and it cost him $11. He went back
to the store the same day to buy school supplies for his younger brother. He spent $11.25 on 3
boxes of pencils and 5 notebooks. How much would notebooks cost?
Exercises:
- A farm raises cows and chickens. The farmer has a total of 42 animals. One day he counts the
legs of all of his animals and realizes he has a total of 114. How many cows does the farmer
have? How many chickens? - The length of a rectangle is 4 times the width. The perimeter of the rectangle is 45 inches.
What is the area of the rectangle? - The sum of the measures of angles x and y is 127″. If the measure of angle x is 34° more
than half the measure of angle y, what is the measure of each angle?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Chapter 6: Polynomials
Solving mixture problems generally involves solving systems of equations. Mixture problems are ones in which two different solutions are mixed together, resulting in a new, final solution. Using a table will help to set up and solve these problems. The basic structure of this table is shown below:
| Name | Amount | Value | Equation |
|---|---|---|---|
The first column in the table (Name) is used to identify the fluids or objects being mixed in the problem. The second column (Amount) identifies the amounts of each of the fluids or objects. The third column (Value) is used for the value of each object or the percentage of concentration of each fluid. The last column (Equation) contains the product of the Amount times the Value or Concentration.
Jasnah has 70 mL of a 50% methane solution. How much of a 80% solution must she add so the final solution is 60% methane? Find the equation.
- The solution names are 50% (S50), 60% (S60), and 80% (S80).
- The amounts are S50 = 70 mL, S80, and S60 = 70 mL + S80.
- The concentrations are S50 = 0.50, S60 = 0.60, and S80 = 0.80.
| Name | Amount | Value | Equation |
|---|---|---|---|
| S50 | 70 mL | 0.50 | 0.50 (70 mL) |
| S80 | S80 | 0.80 | 0.80 (S80) |
| S60 | 70 mL + S80 | 0.60 | 0.60 (70 mL + S80) |
The equation derived from this data is 0.50 (70 mL) + 0.80 (S80) = 0.60 (70 mL + S80).
Sally and Terry blended a coffee mix that sells for [latex]$2.50[/latex] by mixing two types of coffee. If they used 40 mL of a coffee that costs [latex]$3.00,[/latex] how much of another coffee costing [latex]$1.50[/latex] did they mix with the first?
| Name | Amount | Value | Equation |
|---|---|---|---|
| C1.50 | C1.50 | [latex]$1.50[/latex] | [latex]$1.50[/latex] (C1.50) |
| C3.00 | 40 mL | [latex]$3.00[/latex] | [latex]$3.00[/latex] (40 mL) |
| C2.50 | 40 mL + C1.50 | [latex]$2.50[/latex] | [latex]$2.50[/latex] (40 mL + C1.50) |
The equation derived from this data is:
[latex]begin{array}{ccccccc} 1.50(C_{1.50})&+&3.00(40)&=&2.50(40&+&C_{1.50}) \ 1.50(C_{1.50})&+&120&=&100&+&2.50(C_{1.50}) \ -2.50(C_{1.50})&-&120&=&-120&-&2.50(C_{1.50}) \ hline &&-1.00(C_{1.50})&=&-20&& \ \ &&(C_{1.50})&=&dfrac{-20}{-1}&& \ \ &&C_{1.50}&=&20&& end{array}[/latex]
This means 20 mL of the coffee selling for [latex]$1.50[/latex] is needed for the mix.
Nick and Chloe have two grades of milk from their small dairy herd: one that is 24% butterfat and another that is 18% butterfat. How much of each should they use to end up with 42 litres of 20% butterfat?
| Name | Amount | Value | Equation |
|---|---|---|---|
| B24 | B24 | 0.24 | 0.24 (B24) |
| B18 | 42 L − B24 | 0.18 | 0.18 (42 L − B24) |
| B20 | 42 L | 0.20 | 0.20 (42 L) |
The equation derived from this data is:
[latex]begin{array}{rrrrrrr} 0.24(B_{24})&+&0.18(42&- &B_{24})&=&0.20(42) \ 0.24(B_{24})&+&7.56&-&0.18(B_{24})&=&8.4 \ &-&7.56&&&&-7.56 \ hline &&&&0.06(B_{24})&=&0.84 \ \ &&&&B_{24}&=&dfrac{0.84}{0.06} \ \ &&&&B_{24}&=&14 end{array}[/latex]
This means 14 litres of the 24% buttermilk, and 28 litres of the 18% buttermilk is needed.
In Natasha’s candy shop, chocolate, which sells for [latex]$4[/latex] a kilogram, is mixed with nuts, which are sold for [latex]$2.50[/latex] a kilogram. Chocolate and nuts are combined to form a chocolate-nut candy, which sells for [latex]$3.50[/latex] a kilogram. How much of each are used to make 30 kilograms of the mixture?
| Name | Amount | Value | Equation |
|---|---|---|---|
| Chocolate | C | [latex]$4.00[/latex] | [latex]$4.00[/latex] (C) |
| Nuts | 30 kg − C | [latex]$2.50[/latex] | [latex]$2.50[/latex] (30 kg − C) |
| Mix | 30 kg | [latex]$3.50[/latex] | [latex]$3.50[/latex] (30 kg) |
The equation derived from this data is:
[latex]begin{array}{rrrrrrl} 4.00(C)&+&2.50(30&-&C)&=&3.50(30) \ 4.00(C)&+&75&-&2.50(C)&=&105 \ &-&75&&&&-75 \ hline &&&&1.50(C)&=&30 \ \ &&&&C&=&dfrac{30}{1.50} \ \ &&&&C&=&20 end{array}[/latex]
Therefore, 20 kg of chocolate is needed for the mixture.
With mixture problems, there is often mixing with a pure solution or using water, which contains none of the chemical of interest. For pure solutions, the concentration is 100%. For water, the concentration is 0%. This is shown in the following example.
Joey is making a a 65% antifreeze solution using pure antifreeze mixed with water. How much of each should be used to make 70 litres?
| Name | Amount | Value | Equation |
|---|---|---|---|
| Antifreeze (A) | A | 1.00 | 1.00 (A) |
| Water (W) | 70 L − A | 0.00 | 0.00 (70 L − A) |
| 65% Solution | 70 L | 0.65 | 0.65 (70 L) |
The equation derived from this data is:
[latex]begin{array}{rrrrl} 1.00(A)&+&0.00(70-A)&=&0.65(0.70) \ &&1.00A&=&45.5 \ &&A&=&45.5 \ end{array}[/latex]
This means the amount of water added is 70 L − 45.5 L = 24.5 L.
Questions
For questions 1 to 9, write the equations that define the relationship.
- A tank contains 8000 litres of a solution that is 40% acid. How much water should be added to make a solution that is 30% acid?
- How much pure antifreeze should be added to 5 litres of a 30% mixture of antifreeze to make a solution that is 50% antifreeze?
- You have 12 kilograms of 10% saline solution and another solution of 3% strength. How many kilograms of the second should be added to the first in order to get a 5% solution?
- How much pure alcohol must be added to 24 litres of a 14% solution of alcohol in order to produce a 20% solution?
- How many litres of a blue dye that costs [latex]$1.60[/latex] per litre must be mixed with 18 litres of magenta dye that costs [latex]$2.50[/latex] per litre to make a mixture that costs [latex]$1.90[/latex] per litre?
- How many grams of pure acid must be added to 40 grams of a 20% acid solution to make a solution which is 36% acid?
- A 100-kg bag of animal feed is 40% oats. How many kilograms of pure oats must be added to this feed to produce a blend of 50% oats?
- A 20-gram alloy of platinum that costs [latex]$220[/latex] per gram is mixed with an alloy that costs [latex]$400[/latex] per gram. How many grams of the [latex]$400[/latex] alloy should be used to make an alloy that costs [latex]$300[/latex] per gram?
- How many kilograms of tea that cost [latex]$4.20[/latex] per kilogram must be mixed with 12 kilograms of tea that cost [latex]$2.25[/latex] per kilogram to make a mixture that costs [latex]$3.40[/latex] per kilogram?
Solve questions 10 to 21.
- How many litres of a solvent that costs [latex]$80[/latex] per litre must be mixed with 6 litres of a solvent that costs [latex]$25[/latex] per litre to make a solvent that costs [latex]$36[/latex] per litre?
- How many kilograms of hard candy that cost [latex]$7.50[/latex] per kg must be mixed with 24 kg of jelly beans that cost [latex]$3.25[/latex] per kg to make a mixture that sells for [latex]$4.50[/latex] per kg?
- How many kilograms of soil supplement that costs [latex]$7.00[/latex] per kg must be mixed with 20 kg of aluminum nitrate that costs [latex]$3.50[/latex] per kg to make a fertilizer that costs [latex]$4.50[/latex] per kg?
- A candy mix sells for [latex]$2.20[/latex] per kg. It contains chocolates worth [latex]$1.80[/latex] per kg and other candy worth [latex]$3.00[/latex] per kg. How much of each are in 15 kg of the mixture?
- A certain grade of milk contains 10% butterfat and a certain grade of cream 60% butterfat. How many litres of each must be taken so as to obtain a mixture of 100 litres that will be 45% butterfat?
- Solution A is 50% acid and solution B is 80% acid. How much of each should be used to make 100 cc of a solution that is 68% acid?
- A paint that contains 21% green dye is mixed with a paint that contains 15% green dye. How many litres of each must be used to make 600 litres of paint that is 19% green dye?
- How many kilograms of coffee that is 40% java beans must be mixed with coffee that is 30% java beans to make an 80-kg coffee blend that is 32% java beans?
- A caterer needs to make a slightly alcoholic fruit punch that has a strength of 6% alcohol. How many litres of fruit juice must be added to 3.75 litres of 40% alcohol?
- A mechanic needs to dilute a 70% antifreeze solution to make 20 litres of 18% strength. How many litres of water must be added?
- How many millilitres of water must be added to 50 millilitres of 100% acid to make a 40% solution?
- How many litres of water need to be evaporated from 50 litres of a 12% salt solution to produce a 15% salt solution?
Answer Key 6.8
In today’s post, we are going to see a selection of Second Grade word problems that usually appear at the end of a Smartick session for children with a second-grade level. You will also get a chance to see the solution for each problem.
Ready? Let’s go!
How To Correctly Solve Any Problem
- Read the word problem carefully! You should understand what is being asked very clearly.
- Write down the data.
- Complete the operations and always write down the results for each.
- Write the solution very clearly and respond to what the problem asks.
Second Grade Word Problems
Let’s practice with a selection of Second Grade word problems from Smartick.
Word Problem 1
Solution 1
For this word problem, Smartick has given us the solution and it is up to us to select the correct question.
The answer is: ”They were planting 38 chestnut seeds.” Let’s take a look at each option to see which would work with this answer, we’ll use the process of elimination.
- How many more chestnut seeds than oak seeds were they planting? This is asking us about the different types of seeds, but the solution is only asking about chestnuts so this question is not what we are looking for.
- Are fewer chestnut trees or fewer oak trees expected to grow? This answer isn’t the one we are looking for because the answer only gives us information about chestnut seeds.
- How many more poplar seeds than oak seeds were they planting? Nothing was mentioned in the word problem or the answer about poplar trees.
- How many chestnut seeds were they planting? Here were are being asked about the number of chestnut seeds that were planted and the solution tells us the amount that was planted. This is the question that we are looking for.
Word Problem 2
Solution 2
This word problem is asking how many tablespoons of oil have been added to a stew, and we know that there were 20 tablespoons more added than the 9 tablespoons that the recipe called for. So we need to know how many tablespoons in total were added to the stew.
9 + 20 = 29
29 tablespoons of oil were added to the stew.
Word Problem 3
Solution 3
Here, we are being asked to calculate the total number of clocks. To help us solve it, we can create a drawing using the information from the word problem. It tells us that there are 2 clocks on each shelf, and there are 6 shelves.
Word Problem 4
Solution 4
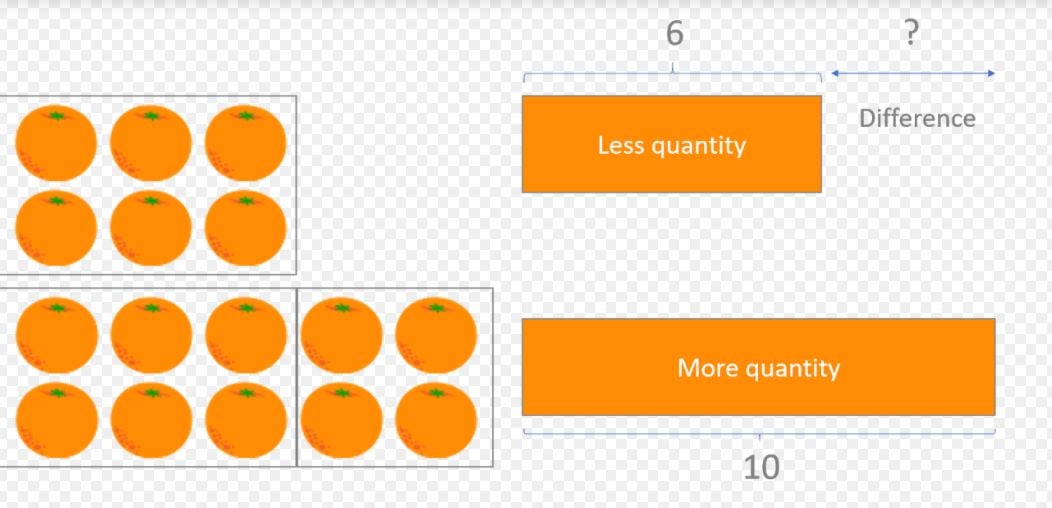
First, we are asked which operation we need to use to solve the problem and are provided with the options of addition and subtraction. Let’s read the word problem carefully to see which would work best…
There were 6 oranges before Diego added more, and now there are 10. Therefore, the difference between the amount in the bowl now, and the amount there was before, is the amount that Diego added. If we add the numbers, adding the larger quantity to the lesser quantity, it does not give us the number of oranges Diego added to the bowl. However, if we subtract the smaller quantity from the larger quantity, we should find the difference.
The answer to the first question would be: 10 – 6.
And the solution to the word problem: 10 – 6 = 4.
Diego added 4 oranges.
I hope you have learned something new from this selection of second grade word problems that appear during our daily Smartick sessions. If you would like to learn more about other primary school math topics, register with Smartick and try it for free.
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
Graph »
Number Line »
Challenge »
Examples »
FAQ »
Correct Answer 
Let’s Try Again 
Try to further simplify
Number Line
Graph
Hide Plot »
Sorry, your browser does not support this application
Examples
-
mathrm{Lauren’s:age:is:half:of:Joe’s:age.:Emma:is:four:years:older:than:Joe.:The:sum:of:Lauren,:Emma,:and:Joe’s:age:is:54.:How:old:is:Joe?}
-
mathrm{Kira:went:for:a:drive:in:her:new:car.:She:drove:for:142.5:miles:at:a:speed:of:57:mph.:For:how:many:hours:did:she:drive?}
-
mathrm{Bob’s:age:is:twice:that:of:Barry’s.:Five:years:ago,:Bob:was:three:times:older:than:Barry.:Find:the:age:of:both.}
-
mathrm{Two:men:who:are:traveling:in:opposite:directions:at:the:rate:of:18:and:22:mph:respectively:started:at:the:same:time:at:the:same:place.:In:how:many:hours:will:they:be:250:apart?}
-
mathrm{If:2:tacos:and:3:drinks:cost:12:and:3:tacos:and:2:drinks:cost:13:how:much:does:a:taco:cost?}
Frequently Asked Questions (FAQ)
-
How do you solve word problems?
- To solve word problems start by reading the problem carefully and understanding what it’s asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
-
How do you identify word problems in math?
- Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
-
Is there a calculator that can solve word problems?
- Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
-
What is an age problem?
- An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as «x years ago,» «in y years,» or «y years later,» which indicate that the problem is related to time and age.
word-problems-calculator
en