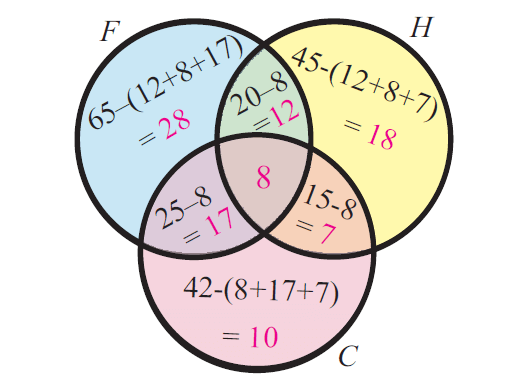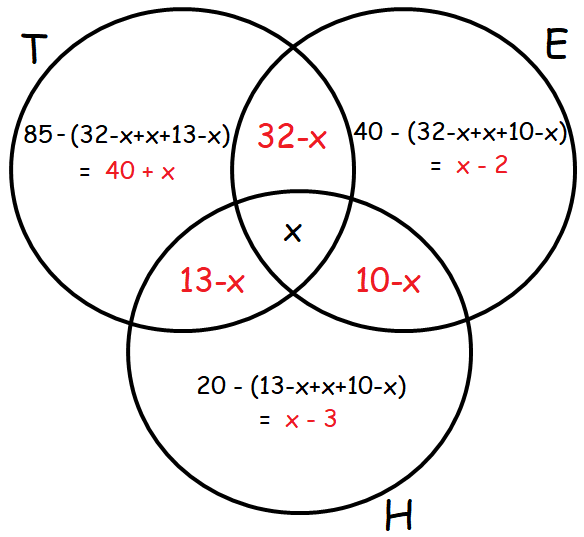Word problems about sets

Word problems on sets are solved here to get the basic ideas how to use the  properties of union and intersection of sets.

Solved basic word problems on sets:

1. Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).

2. If n(A — B) = 18, n(A ∪ B) = 70 and n(A ∩ B) = 25, then find n(B).

Different types on word problems on sets:

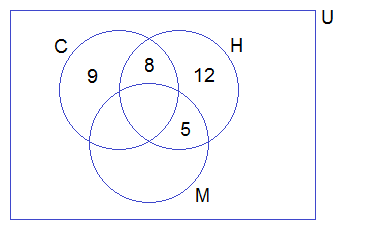
3. In a group of 60 people, 27 like cold drinks and 42 like hot drinks and each person likes at least one of the two drinks. How many like both coffee and tea? 

4. There are 35 students in art class and 57 students in dance class. Find the number of students who are either in art class or in dance class.

Further concept to solve word problems on sets:

5.
In a group of 100 persons, 72 people can speak English and 43 can speak
French. How many can speak English only? How many can speak French only
and how many can speak both English and French?

Word problems on sets using the different properties (Union & Intersection):

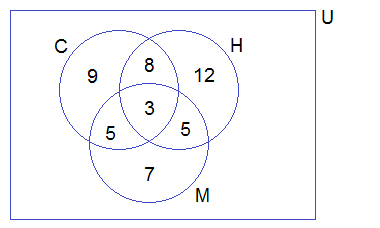
6.
In a competition, a school awarded medals in different categories. 36
medals in dance, 12 medals in dramatics and 18 medals in music. If these
medals went to a total of 45 persons and only 4 persons got medals in
all the three categories, how many received medals in exactly two of
these categories?

Apply set operations to solve the word problems on sets:

7.
Each student in a class of 40 plays at least one indoor game chess,
carrom and scrabble. 18 play chess, 20 play scrabble and 27 play carrom.
7 play chess and scrabble, 12 play scrabble and carrom and 4 play
chess, carrom and scrabble. Find the number of students who play (i)
chess and carrom. (ii) chess, carrom but not scrabble.

Therefore, we learned how to solve different types of word problems on sets without using Venn diagram.

● Set Theory

● Sets Theory

● Representation of a Set

● Types of Sets

● Finite Sets and Infinite Sets

● Power Set

● Problems on Union of Sets

● Problems on Intersection of Sets

● Difference of two Sets

● Complement of a Set

● Problems on Complement of a Set

● Problems on Operation on Sets

● Word Problems on Sets

● Venn Diagrams in Different
Situations

● Relationship in Sets using Venn
Diagram

● Union of Sets using Venn Diagram

● Intersection of Sets using Venn
Diagram

● Disjoint of Sets using Venn
Diagram

● Difference of Sets using Venn
Diagram

● Examples on Venn Diagram

Cardinality Relations
of Three Sets

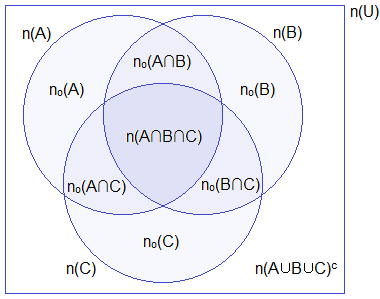
Let, U be the universal set. A, B and C are three overlapping sets which are subsets of the universal set U. 

********************

10 Math Problems officially announces the release of Quick Math Solver, an Android App on the Google Play Store for students around the world.

********************

Look at the following Venn diagram and learn
the cardinal representation for the different portions.

n(A) = Number of elements in
set A

n(B) = Number of elements in set
B

n(C) = Number of elements in
set C

n_o(A) = Number of elements
in set A only

n_o(B) = Number of elements
in set B only

n_o(C) = Number of elements
in set C only

n(A∩B) = Number of elements
common in set A and B

n(A∩C) = Number of elements
common in set A and C

n(B∩C) = Number of elements
common in set B and C

n_o(A∩B) = Number of elements
common in set A and B only

n_o(A∩C) = Number of elements
common in set A and C only

n_o(B∩C) = Number of elements
common in set B and C only

n(A∩B∩C) = Number of elements common
to A, B and C

n(A∪B∪C) = Number of elements belongs to at
least one set A, B or C.

n(A∩B∩C)^c = Number of elements
does not belong to the set A, B or C.

Formula on
Cardinality Relations of Three Sets

If A, B and C are subsets of universal set U then,

1.       
n(A∪B∪C) = n(A) + n(B) + n(C) – n(A∩B) –
n(B∩C) – n(A∩C) + n(A∩B∩C)

2.       
n(A∩B∩C) = n(A∪B∪C) – n(A) – n(B) – n(C) + n(A∩B) + n(B∩C) + n(A∩C)

3.       
n(A∪B∪C)^c = n(U) – n(A∪B∪C)

4.       
n_o(A) = n(A) – n(A∩B) – n(A∩C) + n(A∩B∩C)

5.       
n_o(B) = n(B) – n(A∩B) – n(B∩C) + n(A∩B∩C)

6.       
n_o(C) = n(C) – n(A∩C) – n(B∩C) + n(A∩B∩C)

7.       
n_o(A∩B) = n(A∩B) – n(A∩B∩C)

8.       
n_o(B∩C) = n(B∩C) – n(A∩B∩C)

9.       
n_o(A∩C) = n(A∩C) – n(A∩B∩C)

10.  
Exactly two = n_o(A∩B) + n_o(B∩C) + n_o(A∩C)

11.  
Exactly one = n_o(A) + n_o(B) + n_o(C)

12.  
At least one = n(A∪B∪C)

13.  
All three = n(A∩B∩C)

14.  
None of them = n(A∪B∪C)^c

 

Word Problems Based
on Three Sets

Workout Examples

Example 1: P, Q and R are subsets of a universal set U. If n(U) = 390, n(P) =
210, n(Q) = 165, n(R) = 120, n(P∩Q) = 60, n(Q∩R) = 45, n(A∩R) = 54 and n(P∩Q∩R)
= 24, illustrate this information in a Venn-diagram and find the following:

a.       
n_o(P)

b.       
n_o(Q)

c.       
n_o(R)

d.       
n_o(P∩Q)

e.       
n_o(Q∩R)

f.        
n_o(P∩R)

g.       
n(P∪Q∪R)^c

Solution:

Here,

Venn-diagram,

From the Venn-diagram above,

a.       
n_o(P) = 120

b.       
n_o(Q) = 84

c.       
n_o(R) = 45

d.       
n_o(P∩Q) = 36

e.       
n_o(Q∩R) = 21

f.        
n_o(P∩R) = 30

g.       
n(P∪Q∪R)^c = 30

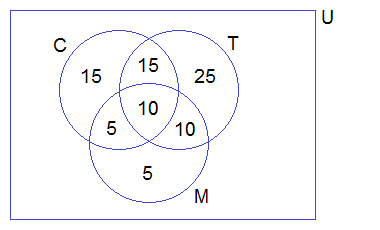
Example 2: In a survey of a group of people, 60 liked tea, 45 liked coffee, 30
liked milk, 25 liked coffee as well as tea, 20 liked tea as well as milk, 15
liked coffee as well as milk and 10 liked all three. How many people were asked
this question? Solve by using Venn-diagram.

Solution:

Let C, T and M represent
the set of people who liked coffee, tea and milk respectively. Then,

∴       n(T) = 60

          n(C) = 45

          n(M) = 30

          n(C∩T) = 25

n(T∩M) = 20

n(C∩M) = 15

n(C∩T∩M) = 10

Venn
diagram,

Now,

n(T∪C∪M)

= n(T) + n(C) + n(M)
– n(C∩T) – n(T∩M) – n(C∩M) + n(C∩T∩M)

= 60 + 45
+ 30 – 25 – 20 – 15 + 10

= 85

Hence, the required number of people = 85.

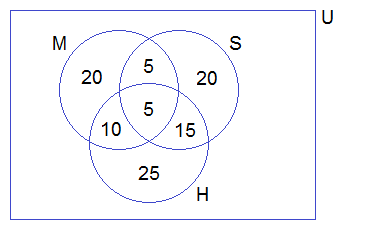
Example 3: In an examination, 40% of candidates passed in mathematics, 45% in
Science, and 55% in Health. If 10% passed in Mathematics and Science, 20% in
Science and Health and 15% in Health and Mathematics,

(i)     Illustrate the above information by drawing a Venn diagram.

(ii)  Find the pass percentage in all three subjects.

Solution:

Let M, S, and H denote the
set of students who passed in Maths, Science and Health respectively.

∴       n(U) = 100% = n(M∪S∪H)

          n(M) = 40%

          n(S) = 45%

          n(H) = 55%

          n(M∩S) = 10%

n(S∩H) = 20%

n(H∩M) = 15%

Since,
there is  no one who failed in all three
subjects,

n(M∪S∪H) = n(U) = 100%

(i)       
Venn-diagram,

(ii)    
n (M∩S∩H)

= n(M∪S∪H) – n(M) – n(S) – n(H) + n(M∩S) + n(S∩H) + n(M∩H)

= 100 – 40 – 45 – 55 + 10 + 20 + 15%

= 5%

∴ 5% passed in all three subjects.

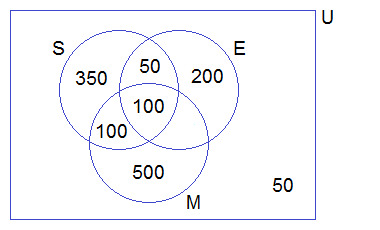
Example 4: Out of 1350 candidates, 600 passed in Science, 700 in Mathematics,
350 in English and 50 failed in all three subjects. If 200 passed in
Science and Mathematics, 150 in Science and English, 100 in Mathematics and
English,

(i)     How many candidates passed in all three subjects?

(ii)  Illustrate the above information in a Venn-diagram.

Solution:

Let, the set of candidates who passed in Science, Mathematics
and English be S, M, and E.

∴       n(U) = 1350

n(S) = 600

n(M) = 700

n(E) = 350

n(S∪M∪E)^c = 50

n(S∩M) = 200

n(M∩E) = 100

n(S∩E) = 150

We know,

n(S∪M∪E)

= n(U) – n(S∪M∪E)^c

= 1350 – 50

= 1300

Now,

n(A∩B∩C)

= n(A∪B∪C) – n(A) – n(B) – n(C) + n(A∩B) + n(B∩C) + n(A∩C)

= 1300 – 600 – 700 – 350 + 200 + 100 + 150

= 100

Therefore,

(i)      100 candidates passed in
all three subjects.

(ii)   Venn-diagram,

Example 5: In a group of students, 25 study computer, 28 study Health, 20
study Mathematics, 9 study Computer only, 12 study Health only, 8 study
Computer and Health only and 5 students study Health and Mathematics only.

(i)       
Draw a Venn diagram to
illustrate the above information.

(ii)    
Find how many students study
all the subjects.

(iii)  How many students are there altogether?

Solution:

Let C, H, and M be the set
of students who study Computer, Health, and Mathematics respectively.

∴       n(C) = 25

          n(H) = 28

          n(M) = 20

          n_o(C) = 9

          n_o(H) = 12

n_o(C∩H) = 8

n_o(H∩M) = 5

Filling the above information in Venn-diagram,
we get

From the above Venn-diagram,

n(C∩H∩M) + 8 + 12 + 5 = n(H)

or,     n(C∩H∩M)
+ 25 = 28

or,     n(C∩H∩M)
= 28 – 25

or,     n(C∩H∩M)
= 3

Again, 

n_o(C∩M)
+ n(C∩H∩M) + 9 + 8 = n(C)

or,     n_o(C∩M) + 3 + 9 + 8 = 25

or,     n_o(C∩M) + 20 = 25

or,     n_o(C∩M) = 25 – 20

or,     n_o(C∩M) = 5

Again, 

n_o(M)
+ n_o(C∩M) + n(C∩H∩M) + 5 = n(M)

or,     n_o(M) + 5 + 3 + 5 = 20

or,     n_o(M) + 13 = 20

or,     n_o(M) = 20 – 13

or,     n_o(M) = 7

(i)       
Venn-diagram:

(ii)    
n(C∩H∩M) = 3 students study all subjects.

(iii) 
From the above venn-diagram,

n(C∪H∪M)

= 9 + 8 + 3 + 5 + 12 + 5 + 7

= 49

∴ There are 49 students altogether.

Example
6: In a group of people, 20 like milk, 30 like tea,
22 like coffee, 12 like coffee only, 6 like milk and coffee only,  2 like tea and coffee only and 8 like milk
and tea only. Show these information in a Venn-diagram and find:

(i)       
How many like
at least one drink?

(ii)    
How many like
exactly one drink?

Solution:

Let the set of people who like milk, tea, and coffee
be M, T, and C.

∴       n(M)
= 20

n(T) = 30

n(C) = 22

n_o(C) = 12

n_o(M∩C) = 6

n_o(T∩C) = 2

n_o(M∩T) = 8

Filling the above information in the
Venn-diagram, we get

From the above Venn-diagram,

n(M∩T∩C) + 6 + 12 + 2 = n(C)

i.e.     n(M∩T∩C)
+ 20 = 22

or,     n(M∩T∩C)
= 22 – 20

or,     n(M∩T∩C)
= 2

Again,

n_o(M) + 6 + n(M∩T∩C) + 8 = n(M)

i.e.     n_o(M)
+ 6 + 2 + 8 = 20

or,     n_o(M)
+ 16 = 20

or,     n_o(M)
= 20 – 16

or,     n_o(M)
= 4

Again,

n_o(T) + 2 + n(M∩T∩C) + 8 = n(T)

i.e.     n_o(T)
+ 2 + 2 + 8 = 30

or,     n_o(T)
+ 12 = 30

or,     n_o(T)
= 30 – 12

or,     n_o(T)
= 18

Venn-diagram,

From the venn-diagram,

(i)       
n(M∪C∪T)

= 4 + 6 + 12 + 2 + 18 + 8 + 2

= 52

∴ 52 like at least one drink.

(ii)    
n_o(M)
+ n_o(C) + n_o(T)

= 4 + 12 +18

= 34

∴ 34 like exactly one drink.

If you have any questions or problems regarding the Word Problems Based on Three Sets, you can ask here, in the comment section below.

Was this article helpful? LIKE
and SHARE with your friends…

Basic Stuff

To understand, how to solve Venn diagram word problems with 3 circles, we have to know the following basic stuff.  

u —-> union (or)

n —-> intersection (and)

Addition Theorem on Sets

Theorem 1 :

n(AuB) = n(A) + n(B) — n(AnB)

Theorem 2 :

n(AuBuC) :

=n(A) + n(B) + n(C) — n(AnB) — n(BnC) — n(AnC) + n(AnBnC)

Explanation :

Let us come to know about the following terms in details.

n(AuB) = Total number of elements related to any of the two events A & B.

n(AuBuC) = Total number of elements related to any of the three events A, B & C.

n(A) = Total number of elements related to A

n(B) = Total number of elements related to B

n(C) = Total number of elements related to C

For  three events A, B & C, we have

n(A) — [n(AnB) + n(AnC) — n(AnBnC)] :

Total number of elements related to A only

n(B) — [n(AnB) + n(BnC) — n(AnBnC)] :

Total number of elements related to B only

n(C) — [n(BnC) + n(AnC) + n(AnBnC)] :

Total number of elements related to C only

n(AnB) :

Total number of elements related to both A & B

n(AnB) — n(AnBnC) :

Total number of elements related to both (A & B) only

n(BnC) :

Total number of elements related to both B & C

n(BnC) — n(AnBnC) :

Total number of elements related to both (B & C) only

n(AnC) :

Total number of elements related to both A & C

n(AnC) — n(AnBnC) :

Total number of elements related to both (A & C) only

For  two events A & B, we have

n(A) — n(AnB) :

Total number of elements related to A only

n(B) — n(AnB) :

Total number of elements related to B only

Practice Problems

Problem 1 :

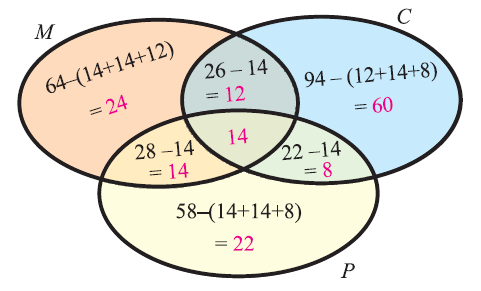
In a survey of university students, 64 had taken mathematics course, 94 had taken chemistry course, 58 had taken physics course, 28 had taken mathematics and physics, 26 had taken mathematics and chemistry, 22 had taken chemistry and physics course, and 14 had taken all the three courses. Find how many had taken one course only.

Solution :

Step 1 :

Let M, C, P represent sets of students who had taken mathematics, chemistry and physics respectively.

Step 2 :

From the given information, we have

n(M) = 64, n(C) = 94, n(P) = 58,

n(MnP) = 28, n(MnC) = 26, n(CnP) = 22

n(MnCnP) = 14

Step 3 :

From the basic stuff, we have

Number of students who had taken only Math

= n(M) — [n(MnP) + n(MnC) — n(MnCnP)]

= 64 — [28 + 26 — 14]

= 64 — 40

= 24

Step 4 :

Number of students who had taken only Chemistry :

= n(C) — [n(MnC) + n(CnP) — n(MnCnP)]

= 94 — [26+22-14]

= 94 — 34

= 60

Step 5 :

Number of students who had taken only Physics :

= n(P) — [n(MnP) + n(CnP) — n(MnCnP)]

= 58 — [28 + 22 — 14]

= 58 — 36

= 22

Step 6 :

Total number of students who had taken only one course :

= 24 + 60 + 22

= 106

Hence, the total number of students who had taken only one course is 106.

Alternative Method (Using venn diagram) :

Step 1 :

Venn diagram related to the information given in the question:

Step 2 :

From the venn diagram above, we have

Number of students who had taken only math = 24

Number of students who had taken only chemistry = 60

Number of students who had taken only physics = 22

Step 3 :

Total Number of students who had taken only one course :

= 24 + 60 + 22

= 106

Hence, the total number of students who had taken only one course is 106.

Problem 2 :

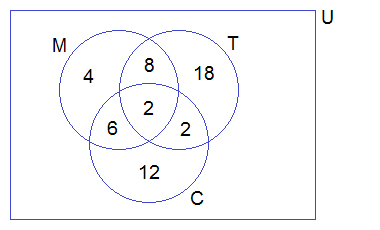
In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game).

Solution :

Step 1 :

Let F, H and C represent the set of students who play foot ball, hockey and cricket respectively.

Step 2 :

From the given information, we have

n(F) = 65, n(H) = 45, n(C) = 42,

n(FnH) = 20, n(FnC) = 25, n(HnC) = 15

n(FnHnC) = 8

Step 3 :

From the basic stuff, we have

Total number of students in the group is n(FuHuC).

n(FuHuC) is equal to

= n(F) + n(H) + n(C) — n(FnH) — n(FnC) — n(HnC) + n(FnHnC)

n(FuHuC) = 65 + 45 + 42 -20 — 25 — 15 + 8

n(FuHuC) = 100

Hence, the total number of students in the group is 100.

Alternative Method (Using Venn diagram) :

Step 1 :

Venn diagram related to the information given in the question :

Step 2 :

Total number of students in the group :

= 28 + 12 + 18 + 7 + 10 + 17 + 8

= 100

So, the total number of students in the group is 100.

Problem 3 :

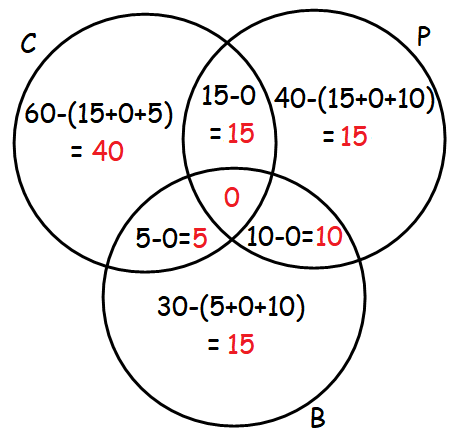
In a college, 60 students enrolled in chemistry,40 in physics, 30 in biology, 15 in chemistry and physics,10 in physics and biology, 5 in biology and chemistry. No one enrolled in all the three. Find how many are enrolled in at least one of the subjects.

Solution :

Let C, P and B represents the subjects Chemistry, Physics  and Biology respectively.

Number of students enrolled in Chemistry :

n(C) = 60

Number of students enrolled in Physics :

n(P) = 40

Number of students enrolled in Biology :

n(B) = 30

Number of students enrolled in Chemistry and Physics :

n(CnP) = 15

Number of students enrolled in Physics and Biology :

n(PnB) = 10

Number of students enrolled in Biology and Chemistry :

n(BnC) = 5

No one enrolled in all the three. So, we have

n(CnPnB) = 0

The above information can be put in a Venn diagram as shown below.

From, the above Venn diagram, number of students enrolled in at least one of the subjects :

= 40 + 15 + 15 + 15 + 5 + 10 + 0

= 100

So, the number of students enrolled in at least one of the subjects is 100.

Problem 4 :

In a town 85% of the people speak Tamil, 40% speak English and 20% speak Hindi. Also 32% speak Tamil and English, 13% speak Tamil and Hindi and 10% speak English and Hindi, find the percentage of people who can speak all the three languages.

Solution :

Let T, E and H represent the people who speak Tamil, English and Hindi respectively.

Percentage of people who speak Tamil :

n(T) = 85

Percentage of people who speak English :

n(E) = 40

Percentage of people who speak Hindi :

n(H)  =  20

Percentage of people who speak English and Tamil :

n(TnE) = 32

Percentage of people who speak Tamil and Hindi :

n(TnH) = 13

Percentage of people who speak English and Hindi :

n(EnH) = 10

Let x be the percentage of people who speak all the three language.

From the above Venn diagram, we can have 

100 = 40 + x + 32 – x + x + 13 – x + 10 – x – 2 + x – 3 + x

100 = 40 + 32 + 13 + 10 – 2 – 3 + x 

100 = 95 – 5 + x

100 = 90 + x

x = 100 — 90

x = 10% 

So, the percentage of people who speak all the three languages is 10%.

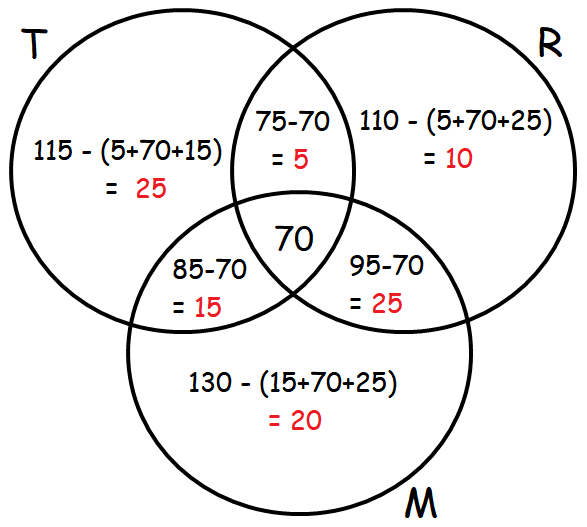
Problem 5 :

An advertising agency finds that, of its 170 clients, 115 use Television, 110 use Radio and 130 use Magazines. Also 85 use Television and Magazines, 75 use Television and Radio, 95 use Radio and Magazines, 70 use all the three. Draw Venn diagram to represent these data. Find 

(i) how many use only Radio?

(ii) how many use only Television?

(iii) how many use Television and Magazine but not radio?

Solution :

Let T, R and M represent the people who use Television, Radio and Magazines respectively.

Number of people who use Television :

n(T) = 115

Number of people who use Radio :

n(R) = 110

Number of people who use Magazine :

n(M) = 130

Number of people who use Television and Magazines

n (TnM) = 85

Number of people who use Television and Radio :

n(TnR) = 75

Number of people who use Radio and Magazine :

n(RnM) = 95

Number of people who use all the three :

n(TnRnM) = 70

From the above Venn diagram, we have

(i) Number of people who use only Radio is 10.

(ii) Number of people who use only Television is 25.

(iii) Number of people who use Television and Magazine but not radio is 15.

Problem 6 :

In a class of 60 students, 40 students like math, 36 like science,
24 like both the subjects. Find the number of students who like

(i)
Math only, (ii) Science only  (iii) Either Math or Science (iv) Neither
Math nor science.

Solution :

Step 1 :

Let M and S represent the set of students who like math and
science respectively.

Step 2 :

From the information given in the question, we have

n(M) = 40, n(S) = 36, n(MnS) = 24

Step
3 :

Answer
(i) :

Number of students who like math only :

= n(M) — n(MnS)

= 40 — 24

= 16

Step
4 :

Answer
(ii) :

Number of students who like science only :

= n(S) — n(MnS)

= 36 — 24

=  12

Step
5 :

Answer
(iii) :

Number of students who like either math or science :

= n(M or S) 

= n(MuS) 

= n(M) + n(S) — n(MnS)

= 40 + 36 — 24

= 52

Step
6 :

Answer
(iv) :

Total number students who like Math or Science subjects :

n(MuS) = 52

Number of students who like neither math nor science

= 60 — 52

= 8

Problem 7 :

At a certain conference of 100 people there are 29 Indian women
and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either
men or doctors. There are no foreign doctors. Find the number of women doctors
attending the conference.

Solution :

Step 1 :

Let M and D represent the set of Indian men and Doctors
respectively.

Step 2 :

From the information given in the question, we have

n(M) = 23, n(D) = 4,
n(MuD) = 24

Step 3 :

From the basic stuff, we have

n(MuD) = n(M) + n(D) — n(MnD)

24 = 23 + 4 — n(MnD)

n(MnD) = 3 

n(Indian Men and Doctors) = 3

Step 4 :

So, out of the 4 Indian doctors,  there are 3 men.

And the remaining 1 is Indian women doctor.

So, the number women doctors attending the conference is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

©All rights reserved. onlinemath4all.com

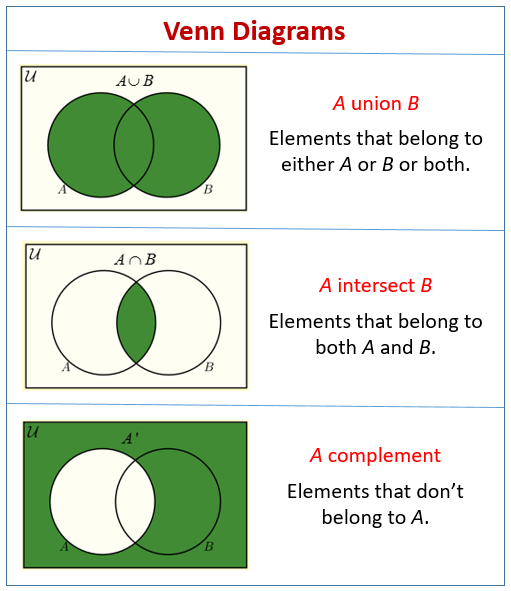
What Are Venn Diagrams?

Venn diagrams are the principal way of showing sets in a diagrammatic form. The method consists primarily
of entering the elements of a set into a circle or ovals.

Before we look at word problems, see the following diagrams to recall how to use Venn Diagrams to
represent Union, Intersection and Complement.

How To Solve Problems Using Venn Diagrams?

This video solves two problems using Venn Diagrams. One with two sets and one with three sets.

Problem 1:
150 college freshmen were interviewed.
85 were registered for a Math class,
70 were registered for an English class,
50 were registered for both Math and English.

a) How many signed up only for a Math Class?
b) How many signed up only for an English Class?
c) How many signed up for Math or English?
d) How many signed up neither for Math nor English?

Problem 2:
100 students were interviewed.
28 took PE, 31 took BIO, 42 took ENG, 9 took PE and BIO, 10 took PE and ENG, 6 took BIO and ENG,
4 took all three subjects.

a) How many students took none of the three subjects?
b) How many students took PE but not BIO or ENG?
c) How many students took BIO and PE but not ENG?

• Show Video Lesson

How And When To Use Venn Diagrams To Solve Word Problems?

Problem:
At a breakfast buffet, 93 people chose coffee and 47 people chose juice. 25 people chose both coffee
and juice. If each person chose at least one of these beverages, how many people visited the buffet?

• Show Video Lesson

How To Use Venn Diagrams To Help Solve Counting Word Problems?

Problem:
In a class of 30 students, 19 are studying French, 12 are studying Spanish and 7 are studying both
French and Spanish. How many students are not taking any foreign languages?

• Show Video Lesson

Probability, Venn Diagrams And Conditional Probability

This video shows how to construct a simple Venn diagram and then calculate a simple conditional
probability.

Problem:
In a class, P(male)= 0.3, P(brown hair) = 0.5, P (male and brown hair) = 0.2
Find
(i) P(female)
(ii) P(male| brown hair)
(iii) P(female| not brown hair)

• Show Video Lesson

Venn Diagrams With Three Categories

Example:
A group of 62 students were surveyed, and it was found that each of the students surveyed liked at
least one of the following three fruits: apricots, bananas, and cantaloupes.

34 liked apricots.
30 liked bananas.
33 liked cantaloupes.
11 liked apricots and bananas.
15 liked bananas and cantaloupes.
17 liked apricots and cantaloupes.
19 liked exactly two of the following fruits: apricots, bananas, and cantaloupes.

a. How many students liked apricots, but not bananas or cantaloupes?
b. How many students liked cantaloupes, but not bananas or apricots?
c. How many students liked all of the following three fruits: apricots, bananas, and cantaloupes?
d. How many students liked apricots and cantaloupes, but not bananas?

• Show Video Lesson

Venn Diagram Word Problem

Here is an example on how to solve a Venn diagram word problem that involves three intersecting sets.

Problem:
90 students went to a school carnival. 3 had a hamburger, soft drink and ice-cream. 24 had hamburgers.
5 had a hamburger and a soft drink. 33 had soft drinks. 10 had a soft drink and ice-cream.
38 had ice-cream. 8 had a hamburger and ice-cream. How many had nothing?
(Errata in video: 90 — (14 + 2 + 3 + 5 + 21 + 7 + 23) = 90 — 75 = 15)

• Show Video Lesson

Venn Diagrams With Two Categories

This video introduces 2-circle Venn diagrams, and using subtraction as a counting technique.

• Show Video Lesson

How To Use 3-Circle Venn Diagrams As A Counting Technique?

Learn about Venn diagrams with two subsets using regions.

• Show Video Lesson

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.