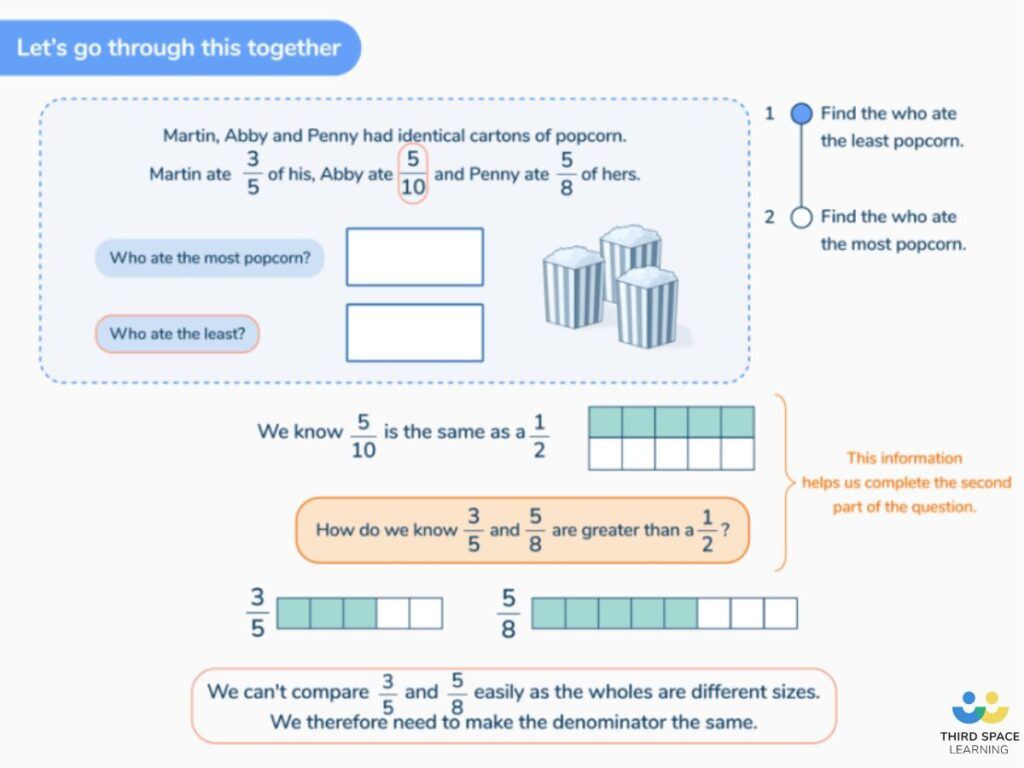
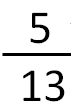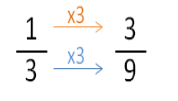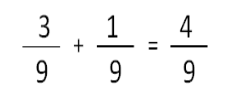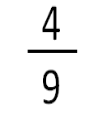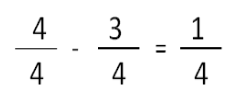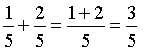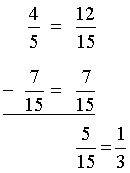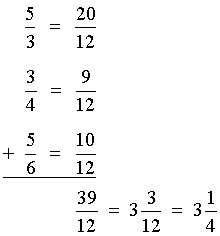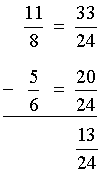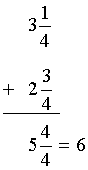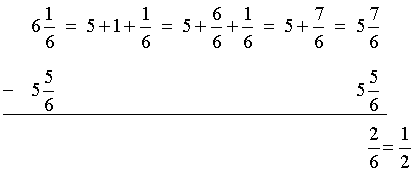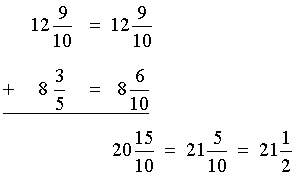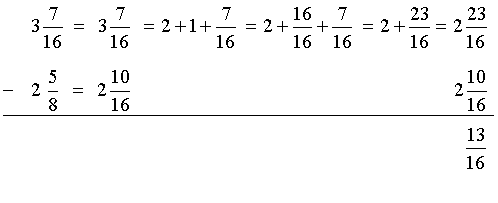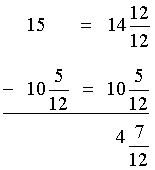Today we are going to look at some examples of word problems with fractions.
Although they may seem more difficult, in reality, word problems involving fractions are just as easy as those involving whole numbers. The only thing we have to do is:
- Read the problem carefully.
- Think about what it is asking us to do.
- Think about the information we need.
- Solve it.
- Simplify, if necessary.
- Think about whether our solution makes sense (in order to check it).
As you can see, the only difference in fraction word problems is step 5 (simplify).
There are some word problems which, depending on the information provided, we should express as a fraction. For example:
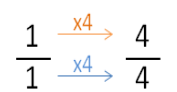
In my fruit basket, there are 13 pieces of fruit, 5 of which are apples.
How can we express the number of apples as a fraction?
5 – The number of apples (5) corresponds to the numerator (the number which expresses the number of parts that we wish to represent).
13 – The total number of fruits (13) corresponds to the denominator (the number which expresses the number of total possible parts).
The solution to this problem is an irreducible fraction (a fraction which cannot be simplified). Therefore, there is nothing left to do.
Word problems with fractions: involving two fractions
In these problems, we should remember how to carry out operations with fractions.
Carefully read the following problem and the steps we have taken to solve it:
Maria spent of the money her grandparents gave her on an adventure book. She also spent
of the money on a bag of candy.
What fraction of the payment has Maria spent?
We find the common denominator:
We calculate:
Answer:
Word problems with fractions: involving a fraction and a whole number
Finally, we are going to look at an example of a word problem with a fraction and a whole number. Now we will have to convert all the information into a fraction with the same denominator (as we did in the example above) in order to calculate
This morning Miguel bought 1 pound of anchovies. In order to eat with his family, he used of a pound. How much does he have left in the refrigerator?
We convert 1 into a fraction with the same denominator:
We calculate:
Answer:
What do you think of this post? Do you see how easy it is to solve word problems with fractions?
To keep learning, try Smartick’s free trial.
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
Here are some examples and solutions of fraction word problems.
The first example is a one-step word problem.
The second example shows how blocks can be used to help illustrate the problem.
The third example is a two-step word problem.
More examples and solutions using the bar modeling method to solve fraction word problems are shown in
the videos. The bar modeling method, also called tape diagrams, are used in Singapore Math and the Common
Core.
Example:
Martha spent
of her allowance on food and shopping. What fraction of her allowance had she left?
Solution:
She had
of her allowance left.
Example:
of a group of children were girls. If there were 24 girls, how many children were there in the group?
Solution:
3 units = 24
1 unit = 24 ÷ 3 = 8
5 units = 5 × 8 = 40
There were 40 children in the group.
Example:
Sam had 120 teddy bears in his toy store. He sold
of them at $12 each. How much did he receive?
Solution:
Step 1: Find the number of teddy bears sold.
He sold 80 teddy bears.
Step 2: Find how much money he received.
80 × 12 = 960
He received $960.
Bar Modeling With Fractions
Examples:
- Grace thought that a plane journey would take 7/10 hr but the actual journey took 1/5 hr longer.
How long did the actual journey take? - Timothy took 2/3 hr to paint a portrait. This was 1/3 hr shorter than the time he took to paint
scenery. How long did he take to paint scenery?
- Show Video Lesson
How To Solve Real World Problems Involving Multiplication Of Fractions By Using Visual Fraction Models Or Equations To Represent The Problem?
Examples:
- At the animal shelter 4/6 of the animals are cats. Of the cats 1/2 are male. What fraction of the
animals at the shelter are male cats? - A taco recipe called for 2/3 cup of cheese per taco. If Andrew wanted to make 3 tacos, how much
cheese would he need?
- Show Video Lesson
How To Solve Word Problems Using Tape Diagrams And Fraction-By-Fraction Multiplication?
Examples:
- Ethan is icing 30 cupcakes. He spreads mint icing on 1/5 of the cupcakes and chocolate on 1/2 of the
remaining cupcakes. The rest will get vanilla frosting. How many cupcakes have vanilla frosting? - Maddox puts 1/4 of her lawn-mowing money in savings and uses 1/2 of the remaining money to pay back
her sister. If she has $15 left, how much did she have at first?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Fraction word problems are an important piece in teaching fractions. Fractions are a key component of the National Curriculum throughout primary, with children introduced to the concept in Year 1 and continuously building upon their knowledge and understanding, through to Year 6 and beyond.
The abstract nature of fractions makes them one of the more difficult areas of maths for children to understand. It is essential that they are taught through the use of concrete resources and visual images, but also through a link to the real world. Word problems are a great way to help children develop this understanding and should be used alongside any fluency work the children do.
To help you with this, we have put together a collection of 20 word problems which can be used with children from Year 2 to Year 6.
Fraction Lessons Resource Pack
Download this free pack of fraction lessons to support your students and help them to practice fractions problems.
Fraction word problems in the national curriculum
Fractions in KS1
Pupils are first introduced to fractions in Year 1, where they begin to recognise a half and quarter of a shape or quantity. As they progress through Key Stage 1, they are introduced to a wider range of fractions.
In Year 2 pupils need to be able to recognise, find, name and write fractions frac{1}{3}, frac{1}{4}, frac{2}{4} and frac{3}{4} of lengths, shape, a set of objects or quantity.
Fractions in lower KS2
Once pupils move into Key Stage 2, there is an increased focus on fractions, with a significant period of time dedicated to developing students’ knowledge and building on previous learning from Year 3 through to Year 6.
In Year 3, pupils are taught to count in tenths; recognise, find and write fractions of a discrete set of objects; understand the term ‘unit’ and ‘non-unit’ fractions; recognise equivalent fractions, compare and order fractions and add/subtract fractions with the same denominator. At this stage, pupils also begin to solve simple problems involving fractions.
As pupils progress into Year 4, they are also introduced to the concept of decimals alongside the work on fractions. They build upon their understanding of equivalent fractions and adding/subtracting fractions (still with the same denominator.
They also learn to count up and down in hundredths, recognise and write decimals equivalent to frac{1}{4}, frac{1}{2} and frac{3}{4} and begin to solve problems with increasingly harder fractions.
Fractions in upper KS2
As pupils continue through the school, into upper Key Stage 2, they continue to build on their learning. They are introduced to mixed numbers and improper fractions. They are also introduced to the concept of percentages alongside fractions and decimals.
In Year 5, children build on the knowledge gained in Year 4, comparing and ordering fractions; recognising equivalent fractions; addition and subtraction of fractions (with different denominators, but multiples of the same number). Fractions appear in addition and subtraction word problems.
They are also introduced to the multiplication of fractions; converting between improper fractions and mixed numbers and the link between fractions, decimals and percentages. By Year 5 pupils will be completing more complex problems, including multi-step word problems and multiplication word problems.
In Year 6, pupils consolidate and build upon the knowledge of fractions they have gained so far. Pupils continue to add and subtract fractions (with different denominators and mixed numbers). They also develop their understanding of how to multiply fractions and begin to divide fractions by whole numbers, combining fraction and division word problems.
Pupils also continue to build upon their understanding of the equivalences between fractions, decimals and percentages and solve increasingly complex one-step, two-step and multi-step percentage word problems.
Why are word problems important for children’s understanding of fractions?
Word problems, alongside the use of concrete resources and visual images, help children to make sense of the abstract nature of fractions.
For example, if children were presented with the question frac{6}{8} ÷ 3, some might find this difficult to access. If children are given it as a word problem, alongside a visual image, it becomes much more accessible.
The above calculation as a word problem:
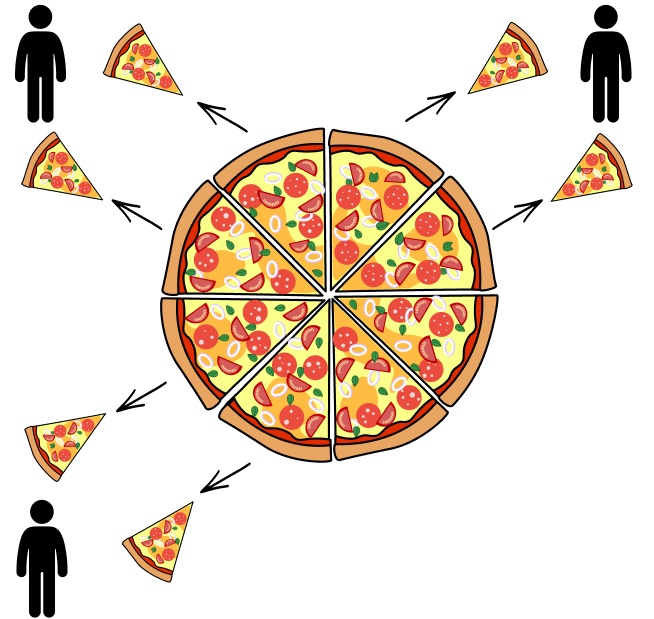
‘3 children shared it{frac{6}{8}} of a pizza, how much did each child get?’
Children can see and understand the concept of 3 children sharing 6 slices of pizza, compared to just seeing the written calculation.
How to teach fraction word problem solving in primary school
As with all word problems, the first thing children need to do is read the question carefully and make sure they understand what is being asked. They then have to decide what calculation is needed and whether they can represent it pictorially.
Here is an example:
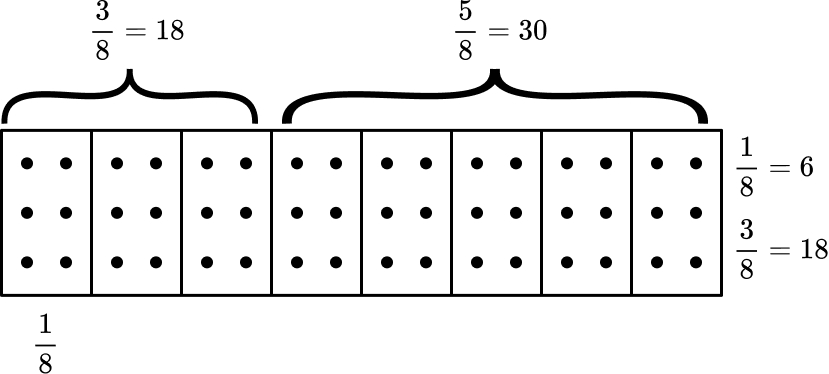
Ben has a bag of 48 sweets.
He gives frac{3}{8} of his bag to his brother
How many sweets does he have left?
How to solve:
What do you already know?
- There are 48 sweets altogether.
- The denominator is 8, so we know we need to divide the 48 by 8. This will tell us how many sweets in frac{1}{8} .
- The numerator is 3, therefore we need to multiply the answer by 3, to tell us how many sweets are frac{3}{8} .
- The last step of the problem is to find out how many sweets Ben has left.
- We can either calculate frac{5}{8} , as we know Ben must have frac{5}{8} left, or we subtract the number of sweets in frac{3}{8} from the total of 48.
How can this be drawn/represented pictorially?
- We can draw a bar model, split into 8 sections.
- The 48 sweets are then shared between the 8 sections (each worth frac{1}{8} ).
- We can see that frac{3}{8} of the 48 sweets equals 18 sweets.
- We can then either subtract 18 from 48, to work out how many sweets were left. 48 – 18 = 30
- Alternatively, we can calculate how many sweets are in frac{5}{8} , which is 30.
Word problems are tied in throughout Third Space Learning’s online one-to-one tuition programmes. Tutors work with students to break down word problems and identify the operations needed to solve problems.
Fraction word problems for primary
The following section lays out the types of fraction word problems that you can expect to see by year group in primary school.
At Third Space Learning we incorporate word problems into our one-to-one online tutoring. With each lesson designed to suit the needs of each individual student, our tutoring programme aims to deepen mathematical understanding and confidence in maths.
Fraction word problems are a great way to strengthen students’ conceptual understanding of fractions and grow their problem solving skills.
Fraction word problems for Year 2
Word problems in Year 2 involve recognising and naming simple fractions and beginning to understand the concept of equivalence.
Question 1
Maisie was having a birthday party.
She invited 16 friends. Half of her friends were from her class and a half were from the other Year 2 class.
How many friends did she invite from each class?
Answer: 8 friends
frac{1}{2} of 16 = 8
Question 2
Ahmed baked 12 cookies.
He ate frac{1}{4} of them.
How many cookies did Ahmed eat?
Answer: 3
frac{1}{4} of 12 = 3
Question 3
Sara says ‘I ate frac{1}{2} a pizza and my friend ate frac{2}{4} . My friend had more than me, as she had 2 pieces’.
Is she correct? Explain why you have chosen your answer.
Answer: Sara is not correct
frac{1}{2} is the same as frac{2}{4}
Question 4
Tom and Zeyn shared a chocolate bar.
They both had a quarter of the chocolate bar.
How much was left?
Answer: frac{1}{2} of the chocolate bar
frac{2}{4} are equivalent to frac{1}{2}
Fraction word problems for Year 3
Word problems for Year 3 include proper fractions, fractions of amounts, simple equivalent fractions and adding and subtracting fractions with the same denominator.
Question 1
Sophie ate frac{1}{4} of her chocolate bar.
If the bar had 20 squares, how many squares did Sophie eat?
Answer: 5 squares
frac{1}{4} of 20 = 20 ÷ 4 = 5
Question 2
Hamza and Khalifa shared a pizza.
Hamza ate two fourths of the pizza and Khalifa ate one fourth.
How much pizza was left?
Answer: frac{1}{4}
frac{2}{4}+frac{1}{4}=frac{3}{4}
1-frac{3}{4}=frac{1}{4}
Question 3
There are 24 hours in a day.
Maise worked out that she spends frac{1}{8} of her day on Saturday, doing exercise.
How long does she spend exercising on a Saturday?
Answer: 3 hours
frac{1}{8} of 24 hours = 24 ÷ 8 = 3
Question 4
There are 30 children in the class.
frac{2}{5} of the children are wearing jumpers.
How many children are wearing jumpers?
Answer: 12 children
frac{1}{5} of 30 = 30 ÷ 5 = 6
frac{2}{5} of 20 = 12
Fraction word problems for Year 4
Word problems for year 4 include equivalent fractions, fractions of quantities (including non-unit fractions and adding/subtracting fractions with the same denominator. Money word problems often appear in Year 4.
Question 1
Abdullah spent frac{1}{3} of his pocket money for the month on a new game.
He receives £18 per month.
How much did he spend on the game?
Answer: £6
frac{1}{3} of 18 = £6
Question 2
Bethan had a bag of sweets.
She gave frac{2}{7} of the bag to her mum and ate frac{3}{7} of herself.
What fraction of the bag was left?
Answer: frac{2}{7}
frac{2}{7} + frac{3}{7} = frac{5}{7}
frac{7}{7}-frac{5}{7}=frac{2}{7}
Question 3
Jamal ate frac{6}{18} of a chocolate bar.
Mason ate frac{1}{3}
Mason said that Jamal ate more than him. Do you agree? Explain your answer.
Answer: No – they both ate the same.
frac{1}{3} is equivalent to frac{6}{18}
Question 4
frac{2}{7} of a piece of ribbon is 10cm.
How long is the whole piece of ribbon?
Answer: 35cm
frac{2}{7} = 10
frac{1}{7} = 5
frac{7}{7} = 5 x 7 = 35
Fraction word problems for Year 5
Word problems for Year 5 include more complex equivalent fractions, problems involving mixed numbers and improper fractions, adding and subtracting fractions (with different denominators) and multiplying fractions.
Question 1
There are 60 pupils in Year 5.
Eden carried out a survey on favourite foods.
frac{1}{5} of the children said pizza, frac{2}{6} said burgers and frac{3}{10} said hot dogs.
How many pupils did she survey altogether?
Answer: 50 pupils
frac{1}{5} of 60 = 12
frac{2}{6} 0f 60 = 20
frac{3}{10} = 18
Question 2
The Johnson family are driving to the zoo.
They have driven frac{5}{9} of their journey, which is 45 miles.
How much further do they have to drive, to reach their holiday home?
Answer: 20 miles left to drive
frac{5}{9} = 45, therefore frac{1}{9} = 45 ÷ 9 = 5.
frac{5}{9} = 5 x 5 = 25 miles
frac{9}{9} = 9 x 5 = 45 miles
45 – 25 = 20
Question 3
Macy is taking part in the school maths challenge.
She is given a word problems worksheet containing 36 questions.
Macy gets frac{7}{9} of the questions correct.
How many does she get wrong?
Answer: 8 questions wrong
frac{1}{9} of 36 = 4
frac{7}{9} = 28
frac{2}{9} = 8
Question 4
Oliver and Zac are making smoothies.
They make 800 ml of smoothies.
frac{2}{5} is made from apples, frac{3}{7} from strawberries and the rest from orange juice.
How many ml of orange juice do they add to the apples and strawberries?
Answer: 180ml orange juice
frac{2}{5} of 800: frac{1}{5} = 160ml, frac{2}{5} = 320 ml apple juice
frac{3}{8} of 800: frac{1}{8} = 100, frac{3}{8} = 300 ml strawberry juice
800 – 620 = 180ml
Fraction word problems for Year 6
Word problems for year 6 include adding and subtracting fractions with different denominators and mixed numbers, multiplying fractions, dividing fractions by whole numbers and finding equivalent fractions, decimals and percentages.
Question 1
Children in a Year 6 Class at Oak Tree Middle School are answering a set of ratio questions.
There are 10 questions and 28 children completing the activity.
If the children got frac{6}{7} of the total number of questions correct between them.
How many did they get wrong?
Answer: 40 questions wrong
28 x 10 = 280 questions
frac{1}{7} of 280 = 40
frac{6}{7} = 40 x 6 = 240
Question 2
Amber and her 5 friends are sharing 4 pizzas for her birthday party.
The pizzas are split into sixths.
If they each eat the same amount of pizza, how many slices does each person at the party get?
Answer: 4 slices
This is a dividing fractions word problem
frac{24}{6} ÷ 6 = frac{4}{6}
Question 3
A group of friends win a quarter of the total lottery prize for the week.
There are 4 friends and each friend shares an equal fraction of the quarter.
What fraction of the total lottery prize does each friend get?
Answer: frac{1}{16} of the prize fund
Each friend gets frac{1}{4} of the frac{1}{4} prize fund
frac{1}{4} times frac{1}{4} = frac{1}{16}
Question 4
There are 30 children in the class
frac{7}{10} of the pupils in the class are girls.
frac{3}{7} of the girls have their ears pierced.
How many girls have their ears pierced?
Answer: 9 girls have their ears pierced
frac{1}{10} = 3, frac{7}{10} = 21 girls
frac{1}{7} of 21 = 3. frac{3}{7} = 3 x 3 = 9
More word problems resources
Third Space Learning offers a wide range of practice word problems for all primary year groups and covering a large number of topics, including; time word problems, ratio word problems, addition word problems and subtraction word problems.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
In word problems on fraction we will solve different types
of problems on multiplication of fractional numbers and division of fractional
numbers.
1. 4/7 of a number is 84. Find the number.
Solution:
According to the problem,
4/7 of a number = 84
Number = 84 × 7/4
[Here we need to multiply 84 by the reciprocal of 4/7]
= 21 × 7
= 147
Therefore, the number is 147.
2. Rachel took (frac{1}{2}) hour to paint a table and (frac{1}{3}) hour to paint a chair. How much time did she take in all?
|
Time taken to paint a table = (frac{1}{2}) hour Time taken to paint a chair = (frac{1}{3}) hour Total time taken = (frac{1}{2}) hour + (frac{1}{3}) hour = (frac{5}{6}) hour |
(frac{1}{2}) + (frac{1}{3}) L.C.M. of 2, 3 is 6. = (frac{3}{6}) + (frac{2}{6}) (frac{1 × 3}{2 × 3}) = (frac{3}{6}) (frac{1 × 2}{3 × 2}) = (frac{2}{6}) |
3. If 3(frac{1}{2}) m of wire is cut from a piece of 10 m
long wire, how much of wire is left?
Total length of the wire = 10 m
Fraction of the wire cut out = 3(frac{1}{2}) m = (frac{7}{2})
m
Length of the wire left = 10 m – 3(frac{1}{2}) m
= [(frac{10}{1}) — (frac{7}{2})] m, [L.C.M. of 1, 2 is 2]
= [(frac{20}{2}) — (frac{7}{2})]
m, [(frac{10}{1}) × (frac{2}{2})]
= [(frac{20 — 7}{2})] m
= (frac{13}{2}) m
= 6(frac{1}{2}) m
4. One half of the students in a school are girls, 3/5 of
these girls are studying in lower classes. What fraction of girls are studying
in lower classes?
Solution:
Fraction of girls studying in school = 1/2
Fraction of girls studying in lower classes = 3/5 of 1/2
=
3/5 × 1/2
= (3 × 1)/(5 × 2)
=
3/10
Therefore, 3/10 of girls studying in lower classes.
5. Maddy reads three-fifth of 75 pages of his lesson. How many more pages he need to complete the lesson?
Solution:
Maddy reads = 3/5 of 75
= 3/5 × 75
= 45 pages.
Maddy has to read = 75 – 45.
= 30 pages.
Therefore, Maddy has to read 30 more pages.
6. A herd of cows gives 4 litres of milk each day. But each cow gives one-third of total milk each day. They give 24 litres milk in six days. How many cows are there in the herd?
Solution:
A herd of cows gives 4 litres of milk each day.
Each cow gives one-third of total milk each day = 1/3 of 4
Therefore, each cow gives 4/3 of milk each day.
Total no. of cows = 4 ÷ 4/3
= 4 × ¾
= 3
Therefore there are 3 cows in the herd.
Questions and Answers on Word problems on Fractions:
1. Shelly walked (frac{1}{3}) km. Kelly walked (frac{4}{15})
km. Who walked farther? How much farther did one walk than the other?
2. A frog took three jumps. The first jump was (frac{2}{3})
m long, the second was (frac{5}{6}) m long and the third was (frac{1}{3})
m long. How far did the frog jump in all?
3. A vessel contains 1(frac{1}{2}) l of milk. John drinks
(frac{1}{4}) l of milk; Joe drinks (frac{1}{2}) l of milk. How much of
milk is left in the vessel?
● Multiplication is Repeated Addition.
● Multiplication of Fractional Number by a Whole Number.
● Multiplication of a Fraction by Fraction.
● Properties of Multiplication of Fractional Numbers.
● Multiplicative Inverse.
● Worksheet on Multiplication on Fraction.
● Division of a Fraction by a Whole Number.
● Division of a Fractional Number.
● Division of a Whole Number by a Fraction.
● Properties of Fractional Division.
● Worksheet on Division of Fractions.
● Simplification of Fractions.
● Worksheet on Simplification of Fractions.
● Word Problems on Fraction.
● Worksheet on Word Problems on Fractions.
5th Grade Numbers
5th Grade Math Problems
From Word Problems on Fraction to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Exercise 1
Determine the fraction that matches the description below:
a. half of a half
b. half of a third
c. a third of a half
d. half of a quarter
The best Maths tutors available
5 (32 reviews)
1st lesson free!
5 (26 reviews)
1st lesson free!
4.9 (40 reviews)
1st lesson free!
5 (33 reviews)
1st lesson free!
4.9 (42 reviews)
1st lesson free!
5 (68 reviews)
1st lesson free!
5 (147 reviews)
1st lesson free!
5 (31 reviews)
1st lesson free!
5 (32 reviews)
1st lesson free!
5 (26 reviews)
1st lesson free!
4.9 (40 reviews)
1st lesson free!
5 (33 reviews)
1st lesson free!
4.9 (42 reviews)
1st lesson free!
5 (68 reviews)
1st lesson free!
5 (147 reviews)
1st lesson free!
5 (31 reviews)
1st lesson free!
Let’s go
Exercise 2
To prepare a cake, you need:
of a package of
g of sugar
of a
kg package of flour
of a bar of butter of weighing
g
Find the quantities that are needed to prepare the cake in grams.
Exercise 3
A well contains liters of water. If
of its original content is consumed, how many liters of water are left in the well?
Exercise 4
A piece of cloth measuring m in length is cut to
of its original length. What is the length of the piece that has been removed?
Exercise 5
A family consumed the following amounts of liquids during their Saturday picnic:
Two bottles of water each measuring a liter and a half
bottles of juice each measuring
of a liter
bottles of lemonade each measuring
of a liter
How many liters of liquid did the family drink during their picnic? Express the result using a mixed number.
Exercise 6
How many thirds of a liter are there in liters?
Exercise 7
A cable measuring m is cut into two pieces. One piece of the cable is
of the original length. What is the length of each piece of cable?
Exercise 8
A box contains chocolates. Eva ate
of the chocolates and Ana ate
of the chocolates.
a. How many chocolates did Eva eat?
b. How many chocolates did Ana eat?
c. What fraction of the chocolates have been eaten so far?
Exercise 9
Adriana has walked m on her way to school. This distance is
of the total distance from her house to the school. What is the total distance from her house to the school?
Exercise 10
Two cars A and B are making the same journey of km. At a particular moment, Car A has traveled
of the trip, while car B has traveled
of it.
a. If the cars continue at the same speed, which of the two will arrive at the destination first?
b. How many kilometers had each car driven at that particular moment?
Exercise 11
After the ballots have been counted in a city’s local election, it was determined that of the votes went to Party A,
went to Party B,
went to Party C and the remainder went to Party D. The total number of votes was
.
Calculate:
a. The number of votes obtained by each party.
b. The number of registered voters who did not cast a ballot if the total amount of voters that did was of the total amount of voters who are registered.
Exercise 12
Helen went to the women’s boutique starting out with dollars. She spent
of that amount on new clothes. How much money does Helen have left?
Exercise 13
A few years ago Peter was , which represents
of the amount of his current age. How old is Peter now?
Exercise 14
A father has divided up dollars among his 3 sons. The eldest son received
of the whole amount, while the middle son received
and the youngest son received the remainder.
a. How much money did each sibling receive?
b. What fraction of the money did the youngest son receive?
Exercise 15
The budget for a residential complex is distributed as follows: th for electricity,
th for water,
th for garbage collection,
th for building maintenance and the remainder is reserved for cleaning the complex.
a. What fraction of the budget is used for cleaning?
b. Order the expenses from least to greatest.
Exercise 16
Alicia had dollars to go shopping with. Thursday she spent
of that amount and Saturday she spent
of what she had left.
a. How much money did she spend each day?
b. How much money does she have left at the end?
Exercise 1 Solution
Determine the fraction that matches the description below:
a. half a half
b. half of a third
c. a third of a half
d. half of a quarter
Exercise 2 Solution
To prepare a cake, you need:
of a package of
g of sugar
of a
kg package of flour
of a bar of butter of
Find the quantities that are needed to prepare the cake in grams.
of
g is
g of sugar
of
g is
g of flour
of
g is
g of butter
Exercise 3 Solution
A well contains liters of water. If
of its original content is consumed, how many liters of water are left in the well?
is the fractional amount left in the well.
liters is the amount of water left in the well.
Exercise 4 Solution
A piece of cloth measuring m in length is cut to
of its original length. What is the length of the piece that has been removed?
is the fractional amount of the piece that was removed.
m is the length of the piece that was removed.
Exercise 5 Solution
A family consumed the following amounts of liquids during their Saturday picnic:
Two bottles of water each measuring a liter and a half
bottles of juice each measuring
of a liter
bottles of lemonade each measuring
of a liter
How many liters of liquid did the family drink during their picnic? Express the result using a mixed number.
amount of water drank: liters
amount of juice drank: liters
amount of lemonade drank: liters
total amount of liquids drank: liters
liters
Exercise 6 Solution
How many thirds of a liter are there in liters?
There are three liters in
liter.
There are thirds
‘s of a liter in
liters.
Exercise 7 Solution
A cable measuring m is cut into two pieces. One piece of the cable is
of the original length. What is the length of each piece of cable?
The fractional length of the second piece of cable: .
The 2 pieces are th and
th of the original length.
The length of the first piece: m.
The length of the second piece: m.
Exercise 8 Solution
A box contains chocolates. Eva ate
of the chocolates and Ana ate
of the chocolates.
a. How many chocolates did Eva eat?
Eva ate chocolates.
b. How many did Ana eat?.
Ana ate chocolates
c. What fraction of the total amount of chocolates has been eaten between them?
Exercise 9 Solution
Adriana has walked m on her way to school. This distance is
th of the total distance from her house to the school. What is the total distance from her house to the school?
of the total distance plus
of the total distance will be the actual total distance.
is
of
Find of the distance
m.
of
m is
m
The total distance is m.
Exercise 10 Solution
Two cars A and B make the same journey of km. At a particular moment, Car A has traveled
of the trip, while Car B has traveled
of it.
a. If the cars continue at the same speed, which of the two will arrive at the destination first?
Car A has traveled of the total trip and car B has traveled
of the total trip.
Car A: of the trip
Car B: of the trip
so Car B will make it to the end of the journey just a hair faster than Car A.
b. How many kilometers have been traveled at this particular moment by each car?
Car A: km
Car B: km
Exercise 11 Solution
After the ballots have been counted in a city’s local election, it was determined that th of the votes went to Party A,
th went to Party B,
th went to Party C and the remainder went to Party D. The total number of votes was
.
Calculate:
a. The number of votes obtained by each party.
Party A has votes
Party B has votes
Party C has votes
Party D has votes
b. The number of registered voters who did not cast a ballot if the number of voters who did was of the total amount of voters who are registered.
of the total amount of registered voters is
voters,
so of the total amount of people who voted,
, will be
of the total amount of registered voters.
is
of the registered voters,
so is the total amount of registered voters.
Exercise 12 Solution
Helen went to the women’s boutique starting out with dollars. She spent
of that amount. How much money does she have left?
dollars
Exercise 13 Solution
A few years ago Peter was 24, which represents of his current age. How old is Peter now?
of Peter’s current age plus
of Peter’s current age will be Peter’s actual current age.
is
of
of
is
present age is
Exercise 14 Solution
A father has divided up dollars among his 3 sons. The eldest son received
of the whole amount, while the middle son received
and the youngest son received the remainder.
a. How much money did each sibling receive?
The eldest son received dollars.
The middle son received dollars.
The youngest son received dollars.
b. What fraction of the money was the amount given to the youngest son?
The youngest son received of the original amount.
Exercise 15 Solution
The budget for a residential complex is distributed as follows: th for electricity,
th for water,
th for garbage collection,
th for building maintenance and the remainder is reserved for cleaning the complex.
a. What fraction of the budget is used for cleaning?
Budget without cleaning expenses:
Cleaning expenses:
b. Order the expenses from least to greatest.
garbage maintenance
cleaning
water
electricity
Exercise 16 Solution
Alicia had dollars to go shopping. Thursday she spent
th of that amount and Saturday she spent
th of what she had left.
a. How much money did she spend each day?
Thursday Alicia spent dollars.
She has dollars left for more shopping.
Saturday Alicia spent dollars.
b. How much does she have left at the end?
She has dollars left.
A great variety of fraction word problems with solutions. These word problems will help you find out when you need to add, subtract, multiply or divide fractions.
1. Sarah knows 8 of the 25 students in her class. Write a fraction showing the number of students Sarah knows.
2. Peter correctly solved 18 out of the 20 math problems the teacher gave him. Write a fraction showing the number of math problems Peter solved correctly.
Solution
18/20
3. Darlene ate 3/5 of her pizza. How much pizza can Darlene share with her sister?
Solution
1 represents the entire pizza. To find how much pizza is left, just do 1 — 3/5
1 — 3/5 = 1/1 — 3/5 = 5/5 — 3/5 = 2/5
Darlene can share 2/5 of the pizza.
4. Last week, Steve spent 3 1/2 hours playing soccer and 4 1/2 hours playing table tennis. How much time did Steve spend playing both sports?
Solution
Just add 3 1/2 and 4 1/2 together.
3 1/2 + 4 1/2 = (3 + 4) + 1/2 + 1/2 = 7 + 1 = 8
Steve spent 8 hours playing both sports.
5. John jogged 1 3/4 miles yesterday and 2 1/2 miles today. How many miles did John spend jogging for the past two days?
Solution
Just add 1 3/4 and 2 1/2 together.
1 + 2 = 3
3/4 + 1/2 = 3/4 + 2/4 = 5/4
John jogged 3 5/4 miles for the past two days.
6. Maria bought a pizza and ate half of it. Then, she gave the leftover to his brother and his brother ate half of it. How much of the pizza did his brother eat?
Solution
The brother ate half of half the pizza.
Half of half = 1/2 of 1/2 = 1/2 × 1/2 = 1/4
7. Anthony caught some fish that weighted 6 1/2 pounds. If he gave 4 1/4 pounds of fish to some friends, how much fish does he have for himself?
Solution
Subtract 4 1/4 from 6 1/2.
6 — 4 = 2
1/2 — 1/4 = 2/4 — 1/4 = 1/4
Anthony has 2 1/4 pounds of fish for himself.
8. 1/4 of a tablespoon of baking soda is needed to make a loaf of bread. How many loaves of bread can be made with 5 tablespoons of baking soda?
Solution
Divide 5 by 1/4
5 ÷ 1/4 = 5/1 ÷ 1/4 = 5/1 × 4/1 = 20/1 = 20
20 loaves of bread can be made.
9. A recipe calls for 2 1/8 cups of butter for a casserole. How much butter is needed to make 6 1/2 casseroles?
Solution
Just multiply 2 1/8 by 6 1/2
2 1/8 × 6 1/2 = (2 × 8 + 1)/8 × (6 × 2 + 1)/2
2 1/8 × 6 1/2 = 17/8 × 13/2 = (17 × 13)/(8 × 2)
2 1/8 × 6 1/2 = 221/16 = 13.8125
To make 6 1/2 casseroles, the recipe will need 13.8125 cups of butter.
10. Kevin cooked 8 1/4 pounds of meat for a dinner. If each serving is 3/4 pound, how many servings did he prepare?
Solution
Just divide 8 1/4 by 3/4
8 1/4 ÷ 3/4 = (8 × 4 + 1)/4 ÷ 3/4 = 33/4 ÷ 3/4 = 33/4 × 4/3 = 132/12 = 11
Kevin prepared 11 servings.
Recent Articles
-
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Let’s learn fractions together! LogicLike has put together word problems on fractions for grades 1-6 students!
1st — 2nd Grade
Unit fractions
Den has nine balls. If four balls are red, what fraction of the balls are red?
Sarah made nine chocolate bars.
She put powdered sugar on three chocolate bars.
Which part of the bars now have powdered sugar?
Meg made a bouquet with seven flowers.
She used two red flowers.
What fraction of the flowers were red?
There are 10 cars in the toy box. Four of them are blue.
What fraction of the cars are blue?
There are 11 houses on Granny’s street.
Six of them are painted green.
What fraction of the houses are green?
What fraction of the week is Tuesday?
What fraction of the week is Saturday and Sunday?
What fraction is the thumb from the fingers on your hand?
What fraction is the thumb from all fingers on your hands?
The girl cut the apple into two equal parts.
She gave one part to her mother.
What fraction of the apple did the girl have?

3rd — 4th Grade
Adding and Subtracting Fractions
Grace ate 3/12 of apple pie and Matthew ate 5/12 of the pie.
How much apple pie did the kids eat in total?
Lori took 2/6 of pencils from the box,
and Mario took 4/6 of pencils from the box.
How many pencils did the children take out of the box?
Mom bought the minced meat, which is 2/6 pork and the rest is beef.
How much beef is in minced meat?
The hippopotamus ate 4/9 fruits for dinner and the rest vegetables.
How many vegetables did the hippopotamus eat for dinner?
Multiplication and Division Fractions
If it takes 4/7 yards of fabric to make a coat,
then how many yards will it take to make 6 coats?
Tom takes 1 1/2 hours to get home.
If he walks twice fast, how many minutes will it take?
Jessica had $200, 1/4 of this money she spent on cosmetics.
How much money did Jessica spend?
Mom bought rice at the market at a price of $0.71 per pound.
How many pounds of rice did mom buy if the purchase amount was $2.13?
Converting Fractions
If 62 out of 100 students in a school are girls, then write a decimal for the part of the school that consists of girls.
Lucas has read 12/20 of the book.
How much of the book has he read as a decimal?
Fraction to/from Decimals
Eric ate 1/2 of the pizza.
How is this fraction written as a decimal number?
Jessica drank 2/5 of the orange juice from the jug.
How is this fraction written as a decimal number?
Each magic stone found in the game gives the same points.
A total of 37.5 points can be earned.
Emma collected 1/2 of the stones.
How many points did Emma get?
—>

5th — 6th Grade
Adding and Subtracting Fractions
The monkey nursery is open two times a day:
3/4 hour at noon and 6/16 hour in the afternoon.
How much time is the monkey nursery open every day?
A construction company bought 4.7 pounds of gravel and 7.9 pounds of sand. How many pounds of material did the company buy in all?
It snowed 3.4 inches on Friday and 6.9 inches on Sunday.
How much did it snow on Friday and Sunday combined?
Sandra bought 8.04 ounces of dark chocolate.
And 5.7 ounces less milk chocolate.
How much milk chocolate did Sandra buy?
Multiplication and Division Fractions
Ms. Sweet decided to make a snack for the 24 students. She gave each student a dish of yogurt and divided 6 cups of blueberries equally among the dishes. How many cups of strawberries did each student get in their yogurt?
WSix friends are eating pizza. They eat 1/2 of pizza each.
How many pizzas do they eat in total?
Donald accidentally cut a coil of rope in two.
The length of one of them is 3.25 feet,
the length of the other is 1.3 times shorter.
How long was the original rope?
Converting Fractions
The travelers walked 3/5 of the route 60 miles.
How many miles are left for travelers to go?
The perimeter of the triangle is 40 inches.
The first side is 3/10 of the perimeter,
the other is 3/2 of the first side.
What is the third side of the triangle?
Join other LogicLikers online!
Become a part of our amazing community
of kids and adults, families and friends, and solve puzzles from everywhere!

Featured here is a vast collection of fraction word problems, which require learners to simplify fractions, add like and unlike fractions; subtract like and unlike fractions; multiply and divide fractions. The fraction word problems include proper fraction, improper fraction, and mixed numbers. Solve each word problem and scroll down each printable worksheet to verify your solutions using the answer key provided. Thumb through some of these word problem worksheets for free!
Represent and Simplify the Fractions: Type 1
Presented here are the fraction pdf worksheets based on real-life scenarios. Read the basic fraction word problems, write the correct fraction and reduce your answer to the simplest form.
Adding Fractions Word Problems Worksheets
Conjure up a picture of how adding fractions plays a significant role in our day-to-day lives with the help of the real-life scenarios and circumstances presented as word problems here.
(15 Worksheets)
Multiplying Fractions Word Problems Worksheets
This set of printables is for the ardently active children! Explore the application of fraction multiplication and mixed-number multiplication in the real world with this exhilarating practice set.
(15 Worksheets)
Fraction Division Word Problems Worksheets
Gift children a broad view of the real-life application of dividing fractions! Let them divide fractions by whole numbers, divide 2 fractions, divide mixed numbers, and solve the word problems here.
(15 Worksheets)
Problem 1 :
A cookie factory uses ¼ of a barrel of oatmeal in each batch of cookies. The factory used ½ of a barrel of oatmeal yesterday. How many batches of cookies did the factory make ?
Solution :
Amount of oatmeal used in each batch of cookies is
= ¼ of a barrel
No. of cookies made yesterday is
= Oatmeal used yesterday/Oatmeal used in each batch
= ½ ÷ ¼
= ½ ⋅ ⁴⁄₁
= 2
The factory made 2 batches of cookies yesterday.
Problem 2 :
Of the students in the band, ¼ play the flute and another ⅒play the clarinet. What fraction of the students in the band play either the flute or the clarinet ?
Solution :
Fraction of the students in the band play either the flute or the clarinet :
= ¼ + ⅒
Least common multiple of the denominators (4, 10) is 20.
Make each denominator as 20 by multiplying the numerator and denominator of the first fraction by 5 and the second fraction by 2.
= ⁽¹ ˣ ⁵⁾⁄₍₄ ₓ ₅₎ + ⁽¹ ˣ ²⁾⁄₍₁₀ ₓ ₂₎
= ⁵⁄₂₀ + ²⁄₂₀
= ⁽⁵ ⁺ ²⁾⁄₂₀
= ⁷⁄₂₀
Fraction of the students who play either the flute or the clarinet is ⁷⁄₂₀.
Problem 3 :
Lily rode her bicycle ⁵⁄₄ miles from her house to the park. Then she rode ³⁄₂ miles from the park to the library. How many miles did Lily ride in all ?
Solution :
Total number of miles that Lily rode in all is
= ⁵⁄₄ + ³⁄₂
Least common multiple of the denominators (4, 2) is 4.
Make each denominator as 4 by multiplying the numerator and denominator of the first fraction by 1 and the second fraction by 2.
= ⁽⁵ ˣ ¹⁾⁄₍₄ ₓ ₁₎ + ⁽³ ˣ ²⁾⁄₍₂ ₓ ₂₎
= ⁵⁄₄ + ⁶⁄₄
= ⁽⁵ ⁺ ⁶⁾⁄₄
= ¹¹⁄₄
= 2¾
Lily rode 2¾ miles in all.
Problem 4 :
At the dealership where Mary works, she fulfilled ⅙ of her quarterly sales goal in January and another ³⁄₁₀ of her sales goal in February. If her quarterly sales goal is $12,000, what amount of sales did she make in January and February ?
Solution :
Fraction of her sales done in January and February is
= ⅙ + ³⁄₁₀
Least common multiple of the denominators (6, 10) is 30.
make each denominator as 30 by multiplying the numerator and denominator of the first fraction by 5 and the second fraction by 3.
Then we have,
= ⁽¹ ˣ ⁵⁾⁄₍₆ ₓ ₅₎ + ⁽³ ˣ ³⁾⁄₍₁₀ ₓ ₃₎
= ⁵⁄₃₀ + ⁹⁄₃₀
= ⁽⁵ ⁺ ⁹⁾⁄₃₀
= ¹⁴⁄₃₀
= ⁷⁄₁₅
Amount of sales she made in January and February is
= ⁷⁄₁₅ of quarterly sales goal
= ⁷⁄₁₅ ⋅ 12000
= 5600
Amount of sales Mary made in January and February is $5,600.
Problem 5 :
Lucy made strawberry jam and raspberry jam. She made enough strawberry jam to fill ⅚ of a jar. If she made 2 times as much raspberry jam as strawberry jam, how many jars would the raspberry jam fill ?
Solution :
Amount of strawberry jam made by Lucy is
= ⅚ of a jar
2 times as much raspberry jam as strawberry jam is
= 2 ⋅ ⅚ of a jar
= ⁵⁄₃ of a jar
= 1⅔ of a jar
Lucy would make enough raspberry jam to fill 1⅔ jars.
Problem 6 :
David’s salary is $1800. David spent 2/3 of the total money for food. He spent 1/2 of the remaining for his kids education and saved the rest. How much did he save ?
Solution :
Money spent on food is
= ⅔ ⋅ 1800
= 1200
Remaining = 1800 — 1200
= 600 —-(1)
Money spent on kids education is
= 1/2 of remaining
= 1/2 ⋅ 600
= 300 —-(2)
Then, his savings is
= (1) — (2)
= 600 — 300
= 300
David saved $300.
Problem 7 :
A, B and C are friends. A has one-third of the money that B has. C has one-half of the money that A has. If they all together have $450. How much money do A, B and C have separately?
Solution :
Let us assume that B has the money y.
Then,
A = (⅓)y = ʸ⁄₃
C = ½ of A
C = ½ ⋅ ʸ⁄₃
C = ʸ⁄₆
Given : A, B and C together have $450.
A + B + C = 450
ʸ⁄₃ + y + ʸ⁄₆ = 450
Least common multiple of the denominators (3, 6) is 6.
Multiply both sides of the equation by 6 to get rid of the denominators 3 and 6.
6(ʸ⁄₃ + y + ʸ⁄₆) = 6(450)
6(ʸ⁄₃) + 6(y) + 6(ʸ⁄₆) = 2700
2y + 6y + y = 2700
9y = 2700
y = 300
ʸ⁄₃ = ³⁰⁰⁄₃ = 100
ʸ⁄₆ = ³⁰⁰⁄₆ = 50
A has $100, B has $300 and C has $50.
Problem 8 :
John’s present age is one-third of David’s age 5 years back. If David is 20 years old now, find the present age of John.
Solution :
Present age of David = 20 years.
David’s age 5 years back = 20 — 5 = 15 years
Given : John’s present age is 1/3 of David’s age 5 years back.
John’s present age :
= ⅓ of 15 years
= (⅓) ⋅ 15
= 5 years
Problem 9 :
In a triangle, the first angle is one-half of the third angle and the second angle is three-fourth of the third angle. Find the three angles of the triangle.
Solution :
In the triangle, since both the first and second angles are linked to the third angle, introduce a variable for the third angle and write the first and second angles in terms of that variable and solve for it.
Let x be the measure of the third angle.
First angle = (½)x = ˣ⁄₂
Second angle = (¾)x = ³ˣ⁄₄
In a triangle, sum of the three angles is equal to 180°.
first angle + second angle + third angle = 180°
ˣ⁄₂ + ³ˣ⁄₄ + x = 180°
Least commpon multiple of the denominator (2, 4) is 4.
Multiply both sides of the equation by 4 to get rid of the denominators 2 and 4.
4(ˣ⁄₂ + ³ˣ⁄₄ + x) = 4(180°)
4(ˣ⁄₂) + 4(³ˣ⁄₄) + 4(x) = 720°
2x + 3x + 4x = 720°
9x = 720°
x = 80°
ˣ⁄₂ = ⁸⁰⁄₂ = 40°
³ˣ⁄₄ = ⁽³ ˣ ⁸⁰⁾⁄₄ = 60°
The three angles of the triangle are 40°, 60° and 80°.
Problem 10 :
The denominator of a fraction is 1 more than thrice the numerarotor. If 2 be added to both numerator and denominator, the fraction would become ⅓. Find the fraction.
Solution :
Let x be the numerator.
Then, the denominator is (4x + 1).
Fraction = ˣ⁄₍₄ₓ ₊ ₁₎
Given : Adding 2 to both numerator and denominator of the fraction results ⅓.
⁽ˣ ⁺ ²⁾⁄₍₄ₓ ₊ ₁ ₊ ₂₎ = ⅓
⁽ˣ ⁺ ²⁾⁄₍₄ₓ ₊ ₃₎ = ⅓
3(x + 2) = 1(4x + 3)
3x + 6 = 4x + 3
6 = x + 3
3 = x
4x + 1 = 4(3) + 1
= 12 + 1
= 13
Sustitute x = 3 and 4x + 1 = 13 in (1).
Fraction = ³⁄₁₃
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Example 1: Rachel rode her bike for one-fifth of a mile on Monday and two-fifths of a mile on Tuesday. How many miles did she ride altogether?
Analysis: To solve this problem, we will add two fractions with like denominators.
Solution:
Answer: Rachel rode her bike for three-fifths of a mile altogether.

Analysis: To solve this problem, we will subtract two fractions with unlike denominators.
Solution:
Answer: Stefanie swam one-third of a lap farther in the morning.

Analysis: To solve this problem, we will add three fractions with unlike denominators. Note that the first is an improper fraction.
Solution:
Answer: It took Nick three and one-fourth hours to complete his homework altogether.

Analysis: To solve this problem, we will subtract two fractions with unlike denominators.
Solution:
Answer:

Analysis: To solve this problem, we will add two mixed numbers, with the fractional parts having like denominators.
Solution:
Answer: Diego and his friends ate six pizzas in all.

Analysis: To solve this problem, we will subtract two mixed numbers, with the fractional parts having like denominators.
Solution:
Answer: The Cocozzelli family took one-half more days to drive home.

Analysis: To solve this problem, we will add two mixed numbers, with the fractional parts having unlike denominators.
Solution:
Answer: The warehouse has 21 and one-half meters of tape in all.

Analysis: To solve this problem, we will subtract two mixed numbers, with the fractional parts having unlike denominators.
Solution:
Answer: The electrician needs to cut 13 sixteenths cm of wire.

Analysis: To solve this problem, we will subtract a mixed number from a whole number.
Solution:
Answer: The carpenter needs to cut four and seven-twelfths feet of wood.
Summary: In this lesson we learned how to solve word problems involving addition and subtraction of fractions and mixed numbers. We used the following skills to solve these problems:
- Add fractions with like denominators.
- Subtract fractions with like denominators.
- Find the LCD.
- Add fractions with unlike denominators.
- Subtract fractions with unlike denominators.
- Add mixed numbers with like denominators.
- Subtract mixed numbers with like denominators.
- Add mixed numbers with unlike denominators.
- Subtract mixed numbers with unlike denominators.
Exercises
Directions: Subtract the mixed numbers in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
Note: To write the fraction three-fourths, enter 3/4 into the form. To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.
| 1. | A recipe needs 3/4 teaspoon black pepper and 1/4 red pepper. How much more black pepper is needed than red pepper for this recipe? |
| 2. | One evening, a restaurant served a total of 1/2 of a loaf of wheat bread and 7/8 of a loaf of white bread. How many loaves were served in all? |
| 3. | Robin and Kelly own neighboring cornfields. Robin harvested 4 and 3/10 acres of corn on Monday and Kelly harvested 2 and 1/10 acres. How many more acres did Robin harvest than Kelly? |
| 4. | Juanita needed 3 and 2/3 hours to take a standardized test, and Jordan needed 5 and 1/4 hours. How much more time did Jordan need than Juanita to take the test? |
| 5. | An airline agent checked in 10 and 1/3 kg of baggage for one passenger and another 8 and 5/6 kg of baggage for his travel companion. How many kilograms of luggage did the agent check in all? |