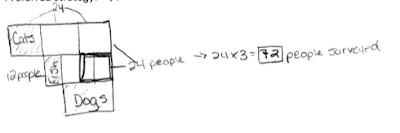It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.
The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!
How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.
Here are the seven strategies I use to help students solve word problems.
1. Read the Entire Word Problem
Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.
2. Think About the Word Problem
Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.
Here are the questions:
A. What exactly is the question?
What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.
B. What do I need in order to find the answer?
Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.
This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better
Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.
One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.
If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?
This is where students will focus in on the numbers which will be used to solve the problem.
3. Write on the Word Problem
This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:
- Circle any numbers you’ll use.
- Lightly cross out any information you don’t need.
- Underline the phrase or sentence which tells exactly what you’ll need to find.
4. Draw a Simple Picture and Label It
Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.
For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!
5. Estimate the Answer Before Solving
Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.
6. Check Your Work When Done
This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable? I want students to do more than to be number crunchers but to really think about what those numbers mean.
Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.
7. Practice Word Problems Often
Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.
When students practice word problems, often several things happen. Word problems become less scary (no, really).
They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.
If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.
This 3rd Grade Math Task Cards Bundle has word problems in almost every one of its 30 task card sets.
There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.
CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.
CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.
CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?
3rd Grade: Rounding Whole Numbers Task Cards
4th Grade: Convert Fractions and Decimals Task Cards
5th Grade: Read, Write, and Compare Decimals Task Cards
Thanks so much for stopping by!

Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
Word problems often confuse students simply because the question does not present itself in a ready-to-solve mathematical equation. You can answer even the most complex word problems, provided you understand the mathematical concepts addressed. While the degree of difficulty may change, the way to solve word problems involves a planned approach that requires identifying the problem, gathering the relevant information, creating the equation, solving and checking your work.
Identify the Problem
Begin by determining the scenario the problem wants you to solve. This might come as a question or a statement. Either way, the word problem provides you with all the information you need to solve it. Once you identify the problem, you can determine the unit of measurement for the final answer. In the following example, the question asks you to determine the total number of socks between the two sisters. The unit of measurement for this problem is pairs of socks.
«Suzy has eight pairs of red socks and six pairs of blue socks. Suzy’s brother Mark owns eight socks. If her little sister owns nine pairs of purple socks and loses two of Suzy’s pairs, how many pairs of socks do the sisters have left?»
Gather Information
Create a table, list, graph or chart that outlines the information you know, and leave blanks for any information you don’t yet know. Each word problem may require a different format, but a visual representation of the necessary information makes it easier to work with.
In the example, the question asks how many socks the sisters own together, so you can disregard the information about Mark. Also, the color of the socks doesn’t matter. This eliminates much of the information and leaves you with only the total number of socks that the sisters started with and how many the little sister lost.
Create an Equation
Translate any of the math terms into math symbols. For example, the words and phrases «sum,» «more than,» «increased» and «in addition to» all mean to add, so write in the «+» symbol over these words. Use a letter for the unknown variable, and create an algebraic equation that represents the problem.
In the example, take the total number of pairs of socks Suzy owns — eight plus six. Take the total number of pairs that her sister owns — nine. The total pairs of socks owned by both sisters is 8 + 6 + 9. Subtract the two missing pairs for a final equation of (8 + 6 + 9) — 2 = n, where n is the number of pairs of socks the sisters have left.
Solve the Problem
Using the equation, solve the problem by plugging in the values and solving for the unknown variable. Double-check your calculations along the way to prevent any mistakes. Multiply, divide and subtract in the correct order using the order of operations. Exponents and roots come first, then multiplication and division, and finally addition and subtraction.
In the example, after adding the numbers together and subtracting, you get an answer of n = 21 pairs of socks.
Verify the Answer
Check if your answer makes sense with what you know. Using common sense, estimate an answer and see if you come close to what you expected. If the answer seems absurdly large or too small, search through the problem to find where you went wrong.
In the example, you know by adding up all the numbers for the sisters that you have a maximum of 23 socks. Since the problem mentions that the little sister lost two pairs, the final answer must be less than 23. If you get a higher number, you did something wrong. Apply this logic to any word problem, regardless of the difficulty.
Word problems can be tricky for a lot of students, but they’re incredibly important to master. After all, in the real world, most math is in the form of word problems. “If one gallon of paint covers 400 square feet, and my wall measures 34 feet by 8 feet, how many gallons do I need?” “This sweater costs $135, but it’s on sale for 35% off. So how much is that?” Here are the best teacher-tested ideas for helping kids get a handle on these problems.
1. Solve word problems regularly
This might be the most important tip of all. Word problems should be part of everyday math practice, especially for older kids. Whenever possible, use word problems every time you teach a new math skill. Even better: give students a daily word problem to solve so they’ll get comfortable with the process.
Learn more: Teaching With Jennifer Findlay
2. Teach problem-solving routines
There are a LOT of strategies out there for teaching kids how to solve word problems (keep reading to see some terrific examples). The important thing to remember is that what works for one student may not work for another. So introduce a basic routine like Plan-Solve-Check that every kid can use every time. You can expand on the Plan and Solve steps in a variety of ways, but this basic 3-step process ensures kids slow down and take their time.
Learn more: Word Problems Made Easy
3. Visualize or model the problem
Encourage students to think of word problems as an actual story or scenario. Try acting the problem out if possible, and draw pictures, diagrams, or models. Learn more about this method and get free printable templates at the link.
Learn more: Math Geek Mama
4. Make sure they identify the actual question
Educator Robert Kaplinsky asked 32 eighth grade students to answer this nonsensical word problem. Only 25% of them realized they didn’t have the right information to answer the actual question; the other 75% gave a variety of numerical answers that involved adding, subtracting, or dividing the two numbers. That tells us kids really need to be trained to identify the actual question being asked before they proceed.
Learn more: Robert Kaplinsky
5. Remove the numbers
It seems counterintuitive … math without numbers? But this word problem strategy really forces kids to slow down and examine the problem itself, without focusing on numbers at first. If the numbers were removed from the sheep/shepherd problem above, students would have no choice but to slow down and read more carefully, rather than plowing ahead without thinking.
Learn more: Where the Magic Happens Teaching
6. Try the CUBES method
This is a tried-and-true method for teaching word problems, and it’s really effective for kids who are prone to working too fast and missing details. By taking the time to circle, box, and underline important information, students are more likely to find the correct answer to the question actually being asked.
Learn more: Teaching With a Mountain View
7. Show word problems the LOVE
Here’s another fun acronym for tackling word problems: LOVE. Using this method, kids Label numbers and other key info, then explain Our thinking by writing the equation as a sentence. They use Visuals or models to help plan and list any and all Equations they’ll use.
Learn more: Teaching With Jennifer Findlay
8. Consider teaching word problem key words
This is one of those methods that some teachers love and others hate. Those who like it feel it offers kids a simple tool for making sense of words and how they relate to math. Others feel it’s outdated, and prefer to teach word problems using context and situations instead (see below). You might just consider this one more trick to keep in your toolbox for students who need it.
Learn more: Book Units Teacher
9. Determine the operation for the situation
Instead of (or in addition to) key words, have kids really analyze the situation presented to determine the right operation(s) to use. Some key words, like “total,” can be pretty vague. It’s worth taking the time to dig deeper into what the problem is really asking. Get a free printable chart and learn how to use this method at the link.
Learn more: Solving Word Problems With Jennifer Findlay
10. Differentiate word problems to build skills
Sometimes students get so distracted by numbers that look big or scary that they give up right off the bat. For those cases, try working your way up to the skill at hand. For instance, instead of jumping right to subtracting 4 digit numbers, make the numbers smaller to start. Each successive problem can be a little more difficult, but kids will see they can use the same method regardless of the numbers themselves.
Learn more: Differentiating Math
11. Ensure they can justify their answers
One of the quickest ways to find mistakes is to look closely at your answer and ensure it makes sense. If students can explain how they came to their conclusion, they’re much more likely to get the answer right. That’s why teachers have been asking students to “show their work” for decades now.
Learn more: Madly Learning
12. Write the answer in a sentence
When you think about it, this one makes so much sense. Word problems are presented in complete sentences, so the answers should be too. This helps students make certain they’re actually answering the question being asked… part of justifying their answer.
Learn more: Multi-Step Word Problems
13. Add rigor to your word problems
A smart way to help kids conquer word problems is to, well… give them better problems to conquer. A rich math word problem is accessible and feels real to students, like something that matters. It should allow for different ways to solve it and be open for discussion. A series of problems should be varied, using different operations and situations when possible, and even include multiple steps. Visit both of the links below for excellent tips on adding rigor to your math word problems.
Learn more: The Routty Math Teacher and Alyssa Teaches
14. Use a problem-solving rounds activity.
Put all those word problem strategies and skills together with this whole-class activity. Start by reading the problem as a group and sharing important information. Then, have students work with a partner to plan how they’ll solve it. In round three, kids use those plans to solve the problem individually. Finally, they share their answer and methods with their partner and the class. Be sure to recognize and respect all problem-solving strategies that lead to the correct answer.
Learn more: Teacher Trap
Like these word problem tips and tricks? Learn more about Why It’s Important to Honor All Math Strategies.
Plus, 60+ Awesome Websites For Teaching and Learning Math.

3-Step System
1. Read: Read the problem and decide what the question is asking.
- Read the problem 2 times or more.
- Underline or circle key words, phrases, and numbers. Draw a line through irrelevant information.
2. Plan: Think about what the story is asking you to do. What information are you given, and what do you need to find out?
- Draw a picture.
- Circle or underline key words. (Use highlighters or crayons to color-code key numbers and phrases.)
- Write out the question in your own words.
3. Solve: What strategy could you use to find the missing information: addition, subtraction, multiplication, or division?
- Write a number sentence and solve.
- Use counters.
- Create charts.
Check your work by explaining your reasoning. Does your answer make sense?
Download this free strategy checklist from Math Fundamentals to help your child solve word problems.
Different Strategies to Solve Word Problems
Everyone learns in a different way. What makes sense to one individual often isn’t the easiest option for another. Incorporating different strategies to solve word problems can help your child discover what strategy works best for him or her. A few tips to use are:
1. Circle numbers in a story and underline key phrases.
Color coding is a fun method to incorporate to help children decide what operation the question is asking for. Assign a color to each operation and highlight the phrase that identifies it. For example, red links to addition and blue links to subtraction.
2. Incorporate a key word list.
Key word lists are best used for teaching younger children how to solve word problems. As math curriculum advances, children should not be dependent on a key word list to solve a problem. The questions get trickier.
Addition
In all
Together
Total
Altogether
Combine
Sum
Join
Subtraction
Difference
Fewer
How many more
How much more
Left
Remain
Less
3. Visuals
If your child is a visual learner, drawing a picture or using counters can help him or her understand what the problem is asking. Use number lines, charts, or counters or draw a picture.
4. Write your own word problem.
Knowing what is needed to write a word problem is the first step in identifying key words to solve a story. Take turns writing your own word problems with your child and exchange them to solve.
5. Stay organized.
It is important to write clearly and keep work space neat so children can read and follow their own computations. Many children need a separate piece of paper to allow them enough space to solve and understand their answer. Graphing paper is a great option to help students record neat work.
Download this free sample word problem from Math Fundamentals, grade 1.
How to solve a two-step word problem
In a two-step word problem children are being asking to solve two related equations. These can get tricky for children to understand when they transition from one-step to two-step problems. Help your child understand his or her relationships within two-step word problems with these strategies:
1. Circle important information.
Circle numbers and important phrases that ask questions. The number sentences needed to solve these equations are hidden in those asking questions. Identify the first and second questions needed to solve.
2. Distinguish the two parts of the problem.
First identify the first step of the first part of the word problem. Write a number sentence and solve.
3. Use the answer from the first-step solution to the whole problem.
Use the answer from the first question to help you solve the next equation. What operation does the second question require?
Check your work by explaining your reasoning. What was the question answered? Is the answer reasonable for the question being asked?
Download this free sample two-strategy word problem from Math Fundamentals, grade 2
Download this free sample multi-strategy word problem from Math Fundamentals, grade 4
Evan-Moor’s Math Fundamentals is a great resource for training students how to solve word problems in 3 simple steps. It provides step-by-step directions for solving questions and guides children with helpful visuals and key phrases.
Check out Daily Word Problems for consistent practice solving word problems.
For more fun math tips and strategies check out our Math- Ideas, Activities and Lessons Pinterest Board.
Save these tips and Pin It now!


A proven step-by-step method for solving word problems is actually quite simple.
- Read the problem out loud to yourself
- Draw a Picture
- Think “What do I need to find?”
- List what is given
- Find the key words
- Solve
- Check your work
Let’s put these steps into practice. Consider the word problem below.
Example: Kevin loves to read. He likes many different types of books. He has 3 large bookcases that each have 9 shelves on it all filled with his books. If each shelf can hold 16 books, how many books does Kevin have?
Read the Problem Out Loud
Kids have a tendency to rush through every problem. This is due to time limits on classwork and tests. If your child does not know what the problem is asking, then they cannot solve the problem. When your child reads the problem aloud, they are saying and hearing the problem. They can form a clearer picture in their head of the problem and they are more prepared to solve it.
Draw a Picture
Students need to visualize a problem to understand it, especially younger students. As they get older, they can start to visualize in their head but at a young age they should be drawing out a picture that explains to them what the problem is about. The picture should take into account all of the aspects of the problem.
Ask “What Do I Need to Find?”
Some word problems are straight forward with their questions. It can be as simple as “Molly has two dogs, Jason has three. How many dogs do Molly and Jason have together?” This one, however, we have to think about. There is more than one step for this problem. We first have to find how many shelves he has and then find out how many books are on all of the shelves to know how many books he has altogether.
List What is Given
It is always good to start with listing the things you know. If you try to solve the problem without knowing what tools you are given to solve it, you will not get the right answer. Think about the last time you tried to fill in the blanks or assume an answer without knowing all the facts. Your outcome probably did not turn out well. It is for this reason that we need to list what is given before any problem. The student should write it down at the top or side of the scrap paper so they always have it as a reference when doing the problem. For this problem, my list of what is given would be:
- Kevin has 3 book cases
- Each book case has 9 shelves
- Each shelve holds 16 books
Find the Key Words
Every word problem has key words to look out for that tell you what operation to do. As your child gets more practice with word problems, finding the key words will get easier. Here are some of the most popular key words for word problems:
|
Operation |
Key Words |
|
Addition |
“all together”, “both”, “combined”, “total”* “additional” |
|
Subtraction |
“decrease”, “difference”, “fewer”, “how many more”, “how much greater”, “have left”, “remain” |
|
Multiplication |
“doubled/tripled”, “each” “equal groups” “in al”, “of”, “per” |
|
Division |
“equal parts” “split between” “separated”, “percent” |
*this can be a key word for addition and multiplication
Solve
According to the chart above, we should use multiplication. First, we should multiply the number of shelves per case by the number of cases. 9 shelves per case x 3 book cases = 27 shelves. Next, we must multiply the number of books per shelf by the number of shelves. 27 shelves x 16 books per shelf = 432 books.
Check your answer
The last step of course is to check your work by seeing if the answer fits the question asked. Mathematically, we can check our work by doing the opposite of whatever operation we used. So for this problem, we can divide 432 by 16 and we will get 27, then divide 27 by 3 and get 9.
As challenging as word problems can be for children, having them follow these simple 7 steps will help them better understand word problems and see beyond the complicated words. Soon enough, world problems will not be so troubling for them after all and they will grow to become more confident, eager learners.
1
Topics:
Math,
Child Education,
Math Skills,
Parenting Tips,
Child Anxiety,
Math Anxiety,
Word Problems
Learning Outcomes
- Approach word problems with a positive attitude
- Use a problem solving strategy for word problems
- Translate more complex word problems into algebraic expressions and equations
Approach Word Problems with a Positive Attitude
The world is full of word problems. How much money do I need to fill the car with gas? How much should I tip the server at a restaurant? How many socks should I pack for vacation? How big a turkey do I need to buy for Thanksgiving dinner, and what time do I need to put it in the oven? If my sister and I buy our mother a present, how much will each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student in the cartoon below?
Negative thoughts about word problems can be barriers to success.
When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts, like the student in the cartoon below. Read the positive thoughts and say them out loud.
When it comes to word problems, a positive attitude is a big step toward success.
If we take control and believe we can be successful, we will be able to master word problems.
Think of something that you can do now but couldn’t do three years ago. Whether it’s driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill. Word problems are no different. Even if you have struggled with word problems in the past, you have acquired many new math skills that will help you succeed now!
Use a Problem-Solving Strategy for Word Problems
In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. Since then, you’ve increased your math vocabulary as you learned about more algebraic procedures, and you’ve had more practice translating from words into algebra.
You have also translated word sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. You had to restate the situation in one sentence, assign a variable, and then write an equation to solve. This method works as long as the situation is familiar to you and the math is not too complicated.
Now we’ll develop a strategy you can use to solve any word problem. This strategy will help you become successful with word problems. We’ll demonstrate the strategy as we solve the following problem.
Example
Pete bought a shirt on sale for $[latex]18[/latex], which is one-half the original price. What was the original price of the shirt?
Solution:
Step 1. Read the problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the Internet.
- In this problem, do you understand what is being discussed? Do you understand every word?
Step 2. Identify what you are looking for. It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the shirt” tell you what you are looking for: the original price of the shirt.
Step 3. Name what you are looking for. Choose a variable to represent that quantity. You can use any letter for the variable, but it may help to choose one that helps you remember what it represents.
- Let [latex]p=[/latex] the original price of the shirt
Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation.
Step 5. Solve the equation using good algebra techniques. Even if you know the answer right away, using algebra will better prepare you to solve problems that do not have obvious answers.
| Write the equation. | [latex]18=Largefrac{1}{2}p[/latex] |
| Multiply both sides by 2. | [latex]color{red}{2}cdot18=color{red}{2}cdotLargefrac{1}{2}normalsize p[/latex] |
| Simplify. | [latex]36=p[/latex] |
Step 6. Check the answer in the problem and make sure it makes sense.
- We found that [latex]p=36[/latex], which means the original price was [latex]text{$36}[/latex]. Does [latex]text{$36}[/latex] make sense in the problem? Yes, because [latex]18[/latex] is one-half of [latex]36[/latex], and the shirt was on sale at half the original price.
Step 7. Answer the question with a complete sentence.
- The problem asked “What was the original price of the shirt?” The answer to the question is: “The original price of the shirt was [latex]text{$36}[/latex].”
If this were a homework exercise, our work might look like this:
We list the steps we took to solve the previous example.
Problem-Solving Strategy
- Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the internet.
- Identify what you are looking for. Determine the constants and variables in the problem. A constant is a number in the problem that is not going to change. A variable is a number that you don’t yet know its value.
- Name what you are looking for. Choose a letter to represent that quantity.
- Translate words into algebraic expressions and equations. Write an equation to represent the problem. It may be helpful to first restate the problem in one sentence before translating.
- Solve the equation using good algebra techniques.
- Check the answer in the problem. Make sure it makes sense.
- Answer the question with a complete sentence.
Translate word problems into expressions
One of the first steps to solving word problems is converting an English sentence into a mathematical sentence. In the table below, words or phrases commonly associated with mathematical operators are categorized. Word problems often contain these or similar words, so it’s good to see what mathematical operators are associated with them.
| Addition [latex]+[/latex] | Subtraction [latex]-[/latex] | Multiplication [latex]times[/latex] | Variable ? | Equals [latex]=[/latex] |
|---|---|---|---|---|
| More than | Less than | Double | A number | Is |
| Together | In the past | Product | Often, a value for which no information is given. | The same as |
| Sum | Slower than | times | After how many hours? | |
| Total | The remainder of | How much will it cost? | ||
| In the future | Difference | |||
| Faster than |
Some examples follow:
- “[latex]xtext{ is }5[/latex]” becomes [latex]x=5[/latex]
- “Three more than a number” becomes [latex]x+3[/latex]
- “Four less than a number” becomes [latex]x-4[/latex]
- “Double the cost” becomes [latex]2cdottext{ cost }[/latex]
- “Groceries and gas together for the week cost $250” means [latex]text{ groceries }+text{ gas }=250[/latex]
- “The difference of [latex]9[/latex] and a number” becomes [latex]9-x[/latex]. Notice how [latex]9[/latex] is first in the sentence and the expression.
Let’s practice translating a few more English phrases into algebraic expressions.
Example
Translate the table into algebraic expressions:
| some number | the sum of the number and [latex]3[/latex] | twice the sum of the number and [latex]3[/latex] |
| a length | double the length | double the length, decreased by [latex]6[/latex] |
| a cost | the difference of the cost and [latex]20[/latex] | [latex]2[/latex] times the difference of the cost and [latex]20[/latex] |
| some quantity | the difference of [latex]5[/latex] and the quantity | the difference of [latex]5[/latex] and the quantity, divided by [latex]2[/latex] |
| an amount of time | triple the amount of time | triple the amount of time, increased by [latex]5[/latex] |
| a distance | the sum of [latex]-4[/latex] and the distance | the sum of [latex]-4[/latex] and the twice the distance |
In this example video, we show how to translate more words into mathematical expressions.
For another review of how to translate algebraic statements into words, watch the following video.
The power of algebra is how it can help you model real situations in order to answer questions about them. Let’s use this approach with another example.
Example
Yash brought apples and bananas to a picnic. The number of apples was three more than twice the number of bananas. Yash brought [latex]11[/latex] apples to the picnic. How many bananas did he bring?
Example
Twenty-eight less than five times a certain number is [latex]232[/latex]. What is the number?
In the video that follows, we show another example of how to translate a sentence into a mathematical expression using a problem solving method.
In the next example, we will apply our Problem-Solving Strategy to applications of percent.
example
Nga’s car insurance premium increased by [latex]text{$60}[/latex], which was [latex]text{8%}[/latex] of the original cost. What was the original cost of the premium?
Contribute!
Did you have an idea for improving this content? We’d love your input.
Improve this pageLearn More
-by Kevin Sonico
“Show me your ‘thinking’.” “Explain your process.” These are two statements that are often used to encourage students to communicate their strategies in solving a word problem. In my experience, what is often produced, written, and described are algorithms, equations, and other symbolic representations. Rarely have students submitted strategies that comprised of visual methods. Because of this, I set out to see if there is an effect of explicitly teaching a visual strategy, namely the model method, in helping students solve problems. Through the use of models, students worked on word problems around the concepts of fractions, decimals, percent, and ratios. Described here are three examples of the many problems posed in class.
In addition to helping students solve word problems through the use of models, I hoped to equip students with a tool that will help them develop their visualization skills. “Students are expected to develop visualization skills to assist in processing information, making connections, and solving problems.” (The Alberta K-9 Mathematics Program of Studies with Achievement Indicators, 2007) The curriculum describes visualization as one of the “critical components that students must encounter in a mathematics program in order to achieve the goals of mathematics education and embrace lifelong learning in mathematics.” Furthermore, this document explicitly outlines four specific outcomes of the Math 8 curriculum that expect students to exhibit their understanding in concrete, pictorial, and symbolic ways (Appendix A).
The model method is sometimes referred to as the Singapore bar model method as students in Singapore are taught how to use bar models in solving word problems. The benefits of teaching this visual strategy have been noted. Hoven and Garelick (2007) stated that “[i]n Singapore, where 4th and 8th grade students consistently come in first on international math exams, students learn how to solve problems using the bar model technique.” Hong, K.T., et al. (2009) wrote, “through the construction of a pictorial model…, students gain better understanding of the problem and develop their abilities in mathematical thinking and problem solving.”
The Transportation Problem
The bar model method is systematic and formulaic; it provides a framework for students to follow when solving word problems. Students draw bars (hence the name) to represent an unknown quantity. They then divide the bars into parts. Within and around the bars, students write labels and other information from the given problem. The set-up of the bars and the labels act as a “picture” of how students visualize the numbers and the relationship between and among the given information. The Transportation problem was one of the first problems that students solved after having been introduced to the model method. (Challenging Word Problems, 2011)
One-third of the students go to school by bus. One-fourth of the remaining students go to school by car. The rest of them either ride a bike or walk to school. If 90 students go to school by car, how many students are there in the school?
To illustrate how the model method works, student exemplars (Figure 1) from the Transportation problem are included below.
Figure 1 A, B, C, and D: Variations of the bar model method. A and B: Both students used similar labeling techniques. C: Student shows intricate knowledge of equivalent fractions and visual division of fractions. D: Student depicts the use of a number line which is similar to the bar models shown in Figures 1A and B.
A.
B.
C.
D.
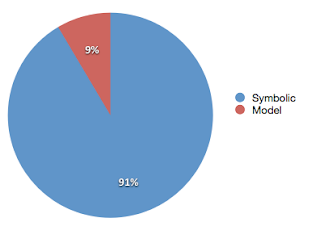
Although it is a set of systematic procedures, students created varying forms of the models to illustrate their understanding of the problem (Figure 1). Based on a survey of all of the strategies employed by students, over half of them chose to solve it in a symbolic manner (Figure 2), that is through the use of numbers, symbols, and algorithms (Figure 3). The second most common strategy was the use models. Interestingly, when students were asked to use a verification strategy, that is, to use another tool to check their solutions, the model method was the most popular, followed by symbolic strategies.
Figure 2: A breakdown of the main and verification strategies used by students in solving the Transportation problem.
Figure 3: Two examples of a symbolic way of solving of the Transportation problem.
After having been introduced to the model method, I expected most students to utilise this strategy in their solution. The results, however, indicated otherwise; most students solved it through symbolic means. This is perhaps due to students’ familiarity and comfort in using symbols and algorithms. When performing a task with a tool, most of us will probably reach for the one with which we are most familiar. We have a preferred way of doing things. This is in no way different from the results of the survey. Students have a preferred method of solving — not necessarily all word problems, but this word problem in particular. The overall survey results also point to the explanation that even though a new skill or strategy has been introduced, it does not necessarily mean that students will readily employ it or easily adopt it in their practice. This leads me to wonder: if students were taught the model method in earlier grades, how familiar would they be by Grade 8 and how frequently would they choose it to solve word problems? Conversely, if students were not exposed to the model method at all, what other tools or strategies would they have employed to verify their solutions? Although a small portion of students were unable to come up with an alternate strategy, most students provided a verification strategy that utilised the model method. With increased exposure to, time with, and practice in using the model method, I expect students to become even more comfortable with it.
The Pet Problem
We typically hold a “congress” after solving word problems. As described by Fosnot & Dolk. (2002), a math congress allows students to share, discuss, and defend individual strategies. Through rich discussions, students can pull common threads among the many methods, and can start to appreciate the interconnectedness among the concepts and different strategies. For the Transportation problem, however, I opted not to conduct the congress. I wanted to see how the students will solve a modified version of the problem, called the Pet problem, after more months of exposure in using models. I also wanted to see if there was an effect or a shift in the number of students who will use the model method as a main strategy. Sharing our strategies through the congress would have also influenced their strategies for the Pet problem. The Pet problem read:
One-third of the people surveyed prefer cats as pets. One-fourth of the remaining participants of the survey preferred fish. The rest of the people surveyed preferred dogs. If 12 people preferred fish, how many people in total were surveyed?
Figure 4: A breakdown of the main and verification strategies used by students in solving the
Pet problem.
After months of using the model method, the results were as I expected them to be (Figure 4) . It indicated that most students used the model method as their main strategy and some form of symbolic method as a verification strategy. This result was the opposite of the results for the earlier Transportation problem, where most students solved it through symbolic means. Students perhaps became more comfortable in using the model method. Perhaps some saw the merit in using and drawing bars over using an algorithm. Or perhaps they found it a better fitting tool for the problem. A student reflected that using models was “easier for [him] to process the question”, and it “helped visualize the problem”. In one instance, a student who used the model method to verify his answer saw that his original solution was incorrect. He wrote, “I think my algorithm was inaccurate because I couldn’t model what the question asks” (Figure 7). In word problems like the Pet or Transportation problem, the abundance of numerical information for students to consider can be overwhelming or confusing. The strength of using the bar model is in its flexibility and its ability to allow for students to visually organize the information in a way that may make more sense to them.
Figure 5: Two examples of students’ solution to the Pet problem using the model method.
After having given the two problems to students, I also wanted to compare the proportion of students who answered the problems correctly. Months earlier, I was not pleased with the percentage of students who answered the Transportation problem incorrectly (Figure 8). About half of them committed errors like using equations and algorithms that were not mathematically logical. In contrast, most students answered the Pet problem correctly. Although a strong, positive correlation between the use of bar models and more accurate answers cannot be made, it is worth suggesting that perhaps it is due to students’ increased confidence in using the bar models that have allowed them to better understand the problem. It is also possible that they have improved their grasp of fraction concepts . For whatever probable reasons there are for this shift, students were readily reaching for the model method as a tool. They saw it as a good fit with the word problem. This is noteworthy because the Pet problem is fundamentally identical to the earlier Transportation problem, which was mainly solved symbolically.
Figure 6: A verification strategy which employed the multiplication of fractions algorithm.
Figure 7: Two strategies used by a student, where the model method was used in verifying the initial solution to the Pet problem. The student reflected how his preferred strategy (through symbolic method) was incorrect.
Figure 8: Percentage of students who incorrectly answered the Transportation and Pet problems.
The Interest Problem
The Transportation and Pet problems were similar in wording and in the relationships among the numbers. Both problems also contained data that students expected to “plug” into some formula or to use in their modeling. The Interest problem, on the other hand, is different in that it is less verbose. Taken from Nrich.Maths.org, the Interest problem asked, “If a sum that is invested gains 10% each year, how long will it be before it has doubled its value?” Posing this word problem encouraged students to make conjectures and “tinker” with numbers. These mathematical skills and habits of mind make the Interest problem a lot richer and more challenging in my opinion. Because the question did not have the degree of detail or data like the Pet and Transportation problems, students who have relied heavily on given data may have found this a bit more challenging. A student commented that this word problem was “more difficult because [he] didn’t have a total number to work with.” Most students, however, managed to choose a number, such as $1, $10, or $100, as a figure to use in their calculations and solutions.
Figure 9: A breakdown of the strategies used by students in solving the Interest problem.
According to the survey of student work, the overwhelming majority of students (approximately 90%) utilised symbolic methods while the rest used models to solve it (Figure 9). Students probably chose to solve it symbollically as they saw the ease and efficiency of using numbers and symbols over drawing models for this particular problem. “Calculating with number sense means that one should look at the numbers first and then decide on a strategy that is fitting — and efficient.” ( Fosnot et al., 2007) A student commented that “using the unit value and a formula worked the best with [the Interest] problem; [He] wasn’t sure how [he] would make a visual representation.” Another student reflected on the restriction of the model method when working with decimals. This is an interesting comment because decimals are essentially fractions. They both signify parts of a whole. Even though the model method was not used by most, a student wrote, “I like visuals because they make me write out what I know. I may not use a complete visual method but it helps me with stating what I know without rewriting the question.”
Although most students chose to solve the Interest problem symbolically, there was not one single algorithm or formula that was utilised by all (Figure 10). Some students preferred to calculate the “unit value”, that is, the 1% value of their sum, then multiplied that by 10 to determine the 10% value (Figure 11A). Others chose to divide the sum by 10 rather than 1, as they saw that 10 is a factor of 100, thereby bypassing the multiplication step performed when calculating the “unit value” (Figure 10B). Then there were others who multiplied their sum by 1.1 to signify 110% growth (Figure 10C). Regardless of the chosen calculation method, it is evident that students did not see the benefit of using models for this problem. An argument, however, can be made that using the model method may have influenced students to represent their understanding symbolically (Hoven et al., 2007). Students may have made the leap from visual to symbolic thinking. For instance, finding the unit value — a strategy that was used symbolically — is a hallmark step used in the model method. In using bars to represent units, students would calculate the value of a bar by dividing a sum by the number of bars. In essence, that is similar to finding the unit value.
Figure 10: A breakdown of the symbolic strategies employed by students in solving the Interest problem.
Figure 11: Exemplars of students’ symbolic strategies in solving the Interest problem. A: student finding the “unit value” then multiplying by 10 to get 10% of sum; B: student using 10% by dividing it by 10; C: student multiplies sum by 1.1 to represent 110% growth. D: model method used to demonstrate student’s understanding of the problem.
A.
C.
D.
Verifying
When we urge students to “check” their work, we expect them to critically look at their processes and evaluate the effectiveness of their methods and the accuracy of their work. We do not expect them to passively read through their solutions. Some students, however, may go through the verification process by simply doing that. “Looking for errors by repeating exactly what has been done is a poor way to check.” (Mason, Burton, & Stacey, 1985). In addition, students sometimes verify their solutions by working backwards. This is not the most effective way to verify an answer to a word problem as students are merely performing the inverse operations of their original algorithms. When the same data (including the solution) is entered into the inverse algorithm, one will mathematically arrive at the original number. For example, if 1 + 1 = 2; then naturally 2 — 1 = 1. This is a flawed form of verification as all it is checking for is the arithmetic — not the mathematical logic and numerical connections behind the data.
For some students, it can be a struggle to think of an alternate method of solving the problem. When students are encouraged to provide another strategy, we are challenging them to see the problem through a different lens. The model method might provide them with a different way of viewing and thinking through a word problem. Before being introduced to drawing bars and using models, some might not even have thought of using a visual strategy in solving and verifying their solutions. One student, who used a symbolic method as his first strategy to solve the Transportation problem and the model method as the second strategy, wrote,
I find the 2nd strategy easier, but if you know what your [sic] doing, the first is faster. Strategy 1 is good because it is fast and efficient but the 2nd is good to check your work.
This sums up a common sentiment among students who have grasped the abstract nature of numbers and have decided on an efficient algorithm to solve it. The challenge with algorithms is that it is difficult to gauge whether or not the student has made sense of the numbers unless further questioning or probing is done. With the model method, we can at least see how students interpret the data as they relate to each other. For students who have a difficult time verbalizing or describing the intricate and complicated calculations that they performed mentally, the model method may also provide them with a way to communicate their complex calculations.
For students who struggled with coming up with their main strategy, in other words, those who are left in the “stuck” phase, they may have benefited from being introduced to the model method. Although it is “natural” to be in the “stuck” phase (Mason et al., 1985), using the model method might allow a student to answer the question “So now what?” after reading a word problem. In the Pet problem, 8% of students, who used the model method as their main strategy, were unable to come up with a verification strategy. Without using the model method, this 8% of students would have been left in the “stuck” phase and not have answered the problem altogether.
Conclusion
The model method can look formulaic and prescriptive, in that it is a generalized procedure, comprised of labeling bars and identifying the given data and missing information. An argument can be made that this is no different from memorizing the algorithm to short or long division, for instance. I do not disagree with the notion that it can be similar because of the procedural nature of the method. However, what distinguishes the model method from other forms of algorithm is that it provides a framework that makes sense to students. Students who have difficulty understanding the logic behind the steps of an algorithm may have an easier time understanding the practice of drawing bars. When reflecting on the model method, a student commented that it was “helpful in visualizing the questions and help[ed] [him] to understand why the formulas work not just how they work.” (Appendix D: Reflections on Model Method)
Figure 12 Students’ responses to the question, “How was the model method helpful in solving and understand word problems
When students were asked about how helpful the model method was in understanding and solving word problems, over half of the students found it either helpful or very helpful; while 33% of students found it only somewhat helpful, and 5% found it not helpful at all (Figure 11). A student commented,
[t]he bar models helped me to visually represent numbers in my head. They are a good method for checking you (sic) work or when you are stuck. It also provided proof that the algorithm method is correct.
Another student wrote,
Models can show you things a (sic) algorithm cannot. A model can show you the magnitude, and can also visually prove to you if something is right or wrong. You can look at it and say “hmm, that doesn’t look right”. A model can also put things into perspective. A (sic) algorithm gives you an answer. A model SHOWS you the answer…
When students struggle with a word problem, the challenge at times is not knowing where to start. Whether we have explicitly taught an algorithm or implicitly modeled a strategy in our practice, we have equipped students in the past with word problem solving strategies like underlining important texts or listing the “knowns”. We have recited “think alouds” — questions that we want students to be asking themselves when thinking through word problems. For one student, the model method helps to “un-jumble” her thoughts. The benefit to using visual models is that it allows for students to start somewhere — to start drawing the situation, to start making sense of the numbers. For others who are able to process the numbers through symbolic means, the model method provides them with a verification strategy. The true strength of the model may also lie in its ability to help students make that connection, a bridge, from concrete to abstract, and vice versa.
The intent of this action research was not to eradicate the use or minimize the power of symbolic representation. . “[The] beauty [of an algorithm] was that they were generalized procedures that could be used as efficient computation strategies.” (Fosnot et al., 2002)
Algorithms…do have an important place in mathematics. After students have a deep understanding of number relationships and operations and have developed a repertoire of computation strategies, they may find it interesting to investigate why the traditional computation algorithms work
Therefore, the power of any symbolic representation including algorithms lies in students’ understanding of how it came about, its derivation. Equally powerful is when a student produces a formula or an algorithm that makes mathematical sense to solve a problem.
A common attitude that was prevalent during this action research was hesitation or resistance. Some students found it tedious and time-consuming to draw a pictorial representation of a concept that can easily be represented with symbols and numbers. “Why do we have to draw this if we can show it with numbers?” or “Why do we have to draw in Grade 8?” To this, I simply replied with an analogy. Think of the model method as a pair of scissors. It is a tool for cutting things. In the world of cutting tools, there are plenty of them: handsaw, jigsaw, bandsaw, paring knife, serrated knife, razor blade, etc. The more tools one owns, the better the choices one has for the job. Learning how to use models adds another tool that one can use.
Some may point out that the method of emphasizing the use of one visual strategy is contrary to the inquiry-based model or problem-based facet of our practice. However, when the focus shifts to the importance placed on having the ability to represent a problem from different perspectives, it is accomplishing that facet of inquiry where students are encouraged to look at multiple points of view.
There are several possible extensions of this action research. First, it might be of interest to see how students will use and adopt the model method in higher grades where there will be increasing demands to symbolically represent their thoughts. Will they abandon the model method or will they use it to help them unpack the complexities of more advanced concepts? A student commented,
the bar model method was very helpful in certain circumstances. However, I was not able to use it in as many situations as I would have liked to. Many times, I didn’t know how the bar model method would have fit into the question, and I just ended up doing the algorithm or doing it in my head. I thought it was made for basic problems, not for some of the problems we had to do. In later years, I will have more challenging problems in math, and I don’t believe I will be able to use the bar model method very often.
As it is closely tied to the model method, observing how students develop their algebraic reasoning would be interesting (Hoven et al., 2007). Second, it might be noteworthy to see how earlier grades can incorporate the model method in their curricula. The resistance and hesitation to drawing models in later years might be mitigated if/when we start/continue to encourage students to visually represent their “thinking”. Third, the impact of technology in demonstrating the model method could be explored. Although students have found it to be effective, some commented on the inefficiency and time-consuming nature of the drawing models. Perhaps apps or online manipulative sites such as the National Library of Virtual Manipulatives could be developed and evaluated for efficiency and effectiveness in helping students develop their skills in solving word problems and in visualizing abstract concepts.
References
Alberta Education, The Alberta K-9 mathematics program of studies with achievement indicators (2007). Alberta, Canada.
Challenging word problems (2011). Singapore: Marshall Cavendish Education.
Fosnot, C. T., & Dolk, M. (2002). Young mathematicians at work, constructing fractions, decimals, and percents. Heinemann Educational Books.
Habits of mind. (2010, September 3). Retrieved from http://www.withoutgeometry.com/2010/09/habits-of-mind.html
Hoven, J. & Garelick, B. (2007). Singapore math: simple or complex?. Educational Leadership (vol. 65 no 3).
Kho, T. H., Yeo, S. M., & Lim, J. (2009). The Singapore model method for learning mathematics. Singapore: Panpac Education.
Mason, J., Burton, L., & Stacey, K. (1985). Thinking mathematically. Essex, UK: Addison-Wesley Publisher Limited.
Resources
Clark, A. (2010). Singapore math: a visual approach to word problems. Houghton Mifflin Harcourt.
https://sites.google.com/a/cusdschools.org/ratio-using-the-bar-model/home/ratio-and-fraction
Habits of mind. (2010, september 3). Retrieved from http://www.withoutgeometry.com/2010/09/habits-of-mind.html
Challenging word problems (2011). Singapore: Marshall Cavendish Education.
Har, Y.B. Bar Modeling: A Problem-solving Tool; from Research to Practice. Singapore: Marshall Cavendish Int Pte Ltd.
Kho, T. H., Yeo, S. M., & Lim, J. (2009). The Singapore model method for learning mathematics. Singapore: Panpac Education.
Appendix A
Specific outcomes that outline expectations for students to demonstrate their understanding of a concept concretely, pictorially, and symbolically. Taken from the Math 8 Program of Studies, The Alberta K-9 Mathematics Program of Studies with Achievement Indicators (2007).
Strand: Number
It is expected that students will:
- Demonstrate an understanding of perfect squares and square roots, concretely, pictorially and symbolically (limited to whole numbers).
- Demonstrate an understanding of multiplying and dividing positive fractions and mixed numbers, concretely, pictorially and symbolically.
- Demonstrate an understanding of multiplication and division of integers, concretely, pictorially and symbolically.
Strand: Patterns and Relations
It is expected that students will:
- Model and solve problems, concretely, pictorially and symbolically, using linear equations…
Appendix B
Accuracy of Solutions to the Interest Problem
An interesting result from the Interest problem was that over half of the students answered the question incorrectly (Fig. 13). And most of these errors came from assuming that the amount or value of 10% is consistent from year to year. Because of this assumption, they predicted for the money to double in 10 years (Fig. 14). Whether or not the model method could have prevented this error is unknown. A source for this mistake may very well be in the wording of the problem. Because it does not specify that 10% would be added to the previous year’s amount, most students who incorrectly answered it assumed that it would be added to the original amount (Fig. 14). In this way, their answers are accurate. The concept of simple interest and compound interest were not explored before this problem was introduced so the notion of earning “interest on interest” was probably not even considered by the students.
Figure 13: Percentage of correct and incorrect answers to the Interest problem, and percentage of students who made an error in assuming that 10% value year to year is consistent.
Figure 14: Student misinterpretation of the Interest problem. The majority of errors were committed with this assumption, that is, 10% was added to the original invested sum, rather than 10% to the previous year’s sum.
Appendix C: Comments of Students Who Found the Model Method Helpful
Appendix D: Comments of students who saw little to no help in using the model method in solving word problems
The techniques and methods we apply to solve word problems in math will vary from problem to problem.
The techniques and methods we apply to solve a word problem in a particular topic in math will not work for another word problem found in some other topic.
For example, the methods we apply to solve the word problems in algebra will not work for the word problems in trigonometry.
Because, in algebra, we will solve most of the problems without any diagram. But, in trigonometry, for each word problem, we have to draw a diagram. Without diagram, always it is bit difficult to solve word problems in trigonometry.
Even though we have different techniques to solve word problems in different topics of math, let us see the steps which are most commonly used.
The following steps would be useful to solve word problems in Mathematics.
Step 1 :
Understanding the question is more important than any other thing. That is, always it is very important to understand the information given in the question rather than solving.
Step 2 :
If it is possible, we have to split the given information. Because, when we split the given information in to parts, we can understand them easily.
Step 3 :
Once we understand the given information clearly, solving the word problem would not be a challenging work.
Step 4 :
When we try to solve the word problems, we have to introduce «x» or «y» or some other alphabet for unknown value (=answer for our question). Finally we have to get value for the alphabet which was introduced for the unknown value.
Step 5 :
If it is required, we have to draw picture for the given information. Drawing picture for the given information will give us a clear understanding about the question.
Step 6 :
Using the alphabet introduced for unknown value, we have to translate the English statement (information) given in the question as mathematical equation.
In translation, we have to translate the following English words as the corresponding mathematical symbols.
of —-> x (multiplication)
am, is, are, was, were, will be, would be —-> = (equal)
Step 7 :
Once we have translated the English Statement (information) given in the question as mathematical equation correctly, 90% of the work will be over. The remaining 10% is just getting the answer. That is solving for the unknown.
Example :
The age of a man is three times the sum of the ages of his two sons and 5 years hence his age will be double the sum of their ages. Find the present age of the man.
Answer :
Step 1 :
Let us understand the given information. There are two information given in the question.
1. The age of a man is three times the sum of the ages of his two sons. (At present)
2. After 5 years, his age would be double the sum of their ages. (After 5 years)
Step 2 :
Target of the question :
Present age of the man = ?
Step 3 :
Introduce required variables for the information given in the question.
Let x be the present age of the man.
Let y be the sum of present ages of two sons.
Clearly, the value of x to be found.
Because that is the target of the question.
Step 4 :
Translate the given information as mathematical equation using x and y.
First information :
The age of a man is three times the sum of the ages of his two sons.
Translation :
The Age of a man —-> x
is —-> =
Three times sum of the ages of his two sons —-> 3y
Equation related to the first information using x and y is
x = 3y —-(1)
Second Information :
After 5 years, his age would be double the sum of their ages.
Translation :
Age of the man after 5 years —-> (x + 5)
Sum of the ages of his two sons after 5 years is
y + 5 + 5 = y + 10
(Because there are two sons, 5 is added twice)
Double the sum of ages of two sons —-> 2(y + 10)
would be —-> =
Equations related to the second information using x and y is
x + 5 = 2(y + 10) —-(2)
Step 5 :
Solve equations (1) & (2).
From (1), substitute 3y for x in (2).
3y + 5 = 2(y + 10)
3y + 5 = 2y + 20
y = 15
Substitute 15 for y in (1).
x = 3(15)
x = 45
So, the present age of the man is 45 years.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com