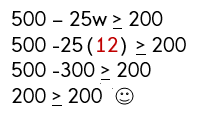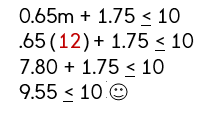Related Pages
Math Word Problems
Singapore Math Word Problems
More Algebra Lessons
Here are some examples of mixed operations word problems. These problems are slightly more challenging,
but they also illustrate how helpful the block diagrams can be. The block diagrams or tape diagrams
(Common Core) can be used to help solve word problems that would usually require algebra.
Example:
Two bowls and three plates cost $1421. The cost of the plate is half the cost of the bowl. What is
the cost of the bowl?
Solution:
Step 1: Draw a block diagram to illustrate the number of bowls
and plates. (In this diagram, the bowls are shown as orange blocks and the plates as blue blocks.)
Step 2: Since a bowl costs twice as much as a plate, we can
replace one orange block (bowl) with two blue blocks (plate).
Step 3: Looking at the block diagram, find the cost of each plate.
7 blue blocks = 1421
1 blue block = 1421 ÷ 7 = 203
The cost of each plate is $203.
The cost of each bowl is 203 × 2 = $406.
Example:
A factory makes 4250 bars of chocolate. There were three kinds of chocolate bars – creamy,
milky and white. The number of white chocolate bars was 715 more than the number of milky chocolate
bars. The number of creamy chocolate bars was 5 times the number of milky chocolate bars. How many
creamy chocolate bars did the factory make?
Solution:
Step 1: Draw a block diagram to illustrate the different types of
chocolate bars. (In this diagram, the creamy chocolate bars are shown as orange blocks, the milky
chocolate bars as blue blocks and the white chocolate bars as red blocks.)
Step 2: Since the number of creamy chocolate bars was 5 times the
number of milky chocolate bars, we can replace one orange block (creamy) with 5 blue blocks (milky).
Since the number of white chocolate bars was 715 more than the number of milky chocolate bars, we
replace one red block with one blue block + 715.
Step 3: Looking at the block diagram, find the number of milky
chocolate bars (blue block)
4250 – 715 = 3535
7 blue blocks = 3535
1 blue block = 3535 ÷ 7 = 505
The number of milky chocolate bars made was 505.
Step 4: Calculate the number of creamy chocolate bars.
The number of creamy chocolate bars was 5 times the number of milky chocolate bars = 5 × 505 = 2525
How to solve word problems with four types of bar models — Comparing, Taking Out, Combining, Missing Part?
Examples:
- Each week, Dwight calculated that he spends 2/3 of his allowance on food and 1/9 on video games.
How much did he spend on food and video games? - Marvin bought 1/2 pound of gummy bears. He ate 1/3 pound on his way to school. How much of gummy bears
does Marvin have left? - A recipe needs 7/8 teaspoons of salt and 2/5 teaspoons of sugar. How much more salt is needed than sugar?
- For the last hour Mr. Negron was awake, he spent 4/8 of the hour making homework and 1/8 of the hour
talking. He spent the rest of the hour watching TV. What fraction of the hour did he spend watching TV?
- Show Video Lesson
Example:
Julian and Stacey need 8 liters of water to fill a tank. Stacey filled the tank with 3 11/12 liters of water.
Julian poured 1 2/5 liters less than Stacey into the tank. How much water is still needed to fill the tank?
- Show Video Lesson
How to solve part-whole word problems with bar modeling?
Examples:
- Danika bought some nail polish for $51. This was 3/5 of her money. How much money did she have to begin with?
- Henry bought 520 cookies for the math competition. If 3/4 were eaten, how many did he have left over?
- Betsy made cupcakes to bring to work. After the Science Department ate 2/7 and the Math Department ate 64,
she had 1/7 left. How many cupcakes did Betsy make? - Fran sold 108 chocolate chip and Snickerdoodle cookies at her lemonade stand. If she made 36 Snickerdoodle
cookies, how many chocolate chip cookies did she make? How much money did she earn selling the chocolate chip
cookies if she sold them in bags of 6 for $1.25 and she sold all of the bags. - Two lbs. of nactarines and one lb. of bananas cost $3.15. Two lbs. of nectarines and three lbs. of bananas
cost $5.65. Find the cost of one lb. of bananas. - Two tennis balls and one racquet cost $75. Two tennis balls and three racquets cost $215. Find the cost of
one racquet. - Carter raised money for a walk-a-thon. On Monday, he earned $0.75 per lap. On Tuesday, he earned $0.80 a
lap and on Wednesday, he earned $0.95 a lap. If he walked 36 laps on Monday, 50% as many laps on Wednesday
as on Monday, how much money did Carter earn for the walk-a-thon?
-
Show Video Lesson
How to solve comparison word problems with bar modeling?
Examples:
- Alex, Sonia and Tini have a total of $580. Sonia has $120 more than Alex, and Toni has $190 more than Sonia.
How much money does Toni have? - Trevor bought a ski jacket, gloves and helmet on clearance for $242 altogether. The jacket cost $71 more
than the gloves while the gloves cost $27 less than the helmet. How much did the jacket cost? - A hard drive costs twice as much as a 64 GB jump drive and a 32 GB jump drive costs half as much as a 64 GB
jump drive. If the hard drive costs $140, find the total cost. - Tracy earned 3/4 as much as Julie. Shannon earned 2/3 as much as Tracy. Julie earned $44. How much less
did Shannon earn than Tracy? - Sadie spent twice as much money as Kim. Kim spent $150 less than Jason. Jason spent $45 more than Sadie.
How much money did they spend altogether? - Harlis is five years younger than Janae. Sherry is three times as old as Janae. Together, Harlis’ and
Janae’s total age is 20 years less than Sherry’s age. How old is Sherry? - Josh has 3/4 as many jelly beans as Lisa. Lisa has 4/5 as many jelly beans as Curt. If Curt has 28 more
jelly beans than Josh, how many jelly beans do they have altogether?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
After you finish this lesson, view all of our Pre-Algebra lessons and practice problems. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
Solving Word Problems
To solve a word problem using a system of equations, it is important to;
– Identify what we don’t know
– Declare variables
– Use sentences to create equations
An example on how to do this:
Mary and Jose each bought plants from the same store. Mary spent $188 on 7 cherry trees and 11 rose bushes. Jose spent $236 on 13 cherry trees and 11 rose bushes. Find the cost of one cherry tree and the cost of one rose bush.
Cost of a cherry tree:
Cost of a rose bush:
7 cherry trees and 11 rose bushes = $188
The y-values cancel each other out, so now you are left with only x-values and real numbers.
Then, you plug in your x-value into an original equation in order to find the y-value.
Cost of a cherry tree: $8
Cost of a rose bush: $12
Example 1
Three coffees and a cupcake cost a total of dollars. Two coffees and four cupcake cost a total of
dollars. What is the individual price for a single coffee and a single cupcake?
Let’s solve this by following steps.
1. What we don’t know:
Cost of a single coffee
Cost of single cupcake
2. Declare variables:
Cost of a single coffee=
Cost of single cupcake=
3. Use sentences to create equations.
Three coffees and a cupcake cost a total of dollars.
Two coffees and four cupcake cost a total of dollars.
Now, we have a system of equations:
Let’s solve for one of the variables in one of the equations and then use that to substitute into the other.
Now, solve for the value of using the first equation.
Let’s solve the value of by substituting the value of
to the bottom equation.
Distribute to each terms inside the parenthesis
Combine like terms
Now, let’s isolate the by subtracting
on both sides.
Then divide both sides by ,
And we’ll have
Then, let’s plug the value of into one equation to get the value of
.
Cost of a single coffee=
Cost of single cupcake=
Example 2
The senior class at High School A rented and filled vans and
buses with
students. High School B rented and filled
vans and
bus with
students. Every van had the same number of students in it as did the buses. Find the number of students in each van and in each bus.
Let’s solve this by following steps.
1. What we don’t know:
Students in each van
Students in each bus
2. Declare variables:
Students in each van=
Students in each bus=
3. Use sentences to create equations.
High School A rented and filled 8 vans and 8 buses with 240 students.
High School B rented and filled 4 vans and 1 bus with 54 students.
Now, we have a system of equations:
Let’s solve for one of the variables in one of the equations and then use that to substitute into the other.
Now, solve for the value of using the second equation.
Let’s solve the value of by substituting the value of
to the bottom equation.
Distribute to each terms inside the parenthesis
Combine like terms
Now, let’s isolate the by subtracting
on both sides.
Then divide both sides by ,
And we’ll have
Then, let’s plug the value of into one equation to get the value of
.
Students in each van=
Students in each bus=
Video-Lesson Transcript
To solve a word problem using system of equations, it is important to:
1. Identify what we don’t know
2. Declare variables.
3. Use sentences to create equations.
Let’s have an example:
Mary and Jose each bought plants from the same store. Mary spent on
cherry trees and
rose bushes. Jose spent
on
cherry trees and
rose bushes. Find the cost of one cherry tree and the cost of one rose bush.
Let’s solve this by following steps above.
1. What we don’t know:
cost of a cherry tree
cost of a rose bush
2. Declare variables:
cost of a cherry tree :
cost of a rose bush :
3. Use sentences to create equations.
For Mary:
cherry trees and
rose bushes
For Jose:
cherry trees and
rose bushes
Now, we have a system of equations
We can solve this by process of substitution, elimination or fraction.
Since the value of is the same for both equations, let’s do the process of elimination.
First, let’s multiply the first equation by
Here we’ll have a negated equation
Let’s do the process of elimination now
We’ll have
Then, let’s isolate by dividing both sides by
Now, we have
Remember, our declared variable?
cost of a cherry tree :
Since
Now we can say that
cost of a cherry tree :
Now, let’s solve for the value of by getting one equation and plugging the value of
.
Let’s use the first equation to plug in
Let’s isolate by subtracting
on both sides of the equation
Then divide by
And we get
Now, we know that cost of a rose bush is .
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
In today’s post, we are going to see a selection of Second Grade word problems that usually appear at the end of a Smartick session for children with a second-grade level. You will also get a chance to see the solution for each problem.
Ready? Let’s go!
How To Correctly Solve Any Problem
- Read the word problem carefully! You should understand what is being asked very clearly.
- Write down the data.
- Complete the operations and always write down the results for each.
- Write the solution very clearly and respond to what the problem asks.
Second Grade Word Problems
Let’s practice with a selection of Second Grade word problems from Smartick.
Word Problem 1
Solution 1
For this word problem, Smartick has given us the solution and it is up to us to select the correct question.
The answer is: ”They were planting 38 chestnut seeds.” Let’s take a look at each option to see which would work with this answer, we’ll use the process of elimination.
- How many more chestnut seeds than oak seeds were they planting? This is asking us about the different types of seeds, but the solution is only asking about chestnuts so this question is not what we are looking for.
- Are fewer chestnut trees or fewer oak trees expected to grow? This answer isn’t the one we are looking for because the answer only gives us information about chestnut seeds.
- How many more poplar seeds than oak seeds were they planting? Nothing was mentioned in the word problem or the answer about poplar trees.
- How many chestnut seeds were they planting? Here were are being asked about the number of chestnut seeds that were planted and the solution tells us the amount that was planted. This is the question that we are looking for.
Word Problem 2
Solution 2
This word problem is asking how many tablespoons of oil have been added to a stew, and we know that there were 20 tablespoons more added than the 9 tablespoons that the recipe called for. So we need to know how many tablespoons in total were added to the stew.
9 + 20 = 29
29 tablespoons of oil were added to the stew.
Word Problem 3
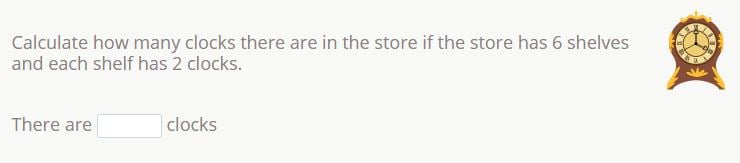
Solution 3
Here, we are being asked to calculate the total number of clocks. To help us solve it, we can create a drawing using the information from the word problem. It tells us that there are 2 clocks on each shelf, and there are 6 shelves.
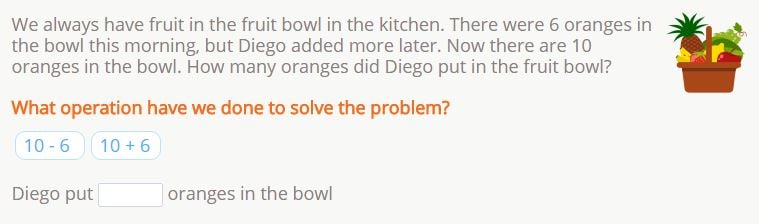
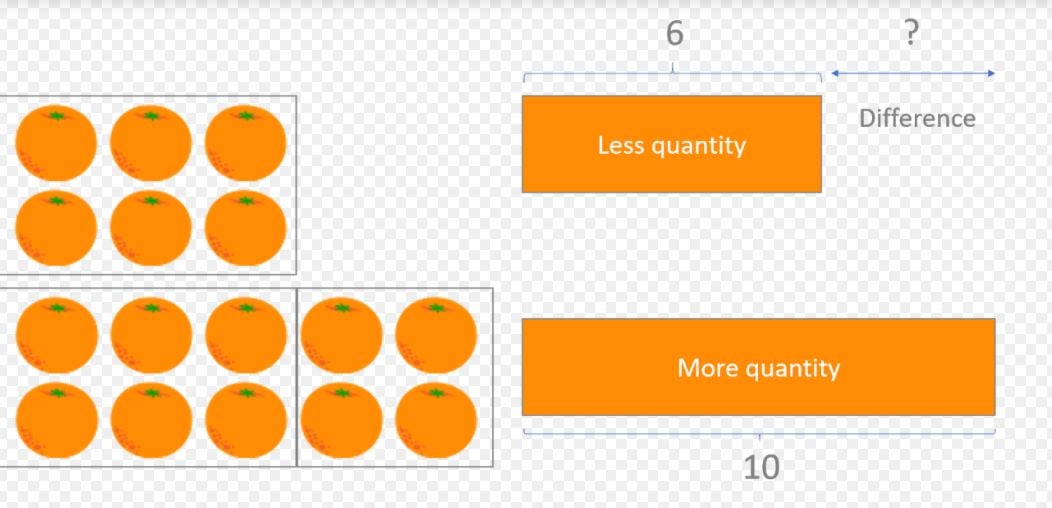
Word Problem 4
Solution 4
First, we are asked which operation we need to use to solve the problem and are provided with the options of addition and subtraction. Let’s read the word problem carefully to see which would work best…
There were 6 oranges before Diego added more, and now there are 10. Therefore, the difference between the amount in the bowl now, and the amount there was before, is the amount that Diego added. If we add the numbers, adding the larger quantity to the lesser quantity, it does not give us the number of oranges Diego added to the bowl. However, if we subtract the smaller quantity from the larger quantity, we should find the difference.
The answer to the first question would be: 10 – 6.
And the solution to the word problem: 10 – 6 = 4.
Diego added 4 oranges.
I hope you have learned something new from this selection of second grade word problems that appear during our daily Smartick sessions. If you would like to learn more about other primary school math topics, register with Smartick and try it for free.
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
What’s the first thing that comes to mind when you hear the phrase Word problems?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
For some, it’s a chance to solve a real-world example, so there’s a level of excitement and sense of wonder. For others, it’s groaning, and frustration on where to even begin.
Well, in this lesson we’re going to make Solving Linear Equation Word Problems manageable with easy to follow tricks and steps.
We already know how to solve all different types of equations. Yay!
And we also know how to translate algebraic expressions and equations. Double Yay!
Now it’s time to bring both of these together.
Solving equations and word problems Example
But, what about the tricks and steps?
Yes, there are some easy to follow steps that we are going to use to solve linear word problems.
- Read the problem carefully and determine what is being asked.
- Create a sidebar! Using different colors, symbols and diagrams and write an equation the relates all the information given.
- Solve your equation and check your answer(s).
Now, these steps might not seem all that remarkable, but once you see them in action I guarantee that writing equations from word problems and solving them will become like second nature!
Again, the secret to success is your Sidebar. This is where you will write down all the information you’ve gleaned from the problem, and formulate a solution by writing an equation to model the situation, as Khan Academy accurately states.
Together we will walk through 9 examples in detail ranging from finding consecutive integers to finding hourly wages, profit and cost, distances for rectangles and triangles, and people’s ages.
Linear Word Problems (How-To) – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Get My Subscription Now
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

Solving Word Problems in Algebra
Inequality Word Problems
How are you with solving word problems in Algebra? Are you ready to
dive into the «real world» of inequalities? I know that solving word
problems in Algebra is probably not your favorite, but there’s no point
in learning the skill if you don’t apply it.
I promise to make this as easy as possible. Pay close attention to
the key words given below, as this will help you to write the
inequality. Once the inequality is written, you can solve the
inequality using the skills you learned in our past lessons.
I’ve tried to provide you with examples that could pertain to your
life and come in handy one day. Think about others ways you might use
inequalities in real world problems. I’d love to hear about them if you do!
Before we look at the examples let’s go over some of the rules and
key words for solving word problems in Algebra (or any math class).
Word Problem Solving Strategies
- Read through the entire problem.
- Highlight the important information and key words that you need to solve the problem.
- Identify your variables.
- Write the equation or inequality.
- Solve.
- Write your answer in a complete sentence.
- Check or justify your answer.
I know it always helps too, if you have key words that help you to write
the equation or inequality. Here are a few key words that we associate
with inequalities! Keep these handy as a reference.
Inequality Key Words
- at least — means greater than or equal to
- no more than — means less than or equal to
- more than — means greater than
- less than — means less than
Ok… let’s put it into action and look at our examples.
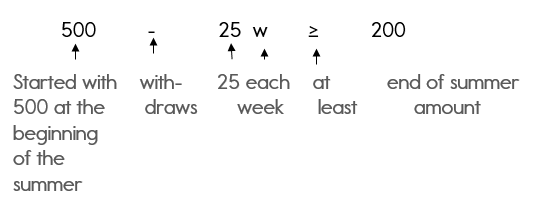
Example 1: Inequality Word Problems
Keith has $500 in a savings account at the beginning of the summer. He wants to have at least $200 in the account by the end of the summer. He withdraws $25 each week for food, clothes, and movie tickets.
- Write an inequality that represents Keith’s situation.
- How many weeks can Keith withdraw money from his account? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: At least is a key word that notes that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know how many weeks.
Let w = the number of weeks
Step 3: Write your inequality.
500 — 25w > 200
I know you are saying, «How did you get that inequality?»
I know the «at least» part is tricky. You would probably think that at least means less than.
But… he wants the amount in his account to be at least $200 which means $200 or greater. So, we must use the greater than or equal to symbol.
Step 4: Solve the inequality.
The number of weeks that Keith can withdraw money from his account is 12 weeks or less.
Step 5: Justify (prove your answer mathematically).
I’m going to prove that the largest number of weeks is 12 by substituting 12 into the inequality for w. You could also substitute any number less than 12.
Since 200 is equal to 200, my answer is correct. Any more than 12 weeks and his account balance would be less than $200. Any number of weeks less than 12 and his account would stay above $200.
That wasn’t too bad, was it? Let’s take a look at another example.
Example 2: More Inequality Word Problems
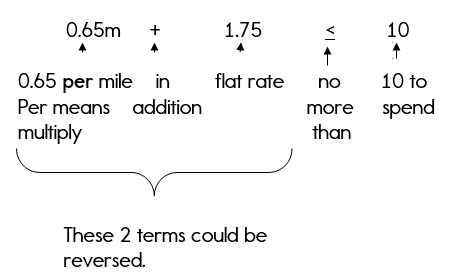
Yellow Cab Taxi charges a $1.75 flat rate in addition to $0.65 per mile. Katie has no more than $10 to spend on a ride.
- Write an inequality that represents Katie’s situation.
- How many miles can Katie travel without exceeding her budget? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: No more than are key words that note that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know the number of miles Katie can travel.
Let m = the number of miles
Step 3: Write the inequality.
0.65m + 1.75 < 10
Are you thinking, «How did you write that inequality?»
The «no more than» can also be tricky. «No more than» means that you can’t have more than something, so that means you must have less than!
Step 4: Solve the inequality.
Since this is a real world problem and taxi’s usually charge by the mile, we can say that Katie can travel 12 miles or less before reaching her limit of $10.
Step 5: Justify (prove your answer mathematically).
Are you ready to try some on your own now? Yes… of course you are! Click here to move onto the word problem practice problems.
Take a look at the questions that other students have submitted:
- Home
- Inequalities
-
Inequality Word Problems
>
>
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Now that we’ve practiced turning words into linear equations, let’s actually solve a couple of word problems. This is usually a three-step process:
- Find the linear equation being described.
- Figure out what question is being asked, and answer that question.
- Check your answer.
The fourth step, «take a nap,» is totally optional.
Sample Problem
Jenna works at a retail shop. Yes, she still works there, even after all her thievery, but she’ll tell you it has nothing to do with her old man owning the joint. She still makes $10 per hour, plus $3 for each item she sells.
- How much does Jenna make in one hour if she sells 5 items during that hour?
- How many items would Jenna need to sell in an hour to make $43 during that hour?
This word problem is describing a line with an equation we found earlier: y = 3x + 10, which describes the amount of cash (y) she makes in an hour if she sells x items.
Since we’ve found the linear equation, now we can answer the questions.
1. How much does Jenna make in one hour if she sells 5 items during that hour?
Since x is the number of items Jenna sells during one hour, we’ve got x = 5.
Then y = 3(5) + 10 = 25, which means Jenna would be paid $25. This amount doesn’t include tips. Yeah, she makes tips, too. What can we say, this girl knows how to turn a buck.
2. How many items would Jenna need to sell in an hour to make $43 during that hour?
Since y is the amount Jenna is paid, if Jenna makes $43, we want to have y = 43. Plug that into our equation:
43 = 3x + 10
We can solve this equation for x to find:
Since x is the number of items Jenna sells during an hour, in order to make $43 Jenna must sell 11 items. Given her foolproof sales technique of breaking down into tears whenever someone decides not to buy something, she shouldn’t have any problem hitting that mark.
Let’s check that this is correct, though: If Jenna sells 11 items she’ll make 3(11) + 10 dollars, which is indeed $43.
Sample Problem
Marcio spent $7 per day. Knowing Marcio, he probably spent it on Lotto scratchers. After five days, he had $8 left. How much money did Marcio start with?
First, we need to come up with a linear equation. The amount of money Marcio has depends on how many days have passed. Let’s have x be the number of days that have passed, and y be the amount of money Marcio has.
The statement «after five days, he had $8 left» tells us that the point (5, 
Since Marcio is spending $7 per day, the slope of the line is -7. We can use this information to find an equation for the line. Let’s use point-slope form, since we have a point and a slope. We find the equation:
y – 8 = -7(x – 5)
Now we can worry about answering the question. The amount of money Marcio started with is the amount of money he had when 0 days had passed. Oh, to go back in time and have all that hard-earned cashola back, eh, Marcio?
We want to find the y-intercept of the line, since that’s the point where x = 0 days. We can do this by rearranging our point-slope equation into slope-intercept form.
The y-intercept is 43, which means Marcio started with $43. Hey…that’s how much Jenna made from selling her 11 items. These two might be in cahoots…
Let’s make sure we’re right. If Marcio started with $43 and spent $7 per day, after 5 days he would have 43 – 5(7) = 43 – 35, which is indeed 8 dollars.
Word problems that involve a linear equation can give us the information we need to write that equation in several different ways. We could be told two points on the line, or a point and a slope, or the y-intercept and the slope, or both intercepts. We could be given a treasure map that will lead us to the information we need, although those problems are more rare. Word problems can ask questions about the intercepts of the line or the slope. They can provide one coordinate of a point on the line and then ask for the other coordinate.
Come to think of it, they ask us for a whole lot of stuff without giving much back in return. We’re in a one-sided relationship and should probably get out of it. We’ll see what our therapist has to say about this on Tuesday.
After we find the line described by the word problem, the trick, as usual, is to figure out what the question is actually asking. Don’t be distracted by any of its mumbo-jumbo.

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.
The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!
How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.
Here are the seven strategies I use to help students solve word problems.
1. Read the Entire Word Problem
Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.
2. Think About the Word Problem
Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.
Here are the questions:
A. What exactly is the question?
What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.
B. What do I need in order to find the answer?
Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.
This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better
Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.
One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.
If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?
This is where students will focus in on the numbers which will be used to solve the problem.
3. Write on the Word Problem
This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:
- Circle any numbers you’ll use.
- Lightly cross out any information you don’t need.
- Underline the phrase or sentence which tells exactly what you’ll need to find.
4. Draw a Simple Picture and Label It
Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.
For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!
5. Estimate the Answer Before Solving
Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.
6. Check Your Work When Done
This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable? I want students to do more than to be number crunchers but to really think about what those numbers mean.
Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.
7. Practice Word Problems Often
Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.
When students practice word problems, often several things happen. Word problems become less scary (no, really).
They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.
If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.
This 3rd Grade Math Task Cards Bundle has word problems in almost every one of its 30 task card sets.
There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.
CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.
CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.
CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?
3rd Grade: Rounding Whole Numbers Task Cards
4th Grade: Convert Fractions and Decimals Task Cards
5th Grade: Read, Write, and Compare Decimals Task Cards
Thanks so much for stopping by!

A Picture is Worth a Thousand Words
“Today, we are going to solve math word problems.” When students hear this from their math teacher, their faces drop, sweat starts to form on their foreheads and they refuse to make eye contact. As a math teacher, I understand. I understand the anxiety and want to make the learning process with word problems more enjoyable. This is where reading, writing and, math collide and the real world of math begins. Let’s talk about how to solve word problems with pictures.
When students struggle with word problems in school, they also have difficulty tackling them for homework. Most students want the “one-size-fits-all” formula for word problems but unfortunately, that does not exist. However, drawing a picture will help students visualize the problem and will start advancing their learning stage from the concrete to the abstract. Let’s take a look at how to solve a word problem using pictures:
Steps for Solving Word Problems using Pictures
- Read the entire problem: Get all the facts – Underline key word
- Answer the question: What am I looking for?
- Draw a picture or diagram: Visualize as a real world situation
- Solve the problem: Set up the equation and solve
- Check your solution: Is this answer reasonable?
Word Problem Examples – Example A
Cody has 6 pencils on his desk, Jonah has 4 more than Cody and Vinny has three less pencils than Jonah. How many pencils are there in all?
- Read the entire problem √
- What am I looking for? How many pencils do Cody, Jonah and Vinny have altogether? √
- Draw a picture or diagram √
- Solve the problem √
6 + 10 + 7 = 23 pencils
- Check your solution √
This answer is reasonable
Example B
There are 3 fish tanks labeled X, Y, and Z. Y weighs 6 times as much as X and twice as much as Z. If Z is 36 lbs. heavier than X, find the total weight of X, Y and Z.
- Read the entire problem √
- What am I looking for? What is thetotal weight of fish tanks X, Y and Z? √
- Draw a picture or diagram √
- Solve the problem √
18 + 108 + 54 = 180 pounds
- Check your solution √
This answer is reasonable
Visualizing a word problem with pictures is a strategy that will help motivate many students to begin the process of solving them. This works especially for students that may become bored by the excess amount of words instead of numbers or for those students who become overwhelmed by the information and want to break it down into a simpler form. Another benefit of using pictures when solving word problems involves communicating the results. The pictures act as justification for answers, make the problems easier to understand and therefore, secure the learning process.
Meet our Guest Blogger: Jan Rowe
Jan is one of Educational Connections’ top tutors. She has twelve years of classroom teaching experience and holds a Virginia and Florida teaching license in middle school mathematics and elementary education. Jan has been with Educational Connections for over a year, working with over twenty students. Her tutoring goal is to help each student understand their learning style so they can improve the speed and quality of that learning. When she is not tutoring or teaching, Jan loves to play scrabble, go hiking and play Frisbee with her new puppy.
Learning Outcomes
- Approach word problems with a positive attitude
- Use a problem solving strategy for word problems
- Translate more complex word problems into algebraic expressions and equations
Approach Word Problems with a Positive Attitude
The world is full of word problems. How much money do I need to fill the car with gas? How much should I tip the server at a restaurant? How many socks should I pack for vacation? How big a turkey do I need to buy for Thanksgiving dinner, and what time do I need to put it in the oven? If my sister and I buy our mother a present, how much will each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student in the cartoon below?
Negative thoughts about word problems can be barriers to success.
When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts, like the student in the cartoon below. Read the positive thoughts and say them out loud.
When it comes to word problems, a positive attitude is a big step toward success.
If we take control and believe we can be successful, we will be able to master word problems.
Think of something that you can do now but couldn’t do three years ago. Whether it’s driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill. Word problems are no different. Even if you have struggled with word problems in the past, you have acquired many new math skills that will help you succeed now!
Use a Problem-Solving Strategy for Word Problems
In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. Since then, you’ve increased your math vocabulary as you learned about more algebraic procedures, and you’ve had more practice translating from words into algebra.
You have also translated word sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. You had to restate the situation in one sentence, assign a variable, and then write an equation to solve. This method works as long as the situation is familiar to you and the math is not too complicated.
Now we’ll develop a strategy you can use to solve any word problem. This strategy will help you become successful with word problems. We’ll demonstrate the strategy as we solve the following problem.
Example
Pete bought a shirt on sale for $[latex]18[/latex], which is one-half the original price. What was the original price of the shirt?
Solution:
Step 1. Read the problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the Internet.
- In this problem, do you understand what is being discussed? Do you understand every word?
Step 2. Identify what you are looking for. It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the shirt” tell you what you are looking for: the original price of the shirt.
Step 3. Name what you are looking for. Choose a variable to represent that quantity. You can use any letter for the variable, but it may help to choose one that helps you remember what it represents.
- Let [latex]p=[/latex] the original price of the shirt
Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation.
Step 5. Solve the equation using good algebra techniques. Even if you know the answer right away, using algebra will better prepare you to solve problems that do not have obvious answers.
| Write the equation. | [latex]18=Largefrac{1}{2}p[/latex] |
| Multiply both sides by 2. | [latex]color{red}{2}cdot18=color{red}{2}cdotLargefrac{1}{2}normalsize p[/latex] |
| Simplify. | [latex]36=p[/latex] |
Step 6. Check the answer in the problem and make sure it makes sense.
- We found that [latex]p=36[/latex], which means the original price was [latex]text{$36}[/latex]. Does [latex]text{$36}[/latex] make sense in the problem? Yes, because [latex]18[/latex] is one-half of [latex]36[/latex], and the shirt was on sale at half the original price.
Step 7. Answer the question with a complete sentence.
- The problem asked “What was the original price of the shirt?” The answer to the question is: “The original price of the shirt was [latex]text{$36}[/latex].”
If this were a homework exercise, our work might look like this:
We list the steps we took to solve the previous example.
Problem-Solving Strategy
- Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the internet.
- Identify what you are looking for. Determine the constants and variables in the problem. A constant is a number in the problem that is not going to change. A variable is a number that you don’t yet know its value.
- Name what you are looking for. Choose a letter to represent that quantity.
- Translate words into algebraic expressions and equations. Write an equation to represent the problem. It may be helpful to first restate the problem in one sentence before translating.
- Solve the equation using good algebra techniques.
- Check the answer in the problem. Make sure it makes sense.
- Answer the question with a complete sentence.
Translate word problems into expressions
One of the first steps to solving word problems is converting an English sentence into a mathematical sentence. In the table below, words or phrases commonly associated with mathematical operators are categorized. Word problems often contain these or similar words, so it’s good to see what mathematical operators are associated with them.
| Addition [latex]+[/latex] | Subtraction [latex]-[/latex] | Multiplication [latex]times[/latex] | Variable ? | Equals [latex]=[/latex] |
|---|---|---|---|---|
| More than | Less than | Double | A number | Is |
| Together | In the past | Product | Often, a value for which no information is given. | The same as |
| Sum | Slower than | times | After how many hours? | |
| Total | The remainder of | How much will it cost? | ||
| In the future | Difference | |||
| Faster than |
Some examples follow:
- “[latex]xtext{ is }5[/latex]” becomes [latex]x=5[/latex]
- “Three more than a number” becomes [latex]x+3[/latex]
- “Four less than a number” becomes [latex]x-4[/latex]
- “Double the cost” becomes [latex]2cdottext{ cost }[/latex]
- “Groceries and gas together for the week cost $250” means [latex]text{ groceries }+text{ gas }=250[/latex]
- “The difference of [latex]9[/latex] and a number” becomes [latex]9-x[/latex]. Notice how [latex]9[/latex] is first in the sentence and the expression.
Let’s practice translating a few more English phrases into algebraic expressions.
Example
Translate the table into algebraic expressions:
| some number | the sum of the number and [latex]3[/latex] | twice the sum of the number and [latex]3[/latex] |
| a length | double the length | double the length, decreased by [latex]6[/latex] |
| a cost | the difference of the cost and [latex]20[/latex] | [latex]2[/latex] times the difference of the cost and [latex]20[/latex] |
| some quantity | the difference of [latex]5[/latex] and the quantity | the difference of [latex]5[/latex] and the quantity, divided by [latex]2[/latex] |
| an amount of time | triple the amount of time | triple the amount of time, increased by [latex]5[/latex] |
| a distance | the sum of [latex]-4[/latex] and the distance | the sum of [latex]-4[/latex] and the twice the distance |
In this example video, we show how to translate more words into mathematical expressions.
For another review of how to translate algebraic statements into words, watch the following video.
The power of algebra is how it can help you model real situations in order to answer questions about them. Let’s use this approach with another example.
Example
Yash brought apples and bananas to a picnic. The number of apples was three more than twice the number of bananas. Yash brought [latex]11[/latex] apples to the picnic. How many bananas did he bring?
Example
Twenty-eight less than five times a certain number is [latex]232[/latex]. What is the number?
In the video that follows, we show another example of how to translate a sentence into a mathematical expression using a problem solving method.
In the next example, we will apply our Problem-Solving Strategy to applications of percent.
example
Nga’s car insurance premium increased by [latex]text{$60}[/latex], which was [latex]text{8%}[/latex] of the original cost. What was the original cost of the premium?
Contribute!
Did you have an idea for improving this content? We’d love your input.
Improve this pageLearn More