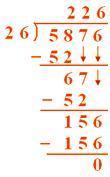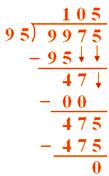1. A
The ratio between black and blue pens is 7 to 28 or 7:28. Bring to the lowest terms by dividing both sides by 7 gives 1:4.
2. A
At 100% efficiency 1 machine produces 1450/10 = 145 m of cloth.
At 95% efficiency, 4 machines produce 4 * 145 * 95/100 = 551 m of cloth.
At 90% efficiency, 6 machines produce 6 * 145 * 90/100 = 783 m of cloth.
Total cloth produced by all 10 machines = 551 + 783 = 1334 m
Since the information provided and the question are based on 8 hours, we did not need to use time to reach the answer.
3. D
The turnout at polling station A is 945 out of 1270 registered voters. So, the percentage turnout at station A is:
(945/1270) × 100% = 74.41%
The turnout at polling station B is 860 out of 1050 registered voters. So, the percentage turnout at station B is:
(860/1050) × 100% = 81.90%
The turnout at polling station C is 1210 out of 1440 registered voters. So, the percentage turnout at station C is:
(1210/1440) × 100% = 84.03%
To find the total turnout from all three polling stations, we need to add up the total number of voters and the total number of registered voters from all three stations:
Total number of voters = 945 + 860 + 1210 = 3015
Total number of registered voters = 1270 + 1050 + 1440 = 3760
The overall percentage turnout is:
(3015/3760) × 100% = 80.12%
Therefore, the total turnout from all three polling stations is 80.12% — rounding to 80%.
4. D
This is a simple direct proportion problem:
If Lynn can type 1 page in p minutes, then she can type x pages in 5 minutes
We do cross multiplication: x * p = 5 * 1
Then,
x = 5/p
5. A
This is an inverse ratio problem.
1/x = 1/a + 1/b where a is the time Sally can paint a house, b is the time John can paint a house, x is the time Sally and John can together paint a house.
So,
1/x = 1/4 + 1/6 … We use the least common multiple in the denominator that is 24:
1/x = 6/24 + 4/24
1/x = 10/24
x = 24/10
x = 2.4 hours.
In other words; 2 hours + 0.4 hours = 2 hours + 0.4•60 minutes
= 2 hours 24 minutes
6. D
The original price of the dishwasher is $450. During a 15% off sale, the price of the dishwasher will be reduced by:
15% of $450 = 0.15 x $450 = $67.50
So the sale price of the dishwasher will be:
$450 – $67.50 = $382.50
As an employee, the person receives an additional 20% off the lowest price, which is $382.50. We can calculate the additional discount as:
20% of $382.50 = 0.20 x $382.50 = $76.50
So the final price that the employee will pay for the dishwasher is:
$382.50 – $76.50 = $306.00
Therefore, the employee will pay $306.00 for the dishwasher.
7. D
Original price = x,
80/100 = 12590/X,
80X = 1259000,
X = 15,737.50.
8. D
We are given that each of the n employees earns s amount of salary weekly. This means that one employee earns s salary weekly. So; Richard has ‘ns’ amount of money to employ n employees for a week.
We are asked to find the number of days n employees can be employed with x amount of money. We can do simple direct proportion:
If Richard can employ n employees for 7 days with ‘ns’ amount of money,
Richard can employ n employees for y days with x amount of money … y is the number of days we need to find.
We can do cross multiplication:
y = (x * 7)/(ns)
y = 7x/ns
9. B
The distribution is done at three different rates and in three different amounts:
$6.4 per 20 kilograms to 15 shops … 20•15 = 300 kilograms distributed
$3.4 per 10 kilograms to 12 shops … 10•12 = 120 kilograms distributed
550 – (300 + 120) = 550 – 420 = 130 kilograms left. This 50
amount is distributed in 5 kilogram portions. So, this means that there are 130/5 = 26 shops.
$1.8 per 130 kilograms.
We need to find the amount he earned overall these distributions.
$6.4 per 20 kilograms : 6.4•15 = $96 for 300 kilograms
$3.4 per 10 kilograms : 3.4 *12 = $40.8 for 120 kilograms
$1.8 per 5 kilograms : 1.8 * 26 = $46.8 for 130 kilograms
So, he earned 96 + 40.8 + 46.8 = $ 183.6
The total distribution cost is given as $10
The profit is found by: Money earned – money spent … It is important to remember that he bought 550 kilograms of potatoes for $165 at the beginning:
Profit = 183.6 – 10 – 165 = $8.6
10. B
We check the fractions taking place in the question. We see that there is a “half” (that is 1/2) and 3/7. So, we multiply the denominators of these fractions to decide how to name the total money. We say that Mr. Johnson has 14x at the beginning; he gives half of this, meaning 7x, to his family. $250 to his landlord. He has 3/7 of his money left. 3/7 of 14x is equal to:
14x * (3/7) = 6x
So,
Spent money is: 7x + 250
Unspent money is: 6×51
Total money is: 14x
Write an equation: total money = spent money + unspent money
14x = 7x + 250 + 6x
14x – 7x – 6x = 250
x = 250
We are asked to find the total money that is 14x:
14x = 14 * 250 = $3500
11. D
First calculate total square feet, which is 15 * 24 = 360 ft2. Next, convert this value to square yards, (1 yards2 = 9 ft2) which is 360/9 = 40 yards2. At $0.50 per square yard, the total cost is 40 * 0.50 = $20.
1). A number consists of two digits. The sum of the digits is 10. On reversing the digits of the number, the number decreases by 36. What is the product of the two digits?
|
||||
2). If a number is multiplied by three-fourth of itself, the value thus obtained is 10800. What is that number?
|
||||
3). The sum of five consecutive numbers is 190. What is the sum of the largest and the smallest numbers?
|
||||
4). The product of two consecutive odd numbers is 19043. Which is the smaller one?
|
||||
5). If the three-fourth of a number is subtracted from the number, the value so obtained is 163. What is that number?
|
||||
6). The sum of two numbers is 10. Their product is 20. Find the sum of the reciprocals of the two numbers.
|
||||
7). Five times of a positive integer is equal to 3 less than twice the square of that number. Find the number.
|
||||
8). A man has given one-fourth part of his property to his daughter, half part to his sons and one-fifth part given as charity. How much part of his property he has given?
|
||||
| 9). A chocolate has 12 equal pieces. Manju gave ( Large frac{1}{4} )th of it to Anju, ( Large frac{1}{3} )rd of it to Sujata and ( Large frac{1}{6} )th of it to Fiza. The number of pieces of chocolate left with Manju is | ||||
| 10). A number consists of two digits whose sum is 10. If the digits of the number are reversed, then the number decreased by 36. Which of the following is/are correct? I. The number is divisible by a composite number. II. The number is a multiple of a prime number.
|
6,738 Answered Questions for the topic Word Problem
The question is in the description.
There are cards in a box. Fifteen of these cards are red, the others are blue, and the rests are white cards. If the probability of drawing a blue card is 0.125 and the probability of drawing a…
more
need answered asap please
A truck enters a highway driving 60 mph. A car enters the highway at the same place 5 minutes later and drives 69 mph in the same direction. From the time the car enters the highway, how long will…
more
Middle school math finding the distance
You and your friend are standing back to back. Your friend runs 13 feet forward and 3 feet right. At the same time, you run 11 feet forward and 7 feet right. You stop and throw a baseball to your…
more
System of equations question!
Afternoon. I’m struggling to understand where to really go with this question! It reads as follows:========================»A lot of people have taken to baking as a pandemic interest. You’ve…
more
word problem Algebra 1
Adam and Jill each improved their yards by planting daylilies and geraniums. They bought theirsupplies from the same store. Adam spent $56 on 7 daylilies and 7 geraniums. Jill spent $94 on14…
more
Word problem!!!!!
Jen has in price speed past train fairs for a group trip to New York. Three adults and four children must pay $129. Two adults and three children must pay $92. Find the price of the adult ticket…
more
algebra word problem
Justin sells tickets at the theatre. At the end of the evening, he had $524.00 in toonies and $5 bills. The total number of coins and bills was 145. How many toonies and $5 bills does he have?
i need help with this word problem
Susan sells beaded necklaces. Each large necklace sells for $5.40 and each small necklace sells for $4.50. How much will she earn from selling 3 large necklaces and 1 small necklace?
i need help with this word problem
Aldo bought 2 CDs that were each the same price. Including sales tax, he paid a total of $25.60. Of that total, $2.40 was tax. What was the price of each CD before tax?
i need help on this word problem
Joe made 4 identical necklaces, each having beads and a pendant. The total cost of the beads and pendants for all 4 necklaces was $23.60. If the beads cost $3.10 for each necklace, how much did…
more
Pre Calc Probability Word Problem
You enter a lottery buying one ticket. There are 45 numbers and you try to choose 5 of them. Then, there are 30 red balls numbered 1-30 and you try to get that number right. How many possible…
more
Pre Calc Probability Word Problem
there are 5 red balls, 30 black balls, and 7 pink balls in a jar. You pull one out, don’t replace it, and pull another one out. Find the probability of getting two of the same color? Please include…
more
Still looking for help? Get the right answer, fast.
OR
Find an Online Tutor Now
Choose an expert and meet online.
No packages or subscriptions, pay only for the time you need.
Question: 1
In each of the following sentences there is a blank space, followed by four choices of words marked (a), (b), (c) and (d).
A. Himalaya is the ___ of the Ganges.
B. The reporter had a valid ___ for the story.
C. He spent hours looking for the ___ of that question.
D. The strategy is to ___ supplies from smaller companies.
(A) source
(B) start
(C) look
(D) mother
Question: 2
In each of the following sentences there is a blank space, followed by four choices of words marked (a), (b), (c) and (d).
A. He has an ___ in ethnic music.
B. They said nothing of great ___.
C. Primary colours can add ___ to a room.
D. How much ____ did you pay for the new loan?
(A) influence
(B) interest
(C) income
(D) interface
Question: 3
In each of the following sentences there is a blank space, followed by four choices of words marked (a), (b), (c) and (d).
A. I cannot ___ the dogma of this church.
B. Please ___ my present.
C. People did not ___ atonal music at that time.
D. I shall have to ___ these unpleasant working conditions.
(A) accept
(B) but
(C) repeat
(D) forget
Question: 4
In each of the following sentences there is a blank space, followed by four choices of words marked (a), (b), (c) and (d).
A. The theatre was her first ___
B. Their __ left them indifferent to their surroundings.
C. It was 40 ___
D. He has a very complicated ___ life.
(A) done
(B) personal
(C) experience
(D) love
Question: 5
In each of the following sentences there is a blank space, followed by four choices of words marked (a), (b), (c) and (d).
A. We ___ the room with an electric heater.
B. The hostess ____ lunch for all the guests.
C. The will ___ that each child should receive half of the money.
D. He ___ for his large family by working their jobs.
(A) added
(B) provided
(C) accepted
(D) notified
Related Questions
- Top 100+ Verbal Reasoning Word Problems Questions & Answers
- Word Utilization Questions and Answers Pdf
- Verbal Ability Word Utilization Questions and Answers
- Top 100+ Logical Reasoning Test Word Utilization Problems
- 1000+ General English Questions & Answers | Word Correction
Recent Articles
Trending Posts
REGISTER TO GET FREE UPDATES
You may love GMAT word problems or you may hate them, but you can’t get around them if you want to ace the GMAT Quant section. No matter what your feelings are about this problem type, though, Magoosh’s experts have put together everything you need to know (and practice!) GMAT word problems in order to master them before test day.
Table of Contents
- What to Expect from GMAT Word Problems
- Strategy Guide: What’s the Trick to Mastering GMAT Word Problems?
- Translate from Words to Math
- Learn to Work with Variables
- Plug in Numbers (the Smart Way)
- Understand Your Strengths and Weaknesses
- GMAT Word Problem Practice Questions
- A Final Word on GMAT Word Problems
What to Expect from GMAT Word Problems
Think of GMAT word problems as questions that ask you to turn real-world situations into math problems. Of course, this can be a lot more complicated than it sounds. After all, it’s one thing to understand algebra in the abstract, and quite another to think about where the rubber meets the road.
Think about it this way: the reason human beings created algebra was to solve problems about real-world situations, and the GMAT loves asking math problems about numbers and about real-world situations, a.k.a. word problems! Even folks who can do algebra in the abstract sometimes find word problems challenging.
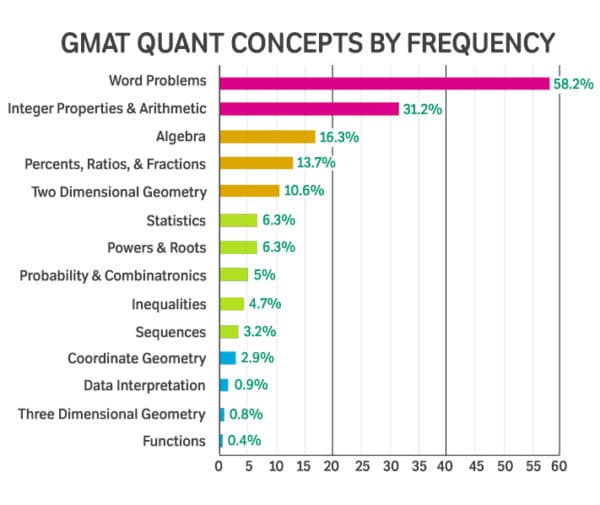
You’ll find GMAT word problems in the GMAT Quant section. How much of the GMAT is word problems? Within the Quant section, actually a whole lot! A study of official GMAT questions from actual tests show that word problems account for 58.2% of all GMAT math questions.
In other words, test-takers should anticipate a word problem cropping up (on average) in three out of every five questions you’ll see in Quant. Because of GMAT word problems’ prevalence, you can expect to see both Data Sufficiency and Problem Solving questions in this format. The question format and answer choices may look different, but the basic premise will be the same.
You may be feeling the pressure, but hang in there! If you’re worried about how to master word problems on the GMAT, keep reading for our GMAT Word Problems strategy guide.
Strategy Guide: What’s the Trick to Mastering GMAT Word Problems?
First, the disappointing news: there’s no one strategy that will work to immediately solve every word problem, every time (where would the fun in that be?). The good news: by using and combining a variety of strategies, you can put together the tools you need to ace even the most complex GMAT word problems, every single time!
With that in mind, here are the four key strategies you’ll need.
1. Translate from Words to Math
Suppose we have the following sentence in a word problem:”Three-fifths of x is 14 less than twice y squared.” How do we change words to math? Here’s a quick guide:
- The verb “is/are” is the equivalent of an equal sign; the equal sign in an equation is, in terms of “mathematical grammar,” the equivalent of a verb in a sentence. Every sentence has a verb and every equation has an equal sign.
- The word “of” means multiply (often used with fractions and percents). Ex. “26% of x” means (0.26x)
- The words “more than” or “greater than” mean addition. Ex. “5 greater than x” means (x + 5) and “7 more than y” means (y + 7)
- The words “less than” means subtraction. Ex. “8 less than Q” means (Q – 8). Notice that the first element is always subtracted: in other words, “J less than K” means (K – J).
With that in mind, let’s go back to the sentence from the hypothetical problem above.
- “three fifths of x” means [(3/5)*x]
- “is” marks the location of the equal sign
- “twice y squared” means 2(y^2)
- “14 less than twice y squared” means 2(y^2) – 14
Altogether, the equation we get is:
Using this strategy, it’s straightforward to translate from a verbal statement about numbers to an equation.
2. Learn to Work with Variables
Working with Variables Part I: Assigning Variables
Most GMAT word problem concern real world quantities and are stated in real world terms, and we need to assign algebraic variables to these real-world quantities.
Sometimes, one quantity is directly related to every other quantity in the problem. For example:
“Sarah spends 2/5 of her monthly salary on rent, 1/12 of her monthly salary on auto costs including gas and insurance, and 1/10 of her monthly salary automatically goes into saving each month. With what she has left each month, she spend she spends $800 on groceries and …”
In that problem, everything is related to “monthly salary,” so it would make a lot of sense to introduce just one variable for that, and express everything else in terms of that variable. Also, please don’t always use the boring choice of x for a variable! If we want a variable for salary, you might use the letter S, which will help you remember what the variable means! If we are given multiple variables that are all related to each other, it’s often helpful to assign a letter to the variable with the lowest value, and then express everything else in terms of this letter.
If there are two or more quantities that don’t depend directly on each other, then you may well have to introduce a different variable for each. Just remember that it’s mathematically problematic to litter a problem with a whole slew of different variables. You see, for each variable, you need an equation to solve it. If we want to solve for two different variables, we need two different equations (this is a common Word Problem scenario). If we want to solve for three different variables, we need three different equations (considerably less common). While the mathematical pattern continues to extend upward from there, more than three completely separate variables is almost unheard of on GMAT math.
When you assign variables, always be hyper-vigilant and over-the-top explicit about exactly what each variable means. Write a quick note to yourself on the scratch paper: T = the price of one box of tissue, or whatever the problem wants. What you want to avoid is the undesirable situation of solving for a number and not knowing what that number means in the problem!
Practice Question
Here’s a word problem practice question that’s a bit easier than what you might see on the GMAT!
Andrew and Beatrice each have their own savings account. Beatrice’s account has $600 less than three times what Andrew’s account has. If Andrew had $300 more dollars, then he would have exactly half what is currently in Beatrice’s account. How much does Beatrice have?
Click here for a text answer and explanation
The obvious choices for variables are A = the amount in Andrew’s account and B = the amount in Beatrice’s account. The GMAT will be good about giving you word problems involving people whose names start with a different letter so that it’s easier to assign variables. We can turn the second & third sentences into equations.
second sentence: B = 3A – 600
Both equations are solved for B, so simply set them equal.
3A – 600 = 2(A + 300)
3A – 600 = 2A + 600
A – 600 = 600
A = 1200
We can plug this into either equation to find B. (BTW, if you have time, an excellent check is to plug it into both equations, and make sure the value of B you get is the same!)
B = 3000
Thus, Andrew has $1200 in his account, and Beatrice, $3000 in hers.
Working with Variables Part II: Choosing Your Approach
When questions have variables in the answer choices, you can decide whether you’d rather take an algebraic approach or a numerical approach. Neither one of these is “better” than the other— it all depends on what works best for you.
An algebraic approach is what you most likely learned back in high school. This means that, to solve the problem, you’ll manipulate the variables according to mathematical rules. For a super-basic example, to solve ( 2x = y ), you would divide both sides by two and end up with ( x = y/2 ).
However, you could also to a numerical approach to this (and many other!) problems. This means putting numbers into both the question and the answer choices. So let’s take the previous example—which, again, is much, much easier than anything you’d see on the GMAT:
If ( 2x = y ), what is x in terms of y?
A. (y/20)
B. (y/2)
C. (4/y)
D. (20/y)
Here, you could pick a number to stand in for x in the original equation. Let’s say x is 2. If x = 2, then the original equation tells us that y = 4.
Now, plug that into the question and the answer. The question becomes: “What is 2 in terms of 4?” It’s ½, or .5. Then, look for the answer choice that gives you this answer. Plugging in the numbers, you get:
A. (y/20) = 0.2
B. (y/2) = 0.5
C. (4/y) = 1
D. (20/y) = 5
So B must be correct.
What does this look like in practice? For some harder examples, take a look over at Mike’s post on Variables in GMAT Answer Choices: 2 Approaches.
3. Plug in Numbers (the Smart Way)
If you choose to use the numerical approach described above, keep in mind that there are some key tips for plugging in numbers that you should use!
Here’s a quick summary of how to quick the best numbers for a particular problem:
- Remember that the GMAT has a broad definition of “number” that goes beyond positive integers! Zero, fractions, and negatives are all included. Work on developing number sense to help select the best numbers in a given scenario.
- For percent problems, think outside the box: GMAT test writers know lots of students pick 100. Try 500 or 1000 instead.
- Don’t try to pick numbers for questions involving more than one percent increase or decrease.
- Pay attention to units and convert them appropriately. This is particularly important in solutions and mixing problems!
- Don’t pick 1 as a number—it has too many unique properties.
A separate case involving plugging in, rather than picking, numbers: When all the answer choices are numerical, one further strategy we have at our disposal is backsolving. Using this strategy, we can pick one answer, plug it into the problem, and see whether it works. If this choice is too big or too small, it guides us in what other answer choices to eliminate. Typically, we would start with answer choice (C), but if another answer choice is a particularly convenient choice, then we would start there.
4. Understand Your Strengths and Weaknesses
With all of the above strategies at your disposal, you have everything you need to improve your answers to GMAT word problems. The most efficient way to do this is to keep an error log of word problems you’ve answered wrong in your practice, then review it. As you go through, think about the following:
- What concept or concepts was the question testing?
- What was tricky about the wording of the question?
- Were you already familiar with the methods used in the explanation video?
- Once you watched the explanation video, could you explain how to solve the problem to somebody else?
Your answers to these questions can help you craft a better strategy for GMAT Math word problems, identifying exactly what you need to review to get better!
GMAT Word Problem Practice Questions
Now that you’ve learned how to approach word problems, we’ve put together a collection of them, direct from Magoosh’s product, for you to try! Video and text answers and explanations follow each question.
- Ann and Bob planted trees on Friday. What is the ratio of the number of trees that Bob planted to the number of trees that Ann planted?
(1) Ann planted 20 trees more than Bob planted.
(2) Ann planted 10 percent more trees than Bob planted.
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 1!
Click here for a text answer and explanation to GMAT Word Problem 1!
Our task is to determine the ratio of Bob’s trees to Ann’s trees. Let’s label these numbers of trees with variables:
Bob’s trees→B, Ann’s trees→A
With these variables, we can express the ratio we want to determine:
(B/A) =?
Statement 1:
Ann planted 20 trees more than Bob planted.
Let’s translate this into an equation using A and B:
( A=B+20 )
Now we can substitute this into our ratio, replacing A:
(B/A) = ( B/(B+20) )
No matter what simplifications we make, we cannot find a numerical value for this fraction. We would need a value for B. We cannot determine the ratio. Statement 1 by itself is not sufficient.
Statement 2:
Ann planted 10 percent more trees than Bob planted.
Let’s translate this into an equation using A and B:
(A=1.10 x B )
Again, let’s substitute this in for A in our ratio:
(B/A) = ( B/(1.10B) )
= (1/1.1 )
We found a value for the ratio of Bob’s trees to Ann’s trees. Statement 2 alone is sufficient.
- The Townville museum was open for 7 consecutive days. If the number of visitors each day was 3 greater than the previous day, how many visitors were there on the first day?
(1) There were a total of 126 visitors for the 7 days.
(2) The number of visitors on the seventh day was three times the number of visitors on the first day.
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 2!
Click here for a text answer and explanation to GMAT Word Problem 2!
If x is the number of visitors on the first day, then:
x = # of visitors on the 1st day
x + 3 = # of visitors on the 2nd day
x + 6 = # of visitors on the 3rd day
x + 9 = # of visitors on the 4th day
x + 12 = # of visitors on the 5th day
x + 15 = # of visitors on the 6th day
x + 18 = # of visitors on the 7th day
1) Adding up the number of visitors gives us:
x + (x + 3) + (x + 9) + (x + 12) + (x + 15) + (x + 18) = 126
We could simplify and solve this for x. So Statement 1 is sufficient.
2) x + 18 = 3x
Again, we can simplify this and solve for x. So Statement 2 is sufficient.
Answer: (D)
- Two teachers, Ms. Ames and Mr. Betancourt, each had N cookies. Ms. Ames was able to give the same number of cookies to each one of her 24 students, with none left over. Mr. Betancourt was also able to give the same number of cookies to each one of his 18 students, with none left over. If N > 0, what is the value of N?
(1) N<100
(2) N > 50
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 3!
Click here for a text answer and explanation to GMAT Word Problem 3!
This question is really about common multiples and the LCM (note that it is different than finding the set of all multiples, though!). If Ms. Ames can give each of her 24 students k cookies, so that they all get the same and none are left over, then 24k = N. Similarly, in Mr. Betancourt’s class, 18s = N.
What are the common multiples of 18 and 24?
18 = 2×9 = 2×3×3 = 6×3
24 = 3×8 = 2×2×2×3 = 6×4
From the prime factorizations, we see that GCF = 6, so the LCM is
LCM = 6×3×4 = 72
and all other common multiples of 18 and 24 are the multiples of 72: {72, 144, 216, 288, 360, …}
Statement #1: if N<100, the only possibility is N = 72. This statement, alone and by itself, is sufficient.
Statement #2: if N > 50, then N could be 72, or 144, or 216, or etc. Many possibilities. This statement, alone and by itself, is not sufficient.
Answer = (A)
- A certain zoo has mammals and reptiles and birds, and no other animals. The ratio of mammals to reptiles to birds is 11:8:5. How many birds are in the zoo?
(1) there are twelve more mammals in the zoo than there are reptiles
(2) if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 4!
Click here for a text answer and explanation to GMAT Word Problem 4!
A short way to do this problem. The prompt gives us ratio information. Each statement gives use some kind of count information, so each must be sufficient on its own. From that alone, we can conclude: answer = D. This is all we have to do for Data Sufficiency.
Here are the details, if you would like to see them.
Statement (1): there are twelve more mammals in the zoo than there are reptiles
From the ratio in the prompt, we know mammals are 11 “parts” and reptiles are 8 “parts”, so mammals have three more “parts” than do reptiles. If this difference of three “parts” consists of 12 mammals, that must mean there are four animals in each “part.” We have five bird “parts”, and if each counts as four animals, that’s 5*4 = 20 birds. This statement, alone and by itself, is sufficient.
Statement (2): if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1
Let’s say there are x animals in a “part”—this means there are currently 11x mammals and 5x birds. Suppose we add 16 mammals. Then the ratio of (11x + 16) mammals to 5x birds is 3:1.
(11x + 16)/(5x) = 3/1 = 3
11x + 16 = 3*(5x) = 15x
16 = 15x – 11x
16 = 4x
4 = x
So there are four animals in a “part”. The birds have five parts, 5x, so that’s 20 birds. This statement, alone and by itself, is sufficient.
Both statements are sufficient. Answer = D.
A Final Word on Word Problems
So, what is the trick to GMAT word problems? As you’ve seen in this post, there’s no one-size-fits-all trick—but there are plenty of strategies!
The strategies you’ve read about here can be used to take the given information and identify key words in a question. With them, you’ll be able to find everything from average speed to total distance traveled, from total time to total amount.
The key now is to put them into practice. Jot down these techniques or bookmark this post so you can come back as you continue your practice with GMAT word problems. You can also check out our posts on compound interest and Venn diagrams for more practice with GMAT word problems. Good luck!
This post was written with contributions from our Magoosh content creator, Rachel Kapelke-Dale.
-
Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as «member of the month» for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.
View all posts
Teaching your pupils to solve 2-step word problems and multi-step word problems at KS2 is one of hardest parts of a mastery led approach in maths. There are several cognitive functions at play, as children have to wrestle with their knowledge of maths vocabulary, maths operations, and often basic comprehension skills.
In this article we set out some of the sorts of maths word problems pupils can expect from the KS2 maths national curriculum and look at strategies for solving them. In total we’ve provided 30 KS2 word problems to work through, showing the variety of 2-step word problems and multi-step word problems pupils are likely to encounter.
What are word problems
Word problems in maths are sentences describing a real life scenario where children must apply their maths knowledge to reach a solution or unpick the maths problem.
To solve maths word problems children must be familiar with the maths language associated with the mathematical symbols they are used to in order to make sense of the word problem; for example: plus, more, total = add; difference, less, minus = subtract, etc.
What are two-step word problems?
Two-step word problems are problems in which two separate calculations (usually different operations) are required to reach the answer. By different operations we mean addition, subtraction, multiplication or division.
What are multi-step word problems?
Multi-step word problems are maths problems that require multiple calculations to solve them. They will usually will involve more than one operation and often more than one strand from the curriculum. For example a multi-step word problem on area and perimeter may also involve ratio and multiplication.
In KS2 SATs multi-step word problems can be awarded up to 3 marks for a correct answer, but 1 or 2 marks can be achieved by solving some of the steps in the problem correctly.
Two-step word problems and multi-step word problems pupils will encounter in KS2
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”.
The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
| Number and place value | 6 | 9 | 5 | 7 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |
As well as varying in content (sometimes by using a combination of strands in one problem, e.g. shape and calculations), word problems will also vary in complexity, from one-step to multi-step problems.
Different word problems will provide a different level of cognitive demand as an alternative method of adapting the level of difficulty. The STA mathematics test framework (2015) sets these out.
| Strand | 1 | 2 | 3 | 4 |
| Depth of understanding | recall of facts or application of procedures | use facts and procedures to solve simple problems | use facts and procedures to solve more complex problems | understand and use facts and procedures creatively to solve complex or unfamiliar problems |
| Computational complexity | no numeric steps | one, or a small number of numeric steps | a larger number of numeric steps all steps are simple | a larger number of numeric steps, at least one of which is more complex |
| Spatial reasoning | no spatial reasoning required | manipulation of the geometric information is required | complex manipulation of the geometric information is required | interpret, infer or generate new geometric information |
| Data interpretation | no data interpretation required | select and retrieve information | select and interpret information | generate or infer new information from data |
| Response strategy | select one or more responses or construct a simple response | construct a small set of responses | construct a straightforward explanation shows evidence of a method | construct a complex explanation |
Skills required for multi-step word problems
There is a high level of cognitive demand on children when they are faced with multi-step word problems: interpreting the question to find the arithmetic behind it and then calculating the arithmetic itself.
Therefore, a secure knowledge of times tables and a confident understanding of arithmetic are essential skills for being able to successfully solve word problems.

Year 3 to 6 Rapid Reasoning (Weeks 1-6)
Download 480 two-step and multi-step word problems for Years 3 to Year 6 (4 a day x 6 weeks for each year group)
Arithmetic within multi-step word problems
A useful strategy to use in class is to provide children with a list of arithmetic questions you have previously ‘extracted’ from some word problems.
Generally, children are much more confident with arithmetic than word problems, so they should be able to answer these with relative ease.
In the next lesson, give the children the word problems – after a while, ask them which they found easier and why.
Then show the children the arithmetic from the previous day and ask if they can see the similarities. They could then try to ‘extract’ the arithmetic from word problems themselves.
How to teach multi-step word problems
Here are two simple strategies that can be applied to most two-step word problems and multi-step word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
How to solve a year 6 multi-step word problem
Here’s an example.
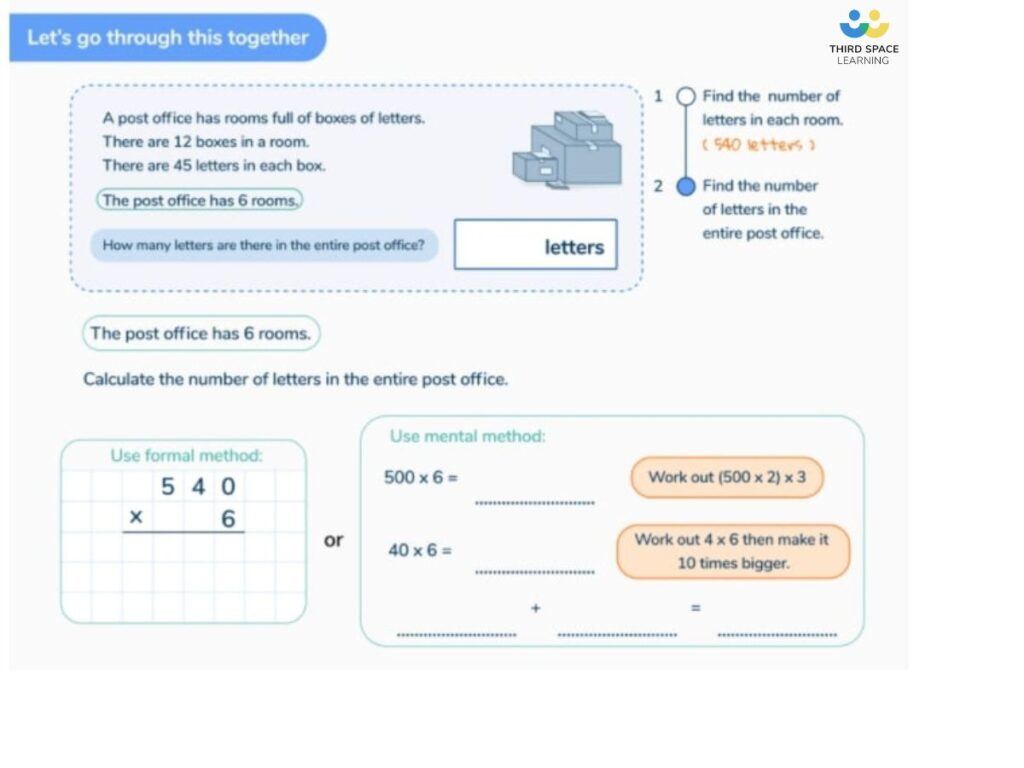
There are 29 pupils in a class. The teacher has 7 litres of apple juice. She pours 215 millilitres of apple juice for every pupil. How much apple juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
Bar modelling is always a brilliant way of representing even multi step word problems in year 6, but there are always other ways of drawing it out. For example, for this question, you could draw 29 pupils (or stick man x 29) with ‘215 ml’ above each one and then a half-empty bottle with ‘7 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
3. How to answer step by step
- There are 29 pupils in a class.
- The teacher has 7 litres of apple juice. 1) 7 litres = 7,000ml
- She pours 215 millilitres of apple juice for every pupil. 2) 215ml x 29 = 6,235ml
- How much apple juice is left over? 3) 7,000ml – 6,235ml = 765ml
How to solve a year 5 multi-step word problem
A similar approach can be used for this one.
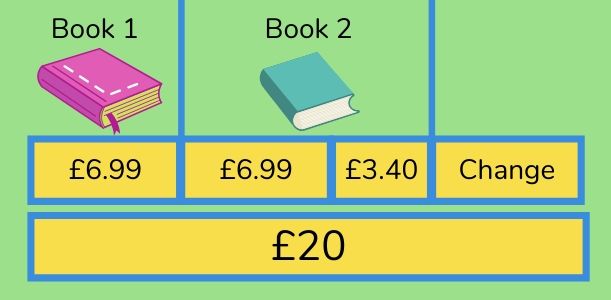
- Mara is in a bookshop. She buys one book for £6.99 and another that costs £3.40 more than the first book. She pays using a £20 notes. What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
3. How to answer step by step
- Mara is in a bookshop.
- She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
- She pays using a £20 note.
- What change does Mara get?
- £20 – £17.38 = £2.62
There are plenty more teacher guides and resources available from Third Space for problem solving in KS2. Find out how to develop maths reasoning skills in KS2, how to balance fluency, reasoning and problem solving in your maths lessons, and get ideas for developing and running maths investigations at KS2.
2-step word problems Year 3
With word problems for Year 3, children will move away from solely using concrete resources when solving word problems and start using written methods. This is also the year in which two-step problems will be introduced.
As some children may not be confident readers, it is important that word problems are explored in a variety of contexts: as a class, in groups, in partners, with an adult, with a list of ‘mathematical vocabulary’ accessible, etc. It is important that children’s literacy skills don’t hinder their progress or in maths.
Example Year 3 word problems
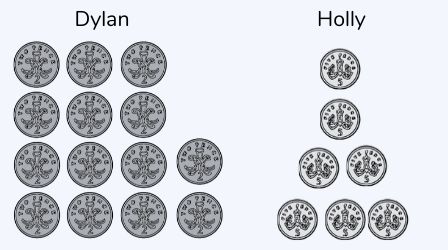
- Dylan and Holly have different amounts of money. Dylan has fifteen 2p coins. Holly has seven 5p coins. Who has the most money, and by how much? Answer: Holly by 5p.
- It takes Jamie 10 minutes to read 3 pages of his book. He reads 18 pages of his book before bed. How long does Jamie spend reading? Answer: 60 minutes.
2-step word problems Year 4
With word problems year 4, children should feel confident using the written method for each of the four operations. This year children will be presented with a variety of problems, including two-step problems, and be expected to work out the appropriate method required to solve each one.
While children should be focusing on formal written methods, it is important that concrete resources and pictorial representations are still used to consolidate their understanding.
Example Year 4 word problem
- Lily, Simon and Rose are each thinking of a number. The sum of their numbers is 9,989. Lily’s number is 1,832. Simon’s number is three thousand more than Lily’s. What is Rose’s number? Answer: 3,325

- Mia has a jug with 2.5 litres of water in it. She pours two glasses of 300ml and three glasses of 500ml. How much water is left in the jug? Give your answer in millilitres. Answer: 400ml
Multi-step word problems: Year 5
Although one and two-step word problems are the mainstay of Year 5 reasoning and problem solving, word problems for year 5 are also when children may start to extend their range to include multi-step problems;
In Upper Key Stage 2, word problems become more complex not only in the calculations (higher numbers, decimals etc.) but also the vocabulary – a subtlety of maths language may mean it is less obvious as to which operation is required.
In the first example below, the children are essentially being asked to add and divide by 7 – or find the ‘mean’ – but the word problem doesn’t use the vocabulary children usually associate with addition or division, such as total, sum, share, split, etc. To reduce the cognitive demand of questions such as these, the numbers could be altered so that children are still required to extract the calculations from the word problems but can then complete those calculations with simpler numbers.
Example Year 5 multi-step word problems
- A writer is working on two projects. She has one week to write 518 maths questions for one project and 476 questions for another project. If she completes the same number of questions every day, how many should she aim to complete each day? Answer: 142
- Walton Wanderers’ new shirt costs £29. In the first month after it was launched, the club shop sold 1,573 shirts. 54 shirts were returned because they did not fit. How much money did the club shop receive by selling the shirts? Answer: £44,051
Multi-step word problems Year 6
With word problems for year 6, children move on from 2-step word problems to multi-step word problems. These could include fractions, decimals and percentages. Some of the most complex problems in KS2 SATS papers are worth 3 marks – these are intended to challenge more able mathematicians.
As previously mentioned, one or two marks can be achieved for correctly solving different ‘steps’ of the problem even without arriving at the correct final answer.
Example Year 6 multi-step word problem
- Sarah makes jewellery with beads. Bracelets have 37 beads. Necklaces have 74 beads. Sarah makes 28 bracelets and 81 necklaces. How many beads does she use altogether? Answer: 7,030
- A field measures 15m by 20m. The field next to it is 300cm longer and 2.5m narrower. What is the difference in area between the two fields? Answer: 15m
For more like this, please refer to this collection of 35 year 6 maths reasoning questions to support teaching in the run up to SATs or if you want to focus specifically on using the bar model as a problem solving tool, try these Year 6 multi-step word problems.
2-step and multi-step word problems by topic
What follows are a series of 2-step word problems and multi-step worded problems based around the national curriculum objectives for each topic in maths. These show you a full range of question and problem types and the type of skills and knowledge your pupils will need to develop. We’ve also added some links to relevant word problems worksheets.

Year 3 to 6 Rapid Reasoning (Weeks 1-6)
Download 480 two-step and multi-step word problems for Years 3 to Year 6 (4 a day x 6 weeks for each year group)
Place value word problems
Place value problems appear throughout KS2. In Year 3, they will be based on five objectives:
- count from 0 in multiples of 4, 8, 50 and 100 (find 10 or 100 more or less than a given number)
- recognise the place value of each digit in a three-digit number
- compare and order numbers up to 1000
- identify, represent and estimate numbers using different representations
- read and write numbers up to 1000 in numerals and in words.
The progression in place value through KS2 ends in Year 6 with problems being based on three objectives:
- read, write, order and compare numbers up to 10 000 000 and determine the value of each digit
- round any whole number to a required degree of accuracy
- use negative numbers in context, and calculate intervals across zero.
Place value multi-step word problem: Year 6
- Mo uses four-digit cards and some zeros to make a seven-digit number on a place-value grid. Mo places the digit with the lowest value in the place with the highest value. He then places the 6 so that it has a value of 60,000. Finally, he places the digit with the highest value in the place with the lowest value. What could Mo’s number be? Write your answer in words.
- Answer: any of the following numbers: one million two hundred and sixty thousand and nine, one million sixty-two thousand and nine, one million sixty thousand two hundred and nine, one million sixty thousand and twenty-nine
For free multi-step word problems worksheets download these free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction problems appear throughout KS2. In Year 3, they will be based on three objectives:
- add and subtract numbers mentally
- add and subtract numbers with up to three digits, using formal written methods of columnar addition and subtraction estimate the answer to a calculation and use inverse operations to check answers
- solve problems, including missing number problems, using number facts, place value, and more complex addition and subtraction.
The progression in addition and subtraction through KS2 ends in Year 6 with problems being based on three objectives:
- perform mental calculations, including with mixed operations and large numbers
- solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why
- use estimation to check answers to calculations and determine, in the context of a problem, an appropriate degree of accuracy.
Addition and subtraction multi-step word problem: Year 6
- Buzzard Sky Diving Company have taken individual bookings worth £12,584 and group bookings worth £15,992. Some people have cancelled at the last minute. £1,629 has had to be returned to them. How much money has the sky diving company taken altogether? Answer: £26,947
For free multi-step and two-step word problems worksheets download these free addition and subtraction word problems for Years 3, 4, 5 and 6 and take a look at our collection of addition and subtraction word problems for Year 3- Year 6.
Tips for solving addition multi-step word problems
Children should be taught to recognise the vocabulary used in addition word problems to signify that the addition operation is required, for example, altogether, combined, total, sum etc. Be mindful that although more can be used for addition (e.g. What is 7 more than 9?), it can also be used for subtraction (e.g. How many more is 9 than 7?).
Addition multi-step word problem: Year 6
- Two different numbers add together to make an even total less than 20. Both numbers are greater than 6 and less than 12. What could the numbers be? Answer: 7 and 9, 7 and 11, 8 and 10
Tips for solving subtraction multi-step word problems
Children should be taught to recognise the vocabulary used in subtraction word problems to signify that the subtraction operation is required, for example, change (money), difference, fewer than, minus etc. They should also by now know their subtraction facts.
Subtraction two-step word problem: Year 5
- Carlos Varqueri – United’s star striker – has asked for a pay rise. He would like another £154,875 a year, so that his wage becomes £800,000 per year. How much money does Carlos earn at the moment? Answer: £645,125
Multiplication and division word problems
Multiplication and division problems appear throughout KS2. In Year 3, they will be based on three objectives:
- recall and use multiplication and division facts for the 3, 4 and 8 multiplication tables
- write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for two-digit numbers times one-digit numbers, using mental and progressing to formal written methods
- solve problems, including missing number problems, involving multiplication and division, including positive integer scaling problems and correspondence problems in which n objects are connected to m objects.
The progression in multiplication and division through KS2 ends in Year 6 with problems being based on six objectives:
- multiply multi-digit numbers up to 4 digits by a two-digit whole number using the formal written method of long multiplication
- divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context
- divide numbers up to 4 digits by a two-digit number using the formal written method of short division where appropriate, interpreting remainders according to the context
- perform mental calculations, including with mixed operations and large numbers
- identify common factors, common multiples and prime numbers
- use estimation to check answers to calculations and determine, in the context of a problem, an appropriate degree of accuracy.
Multiplication and division multi-step word problem: Year 6 (crossover with decimals)
- Lottie is playing a computer game. She has scored 67 points so far. She defeats a giant, which means that her score becomes ten times greater. However, she then gets lots in a maze, which means that her score becomes 1,000 times smaller. What is Lottie’s new score? Answer: 0.67
Tips for solving multiplication multi-step word problems
Children should be taught to recognise the vocabulary used in word problems to signify that the multiplication operation is required, for example, product, double, triple, groups etc. Be mindful that groups can be used in both multiplication and division problems, e.g. ‘What are 7 groups of 5?’ (multiplication) or ‘How many groups of 4 fit into 28?’ (division).
Multiplication multi-step word problem: Year 6
- There are 32 levels in a computer game. The maximum number of points that can be achieved for each level is 1,450. Hauwa completes the game and scores maximum points. How many points does Hauwa score altogether? Answer: 46,400
For free multi-step and two-step word problems worksheets download free multiplication word problems worksheets for Years 3, 4, 5 and 6
Children can practice can practice multiplication word problems in Third Space Learning’s online tuition programmes.
Tips for solving division multi-step word problems
Children should be taught to recognise the vocabulary used in division word problems to signify that the division operation is required, for example, halve, share, groups, split etc.
Division two-step word problem: Year 4
- A group of friends earn £120 by mowing lawns. They share the money equally. They get £15 each. How many friends are there in the group? Answer: 8
For free multi-step and two-step word problems worksheets download this free division word problems worksheet for Years 3, 4, 5 and 6
Mixed operations word problems
In the Year 3 non-statutory notes and guidance of the National Curriculum, it is recommended that pupils practise solving varied addition and subtraction questions and simple multiplication and division problems in contexts, deciding which of the four operations to use and why. These include measuring and scaling contexts, and correspondence problems in which m objects are connected to n objects.
At the end of KS2, the guidance states that pupils could practise addition, subtraction, multiplication and division for larger numbers, using the formal written methods of columnar addition and subtraction, short and long multiplication, and short and long division.
Mixed operations two-step word problem: Year 6 (crossover with money)

- A customer visits Dave’s DIY and buys 18 packs of screws, 18 packs of washers and a screwdriver. How much change is given from £20? Answer: £1.67
Four operations multi-step word problem: Year 5
- Oakthorpe Academy have been given a donation of £5,460 by the PTA. The School Council decide to use £1,755 on buying some new computer equipment. The rest is split equally between five year groups so they can decide for themselves how to spend the money. How much money will each year group have? Answer: £741
Read more
- 33 mental maths strategies you should be teaching in KS1 and KS2
- What are number facts? Activities to support memorisation.
- How primary schools develop fluency in maths
Fraction word problems
Fraction word problems require a good understanding of division and multiplication. Bar models or other pictorial representations are useful strategies in helping children solve problems like these.
Fraction problems appear throughout KS2. In Year 3, they will be based on seven objectives:
- count up and down in tenths
- recognise that tenths arise from dividing an object into 10 equal parts and in dividing one-digit numbers or quantities by 10
- recognise, find and write fractions of a discrete set of objects: unit fractions and non-unit fractions with small denominators
- recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators
- recognise and show, using diagrams, equivalent fractions with small denominators
- add and subtract fractions with the same denominator within one whole
- compare and order unit fractions, and fractions with the same denominators.
The progression in fractions through KS2 ends in Year 6 with problems being based on seven objectives:
- use common factors to simplify fractions and use common multiples to express fractions in the same denomination
- compare and order fractions, including fractions > 1
- add and subtract fractions with different denominators and mixed numbers, using the concept of equivalent fractions
- multiply simple pairs of proper fractions, writing the answer in its simplest form
- divide proper fractions by whole numbers
- associate a fraction with division and calculate decimal fraction equivalents
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
Fraction multi-step word problem: Year 6
- A bakery has 2 and 1/3 rhubarb pies left for sale. A customer buys 3/12 of a pie. What fraction of the pies is left? Write your answer as a mixed number. Answer: 2 and 1/12
For free multi-step and two-step word problems worksheets download fractions and decimals word problems for Years 3, 4, 5 and 6
Decimals word problems
Decimal word problems are commonly used in questions involving money, although they also often appear alongside fractions and/or percentages, requiring children to calculate their equivalences.
Decimal problems begin in Year 4 and will be based on six objectives:
- recognise and write decimal equivalents of any number of tenths or hundredths
- recognise and write decimal equivalents to ¼, ½, ¾
- find the effect of dividing a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths
- round decimals with one decimal place to the nearest whole number
- compare numbers with the same number of decimal places up to two decimal places; solve simple measure and money problems involving fractions and decimals to two decimal places.
The progression in decimals from Year 4 ends in Year 6 with problems being based on six objectives
- associate a fraction with division and calculate decimal fraction equivalents for a simple fraction
- identify the value of each digit in numbers given to three decimal places and multiply and divide numbers by 10, 100 and 1000 giving answers up to three decimal places
- multiply one-digit numbers with up to two decimal places by whole numbers
- use written division methods in cases where the answer has up to two decimal places; solve problems which require answers to be rounded to specified degrees of accuracy
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
Decimals two-step word problem: Year 6 (crossover with multiplication)
- A teaspoon contains 5.26ml of cough medicine. Amber takes 5 teaspoons full every day. How many millilitres of cough medicine does Amber take each day? Answer: 26.3ml
Percentage word problems
Children need a secure understanding in fractions before attempting percentage problems; they are therefore not introduced until Upper Key Stage 2. Percentage word problems begin in Year 5 and will be based on two objectives:
- recognise the per cent symbol (%) and understand that per cent relates to ‘number of parts per hundred’, and write percentages as a fraction with denominator 100, and as a decimal
- solve problems which require knowing percentage and decimal equivalents of ½, ¼, 1/5, 2/5, 4/5 and those fractions with a denominator of a multiple of 10 or 25.
The progression in percentage continues into Year 6 with problems being based on two objectives:
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts
- solve problems involving the calculation of percentages and the use of percentages for comparison.
Percentage multi-step word problem: Year 6
- Rachel and Max are playing a computer game. The game has 160 levels. Rachel’s counter says she has completed 60% of the game. Max’s counter says that he has completed 45% of the game. What levels are they each on? Answer: Rachel = Level 96, Max = Level 72
For free multi-step and two-step word problems worksheets download decimals and percentages word problems for Years 3, 4, 5 and 6
Measurement word problems
Many measurement word problems require children to convert between metric measures, thus children should be confident in multiplying and dividing by powers of 10. More complex measurement word problems (such as those involving imperial measures) may require children to have an understanding of ratio and proportion.
Word problems involving measures begin in Year 3 and will be based on six objectives:
- measure, compare, add and subtract: lengths (m/cm/mm); mass (kg/g), volume/capacity (l/ml)
- time word problems where children tell and write the time from an analogue clock, including using Roman numerals from I to XII, and 12-hour and 24-hour clocks
- estimate and read time with increasing accuracy to the nearest minute
- record and compare time in terms of seconds, minutes and hours
- use vocabulary such as o’clock, a.m./p.m., morning, afternoon, noon and midnight
- know the number of seconds in a minute and the number of days in each month, year and leap year; compare durations of events
The progression continues into Year 6 with problems being based on three objectives:
- solve problems involving the calculation and conversion of units of measure, using decimal notation up to three decimal places where appropriate
- use, read, write and convert between standard units, converting measurements of length, mass, volume and time from a smaller unit of measure to a larger unit, and vice versa, using decimal notation to up to three decimal places
- convert between miles and kilometres.
Measurement multi-step word problem: Year 6 (crossover with ratio)
- 5 miles are approximately equivalent to 8 km. Mr Norton’s car speedometer shows that he is travelling at 104 km/h. About how many miles per hour (mph) is the car travelling? Answer: 65 mph
Money word problems
Problems involving money link with decimals (money notation) and measures (converting between £ and p). Where possible, especially until their understanding is secure, children should be handling real money to help them solve problems.
Money word problems begin in Year 3 and will be based on one objective: add and subtract amounts of money to give change, using both £ and p in practical contexts. The non-statutory guidance in the curriculum recommends that pupils continue to become fluent in recognising the value of coins, by adding and subtracting amounts, including mixed units, and giving change using manageable amounts.
The decimal recording of money is introduced formally in year 4, where word problems will be based on one objective: solve simple measure and money problems involving fractions and decimals to two decimal places.
Money problems continue throughout KS2 but are not specifically mentioned in the National Curriculum beyond Year 4.
Two-step money word problem: Year 6 (crossover with mixed operations)
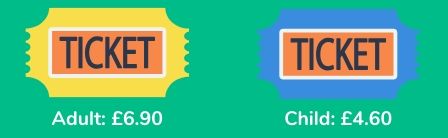
These are the different prices of tickets at a cinema.
- Jamaal’s dad buys two adults’ tickets and four children’s tickets. How much money do the tickets cost altogether? Answer: £32.20
Area word problems
Mathematical questions related to area require a secure understanding of arrays, times tables, multiplication, division and factors. Concrete resources such as Numicon and multilink can be used to support children to solve these problems.
Word problems involving area begin in Year 4 and will be based on one objective: find the area of rectilinear shapes by counting squares. The progression continues into Year 6 with problems being based on three objectives:
- recognise that shapes with the same areas can have different perimeters and vice versa
- recognise when it is possible to use formulae for area and volume of shapes
- calculate the area of parallelograms and triangles
Area multi-step word problem: Year 6
- A square has a side length of 6cm. A triangle has a base of 8cm and a perpendicular height of 7cm. What is the difference in their areas? Answer: 8cm2
Perimeter word problems
As well as being an important life skill, it is important for children to be able to measure accurately with a ruler for some aspects of this mathematical strand. As above, Numicon and multilink are extremely useful resources in supporting children in their calculation of perimeter word problems.
These problems begin in Year 3 and will be based on one objective: measure the perimeter of simple 2-D shapes. The progression continues into Year 6 with problems being based on one objective: recognise that shapes with the same areas can have different perimeters and vice versa.
Perimeter word problem: Year 6 (crossover with decimals and multiplication)
- Josh has drawn a square. Each side is 7.5cm. What is the perimeter of the square? Answer: 30cm
Ratio word problems
In my experience, ratio is most successful when taught with concrete resources such as multilink, Cuisenaire rods or beads. Once children are taught how to represent ratio word problems using equipment (and eventually transferring to a pictorial representation, such as a bar model), the process is a lot easier.
Children won’t encounter ratio word problems until Year 6, where they will be based on three objectives:
- solve problems involving the relative sizes of two quantities where missing values can be found by using integer multiplication and division facts
- solve problems involving similar shapes where the scale factor is known or can be found
- solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
Ratio word problem: Year 6 (crossover with measurement)
- A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
Order of operations word problems
Children won’t encounter word problems about the order of operations until Year 6, where they will be based on one objective: use knowledge of the order of operations to carry out calculations involving the four operations. The non-statutory guidance in the National Curriculum also recommends that children explore the order of operations using brackets (otherwise known as BODMAS or BIDMAS); for example, 2 + 1 x 3 = 5 and (2 + 1) x 3 = 9.
Bodmas word problem: Year 6
- Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
- 50 – 10 × 5 =
- 50 – 10 × 5 =
Volume word problems
Children won’t encounter volume-related word problems until Year 6, where they will be based on two objectives:
- recognise when it is possible to use formulae for area and volume of shapes
- calculate, estimate and compare volume of cubes and cuboids using standard units, including cubic centimetres and cubic metres, and extending to other units
Volume word problem: Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
Algebra word problems
Again algebra word problems only really come up in Year 6; the objectives they will be based on are:
- use simple formulae
- generate and describe linear number sequences
- express missing number problems algebraically
- find pairs of numbers that satisfy an equation with 2 unknowns
- enumerate possibilities of combinations of 2 variables
Algebra word problem: Year 6
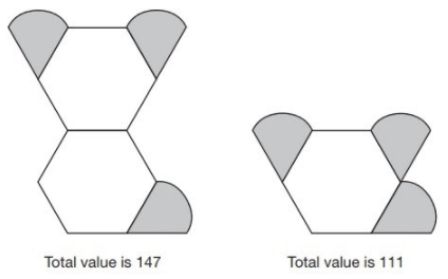
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
Amina is making designs with two different shapes. She gives each shape a value. Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
More support with KS2 word problems
For more multi-step and 2-step word problems register for free on the Third Space Learning Maths Hub which includes lots more printable word problems worksheets including as part of the free resources on offer a complete set of place value word problems with answer sheets for Year 3 to Year 6: All Kinds of Word Problems on Number and Place Value
If you have any pupils who are struggling to master word problems they may need a more intensive personalised intervention. Third Space Learning’s tuition follows a rigorous step by step process to teaching problem solving with excellent success – pupils make on average double their expected progress with us.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Word problems on division for fourth grade students are solved here step by step.
Consider the following examples on word problems involving division:
1. $5,876 are distributed equally among 26 men. How much money will each person get?
Solution:
Money received by 26 men = 5876 So, money received by one man = 5876 ÷ 26
= 226
Each man will get $226.
2. If 9975 kg of wheat is packed in 95 bags, how much wheat will each bag contain?
Solution:
Since 95 bags contain wheat 9975 kg
Therefore, 1 bag contains wheat (9975 ÷ 95) kg
= 105 kg
Each bag contains wheat = 105 kg
In a problem sum involving division, we have to be careful about using the remainder.
3. 89
people have been invited to a banquet. The caterer is arranging tables.
Each table can seat 12 people. How many tables are needed?
Solution:
To answer this question, we need to divide 89 by 12
89 ÷ 12
Quotient — 7
Remainder — 5
If the caterer arranges 7 tables, then 5 people will have no place to sit.
So he needs to arrange 7 + 1 = 8 tables.
4. How many hours are there in 1200 minutes?
Solution:
We know that there are 60 minutes in 1 hour.Divide the number of minutes by the number of minutes in 1 hour. We get, divide 1200 by 601200 ÷ 60 = 20
So there are 20 hours in 1200 minutes.
Answer: 20 hours.
5. A bus can hold 108 passengers. If there are 12 rows of seats on the bus, how many seats are in each row?
Solution:
Total number of passengers = 108
There are 12 rows of seats on the bus.
To find how many seats are there in each row, divide the total number of passengers by the number of rows of seats on the bus.
We get, divide 108 by 12
108 ÷ 12 = 9
Therefore, there are 9 seats in each row.
Answer: 9 seats.
6. Tom had 63 apples. He divides all apples evenly among 9 friends. How many apples did Tom give to each of his friends?
Solution:
Total number of apples = 63
There are 9 friends of seats on the bus.
To find how many apples Tom gave to each of his friends, divide the total number of apples by the number of friends.
We get, divide 63 by 9
63 ÷ 9 = 7
Therefore, Tom gives 7 apples to each of his friends.
Answer: 7 Apples
7. Mark baked 195 cookies and divided them equally into 13 packs. How many cookies did Mark put in each packet?
Solution:
Total number of cookies = 195
There are 13 packs.
To find how many cookies did Mark put in each packet, divide the total number of cookies by the number of packs.
We get, divide 195 by 13
195 ÷ 13 = 15
Therefore, Mark put 15 cookies in each pack.
Answer: 15 cookies.
9.
Nancy needs 5 lemons to make a glass of orange juice. If Nancy has 250
oranges, how many glasses of orange juice can she make?
Solution:
Total number of oranges = 250
She needs 5 lemons to make a glass of orange juice.
To
find how many glasses of orange juice can Nancy make, divide the total
number of oranges by the number of oranges needed for each glass of
orange juice.
We get, divide 250 by 5
250 ÷ 5 = 50
Therefore, Nancy can make 50 glasses of orange juice.
Answer: 50 glasses of orange juice.
10. In your classes you counted 120 hands. How many students were at the class?
Solution:
Total number of hands = 120
We have 2 hands.
To find how many students were at the class, divide the total number of hands by the number of hands we have.
We get, divide 120 by 2
220 ÷ 2 = 60
Therefore, there were 60 students at the class.
Answer: 60 students.
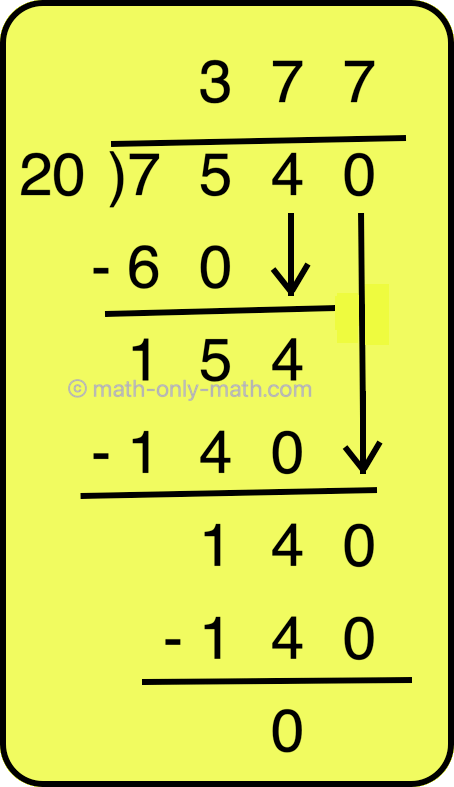
11. The total train fare for 20 persons is 7540 rupees. What is the fare for 1 person.
|
Solution: The total train fare = 7540 rupees Number of persons = 20 Train fare for 1 person = 7540 ÷ 20 = 377 |
|
These are the basic word problems on division.
Questions and Answers on Word Problems on Division:
1. 92 bags of cement can be
loaded in a truck. How many such trucks will be needed to load 2208 bags?
Answer: 24 trucks
2. The total train fare for 11
persons was $3850. What was the fare for one person?
Answer: $350
Related Concept
● Addition
● Word
Problems on Addition
● Subtraction
● Check
for Subtraction and Addition
● Word
Problems Involving Addition and Subtraction
● Estimating
Sums and Differences
● Find the
Missing Digits
● Multiplication
● Multiply
a Number by a 2-Digit Number
● Multiplication
of a Number by a 3-Digit Number
● Multiply a Number
● Estimating Products
● Word
Problems on Multiplication
● Multiplication
and Division
● Terms Used in
Division
● Division
of Two-Digit by a One-Digit Numbers
● Division
of Four-Digit by a One-Digit Numbers
● Division
by 10 and 100 and 1000
● Dividing Numbers
● Estimating
the Quotient
● Division
by Two-Digit Numbers
● Word
Problems on Division
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
If you looking for different questions on Sets you have come the right way. We have curated Word Problems on Sets with Step by Step Solutions for your understanding. Make use of them while practicing Sets Problems and increase your conceptual knowledge. In this, you will understand how to Solve Sets Word Problems using Venn Diagrams easily. If you need help on different concepts of Sets refer to Set Theory and learn the representation of a set, types of sets, etc. Check out the Solved Examples provided and learn how to solve related problems during your work.
1. Let A and B be two finite sets such that n(A) = 30, n(B) = 18 and n(A ∪ B) = 26, find n(A ∩ B)?
Solution:
Formula for n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
Rearranging it we get the n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
=30+18 – 26
= 22
Therefore, n(A ∩ B) = 22.
2. If If n(A – B) = 12, n(A ∪ B) = 45 and n(A ∩ B) = 15, then find n(B)?
Solution:
n(A∪B) = n(A – B) + n(A ∩ B) + n(B – A)
45 = 12+15 +n(B-A)
n(B-A) = 45-12-15
= 45-27
= 18
n(B) = n(A ∩ B) + n(B – A)
= 15+18
= 33
3. In a group of 80 people, 37 like cold drinks and 52 like hot drinks and each person likes at least one of the two drinks. Find How many people like both coffee and tea?
Solution:
Let A = Set of people who like cold drinks.
B = Set of people who like hot drinks.
Given
(A ∪ B) = 80 n(A) = 37 n(B) = 22 then;
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 37+52-80
= 89 – 80
= 9
Therefore, 9 people like both tea and coffee.
4. Let S={4, 5, 6}. Write all the possible partitions of S?
Solution:
Remember that partition of S is a collection of nonempty sets that are disjoint and their union is S.
Possible Partitions of S are
{4},{5},{6}
{4,5},{6}
{4,6},{5}
{5,6},{4}
{4,5,6}.
5. In a school, there are 30 teachers who teach Mathematics or Physics. Of these, 18 teach Mathematics and 6 teach both Physics and Mathematics. How many teach Physics only?
Solution:
Total Number of Teachers who teach Mathematics or Physics = 30
Number of Teachers who teach Mathematics n(M) = 18
Number of Teachers who teach both Mathematics and Physics n( M ∩ P) = 6
n(M) = 18 n( M ∩ P) = 6 and n (M ∪ P )= 30
n (M ∪ P ) = n(M) + n(P) – n(M ∩ P)
30 = 18 + n(P) – 6
30 = 12 + n(P)
⇒ n(P) = 30 – 12
⇒ n(P) = 18
Number of teachers teach Physics only = n( P – M)
n( P – M) = n(P) – n( M ∩ P )
= 18 – 6
n( P – M) = 12
Number of teachers who teach physics only is 12.
6. In a survey of 80 people, it was found that 35 people read newspaper H, 20 read newspaper T, 15 read the newspaper I, 5 read both H and I, 10 read both H and T, 7 read both T and I, 4 read all three newspapers. Find the number of people who read at least one of the newspapers?
Solution:
n(H) is the Number of People who read the newspaper H i.e. 35
n(I) is the Number of People who read the newspaper I i.e. 15
n(T) is the Number of People who read the newspaper T i.e. 20
n(H ∩ I) is the Number of People who read H and I i.e. 5
n(H ∩ T) is the Number of People who read H and T i.e 10
n(T ∩ I) is the Number of People who read T and I i.e. 7
n(H ∩ T ∩ I) is the Number of People who read all three Newspapers H, T, I i.e. 4
n(H ∪T ∪ I ) is the Number of people who read at least one of the newspapers
n(H ∪T ∪ I ) = n(H) + n(T) + n(I) – n(H ∩ T) – n(T ∩ I) – n(H ∩ I) + n(H ∩ T ∩ I)
n(H ∪T ∪ I )= 35+20+15-10-7-5+4
= 74-22
= 52
Therefore, the number of people who read at least one of the newspapers is 52.
7. In a school, all pupils play either Hockey or Football or both. 400 play Football, 150 play Hockey, and 130 play both the games. Find
(i) The number of pupils who play Football only,
(ii) The number of pupils who play Hockey only,
(iii) The total number of pupils in the school.
H = Hockey and F = Football
n (H ) = 150 n (F)= 400
n ( H ∩ F) = 130
(i) The number of pupils who only play Football = n (F – H )
n (F – H ) = n(F) – n( F ∩ H )
= 400 – 130
= 270
(ii) The number of pupils who only play Hockey = n (H – F )
n (H– F ) = n(H) – n( F ∩ H )
= 150 – 130
= 20
(iii) The total number of pupils in school
= n(H) + n(F) – n (F ∩ H)
= 150 + 400 – 130
= 420
Homework Q&A
•
Assignments
•
Essays
•
Papers
•
Study Guides
Homework help
Exam prep
Writing support
TOP WORD PROBLEM QUESTIONS
visibility_off Private questions are not visible.
|
|
Algebra Word Problem Graphing Utility on Desmos Webpage Assignment Algebraic equations college algebra Answered by |
|
|
College Algebra Miniature Golf Word Problem 6 college algebra Word Problem Answered by |
|
|
Criminal justice 3-1 APA Word Problem Answered by |
|
|
Ez pz math algebra Word Problem Answered by |
|
|
One word problem. Right triangle problems. right triangles Word Problem Answered by |
|
|
Please solve for the height of the tree in this word problem. Word Problem height of a tree Answered by |
|
|
The problem and the hints of how to solve the question attached in the file. Economic Word Problem Answered by |
|
|
Assignment Word Problem work Answered by |
|
|
Where will they meet? Describe in a brief sentence or two the approximate shape of the path taken by each. What is the exact value of the path length of each? calculus Word Problem Answered by |
|
|
Needing help on two math questions triangles Word Problem Answered by |
|
|
Answer the question showing steps physics Word Problem Answered by |
|
|
Calculus Matrices calculus Word Problem Answered by |
|
|
Random variable Word Problem answer Answered by |
|
|
Word problem What brand of appliance do you prefer Word Problem answer Answered by |
|
|
Cost Volume Profit Analysis excel memo Answered by |
|
|
Market analysis, accounting homework help excel accounting Answered by |
|
|
Word problem 2, math homework help Word Problem solve Answered by |
|
|
Word problem, math homework help Word Problem SHOW WORK Answered by |
|
|
In how many ways can the team of 4 be selected, assignment help Word Problem solve Answered by |
|
|
An identification code is to consist of three letters followed by four digits, homework help Word Problem solve Answered by |
|
|
Sample probability, math homework help Word Problem solve Answered by |
|
|
Attached word problem, math homework help Word Problem solve Answered by |
|
|
probability marbles probability Word Problem Answered by |
|
|
Expectation, math homework help Word Problem Expectation Answered by |
|
|
word problem, math homework help Word Problem determine Answered by |
|
|
What are the odds, math homework help Word Problem Odds Answered by |
|
|
probability, math homework help probability Word Problem Answered by |
|
|
Probability 2, math homework help probability Word Problem Answered by |
|
|
Probability, math homework help probability Word Problem Answered by |
|
|
Word problem, math homework help graph Word Problem Answered by |
|
|
Word math problem, math homework help graph Word Problem Answered by |
|
|
Word problem, math homework help Word Problem SHOW WORK Answered by |
|
|
QRB 501 Final Exam, accounting homework help excel Word Problem Answered by |
|
|
QRB/501 » Assignment research Word Problem Answered by |
|
|
2 Questions QRB 501 excel Word Problem Answered by |
|
|
5 questions Word problems excel Word Problem Answered by |
|
|
Write the standard form, math homework help equation algebra Answered by |
SITE RATINGS

Studypool

4.7

Trustpilot

4.5

Sitejabber

4.4