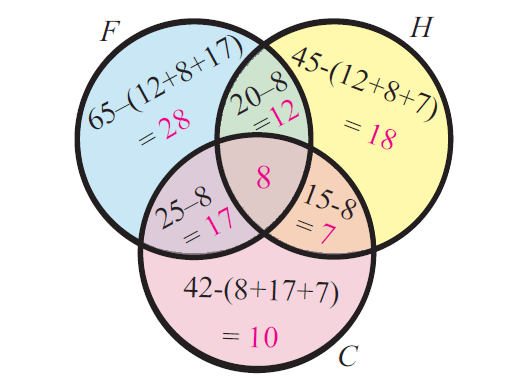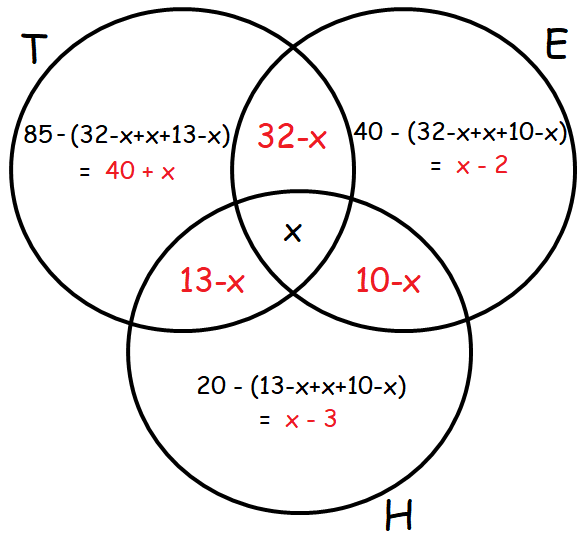Word problems on sets are solved here to get the basic ideas how to use the properties of union and intersection of sets.
Solved basic word problems on sets:
1. Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).
Solution:
Using the formula n(A ∪ B) = n(A) + n(B) — n(A ∩ B).
then n(A ∩ B) = n(A) + n(B) — n(A ∪ B)
= 20 + 28 — 36
= 48 — 36
= 12
2. If n(A — B) = 18, n(A ∪ B) = 70 and n(A ∩ B) = 25, then find n(B).
Solution:
Using the formula n(A∪B) = n(A — B) + n(A ∩ B) + n(B — A)
70 = 18 + 25 + n(B — A)
70 = 43 + n(B — A)
n(B — A) = 70 — 43
n(B — A) = 27
Now n(B) = n(A ∩ B) + n(B — A)
= 25 + 27
= 52
Different types on word problems on sets:
3. In a group of 60 people, 27 like cold drinks and 42 like hot drinks and each person likes at least one of the two drinks. How many like both coffee and tea?
Solution:
Let A = Set of people who like cold drinks.
B = Set of people who like hot drinks.
Given
(A ∪ B) = 60 n(A) = 27 n(B) = 42 then;
n(A ∩ B) = n(A) + n(B) — n(A ∪ B)
= 27 + 42 — 60
= 69 — 60 = 9
= 9
Therefore, 9 people like both tea and coffee.
4. There are 35 students in art class and 57 students in dance class. Find the number of students who are either in art class or in dance class.
• When two classes meet at different hours and 12 students are enrolled in both activities.
• When two classes meet at the same hour.
Solution:
n(A) = 35, n(B) = 57, n(A ∩ B) = 12
(Let A be the set of students in art class.
B be the set of students in dance class.)
(i) When 2 classes meet at different hours n(A ∪ B) = n(A) + n(B) — n(A ∩ B)
= 35 + 57 — 12
= 92 — 12
= 80
(ii) When two classes meet at the same hour, A∩B = ∅ n (A ∪ B) = n(A) + n(B) — n(A ∩ B)
= n(A) + n(B)
= 35 + 57
= 92
Further concept to solve word problems on sets:
5.
In a group of 100 persons, 72 people can speak English and 43 can speak
French. How many can speak English only? How many can speak French only
and how many can speak both English and French?
Solution:
Let A be the set of people who speak English.
B be the set of people who speak French.
A — B be the set of people who speak English and not French.
B — A be the set of people who speak French and not English.
A ∩ B be the set of people who speak both French and English.
Given,
n(A) = 72 n(B) = 43 n(A ∪ B) = 100
Now, n(A ∩ B) = n(A) + n(B) — n(A ∪ B)
= 72 + 43 — 100
= 115 — 100
= 15
Therefore, Number of persons who speak both French and English = 15
n(A) = n(A — B) + n(A ∩ B)
⇒ n(A — B) = n(A) — n(A ∩ B)
= 72 — 15
= 57
and n(B — A) = n(B) — n(A ∩ B)
= 43 — 15
= 28
Therefore, Number of people speaking English only = 57
Number of people speaking French only = 28
Word problems on sets using the different properties (Union & Intersection):
6.
In a competition, a school awarded medals in different categories. 36
medals in dance, 12 medals in dramatics and 18 medals in music. If these
medals went to a total of 45 persons and only 4 persons got medals in
all the three categories, how many received medals in exactly two of
these categories?
Solution:
Let A = set of persons who got medals in dance.
B = set of persons who got medals in dramatics.
C = set of persons who got medals in music.
Given,
n(A) = 36 n(B) = 12 n(C) = 18
n(A ∪ B ∪ C) = 45 n(A ∩ B ∩ C) = 4
We know that number of elements belonging to exactly two of the three sets A, B, C
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) — 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) — 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) — n(A ∩ B) — n(B ∩ C) — n(A ∩ C) + n(A ∩ B ∩ C)
Therefore, n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) — n(A ∪ B ∪ C)
From (i) required number
= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) — n(A ∪ B ∪ C) — 12
= 36 + 12 + 18 + 4 — 45 — 12
= 70 — 57
= 13
Apply set operations to solve the word problems on sets:
7.
Each student in a class of 40 plays at least one indoor game chess,
carrom and scrabble. 18 play chess, 20 play scrabble and 27 play carrom.
7 play chess and scrabble, 12 play scrabble and carrom and 4 play
chess, carrom and scrabble. Find the number of students who play (i)
chess and carrom. (ii) chess, carrom but not scrabble.
Solution:
Let A be the set of students who play chess
B be the set of students who play scrabble
C be the set of students who play carrom
Therefore, We are given n(A ∪ B ∪ C) = 40,
n(A) = 18, n(B) = 20 n(C) = 27,
n(A ∩ B) = 7, n(C ∩ B) = 12 n(A ∩ B ∩ C) = 4
We have
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) — n(A ∩ B) — n(B ∩ C) — n(C ∩ A) + n(A ∩ B ∩ C)
Therefore, 40 = 18 + 20 + 27 — 7 — 12 — n(C ∩ A) + 4
40 = 69 – 19 — n(C ∩ A)
40 = 50 — n(C ∩ A) n(C ∩ A) = 50 — 40
n(C ∩ A) = 10
Therefore, Number of students who play chess and carrom are 10.
Also, number of students who play chess, carrom and not scrabble.
= n(C ∩ A) — n(A ∩ B ∩ C)
= 10 – 4
= 6
Therefore, we learned how to solve different types of word problems on sets without using Venn diagram.
● Set Theory
● Sets Theory
● Representation of a Set
● Types of Sets
● Finite Sets and Infinite Sets
● Power Set
● Problems on Union of Sets
● Problems on Intersection of Sets
● Difference of two Sets
● Complement of a Set
● Problems on Complement of a Set
● Problems on Operation on Sets
● Word Problems on Sets
● Venn Diagrams in Different
Situations
● Relationship in Sets using Venn
Diagram
● Union of Sets using Venn Diagram
● Intersection of Sets using Venn
Diagram
● Disjoint of Sets using Venn
Diagram
● Difference of Sets using Venn
Diagram
● Examples on Venn Diagram
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Basic Stuff
To understand, how to solve Venn diagram word problems with 3 circles, we have to know the following basic stuff.
u —-> union (or)
n —-> intersection (and)
Addition Theorem on Sets
Theorem 1 :
n(AuB) = n(A) + n(B) — n(AnB)
Theorem 2 :
n(AuBuC) :
=n(A) + n(B) + n(C) — n(AnB) — n(BnC) — n(AnC) + n(AnBnC)
Explanation :
Let us come to know about the following terms in details.
n(AuB) = Total number of elements related to any of the two events A & B.
n(AuBuC) = Total number of elements related to any of the three events A, B & C.
n(A) = Total number of elements related to A
n(B) = Total number of elements related to B
n(C) = Total number of elements related to C
For three events A, B & C, we have
n(A) — [n(AnB) + n(AnC) — n(AnBnC)] :
Total number of elements related to A only
n(B) — [n(AnB) + n(BnC) — n(AnBnC)] :
Total number of elements related to B only
n(C) — [n(BnC) + n(AnC) + n(AnBnC)] :
Total number of elements related to C only
n(AnB) :
Total number of elements related to both A & B
n(AnB) — n(AnBnC) :
Total number of elements related to both (A & B) only
n(BnC) :
Total number of elements related to both B & C
n(BnC) — n(AnBnC) :
Total number of elements related to both (B & C) only
n(AnC) :
Total number of elements related to both A & C
n(AnC) — n(AnBnC) :
Total number of elements related to both (A & C) only
For two events A & B, we have
n(A) — n(AnB) :
Total number of elements related to A only
n(B) — n(AnB) :
Total number of elements related to B only
Practice Problems
Problem 1 :
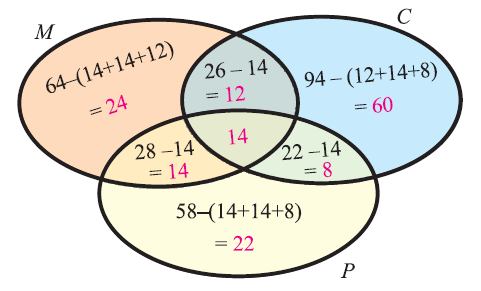
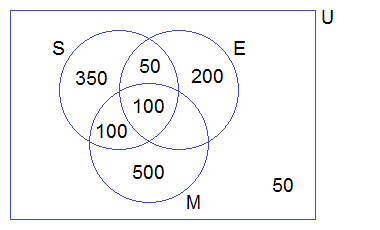
In a survey of university students, 64 had taken mathematics course, 94 had taken chemistry course, 58 had taken physics course, 28 had taken mathematics and physics, 26 had taken mathematics and chemistry, 22 had taken chemistry and physics course, and 14 had taken all the three courses. Find how many had taken one course only.
Solution :
Step 1 :
Let M, C, P represent sets of students who had taken mathematics, chemistry and physics respectively.
Step 2 :
From the given information, we have
n(M) = 64, n(C) = 94, n(P) = 58,
n(MnP) = 28, n(MnC) = 26, n(CnP) = 22
n(MnCnP) = 14
Step 3 :
From the basic stuff, we have
Number of students who had taken only Math
= n(M) — [n(MnP) + n(MnC) — n(MnCnP)]
= 64 — [28 + 26 — 14]
= 64 — 40
= 24
Step 4 :
Number of students who had taken only Chemistry :
= n(C) — [n(MnC) + n(CnP) — n(MnCnP)]
= 94 — [26+22-14]
= 94 — 34
= 60
Step 5 :
Number of students who had taken only Physics :
= n(P) — [n(MnP) + n(CnP) — n(MnCnP)]
= 58 — [28 + 22 — 14]
= 58 — 36
= 22
Step 6 :
Total number of students who had taken only one course :
= 24 + 60 + 22
= 106
Hence, the total number of students who had taken only one course is 106.
Alternative Method (Using venn diagram) :
Step 1 :
Venn diagram related to the information given in the question:
Step 2 :
From the venn diagram above, we have
Number of students who had taken only math = 24
Number of students who had taken only chemistry = 60
Number of students who had taken only physics = 22
Step 3 :
Total Number of students who had taken only one course :
= 24 + 60 + 22
= 106
Hence, the total number of students who had taken only one course is 106.
Problem 2 :
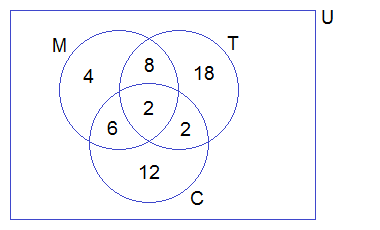
In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game).
Solution :
Step 1 :
Let F, H and C represent the set of students who play foot ball, hockey and cricket respectively.
Step 2 :
From the given information, we have
n(F) = 65, n(H) = 45, n(C) = 42,
n(FnH) = 20, n(FnC) = 25, n(HnC) = 15
n(FnHnC) = 8
Step 3 :
From the basic stuff, we have
Total number of students in the group is n(FuHuC).
n(FuHuC) is equal to
= n(F) + n(H) + n(C) — n(FnH) — n(FnC) — n(HnC) + n(FnHnC)
n(FuHuC) = 65 + 45 + 42 -20 — 25 — 15 + 8
n(FuHuC) = 100
Hence, the total number of students in the group is 100.
Alternative Method (Using Venn diagram) :
Step 1 :
Venn diagram related to the information given in the question :
Step 2 :
Total number of students in the group :
= 28 + 12 + 18 + 7 + 10 + 17 + 8
= 100
So, the total number of students in the group is 100.
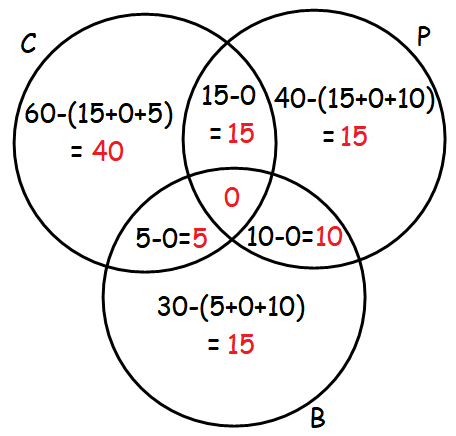
Problem 3 :
In a college, 60 students enrolled in chemistry,40 in physics, 30 in biology, 15 in chemistry and physics,10 in physics and biology, 5 in biology and chemistry. No one enrolled in all the three. Find how many are enrolled in at least one of the subjects.
Solution :
Let C, P and B represents the subjects Chemistry, Physics and Biology respectively.
Number of students enrolled in Chemistry :
n(C) = 60
Number of students enrolled in Physics :
n(P) = 40
Number of students enrolled in Biology :
n(B) = 30
Number of students enrolled in Chemistry and Physics :
n(CnP) = 15
Number of students enrolled in Physics and Biology :
n(PnB) = 10
Number of students enrolled in Biology and Chemistry :
n(BnC) = 5
No one enrolled in all the three. So, we have
n(CnPnB) = 0
The above information can be put in a Venn diagram as shown below.
From, the above Venn diagram, number of students enrolled in at least one of the subjects :
= 40 + 15 + 15 + 15 + 5 + 10 + 0
= 100
So, the number of students enrolled in at least one of the subjects is 100.
Problem 4 :
In a town 85% of the people speak Tamil, 40% speak English and 20% speak Hindi. Also 32% speak Tamil and English, 13% speak Tamil and Hindi and 10% speak English and Hindi, find the percentage of people who can speak all the three languages.
Solution :
Let T, E and H represent the people who speak Tamil, English and Hindi respectively.
Percentage of people who speak Tamil :
n(T) = 85
Percentage of people who speak English :
n(E) = 40
Percentage of people who speak Hindi :
n(H) = 20
Percentage of people who speak English and Tamil :
n(TnE) = 32
Percentage of people who speak Tamil and Hindi :
n(TnH) = 13
Percentage of people who speak English and Hindi :
n(EnH) = 10
Let x be the percentage of people who speak all the three language.
From the above Venn diagram, we can have
100 = 40 + x + 32 – x + x + 13 – x + 10 – x – 2 + x – 3 + x
100 = 40 + 32 + 13 + 10 – 2 – 3 + x
100 = 95 – 5 + x
100 = 90 + x
x = 100 — 90
x = 10%
So, the percentage of people who speak all the three languages is 10%.
Problem 5 :
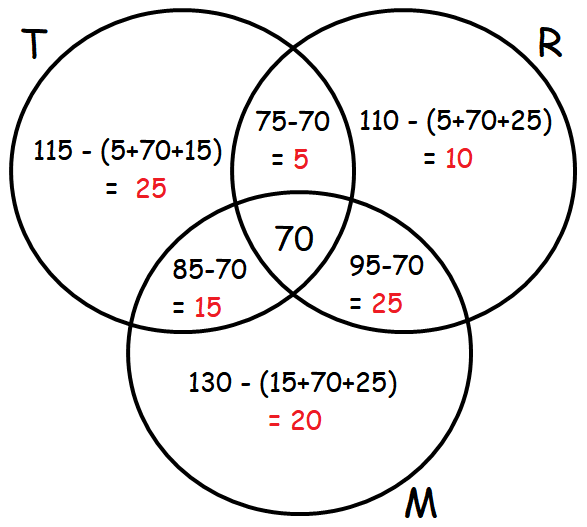
An advertising agency finds that, of its 170 clients, 115 use Television, 110 use Radio and 130 use Magazines. Also 85 use Television and Magazines, 75 use Television and Radio, 95 use Radio and Magazines, 70 use all the three. Draw Venn diagram to represent these data. Find
(i) how many use only Radio?
(ii) how many use only Television?
(iii) how many use Television and Magazine but not radio?
Solution :
Let T, R and M represent the people who use Television, Radio and Magazines respectively.
Number of people who use Television :
n(T) = 115
Number of people who use Radio :
n(R) = 110
Number of people who use Magazine :
n(M) = 130
Number of people who use Television and Magazines
n (TnM) = 85
Number of people who use Television and Radio :
n(TnR) = 75
Number of people who use Radio and Magazine :
n(RnM) = 95
Number of people who use all the three :
n(TnRnM) = 70
From the above Venn diagram, we have
(i) Number of people who use only Radio is 10.
(ii) Number of people who use only Television is 25.
(iii) Number of people who use Television and Magazine but not radio is 15.
Problem 6 :
In a class of 60 students, 40 students like math, 36 like science,
24 like both the subjects. Find the number of students who like
(i)
Math only, (ii) Science only (iii) Either Math or Science (iv) Neither
Math nor science.
Solution :
Step 1 :
Let M and S represent the set of students who like math and
science respectively.
Step 2 :
From the information given in the question, we have
n(M) = 40, n(S) = 36, n(MnS) = 24
Step
3 :
Answer
(i) :
Number of students who like math only :
= n(M) — n(MnS)
= 40 — 24
= 16
Step
4 :
Answer
(ii) :
Number of students who like science only :
= n(S) — n(MnS)
= 36 — 24
= 12
Step
5 :
Answer
(iii) :
Number of students who like either math or science :
= n(M or S)
= n(MuS)
= n(M) + n(S) — n(MnS)
= 40 + 36 — 24
= 52
Step
6 :
Answer
(iv) :
Total number students who like Math or Science subjects :
n(MuS) = 52
Number of students who like neither math nor science
= 60 — 52
= 8
Problem 7 :
At a certain conference of 100 people there are 29 Indian women
and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either
men or doctors. There are no foreign doctors. Find the number of women doctors
attending the conference.
Solution :
Step 1 :
Let M and D represent the set of Indian men and Doctors
respectively.
Step 2 :
From the information given in the question, we have
n(M) = 23, n(D) = 4,
n(MuD) = 24
Step 3 :
From the basic stuff, we have
n(MuD) = n(M) + n(D) — n(MnD)
24 = 23 + 4 — n(MnD)
n(MnD) = 3
n(Indian Men and Doctors) = 3
Step 4 :
So, out of the 4 Indian doctors, there are 3 men.
And the remaining 1 is Indian women doctor.
So, the number women doctors attending the conference is 1.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
If you looking for different questions on Sets you have come the right way. We have curated Word Problems on Sets with Step by Step Solutions for your understanding. Make use of them while practicing Sets Problems and increase your conceptual knowledge. In this, you will understand how to Solve Sets Word Problems using Venn Diagrams easily. If you need help on different concepts of Sets refer to Set Theory and learn the representation of a set, types of sets, etc. Check out the Solved Examples provided and learn how to solve related problems during your work.
1. Let A and B be two finite sets such that n(A) = 30, n(B) = 18 and n(A ∪ B) = 26, find n(A ∩ B)?
Solution:
Formula for n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
Rearranging it we get the n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
=30+18 – 26
= 22
Therefore, n(A ∩ B) = 22.
2. If If n(A – B) = 12, n(A ∪ B) = 45 and n(A ∩ B) = 15, then find n(B)?
Solution:
n(A∪B) = n(A – B) + n(A ∩ B) + n(B – A)
45 = 12+15 +n(B-A)
n(B-A) = 45-12-15
= 45-27
= 18
n(B) = n(A ∩ B) + n(B – A)
= 15+18
= 33
3. In a group of 80 people, 37 like cold drinks and 52 like hot drinks and each person likes at least one of the two drinks. Find How many people like both coffee and tea?
Solution:
Let A = Set of people who like cold drinks.
B = Set of people who like hot drinks.
Given
(A ∪ B) = 80 n(A) = 37 n(B) = 22 then;
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 37+52-80
= 89 – 80
= 9
Therefore, 9 people like both tea and coffee.
4. Let S={4, 5, 6}. Write all the possible partitions of S?
Solution:
Remember that partition of S is a collection of nonempty sets that are disjoint and their union is S.
Possible Partitions of S are
{4},{5},{6}
{4,5},{6}
{4,6},{5}
{5,6},{4}
{4,5,6}.
5. In a school, there are 30 teachers who teach Mathematics or Physics. Of these, 18 teach Mathematics and 6 teach both Physics and Mathematics. How many teach Physics only?
Solution:
Total Number of Teachers who teach Mathematics or Physics = 30
Number of Teachers who teach Mathematics n(M) = 18
Number of Teachers who teach both Mathematics and Physics n( M ∩ P) = 6
n(M) = 18 n( M ∩ P) = 6 and n (M ∪ P )= 30
n (M ∪ P ) = n(M) + n(P) – n(M ∩ P)
30 = 18 + n(P) – 6
30 = 12 + n(P)
⇒ n(P) = 30 – 12
⇒ n(P) = 18
Number of teachers teach Physics only = n( P – M)
n( P – M) = n(P) – n( M ∩ P )
= 18 – 6
n( P – M) = 12
Number of teachers who teach physics only is 12.
6. In a survey of 80 people, it was found that 35 people read newspaper H, 20 read newspaper T, 15 read the newspaper I, 5 read both H and I, 10 read both H and T, 7 read both T and I, 4 read all three newspapers. Find the number of people who read at least one of the newspapers?
Solution:
n(H) is the Number of People who read the newspaper H i.e. 35
n(I) is the Number of People who read the newspaper I i.e. 15
n(T) is the Number of People who read the newspaper T i.e. 20
n(H ∩ I) is the Number of People who read H and I i.e. 5
n(H ∩ T) is the Number of People who read H and T i.e 10
n(T ∩ I) is the Number of People who read T and I i.e. 7
n(H ∩ T ∩ I) is the Number of People who read all three Newspapers H, T, I i.e. 4
n(H ∪T ∪ I ) is the Number of people who read at least one of the newspapers
n(H ∪T ∪ I ) = n(H) + n(T) + n(I) – n(H ∩ T) – n(T ∩ I) – n(H ∩ I) + n(H ∩ T ∩ I)
n(H ∪T ∪ I )= 35+20+15-10-7-5+4
= 74-22
= 52
Therefore, the number of people who read at least one of the newspapers is 52.
7. In a school, all pupils play either Hockey or Football or both. 400 play Football, 150 play Hockey, and 130 play both the games. Find
(i) The number of pupils who play Football only,
(ii) The number of pupils who play Hockey only,
(iii) The total number of pupils in the school.
H = Hockey and F = Football
n (H ) = 150 n (F)= 400
n ( H ∩ F) = 130
(i) The number of pupils who only play Football = n (F – H )
n (F – H ) = n(F) – n( F ∩ H )
= 400 – 130
= 270
(ii) The number of pupils who only play Hockey = n (H – F )
n (H– F ) = n(H) – n( F ∩ H )
= 150 – 130
= 20
(iii) The total number of pupils in school
= n(H) + n(F) – n (F ∩ H)
= 150 + 400 – 130
= 420
Cardinality Relations
of Three Sets
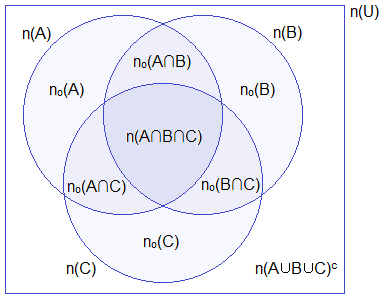
Let, U be the universal set. A, B and C are three overlapping sets which are subsets of the universal set U.
********************
10 Math Problems officially announces the release of Quick Math Solver, an Android App on the Google Play Store for students around the world.
********************
Look at the following Venn diagram and learn
the cardinal representation for the different portions.
n(A) = Number of elements in
set A
n(B) = Number of elements in set
B
n(C) = Number of elements in
set C
no(A) = Number of elements
in set A only
no(B) = Number of elements
in set B only
no(C) = Number of elements
in set C only
n(A∩B) = Number of elements
common in set A and B
n(A∩C) = Number of elements
common in set A and C
n(B∩C) = Number of elements
common in set B and C
no(A∩B) = Number of elements
common in set A and B only
no(A∩C) = Number of elements
common in set A and C only
no(B∩C) = Number of elements
common in set B and C only
n(A∩B∩C) = Number of elements common
to A, B and C
n(A∪B∪C) = Number of elements belongs to at
least one set A, B or C.
n(A∩B∩C)c = Number of elements
does not belong to the set A, B or C.
Formula on
Cardinality Relations of Three Sets
If A, B and C are subsets of universal set U then,
1.
n(A∪B∪C) = n(A) + n(B) + n(C) – n(A∩B) –
n(B∩C) – n(A∩C) + n(A∩B∩C)
2.
n(A∩B∩C) = n(A∪B∪C) – n(A) – n(B) – n(C) + n(A∩B) + n(B∩C) + n(A∩C)
3.
n(A∪B∪C)c = n(U) – n(A∪B∪C)
4.
no(A) = n(A) – n(A∩B) – n(A∩C) + n(A∩B∩C)
5.
no(B) = n(B) – n(A∩B) – n(B∩C) + n(A∩B∩C)
6.
no(C) = n(C) – n(A∩C) – n(B∩C) + n(A∩B∩C)
7.
no(A∩B) = n(A∩B) – n(A∩B∩C)
8.
no(B∩C) = n(B∩C) – n(A∩B∩C)
9.
no(A∩C) = n(A∩C) – n(A∩B∩C)
10.
Exactly two = no(A∩B) + no(B∩C) + no(A∩C)
11.
Exactly one = no(A) + no(B) + no(C)
12.
At least one = n(A∪B∪C)
13.
All three = n(A∩B∩C)
14.
None of them = n(A∪B∪C)c

Word Problems Based
on Three Sets
Workout Examples
Example 1: P, Q and R are subsets of a universal set U. If n(U) = 390, n(P) =
210, n(Q) = 165, n(R) = 120, n(P∩Q) = 60, n(Q∩R) = 45, n(A∩R) = 54 and n(P∩Q∩R)
= 24, illustrate this information in a Venn-diagram and find the following:
a.
no(P)
b.
no(Q)
c.
no(R)
d.
no(P∩Q)
e.
no(Q∩R)
f.
no(P∩R)
g.
n(P∪Q∪R)c
Solution:
Here,
Venn-diagram,
From the Venn-diagram above,
a.
no(P) = 120
b.
no(Q) = 84
c.
no(R) = 45
d.
no(P∩Q) = 36
e.
no(Q∩R) = 21
f.
no(P∩R) = 30
g.
n(P∪Q∪R)c = 30
Example 2: In a survey of a group of people, 60 liked tea, 45 liked coffee, 30
liked milk, 25 liked coffee as well as tea, 20 liked tea as well as milk, 15
liked coffee as well as milk and 10 liked all three. How many people were asked
this question? Solve by using Venn-diagram.
Solution:
Let C, T and M represent
the set of people who liked coffee, tea and milk respectively. Then,
∴ n(T) = 60
n(C) = 45
n(M) = 30
n(C∩T) = 25
n(T∩M) = 20
n(C∩M) = 15
n(C∩T∩M) = 10
Venn
diagram,
Now,
n(T∪C∪M)
= n(T) + n(C) + n(M)
– n(C∩T) – n(T∩M) – n(C∩M) + n(C∩T∩M)
= 60 + 45
+ 30 – 25 – 20 – 15 + 10
= 85
Hence, the required number of people = 85.
Example 3: In an examination, 40% of candidates passed in mathematics, 45% in
Science, and 55% in Health. If 10% passed in Mathematics and Science, 20% in
Science and Health and 15% in Health and Mathematics,
(i) Illustrate the above information by drawing a Venn diagram.
(ii) Find the pass percentage in all three subjects.
Solution:
Let M, S, and H denote the
set of students who passed in Maths, Science and Health respectively.
∴ n(U) = 100% = n(M∪S∪H)
n(M) = 40%
n(S) = 45%
n(H) = 55%
n(M∩S) = 10%
n(S∩H) = 20%
n(H∩M) = 15%
Since,
there is no one who failed in all three
subjects,
n(M∪S∪H) = n(U) = 100%
(i)
Venn-diagram,
(ii)
n (M∩S∩H)
= n(M∪S∪H) – n(M) – n(S) – n(H) + n(M∩S) + n(S∩H) + n(M∩H)
= 100 – 40 – 45 – 55 + 10 + 20 + 15%
= 5%
∴ 5% passed in all three subjects.
Example 4: Out of 1350 candidates, 600 passed in Science, 700 in Mathematics,
350 in English and 50 failed in all three subjects. If 200 passed in
Science and Mathematics, 150 in Science and English, 100 in Mathematics and
English,
(i) How many candidates passed in all three subjects?
(ii) Illustrate the above information in a Venn-diagram.
Solution:
Let, the set of candidates who passed in Science, Mathematics
and English be S, M, and E.
∴ n(U) = 1350
n(S) = 600
n(M) = 700
n(E) = 350
n(S∪M∪E)c = 50
n(S∩M) = 200
n(M∩E) = 100
n(S∩E) = 150
We know,
n(S∪M∪E)
= n(U) – n(S∪M∪E)c
= 1350 – 50
= 1300
Now,
n(A∩B∩C)
= n(A∪B∪C) – n(A) – n(B) – n(C) + n(A∩B) + n(B∩C) + n(A∩C)
= 1300 – 600 – 700 – 350 + 200 + 100 + 150
= 100
Therefore,
(i) 100 candidates passed in
all three subjects.
(ii) Venn-diagram,
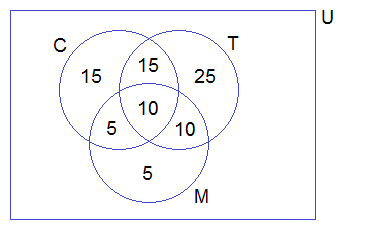
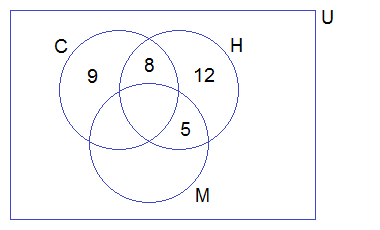
Example 5: In a group of students, 25 study computer, 28 study Health, 20
study Mathematics, 9 study Computer only, 12 study Health only, 8 study
Computer and Health only and 5 students study Health and Mathematics only.
(i)
Draw a Venn diagram to
illustrate the above information.
(ii)
Find how many students study
all the subjects.
(iii) How many students are there altogether?
Solution:
Let C, H, and M be the set
of students who study Computer, Health, and Mathematics respectively.
∴ n(C) = 25
n(H) = 28
n(M) = 20
no(C) = 9
no(H) = 12
no(C∩H) = 8
no(H∩M) = 5
Filling the above information in Venn-diagram,
we get
From the above Venn-diagram,
n(C∩H∩M) + 8 + 12 + 5 = n(H)
or, n(C∩H∩M)
+ 25 = 28
or, n(C∩H∩M)
= 28 – 25
or, n(C∩H∩M)
= 3
Again,
no(C∩M)
+ n(C∩H∩M) + 9 + 8 = n(C)
or, no(C∩M) + 3 + 9 + 8 = 25
or, no(C∩M) + 20 = 25
or, no(C∩M) = 25 – 20
or, no(C∩M) = 5
Again,
no(M)
+ no(C∩M) + n(C∩H∩M) + 5 = n(M)
or, no(M) + 5 + 3 + 5 = 20
or, no(M) + 13 = 20
or, no(M) = 20 – 13
or, no(M) = 7
(i)
Venn-diagram:
(ii)
n(C∩H∩M) = 3 students study all subjects.
(iii)
From the above venn-diagram,
n(C∪H∪M)
= 9 + 8 + 3 + 5 + 12 + 5 + 7
= 49
∴ There are 49 students altogether.
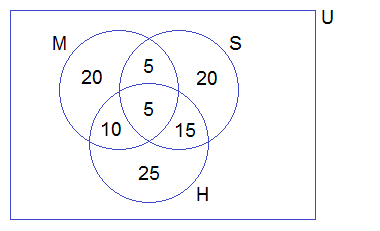
Example
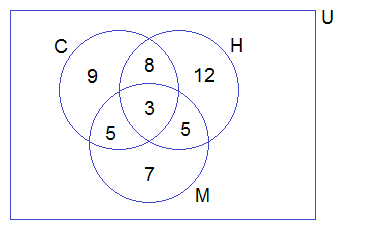
6: In a group of people, 20 like milk, 30 like tea,
22 like coffee, 12 like coffee only, 6 like milk and coffee only, 2 like tea and coffee only and 8 like milk
and tea only. Show these information in a Venn-diagram and find:
(i)
How many like
at least one drink?
(ii)
How many like
exactly one drink?
Solution:
Let the set of people who like milk, tea, and coffee
be M, T, and C.
∴ n(M)
= 20
n(T) = 30
n(C) = 22
no(C) = 12
no(M∩C) = 6
no(T∩C) = 2
no(M∩T) = 8
Filling the above information in the
Venn-diagram, we get
From the above Venn-diagram,
n(M∩T∩C) + 6 + 12 + 2 = n(C)
i.e. n(M∩T∩C)
+ 20 = 22
or, n(M∩T∩C)
= 22 – 20
or, n(M∩T∩C)
= 2
Again,
no(M) + 6 + n(M∩T∩C) + 8 = n(M)
i.e. no(M)
+ 6 + 2 + 8 = 20
or, no(M)
+ 16 = 20
or, no(M)
= 20 – 16
or, no(M)
= 4
Again,
no(T) + 2 + n(M∩T∩C) + 8 = n(T)
i.e. no(T)
+ 2 + 2 + 8 = 30
or, no(T)
+ 12 = 30
or, no(T)
= 30 – 12
or, no(T)
= 18
Venn-diagram,
From the venn-diagram,
(i)
n(M∪C∪T)
= 4 + 6 + 12 + 2 + 18 + 8 + 2
= 52
∴ 52 like at least one drink.
(ii)
no(M)
+ no(C) + no(T)
= 4 + 12 +18
= 34
∴ 34 like exactly one drink.
If you have any questions or problems regarding the Word Problems Based on Three Sets, you can ask here, in the comment section below.
Was this article helpful? LIKE
and SHARE with your friends…
Word problems on sets are solved here to get the basic ideas how to use the properties of union and intersection of sets.
Solved basic word problems on sets:
1. Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).
Solution:
Using the formula n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
then n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 20 + 28 – 36
= 48 – 36
= 12
2. If n(A – B) = 18, n(A ∪ B) = 70 and n(A ∩ B) = 25, then find n(B).
Solution:
Using the formula n(A∪B) = n(A – B) + n(A ∩ B) + n(B – A)
70 = 18 + 25 + n(B – A)
70 = 43 + n(B – A)
n(B – A) = 70 – 43
n(B – A) = 27
Now n(B) = n(A ∩ B) + n(B – A)
= 25 + 27
= 52
Different types on word problems on sets:
3. In a group of 60 people, 27 like cold drinks and 42 like hot drinks and each person likes at least one of the two drinks. How many like both coffee and tea?
Solution:
Let A = Set of people who like cold drinks.
B = Set of people who like hot drinks.
Given
(A ∪ B) = 60 n(A) = 27 n(B) = 42 then;
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 27 + 42 – 60
= 69 – 60 = 9
= 9
Therefore, 9 people like both tea and coffee.
4. There are 35 students in art class and 57 students in dance class. Find the number of students who are either in art class or in dance class.
• When two classes meet at different hours and 12 students are enrolled in both activities.
• When two classes meet at the same hour.
Solution:
n(A) = 35, n(B) = 57, n(A ∩ B) = 12
(Let A be the set of students in art class.
B be the set of students in dance class.)
(i) When 2 classes meet at different hours n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 35 + 57 – 12
= 92 – 12
= 80
(ii) When two classes meet at the same hour, A∩B = ∅ n (A ∪ B) = n(A) + n(B) – n(A ∩ B)
= n(A) + n(B)
= 35 + 57
= 92
Further concept to solve word problems on sets:
5.
In a group of 100 persons, 72 people can speak English and 43 can speak
French. How many can speak English only? How many can speak French only
and how many can speak both English and French?
Solution:
Let A be the set of people who speak English.
B be the set of people who speak French.
A – B be the set of people who speak English and not French.
B – A be the set of people who speak French and not English.
A ∩ B be the set of people who speak both French and English.
Given,
n(A) = 72 n(B) = 43 n(A ∪ B) = 100
Now, n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 72 + 43 – 100
= 115 – 100
= 15
Therefore, Number of persons who speak both French and English = 15
n(A) = n(A – B) + n(A ∩ B)
⇒ n(A – B) = n(A) – n(A ∩ B)
= 72 – 15
= 57
and n(B – A) = n(B) – n(A ∩ B)
= 43 – 15
= 28
Therefore, Number of people speaking English only = 57
Number of people speaking French only = 28
Word problems on sets using the different properties (Union & Intersection):
6.
In a competition, a school awarded medals in different categories. 36
medals in dance, 12 medals in dramatics and 18 medals in music. If these
medals went to a total of 45 persons and only 4 persons got medals in
all the three categories, how many received medals in exactly two of
these categories?
Solution:
Let A = set of persons who got medals in dance.
B = set of persons who got medals in dramatics.
C = set of persons who got medals in music.
Given,
n(A) = 36 n(B) = 12 n(C) = 18
n(A ∪ B ∪ C) = 45 n(A ∩ B ∩ C) = 4
We know that number of elements belonging to exactly two of the three sets A, B, C
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
Therefore, n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C)
From (i) required number
= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C) – 12
= 36 + 12 + 18 + 4 – 45 – 12
= 70 – 57
= 13
Apply set operations to solve the word problems on sets:
7.
Each student in a class of 40 plays at least one indoor game chess,
carrom and scrabble. 18 play chess, 20 play scrabble and 27 play carrom.
7 play chess and scrabble, 12 play scrabble and carrom and 4 play
chess, carrom and scrabble. Find the number of students who play (i)
chess and carrom. (ii) chess, carrom but not scrabble.
Solution:
Let A be the set of students who play chess
B be the set of students who play scrabble
C be the set of students who play carrom
Therefore, We are given n(A ∪ B ∪ C) = 40,
n(A) = 18, n(B) = 20 n(C) = 27,
n(A ∩ B) = 7, n(C ∩ B) = 12 n(A ∩ B ∩ C) = 4
We have
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
Therefore, 40 = 18 + 20 + 27 – 7 – 12 – n(C ∩ A) + 4
40 = 69 – 19 – n(C ∩ A)
40 = 50 – n(C ∩ A) n(C ∩ A) = 50 – 40
n(C ∩ A) = 10
Therefore, Number of students who play chess and carrom are 10.
Also, number of students who play chess, carrom and not scrabble.
= n(C ∩ A) – n(A ∩ B ∩ C)
= 10 – 4
= 6
Therefore, we learned how to solve different types of word problems on sets without using Venn diagram.
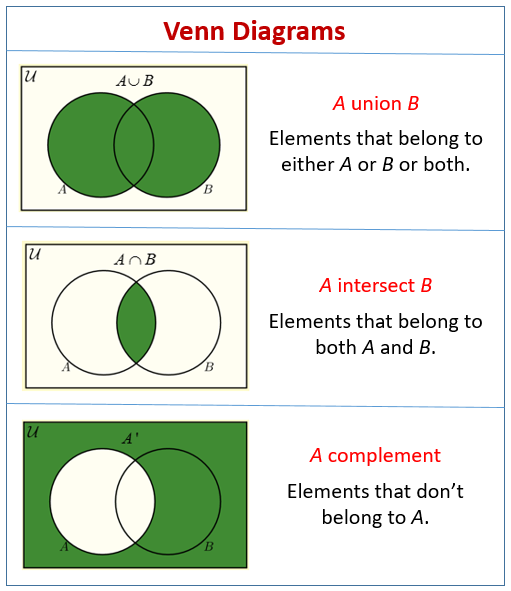
What Are Venn Diagrams?
Venn diagrams are the principal way of showing sets in a diagrammatic form. The method consists primarily
of entering the elements of a set into a circle or ovals.
Before we look at word problems, see the following diagrams to recall how to use Venn Diagrams to
represent Union, Intersection and Complement.
How To Solve Problems Using Venn Diagrams?
This video solves two problems using Venn Diagrams. One with two sets and one with three sets.
Problem 1:
150 college freshmen were interviewed.
85 were registered for a Math class,
70 were registered for an English class,
50 were registered for both Math and English.
a) How many signed up only for a Math Class?
b) How many signed up only for an English Class?
c) How many signed up for Math or English?
d) How many signed up neither for Math nor English?
Problem 2:
100 students were interviewed.
28 took PE, 31 took BIO, 42 took ENG, 9 took PE and BIO, 10 took PE and ENG, 6 took BIO and ENG,
4 took all three subjects.
a) How many students took none of the three subjects?
b) How many students took PE but not BIO or ENG?
c) How many students took BIO and PE but not ENG?
- Show Video Lesson
How And When To Use Venn Diagrams To Solve Word Problems?
Problem:
At a breakfast buffet, 93 people chose coffee and 47 people chose juice. 25 people chose both coffee
and juice. If each person chose at least one of these beverages, how many people visited the buffet?
- Show Video Lesson
How To Use Venn Diagrams To Help Solve Counting Word Problems?
Problem:
In a class of 30 students, 19 are studying French, 12 are studying Spanish and 7 are studying both
French and Spanish. How many students are not taking any foreign languages?
- Show Video Lesson
Probability, Venn Diagrams And Conditional Probability
This video shows how to construct a simple Venn diagram and then calculate a simple conditional
probability.
Problem:
In a class, P(male)= 0.3, P(brown hair) = 0.5, P (male and brown hair) = 0.2
Find
(i) P(female)
(ii) P(male| brown hair)
(iii) P(female| not brown hair)
- Show Video Lesson
Venn Diagrams With Three Categories
Example:
A group of 62 students were surveyed, and it was found that each of the students surveyed liked at
least one of the following three fruits: apricots, bananas, and cantaloupes.
34 liked apricots.
30 liked bananas.
33 liked cantaloupes.
11 liked apricots and bananas.
15 liked bananas and cantaloupes.
17 liked apricots and cantaloupes.
19 liked exactly two of the following fruits: apricots, bananas, and cantaloupes.
a. How many students liked apricots, but not bananas or cantaloupes?
b. How many students liked cantaloupes, but not bananas or apricots?
c. How many students liked all of the following three fruits: apricots, bananas, and cantaloupes?
d. How many students liked apricots and cantaloupes, but not bananas?
- Show Video Lesson
Venn Diagram Word Problem
Here is an example on how to solve a Venn diagram word problem that involves three intersecting sets.
Problem:
90 students went to a school carnival. 3 had a hamburger, soft drink and ice-cream. 24 had hamburgers.
5 had a hamburger and a soft drink. 33 had soft drinks. 10 had a soft drink and ice-cream.
38 had ice-cream. 8 had a hamburger and ice-cream. How many had nothing?
(Errata in video: 90 — (14 + 2 + 3 + 5 + 21 + 7 + 23) = 90 — 75 = 15)
- Show Video Lesson
Venn Diagrams With Two Categories
This video introduces 2-circle Venn diagrams, and using subtraction as a counting technique.
- Show Video Lesson
How To Use 3-Circle Venn Diagrams As A Counting Technique?
Learn about Venn diagrams with two subsets using regions.
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
See the word problems solved here to get the basic ideas on how you should be using properties of set’s union and intersection.
Word Problems:
Example 1. Let finite sets, Set A and Set B like n (A) = 25, n (B) = 29; n (A ∪ B) = 38, so, find –
n (A ∩ B).
Solution:
Using formula of union
= n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
then, n (A ∩ B) = n (A) + n (B) – n (A ∪ B)
= 25 + 29 – 38
= 54 – 38
= 16
Example 2. If n (A – B) = 20, n(A ∪ B) = 60 and n(A ∩ B) = 30, then find n(B).
Solution:
Using formula,
n (A∪B) = n (A – B) + n (A ∩ B) + n (B – A)
60 = 20 + 30 + n(B – A)
60 = 50 + n(B – A)
n(B – A) = 60 – 50
n(B – A) = 10
Now, n(B) = n(A ∩ B) + n(B – A)
= 30 + 10
= 40
Different categories of word problems regarding sets:
Question 3. A group of 70 people is there, 50 people like hot soups, and 28 people like cold soups, and each individual like at least one out of 2 soups. How many people like tea and coffee?
Solution:
Let take,
A = Set of individuals liking cold soups.
B = Set of individuals liking hot soups.
Given,
- (A ∪ B) = 70n
- (A) = 50
- n(B) = 28 then;
As per formula , n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 50 + 28 – 70
= 78 – 70 = 8
= 8
Thus, 8 people like coffee and tea
Another Example:
In a school where 600 students are there, 200 like history subject, 160 like English and 50 like both History and English. Find the number of students who like
- Students who like History; not English
- Students who like English; not History
- Students who either like History or English
Solution
Let the total number of students be U that is, the universal set.
Assuming A = set of a number of students who favor History.
Assuming B = set of a number of students who favor English.
Here, n (U) = 600 n (A) = 200 n (B) = 160 n (A∩B) = 50
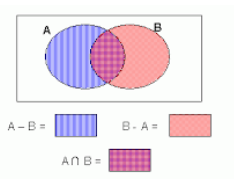
Here, you have to determine the number of students who favor History but not English, so to find A-B:
As shown in the Venn diagram,
A = (A-B) ∪ (A∩B)
n (A) = n (A-B) + n (A∩B)
n (A-B) = n (A) – n (A∩B)
= 200 – 50 = 150
Therefore, the numbers of students who favor only History but not English = 150
Here, you have to determine the number of students who favor English but not like History, so to find B-A:
B = (B-A) ∪ (A∩B)
n (B) = n (B-A) +n (A∩B)
n (B-A) = n (B)- n (A∩B)
= 160 – 50 = 110
Therefore, the numbers of students who favor only English but not History are= 110.
Here we have to find the number of students who like either English or History.
n (A∪B) = n (A) + n (B) – n (A∩B)
= 200 + 160 – 50
= 310
Next Word Problem:
Question: A competition was held in the school where students were given awards in different groups. 46 medals were given in dance, 22 medals in sports, and a total of 15 medals in English debate. If these medals were given to 44 total students and only 5 students got medals in each of the 3 groups, then how many medals are acknowledged in exactly 2 of these groups?
In a competition, a school awarded medals in different categories. 36 medals in dance, 12 medals in dramatics and 18 medals in music. If these medals went to a total of 45 persons and only 4 persons got medals in all the three categories, how many received medals in exactly two of these categories?
Solution:
Assuming A = set of students who got medals in dance.
B = set of students who got medals in sports.
C = set of persons who got medals in English Debate.
Given,
n(A) = 46 n(B) = 22 n(C) = 15
n(A ∪ B ∪ C) = 44 n(A ∩ B ∩ C) = 5
As we know the number of elements which belongs to exactly 2 out of three sets A, B, C
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C)
Therefore, n(A ∩ B) + n(A ∩ C) + n(B ∩ C) = n(A) + n(B) + n(C) – n(A ∪ B ∪ C) + n(A ∩ B ∩ C)
From (i) the required number
= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C) – 12
= 46 + 22 + 15 + 4 – 44 – 12
= 85 – 12
= 73

Venn diagram word problems are based on union, intersection, complement and difference of two sets. This batch of printable word problems on Venn diagram with two circles for students of grade 5 through grade 8 is illustrated with images, numbers, words and symbols. Few word problems may contain universal set. Use the key information from the given data to solve the word problems. Click on our free worksheets and kick-start your practice!
Reading Venn Diagram — Type 1
The elements of the set are represented as pictures on the two circles of these Venn diagrams. Read each Venn diagram and answer the given questions.
Reading Venn Diagram — Type 2
The elements of the set are multiples, names, days, etc. Answer the word problems that follow the Venn diagram on each printable worksheet. Children should learn to differentiate the overlapping regions and the relation between the sets at the end of the practice.
Reading Venn Diagram — Type 3
These Venn diagram word problem pdfs require the 5th grade and 6th grade children to count the number of elements in the region. The cross-markings represent the customers in cafes, pizzeria, books in the library, park goers, or members of a gym.
Drawing Venn Diagram — No Universal Set
Follow the direction and create a Venn diagram with two intersecting circles for the given data. Fill in the key information to complete the Venn diagram with 2 circles. Use all the available information to answer the questions.
Drawing Venn Diagram — With a Universal Set
Task 7th grade and 8th grade students to draw a Venn diagram with a universal set and fill in each region with the information provided. Interpret the Venn diagram and answer the word problems given below.
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivationEdit
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that are symbols representing real numbers — then a relevant solution to the word problem would, given the input , produce the output EQUAL, and similarly produce NOT_EQUAL from .
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that is the normal form of , , and , and devise a transformation system to rewrite those expressions to that form, in the process proving that all equivalent expressions will be rewritten to the same normal form.[2] But not all solutions to the word problem use a normal form theorem — there are algebraic properties which indirectly imply the existence of an algorithm.[1]
While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms containing variables have instances that are equal, or in other words whether the equation has any solutions. As a common example, is a word problem in the integer group ℤ,
while is a unification problem in the same group; since the former terms happen to be equal in ℤ, the latter problem has the substitution as a solution.
HistoryEdit
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systemsEdit
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system and two words (strings) , can be transformed into by applying rules from ? Note that the rewriting here is one-way. The word problem is the accessibility problem for symmetric rewrite relations, i.e. Thue systems.[27]
The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groupsEdit
Given a presentation for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max Dehn in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable.[31]
The word problem in combinatorial calculus and lambda calculusEdit
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systemsEdit
Solving the word problem: deciding if usually requires heuristic search (red, green), while deciding is straightforward (grey).
The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under ?[29] The word problem for an ARS is undecidable in general. However, there is a computable solution for the word problem in the specific case where every object reduces to a unique normal form in a finite number of steps (i.e. the system is convergent): two objects are equivalent under if and only if they reduce to the same normal form.[33]
The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebraEdit
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free latticesEdit
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free groupEdit
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
- , and
share the same normal form, viz. ; therefore both terms are equal in every group.
As another example, the term and has the normal form and , respectively. Since the normal forms are literally different, the original terms cannot be equal in every group. In fact, they are usually different in non-abelian groups.
| A1 | ||
| A2 | ||
| A3 |
| R1 | ||
| R2 | ||
| R3 | ||
| R4 | ||
| R8 | ||
| R11 | ||
| R12 | ||
| R13 | ||
| R14 | ||
| R17 |
See alsoEdit
- Conjugacy problem
- Group isomorphism problem
ReferencesEdit
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.