In today’s post, we are going to work with time word problems. We’ll take a look at some examples and solve them together.
Let’s begin!
Time Word Problem 1: The Sailboat Race
In a sailboat race, the winning boat completed two distances in the following times: 2 min 22 seconds and 3 min 45 seconds. How much time did it take the sailboat to finish from the beginning to the end?
We want to know the total time that it took for the sailboat to finish. So, we’ll need to add the times of the two distances. 
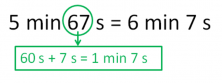
Time Word Problem 2: Flight to NYC
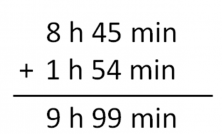
When Alex arrived at the airport, he looked at his watch and it was 5:45 a.m., exactly 3 hours before his next flight to NYC. If his next flight left on time and took exactly 114 minutes, what was the time on his watch when he arrived in NYC?
We need to calculate the amount of time that passed since the moment Alex looked at his watch until when he landed in NYC. The first thing we need to do is figure out when the plane took off. The text told us that exactly 3 hours passed, so he left at 8:45 a.m.
Now, we need to calculate when he landed. The flight took 114 minutes, which is more than 60 minutes. That means we need to change it so the answer is expressed in hours and minutes: 

What did you think about this post? Did it help you understand how to solve time word problems?
If you want to practice more time word problems, and others, create an account on Smartick and try it for free!
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
Reading & Math for K-5
- Math
-
-
Numbers
- Learning numbers
- Counting
- Comparing numbers
- Place Value
- Rounding
- Roman numerals
- Fractions & Decimals
- Fractions
- Decimals
-
4 Operations
- Addition
- Subtraction
- Multiplication
- Division
- Order of operations
- Flashcards
- Drills & practice
- Measurement
- Measurement
- Money
- Time
-
Advanced
- Factoring & prime factors
- Exponents
- Proportions
- Percents
- Integers
- Algebra
- More
- Shape & geometry
- Data & graphing
- Word problems
-
-
- Reading
-
- Kindergarten
-
- Vocabulary
-
- Spelling
-
- Grammar & Writing
-
- Science
-
- Cursive
-
- |
- Bookstore
- Math
- Reading
- Kindergarten
- Vocabulary
- Spelling
- Grammar & Writing
- More
- Science
- Cursive
- Bookstore
- Math
- Reading
- Kindergarten
- More
- Vocabulary
- Spelling
- Grammar & Writing
- Science
- Cursive
- Bookstore

Download & Print
Only $7.70
Word problem worksheets: Time and elapsed time
Below are three versions of our grade 4 math worksheet with word problems involving time and elapsed time. Students must figure out what time it was, will be or how much time went by in the various scenarios described. Use of «am» and «pm» is emphasized. These worksheets are pdf files.
Help us give away worksheets
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits

Become a Member
This content is available to members only.
Join K5 to save time, skip ads and access more content.
Learn More
Time word problems are an important element of teaching children how to tell the time. Children are introduced to the concept of time in Year 1. At this early stage, they learn the basics of analogue time; reading to the hour and half past and learn how to draw hands on the clocks to show these times.
As they move through primary school, pupils progress onto reading the time in analogue, digital and 24 hour clocks and being able to compare the duration of events. By the time children reach upper Key Stage 2, they should be confident in reading the time in all formats and solving problems involving converting between units of time.

Let’s Practice Telling The Time
Download this free printable worksheet to let your students practice telling the time.
When students are first introduced to time and time word problems, it is important for them to have physical clocks, to hold and manipulate the hands. Pictures on worksheets are helpful, but physical clocks enable them to work out what is happening with the hands and to solve word problems involving addition word problems and subtraction word problems.
Time word problems are important for helping children to understand how time is used in the real-world. We have put together a collection of 25 time word problems, which can be used with pupils from Year 2 to Year 6.
Time word problems in the National Curriculum
Time in Year 1
In Year 1, students are introduced to the basics of time. They learn to recognise the hour and minute hand and use this to help read the time to the hour and half past the hour. They also draw hands on clock faces to represent these times.
Time in Year 2
By the end of Year 2, pupils should be able to tell the time to five minutes, including quarter past/to the hour and draw the hands on a clock face to show these times. They should also know the number of minutes in an hour and the number of hours in a day.
Time in Year 3
In Year 3, children read the time in analogue (including using Roman Numerals). By this stage they are also learning to read digital time in 12 and 24 hour clock, using the AM and PM suffixes. Pupils record and compare time in terms of seconds, minutes and hours; know the number of seconds in a minute, days in a month and year and compare durations of events.
Time in Year 4
By Year 4, pupils should be confident telling the time in analogue to the nearest minute, digital and 24 hour clock. They also need to be able to read, write and convert time between analogue and digital 12 and 24 hour clocks and solve problems involving converting from hours to minutes; minutes to seconds; years to months and weeks to days.
Time in Year 5 & 6
By Year 5 and 6, there is only limited mention of time in the curriculum. Pupils continue to build on the knowledge they have picked up so far and should be confident telling the time and solving a range of problems, including: converting units of time; elapsed time word problems, working with timetables and tackling multi-step word problems.
Time word problems have been known to appear on Year 6 SATs tests. Third Space Learning’s online one-to-one SATs revision programme incorporates a wide range of word problems to develop students’ problem solving skills and prepare them the SATs tests. Available for all primary year groups as well as Year 7 and GCSE, our online tuition programmes are personalised to suit the needs of each individual student, fill learning gaps and build confidence in maths.
Why are word problems important for children’s understanding of time
Word problems are important for helping children to develop their understanding of time and the different ways time is used on an every-day basis. Confidence in telling the time and solving a range of time problems is a key life skill. Time word problems provide children with the opportunity to build on the skills they have picked up and apply them to real-world situations.
How to teach time word problem solving in primary school
It’s important children learn the skills needed to solve word problems. Key things they need to remember are: to make sure they read the question carefully; to think whether they have fully understood what is being asked and then identify what they will need to do to solve the problem and whether there are any concrete resources or pictorial representations which will help them.
Here is an example:
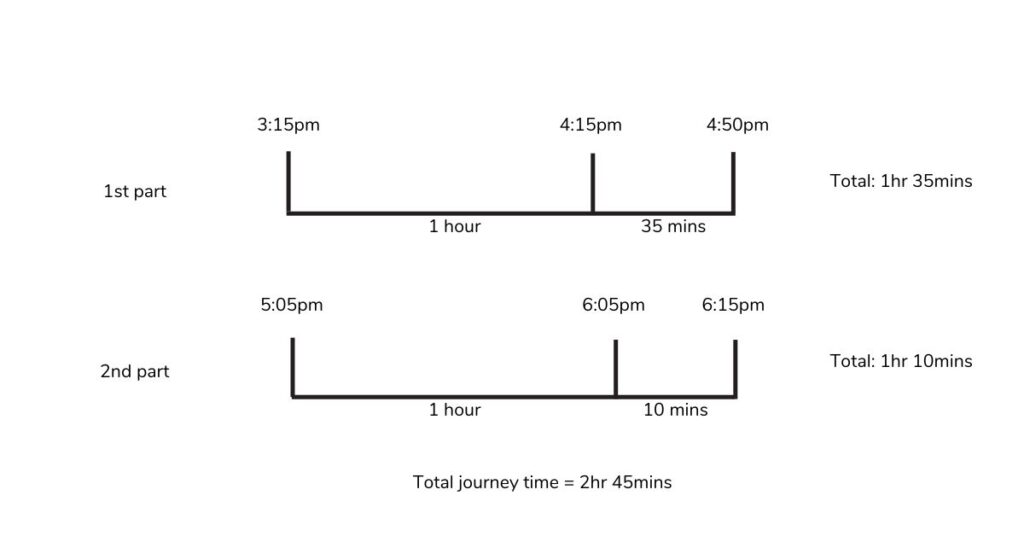
Mr Arrowsmith drives to Birmingham. He sets off at 3:15pm. He stops for a break of 15 minutes at 4:50 and arrives in Birmingham at 6:15pm.
How long did Mr Arrowsmith spend driving?
How to solve:
What do you already know?
- We know that he set off at 3:15pm and stopped for a break at 4:50. We can calculate how long the first part of his journey was, by counting on from 3:15 to 4:50.
- He had a break at 4:50pm for 15 minutes, so we won’t include that in our driving time calculation.
- He then must have set off again at 5:05pm, before arriving at 6:15pm. We can use this information to work out the length of the second part of his journey.
- We can then add the 2 journey times together, to calculate the total amount of time spent driving.
How can this be represented pictorially?
- We can use a number line to calculate the length of time each journey takes.
- If we start by adding on an hour, we can then calculate how many more minutes for each section of the journey.
- Once we have calculated the journey time for each part of the journey, we can add these together to calculate the total journey time.
Time word problems for year 2
Time word problems in Year 2 require students to read the time to o’clock and half past the hour and compare and sequence time intervals.
Question 1
Oliver went for a bike ride with his friend.
He left home at 2 o’clock and came home at 4 o’clock.
How long was he out on his bike for?
Answer: 2 hours
Count on from 2 o’ clock to 4 o’clock or subtract 2 from 4.
Question 2
Mum went shopping at 3 o’clock and got home an hour later.
Draw the time she got home on the clock below.
Answer
Question 3
Tom baked a cake.
The cake was in the oven for one hour.
If he took the cake out at half past 11, what time did he put the cake in?
Answer: Half past 10
Use an hour from half past 11.
Question 4
Arlo starts school at 9 o’clock and has his first break at half past 10.
How long does he have to wait for his first break?
Answer: One and a half hours.
(Use a number line to count on from 9 to half past 10)
Question 5
The Smith family are going to the beach.
They plan to leave home at 10 o’clock and the journey take two hours.
What time will they arrive at the beach?
Answer: 12 o’clock
(Use a number line to count on 2 hours from 10 o’clock)
Time word problems for year 3
With time word problems for year 3, students build on their understanding of analogue time from Year 2 and also begin to read the time in digital (12 and 24 hour clock). Children also need to be able to compare time and durations of events.
Question 1
Chloe is walking to football training.
She sets off at 8:40am and takes 17 minutes to get there.
What time does she arrive?
Answer: 8:57
(Count on 17 minutes from 8:40 – use a number line if needed)
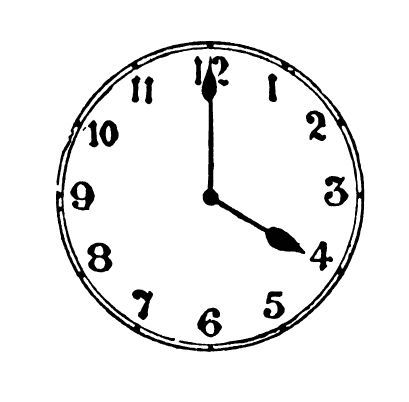
Question 2
(Picture of analogue clock with 2:30 showing here)
Maisie says that in 1 hour and 48 minutes it will be 4:28.
Do you agree? Explain how you worked out your answer.
Answer: Maisie is wrong. It will be 4:18.
This can be worked out by counting on an hour from 2:30 to 3:30 and then another 48 minutes to 4:18.
Question 3
The Baker family are driving to their campsite.
They set off at 8:30 am, drive for 2 hours and 15 minutes, then had a 30 minute break.
If they drive for another 1 hour and 45 minutes, what time do they arrive at the campsite?
Answer: 12:45pm
Use a number line to show what time they arrive at the break. From 8:30, count on 2 hours and 15 minutes to get to 10:45. Add on the 30 minute break. It is now 11:15. They count on another hour and a half to 12:45
Question 4
Ahmed looks at his watch and says ‘it is half past 4 in the afternoon’
Jude says that it is 17:30 in a 24 hour clock.
Is Jude correct? Explain your answer.
Answer: Jude is not correct. Half past 4 in the afternoon is 16:30 not 17:30
Question 5
How many minutes are there in 2 hours and 30 minutes?
Answer: 150 minutes
60 + 60 + 30 = 150
Time word problems for year 4
When solving time word problems for year 4, pupils need to be confident telling time in analogue, and digital, as well as converting between analogue, 12 hour and 24 hour clock. They also begin to solve more challenging problems involving duration of time and converting time.
Question 1
If there are 60 seconds in 1 minute. How many seconds are there in 8 minutes?
Answer: 480 seconds
60 x 8 = 480 seconds (calculate 6 x 8, then multiply by 10)
Question 2
Mason played on his VR from 3:35 to 5:25.
How long did he play on his VR?
Answer: 1 hour and 50 minutes.
Count on from 3:35 (using a numberline if needed)
Question 3
Jamie started his homework at 3:45pm. He finished 43 minutes later.
What time did Jamie finish? Give your answer in 24 hour clock.
Answer: 16:28
Count on 43 minutes from 3:45 (use a number line, if needed) = 4:28. Convert to 24 hour clock.
Question 4
Chloe and Freya went to the cinema to watch a film. The film started at 2:05pm and lasted for 1 hour and 43 minutes.
What time did the film end?
Answer: 3:48pm
Count on one hour from 2:05 pm to 3:05pm, then add another 43 minutes – 3:48pm
Question 5
A family is driving on their holiday.
They drive for 2 hours and 28 minutes, stop for 28 minutes and then drive a further 1 hour and 52 minutes.
If they left at 8:30am, what time did they arrive?
Answer: 1:18pm
2 hours and 28 minutes from 8:30am = 10:58am
10:58am with a 28 minute break = 11:26am
1 hour 52 minute drive from 11:26 am = 1:18pm
Time word problems for year 5
With word problems for year 5, pupils should be confident telling the time in analogue and digital and solving a wider range of time problems including: converting units of time; interpreting and answering questions on timetables and elapsed time.
Question 1
The sun set at 19:31 and rose again at 6:28.
How many hours passed between the sun setting and rising again?
Answer: 10 hours and 57 minutes
Count on from 19:31 to 5:31 (10 hours)
Then count on from 5:31 to 6:28 (57 minutes)
Question 2
A play started at 14:45 and finished at 16:58.
How long was the play?
Answer: 2 hours and 13 minutes
Count on 2 hours from 14:45 to 16:45, then add another 13 minutes to get to 16:58
Question 3
How many seconds are there in 23 minutes?
Answer: 1380 seconds
Show as column method: 60 x 23 = 1380
Question 4
Max ran a race in 2 minutes 13 seconds, Oscar ran it in 125 seconds.
What was the difference in time between Max and Oscar?
Answer: Oscar was 8 seconds faster.
Max – 2 minutes 13 seconds, Oscar – 2 minutes 5 seconds (difference of 8 seconds)
Question 5
4 children take part in a freestyle swimming relay.
There times were:
Maisie: 42.8 seconds
Amber 36.3 seconds
Megan 48.7 seconds
Zymal 45.6 seconds
What was the final time for the relay in minutes and seconds?
Answer: 2:53.4
(Show as column method) 42.8 + 36.3 + 48.7 + 45.6 = 173.4 seconds
173.4 seconds = 2:53.4
Time word problems for year 6
No new time concepts are taught to pupils in word problems for year 6. By this stage they are continuing to build confidence and develop skills within the concepts already taught.
Question 1
Chess: 25 minutes
Basketball: 40 minutes.
Trampolining: 30 minutes
Gymnastics: 50 minutes
Tennis 40 minutes
Tri golf – 45 minutes
Hamza is choosing activities to take part in at his holiday club.
The activities can’t add up to more than 2 hours.
Which 3 activities could he do, which add up to exactly 2 hours?
Answer: Trampolining, gymnastics and tennis: Trampolining: 30 minutes, gymnastics: 50 minutes, tennis: 40 minutes.
Question 2
5 children took part in a sponsored swim. The children swam for the following lengths of time:
Sam: 27 minutes 37 seconds
Jemma: 33 minutes 29 seconds.
Ben: 23 minutes 18 seconds
Lucy: 41 minutes 57 seconds
Oliver: 39 minutes 21 seconds
Answer: 18 minutes 30 seconds
Longest: Lucy: 41 minutes 57 seconds
Shortest: Ben: 23 minutes 18 seconds.
Difference – count up from 23 minutes 18 seconds to 41 minutes 57 seconds = 18 minutes 39 seconds
Question 3
What is 6 minutes 47 seconds in seconds?
Answer: 407 minutes
60 x 6 = 360
360 + 47 = 407 minutes
Question 4
Bethany’s goal is to run round her school running track in under 8 minutes.
She runs it in 440 seconds. Does she achieve her goal? How far above or below the target is she?
Answer: Bethany beats her target by 40 seconds
8 minutes = 8 x 60 = 480 minutes
Question 5
Lucy’s favourite programme is on TV twice a week for 35 minutes.
In 6 weeks, how many hours does Lucy spend watching her favourite programme?
Answer: 7 hours
420 minutes = 7 hours
(Show as column method) 35 x 12 = 420 minutes
420 ÷ 60 = 7
More time and word problems resources
For more time resources, take a look at our collection of printable time worksheets. Third Space Learning also offers a wide collection of word problems covering a range of topics such as place value, decimals and fractions word problems, percentages word problems, division word problems, ratio word problems, addition and subtraction word problems, multiplication word problems, money word problems and other word problem challenge cards.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Let us consider some of the word problems on measurement of time i.e. hours, minutes and seconds.
Examples on addition of hours, minutes and seconds:
1. A train leaves Delhi for Tundla at 7:30 a.m. It takes 5 ours to reach at Tundla. At what time it reach at Tundal?
The train departs at hr. min.
Time taken to reach at Tundla 7 30
The train will reach at Tundla + 5 00
12 30
Therefore, the train will reach Tundla at 12:30 p.m.
2. Sam leaves for school at 6:35 a.m. It takes him 1 hr. 45 min.
to reach the school. At what time will he reach the school?
Sam leaves for school at hr. min.
Time taken to reach the school 6 35
Sam will reach the school at + 1 45
7 80
7 hr. 80 min. = 7 hr. + 60 min. + 20 min.
= 7 hr. + 1 hr. + 20 min.
= 8
hr. 20 minutes.
Therefore, Sam will reach the school at 8:20 a.m.
Examples on
subtraction of hours, minutes and
seconds:
1. Ron left for his school at 6:35 a.m. He reached the school at
8:25 a.m. How much time did Ron take to reach the school?
Ron reached his school at 7:25 a.m.
He left for his school at 6:35 a.m.
Time taken by him to reach the school
= 7 hr. 25 min — 6hr. 35 min
= 0 hr. 50 min.
Therefore, time taken by Ron to reach the school is 50 minutes.
2. Ken left his home at 4:30 p.m. to play cricket. He came at 7:15
p.m. How long was he away from his home?
Ken came back at 7:15 p.m.
He left home at 4:30 p.m.
He was away from home = 7 hr. 15 min. — 4 hr. 30 min.
= 2 hr. 45 min.
Therefore, Ron was away from home 2 hours 45 minutes
4th Grade Math Activities
From Word problems on Measurement of Time to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Today we are going to learn the Word Problems on Measurement of Time, which helps students in every phase of their life. In order to solve problems on measuring time, first, we need to get knowledge on units of time and how to calculate and measure the time correctly. As you know, how time varies in different types of units, let’s have a glance at this Measurement of Time Word Problems.
While solving the time problems, time can be in the format of a.m. and p.m where the clock is 12-hour clock format. Here, we have compiled some examples for students to explain and understand the Time Problem Solving with Solution. So, practice with these Measuring Time Word Problems with Solutions PDF and improve your knowledge on 4th grade math time concepts.
Also Read:
- Time Duration
- Adding and Subtracting Time
- Worksheet on Conversion of Time
Example 1:
Navya went to college at 7:00 a.m. It takes her 1 hr 30 min to reach the college. At what time will she reach the college?
Solution:
Navya went to college at 7 hr 00 min
Time taken to reach the college for her is 1 hr 30 min +
Now, the time she reached college is 8 hr 30 min
Therefore, Navya reaches the college at 8:30 a.m.
Example 2:
Chaitanya is feeding a dog. He starts at 10:45 a.m. and continues feeding for 15 minutes. When did he complete his feeding?
Solution:
Chaitanya started feeding a dog at 10:45 a.m.
He continued feeding for 15 minutes.
Now, have to find the time when he completed feeding.
We add both the timings and we will get the answer.
i.e., 10 hr 45 min + 15 min = 10 hr + 60 min = 10 hr + 1 hr = 11 hrs.
Hence, at 11:00 a.m. Chaitanya completed the feeding for his dog.
Example 3:
Sam is getting her exam. She starts at 9:05 a.m. and continues her exam for 58 minutes. When did she finish her exam?
Solution:
Sam starts her exam at 9:05 a.m.
It continues for 58 minutes.
Now, add both the exam times to get the finish time of the exam.
9 hr 05 min + 58 min = 9 hr 63 min = 9 hr + 60 min + 3 min = 9 hr + 1 hr + 3 min = 10 hr 3 min.
So, Sam finishes her exam at 10:03 a.m.
Example 4:
The train was scheduled to arrive at 6:40 p.m. However, it was delayed for 35 minutes. What is the time when the train arrives?
Solution:
The train schedules at 6:40 p.m. i.e., 6 hr 40 min.
The train delays for 35 minutes.
Arrived time of the train = 6 hr 40 min + 35 min = 6 hr 75 min = 6 hr + 60 min + 15 min = 6 hr + 1 hr + 15 min = 7 hr 15 min.
The train arrives at 7:15 p.m.
Example 5:
Chetan’s birthday party started at 5:30 p.m. The last guest left at 7:05 p.m. How long did Chetan’s party last?
Solution:
Chetan’s birthday party starts at 5:30 p.m. i.e., 5 hr 30 min.
The last guest left the party at the time of 7:05 p.m i.e., 7 hr 5 min.
To know the time how long did Chetan’s party be. We subtract the left guest time with the time when the party started.
i.e., 7 hr 05 min – 5 hr 30 min = 2 hr 25 min.
Thus, Chetan’s party lasts for 2 hrs 25 min.
Example 6:
Karan is practicing his violin. He finishes at 2:40 p.m. after 30 minutes. When did he start his violin?
Solution:
Karan completes his practice at 2:40 p.m. i.e., 2 hrs 40 min.
Next, we have to know when he starts his violin practice time.
From the given question, we have a clue that after 30 minutes. So, we subtract this 30 min time from the completed practice time i.e., 2 hr 40 min.
Now, 2 hr 40 min – 30 min = 2 hr 10 min.
Hence, Karan starts his violin practice session at 2:10 p.m.
Distance problems are word problems that involve the distance
an object will travel at a certain average rate for a given
period of time.
The formula for distance problems is: distance =
rate × time or
d = r × t.
Things to watch out for:
Make sure that you change the units when necessary. For example, if the rate is given in miles per
hour and the time is given in minutes then change the units appropriately.
It would be helpful to use a table to organize the information for distance problems. A table helps
you to think about one number at a time instead being confused by the question.
The following diagrams give the steps to solve Rate Time Distance Word Problems. Scroll down
the page for examples and solutions.
Distance Problems: Traveling In Opposite Directions
Example:
A bus and a car leave the same place and traveled in opposite directions. If the bus is
traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?
Solution:
Step 1: Set up a rtd table.
| r | t | d | |
|---|---|---|---|
| bus | |||
| car |
Step 2: Fill in the table with information given in the question.
If the bus is traveling at 50 mph and the car is traveling
at 55 mph, in how many hours will they be 210 miles apart?
Let t = time when they are 210 miles apart.
| r | t | d | |
|---|---|---|---|
| bus | 50 | t | |
| car | 55 | t |
Step 3: Fill in the values for d using the formula d = rt
| r | t | d | |
|---|---|---|---|
| bus | 50 | t | 50t |
| car | 55 | t | 55t |
Step 4: Since the total distance is 210, we get the equation:
50t + 55t = 210
105t = 210
Isolate variable t
Answer: They will be 210 miles apart in 2 hours.
Example of a distance word problem with vehicles moving in opposite directions
In this video, you will learn to solve introductory distance or motion word problems — for example,
cars traveling in opposite directions, bikers traveling toward each other, or one plane overtaking
another. You should first draw a diagram to represent the relationship between the distances
involved in the problem, then set up a chart based on the formula rate times time = distance.
The chart is then used to set up the equation.
Example:
Two cars leave from the same place at the same time and travel in opposite directions. One car
travels at 55 mph and the other at 75 mph. After how many hours will they be 520 miles apart?
- Show Video Lesson
Rate-Time-Distance Problem
Solve this word problem using uniform motion rt = d formula:
Example:
Two cyclists start at the same corner and ride in opposite directions. One cyclist rides twice as
fast as the other. In 3 hours, they are 81 miles apart. Find the rate of each cyclist.
- Show Video Lesson
Distance — Opposite Directions
Example:
Brian and Jennifer both leave the convention at the same time traveling in opposite directions.
Brian drove at 35 mph and Jennifer drove at 50 mph. After how much time were they 340 miles apart?
- Show Video Lesson
Distance — Opposite Directions find t
Example:
Two joggers start from opposite ends of an 8 mile course running towards each other. One
jogger is running at a rate of 4 mph. The other is running at a rate of 6 mph. After how
long will the joggers meet?
- Show Video Lesson
Distance — Opposite Directions find r
Example:
Bob and Fred start from the same point and walk in opposite directions. Bob walks 2 mph faster
than Fred. After 3 hours they are 30 miles apart. How fast does each walk?
- Show Video Lesson
GMAT Challenge Question: Distance/Rate/Time
Example:
Trains A and B left stations R and S simultaneously on two separate parallel rail tracks that
are 350 miles long. The trains pass each other at point X after traveling for a certain amount
of time. How many miles of the rail tracks has train A traveled when the two trains passed each other?
- Up to point X, the average speed of train B was 25% less than the average speed of train A.
- Up to point X, the average speed of train B was 60 mph and it took two and a half hours for
train B to arrive at point X.
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Classen Rafael / EyeEm / Getty Images
Updated on October 22, 2018
Elapsed time is the amount of time that passes between the beginning and the end of an event. The concept of elapsed time fits nicely in the elementary school curriculum. Beginning in third grade, students should be able to tell and write time to the nearest minute and solve word problems involving addition and subtraction of time. Reinforce these essential skills with the following elapsed time word problems and games.
Elapsed Time Word Problems
These quick and easy elapsed time word problems are perfect for parents and teachers who want to help students practice elapsed time to the nearest minute with simple mental math problems. Answers are listed below.
- Sam and his mom arrive at the doctor’s office at 2:30 p.m. They see the doctor at 3:10 p.m. How long was their wait?
- Dad says dinner will be ready in 35 minutes. It’s 5:30 p.m. now. What time will dinner be ready?
- Becky is meeting her friend at the library at 12:45 p.m. It takes her 25 minutes to get to the library. What time will she need to leave her house to arrive on time?
- Ethan’s birthday party started at 4:30 p.m. The last guest left at 6:32 p.m. How long did Ethan’s party last?
- Kayla put cupcakes in the oven at 3:41 p.m. The directions say that the cupcakes need to bake for 38 minutes. What time will Kayla need to take them out of the oven?
- Dakota arrived at school at 7:59 a.m. He left at 2:33 p.m. How long was Dakota at school?
- Dylan started working on homework at 5:45 p.m. It took him 1 hour and 57 minutes to complete it. What time did Dylan complete his homework?
- Dad arrives home at 4:50 p.m. He left work 40 minutes ago. What time did Dad get off work?
- Jessica’s family is traveling from Atlanta, Georgia to New York by plane. Their flight leaves at 11:15 a.m. and should take 2 hours and 15 minutes. What time will their plane arrive in New York?
- Jordan got to football practice at 7:05 p.m. Steve showed up 11 minutes later. What time did Steve get to practice?
- Jack ran a marathon in 2 hours and 17 minutes. He crossed the finish line at 10:33 a.m. What time did the race start?
- Marci was babysitting for her cousin. Her cousin was gone for 3 hours and 40 minutes. Marci left at 9:57 p.m. What time did she start babysitting?
- Caleb and his friends went to see a movie at 7:35 p.m. They left at 10:05 p.m. How long was the movie?
- Francine got to work at 8:10 a.m. She left at 3:45 p.m. How long did Francine work?
- Brandon went to bed at 9:15 p.m. It took him 23 minutes to fall asleep. What time did Brandon fall asleep?
- Kelli had to wait in a long, slow-moving line to purchase a popular new video game that was just released. She got in line at 9:15 a.m. She left with the game at 11:07 a.m. How long did Kelli wait in line?
- Jaydon went to batting practice Saturday morning at 8:30 a.m. He left at 11:42 a.m. How long was he at batting practice?
- Ashton got behind on her reading assignment, so she had to read four chapters last night. She started at 8:05 p.m. and finished at 9:15 p.m. How long did it take Ashton to catch up on her assignment?
- Natasha has a dentist appointment at 10:40 a.m. It should last 35 minutes. What time will she finish?
- Mrs. Kennedy’s 3rd-grade class is going to the aquarium on a field trip. They are scheduled to arrive at 9:10 a.m. and leave at 1:40 p.m. How long will they spend at the aquarium?
Elapsed Time Games
Try these games and activities at home to help your children practice elapsed time.
Daily Schedule
Let your children keep track of their schedule and ask them to figure the elapsed time for each activity. For example, how long did your child spend eating breakfast, reading, taking a bath, or playing video games?
How Long Will It Take?
Give your kids practice with elapsed time by encouraging them to figure out how long daily activities take. For example, the next time you order a pizza online or by phone, you’ll probably be given an estimated delivery time. Use that information to create a word problem that’s relevant to your child’s life, such as, «It’s 5:40 p.m. now and the pizza shop says the pizza will be here at 6:20 p.m. How long will it take for the pizza to arrive?»
Time Dice
Order a set of time dice from online retailers or teacher supply stores. The set contains two twelve-sided dice, one with numbers representing the hours and the other with numbers representing minutes. Take turns rolling the time dice with your child. Each player should roll twice, then calculate the elapsed time between the two resulting dice times. (A pencil and paper will come in handy, as you’ll want to jot down the time of the first roll.)
Elapsed Time Word Problem Answers
- 40 minutes
- 6:05 p.m.
- 12:20 p.m.
- 2 hours and 2 minutes
- 4:19 p.m.
- 6 hours and 34 minutes
- 7:42 p.m.
- 4:10 p.m.
- 1:30 p.m.
- 7:16 p.m.
- 8:16 a.m.
- 6:17 p.m.
- 2 hours and 30 minutes
- 7 hours and 35 minutes
- 9:38 p.m.
- 1 hour and 52 minutes
- 3 hours and 12 minutes
- 1 hour and 10 minutes
- 11:15 a.m.
- 4 hours and 30 minutes
Before you get into distance, time and speed word problems, take a few minutes to read this first and understand: How to build your credit score in USA as an international student.
Problems involving Time, Distance and Speed are solved based on one simple formula.
Distance = Speed * Time
Which implies →
Speed = Distance / Time and
Time = Distance / Speed
Let us take a look at some simple examples of distance, time and speed problems.
Example 1. A boy walks at a speed of 4 kmph. How much time does he take to walk a distance of 20 km?
Solution
Time = Distance / speed = 20/4 = 5 hours.
Example 2. A cyclist covers a distance of 15 miles in 2 hours. Calculate his speed.
Solution
Speed = Distance/time = 15/2 = 7.5 miles per hour.
Example 3. A car takes 4 hours to cover a distance, if it travels at a speed of 40 mph. What should be its speed to cover the same distance in 1.5 hours?
Solution
Distance covered = 4*40 = 160 miles
Speed required to cover the same distance in 1.5 hours = 160/1.5 = 106.66 mph
Now, take a look at the following example:
Example 4. If a person walks at 4 mph, he covers a certain distance. If he walks at 9 mph, he covers 7.5 miles more. How much distance did he actually cover?
Now we can see that the direct application of our usual formula Distance = Speed * Time or its variations cannot be done in this case and we need to put in extra effort to calculate the given parameters.
Let us see how this question can be solved.
Solution
For these kinds of questions, a table like this might make it easier to solve.
| Distance | Speed | Time |
| d | 4 | t |
| d+7.5 | 9 | t |
Let the distance covered by that person be ‘d’.
Walking at 4 mph and covering a distance ‘d’ is done in a time of ‘d/4’
IF he walks at 9 mph, he covers 7.5 miles more than the actual distance d, which is ‘d+7.5’.
He does this in a time of (d+7.5)/9.
Since the time is same in both the cases →
d/4 = (d+7.5)/9 → 9d = 4(d+7.5) → 9d=4d+30 → d = 6.
So, he covered a distance of 6 miles in 1.5 hours.
Example 5. A train is going at 1/3 of its usual speed and it takes an extra 30 minutes to reach its destination. Find its usual time to cover the same distance.
Solution
Here, we see that the distance is same.
Let us assume that its usual speed is ‘s’ and time is ‘t’, then
| Distance | Speed | Time |
| d | s | t min |
| d | S+1/3 | t+30 min |
s*t = (1/3)s*(t+30) → t = t/3 + 10 → t = 15.
So the actual time taken to cover the distance is 15 minutes.
Note: Note the time is expressed in terms of ‘minutes’. When we express distance in terms of miles or kilometers, time is expressed in terms of hours and has to be converted into appropriate units of measurement.
Solved Questions on Trains
Example 1. X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70 mph. After 2 hours, another train starts from Y and travels towards X at 20 mph. At what time do they meet?
Solution
Let the time after which they meet be ‘t’ hours.
Then the time travelled by second train becomes ‘t-2’.
Now,
Distance covered by first train+Distance covered by second train = 320 miles
70t+20(t-2) = 320
Solving this gives t = 4.
So the two trains meet after 4 hours.
Example 2. A train leaves from a station and moves at a certain speed. After 2 hours, another train leaves from the same station and moves in the same direction at a speed of 60 mph. If it catches up with the first train in 4 hours, what is the speed of the first train?
Solution
Let the speed of the first train be ‘s’.
Distance covered by the first train in (2+4) hours = Distance covered by second train in 4 hours
Therefore, 6s = 60*4
Solving which gives s=40.
So the slower train is moving at the rate of 40 mph.
Questions on Boats/Airplanes
For problems with boats and streams,
Speed of the boat upstream (against the current) = Speed of the boat in still water – speed of the stream
[As the stream obstructs the speed of the boat in still water, its speed has to be subtracted from the usual speed of the boat]
Speed of the boat downstream (along with the current) = Speed of the boat in still water + speed of the stream
[As the stream pushes the boat and makes it easier for the boat to reach the destination faster, speed of the stream has to be added]
Similarly, for airplanes travelling with/against the wind,
Speed of the plane with the wind = speed of the plane + speed of the wind
Speed of the plane against the wind = speed of the plane – speed of the wind
Let us look at some examples.
Example 1. A man travels at 3 mph in still water. If the current’s velocity is 1 mph, it takes 3 hours to row to a place and come back. How far is the place?
Solution
Let the distance be ‘d’ miles.
Time taken to cover the distance upstream + Time taken to cover the distance downstream = 3
Speed upstream = 3-1 = 2 mph
Speed downstream = 3+1 = 4 mph
So, our equation would be d/2 + d/4 = 3 → solving which, we get d = 4 miles.
Example 2. With the wind, an airplane covers a distance of 2400 kms in 4 hours and against the wind in 6 hours. What is the speed of the plane and that of the wind?
Solution
Let the speed of the plane be ‘a’ and that of the wind be ‘w’.
Our table looks like this:
| Distance | Speed | Time | |
| With the wind | 2400 | a+w | 4 |
| Against the wind | 2400 | a-w | 6 |
4(a+w) = 2400 and 6(a-w) = 2400
Expressing one unknown variable in terms of the other makes it easier to solve, which means
a+w = 600 → w=600-a
Substituting the value of w in the second equation,
a-w = 400
a-(600-a) = 400 → a = 500
The speed of the plane is 500 kmph and that of the wind is 100 kmph.
More solved examples on Speed, Distance and Time
Example 1. A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus.
Solution
| Distance | Speed | Time | |
| Train | d | 30 | t |
| Bus | 100-d | 40 | 3-t |
Let the time taken by the train be ‘t’. Then that of bus is ‘3-t’.
The entire distance covered was 100 miles
So, 30t + 40(3-t) = 100
Solving which gives t=2.
Substituting the value of t in 40(3-t), we get the distance travelled by bus is 40 miles.
Alternatively, we can add the time and equate it to 3 hours, which directly gives the distance.
d/30 + (100-d)/40 = 3
Solving which gives d = 60, which is the distance travelled by train. 100-60 = 40 miles is the distance travelled by bus.
Example 2. A plane covered a distance of 630 miles in 6 hours. For the first part of the trip, the average speed was 100 mph and for the second part of the trip, the average speed was 110 mph. what is the time it flew at each speed?
Solution
Our table looks like this.
| Distance | Speed | Time | |
| 1st part of journey | d | 100 | t |
| 2nd part of journey | 630-d | 110 | 6-t |
Assuming the distance covered in the 1st part of journey to be ‘d’, the distance covered in the second half becomes ‘630-d’.
Assuming the time taken for the first part of the journey to be ‘t’, the time taken for the second half becomes ‘6-t’.
From the first equation, d=100t
The second equation is 630-d = 110(6-t).
Substituting the value of d from the first equation, we get
630-100t = 110(6-t)
Solving this gives t=3.
So the plane flew the first part of the journey in 3 hours and the second part in 3 hours.
Example 2. Two persons are walking towards each other on a walking path that is 20 miles long. One is walking at the rate of 3 mph and the other at 4 mph. After how much time will they meet each other?
Solution
| Distance | Speed | Time | |
| First person | d | 3 | t |
| Second person | 20-d | 4 | t |
Assuming the distance travelled by the first person to be ‘d’, the distance travelled by the second person is ’20-d’.
The time is ‘t’ for both of them because when they meet, they would have walked for the same time.
Since time is same, we can equate as
d/3 = (20-d)/4
Solving this gives d=60/7 miles (8.5 miles approximately)
Then t = 20/7 hours
So the two persons meet after 2 6/7 hours.
Practice Questions for you to solve
Problem 1: Click here
Answer 1: Click here
Problem 2: Click here
Answer 2: Click here
Time Riddles (harder)
Welcome to our Time Word Problems Worksheets page.
Here you find our selection of more challenging Time Riddles to help your child learn to read, record and solve problems involving time and clocks.
Time Word Problems Worksheets
Time Riddles (harder)
Looking for some 24 hour clock problem sheets?
Do you need some challenging time problems for older children?
Then hopefully you have found the right place!
The printable time sheets in this section involve being able to tell the time to the nearest minute,
as well as converting times between the 12 and 24 clock.
These worksheets are great to use when your child is confident telling the time and needs to extend
their knowledge by solving time problems.
The sheets are also very good at developing an understanding of mathematical language associated with time.
Each sheet has 2 different Time Riddles with 8 possible solutions.
The aim of each puzzle is to use the clues to work out the correct solution.
Using these sheets will help your child to:
- read times to the nearest minute;
- convert analogue to digital times;
- use ‘past’ and ‘to’ language correctly to tell the time;
- convert times between the 12 and 24 hour clock;
- solve problems involving time;
Our time word problems worksheets will help you practice applying your time skills and knowledge to solve problems.
Time Word Problems Worksheets : to the nearest minute
-
Time Riddles 4a
-
Answers
-
PDF version
-
Time Riddles 4b
-
Answers
-
PDF version
-
Time Riddles 4c
-
Answers
-
PDF version
Time Word Problems Worksheets: 24 hour clock
Extension Activity Ideas
If you are looking for a way to extend learning with these Time Riddles, why not…
-
Get children to work in partners with one child choosing one of the 8 possible times and the other child asking ‘yes/no’ questions.
E.g. Is it earlier than…? Is the minute hand on number 6…? Is it later than 4pm? … etc - Children could write their own set of clues down to identify one of the clocks.
Looking for something easier?
Here you will find our selection of easier Time Riddles.
The sheets in this section are similar to those on this page, but involve telling the times:
o’clock and half-past, quarter past and quarter to, and to 5 minute intervals.
Need help telling the time?
Here you will find our selection of telling time clock worksheets to help your child to
learn their o’clock, half-past, quarter past and to, and 5 minute intervals.
Using these sheets will help your child to:
- read o’clock, half-past times;
- read quarter past and quarter to;
- read time going up in 5 minute intervals;
- convert analogue times to digital;
The sheets in this section are a great way of starting your child off with learning to tell the time.
Time Interval Worksheets
These sheets will help you learn to add and subtract hours and minutes from times as well
as working out a range of time intervals.
There are also sheets to help you practice adding and subtracting time intervals.
Online Age Calculator
Do you want to know exactly how old you are to the nearest minute?
Have you been alive for more than a billion seconds?
Do you know how many days old you are?
Our online age calculator will tell you all you need to know…
How to Print or Save these sheets
Need help with printing or saving?
Follow these 3 easy steps to get your worksheets printed out perfectly!
-
How to Print support
How to Print or Save these sheets
Need help with printing or saving?
Follow these 3 easy steps to get your worksheets printed out perfectly!
-
How to Print support
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets
and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.
| Time word problems | |
|---|---|
 |
|
| Description | |
| Exercise Name: | Time word problems |
| Math Missions: | 4th grade (U.S.) Math Mission |
| Types of Problems: | 2 |
The first instance of Time word problems is under the 4th grade (U.S.) Math Mission. This exercise practices telling time on a clock in word problems.
Types of Problems
There are two types of problems in this exercise:
- Time to catch: This problem has a situation involving someone who is timed. Another person starts, let’s time pass, and the student is asked how much longer the second person should take to tie the first person.
Time to catch
- Find time: This problem has an involved word problem and asks the student to find the time a person should start a certain thing or will arrive at a particular place.
Find time
Strategies
This exercise is easy to get accuracy badges as long as user is familiar with a clock. However, since they need to patient with user reading is should be considered medium to attain speed badges.
- The phrase «quarter of» means 15 minutes before.
- A program or resource that could count modulo 60 could make these problem run faster in a calculator and thereby help with speed badges.
Real-life Applications
- Knowledge of telling time is needed for getting to meetings at the right time.