Word problem of speed

The speed word problems to follow don’t have complicated math equations at all. Instead, the focus is on understanding how to apply the concept of speed, distance, and time. 

Interesting speed word problems

Problem #1: Calculate the average speed of a lion that runs 45 meters in 5 seconds . What could be some possible instantaneous speeds?

Solution:  The formula to get the average speed is 

The total distance is 45 meters, so d = 45 meters.

It took the lion 5 seconds to reach a distance of 45 meters.

The total time is 5 seconds, so t = 5.

Just plug these into the formula. 

d = 9 meters per second.

You could also write d = 9 m/s.

Some possible instantaneous speed for the lion could be the followings:

13 meters in 1 second      v = 13 m/s

9 meters in 1 second        v  = 9 m/s

10 meters in 1 second      v  = 10 m/s 

8 meters in 1 second        v = 8 m/s

5 meters in 1 second        v = 5 m/s

As you can see the total distance is 13 + 9 + 10 + 8 + 5 = 45

and the total time is 1 + 1  + 1 + 1  + 1 = 5  

Challenging speed word problems

Problem #2: How far is a house in New York if it takes you 5 hours to get there and your average speed is 35 miles per half hour?

First,
notice that in the problem we said average speed instead of just
speed. It is because you did not just do 35 miles per hour during the
entire trip. Your speed changed from times to times, but the
average comes to 35 miles per hour.

Second, it is convenient to convert miles per half hour to miles per hour.

35 miles per half hour is 70 miles per hour.

Lastly, convert the formula from speed to distance. 

By the same fashion,

Now, we have the speed and the time, we can get the distance.

d = speed × t

d = 70 × 5

d = 350 miles

Problem #3: Your turn!

How far is a house
in Florida if it takes you 4 hours to get there and your instantaneous
speeds were 70 miles per hour, 50 miles per hour,  60 miles per hour, 10
miles per hour, and 0 miles per hour? 

Take a look also at the speed word problem below

Before you get into distance, time and speed word problems, take a few minutes to read this first and understand: How to build your credit score in USA as an international student.

Problems involving Time, Distance and Speed are solved based on one simple formula.

Distance = Speed * Time

Which implies →

Speed = Distance / Time   and

Time = Distance / Speed

Solution

Solution

Solution

Distance covered = 4*40 = 160 miles

Example 4. If a person walks at 4 mph, he covers a certain distance. If he walks at 9 mph, he covers 7.5 miles more. How much distance did he actually cover?

Now we can see that the direct application of our usual formula Distance = Speed * Time or its variations cannot be done in this case and we need to put in extra effort to calculate the given parameters.

Let us see how this question can be solved.

Solution

For these kinds of questions, a table like this might make it easier to solve.

Distance	Speed	Time
d	4	t
d+7.5	9	t

 
Let the distance covered by that person be ‘d’.

Walking at 4 mph and covering a distance ‘d’ is done in a time of ‘d/4’

IF he walks at 9 mph, he covers 7.5 miles more than the actual distance d, which is ‘d+7.5’.

He does this in a time of (d+7.5)/9.

Since the time is same in both the cases →

d/4 = (d+7.5)/9            →        9d = 4(d+7.5)   →        9d=4d+30        →        d = 6.

Solution

Here, we see that the distance is same.

Let us assume that its usual speed is ‘s’ and time is ‘t’, then

Distance	Speed	Time
d	s	t min
d	S+1/3	t+30 min

 
s*t = (1/3)s*(t+30)      →        t = t/3 + 10      →        t = 15.

So the actual time taken to cover the distance is 15 minutes.

Note: Note the time is expressed in terms of ‘minutes’. When we express distance in terms of miles or kilometers, time is expressed in terms of hours and has to be converted into appropriate units of measurement.

Solved Questions on Trains

Example 1. X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70 mph. After 2 hours, another train starts from Y and travels towards X at 20 mph. At what time do they meet?

Solution

Let the time after which they meet be ‘t’ hours.

Then the time travelled by second train becomes ‘t-2’.

Now,

Distance covered by first train+Distance covered by second train = 320 miles

70t+20(t-2) = 320

Solving this gives t = 4.

Solution

Let the speed of the first train be ‘s’.

Distance covered by the first train in (2+4) hours = Distance covered by second train in 4 hours

Therefore, 6s = 60*4

Solving which gives s=40.

So the slower train is moving at the rate of 40 mph.
 

Questions on Boats/Airplanes

For problems with boats and streams,

Speed of the boat upstream (against the current) = Speed of the boat in still water – speed of the stream

[As the stream obstructs the speed of the boat in still water, its speed has to be subtracted from the usual speed of the boat]

Speed of the boat downstream (along with the current) = Speed of the boat in still water + speed of the stream

[As the stream pushes the boat and makes it easier for the boat to reach the destination faster, speed of the stream has to be added]

Similarly, for airplanes travelling with/against the wind,

Speed of the plane with the wind = speed of the plane + speed of the wind

Speed of the plane against the wind = speed of the plane – speed of the wind

Let us look at some examples.

Example 1. A man travels at 3 mph in still water. If the current’s velocity is 1 mph, it takes 3 hours to row to a place and come back. How far is the place?

Solution

Let the distance be ‘d’ miles.

Time taken to cover the distance upstream + Time taken to cover the distance downstream = 3

Speed upstream = 3-1 = 2 mph

Speed downstream = 3+1 = 4 mph

Solution

Let the speed of the plane be ‘a’ and that of the wind be ‘w’.

Our table looks like this:
 

	Distance	Speed	Time
With the wind	2400	a+w	4
Against the wind	2400	a-w	6

 
4(a+w) = 2400 and 6(a-w) = 2400

Expressing one unknown variable in terms of the other makes it easier to solve, which means

a+w = 600 → w=600-a

Substituting the value of w in the second equation,

a-w = 400

a-(600-a) = 400 → a = 500

The speed of the plane is 500 kmph and that of the wind is 100 kmph.
 

More solved examples on Speed, Distance and Time

Example 1. A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus.

Solution

	Distance	Speed	Time
Train	d	30	t
Bus	100-d	40	3-t

Let the time taken by the train be ‘t’. Then that of bus is ‘3-t’.

The entire distance covered was 100 miles

So, 30t + 40(3-t) = 100

Solving which gives t=2.

Substituting the value of t in 40(3-t), we get the distance travelled by bus is 40 miles.

Alternatively, we can add the time and equate it to 3 hours, which directly gives the distance.

d/30 + (100-d)/40 = 3

Solution

Our table looks like this.

	Distance	Speed	Time
1st part of journey	d	100	t
2nd part of journey	630-d	110	6-t

Assuming the distance covered in the 1^st part of journey to be ‘d’, the distance covered in the second half becomes ‘630-d’.

Assuming the time taken for the first part of the journey to be ‘t’, the time taken for the second half becomes ‘6-t’.

From the first equation, d=100t

The second equation is 630-d = 110(6-t).

Substituting the value of d from the first equation, we get

630-100t = 110(6-t)

Solving this gives t=3.

Solution

	Distance	Speed	Time
First person	d	3	t
Second person	20-d	4	t

 
Assuming the distance travelled by the first person to be ‘d’, the distance travelled by the second person is ’20-d’.

The time is ‘t’ for both of them because when they meet, they would have walked for the same time.

Since time is same, we can equate as

d/3 = (20-d)/4

Solving this gives d=60/7 miles (8.5 miles approximately)

Then t = 20/7 hours

So the two persons meet after 2 6/7 hours.
 

Practice Questions for you to solve

---

Problem 1: Click here

Answer 1: Click here

---

Problem 2: Click here

Answer 2: Click here

---

Problem 1 :

David drove for 3 hours at a rate of 50 miles per hour, for 2 hours at 60 miles per hour and for 5 hours at a rate of 70 miles per hour. What was his average speed for the whole journey?

Solution :

Step 1 :

Formula for average speed is

= Total distance/Total time taken

And also, formula for the distance is

= Rate ⋅ Time

Step 2 :

Distance covered in the first 3 hours is

= 50 ⋅ 3

= 150 miles

Distance covered in the next 2 hours is

= 60 ⋅ 2

= 120 miles

Distance covered in the last 5 hours is

= 70 ⋅ 5

= 350 miles

Step 3 :

Then, total distance is

= 150 + 120 + 350

= 620 miles

Total time is

= 3 + 2 + 5

= 10 hours

Step 4 :

So, the average speed is

= 620/10

= 62

So, the average speed for the whole journey is 62 miles per hour.

Problem 2 :

Jose travels from the place A to place B at a certain speed. When he comes back from place B to place A, his speed is 60 miles per hour. If the average speed for the whole journey is 72 miles per hour, find his speed when he travels from the place A to B.

Solution :

Step 1 :

Let a be the speed from place A to B.

Speed from place B to A = 60 miles/hour.

Step 2 :

Here, both the ways, he covers the same distance.

Then, formula to find average speed is

= 2xy/(x + y)

Step 3 :

x —-> speed from place A to B

x = a

y —-> speed from place B to A

y = 60

Step 4 :

Given : Average speed  is 72 miles/hour.

(2 ⋅ a ⋅ 60)/(a + 60) = 72

120a = 72(a + 60)

120a = 72a + 4320

48a = 4320

a = 90

So, the speed from place A to B is 90 miles per hour.

Problem 3 :

David travels from the place A to place B at a certain speed. When he comes back from place B to place A, he increases his speed 2 times. If the constant-speed for the whole journey is 80 miles per hour, find his speed when he travels from the place A to B.

Solution :

Step 1 :

Let a be the speed from place A to B.

Then, speed from place B to A = 2a

Step 2 :

The distance traveled in both the ways (A to B and B to A) is same.

So, the formula to find average speed is

= 2xy/(x + y)

Step 3 :

x —-> Speed from place A to B

x = a

y —-> Speed from place B to A

y = 2a

Step 4 :

Given : Average speed = 80 miles/hour

(2 ⋅ a ⋅ 2a)/(a + 2a) = 80

4a²/3a = 80

4a/3 = 80

a = 60

So, the speed from place A to B is 60 miles per hour. 

Problem 4 :

A person takes 5 hours to travel from place A to place B at the rate of 40 miles per hour. He comes back from place B to place A with 25% increased speed. Find the average speed for the whole journey.

Solution :

Step 1 :

Speed (from A to B) = 40 miles/hour

Speed (from B to A) = 50 miles/hour (25% increased)

Step 2 :

The distance traveled in both the ways (A to B and B to A) is same.

So, the formula to find average distance is

= 2xy/(x + y)

Step 3 :

x —-> speed from place A to B

x = 40

y —-> speed from place B to A

y = 50

Step 4 :

Average speed = (2 ⋅ 40 ⋅ 50)/(40 + 50)

= 44.44

So, the average speed for the whole journey is about 44.44 miles/hour.

Problem 5 :

Speed (A to B) = 20 miles/hour

Speed (B to C) = 15 miles/hour

Speed (C to D) = 30 miles/hour

If the distances from A to B, B to C and C to D are equal and it takes 3 hours to travel from A to B, find the average speed from A to D.

Solution :

Step 1 :

Formula to find distance is

= Rate ⋅ Time

Distance from A to B is

= 20 ⋅ 3

= 60 miles

Given : Distance from A to B, B to C and C to D are equal.

Total distance from A to D is

= 60 + 60 + 60

= 180  miles

Step 2 :

Formula to find time is

= Distance/Speed

Time (A to B) = 60/20 = 3 hours

Time (B to C) = 60/15 = 4 hours

Time (C to D) = 60/30 = 2 hours

Total time taken from A to D is

= 3 + 4 + 2

= 9 hours

Step 3 :

Formula to find average speed is

= Total distance/Total time

= 180/9

= 20

So, the average speed from A to D is 20 miles per hour.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

©All rights reserved. onlinemath4all.com

To solve the word problems on speed distance time we need to
know the relationship between speed (rate), distance and time.

  Speed = Distance
                Time

    Time = Distance
               Speed

                                           Distance = Speed × Time

The formula is used to solve different questions on distance
covered, time taken, uniform speed and variable speed problems.

The detailed explanation will help us to understand how to
solve the word problems on speed distance time.

1. An airplane travels 4362 km against the wind in 6 hours and 5322 km with the wind in the same amount of time. What is the rate of the plane in still air and what is the rate of the wind?

Solution:

Let the speed of the
air plane in still air be x km/hr

And the speed of the
wind be y km/hr.

Then speed of the
airplane going with the wind = (x + y) km/hr

and speed of the
airplane going against the wind = (x — y) km/hr.

We know that,

                                 Distance = Speed
× Time

                     or,     Speed = Distance
                                                Time

According to the
problem,

An airplane travels 4362 km against the wind in 6 hours

     x — y = 4362/6

or, x — y = 727 ———— (1)

Again, the
airplane travels 5322 km with the wind in the same amount of time i.e. 6 hours

     x + y = 5322/6

or, x + y = 887 ————
(2)

Now add (1) and (2) we get,

 x — y =  727

 x + y =  887

2x     = 1614

or, 2x/2 = 1614/2,
(Divide both sides by 2)

or, x = 807

Now substitute the
value of value of x = 807 in equation (2) we get,

  807 + y = 887

-807        -807, (Subtract 407 from both sides)

          y = 80

Answer: Rate
of the plane in still air = 807 km/hr

            Rate
of the wind = 80km/hr

Related Concepts

● Math Questions Answers
● Help with Math Problems
● Answer Math Problems
● Math Problem Solver
● Math Unsolved Questions
● Math Questions
● Math Word Problems
● Word Problems on Speed Distance Time
● Algebra Word Problems – Money

Related Pages
Rate Distance Time Word Problems
Distance Word Problems
Average Speed Problems

What Are Distance Word Problems Or Distance Rate Time Problems?

Distance problems are word problems that involve the distance
an object will travel at a certain average rate for a given
period of time.

The formula for distance problems is:
distance = rate × time or
d = r × t

Things to watch out for:
Make sure that you change the units when necessary. For example, if the rate is given in miles
per hour and the time is given in minutes then change the units appropriately.

It would be helpful to use a table to organize the information for distance problems. A table
helps you to think about one number at a time instead being confused by the question.

The following diagrams give the steps to solve Distance-Rate-Time Problems. Scroll down the page
for examples and solutions.

We will show you how to solve distance problems by the following examples:

• Traveling At Different Rates
• Traveling In Different Directions
• Given Total Time
• Wind and Current Problems

How To Solve Distance Problems: Traveling At Different Rates

Example:
A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours.
If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make
the trip?

Solution:
Step 1: Set up a rtd table.

	r	t	d
Case 1
Case 2

Step 2: Fill in the table with information given in the question.

A bus traveling at an average rate of 50 kilometers per hour
made the trip to town in 6 hours. If it had traveled at
45 kilometers per hour, how many more minutes would it
have taken to make the trip?

Let t = time to make the trip in Case 2.

	r	t	d
Case 1	50	6
Case 2	45	t

Step 3: Fill in the values for d using the formula d = rt

	r	t	d
Case 1	50	6	50 × 6 = 300
Case 2	45	t	45t

Step 4: Since the distances traveled in both cases are the same,
we get the equation:

45t = 300
Isolate variable t

Step 5: Beware — the
question asked for “how many more minutes would it
have taken to make the trip”, so we need to deduct the original 6 hours taken.

Answer: The time taken would have been 40 minutes longer.

How To Solve Distance Problems: Two Objects Traveling In The Same Direction

Example:
This motion problem (or distance rate time problem or uniform rate problem) involves traveling
in the same direction, solving for “how long” one moving object traveling until it meets up with
the second moving object.

It uses d = rt (distance equals rate times time).

Car 1 starts from point A and heads for point B at 60 mph. Fifteen minutes later, car 2 leaves the
same point A and heads for point B at 75 mph. How long before car 2 overtakes car 1?

• Show Video Lesson

How To Solve Distance Problems: Two Objects Traveling In The Opposite Directions

Example:
A bus and a car leave the same place and traveled in opposite directions. If the bus is traveling
at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

Solution:
Step 1: Set up a rtd table.

	r	t	d
bus
car

Step 2: Fill in the table with information given in the question.

If the bus is traveling at 50 mph and the car is traveling
at 55 mph, in how many hours will they be 210 miles apart?

Let t = time when they are 210 miles apart.

	r	t	d
bus	50	t
car	55	t

Step 3: Fill in the values for d using the formula d = rt

	r	t	d
bus	50	t	50t
car	55	t	55t

Step 4: Since the total distance is 210, we get the equation:

50t + 55t = 210
105t = 210

Isolate variable t

Answer: They will be 210 miles apart in 2 hours.

Objects Traveling At Opposite Directions, Calculate How Long It Takes For Them To Be A Given Distance Apart

This motion problem (or distance rate time problem or uniform rate problem) involves one object
traveling in one direction and the other in the opposite direction, solving for “how long”
(or the amount of time) two moving objects traveling until they are certain distance apart.

Example:
Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at
450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart?
How far has each plane traveled?

• Show Video Lesson

How To Solve Distance Problems: Given The Total Time

Example:
John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph.
If he spent a total of 7 hours traveling, what is the distance traveled by John?

Solution:
Step 1: Set up a rtd table.

	r	t	d
Case 1
Case 2

Step 2: Fill in the table with information given in the question.

John took a drive to town at an average rate of 40 mph. In the
evening, he drove back at 30 mph. If he spent a total of
7 hours traveling, what is the distance traveled by John?

Let t = time to travel to town.

7 – t = time to return from town.

	r	t	d
Case 1	40	t
Case 2	30	7 – t

Step 3: Fill in the values for d using the formula d = rt

	r	t	d
Case 1	40	t	40t
Case 2	30	7 – t	30(7 – t)

Step 4: Since the distances traveled in both cases are the same,
we get the equation:

40t = 30(7 – t)
Use distributive property
40t = 210 – 30t

Isolate variable t
40t + 30t = 210
70t = 210

Step 5: The distance traveled by John to town is

40t = 120
The distance traveled by John to go back is also 120
So, the total distance traveled by John is 240

Answer: The distance traveled by John is 240 miles.

How To Find The Total Distance Given Total Time And Two Rates?

Example:
Roy took 5 hours to complete a journey. For the first 2 hours, he traveled at an average speed
of 65 km/h. For the rest of the journey, he traveled at an average speed of 78 km/h. What was
the total distance of the journey?

• Show Video Lesson

How To Solve Wind And Current Word Problems?

There is another group of distance-time problems that involves the speed of the water current or
the speed of wind affecting the speed of the vehicle. The following video shows an example of
such a problem.

How to solve Wind Word Problems?

Example:
Into the headwind, the plane flew 2000 miles in 5 hours. With a tailwind, the return trip took 4
hours. Find the speed of the plane in still air and the speed of the wind.

• Show Video Lesson

How to find the speed of the current of a stream?

Example:
The speed of a boat in still water is 10 mph. It travels 24 miles upstream and 24 miles downstream
in 5 hours. What is the speed of the current?

• Show Video Lesson

How to solve Current Word Problems?

Example:
Traveling downstream, Elmo can go 6 km in 45 minutes. On the return trip, it takes him 1.5 hours.
What is the boat’s speed in still water and what is the rate of the current?

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Microsoft Word is one of the popular text processing applications available. Though there are many alternate apps, Word is an ultimate document app due to universal use. However, slow performance of Microsoft Word is quite common on many computers due to various reasons. This may result in reduced productivity for business professionals and normal computer users. In this article let us explain how to fix slow Word when opening, typing and saving documents to speedup productivity.

Related: How to fix slow Microsoft Excel and speedup your productivity.

Fix Slow Microsoft Office Problems

Here are the fixes to solve the performance problem with Microsoft Word.

1. Deleting default template file
2. Disable graphics acceleration in Word settings
3. Use registry editor to disable graphics acceleration
4. Install updates
5. Update your OS
6. Reinstall Microsoft Office
7. Delete temporary files
8. Optimize the document
9. Open Word in safe mode
10. Check locked files
11. Disable add-ins

Method #1: Delete Normal.dot File

Microsoft Word uses template files to create documents. Normal.dot is the global template file that Word uses for creating a blank document file. This essentially means, the template file is always in use when Word is in use. Word also stores all style related settings, such as font size and font type in this template. So, problematic or corrupted ‘Normal.dot’ template can cause slow performance when opening or closing your documents.

An effective solution is to delete the Nomal.dot or Normal.dotm template file. You don’t need to worry about deleting this file as Word will recreate a fresh Normal.dot file when you open the application. However, it is a bit tricky task, since Normal.dot or Normal.dotm file is a hidden file. Therefore, you need to first enable the option in Windows to show hidden files. Then save all your open documents and close Microsoft Word.

The file location may be different depending upon your Windows version. Generally you can find the Normal.dot (Word 2007) or Normal.dotm (Word 2007/10) or Normal.dotx (Word 2013 and above) file in the following location:

C:UsersUsernameappdataMicrosoftTemplates

In Windows 10, you can look for the file in the below path:

C:UsersYour User NameAppDataRoamingMicrosoftTemplates

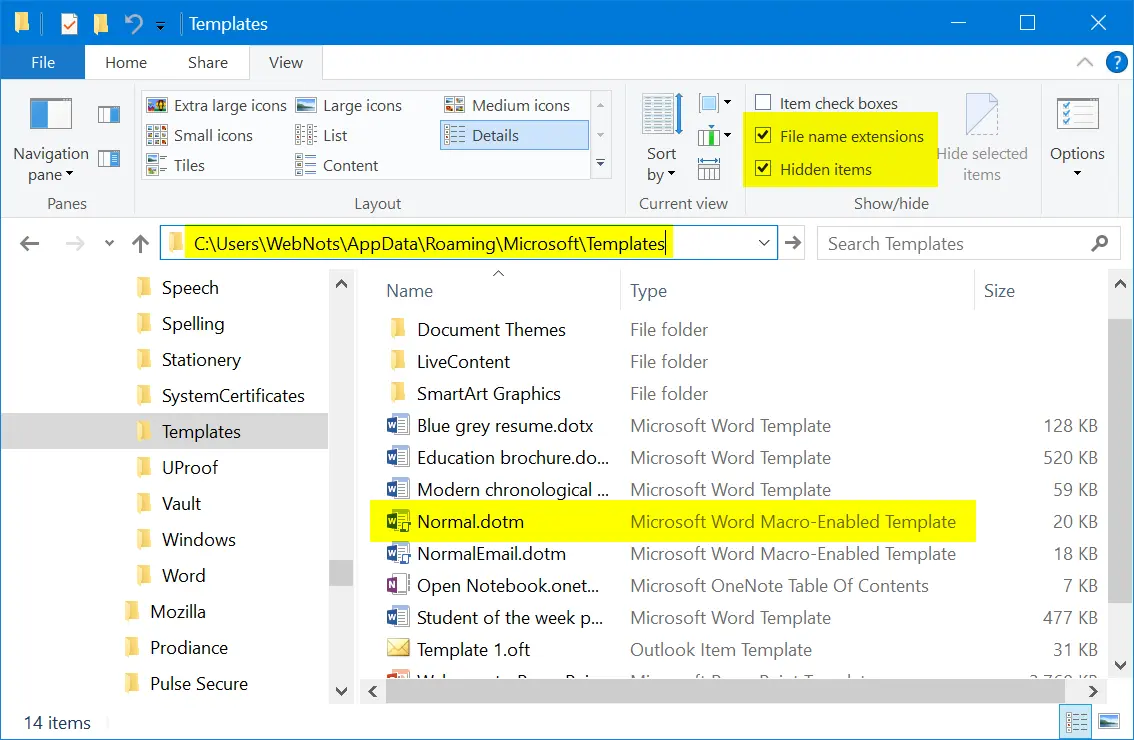
If you use Office on Mac, go to Finder and press “Command + Shift + G” to open “Go to folder” box. Type the following location and press enter key.

~/Library/Application Support/Microsoft/Office/User Templates/

After locating the template file in your PC or Mac, simply delete it. Now, open Microsoft Word to create a new Normal.dot/dotm/dotx file. Check whether this helps to solve the slow processing issues in Microsoft Word.

Related: How to quickly insert dividers in Microsoft Word?

Method #2: Disable Hardware Graphics Acceleration

In some cases, when you type on a Word document, it will lag for few seconds or longer from the moment you press the key. This will badly affect your productivity by causing delay and diverting your concentration when doing important work. Newer Office versions use hardware graphics acceleration to speed up the performance. However, slow computers often have limited hardware resources, which make Word less responsive. Follow these steps to disable hardware acceleration in Word:

• Open Microsoft Word and create a blank document.
• Click “File” menu and choose “Options” in the left pane to go to backstage view.
• On the “Word Options” screen, choose “Advanced” in the left pane.
• Look for “Disable hardware graphics acceleration” option at the right pane under the “Display” section and enable it.
• Click the OK button to apply your changes.

Restart Microsoft Word and verify whether the problem has been resolved.

Method #3: Disable Hardware Acceleration in Registry Editor

If Microsoft Word still performs slowly, it may be a good idea to perform changes in the registry. Note that modifying registry is not recommended and you may not have access in the administered computers. If you have access to registry editor then backup your data and follow the below steps:

• Press “Win + R” keys to open Run prompt. Type the command “regedit” and hit enter. Alternatively, use Windows search box and type in “regedit” to open Registry Editor.
• Navigate to the entry HKEY_CURRENT_USERSoftwareMicrosoftOffice16.0common.
• Note that 16.0 is the version of Microsoft Office 2016, your version could be different.
• Right click on the right pane select “New > Key” to create a new key under the “common” folder.

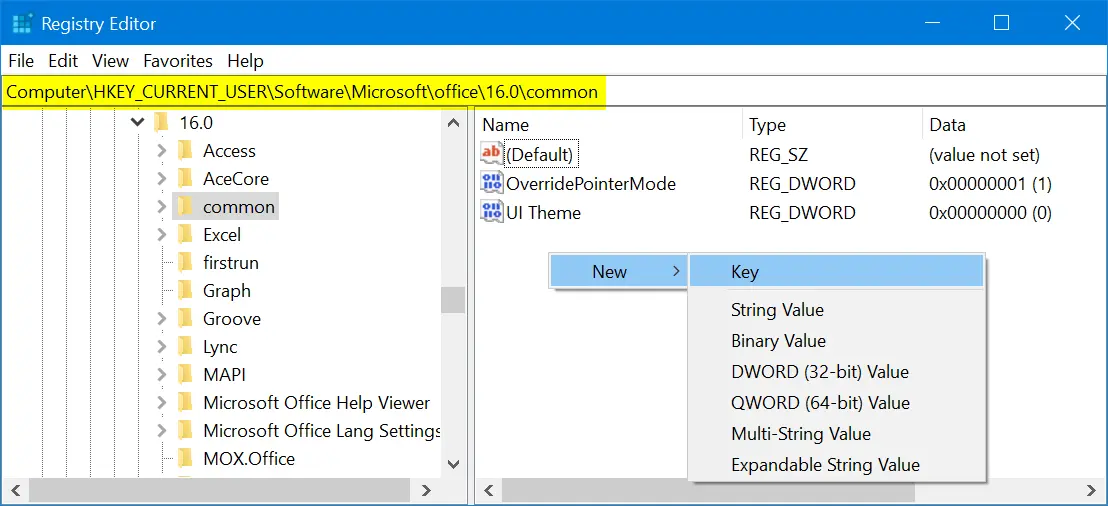
• Windows will create a key with the name as “New Key #1” with an option to edit. Type in “Graphics” for the name of the key.
• Click the newly created “Graphics” key and right click on the right pane. Select “New > DWORD (32-bit) Value” option.

• Type in “DisableHardwareAcceleration” as the name of the new DWORD value.
• Double click on the new DWORD and change its value from 0 to 1.

Close the registry editor and restart your computer. Check Word works smoother now.

Related: Fix slow Microsoft PowerPoint presentations.

Method #4: Install Latest Updates

If Microsoft Word seems to react poorly to any command for processing a task, you may need to look for updating to the latest service pack. The latest service pack may provide you with bug fixes and performance optimization. Microsoft releases service pack regularly, generally they are installed automatically if you have auto update enabled. Otherwise you need to check and update them manually. Often, by installing a new service pack, you can regain lost performance.

Note that Apple stopped supporting 32-bit applications from macOS Catalina. Hence the 32-bit Mac Word 2011 or 2016 apps will no more work on your Mac. Ensure to purchase Office 365 subscription to work with 64-bit compatible Office apps on your Mac.

Method #5: Update Your OS

Also ensure your Windows OS is getting automatic security updates to make sure that rest of the system is working properly. Microsoft updates Windows 10 automatically, however follow the below steps to check the status and manually update:

• Press “Win + I” keys to open Windows Settings app.
• Click on “Update & Security” section.
• Click on the “Check for updates” button to update your Windows 10 to the latest version.

If you have Mac, you can install the latest updates by following the below instructions:

• Go to “Apple menu” by clicking the Apple icon on top left corner of your Mac.
• Select “System Preferences…” and click on the “Software Update” option.
• Check any update is available and install the latest version.

Related: How to change embedded document name in Word?

Method #6: Reinstall Microsoft Office

If you use Microsoft Office regularly for creating complex documents, spreadsheets and presentations, there’s a possibility that it will become faulty or corrupted. You may remedy it easily by reinstalling Office package. Prepare your Microsoft Office DVD and product key to complete the re-installation process. Follow these steps to uninstall and re-install Office in Windows 10:

• Go to “Control Panel” and choose “Uninstall a program” under “Programs” section.
• Find Microsoft Office and click the “Change” button. Follow steps on the screen to remove the program.
• Use the installation disk or download from the Windows Store for re-installing again.

Note that Word 2000, 2002 and 2003 can be restored to original settings by choosing ‘”Detect and Repair” in the “Help” menu.

On Mac, you can simply drag the application file to trash bin and reinstall from the App Store.

Method #7: Delete “~.dot” or “~.doc” Files

When you open a document, Word will have a temporary file in the same folder indicated by the ~ (tilde) sign at the beginning. Generally, Word will delete them automatically when you save and close your document. however, if you accumulate lot of these temporary files, Word would become slow and sluggish. For example, if you zip the content when the document is open then the compressed folder will include the temporary file in addition to the original file. Follow these steps to cleanup the temporary files:

• Go to Windows Search box and type in ~*.dot.
• Hit enter and wait until you get all the files on your computer. Select all of them, right click and choose “Delete”.
• Repeat the process by typing in ~*.doc in the search box. Also select all of them, right click and choose “Delete”.
• You can also empty your Recycle Bin to save storage space on your PC.

Open Microsoft Word and make sure that the problem has been resolved

Method #8: Optimize Document Files

Often, less optimized document files cause slow performance. Check whether your document has plenty of embedded macros and remove any of them if possible. Many people also put high quality pictures with large resolution inside documents. You need to optimize the pictures by changing the dimension that matches the size of the page. You may also use Adobe Photoshop or Snagit to save these images in optimized format to reduce the file sizes without sacrificing the quality too much.

Method #9: Open Word in Safe Mode

One of the reasons for slow Word app is the corrupted documents. When you try to open corrupted document, Word will show a message like “Microsoft Word is not responding” indicating the problem. You can choose “Restart the program” option to cancel the current operation and try to reopen the file again.

If that does not help, then press “Win + R” keys and open Run Command box. Type “winword /safe” to open Word in safe mode. This will help you to speedup the document as Word will disable extensions and other unnecessary stuffs in safe mode. Sometimes, Word will also suggest to open a document in safe mode. Choose “Yes” to check whether the safe mode can help in improving the performance at least when processing that document.

Related: Fix slow Microsoft Outlook emails.

Method #10: Check File Lock

Some times people share the locked file in chat, emails or SharePoint. When you try to open locked file, Word will show you the “File in Use” warning and ask you to choose the action.

You may notice, slow response time in Word when you open and read locked documents. We recommend you to open the locked file in “Read Only” mode to open it faster. Otherwise, you can request the owner to share the file without edit lock.

Method #11: Disable Add-ins

If you use add-ins to enhance the functionalities then ensure to disable them when you have problem with Word.

• Go to “File > Options” menu in Word.
• Choose “Add-ins” to view all installed on your Word installation. you can click each add-in to check the function it does.
• Select the add-ins type from the “Manage” drop-down and click on “Go…” button.
• Uncheck the add-ins to disable them.

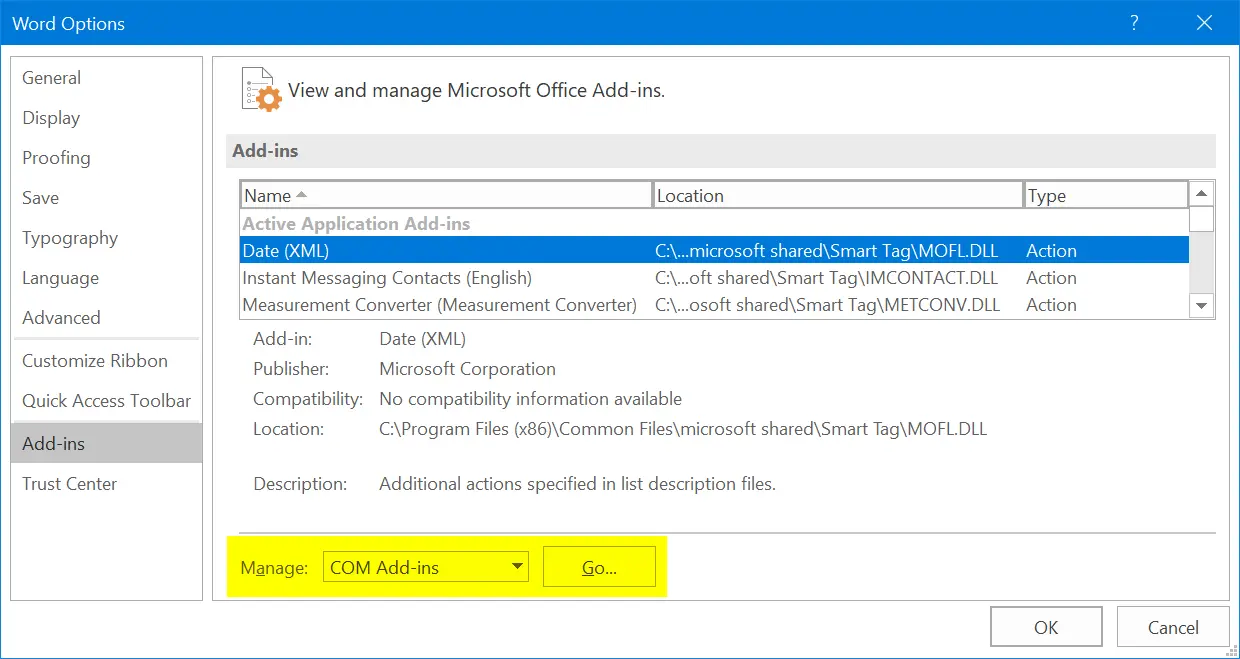
Check whether this helps to resolve your problems. You can enable the add-ins back any time when needed.

Conclusion

Microsoft Word is almost an essential utility in office workers and many user’s daily life. So when you experience slow response, typing delay or any other problem, it is a good idea to check all the above steps. This will ensure to fix the problems and focus on creating documents with improved productivity.