Сводка
В этой статье описано, как устранять проблемы, которые могут возникнуть при запуске или использовании Microsoft Word. Используйте следующие методы в том порядке, в котором они представлены. Если вы попробуйте один из этих способов, но он не помогает, перейдите к следующему методу.
Решение
Проверка и установка последних обновлений
Возможно, вам придется настроить Windows обновления, чтобы автоматически скачивать и устанавливать рекомендуемые обновления. Установка важных, рекомендуемых и необязательных обновлений часто устраняет проблемы, заменяя их и устраняя уязвимости. Чтобы установить последние обновления Microsoft Office, см. Office Обновления Майкрософт на компьютере и на компьютере.
Список последних обновлений Office см. в Office обновления. Если после установки последних обновлений Windows и Office проблема не устранена, перейдите к методу 2.
Убедитесь, что на компьютере установлены последние обновления для Windows. Обновления часто устраняют проблемы с программным обеспечением. Прежде чем использовать один из следующих способов, сначала попробуйте установить обновления. После установки обновлений перезагрузите компьютер и запустите Word.
Устранение неполадок, которые возникают при запуске Word
ВАЖНО:Будьте внимательны, выполняя действия, описанные в этом разделе. Ошибки при изменении реестра могут привести к серьезным проблемам. Перед внесением изменений зарегистрировать реестр на случай проблем и его потребуется восстановить позже.
Способ 1. Вставка документа в другой файл
Последний знак абзаца в документе Word содержит сведения о документе. Если документ поврежден, вы можете получить его текст, если можете опустить последний знак абзаца.
Чтобы получить доступ к документу, но оставить знак последнего абзаца, выполните следующие действия:
-
Щелкните Файл > новый > новый документ.
-
На вкладке Вставка нажмите кнопку Объекти выберите текст из файла.
-
Выберите файл, который вы хотите открыть и вставить, а затем нажмите кнопку Вставить.
Способ 2. Запуск Word с помощью переключателя /a
Переключатель/ — это средство устранения неполадок, с помощью которой можно определить, где может возникнуть проблема в Word. Переключатель /предотвращает автоматическое загрузку надстройок и глобальных шаблонов. Переключатель /a также блокирует файлы параметров, чтобы предотвратить его чтение или изменение. Чтобы запустить Word с помощью переключателя /a, выполните следующие действия:
-
Нажмите кнопку > поиск,введите «Выполнить» и нажмите ввод.
-
Во всплывающее окно Выполнить введите «winword /a» и нажмите ввод.
Дополнительные сведения о переключателье / см. в описании переключателя запуска «/a» в Word.
Если проблема не возникает при запуске Word с помощью переключателя /, попробуйте следующий способ определить ее источник.
Способ 3. Удаление подменю реестра данных Word
Большинство часто используемых параметров в Word хранятся в подменю реестра данных Word. Распространенный этап устранения неполадок — удаление подменю реестра данных Word. При перезапуске Word программа перестраит ключ реестра данных Word, используя параметры по умолчанию.
ПРИМЕЧАНИЕ: При удалении подменю реестра данных Word некоторые параметры заменяются настройками по умолчанию. Например, Word сбрасывает список «последний использованный файл» в меню Файл. Кроме того, Word сбрасывает многие параметры, настроенные во всплывающее окно Параметры.
ВАЖНО: Будьте внимательны, следуя этим шагам. Ошибки при изменении реестра могут привести к серьезным проблемам. Перед внесением изменений зарегистрировать реестр на случай проблем и его потребуется восстановить позже.
Чтобы удалить подменю реестра данных Word, выполните указанные здесь действия.
-
Выйдите из Office программ.
-
Введите «regedit» в поле Поиск и нажмите ввод.
-
Найдите следующий подменю реестра, соответствующий используемой версии Word:
Word 2016: HKEY_CURRENT_USERSoftwareMicrosoftOffice16.0WordData
Word 2013: HKEY_CURRENT_USERSoftwareMicrosoftOffice15.0WordData
Word 2010: HKEY_CURRENT_USERSoftwareMicrosoftOffice14.0WordData
Word 2007: HKEY_CURRENT_USERSoftwareMicrosoftOffice12.0WordData
Word 2003: HKEY_CURRENT_USERSoftwareMicrosoftOffice11.0WordData -
Щелкните Данныеи выберите файл > экспорт.
-
Назовите файл «Wddata.reg» и сохраните его на рабочем столе.
-
Нажмите кнопку > удалитьи нажмите кнопку Да.
-
Зайдите из редактора реестра и запустите Word.
Если Word запускается и работает правильно, проблема устранена (поврежденный ключ реестра данных Word). Для восстановления избранных параметров в Word может потребоваться изменить несколько параметров.
Если проблема не устранена, восстановите исходный подменю реестра данных Word и попробуйте следующий способ:
Восстановление исходного ключа реестра данных Word
Чтобы восстановить исходный подменю реестра данных Word, выполните указанные здесь действия.
-
Выйдите из Office программ.
-
Дважды щелкните значок Wddata.reg на рабочем столе.
-
Нажмите кнопку Даи нажмите кнопку ОК.
Если восстановление подменю реестра данных Word не работает, перейдите к следующей процедуре.
Способ 4. Удаление ключа реестра «Параметры Word»
В параметрах реестра Word есть параметры, которые можно настроить в Word. Эти параметры разделены на группы по умолчанию и необязательные. Параметры по умолчанию создаются во время настройки программы. Необязательные параметры не создаются во время настройки. Вы можете изменить как стандартные, так и необязательные параметры в Word.
Чтобы удалить параметры реестра Word, выполните следующие действия:
-
Выйдите из Office программ.
-
Введите regedit в поле Поиск (в Windows 10, Windows 8.1 или Windows
или в поле Начать поиск в меню Пуск (в более ранних версиях Windows) и нажмите ввод.
-
Найдите следующий подменю реестра, подходящий для запущенной версии Word:
Word 2016: HKEY_CURRENT_USERSoftwareMicrosoftOffice16.0WordOptions
Word 2013: HKEY_CURRENT_USERSoftwareMicrosoftOffice15.0WordOptions
Word 2010: HKEY_CURRENT_USERSoftwareMicrosoftOffice14.0WordOptions
Word 2007: HKEY_CURRENT_USERSoftwareMicrosoftOffice12.0WordOptions
Word 2003: HKEY_CURRENT_USERSoftwareMicrosoftOffice11.0WordOptions -
Нажмите кнопкуПараметры и выберите файл > экспорт.
-
Назовите файл «Wddata.reg» и сохраните его на рабочем столе.
-
Нажмите кнопку > удалитьи нажмите кнопку Да.
-
Зайдите из редактора реестра и запустите Word.
Если Word запускается и работает правильно, проблема устранена (поврежденный параметр реестра Параметры Word). Для восстановления избранных параметров в Word может потребоваться изменить несколько параметров.
Если проблема не устранена, восстановите исходный ключ реестра Параметры Word и попробуйте следующий способ.
Восстановление исходного ключа реестра «Параметры Word»
Чтобы восстановить исходный подменю «Параметры Word», выполните указанные здесь действия.
-
Выйдите из Office программ.
-
Дважды щелкните значок Wdoptn.reg на рабочем столе.
-
Нажмите кнопку Даи нажмите кнопку ОК.
Способ 5. Замените глобальный файл шаблонов Normal.dot или Normal.dotm
Форматирование, автотекст и макрос, хранимые в глобальном файле шаблонов, могут повлиять на работу Word и любых открытых документов. Для этого замените глобальный файл шаблона.
ВАЖНО: Этот метод включает переименование глобального файла шаблона, чтобы Word не нашел его, как ожидалось, при перезапуске. В связи с этим Word повторно создаст глобальный файл шаблона. Таким образом вы сохраняете исходный файл на тот случай, если его придется восстановить. При переименовании глобального файла шаблона по умолчанию сбрасываются некоторые параметры, включая пользовательские стили, настраиваемые панели инструментов, макрос и элементы автотекста. Поэтому мы настоятельно рекомендуем сохранить глобальный файл шаблона и не удалять его.
ДОПОЛНИТЕЛЬНОЕ ПРИМЕЧАНИЕ. В некоторых ситуациях может быть несколько глобальных файлов шаблонов. Например, это происходит, если на одном компьютере запущено несколько версий Word или на одном компьютере работает несколько установок рабочих станции. В таких ситуациях необходимо переименовать каждый глобальный файл шаблона, чтобы он четко отражал соответствующую установку Word.
Чтобы переименовать глобальный файл шаблона, выполните следующие действия:
-
Выйдите из Office программ.
-
Нажмите кнопку > поиск, введите «cmd» и нажмите ввод.
-
В командной области введите команду, соответствующую вашей версии Word:
Word 2016, Word 2013, Word 2010 или Word 2007: «ren %userprofile%AppDataRoamingMicrosoftTemplatesNormal.dotm OldNormal.dotm»
Word 2003: «ren %userprofile%AppDataRoamingMicrosoftTemplatesNormal.dot OldNormal.dot»
-
Нажмите клавишу ВВОД.
-
В командной области введите «выход» и нажмите ввод.
-
Запустите программу Word.
Если Word запускается правильно, проблема решена. В этом случае проблема заключается в поврежденного глобальном файле шаблона. Теперь для восстановления избранных параметров может потребоваться изменить несколько параметров.
ПРИМЕЧАНИЕ: Старый глобальный файл шаблона может содержать настройки, которые нельзя легко создать. Эти настройки могут включать стили, макрос и элементы автотекста. В этом случае вы можете скопировать настройки из старого глобального файла шаблона в новый глобальный файл шаблона с помощью организатора. Чтобы получить дополнительные сведения об использовании организатора для копирования макроса и стилей, нажмите F1 в Word, чтобы открыть справку Microsoft Word, введите «переименовать макрос» в поле Поиск и нажмите кнопку Поиск, чтобы просмотреть эту тему.
Если проблема не устранена, восстановим исходный глобальный файл шаблона и перейдите к следующему разделу.
Восстановление исходного глобального файла шаблона
Чтобы восстановить исходный глобальный файл шаблона, выполните следующие действия:
-
Выйдите из Office программ.
-
Нажмите кнопку > поиск, введите «cmd» и нажмите ввод.
-
В командной области введите команду, соответствующую вашей версии Word:
Word 2016, Word 2013, Word 2010 или Word 2007: «ren %userprofile%AppDataRoamingMicrosoftTemplatesNormal.dotm OldNormal.dotm»
Word 2003: «ren %userprofile%AppDataRoamingMicrosoftTemplatesNormal.dot OldNormal.dot»
-
Нажмите клавишу ВВОД.
-
В командной области введите «выход» и нажмите ввод.
-
Запустите программу Word.
Способ 6. Отключение надстройки для папки «Загрузка»
При запуске Word Word автоматически загружает шаблоны и надстройки, которые находятся в папках «Загрузка». Конфликты или проблемы, влияющие на надстройки, могут привести к проблемам в Word. Чтобы определить, является ли элемент в папке «Загрузка» причиной проблемы, временно отключите параметр реестра, который указывает на эти надстройки.
Для этого выполните следующие действия:
-
Выйдите из Office программ.
-
Запустите Windows проводника, введите «windows ex» в поле Поиск и нажмите ввод.
-
В командной области введите команду, соответствующую вашей версии Word:
Word 2016, 64-битная установка C2R: «%programfiles%Microsoft Officerootoffice16Startup»
Word 2016, 32-битная установка C2R: «%programfiles% (x86)Microsoft Officerootoffice16Startup»
Word 2016, 64-битная установка MSI:
«%programfiles%Microsoft Officeoffice16Startup» Word 2016, 32-bit MSI installation: «%programfiles% (x86)Microsoft Officeoffice16Startup»
Word 2013, 64-битная установка C2R: «%programfiles%Microsoft Officerootoffice15Startup»
Word 2013, 32-битная установка C2R: «%programfiles% (x86)Microsoft Officerootoffice15Startup»
64-битная установка MSI в Word 2013: «%programfiles%Microsoft Officeoffice15Startup»
Word 2013, 32-bit MSI installation: » %programfiles% (x86)Microsoft Officeoffice15Startup»
Word 2010: «%programfiles%Microsoft OfficeOffice14Startup»
Word 2007: «%programfiles%Microsoft OfficeOffice12Startup»
Word 2003: «%programfiles%MicrosoftOfficeOffice11Startup» -
Нажмите клавишу ВВОД.
-
Щелкните правой кнопкой мыши один из файлов, содержащихся в папке, и выберите переименовать.
-
После имени файла введите .old и нажмите ввод.
ВАЖНО: Внимание! Заметьте исходное имя файла, чтобы при необходимости его можно было восстановить.
-
Запустите программу Word.
-
Если воспроизвести проблему больше не удалось, найдена надстройка, которая вызывает проблему. Если вам необходимо иметь функции, которые предоставляет надстройка, обратитесь к ее поставщику для обновления.
Если проблема не устранена, переименуйте надстройки, используя исходное имя, и повторите шаги 3–6 для каждого файла в папке «Запуск».
-
Если проблему по-прежнему можно воспроизвести, введите следующий путь в адресной Windows проводника и нажмите кнопку ОК.
Windows 10, 8.1, 8 или 7: «%userprofile%AppDataRoamingMicrosoftWordStartup»
Windows XP: «%userprofile%Application DataMicrosoftWordStartup» -
Повторите действия 3–6 для каждого файла в этой папке startup.
Если после отключения надстройки «Папка для загрузки» проблема не устранена, перейдите к следующему способу.
Способ 7. Удаление реестра надстройки COM
Надстройки COM можно установить в любом месте. Программы, взаимодействующие с word, устанавливают надстройки COM. Чтобы определить, вызывает ли проблема надстройка COM, временно отключать ее, удаляя ключи реестра для надстройки COM.
Чтобы удалить ключи реестра надстроек COM, выполните следующие действия:
-
Выйдите из Office программ.
-
Нажмите кнопку < поиск, введите «regedit» и нажмите ввод.
-
Найдите подменю реестра: HKEY_CURRENT_USERSoftwareMicrosoftOfficeWordAddins.
-
Нажмите кнопку Добавить ивыберите файл > экспорт.
-
Назовите файл «WdaddinHKCU.reg» и сохраните его на рабочем столе.
-
Нажмите кнопку > удалитьи нажмите кнопку Да.
-
Найдите подменю реестра: HKEY_LOCAL_MACHINESoftwareMicrosoftOfficeWordAddins
-
Нажмите кнопку Добавить ивыберите файл > экспорт.
-
Примените к файлу имя WdaddinHKLM.reg, а затем сохраните его на рабочем столе.
-
Нажмите кнопку > удалитьи нажмите кнопку Да.
-
Зайдите из редактора реестра и запустите Word.
Если проблема устранена, вы определили, что проблема возникает из-за надстройки COM. Затем необходимо определить, какая надстройка COM вызывает проблему.
Определение программы надстройки COM, которая вызывает проблему
Чтобы определить, какая надстройка COM вызывает проблему, выполните указанные здесь действия.
-
Выйдите из Office программ.
-
Дважды щелкните значок Wdaddin.reg на рабочем столе.
-
Нажмите кнопку Да, а затем — кнопку ОК.
-
Если вы используете Word 2016, Word 2013 или Word 2010:
-
Щелкните Параметры > файла.
-
Щелкните Надстройки.
-
В списке Управление нажмите Надстройки COM, а затем — Перейти.
ПРИМЕЧАНИЕ: Если надстройка указана во всплывающее Add-Ins COM, отвяжем ее. Если в списке несколько надстроек, каждый раз отсвейте только одну надстройку. Эта процедура помогает определить, какая надстройка вызывает проблему.
-
Нажмите кнопку ОК, чтобы закрыть всплывающее Add-Ins COM.
-
Выберите файл > Выход.
-
-
Если вы используете Word 2007:
-
Нажмите кнопку Microsoft Office и выберите параметры Word.
-
Щелкните Надстройки.
-
В списке Управление нажмите Надстройки COM, а затем — Перейти.
ПРИМЕЧАНИЕ: Если надстройка указана во всплывающее Add-Ins COM, отвяжем ее. Если в списке несколько надстроек, каждый раз отсвейте только одну надстройку. Эта процедура помогает определить, какая надстройка вызывает проблему.
-
Нажмите кнопку ОК, чтобы закрыть всплывающее Add-Ins COM.
-
Нажмите кнопку Microsoft Office и выберите выход из Word.
-
Выберите файл > Выход.
-
-
Запустите программу Word.
Если проблема устранена при запуске Word, вы определили, какая надстройка COM является причиной проблемы. Если у вас должны быть функции, которые предоставляет надстройка, необходимо определить, какая надстройка включает эти функции, чтобы связаться с поставщиком обновления.
Если проблема не устранена при запуске Word, повторите шаги 4 и 5 для каждой надстройки COM, которая указана в списке, пока не определите, какая надстройка вызывает проблему.
Чтобы восстановить надстройки COM, повторите шаг 4, но выберите для каждой надстройки COM, которую вы хотите восстановить.
Способ 8. Изменение принтера по умолчанию
Чтобы изменить принтер по умолчанию, выполните следующие действия:
-
Выйдите из Office программ.
-
Нажмите кнопку < поиск, введите «regedit» и нажмите ввод.
-
Щелкните правой кнопкой мыши Microsoft XPS Document Writerи выберите установить принтер по умолчанию.
-
Запустите программу Word.
Если проблема устранена после запуска Word, вы определили, что проблема обусловлена принтером. В этом случае обратитесь к поставщику, чтобы узнать, есть ли обновление драйвера принтера.
Варианты поддержки Майкрософт
Если вы не можете решить эту проблему, воспользуйтесь службой поддержки Майкрософт для поиска ответов в базе знаний Майкрософт и других технических ресурсах. Вы также можете настроить сайт для управления поиском. Чтобы начать поиск, перейдите на веб-сайт службы поддержки Майкрософт.
The halting problem can serve as the origin for a chain of provably undecidable problems. A standard and in fact the by far most common way for proving that a problem is undecidable, is to show that the halting problem can be reduced to it in the sense that any algorithmic solution of the considered problem would imply a solution for the halting problem. In many cases there is in fact a longer chain of reductions through intermediate problems.
Since Axel Thue was a Norwegian mathematician the German way of pronouncing ‘Thue’ is likely to be much closer to the truth than the English one.
In this lecture we will provide a first (and second) link in such chains by proving a reduction of the halting problem to the word problem for semi-Thue systems (and finally for Thue systems). Here and in the following lectures (until we say something different) undecidable will always mean algorithmically undecidable by recursive means. Having in mind the Church-Turing thesis we will drop ‘by recursive means’ and since we haven’t talked about axiomatic undecidability yet, we will be even more sloppy and also omit ‘algorithmically’ …
Terminology and notation
In principle we could talk about sets, their elements, ordered pairs and sequences, but in this business a different terminology is commonly used: we consider a finite set which we call alphabet, the elements of which are called symbols. A finite sequence of symbols
is called a word over the alphabet, and the set of all words of length
will be denoted by
. It is convenient to use an extra symbol, say
, for the word of zero length and to include this into the set of all words
.
Definition [semi-Thue system]
A semi-Thue system is a pair of a finite alphabet
and a finite set of ordered pairs
called substitution rules.
Furthermore, we will write for a pair of words
iff there is a substitution rule
and words
(possibly of zero length) so that
and
(hence, the name substitution rule). Note that here we make use of the natural operation on words, namely concatenation which is, needless to say, associative.
In a similar vein, we will write iff there is a finite sequence of words
so that
which for
means
. Keep in mind that all this is always w.r.t. a given semi-Thue system. The word problem for a fixed semi-Thue system is then the problem of deciding whether or not
for given words
. The following specifies in which sense the word problem is undecidable:
Proposition [Undecidable word problem for semi-Thue systems]
There is a semi-Thue system and a word
such that there is no algorithm which upon input
is capable of deciding whether or not
. (That is, every algorithm attempting to compute this predicate will necessarily fail on an infinite subset of inputs.)
proof: As mentioned before, the idea is to reduce the halting problem to this word problem. So we will construct a semi-Thue process for every Turing machine for which the corresponding map is defined for any internal state apart from the halting state. Let us denote the internal states as
where
and
are the starting state and halting state, respectively. In order to encode a Turing machine into a semi-Thue system we characterize the entire tape&head configuration by a string of the form
where
is the current internal state,
is the content of the tape (in a sufficiently large region to be specified in a moment) and the scanned symbol
is the left most symbol of
. If we denote the rightmost symbol of
as
, then a single step in the TM evolution only alters the triple
in the way
Here the case to be chosen (R or L) and the primed=new symbols for the internal state and the tape cell depend on and
from which they are determined by the map
which characterizes the TM. Hence, the evolution of a TM corresponds to a finite set of substitution rules so that we almost have a semi-Thue process assigned to any TM. What has yet to be taken care of is the fact that the tape is infinite while a word has to be finite. In order to cure this apparent conflict we introduce the marker
which does nothing but setting a virtual mark at the outmost points of the ‘relevant’ part of the tape. Since we do not know beforehand how big this is to be chosen, we allow the marks to move. This is done by adding the substitution rules
and
for all
.
Finally, we want to assure that if the halting state appears, then there is a unique squence of substitutions which collaps the entire head&tape configuration to a unique word. To this end we add a new symbol and the substitution rules
,
and
for all . Taking it all together we have achieved that the TM halts upon starting with the head on the leftmost symbol of a string
iff
holds for the constructed semi-Thue system with alphabet . Applying this to a universal TM we see that a solution to the above word problem would imply a solution to the halting problem. Hence, there cannot be an algorithm deciding the word problem.
The construction in the proof is such that an -state TM with binary tape alphabet gives rise to a semi-Thue system with
substitution rules and an alphabet with
symbols. While the latter number can easily always be reduced to 2, the size of
is more tricky – the current record is
.
Definition [Thue system]
A Thue system is a semi-Thue system for which implies that
.
It follows dirctly from the definition of a Thue system that the relation becomes an equivalence relation since it is reflexive, symmetric and transitive. We will thus write
in this case.
From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Word problems for systems of linear equations are troublesome for most of the students in understanding the situations and bringing the word problem into equations. We tried to explain the trick of solving word problems for equations with two variables with an example.
Example:
2000 tickets were sold in an exhibition on Saturday. The cost of a ticket for an adult is $4 and for a child is $2. The total amount collected on Saturday was $6400. Find the number of adult tickets and child tickets sold on Saturday.
Solution:
Step 1:
Total number of tickets sold = 2000
Cost of ticket for an adult = $4
Cost of ticket for a child = $2
Total amount collected = $6400
We are asked to find the number of adult tickets and children tickets sold.
Let x be the number of adult tickets sold and y the number of child tickets sold on Saturday.
Step 2:
Total number of tickets sold = 2000
Number of adults tickets sold + Number of child tickets sold = 2000
x + y = 2000 ————— (1)
Total amount collected = Amount collected from adult tickets + Amount collected from child tickets
Since there are x adults and the adult ticket cost is $4 per, the amount collected from adult tickets is 4x and since there are y children and the child ticket costs $2 per child, the amount collected from child tickets is 2y.
6400 = 4x + 2y
It can be written as 4x + 2y = 6400 —————- (2)
Now, we got a system of two linear equations in two variables.
x + y = 2000 ————— (1)
4x + 2y = 6400 —————- (2)
Step 3:
Solve the above two linear equations to find the value of x and y.
Multiply equation (1) with -2 and add the resulting equation and equation (2) to eliminate the variable y.
-2x — 2y = -4000
(+) 4x + 2y = 6400
———————————
2x = 2400
Divide by 2 on both the sides and simplify.
x = 1200
Step 4:
Now, substitute the value of x = 1200 in either of the two equations.
Let us substitute in equation (1). So, it becomes
1200 + y = 2000
Subtract 1200 from both sides of the equation and simplify.
1200 + y — 1200 = 2000 — 1200
y = 800
Step 5:
So, the solution for the given system of equations is (1200, 800), which means 1200 adult tickets and 800 child tickets were sold on Saturday.
Note: The above problem can be also solved using substitution method since the coefficients of x and y in the first equation is 1.
Practice Problems:
1. James bought 5 apples and 10 oranges for $4. Donald bought 3 apples and 9 oranges for $3. The shop keeper strictly told that there will not be any discounts. What is the cost of an apple and an orange?
Show Answer
2. Ana writes test to upgrade her level. The test has 25 questions for a total score of 150 points. Among the 25 questions, each multiple choice questions carries 3 points and the descriptive type questions carries 8 points. How many multiple choice questions and descriptive type questions are there in the test?
Show Answer
3. The sum of the digits of a two digit number is 7. When the digits are reversed, then number is decreased by 9. Find the number.
Show Answer
4. The perimeter of a rectangle is 12 meters. The length is 3 more than twice its width. Find the dimensions of the rectangle.(This can also be solved just with one variable)
Show Answer
5. The sum of two numbers is 12. When three times the first number is added to 5 times the second number, the resultant number is 44. Find the two numbers.
Show Answer
Having problem in solving any of these questions? Post your doubt in comment. We will help you how to solve this.
Related Articles:
Если вы столкнулись с тем, что текстовый редактор Microsoft Word работает с ошибками или вообще не запускается на Windows 10, не стоит беспокоиться, эти проблемы вполне реально решить. В данной статье мы рассмотрим наиболее вероятные причины подобных сбоев в работе этого популярного приложения и подскажем способы их устранения.
Вы можете столкнуться с ситуацией, когда Word отказывается запускаться по причине отсутствия у вас прав администратора. См. также: как получить права администратора в Windows 10.
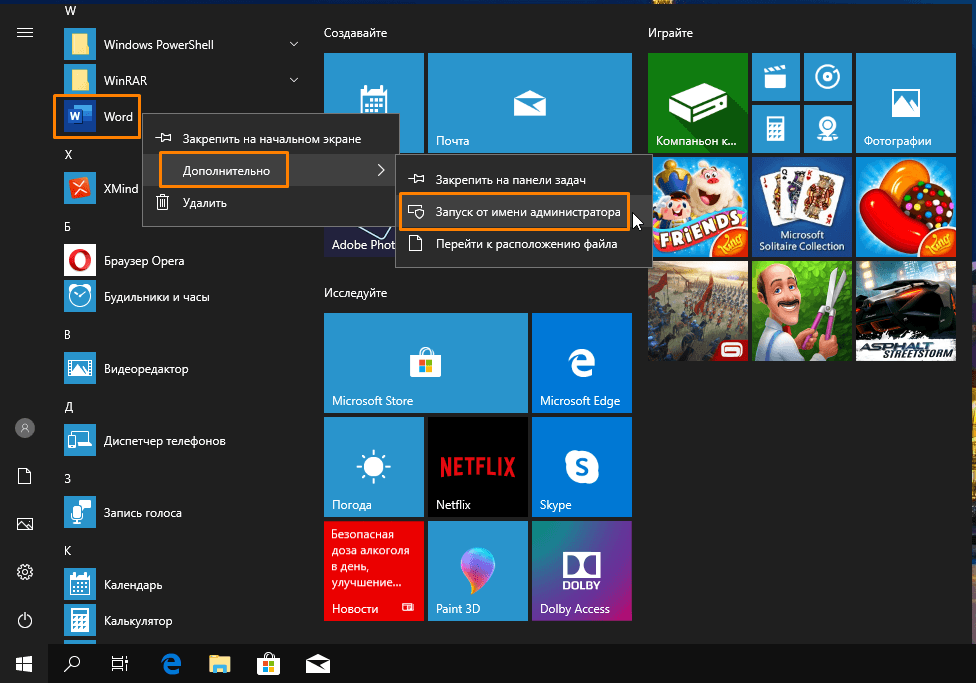
- Найдите ярлык Word в меню «Пуск», щелкните на него правой кнопкой мыши и в контекстном меню выберите команду «Дополнительно», а после — «Запуск от имени администратора».
Запускаем Word от имени администратора
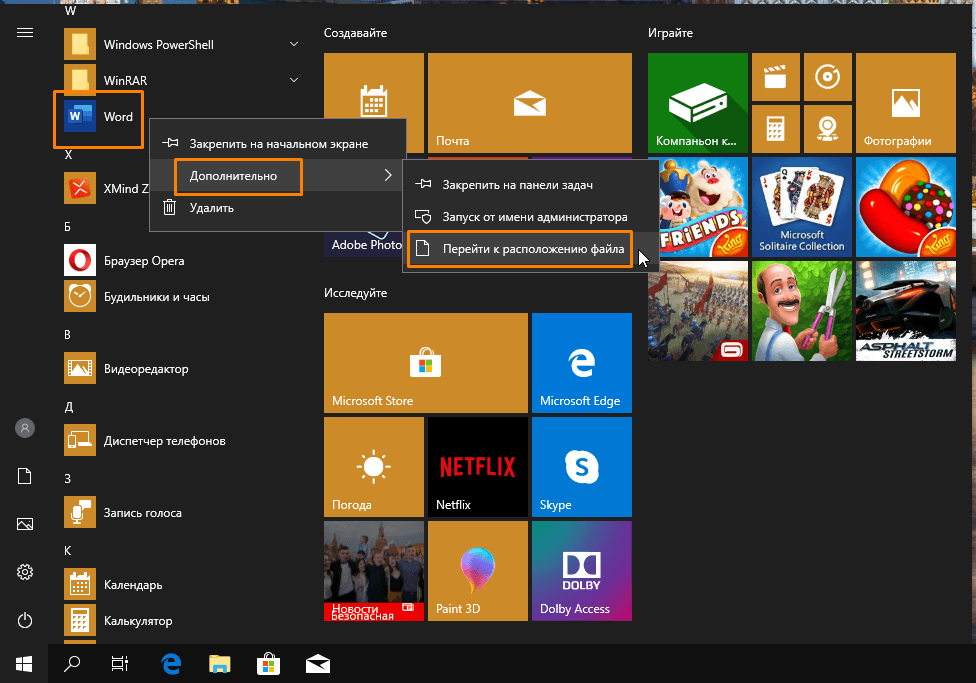
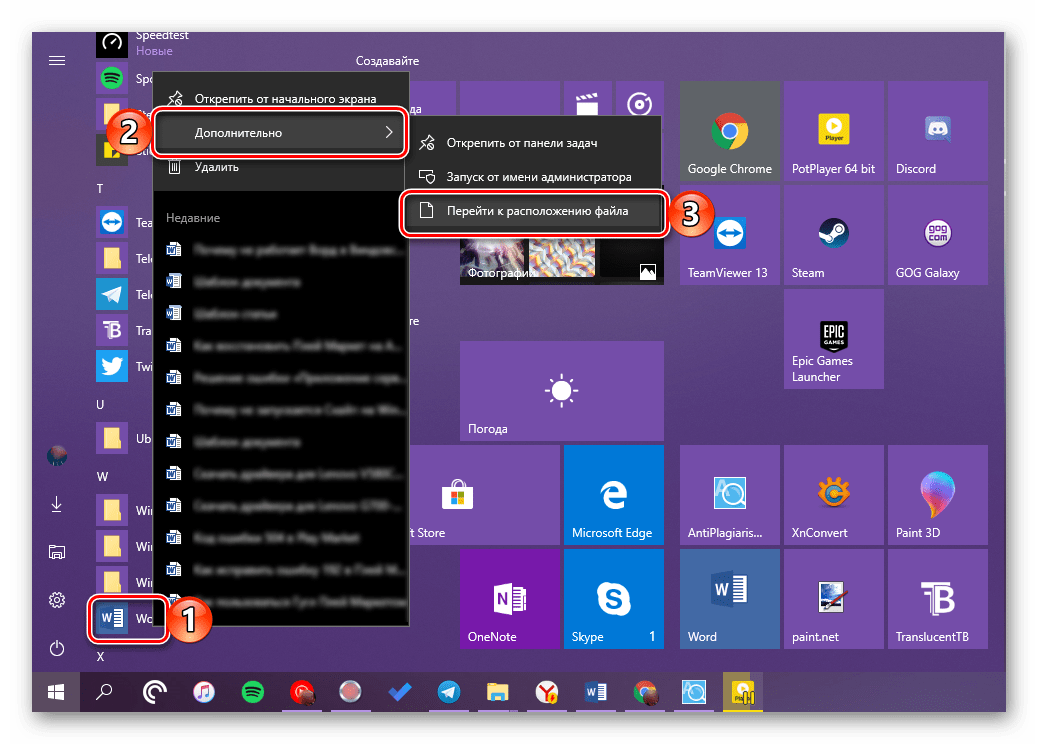
- Если приложение запустилось, считайте, что причина неработоспособности Word найдена. Чтобы не проделывать вышеописанные действия каждый раз, изменим свойства ярлыка программы. Для этого снова кликаем ярлык Word в меню «Пуск» правой кнопкой мыши и в подменю «Дополнительно» выбираем команду «Перейти к расположению файла».
Переходим к расположению файла
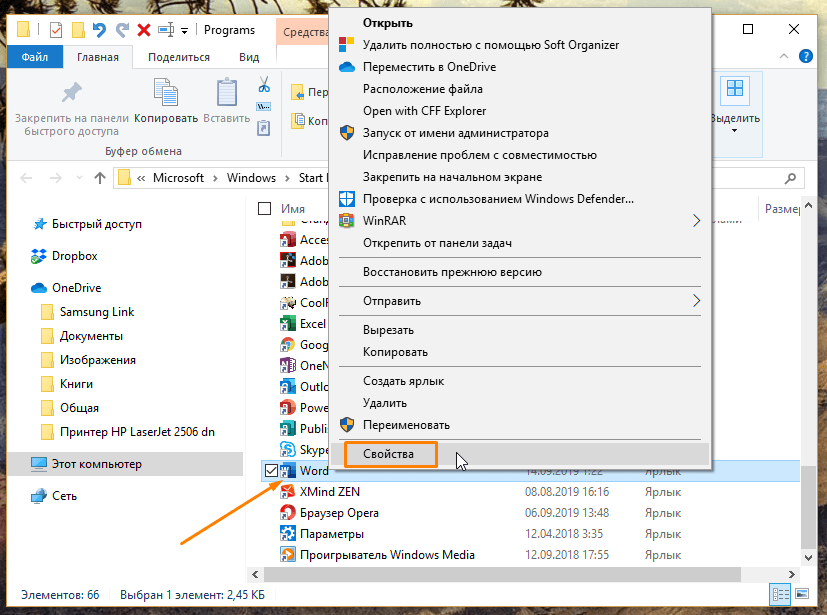
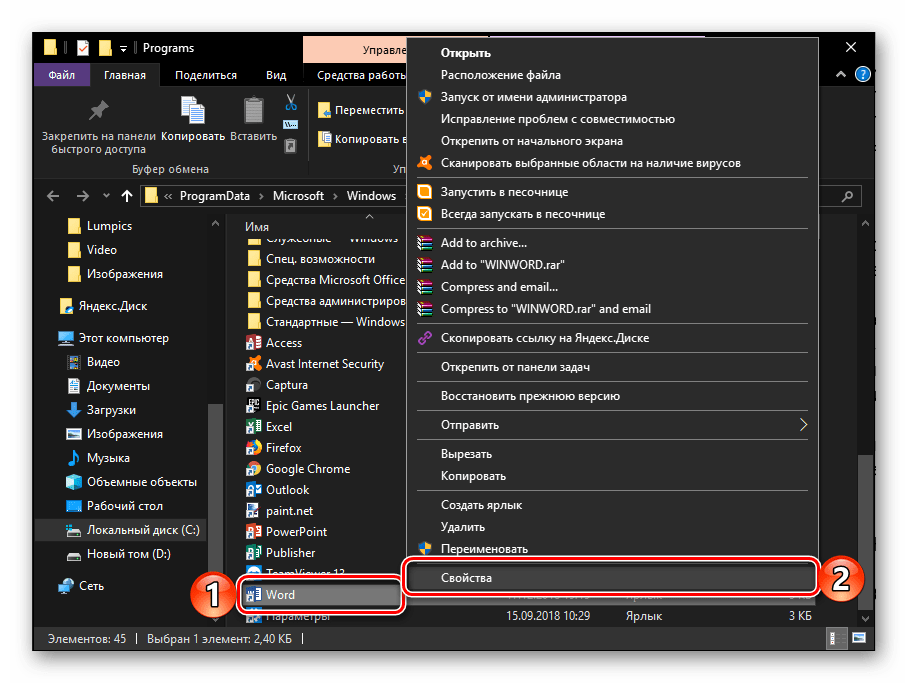
- Откроется окно папки, содержащей файлы ярлыков из меню «Пуск». С помощью правой кнопки мыши открываем контекстное меню ярлыка Word и выбираем команду «Свойства».
Открываем свойства ярлыка Word
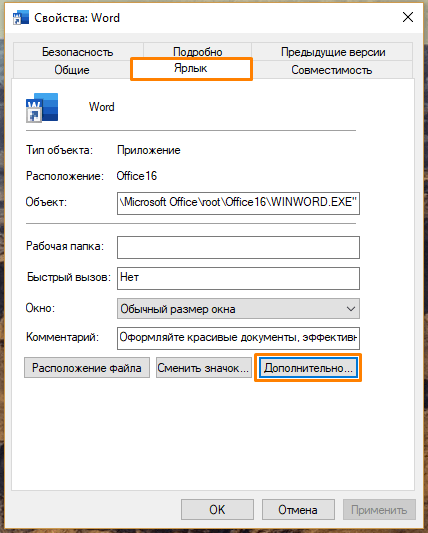
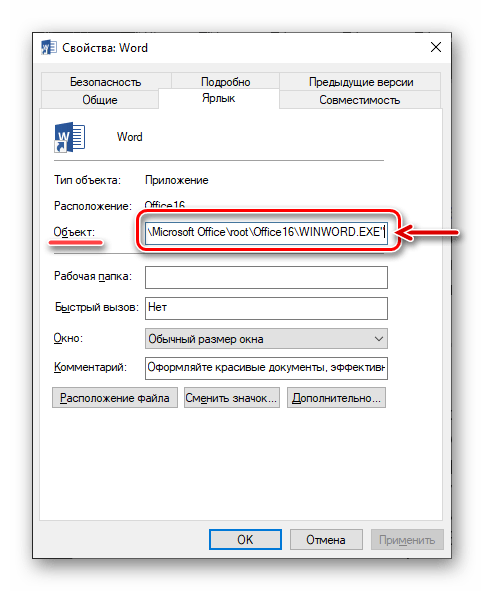
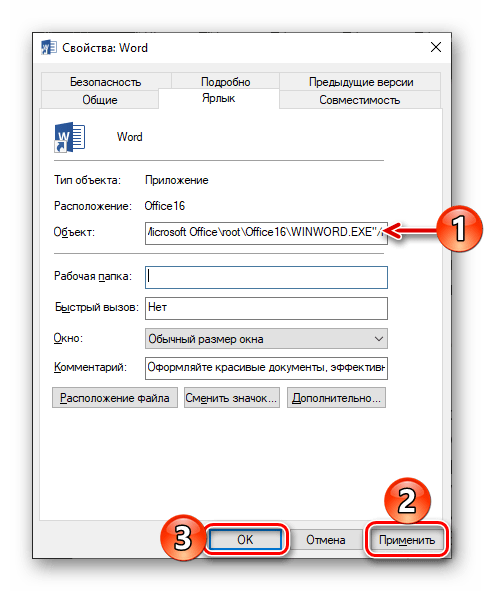
- В появившемся окне на вкладке «Ярлык» нажимаем кнопку «Дополнительно».
Переходим к дополнительным параметрам ярлыка
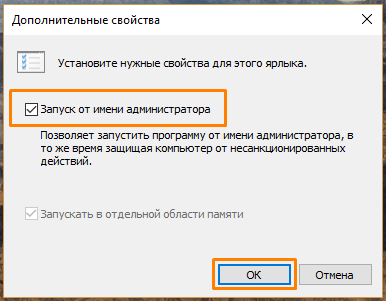
- В окне «Дополнительные свойства» ставим флажок «Запуск от имени администратора» и нажимаем кнопку «ОК» в этом и в предыдущем окне, а затем кнопку «Продолжить» в окне предупреждения для завершения операции.
- Теперь Word каждый раз будет запускаться с правами администратора.
Загрузка …
Восстанавливаем Word через «Параметры Windows»
Проблемы в работе текстового редактора Word могут быть вызваны повреждением, изменением либо удалением отдельных компонентов Microsoft Office. Это может касаться как версии 2007 года, так и 2013 или даже 365. Для восстановления офисного пакета проделаем следующие шаги:
- Кликаем на кнопку «Пуск» правой кнопкой мыши и в контекстном меню выбираем пункт «Приложения и возможности».
Открываем «Приложения и возможности» из контекстного меню кнопки «Пуск»
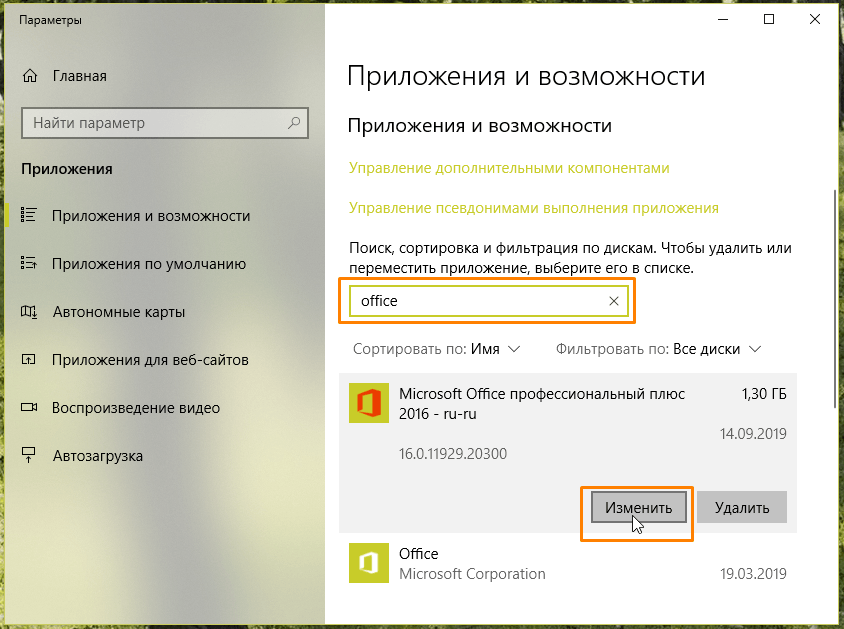
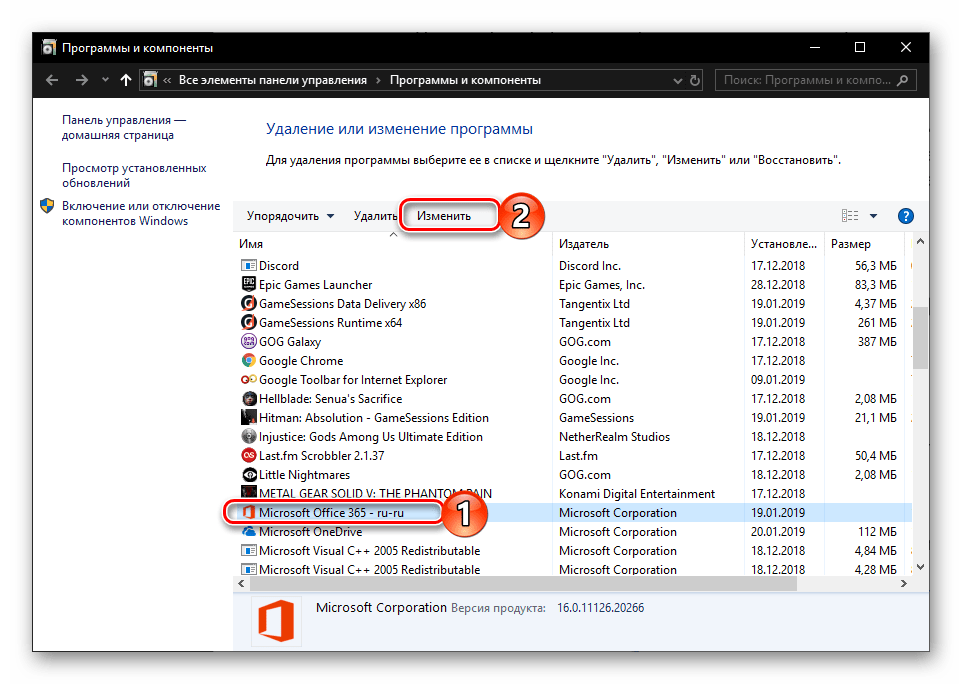
- В появившемся окне «Параметры» мы увидим перечень всех установленных на компьютере программ. Находим в списке Microsoft Office. Для этого можно воспользоваться поисковой строкой «Искать в этом списке»: вводим в нее слово «office» и, когда офисный пакет будет найден, выбираем его, а затем нажимаем на кнопку «Изменить».
Находим Microsoft Office и жмем на кнопку «Изменить»
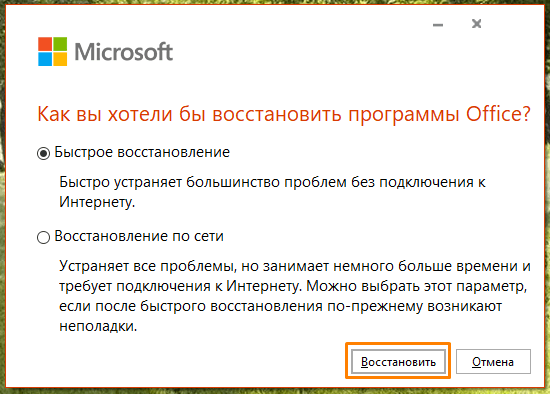
- Появится окно, в котором нужно указать способ восстановления и нажать кнопку «Восстановить». Вначале попробуйте воспользоваться быстрым восстановлением, а если оно не решит проблему, выберите восстановление по сети. Так или иначе, данная операция восстановит оригинальные файлы офисного пакета Microsoft и, скорее всего, решит проблему с запуском Word.
Запускаем восстановление Microsoft Office
Загрузка …
Исправляем работу Word с помощью утилиты от разработчика
На официальном сайте поддержки пользователей продуктов Microsoft при получении сообщения «Прекращена работа программы Microsoft Word» рекомендуется скачать специальную утилиту «Средство простого исправления».
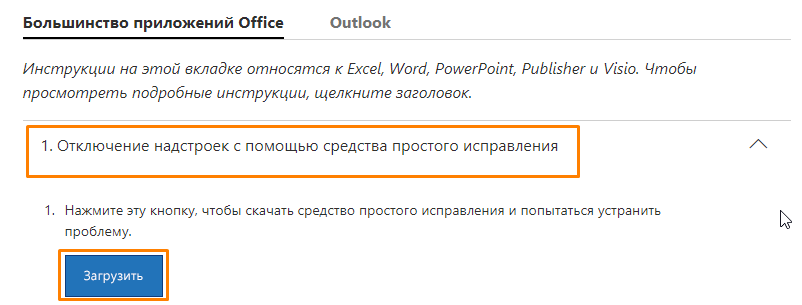
- Перейдите по ссылке https://support.office.com/ru-ru/article/Я-получаю-сообщение-об-ошибке-Прекращена-работа-при-запуске-приложений-office-на-моем-компьютере-52bd7985-4e99-4a35-84c8-2d9b8301a2fa, кликните на пункт «1. Отключение надстроек с помощью средства простого исправления» и нажмите кнопку «Загрузить».
Скачиваем средство простого исправления с сайта Microsoft
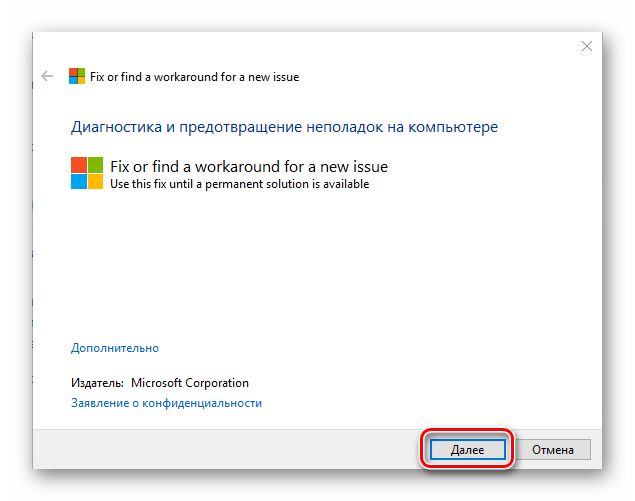
- После окончания загрузки запустите скачанный файл CSSEmerg6619.diagcab и нажмите кнопку «Далее».
Запускаем утилиту для исправления Microsoft Office
- Программа проведет диагностику и исправит найденные ошибки, после чего средство устранения неполадок можно закрыть.
Утилита обнаружила и исправила проблему
Загрузка …
Отключаем надстройки Word в безопасном режиме
При установке различных приложений в текстовый редактор Word могут быть добавлены надстройки, расширяющие возможности программы, однако нередко они являются причиной нестабильной работы и невозможности запуска Word в обычном режиме.
- Запустим Word в безопасном режиме. Для этого в контекстном меню кнопки «Пуск» выберем команду «Выполнить».
Открываем окно «Выполнить» из контекстного меню кнопки «Пуск»
- В появившемся окне вводим команду winword /safe и нажимаем кнопку «ОК».
Запускаем Word в безопасном режиме
- После запуска Word открываем меню «Файл» и выбираем команду «Параметры».
Открываем меню «Файл»
Кликаем команду «Параметры»
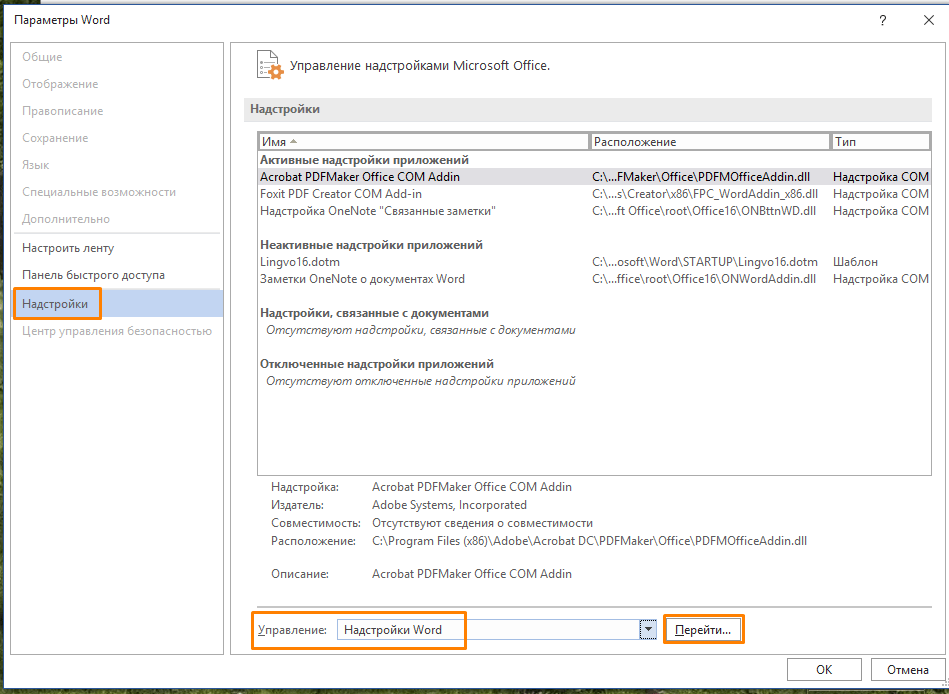
- В левой части окна «Параметры Word» находим раздел «Надстройки», затем в раскрывающемся списке «Управление» справа выбираем «Надстройки Word» и нажимаем кнопку «Перейти».
Переходим к надстройкам Word
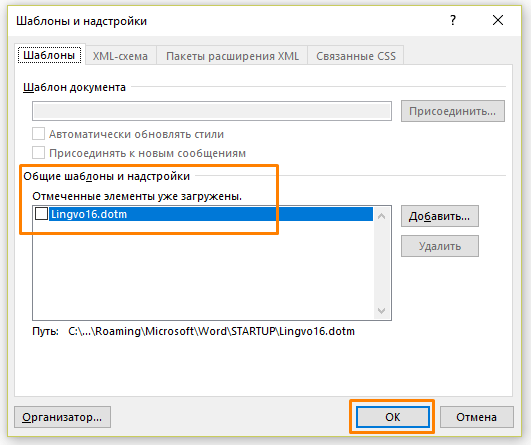
- В окне «Шаблоны и надстройки» снимаем галочки со всех элементов и нажимаем кнопку «ОК».
Отключаем надстройки Word
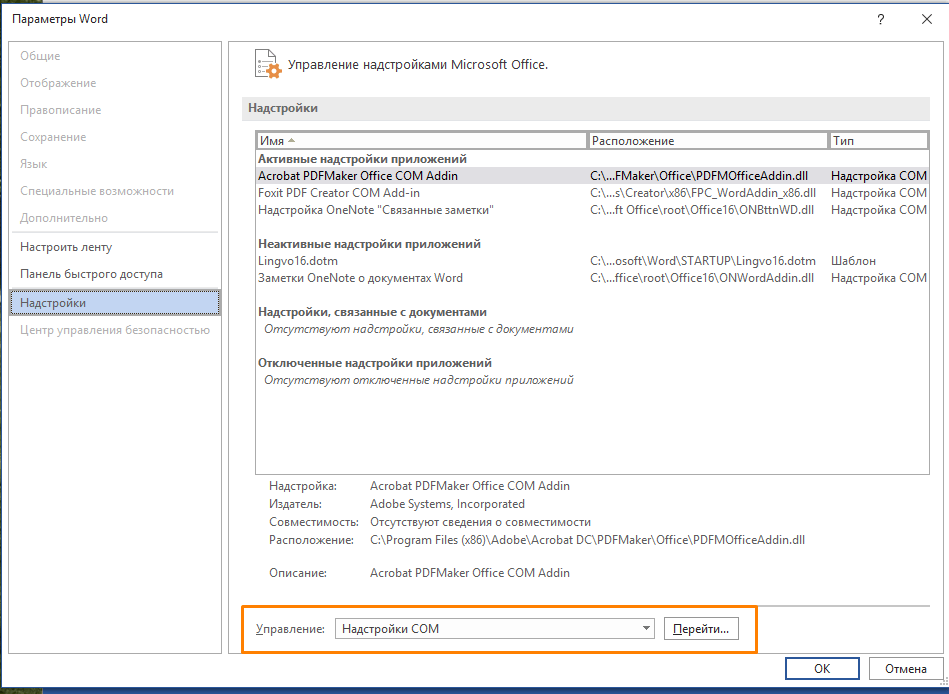
- Вернемся в окно «Параметры Word» и перейдем к управлению «Надстройками COM».
Переходим к надстройкам COM
- В открывшемся окне также можно отключить доступные надстройки. Чтобы выяснить, какая именно надстройка вызывает ошибку в работе Word, их следует отключать поочередно, после чего выходить из безопасного режима и запускать Word в обычном режиме, пока виновница сбоя не будет найдена.
Отключаем надстройки COM
Загрузка …
Кроме перечисленных выше причин неработоспособности Word, могут возникнуть проблемы с активацией Microsoft Office. После установки пакета офисных приложений пользователю доступен тридцатидневный пробный бесплатный период использования, по окончании которого офисные программы прекращают работать. Чтобы продолжить пользоваться ими, необходимо приобрести лицензию на официальном сайте Microsoft. Если вы оплатили лицензию, но столкнулись с проблемами в работе Word, обратитесь в службу поддержки продуктов Microsoft Office https://support.office.com/.
Загрузка …
Post Views: 20 824
After you finish this lesson, view all of our Pre-Algebra lessons and practice problems. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
Solving Word Problems
To solve a word problem using a system of equations, it is important to;
– Identify what we don’t know
– Declare variables
– Use sentences to create equations
An example on how to do this:
Mary and Jose each bought plants from the same store. Mary spent $188 on 7 cherry trees and 11 rose bushes. Jose spent $236 on 13 cherry trees and 11 rose bushes. Find the cost of one cherry tree and the cost of one rose bush.
Cost of a cherry tree:
Cost of a rose bush:
7 cherry trees and 11 rose bushes = $188
The y-values cancel each other out, so now you are left with only x-values and real numbers.
Then, you plug in your x-value into an original equation in order to find the y-value.
Cost of a cherry tree: $8
Cost of a rose bush: $12
Example 1
Three coffees and a cupcake cost a total of dollars. Two coffees and four cupcake cost a total of
dollars. What is the individual price for a single coffee and a single cupcake?
Let’s solve this by following steps.
1. What we don’t know:
Cost of a single coffee
Cost of single cupcake
2. Declare variables:
Cost of a single coffee=
Cost of single cupcake=
3. Use sentences to create equations.
Three coffees and a cupcake cost a total of dollars.
Two coffees and four cupcake cost a total of dollars.
Now, we have a system of equations:
Let’s solve for one of the variables in one of the equations and then use that to substitute into the other.
Now, solve for the value of using the first equation.
Let’s solve the value of by substituting the value of
to the bottom equation.
Distribute to each terms inside the parenthesis
Combine like terms
Now, let’s isolate the by subtracting
on both sides.
Then divide both sides by ,
And we’ll have
Then, let’s plug the value of into one equation to get the value of
.
Cost of a single coffee=
Cost of single cupcake=
Example 2
The senior class at High School A rented and filled vans and
buses with
students. High School B rented and filled
vans and
bus with
students. Every van had the same number of students in it as did the buses. Find the number of students in each van and in each bus.
Let’s solve this by following steps.
1. What we don’t know:
Students in each van
Students in each bus
2. Declare variables:
Students in each van=
Students in each bus=
3. Use sentences to create equations.
High School A rented and filled 8 vans and 8 buses with 240 students.
High School B rented and filled 4 vans and 1 bus with 54 students.
Now, we have a system of equations:
Let’s solve for one of the variables in one of the equations and then use that to substitute into the other.
Now, solve for the value of using the second equation.
Let’s solve the value of by substituting the value of
to the bottom equation.
Distribute to each terms inside the parenthesis
Combine like terms
Now, let’s isolate the by subtracting
on both sides.
Then divide both sides by ,
And we’ll have
Then, let’s plug the value of into one equation to get the value of
.
Students in each van=
Students in each bus=
Video-Lesson Transcript
To solve a word problem using system of equations, it is important to:
1. Identify what we don’t know
2. Declare variables.
3. Use sentences to create equations.
Let’s have an example:
Mary and Jose each bought plants from the same store. Mary spent on
cherry trees and
rose bushes. Jose spent
on
cherry trees and
rose bushes. Find the cost of one cherry tree and the cost of one rose bush.
Let’s solve this by following steps above.
1. What we don’t know:
cost of a cherry tree
cost of a rose bush
2. Declare variables:
cost of a cherry tree :
cost of a rose bush :
3. Use sentences to create equations.
For Mary:
cherry trees and
rose bushes
For Jose:
cherry trees and
rose bushes
Now, we have a system of equations
We can solve this by process of substitution, elimination or fraction.
Since the value of is the same for both equations, let’s do the process of elimination.
First, let’s multiply the first equation by
Here we’ll have a negated equation
Let’s do the process of elimination now
We’ll have
Then, let’s isolate by dividing both sides by
Now, we have
Remember, our declared variable?
cost of a cherry tree :
Since
Now we can say that
cost of a cherry tree :
Now, let’s solve for the value of by getting one equation and plugging the value of
.
Let’s use the first equation to plug in
Let’s isolate by subtracting
on both sides of the equation
Then divide by
And we get
Now, we know that cost of a rose bush is .
The word problem for one-relation monoids: a survey
-
Mathematics
Semigroup Forum
- 2021
This survey is intended to provide an overview of one of the oldest and most celebrated open problems in combinatorial algebra: the word problem for one-relation monoids. We provide a history of the…
Adventures in applying iteration lemmas
- M. Pfeiffer
-
Mathematics
- 2013
The word problem of a finitely generated group is commonly defined to be a formal language over a finite generating set. The class of finite groups has been characterised as the class of finitely…
The word problem for semigroups with two generators
- M. Hall
-
Mathematics
Journal of Symbolic Logic
- 1949
Emil Post has shown that the word problem for Thue systems is unsolvable. A Thue system is a system of strings of letters x1, x2, …, xr, where a string or word is either void or a succession of…
THE WORD PROBLEM.
- W. W. Boone
-
Computer Science
Proceedings of the National Academy of Sciences of the United States of America
- 1958
I have been involved with typesetting relatively complex mathematical and engineering textbooks using l&X since late 1982, and the page make-up abilities are woefully lacking for this application.
Recursive Unsolvability of a problem of Thue
- Emil L. Post
-
Mathematics
Journal of Symbolic Logic
- 1947
Thue’s problem is the problem of determining for arbitrarily given strings A, B on al, whether, or no, A and B are equivalent, and this problem is more readily placed if it is restated in terms of a special form of the canonical systems of [3].
On Ground AC-Completion
- C. Marché
-
Mathematics
RTA
- 1991
We prove that a canonical set of rules for an equational theory defined by a finite set of ground axioms plus the associativity and commutativity of any number of operators must be finite.
Word – самый популярный текстовый редактор, который по умолчанию устанавливается на все компьютеры под управлением Windows 10 в рамках пакета Microsoft Office.
Им пользуются десятки миллионов людей, а потому проблемы, когда не открывается Ворд в операционной системе Виндовс 10, возникают нередко. К счастью, любые неполадки можно устранить, но только при полном соблюдении требований инструкции.
Чтобы сэкономить время, сначала рекомендуется установить причину возникновения проблемы.
Для этого стоит обратить внимание на следующие факторы, которые чаще всего блокируют запуск Microsoft Word:
- отсутствие лицензии;
- недостаточное количество пользовательских прав;
- использование некорректной сборки приложения;
- повреждение файлов Word;
- воздействие вирусов.
Понять, что именно послужило причиной, бывает очень сложно. Но даже в таком случае не стоит отчаиваться, поскольку проблему, рано или поздно, все равно удастся решить. Главное – не закрывать глаза даже на мельчайшие ошибки в работе текстового редактора. Это может быть косвенным свидетельством появления неполадок.
Как восстановить работоспособность Word в Windows 10
Определив причину возникновения проблемы, вы сэкономите время на ее устранении. Однако не каждый пользователь способен с точностью выявить вредителя. В таком случае рекомендуется действовать по инструкции, рассматривая наиболее вероятные факторы, которые привели к сбою в работе приложения.
Проверка лицензии
Некоторые люди ошибочно полагают, что Word – это бесплатный софт. Но, на самом деле, текстовый редактор распространяется по модели подписки. Получить доступ к одному лишь Ворду не получится. Придется оформлять подписку на все сервисы Microsoft Office, в число которых входят PowerPoint, Excel и другие программы.
При первом запуске Word владельцу компьютера дается 30 дней на бесплатное использование сервиса. Если по истечении этого срока он не оформит подписку, то доступ к редактору будет заблокирован, и совершенно не удивительно, что Ворд не работает. Вне зависимости от того, являетесь вы владельцем лицензионной версии ПО, или только что исчерпали 30-дневный лимит, стоит проверить состояние подписки:
- Щелкните ПКМ по иконке «Пуск».
- Через контекстное меню откройте Командную строку с правами Администратора.
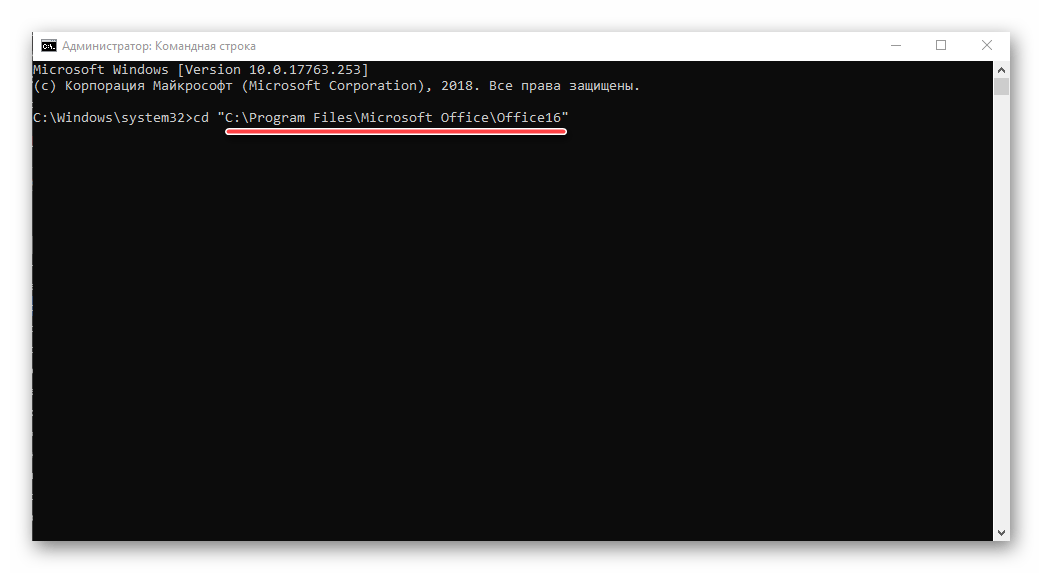
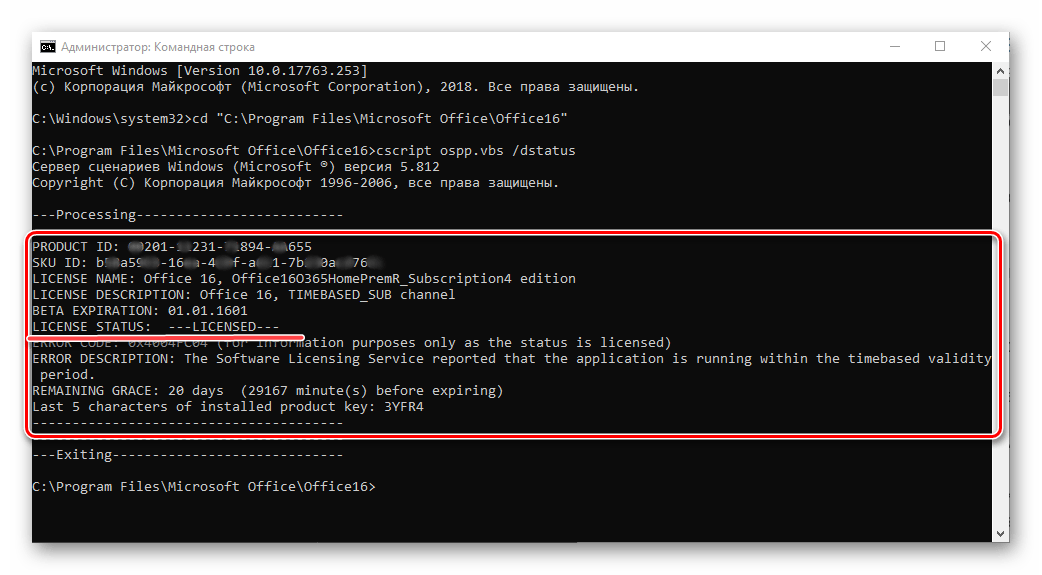
- Введите запрос «cd “C:Program FilesMicrosoft OfficeOffice16”» для 64-битной Windows или «cd “C:Program Files (x86)Microsoft OfficeOffice16”» для 32-битной. Обратите внимание, что название пакета может отличаться, так как Office 2016 – далеко не самая актуальная версия пакета.
- Нажмите на клавишу «Enter».
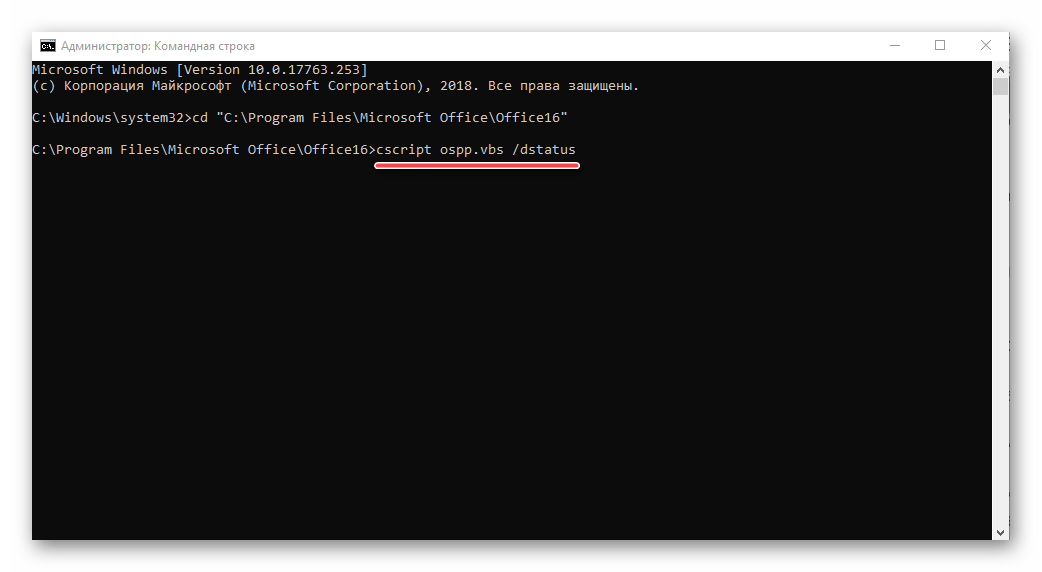
- Предыдущей командой мы указали терминалу, какое приложение нуждается в проверке. Далее нужно вбить запрос «cscript ospp.vbs /dstatus» и подтвердить его нажатием на «Enter».
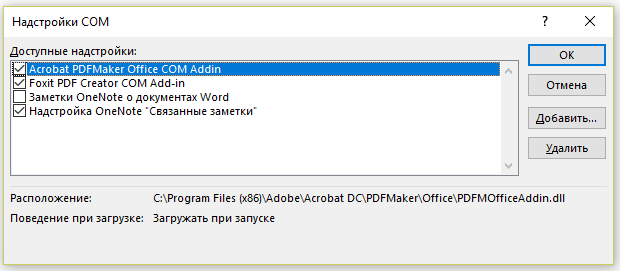
- Изучите информацию, представленную в пункте «LICENSE STATUS». Если продукт активирован, то будет установлено значение «LICENSED».
На заметку. Людям, которые не хотят пользоваться платной версией офиса, рекомендуется обратить внимание на Microsoft Office Online. Это онлайн-сервис с аналогичным функционалом, который работает бесплатно, но только через браузер в интернете.
Отсутствие статуса «LICENSED» может свидетельствовать о том, что ранее вам не удалось корректно активировать продукт. Придется повторить операцию на сайте Microsoft или обратиться в службу поддержки для выяснения обстоятельств.
Запуск от имени Администратора
Если предыдущий метод подтвердил отсутствие проблем с лицензией, но редактор все равно не запускается, то причина возникновения проблемы кроется в другом факторе. Возможно, для приложения случайно или намеренно было выставлено ограничение по запуску, когда пользоваться приложением может только человек с правами Администратора. Исправляется ошибка следующим образом:
- Найдите исполняемый файл приложения (например, в меню «Пуск»).
- Щелкните по нему ПКМ.
- Выберите опцию «Запуск с правами Администратора».
Успешный запуск подтвердит, что проблема заключалась в недостаточном количестве прав. Для корректного использования программы без принудительной активации профиля Администратора действуйте по алгоритму:
- Щелкните ПКМ по иконке Word в меню «Пуск».
- Выберите «Дополнительно», а затем – «Перейти к расположению файла».
- В корневой папке найдите исполняемый файл редактора и откройте его свойства из контекстного меню, которое вызывается щелчком ПКМ.
- Во вкладке «Ярлык» обратитесь к пункту «Объект». Здесь нужно дописать значение «/r».
- Нажмите на кнопку «Применить» для сохранения настроек.
После выполнения изменений Ворд будет автоматически запускаться с правами Администратора. Следовательно, проблема больше не побеспокоит вас. Если ничего не изменилось – рассмотрите еще несколько вариантов устранения неполадок.
Восстановление через «Параметры»
Далее стоит рассмотреть вариант, при котором программа отказывается работать из-за повреждения собственных файлов. Это могло произойти как по неосторожности пользователя, так и вследствие вмешательства вредоносного ПО. Решение заключается в восстановлении параметров Word и всего офисного пакета:
- Щелкните ПКМ по иконке «Пуск».
- Выберите пункт «Приложения и возможности», чтобы сразу запустить необходимый раздел «Параметров».
- Найдите в списке офисный пакет и кликните по нему ЛКМ.
- Нажмите на кнопку «Изменить».
- Подтвердите восстановление софта.
По завершении не забудьте перезагрузить компьютер. После повторного запуска ПК попробуйте снова открыть текстовый редактор.
Исправляем работу Word с помощью утилиты от разработчика
В ситуации, когда не запускается Ворд или другая офисная программа Microsoft, разработчики рекомендуют обращаться к помощи утилиты «Средство простого исправления». Ее можно скачать через официальный сайт американской компании.
Утилита поможет отключить надстройки, которые нередко вызывают сбои в работе программного обеспечения. С высокой долей вероятности вам удастся решить проблему. В крайнем случае, обратитесь к последнему варианту.
Отключение надстроек в безопасном режиме
Так или иначе, проблема связана с надстройками. Если они не отключаются средствами ПО разработчика, то выполнить операцию придется вручную:
- Перезагрузите компьютер в безопасном режиме.
- Запустите Word (в безопасном режиме он должен работать без нареканий).
- Щелкните ЛКМ по вкладке «Файл».
- Перейдите в «Параметры».
- Опуститесь в раздел «Надстройки» и нажмите на кнопку «Перейти».
- Снимите галочки со всех надстроек, которые отображаются в меню параметров. Сохраните изменения.
То, что Word функционирует в безопасном режиме – не показатель. Вам нужно покинуть профиль, переведя устройство в обычное состояние. Только так можно быть уверенным в устранении неполадок. Если положительных изменений не произойдет, то попробуйте еще раз повторить все рекомендации из материала. Заключительный вариант решения проблемы – обращение в службу поддержки Microsoft.
Содержание
- Восстановление работоспособности Ворд в Виндовс 10
- Способ 1: Проверка лицензии
- Способ 2: Запуск от имени администратора
- Способ 3: Исправление ошибок в работе программы
- Дополнительно: Распространенные ошибки и их решение
- Заключение
- Вопросы и ответы
Word, несмотря на множество аналогов, в том числе и бесплатных, все еще является неоспоримым лидером среди текстовых редакторов. Эта программа содержит в себе множество полезных инструментов и функций для создания и редактирования документов, но, к сожалению, не всегда стабильно работает, особенно, если используется она в среде Windows 10. В нашей сегодняшней статье расскажем, как устранить возможные ошибки и сбои, нарушающие работоспособность одного из главных продуктов Microsoft.
Читайте также: Установка Microsoft Office
Причин, из-за которых Microsoft Word может не работать в Windows 10, не очень много, и каждая из них имеет свой вариант решения. Так как на нашем сайте есть довольно много статей, рассказывающих в целом об использовании этого текстового редактора и конкретно об устранении проблем в его работе, этот материал мы разделим на две части – общую и дополнительную. В первой рассмотрим ситуации, в которых программа именно не работает, не запускается, а во второй кратко пройдемся по наиболее распространенным ошибкам и сбоям.
Читайте также: Инструкции по работе с Microsoft Word на Lumpics.ru
Способ 1: Проверка лицензии
Ни для кого не секрет, что приложения из пакета Майкрософт Офис являются платными и распространяются по подписке. Но, зная это, многие пользователи продолжают пользоваться пиратскими версиями программы, степень стабильности которых напрямую зависит от прямоты рук автора дистрибутива. Мы не будем рассматривать возможные причины того, почему не работает взломанный Word, но если вы, будучи добросовестным обладателем лицензии, столкнулись с проблемами, используя приложения из оплаченного пакета, первым делом следует проверить их активацию.
Примечание: Microsoft предоставляют возможность бесплатного использования Office в течение месяца, и если этот срок истек, офисные программы не будут работать.
Лицензия Офис может распространяться в разном виде, но проверить ее состояние можно через «Командную строку». Для этого:
Читайте также: Как запустить «Командную строку» от имени администратора в Windows 10
- Запустите «Командную строку» от имени администратора. Сделать это можно путем вызова меню дополнительных действия (клавиши «WIN+X») и выбора соответствующего пункта. Другие возможные варианты описаны в представленной по ссылке выше статье.
- Введите в нее команду, обозначающую путь установки Microsoft Office на системном диске, точнее, переход по нему.
Для приложений из пакета Офис 365 и 2016 в 64-битных версиях этот адрес выглядит следующим образом:
cd “C:Program FilesMicrosoft OfficeOffice16”
Путь к папке 32-битного пакета:cd “C:Program Files (x86)Microsoft OfficeOffice16”Примечание: Для Офис 2010 конечная папка будет иметь название «Office14», а для 2012 – «Office15».
- Нажмите клавишу «ENTER» для подтверждения ввода, а затем введите представленную ниже команду:
cscript ospp.vbs /dstatus
Будет начата проверка лицензии, которая займет буквально несколько секунд. После вывода результатов обратите внимание на строку «LICENSE STATUS» — если напротив нее указано «LICENSED», значит, лицензия активна и проблема не в ней, следовательно, можете переходить к следующему способу.
Но если там указано иное значение, активация по какой-то причине слетала, а значит, ее нужно произвести повторно. О том, как это делается, мы ранее рассказывали в отдельной статье:
Подробнее: Активация, скачивание и установка Microsoft Office
В случае возникновения проблем с повторным получением лицензии вы всегда можете обратиться в службу поддержки продуктов Майкрософт Офис, ссылка на страницу которой представлена ниже.
Страница поддержки пользователей Microsoft Office
Способ 2: Запуск от имени администратора
Возможно и такое, что работать, а точнее запускаться Ворд отказывается по более простой и банальной причине – у вас нет прав администратора. Да, это не обязательное требование для использования текстового редактора, но в среде Windows 10 это нередко помогает устранить аналогичные проблемы с другими программами. Вот что нужно сделать для запуска программы с административными полномочиями:
- Отыщите ярлык Word в меню «Пуск», кликните по нему правой кнопкой мышки (ПКМ), выберите пункт «Дополнительно», а затем – «Запуск от имени администратора».
- Если программа запустится, значит, проблема заключалась именно в ограниченности ваших прав в системе. Но, так как у вас наверняка нет желания каждый раз открывать Ворд таким способом, необходимо изменить свойства его ярлыка, чтобы запуск всегда происходил с административными полномочиями.
- Для этого снова найдите ярлык программы в «Пуске», нажмите по нему ПКМ, затем «Дополнительно», но в этот раз выберите в контекстном меню пункт «Перейти к расположению файла».
- Оказавшись в папке с ярлыками программ из стартового меню, найдите в их перечне Word и снова кликните по нему ПКМ. В контекстном меню выберите пункт «Свойства».
- Кликните по адресу, указанному в поле «Объект», перейдите в его конец, и допишите туда следующее значение:
/r
Нажмите расположенные внизу диалогового окна кнопки «Применить» и «ОК».
С этого момента Ворд всегда будет запускаться с правами администратора, а значит, вы больше не столкнетесь с проблемами в его работе.
Читайте также: Обновление Microsoft Office до последней версии
Способ 3: Исправление ошибок в работе программы
Если же после выполнения предложенных выше рекомендаций Microsoft Word так и не запустился, следует попробовать выполнить восстановление всего пакета Office. О том, как это делается, мы ранее рассказывали в одной из наших статей, посвященной другой проблеме – внезапному прекращению работы программы. Алгоритм действий в данном случае будет точно таким же, для ознакомления с ним просто перейдите по представленной ниже ссылке.
Подробнее: Восстановление работоспособности приложений Microsoft Office
Дополнительно: Распространенные ошибки и их решение
Выше мы рассказали о том, что делать есть Ворд в принципе отказывается работать на компьютере или ноутбуке с Виндовс 10, то есть попросту не запускается. Остальные же, более конкретные ошибки, которые могут возникнуть в процессе использования этого текстового редактора, как и действенные способы их устранения, нами были рассмотрены ранее. Если вы столкнулись с одной из представленных в списке ниже проблем, просто перейдите по ссылке на подробный материал и воспользуйтесь предложенными там рекомендациями.
Подробнее:
Исправление ошибки «Прекращена работа программы…»
Решение проблем с открытием текстовых файлов
Что делать, если документ не редактируется
Отключение режима ограниченной функциональности
Устранение ошибки при направлении команды
Недостаточно памяти, чтобы закончить операцию
Заключение
Теперь вы знаете, как заставить работать Microsoft Word, даже если он отказывается запускаться, а также о том, как исправить ошибки в его работе и устранить возможные проблемы.

 или в поле Начать поиск в меню Пуск (в более ранних версиях Windows) и нажмите ввод.
или в поле Начать поиск в меню Пуск (в более ранних версиях Windows) и нажмите ввод.