Here are some carefully chosen combination word problems that will show you how to solve word problems involving combinations.
Use the combination formula shown below when the order does not matter
The combination word problems will show you how to do the followings:
- Use the combination formula
- Use the multiplication principle and the combination formula
- Use the addition principle and the combination formula
- Use the multiplication principle, addition principle, and combination formula
Word problem #1
There are 18 students in a classroom. How many different eleven-person students can be chosen to play in a soccer team?
Solution
The order in which students are listed once the students are chosen does not distinguish one student from another. You need the number of combinations of 18 potential students chosen 11 at a time.
Evaluate nCr with n = 18 and r = 11
18C11 =
18!
/
11!(18 — 11)!
18C11 =
18×17×16×15×14×13×12×11!
/
11!(7×6×5×4×3×2)
18C11 =
18×17×16×15×14×13×12
/
(7×6×5×4×3×2)
18C11 = 31824
There are 31824 different eleven-person students that can be chosen from a group of 18 students.
Word problem #2
For your biology report, you can choose to write about three of a list of four different animals. Find the number of combinations possible for your report.
Solution
The order in which you write about these 3 animals does not matter as long as you write about 3 animals.
Evaluate nCr with n = 4 and r = 3
There are 4 different ways you can choose 3 animals from a list of 4.
Word problem #3
A math teacher would like to test the usefulness of a new math game on 4 of the 10 students in the classroom. How many different ways can the teacher pick students?
Solution
The order in which the teacher picks students does not matter.
Evaluate nCr with n = 10 and r = 4
10C4 =
10×9×8×7×6!
/
4×3×2(6)!
There are 210 ways the teacher can pick students
More challenging combination word problems
These combination word problems will also show you how to use the multiplication principle and the addition principle.
Word problem #4
A company has 20 male employees and 30 female employees. A grievance committee is to be established. If the committee will have 3 male employees and 2 female employees, how many ways can the committee be chosen?
Solution
This problem has the following two tasks:
Task 1: choose 3 males from 20 male employees
Task 2: choose 2 females from 30 female employees
We need to use the fundamental counting principle, also called the multiplication principle, since we have more than 1 task.
Fundamental counting principle
If you have n choices for a first task and m choices for a second task, you have n × m choices for both tasks.
Therefore, evaluate 20C3 and 30C2 and then multiply 20C3 by 30C2
20C3 =
20×19×18×17!
/
3×2(17)!
20C3 =
30×29×28!
/
2×1(28)!
20C3 × 30C2 = 1140 × 435 = 495900
The number of ways the committee can be chosen is 495900
Word problem #5
Eight candidates are competing to get a job at a prestigious company. The company has the freedom to choose as many as two candidates. In how many ways can the company choose two or fewer candidates.
Solution
The company can choose 2 people, 1 person, or none.
Notice that this time we need to use the addition principle as opposed to using the multiplication principle.
What is the difference? The key difference here is that the company will choose either 2, 1, or none. The company will not choose 2 people and 1 person at the same time. This does not make sense!
Addition principle
Let A and B be two events that cannot happen together. If n is the number of choices for A and m is the number of choices for B, then n + m is the number of choices for A and B.
Therefore you need to evaluate 8C2, 8C1, and 8C0 and then add 8C2, 8C1, and 8C0 together.
Useful shortcuts to find combinations
nC1 = n and nC0 = 1
Therefore, 10C1 = 10 and 10C0 = 1
8C2 + 8C1 + 8C0 = 28 + 10 + 1 = 39
The company has 39 ways to choose two or fewer candidates.
Word problem #6
A company has 20 male employees and 30 female employees. A grievance committee is to be established. If the committee will have as many as 3 male employees and as many as 2 female employees, how many ways can the committee be chosen?
Solution
The expression as many as makes the problem quite complex now since we now have all the following cases to consider.
Choose 3 males, 2 males, 1 male, or 0 male
Choose 2 females, 1 female, or 0 female.
Here is a complete list of all the different cases.
- 3 males and 2 females
- 3 males and 1 female
- 3 males and 0 female
- 2 males and 2 females
- 2 males and 1 female
- 2 males and 0 female
- 1 male and 2 females
- 1 male and 1 female
- 1 male and 0 female
- 0 male and 2 females
- 0 male and 1 female
- 0 male and 0 female
We only need to find 20C2
20C2 =
20×19×18!
/
2(18)!
3 males and 2 females: 20C3 × 30C2 = 1140 × 435 = 495900 (done in problem #4)
3 males and 1 female: 20C3 × 30C1 = 1140 × 30 = 34200
3 males and 0 female: 20C3 × 30C0 = 1140 × 1 = 1140
2 males and 2 females: 20C2 × 30C2 = 190 × 435 = 82650
2 males and 1 female: 20C2 × 30C1 = 190 × 30 = 5700
2 males and 0 female: 20C2 × 30C0 = 190 × 1 = 190
1 male and 2 females: 20C1 × 30C2 = 20 × 435 = 8700
1 male and 1 female: 20C1 × 30C1 = 20 × 30 = 600
1 male and 0 female: 20C1 × 30C0 = 20 × 1 = 20
0 male and 2 females: 20C0 × 30C2 = 1 × 435 = 435
0 male and 1 female: 20C0 × 30C1 = 1 × 30 = 30
0 male and 0 female: 20C0 × 30C0 = 1 × 1 = 1
Add everything:
495900 + 34200 + 1140 + 82650 + 5700 + 190 + 8700 + 600 + 20 + 435 + 30 + 1 = 629566.
The number of ways to choose the committee is 629566
Recent Articles
-
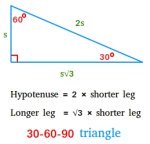
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
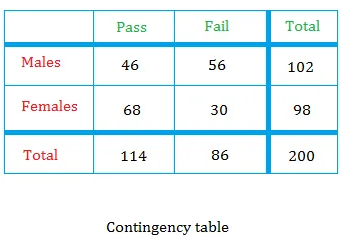
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
From Ramanujan to calculus co-creator Gottfried Leibniz, many of the world’s best and brightest mathematical minds have belonged to autodidacts. And, thanks to the Internet, it’s easier than ever to follow in their footsteps (or just finish your homework or study for that next big test). With this installment from Internet pedagogical superstar Salman Khan’s series of free math tutorials, you’ll learn how to unpack and solve word problems invplving permutations and combinations in basic statistics.
Want to master Microsoft Excel and take your work-from-home job prospects to the next level? Jump-start your career with our Premium A-to-Z Microsoft Excel Training Bundle from the new Gadget Hacks Shop and get lifetime access to more than 40 hours of Basic to Advanced instruction on functions, formula, tools, and more.
Buy Now (97% off) >
Other worthwhile deals to check out:
- 97% off The Ultimate 2021 White Hat Hacker Certification Bundle
- 98% off The 2021 Accounting Mastery Bootcamp Bundle
- 99% off The 2021 All-in-One Data Scientist Mega Bundle
- 59% off XSplit VCam: Lifetime Subscription (Windows)
- 98% off The 2021 Premium Learn To Code Certification Bundle
- 62% off MindMaster Mind Mapping Software: Perpetual License
- 41% off NetSpot Home Wi-Fi Analyzer: Lifetime Upgrades
In today’s post, we are going to present the way that we work on combined operations through word problems in Smartick.
In the field of mathematics in school, combined operations are those problems where we need to use more than one operation. If you don’t remember exactly what they were, click here to refresh your memory! On the other hand, a word problem is a problem that describes a real-life scenario which, as explained in this post, the method needed to solve it is unknown.
Let’s look at an example!
Example of Combined Operations with Word Problems: Counting Signs
In this word problem, there are three pieces of numerical data (2, 6, and 7). It is up to you to determine what to do with them. In particular, you have to decide what data is needed, what operation (or operations) to perform with it, and in what order. If you look at the units that those numbers have, we can see that the data is actually ”2 hours’‘, ”6 hours” and ”7 signs per hour.” On the other hand, the question is asking for the number of signs counted. Thus, one way to solve it is to first get the total number of hours Noah has driven and then apply the ratio of signs counted per hour. Let’s put it in mathematical language!
In order to calculate the total number of hours that Noah drove, you need to group the hours he drove before the stop in Edinburgh with those that he drove after. Then you will have the total number of hours…
2 + 6
Our result looks good so far because we are adding hours with hours, which gives us a result in hours. Now we have to multiply the result by the number of signs per hour. However, if we wrote it without making any changes, we would be wrong. Let’s see why. If we wrote…
2 + 6 × 7
we would have to first multiply 6 by 7 according to the order of operations. To solve this, we would use parentheses to represent what we want to be done first. In other words,
( 2 + 6 ) × 7
At this point, it is clear that by formalizing these problems we are also working on the combined operations. Finally, we just need to solve it.
( 2 + 6 ) × 7
8 × 7
56
So, the solution to the problem is ”His daughter counted 56 signs.”
I hope that this post has helped you realize that combined operations appear in various situations that happen every day and are critical to addressing everyday issues. If you would like to practice some more and continue learning mathematics, try the Smartick method for free. What are you waiting for?!
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
The number of ways of choosing 2 blue out of 4 is $binom{4}{2}.$ After that you have 4 chips remaining which can be chosen from either 9 red or 6 yellow or both. So you are choosing 4 chips from $9 + 6 =15$ chips.
Putting all together, you get $$binom{4}{2}binom{15}{4}.$$
Related videos on Youtube
17 : 41
Permutations and Combinations Tutorial
The Organic Chemistry Tutor
21 : 17
Permutations, Combinations & Probability (14 Word Problems)
08 : 40
Permutations and Combinations — word problems 128-1.11
11 : 25
Combinations and Permutations Word Problems
16 : 56
SOLVING WORD PROBLEMS INVOLVING PERMUTATIONS AND COMBINATIONS || GRADE 10 MATHEMATICS Q3
Comments
-
I’m continuing to work through permutations and combinations and my book has the following question:
A box contains 9 red, 4 blue, and 6 yellow chips. In how many ways can
6 chips be chosen if:
a) all 6 chips are red
b) all 6 chips are yellow
c) 2 chips are blueI had no problem answering a) and b); however c) is stumping me. The answer, according to the text, is 8,190 however I can’t figure out how they’re arriving at that number.
I thought it would be:
$$(19cdot 18cdot 17cdot 16/4!)/2! = frac{19cdot 18cdot 17cdot 16}{4!cdot 2!}$$
but that returns $1938$, not $8,190$.At this point in the text we’ve only covered the Permutation and Combination formulas: nPr and nCr.
Help?
-
Thanks so much for the textual explanation (not to mention the calculation)! Really helpful.
-
No problem. glad to help..:)
-
Sorry, one more question on this. After choosing 2 blue out of 4, why would the the 4 chips remaining not be chosen from 9 red, 6 yellow and/OR 2 blue? In other words after you choose the 2 blue chips aren’t there still 2 other blue chips remaining that could be chosen to fill the remaining 4 places?
-
Never mind. Got it. The problem states only 2 chips are blue, so we don’t include them. If the problem said «at least 2 chips are blue» then we’d include the remaining 2 blue chips in the second combination: 17C4, as opposed to 15C4.
-
Im glad you got it. If it however said at least 2 blue chips, then we could have 2 blue, 3 blue or 4 blue chips.So that will be (4C2*15C4)+(4C3*15C3)+(4C4*15C2)
-
Ahh, of course…Thank you so much! Just so I’m clear: if the problem said «4 chips are yellow», we’d take: 6C4 * 13C2. Correct?
-
Yes, Correct!!!
Recents
Related
Exercise 10
How many groups can be made from the word «house» if each group consists of 3 alphabets?
Exercise 11
Sarah has 8 colored pencils that are all unique. She wants to pick three colored pencils from her collection and give them to her younger sister. How many different combinations of colored pencils can Sarah make from 8 pencils?
Exercise 12
Alice has 6 chocolates. All of the chocolates are of different flavors. She wants to give two of her chocolates to her friend. How many different combinations of chocolates can Alice make from six chocolates?
Solution of exercise 1
How many different combinations of management can there be to fill the positions of president, vice-president and treasurer of a football club knowing that there are 12 eligible candidates?
The order of the elements does matter.
The elements cannot be repeated.
Solution of exercise 2
How many different ways can the letters in the word «micro» be arranged if it always has to start with a vowel?
The words will begin with i or o followed by the remaining 4 letters taken from 4 by 4.
The order of the elements does matter.
The elements cannot be repeated.
Solution of exercise 3
How many combinations can the seven colors of the rainbow be arranged into groups of three colors each?
The order of the elements does not matter.
The elements cannot be repeated.
Solution of exercise 4
How many different five-digit numbers can be formed with only odd numbered digits? How many of these numbers are greater than 70,000?
The order of the elements does matter.
The elements cannot be repeated.
n = 5 k = 5
The odd numbers greater than 70,000 have to begin with 7 or 9. Therefore:
Solution of exercise 5
How many games will take place in a league consisting of four teams? (Each team plays each other twice, once at each teams respective «home» location)
The order of the elements does matter.
The elements cannot be repeated.
Solution of exercise 6
10 people exchange greetings at a business meeting. How many greetings are exchanged if everyone greets each other once?
The order of the elements does not matter.
The elements cannot be repeated.
Solution of exercise 7
How many five-digit numbers can be formed with the digits 1, 2 and 3? How many of those numbers are even?
The order of the elements does matter.
The elements are repeated.
If the number is even it can only end in 2.
Solution of exercise 8
How many lottery tickets must be purchased to complete all possible combinations of six numbers, each with a possibility of being from 1 to 49?
The order of the elements does not matter.
The elements cannot be repeated.
Solution of exercise 9
How many ways can 11 players be positioned on a soccer team considering that the goalie cannot hold another position other than in goal?
Therefore, there are 10 players who can occupy 10 different positions.
The order of the elements does matter.
The elements cannot be repeated.
Solution of exercise 10
The word house has 5 alphabets. If each new word should have 3 alphabets, then we should use the following formula:
, where
Substitute the values in this example in the above formula:
Solution of exercise 11
Number of pencils Sarah have = 8
Number of pencils she wants to give to her younger sister = 3
We will use the binomial coefficients formula to determine the number of combinations:
, where
After substitution we will get the number of combinations:
Hence, Sarah can make 56 combinations of 8 colored pencils given the fact that she can choose 3 at a time.
Solution of exercise 12
Number of chocolates Alice have = 6
Number of chocolates she wants to give to her friend= 2
We will use the binomial coefficients formula to determine the number of combinations:
, where
After substitution we will get the number of combinations:
Hence, Alice can make 15 combinations of 6 chocolates given the fact that she can choose 2.