The so-called Platonic Solids are convex regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.” There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles:
 |
tetrahedron Four triangular faces, four vertices, and six edges. |
 |
cube Six square faces, eight vertices, and twelve edges. |
 |
octahedron Eight triangular faces, six vertices, and twelve edges. |
 |
dodecahedron Twelve pentagonal faces, twenty vertices, and thirty edges. |
 |
icosahedron Twenty triangular faces, twelve vertices, and thirty edges. |
It is natural to wonder why there should be exactly five Platonic solids, and whether there might conceivably be one that simply hasn’t been discovered yet. However, it is not difficult to show that there must be five—and that there cannot be more than five.
First, consider that at each vertex (point) at least three faces must come together, for if only two came together they would collapse against one another and we would not get a solid. Second, observe that the sum of the interior angles of the faces meeting at each vertex must be less than 360°, for otherwise they would not all fit together.
Now, each interior angle of an equilateral triangle is 60°, hence we could fit together three, four, or five of them at a vertex, and these correspond to to the tetrahedron, the octahedron, and the icosahedron. Each interior angle of a square is 90°, so we can fit only three of them together at each vertex, giving us a cube. (We could fit four squares together, but then they would lie flat, giving us a tesselation instead of a solid.) The interior angles of the regular pentagon are 108°, so again we can fit only three together at a vertex, giving us the dodecahedron.
And that makes five regular polyhedra. What about the regular hexagon, that is, the six-sided figure? Well, its interior angles are 120°, so if we fit three of them together at a vertex the angles sum to precisely 360°, and therefore they lie flat, just like four squares (or six equilateral triangles) would do. For this reason we can use hexagons to make a tesselation of the plane, but we cannot use them to make a Platonic solid. And, obviously, no polygon with more than six sides can be used either, because the interior angles just keep getting larger.
The Greeks, who were inclined to see in mathematics something of the nature of religious truth, found this business of there being exactly five Platonic solids very compelling. The philosopher Plato concluded that they must be the fundamental building blocks—the atoms—of nature, and assigned to them what he believed to be the essential elements of the universe. He followed the earlier philosopher Empedocles in assigning fire to the tetrahedron, earth to the cube, air to the octahedron, and water to the icosahedron. To the dodecahedron Plato assigned the element cosmos, reasoning that, since it was so different from the others in virtue of its pentagonal faces, it must be what the stars and planets are made of.
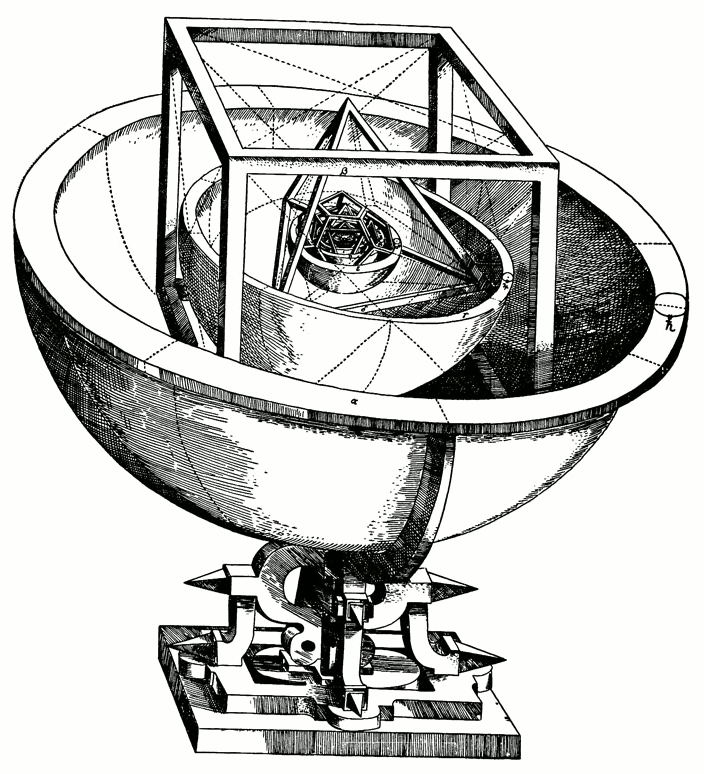
Kepler’s Platonic Solids Model of the Cosmos
Although this might seem naive to us, we should be careful not to smile at it too much: these were powerful ideas, and led to real knowledge. As late as the 16th century, for instance, Johannes Kepler was applying a similar intuition to attempt to explain the motion of the planets. Early in his life he concluded that the distances of the orbits, which he assumed were circular, were related to the Platonic solids in their proportions. This model is represented in this woodcut from his treatise Mysterium Cosmographicum. Only later in his life, after his friend the great astronomer Tycho Brahe bequeathed to him an enormous collection of astronomical observations, did Kepler finally reason to the conclusion that this model of planetary motion was mistaken, and that in fact planets moved around the sun in ellipses, not circles. It was this discovery that led Isaac Newton, less than a century later, to formulate his law of gravity—which governs planetary motion—and which ultimately gave us our modern conception of the universe.
The beauty and interest of the Platonic solids continue to inspire all sorts of people, and not just mathematicians. For a look at how one artist used these shapes, you may wish to study the M.C. Escher Minitext.
determiner
1 sometimes preceded by: a great or a good
a a large number of
many coaches, many times
b (as pronoun; functioning as pl)
many are seated already
2 foll by: a, an, or another, and a sing noun each of a considerable number of
many a man
3 preceded by: as, too, that, etc.
a a great number of
as many apples as you like, too many clouds to see
b (as pronoun; functioning as pl)
I have as many as you
n
4 ♦
the many the majority of mankind, esp. the common people
the many are kept in ignorance while the few prosper Compare →
few →
7 (See also)
→
more →
most
(Old English manig; related to Old Frisian manich, Middle Dutch menech, Old High German manag)
fallacy of many questions
n (Logic) the rhetorical trick of asking a question that cannot be answered without admitting a presupposition that may be false, as have you stopped beating your wife?
many-one
adj (Maths, logic) (of a function) associating a single element of a range with more than one member of the domain
many-sided
adj having many sides, aspects, etc.
a many-sided personality
♦
many-sidedness n
many-valued logic
n
a the study of logical systems in which the truth-values that a proposition may have are not restricted to two, representing only truth and falsity
one-many
adj (Maths, logic) (of a relation) holding between more than one ordered pair of elements with the same first member
English Collins Dictionary — English Definition & Thesaurus
Collaborative Dictionary English Definition
|
! many |
n. |
muchos, muchas |
||
|
! many |
n. |
muchos, muchas |
||
|
! comressions |
n. |
many compresses |
||
|
! many compress |
n. |
compressions |
||
|
fizzog |
n. |
face |
British slang in use at least from the 1940`s — abbreviation of ‘physiognomy’ |
|
|
noob |
n. |
a player who asks too many funny questions that can be related as being stupid |
Origin of the word is a «newbie» that can be shortened as a Newb |
|
|
! compiled
|
v. |
When you compile something such as a report, book, or program, you produce it by collecting and putting together many pieces of information. |
||
|
! SundryShop |
n. |
One place to find many different unique antiques, collectibles, and novelty items |
||
|
career woman |
n. |
an ambitious woman who thinks her career really matters more than many things and is not willing to compromise on it |
||
|
! FOTD |
exp. |
Face Of The Day |
langage internet |
|
|
to man up |
v. |
to face a situation courageously |
colloquial |
|
|
knuckle sandwich |
n. |
a punch in the face |
[Fam.];[Fig.];[Hum.] Ex.: French: «What do they call a knuckle sandwich?» English friend: «If someone offers you a knuckle sandwich, you’d better decline it; he’s about to thump you in the face!» |
|
|
o-face |
n. |
face that people are showing during orgasm |
SLANG |
To add entries to your own vocabulary, become a member of Reverso community or login if you are already a member.
It’s easy and only takes a few seconds:
In Geometry, a polyhedron is a closed space figure whose faces are polygons. The word polyhedron has Greek origins, meaning many faces. The following are a few examples of polyhedra.
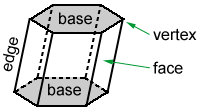
Characteristics of a polyhedron
The polygons that form a polyhedron are called faces. The line segments created by two intersecting faces are called edges. The vertices are points where three or more edges meet.
The hexagonal prism above is a polyhedron that has 6 lateral faces that are parallelograms, and 2 faces on the top and bottom, called bases, that are hexagons.
Euler’s Theorem
Euler’s Theorem shows a relationship between the number of faces, vertices, and edges of a polyhedron. It states that the sum of the faces and vertices minus the number of edges always equals two:
F + V — E = 2
where F is the number of faces, V is the number of vertices, and E is the number of edges of a polyhedron.
Example:
For the hexagonal prism shown above, F = 8 (six lateral faces + two bases), V = 12, and E = 18:
8 + 12 — 18 = 2
Classifications of polyhedra
Polyhedra can be classified in many ways. For example, they can be classified as regular and irregular polyhedra. A regular polyhedron is a polyhedron whose faces are all congruent regular polygons; any polyhedron that does not meet these conditions is considered irregular.
Polyhedra can also be classified as convex and concave. A concave polyhedron has at least one face that is a concave polygon. A polyhedron that is not concave, is convex. Polyhedra can also be classified based on the number of faces it has. For example, a tetrahedron has 4 faces, a pentahedron has 5 faces, and a hexahedron has 6 faces.
The following is a list of terms often used to describe polyhedra based on their characteristics.
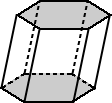
Prisms
Prisms are polyhedra that have two congruent faces, called bases, lying in parallel planes. A prism is typically named by the shape of its polygonal bases. The lateral faces (the sides that are not bases) are parallelograms, rectangles, or squares.
| Regular prism | Irregular prism |
|---|---|
 |
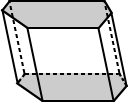 |
| The bases for the regular hexagonal prism above have bases that are regular hexagons. | The bases for the hexagonal prism above are irregular hexagon. |
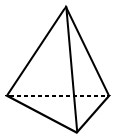
Pyramids
Pyramids are polyhedra that has a polygon as its base and triangles as all its other faces. A pyramid is also typically named by the shape of its polygonal base.
| Regular pyramid | Irregular pyramid |
|---|---|
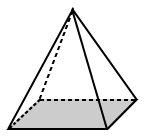 |
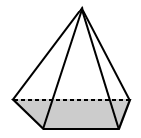 |
| The base of the square pyramid above has a base that is a square (a regular polygon). | The base for the trapezoidal pyramid above is a trapezoid with unequal sides (so it is an irregular polygon). |
Regular polyhedra
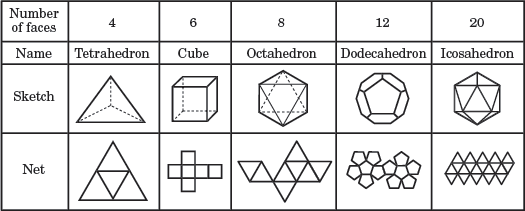
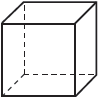
A regular polyhedron is a polyhedron whose faces are all congruent, regular polygons. A regular polyhedron is named based on its number of faces. There are only five polyhedra that are regular polyhedra; these are referred to as Platonic solids.
The five Platonic solids
In the diagram above, each regular polyhedra is named based on its number of faces. The net below each sketch shows a 2D picture of all of the faces of the polyhedron.
Most regular prisms are generally not considered regular polyhedra. A cube is the only regular prism that can also be classified as a regular polyhedron.
Likewise, a regular tetrahedron is the only regular pyramid that is also a regular polyhedron.
Multifaceted means having many aspects or sides. Diamonds are usually cut to be multifaceted, that is, with many angled flat surfaces, because this increases their ability to reflect light.
Since facet means «aspect,» «side,» or «face,» multifaceted means «many aspects, sides, or faces.» This can apply to jewels or other physical objects, like the eyes of a dragonfly, but it can also refer to complicated issues that have lots of contributing factors and generate more than two sides to an argument. A multifaceted person has many abilities, or a personality with many sides to it.
DISCLAIMER: These example sentences appear in various news sources and books to reflect the usage of the word ‘multifaceted’.
Views expressed in the examples do not represent the opinion of Vocabulary.com or its editors.
Send us feedback
EDITOR’S CHOICE
Look up multifaceted for the last time
Close your vocabulary gaps with personalized learning that focuses on teaching the
words you need to know.
Sign up now (it’s free!)
Whether you’re a teacher or a learner, Vocabulary.com can put you or your class on the path to systematic vocabulary improvement.
Get started
Sounds, visual images, and faces remind the players of people or events of the past.
A possible extension of the method was also presented which takes into account qualitative sur face height information.
Philosophical arguments address one of the most fundamental yet elusive questions facing behavioral scientists, namely, what constitutes a disorder?
The sections have been photographed so that the lateral surface of the brain faces upwards with the ventrolateral edge of the brain to the left.
But the great body of solar lines give, on the face of the returns, great difficulty in the relativity view.
In approaching their prospects, network marketers enjoy the privilege of exploiting the element of intimacy by reducing the potential threat to their prospects’ negative face.
The transactions for both parties were done face to face (and privately) with the game administrator.
With rare, athletic exceptions, the threat environment we now face is more symbolic than physical.
Countries are facing this challenge in many different ways, but one common factor is the increasing reliance on electronics and systems.
For metals, par t of the laser-evaporated material can then be redeposited on the sur face in and around the ablation site.
One of the challenges facing simulation studies is to relate the molecular structures of channel components to the physiological properties of ion channels.
The results suggest that many students are faced with a situation in which the cognitively demanding language of the classroom is beyond their grasp.
Recently, for foreign, liberal commentators these marginal groups represent the authentic face of the nation, suffering urban decadence and state repression.
It is also not unique in suffering high levels of air and water pollution and facing severe threats to its biological resources.
We are not targeting accurate predictions in the face of drastic unseen-before changes in workload patterns.
These examples are from corpora and from sources on the web. Any opinions in the examples do not represent the opinion of the Cambridge Dictionary editors or of Cambridge University Press or its licensors.