One way to help understand place value is by writing numbers in standard form, word form, and expanded form. For example, 9 in 129 has a different value than the 9 in 192. Knowing how to represent numbers in these three different ways will help build place value concepts.
What are these three forms of writing numbers?
Standard form is the usual way of writing numbers. One example is 756. This is how we see numbers everyday in the grocery, on our phones, computers, etc.
Expanded form is breaking down the numbers in such a way that you see the value of each number. So, the expanded form of 756 is 700 + 50 + 6.
Word form is when you write a number the way that you read it. When you see the number 756, you write it as “seven hundred fifty-six”.
How do you write numbers in standard form to word form?
When writing numbers from standard form to word form, having a place value chart will be very helpful. A place value chart shows how each digit in a number is related. It helps you read and separate the values into groups of three especially with big numbers.
Just look at this number 612,321,589. This number is read as “six hundred twelve million, three hundred twenty-one thousand, five hundred eighty-nine”. Notice that for each group of three, there is a comma or sometimes a space. These commas or spaces are not just for ease of reading. Commas also indicate the period or the group of digits in your number.
How do you write numbers in standard form to expanded form?
When writing numbers in expanded form, you will also find a place value chart helpful. Place value chart not just shows how the numbers are grouped, but also shows that each digit in a number increases by a power of ten from right to left. This will help decompose a number so that your students will know that having a 9 in the tens place has a different value than having a 9 in the hundreds place.
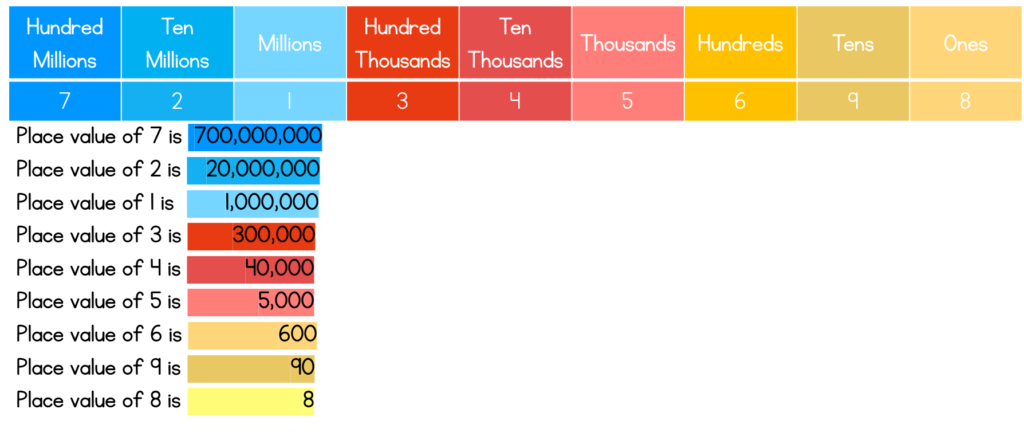
Here’s a place value chart showing the value of a number.
When the number 721,345,698 is placed in a place value chart, you will see the following:
- 7 is in the hundred millions place and has a value of 700,000,000
- 2 is in the ten millions place and has a value of 20,000,000
- 1 is in the millions place and has a value of 1,000,000
- 3 is in the hundred thousands place and has a value of 300,000
- 4 is the ten thousands place and has a value of 40,000
- 5 is in the thousands place and has a value of 5,000
- 6 is in the hundreds place and has a value of 600
- 9 is in the tens place and has a value of 90
- 8 is in the ones place and has a value of 8
When you put them all together, you will have a number written in expanded form. So 721,345,698 written in expanded form is 700,000,000 + 20,000,000 + 1,000,000 + 300,000 + 40,000 + 5,000 + 600 + 90 + 8.
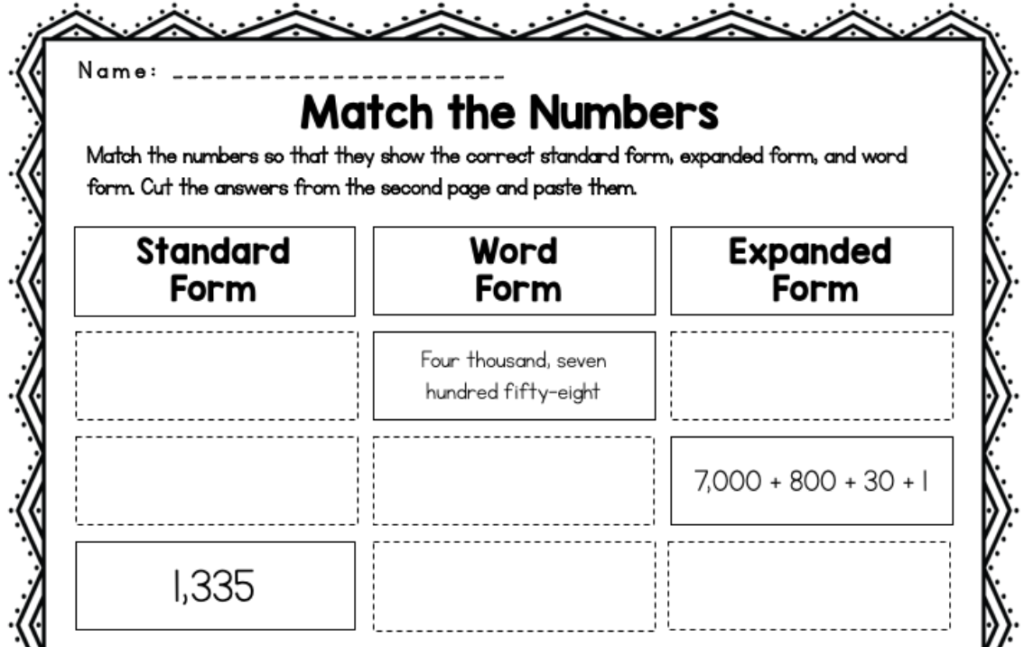
To start practicing converting numbers into their different forms, you can try our Match the Numbers worksheet. This activity asks the students to match the standard, expanded, and word forms of each number. This is a cut-and-paste activity but is easily convertible to just a pen-and-paper activity. An answer key is included on the second page.
Need a more comprehensive worksheet on reading and writing numbers? Check out these activities on Teachers Pay Teachers.
Using base-ten blocks is another good tool to help decompose a number in expanded form. You can start with our Place Value with Base-ten Blocks activity.
-
Feedback
Login to rate activities and track progress.
Login to rate activities and track progress.
A superb video lesson designed for children to teach them about «number forms» in an innovative way. With the help of this lesson, they will learn about different number forms like standard form, expanded form, and word form with the help of suitable examples. With the help of this engaging lesson, kids will become familiar with this topic in no time. No wonder, it will help kids’ build a strong foundation in maths from a young age.
A concept regularly taught along with place value is “expanded form”, a way to write a number that displays each place separately. As we’ll see, there is considerable variation in terminology here, so parents may have to check what form a teacher wants, rather than look it up and expect a single answer!
Whole numbers
Here is a question from 1998:
Expanded and Standard FormsMy teacher has asked me to write numbers in standard form and expanded form. For example 4,017. What exactly does she want me to do?
Doctor Ameis replied:
Hello Mark, Expanded form is a way of writing numbers so that all that is hidden about them comes out into the open. The simplest way to write numbers in expanded form is to write them sort of in English. For 4,017, this becomes 4 thousands and 0 hundreds and 1 ten and 7 ones. This can be made to look like math by changing the words to math symbols.The expanded form for 4,017, then, is: 4 x 1000 + 0 x 100 + 1 x 10 + 7 x 1 The expanded form shows what each digit is worth (for example, the 4 is worth 4 x 1000, which is the same as 4 thousands, which equals 4000).
I love that initial description. We want to “expand” a number, sort of unfurling it, to show what is hidden in the compact form we call positional notation, making explicit what is implied by the position of each digit.
He says “sort of in English” because normal English would be “four thousand seventeen”, which is not so fully unfurled! We have to make it clear that 4 thousand means 4 times one thousand, and break up the clump that is “seventeen” as one ten and seven ones. So we have $$4017 = 4times 1000 + 0times 100 + 1times 10 + 7times 1$$ We’ll discuss below whether the zero should be included.
Here is another example. 12,345 becomes 1 ten thousand and 2 thousands and 3 hundreds and 4 tens and 5 ones. Changing the words to math symbols, 12,345 in expanded form is: 1 x 10,000 + 2 x 1,000 + 3 x 100 + 4 x 10 + 5 x 1
What is standard form? It’s just the form we started with, like Mark’s 4017. What if you’re given the expanded form first?
Standard form is the reverse of expanded form. You begin with expanded form and change it to the way we normally write numbers. For example, 3 x 1,000 + 5 x 100 + 7 x 10 + 4 x 1 can be changed to 3 thousands and 5 hundreds and 7 tens and 4 ones. This becomes: 3000 + 500 + 70 + 4 Do the addition and you get 3574 (the standard form).
Writing in standard form just means doing the arithmetic indicated by the expanded form. We’re putting the number back together again.
The intermediate form here, as we’ll see, is also sometimes called “expanded form”: $$3574 = 3000 + 500 + 70 + 4$$
But “standard form” doesn’t mean the same thing everywhere; in many countries that term refers to what we in America call “scientific notation”. As I have often commented, the least standardized word in all of math is the word “standard”.
In between: Short word form
A closely related question is represented by this from 2002:
Short Word FormHow is 474,136 written in short word form vs. standard form?
Doctor Sarah answered:
Hi Nicholas - thanks for writing to Dr. Math. The standard form of a number is written with commas separating every three digits. Your number 474,136 is already in standard form. In short word form, the number is written using a combination of numerals and letters. Your number would be 474 thousand 136
This form focuses on the “periods” (groups of three digits, separated by commas) in a number, which represent powers of 1000 (thousand, million, billion, …).
Another form (which one teacher who asked about it called “mixed form”) looks like “3 hundreds, 4 tens, 5 ones”, which is essentially the “sort of English” form of Doctor Ameis. A student once asked about “word-and-number” form, which might be what his teacher calls either of these.
In word form, the number is written in words: four hundred seventy-four thousand one hundred thirty-six
This could be called “long word form” or “standard word form”; it doesn’t directly relate to place value.
In expanded form or expanded notation, your number is written as: 4 x 100,000 + 7 x 10,000 + 4 x 1,000 + 1 x 100 + 3 x 10 + 6 x 1
This is the same expanded form we saw before. But we’ve seen teachers use that term for a couple variations.
Three kinds of “expanded”
A similar question (never archived) comes from 2009:
How do I write 680034987 in expanded notation?
Doctor Ian answered, taking a slightly different approach to the form:
Hi Monique,
Suppose I want to write 4098 in expanded form. I can write it as a column addition,
4000
90
+ 8
-----
4098
If I write it on a single line,
4000 + 90 + 8
then it's in 'expanded form'.
This is the simplest “expanded form”; there are a couple others:
Note that this isn't really a mathematical thing. It's a math-teacher thing. So the 'right' answer will depend on what it is your teacher wants to see. Some teachers might require it to be written like 4*1000 + 9*10 + 8*1 and some might require it to be written as 4*10^3 + 9*10^1 + 8*10^0 It's really a matter of taste. Any one of those would be correct, but any teacher might decide to mark only one of them as 'right'. Anyway, do you see the main idea? Can you apply it to your number? Try that, and let me know what you come up with.
We’ve seen the first of these; the second we haven’t yet. This can be called exponential expanded form, or expanded form with powers of ten.
Incidentally, we have had a number of teachers or students ask us about the difference between “expanded form” and “expanded notation”, and it seems that some authors do distinguish these terms (e.g. here), saying that (400+90+8) is “expanded form” while (4times 1000+9times 10+8times 1) is “expanded notation”. But Common Core (here) calls the latter “expanded form”; and other sources (e.g. here) call the former “expanded notation”. I don’t think any of these naming conventions are standard. As Doctor Ian said, it’s just a matter of taste.
I’ll call the three forms “short expanded form“, $$498 = 4000+90+8$$
“long expanded form“, $$498 = 4times 1000 + 9times 10 + 8times 1$$
and “exponential expanded form“, $$498 = 4times 10^3 + 9times 10^1 + 8times 10^0$$
That’s just my choice of names, made up this minute!
Should you include zeros?
Here is a question (from 2012) that should have been archived, because it is surely a common issue:
How would you write a single digit number in expanded form? For example the number 6. We know that 16 is 10+6, but we are confused about the right way to do a single digit number. My teacher asks me to do 5 different things with the date everyday. Tally marks, money, place value blocks, odd/even, and expanded form. We are all confused about the right way to write single digit numbers in expanded form. I say it's just the number itself. My friend says you would do 0+6 like you do in money or time for single digit numbers. We really want to know what the right way to do it is.
Emily is right; but her friend isn’t terribly wrong. (Note that they are using “short expanded form”.) Doctor Ian answered:
Hi Emily, A single digit number is *already* expanded. You don't have to do anything. The problem with writing 0+6 is that you could also write 0+0+6, or 0+0+0+6, and so on. There would be no end to it. Just out of curiosity, if asked to write something like 1506 in expanded form, how would you do that?
If you require an added zero, how do you know when to stop? It seems best to stop before you start.
The new question is a good way to stimulate thought. We’ve already seen examples like this, probably chosen specifically to bring up this point.
Emily replied,
Thank you for helping us to understand math. Just to be sure I have this right, if the number is a single digit, I should just rewrite the number in the answer spot. Would it be better to leave it blank or to write, no expanded form? Emily
To answer your question 1506 in expanded form is 1000+500+6 right? I used to think I had to put a +0 in there where the tens go, but my teacher said that it wasn't needed.Well, now that brings up another question. What if the number is 40? 40 + 0?
Emily already has been told about zeros in the middle; but zeros on the left, and zeros on the right, seem different!
Doctor Ian responded first to the question about “no expanded form”:
Hi Emily, It would be better to just put the number there. For a single-digit number, the regular form and the expanded form are the same.
So there is an expanded form; it just isn’t different.
Next, about the zero in 1506 not being needed in expanded form:
I would agree.
The reason it’s needed in standard form is as a place-holder. In expanded form, places are explicit, so they don’t need to be “held”.
And then, on 40:
That *is* a good question. If we don't have to write the 0 for 1506, we probably wouldn't want to write it for 40, either.
It might help to think about what 'expanded notation' is good for. For example, it's useful if we want to do 'lattice multiplication'. That is, if we want to multiply 234 by 56, we can make up a table:
50 6
200
30
4
We can multiply the individual parts,
50 6
200 10000 1200
30 1500 180
4 200 24
and then add those up to get the product:
234 * 56 = 10000 + 1500 + 200 + 1200 + 180 + 24
= 13104
Don't worry if you haven't learned about this yet. You will.
But let's think about doing something like multiplying 40 by 56. The table would look like
50 6
40 2000 240
0 0 0
That last row isn't making much of a contribution, is it? So there's no real reason to include it. That's also why we wouldn't bother to write 1506 as 1000+500+0+6. Let's look at a table for that:
1000 500 0 6
30 30000 15000 0 180
9 9000 4500 0 54
Again, that third row isn't making much of a contribution. So there's no real reason to include it.
This is the kind of thing that leads us to the decision not to include entries for places where the digit is zero. It just takes up space, without really being useful.
Does this make sense?
A lot of math comes down to a question of what is useful.
Expanded form with decimals
A couple new issues arise when we include decimals, which are only mentioned in the archive in this question from 2001:
What is Expanded Notation?
We get more details in this unarchived question from 2010 explicitly about decimals:
My math assignment says I have to write expanded notation with numbers under 1, for example 0.05 and 0.7805
How do you do it? Especially the zero's. 0.00+ 0.05 0.000+ 0.7805Thanks Katie
The leading zeros might make a student trip up; it appears that Katie is trying to include terms for them, which would be confusing. I answered:
Weren't you given any examples in class? Or is this an assignment to test what you already know, and you have never been taught this before? I'd like to have seen some attempt (or an example of how you would write expanded notation for a number greater than 1) in order to give me a better idea where to start.
Students do sometimes ask questions about topics they missed, or on tests not associated with what they have already learned; it’s helpful when we can get such background information. Also, as we’ve seen, an example would clarify what kind of expanded form they are (or will be) learning. Lacking that information, I offered several options:
There are slightly different ways to write "expanded notation", but one form is to show the value of each digit in the number, like this: 123 = 100 + 20 + 3 or 123 = 1x100 + 2x10 + 3x1 That is, the 1 means 1 hundred, so we write either 100 or 1x100. The 2 means 2 tens, so we write 20 or 2x10; and the 3 means 3 ones, so we write 3 or 3x1.
These are my “short” and “long” extended forms, so far applied only to whole numbers. Now we extend the idea, using fractions:
The digit after the decimal point is the number of tenths, and the one after that is hundredths. So we would write 1.23 as 1.23 = 1 + 2/10 + 3/100 or 1.23 = 1x1 + 2x1/10 + 3x1/100 Does that remind you of something you've been taught? Can you tell whether one of these forms, or something like them, is the way you have been taught to write expanded form?
The short extended form is $$1.23 = 1times 1 + frac{2}{10} + frac{3}{100}$$ and the long extended form is $$1.23 = 1times 1 + 2timesfrac{1}{10} + 3timesfrac{1}{100}.$$
It looks like you may have been trying to write something like my first form, but using decimals rather than fractions: 1.23 = 1 + .2 + .03. That's a possible form, but I don't think it's very useful, and so I doubt it is what you would be expected to do. But you'd have to show me an example of what your teacher means by expanded notation in order for me to be sure.
I’m not sure whether anyone teaches this form, $$1.23 = 1times 1 + 2times .1 + 3times .01.$$
How many ways to name a number?
Occasionally, we got questions like this (unarchived) from 2007:
What are the five ways to name a number? e.g. 127
I have1. pictorial (drawing blocks)
2. words (one hundred twenty-seven)
3. expanded notation (100 + 2 10's + 7 1's) I suppose 127 is called standard notation. If so I have four of the five ways to name a number.
Doctor Rick answered:
Who says there are just five ways to name a number? That must be some educator's pronouncement, in which case you'll have to read the educator's book to get the full list. You can use scientific notation: 1.27*10^2. Or Roman numerals: CXXVII. Or hexadecimal: 7F. Or binary: 1111111. Or ancient Egyptian hieratic numerals. Or modern Arabic numerals. Or ancient Babylonian base-60 numerals. Or French words ... Honestly, I don't know what the answer is supposed to be.
Someone else asked about the four ways to name a number. I imagine each of these was really “the ___ ways we discussed in class”; such questions are particularly frustrating to parents when they don’t know what was taught, and assume it must be something universal.
Why so many ways to name a number?
Let’s look at one more unarchived question, this one from 2009:
Why are there so many forms or notations for numbers?Like Standard notation = 782
But there's also
Expanded notation = 782 = (7*100)+ (8*10)+(2*1)
Scientific notation = 1,000,000 = 10^6 (ten to the sixth power) * 1 = 1,000,000
Word form = seven hundred and eighty two
Word and Number form = (1,000) 1 thousandIt's just my teacher has taught us all these and I just find that there are A LOT.
Like here's an example of a question: "Write 107 in word form"
Answer: one hundred seven
We see here (long) expanded form, (long) word form, the “mixed” form I’ve mentioned, and also scientific notation, which uses a single power of ten. Doctor Ian answered:
I'll bet you have more than one pair of shoes, right? How come? Because different kinds of shoes are good for different situations, right? The shoes you wear to church aren't so good for the beach, and shoes for going out in the snow aren't so good for playing soccer, and so on. Each form for writing a number has its own uses, things it's good for. And it's not so good for other things!
This is the standard way to think about any such question. How about some specifics?
For example, we use word form when writing checks. If I wrote you a check for, say, 15.00 dollars, it would be easy for you to put some numbers in front of that when you go to cash it. You might change it to 915.00, for example. But if I write out 'fifteen and no/100', it's a lot harder to alter that. It's also useful for catching errors, e.g., some people write their sevens the way other people write their ones. So if you just see '15', that might mean fifteen, or it might mean seventy-five, depending on who wrote it. But if the words are written out, it's hard to confuse the two, isn't it?
These two reasons are fraud prevention (which was also one reason Europe held on to Roman numerals for so long!) and error detection (as when people write something like “two (2) copies”).
(We also use word form just to read numbers aloud, of course.)
Scientific notation makes really big numbers (like 602,000,000,000,000,000,000,000) or really small numbers (like 0.00000000056) easier to compare with other numbers, because we can just look at the exponents. It also makes them easier to work with, because we can manipulate the exponent and non-exponent parts independently.
For example, to multiply
602,000,000,000,000,000,000,000
* 0.00000000056
---------------------------------
would be really hard to do, even with a calculator, without making a mistake of some kind. But if we write it as
6.02 * 10^23
* 5.6 * 10^-10
-----------------
we can just multiply 6.02 and 5.6, to get 33.7, and add the exponents,
6.02 * 10^23
* 5.6 * 10^-10
-----------------
33.7 * 10^13
and adjust it back to scientific notation (i.e., so the first part is between 1 and 10),
6.02 * 10^23
* 5.6 * 10^-10
-----------------
33.7 * 10^13 = 3.37 * 10^14
and it's pretty straightforward.
Each has its place.
Now, just as you don't want to wear your snow boots everywhere, using scientific notation is a bad idea for numbers that aren't very large, or very small! But for the right situation, it's a great tool to have. So basically, if mathematicians have invented a way of writing a number, it means that there is at least one situation where it solves a problem for them. Does this make sense?
Finally:
An exception is 'expanded notation'. This isn't used anywhere except in classrooms, as a way of teaching about place value. It's really not used outside of school.
And this is why the names and notations for expanded form(s) are not standardized: They are just teaching tools, not concepts mathematicians or scientists have to use (and therefore agree on).
Next time, we’ll look at some details of “word form”.
Presentation on theme: «Forms of Numbers Standard Form, Expanded Form, and Word Form»— Presentation transcript:
1
Forms of Numbers Standard Form, Expanded Form, and Word Form
2
Standard Form What is the standard form for one hundred twenty-three thousand, fifty-eight? ,58 ,058 ,508 The correct answer would be number 2.
3
Expanded Form What is the expanded form for 603,478?
600, , 60, , 600, , The correct answer would be number 1.
4
Place Value What place is the number 6 in? 13,568,792 1. thousands
2. ten thousands 3. hundred thousands The correct answer is number 2. What is the value of the number 6? 1. 60,000 2. 6,000 ,000 The correct answer is number 1.
5
Place Value What is the value of the number 5 in the number 50,678,123? 5 million 50,000,000 5 hundred million The correct answer would be number 2.
Standard form in maths is the method of representing a particular element in the most common manner. From large numbers to small numbers to equations to lines, every element in maths is denoted in a standard form. Let us explore this interesting concept of standard form in various elements of maths such as fractions, equations, algebra, slope along with learning the standard from formula. Solving examples and understanding the basic thumb rule will help in understanding the concept better.
| 1. | What is Standard Form? |
| 2. | Standard Form of Number |
| 3. | Standard Form of Fraction |
| 4. | Standard Form of Equations |
| 5. | Standard Form of Polynomial |
| 6. | Standard Form of a Linear Equation |
| 7. | Standard Form of Quadratic Equations |
| 8. | Standard Form Formula |
| 9. | FAQs on Standard Form |
What is Standard Form?
A standard form is a form of writing a given mathematical concept like an equation, number, or an expression in a form that follows certain rules. Representing very large or very small numbers concisely, the standard form is used. For example, 4.5 billion years is written as 4,500,000,000 years. As you can see here, writing a large number like 4.5 billion in its number form is not just ambiguous but also time-consuming and there are chances that we may write a few 0’s less or more while writing in the number form. In this case, writing the number in standard form is very helpful. For example, the standard form of 4,500,000,000 = 4.5 × 109. Not only numbers but the fractions, equations, expressions, polynomials, etc also can be written in the standard form.
Let us study the standard form of each of these in detail.
Standard Form of Number
The standard form of numbers (which is also known as «scientific notation» of numbers) has different meanings depending on which country you are in. In the United Kingdom and countries using UK conventions, the standard form is another name for scientific notation. Scientific notation is the process of writing a very large or very small number using numbers between 1 to 10 multiplied by the power of 10. For example, 3890 is written as 3.89 × 103. These are numbers that are greater than 1 use positive powers of 10. Numbers less than 1 use the negative power of 10. For example, 0.0451 is written as 4.51 × 10-2.
In the United States and countries using US conventions, the standard form is the usual way of writing numbers in decimal notation. Using the same example,
Standard form = 3890, Expanded form = 3000 + 800 + 90, and Written form = Three thousand eight hundred and ninety.
Standard Form of Fraction
In the case of fractions, we need to ensure that in the standard form of fractions, the numerator and denominator must be co-prime numbers. That means they have no common factor other than 1, hence the standard form is also called the simplest form of a fraction. For example, 14/22 and 13/6. The simplest form of 14/22 = 7/22 and 13/6 is already in its simplest form as 13 and 6 are co-prime.
Standard Form of Equations
The standard form of an equation is where zero goes on the right and everything else goes on the left. i.e., it is of the form
- Expression = 0.
This helps in solving the equation in a simple manner. Equations used for polynomials, linear and quadratic have a standard form, let us look at what they are.
Standard Form of Polynomial
The standard form polynomial is written with the exponents in decreasing order to make calculations easier. A polynomial is said to be in its standard form, if it is expressed in such a way that the term with the highest degree is placed first, followed by the term which has the next highest degree, and so on. There are two very simple rules of writing a polynomial in a standard form, they are:
- Write the terms in the descending order of their powers (also called exponents).
- Ensure the polynomial contains no like terms.
Hence, the standard form is anxn + an-1xn-1 + an-2xn-2 + … + a1x1 + a0. For example, the standard form of equation y2 + 7y6 — 8y — y9 is written as -y9 + 7y6 + y2 — 8y.
Note: The thumb rule for writing a polynomial in its standard form is D-U. D stands for Descending and U stands for unlike terms.
Standard Form of a Linear Equation
The standard form of linear equations also known as the general form is a method of writing linear equations. A linear equation can be written in different forms like the standard form, the slope-intercept form, and the point-slope form. The standard form of a linear equation is expressed in two ways, with one variable and with two variables. The standard form of linear equation with one variable is expressed as ax + b = 0 where a and b are constants and the letters x is the variable. The standard form of a linear equation with two variables is expressed as ax + by = c. where a, b, and c are real numbers and the letters x and y are the variables. Look at the image below.

Let’s see how to convert the two lines into the standard form of a linear equation ax + by = c.
Line 1: x + y = 7 i.e. 1x +1y = 7. Here, a = 1, b =1 , c = 7
Line 2: y = 3x i.e. 3x -1y = 0. Here, a = 3, b = -1 , c = 0
Therefore, what we see here is the standard form of equation which is linear i.e. ax + by = c.
Standard Form of Slope of a Line
The slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line. Representing a line geometrically, we use the standard form of a linear equation (mentioned above). To determine the slope of a line that is expressed graphically, the equation must be converted to a slope-intercept form. To do this, we must solve the equation for y, and the standard form of a slope is expressed as y = mx + c, where m is the slope of the line. This formula is used when the line is straight.
When there are two points in a plane, the slope can be defined as the ratio of change in the value of y to the change in the value of x. The standard form of slope of a line is expressed as m = (y2 – y1)/(x2 – x1). The image below represents both the coordinates on a graph.
Standard Form of Quadratic Equations
The standard form of quadratic equation in a variable x is of the form ax2 + bx + c = 0, where a ≠ 0, and a, b, and c are real numbers. Here, b and c can be either zeros or non-zero numbers and
- ‘a’ is the coefficient of x2
- ‘b’ is the coefficient of x
- ‘c’ is the constant
Apart from the standard form of a quadratic equation, a quadratic equation can be written in several other forms.
- Vertex Form: a (x — h)2 + k = 0
- Intercept Form: a (x — p)(x — q) = 0
A parabola is a graph of a quadratic function that refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point, and a fixed-line. The fixed point is called the focus of the parabola, and the fixed line is called the directrix of the parabola. The following graphs are two typical parabolas; their x and y-intercepts are marked by green dots, and the vertex of each parabola is marked by a blue dot.
The graph will have one of the two shapes as shown above.
- When a > 0, it represents the first parabola (figure 1) which opens upward (U-shaped).
- When a < 0, we obtain a parabola that opens downward (inverted U-shaped) as shown in figure 2.
When we put y = 0 in the above equation, we get the x-intercept which is also called the roots of the equation. Finding the roots provides us with the turning point of the parabola and the vertical line which is drawn from the turning point is called the axis of symmetry. Look at the image below for reference.
Standard Form Formula
The standard form formula represents the standard form of an equation which is the commonly accepted form of an equation. The formula to represent the standard form formula is based on the degree of the equations.
-
The standard form of a linear equation is the basic form of an equation. The standard form of a linear equation with two variables and more than two variables is presented below. Here x, y, or x1, x2, x3,…. represent the variables and a, b, a1, a2, a3, …….. an are referred to as the coefficients. The numerics placed to the right of the equals to sign are called constants.
ax + by = c
a1x1 +a2 x2+ a3 x3 + …….. + an xn = D
-
The standard form of a quadratic equation is a second-degree equation and has a variable, coefficients, and constant term. Here it is a single variable x of degree 2. The standard form of a quadratic equation is ax2 + bx + c = 0, where a ≠ 0.
Further, we have standard form formulas for equations of higher degrees. Also in coordinate geometry, we have a standard form for different geometric representations such as a straight line, circle, ellipse, hyperbola, and parabola.
- Straight-line: ax + by = c, where a is a positive integer, and b, and c are integers.
- Circle: (x — h)2 + (y — k)2 = (r)2, where ( h, k) is the center and r is the radius.
- Ellipse: x2/a2 + y2/b2 = 1
- Hyperbola: (x-x0)2/a2 — (y-y0)2/b2 = 1, where x0, x0 are the center points, a = semi-major axis and b = semi-minor axis.
- Parabola: (x — h)2 = 4p(y — k)
☛Related Topics
Listed below are a few topics that are related to a standard form.
- Standard Form Calculator
- Standard Form to Vertex Form
- Polynomial in One Variable in Standard Form
FAQs on Standard Form
What is the Definition of Standard Form in Math?
Standard form in math is the method of representing a particular element (numbers, fractions, equations, etc) in the most common way. Very large numbers or very small numbers are expressed in the standard form. Mathematical elements such as equations are expressed in a standard form to better solve the problem. In other words, a standard form is a form of writing a given mathematical concept like an equation, number, or expression in a form that follows certain rules.
How Do We Write Standard Form in Maths?
The process of writing a given mathematical concept like an equation, number, or expression in certain rules is called the standard form. Depending upon which mathematical concept we are dealing with, the standard form formula will vary.
How Do You Write Standard Form of Number?
Standard form in math of numbers is written differently depending on the country. In the UK, numbers that are greater than 1 use positive powers of 10, and numbers less than 1 use the negative power of 10. For example, 3670000 is written as 3.67 × 106 and 0.0763 is written as 7.63 × 10-2. This is commonly known as scientific notation of numbers.
What is Standard Form Formula?
The standard form formula refers to the formula presenting the general representation for different types of notation. For example, the standard form of
- a linear equation is ax + by = c.
- a quadratic equation is ax2 + bx + c = 0
- a cubic equation is ax3 + bx2 + cx + d = 0
What is the Standard Form Formula for Parabola?
The standard form formula of the equation of the parabola is this: (y — k)2 = 4p(x — h), where p≠ 0 only in case a parabola has a horizontal axis.
- The vertex of this parabola is at (h, k).
- The focus is at (h + p, k).
What is the Standard Form for Slope Formula?
The standard form of the slope-intercept form of a linear equation is y = mx + b, where m is the slope of the line whereas the standard form of a linear equation is Ax + By = C and the slope in this form is -A/B.
How to Use Standard Form Formula?
We can use the standard form formula depending on the equation, if it’s linear, quadratic, etc. Just rewrite the given formulas in the standard form.
- Standard form of linear equation: ax + by = c
- Standard form of a quadratic equation is a second degree equation: ax2 + bx + c = 0
What is the Standard Form of Equation?
In the standard form of an equation, 0 is usually present on the right side, whereas the rest of the expressions are on the left. Also, the terms are arranged in the descending order of their exponents. To convert an equation into stadard form, just apply arithmetic operations on both sides to turn the right side to be 0.