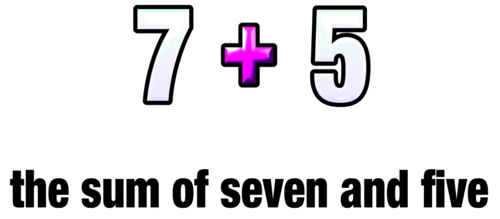What is a word phrase in math?
A mathematical phrase is a verbal phrase that contains words and/or numbers that can be translated into a mathematical expression, where a…
How do you write an expression?
To write an expression, we often have to interpret a written phrase. For example, the phrase “6 added to some number” can be written as the expression x + 6, where the variable x represents the unknown number.
What is expression example?
The definition of an example of expression is a frequently used word or phrase or it is a way to convey your thoughts, feelings or emotions. An example of an expression is the phrase “a penny saved is a penny earned.” An example of an expression is a smile. noun. 67.
What are some good expressions?
Common English idioms & expressions
| Idiom | Meaning | Usage |
|---|---|---|
| It’s a piece of cake | It’s easy | by itself |
| It’s raining cats and dogs | It’s raining hard | by itself |
| Kill two birds with one stone | Get two things done with a single action | by itself |
| Let the cat out of the bag | Give away a secret | as part of a sentence |
What are the expressions explain?
Expression: An expression is a combination of operators, constants and variables. An expression may consist of one or more operands, and zero or more operators to produce a value.
What is C expression write an example?
An expression is a formula in which operands are linked to each other by the use of operators to compute a value. An operand can be a function reference, a variable, an array element or a constant.
What are the two types of expression?
In this article
- Primary expressions.
- Postfix expressions.
- Expressions formed with unary operators.
- Expressions formed with binary operators.
- Expressions with the conditional operator.
- Constant expressions.
- Expressions with explicit type conversions.
- Expressions with pointer-to-member operators.
What are different types of expressions?
There are three kinds of expressions: An arithmetic expression evaluates to a single arithmetic value. A character expression evaluates to a single value of type character. A logical or relational expression evaluates to a single logical value.
What are the 5 types of expression?
Types of Expressions
- Numeric. Use a numeric expression to perform calculations that use numeric constants (integer or decimal) and variables.
- Date. Use date expressions to perform numeric calculations on dates.
- Character.
- Logical.
- Conditional.
Which code example is an expression?
Examples. For example, 2 + 3 is both an arithmetic and programming expression, which evaluates to 5 . A variable is an expression because it denotes a value in memory, so y + 6 is also an expression. An example of a relational expression is 4 ≠ 4 , which evaluates to false .
What are the different types of algebraic expressions?
There are 3 main types of algebraic expressions which include:
- Monomial Expression.
- Binomial Expression.
- Polynomial Expression.
What is algebra example?
Algebra helps in the representation of problems or situations as mathematical expressions. It involves variables like x, y, z, and mathematical operations like addition, subtraction, multiplication, and division to form a meaningful mathematical expression. One simple example of algebra is 2x + 4 = 8. …
Is 2x YZ a Monomial?
2x yz D. 2 + xyz. 2xyz2 is a monomial.
Is 10x a polynomial?
10x is a polynomial. In particular, for an expression to be a polynomial term, it must contain no square roots of variables, no fractional or negative powers on the variables, and no variables in the denominators of any fractions. That’s why 10x is a polynomial because it obeys all the rules.
Is 5x 3 a Monomial?
Step-by-step explanation: A monomial refers to an expression that involves one term, like 5xy. Monomials include variables, numbers, and whole numbers whose multiplication takes place together. Any number, all by itself, can be a monomial, like the number 5 or the number 2,700.
What is Monomial example?
A monomial is an expression in algebra that contains one term, like 3xy. Any number all by itself is a monomial, like 5 or 2,700. A monomial can also be a variable, like “b” or “y.” It can also be a combination of these, like 98b or xy.
Which is called Monomial?
A monomial, also called power product, is a product of powers of variables with nonnegative integer exponents, or, in other words, a product of variables, possibly with repetitions. For example, is a monomial. The constant 1 is a monomial, being equal to the empty product and to x0 for any variable x.
How do you identify a Monomial?
A monomial is an expression in algebra that contains one term, like 3xy. Monomials include numbers, whole numbers and variables that are multiplied together, and variables that are multiplied together. A polynomial is a sum of monomials where each monomial is called a term.
Is 2x one or two terms?
Even though 2x has two parts (2 and x), since they are being multiplied together, 2x is considered a single term (a monomial expression). In expressions containing more than one term, terms are generally separated by addition, subtraction, or division.
Is 2x a coefficient?
In 2x, the coefficient of 2x is 2, and 3 is a constant. Therefore, the coefficients are 1 and 2.
Is 2B a term?
2B is defined as a cyber term because some of its characters are used as substitutes for letters.
What is the constant of 2x?
the 3 is a constant term. where x is the variable, and has a constant term of c. If c = 0, then the constant term will not actually appear when the quadratic is written. when x is multiplied by 2, the result, 2x, is not constant; while 1 * -2 is -2 and still a constant.
What is constant give example?
In Algebra, a constant is a number on its own, or sometimes a letter such as a, b or c to stand for a fixed number. Example: in “x + 5 = 9”, 5 and 9 are constants.
What is constant term example?
A constant term is a term that contains only a number. In other words, there is no variable in a constant term. Examples of constant terms are 4, 100, and -5.
What is the constant of y =- 2x?
Answer. Answer: 2 is the constant of proportionality in the equation y = 2x .
What is the constant of proportionality in an equation?
When two variables are directly or indirectly proportional to each other, then their relationship can be described as y = kx or y = k/x, where k determines how the two variables are related to one another. This k is known as the constant of proportionality.
Is Y 2x a constant variation?
It is a direct variation and the constant of variation is the slope of the line, which is 2. Alan P. y=2x+1 is not a direct variation.
Is Y 2x a linear function?
the equation y = 2x represents a linear or non linear function. y/x = 2, which is a constant. So, the slope is constant, meaning the graph is a straight line. So, it is linear.
Welcome to this complete guide to translating words into algebraic expressions (also known as algebraic translation), where you will learn how to identify and apply key information, in the form of words and phrases, to accurately translate a given set of words into an algebraic expression involving both numbers and variables.
Why is learning how to translate words into algebraic expressions a crucial skill that every math student must learn? Because it is often the case that math problems are expressed completely in words without any explicit use of numbers, expressions, or equations. In order to solve these types of math word problems, students have to be able to translate words into expressions or equations so they may model and solve such scenarios.
Are you ready to learn everything there is to know about algebraic translation?
The following free Translating Words into Algebraic Expressions lesson guide is a step-by-step tutorial that will teach you how to easily and accurately translate any given word phrase into a mat equation.
How can you translate written expressions into numerical form?
The key skill associated with algebraic translation is being able to rewrite mathematical situations expressed in words as a mathematical expression involving numbers, operations, and variables.
Before we get to actually translating words into algebraic expressions, let’s lay some important groundwork!
Tip #1: Expressing Variables
For example, what if we wanted to translate the phrase the sum of seven and five into an expression. It would be pretty easy to translate this phrase into 7 + 5 and your job would be done.
But what if we changed the phrase to the sum of a number and five? How would our numerical expression change? Since a number could represent any value, we have to use a variable (since a variable can represent any value).
In this case, you could translate the sum of a number and five into x + 5 where x represents a number.
When using letters as variables in a math expression or equation, x is the most commonly chosen letter, but you can actually choose any letter to represent an unknown value.
Example A: Translate the phrase ten plus a number into an algebraic expression.
To complete this translation, we can break the given phrase down into three parts:
I: ten ➔ 10
II: plus ➔ +
III: a number ➔ x
Now, you can translate ten into 10, plus into an addition sign, and a number into a variable leaving you with:
ten plus a number ➔ 10 + x
Tip #2: More Than/Less Than
Now, let’s slightly change the words given in Example A as follows:
Example B: Translate the phrase ten more than a number into an algebraic expression.
You probably already know that more than is associated with addition so the sign is not going to change. But what about the order of the terms?
Think about it this way: we have a number (some unknown value) and this phrase represents ten more than whatever that value is. So, in this case, you will start with the variable first and then add ten to it as follows:
ten more than a number ➔ x+ 10
You would be correct to wonder whether or not the order of the terms matters in this example. Technically, it does not because addition is commutative. But what about subtraction, which is not commutative?
See Also: The Commutative Property: Everything You Need to Know
Example C: Translate the phrase six less than a number into an algebraic expression.
Notice again that we are seeing the word than.
You probably already know that less than is associated with subtraction so you already know what sign you will be using.
This phrase represents a value that is six units smaller than whatever our unknown value is. So, to find that number, we would have to take our variable and subtract six from it as follows:
six less than a number ➔ n-6
In cases like Example B and Example C, the second term comes first and the first term comes second (you have to switch the order).
So, we can conclude that than is a switch word, which means that the operator in the middle stays the same, but the first term and the last term are switched. Look out for this relationship when you see the phrase more than or less than in words.
Tip #3: Groupings and Parenthesis
Lets move onto another example…
Example D: Translate the phrase the difference of three and a number into an algebraic expression.
Translating this phrase into an expression should be pretty straightforward.
Since difference means subtraction, we can easily perform the following algebraic translation:
the difference of three and a number ➔ 3 — p
Now, what if we changed this expression to the difference of three and twice a number plus one
Example D: Translate the phrase the difference of three and twice a number plus one into an algebraic expression.
So, now instead of 3 — p, we have to write the expression as 3 — the entire expression twice a number plus one, which we can call 2p + 1.
Note that you will have to use parenthesis to enclose the entire expression twice a number plus one as follows:
the difference of three and twice a number plus one ➔ 3 — (2p+1)
So, whenever you are performing algebraic translations, you can use parenthesis to separate independnt groupings.
Translate Algebraic Expressions Practice
Now that you understand some key elements of translating words into algebraic expressions, you are ready to practice on your own. Go ahead and translate the following words into algebraic expressions on your own and then check the answer key at the end of this post to see how you did!
Practice Problems: Translate each phrase into an algebraic expression.
1.) nine times a number
2.) the sum of a number and twelve
3.) twice a number decreased by eleven
4.) twenty less than a number
5.) half a number plus two
6.) the quotient of five and a number
7.) five times the difference of a number and one
8.) the sum of sixteen and three times a number minus four
Wait! Don’t scroll further until you’re ready to see the answer key.
Answer Key:
1.) nine times a number ➔ 9x
2.) the sum of a number and twelve ➔ n + 12
3.) twice a number decreased by eleven ➔ 2y — 11
4.) twenty less than a number ➔ m — 20
5.) half a number plus two ➔ (x/2) + 2
6.) the quotient of five and a number ➔ 5 ÷ p
7.) five times the difference of a number and one ➔ 5(x-1)
8.) the sum of sixteen and three times a number minus four ➔ 16 + (3y — 4)
How to Translate Algebraic Expressions Video
Are you looking for more help with translating algebraic expressions? Check out our free step-by-step video lesson below:
Keep Learning:
2 Comments
Verbal expressions in mathematics are standardized terms that help alleviate confusion created by the attempts to explain mathematical expressions using words. Each element and operator in a mathematical equation has its own name and there are standardized phrases that are used to describe the relationships between them. Putting it plainly, they help you turn sentences like: “The second number on the left, behind the little cross, has a small number 2 a bit to the right and above it and then there is the small letter x and then 17 and after that two, short lines on top of one another then number 4” into something people can actually understand. Using examples, we are going to list the verbal expressions you are going to need to communicate all the basic mathematical expressions you want.
Verbal expressions in algebra exams for teachers
| Exam Name | File Size | Downloads | Upload date |
|
Express algebraically |
|||
|
Without variables |
|||
| Verbal expressions algebraically – No variables – sum | 10.0 kB | 6591 | December 5, 2011 |
| Verbal expressions algebraically – No variables – difference | 460.4 kB | 3684 | September 3, 2019 |
| Verbal expressions algebraically – No variables – product | 460.1 kB | 3022 | September 3, 2019 |
| Verbal expressions algebraically – No variables – quotient | 460.5 kB | 3822 | September 3, 2019 |
| Verbal expressions algebraically – No variables – exponenting | 459.6 kB | 3059 | September 3, 2019 |
|
Into equations |
|||
| Verbal expressions algebraically – Equation – sum | 461.3 kB | 5997 | September 3, 2019 |
| Verbal expressions algebraically – Equation – difference | 461.4 kB | 3933 | September 3, 2019 |
| Verbal expressions algebraically – Equation – product | 7.9 kB | 3544 | December 5, 2011 |
| Verbal expressions algebraically – Equation – quotient | 460.7 kB | 3528 | September 3, 2019 |
| Verbal expressions algebraically – Equation – exponenting | 461.6 kB | 2940 | September 3, 2019 |
|
Into expression |
|||
| Verbal expressions algebraically – Expression – sum | 8.0 kB | 5112 | December 5, 2011 |
| Verbal expressions algebraically – Expression – difference | 460.9 kB | 3487 | September 3, 2019 |
| Verbal expressions algebraically – Expression – product | 460.7 kB | 3216 | September 3, 2019 |
| Verbal expressions algebraically – Expression – quotient | 461 kB | 6381 | September 3, 2019 |
| Verbal expressions algebraically – Expression – exponenting | 461.4 kB | 3049 | September 3, 2019 |
|
Into inequalities |
|||
| Verbal expressions algebraically – Inequality – sum | 461.6 kB | 10363 | September 3, 2019 |
| Verbal expressions algebraically – Inequality – difference | 461.8 kB | 2593 | September 3, 2019 |
| Verbal expressions algebraically – Inequality – product | 461.8 kB | 6042 | September 3, 2019 |
| Verbal expressions algebraically – Inequality – quotient | 462.6 kB | 10002 | September 3, 2019 |
| Verbal expressions algebraically – Inequality – exponenting | 462.1 kB | 2201 | September 3, 2019 |
|
Express with words |
|||
|
Without variables |
|||
| Algebraic expressions with words – No variables – sum | 7.3 kB | 2953 | December 5, 2011 |
| Algebraic expressions with words – No variables – difference | 461.5 kB | 2275 | September 3, 2019 |
| Algebraic expressions with words – No variables – product | 461.2 kB | 2107 | September 3, 2019 |
| Algebraic expressions with words – No variables – quotient | 462.3 kB | 2590 | September 3, 2019 |
| Algebraic expressions with words – No variables – exponenting | 461.7 kB | 2145 | September 3, 2019 |
|
Into equations |
|||
| Algebraic expressions with words – Equation – sum | 462.7 kB | 3084 | September 3, 2019 |
| Algebraic expressions with words – Equation – difference | 463.1 kB | 6018 | September 3, 2019 |
| Algebraic expressions with words – Equation – product | 461.8 kB | 2463 | September 3, 2019 |
| Algebraic expressions with words – Equation – quotient | 462.2 kB | 2776 | September 3, 2019 |
| Algebraic expressions with words – Equation – exponenting | 463.7 kB | 2341 | September 3, 2019 |
|
Into expressions |
|||
| Algebraic expressions with words – Expression – sum | 462.3 kB | 2518 | September 3, 2019 |
| Algebraic expressions with words – Expression – difference | 462.5 kB | 1938 | September 3, 2019 |
| Algebraic expressions with words – Expression – product | 462.2 kB | 2371 | September 3, 2019 |
| Algebraic expressions with words – Expression – quotient | 462.9 kB | 2383 | September 3, 2019 |
| Algebraic expressions with words – Expression – exponenting | 462 kB | 2081 | September 3, 2019 |
|
Into inequalities |
|||
| Algebraic expressions with words – Inequality – sum | 462.8 kB | 3154 | September 3, 2019 |
| Algebraic expressions with words – Inequality – difference | 463.3 kB | 2280 | September 3, 2019 |
| Algebraic expressions with words – Inequality – product | 463.1 kB | 2767 | September 3, 2019 |
| Algebraic expressions with words – Inequality – quotient | 463.9 kB | 4576 | September 3, 2019 |
| Algebraic expressions with words – Inequality – exponenting | 464 kB | 2045 | September 3, 2019 |
|
Evaluate expression of number |
|||
| Evaluate verbal expressions of number – sum | 459.8 kB | 3014 | September 3, 2019 |
| Evaluate verbal expressions of number – difference | 459.9 kB | 2181 | September 3, 2019 |
| Evaluate verbal expressions of number – product | 459.8 kB | 2214 | September 3, 2019 |
| Evaluate verbal expressions of number – quotient | 459.8 kB | 3064 | September 3, 2019 |
| Evaluate verbal expressions of number – exponenting | 459.7 kB | 3041 | September 3, 2019 |
Verbal expressions in algebra worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
|
Verbal expressions algebraically |
|||
| Verbal expressions algebraically – No variables | 490.2 kB | 3442 | September 3, 2019 |
| Verbal expressions algebraically – Equations | 515.9 kB | 92853 | September 3, 2019 |
| Verbal expressions algebraically – Expressions | 501.8 kB | 4439 | September 3, 2019 |
| Verbal expressions algebraically – Inequalities | 515.9 kB | 92853 | September 3, 2019 |
|
Algebraic expressions with words |
|||
| Algebraic expressions with words – No variables | 47.7 kB | 2384 | September 3, 2019 |
| Algebraic expressions with words – Equations | 87.4 kB | 5467 | September 3, 2019 |
| Algebraic expressions with words – Expressions | 74.8 kB | 3494 | September 3, 2019 |
| Algebraic expressions with words – Inequalities | 102.3 kB | 2282 | September 3, 2019 |
|
Evaluate verbal expressions of number |
|||
| Evaluate verbal expressions of number | 29 kB | 3959 | September 3, 2019 |
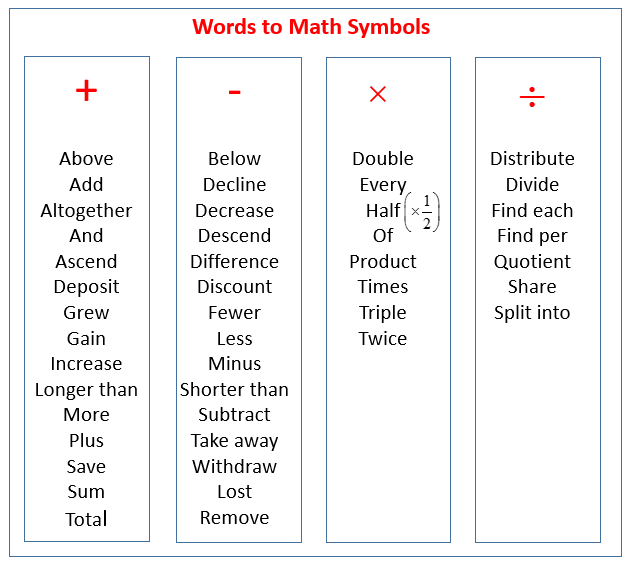
To solve any mathematical problem, it is important to understand and know the mathematical meaning of the words used in the problem. Many mathematical expressions or even general expressions have the same meaning and may indicate a relationship between quantities or a mathematical operation (such as addition, subtraction, multiplication, and division).
Equality Expressions
All of the following expressions represents that two quantities are equal (=).
- is equal to (or equals)
- is the same as
- the result is
- yields
- gives
For example, 2+5 is equal to 7.
Note: The word “is” is also used to mean “equals”. For example, 8 is 5 more than 3, or 8 equal 5 + 3.
Addition Expressions
All of the following expression shows that the number $X$ and $Y$ are added
| Expression Description | Example |
| $X+Y$ | $2+3$ |
| The sum of $X$ and $Y$ | The sum of 2 and 3 |
| The total of $X$ and $Y$ | The total of 2 and 3 |
| $X$ added to $Y$ | 2 added to 3 |
| $X$ increased by $Y$ | 2 increased by 3 |
| $X$ more than $Y$ | 2 more than 3 |
| $X$ greater than $Y$ | 2 greater than 3 |
Subtraction Expressions
All of the following expressions show that the number $Y$ is to be subtracted from the number $X$
| Expression Description | Example |
| $X-Y$ | $7-2$ |
| $X$ minus $Y$ | 7 minus 3 |
| $X$ less $Y$ | 7 less 3 |
| The difference of $X$ and $Y$ | The difference between 7 and 3 |
| from $X$ subtract $Y$ | from 7 subtract 3 |
| $X$ take away $Y$ | 7 take away 3 |
| $X$ decreased by $Y$ | 7 decreased by 3 |
| $X$ diminished by $Y$ | 7 diminished by 3 |
| $Y$ is subtracted from $X$ | 7 is subtracted from 3 |
| $Y$ less than $X$ | 3 less than 7 |
Multiplication Expressions
The following expression can be used if the numbers $X$ and $Y$ need to be multiplied.
| Expression Description | Example |
| $X times Y$ | $2times 3$ |
| $X$ multiplied by $Y$ | 2 multiplied by 3 |
| The product of $X$ and $Y$ | The product of 2 and 3 |
| $X$ times $Y$ | 2 times 3 |
For multiplication of two or more numbers symbol $times$ or $cdot$ is used. In algebra, a number before a variable is a coefficient, such as $4Y$ means 4 times $Y$, where 4 is coefficient.
Division Expressions
All of the following expression indicate the division of the numbers $X$ and $Y$ (in the order $X div Y$.
| Expression | Example |
| $X div Y$ | $10 div 2$ |
| $X$ divided by $Y$ | 10 divided by 2 |
| The quotient of $X$ and $Y$ | The quotient of 10 and 2 |
Read about Significant Figures
Muhammad Imdad Ullah
Currently working as Assistant Professor of Statistics in Ghazi University, Dera Ghazi Khan.
Completed my Ph.D. in Statistics from the Department of Statistics, Bahauddin Zakariya University, Multan, Pakistan.
l like Applied Statistics, Mathematics, and Statistical Computing.
Statistical and Mathematical software used is SAS, STATA, GRETL, EVIEWS, R, SPSS, VBA in MS-Excel.
Like to use type-setting LaTeX for composing Articles, thesis, etc.
Related Pages
Writing Expressions (Lesson 16)
Writing Expressions (Lesson 17)
Algebraic Expressions
The following table gives some common words or phrases that are usually imply one of the four operations:
add, subtract, multiply, divide. However, depending on the word problem, there are exceptions.
Scroll down the page for more examples and explanations.
Phrase To Algebraic Expression
To write an expression, we often have to interpret a written phrase.
For example, the phrase “6 added to some number” can be written as the expression
x + 6, where the variable x represents the unknown number.
Some examples of common phrases and corresponding expressions that involve
addition are:
| Phrase | Expression |
| 4 more than some number | x + 4 |
| a number increased by 10 | y + 10 |
| 8 plus some number | t + 8 |
| the sum of a number and 12 | w + 12 |
Some examples of common phrases and corresponding expressions that involve
subtraction are:
| Phrase | Expression |
| 4 less than some number | x – 4 |
| a number decreased by 10 | y – 10 |
| 8 minus some number | 8 – t |
| the difference between a number and 12 | w – 12 |
Some examples of common phrases and corresponding expressions that involve
multiplication are:
| Phrase | Expression |
| 4 times some number | 4x |
| twice a number | 2y |
| one-third of some number | |
| the product of a number and 12 | 12w |
Some examples of common phrases and corresponding expressions that involve
division are:
Some examples of common phrases and corresponding expressions that involve
two operations are:
| Phrase | Expression |
| 6 more than 5 times a number | 5x + 6 |
| 4 times the sum of a number and 7 | 4(y + 7) |
| 5 less than the product of 3 and a number | 3w – 5 |
| twice the difference between a number and 9 | 2(z – 9) |
How Do You Write Mathematical Expressions From Word Problems?
There are so many words that you come across when you’re working on algebra problems,
and these words are really code for very specific mathematical symbols.
- Show Video Lesson
How To Write Algebraic Expressions For Word Phrases, By Analyzing The Language Used?
An algebraic expression is a mathematical phrase that contains a combination of numbers,
variables and operational symbols.
A variable is a letter that can represent one or more numbers.
How to write expressions with variables?
Examples:
Write the algebraic expressions to represent the statements.
a) The sum of -7 and the quantity 8 times x
b) Take the quantity -3 times x and then add 1.
c) -6 plus the product of -1 and x.
- Show Video Lesson
How to write algebraic expressions with parentheses?
Examples:
-
First consider the expression for
-5 plus the quantity of 4 times x
Now take the product of -8 and that expression and then add 6. -
First consider the expression for
the sum of 7 and the product of -2 and x
What expression would be:
4 plus the quantity of 2 times that expression.
- Show Video Lesson
How to Write Equations from Word Problems?
This video teaches how to dissect a word problem in order to define a variable and write an equation.
Examples:
-
Half of a number is 16. Write an equation to represent the situation. Define your variable and solve.
-
Mrs. Gaddie has two dogs. Her friend Anna-Marie has three less than twice as many as Mtr. Gaddie.
How many dogs does Anna-Marie have? -
A recycling plant recycles 2 tons of cans yesterday. This is a third of their usual amount.
How much does the plant usually recycle?
-
Show Video Lesson
How to Write Algebraic Expressions for Situations?
Example:
Translate the following phrases into algebraic or numeric expressions.
a) 173 less than a number ‘b’
b) Quotient of 173 and ‘b’
c) ‘b’ times 173
d) 173 more than ‘b’
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.