In this question type you have to work out a code. The code uses numbers as letters. You might have to change a code word into English or English word into code.
Look at this first example and then we can work our way through the question until we get the answer: —
(For ease of learning we have marked the important parts of this explanation in RED.)
Here are four words and below the four words are three of the words written in a secret code. The codes are in a different order from the words.
PACE CAPE PART TAPE
1234 3214 3267
Q1 What does the code 1234 stand for? (________________)
The question may refer to one of the words already given in the question or it might refer to another word that is made from some of the letters in the words.
We can start by writing the codes above each other in numerical order like this:-
1 2 3 4
3 2 1 4
3 2 6 7
1 2 3 4
A
3 2 1 4
A
3 2 6 7
A
It then becomes easier to see patterns in the code. Already it becomes clear that the number 2 in the code is actually the letter A in the real words. This is because 2 is used as the second number in the codes three times and all four words have the letter A as their second letter, so 2 must be code for the letter A.
We can write the letter A below the number 2.
We can also see that the number 3 is used twice at the start of two of the codes. We can then ask ourselves if there are at least two words that start with the same letter?
We can see that PACE and PART start with the same letter – P.
We can write the letter P below the number 3.
1 2 3 4
A P
3 2 1 4
P A
3 2 6 7
P A
We can also see that the number 4 is used twice at the end of the codes. We can then ask ourselves if there are at least two words that end with the same letter?
We can see that PACE and CAPE and TAPE all end with the same letter – E.
We can write the letter E below the number 4.
1 2 3 4
A P E
3 2 1 4
P A E
3 2 6 7
P A
We are now very close to breaking the code!! We now have three letters of one of the words and the code that goes with it. This word must be PACE and it also gives us another letter and its code because we now know that the code 1 is actually the letter C.
3 2 1 4
P A C E
We can now complete more of our table.
1 2 3 4
C A P E
3 2 1 4
P A C E
3 2 6 7
P A
We now know that 1234 is actually the word CAPE and this is our answer.
Q1 What does the code 1234 stand for? ( CAPE )
We also know that 3267 must be PART because this is the only other word that starts with P.
1 2 3 4
C A P E
3 2 1 4
P A C E
3 2 6 7
P A R T
Once we have broken the code we can answer other questions such as :-
Q2 What is PEAR in code? (________________)
THINGS TO LOOK OUT FOR!!!!
Make sure that you work systemically and neatly writing the correct letter below the correct number.
It might take time to break the code but once broken it will allow you to answer lots of questions based on the code.
Once you start to break the code it usually falls into place quite quickly.
You can also work out the code by placing the letters “on top” in your table and placing the numbers underneath — use whatever method you are most comfortable with.
If you follow a system similar to this you should be able to break the code.
Avoid guessing the answer – though if you are completely stuck a guess is better than a blank answer space.
NB When you are completing a Verbal Reasoning test in Multiple-Choice format the correct answer will always be one of the choices that you are given on your answer sheet. If your answer does not match one of the answers that you are given then your answer is wrong.
Change the Format of a Number Field in a Microsoft Word Mail Merge Document Using Switches
by Avantix Learning Team | Updated January 16, 2021
Applies to: Microsoft® Word® 2010, 2013, 2016, 2019 and 365 (Windows)
You can change or fix the format of a number field in a Word mail merge document using switches in field codes. Number formatting issues typically occur when the source document for the mail merge is an Excel workbook or Access database. You can use switches to change the format of a number field to display currency symbols as well as commas or decimals.
A number field is typically inserted in the main document using Insert Merge Field on the Mailings tab in the Ribbon.
Related article: How to Use Mail Merge in Microsoft Word to Generate Form Letters
Do you want to learn more about Microsoft Word? Check out our virtual classroom or live classroom Word courses >
Using codes in a number field switch
The common codes used in a number switch are 0 for a required digit and # for a variable number. Codes entered in switches can contain multiple parts separated by semi-colons:
# = variable number
0 (zero) = required digit
The # code will be replaced by a digit only if it is not a leading or trailing zero. You can also enter commas (,), decimals (.) and currency signs ($). Since # specifies the minimum numeric places to display, if a place has no digit, it is replaced with a space.
Number switches start with # and the codes that follow represent the format for the number. The merge codes may appear in quotes or double quotes.
The syntax of the full mail merge number field code with the switch is:
{MERGEFIELD FieldName # number codes} or
{MERGEFIELD FieldName # «number codes»}
If you want to include negative formatting, add a semi-colon after the first part. This follows the same logic as Excel custom number formatting. The first part formats positive numbers, the second part (after the semi-colon) formats negative numbers. If you add another semi-colon, this creates a third part that formats zero (0) values.
Quotation marks are not required for simple number formats that do not include spaces such as {Salary # $#,##0.00}. For more complex number formats and those that include text or spaces, enclose the number format codes in quotation marks.
Changing the format of Word mail merge number field using a switch
To use a switch to change the format of a mail merge number field in Word, you will first need to display the field code and then type the switch starting with #:
- In the main Word mail merge document, select the number field.
- Right-click the field and choose Toggle Field Codes from the drop-down menu to display the field code. You can also press Shift + F9 to display the field code.
- If necessary, delete *MERGEFORMAT from the field code.
- Enter the switch after the field name (such as # $#,##0). Be sure to type a space after #.
- Right-click the field and choose Toggle Field Codes from the drop-down menu to hide the field code. You can also press Shift + F9 to hide the field code.
- Right-click in the field and select Update Field from the drop-down menu. You can also press F9 to update the field.
- Run the merge by selecting Edit Individual documents from the Mailings tab in the Ribbon and then click OK in the dialog box. In the merged document, the number should appear in the switch format.
Number field formatting examples
The following are examples of mail merge number fields formatted using switches. Number switches apply rounding by default.
To change the number field formatting to a format to display a dollar sign and insert a comma as a thousands separator, we used the following switch:
{MERGEFIELD Salary # $#,##0}
To change the number field formatting to display a comma as a thousands separator and two decimal places, we used the following switch:
{MERGEFIELD SalesAmount # #,##0.00}
To change the number field formatting to display a number under one thousand with two decimal places and a number of one thousand or more with a comma as a thousands separator, we used the following switch (the benefit of this switch is that Word will not include a space for missing digits):
{MERGEFIELD AmountOwing # ,#.00}
The following switch could be used with negative numbers (if the original value was 1500.57 or -1500.57, this would display $1,500.57 for a positive number and ($1,500.57) for a negative number):
{MERGEFIELD AmountOwing # «$,#.00;($,#.00)»}
The following switch is similar to the switch above but formats zeros as a dash (the dash is considered to be text so must be enclosed in single quotes):
{MERGEFIELD AmountOwing # «$,#.00;($,#.00);’-‘»}
Zero values can be suppressed by adding a final semicolon (;) in the switch but nothing after it. This suppresses zeros from empty fields and from fields containing zeros.
In the examples above, commas would be inserted only if the number was one thousand or more. The name of the number merge field in the above examples comes from the Excel source file. The curly brackets cannot be typed.
Subscribe to get more articles like this one
Did you find this article helpful? If you would like to receive new articles, join our email list.
More resources
How to Create a Table of Contents in Word
How to Insert a Watermark in Word (like DRAFT)
How to Remove Hard Returns in Word Documents
How to Find and Replace in Word (and use Wildcards)
How to Superscipt or Subscript in Word (with Shortcuts)
Related courses
Microsoft Word: Intermediate / Advanced
Microsoft Word: Designing Dynamic Word Documents Using Fields
Microsoft Word: Long Documents Master Class
Microsoft Word: Accessible Word Documents
Microsoft Excel: Intermediate / Advanced
Microsoft PowerPoint: Intermediate / Advanced
VIEW MORE COURSES >
Our instructor-led courses are delivered in virtual classroom format or at our downtown Toronto location at 18 King Street East, Suite 1400, Toronto, Ontario, Canada (some in-person classroom courses may also be delivered at an alternate downtown Toronto location). Contact us at info@avantixlearning.ca if you’d like to arrange custom instructor-led virtual classroom or onsite training on a date that’s convenient for you.
Copyright 2023 Avantix® Learning
Microsoft, the Microsoft logo, Microsoft Office and related Microsoft applications and logos are registered trademarks of Microsoft Corporation in Canada, US and other countries. All other trademarks are the property of the registered owners.
Avantix Learning |18 King Street East, Suite 1400, Toronto, Ontario, Canada M5C 1C4 | Contact us at info@avantixlearning.ca
The ABZZ word code system is a method that can be used to convert any given number to word code equivalents. With this method, any given number from zero to zillion can be converted to word codes. The principles of this method are explained in this book. This book also contains a thesaurus that gives two examples of easily derivable and meaningful word code equivalents of every number from 0 to 9,999. It is a forerunner to a proposed online thesaurus that would list word code alternatives of every number from zero to one billion (0-1,000,000,000). For centuries, people have been attracted to the idea of converting numbers to words. One of the major advantages of this is that people would be able to find meaningful word names for phone numbers, passwords, pin numbers, log-in numbers, access codes, etc. Other advantages include the ability to generate prospective number codes based on any words of your choice. Numerous other advantages and uses are elaborated in this book. Word code systems for numbers devised over the centuries have been cumbersome and difficult to use. This has limited their use in everyday life. The ABZZ word code system introduces a new, simpler, and user-friendly system of converting any given numbers to words and vice versa. The principles of the system can be mastered in a few minutes. Regular usage would engrain it as one of our basic thinking processes. The ABZZ is an idea whose time has come.
This article was formerly combined with another which explained how to solve codes involving letters for symbols. To read how to do that, you can look at another new article,VR — Codes Using Letters for Symbols.
Letters for Numbers are another type of code question. Similar to Letters For Letters, they are codes in which numbers are used this time, to represent other letters.
Letters for Numbers are a logic-based question rather than one which needs knowledge of words or of maths. They are similar to a Sudoku puzzle in the sense that you get presented with numbers and yet it needs no mathematics whatsoever.
How Are Letters for Numbers Codes Used In The Exam?
Candidates are shown three four-letter words. They are also shown three sets of four numbers which represent the words in code. They are not told which code represents which word – they have to work that out for themselves. They are then asked to find the code for a fourth word.
This may sound really tricky but, once you know the techniques to solve them, they’re not so hard after all.
Now let’s look at some examples:
Example Question One
These three words are given in code. The order is mixed up.
DEAL CLAD LIED
5431 4621 1234
Find the code for the word DELL.
If you are presented with a multiple-choice answer list then you will be able to find the solution in a different (some might say easier) way. Let’s start with the slightly harder ‘no choices’ situation.
In order to sort out which code goes with which word, see what they have in common. The first two code numbers end in ‘1’ so these must relate to ‘CLAD’ and ‘LIED’ as both of these words end in the same letter. This means ‘1’ represents ‘D’.
If ‘1’ is ‘D’, it means ‘1234’ must be the code for ‘DEAL’. Now we know ‘E’ is represented by ‘2’, ‘A’ by ‘3’ and ‘L’ by ‘4’. This is all we need to work out the code for ‘DELL’ — it must be ‘1244’.
Now let’s look at a slightly quicker method should there be a set of multiple-choice answers provided.
Example Question Two
These three words are given in code. The order is mixed up.
DEAL CLAD LIED
5431 4621 1234
Find the code for the word DELL.
Choose the correct answer:
5422
1234
1244
4621
4612.
We immediately know it must end in two of the same number as ‘DELL’ ends in a double letter. The only possibilities are therefore ‘1244’ and ‘5422’.
We might then use the previous method to be certain or use a different approach — perhaps we could see that ‘L’ must be either ‘2’ or ‘4’. Look at the original codes. Given that ‘DEAL’ ends in ‘L’ we would need there to be a ‘2’ at the end of a code but there isn’t, so it’s not possible that ‘L’ is ‘2’. The only possible answer is ‘1244’.
Sample Tests
So, now that you have learnt how to crack Letter For Number codes in Verbal Reasoning. Hopefully you and our child have the hang of them now, but let’s find out!
The Education Quizzes website has four quizzes on Letter For Number codes. You may find that your child has a natural knack for them, especially if they like the puzzles found in puzzle magazines. If not, teach them the techniques we’ve learned in this lesson and they should soon find them easy to crack.
You’ll find the quizzes in our Eleven Plus Verbal Reasoning section or, alternatively, you can follow these links:
Word-Number Codes 1
Word-Number Codes 2
Word-Number Codes 3
Word-Number Codes 4
As always, practise makes perfect, so be sure to try all forty questions. Good luck!
Set is a collection of different elements. It could be numbers, alphabets, etc. Various symbols are used to denote them (like ℝ denote set of Real Numbers) and their relationship and operation (subset, union, etc).
These set symbols helps to represent mathematical ideas in a concise way and saves space and time. In this blog we have listed all the commonly used Set symbols together and how to get them in Ms Word along with their keyboard shortcuts
List of set symbols along with their meaning and how to get them in Ms Word
Three methods to get symbols in Ms Word
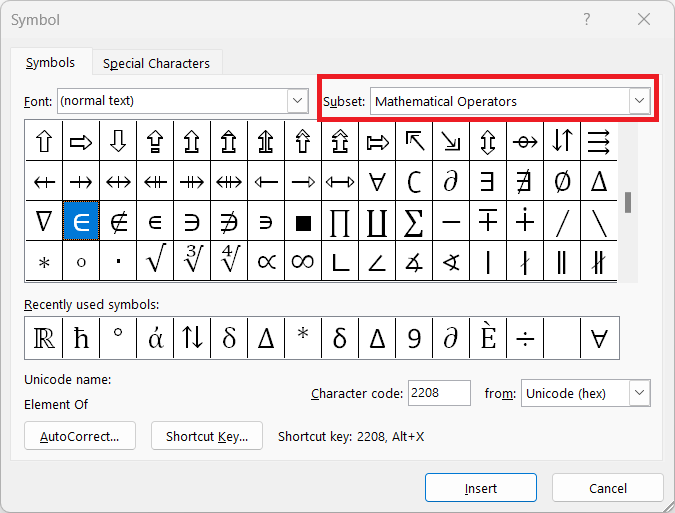
Insert Symbol Method: Go to Insert > Symbols and select More Symbols. In the symbol window, click the desired symbol and hit insert. Following table gives the subset dropdown option of each symbol that can help you find a symbol.
Math AutoCorrect: This is the smartest way to get any symbol in Ms Word. Simply type the Math AutoCorrect text and hit space to get symbol. It works inside Equation editor. However, you can make it work outside equation editor, with following one time setting.
- Go to File > Options to open Word Options
- In Proofing and select AutoCorrect Options
- In Math Autocorrect tab, check box against “Use Math AutoCorrect rules outside of math regions”
Alt X Method: Type the Alt X code of symbol and press Alt + X immediately after it to get symbol.
Let’s say, P = {1, 2, 3, 4} and Q = {1, 3, 5}
| Symbol | Name & Meaning | Example | Subset of Symbol | Math Autocorrect Shortcut (press space after shortcut to get symbol) | Alt X Code (type this code and press Alt+X) |
|---|---|---|---|---|---|
| ℕ | Natural number: All positive integers from 1 till infinity | ℕ = {1, 2, 3, …} | letterlike symbols | doubleN | 2115 |
| ℤ | Integers: A whole number (not fractional ) that are +ve, -ve or 0 | ℤ = {…, -2, -1,0 ,1 ,2 ,…} | letterlike symbols | doubleZ | 2124 |
| ℚ | Rational Numbers: a number that is of the form p/q where p and q are integers and q is not equal to 0 | 5, 10.45, 3/7 | letterlike symbols | doubleQ | 211A |
| 𝔸 | Algebraic numbers: Number that is the solution to a polynomial with rational coefficients | 1, 3/7, √2 | Extended characters – Plane 1 | doubleA | 1D538 |
| ℝ | Real numbers: A number that includes rational and irrational numbers | 2, π, 2/7 | letterlike symbols | doubleR | 211D |
| 𝕀 | Imaginary numbers: a real number multiplied by an imaginary unit which is defined by its property i2 = −1 | 5i, πi | Extended characters – Plane 1 | doubleI | 1D540 |
| ℂ | Complex number: a number of the form a + bi, where a and b are real numbers | 2+3i, 1.5-1i | letterlike symbols | doubleC | 2102 |
| { } | Set: collection of elements | Q = {1, 3, 5} | – | – | – |
| A ∪ B | Union: in A or B (or both) | P ∪ Q = {1, 2, 3, 4, 5} | Mathematical operators | bigcup | 222A |
| A ∩ B | Intersection: in both A | P ∩ Q = {1, 3} | Mathematical operators | bigcap | 2229 |
| A ⊆ B | Subset: every element of A is in B | {1, 3, 5} ⊆ Q or {2, 4} ⊆ P | Mathematical operators | subseteq | 2286 |
| A ⊂ B | Proper Subset: every element of A is in B, but B has more elements. |
Correct: {1, 3} ⊂ Q Incorrect: {1, 3, 5} ⊂ Q |
Mathematical operators | subset | 2282 |
| A ⊄ B | Not a Subset: A is not a subset of B | {5, 6} ⊄ Q | Mathematical Operators | 2284 | |
| A ⊇ B | Superset: A has same elements as B, or more | {1, 3, 5, 7} ⊇ {1, 3, 7} or {1, 3, 5, 7} ⊇ {1, 3, 5, 7} | Mathematical operators | superseteq | 2287 |
| A ⊃ B | Proper Superset: A has B’s elements and more | Correct: {1, 3, 5, 7} ⊃ {3, 5, 7} Incorrect: {1, 3, 5, 7} ⊃ {1, 3, 5, 7} | Mathematical operators | superset | 2283 |
| A ⊅ B | Not a Superset: A is not a superset of B | {1, 3, 5, 7} ⊅ {1, 9} | 2285 | ||
| Ac | Complement: Elements not in A | Qc = {1, 2, 6, 7} | – | – | – |
| A − B | Difference: In A but not in B | Let X = {1, 2, 3, 4} and Y = {2, 4}, then X – Y = {1, 3} | – | – | – |
| a ∈ A | Element: a is an element of A | 3 ∈ {1, 2, 3, 4} | Mathematical operator | in | 2208 |
| b ∉ C | Not an element: b is not an element of C | 2 ∉ {1, 3, 5} | Mathematical operator | notelement | 2209 |
| Ø | Empty set: { } | {1, 3} ∩ {2, 4} = Ø | Mathematical operator | emptyset | 2205 |
| 𝕌 | Universal set: the set of all elements or members of all related sets | Extended Characters – Plane 1 | doubleU | 1D54C | |
| P(A) | Power set: all subset of A | P({a, b}) = { {}, {a}, {b}, {a, b} } | – | – | – |
| A = B | Equality: both sets have the same members | {2, 5, 8} = {8, 2, 5} | – | – | – |
| A×B | Cartesian Product: (set of ordered pairs from A and B) |
{1, 2} × {a, b} = {(1, a), (1, b), (2, a), (2, b)} |
Latin-1 Supplement | times | 00D7 |
| |A| | Cardinality: number of elements of set A | |{5, 6}| = 2 | – | – | |
| | | Such that | { n | n > 0 } = {1, 2, 3,…} | – | – | – |
| : | Such that | { n : n > 0 } = {1, 2, 3,…} | – | – | – |
| ∀ | For all | ∀ x >1, x2 > x (for all x greater than 1, x square is greater than x) |
Mathematical operators | forall | 2200 |
| ∃ | There exists | ∃ x | x2 < x (there exists x such that x squared is less than x) |
Mathematical operators | exists | 2203 |
| ∄ | There does not exist | ∄ x | x +1 < x | Mathematical operator | 2204 | |
| ∴ | Therefore | a=b ∴ b=a | Mathematical operators | therefore | 2234 |