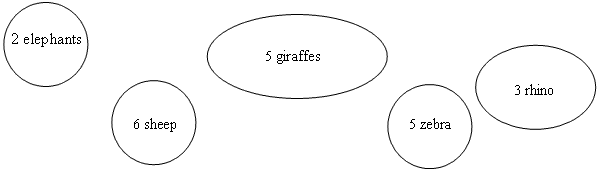From Wikipedia, the free encyclopedia
In computing, a word is the natural unit of data used by a particular processor design. A word is a fixed-sized datum handled as a unit by the instruction set or the hardware of the processor. The number of bits or digits[a] in a word (the word size, word width, or word length) is an important characteristic of any specific processor design or computer architecture.
The size of a word is reflected in many aspects of a computer’s structure and operation; the majority of the registers in a processor are usually word-sized and the largest datum that can be transferred to and from the working memory in a single operation is a word in many (not all) architectures. The largest possible address size, used to designate a location in memory, is typically a hardware word (here, «hardware word» means the full-sized natural word of the processor, as opposed to any other definition used).
Documentation for older computers with fixed word size commonly states memory sizes in words rather than bytes or characters. The documentation sometimes uses metric prefixes correctly, sometimes with rounding, e.g., 65 kilowords (KW) meaning for 65536 words, and sometimes uses them incorrectly, with kilowords (KW) meaning 1024 words (210) and megawords (MW) meaning 1,048,576 words (220). With standardization on 8-bit bytes and byte addressability, stating memory sizes in bytes, kilobytes, and megabytes with powers of 1024 rather than 1000 has become the norm, although there is some use of the IEC binary prefixes.
Several of the earliest computers (and a few modern as well) use binary-coded decimal rather than plain binary, typically having a word size of 10 or 12 decimal digits, and some early decimal computers have no fixed word length at all. Early binary systems tended to use word lengths that were some multiple of 6-bits, with the 36-bit word being especially common on mainframe computers. The introduction of ASCII led to the move to systems with word lengths that were a multiple of 8-bits, with 16-bit machines being popular in the 1970s before the move to modern processors with 32 or 64 bits.[1] Special-purpose designs like digital signal processors, may have any word length from 4 to 80 bits.[1]
The size of a word can sometimes differ from the expected due to backward compatibility with earlier computers. If multiple compatible variations or a family of processors share a common architecture and instruction set but differ in their word sizes, their documentation and software may become notationally complex to accommodate the difference (see Size families below).
Uses of words[edit]
Depending on how a computer is organized, word-size units may be used for:
- Fixed-point numbers
- Holders for fixed point, usually integer, numerical values may be available in one or in several different sizes, but one of the sizes available will almost always be the word. The other sizes, if any, are likely to be multiples or fractions of the word size. The smaller sizes are normally used only for efficient use of memory; when loaded into the processor, their values usually go into a larger, word sized holder.
- Floating-point numbers
- Holders for floating-point numerical values are typically either a word or a multiple of a word.
- Addresses
- Holders for memory addresses must be of a size capable of expressing the needed range of values but not be excessively large, so often the size used is the word though it can also be a multiple or fraction of the word size.
- Registers
- Processor registers are designed with a size appropriate for the type of data they hold, e.g. integers, floating-point numbers, or addresses. Many computer architectures use general-purpose registers that are capable of storing data in multiple representations.
- Memory–processor transfer
- When the processor reads from the memory subsystem into a register or writes a register’s value to memory, the amount of data transferred is often a word. Historically, this amount of bits which could be transferred in one cycle was also called a catena in some environments (such as the Bull GAMMA 60 [fr]).[2][3] In simple memory subsystems, the word is transferred over the memory data bus, which typically has a width of a word or half-word. In memory subsystems that use caches, the word-sized transfer is the one between the processor and the first level of cache; at lower levels of the memory hierarchy larger transfers (which are a multiple of the word size) are normally used.
- Unit of address resolution
- In a given architecture, successive address values designate successive units of memory; this unit is the unit of address resolution. In most computers, the unit is either a character (e.g. a byte) or a word. (A few computers have used bit resolution.) If the unit is a word, then a larger amount of memory can be accessed using an address of a given size at the cost of added complexity to access individual characters. On the other hand, if the unit is a byte, then individual characters can be addressed (i.e. selected during the memory operation).
- Instructions
- Machine instructions are normally the size of the architecture’s word, such as in RISC architectures, or a multiple of the «char» size that is a fraction of it. This is a natural choice since instructions and data usually share the same memory subsystem. In Harvard architectures the word sizes of instructions and data need not be related, as instructions and data are stored in different memories; for example, the processor in the 1ESS electronic telephone switch has 37-bit instructions and 23-bit data words.
Word size choice[edit]
When a computer architecture is designed, the choice of a word size is of substantial importance. There are design considerations which encourage particular bit-group sizes for particular uses (e.g. for addresses), and these considerations point to different sizes for different uses. However, considerations of economy in design strongly push for one size, or a very few sizes related by multiples or fractions (submultiples) to a primary size. That preferred size becomes the word size of the architecture.
Character size was in the past (pre-variable-sized character encoding) one of the influences on unit of address resolution and the choice of word size. Before the mid-1960s, characters were most often stored in six bits; this allowed no more than 64 characters, so the alphabet was limited to upper case. Since it is efficient in time and space to have the word size be a multiple of the character size, word sizes in this period were usually multiples of 6 bits (in binary machines). A common choice then was the 36-bit word, which is also a good size for the numeric properties of a floating point format.
After the introduction of the IBM System/360 design, which uses eight-bit characters and supports lower-case letters, the standard size of a character (or more accurately, a byte) becomes eight bits. Word sizes thereafter are naturally multiples of eight bits, with 16, 32, and 64 bits being commonly used.
Variable-word architectures[edit]
Early machine designs included some that used what is often termed a variable word length. In this type of organization, an operand has no fixed length. Depending on the machine and the instruction, the length might be denoted by a count field, by a delimiting character, or by an additional bit called, e.g., flag, or word mark. Such machines often use binary-coded decimal in 4-bit digits, or in 6-bit characters, for numbers. This class of machines includes the IBM 702, IBM 705, IBM 7080, IBM 7010, UNIVAC 1050, IBM 1401, IBM 1620, and RCA 301.
Most of these machines work on one unit of memory at a time and since each instruction or datum is several units long, each instruction takes several cycles just to access memory. These machines are often quite slow because of this. For example, instruction fetches on an IBM 1620 Model I take 8 cycles (160 μs) just to read the 12 digits of the instruction (the Model II reduced this to 6 cycles, or 4 cycles if the instruction did not need both address fields). Instruction execution takes a variable number of cycles, depending on the size of the operands.
Word, bit and byte addressing[edit]
The memory model of an architecture is strongly influenced by the word size. In particular, the resolution of a memory address, that is, the smallest unit that can be designated by an address, has often been chosen to be the word. In this approach, the word-addressable machine approach, address values which differ by one designate adjacent memory words. This is natural in machines which deal almost always in word (or multiple-word) units, and has the advantage of allowing instructions to use minimally sized fields to contain addresses, which can permit a smaller instruction size or a larger variety of instructions.
When byte processing is to be a significant part of the workload, it is usually more advantageous to use the byte, rather than the word, as the unit of address resolution. Address values which differ by one designate adjacent bytes in memory. This allows an arbitrary character within a character string to be addressed straightforwardly. A word can still be addressed, but the address to be used requires a few more bits than the word-resolution alternative. The word size needs to be an integer multiple of the character size in this organization. This addressing approach was used in the IBM 360, and has been the most common approach in machines designed since then.
When the workload involves processing fields of different sizes, it can be advantageous to address to the bit. Machines with bit addressing may have some instructions that use a programmer-defined byte size and other instructions that operate on fixed data sizes. As an example, on the IBM 7030[4] («Stretch»), a floating point instruction can only address words while an integer arithmetic instruction can specify a field length of 1-64 bits, a byte size of 1-8 bits and an accumulator offset of 0-127 bits.
In a byte-addressable machine with storage-to-storage (SS) instructions, there are typically move instructions to copy one or multiple bytes from one arbitrary location to another. In a byte-oriented (byte-addressable) machine without SS instructions, moving a single byte from one arbitrary location to another is typically:
- LOAD the source byte
- STORE the result back in the target byte
Individual bytes can be accessed on a word-oriented machine in one of two ways. Bytes can be manipulated by a combination of shift and mask operations in registers. Moving a single byte from one arbitrary location to another may require the equivalent of the following:
- LOAD the word containing the source byte
- SHIFT the source word to align the desired byte to the correct position in the target word
- AND the source word with a mask to zero out all but the desired bits
- LOAD the word containing the target byte
- AND the target word with a mask to zero out the target byte
- OR the registers containing the source and target words to insert the source byte
- STORE the result back in the target location
Alternatively many word-oriented machines implement byte operations with instructions using special byte pointers in registers or memory. For example, the PDP-10 byte pointer contained the size of the byte in bits (allowing different-sized bytes to be accessed), the bit position of the byte within the word, and the word address of the data. Instructions could automatically adjust the pointer to the next byte on, for example, load and deposit (store) operations.
Powers of two[edit]
Different amounts of memory are used to store data values with different degrees of precision. The commonly used sizes are usually a power of two multiple of the unit of address resolution (byte or word). Converting the index of an item in an array into the memory address offset of the item then requires only a shift operation rather than a multiplication. In some cases this relationship can also avoid the use of division operations. As a result, most modern computer designs have word sizes (and other operand sizes) that are a power of two times the size of a byte.
Size families[edit]
As computer designs have grown more complex, the central importance of a single word size to an architecture has decreased. Although more capable hardware can use a wider variety of sizes of data, market forces exert pressure to maintain backward compatibility while extending processor capability. As a result, what might have been the central word size in a fresh design has to coexist as an alternative size to the original word size in a backward compatible design. The original word size remains available in future designs, forming the basis of a size family.
In the mid-1970s, DEC designed the VAX to be a 32-bit successor of the 16-bit PDP-11. They used word for a 16-bit quantity, while longword referred to a 32-bit quantity; this terminology is the same as the terminology used for the PDP-11. This was in contrast to earlier machines, where the natural unit of addressing memory would be called a word, while a quantity that is one half a word would be called a halfword. In fitting with this scheme, a VAX quadword is 64 bits. They continued this 16-bit word/32-bit longword/64-bit quadword terminology with the 64-bit Alpha.
Another example is the x86 family, of which processors of three different word lengths (16-bit, later 32- and 64-bit) have been released, while word continues to designate a 16-bit quantity. As software is routinely ported from one word-length to the next, some APIs and documentation define or refer to an older (and thus shorter) word-length than the full word length on the CPU that software may be compiled for. Also, similar to how bytes are used for small numbers in many programs, a shorter word (16 or 32 bits) may be used in contexts where the range of a wider word is not needed (especially where this can save considerable stack space or cache memory space). For example, Microsoft’s Windows API maintains the programming language definition of WORD as 16 bits, despite the fact that the API may be used on a 32- or 64-bit x86 processor, where the standard word size would be 32 or 64 bits, respectively. Data structures containing such different sized words refer to them as:
- WORD (16 bits/2 bytes)
- DWORD (32 bits/4 bytes)
- QWORD (64 bits/8 bytes)
A similar phenomenon has developed in Intel’s x86 assembly language – because of the support for various sizes (and backward compatibility) in the instruction set, some instruction mnemonics carry «d» or «q» identifiers denoting «double-«, «quad-» or «double-quad-«, which are in terms of the architecture’s original 16-bit word size.
An example with a different word size is the IBM System/360 family. In the System/360 architecture, System/370 architecture and System/390 architecture, there are 8-bit bytes, 16-bit halfwords, 32-bit words and 64-bit doublewords. The z/Architecture, which is the 64-bit member of that architecture family, continues to refer to 16-bit halfwords, 32-bit words, and 64-bit doublewords, and additionally features 128-bit quadwords.
In general, new processors must use the same data word lengths and virtual address widths as an older processor to have binary compatibility with that older processor.
Often carefully written source code – written with source-code compatibility and software portability in mind – can be recompiled to run on a variety of processors, even ones with different data word lengths or different address widths or both.
Table of word sizes[edit]
| key: bit: bits, c: characters, d: decimal digits, w: word size of architecture, n: variable size, wm: Word mark | |||||||
|---|---|---|---|---|---|---|---|
| Year | Computer architecture |
Word size w | Integer sizes |
Floatingpoint sizes |
Instruction sizes |
Unit of address resolution |
Char size |
| 1837 | Babbage Analytical engine |
50 d | w | — | Five different cards were used for different functions, exact size of cards not known. | w | — |
| 1941 | Zuse Z3 | 22 bit | — | w | 8 bit | w | — |
| 1942 | ABC | 50 bit | w | — | — | — | — |
| 1944 | Harvard Mark I | 23 d | w | — | 24 bit | — | — |
| 1946 (1948) {1953} |
ENIAC (w/Panel #16[5]) {w/Panel #26[6]} |
10 d | w, 2w (w) {w} |
— | — (2 d, 4 d, 6 d, 8 d) {2 d, 4 d, 6 d, 8 d} |
— — {w} |
— |
| 1948 | Manchester Baby | 32 bit | w | — | w | w | — |
| 1951 | UNIVAC I | 12 d | w | — | 1⁄2w | w | 1 d |
| 1952 | IAS machine | 40 bit | w | — | 1⁄2w | w | 5 bit |
| 1952 | Fast Universal Digital Computer M-2 | 34 bit | w? | w | 34 bit = 4-bit opcode plus 3×10 bit address | 10 bit | — |
| 1952 | IBM 701 | 36 bit | 1⁄2w, w | — | 1⁄2w | 1⁄2w, w | 6 bit |
| 1952 | UNIVAC 60 | n d | 1 d, … 10 d | — | — | — | 2 d, 3 d |
| 1952 | ARRA I | 30 bit | w | — | w | w | 5 bit |
| 1953 | IBM 702 | n c | 0 c, … 511 c | — | 5 c | c | 6 bit |
| 1953 | UNIVAC 120 | n d | 1 d, … 10 d | — | — | — | 2 d, 3 d |
| 1953 | ARRA II | 30 bit | w | 2w | 1⁄2w | w | 5 bit |
| 1954 (1955) |
IBM 650 (w/IBM 653) |
10 d | w | — (w) |
w | w | 2 d |
| 1954 | IBM 704 | 36 bit | w | w | w | w | 6 bit |
| 1954 | IBM 705 | n c | 0 c, … 255 c | — | 5 c | c | 6 bit |
| 1954 | IBM NORC | 16 d | w | w, 2w | w | w | — |
| 1956 | IBM 305 | n d | 1 d, … 100 d | — | 10 d | d | 1 d |
| 1956 | ARMAC | 34 bit | w | w | 1⁄2w | w | 5 bit, 6 bit |
| 1956 | LGP-30 | 31 bit | w | — | 16 bit | w | 6 bit |
| 1957 | Autonetics Recomp I | 40 bit | w, 79 bit, 8 d, 15 d | — | 1⁄2w | 1⁄2w, w | 5 bit |
| 1958 | UNIVAC II | 12 d | w | — | 1⁄2w | w | 1 d |
| 1958 | SAGE | 32 bit | 1⁄2w | — | w | w | 6 bit |
| 1958 | Autonetics Recomp II | 40 bit | w, 79 bit, 8 d, 15 d | 2w | 1⁄2w | 1⁄2w, w | 5 bit |
| 1958 | Setun | 6 trit (~9.5 bits)[b] | up to 6 tryte | up to 3 trytes | 4 trit? | ||
| 1958 | Electrologica X1 | 27 bit | w | 2w | w | w | 5 bit, 6 bit |
| 1959 | IBM 1401 | n c | 1 c, … | — | 1 c, 2 c, 4 c, 5 c, 7 c, 8 c | c | 6 bit + wm |
| 1959 (TBD) |
IBM 1620 | n d | 2 d, … | — (4 d, … 102 d) |
12 d | d | 2 d |
| 1960 | LARC | 12 d | w, 2w | w, 2w | w | w | 2 d |
| 1960 | CDC 1604 | 48 bit | w | w | 1⁄2w | w | 6 bit |
| 1960 | IBM 1410 | n c | 1 c, … | — | 1 c, 2 c, 6 c, 7 c, 11 c, 12 c | c | 6 bit + wm |
| 1960 | IBM 7070 | 10 d[c] | w, 1-9 d | w | w | w, d | 2 d |
| 1960 | PDP-1 | 18 bit | w | — | w | w | 6 bit |
| 1960 | Elliott 803 | 39 bit | |||||
| 1961 | IBM 7030 (Stretch) |
64 bit | 1 bit, … 64 bit, 1 d, … 16 d |
w | 1⁄2w, w | bit (integer), 1⁄2w (branch), w (float) |
1 bit, … 8 bit |
| 1961 | IBM 7080 | n c | 0 c, … 255 c | — | 5 c | c | 6 bit |
| 1962 | GE-6xx | 36 bit | w, 2 w | w, 2 w, 80 bit | w | w | 6 bit, 9 bit |
| 1962 | UNIVAC III | 25 bit | w, 2w, 3w, 4w, 6 d, 12 d | — | w | w | 6 bit |
| 1962 | Autonetics D-17B Minuteman I Guidance Computer |
27 bit | 11 bit, 24 bit | — | 24 bit | w | — |
| 1962 | UNIVAC 1107 | 36 bit | 1⁄6w, 1⁄3w, 1⁄2w, w | w | w | w | 6 bit |
| 1962 | IBM 7010 | n c | 1 c, … | — | 1 c, 2 c, 6 c, 7 c, 11 c, 12 c | c | 6 b + wm |
| 1962 | IBM 7094 | 36 bit | w | w, 2w | w | w | 6 bit |
| 1962 | SDS 9 Series | 24 bit | w | 2w | w | w | |
| 1963 (1966) |
Apollo Guidance Computer | 15 bit | w | — | w, 2w | w | — |
| 1963 | Saturn Launch Vehicle Digital Computer | 26 bit | w | — | 13 bit | w | — |
| 1964/1966 | PDP-6/PDP-10 | 36 bit | w | w, 2 w | w | w | 6 bit 7 bit (typical) 9 bit |
| 1964 | Titan | 48 bit | w | w | w | w | w |
| 1964 | CDC 6600 | 60 bit | w | w | 1⁄4w, 1⁄2w | w | 6 bit |
| 1964 | Autonetics D-37C Minuteman II Guidance Computer |
27 bit | 11 bit, 24 bit | — | 24 bit | w | 4 bit, 5 bit |
| 1965 | Gemini Guidance Computer | 39 bit | 26 bit | — | 13 bit | 13 bit, 26 | —bit |
| 1965 | IBM 1130 | 16 bit | w, 2w | 2w, 3w | w, 2w | w | 8 bit |
| 1965 | IBM System/360 | 32 bit | 1⁄2w, w, 1 d, … 16 d |
w, 2w | 1⁄2w, w, 11⁄2w | 8 bit | 8 bit |
| 1965 | UNIVAC 1108 | 36 bit | 1⁄6w, 1⁄4w, 1⁄3w, 1⁄2w, w, 2w | w, 2w | w | w | 6 bit, 9 bit |
| 1965 | PDP-8 | 12 bit | w | — | w | w | 8 bit |
| 1965 | Electrologica X8 | 27 bit | w | 2w | w | w | 6 bit, 7 bit |
| 1966 | SDS Sigma 7 | 32 bit | 1⁄2w, w | w, 2w | w | 8 bit | 8 bit |
| 1969 | Four-Phase Systems AL1 | 8 bit | w | — | ? | ? | ? |
| 1970 | MP944 | 20 bit | w | — | ? | ? | ? |
| 1970 | PDP-11 | 16 bit | w | 2w, 4w | w, 2w, 3w | 8 bit | 8 bit |
| 1971 | CDC STAR-100 | 64 bit | 1⁄2w, w | 1⁄2w, w | 1⁄2w, w | bit | 8 bit |
| 1971 | TMS1802NC | 4 bit | w | — | ? | ? | — |
| 1971 | Intel 4004 | 4 bit | w, d | — | 2w, 4w | w | — |
| 1972 | Intel 8008 | 8 bit | w, 2 d | — | w, 2w, 3w | w | 8 bit |
| 1972 | Calcomp 900 | 9 bit | w | — | w, 2w | w | 8 bit |
| 1974 | Intel 8080 | 8 bit | w, 2w, 2 d | — | w, 2w, 3w | w | 8 bit |
| 1975 | ILLIAC IV | 64 bit | w | w, 1⁄2w | w | w | — |
| 1975 | Motorola 6800 | 8 bit | w, 2 d | — | w, 2w, 3w | w | 8 bit |
| 1975 | MOS Tech. 6501 MOS Tech. 6502 |
8 bit | w, 2 d | — | w, 2w, 3w | w | 8 bit |
| 1976 | Cray-1 | 64 bit | 24 bit, w | w | 1⁄4w, 1⁄2w | w | 8 bit |
| 1976 | Zilog Z80 | 8 bit | w, 2w, 2 d | — | w, 2w, 3w, 4w, 5w | w | 8 bit |
| 1978 (1980) |
16-bit x86 (Intel 8086) (w/floating point: Intel 8087) |
16 bit | 1⁄2w, w, 2 d | — (2w, 4w, 5w, 17 d) |
1⁄2w, w, … 7w | 8 bit | 8 bit |
| 1978 | VAX | 32 bit | 1⁄4w, 1⁄2w, w, 1 d, … 31 d, 1 bit, … 32 bit | w, 2w | 1⁄4w, … 141⁄4w | 8 bit | 8 bit |
| 1979 (1984) |
Motorola 68000 series (w/floating point) |
32 bit | 1⁄4w, 1⁄2w, w, 2 d | — (w, 2w, 21⁄2w) |
1⁄2w, w, … 71⁄2w | 8 bit | 8 bit |
| 1985 | IA-32 (Intel 80386) (w/floating point) | 32 bit | 1⁄4w, 1⁄2w, w | — (w, 2w, 80 bit) |
8 bit, … 120 bit 1⁄4w … 33⁄4w |
8 bit | 8 bit |
| 1985 | ARMv1 | 32 bit | 1⁄4w, w | — | w | 8 bit | 8 bit |
| 1985 | MIPS I | 32 bit | 1⁄4w, 1⁄2w, w | w, 2w | w | 8 bit | 8 bit |
| 1991 | Cray C90 | 64 bit | 32 bit, w | w | 1⁄4w, 1⁄2w, 48 bit | w | 8 bit |
| 1992 | Alpha | 64 bit | 8 bit, 1⁄4w, 1⁄2w, w | 1⁄2w, w | 1⁄2w | 8 bit | 8 bit |
| 1992 | PowerPC | 32 bit | 1⁄4w, 1⁄2w, w | w, 2w | w | 8 bit | 8 bit |
| 1996 | ARMv4 (w/Thumb) |
32 bit | 1⁄4w, 1⁄2w, w | — | w (1⁄2w, w) |
8 bit | 8 bit |
| 2000 | IBM z/Architecture (w/vector facility) |
64 bit | 1⁄4w, 1⁄2w, w 1 d, … 31 d |
1⁄2w, w, 2w | 1⁄4w, 1⁄2w, 3⁄4w | 8 bit | 8 bit, UTF-16, UTF-32 |
| 2001 | IA-64 | 64 bit | 8 bit, 1⁄4w, 1⁄2w, w | 1⁄2w, w | 41 bit (in 128-bit bundles)[7] | 8 bit | 8 bit |
| 2001 | ARMv6 (w/VFP) |
32 bit | 8 bit, 1⁄2w, w | — (w, 2w) |
1⁄2w, w | 8 bit | 8 bit |
| 2003 | x86-64 | 64 bit | 8 bit, 1⁄4w, 1⁄2w, w | 1⁄2w, w, 80 bit | 8 bit, … 120 bit | 8 bit | 8 bit |
| 2013 | ARMv8-A and ARMv9-A | 64 bit | 8 bit, 1⁄4w, 1⁄2w, w | 1⁄2w, w | 1⁄2w | 8 bit | 8 bit |
| Year | Computer architecture |
Word size w | Integer sizes |
Floatingpoint sizes |
Instruction sizes |
Unit of address resolution |
Char size |
| key: bit: bits, d: decimal digits, w: word size of architecture, n: variable size |
[8][9]
See also[edit]
- Integer (computer science)
Notes[edit]
- ^ Many early computers were decimal, and a few were ternary
- ^ The bit equivalent is computed by taking the amount of information entropy provided by the trit, which is
. This gives an equivalent of about 9.51 bits for 6 trits.
- ^ Three-state sign
References[edit]
- ^ a b Beebe, Nelson H. F. (2017-08-22). «Chapter I. Integer arithmetic». The Mathematical-Function Computation Handbook — Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. p. 970. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721.
- ^ Dreyfus, Phillippe (1958-05-08) [1958-05-06]. Written at Los Angeles, California, USA. System design of the Gamma 60 (PDF). Western Joint Computer Conference: Contrasts in Computers. ACM, New York, NY, USA. pp. 130–133. IRE-ACM-AIEE ’58 (Western). Archived (PDF) from the original on 2017-04-03. Retrieved 2017-04-03.
[…] Internal data code is used: Quantitative (numerical) data are coded in a 4-bit decimal code; qualitative (alpha-numerical) data are coded in a 6-bit alphanumerical code. The internal instruction code means that the instructions are coded in straight binary code.
As to the internal information length, the information quantum is called a «catena,» and it is composed of 24 bits representing either 6 decimal digits, or 4 alphanumerical characters. This quantum must contain a multiple of 4 and 6 bits to represent a whole number of decimal or alphanumeric characters. Twenty-four bits was found to be a good compromise between the minimum 12 bits, which would lead to a too-low transfer flow from a parallel readout core memory, and 36 bits or more, which was judged as too large an information quantum. The catena is to be considered as the equivalent of a character in variable word length machines, but it cannot be called so, as it may contain several characters. It is transferred in series to and from the main memory.
Not wanting to call a «quantum» a word, or a set of characters a letter, (a word is a word, and a quantum is something else), a new word was made, and it was called a «catena.» It is an English word and exists in Webster’s although it does not in French. Webster’s definition of the word catena is, «a connected series;» therefore, a 24-bit information item. The word catena will be used hereafter.
The internal code, therefore, has been defined. Now what are the external data codes? These depend primarily upon the information handling device involved. The Gamma 60 [fr] is designed to handle information relevant to any binary coded structure. Thus an 80-column punched card is considered as a 960-bit information item; 12 rows multiplied by 80 columns equals 960 possible punches; is stored as an exact image in 960 magnetic cores of the main memory with 2 card columns occupying one catena. […] - ^ Blaauw, Gerrit Anne; Brooks, Jr., Frederick Phillips; Buchholz, Werner (1962). «4: Natural Data Units» (PDF). In Buchholz, Werner (ed.). Planning a Computer System – Project Stretch. McGraw-Hill Book Company, Inc. / The Maple Press Company, York, PA. pp. 39–40. LCCN 61-10466. Archived (PDF) from the original on 2017-04-03. Retrieved 2017-04-03.
[…] Terms used here to describe the structure imposed by the machine design, in addition to bit, are listed below.
Byte denotes a group of bits used to encode a character, or the number of bits transmitted in parallel to and from input-output units. A term other than character is used here because a given character may be represented in different applications by more than one code, and different codes may use different numbers of bits (i.e., different byte sizes). In input-output transmission the grouping of bits may be completely arbitrary and have no relation to actual characters. (The term is coined from bite, but respelled to avoid accidental mutation to bit.)
A word consists of the number of data bits transmitted in parallel from or to memory in one memory cycle. Word size is thus defined as a structural property of the memory. (The term catena was coined for this purpose by the designers of the Bull GAMMA 60 [fr] computer.)
Block refers to the number of words transmitted to or from an input-output unit in response to a single input-output instruction. Block size is a structural property of an input-output unit; it may have been fixed by the design or left to be varied by the program. […] - ^ «Format» (PDF). Reference Manual 7030 Data Processing System (PDF). IBM. August 1961. pp. 50–57. Retrieved 2021-12-15.
- ^ Clippinger, Richard F. [in German] (1948-09-29). «A Logical Coding System Applied to the ENIAC (Electronic Numerical Integrator and Computer)». Aberdeen Proving Ground, Maryland, US: Ballistic Research Laboratories. Report No. 673; Project No. TB3-0007 of the Research and Development Division, Ordnance Department. Retrieved 2017-04-05.
{{cite web}}: CS1 maint: url-status (link) - ^ Clippinger, Richard F. [in German] (1948-09-29). «A Logical Coding System Applied to the ENIAC». Aberdeen Proving Ground, Maryland, US: Ballistic Research Laboratories. Section VIII: Modified ENIAC. Retrieved 2017-04-05.
{{cite web}}: CS1 maint: url-status (link) - ^ «4. Instruction Formats» (PDF). Intel Itanium Architecture Software Developer’s Manual. Vol. 3: Intel Itanium Instruction Set Reference. p. 3:293. Retrieved 2022-04-25.
Three instructions are grouped together into 128-bit sized and aligned containers called bundles. Each bundle contains three 41-bit instruction slots and a 5-bit template field.
- ^ Blaauw, Gerrit Anne; Brooks, Jr., Frederick Phillips (1997). Computer Architecture: Concepts and Evolution (1 ed.). Addison-Wesley. ISBN 0-201-10557-8. (1213 pages) (NB. This is a single-volume edition. This work was also available in a two-volume version.)
- ^ Ralston, Anthony; Reilly, Edwin D. (1993). Encyclopedia of Computer Science (3rd ed.). Van Nostrand Reinhold. ISBN 0-442-27679-6.
Bits
Definitions of Bits not found.
Parts and bits are semantically related. In some cases you can use «Parts» instead a noun «Bits».
Parts
Parts noun — The local environment.
Bits and parts are semantically related. Sometimes you can use «Bits» instead a noun «Parts».
Both words in one sentence
- APA
- MLA
- CMS
Google Ngram Viewer shows how «bits» and «parts» have occurred on timeline
Purpose
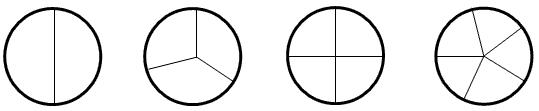
This unit explores the beginnings of proportional thinking by introducing fractions and associated language. The purpose for this unit is to make, name, and recognise wholes, halves, third parts, fourth parts and fifth parts of a variety of objects.
NA2-1: Use simple additive strategies with whole numbers and fractions.
NA2-7: Generalise that whole numbers can be partitioned in many ways.
Specific Learning Outcomes
- count in fractions forwards and backwards to a named whole number.
- recognise the whole of an object, part of an object, and equal parts and their names.
Description of Mathematics
This unit is based on the work of Richard Skemp. His ideas for teaching fractions can be used successfully with year 2 students, and also with students up to year 8 who are having difficulty understanding fractions. Skemp’s use of the word ‘parts’ is deliberate in that he uses it to refer to ‘equal parts’ whereas ‘bits’ refers to non-equal parts.
The use of two different physical representations, the whole and parts of a whole, are used to develop the concept of a fraction. Language also plays an important role. Being able to count in fractions helps students understand that you can have 5 thirds or 6 halves.
Using denominators that are the same, students need to know:
- a whole can be divided (partitioned) into equal parts, e.g. one whole is equal to two half parts or 1 = 1/2 + 1/2
- each of those parts can be put back together to make a whole, e.g. two half parts is equal to one whole or 1/2 + 1/2 = 1
- parts can be joined to make a fraction less than 1, e.g. one fourth and one fourth and one fourth is equal to three fourths or 1/4 + 1/4 + 1/4 = 3/4
- parts can be joined to make a number more than 1, e.g. three fourths (quarters) and one fourth and one fourth is equal to one whole and one fourth or 3/4 + 1/4 + 1/4 = 1 1/4
Opportunities for Adaptation and Differentiation
This unit can be differentiated by varying the scaffolding provided and altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- Support students thinking by clearly and deliberately modelling how to partition a whole into equal parts, and the result of the partitioning.
- Support students to describe the process of partitioning and their understanding of equal parts in their own words. Introduce mathematical terms naturally, alongside students’ explanations (whole, equal parts, fractional names such as one half and one third).
- Use the terms “numerator” and “denominator” only once the underlying ideas are understood, and can be articulated in students’ own words.
- Provide additional experiences of physically partitioning materials and discussing the resultant parts, until students understand the underlying ideas.
The context of equal shares can be adapted to recognise diversity and student interests to encourage engagement. Support students to identify and explore other situations in their lives where equal sharing occurs. For example, sharing kai at home or sharing cards to play a game (the pack of cards represents one whole). Rēwena bread modelled out of playdough could be used as another context for eels.
Activity
Prior Experiences
- Idea of fair shares
- Know 1/2, 1/3 and 1/4 of shapes such as rectangles and circles
- Doubles and their corresponding halves
Although the unit is planned around 5 sessions it can be extended over a longer period of time.
Session 1
The purpose of this session is to develop students’ understanding of equal parts (the denominator).
Resources:
- Copymaster 1
- Playdough (see recipe)
- Plastic knives
- Cutting boards
- Ask the students how they would share a bale of hay (block of chocolate) between 4 sheep (4 people) fairly. Other contexts could be the sharing of pizzas but the shape of the rectangle is easier for students to cut into equal shapes. Introduce the word equal – what do you think it means?
- Distribute copies of the eels start, action, results boards (Copymaster 1), some playdough, a cutting board and a plastic knife each. If it is possible it would be better to have 1 board between 2 students.
- Have each student or pair of students make six equal sized round eels, by rolling 6 equal amounts of play dough. Put one eel in each of the outlines on the left hand side of the board. The eels are small as they have their heads and tails cut off. The eels we are making today are miniatures of the big eels. That means we are making small copies of the big ones.
- The following story can be used to guide students through the actions as described on the board. The story could be adapted to a different context, such as the sharing of rēwena bread, to suit your students.
Hoepo and his brothers and sisters are at their Poua’s tangi and although they are sad they are looking forward to the hakari because shortfin eel is always on the menu.
Hoepo is planning to go early to the marquee because he wants one eel all to himself. He is given one whole eel. Hoepo doesn’t know it but he is going to be one sick boy!
The twins appear and they are told they have to share one eel evenly between the two of them. There are now two half parts.
The triplets come next and Aunty Wai says we will have to cut another eel into three equal parts. There are now three third parts.
Hoepo’s sister has come with her three friends. Aunty Wai says that they will have to cut the eel into four equal parts. There are now four fourth parts. Aunty Wai says they are also known as quarters.
Hoepo’s five baby cousins are only allowed to eat small portions so Aunty Wai cuts the last eel into five equal parts. There are now five fifth parts.
- Ask the students to mark the lines and cut lightly then if they haven’t made equal parts they can smooth the playdough out and start again.
- After cutting, the separated parts are put in the RESULT column next to their descriptions.
- Ask the students to share with the person next to them what they can see. Hopefully someone may say, «The more cuts we made, the smaller the equal part.» Prompt them towards that knowledge.
I want you to look at one of the third parts and one of the fifth parts. Which is bigger?
Have the students take one of each of the equal parts and put them on another blank board.
Order the equal parts from smallest to biggest.
Let’s say the names.
Students should order from 1/5 – 1
Put them back on the original board.
How many halves are equal to the whole?
How many fourths are equal to the whole?
How many thirds are equal to a whole?
How many wholes are equal to a whole?
Depending on the age of the students symbolic notation can be introduced, using the terms like 1/2 and one half part interchangeably.
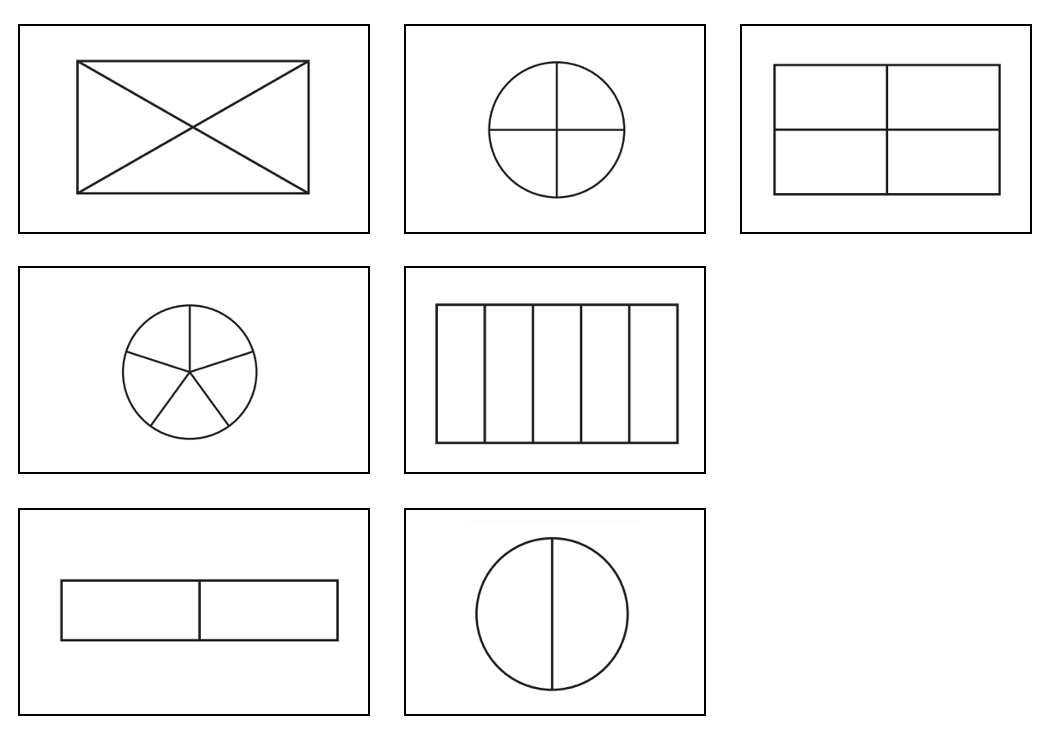
- Repeat the steps above using the biscuits start, action, results boards and fresh playdough. The first boards should, if possible, remain on view. With this second board a variety of division lines are easily found, eg fourth parts. Rēwena bread could be used as another context instead of biscuits or pies (as in number 9).
- Repeat the steps above using the pies start, action, results boards. If possible, fresh play dough should be used, the other two boards remaining on view. The lines of division should be radial as shown below.
Session 2
The purpose of this session is to develop the idea that parts of the same kind may not look alike. In Activity 1 this arose from the use of different objects. Here we see that this can be so, even with the same object.
Resources:
- Copymaster 2
- Playdough
- Plastic knives
- Cutting boards
Revise knowledge about equal parts.
What can we remember from yesterday? Write students’ comments in your modeling book.
- Begin with the first page. This is used in the same way as the board for Activity 1. Ask students to complete the first 3 lines (making halves in three different ways). There are three simple ways, see if you can find them.
The three straightforward ways are:
- Next, they complete the next two lines (the third parts) which offers only two straightforward ways.
- Complete the second page (the fourth-parts). There are six ways of doing this which are fairly easy to find.
- Students may want to go back to the halves, thirds or fourths/quarters boards and see if they can find some more.
Session 3
The purpose of this session is to consolidate the concepts formed in Sessions 1 and 2, moving onto a pictorial representation.
Resources:
- Copymaster 3
- Copymaster 4
- Begin by looking at some of the parts cards from Copymaster 3 together. Explain that these represent the objects which they made from playdough in the last activity, eels, chocolate bars, biscuits and some new ones. They also represent the parts into which the objects have been cut, e.g. third-parts, fourth-parts, halves, fifth-parts. Some have not been cut: these are wholes.
- Shuffle the parts cards and spread them out on the table, face upwards.
- Give each student one of the set names from Copymaster 4.
- Each student should collect the parts cards that match the name of the set they have been given, for example, halves.
- Students check each other’s sets and discuss if necessary.
- Next, introduce Skemp’s mix and match game. This is a great game in that the students are consolidating what they know about denominator without being introduced to the word. Older students may have heard that word and it is important that they understand what it is. The denominator names the number of equal parts.
Mix and Match: Rules of the Game
This game is best played by groups of 2-4 people (a tuakana/teina model could be used here).
- Share the parts cards from Copymaster 3 evenly between all players. Each player should have their cards in front of them in a single pile, face down.
- Place the mix and match card somewhere where all players can see it. The purpose of the mix and match card is to remind players of the directions in which they can build.
- The first player turns over their top card and places it in the middle of the playing area.
- Players take it in turns to turn over a card and place it alongside a card already on the playing area. When placing cards they must ensure that:
- cards in a line in the ‘match’ direction are each split into the same number of parts (e.g. halves, thirds…).
- cards in a line in the ‘mix’ direction are each split into different numbers of parts
- If a player cannot place their card they put it back on the bottom of their pile and it is the next player’s turn.
- To make the game into a contest you can give a point to any player that makes ‘three in a row’ in either direction, and add a rule that says you can not have more than three cards in a row at any time. It is possible to gain 2 points by completing both a match and a mix by placing your card in the right place. The player with the most points wins.
Session 4
The purpose of this session is to develop students’ understanding of a number of like parts (the numerator).
This is the next step towards the concept of a fraction. It is much more straightforward than that of session 1 -3 which involved (i) separating a single object into part objects (ii) of a given number (iii) all of the same amount. Here we only have to put together a given number of these parts and to recognise and name the combination.
Resources:
- 3 sets of animals (these could be models or pictures)
- Copymaster 5
- Copymaster 6
- Five trays or plates
- Playdough
- Plastic knives
- Cutting boards
- Five set loops
Warm up
- Count in halves up to a number such as 3.
1/2, 2/2, 3/2, 4/2, 5/2, 6/2 (be prepared for students to carry on counting and not realise that 6/2 is equal to 3).
- Ask the students:
How many halves did we count (six halves = three wholes, write on the board)
How many halves do you think would equal 6? Write on the board
How many halves do you think would equal 9? Write on the board
- Relate back to their knowledge of doubles and halves.
A Number of Like Parts
This is an activity for up to six students working in two teams (mahi tahi). Its purpose is to introduce the concept described above.
Set the scene for your students:
Yesterday we went to the zoo and saw the zoo keepers feeding some of the animals. We are going to pretend that some of us are the animal keepers feeding the animals and some of us are the zoo kitchen staff, preparing and cutting up all the food.
- One team acts as animal keepers, the other works in the zoo kitchen. The latter need to be more numerous, since there is more work for them to do.
- A set of animals is chosen. Suppose that this is set 1. The kitchen staff look at the menu and set to work preparing eels, as in Making Equal parts. The animal keepers put the animals in their separate enclosures. They may choose how many of each. For example:
- The animal keepers, one at a time, come to the kitchen and ask for food for each kind of animal in turn. The kitchen staff cut the hay as required (using the shaped playdough, plastic knives and cutting boards), e.g.
Animal Keepers may say: Zoo Kitchen Staff may say: Food for 2 elephants please Here it is, 2 whole bales of hay. Food for 5 giraffes please 5 third parts. Tell them not to leave any scraps. Food for 3 rhino please Here you are. 3 half parts from 2 bales of hay. There is one half part left. Food for 5 zebra please Here you are, 5 quarters or 5 fourth parts. Food for 6 sheep please 6 fifth parts. Lucky sheep. - Each time the animal keeper checks that the amounts are correct, and then gives its ration to each animal. The keepers check each other’s work.
- When feeding time is over, the food is returned to the kitchen for reprocessing. Steps 1 to 4 are then repeated with different animals, keepers and kitchen staff.
Note that the eels, slabs, and hay should be of a standard size.
Note also that the eels, after their head and tails are removed, resemble the eels in a cylinder shape and the slabs of meat and hay are oblongs.
Session 5
So far we have covered denominator and numerator without mentioning their names. Students need to understand that the denominator names the equal parts and numerator names the number of like parts.
Resources:
- Copymaster 7
- Copymaster 8
Revise some of the ideas from sessions 1-4, selecting from these activities:
- You may want to give them some unit fraction cards and ask them to order from smallest to biggest.
- Give simple fraction addition problems to add below 1.
- Give them a piece of paper and ask them to fold the paper into equal parts that they have chosen. For example, a student may choose to fold the paper into 4 equal parts. They need to verbalise what they have done. Ask them to tell you about three of the sections.
- An activity for students if the symbolic notation has been introduced could be to have a pack of cards which they can use to match pairs, e.g. 1/4 goes with one fourth. When they have matched the cards, ask each student to solve a simple addition problem for you.
I want you to give me one fourth + one fourth (write on the board). Can anyone give me cards that mean the same but are written in a different way? (1/4 + 1/4)
I want you to find one fifth and one fifth and one fifth. How many fifths are there? Can anyone give me cards that mean the same but are written in a different way? (1/5 + 1/5 + 1/5) - Give the students three problems to solve with a partner (tuakana-teina model could be used).
What happens if we had to feed 5 giraffes and they were allowed 1/3 of a bale of hay each?
What happens if we had to feed 5 rhinos and they are allowed 1/2 a bale of hay each?
What happens if we had to feed 6 zebras and they are allowed 1/4 of a bale of hay each?
To conclude the session, ask the students to work in pairs and complete a think board (Copymaster 7 provides a blank think board and Copymaster 8 shows a completed example.) Suitable fractions for think boards include 2 halves, 3 fourth parts, 2 fifth parts, 4 third parts, 2 quarters. Show and discuss the example of a completed think board for 3/5.
Home Link
Dear family and whānau,
This week we have been learning about dividing things into equal parts so people get fair shares. Please draw your child’s attention to any fractions you use over the week in cooking or when sharing kai or meals. For example if you are having pizza, show them how it is sliced into 4 or 6 or 8 equal sliced parts. Ask them to help share out food when dishing up dinner or making lunches. They can draw pictures or take photos of the things you talk about and bring these to class to share.
On x86/x64 processors, a byte is 8 bits, and there are 256 possible binary states in 8 bits, 0 thru 255. This is how the OS translates your keyboard key strokes into letters on the screen. When you press the ‘A‘ key, the keyboard sends a binary signal equal to the number 97 to the computer, and the computer prints a lowercase ‘a‘ on the screen. You can confirm this in any Windows text editing software by holding an ALT key, typing 97 on the NUMPAD, then releasing the ALT key. If you replace ’97’ with any number from 0 to 255, you will see the character associated with that number on the system’s character code page printed on the screen.
If a character is 8 bits, or 1 byte, then a WORD must be at least 2 characters, so 16 bits or 2 bytes. Traditionally, you might think of a word as a varying number of characters, but in a computer, everything that is calculable is based on static rules. Besides, a computer doesn’t know what letters and symbols are, it only knows how to count numbers. So, in computer language, if a WORD is equal to 2 characters, then a double-word, or DWORD, is 2 WORDs, which is the same as 4 characters or bytes, which is equal to 32 bits. Furthermore, a quad-word, or QWORD, is 2 DWORDs, same as 4 WORDs, 8 characters, or 64 bits.
Note that these terms are limited in function to the Windows API for developers, but may appear in other circumstances (eg. the Linux dd command uses numerical suffixes to compound byte and block sizes, where c is 1 byte and w is bytes).
1680 ₽
Word Bits отличная и легкая игра. Подойдет для всех!
1.Возьмите карточку и киньте то количество кубиков, которое указано на карточке.
2.Первый игрок, который назовет слово на заданную категорию забирает карту, но не все так просто! Это слово должно содержать все выпавшие на кубиках буквы!
3.Тот, кто собрал больше всех карточек за определенный промежуток времени, выиграл!
-
Описание
-
Детали
-
Отзывы (0)
Описание
В комплекте:
81 карточка
4 кубика с буквами
Инструкция на английском языке
Детали
| Вес | 0.24 kg |
|---|---|
| Габариты | 12 × 12 × 4 cm |