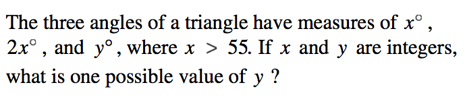Wednesday, November 28, 2012
What math word problems look like to me:
If I have two apples and you have 7 pencils, how many pancakes will fit on the roof? Explain.
ANSWER:
Giraffe. Because aliens don’t wear hats.
-Sam
Posted by
Unknown
at
11:11 AM
No comments:
Post a Comment

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.
The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!
How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.
Here are the seven strategies I use to help students solve word problems.
1. Read the Entire Word Problem
Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.
2. Think About the Word Problem
Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.
Here are the questions:
A. What exactly is the question?
What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.
B. What do I need in order to find the answer?
Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.
This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better
Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.
One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.
If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?
This is where students will focus in on the numbers which will be used to solve the problem.
3. Write on the Word Problem
This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:
- Circle any numbers you’ll use.
- Lightly cross out any information you don’t need.
- Underline the phrase or sentence which tells exactly what you’ll need to find.
4. Draw a Simple Picture and Label It
Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.
For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!
5. Estimate the Answer Before Solving
Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.
6. Check Your Work When Done
This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable? I want students to do more than to be number crunchers but to really think about what those numbers mean.
Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.
7. Practice Word Problems Often
Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.
When students practice word problems, often several things happen. Word problems become less scary (no, really).
They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.
If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.
This 3rd Grade Math Task Cards Bundle has word problems in almost every one of its 30 task card sets.
There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.
CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.
CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.
CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?
3rd Grade: Rounding Whole Numbers Task Cards
4th Grade: Convert Fractions and Decimals Task Cards
5th Grade: Read, Write, and Compare Decimals Task Cards
Thanks so much for stopping by!

About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.
This post will be your complete guide to SAT Math word problems. We’ll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.
Feature Image: Antonio Litterio/Wikimedia
What Are SAT Math Word Problems?
A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.
You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.
Secondly, these types of questions allow test makers to ask questions that’d be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it’d be difficult to demonstrate and ask this with only a diagram.
Translating Math Word Problems Into Equations or Drawings
In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.
For instance, the word «sum» means the value when two or more items are added together. So if you need to find the sum of a and b, you’ll need to set up your equation like this: a+b.
Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.
Here is a chart with all the key terms and symbols you should know for SAT Math word problems:
| Key Terms | Mathematical Action |
| Sum, increased by, added to, more than, total of | + |
| Difference, decreased by, less than, subtracted from | − |
| Product, times, __ times as much, __ times as many (a number, e.g., “three times as many”) | * or x |
| Divided by, per, __ as many, __ as much (a fraction, e.g., “one-third as much”) | / or ÷ |
| Equals, is, are, equivalent | = |
| Is less than | < |
| Is greater than | > |
| Is less than or equal to | ≤ |
| Is greater than or equal to | ≥ |
Now, let’s look at these math terms in action using a few official examples:
We can solve this problem by translating the information we’re given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let’s write this out in algebraic form.
We’ll say that the number of salads sold = S, and the number of drinks sold = D. The problem tells us that 209 salads and drinks have been sold, which we can think of as this:
S + D = 209
Finally, we’ve been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don’t know the exact numbers of S and D, but we do know how much each unit costs. Therefore, we can write this equation:
6.50S + 2D = 836.5
We now have two equations with the same variables (S and D). Since we want to know how many salads were sold, we’ll need to solve for D so that we can use this information to solve for S. The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S:
S + D = 209
Now, just subtract S from both sides to get what D equals:
D = 209 − S
Finally, plug this expression in for D into our other equation, and then solve for S:
6.50S + 2(209 − S) = 836.5
6.50S + 418 − 2S = 836.5
6.50S − 2S = 418.5
4.5S = 418.5
S = 93
The correct answer choice is (B) 93.
This word problem asks us to solve for one possible solution (it asks for «a possible amount»), so we know right away that there will be multiple correct answers.
Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.
If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.
Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.
Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.
Typical SAT Word Problems
Word problems on the SAT can be grouped into three major categories:
- Word problems for which you must simply set up an equation
- Word problems for which you must solve for a specific value
- Word problems for which you must define the meaning of a value or variable
Below, we look at each world problem type and give you examples.
Word Problem Type 1: Setting Up an Equation
This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You’ll also most likely see it first on the section.
For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.
Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.
To solve this problem, we’ll need to know both Armand’s and Tyrone’s situations, so let’s look at them separately:
Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m—the number of texts he sent per hour multiplied by the total number of hours he texted.
Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4p—the number of texts he sent per hour multiplied by the total number of hours he texted.
We now know that Armand’s situation can be written algebraically as 5m, and Tyrone’s can be written as 4p. Since we’re being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:
5m + 4p
The correct answer is choice (C) 5m + 4p
Word Problem Type 2: Solving for a Missing Value
The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics, such as averages, single-variable equations, and ratios. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
Let’s try to think about this problem in terms of x. If Type A trees produced 20% more pears than Type B did, we can write this as an expression:
x + 0.2x = 1.2x = # of pears produced by Type A
In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2x) to x, we get the number of pears produced by Type A trees.
The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2x is equal to the number of pears produced by Type A, we can write the following equation:
1.2x = 144
Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:
x = 144 / 1.2
x = 120
The correct answer choice is (B) 120.
You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math.)
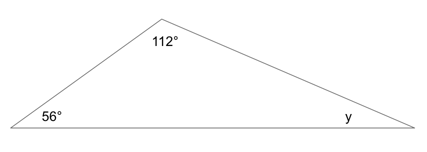
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.
Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it’s the smallest integer larger than 55. Basically, it’s a safe bet!)
Now, because x = 56, the next angle in the triangle—2x—must measure the following:
56*2 = 112
Let’s make a rough (not to scale) sketch of what we know so far:
Now, we know that there are 180° in a triangle, so we can find the value of y by saying this:
y = 180 − 112 − 56
y = 12
One possible value for y is 12. (Other possible values are 3, 6, and 9.)
Word Problem Type 3: Explaining the Meaning of a Variable or Value
This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.
This question might sound tricky at first, but it’s actually quite simple.
We know that P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she’s worked 0 days (i.e., if we plug 0 into the equation), here’s what we get:
P = 108 − 23(0)
P = 108
This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.
To help juggle all the various SAT word problems, let’s look at the math strategies and tips at our disposal.
Ready to go beyond just reading about the SAT? Then you’ll love the free five-day trial for our SAT Complete Prep program. Designed and written by PrepScholar SAT experts, our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.
Click on the button below to try it out!
SAT Math Strategies for Word Problems
Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.
#1: Draw It Out
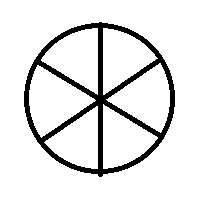
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you’re working with. For instance, let’s look at how a picture can help you solve a word problem about a circle (specifically, a pizza):
If you often have trouble visualizing problems such as these, draw it out. We know that we’re dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.
Because we’ll need to solve the weight of each slice in ounces, let’s first convert the total weight of our pizza from pounds into ounces. We’re given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:
3 * 16 = 48 ounces (for whole pizza)
Now, let’s draw a picture. First, the pizza is divided in half (not drawn to scale):
We now have two equal-sized pieces. Let’s continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):
This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:
48 / 6 = 8 ounces per piece
The correct answer choice is (C) 8.
As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.
#2: Memorize Key Terms
If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.
There are free SAT Math questions available online, so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.
#3: Underline and/or Write Out Important Information
The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.
#4: Pay Close Attention to What’s Being Asked
It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?
It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.
#5: Brush Up on Any Specific Math Topic You Feel Weak In
You’re likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.
For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!
Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now’s a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!
All set? Let’s go!
Test Your SAT Math Word Problem Knowledge
Finally, it’s time to test your word problem know-how against real SAT Math problems:
Word Problems
1. No Calculator
2. Calculator OK
3. Calculator OK
4. Calculator OK
Answers: C, B, A, 1160
Answer Explanations
1. For this problem, we have to use the information we’re given to set up an equation.
We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:
x + 1
Ken and Paul split the bill evenly. This means that we’ll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken’s sandwich cost x dollars and Paul’s cost x + 1, here’s what our equation looks like when we combine the two expressions:
x + x + 1
2x + 1
Now, we can divide this expression by 2 to get the price each person paid:
(2x + 1) / 2
x + 0.5
But we’re not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:
(x + 0.5) + 0.2(x + 0.5)
x + 0.5 + 0.2x + 0.1
1.2x + 0.6
The correct answer choice is (C) 1.2x + 0.6
2. You’ll have to be familiar with statistics in order to understand what this question is asking.
Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.
Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:
225 * 0.256 = 57.6
Since the question is asking «about how many students»—and since we obviously can’t have a fraction of a person!—we’ll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).
3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don’t be scared—it’s actually not as difficult as it appears!
First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here’s what happens to the equation when we plug in 0 for t:
h(0) = -16(0)2 + 110(0) + 72
h(0) = 0 + 0 + 72
h(0) = 72
As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).
4. You might be tempted to draw a diagram for this problem since it’s talking about a pool (rectangle), but it’s actually quicker to just look at the numbers given and work from there.
We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.
To find the amount of water in the pool now, we’ll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:
8 * 70 = 560 gallons
This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:
560 + 600 = 1160
The correct answer is 1160.
Aaaaaaaaaaand time for a nap.
Key Takeaways: Making Sense of SAT Math Word Problems
Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.
Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.
Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.
What’s Next?
Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math. From polygons and slopes to probabilities and sequences, we’ve got you covered!
Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score.
Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.
Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math, written by a perfect scorer.
Want to improve your SAT score by 160 points?
Check out our best-in-class online SAT prep program. We guarantee your money back if you don’t improve your SAT score by 160 points or more.
Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math strategy guide, you’ll love our program. Along with more detailed lessons, you’ll get thousands of practice problems organized by individual skills so you learn most effectively. We’ll also give you a step-by-step program to follow so you’ll never be confused about what to study next.
Check out our 5-day free trial:
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
One important reason for studying mathematics is to nurture an aptitude for and a confidence in problem solving. To be good at problem solving, one must be able to sort through the unknown, make sense of it, persevere in it, and come away with a solution. This ability is not only critical to mathematics, but learning to solve problems successfully crosses over all aspects of life, in school and out.
George Polya’s book, How to Solve It was published in 1945. Polya, frequently referred to as “The Father of Problem Solving,” is best known for the following four basic principles of problem solving.
| George Polya’s 4 – Step Problem Solving Principles |
| 1. First Principle: Understand the problem. |
| 2. Second Principle: Devise a Plan. |
| 3. Third Principle: Carry out the plan & Solve the problem. |
| 4. Fourth Principle: Look back & Check for reasonableness & accuracy. |
These principles still stand today as reliable strategies for problem solving. Unfortunately, over time, the original significance inherent in each of Polya’s steps became less like real problem solving and more like a trick for quick calculating.
As a result unfortunately, an approach to solving word problems known as “find the magic words” was born. Instead of actually reading the problem, students just followed a scripted formula – underline numbers, find and circle magic words and Presto, put them together and problem solved. But is it?
Tracy Johnston Zager (@TracyZager), a highly respected math coach and author, shared the following two problems with her twitter followers.
First grade word problem
Lois has 16 counters.
She gets 10 more counters.
How many counters does Lois have in all?
HINT for students usually written in textbook:
Now here is another first grade word problem.
There are 20 pens.
10 pens are in each box.
How many boxes in all?
a. 1
b. 2
c. 20
d. 30
Several of the students she observed chose D. This answer proves more students are adopting the “magic words” method to problem solving. In fact, this is just a small sampling of what is now seen as routine in solving word problems; students don’t see a need to even read the words in context any longer. They simply circle the magic words; in this case, “in all,” underline the numbers; in this case 20 and 10, and then just “put them together”; in this case 20 + 10 = 30.
But 30 boxes of pencils is not a reasonable solution to this problem. The truth is, when students only use finding magic words as their method for understanding a word problem, the meaning behind the math-at-hand is missing.
Here’s another dilemma; as children get older and the problems get bigger, the magic-word approach rarely works.
When students mindlessly pull out and put together isolated words and numbers, the essence of the problem gets lost and the meaning within that context gets watered down to a few scripted steps, regardless of what the problem really means.
The acronym CUBES as a similar pick-pull-and-calculate method to problem solving is getting popular. Check out the premise behind the problem solving; circle, underline, calculate.

The problem with CUBES and similar strategies is that as students get older, the problems require more thinking, with layers that cannot be solved with a simple pull and put together method.
Without a real understanding of how to comprehend a word problem, students are not only led astray, but grow up thinking that problems are not worth investigating. In fact, students using these approaches can get the impression that problems are neat and tidy; when actually problems can get quite messy requiring logic, persistence, and creativity as trying alternative strategies can help clear the muddy waters a bit.
What’s a teacher to do?
One answer is for teachers to first spend valuable instructional time investigating and modeling what it means to actually understand a word problem.
Below you will find a sample anchor lesson for modelling how to think like a real mathematician when understanding word problems.
Anchor Lesson for what it looks like and sounds like to understand a word problem like a Real Mathematician
Purpose:
- Students will notice how a mathematician understands a word problem.
- Students will relate the skills a mathematician uses in understanding to that of a reader, scientist, historian, etc.
- Students will identify how using the strategies makes comprehension easier.
Directions:
Setting the Stage:
- Put up the following text (or something just as difficult) on Smartboard.
(Students should not have a copy of this.)
We now know that we can find equilibria solutions to a differential equation by finding values of the population for which dP/dt=0. But we also observed that the two equilibria solutions for the logistic population model differ: for equilibrium, nearby trajectories (solutions to the differential equation) are “attracted” to the equilibrium; for the other equilibrium, nearby trajectories are “repelled.” We call the first case a stable equilibrium (also called a sink) and we call the second case an unstable equilibrium (also called a source).
- Challenge your students to switch roles with you. They are now the teacher and you are the student. They will be “grading” you in how they think you did as a reader.
- Make sure you have read this ahead of time several times. Really impress the students with your oral reading. Exaggerate your reading so it sounds like you really understand the piece.
- Have the students talk to a partner and come up with a grade on how you did as a reader.
- Ask them what grade they gave you and why they gave you that grade. They will more than likely give you an “A.” (I always get one “C+” from the student who is going for the laugh.)
- Here’s the powerful part – reveal that you have no idea what you read. Share what Cris Tovanni calls “fake reading.” That is reading without thinking. Reveal that if they asked you anything about what you read, you would not be able to answer it because you really have no idea what you read. Add that real reading means you are actively involved. It takes both text and thinking.
- Let the students know the same thing happens in mathematics. Sometimes we just keep moving along in our problem solving without thinking. When that happens, we really can’t get any real meaning out of it. Sometimes we even just circle magic words and underline numbers thinking this alone will help us make meaning of the problem. But, without any real connections to what we underline, we rush into strategies without thinking and that can sometimes lead us astray.
- Ask students how many of them have ever faked their way through a math problem – they didn’t think, they just kept moving along. Raise your own hand. We’ve all done it.
Think Aloud:
- Put the following problem (or any open-ended math prompt) on your Smartboard. Students should not have a copy of the problem. That can be distracting. You want them to pay attention to your Think Aloud.
A total of 8,000 runners started a long distance race. The results of the race are listed below.
- 3/15 of the runners finished the race in less than 4 hours.
- 0.6 of the runners finished the race in 4 or more hours.
- The rest of the runners did not finish the race.
A. Calculate the number of runners who finished the race in less than 4 hours. Show and explain all your work, even if you used a calculator.
B. Calculate the number of runners who did not finish the race. Show all your work. Explain why you did each step.
- Give out the following T-Chart for students to complete during your Think Aloud. Make a copy on chart paper to use as an anchor reference in future problem solving.
| How to think & UNDERSTAND a word problem like a REAL mathematician | |
| What did you notice your teacher doing to understand a word problem like a real mathematician? | How did what you noticed help your teacher better understand the problem? |
3. Tell students that you are going to think aloud through this problem. Challenge them to notice and write anything you did to help you make meaning of the text and think like a real mathematician.
- Read the entire problem through one time (Do not read parts A or B yet). Then say, “Wow, that’s a lot of information. I think I better reread it slowly and take it apart.”
- Start over and read the first sentence. Stop and make a personal connection that helps you visualize the scenario, but get off track a little. (Use this step if you are noticing students losing focus during problem solving). Say something like, “I can make a connection to this. I went to a marathon once. I can picture that day. That was a really hot day. Oh wait, I’m getting off track. That connection is not helping me make meaning of the text. I’m going to have to ‘turn down the volume’ to that and get back to the problem. I better reread it from the beginning to get myself back on track.”
- Continue reading. Share that you first want to remove the numbers in your mind so you can connect to the story. Now replace the numbers accordingly:
- with “the total number of runners” for 8,000
- “one part” for 3/15
- “another part” for 0.6
- “a third part” for the words “the rest” in the third bullet.
- Identify there are three parts that make up the total number the runners in the race. (This will give your students a sense of the part/part/whole relationship).
- Reread the problem again, this time with the numbers included. Make a connection to 3/15 of 8,000. Say something like, “Hmmm, 3/15 of 8,000. Let me make sense of this before I move on. I know that 3/15 expressed as a friendlier fraction is 1/5. Write 1/5 in front of 3/15. Draw a visual. It can be the race (an open number line) showing what 1/5 would look like. I know in my brain that 1/5 of 8,000 is 1,600. So 1,600 runners finished the race in less than 4 hours. That’s not a lot of the runners. Point out the remaining part of the open number line (leaving four more fifths).
- Read aloud the next sentence, “0.6 of the runners finished the race in four or more hours.” Say a connection to your math class and say something like, “I remember when we were working with fractions and decimals and I found it easiest to work with either all fractions or all decimals.” Now depending on your students, you choose what you would like to do. If you want to focus on the part/part/whole relationship using fractions, say something like, “I think I’d like to continue my drawing using fractions, so I started with 1/5 and now I have 0.6 of the runners. If I think of 0.6 as a fraction, I am thinking of 6/10. Since I already am working with fifths, I’m going to rename 6/10 as 3/5.” Now draw what three more fifths would look like on your open number line. And say “If 1/5 is 1,600, then 3 times that or 3/5 would be 4,800 runners. That means most of the runners finished the race in 4 or more hours. (Purposely do not underline numbers and circle magic words. Just connect to context and meaning. Estimate and make numbers friendly and reasonable.)
- Notice that “If 1/5 finished in less than four hours, and 3/5 finished in four or more hours, that leaves 1/5 that did not finish. You know this because 1/5 + 3/5 + 1/5 = 1. (Draw as a fraction bar or show it on your open number line). That means the same amount of runners that finished in less than four hours also didn’t finish the race.
- Saying something like, “Wow, this is easy. I really understand the story in this math. I’m ready to begin reading my questions and solving my problem.”
Reflecting on Student Noticings:
- Stop and have partners share what they noticed you doing to think like a real mathematician and not just do fake math.
- Discuss with the whole class and write down what the students noticed as a T-chart on chart paper to use as a reference. Take ideas and reframe them to include good thinking strategies. Do they notice you visualizing, making connections, and looking for the mathematical patterns in the numbers; ‘turning down the volume” to connections that distract; making sense of the problem; rereading to clarify; rereading to get back on track; making a model; asking questions; using friendly numbers to help with mental math; staying in the context; and estimating?
- Challenge the students to discover how this all helped you make meaning of the text. Remember to share that is how mathematicians think. In fact, it is how scientists think, and historians, etc. Good thinking is good thinking. It crosses over content area. Students should now record their reflections on the right side of the T-Chart.
- Point out that you didn’t even begin answering the questions yet; you were making sense of the problem first.
- Do not solve the problem. It can be a problem they solve later on.
Students Give it a Go:
- Hand out copies of similar problems and have partners use active reading strategies to think through the problems out loud to each other. While one student thinks aloud, the other student notices what critical thinking habits they used to make meaning of the text.
- If you have time, they can solve the problem. Be careful not to rush into this. The focus here is how to think critically through problem solving.
A Student Resource for Math Fix-up Tools
One of the best math consultants in the country, Donna Boucher (@mathcoachcorner), and I collaborated on a list of Fix-up Tools for Mathematics. We have found this to be very useful in helping students recognize when their attention wavers and then have the tools they need to get back on track in their problem solving.
Feel free to download and share!
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more