What the word mean means in math - Word и Excel - помощь в работе с программами

From Wikipedia, the free encyclopedia

This article is about the mathematical concept. For other uses, see Mean (disambiguation). For the state of being mean or cruel, see Meanness. For broader coverage of this topic, see Average.

There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set.

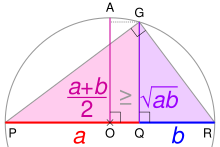
Pythagorean means consist of arithmetic mean (AM), geometric mean (GM), and harmonic mean (HM). The AM is the sum of numbers divided by the number of numbers, GM is an average for sets of positive numbers based on their product, and HM is an average for sets of numbers defined in relation to a unit of measurement. The relationship between AM, GM, and HM is represented by the inequality AM ≥ GM ≥ HM.

Statistical location covers mean, median, and mode, where mean may not always be the same as the median or mode for skewed distributions. The mean of a probability distribution is the long-run average value of a random variable with that distribution.

Generalized means include power mean and f-mean. The power mean is an abstraction of quadratic, arithmetic, geometric, and harmonic means, while the f-mean generalizes the concept further.

Other specialized means discussed are weighted arithmetic mean, truncated mean, interquartile mean, mean of a function, mean of angles and cyclical quantities, Fréchet mean, triangular sets, and Swanson’s rule.

For a data set, the arithmetic mean, also known as «arithmetic average», is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers x₁, x₂, …, x_n is typically denoted using an overhead bar, .^{[note 1]} If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the sample mean () to distinguish it from the mean, or expected value, of the underlying distribution, the population mean (denoted or $mu _{x}$ ^{[note 2]}).^[1]

Outside probability and statistics, a wide range of other notions of mean are often used in geometry and mathematical analysis; examples are given below.

Types of means[edit]

Pythagorean means[edit]

Arithmetic mean (AM)[edit]

The arithmetic mean (or simply mean) of a list of numbers, is the sum of all of the numbers divided by the number of numbers. Similarly, the mean of a sample $x_{1},x_{2},ldots ,x_{n}$ , usually denoted by , is the sum of the sampled values divided by the number of items in the sample.

${displaystyle {bar {x}}={frac {1}{n}}left(sum _{i=1}^{n}{x_{i}}right)={frac {x_{1}+x_{2}+cdots +x_{n}}{n}}}$

For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:

${displaystyle {frac {4+36+45+50+75}{5}}={frac {210}{5}}=42.}$

Geometric mean (GM)[edit]

The geometric mean is an average that is useful for sets of positive numbers, that are interpreted according to their product (as is the case with rates of growth) and not their sum (as is the case with the arithmetic mean):

${displaystyle {bar {x}}=left(prod _{i=1}^{n}{x_{i}}right)^{frac {1}{n}}=left(x_{1}x_{2}cdots x_{n}right)^{frac {1}{n}}}$

^[2]

For example, the geometric mean of five values: 4, 36, 45, 50, 75 is:

${displaystyle (4times 36times 45times 50times 75)^{frac {1}{5}}={sqrt[{5}]{24;300;000}}=30.}$

Harmonic mean (HM)[edit]

The harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, as in the case of speed (i.e., distance per unit of time):

${displaystyle {bar {x}}=nleft(sum _{i=1}^{n}{frac {1}{x_{i}}}right)^{-1}}$

For example, the harmonic mean of the five values: 4, 36, 45, 50, 75 is

${frac {5}{{tfrac {1}{4}}+{tfrac {1}{36}}+{tfrac {1}{45}}+{tfrac {1}{50}}+{tfrac {1}{75}}}}={frac {5}{;{tfrac {1}{3}};}}=15.$

Relationship between AM, GM, and HM[edit]

AM, GM, and HM satisfy these inequalities:

{displaystyle mathrm {AM} geq mathrm {GM} geq mathrm {HM} ,}

Equality holds if all the elements of the given sample are equal.

Statistical location[edit]

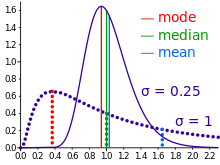
Geometric visualization of the mode, median and mean of an arbitrary probability density function.^[3]

In descriptive statistics, the mean may be confused with the median, mode or mid-range, as any of these may incorrectly be called an «average» (more formally, a measure of central tendency). The mean of a set of observations is the arithmetic average of the values; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely value (mode). For example, mean income is typically skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income and favors the larger number of people with lower incomes. While the median and mode are often more intuitive measures for such skewed data, many skewed distributions are in fact best described by their mean, including the exponential and Poisson distributions.

Mean of a probability distribution[edit]

The mean of a probability distribution is the long-run arithmetic average value of a random variable having that distribution. If the random variable is denoted by , then it is also known as the expected value of (denoted E(X) ). For a discrete probability distribution, the mean is given by , where the sum is taken over all possible values of the random variable and P(x) is the probability mass function. For a continuous distribution, the mean is $textstyle int _{-infty }^{infty }xf(x),dx$ , where f(x) is the probability density function.^[4] In all cases, including those in which the distribution is neither discrete nor continuous, the mean is the Lebesgue integral of the random variable with respect to its probability measure. The mean need not exist or be finite; for some probability distributions the mean is infinite (+∞ or −∞), while for others the mean is undefined.

Generalized means[edit]

Power mean[edit]

The generalized mean, also known as the power mean or Hölder mean, is an abstraction of the quadratic, arithmetic, geometric, and harmonic means. It is defined for a set of n positive numbers x_i by

${displaystyle {bar {x}}(m)=left({frac {1}{n}}sum _{i=1}^{n}x_{i}^{m}right)^{frac {1}{m}}}$ ^[2]

By choosing different values for the parameter m, the following types of means are obtained:

${displaystyle lim _{mto infty }}$: maximum of $x_{i}$
${displaystyle lim _{mto 2}}$: quadratic mean
${displaystyle lim _{mto 1}}$: arithmetic mean
${displaystyle lim _{mto 0}}$: geometric mean
${displaystyle lim _{mto -1}}$: harmonic mean
${displaystyle lim _{mto -infty }}$: minimum of $x_{i}$

f-mean[edit]

This can be generalized further as the generalized f-mean

${displaystyle {bar {x}}=f^{-1}left({{frac {1}{n}}sum _{i=1}^{n}{fleft(x_{i}right)}}right)}$

and again a suitable choice of an invertible f will give

Weighted arithmetic mean[edit]

The weighted arithmetic mean (or weighted average) is used if one wants to combine average values from different sized samples of the same population:

${displaystyle {bar {x}}={frac {sum _{i=1}^{n}{w_{i}{bar {x_{i}}}}}{sum _{i=1}^{n}w_{i}}}.}$

^[2]

Where ${displaystyle {bar {x_{i}}}}$ and $w_{i}$ are the mean and size of sample respectively. In other applications, they represent a measure for the reliability of the influence upon the mean by the respective values.

Truncated mean[edit]

Sometimes, a set of numbers might contain outliers (i.e., data values which are much lower or much higher than the others). Often, outliers are erroneous data caused by artifacts. In this case, one can use a truncated mean. It involves discarding given parts of the data at the top or the bottom end, typically an equal amount at each end and then taking the arithmetic mean of the remaining data. The number of values removed is indicated as a percentage of the total number of values.

Interquartile mean[edit]

The interquartile mean is a specific example of a truncated mean. It is simply the arithmetic mean after removing the lowest and the highest quarter of values.

${displaystyle {bar {x}}={frac {2}{n}};sum _{i={frac {n}{4}}+1}^{{frac {3}{4}}n}!!x_{i}}$

assuming the values have been ordered, so is simply a specific example of a weighted mean for a specific set of weights.

Mean of a function[edit]

In some circumstances, mathematicians may calculate a mean of an infinite (or even an uncountable) set of values. This can happen when calculating the mean value ${displaystyle y_{text{avg}}}$ of a function f(x) . Intuitively, a mean of a function can be thought of as calculating the area under a section of a curve, and then dividing by the length of that section. This can be done crudely by counting squares on graph paper, or more precisely by integration. The integration formula is written as:

${displaystyle y_{text{avg}}(a,b)={frac {1}{b-a}}int limits _{a}^{b}!f(x),dx}$

In this case, care must be taken to make sure that the integral converges. But the mean may be finite even if the function itself tends to infinity at some points.

Mean of angles and cyclical quantities[edit]

Angles, times of day, and other cyclical quantities require modular arithmetic to add and otherwise combine numbers. In all these situations, there will not be a unique mean. For example, the times an hour before and after midnight are equidistant to both midnight and noon. It is also possible that no mean exists. Consider a color wheel—there is no mean to the set of all colors. In these situations, you must decide which mean is most useful. You can do this by adjusting the values before averaging, or by using a specialized approach for the mean of circular quantities.

Fréchet mean[edit]

The Fréchet mean gives a manner for determining the «center» of a mass distribution on a surface or, more generally, Riemannian manifold. Unlike many other means, the Fréchet mean is defined on a space whose elements cannot necessarily be added together or multiplied by scalars.
It is sometimes also known as the Karcher mean (named after Hermann Karcher).

Trianglar sets[edit]

In geometry, there are thousands of different
definitions for the center of a triangle that can all be interpretted as the mean of a triangular set of points in the plane.^{[citation needed]}

Swanson’s rule[edit]

This is an approximation to the mean for a moderately skewed distribution.^[5] It is used in hydrocarbon exploration and is defined as:

${displaystyle m=0.3P_{10}+0.4P_{50}+0.3P_{90}}$

where P₁₀, P₅₀ and P₉₀ 10th, 50th and 90th percentiles of the distribution.

Other means[edit]

Arithmetic-geometric mean
Arithmetic-harmonic mean
Cesàro mean
Chisini mean
Contraharmonic mean
Elementary symmetric mean
Geometric-harmonic mean
Grand mean
Heinz mean
Heronian mean
Identric mean
Lehmer mean
Logarithmic mean
Moving average
Neuman–Sándor mean
Quasi-arithmetic mean
Root mean square (quadratic mean)
Rényi’s entropy (a generalized f-mean)
Spherical mean
Stolarsky mean
Weighted geometric mean
Weighted harmonic mean

Notes[edit]

^ Pronounced «x bar».
^ Greek letter μ, for «mean», pronounced /’mjuː/.

References[edit]

^ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 0-7021-3838-X p. 181
^ ^a ^b ^c «Mean | mathematics». Encyclopedia Britannica. Retrieved 2020-08-21.
^ «AP Statistics Review — Density Curves and the Normal Distributions». Archived from the original on 2 April 2015. Retrieved 16 March 2015.
^ Weisstein, Eric W. «Population Mean». mathworld.wolfram.com. Retrieved 2020-08-21.
^ Hurst A, Brown GC, Swanson RI (2000) Swanson’s 30-40-30 Rule. American Association of Petroleum Geologists Bulletin 84(12) 1883-1891

Источник

Mean is one of the important and most commonly used measures of central tendency. There are several types of means in mathematics. In statistics, the mean for a given set of observations is equal to the sum of all the values of a collection of data divided by the total number of values in the data. In other words, we can simply add all the values in a data set and divide it by the total number of values to calculate mean. However, the general method and formulas vary depending upon the type of data given, grouped data, or ungrouped data.

Grouped data is the data set formed by aggregating individual observations of a variable into different groups, while ungrouped data is a random set of observations. Let us understand the different mean formulas and methods to find the mean of the given set of observations using examples.

1.	What is Mean in Statistics?
2.	Mean Formula
3.	Mean of Ungrouped Data
4.	Mean of Grouped Data
5.	How to Find Mean?
6.	Types of Mean in Math
7.	FAQs on Mean

What is Mean in Statistics?

«Mean» is commonly known as «average». For example, if we say, the average height of the class of students of grade 9 is 150 cm, then it means that the mean of their heights is 150 cm. Mean is a statistical concept that carries a major significance in finance and is used in various financial fields and business valuation. Mean, median, and mode are the three statistical measures of the central tendency of data.

Mean Meaning

The mean is the average or a calculated central value of a set of numbers and is used to measure the central tendency of the data. Central tendency is the statistical measure that recognizes the entire set of data or distribution through a single value. It provides an exact description of the whole data. In statistics, the mean can also be defined as the ratio of sum of all observations to the total number of observations.

⇒ Given a data set, X = {x₁,x₂, . . . ,x_n}, the mean (or arithmetic mean, or average), denoted x̄, is the mean of the n values x₁,x₂, . . . ,x_n.

Mean Symbol: The mean is represented as x-bar, x̄.

Examples:

Examples of mean in real life are:

Mean of the runs scored by a cricketer in test matches.
Mean price of houses in a particular area calculated by real estate agents.

Mean Formula

The mean formula in statistics for a set is defined as the sum of the observations divided by the total number of observations. But the formula is different if the data is grouped (i.e., if the data is seggrated as categories). We are going to study two types of mean formulas in this page:

Mean formula of grouped data
Mean formula of ungrouped data

But the common formula of mean (of ungrouped data) is:

Mean = (Sum of all data points) ÷ (Number of data points)

Example: Find the mean of the first five natural odd numbers, using the mean formula.

Solution:

The first five natural odd numbers = 1, 3, 5, 7, and 9

Using mean formula,

Mean = (1 + 3 + 5 + 7 + 9) ÷ 5 = 25/5 = 5

Answer: The mean of the first five natural odd numbers {1, 3, 5, 7, 9} is 5.

Mean of Ungrouped Data

Ungrouped data is the raw data gathered from an experiment or study. In other words, an ungrouped set of data is basically a list of numbers. To find the mean of ungrouped data, we simply calculate the sum of all collected observations and divide by the total number of the observations. Follow the below-given steps to find the mean of a given set of data,

Note down the given set of data whose mean is to be calculated.
Apply any of the following formulas based on the type of information available.
x̄ = (x₁+ x₂+ x₃+ … + x_n )/n where x₁, x₂, . . ., x_n are n observations.

Example: The heights of five students are 161 in, 130 in, 145 in, 156 in, and,162 in respectively. Find the mean height of the students.

Solution: To find: the mean height of the students.

The heights of five students = 161 in, 130 in, 145 in, 156 in, and,162 in (given)

Sum of the heights of five students = (161 + 130 + 145 + 156 + 162) = 754

Using mean formula,

Mean = 754/5 = 150.8

Answer: The mean height of the students is 150.8 inches.

Mean of Grouped Data

Grouped data is a set of given data that has been bundled together in categories. For a mean of grouped data, a frequency distribution table is created, which shows the frequencies of the given data set. We can calculate the mean of the given data using the following methods:

Direct Method
Assumed Mean Method
Step Deviation Method

Calculating Mean Using Direct Method

The direct method is the simplest and the most popular method to find the mean of the grouped data. The steps that can be followed to find the mean for grouped data using the direct method are given below,

Create a table containing four columns as given below,
Column 1- Class interval.
Column 2- Class marks (corresponding), denoted by x_i. The class mark is the middle value of the interval. i.e., x_i = (upper limit) + (lower limit) / 2.
Column 3- Frequencies (f_i) (corresponding)
Column 4- x_if_i (corresponding product of column 2 and column 3)
Calculate mean by the formula ∑x_if_i/∑f_i

Example: There are 100 members in a basketball club. The different age groups of the members and the number of members in each age group are tabulated below. Calculate the mean age of the club members.

Age Group	Number of members
10-20	17
20-30	22
30-40	20
40-50	21
50-60	20

Solution:

In this case, we first need to calculate the Class Mark for each age group.

We will use the formula given below and calculate the Class Mark for each age group.

Class mark = (Upper Limit + Lower Limit)/2. For example, for the first interval 10-20, class mark = (10 + 20) / 2 = 30/2 = 15.

Age Group	Class Mark (x_i)	Frequencies (f_i)	x_if_i
10-20	15	17	x₁f₁ =15 × 17 = 255
20-30	25	22	x₂f₂ = 25 × 22 = 550
30-40	35	20	x₃f₃ = 35 × 20 = 700
40-50	45	21	x₄f₄ = 45 × 21 = 945
50-60	55	20	x₅f₅ = 55 × 20 = 1100

Now,

Σf_ix_i = f₁x₁ + f₂x₂ + f₃x₃ + f₄x₄ + f₅x₅
= 255 + 550 + 700 + 945 + 1100
= 3550

Σf_i = f₁ + f₂ + f₃ + f₄ + f₅
= 17 + 22 + 20 + 21 + 20
= 100

We will use the formula given below.

x̄ = Σf_ix_i/Σf_i

The mean age = 3550/100

= 35.5

The mean age of the members = 35.5

Calculating Mean Using Assumed Mean Method

We apply the assumed mean method to find the mean of a set of grouped data when the direct method becomes tedious. We can follow the below-given steps to find mean using the assumed mean method,

Create a table containing five columns as stated below,
Column 1- Class interval.
Column 2- Classmarks (corresponding), denoted by x_i. Take the central value from the class marks as the assumed mean and denote it as A.
Column 3- Calculate the corresponding deviations using, i.e. d_i = x_i — A
Column 4- Frequencies (f_i) (corresponding)
Finally, calculate the mean by the formula, A + ∑f_id_i/∑f_i

Calculating Mean Using Step Deviation Method

Step deviation is also called the shift of origin and scale method. We apply the step deviation method to reduce the tedious calculations while calculating the mean for grouped data. Steps to be followed while applying the step deviation method are given below,

Create a table containing five columns as given below,
Column 1- Class interval.
Column 2- Classmarks (corresponding), denoted by x_i. Take the central value from the class marks as the assumed mean (A).
Column 3- Calculate the corresponding deviations, i.e. d_i = x_i — A
Column 4- Calculate the values of u_i using the formula, u_i = d_i/h, where h is the class width.
Column 5- Frequencies (f_i) (corresponding)
Finally, calculate the mean by using the formula A + h (∑f_iu_i / ∑f_i).

How to Find Mean?

Mean is the most common central tendency we know about and use. It is also commonly used as average. We can calculate the mean for a given set of data using different methods based on the type of given data. Let us see how to find mean for a few different cases.

Case 1: Let there be «n» number of items in a list. {x₁, x₂, x₃, … , x_n }

Mean can be calculated using the formula given below,

x̄ = (x₁+ x₂+ x₃+ … + x_n )/n

x̄ = Σx_i/n

Case 2: Let there be n number of items in a list, given as, {x₁, x₂, x₃, … , x_n } and the frequency of each item be {f₁, f₂, f₃, … , f_n } respectively.

Mean can be calculated using the formula given below,

x̄ = (f₁x₁ + f₂x₂ + f₃x₃ + . . . + f_nx_n)/(f₁ + f₂ + f₃ + . . . + f_n)

x̄ = Σf_ix_i/Σf_i

Case 3: When the items in a list are written in the form of intervals, for example, 10 — 20, we need to first calculate the class mark using x_i = (lower limit + upper limit) / 2.

Then, the mean can be calculated using the formula given below,

x̄ = Σf_ix_i/Σf_i

Types of Mean in Math

There are different types of means in mathematics, which are arithmetic mean, weighted mean, geometric mean (GM), and harmonic mean (HM). If mentioned without an adjective (as mean), mean generally refers to the arithmetic mean in statistics. Some of the types of the mean are explained in brief as given below,

Arithmetic Mean
Weighted Mean
Geometric Mean
Harmonic Mean

Arithmetic Mean

Arithmetic mean is often referred to as the mean or arithmetic average, which is calculated by adding all the numbers in a given data set and then dividing it by the total number of items within that set. The general formula to find the arithmetic mean is given as,

x̄ = Σx_i/n (or) x̄ = Σf_ix_i / Σf_i.

where,

x̄ = the mean value of the set of given data.
x_i = data value
f_i = corresponding frequency
n = total number of data values

Weighted Mean

The weighted mean is calculated when certain values that are given in a data set are more important than the others. A weight w_i is attached to each of the values x_i. The general formula to find the weighted mean is given as,

Weighted mean = Σw_ix_i/Σw_i

where,

x_i = data value
w_i = corresponding weight

Geometric Mean

The geometric mean is defined as the n^th root of the product of n numbers in the given data set. The formula to find the geometric mean for a given set of data, x₁, x₂, x₃, … , x_n ,

G.M. = ⁿ√(x₁ · x₂ · x₃ · … · x_n)

Harmonic Mean

For a given set of observations, harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations, given using the formula,

Harmonic mean = 1/[Σ(1/x_i)]/N = N/Σ(1/x_i)

Related Topics on Mean:

Categorical Data
Range in Statistics
Average

FAQs on Mean

What is the Definition of Mean?

Mean, one of the important and most commonly used measures of central tendency is the average or a calculated central value of a set of numbers. The process of calculating the mean is different based on the type of data (grouped or ungrouped data).

What is Mean Formula?

There are different formulas to find the mean of a given set of data, as given below,

For ungrouped data, mean, x̄ = (sum of observations) ÷ (number of observations)
For grouped data, mean, x̄ = Σfx/Σf
where,
f = frequency of each class
x = mid-interval value of each class

What is Mean Formula for Grouped Data?

The mean formula to find the mean of a grouped set of data can be given as, x̄ = Σf_ix/_iΣf_i, where, x̄ is the mean, f_i is frequency of a class and x_i is mid-interval value of corresponding class.

What is Population Mean Symbol?

The population mean refers to the mean of all the data values that are there in the population. It is represented by the symbol μ.

What is the Mean Formula for Ungrouped Data?

The mean formula to find the mean for an ungrouped set of data can be given as, mean = (sum of data values) / (number of data values).

What is the Difference Between Mean and Median?

The mean formula is given as the average of all the observations. It is expressed as mean = (sum of observations) ÷ (total number of observations). Whereas, the median formula is totally dependent on the number of observations (n). If the number of observations is even then the median formula is [median = ((n/2)^th term + ((n/2) + 1)^thterm)/2] and if n = odd then the median formula is [median = {(n + 1)/2} ^thterm].

How To Find the Mean Using Mean Formula?

If the data is not grouped, then just divide the sum of observations by total number to find the mean. If the data is grouped, then to find the mean, first multiply the mid point of each class by the corresponding frequency first, then divide the sum of all products obtained by the sum of all frequencies.

What are Different Types of Mean?

The different types of means in mathematics are,

Arithmetic Mean
Geometric Mean
Harmonic Mean
Weighed Mean

What is the Difference Between Arithmetic Mean and Weighted Mean?

Arithmetic mean is calculated when all data values have equal importance, while weighted mean is calculated when certain values that are given in a data set are more important than the others.

What are the Applications of Mean in our Daily Lives?

Mean is used to understand the whole data by a single number. For example, to analyze how high the students of a class are, it is enough to just find the mean instead of looking into each student’s height.

How To Use the Mean Formula?

The usage of mean formula is shown using an example here.
Example: Find the mean of (1, 2, 3, 4, 5, 6, 7).
Solution: Total number of observations = 7
Mean = (sum of observations) ÷ (total numbers of observations)
Mean = (1 + 2 + 3 + 4 + 5 + 6 + 7) ÷ 7 = 28/7 = 4
Mean of (1, 2, 3, 4, 5, 6, 7) is 4.

What is Sample Mean Symbol?

The sample mean refers to the mean of only selected data values from the population. It is represented by the symbol x̄.

Источник

Mean Definition: A mean in simple words can be understood as the mathematical average of a set of two or more numbers. The mean for a provided set of numbers can be estimated in more than one way, comprising the arithmetic mean method, which is practiced to compute the sum of the numbers in the series, and the geometric mean approach, which is the average of a set of products. Though, all of the primary means of computing a simple average produce the same estimated result is obtained most of the time.

With this article on mean, you will be able to answer questions like what is meant by mean? or what is the meaning of mean? define mean in math, statistics and every information related to meaning. So go through the entire article and develop your knowledge regarding Mean.

Learn about Mean Median Mode

What is the Meaning of Mean in Maths?

Mean, in Maths, is the final average value of the provided numbers or data. To determine the mean, we first require to add the total values provided in a datasheet and then divide the total sum by the total number of values/number given. Assume, in a given data table, the price values of 14 chairs are mentioned. If we have to determine the mean of the prices, then add the prices of each chair and divide the total sum by 14. It will appear in an average value.

Mean = (Sum of all the observations/Total number of observations)

Example: What is the mean of 2, 4, 8, 6 and 12?

Step 1: First add all the numbers.

2+4+6+8+12 = 32

Step 2: Now divide by 5 (here 5 is the total number of observations).

Mean = 32/5 = 6.4

Consider another example, where we have to determine the average age of teachers in a school. Here also we will apply the same procedure. First, add the individual age of all the teachers and then divide the sum by the total number of teachers present in the school.

Mean is an approach that is generally used in Statistics. At our school level, we learned the theory behind the average calculation. However, in higher levels, we are introduced to the topic called mean.

Mean is a fundamental concept in mathematics and statistics. In statistics, it is defined as the measure of the central tendency of a probability distribution with median and mode. It is also recognized as the expected value.

Mean is nothing but the advanced version of average for a sequence or series of a number. In the actual world, when there is enormous data prepared, we practice statistics to deal with the calculations. Along with mean, statistics also include important terms like median and mode.

The Median is defined as the middle value of a given data/information/number when all the values are arranged in ascending order. The Mode is the number in the list, which appears for the maximum number of times. Mean is a statistical concept that carries major importance in finance. The concept is applied in various financial fields, including management and business valuation.

Check Rolle’s Theorem and Lagrange’s Mean Value Theorem

Types of Mean

There are majorly 3 distinct types of mean value that you will find in statistics.

Arithmetic Mean
Geometric Mean
Harmonic Mean

Arithmetic Mean

The Arithmetic Mean is the average of the numbers/data or can be understood as the calculated central value of a set of numbers. To determine Arithmetic Mean:

Add all the numbers/data given.
Divide the total obtained in the above steps by the total numbers/data.

(X=frac{sum_{i=1}^nX_i}{N})

Here N= Total number of observations.

Learn about Assumed Mean Method

Geometric Mean

The Geometric Mean or GM is the average value or mean which implies the central tendency of the set of numbers by using the root of the product of the values. Below is the formula for the Geometric Mean calculation.

(Consider, if x_1,x_2dots. x_n are the observation, then the G.M is defined as)

(GM=sqrt[n] {x_1times x_2times x_3…..x_n})

(GM=(x_1times x_2times x_3…..x_n)^{frac{1}{n}})

This can also be written as;

(log G.M=frac{sum_{ }^{ }log x_i}{n})

(GM=Antilog frac{sum_{ }^{ }log x_i}{n})

(G.M.=sqrt[n]{prod_{i=1}^nx_i})

(For any Grouped Data, G.M can be written as:GM=Antilog frac{sum_{ }^{ }f.log x_i}{n})

Thus, the geometric mean is also represented as the nth root of the product of n numbers. values.

Harmonic Mean

Harmonic Mean or HM is determined as the reciprocal of the average of the reciprocals of the data values. The harmonic mean formula is applied to calculate the average of a set of numbers.

(Ifx_1, x_2 , x_3,dots, x_{n }are the individual items then;)

(H.M=frac{n}{frac{1}{x_1}+frac{1}{x_2}+frac{1}{x_3}+dots+frac{1}{x_n}}=frac{n}{sum_{i=1}^nfrac{1}{x_i}})

(For a frequency distribution, the harmonic mean formula is:)

(H.M=frac{N}{sum_{i=1}^nffrac{1}{x_i}})

Here N=summation of f.

In general, the harmonic mean is used when there is a requirement to give higher weight to the smaller items. It is used in the case of times and average rates.

Important Points on Mean

The mean is the arithmetical average of a set of two or more numbers.
Arithmetic mean geometric mean and harmonic mean are three types of mean that can be calculated.
Summing the numbers/data in a set and dividing it by the total number provides the arithmetic mean.
The geometric mean is somewhat complicated and includes the multiplication of the numbers using the nth root.
The mean serves to evaluate the performance of an investment or company over a while, and several other uses.
Average is different from an Arithmetic Mean.

We hope that the above article on Mean is helpful for your understanding and exam preparations. Stay tuned to the Testbook app for more updates on related topics from Mathematics, and various such subjects. Also, reach out to the test series available to examine your knowledge regarding several exams

Mean FAQs

Q.1 How do you define the mean?

Ans.1 The mean in mathematics is defined as the average of a set of two or more numbers. Summing the numbers in a set and dividing by the total number provides the arithmetic mean.

Q.2 What is the “mean” in maths?

Ans.2 The mean is the sum of the numbers divided by the total numbers present. To find the mean, add all the numbers commonly then divide by the number of numbers. Eg 3 + 6 + 100 + 13 + 3 = 125 ÷ 5 = 25. The mean of the range of numbers is 25.

Q.3 What is “mean” in statistics?

Ans.3 The mean or the average of a data set is determined by adding all numbers in the data set and then dividing by the number of values available in the set.

Q.4 What is the difference between mean and average?

Ans.4 The term Average is the sum of all the data divided by the total number of values in the set. Whereas in Mean we find the average of a sample data. In other words average is finding the central value in mathematics, whereas mean is finding the central value in statistics.

Q.5 What is “mean” and its uses?

Ans.5 The mean is the sum of the numbers in a data set divided by the total number of values in the set. The mean is also understood as the average. Mean is suitably used for a data set with numbers that are nearby together.

Q.6 What is “mean” and its types?

Ans.6 Mean is the most generally adopted model of central tendency. There are different types of the mean; arithmetic means, geometric mean (GM) and harmonic mean (HM).

Источник

What Is a Mean?

Mean is the simple mathematical average of a set of two or more numbers.

The mean for a given set of numbers can be computed in more than one way, including the arithmetic mean method, which uses the sum of the numbers in the series, and the geometric mean method, which is the average of a set of products. However, all the primary methods of computing a simple average produce the same approximate result most of the time.

Key Takeaways

The mean is the mathematical average of a set of two or more numbers.
The arithmetic mean and the geometric mean are two types of mean that can be calculated.
The formula for calculating the arithmetic mean is to add up the numbers in a set and divide by the total quantity of numbers in the set.
The formula for calculating the geometric mean is to multiply all the values in a data set, then take the root of the sum equal to the quantity of values within that data set.
A mean helps you to assess a set of numbers by telling you the average, helping to contextualize each data point.

Calculating The Means

Understanding Mean

The mean is a statistical indicator that can be used to gauge performance over time. Specific to investing, the mean is used to understand the performance of a company’s stock price over a period of days, months, or years.

An analyst who wants to measure the trajectory of a company’s stock value in, say, the last 10 days would sum up the closing price of the stock in each of the 10 days. The sum total would then be divided by the number of days to get the arithmetic mean. The geometric mean will be calculated by multiplying all of the values together. The nth root of the product total is then taken—in this case, the 10^th root—to get the mean.

Formulas for Arithmetic Mean and Geometric Mean

Calculations for both the arithmetic and geometric means are fairly similar. The calculated amount for one will not substantially vary from another. However, there are subtle differences between the two approaches that do lead to different numbers.

Arithmetic Mean

The formula for calculating the arithmetic mean is to add up all figures and divide by the quantity of figures used. For example, the arithmetic mean of the numbers 4 and 9 is found by adding 4 and 9 together, then dividing by 2 (the quantity of numbers we are using). The arithmetic mean in this example is 6.5.

Arithmetic Mean

Pros

It is easier to calculate.
It is simpler for following along and audit results.
Its calculated value is a finite number.
It has more widespread use in algebraic computations.
It is often the fastest type of mean to calculate.

Cons

It is highly affected by material outliers or extreme numbers outside of a data set.
It is not as useful for skewed distributions.
It is not useful when using time series data (or other series of data with varying basis).
It weighs every item equally, diminishing the importance of more impactful data points.

Geometric Mean

The geometric mean is more complicated and uses a more complex formula. To get the formula for calculating the geometric mean is to multiply all values within a data set. Then, take the root of the sum equal to the quantity of values within that data set. For example, to calculate the geometric of the values 4 and 9, multiply the two numbers together to get 36. Then, take the square root (since there are two values). The geometric mean in this example is 6.

Geometric Mean

Pros

It is less likely to be impacted by extreme outliers.
It returns a more accurate measurement for more volatile data sets.
It considers the effects of compounding.
It is more accurate when using a data set over a long period of time (due to compounding).

Cons

It can’t be used if any value within the data set is 0 or negative.
Its formula is more complex and not easily used.
Its calculation is not transparent and more difficult to audit.
It is less prevalent and not used as much as other methods.

Example Mean Calculations

Let’s put this into practice by examining the price of a stock over a 10-day period. Imagine an investor purchased one share of stock for $148.01. The price of the stock over the next 10 days is also included.

The arithmetic mean is 0.67%, and is simply the sum total of the returns divided by 10. However, the arithmetic mean of returns is only accurate when there is no volatility, which is nearly impossible with the stock market.

In addition to the arithmetic and geometric means, the harmonic mean is calculated by dividing the number of observations by the reciprocal (one over the value) of each number in the series. Harmonic means are often used in finance to average data that occurs in fractions, ratios, or percentages, such as yields, returns, or price multiples.

The geometric mean factors in compounding and volatility, making it a better metric of average returns. Because it is impossible to take the root of a negative value, add one to all the percentage returns so that the product total yields a positive number. Take the 10^th root of this number and remember to subtract from one to get the percentage figure. The geometric mean of returns for the investor in the last five days is 0.61%. As a mathematical rule, the geometric mean will always be equal to or less than the arithmetic mean.

Arithmetic Mean

(

0.0045

)

0.0121

0.0726

0.0043

(

0.0049

)

0.0376

0.0067

0.67

begin{aligned}text{Arithmetic Mean} &= tiny{frac{ (0.0045) + 0.0121 + 0.0726 + … + 0.0043 + (0.0049) + 0.0376 }{ 10 } } \&= 0.0067 \&= 0.67% \end{aligned}

Arithmetic Mean=10(0.0045)+0.0121+0.0726+…+0.0043+(0.0049)+0.0376=0.0067=0.67%

Geometric Mean

0.9955

1.0121

1.0726

1.0043

0.9951

1.0376

−

0.0061

0.61

begin{aligned}text{Geometric Mean} &= tiny{sqrt[10]{ 0.9955 times 1.0121 times 1.0726 times … times 1.0043 times 0.9951 times 1.0376 } — 1} \&= 0.0061 \&= 0.61% \end{aligned}

Geometric Mean=100.9955×1.0121×1.0726×…×1.0043×0.9951×1.0376−1=0.0061=0.61%

Analyzing the table shows why the geometric mean provides a better value. When the arithmetic mean of 0.67% is applied to each of the stock prices, the end value is $152.63. However, the stock traded for $157.32 on the last day. This means that the arithmetic mean of returns is understated.

On the other hand, when each of the closing prices is raised by the geometric average return of 0.61%, the exact price of $157.32 is calculated. In this example, and often in many calculations, the geometric mean is a more accurate reflection of the true return of a portfolio.

While the mean is a good tool to evaluate the performance of a company or portfolio, it should also be used with other fundamentals and statistical tools to get a better and broader picture of the investment’s historical and future prospects.

Examples of When Means Are Important in Investing

Within business and investing, mean is used extensively to analyze performance. Examples of situations in which you may encounter mean include:

Determining whether an equity is trading above or below its average over a specified time period.
Looking back to see how comparative trading activity may determine future outcomes. For example, seeing the average rate of return for broad markets during prior recessions may guide decision making in future economic downturns.
Seeing whether trading volume or the quantity of market orders is in line with recent market activity.
Analyzing the operational performance of a company. For instance, some financial ratios like days sales outstanding require determining the average accounts receivable balance for the numerator.
Quantifying macroeconomic data like average unemployment over a period of time to determine general health of an economy.

What is a mean in math?

In mathematics and statistics, the mean refers to the average of a set of values. The mean can be computed in a number of ways, including the simple arithmetic mean (add up the numbers and divide the total by the number of observations), the geometric mean, and the harmonic mean.

How do you find the mean?

The mean is a characteristic of a set of data that describes some sort of average. To find the mean, you can compute it mathematically using one of several methods, depending on the structure of the data and the type of average you need. You can also visually identify the mean in many cases by plotting the data distribution. In a normal distribution, the mean, mode, and median are all the same value that occurs at the center of the plot.

What is the difference between mean, median, and mode?

The mean is the average that appears in a set of data.

The median is the midway point above (below) where 50% of the values in the data sits.

The mode refers to the most frequently observed value in the data (the one that occurs the most).

Why is mean important?

Mean is a valuable statistical measurement that tells you what the expected outcome is when comparing all data points together. Although it doesn’t guarantee future results, the mean helps set the expectation of a future outcome based on what already has happened.

Is a mean the same as an average?

Yes. A mean is the mathematical average of a set of two or more numbers.

The Bottom Line

The mean is another word for a mathematical «average.» The simple or arithmetic mean is the average calculated by summing up the values of some observations and dividing by the number of observations. The geometric mean is calculated by multiplying all the numbers in a dataset and then taking the n^th root of the product, where n is the total number of values in the dataset. The geometric mean is particularly useful when dealing with quantities that have a multiplicative or exponential relationship, such as growth rates, percentages, or ratios. The harmonic mean is calculated by dividing the total number of values in the dataset by the sum of the reciprocals of the individual values. It is also used when dealing with rates, ratios, or situations where the relationship between the values is inversely proportional.

The mean is an important descriptive statistic, but should not be interpreted in isolation. One should also keep in mind the shape of the data distribution and other metrics like the standard deviation, median, and mode.

Источник

The term ‘Mean’ is used constantly in the field of Statistics and is one of the basic methods used to obtain a result. It is also known as arithmetic mean or the average of a given set of data. It also measures the central tendency of data. The definition of a mean for a given set of data is the average calculated for a given set of numbers or data. This is referred to as the total of all the values of data provided divided by the number of data values in total for any given set of data.

The mathematical symbol or notation for the mean is ‘x-bar’. This symbol appears on scientific calculators and in mathematical and statistical notations.

The ‘mean’ or ‘arithmetic mean is the most commonly used form of average. To calculate the mean, you need a set of related numbers (or data set). At least two numbers are needed in order to calculate the mean.

The formula denoting the mean of a given set of data is as follows:

Mean = Sum of Observations/Total number of observations

The other two statistical methods used are median and mode to obtain a result for a given set of data. The median is defined as the value present in the middle of a given set of data and the mode is the frequency with which a particular number occurs in a given set of data.

(Image will be uploaded soon)

In order to find the mean of 4, 5, 6, 3, and 7, first, we have to add the numbers and then divide the sum by the number of items.

4 + 5 + 6 + 3 + 7 = 25 i.e. the sum of the numbers is 25.

Mean = = = = 5

So, the mean of the data set 4, 5, 6, 3, and 7 is 5.

How to Find Mean?

The mean value for a given set of data is calculated in a two-step process:

The values given in the data set are added up together.
The total of the values obtained is then divided by the number of values given.

Mean Formula

The measure of central tendencies is used to describe data clusters around a central value. The mean definition indicates a varied formula used to calculate the mean depending on the data provided. The general formula to calculate the mean is as follows:

[Mean = frac{text{Sum of Given Data}}{text{Total Number of Data}}]

When using the Sigma (∑) notation, the mean formula is:

[frac{sum_{i=1}^{n} X_{i}}{N}]

Here,

N = it is the Total number provided in a given data set.

∑ Xi = Total sum of all the data values.

Mean of Negative Numbers

We have seen examples of finding the mean of positive numbers till now. But what if the numbers in the observation list include negative numbers. Let us understand with an instance,

Example: Find the mean of 9, 6, -3, 2, -7, 1.

Add all the numbers first:

Total: 9+6+(-3)+2+(-7)+1 = 9+6-3+2-7+1 = 8

Now divide the total from 6, to get the mean.

Mean = 8/6 = 1.33

Mean Formula with Example

Find the mean for the given set of random data,

3, 5, 9, 17, 19

The given set of data contains the numbers 3, 5, 9, 17, 19
The total number of numerals given is 5
Sum of the given numbers in the data set = 3 + 5 + 9 + 17 + 19 = 53

Therefore, Mean = Sum of given data/Total number of data

=[ frac{53}{5}] =10.6

Hence, the mean for the given data is 10.6.

Different Types of Mean

A. Arithmetic Mean

The arithmetic mean is one of the foremost methods used to obtain the central tendency of a set of data. It encompasses all the values provided by the data set. It is referred to as the ratio of the total sum of given observations to the total number of observations. The arithmetic mean can be positive, negative, or zero. There are two types of Arithmetic Mean,

Simple Arithmetic Mean.
Weighted Arithmetic Mean.

The formula to calculate Arithmetic mean is as follows:

[X = frac{sum_{i=1}^{n} x_{i}p_{i}}{N}]

The arithmetic mean is easy to calculate and is rigidly defined.

B. Geometric Mean

The second type of Mean is the Geometric Mean (GM). It is defined as the average value signifying the set of numbers of central tendencies by calculating the product of their values. Multiplication of the numbers provided and take out the nth root of the multiplied numbers.

Here, n is the total number of values.

Taking an example of two numbers in a given set of data as 4 and 2, the geometric mean is equal to. [sqrt{(4+2)} = sqrt{6} = 2.5]

The difference between the arithmetic mean and the geometric mean is the method. In the arithmetic mean, we add the numbers whereas in the geometric mean we calculate the product of the numbers.

[text{Geometric Mean = } sqrt[n]{prod_{i=1}^{n} x_{i}}]

C. Harmonic Mean

This is one of the methods of central tendency used in Statistics. It is the reciprocal of the arithmetic mean for a given set of data. The Harmonic Mean is based on all values from the data set and it is defined rigidly. It also provides the weightage of the mean in terms of large or small values depending on the data set. This is applied in time and average analysis.

To calculate the harmonic mean for a given set of data, where x1, x2, x3,…, xn are the individual items up to n terms, then,

[text{Harmonic Mean = } frac{n}{[(frac{1}{x_{1}}) + (frac{1}{x_{2}}) + (frac{1}{x_{3}}) + . . . + (frac{1}{x_{n}})]}]

(Image will be uploaded soon)

Properties of Mean

The sum of the deviations taken from the arithmetic mean is zero.
If the mean of n observations x1, x2, x3….,xn is x then (x1-x)+(x2-x)+(x3-x)…+(xn-x)=0. In short, ∑ (x-x)=0
If each observation is increased by p, the mean of new observations is also increased by p.
If the mean of n observations x1, x2, x3….,xn is x then the mean of (x1+p), (x2+p), (x3+p),….,(xn+p) is (x+p).
If each observation is decreased by p, the mean of new observations is also decreased by p.
If the mean of n observations x1, x2, x3….,xnis x then the mean of (x1-p), (x2-p), (x3-p),….,(xn-p) is (x-p).
If each observation is multiplied by p (where p≠0), the mean of new observations is also multiplied by p.
If the mean of n observations x1, x2, x3….,xn is x then the mean of px1, px2,px3,pxn is px.
If each observation is divided by p (where p≠0), the mean of new observations is also divided by p.
If the mean of n observations x1, x2, x3….,xn is x then the mean of

[ frac{X_{1}}{p} ,frac{X_{2}}{p} ,frac{X_{3}}{p} ,…frac{X_{n}}{p} is frac{bar{X}}{p}]

Why is the Average Called the Mean?

To find the mean, add all the data points and divide it by the total number of data points. In the case of Mathematics, we have been always taught that the average is the middle point of all the given numbers. The central value which is called the average in mathematics is called the mean in statistics.

Important points:

The mean is the mathematical average of a set of two or more numbers.
The arithmetic mean and the geometric mean are two types of mean that can be calculated.
Summing the numbers in a set and dividing by the total number gives you the arithmetic mean.
The geometric mean is more complicated and involves the multiplication of the numbers taking the nth root.
The mean helps to assess the performance of an investment or company over a period of time, and many other uses.

Источник

Types of means[edit]

Pythagorean means[edit]

Arithmetic mean (AM)[edit]

Geometric mean (GM)[edit]

Harmonic mean (HM)[edit]

Relationship between AM, GM, and HM[edit]

Statistical location[edit]

Mean of a probability distribution[edit]

Generalized means[edit]

Power mean[edit]

f-mean[edit]

Weighted arithmetic mean[edit]

Truncated mean[edit]

Interquartile mean[edit]

Mean of a function[edit]

Mean of angles and cyclical quantities[edit]

Fréchet mean[edit]

Trianglar sets[edit]

Swanson’s rule[edit]

Other means[edit]

See also[edit]

Notes[edit]

References[edit]

What is Mean in Statistics?

Mean Meaning

Mean Formula

Mean of Ungrouped Data

Mean of Grouped Data

Calculating Mean Using Direct Method

Calculating Mean Using Assumed Mean Method

Calculating Mean Using Step Deviation Method

How to Find Mean?

Types of Mean in Math

Arithmetic Mean

Weighted Mean

Geometric Mean

Harmonic Mean

FAQs on Mean

What is the Definition of Mean?

What is Mean Formula?

What is Mean Formula for Grouped Data?

What is Population Mean Symbol?

What is the Mean Formula for Ungrouped Data?

What is the Difference Between Mean and Median?

How To Find the Mean Using Mean Formula?

What are Different Types of Mean?

What is the Difference Between Arithmetic Mean and Weighted Mean?

What are the Applications of Mean in our Daily Lives?

How To Use the Mean Formula?

What is Sample Mean Symbol?

What is the Meaning of Mean in Maths?

Types of Mean

Arithmetic Mean

Geometric Mean

Harmonic Mean

Important Points on Mean

Mean FAQs

What Is a Mean?

Key Takeaways

Calculating The Means

Understanding Mean

Formulas for Arithmetic Mean and Geometric Mean

Arithmetic Mean

Arithmetic Mean

Geometric Mean

Geometric Mean

Example Mean Calculations

Examples of When Means Are Important in Investing

What is a mean in math?

How do you find the mean?

What is the difference between mean, median, and mode?

Why is mean important?

Is a mean the same as an average?

The Bottom Line

How to Find Mean?

Mean Formula

Mean of Negative Numbers

Mean Formula with Example

Different Types of Mean

Properties of Mean