From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Solving Word Problems in Mathematics
What Is a Word Problem? (And How to Solve It!)
Learn what word problems are and how to solve them in 7 easy steps.
Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances.
As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem.
As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.
If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?
Steps of Solving a Word Problem
To work through any word problem, students should do the following:
1. Read the problem: first, students should read through the problem once.
2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
3. Visualize the problem: drawing a picture or creating a diagram can be helpful.
Students can start visualizing simple or more complex problems by creating relevant images, from concrete (like drawings of putting away cookies from a jar) to more abstract (like tape diagrams). It can also help students clarify the operations they need to carry out. (next step!)
4. Determine the operation(s): next, students should determine the operation or operations they need to perform. Is it addition, subtraction, multiplication, division? What needs to be done?
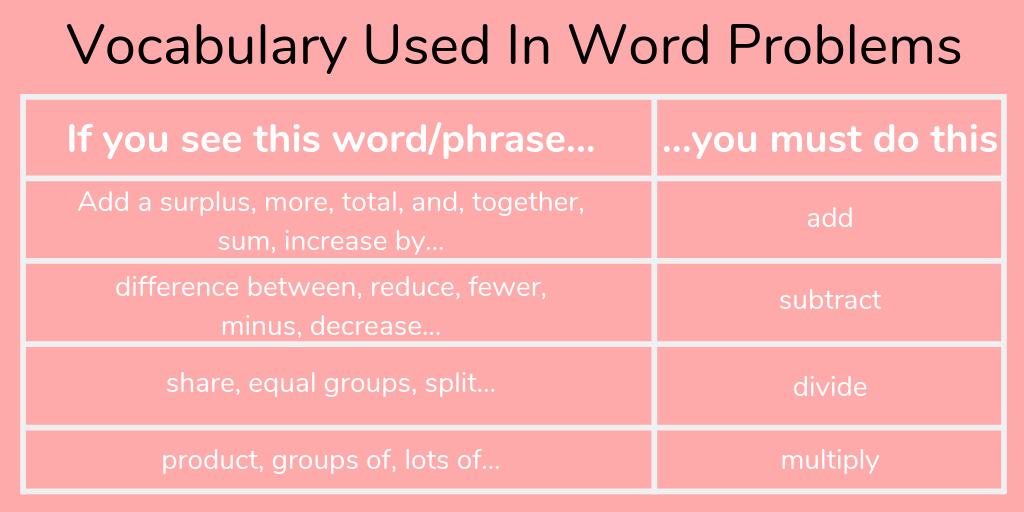
Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:
– Addition: add, more, total, altogether, and, plus, combine, in all;
– Subtraction: fewer, than, take away, subtract, left, difference;
– Multiplication: times, twice, triple, in all, total, groups;
– Division: each, equal pieces, split, share, per, out of, average.
These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems.
Another way to determine the operation is to search for certain situations, Jennifer Findley suggests. She has a great resource that lists various situations you might find in the most common word problems and the explanation of which operation applies to each situation.
5. Make a math sentence: next, students should try to translate the word problem and drawings into a math or number sentence. This means students might write a sentence such as 3 + 8 =.
Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence.
6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
7. Check the answer: finally, students should check their work to make sure that the answer is correct.
These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that!
At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises!
Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience.
Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.
For example, during the first steps, simple wording and animation help students realize what action the problem represents and find the connection between these actions and key words like “take away” and “left” that may signal them.
From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes.
Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.
Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations.
Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams!
To see the full exercise, follow this link.
The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task.
Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language.
These are the common steps that may help students overcome initial feelings of anxiety and fear of difficulty of the task they are given. Together with a teacher, they can master these foundational skills and build their confidence toward solving word problems. And Happy Numbers can facilitate this growth, providing varieties of engaging exercises and challenging word problems!
Solving word problems at KS1 and KS2 is an essential part of the new maths curriculum. Here you can find expert guidance on how to solve maths word problems as well as examples of the many different types of word problems primary school children will encounter with links to hundreds more.
What is a word problem?
A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem.
For example:
Importance of word problems within the national curriculum
The National Curriculum states that its mathematics curriculum “aims to ensure that all pupils:
- become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately;
- reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
- can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.”
To support this schools are adopting a ‘mastery’ approach to maths
The National Centre for Excellence in the Teaching of Mathematics (NCETM) have defined “teaching for mastery”, with some aspects of this definition being:
- Maths teaching for mastery rejects the idea that a large proportion of people ‘just can’t do maths’.
- All pupils are encouraged by the belief that by working hard at maths they can succeed.
- Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other.
- Significant time is spent developing deep knowledge of the key ideas that are needed to underpin future learning. The structure and connections within the mathematics are emphasised, so that pupils develop deep learning that can be sustained.
(The Essence of Maths Teaching for Mastery, 2016)

Year 3 to 6 Rapid Reasoning Worksheet for Weeks 1-6
Download for FREE 6 weeks of Rapid Reasoning worksheets. That include six weeks of daily reasoning and problem-solving questions for years 3, 4, 5 and 6!
Mastery helps children to explore maths in greater depth
One of NCETM’s Five Big Ideas in Teaching for Mastery (2017) is “Mathematical Thinking: if taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others”.
In other words – yes, fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learnt the number skills appropriate to their level/age, they should be progressed to the next level/age of number skills.
The mastery approach encourages exploring the breadth and depth of these concepts (once fluency is secure) through reasoning and problem solving.
See the following example:
| Year 6 objective | Fluency | Reasoning | Problem solving |
|---|---|---|---|
| Solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why. | 7,208 females attended a concert as well as 8,963 males. There were originally 20,000 seats on sale. How many empty seats were there at the concert? | Abdul says, “If I add any two 4-digit numbers together, it will make a 5-digit number.” Do you agree? Explain why. | Three pandas are eating bamboo sticks. There are 51 altogether. They all eat an odd number of sticks. How many bamboo sticks did they each eat? How many different ways can you do it? |
What sort of word problems might my child encounter at school?
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”. The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
|---|---|---|---|---|---|
| Number and place value | 6 | 9 | 7 | 5 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |
How to teach children to solve word problems?
Here are two simple strategies that can be applied to many word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
Let’s see how this can be applied to a word problem to help achieve the answer.
Solving a simple word problem
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
The bar model is always a brilliant way of representing problems, but if you are not familiar with this, there are always other ways of drawing it out.
Read more: What is a bar model
For example, for this question, you could draw 28 pupils (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
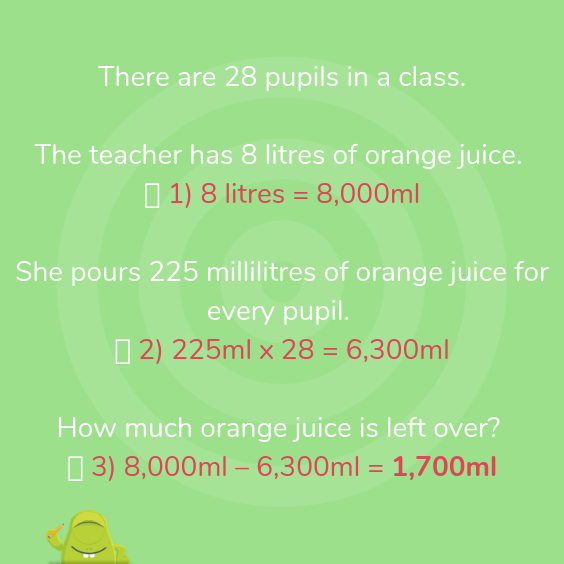
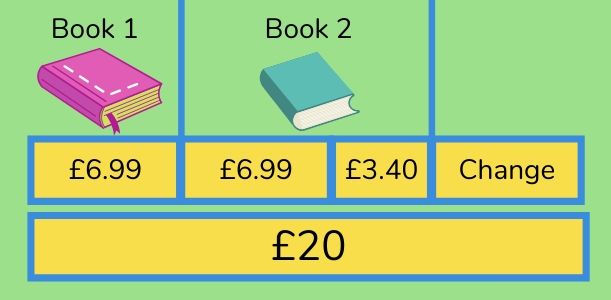
Solving a more complex word problem
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book.
She pays using a £20 notes.
What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
She pays using a £20 note.
What change does Mara get? 2) £20 – £17.38 = £2.62
Maths word problems for years 1 to 6
The more children learn about maths as the go through primary school, the trickier the word problems they face will become.
Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each primary year group
Word problems in Year 1
Throughout Year 1 a child is likely to be introduced to word problems with the help of concrete resources (pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.
An example of a word problem for Year 1 would be:
Chris is going to buy a cake for his mum which costs 80p. How many 20p coins would he need to do this?
Word problems in Year 2
Year 2 is a continuation of Year 1 when it comes to word problems, with children still using concrete maths resources to help them understand and visualise the problems they are working on
An example of a word problem for Year 2 would be:
A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?
Word problems in Year 3
With word problems for year 3, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the four operations such as addition and subtraction word problems, multiplication and division problems too.
This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.
Year 3 word problem: Geometry properties of shape
Shaun is making 3-D shapes out of plastic straws.
At the vertices where the straws meet, he uses blobs of modelling clay to fix them together
Here are some of the shapes he makes:
| Shape | Number of straws | Number of blobs of modelling clay |
|---|---|---|
| A | 8 | 5 |
| B | 12 | 8 |
| C | 6 | 4 |
One of Sean’s shapes is a cuboid. Which is it? Explain your answer.
Answer: shape B as a cuboid has 12 edges (straws) and 8 vertices (clay)
Year 3 word problem: Statistics
Year 3 are collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.

Answer: a) 9 b) 3 pebbles drawn
Top tip
By the time children are in Year 3 many of the word problems, even one-step story problems tend to be a variation on a multiplication problem. For this reason learning times tables becomes increasingly essential at this stage. One of the best things you can do to help with Year 3 maths at home is support your child to do this.
Word problems in Year 4
At this stage of their primary school career, children should feel confident using the written method for each of the four operations.
Word problems for year 4 will include a variety of problems, including 2-step problems and be children will be expected to work out the appropriate method required to solve each one.
Year 4 word problem: Number and place value
My number has four digits and has a 7 in the hundreds place.
The digit which has the highest value in my number is 2.
The digit which has the lowest value in my number is 6.
My number has 3 fewer tens than hundreds.
What is my number?
Answer: 2,746
Word problems in Year 5
One and 2-step word problems continue with word problems for year 5, but this is also the year that children will be introduced to word problems containing decimals.
These are some examples of Year 5 maths word problems.
Year 5 word problem: Fractions, decimals and percentages
Stan, Frank and Norm are washing their cars outside their houses.
Stan has washed 0.5 of his car.
Frank has washed 1/5 of his car.
Norm has washed 5% of his car.
Who has washed the most?
Explain your answer.
Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.05)
Word problems in Year 6
Word problems for year 6 shift from 2-step word problems to multi-step word problems. These will include fractions, decimals, percentages and time word problems.
Here are some examples of the types of maths word problems Year 6 will have to solve.
Year 6 word problem – Ratio and proportion
This question is from the 2018 key stage 2 SATs paper. It is worth 1 mark.
The Angel of the North is a large statue in England. It is 20 metres tall and 54 metres wide.
Ally makes a scale model of the Angel of the North. Her model is 40 centimetres tall. How wide is her model?
Answer: 108cm
Year 6 word problem – Algebra
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
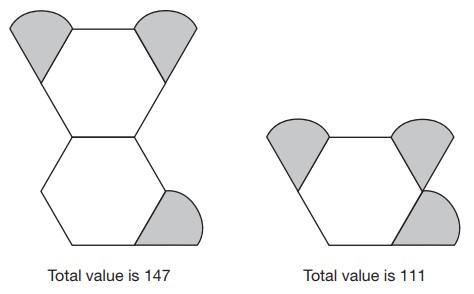
Amina is making designs with two different shapes.
She gives each shape a value.
Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
Year 6 word problem: Measurement
This question is from the 2018 KS2 SATs paper. It is worth 3 marks as it is a multi-step problem.
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
Answer: 1.7 litres or 1,700ml
Topic based word problems
The following examples give you an idea of the kinds of maths word problems your child will encounter for each of the 9 strands of maths in KS2.
Place value word problems
Place value word problem Year 5
This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37
Download free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction word problem Year 3
In Year 3 pupils will solve addition word problems and subtraction word problems with 2 and 3 digits.
Sam has 364 sweets. He gets given 142 more. He then gives 277 away. How many sweets is he left with? Answer: 229
Download free addition and subtraction word problems for Years 3, 4, 5 and 6
Addition word problem Year 3
Alfie thinks of a number. He subtracts 70. His new number is 12. What was the number Alfie thought of? Answer: 82
Subtraction word problem Year 6
The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC
More here: 25 addition and subtraction word problems
Multiplication and division word problems
Multiplication and division word problem Year 3
A baker is baking chocolate cupcakes. She melts 16 chocolate buttons to make the icing for 9 cakes. How many chocolate buttons will she need to melt to make the icing for 18 cakes? Answer: 32
Multiplication word problem Year 4
Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108
Download free multiplication word problems for Years 3, 4, 5 and 6
Division word problem Year 6
A factory produces 1,692 paintbrushes every day. They are packaged into boxes of 9. How many boxes does the factory produce every day? Answer: 188
Download our free division word problems worksheets for Years 3, 4, 5 and 6.
More here: 20 multiplication word problems
More here: 25 division word problems
Free resource: Use these four operations word problems to practise addition, subtraction, multiplication and division all together.
Fraction word problems
Fraction word problem Year 5
At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3
Download free fractions and decimals word problems worksheets for Years 3, 4, 5 and 6
More here: 28 fraction word problems
Decimals word problem Year 4 (crossover with subtraction)
Which two decimals that have a difference of 0.5? 0.2, 0.25, 0.4, 0.45, 0.6, 0.75. Answer: 0.25 and 0.75
Download free decimals and percentages word problems resources for Years 3, 4, 5 and 6
Percentage word problem Year 5
There are 350 children in a school. 50% are boys. How many boys are there? Answer: 175
Measurement word problem Year 3 (crossover with subtraction)
Lucy and Ffion both have bottles of strawberry smoothie. Each bottle contains 1 litre. Lucy drinks ½ of her bottle. Ffion drinks 300ml of her bottle. How much does each person have left in both bottles? Answer: Lucy = 500ml, Ffion = 300ml
More here: 25 percentage word problems
Money word problem Year 3
James and Lauren have different amounts of money. James has twelve 2p coins. Lauren has seven 5p coins. Who has the most money and by how much? Answer: Lauren by 11p.
More here: 25 money word problems
Area word problem Year 4
A rectangle measures 6cm by 5cm.
What is its area? Answer: 30cm2
Perimeter word problem Year 4
The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many metres has she swum? Answer: 108m
Ratio word problem Year 6 (crossover with measurement)
A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
More here: 24 ratio word problems
Bodmas word problem Year 6
Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
50 – 10 × 5 =
50 – 10 × 5 =
Volume word problem Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
How important are word problems when it comes to the SATs?
In the KS1 SATs, 58% (35/60 marks) of the test is comprised of maths ‘reasoning’ (word problems).
In KS2, this increases to 64% (70/110 marks) spread over two reasoning papers, each worth 35 marks. Considering children have, in the past, needed approximately 55-60% to reach the ‘expected standard’, it’s clear that children need regular exposure to and a solid understanding of how to solve a variety of word problems.
Children have the opportunity to practice SATs style word problems in Third Space Learning’s online one-to-one SATs revision programme. Personalised to meet the needs of each student, our programme helps to fill gaps and give students more confidence going in to the SATs exams.
Remember: The word problems can change but the maths won’t
It can be easy for children to get overwhelmed when they first come across word problems in KS2, but it is important that you remind them that whilst the context of the problem may be presented in a different way, the maths behind it remains the same.
Word problems are a good way to bring maths into the real world and make maths more relevant for your child, so help them practise, or even ask them to turn the tables and make up some word problems for you to solve.
This article while written by a teacher for teachers is also suitable for those at home supporting children with home learning. More free home learning resources are also available.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/
: Decision problem pertaining to equivalence of expressions
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that [math]displaystyle{ x,y,z }[/math] are symbols representing real numbers — then a relevant solution to the word problem would, given the input [math]displaystyle{ (x cdot y)/z mathrel{overset{?}{=}} (x/z)cdot y }[/math], produce the output EQUAL, and similarly produce NOT_EQUAL from [math]displaystyle{ (x cdot y)/z mathrel{overset{?}{=}} (x/x)cdot y }[/math].
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in a equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that [math]displaystyle{ x cdot y cdot z^{-1} }[/math] is the normal form of [math]displaystyle{ (x cdot y)/z }[/math], [math]displaystyle{ (x/z)cdot y }[/math], and [math]displaystyle{ (y/z)cdot x }[/math], and devise a transformation system to rewrite those expressions to that form, in the process proving that all equivalent expressions will be rewritten to the same normal form.[2] But not all solutions to the word problem use a normal form theorem — there are algebraic properties which indirectly imply the existence of an algorithm.[1]
While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms [math]displaystyle{ t_1,t_2 }[/math] containing variables have instances that are equal, or in other words whether the equation [math]displaystyle{ t_1 = t_2 }[/math] has any solutions. As a common example, [math]displaystyle{ 2 + 3 stackrel{?}{=} 8 + (-3) }[/math] is a word problem in the integer group ℤ,
while [math]displaystyle{ 2 + x stackrel{?}{=} 8 + (-x) }[/math] is a unification problem in the same group; since the former terms happen to be equal in ℤ, the latter problem has the substitution [math]displaystyle{ {x mapsto 3} }[/math] as a solution.
History
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]:342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]:354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]:355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]:355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system [math]displaystyle{ T:=(Sigma, R) }[/math] and two words (strings) [math]displaystyle{ u, v in Sigma^* }[/math], can [math]displaystyle{ u }[/math] be transformed into [math]displaystyle{ v }[/math] by applying rules from [math]displaystyle{ R }[/math]? Note that the rewriting here is one-way. The word problem is the accessibility problem for symmetric rewrite relations, i.e. Thue systems.[27]
The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finally presented semigroups.[29][30]
The word problem for groups
- Main page: Word problem for groups
Given a presentation [math]displaystyle{ langle Smid mathcal{R} rangle }[/math] for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max Dehn in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable.[31]
The word problem in combinatorial calculus and lambda calculus
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems
Solving the word problem: deciding if [math]displaystyle{ x stackrel{*}{leftrightarrow} y }[/math] usually requires heuristic search (red, green), while deciding [math]displaystyle{ xdownarrow = ydownarrow }[/math] is straightforward (grey).
The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under [math]displaystyle{ stackrel{*}{leftrightarrow} }[/math]?[29] The word problem for an ARS is undecidable in general. However, there is a computable solution for the word problem in the specific case where every object reduces to a unique normal form in a finite number of steps (i.e. the system is convergent): two objects are equivalent under [math]displaystyle{ stackrel{*}{leftrightarrow} }[/math] if and only if they reduce to the same normal form.[33]
The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity (typically binary operations), and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 =a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient space W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
- [math]displaystyle{ ((a^{-1} cdot a) cdot (b cdot b^{-1}))^{-1} stackrel{R2}{rightsquigarrow} (1 cdot (b cdot b^{-1}))^{-1} stackrel{R13}{rightsquigarrow} (1 cdot 1)^{-1} stackrel{R1}{rightsquigarrow} 1 ^{-1} stackrel{R8}{rightsquigarrow} 1 }[/math], and
- [math]displaystyle{ b cdot ((a cdot b)^{-1} cdot a) stackrel{R17}{rightsquigarrow} b cdot ((b^{-1} cdot a^{-1}) cdot a) stackrel{R3}{rightsquigarrow} b cdot (b^{-1} cdot (a^{-1} cdot a)) stackrel{R2}{rightsquigarrow} b cdot (b^{-1} cdot 1) stackrel{R11}{rightsquigarrow} b cdot b^{-1} stackrel{R13}{rightsquigarrow} 1 }[/math]
share the same normal form, viz. [math]displaystyle{ 1 }[/math]; therefore both terms are equal in every group.
As another example, the term [math]displaystyle{ 1 cdot (a cdot b) }[/math] and [math]displaystyle{ b cdot (1 cdot a) }[/math] has the normal form [math]displaystyle{ a cdot b }[/math] and [math]displaystyle{ b cdot a }[/math], respectively. Since the normal forms are literally different, the original terms cannot be equal in every group. In fact, they are usually different in non-abelian groups.
| A1 | [math]displaystyle{ 1 cdot x }[/math] | [math]displaystyle{ = x }[/math] |
| A2 | [math]displaystyle{ x^{-1} cdot x }[/math] | [math]displaystyle{ = 1 }[/math] |
| A3 | [math]displaystyle{ (x cdot y) cdot z }[/math] | [math]displaystyle{ = x cdot (y cdot z) }[/math] |
| R1 | [math]displaystyle{ 1 cdot x }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R2 | [math]displaystyle{ x^{-1} cdot x }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R3 | [math]displaystyle{ (x cdot y) cdot z }[/math] | [math]displaystyle{ rightsquigarrow x cdot (y cdot z) }[/math] |
| R4 | [math]displaystyle{ x^{-1} cdot (x cdot y) }[/math] | [math]displaystyle{ rightsquigarrow y }[/math] |
| R8 | [math]displaystyle{ 1^{-1} }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R11 | [math]displaystyle{ x cdot 1 }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R12 | [math]displaystyle{ (x^{-1})^{-1} }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R13 | [math]displaystyle{ x cdot x^{-1} }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R14 | [math]displaystyle{ x cdot (x^{-1} cdot y) }[/math] | [math]displaystyle{ rightsquigarrow y }[/math] |
| R17 | [math]displaystyle{ (x cdot y)^{-1} }[/math] | [math]displaystyle{ rightsquigarrow y^{-1} cdot x^{-1} }[/math] |
See also
- Conjugacy problem
- Group isomorphism problem
References
- ↑ 1.0 1.1 1.2 1.3 Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ↑ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Miller, Charles F. (2014). Downey, Rod. ed. «Turing machines to word problems». Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. ISBN 9781107338579. http://minerva-access.unimelb.edu.au/bitstream/11343/51723/1/cfm-lnl42-turings-legacy-pp329-385-2014.pdf. Retrieved 6 December 2021.
- ↑ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ↑ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ↑ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue» (in English). Bulletin of the European Association for Theoretical Computer Science 72: 256–269.
- ↑ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0071&DMDID=DMDLOG_0013&L=1.
- ↑ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0072&DMDID=DMDLOG_0039&L=1.
- ↑ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ↑ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen 166 (3): 208–228. doi:10.1007/BF01361168. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002296799&L=1.
- ↑ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen 178 (2): 119–130. doi:10.1007/BF01350654. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002300036&L=1.
- ↑ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ↑ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ↑ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue». Journal of Symbolic Logic 12 (1): 1–11. doi:10.2307/2267170. https://www.wolframscience.com/prizes/tm23/images/Post2.pdf. Retrieved 6 December 2021.
- ↑ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20.». Journal of Symbolic Logic 16 (3): 215. doi:10.2307/2266407.
- ↑ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics 52 (2): 491–505. doi:10.2307/1969481.
- ↑ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory» (in ru). Proceedings of the Steklov Institute of Mathematics 44: 1–143.
- ↑ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings) 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ↑ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings) 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ↑ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ↑ Boone, William W. (1958). «The word problem». Proceedings of the National Academy of Sciences 44 (10): 1061–1065. doi:10.1073/pnas.44.10.1061. PMID 16590307. PMC 528693. Bibcode: 1958PNAS…44.1061B. http://www.pnas.org/cgi/reprint/44/10/1061.pdf.
- ↑ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics 70 (2): 207–265. doi:10.2307/1970103.
- ↑ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 262 (1311): 455–475. doi:10.1098/rspa.1961.0132. Bibcode: 1961RSPSA.262..455H.
- ↑ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics 77 (1): 16–32. doi:10.2307/1970200.
- ↑ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups». http://www.personal.psu.edu/t20/logic/seminar/050517.pdf.
- ↑ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ↑ 27.0 27.1 Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ↑ Davis, Martin (1978). «What is a Computation?». Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. https://www.cs.princeton.edu/courses/archive/spring11/cos116/handouts/daviscomputation.pdf. Retrieved 5 December 2021.
- ↑ 29.0 29.1 Baader, Franz; Nipkow, Tobias (5 August 1999) (in en). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3. https://www.google.com/books/edition/Term_Rewriting_and_All_That/N7BvXVUCQk8C?hl=en&gbpv=1&pg=PA59.
- ↑
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» (in Russian). Doklady Akademii Nauk SSSR 173 (6): 1264–1266. ISSN 0869-5652. http://mi.mathnet.ru/eng/dan/v173/i6/p1264.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics 8 (2): 555–557. ISSN 0197-6788.
- ↑ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory» (in ru). Trudy Mat. Inst. Steklov 44: 1–143.
- ↑ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ↑ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ↑ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ↑ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics 42 (1): 325–329. doi:10.2307/1969001.
- ↑ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics 43 (1): 104–115. doi:10.2307/1968883.
- ↑ K. H. Bläsius and H.-J. Bürckert, ed (1992). Deduktionsssysteme. Oldenbourg. pp. 291.; here: p.126, 134
- ↑ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.

Word Problems: Word Problems are an important aspect of the primary curriculum because they require students to apply their understanding of various topics to “real-life” circumstances. They also assist students in becoming acquainted with mathematical terminology like more, fewer, subtract, difference, altogether, equal, share, multiply, reduced, etc.
A word problem consists of a description of a real-life scenario where a mathematical calculation is required to solve a problem. Students need to learn how to solve word problems as it enables them to apply mathematical concepts to various real-life scenarios. This means that to understand the word problem, students must be familiar with the terminology linked with the mathematical symbols they are used to. Let us learn in detail about Word Problems in this article.
What is a Word Problem?
In real life, mathematical problems do not usually present themselves as (2+3) or (6-4.) Instead, they are a bit more complex than we think. Authors of mathematical curriculum sometimes implement word problems to help students understand how they are related to the real world.
Learn 10th CBSE Exam Concepts
Word problems often show mathematics happening more naturally in the real world. Word problems can vary from simple to complex.
Examples:
Here are a few examples to get you some ideas:
1. Keerthi had (5) apples. Her mother gave her (7) more apples. Now, how many apples does Keerthi have altogether?
2. There were (18) pencils and (9) pens. How many more pencils than pens are there?
3. Spurti has one dozen eggs. Her friends ate (4) for breakfast. Now, how many eggs are left with Spurti?
4. There are (18) apples. Swetha, Priya, and Rachana want to eat them in equal share. How many apples will each of the friends get?
As you can notice, word problems involve addition, subtraction, multiplication, division, or even multiple operations.
Word Problems on Quadratic Equation
Handling Maths Word Problems in General
Steps for Solving a Word Problem:
To work out any word problem, follow the steps given below:
1. Read the Problem: First, read through the problem once.
2. Highlight Facts: Then, read through the problem again and underline or highlight important facts such as numbers or words that indicate an operation.
3. Draw a Picture: Drawing a picture sometimes help visualise the problem more clearly. It can also help understand clearly the algebraic operations that need to be carried out.
4. Determine the Operation(s): Next, determine the operation or operations that need to be performed. Is it addition, subtraction, multiplication, division? What needs to be done? Drawing the picture should be a big help in figuring this out. However, look for clues in words such as:
(i) Addition: add, total, brought, plus, altogether, and, combine, more, in all
(ii) Subtraction: subtract, fewer, take away, than, left
(iii) Multiplication: total, times, triple, twice, in all
(iv) Division: each, per, out of, equal pieces, split, average
Practice 10th CBSE Exam Questions
5. Make a Math Sentence: Next, translate the word problem and drawings into a math or number sentence. This means write a sentence such as (18+3=)
6. Solve the Problem: Then, solve the number sentence and find the solution—for example, (3+8=11.)
7. Check Your Answer: Finally, check the result obtained to ensure the correct answer.
With the above (7) steps, solving word problems in mathematics becomes easy.
Addition Word Problems
Addition word problems arise in situations where there is an increase of something or gain as a result of combining one or more numbers. Think of addition as combining parts to form a whole.
Example: Teena has (6) chocolates, her brother gives her (4) chocolates. How many chocolates in total does Teena have?
To find the total chocolates, we add the number of chocolates Teena has and the number of chocolates her brother gave her.

Thus, Teena has (10) chocolates now.
Attempt 10th CBSE Exam Mock Tests
Subtraction Word Problems
Subtraction word problems arise in situations where there is a decrease of something or loss as a result of deducting a number from another.
Example: Arya plucked (10) cherries from the tree, and her friend asked her to give (4) cherries to her. How many cherries are left with Arya?
Here we subtract the number of cherries given to Arya’s friend from the total cherries plucked by Arya.

Thus, the number of cherries left with Arya is (6.)
Multiplication Word Problems
Multiplication word problems are helpful for students to develop their multiplication knowledge by applying it to real-life situations. In this kind of multiplication word problem, one quantity is compared with another quantity, larger or smaller. Work out the multiplication problem using the clues provided.
Example: Ajay has two bunch of tomatoes. Each bunch has (4) tomatoes. What is the total number of tomatoes does Ajay have?
Here, we multiply the number of the bunch by the number of tomatoes in each bunch

Thus, Ajay has (8) tomatoes in total.
Division Word Problems
Division word problems are more confusing for students to understand. The words generally used in division word problems are “shared among” or “given to each” or similar phrases that imply total quantity to be split evenly into groups. We use division or multiplication when the problem involves equal parts of a whole.
Example: He divides (12) apples evenly among (4) friends. How many apples did John give to each of his friends?
To find how many apples John gave to each of his friends, we divide the total number of apples by the number of friends.

Hence, each of John’s friends gets (3) apples.
Fraction Word Problems
Fraction word problems look more complex, but in reality, fraction word problems are just as easy as those involving whole numbers. Here, one extra step of simplification may be needed in some cases. Students should know the operations with fractions to solve word problems on fractions.
Example: Swaroop had half an apple, and his mother gave him another quarter of an apple. What portion of apple does Swaroop have?
The given example is the addition word problem that involves fractions.
Here, we add the portion of apple Swaroop initially had with the portion his mother gives. i.e., (frac{1}{2} + frac{1}{4} = frac{{2 + 1}}{4} = frac{3}{4}.)

Thus, Swaroop has (frac{3}{4})th of apple.
Solved Examples
Q.1. The male population of a village is (76138,) and the female population is (13776.) What is the total population of the village?
Ans: Male population (=76138)
Female population (=13776)
Total population of the village (=) male population (+) female population (=76138+13776 )
(=89914 )

Thus, the total population of the village is (89914.)
Q.2. Likith had collected (208) coins. He lost of (52) coins. How many coins are left with Likith?
Ans: Total coins Likith collected (=208)
The number of coins lost (=52)
Number of coins left (=208 – 52=156)

Thus, the number of coins left is (156.)
Q.3. The cost of one shirt is (₹206.) A retailer wants to buy (68) such shirts. How much should he pay?
Ans: Given that the cost of one shirt (=₹206)
Number of shirts a retailer wants to buy (=68)
Total amount to be paid (=₹206×68)

Therefore, the total amount to be paid is (₹14008.)
Q.4 If (4472,{rm{kg}}) of rice is packed in (52) bags, how much rice will each bag contain?
Ans: Since (52) bags contain rice of (4472,{rm{kg}})
Therefore, (1) bag contains rice ( = left( {frac{{4472}}{{52}}} right){rm{kg}})
( = 86,{rm{kg}})

Thus, each bag of rice contains ( = 86,{rm{kg}}.)
Q.5. One-half of the students in a school are boys, (frac{4}{5}) of these boys are studying in lower classes. What fraction of boys are studying in lower classes?
Ans: Fraction of boys studying in school ( = frac{1}{2})
Fraction of boys studying in lower classes ( = frac{4}{5}) of (frac{1}{2})
( = frac{4}{5} times frac{1}{2})
( = frac{2}{5})
Therefore, (frac{2}{5}) of boys studying in lower classes.
Q.6. Celena planned to interview some candidates for a position in her office. If she scheduled half an hour to meet each of them, how much time did she schedule for all (6) candidates?
Ans: Time spent to meet each candidate ( = frac{1}{2}) hour
Number of applicants (=6)
Time scheduled for all (6) candidates ( = frac{1}{2} times 6 = 3) hours
Thus, Celena scheduled (3) hours for the interview.
Summary
In this article, we studied the meaning and steps to solve word problems. Then we have discussed in detail taking an example of how to do the addition word problem, subtraction, multiplication, division and fraction word problem.
We have solved word problem examples for students to understand the concept clearly.
Learn the Concepts on Unitary Method
Frequently Asked Questions on Word Problems
We have provided some frequently asked questions on Word Problems here:
Q.1. What are word problems in maths?
Ans: A word problem is a few sentences describing a real-life scenario where a problem needs to be solved by a mathematical calculation.
Q.2. What are numberless word problems?
Ans: Numberless word problems are designed to provide scaffolding that allows students to understand the underlying structure of word problems.
Q.3. What is addition word problems?
Ans: Addition word problems appear when there is a gain or an increase of something due to combining one or more numbers. Think of addition as combining parts to form a whole.
Q.4. What are the steps in solving word problems?
Ans: Solving word problem requires the following steps:
1. Read the problem
2. Highlight facts
3. Draw a picture
4. Determine the operation/s.
(i) Addition
(ii) Subtraction
(iii) Multiplication
(iv) Division
5. Make a mathematical sentence
6. Solve the problem
7. Verify your answer
Q.5. What is an example of a word problem?
Ans: The typical examples of word problems in algebra are distance problems, age problems, percentage problems, work problems, mixtures problems and number problems.
Now you are provided with all the necessary information on Maths word problems and we hope this detailed article is helpful to you. If you have any queries regarding this article, please ping us through the comment section below and we will get back to you as soon as possible.
: «Abstract algebra has an unrelated term word problem for groups.»
In mathematics education, the term word problem is often used to refer to any mathematical exercise where significant background information on the problem is presented as text rather than in mathematical notation [L Verschaffel, B Greer, E De Corte (2000) «Making Sense of Word Problems», Taylor & Francis] . As word problems often involve a narrative of some sort, they are occasionally also referred to as «story problems» and may vary in the amount of language used. John C. Moyer; Margaret B. Moyer; Larry Sowder; Judith Threadgill-Sowder (1984) «Story Problem Formats: Verbal versus Telegraphic» Journal for Research in Mathematics Education, Vol. 15, No. 1. (Jan., 1984), pp. 64-68. http://links.jstor.org/sici?sici=0021-8251%28198401%2915%3A1%3C64%3ASPFVVT%3E2.0.CO%3B2-V]
Example
A mathematical problem in mathematical notation:
: Solve for J::: «J» = «A» − 20:: «J» + 5 = («A» + 5)/2
might be presented in a word problem as follows:
:»John is twenty years younger than Amy, and in five years’ time he will be half her age. What is John’s age now?»
The answer to the word problem is that John is 15 years old. While the answer to the mathematical problem is J = 15 (and A =35).
Structure
Word problems can be examined on three levels:Perla Nesher Eva Teubal (1975)»Verbal Cues as an Interfering Factor in Verbal Problem Solving» Educational Studies in Mathematics, Vol. 6, No. 1. (Mar., 1975), pp. 41-51. http://links.jstor.org/sici?sici=0013-1954%28197503%296%3A1%3C41%3AVCAAIF%3E2.0.CO%3B2-H]
:Level a: the verbal formulation;:Level b: the underlying mathematical relations;:Level c: the symbolic mathematical expression.Word problems can be further analysed by examining their linguistic properties (Level a), their logico-mathematical properties (Level b) or their symbolic representations (Level c). Linguistic properties can include such variables as the number of words in the problem or the mean sentence length.Madis Lepik (1990) «Algebraic Word Problems: Role of Linguistic and Structural Variables», Educational Studies in Mathematics, Vol. 21, No. 1. (Feb., 1990), pp. 83-90., http://links.jstor.org/sici?sici=0013-1954%28199002%2921%3A1%3C83%3AAWPROL%3E2.0.CO%3B2-8.] The logico-mathematical properties can be classified in numerous ways, but one such scheme is too classify the quantities in the problem (assuming the word problem is primarily numerical) into known quantities (the values given in the text of the problem), wanted quantities (the values that need to be found) and auxiliary quantities (values that may need to be found as intermediate stages of the problem).
Purpose and use
Word problems commonly include mathematical modelling questions, where data and information about a certain system is given and a student is required to develop a model. For example:
# Jane has $5 and she uses $2 to buy something. How much does she have now?
# If the water level in a cylinder of radius 2 m is rising at a rate of 3 m per second, what is the rate of increase of the volume of water?
These examples are not only intended to force the students into developing mathematical models on their own, but may also be used to promote mathematical interest and understanding by relating the subject to real-life situations. The relevance of these situations to the students is varying. The situation in the first example is well-known to most people and may be useful in helping primary school students to understand the concept of subtraction. The second example, however, does not necessarily have to be «real-life» to a high school student, who may find that it is easier to handle the following problem:
: Given «r» = 2 and «dh»/»dt» = 3, find «d/dt» (π «r» 2× «h»).
Word problems are a common way to train and test understanding of underlying concepts within a descriptive problem, instead of solely testing the student’s capability to perform algebraic manipulation or other «mechanical» skills.
History and Culture
Word problems have a long history and examples can be found dating back to Babylonian times.
The Babylonians were strong believers in word problems. Apart from a few procedure texts for finding things like square roots, most Old Babylonian problems are couched in a language of measurement of everyday objects and activities. Students had to find lengths of canals dug, weights of stones, lengths of broken reeds, areas of fields, numbers of bricks used in a construction, and so on. Duncan J Melville (1999) «Old Babylonian Mathematics» http://it.stlawu.edu/%7Edmelvill/mesomath/obsummary.html] .
Ancient Egyptian mathematics also has examples of word problems. The Rhind Mathematical Papyrus includes a problem that can be translated as:
There are seven houses; in each house there are seven cats; each cat kills seven mice; each mouse has eaten seven grains of barley; each grain would have produced seven hekat. What is the sum of all the enumerated things. [http://www.math.buffalo.edu/mad/Ancient-Africa/mad_ancient_egypt_algebra.html#rhind79 Egyptian Algebra — Mathematicians of the African Diaspora ] ]
In more modern times the sometimes confusing and arbitrary nature of word problems has been the subject of satire. Gustav Flaubert wrote this nonsensical problem:
Since you are now studying geometry and trigonometry, I will give you a problem. A ship sails the ocean. It left Boston with a cargo of wool. It grosses 200 tons. It is bound for Le Havre. The mainmast is broken, the cabin boy is on deck, there are 12 passengers aboard, the wind is blowing East-North-East, the clock points to a quarter past three in the afternoon. It is the month of May. How old is the captain? [http://math.furman.edu/~mwoodard/ascquotf.html Mathematical Quotations — F ] ]
Word problems have also been satirised in The Simpsons:
Bart: 7:30am an express train traveling 60 miles per hour leaves Santa Fe bound for Phoenix, 520 miles away. At the same time, a local train traveling 30 miles an hour carrying 40 passengers leaves Phoenix bound for Santa Fe. It’s 8 cars long and always carries the same number of passengers in each car. An hour later, the number of passengers equal to half the number of minutes past the hour get off, but three times as many plus six get on. At the second stop, half the passengers plus two get off but twice as many get on as got on at the first stop.
Train conductor: Ticket, please.
Bart: I don’t have a ticket!
Train conductor: Come with me, boy.
[drags Bart off. Numbers circle Bart’s head]
We’ve got a stowaway, sir.
Bart: I’ll pay! How much?
[the train engineer is Martin, shoveling numbers into the engine.]
Martin: Twice the fare from Tucson to Flagstaff minus two-thirds of the fare from Albuquerque to El Paso! Ha ha ha ha!
[http://homepage.smc.edu/nestler_andrew/SimpsonsMath.htm Andrew Nestler’s Guide to Mathematics and Mathematicians on The Simpsons ] ]
References
External links
* [http://www.cut-the-knot.org/arithmetic/WProblem.shtml Word problems that lead to simple linear equations] at cut-the-knot
* [http://www.superteacherworksheets.com/word-problems.html Simpler Math Word Problems] that cover a variety of Mathematical topics
* [http://www.kwiznet.com/p/showCurriculum.php?curriculumID=40 Word Problems Lessons, Examples, & Quizzes]
* [http://www.mytestbook.com Math Word Problems Worksheets and Online Tests]
* [http://www.math10.com/en/algebra/word-problems.html Math Word Problems and Solutions]
Wikimedia Foundation.
2010.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
Though the majority of ACT math problems use diagrams or simply ask you to solve given mathematical equations, you will also see approximately 15-18 word problems on any given ACT (between 25% and 30% of the total math section). This means that knowing how best to deal with word problems will help you significantly when taking the test. Though there are many different types of ACT word problems, most of them are not nearly as difficult or cumbersome as they may appear.
This post will be your complete guide to ACT word problems: how to translate your word problems into equations and diagrams, the different types of word problems you’ll see on the test, and how best to go about solving your word problems for test day.
What Are Word Problems?
A word problem is any problem that is based mostly or entirely on written description and does not provide you with an equation, diagram, or graph. You must use your reading skills to translate the words of the question into a workable math problem and then solve for your information.
Word problems will show up on the test for a variety of reasons. Most of the time, these types of questions act to test your reading and visualization skills, as well act as a medium to deliver questions that would otherwise be untestable. For instance, if you must determine the number of sides of an unknown polygon based on given information, a diagram would certainly give the game away!
Translating Word Problems Into Equations or Drawings
In order to translate your word problems into actionable math equations that you can solve, you’ll need to know and utilize some key math terms. Whenever you see these words, you can translate them into the proper action. For instance, the word “product” means “the value of two or more values that have been multiplied together,” so if you need to find “the product of a and b,” you’ll need to set up your equation with $a * b$.
|
Key Terms |
Mathematical Action |
|
Sum, increased by, added to, total of |
+ |
|
Difference, decreased by, subtracted from |
— |
|
Product, times |
* or x |
|
Divided by |
/ or ÷ |
|
Equals, is, are, equivalent, same |
= |
|
Is less than |
< |
|
Is greater than |
> |
|
Is less than or equal to |
≤ |
|
Is greater than or equal to |
≥ |
Let’s take a look at this in action with an example problem:
We have two different cable companies that each have different rates for installation and different monthly fees. We are asked to find out how many months it will take for the cost for each company to be the «same,» which means we must set the two rates equal.
Uptown Cable charges 120 dollars for installation plus 25 dollars a month. We do not know how many months we’re working with, so we will have:
$120 + 25x$
Downtown Cable charges 60 dollars for installation and 35 dollars per month. Again, we don’t know how many months we’re working with, but we know they will be the same, so we will have:
$60 + 35x$
And, again, because we are finding the amount of months when the cost is the «same,» we must set our rates equal.
$120 + 25x = 60 + 35x$
From here, we can solve for $x$, since it is a single variable equation.
[Note: the final answer is G, 6 months]
Learning the language of ACT word problems will help you to unravel much of the mystery of these types of questions.
Typical ACT Word Problems
ACT word problems can be grouped into two major categories: word problems where you must simply set up an equation and word problems in which you must solve for a specific piece of information.
Word Problem Type 1: Setting Up an Equation
This is the less common type of word problem on the test, but you’ll generally see it at least once or twice. You’ll also usually see this type of word problem first. For this type of question, you must use the given information to set up the equation, even though you don’t need to solve for the missing variable.
Almost always, you’ll see this type of question in the first ten questions on the test, meaning that the ACT test-makers consider them fairly “easy.” This is due to the fact that you only have to provide the set-up and not the execution.
We consider a “profit” to be any money that is gained, so we must always subtract our costs from our earnings. We know that Jones had to invest 10 million starting capital, so he is only making a profit if he has earned more than 10 million dollars. This means we can eliminate answer choices C, D, and E, as they do not account for this 10 million.
Now each boat costs Jones 7,000 dollars to make and he sells them for 20,000. This means that he earns a profit of:
$20,000 — 7,000$
$13,000$ per boat.
If $x$ represents our number of boats, then our final equation will be:
$13,000x — 10,000,000$
Our final answer is A, $13,000x — 10,000,000$
Word Problem Type 2: Solving for Your Information
Other than the few set-up word questions you’ll see, the rest of your ACT word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of ACT math topics, including averages, single variable equations, and probabilities, among others. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
This question is a rare example of a time in which not every piece of given information is needed to solve the problem. For most ACT word questions, all your given information will come into play at some point, but this is not the case here (though you can use all of your information, should you so choose).
For example, we are told that 25% of a given set of jelly beans are red. 25% translates to $1/4$ because 25% is the same as $25/100$ (or $1/4$). If we are being asked to find how many jelly beans are NOT red, then we know it would be $3/4$ because 100% is the same as 1, and 1 — $1/4$ = $3/4$.
So we didn’t need to know that there were 400 jellybeans to know that our final answer is H, $3/4$.
Alternatively, we could use all of our given information and find 25% of 400 in order to find the remaining jelly beans.
$400 * {1/4}$ or $400/4$
$100$
If 100 jellybeans are red, then 400 — 100 = 300 jelly beans are NOT red. This means that the not-red jelly beans make up,
$300/400$
$3/4$ of the total number of jelly beans.
Again, our final answer is H, $3/4$
You might also be given a geometry problem as a word problem, which may or may not be set up with a scenario as well.
Geometry questions will be presented as word problems typically because the test-makers felt the problem would be too easy to solve had you been given a diagram.
The test-makers didn’t give us a diagram, so let’s make ourselves one and fill it in with what we know so far.
We know from our studies of parallelograms that opposite side pairs will be equal, so we know that the opposite side of our given will also be 12.
Now we can use this information to subtract from our total perimeter.
$72 — 12 — 12$
$48$
Again, opposite sides will be equal and we know that the sum of the two remaining sides will be 48. This means that each remaining side will be:
$48/2$
$24$
Now we have four sides in the pairings of 12 and 24.
Our final answer is C, 12, 12, 24, 24.
Now, how do we put our knowledge to its best effect? Let’s take a look.
ACT Math Strategies for Your Word Problems
Though you’ll see word problems on a myriad of different types of ACT math topics, there are still a few techniques you can apply to solve your word problems as a whole.
#1: Draw It Out
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what, exactly, you’re working with. For instance, let’s look at how a picture can help you solve a ratio/division problem:
Let’s start by first drawing our sandwich and Jerome’s portion of it.
Now let’s divvy off Kevin’s portion and, by the remainder, Seth’s as well.
By seeing the problem visually, we can see that the ratio of Jerome’s share, to Kevin’s, to Seth’s will go in descending order of size. This let’s us eliminate answer choices A, B, and C, and leaves us with answer choices D and E.
Just by drawing it out and using process of elimination, and without knowing anything else about ratios, we have a 50-50 shot of guessing the right answer. And, again, without knowing anything else about fractions or ratios, we can make an educated guess between the two options. Since Jerome’s share doesn’t look twice as large as Kevin’s, our answer is probably not E.
This leaves us with our final answer D, 3:2:1.
[Note: for a breakdown on how to solve this problem using fractions and ratios instead of using a diagram and educated guessing, check out our guide to ACT fractions and ratios.]
As for geometry problems, remember—you’re often given a word problem as a word problem because it would be too simple to solve had you had a diagram to work with from the get-go. So take back the advantage and draw the picture yourself. Even a quick and dirty sketch can help you visualize the problem much easier than you can in your head and help keep all your information clear.
#2: Memorize Important Terms
If you’re not used to translating English words into mathematical equations, then ACT word problems can sound like so much nonsense and leave you floundering to set up the proper equation. Look to the chart and learn how to translate your keywords into their math equivalents. Doing so will help you to understand exactly what the problem is asking you to find.
There are free ACT math questions available online, so memorize your terms and then practice on real ACT word problems to make sure you’ve got your definitions down and can apply them to real problems.
#3: Underline and Write Out the Key Information
The key to solving a word problem is bringing together all the relevant pieces of given information and putting them in the right places. Make sure you write out all your givens on the diagram you’ve drawn (if the problem calls for a diagram) and that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline them in the problem and then write them out yourself before you set up your equation, so take a moment to perform this step.
#4: Pay Close Attention to Exactly What Is Being Asked of You
Little is more frustrating than solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of $x$ or $x + y$? Better to make sure before you start what you’re supposed to find than realize two minutes down the line that you have to solve the problem all over again.
#5: Brush Up on Any Specific Math Topic in Which You Feel Weak
You are likely to see both diagram/equation problems and word problems for any given ACT math topic on the test. Many of the topics can swing either way, which is why there are so many different types of word problems and why you’ll need to know the ins and outs of any particular math topic in order to solve its corresponding word problem. For example, if you don’t know how to properly set up a system of equations problem, you will have a difficult time of it when presented with a word problem on the topic.
So understand that solving a word problem is a two-step process: it requires you to both understand how word problems themselves work and to understand the math topic in question. If you have any areas of mathematical weakness, now is a good time to brush up on them, or else the word problem might be trickier than you were expecting.
All set? Time to shine!
Test Your Knowledge
Now to put your word problem know-how to the test with real ACT math problems.
Answers: K, C, A, E
Answer Explanations:
1) First, let us make a sketch of what we have, just so we can keep our measurements straight. We know we have two triangles, one smaller than the other, and the hypotenuse of the smaller triangle is 5.
Now our triangles are in a ratio of 2:5, so if the hypotenuse of the smaller triangle is 5, we can find the hypotenuse of the larger triangle by setting them up in a proportion.
$2/5 = 5/x$
$2x = 25$
$x = 12.5$
Our final answer is K, 12.5.
2) Because we are dealing with a hypothetical number that is increasing and decreasing based on percentage, we can solve this problem in one of two ways—by using algebra or by plugging in our own numbers.
Solving Method 1: Algebra
If we assign our hypothetical number as $x$, we can say that $x$ is increased by 25% by saying:
$x + 0.25x$
Which gives us:
$1.25x$
Now, we can decrease this value by 20% by saying:
$1.25x — (1.25x * 0.2)$
$1.25x — 0.25x$
This leaves us with:
$1x$ or 100% of our original number.
Our final answer is C, 100%.
Solving Method 2: Plugging in Numbers
Alternatively, we can use the same basic process, but make it a little simpler by using numbers instead of variables.
Let’s say our original number is 100. (Why 100? Why not! Our number can literally be anything and 100 is an easy number to work with.)
So if we need to increase 100 by 25%, we first need to find 25% of 100 and then add that to 100.
$100 + (0.25)100$
$100 + 25$
$125$
Now we need to decrease this value by 20%, so we would say:
$125 — (0.2)125$
$125 — 25$
$100$
We are left with the same number we started with, which means we are left with 100% of the number we started with.
Again, our final answer is C, 100%.
3) Let’s first begin by drawing a picture of our scene. We know that one vertex of the square is at (3, 0), so we can mark it on a coordinate plane.
Now, we are told that each side of the square is 3 cm long. To make life simple, we can start by marking all the possible vertexes attached to our known vertex at (3, 0) straight up, down, and side to side. If no answers match, we can then look to vertexes at different angles.
Our possible vertexes are:
(0, 0), (6, 0), 3, 3) and (3, -3)
One of our possible vertexes is at (6, 0 and this matches one of our answer choices, so we can stop here.
Our final answer is A, (6, 0).
4) We are told that Ms. Lopez throws out the lowest test score and then averages the remaining scores. Because Victor’s scores are already in ascending order, we can throw out the first score of 62.
Now to find the average of the remaining 4 scores, let us add them together and then divide by the number of scores.
$(78 + 83 + 84 + 93)/4$
$338/4$
$84.5$
Our final answer is E, 84.5.

Picture: John Morris/Flickr
The Take-Aways
Word problems comprise a significant portion of the ACT, so it’s a good idea to understand how they work and how to translate the words into a proper equation. But remember that translating your word problems is still only half the battle.
You must also supplement this knowledge of how to solve word problems with a solid understanding of the math topic in question. For example, it won’t do a lot of good if you can translate a probability word problem if you don’t understand exactly how probabilities work. So be sure to not only learn how to approach your word problems, but also hone your focus on any math topics you feel you need to improve upon. You can find links to all of our ACT math topic guides here to help your studies.
What’s Next?
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.