What is word embeddings

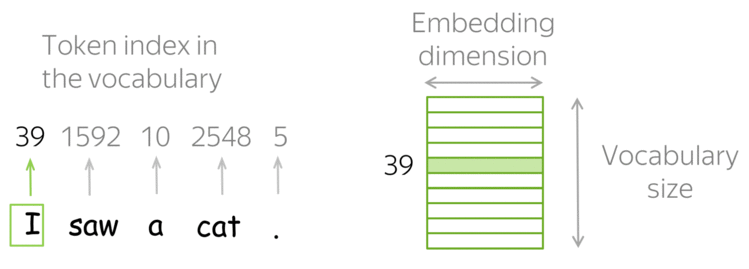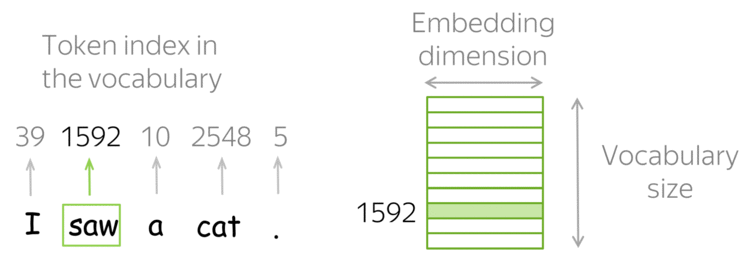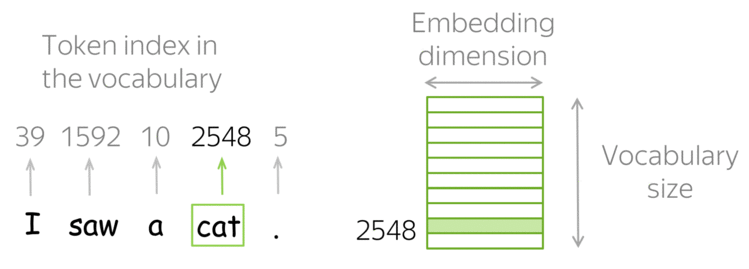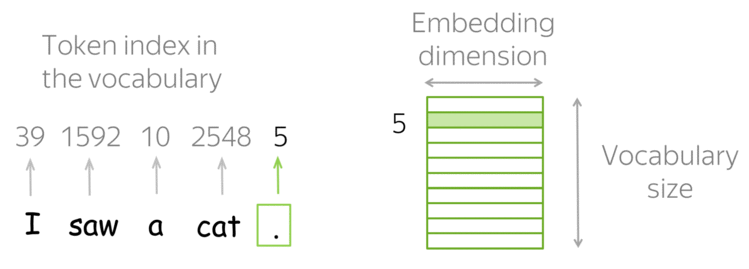
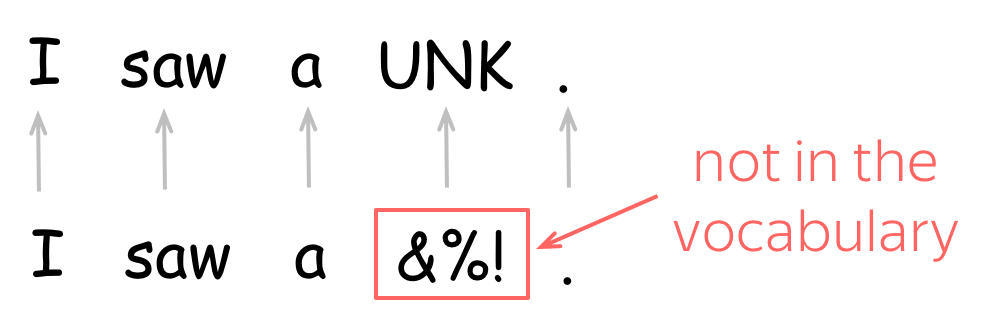
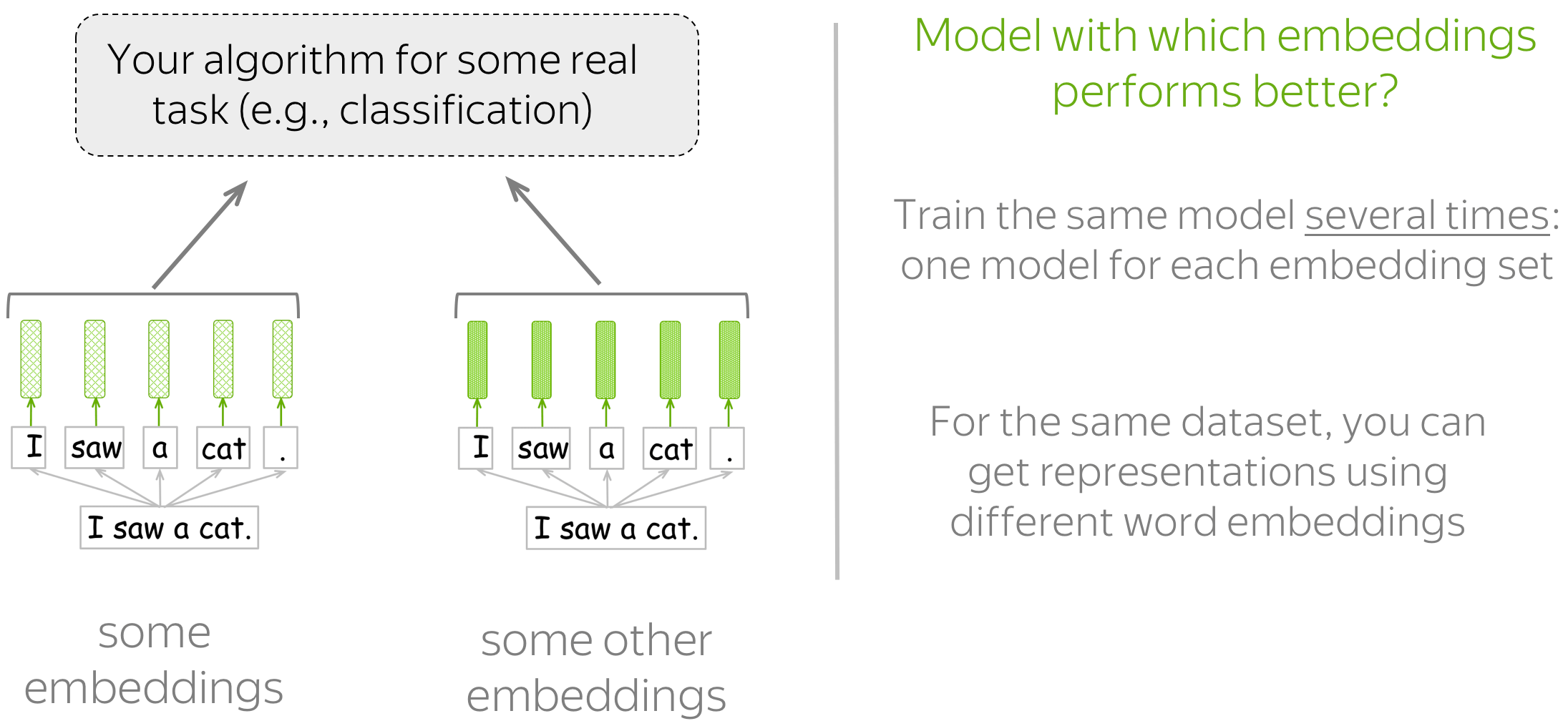
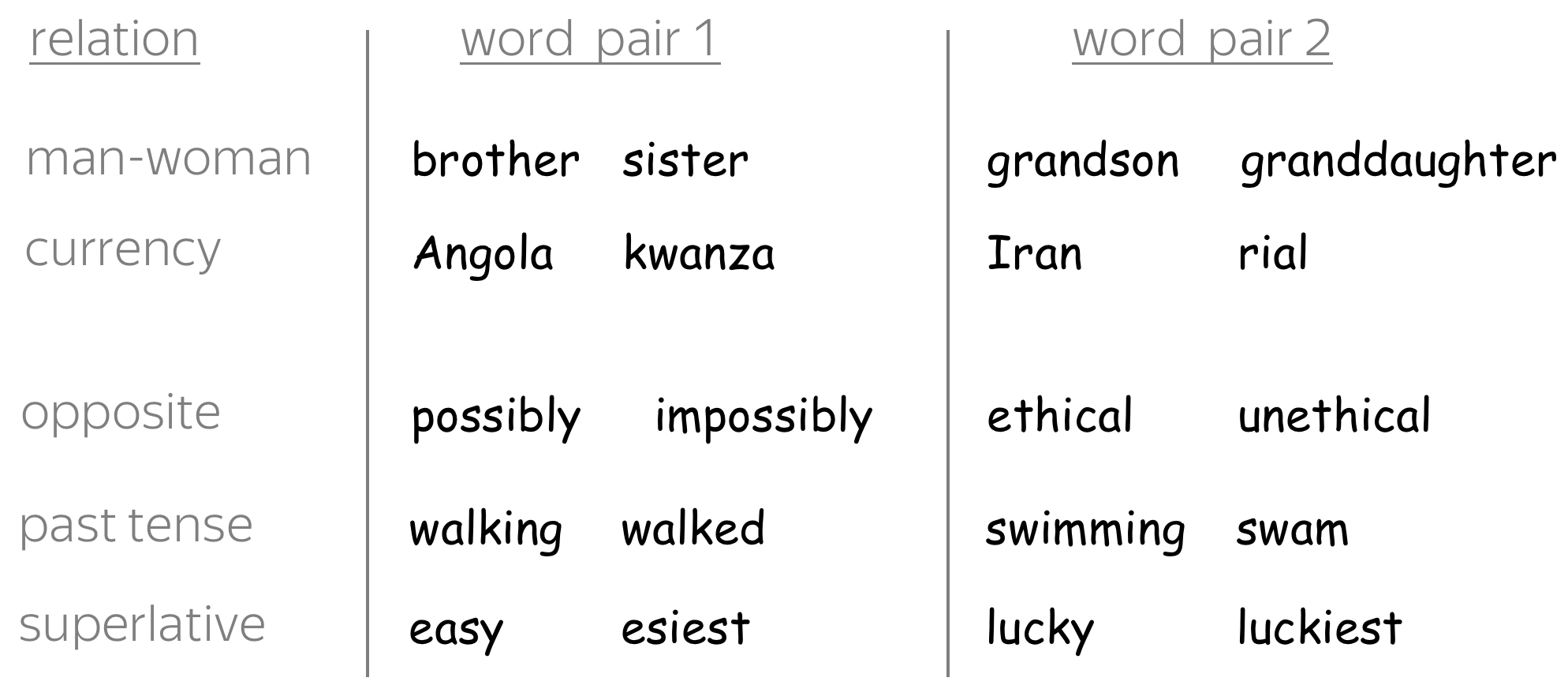
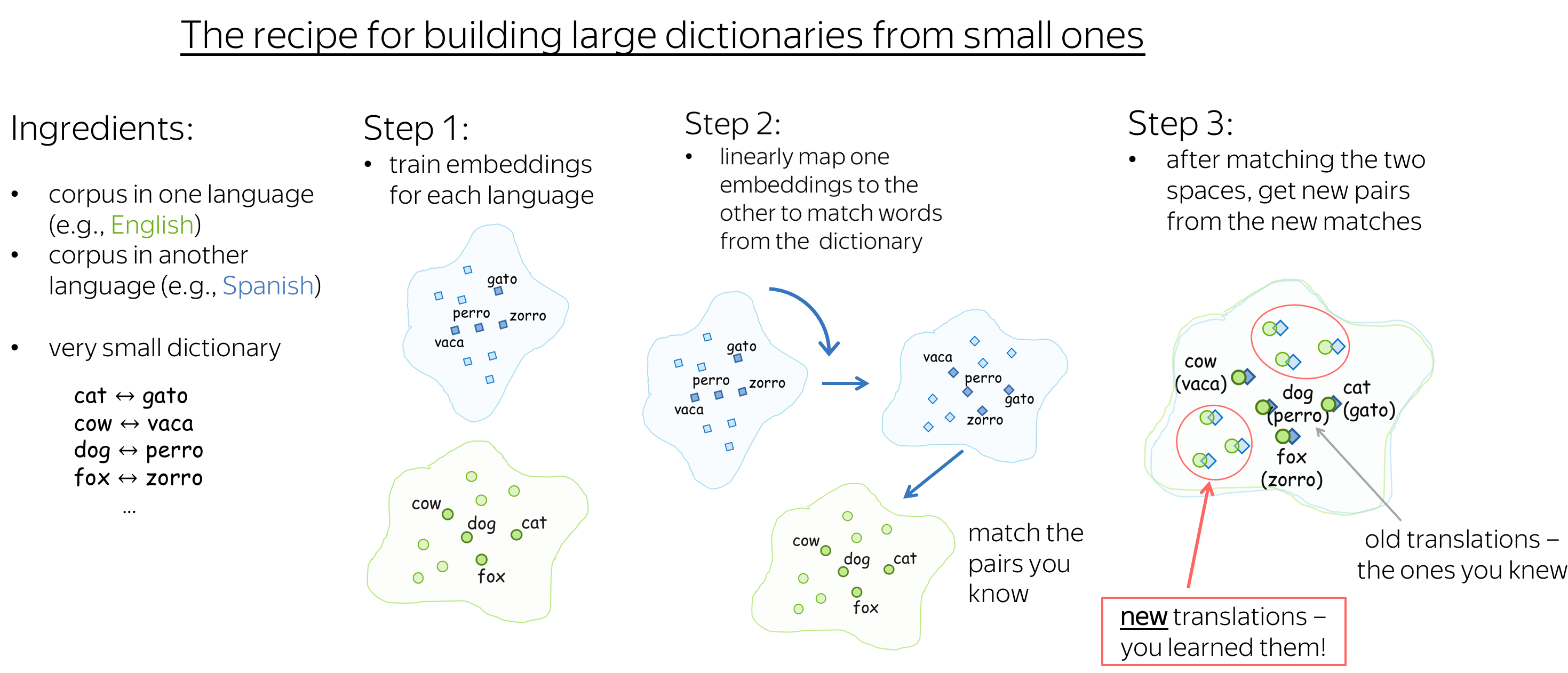
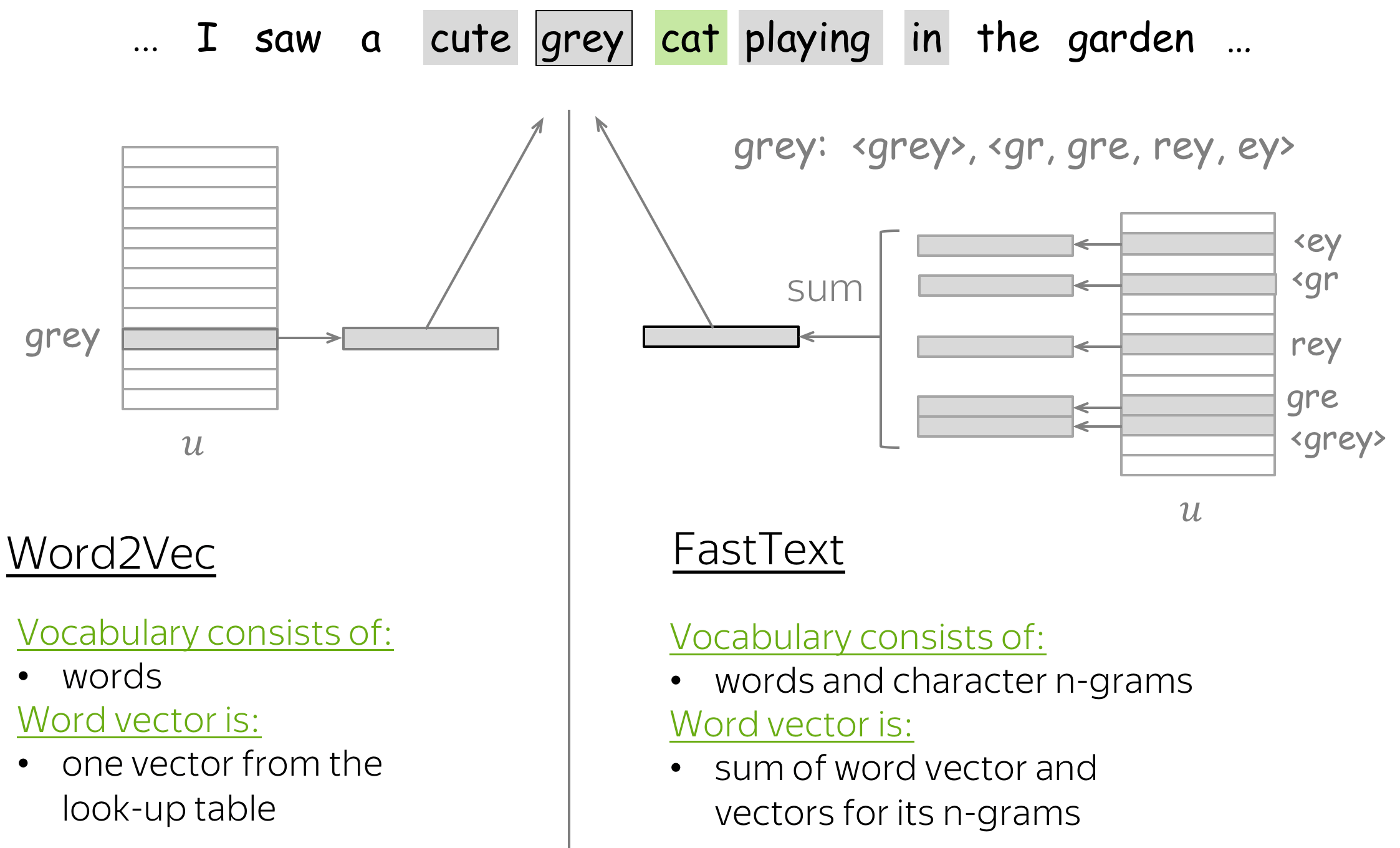
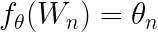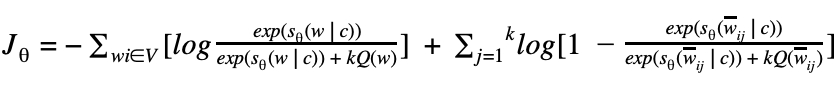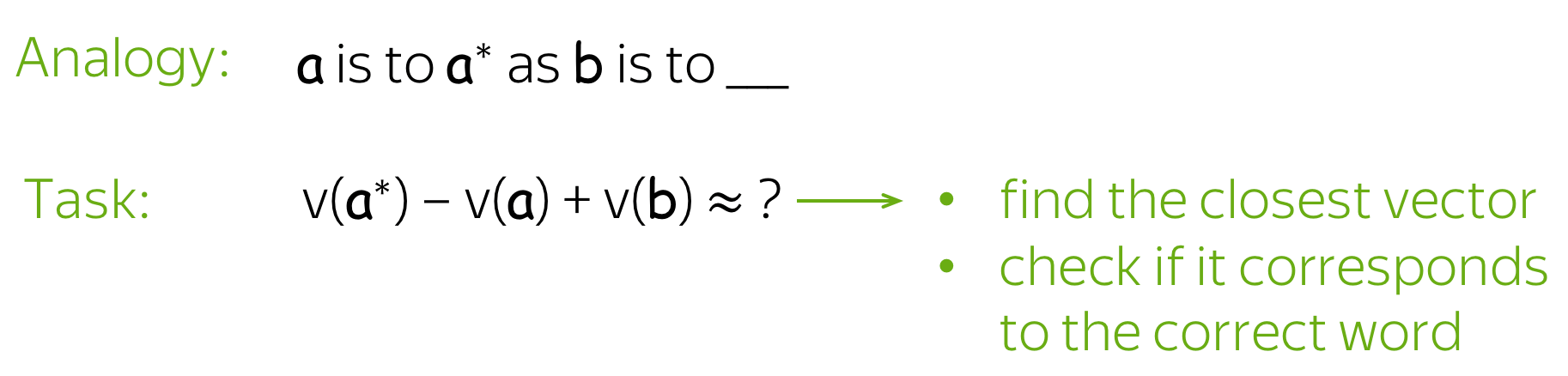From Wikipedia, the free encyclopedia

In natural language processing (NLP), a word embedding is a representation of a word. The embedding is used in text analysis. Typically, the representation is a real-valued vector that encodes the meaning of the word in such a way that words that are closer in the vector space are expected to be similar in meaning.^[1] Word embeddings can be obtained using language modeling and feature learning techniques, where words or phrases from the vocabulary are mapped to vectors of real numbers.

Methods to generate this mapping include neural networks,^[2] dimensionality reduction on the word co-occurrence matrix,^[3][4][5] probabilistic models,^[6] explainable knowledge base method,^[7] and explicit representation in terms of the context in which words appear.^[8]

Word and phrase embeddings, when used as the underlying input representation, have been shown to boost the performance in NLP tasks such as syntactic parsing^[9] and sentiment analysis.^[10]

Development and history of the approach[edit]

In Distributional semantics, a quantitative methodological approach to understanding meaning in observed language, word embeddings or semantic vector space models have been used as a knowledge representation for some time.^[11] Such models aim to quantify and categorize semantic similarities between linguistic items based on their distributional properties in large samples of language data. The underlying idea that «a word is characterized by the company it keeps» was proposed in a 1957 article by John Rupert Firth,^[12] but also has roots in the contemporaneous work on search systems^[13] and in cognitive psychology.^[14]

The notion of a semantic space with lexical items (words or multi-word terms) represented as vectors or embeddings is based on the computational challenges of capturing distributional characteristics and using them for practical application to measure similarity between words, phrases, or entire documents. The first generation of semantic space models is the vector space model for information retrieval.^[15][16][17] Such vector space models for words and their distributional data implemented in their simplest form results in a very sparse vector space of high dimensionality (cf. Curse of dimensionality). Reducing the number of dimensions using linear algebraic methods such as singular value decomposition then led to the introduction of latent semantic analysis in the late 1980s and the Random indexing approach for collecting word cooccurrence contexts.^{[18][19][20][21]} In 2000 Bengio et al. provided in a series of papers the «Neural probabilistic language models» to reduce the high dimensionality of words representations in contexts by «learning a distributed representation for words».^[22][23]

A study published in NeurIPS (NIPS) 2002 introduced the use of both word and document embeddings applying the method of kernel CCA to bilingual (and multi-lingual) corpora, also providing an early example of self-supervised learning of word embeddings ^[24]

Word embeddings come in two different styles, one in which words are expressed as vectors of co-occurring words, and another in which words are expressed as vectors of linguistic contexts in which the words occur; these different styles are studied in (Lavelli et al., 2004).^[25] Roweis and Saul published in Science how to use «locally linear embedding» (LLE) to discover representations of high dimensional data structures.^[26] Most new word embedding techniques after about 2005 rely on a neural network architecture instead of more probabilistic and algebraic models, since some foundational work by Yoshua Bengio and colleagues.^[27][28]

The approach has been adopted by many research groups after advances around year 2010 had been made on theoretical work on the quality of vectors and the training speed of the model and hardware advances allowed for a broader parameter space to be explored profitably. In 2013, a team at Google led by Tomas Mikolov created word2vec, a word embedding toolkit that can train vector space models faster than the previous approaches. The word2vec approach has been widely used in experimentation and was instrumental in raising interest for word embeddings as a technology, moving the research strand out of specialised research into broader experimentation and eventually paving the way for practical application.^[29]

Polysemy and homonymy[edit]

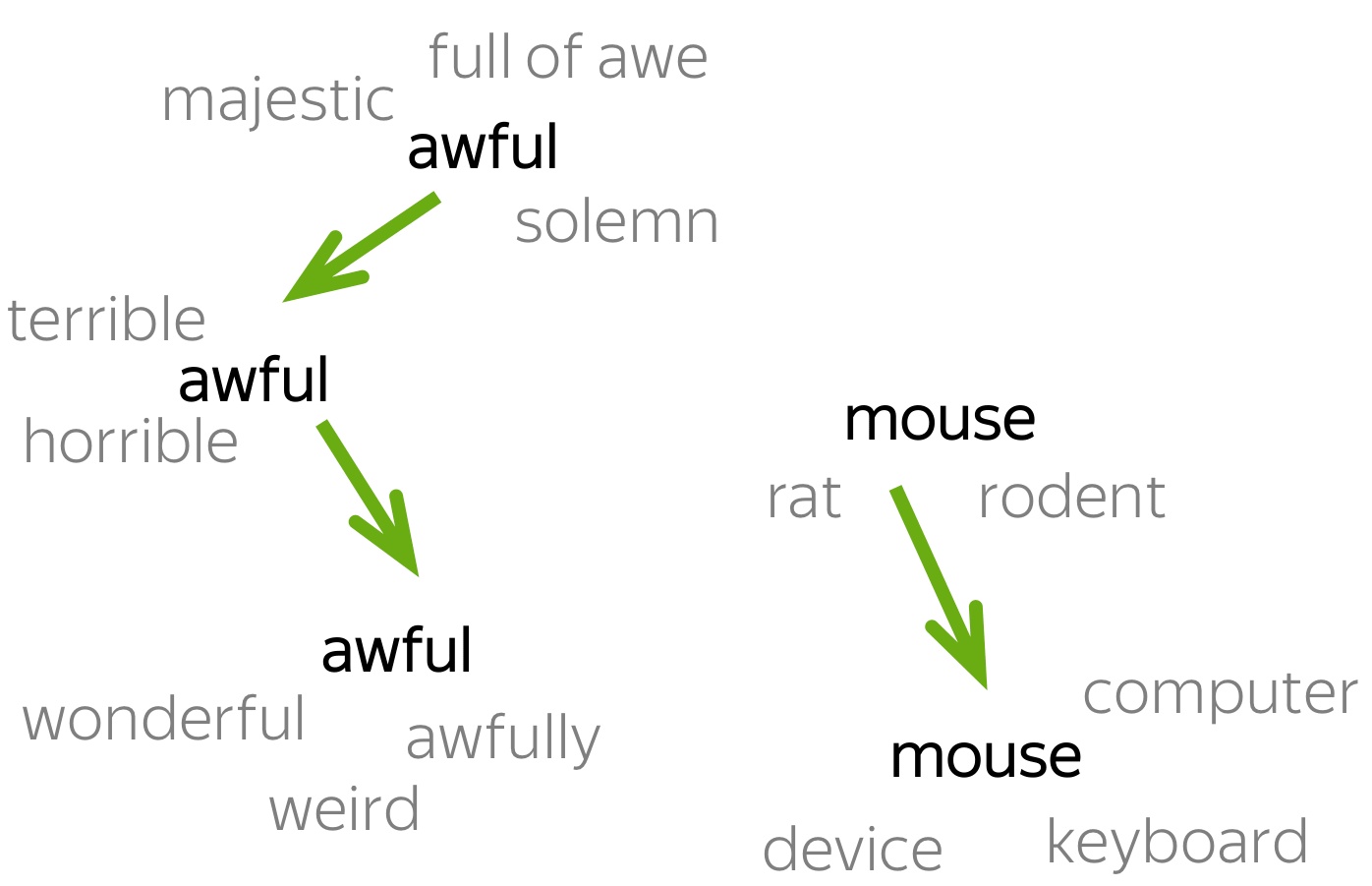
Historically, one of the main limitations of static word embeddings or word vector space models is that words with multiple meanings are conflated into a single representation (a single vector in the semantic space). In other words, polysemy and homonymy are not handled properly. For example, in the sentence «The club I tried yesterday was great!», it is not clear if the term club is related to the word sense of a club sandwich, baseball club, clubhouse, golf club, or any other sense that club might have. The necessity to accommodate multiple meanings per word in different vectors (multi-sense embeddings) is the motivation for several contributions in NLP to split single-sense embeddings into multi-sense ones.^[30][31]

Most approaches that produce multi-sense embeddings can be divided into two main categories for their word sense representation, i.e., unsupervised and knowledge-based.^[32] Based on word2vec skip-gram, Multi-Sense Skip-Gram (MSSG)^[33] performs word-sense discrimination and embedding simultaneously, improving its training time, while assuming a specific number of senses for each word. In the Non-Parametric Multi-Sense Skip-Gram (NP-MSSG) this number can vary depending on each word. Combining the prior knowledge of lexical databases (e.g., WordNet, ConceptNet, BabelNet), word embeddings and word sense disambiguation, Most Suitable Sense Annotation (MSSA)^[34] labels word-senses through an unsupervised and knowledge-based approach, considering a word’s context in a pre-defined sliding window. Once the words are disambiguated, they can be used in a standard word embeddings technique, so multi-sense embeddings are produced. MSSA architecture allows the disambiguation and annotation process to be performed recurrently in a self-improving manner.^[35]

The use of multi-sense embeddings is known to improve performance in several NLP tasks, such as part-of-speech tagging, semantic relation identification, semantic relatedness, named entity recognition and sentiment analysis.^[36][37]

As of the late 2010s, contextually-meaningful embeddings such as ELMo and BERT have been developed.^[38] Unlike static word embeddings, these embeddings are at the token-level, in that each occurrence of a word has its own embedding. These embeddings better reflect the multi-sense nature of words, because occurrences of a word in similar contexts are situated in similar regions of BERT’s embedding space.^[39][40]

For biological sequences: BioVectors[edit]

Word embeddings for n-grams in biological sequences (e.g. DNA, RNA, and Proteins) for bioinformatics applications have been proposed by Asgari and Mofrad.^[41] Named bio-vectors (BioVec) to refer to biological sequences in general with protein-vectors (ProtVec) for proteins (amino-acid sequences) and gene-vectors (GeneVec) for gene sequences, this representation can be widely used in applications of deep learning in proteomics and genomics. The results presented by Asgari and Mofrad^[41] suggest that BioVectors can characterize biological sequences in terms of biochemical and biophysical interpretations of the underlying patterns.

Game design[edit]

Word embeddings with applications in game design have been proposed by Rabii and Cook^[42] as a way to discover emergent gameplay using logs of gameplay data. The process requires to transcribe actions happening during the game within a formal language and then use the resulting text to create word embeddings. The results presented by Rabii and Cook^[42] suggest that the resulting vectors can capture expert knowledge about games like chess, that are not explicitly stated in the game’s rules.

Sentence embeddings[edit]

The idea has been extended to embeddings of entire sentences or even documents, e.g. in the form of the thought vectors concept. In 2015, some researchers suggested «skip-thought vectors» as a means to improve the quality of machine translation.^[43] A more recent and popular approach for representing sentences is Sentence-BERT, or SentenceTransformers, which modifies pre-trained BERT with the use of siamese and triplet network structures.^[44]

Software[edit]

Software for training and using word embeddings includes Tomas Mikolov’s Word2vec, Stanford University’s GloVe,^[45] GN-GloVe,^[46] Flair embeddings,^[36] AllenNLP’s ELMo,^[47] BERT,^[48] fastText, Gensim,^[49] Indra,^[50] and Deeplearning4j. Principal Component Analysis (PCA) and T-Distributed Stochastic Neighbour Embedding (t-SNE) are both used to reduce the dimensionality of word vector spaces and visualize word embeddings and clusters.^[51]

Examples of application[edit]

For instance, the fastText is also used to calculate word embeddings for text corpora in Sketch Engine that are available online.^[52]

Ethical Implications[edit]

Word embeddings may contain the biases and stereotypes contained in the trained dataset, as Bolukbasi et al. points out in the 2016 paper “Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddings” that a publicly available (and popular) word2vec embedding trained on Google News texts (a commonly used data corpus), which consists of text written by professional journalists, still shows disproportionate word associations reflecting gender and racial biases when extracting word analogies (Bolukbasi et al. 2016). For example, one of the analogies generated using the aforementioned word embedding is “man is to computer programmer as woman is to homemaker”.^[53]

The applications of these trained word embeddings without careful oversight likely perpetuates existing bias in society, which is introduced through unaltered training data. Furthermore, word embeddings can even amplify these biases (Zhao et al. 2017).^[54] Given word embeddings popular usage in NLP applications such as search ranking, CV parsing and recommendation systems, the biases that exist in pre-trained word embeddings may have further reaching impact than we realize.

See also[edit]

• Brown clustering
• Distributional–relational database

References[edit]

Начать стоит от печки, то есть с постановки задачи. Откуда берется сама задача word embedding?
Лирическое отступление: К сожалению, русскоязычное сообщество еще не выработало единого термина для этого понятия, поэтому мы будем использовать англоязычный.
Сам по себе embedding — это сопоставление произвольной сущности (например, узла в графе или кусочка картинки) некоторому вектору.

Сегодня мы говорим про слова и стоит обсудить, как делать такое сопоставление вектора слову.
Вернемся к предмету: вот у нас есть слова и есть компьютер, который должен с этими словами как-то работать. Вопрос — как компьютер будет работать со словами? Ведь компьютер не умеет читать, и вообще устроен сильно иначе, чем человек. Самая первая идея, приходящая в голову — просто закодировать слова цифрами по порядку следования в словаре. Идея очень продуктивна в своей простоте — натуральный ряд бесконечен и можно перенумеровать все слова, не опасаясь проблем. (На секунду забудем про ограничения типов, тем более, в 64-битное слово можно запихнуть числа от 0 до 2^64 — 1, что существенно больше количества всех слов всех известных языков.)

Но у этой идеи есть и существенный недостаток: слова в словаре следуют в алфавитном порядке, и при добавлении слова нужно перенумеровывать заново большую часть слов. Но даже это не является настолько важным, а важно то, буквенное написание слова никак не связано с его смыслом (эту гипотезу еще в конце XIX века высказал известный лингвист Фердинанд де Соссюр). В самом деле слова “петух”, “курица” и “цыпленок” имеют очень мало общего между собой и стоят в словаре далеко друг от друга, хотя очевидно обозначают самца, самку и детеныша одного вида птицы. То есть мы можем выделить два вида близости слов: лексический и семантический. Как мы видим на примере с курицей, эти близости не обязательно совпадают. Можно для наглядности привести обратный пример лексически близких, но семантически далеких слов — «зола» и «золото». (Если вы никогда не задумывались, то имя Золушка происходит именно от первого.)
Чтобы получить возможность представить семантическую близость, было предложено использовать embedding, то есть сопоставить слову некий вектор, отображающий его значение в “пространстве смыслов”.

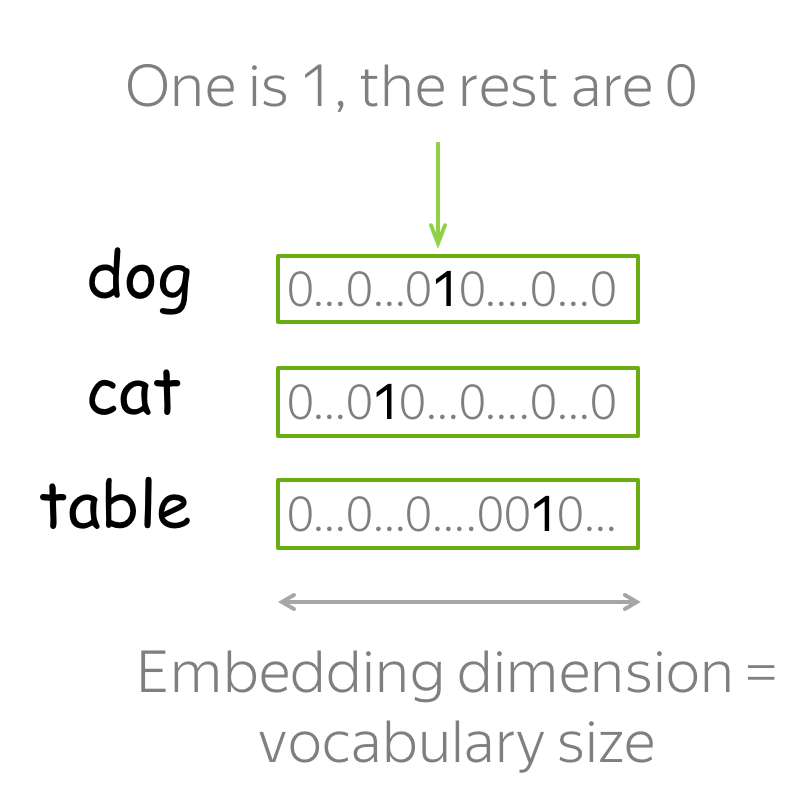
Какой самый простой способ получить вектор из слова? Кажется, что естественно будет взять вектор длины нашего словаря и поставить только одну единицу в позиции, соответствующей номеру слова в словаре. Этот подход называется one-hot encoding (OHE). OHE все еще не обладает свойствами семантической близости:

Значит нам нужно найти другой способ преобразования слов в вектора, но OHE нам еще пригодится.

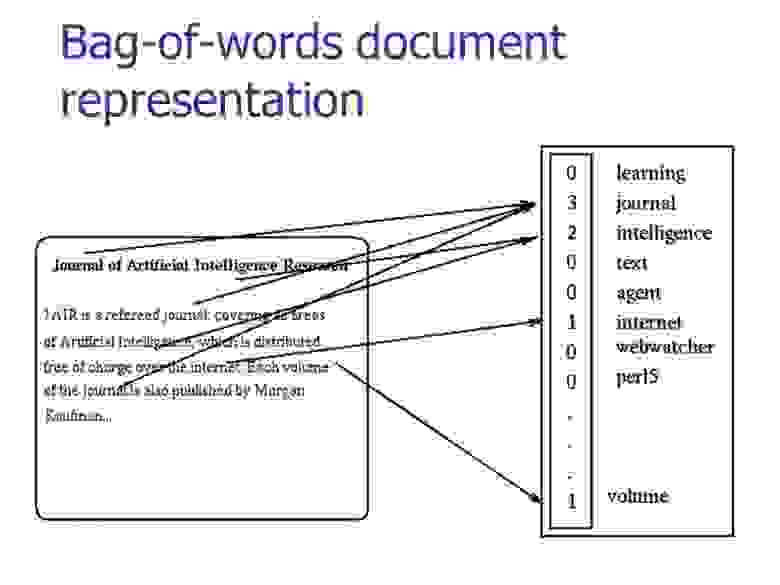
Отойдем немного назад — значение одного слова нам может быть и не так важно, т.к. речь (и устная, и письменная) состоит из наборов слов, которые мы называем текстами. Так что если мы захотим как-то представить тексты, то мы возьмем OHE-вектор каждого слова в тексте и сложим вместе. Т.е. на выходе получим просто подсчет количества различных слов в тексте в одном векторе. Такой подход называется “мешок слов” (bag of words, BoW), потому что мы теряем всю информацию о взаимном расположении слов внутри текста.

Но несмотря на потерю этой информации так тексты уже можно сравнивать. Например, с помощью косинусной меры.

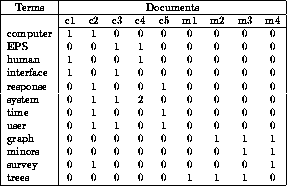
Мы можем пойти дальше и представить наш корпус (набор текстов) в виде матрицы “слово-документ” (term-document). Стоит отметить, что в области информационного поиска (information retrieval) эта матрица носит название «обратного индекса» (inverted index), в том смысле, что обычный/прямой индекс выглядит как «документ-слово» и очень неудобен для быстрого поиска. Но это опять же выходит за рамки нашей статьи.

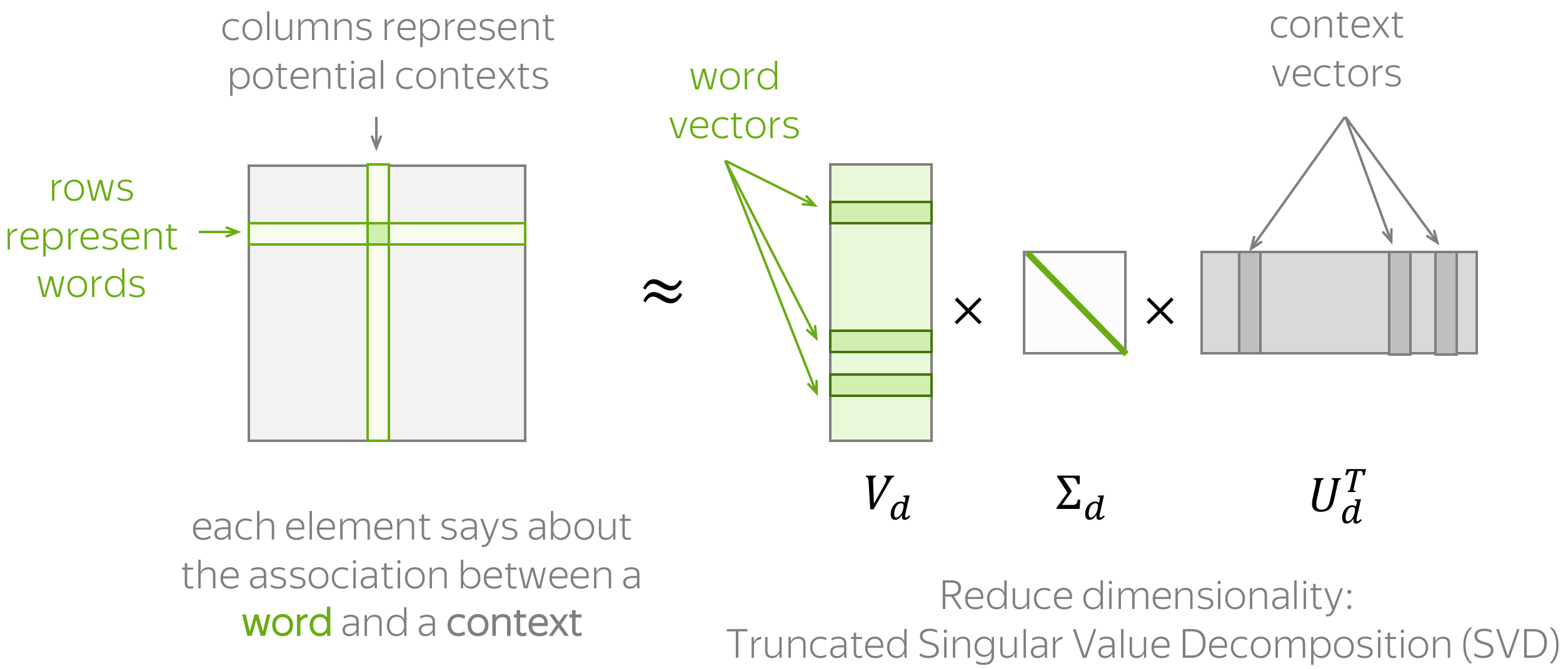
Эта матрица приводит нас к тематическим моделям, где матрицу “слово-документ” пытаются представить в виде произведения двух матриц “слово-тема” и “тема-документ”. В самом простом случае мы возьмем матрицу и с помощью SVD-разложения получим представление слов через темы и документов через темы:

Здесь — слова, — документы. Но это уже будет предметом другой статьи, а сейчас мы вернемся к нашей главной теме — векторному представлению слов.

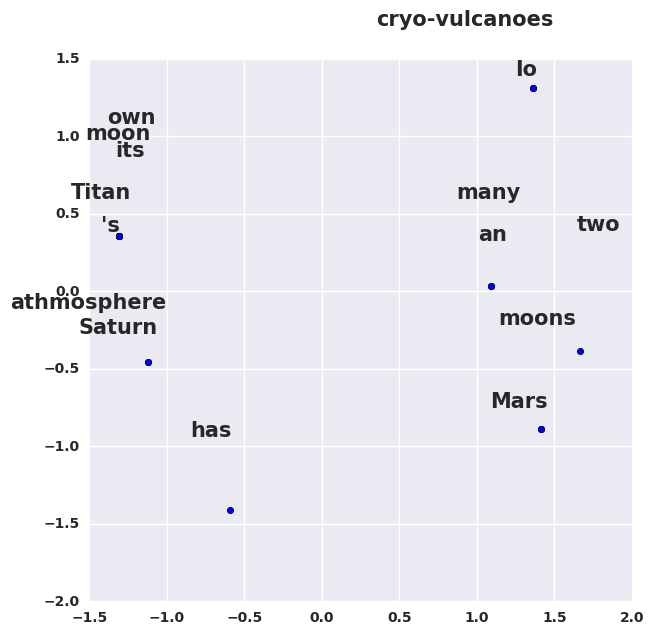
Пусть у нас есть такой корпус:

s = ['Mars has an athmosphere', "Saturn 's moon Titan has its own athmosphere",
     'Mars has two moons', 'Saturn has many moons', 'Io has cryo-vulcanoes']

С помощью SVD-преобразования, выделим только первые две компоненты, и нарисуем:

Что интересного на этой картинке? То, что Титан и Ио — далеко друг от друга, хотя они оба являются спутниками Сатурна, но в нашем корпусе про это ничего нет. Слова «атмосфера» и «Сатурн» очень близко друг другу, хотя не являются синонимами. В то же время «два» и «много» стоят рядом, что логично. Но общий смысл этого примера в том, что результаты, которые вы получите очень сильно зависят от корпуса, с которым вы работаете. Весь код для получения картинки выше можно посмотреть здесь.

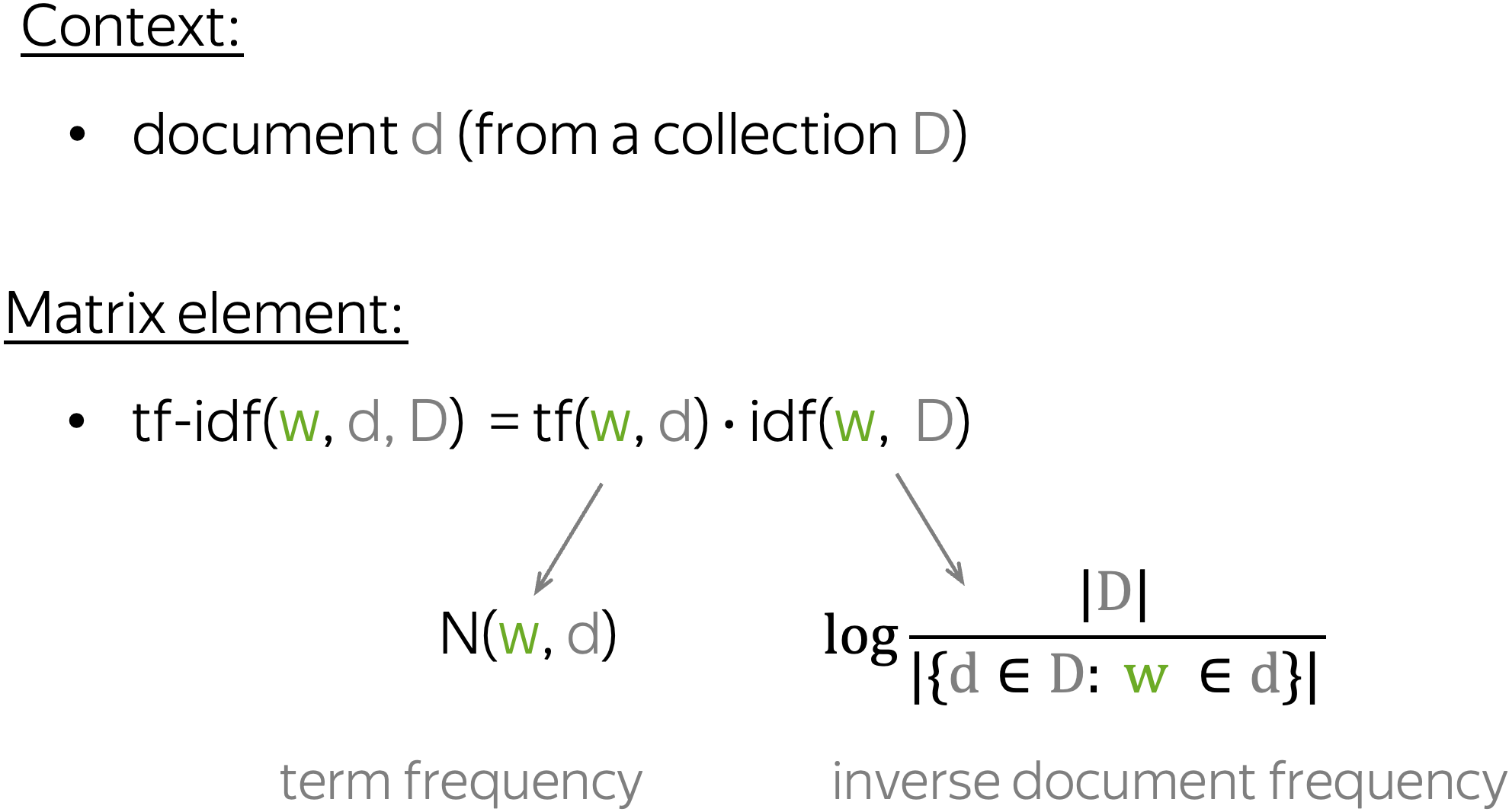
Логика повествования выводит на следующую модификацию матрицы term-document — формулу TF-IDF. Эта аббревиатура означает «term frequency — inverse document frequency».

Давайте попробуем разобраться, что это такое. Итак, TF — это частота слова в тексте , здесь нет ничего сложного. А вот IDF — существенно более интересная вещь: это логарифм обратной частоты распространенности слова в корпусе . Распространенностью называется отношение числа текстов, в которых встретилось искомое слово, к общему числу текстов в корпусе. С помощью TF-IDF тексты также можно сравнивать, и делать это можно с меньшей опаской, чем при использовании обычных частот.

Новая эпоха

Описанные выше подходы были (и остаются) хороши для времен (или областей), где количество текстов мало и словарь ограничен, хотя, как мы видели, там тоже есть свои сложности. Но с приходом в нашу жизнь интернета все стало одновременно и сложнее и проще: в доступе появилось великое множество текстов, и эти тексты с изменяющимся и расширяющимся словарем. С этим надо было что-то делать, а ранее известные модели не могли справиться с таким объемом текстов. Количество слов в английском языке очень грубо составляет миллион — матрица совместных встречаемостей только пар слов будет 10^6 x 10^6. Такая матрица даже сейчас не очень лезет в память компьютеров, а, скажем, 10 лет назад про такое можно было не мечтать. Конечно, были придуманы множество способов, упрощающих или распараллеливающих обработку таких матриц, но все это были паллиативные методы.

И тогда, как это часто бывает, был предложен выход по принципу “тот, кто нам мешает, тот нам поможет!” А именно, в 2013 году тогда мало кому известный чешский аспирант Томаш Миколов предложил свой подход к word embedding, который он назвал word2vec. Его подход основан на другой важной гипотезе, которую в науке принято называть гипотезой локальности — “слова, которые встречаются в одинаковых окружениях, имеют близкие значения”. Близость в данном случае понимается очень широко, как то, что рядом могут стоять только сочетающиеся слова. Например, для нас привычно словосочетание «заводной будильник». А сказать “заводной апельсин” мы не можем* — эти слова не сочетаются.

Основываясь на этой гипотезе Томаш Миколов предложил новый подход, который не страдал от больших объемов информации, а наоборот выигрывал [1].

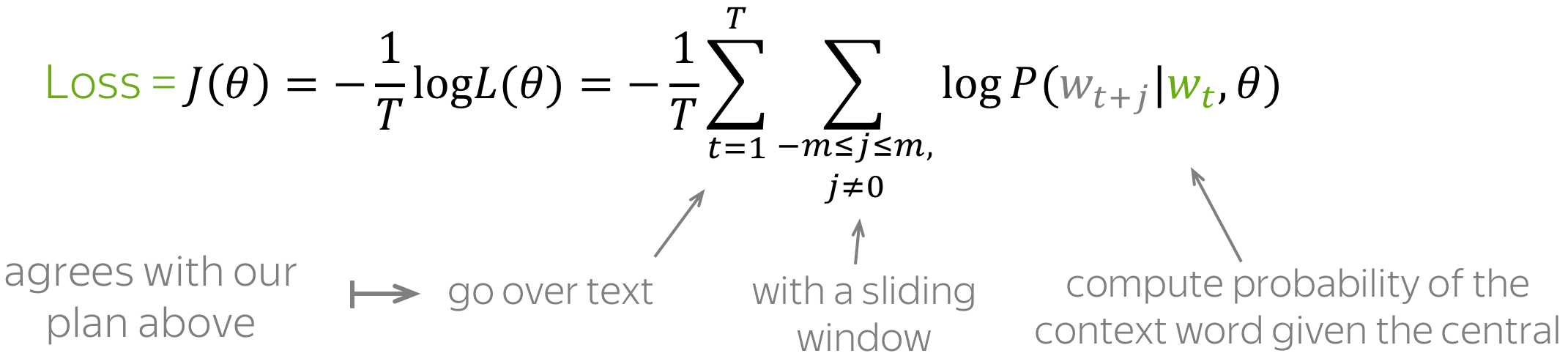
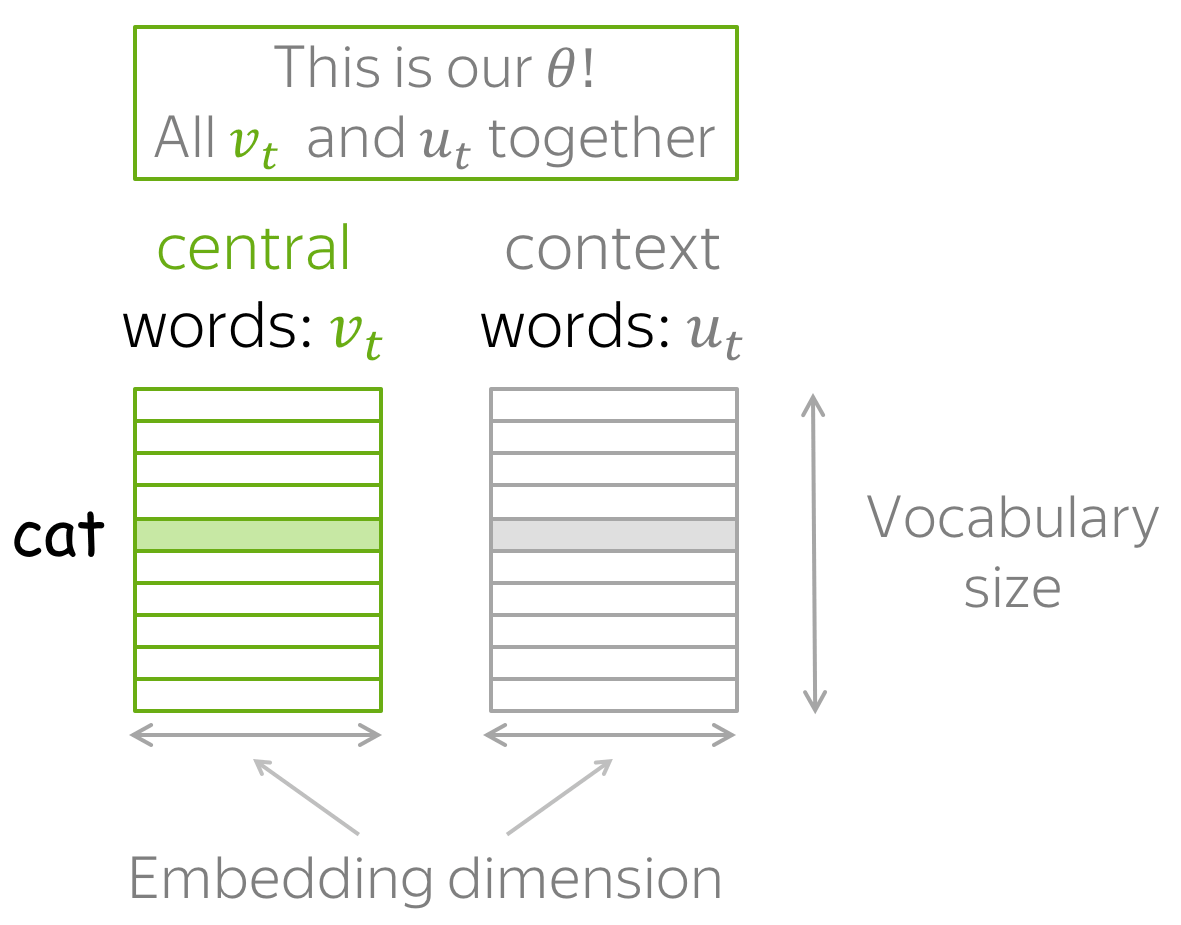
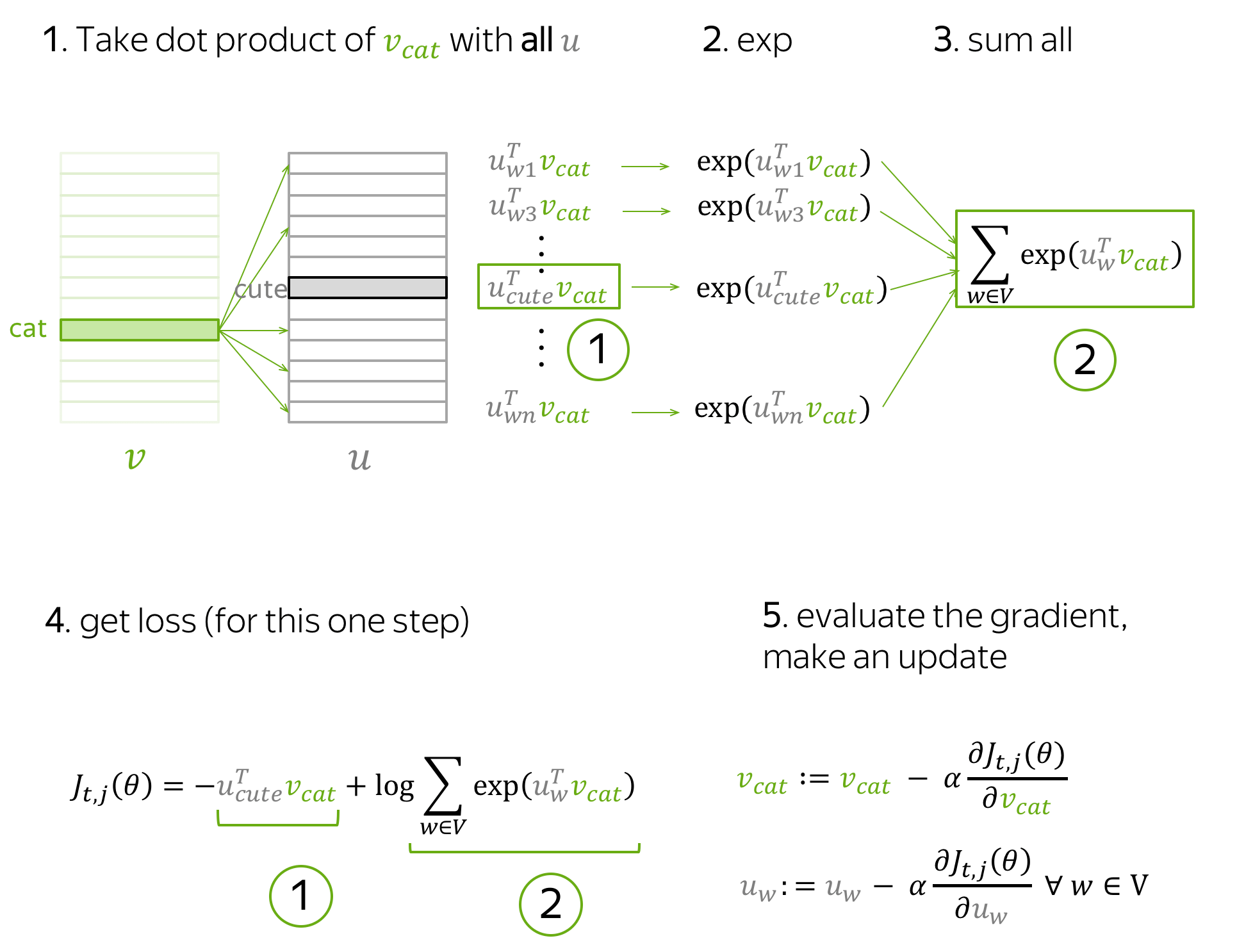
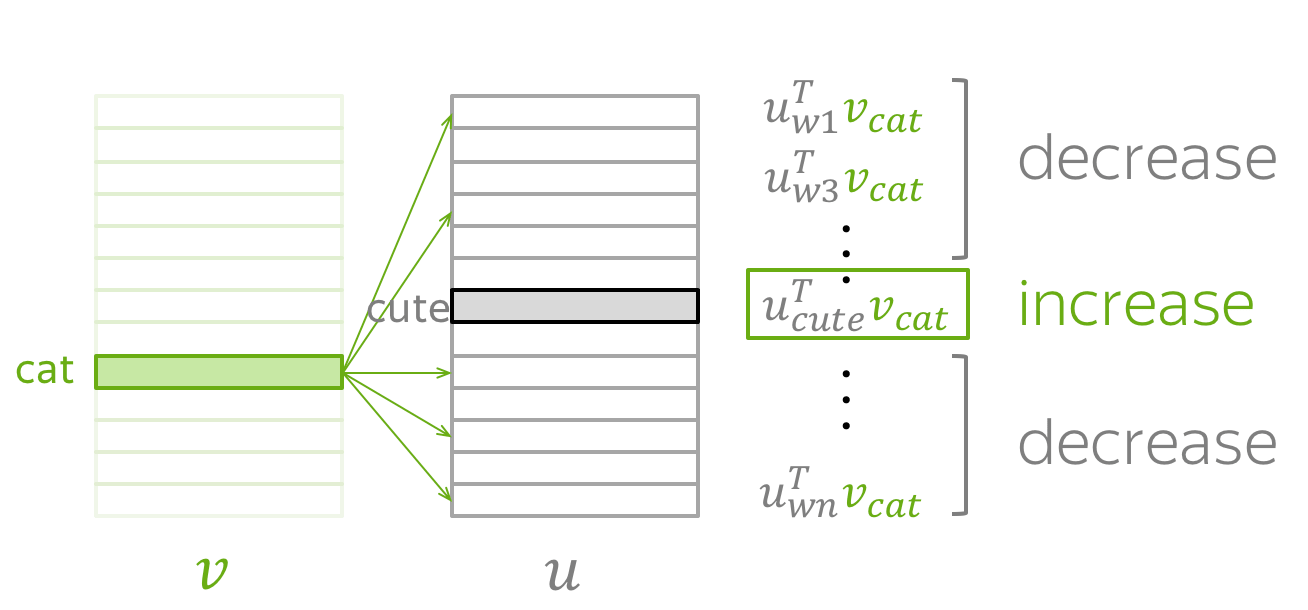
Модель, предложенная Миколовым очень проста (и потому так хороша) — мы будем предсказывать вероятность слова по его окружению (контексту). То есть мы будем учить такие вектора слов, чтобы вероятность, присваиваемая моделью слову была близка к вероятности встретить это слово в этом окружении в реальном тексте.

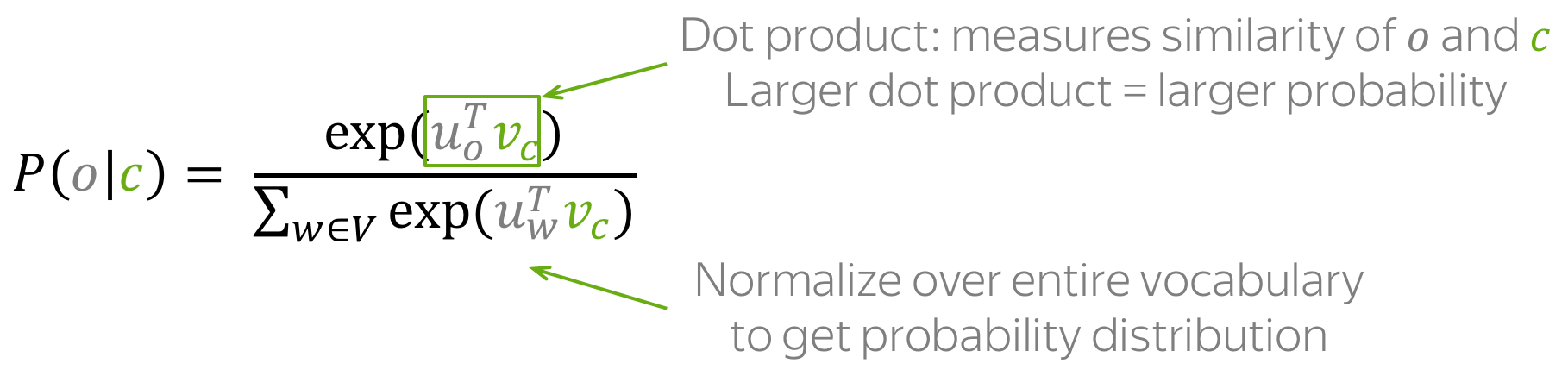
Здесь — вектор целевого слова, — это некоторый вектор контекста, вычисленный (например, путем усреднения) из векторов окружающих нужное слово других слов. А — это функция, которая двум векторам сопоставляет одно число. Например, это может быть упоминавшееся выше косинусное расстояние.

Приведенная формула называется softmax, то есть “мягкий максимум”, мягкий — в смысле дифференцируемый. Это нужно для того, чтобы наша модель могла обучиться с помощью backpropagation, то есть процесса обратного распространения ошибки.

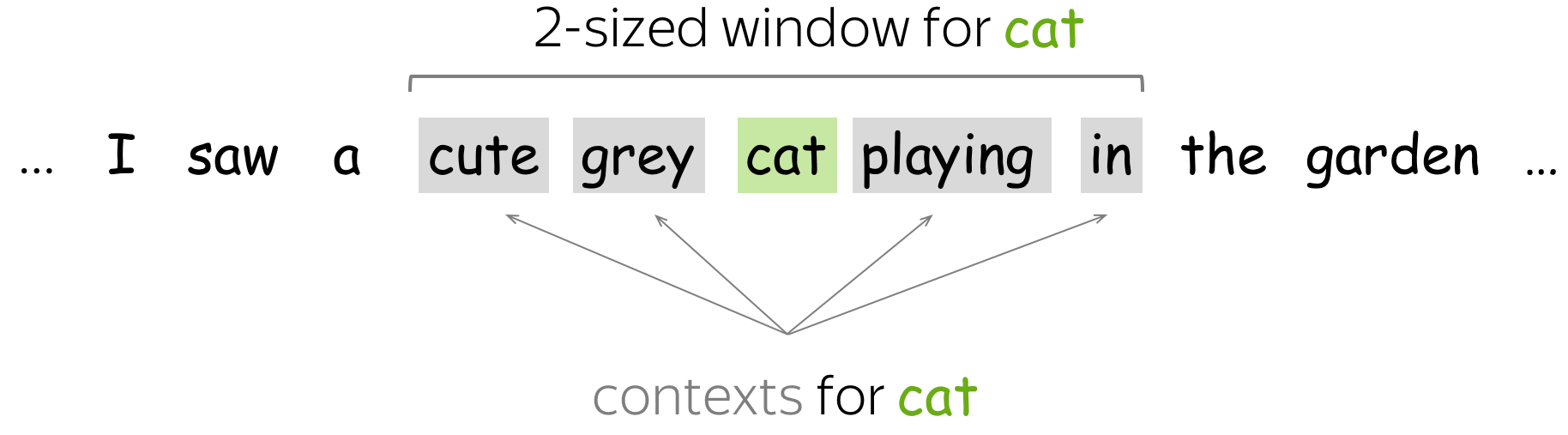
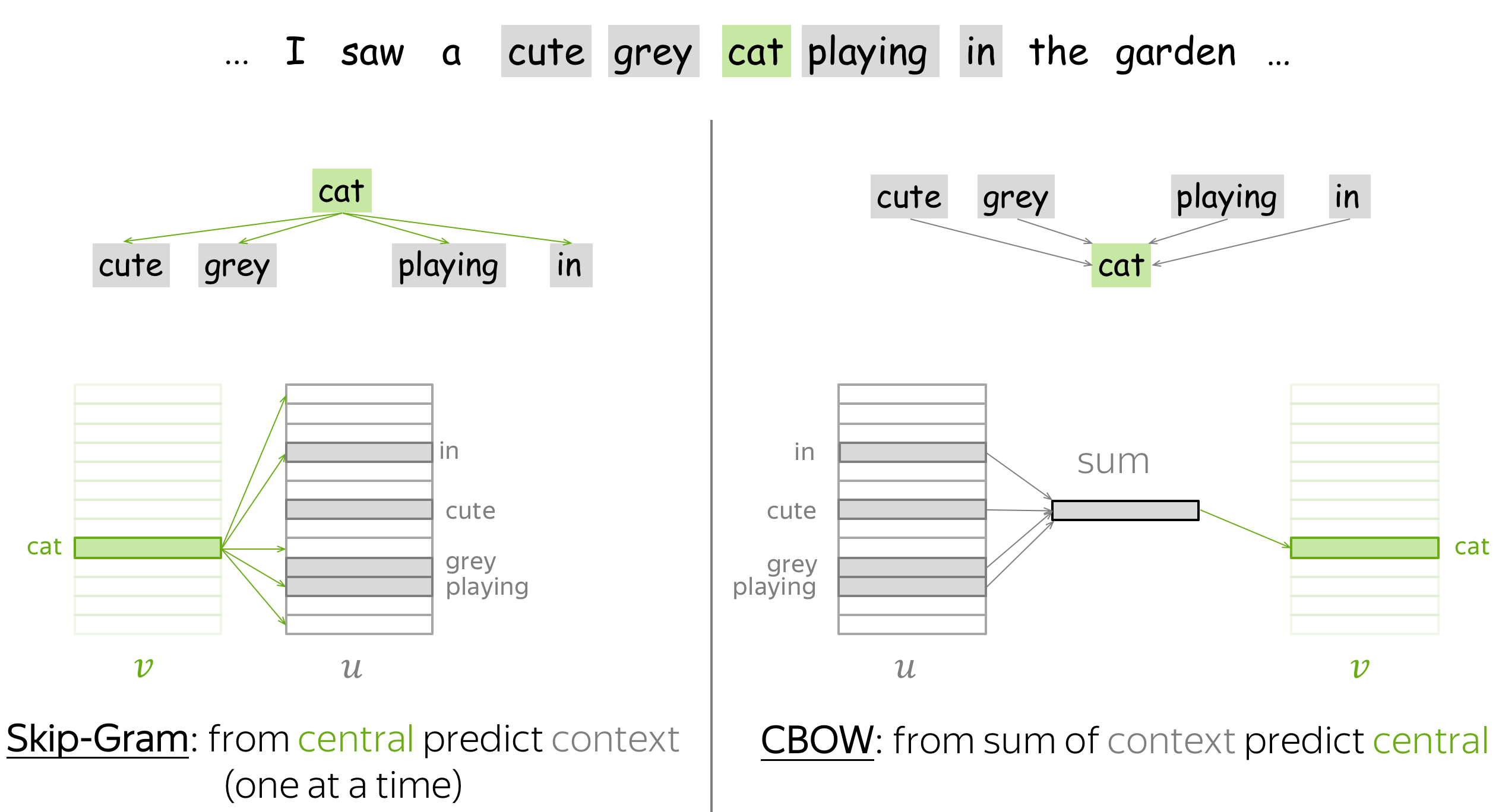
Процесс тренировки устроен следующим образом: мы берем последовательно (2k+1) слов, слово в центре является тем словом, которое должно быть предсказано. А окружающие слова являются контекстом длины по k с каждой стороны. Каждому слову в нашей модели сопоставлен уникальный вектор, который мы меняем в процессе обучения нашей модели.

В целом, этот подход называется CBOW — continuous bag of words, continuous потому, что мы скармливаем нашей модели последовательно наборы слов из текста, a BoW потому что порядок слов в контексте не важен.

Также Миколовым сразу был предложен другой подход — прямо противоположный CBOW, который он назвал skip-gram, то есть “словосочетание с пропуском”. Мы пытаемся из данного нам слова угадать его контекст (точнее вектор контекста). В остальном модель не претерпевает изменений.

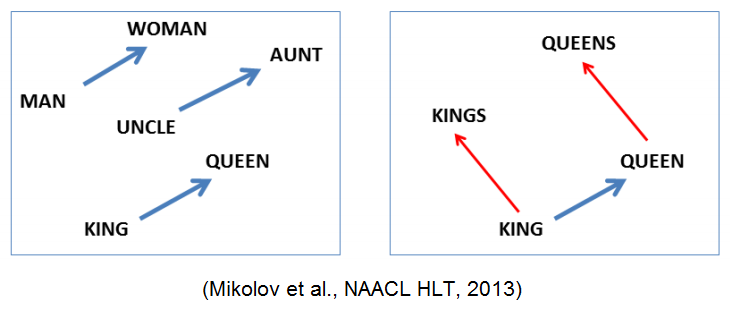
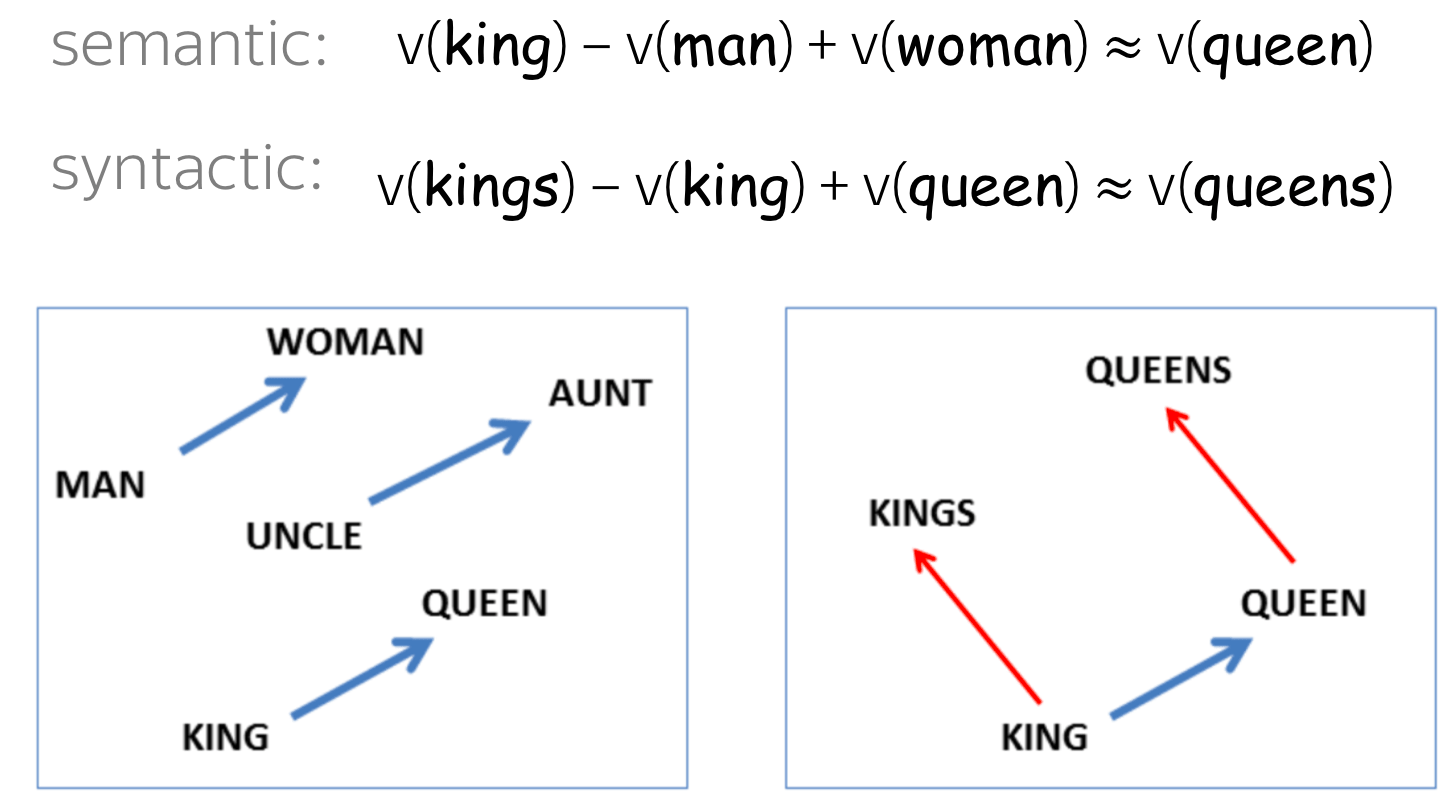
Что стоит отметить: хотя в модель не заложено явно никакой семантики, а только статистические свойства корпусов текстов, оказывается, что натренированная модель word2vec может улавливать некоторые семантические свойства слов. Классический пример из работы автора:

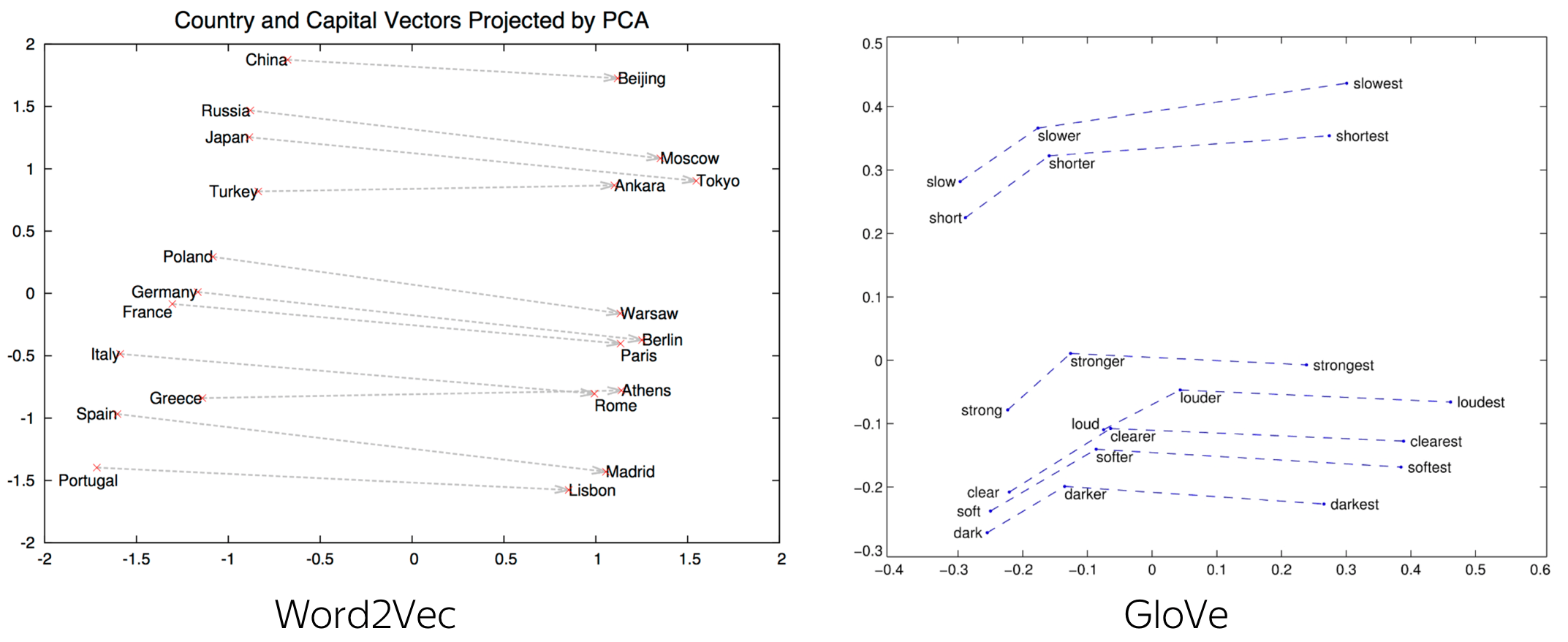
Слово «мужчина» относится к слову «женщина» так же, как слово «дядя» к слову «тётя», что для нас совершенно естественно и понятно, но в других моделям добиться такого же соотношения векторов можно только с помощью специальных ухищрений. Здесь же — это происходит естественно из самого корпуса текстов. Кстати, помимо семантических связей, улавливаются и синтаксические, справа показано соотношение единственного и множественного числа.

Более сложные вещи

На самом деле, за прошедшее время были предложены улучшения ставшей уже также классической модели Word2Vec. Два самых распространенных будут описаны ниже. Но этот раздел может быть пропущен без ущерба для понимания статьи в целом, если покажется слишком сложным.

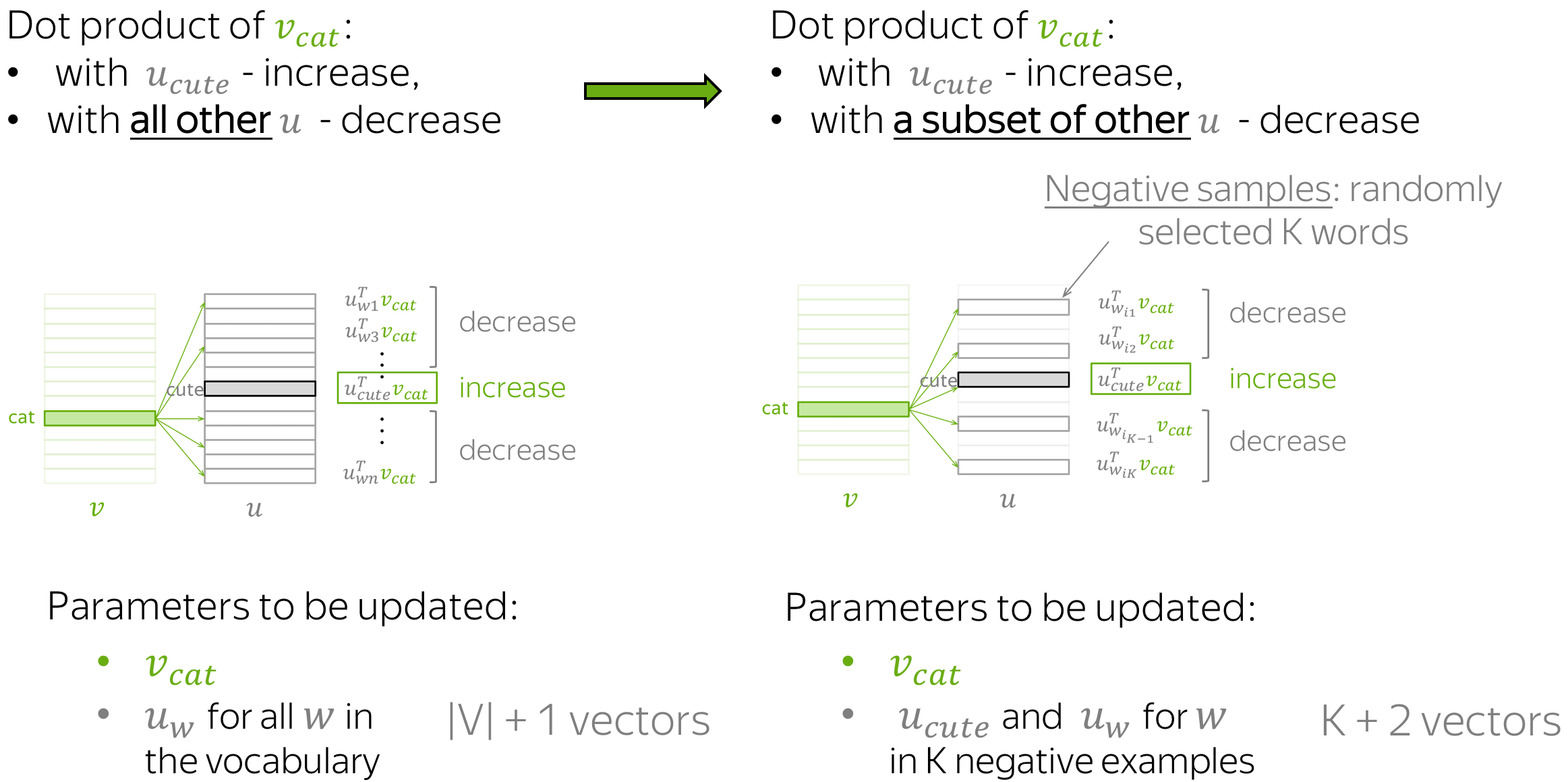
Negative Sampling

В стандартной модели CBoW, рассмотренной выше, мы предсказываем вероятности слов и оптимизируем их. Функцией для оптимизации (минимизации в нашем случае) служит дивергенция Кульбака-Лейблера:

Здесь — распределение вероятностей слов, которое мы берем из корпуса, — распределение, которое порождает наша модель. Дивергенция — это буквально «расхождение», насколько одно распределение не похоже на другое. Т.к. наши распределения на словах, т.е. являются дискретными, мы можем заменить в этой формуле интеграл на сумму:

Оказалось так, что оптимизировать эту формулу достаточно сложно. Прежде всего из-за того, что рассчитывается с помощью softmax по всему словарю. (Как мы помним, в английском сейчас порядка миллиона слов.) Здесь стоит отметить, что многие слова вместе не встречаются, как мы уже отмечали выше, поэтому большая часть вычислений в softmax является избыточной. Был предложен элегантный обходной путь, который получил название Negative Sampling. Суть этого подхода заключается в том, что мы максимизируем вероятность встречи для нужного слова в типичном контексте (том, который часто встречается в нашем корпусе) и одновременно минимизируем вероятность встречи в нетипичном контексте (том, который редко или вообще не встречается). Формулой мысль выше записывается так:

Здесь — точно такой же, что и в оригинальной формуле, а вот остальное несколько отличается. Прежде всего стоит обратить внимание на то, что формуле теперь состоит из двух частей: позитивной () и негативной (). Позитивная часть отвечает за типичные контексты, и здесь — это распределение совместной встречаемости слова и остальных слов корпуса. Негативная часть — это, пожалуй, самое интересное — это набор слов, которые с нашим целевым словом встречаются редко. Этот набор порождается из распределения , которое на практике берется как равномерное по всем словам словаря корпуса. Было показано, что такая функция приводит при своей оптимизации к результату, аналогичному стандартному softmax [2].

Hierarchical SoftMax

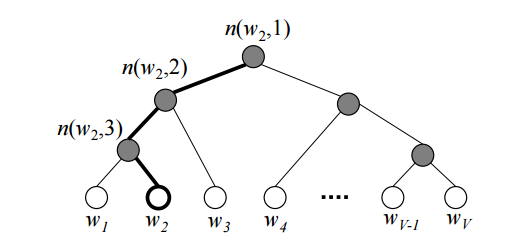
Также люди зашли и с другой стороны — можно не менять исходную формулу, а попробовать посчитать сам softmax более эффективно. Например, используя бинарное дерево [3]. По всем словам в словаре строится дерево Хаффмана. В полученном дереве слов располагаются на листьях дерева.

На рисунке изображен пример такого бинарного дерева. Жирным выделен путь от корня до слова . Длину пути обозначим , а -ую вершину на пути к слову обозначим через . Можно доказать, что внутренних вершин (не листьев) .

С помощью иерархического softmax вектора предсказывается для внутренних вершин. А вероятность того, что слово будет выходным словом (в зависимости от того, что мы предсказываем: слово из контекста или заданное слово по контексту) вычисляется по формуле:

где — функция softmax; ; — левый сын вершины ; , если используется метод skip-gram, , то есть, усредненный вектор контекста, если используется CBOW.

Формулу можно интуитивно понять, представив, что на каждом шаге мы можем пойти налево или направо с вероятностями:

Затем на каждом шаге вероятности перемножаются ( шагов) и получается искомая формула.

При использовании простого softmax для подсчета вероятности слова, приходилось вычислять нормирующую сумму по всем словам из словаря, требовалось операций. Теперь же вероятность слова можно вычислить при помощи последовательных вычислений, которые требуют .

Другие модели

Помимо word2vec были, само собой, предложены и другие модели word embedding. Стоит отметить модель, предложенную лабораторией компьютерной лингвистики Стенфордского университета, под названием Global Vectors (GloVe), сочетающую в себе черты SVD разложения и word2vec [4].

Также надо упомянуть о том, что т.к. изначально все описанные модели были предложены для английского языка, то там не так остро стоит проблема словоизменения, характерная для синтетических языков (это — лингвистический термин), вроде русского. Везде выше по тексту неявно предполагалось, что мы либо считаем разные формы одного слова разными словами — и тогда надеяться, что нашего корпуса будет достаточно модели, чтобы выучить их синтаксическую близость, либо используем механизмы стеммирования или лемматизации. Стеммирование — это обрезание окончания слова, оставление только основы (например, “красного яблока” превратится в “красн яблок”). А лемматизация — замена слова его начальной формой (например, “мы бежим” превратится в “я бежать”). Но мы можем и не терять эту информацию, а использовать ее — закодировав OHE в новый вектор, и сконкатинировать его с вектором для основы или леммы.
Еще стоит сказать, что то, с чем мы начинали — буквенное представление слова — тоже не кануло в Лету: предложены модели по использованию буквенного представления слова для word embedding [5].

Практическое применение

Мы поговорили о теории, пришло время посмотреть, к чему все вышеописанное применимо на практике. Ведь любая самая красивая теория без практического применения — не более чем игра ума. Рассмотрим применение Word2Vec в двух задачах:
1) Задача классификации, необходимо по последовательности посещенных сайтов определять пользователя;
2) Задача регрессии, необходимо по тексту статьи определить ее рейтинг на Хабрахабре.

Классификация

# загрузим библиотеки и установим опции
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
#%matplotlib inline
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_score

Cкачать данные для первой задачи можно со страницы соревнования «Catch Me If You Can»

# загрузим обучающую и тестовую выборки
train_df = pd.read_csv('data/train_sessions.csv')#,index_col='session_id')
test_df = pd.read_csv('data/test_sessions.csv')#, index_col='session_id')

# приведем колонки time1, ..., time10 к временному формату
times = ['time%s' % i for i in range(1, 11)]
train_df[times] = train_df[times].apply(pd.to_datetime)
test_df[times] = test_df[times].apply(pd.to_datetime)

# отсортируем данные по времени
train_df = train_df.sort_values(by='time1')

# посмотрим на заголовок обучающей выборки
train_df.head()

sites = ['site%s' % i for i in range(1, 11)]
#заменим nan на 0
train_df[sites] = train_df[sites].fillna(0).astype('int').astype('str')
test_df[sites] = test_df[sites].fillna(0).astype('int').astype('str')
#создадим тексты необходимые для обучения word2vec
train_df['list'] = train_df['site1']
test_df['list'] = test_df['site1']
for s in sites[1:]:
    train_df['list'] = train_df['list']+","+train_df[s]
    test_df['list'] = test_df['list']+","+test_df[s]
train_df['list_w'] = train_df['list'].apply(lambda x: x.split(','))
test_df['list_w'] = test_df['list'].apply(lambda x: x.split(','))

#В нашем случае предложение это набор сайтов, которые посещал пользователь
#нам необязательно переводить цифры в названия сайтов, т.к. алгоритм будем выявлять взаимосвязь их друг с другом.
train_df['list_w'][10]

['229', '1500', '33', '1500', '391', '35', '29', '2276', '40305', '23']

# подключим word2vec
from gensim.models import word2vec

#объединим обучающую и тестовую выборки и обучим нашу модель на всех данных 
#с размером окна в 6=3*2 (длина предложения 10 слов) и итоговыми векторами размерности 300, параметр workers отвечает за количество ядер
test_df['target'] = -1
data = pd.concat([train_df,test_df], axis=0)

model = word2vec.Word2Vec(data['list_w'], size=300, window=3, workers=4)
#создадим словарь со словами и соответсвующими им векторами
w2v = dict(zip(model.wv.index2word, model.wv.syn0))

Т.к. сейчас мы каждому слову сопоставили вектор, то нужно решить, что сопоставить целому предложению из слов.
Один из возможных вариантов это просто усреднить все слова в предложении и получить некоторый смысл всего предложения (если слова нет в тексте, то берем нулевой вектор).

class mean_vectorizer(object):
    def __init__(self, word2vec):
        self.word2vec = word2vec
        self.dim = len(next(iter(w2v.values())))

    def fit(self, X):
        return self 

    def transform(self, X):
        return np.array([
            np.mean([self.word2vec[w] for w in words if w in self.word2vec] 
                    or [np.zeros(self.dim)], axis=0)
            for words in X
        ])

data_mean=mean_vectorizer(w2v).fit(train_df['list_w']).transform(train_df['list_w'])
data_mean.shape

(253561, 300)

Т.к. мы получили distributed representation, то никакое число по отдельности ничего не значит, а значит лучше всего покажут себя линейные алгоритмы. Попробуем нейронные сети, LogisticRegression и проверим нелинейный метод XGBoost.

# Воспользуемся валидацией
def split(train,y,ratio):
    idx = round(train.shape[0] * ratio)
    return train[:idx, :], train[idx:, :], y[:idx], y[idx:]
y = train_df['target']
Xtr, Xval, ytr, yval = split(data_mean, y,0.8)
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()

((202849, 300), (50712, 300), 0.009726446765820882, 0.006389020350212968)

# подключим библиотеки keras 
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Activation, Input
from keras.preprocessing.text import Tokenizer
from keras import regularizers

# опишем нейронную сеть
model = Sequential()
model.add(Dense(128, input_dim=(Xtr.shape[1])))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy',
              optimizer='adam',
              metrics=['binary_accuracy'])

history = model.fit(Xtr, ytr,
                    batch_size=128,
                    epochs=10,
                    validation_data=(Xval, yval),
                    class_weight='auto',
                    verbose=0)

classes = model.predict(Xval, batch_size=128)
roc_auc_score(yval, classes)

0.91892341356995644

Получили неплохой результат. Значит Word2Vec смог выявить зависимости между сессиями.
Посмотрим, что произойдет с алгоритмом XGBoost.

import xgboost as xgb

dtr = xgb.DMatrix(Xtr, label= ytr,missing = np.nan)
dval = xgb.DMatrix(Xval, label= yval,missing = np.nan)
watchlist = [(dtr, 'train'), (dval, 'eval')]
history = dict()

params = {
    'max_depth': 26,
    'eta': 0.025,
    'nthread': 4,
    'gamma' : 1,
    'alpha' : 1,
    'subsample': 0.85,
    'eval_metric': ['auc'],
    'objective': 'binary:logistic',
    'colsample_bytree': 0.9,
    'min_child_weight': 100,
    'scale_pos_weight':(1)/y.mean(),
    'seed':7
}

model_new = xgb.train(params, dtr, num_boost_round=200, evals=watchlist, evals_result=history, verbose_eval=20)

[0] train-auc:0.954886  eval-auc:0.85383
[20]    train-auc:0.989848  eval-auc:0.910808
[40]    train-auc:0.992086  eval-auc:0.916371
[60]    train-auc:0.993658  eval-auc:0.917753
[80]    train-auc:0.994874  eval-auc:0.918254
[100]   train-auc:0.995743  eval-auc:0.917947
[120]   train-auc:0.996396  eval-auc:0.917735
[140]   train-auc:0.996964  eval-auc:0.918503
[160]   train-auc:0.997368  eval-auc:0.919341
[180]   train-auc:0.997682  eval-auc:0.920183

Видим, что алгоритм сильно подстраивается под обучающую выборку, поэтому возможно наше предположение о необходимости использовать линейные алгоритмы подтверждено.
Посмотрим, что покажет обычный LogisticRegression.

from sklearn.linear_model import LogisticRegression
def get_auc_lr_valid(X, y, C=1, seed=7, ratio = 0.8):
    # разделим выборку на обучающую и валидационную
    idx = round(X.shape[0] * ratio)
    # обучение классификатора
    lr = LogisticRegression(C=C, random_state=seed, n_jobs=-1).fit(X[:idx], y[:idx])
    # прогноз для валидационной выборки
    y_pred = lr.predict_proba(X[idx:, :])[:, 1]
    # считаем качество
    score = roc_auc_score(y[idx:], y_pred)

    return score

get_auc_lr_valid(data_mean, y, C=1, seed=7, ratio = 0.8)

0.90037148150108237

Попробуем улучшить результаты.

Теперь вместо обычного среднего, чтобы учесть частоту с которой слово встречается в тексте, возьмем взвешенное среднее. В качестве весов возьмем IDF. Учёт IDF уменьшает вес широко употребительных слов и увеличивает вес более редких слов, которые могут достаточно точно указать на то, к какому классу относится текст. В нашем случае, кому принадлежит последовательность посещенных сайтов.

#пропишем класс выполняющий tfidf преобразование.
from sklearn.feature_extraction.text import TfidfVectorizer
from collections import defaultdict

class tfidf_vectorizer(object):
    def __init__(self, word2vec):
        self.word2vec = word2vec
        self.word2weight = None
        self.dim = len(next(iter(w2v.values())))

    def fit(self, X):
        tfidf = TfidfVectorizer(analyzer=lambda x: x)
        tfidf.fit(X)
        max_idf = max(tfidf.idf_)
        self.word2weight = defaultdict(
            lambda: max_idf,
            [(w, tfidf.idf_[i]) for w, i in tfidf.vocabulary_.items()])

        return self

    def transform(self, X):
        return np.array([
                np.mean([self.word2vec[w] * self.word2weight[w]
                         for w in words if w in self.word2vec] or
                        [np.zeros(self.dim)], axis=0)
                for words in X
            ])

data_mean = tfidf_vectorizer(w2v).fit(train_df['list_w']).transform(train_df['list_w'])

Проверим изменилось ли качество LogisticRegression.

get_auc_lr_valid(data_mean, y, C=1, seed=7, ratio = 0.8)

0.90738924587178804

видим прирост на 0.07, значит скорее всего взвешенное среднее помогает лучше отобразить смысл всего предложения через word2vec.

Предсказание популярности

Попробуем Word2Vec уже в текстовой задаче — предсказании популярности статьи на Хабрхабре.

Испробуем силы алгоритма непосредственно на текстовых данных статей Хабра. Мы преобразовали данные в csv таблицы. Скачать их вы можете здесь: train, test.

Xtrain = pd.read_csv('data/train_content.csv')
Xtest = pd.read_csv('data/test_content.csv')
print(Xtrain.shape,Xtest.shape)
Xtrain.head()

Будем обучать модель на всем содержании статьи. Для этого совершим некоторые преобразования над текстом.

Напишем функцию, которая будет преобразовывать тестовую статью в лист из слов необходимый для обучения Word2Vec.
Функция получает строку, в которой содержится весь текстовый документ.

1) Сначала функция будет удалять все символы кроме букв верхнего и нижнего регистра;

2) Затем преобразовывает слова к нижнему регистру;

3) После чего удаляет стоп слова из текста, т.к. они не несут никакой информации о содержании;

4) Лемматизация, процесс приведения словоформы к лемме — её нормальной (словарной) форме.

Функция возвращает лист из слов.

# подключим необходимые библиотеки
from sklearn.metrics import mean_squared_error
import re
from nltk.corpus import stopwords
import pymorphy2
morph = pymorphy2.MorphAnalyzer()

stops = set(stopwords.words("english")) | set(stopwords.words("russian"))
def review_to_wordlist(review):
    #1)
    review_text = re.sub("[^а-яА-Яa-zA-Z]"," ", review)
    #2)
    words = review_text.lower().split()
    #3)
    words = [w for w in words if not w in stops]
    #4)
    words = [morph.parse(w)[0].normal_form for w in words ]
    return(words)

Лемматизация занимает много времени, поэтому ее можно убрать в целях более быстрых подсчетов.

# Преобразуем время
Xtrain['date'] = Xtrain['date'].apply(pd.to_datetime)
Xtrain['year'] = Xtrain['date'].apply(lambda x: x.year)
Xtrain['month'] = Xtrain['date'].apply(lambda x: x.month)

Будем обучаться на 2015 году, а валидироваться по первым 4 месяцам 2016, т.к. в нашей тестовой выборке представлены данные за первые 4 месяца 2017 года. Более правдивую валидацию можно сделать, идя по годам, увеличивая нашу обучающую выборку и смотря качество на первых четырех месяцах следующего года

Xtr = Xtrain[Xtrain['year']==2015]
Xval = Xtrain[(Xtrain['year']==2016)& (Xtrain['month']<=4)]
ytr = Xtr['favs_lognorm']
yval = Xval['favs_lognorm']
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()

((23425, 15), (7556, 15), 3.4046228249071526, 3.304679829935242)

data = pd.concat([Xtr,Xval],axis = 0,ignore_index = True)

#у нас есть nan, поэтому преобразуем их к строке
data['content_clear'] = data['content'].apply(str)

%%time
data['content_clear'] = data['content_clear'].apply(review_to_wordlist)

model = word2vec.Word2Vec(data['content_clear'], size=300, window=10, workers=4)
w2v = dict(zip(model.wv.index2word, model.wv.syn0))

Посмотрим чему выучилась модель:

model.wv.most_similar(positive=['open', 'data','science','best'])

Модель обучилась достаточно неплохо, посмотрим на результаты алгоритмов:

data_mean = mean_vectorizer(w2v).fit(data['content_clear']).transform(data['content_clear'])
data_mean.shape

def split(train,y,ratio):
    idx = ratio
    return train[:idx, :], train[idx:, :], y[:idx], y[idx:]
y = data['favs_lognorm']
Xtr, Xval, ytr, yval = split(data_mean, y,23425)
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()

((23425, 300), (7556, 300), 3.4046228249071526, 3.304679829935242)

from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
model = Ridge(alpha = 1,random_state=7)
model.fit(Xtr, ytr)
train_preds = model.predict(Xtr)
valid_preds = model.predict(Xval)
ymed = np.ones(len(valid_preds))*ytr.median()
print('Ошибка на трейне',mean_squared_error(ytr, train_preds))
print('Ошибка на валидации',mean_squared_error(yval, valid_preds))
print('Ошибка на валидации предсказываем медиану',mean_squared_error(yval, ymed))

Ошибка на трейне 0.734248488422
Ошибка на валидации 0.665592676973
Ошибка на валидации предсказываем медиану 1.44601638512

data_mean_tfidf = tfidf_vectorizer(w2v).fit(data['content_clear']).transform(data['content_clear'])

y = data['favs_lognorm']
Xtr, Xval, ytr, yval = split(data_mean_tfidf, y,23425)
Xtr.shape,Xval.shape,ytr.mean(),yval.mean()

((23425, 300), (7556, 300), 3.4046228249071526, 3.304679829935242)

model = Ridge(alpha = 1,random_state=7)
model.fit(Xtr, ytr)
train_preds = model.predict(Xtr)
valid_preds = model.predict(Xval)
ymed = np.ones(len(valid_preds))*ytr.median()
print('Ошибка на трейне',mean_squared_error(ytr, train_preds))
print('Ошибка на валидации',mean_squared_error(yval, valid_preds))
print('Ошибка на валидации предсказываем медиану',mean_squared_error(yval, ymed))

Ошибка на трейне 0.743623730976
Ошибка на валидации 0.675584372744
Ошибка на валидации предсказываем медиану 1.44601638512

Попробуем нейронные сети.

# подключим библиотеки keras 
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Activation, Input
from keras.preprocessing.text import Tokenizer
from keras import regularizers
from keras.wrappers.scikit_learn import KerasRegressor

# Опишем нашу сеть.
def baseline_model():
    model = Sequential()
    model.add(Dense(128, input_dim=Xtr.shape[1], kernel_initializer='normal', activation='relu'))
    model.add(Dropout(0.2))
    model.add(Dense(64, activation='relu'))
    model.add(Dropout(0.5))
    model.add(Dense(1, kernel_initializer='normal'))

    model.compile(loss='mean_squared_error', optimizer='adam')
    return model
estimator = KerasRegressor(build_fn=baseline_model,epochs=20, nb_epoch=20, batch_size=64,validation_data=(Xval, yval), verbose=2)

estimator.fit(Xtr, ytr)

Получили более хороший результат по сравнению с гребневой регрессией.

Заключение

Word2Vec показал свою пользу на практических задачах анализа текстов, все-таки не зря на текущий момент на практике используется в основном именно он и — гораздо менее популярный — GloVe. Тем не менее, может быть в вашей конкретной задаче, вам пригодятся подходы, которым для эффективной работы не требуются такие объемы данных, как для word2vec.

Код ноутбуков с примерами можно взять здесь. Код практического применения — вот тут.

Пост написан совместно с demonzheg.

Литература

1. Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean. Efficient estimation
   of word representations in vector space. CoRR, abs/1301.3781,
2. Tomas Mikolov, Ilya Sutskever, Kai Chen, Gregory S. Corrado, and Jeffrey Dean. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, pages 3111–3119, 2013.
3. Morin, F., & Bengio, Y. Hierarchical Probabilistic Neural Network Language Model. Aistats, 5, 2005.
4. Jeffrey Pennington, Richard Socher, and Christopher D. Manning. GloVe: Global Vectors for Word Representation. 2014.
5. Piotr Bojanowski, Edouard Grave, Armand Joulin, and Tomas Mikolov. Enriching word vectors
   with subword information. arXiv preprint arXiv:1607.04606, 2016.

* Да, это специальная пасхалка для любителей творчества Энтони Бёрджеса.

Word embedding in NLP is an important term that is used for representing words for text analysis in the form of real-valued vectors. It is an advancement in NLP that has improved the ability of computers to understand text-based content in a better way. It is considered one of the most significant breakthroughs of deep learning for solving challenging natural language processing problems.

In this approach, words and documents are represented in the form of numeric vectors allowing similar words to have similar vector representations. The extracted features are fed into a machine learning model so as to work with text data and preserve the semantic and syntactic information. This information once received in its converted form is used by NLP algorithms that easily digest these learned representations and process textual information.

Due to the perks this technology brings on the table, the popularity of ML NLP is surging making it one of the most chosen fields by the developers.

Now that you have a basic understanding of the topic, let us start from scratch by introducing you to word embeddings, its techniques, and applications.

What is word embedding?

Word embedding or word vector is an approach with which we represent documents and words. It is defined as a numeric vector input that allows words with similar meanings to have the same representation. It can approximate meaning and represent a word in a lower dimensional space. These can be trained much faster than the hand-built models that use graph embeddings like WordNet.

For instance, a word embedding with 50 values holds the capability of representing 50 unique features. Many people choose pre-trained word embedding models like Flair, fastText, SpaCy, and others.

We will discuss it further in the article. Let’s move on to learn it briefly with an example of the same.

The problem

Given a supervised learning task to predict which tweets are about real disasters and which ones are not (classification). Here the independent variable would be the tweets (text) and the target variable would be the binary values (1: Real Disaster, 0: Not real Disaster).

Now, Machine Learning and Deep Learning algorithms only take numeric input. So, how do we convert tweets to their numeric values? We will dive deep into the techniques to solve such problems, but first let’s look at the solution provided by word embedding.

The solution

Word Embeddings in NLP is a technique where individual words are represented as real-valued vectors in a lower-dimensional space and captures inter-word semantics. Each word is represented by a real-valued vector with tens or hundreds of dimensions.

Term frequency-inverse document frequency (TF-IDF)

Term frequency-inverse document frequency is the machine learning algorithm that is used for word embedding for text. It comprises two metrics, namely term frequency (TF) and inverse document frequency (IDF).

This algorithm works on a statistical measure of finding word relevance in the text that can be in the form of a single document or various documents that are referred to as corpus.

The term frequency (TF) score measures the frequency of words in a particular document. In simple words, it means that the occurrence of words is counted in the documents.

The inverse document frequency or the IDF score measures the rarity of the words in the text. It is given more importance over the term frequency score because even though the TF score gives more weightage to frequently occurring words, the IDF score focuses on rarely used words in the corpus that may hold significant information.

TF-IDF algorithm finds application in solving simpler natural language processing and machine learning problems for tasks like information retrieval, stop words removal, keyword extraction, and basic text analysis. However, it does not capture the semantic meaning of words efficiently in a sequence.

Now let’s understand it further with an example. We will see how vectorization is done in TF-IDF.

To create TF-IDF vectors, we use Scikit-learn’s TF-IDF Vectorizer. After applying it to the previous 4 sample tweets, we obtain —

Output of TfidfVectorizer

The rows represent each document, the columns represent the vocabulary, and the values of tf-idf(i,j) are obtained through the above formula. This matrix obtained can be used along with the target variable to train a machine learning/deep learning model.

Let us now discuss two different approaches to word embeddings. We’ll also look at the hands-on part!

Bag of words (BOW)

A bag of words is one of the popular word embedding techniques of text where each value in the vector would represent the count of words in a document/sentence. In other words, it extracts features from the text. We also refer to it as vectorization.

To get you started, here’s how you can proceed to create BOW.

• In the first step, you have to tokenize the text into sentences.
• Next, the sentences tokenized in the first step have further tokenized words.
• Eliminate any stop words or punctuation.
• Then, convert all the words to lowercase.
• Finally, move to create a frequency distribution chart of the words.

We will discuss BOW with proper example in the continuous bag of word selection below.

Word2Vec

Word2Vec method was developed by Google in 2013. Presently, we use this technique for all advanced natural language processing (NLP) problems. It was invented for training word embeddings and is based on a distributional hypothesis.

In this hypothesis, it uses skip-grams or a continuous bag of words (CBOW).

These are basically shallow neural networks that have an input layer, an output layer, and a projection layer. It reconstructs the linguistic context of words by considering both the order of words in history as well as the future.

The method involves iteration over a corpus of text to learn the association between the words. It relies on a hypothesis that the neighboring words in a text have semantic similarities with each other. It assists in mapping semantically similar words to geometrically close embedding vectors.

It uses the cosine similarity metric to measure semantic similarity. Cosine similarity is equal to Cos(angle) where the angle is measured between the vector representation of two words/documents.

• So if the cosine angle is one, it means that the words are overlapping.

• And if the cosine angle is a right angle or 90°, It means words hold no contextual similarity and are independent of each other.

To summarize, we can say that this metric assigns similar vector representations to the same boards.

Two variants of Word2Vec

Word2Vec has two neural network-based variants: Continuous Bag of Words (CBOW) and Skip-gram.

1. CBOW — The continuous bag of words variant includes various inputs that are taken by the neural network model. Out of this, it predicts the targeted word that closely relates to the context of different words fed as input. It is fast and a great way to find better numerical representation for frequently occurring words. Let us understand the concept of context and the current word for CBOW.

In CBOW, we define a window size. The middle word is the current word and the surrounding words (past and future words) are the context. CBOW utilizes the context to predict the current words. Each word is encoded using One Hot Encoding in the defined vocabulary and sent to the CBOW neural network.

The hidden layer is a standard fully-connected dense layer. The output layer generates probabilities for the target word from the vocabulary.

As we have discussed earlier about the bag of words (BOW) and it being also termed as vectorizer, we will take an example here to clarify it further.

Let’s take a small part of disaster tweets, 4 tweets, to understand how BOW works:-

‘kind true sadly’,

‘swear jam set world ablaze’,

‘swear true car accident’,

‘car sadly car caught up fire’

To create BOW, we use Scikit-learn’s CountVectorizer, which tokenizes a collection of text documents, builds a vocabulary of known words, and encodes new documents using that vocabulary.

Output of CountVectorizer

Here the rows represent each document (4 in our case), the columns represent the vocabulary (unique words in all the documents) and the values represent the count of the words of the respective rows.

In the same way, we can apply CountVectorizer to the complete training data tweets (11,370 documents) and obtain a matrix that can be used along with the target variable to train a machine learning/deep learning model.

2. Skip-gram — Skip-gram is a slightly different word embedding technique in comparison to CBOW as it does not predict the current word based on the context. Instead, each current word is used as an input to a log-linear classifier along with a continuous projection layer. This way, it predicts words in a certain range before and after the current word.

This variant takes only one word as an input and then predicts the closely related context words. That is the reason it can efficiently represent rare words.

The end goal of Word2Vec (both variants) is to learn the weights of the hidden layer. The hidden consequences will be used as our word embeddings!! Let’s now see the code for creating custom word embeddings using Word2Vec-

Import Libraries
from gensim.models import Word2Vec
import nltk
import re
from nltk.corpus import stopwords

Preprocess the Text

#Word2Vec inputs a corpus of documents split into constituent words.
corpus = []
for i in range(0,len(X)):
 tweet = re.sub(“[^a-zA-Z]”,” “,X[i])
 tweet = tweet.lower()
 tweet = tweet.split()
 corpus.append(tweet)

Here is the exciting part! Let’s try to see the most similar words (vector representations) of some random words from the tweets —
model.wv.most_similar(‘disaster’)

Output —

List of tuples of words and their predicted probability
The embedding vector of ‘disaster’ —

dimensionality = 100

Challenges with the bag of words and TF-IDF

Now let’s discuss the challenges with the two text vectorization techniques we have discussed till now.

In BOW, the size of the vector is equal to the number of elements in the vocabulary. If most of the values in the vector are zero then the bag of words will be a sparse matrix. Sparse representations are harder to model both for computational reasons and also for informational reasons.

Also, in BOW there is a lack of meaningful relations and no consideration for the order of words. Here’s more that adds to the challenge with this word embedding technique.

• Massive amount of weights: Large amounts of input vectors invite massive amounts of weight for a neural network.

• No meaningful relations or consideration for word order: The bag of words does not consider the order in which the words appear in the sentences or a text.

• Computationally intensive: With more weight comes the need for more computation to train and predict.

While the TF-IDF model contains the information on the more important words and the less important ones, it does not solve the challenge of high dimensionality and sparsity, and unlike BOW it also makes no use of semantic similarities between words.

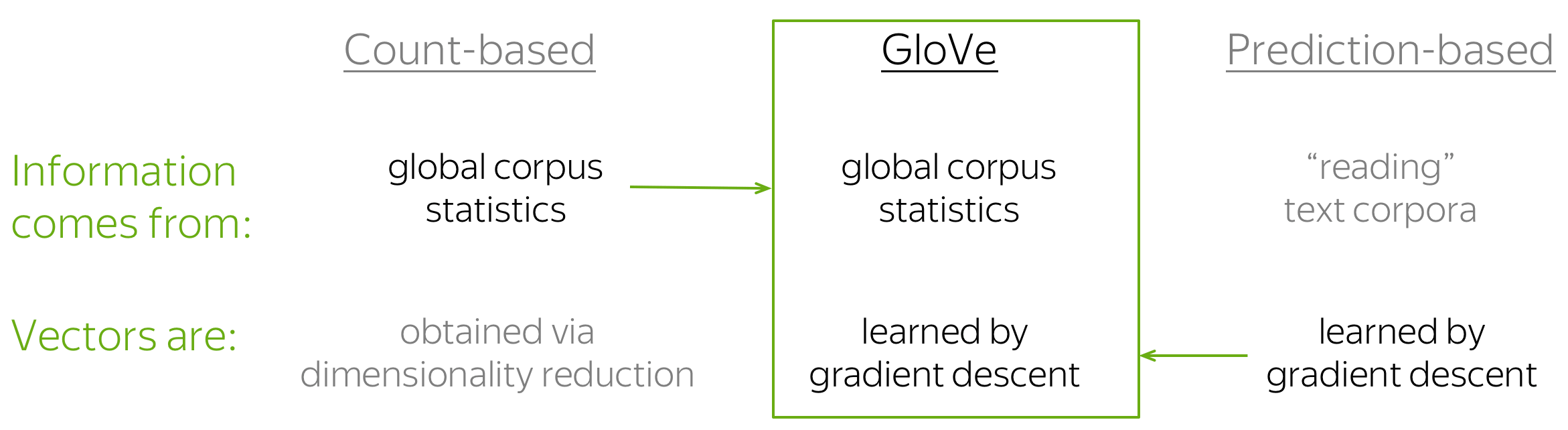
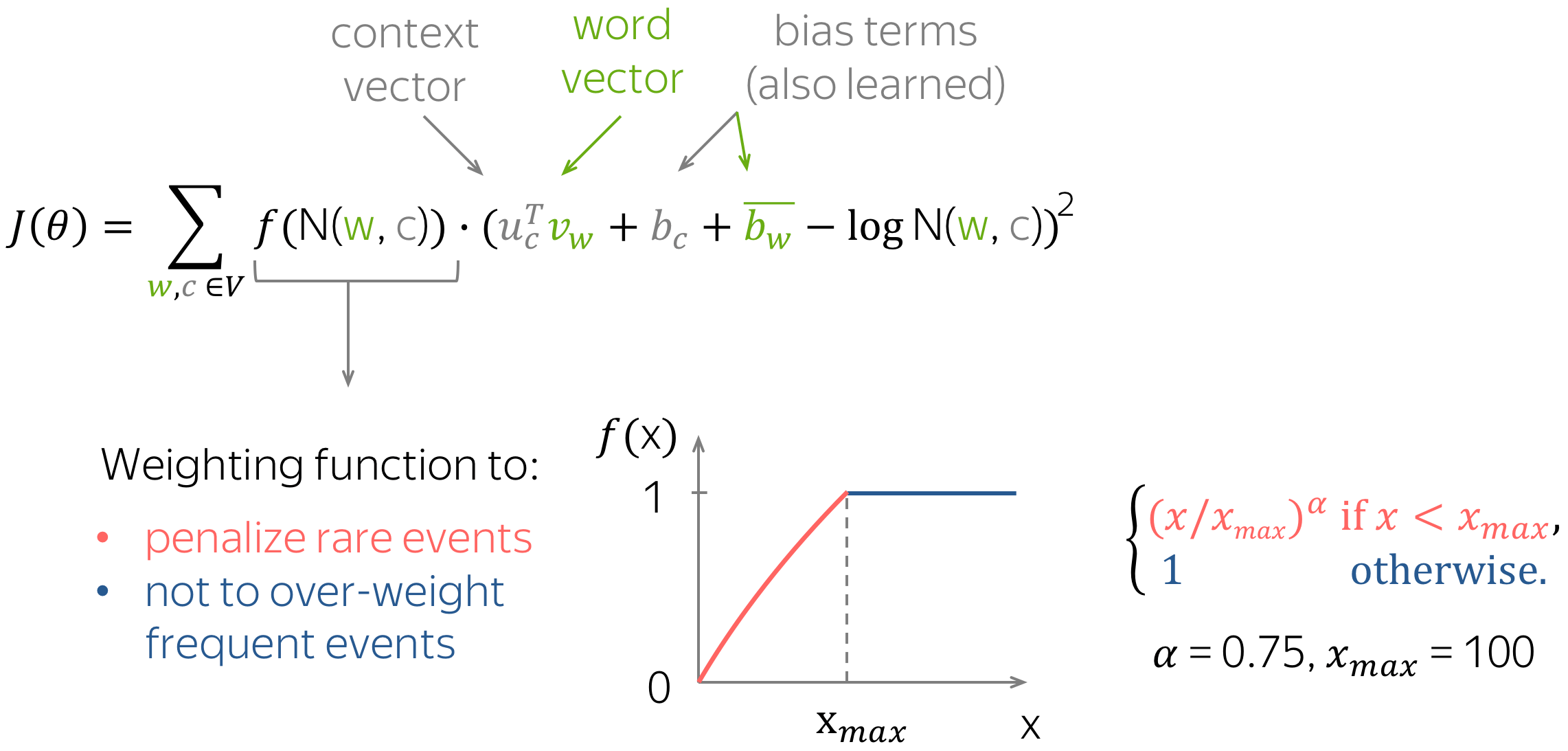
GloVe: Global Vector for word representation

GloVe method of word embedding in NLP was developed at Stanford by Pennington, et al. It is referred to as global vectors because the global corpus statistics were captured directly by the model. It finds great performance in world analogy and named entity recognition problems.

This technique reduces the computational cost of training the model because of a simpler least square cost or error function that further results in different and improved word embeddings. It leverages local context window methods like the skip-gram model of Mikolov and Global Matrix factorization methods for generating low dimensional word representations.

Latent semantic analysis (LSA) is a Global Matrix factorization method that does not do well on world analogy but leverages statistical information indicating a sub-optimal vector space structure.

On the contrary, the skip-gram method performs better on the analogy task. However, it does not utilize the statistics of the corpus properly because of no training on global co-occurrence counts.

So, unlike Word2Vec, which creates word embeddings using local context, GloVe focuses on global context to create word embeddings which gives it an edge over Word2Vec. In GloVe, the semantic relationship between the words is obtained using a co-occurrence matrix.

Consider two sentences —

I am a data science enthusiast

I am looking for a data science job

The co-occurrence matrix involved in GloVe would look like this for the above sentences —

Window Size = 1

Each value in this matrix represents the count of co-occurrence with the corresponding word in row/column. Observe here — this co-occurrence matrix is created using global word co-occurrence count (no. of times the words appeared consecutively; for window size=1). If a text corpus has 1m unique words, the co-occurrence matrix would be 1m x 1m in shape. The core idea behind GloVe is that the word co-occurrence is the most important statistical information available for the model to ‘learn’ the word representation.

Let’s now see an example from Stanford’s GloVe paper of how the co-occurrence probability rations work in GloVe. “For example, consider the co-occurrence probabilities for target words ice and steam with various probe words from the vocabulary. Here are some actual probabilities from a corpus of 6 billion words:”

Here,

Let’s take k = solid i.e, words related to ice but unrelated to steam. The expected Pik /Pjk ratio will be large. Similarly, for words k which are related to steam but not to ice, say k = gas, the ratio will be small. For words like water or fashion, which are either related to both ice and steam or neither to both respectively, the ratio should be approximately one.

The probability ratio is able to better distinguish relevant words (solid and gas) from irrelevant words (fashion and water) than the raw probability. It is also able to better discriminate between two relevant words. Hence in GloVe, the starting point for word vector learning is ratios of co-occurrence probabilities rather than the probabilities themselves.

Enough of the theory. Time for the code!

Import Libraries
import nltk
import re
from nltk.corpus import stopwords
from glove import Corpus, Glove
Text Preprocessing
#GloVe inputs a corpus of documents splitted into constituent words
corpus = []
for i in range(0,len(X)):
 tweet = re.sub(“[^a-zA-Z]”,” “,X[i])
 tweet = tweet.lower()
 tweet = tweet.split()
 corpus.append(tweet)
Train the word Embeddings
corpus = Corpus()
corpus.fit(text_corpus,window = 5)
glove = Glove(no_components=100, learning_rate=0.05)
#no_components = dimensionality of word embeddings = 100
glove.fit(corpus.matrix, epochs=100, no_threads=4, verbose=True)
glove.add_dictionary(corpus.dictionary)
Find most similar -
glove.most_similar(“storm”,number=10)

Output —

List of tuples of words and their predicted probability

BERT (Bidirectional encoder representations from transformers)

This natural language processing (NLP) based language algorithm belongs to a class known as transformers. It comes in two variants namely BERT-Base, which includes 110 million parameters, and BERT-Large, which has 340 million parameters.

It relies on an attention mechanism for generating high-quality world embeddings that are contextualized. So when the embedding goes through the training process, they are passed through each BERT layer so that its attention mechanism can capture the word associations based on the words on the left and those on the right.

It is an advanced technique in comparison to the discussed above as it creates better word embedding. The credit goes to the pre-trend model on Wikipedia data sets and massive word corpus. This technique can be further improved for task-specific data sets by fine-tuning the embeddings.

It finds great application in language translation tasks.

Conclusion

Word embeddings can ‌train deep learning models like GRU, LSTM, and Transformers, which have been successful in NLP tasks such as sentiment classification, name entity recognition, speech recognition, etc.

Here’s a final checklist for a recap.

• Bag of words: Extracts features from the text
• TF-IDF: Information retrieval, keyword extraction
• Word2Vec: Semantic analysis task
• GloVe: Word analogy, named entity recognition tasks
• BERT: language translation, question answering system

In this blog, we discussed the two techniques for vectorizations in NLP: the Bag of Words and TF-IDF, their drawbacks, and how word-embedding techniques like GloVe and Word2Vec overcome their drawbacks by dimensionality reduction and context similarity. With all said above, you would have a better understanding of how word embeddings benefits your day-to-day life as well.

Word embeddings is one of the most used techniques in natural language processing (NLP). It’s often said that the performance and ability of SOTA models wouldn’t have been possible without word embeddings. It’s precisely because of word embeddings that language models like RNNs, LSTMs, ELMo, BERT, AlBERT, GPT-2 to the most recent GPT-3 have evolved at a staggering pace. 

These algorithms are fast and can generate language sequences and other downstream tasks with high accuracy, including contextual understanding, semantic and syntactic properties, as well as the linear relationship between words.

At the core, these models use embedding as a method to extract patterns from text or voice sequences. But how do they do that? What is the exact mechanism and the math behind word embeddings?

In this article, we’ll explore some of the early neural network techniques that let us build complex algorithms for natural language processing. For certain topics, there will be a link to the paper and a colab notebook attached to it, so that you can understand the concepts through trying them out. Doing so will help you learn quicker.

Topics we’ll be covering:

1. What are word embeddings?
2. Neural Language Model
3. Word2Vec
   1. Skipgrams
   2. Continuous bag of words
4. On softmax function
5. Improving approximation 
   1. Softmax-based approaches
      1. Hierarchical Softmax
   2. Sampling-based approaches
      1. Noise contrastive estimation
      2. Negative sampling

What are word embeddings?

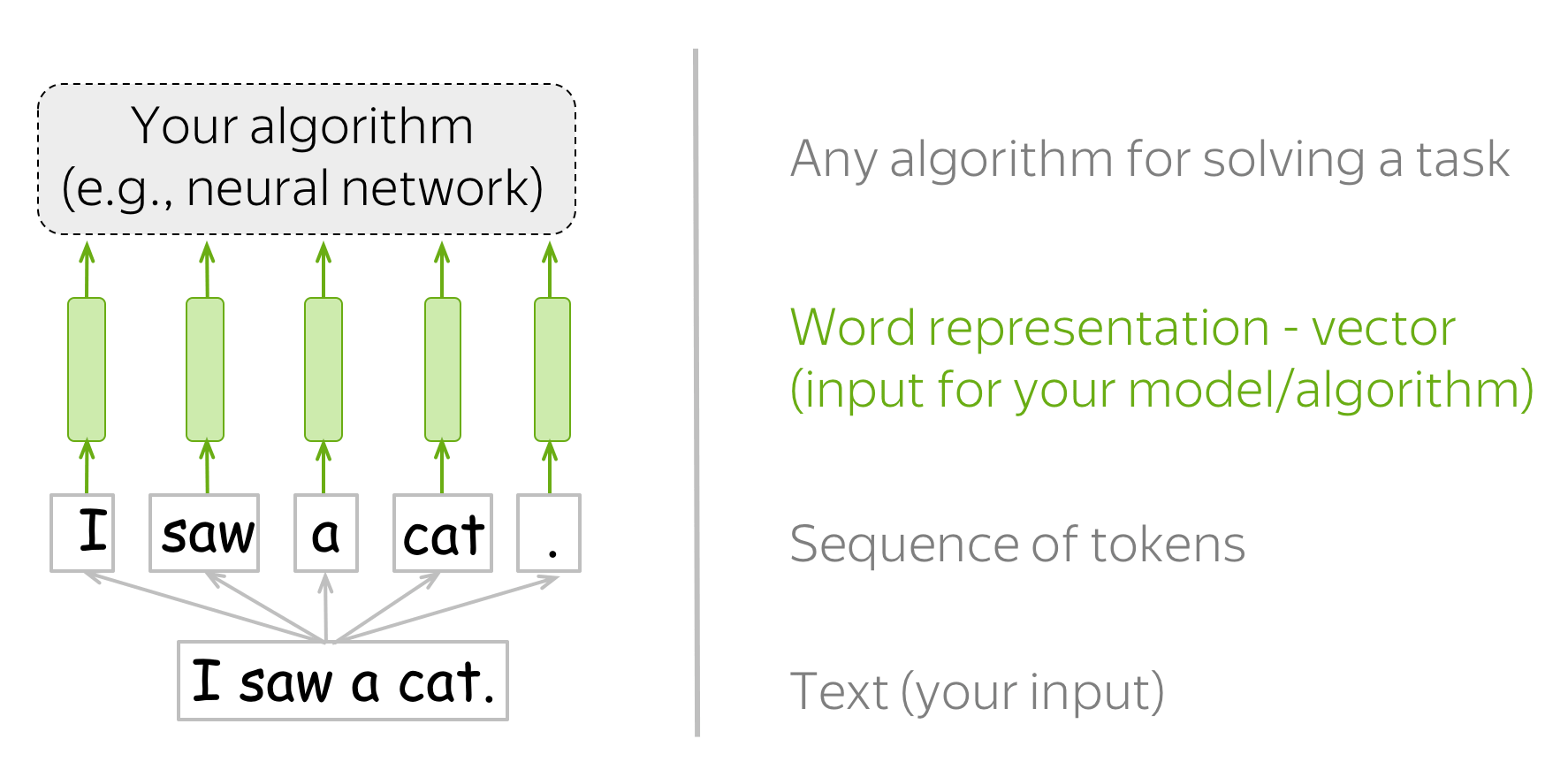
Word embeddings are a way to represent words and whole sentences in a numerical manner. We know that computers understand the language of numbers, so we try to encode words in a sentence to numbers such that the computer can read it and process it. 

But reading and processing are not the only things that we want computers to do. We also want computers to build a relationship between each word in a sentence, or document with the other words in the same. 

We want word embeddings to capture the context of the paragraph or previous sentences along with capturing the semantic and syntactic properties and similarities of the same. 

For instance, if we take a sentence:

“The cat is lying on the floor and the dog was eating”, 

…then we can take the two subjects (cat and dog) and switch them in the sentence making it:

 “The dog is lying on the floor and the cat was eating”. 

In both sentences, the semantic or meaning-related relationship is preserved, i.e. cat and dog  are animals. And the sentence makes sense. 

Similarly, the sentence also preserved syntactic relationship, i.e. rule-based relationship or grammar.  

In order to achieve that kind of semantic and syntactic relationship we need to demand more than just mapping a word in a sentence or document to mere numbers. We need a larger representation of those numbers that can represent both semantic and syntactic properties. 

We need vectors. Not only that, but learnable vectors. 

In a mathematical sense, a word embedding is a parameterized function of the word:

where is the parameter and W is the word in a sentence. 

A lot of people also define word embedding as a dense representation of words in the form of vectors. 

For instance, the word cat and dog can be represented as:

W(cat) = (0.9, 0.1, 0.3, -0.23 … ) 

W(dog) = (0.76, 0.1, -0.38, 0.3 … ) 

Now, hypothetically speaking, if the model is able to preserve the contextual similarity, then both words will be close in a vector space. 

So far we’ve dealt with two words (cat and dog), but what if there are more words? The job of a work embedding model is to cluster similar information and establish a relationship between them.

As you can see, word embeddings clusters similar words together. 

There are a lot of shallow algorithms present that work well for clustering. Why do we need neural networks?

One of the biggest misconceptions is that word embeddings require deep neural networks. As we build different word embedding models, you will see that for all the embeddings, the model is a shallow neural network, and some are linear models as well.

The reasons we use neural networks to create word embeddings are:

1. It’s useful in finding nearest neighbors in the embedding space. 
2. It can be used as an input to supervised learning tasks. 
3. It creates a mapping of discrete variables, such as words to a vector, of continuous variables. 
4. It also tackles the curse of dimensionality. 

Neural Language Model

Word embeddings were proposed by Bengio et. al. (2001, 2003) to tackle what’s known as the curse of dimensionality, a common problem in statistical language modelling. 

It turns out that Bengio’s method could train a neural network such that each training sentence could inform the model about a number of semantically available neighboring words, which was known as distributed representation of words. The neural network not established relationships between different words, but it also preserved relationships in terms of both semantic and syntactic properties.   

This introduced a neural network architecture approach that laid the foundation for many current approaches. 

This neural network has three components:

1. An embedding layer that generates word embedding, and the parameters are shared across words.
2. A hidden layer of one or more layers, which introduces non-linearity to the embeddings.
3. A softmax function that produces probability distribution over all the words in the vocabulary. 

Let’s understand how a neural network language model works with the help of code.

(here are links to the Notebook and original Paper) 

Step 1: Indexing the words. We start by indexing the words. For each word in the sentence, we’ll assign a number to it.

word_list = " ".join(raw_sentence).split()
word_list = list(set(word_list))
word2id = {w: i for i, w in enumerate(word_list)}
id2word = {i: w for i, w in enumerate(word_list)}
n_class = len(word2id)

Step 2: Building the model.

We will build the model exactly as described in the paper.

class NNLM(nn.Module):
   def __init__(self):
       super(NNLM, self).__init__()
       self.embeddings = nn.Embedding(n_class, m) 

       self.hidden1 = nn.Linear(n_step * m, n_hidden, bias=False)
       self.ones = nn.Parameter(torch.ones(n_hidden))

       self.hidden2 = nn.Linear(n_hidden, n_class, bias=False)
       self.hidden3 = nn.Linear(n_step * m, n_class, bias=False) 

       self.bias = nn.Parameter(torch.ones(n_class))

   def forward(self, X):
       X = self.embeddings(X) 
       X = X.view(-1, n_step * m) 
       tanh = torch.tanh(self.d + self.hidden1(X)) 
       output = self.b + self.hidden3(X) + self.hidden2(tanh) 
       return output

We’ll start by initializing an embedding layer. An embedding layer is a lookup table. 

Once the input index of the word is embedded through an embedding layer, it’s then passed through the first hidden layer with bias added to it. The output of these two is then passed through a tanh function. 

If you remember from the diagram in the original paper, the output from the embedded layer is also passed into the final hidden layer, where the output of the tanh is summed together.

output = self.b + self.hidden3(X) + self.hidden2(tanh)

Now, in the last step we will calculate the probability distribution over the entire vocabulary. 

Step 3: Loss and optimization function.

Now that we have the output from the model, we need to make sure that we pass it through the softmax function to get the probability distribution. 

We’re using cross entropy loss. 

criterion = nn.CrossEntropyLoss()

The cross entropy loss is made up of two equations: log softmax function, and negative log likelihood loss or NLLLoss. The former calculates the softmax normalization, while the latter calculates the negative log likelihood loss. 

For optimization, we use Adam optimizer. 

Step 4: Training.

Finally, we train the model. 

In a nutshell, word embeddings can be defined as a dense representation of words in the form of vectors in low-dimensional space. These embeddings are accompanied by learnable vectors, or parameterized functions. They update themselves during backpropagation using a loss function, and try to find a good relationship between words, preserving both semantic and synaptic properties. 

“As it turned out that neural network based models significantly outperformed statistical based models” Mikolov et. al. (2013).  

Word2Vec

The approach introduced by Bengio opened new opportunities for NLP researchers to modify the technique and the architecture itself, to create a method that’s computationally less expensive. Why?

The method that Bengio et al proposed takes words for the vocabulary, and feeds them into a feed forward neural network with an embedding layer, hidden layer(s) and a softmax function.

These embeddings have associated learnable vectors, which optimize themselves through back propagation. Essentially, the first layer of the architecture yields word embeddings, since it’s a shallow network. 

The problem with this architecture is that it’s computationally expensive between the hidden layer and the projection layer. The reason for it is complex:

1. The values produced in the projection are dense.
2. The hidden layer computes probability distribution for all the words in the vocabulary.

To address this issue, researchers (Mikolov et al. in 2013) came along with a model called ‘Word2Vec’. 

A Word2Vec model essentially addresses the issues of Bengio’s NLM. 

It removes the hidden layer altogether, but the projection layer is shared for all words, just like Bengio’s model. The downside is that this simple model without a neural network won’t be able to represent data as precisely as the neural network can, if there’s less data. 

On the other hand, with a larger dataset, it can represent the data precisely in the embedding space. Along with it, it also reduces complexity, and the model can be trained in larger datasets.

Mikolov et al. in 2013 proposed two models:

1. Continuous Bag-of-Words Model
2. Continuous Skip-gram Model

Continuous bag-of-words model

A Continuous Bag-of-Words or CBOW model basically takes ‘n’ words before and after the target word (wt), and predicts the latter. n can be any number. 

For instance, if n=2 and the sentence is ‘the dog is playing in the park”, then the words fed into the model will be ([the, dog, is, in, the, park] ), followed by the target word ‘playing’. 

This model takes out the complexity of calculating probability distribution over all the words in the vocabulary by just calculating the log2(V), where V is the vocabulary size. Hence this model is faster and efficient. 

Let’s understand how a CBOW model works with the help of code.

(here are links to the Notebook and original paper) 

To begin with, we won’t change the word encoding method to numbers. That will stay the same. 

Step 1: Define a function to create a context window with n words from the right and left of the target word.

def CBOW(raw_text, window_size=2):
   data = []
   for i in range(window_size, len(raw_text) - window_size):
       context = [raw_text[i - window_size], raw_text[i - (window_size - 1)], raw_text[i + (window_size - 1)], raw_text[i + window_size]]
       target = raw_text[i]
       data.append((context, target))

   return data

The function should take two arguments: data and window size. The window size will define how many words we are supposed to take from the right and from the left. 

The for loop: for i in range(window_size, len(raw_text) – window_size): iterates through a range starting from the window size, i.e. 2 means it will ignore words in index 0 and 1 from the sentence, and end 2 words before the sentence ends. 

Inside the for loop, we try separate context and target words and store them in a list.

For example, if the sentence is “The dog is eating and the cat is lying on the floor”, CBOW with window 2 will consider words ‘The’, ‘dog’,  ‘eating’ and ‘and’. Essentially making the target word ‘is’.

Let i = window size = 2, then:

context = [raw_text[2 - 2], raw_text[2 - (2 - 1)], raw_text[i + (2 - 1)], raw_text[i + 2]]

target = raw_text[2]

Let’s call the function and see the output. 

data = CBOW(raw_text)
print(data[0])

Output:
(['The', 'dog', 'eating', 'and'], 'is')

Step 2: Build the model.

Building a CBOW is similar to building the NNLM we did earlier, but actually much simpler. 

In the CBOW model, we reduce the hidden layer to only one. So all together we have: an embedding layer, a hidden layer which passes through the ReLU layer, and an output layer.

class CBOW_Model(torch.nn.Module):
   def __init__(self, vocab_size, embedding_dim):
       super(CBOW_Model, self).__init__()

       self.embeddings = nn.Embedding(vocab_size, embedding_dim)
       self.linear1 = nn.Linear(embedding_dim, 128)
       self.activation_function1 = nn.ReLU()

       self.linear2 = nn.Linear(128, vocab_size)


   def forward(self, inputs):
       embeds = sum(self.embeddings(inputs)).view(1,-1)
       out = self.linear1(embeds)
       out = self.activation_function1(out)
       out = self.linear2(out)
       return out

This model is pretty straightforward. The context words index is fed into the embedding layers, which is then passed through the hidden layer followed by the nonlinear activation layer, i.e. ReLU, and finally we get the output. 

Step 3: Loss and optimization function. 

Similar to NNLM, we use the same technique for calculating probability distribution over all the words in the vocabulary, ie. nn.CrossEntropyLoss(). 

For optimization, we use Stochastic Gradient Descent. You can use Adam optimizer as well. In NLP, Adam is the go-to optimizer because it converges faster than SGD.

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

Step 4: Training

Training is the same as the NNLM model.  

for epoch in range(50):
   total_loss = 0

   for context, target in data:

       context_vector = make_context_vector(context, word_to_ix)

       output = model(context_vector)

       target = torch.tensor([word_to_ix[target]])
       total_loss += loss_function(output, target)

   
   optimizer.zero_grad()
   total_loss.backward()
   optimizer.step()

make_context_vector turns words into numbers. 

It’s worth noting that authors of this paper found that NNLM preserves linear relationships between words with similarity. For example, ‘king’ and ‘queen’ are the same as ‘men’ and ‘women’, i.e. NNLM preserves gender linearity. 

Similarly, models such as CBOW and any neural network model that we’ll be discussing next will preserve linear relationships, even though we specifically define nonlinearity in the neural network. 

Continuous skip-gram model

Continuous skip-gram, or skip-gram, is similar to CBOW. Instead of predicting the target word (wt), it predicts the word surrounding it with context. The training objective is to learn representations, or embeddings, that are good at predicting nearby words. 

It also takes an “n” number of words. For instance, if n=2 and the sentence is ‘the dog is playing in the park”, then the word fed into the model will be playing, and the target words will be (the, dog, is, in, the, park).

Let’s understand how a skip-gram model works with the help of code.

(here are links to the Notebook and original paper)

A skipgram model is the same as the CBOW model with one difference. The difference lies in creating the context and the target word. 

Step 1: Setting target and context variable. 

Since skipgram takes a single context word and n number of target variables, we just need to flip the CBOW from the previous model.

def skipgram(sentences, window_size=1):
   skip_grams = []
   for i in range(window_size, len(word_sequence) - window_size):
       target = word_sequence[i]
       context = [word_sequence[i - window_size], word_sequence[i + window_size]]
       for w in context:
           skip_grams.append([target, w])

   return skip_grams

As you can see, the function is almost the same. 

Here, you need to understand that when the window size is 1, we take one word before and after the target word.

When we call the function, the output looks something like this:

print(skipgram(word_sequence)[0:2])

Output:
[['my', 'During'], ['my', 'second']]

As you can see, the target word is ‘my’ and the two words are ‘During’ and ‘second’.

Essentially, we’re trying to create a pair of words such that each pair will contain a target word. Depending on the context window, it will contain the neighboring words.

Step 2: Building the model.

The model is pretty straightforward. 

class skipgramModel(nn.Module):
   def __init__(self):
       super(skipgramModel, self).__init__()
       self.embedding = nn.Embedding(voc_size, embedding_size)
       self.W = nn.Linear(embedding_size, embedding_size, bias=False)
       self.WT = nn.Linear(embedding_size, voc_size, bias=False)

   def forward(self, X):
       embeddings = self.embedding(X)
       hidden_layer = nn.functional.relu(self.W(embeddings))
       output_layer = self.WT(hidden_layer)
       return output_layer

The loss function and optimisation remains the same. 

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

Once we’ve defined everything, we can train the model. 

for epoch in range(5000):
        input_batch, target_batch = random_batch()
        input_batch = torch.Tensor(input_batch)
        target_batch = torch.LongTensor(target_batch)

        optimizer.zero_grad()
        output = model(input_batch)

        
        loss = criterion(output, target_batch)
        if (epoch + 1) % 1000 == 0:
            print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))

        loss.backward()
        optimizer.step()

The skip-gram model increases computational complexity because it has to predict nearby words based on the number of neighboring words. The more distant words tend to be slightly less related to the current word.

Summary so far:

1. Neural Network Language Model (NNLM) or Bengio’s model outperforms the earlier statistical model like the n-gram model.   
2. NNLM also tackles the curse of dimensionality and preserves contextual, linguistic regularities and patterns through its distributed representation.
3. NNLM is computationally expensive.
4. Word2Vec models tackles computational complexity by removing the hidden layer and sharing the weights 
5. The downside of Word2Vec is it does not have a neural network which makes it hard to represent the data but the upside is that if it can be trained on a large number of data then because it is much more efficient than neural networks it is possible to compute very accurate high dimensional word vectors.
6. Word2Vec has two models: CBOW and Skipgram. The former is faster than the latter.

On softmax function

So far, you’ve seen how the softmax function plays a vital role in predicting the words around a given context. But it suffers from a complexity issue. 

Recall the equation of softmax function:

Where w_t is the target word, c is the context words, and y is the output for each target word. 

If you look at the equation above, the complexity of the softmax function arises when the number of predictors is high. If i=3, then the softmax function will return a probability distribution over three categories. 

But, in NLP we usually deal with thousands, sometimes millions of words. Getting a probability distribution over that many words will make the computation really expensive and slow. 

Keep in mind that softmax functions return the exact probability distribution, so they tend to get slower with increasing parameters. For each word (w_t), it sums over the entire vocabulary in the denominator. 

So what are the different approaches that will make computation inexpensive and fast, while making sure that the approximation is not compromised?

In the next section, we’ll cover different approaches that can reduce the computational time. Instead of getting exact probabilities over the full vocabulary, we’ll try to approximate over the full vocabulary, or even a sample vocabulary. This reduces complexity and increases processing speed. 

We will discuss two approaches: softmax-based approaches and sampling-based approaches.

Improving predictive functions

In this section, we explore three possible methods for improving prediction, by modifying the softmax function for approximating better results, and replacing the softmax with new methods. 

Softmax-based approaches

Softmax-based approaches are more inclined towards modifying the softmax to get a better approximation of the predicted word, rather than eliminating it altogether. We will discuss two methods: hierarchical softmax approach and CNN approach.

Hierarchical softmax

Hierarchical softmax was introduced by Morin and Bengio in 2005, as an alternative to the full softmax function, where it replaces it with a hierarchical layer. It borrows the technique from the binary huffman tree, which reduces the complexity of calculating the probability from the whole vocabulary V to log₂(V), i.e. binary.

Coding a huffman tree is very complicated. I’ll try to explain it without using code, but you can find the notebook here and try it out.

To understand the H-softmax, we need to understand the workings of the huffman tree. 

The huffman tree is a binary tree that takes the words from the vocabulary; based on their frequency in the document, it creates a tree. 

Take for example this text: “the cat is eating and the dog is barking”. In order to create a huffman tree, we need to calculate the frequency of words from the whole vocabulary. 

word_to_id = {w:i for i, w in enumerate(set(raw_text))}
id_to_word = {i:w for w, i in word_to_id.items()}
word_frequency = {w:raw_text.count(w) for w,i in word_to_id.items()}

print(word_frequency)

Output:

{'and': 1, 'barking': 1, 'cat': 1, 'dog': 1, 'eating': 1, 'is': 2, 'the': 2}

The next step is to create a huffman tree. The way we do it is by taking the least frequent word. In our example, we have a lot of words that are occurring only once, so we’re free to take any two. Let’s take ‘dog’ and ‘and’. We will then join the two leaf nodes by a parent node, and add the frequency. 

In the next step, we’ll take another word that is least frequent (again, the word that occurs only once) and we’ll put it beside the node that has the sum of two. Remember that less frequent words go to the left side, and more frequent words go to the right side. 

Similarly, we’ll keep on building the words until we’ve used all the words from the vocabulary. 

Remember, all the words with the least frequency are at the bottom. 

print(Tree.wordid_code)

Output:
{0: [0, 1, 1],
 1: [0, 1, 0],
 2: [1, 1, 1, 1],
 3: [1, 1, 1, 0],
 4: [0, 0],
 5: [1, 1, 0],
 6: [1, 0]}

Once the tree is created, we can then start the training. 

In the huffman tree, we no longer calculate the output embeddings w`. Instead, we try to calculate the probability of turning right or left at each leaf node, using a sigmoid function. 

p(right | n,c)=σ(h⊤w′n), where n is the node and c is the context.

As you will find in the code below, a sigmoid function is used to decide whether to go right or to left. It’s also important to know that the probabilities of all the words should sum up to 1. This ensures that the H-softmax has a normalized probability distribution over all the words in the vocabulary. 

class SkipGramModel(nn.Module):
   def __init__(self, emb_size, emb_dimension):
       super(SkipGramModel, self).__init__()
       self.emb_size = emb_size
       self.emb_dimension = emb_dimension
       self.w_embeddings = nn.Embedding(2*emb_size-1, emb_dimension, sparse=True)
       self.v_embeddings = nn.Embedding(2*emb_size-1, emb_dimension, sparse=True)
       self._init_emb()

   def _init_emb(self):
       initrange = 0.5 / self.emb_dimension
       self.w_embeddings.weight.data.uniform_(-initrange, initrange)
       self.v_embeddings.weight.data.uniform_(-0, 0)

   def forward(self, pos_w, pos_v,neg_w, neg_v):

       emb_w = self.w_embeddings(torch.LongTensor(pos_w))
       neg_emb_w = self.w_embeddings(torch.LongTensor(neg_w))
       emb_v = self.v_embeddings(torch.LongTensor(pos_v))
       neg_emb_v = self.v_embeddings(torch.LongTensor(neg_v))

       score = torch.mul(emb_w, emb_v).squeeze()
       score = torch.sum(score, dim=1)
       score = F.logsigmoid(-1 * score)
       neg_score = torch.mul(neg_emb_w, neg_emb_v).squeeze()
       neg_score = torch.sum(neg_score, dim=1)
       neg_score = F.logsigmoid(neg_score)
       
       loss = -1 * (torch.sum(score) + torch.sum(neg_score))
       return loss

Sampling-based approaches

Sampling-based approaches completely eliminate the softmax layer. 

We’ll discuss two approaches: noise contrastive estimation, and negative sampling.

Noise contrastive estimation

Noise contrastive estimation (NCE) is an approximation method that replaces the softmax layer and reduces the computational cost. It does so by converting the prediction problem into a classification problem. 

This section will contain a lot of mathematical explanations. 

NCE takes an unnormalised multinomial function (i.e. the function that has multiple labels and its output has not been passed through a softmax layer), and converts it to a binary logistic regression. 

In order to learn the distribution to predict the target word (w_t) from some specific context (c), we need to create two classes: positive and negative. The positive class contains samples from training data distribution, while the negative class contains samples from a noise distribution Q, and we label them 1 and 0 respectively. Noise distribution is a unigram distribution of the training set. 

For every target word given context, we generate sample noise from the distribution Q as Q(w), such that it’s k times more frequent than the samples from the data distribution P(w | c). 

These two probability distributions can be represented as the sum of each other because we are effectively sampling words from the two distributions. Hence,

As mentioned earlier, NCE is a binary classifier which consists of a true label as ‘1’ and false label as ‘0’. Intuitively, 

When y=1, 

When y=0, 

Our aim is to develop a model with parameters θ, such that given a context c, its predicted probability P(w,c) approximates the original data distribution P_d(w,c). 

Generally, the noise distribution is approximated by sampling. We do that by generating k noise samples {wij}:

Where Z_θ(c) is a normalizing term from the softmax, and you recall this is what we are trying to eliminate. The way we can eliminate Z_θ(c) is by making it a learnable parameter. Essentially, we transform the softmax function from absolute value, i.e. the value which sums over all the words in vocabulary again and again, to a dynamic value which changes to find a better for itself – it’s learnable. 

But, as it turns out, Mnih et al. (2013) stated that Z_θ(c) can be fixed at 1. Even though it’s static again but it normalizes quite well, Zoph et al. (2016) found that Z_θ(c)=1 produces a model with low variance. 

We can replace P_θ(w | c) with exp(s_θ(w | c)) such that the loss function can be written as:

One thing to keep in mind is that as we increase the number of noise samples k, the NCE derivative approaches the likelihood gradient, or the softmax function of the normalised model. 

In conclusion, NCE is a way of learning a data distribution by comparing it against a noise distribution, and modifying the learning parameters such that the model P_θ is almost equal to P_d.

Negative sampling

It’s important to understand NCE, because negative sampling is the modified version of the same. It’s a more simplified version as well. 

To begin with, we learned that as we increase the number of noise samples k, the NCE derivative approaches the likelihood gradient, or the softmax function of the normalised model. 

The way negative sampling works is, it gets rid of the noise by replacing it with 1.  Intuitively, 

When y=1, 

In negative sampling we use a sigmoid function, so we’ll transform the above equation to:

We know that P_θ(w | c) is replaced with exp(s_θ(w | c)).

Therefore, 

This makes the equation shorter. It has to compute 1 instead of noise, so the equation becomes computationally efficient. But why do we care to simplify NCE? 

One reason is that we’re concerned with the high representation of the word vector, so it can simplify the model as long as the word embeddings produced by the model retain their quality. 

If we replace the final NCE equation with the equation above, we get:

Since log(1)=0, 

therefore,

Since we’re dealing with sigmoid function i.e. 

we can modify the equation above to:

(Here are the links to the Notebook and original paper)

Final thoughts and conclusion

We explored the evolution of neural-based modelling for NLP or machine translation. We covered word embedding, a method to find semantic, syntactic and linear relationship in the vocabulary. Although some of the methods mentioned earlier are no longer used, they lay the basic foundation of the subject, and make further learning easier. 

We saw how Begio and his team introduced neural language models to find better representation through their word embedding method, followed by how Mikolov and his team modified Begio’s method and introduced a computationally less expensive method by removing the hidden layer. Although the word2vec model is a simple model, it became computationally expensive once the vocabulary size increased. 

Different methods were introduced to rectify the issue of complexities, and the three models that we saw later in the post addressed the issue with the softmax function. 

In the end, we saw how negative sampling outranks all the two methods (hierarchical softmax and NCE), and modifies word2vec model with a much more efficient approximation technique that captures better representation like semantic, syntactic, and preserves linear representation as well reduces the computational cost. 

Word embedding opened new doors for NLP research and development. These models work well, but they still lack conceptual understanding. It was only in 2018 that Peters et. al. introduced ELMo: Embeddings from Language Model, which linked the missing piece of finding contextual representation through word embeddings. 

For better understanding and clarity, check out the notebooks for each topic. 

Resources

• On word embeddings – Part 1
• On word embeddings – Part 2: Approximating the Softmax
• Noise Contrastive Estimation
• The Illustrated Word2vec
• Distributed Representations of Words and Phrases and their Compositionality 
• Efficient Estimation of Word Representations in Vector Space 
• A Neural Probabilistic Language Model
• Notes on Noise Contrastive Estimation and Negative Sampling