Add your answer:
Earn +
20
pts
Q: What is the word coiled inside this circle N G O E R R T S?
Write your answer…
Made with 💙 in St. Louis
Copyright ©2023 Infospace Holdings LLC, A System1 Company. All Rights Reserved. The material on this site can not be reproduced, distributed, transmitted, cached or otherwise used, except with prior written permission of Answers.
I’d like to know what is the word to describe the entire interior within a circle. Circle is for the boundary only and does not include the interior of it.
asked May 17, 2019 at 17:25
2
Mathematically speaking, it’s a closed disk.
In geometry, a disk (also spelled disc) is the region in a plane bounded by a circle. A disk is said to be closed if it contains the circle that constitutes its boundary, and open if it does not.
Non-mathematicians will be satisfied to call it just a disk.
answered May 17, 2019 at 17:28
Glorfindel♦Glorfindel
14.7k15 gold badges69 silver badges75 bronze badges
2
Euclidean geometry deals with figures such as: circles, rectangles, etc.
The parts inside the figures are simply an area or space.
It refers to the space inside the line or lines. Beyond that, there are all sorts of complexities I am not really trained for. 
«Any time you need to determine the space inside a circle or the amount of space a circle covers, you can use the equation for the area of a circle. Especially for real world applications of this skill, measuring diameter is often the simplest way to start.»
space inside a circle or amount of spaced a circle covers
answered May 17, 2019 at 17:52
LambieLambie
39.5k3 gold badges29 silver badges84 bronze badges
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
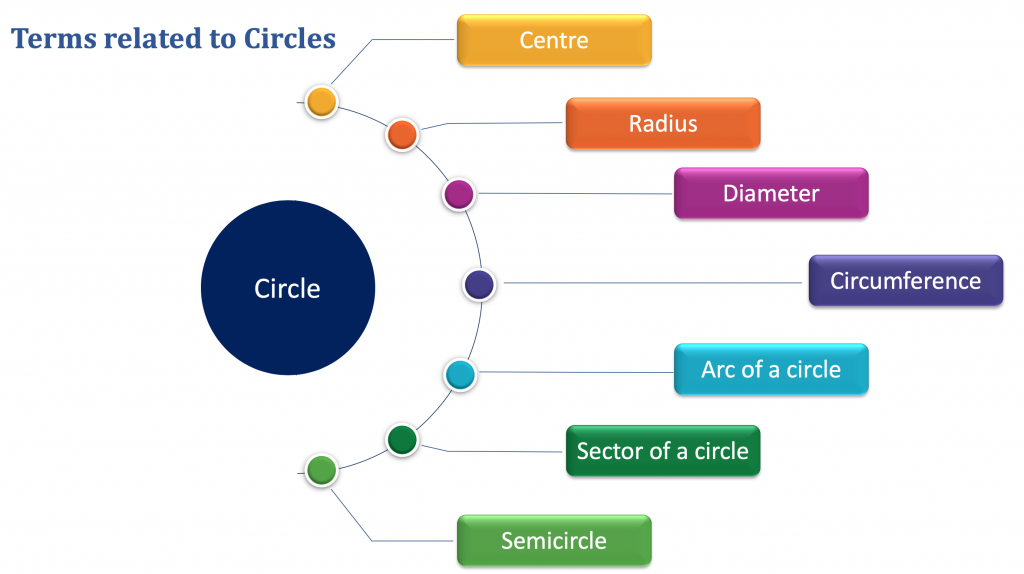
There are many parts of a circle that make it a circle. A circle is a 2D shape and is measured in terms of its radius. The word ‘Circle’ is derived from the Greek word ‘kirkos’ meaning ‘ring’ or ‘hoop’. The parts of a circle include the radius, diameter, circumference, and so on. Let us learn about the circle and its parts in detail.
| 1. | Definition of a Circle |
| 2. | What are the Parts of a Circle? |
| 3. | FAQs on Parts of a Circle |
Definition of a Circle
A circle can be defined as a 2D figure formed by a set of points that are adjacent to each other and are equidistant from a fixed point. The fixed point in this curved plane figure is called the center of the circle, the common distance between the points from the center is called a radius, and a line that crosses from the center of the circle starting from one point to the other is called a diameter. A circle has two main regions namely, the interior of a circle and the exterior of a circle. The interior of a circle consists of the region inside the circle and the exterior of a circle is the region outside the circle.
What are the Parts of a Circle?
A circle is a closed figure with a curved boundary and has many parts that represent the properties and characteristics of a circle.
Circle and its Parts
The different parts of a circle are listed below:
- Circumference
- Radius
- Diameter
- Chord
- Tangent
- Secant
- Arc
- Segment
- Sector
Let us discuss each of the parts in detail.
Circumference of a Circle
The circumference of a circle is its boundary. In other words, when we measure the boundary or the distance around the circle, that measure is called the circumference and it is expressed in units of length like centimeters, meters, or kilometers. The circumference of a circle has three most important elements namely, the center, the diameter, and the radius.
Since we cannot use the ruler (scale) to measure the distance of this curved figure, we apply a formula that uses the radius, diameter, and the value of Pi (π). The formulas for the circumference of a circle are given as follows:
- When the radius is given: Circumference of a circle formula = 2πr
- When the diameter is given: Circumference of a circle formula = π × D
Where,
- r = radius of the circle.
- D = diameter of the circle.
- π = Pi with the value approximated to 3.14159 or 22/7.
Radius of a Circle
The radius of a circle is the length of the line segment joining the center of the circle to any point on the circumference of the circle. A circle can have many radii (the plural form of radius) and they measure the same. Usually, the radius of a circle is denoted by ‘r’.
To calculate the radius of a circle when the diameter, area of a circle, and circumference is known, we use the following formulas:
- Radius of Circle = Diameter / 2 — The diameter is twice the length of the radius and is also the longest chord of the circle. When the diameter is known, we use this formula.
- Radius of Circle = Circumference / 2π — The circumference is the perimeter of the circle and when the circumference is given, we use this formula.
- Radius of Circle = √(Area/π) — The area of a circle is the space inside the circle. Hence, when the area of the circle is given, we use this formula.
Diameter of a Circle
The diameter of a circle is a line segment that passes through the center of the circle and with endpoints that lie on the circumference of a circle. The diameter is also known as the longest chord of the circle and is twice the length of the radius. The diameter is measured from one end of the circle to a point on the other end of the circle, passing through the center. The diameter is denoted by the letter D. There can be an infinite number of diameters where the length of each diameter of the circle is length.
To calculate the diameter of a circle when the radius, area of a circle, and circumference is known, we use the following formulas:
- Diameter = Circumference/π (used when the circumference is given)
- Diameter = Radius × 2 (used when the radius is given)
- Diameter = 2√(Area/π) (used when the area of the circle is given)
Chord of a Circle
A chord of a circle is a line segment that joins two points on the circumference of the circle. A chord divides the circle into two regions known as the segment of the circle which can be referred to as minor segment and major segment depending on the area covered by the chord. In a circle, when the chord is extended infinitely on both sides it becomes a secant. In the figure given below, PQ is represented as the chord of the circle with O as the center.
To calculate the chord of a circle, we use two basic formulas:
- Chord Length = 2 × √(r2 − d2) (using perpendicular distance from the center)
- Chord Length = 2 × r × sin(c/2) (using trigonometry)
Where,
- r is the radius of the circle
- c is the angle subtended at the center by the chord
- d is the perpendicular distance from the chord to the circle center.
Tangent of a Circle
The tangent of a circle is defined as a straight line that touches the curve of the circle at only one point and does not enter the circle’s interior. The tangent touches the circle’s radius at a right angle. The two main aspects to remember in the tangent is the slope (m) and a point on the line. The general equation or formula of the tangent to a circle is:
- The tangent to a circle equation x2 + y2 = a2 for a line y = mx + c is given by the equation y = mx ± a √[1+ m2]
- The tangent to a circle equation x2+ y2 = a2 at (a1, b1) is xa1 + yb1 = a2. This means that the equation of the tangent is expressed as xa1 + yb1 = a2, where a1 and b1 are the coordinates at which the tangent is made.
Secant of a Circle
The secant of a circle is the line that cuts across the circle intersecting the circle at two distinct points. The difference between a chord and a secant is that a chord is a line segment whose endpoints are on the circumference of the circle whereas a secant passes through the circle forming a chord or diameter of the circle.
There are three secant theorems used in the circle which are given below:
- Theorem 1: When two secants intersect at an exterior point, the product of the one whole secant segment and its external segment is equal to the product of the other whole secant segment and its external segment.
- Theorem 2: Two secants can intersect inside or outside a circle.
- Theorem 3: If a secant and a tangent are drawn to a circle from a common exterior point, then the product of the length of the whole secant segment and its external secant segment is equal to the square of the length of the tangent segment.
The figure given below shows the secant PQ and the chord AB.
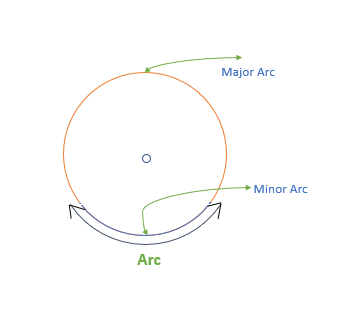
Arc of a Circle
The arc of a circle is the curved part or a part of the circumference of a circle. In other words, the curved portion of an object is mathematically called an arc. The arc of a circle has two arcs namely, minor arc and major arc. To find the measure of these arcs we need to find the length of the arc along with the angle suspended by the arc of any two points. To calculate the length of the arc we use different formulas based on the unit of the central angle (degrees or radians). For a circle, the arc length formula is θ times the radius of a circle. The formulas are:
- Arc Length = θ × r (used for radians)
- Arc Length = θ × (π/180) × r (used for degrees)
Where,
- L = Length of an Arc
- θ = Central angle of Arc
- r = Radius of the circle
Segment of a Circle
A segment of a circle is the region that is bounded by an arc and a chord of the circle. There are two types of segments — minor segment and major segment. A minor segment is made by a minor arc and a major segment is made by a major arc of the circle. To calculate the segment of a circle, we consider the area of the segment which consists of a sector (arc + 2 radii) and a triangle. Hence, the formula for the area of a segment can be expressed as follows
- Area of a segment of circle = area of the sector — area of the triangle
Note: To find the area of the major segment of a circle, we just subtract the corresponding area of the minor segment from the total area of the circle.
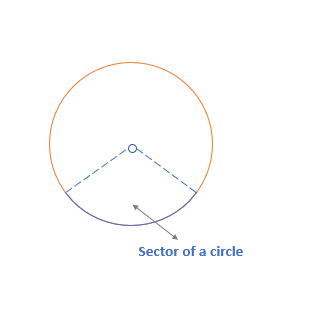
Sector of a Circle
A sector of a circle is a pie-shaped part of a circle made of the arc along with its two radii dividing the circle into a minor sector and a major sector. The larger portion of the circle is called the major sector whereas the smaller portion of the circle is called the minor sector. The 2 radii meet at the part of the circumference of a circle known as an arc, forming a sector of a circle. The formulas to calculate the sector of the circle are:
- Area of a sector (A) = (θ/360°) × πr2 (when the angle is given)
- Length of a section (l) = (θπr) /180 (when the length is given)
- Area of a sector of a circle = (l × r)/2 (when the length and radius is given)
- Perimeter of a sector of a circle = 2 Radius + ((θ/360) × 2πr )
Where,
- r = radius of the circle.
- l = length of the arc.
- θ = angle in degrees.
- π = Pi with the value approximated to 3.14159 or 22/7.
☛ Related Topics
- Circumference to Diameter
- Semicircle
- 3D shapes
FAQs on Parts of Circle
What are the Parts of a Circle?
The parts of a circle include the circumference, radius, diameter, chord, tangent, secant, arc, segment, and sector. Each of these parts of a circle plays a significant role in forming a circle.
Which Part of a Circle is the Longest?
The longest part of the circle is the diameter, i.e., the distance from one end of the circle to the other end of the circle. The line segment that passes through the center joining the two points on the circle is considered to be the longest part. It is to be noted that the diameter is the longest chord of the circle.
What are the 4 Main Parts of a Circle?
The 4 main parts of a circle are radius, diameter, center, and circumference. The center of the circle is the point that is equidistant from all the sides of the circle. The radius is the length of the line from the center of the circle to any point on the curve of the circle. A diameter is a line segment that crosses the center of the circle from one end of the circle to the other end. A circumference of a circle is the boundary or the distance that completes a circle.
How Many Parts is a Segment of a Circle Divided Into?
A segment of a circle is divided into two parts — the minor segment and the major segment. The smaller part of the segment of the circle is called the minor segment whereas the larger part of the segment of the circle is called the major segment.
What is the Center of a Circle?
The center of a circle is the point inside the circle that is equidistant from all the points on the curve of the circle. The center of the circle also helps in creating a circle according to any measurement.
What are Secants in a Circle?
The secant of a circle is the line that cuts across the circle intersecting the circle at two distinct points. The difference between a chord and a secant is that a chord is a line segment whose endpoints are on the curved part of the circle whereas a secant passes through the circle forming a chord or diameter of the circle.
A 7 min read
A circle is a closed shape formed by tracing a point that moves in a plane such that its distance from a given point is constant. The word circle is derived from the Greek word kirkos, meaning hoop or ring. In this article, we cover the properties of a circle, important terms related to circles, and the various circle formulas.
Following is a brief outline of the topics that we will cover in this article:
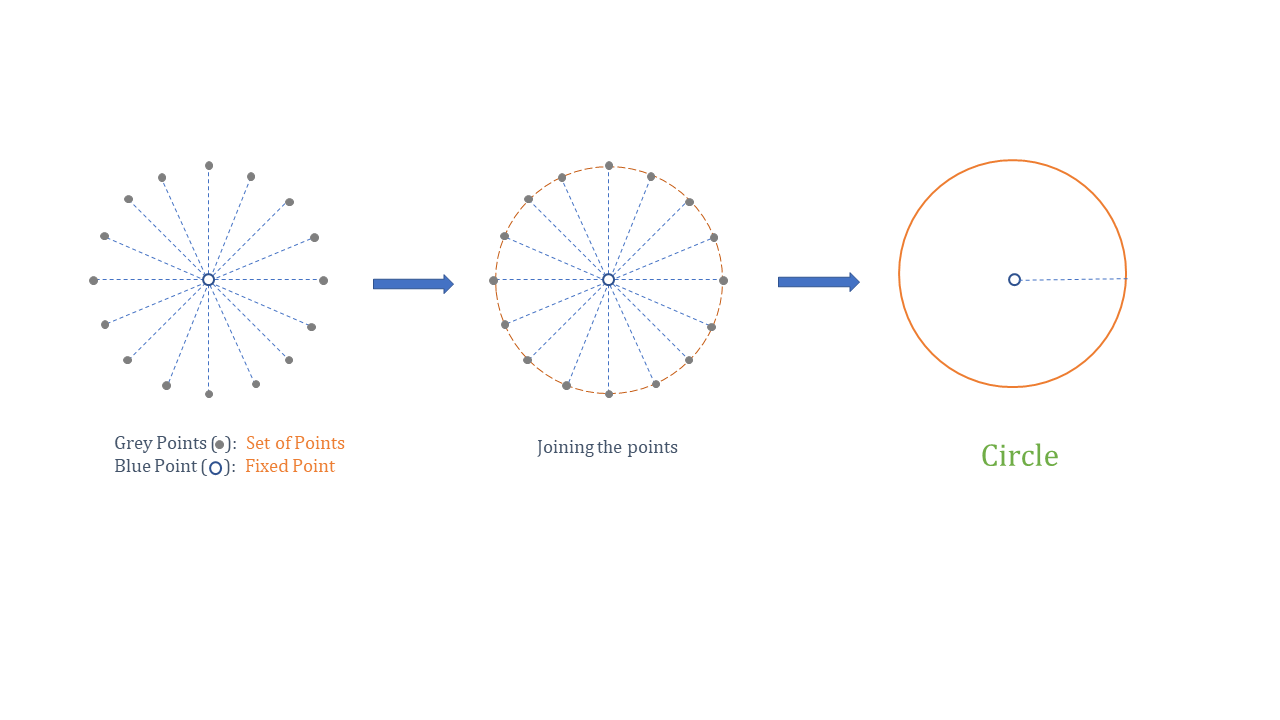
When a set of all points that are at a fixed distance from a fixed point are joined then the geometrical figure obtained is called circle.
Let us now learn a bit about the terminology used in circles.
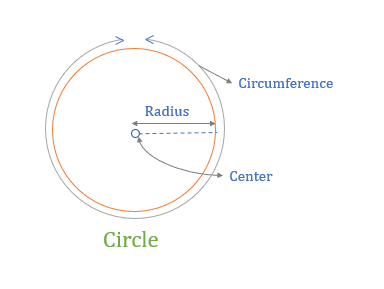
Center
The fixed point in the circle is called the center.
- So, the set of points are at a fixed distance from the center of the circle.
Radius
Radius is the fixed distance between the center and the set of points. It is denoted by “R”.
Diameter
Diameter is a line segment, having boundary points of circles as the endpoints and passing through the center.
- So, logically a diameter can be broken into two parts:
- One part from one boundary point of the circle to the center
- And, the other part from the center to another boundary point.
- Hence, Diameter = Twice the length of the radius or “D = 2R”
Circumference
It is the measure of the outside boundary of the circle.
So, the length of the circle or the perimeter of the circle is called Circumference.
Arc of a circle
The arc of a circle is a portion of the circumference.
From any two-points that lie on the boundary of the circle, two arcs can be created: A Minor and a Major Arc.
- Minor arc: The shorter arc created by two points.
- Major Arc: The longer arc created by two points.
Sector of a circle:
A Sector is formed by joining the endpoints of an arc with the center.
- On joining the endpoints with the center, two sectors will be obtained: Minor and Major.
- By default, we only consider the Minor sector unless it is mentioned otherwise.
Semi-circle
A semi-circle is half part of the circle or,
- A semi-circle is obtained when a circle is divided into two equal parts.
Now that we know all the terminologies related to the circles, let us learn about the properties of a circle.
Geometry is an essential topic to ace if you plan to score 700+ on the GMAT. Let us help you achieve mastery in GMAT Geometry. Start by signing up for a free trial and learn from the best in the industry. After all, we are the most reviewed company on gmatclub.
Richa, Guillermo, Sireesh, and Raghav are just a few of the students that have achieved a Q50+ score in the GMAT Quant section using e-GMAT. Get started with our free trial today if you too wish to score Q50+ on the GMAT!
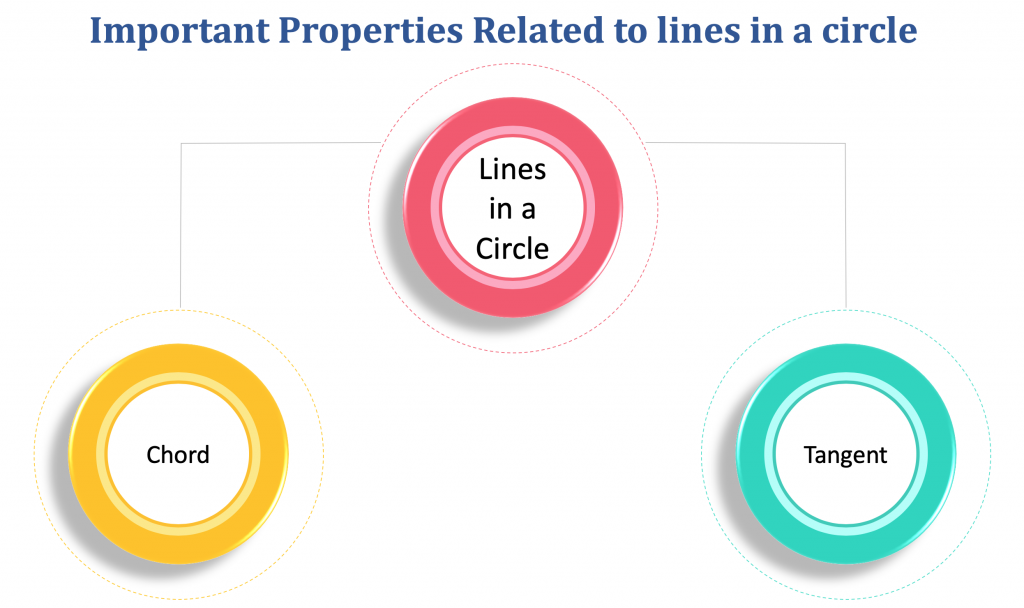
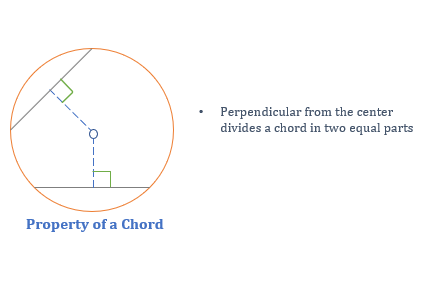
Chord
A chord is a line segment whose endpoints lie on the boundary of the circle.
Properties of Chord
- Perpendicular dropped from the center divides a chord into two equal parts.
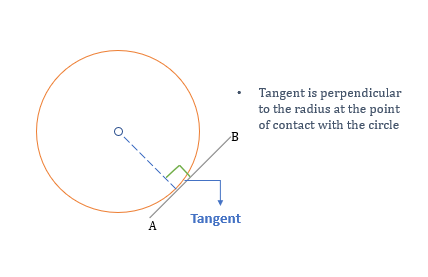
Tangent
Tangent is a line that touches the circle at any point.
Properties of Tangent
- Radius is always perpendicular to the tangent at the point where it touches the circle.
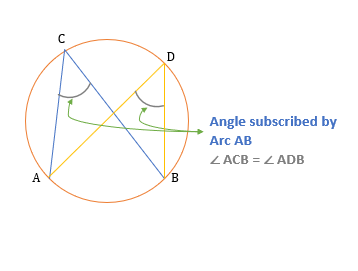
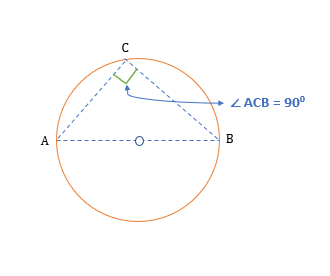
Inscribed Angle
An inscribed angle is the angle formed between two chords when they meet on the boundary of the circle.
Properties of Inscribed Angles
1. Angles formed by the same arc on the circumference of the circle is always equal.
2. The angle in a semi-circle is always 90°.Central Angle
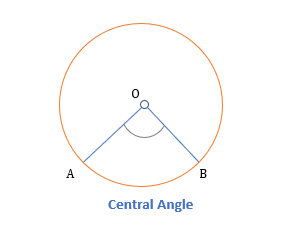
A central angle is the angle formed when two-line segments meet such that one of the endpoints of both the line segment is at the center and another is at the boundary of the circle.
Property of Central Angles
- An angle formed by an arc at the center is twice the inscribed angle formed by the same arc.
Important Circle Formulas: Area and Perimeter
The following are some mathematical formulae that will help you calculate the area and perimeter/circumference of a circle.
Perimeter:
- Perimeter or the Circumference of the circle = 2 × π × R.
- Length of an Arc = (Central angle made by the arc/360°) × 2 × π × R.
Area:
- Area of the circle = π × R²
- Area of the sector =(Central angle made by the sector/360°) × π × R².
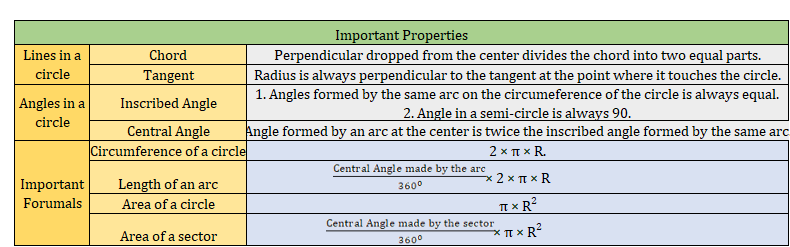
Summary of all the Properties of a Circle
Here is a summarized list of all the properties we have learned in the article up to this point.
| Property | Element | Description |
| Lines in a circle | Chord | Perpendicular dropped from the center divides the chord into two equal parts. |
| Tangent | The radius is always perpendicular to the tangent at the point where it touches the circle. | |
| Angles in a circle | Inscribed Angle | 1. Angles formed by the same arc on the circumference of the circle is always equal. 2. The angle in a semi-circle is always 90. |
| Central Angle | The angle formed by an arc at the center is twice the inscribed angle formed by the same arc. | |
| Important Formulae | Circumference of a circle | 2 × π × R. |
| Length of an arc | (Central angle made by the arc/360°) × 2 × π × R | |
| Area of a circle | π × R² | |
| Area of a sector | (Central angle made by the arc/360°) × π × R² |
Begin your GMAT preparation with the only prep company that has delivered more 700+ scores than any other GMAT club partner. Achieve GMAT 740+ with our AI driven tools that you personilzed feedback at every step of your GMAT journey. Take our free trial today!
Application of the circle properties in the questions
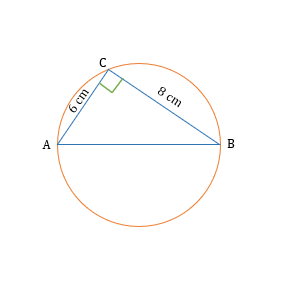
Question 1
The lengths of two sides in a right-angle triangle other than hypotenuse are 6 cm and 8 cm. If this right-angle triangle is inscribed in a circle, then what is the area of the circle?
- 5 π
- 10 π
- 15 π
- 20 π
- 25 π
Solution
Step 1: Given
- The lengths of two sides other than hypotenuse of a right triangle are 6 cm and 8 cm.
- This triangle is inscribed in a circle.
Step 2: To find
- Area of the circle.
Step 3: Approach and Working out
Let us draw the diagrammatic representation.
By applying the property that the angle in a semi-circle is 90º, we can say that AB is the diameter of the circle.
- And, once we find the length of the diameter, we can find the radius, and then we can find the area of the circle as well.
Applying Pythagoras theorem in △ ABC,
- AB² = AC² + BC²
- AB² = 6² + 8² = 36 +64 = 100
- AB = 10 cm
Since AB is the diameter, AB = 2R = 10
- Hence, R = 5 cm.
Area of the circle = π × R²= π × 5² = 25 π.
Hence, the correct answer is option E.
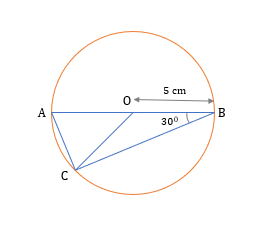
Question 2
In the diagram given above, O is the center of the circle. If OB = 5 cm and ∠ABC = 300 then what the length of the arc AC?
- 5π/6
- 5π/3
- 5π/2
- 5π
- 10π
Solution
Step 1: Given
- OB = 5 cm
- ∠ABC = 30°
Step 2: To find
- Length of the arc
Step 3: Approach and Working out
- Length of the arc = (Central angle made by the arc/360°) × 2 × π × R.
To find the length of the arc, we need the value of two variable, the center angle made by the arc and the radius.
- We are already given radius as OB = 5cm
- We need to find the ∠AOC
On visualizing the diagram, the inscribed angle by the arc AC is ∠ABC, and the center angle by arc AC is ∠AOC.
- Hence, we can apply the property that the angle made at the center by an arc is twice the inscribed angle formed by the same arc.
- Thus, ∠AOC = 2 × ∠ABC = 2 × 30° = 60°
Now, we know the central angle formed by the arc as well.
- Hence, length of the arc AC =(Central angle made by the arc/360°) × 2 × π × R.
- =(60°/360°) × 2 × π × 5.
- =(1/6) × 2 × π × 5.
- =(5π/3) cm
Thus, the correct answer is option B.
If you like this article here are a few more article related to geometry:
- Triangle – Formulas and Concepts (Part-1)
- Triangle – Formulas and Concepts (Part-2)
- Triangle – Formulas and Concepts (Part-3)
- Most common mistakes in Geometry Questions – GMAT Quant
Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2160+ reviews on GMATClub
-
- -1
-
1,299.1K Views
-
- 1
-
-
- 0
-
Answer – 6
EXPLANATION-
Looking at the diagram in rows,
The central circle equals half the sum of the numbers in the other circles to the left and right of the centre.
-
- 0
-
-
- 0
-
Your Answer
What is the logic behind these ?
3 + 3 = 3 5 + 4 = 4 1 + 0 = 3 2 + 3 = 4 …Read More »
Defective stack of coins puzzle
There are 10 stacks of 10 coins each. Each coin weights 10 gms. However, one stack of coins is defective …Read More »
Which clock works best?
Which clock works best? The one that loses a minute a day or the one that doesn’t work at all?Read More »
(Advanced) Cheryl’s Birthday Puzzle
Paul, Sam and Dean are assigned the task of figuring out two numbers. They get the following information: Both numbers …Read More »
Five greedy pirates and gold coin distribution Puzzle
Five puzzleFry ship’s pirates have obtained 100 gold coins and have to divide up the loot. The pirates are all …Read More »
Magical flowers!!
A devotee goes to three temples, temple1, temple2 and temple3 one after the other. In front of each temple, there …Read More »
Tuesday, Thursday what are other two days staring with T?
Four days are there which start with the letter ‘T‘. I can remember only two of them as “Tuesday , Thursday”. …Read More »
How could only 3 apples left
Two fathers took their sons to a fruit stall. Each man and son bought an apple, But when they returned …Read More »
How Many Eggs ?
A farmer is taking her eggs to the market in a cart, but she hits a pothole, which knocks over …Read More »
HARD MATHS – How much faster is one train from other Puzzle
Two trains starting at same time, one from Bangalore to Mysore and other in opposite direction arrive at their destination …Read More »
Most Analytical GOOGLE INTERVIEW Question Revealed
Let it be simple and as direct as possible. Interviewer : Tell me how much time (in days) and money would …Read More »
Lateral thinking sequence Puzzle
Solve this logic sequence puzzle by the correct digit- 8080 = 6 1357 = 0 2022 = 1 1999 = …Read More »
How did he know?
A man leaves his house in the morning to go to office and kisses his wife. In the evening on …Read More »
Pizza Cost Math Brain Teaser
Jasmine, Thibault, and Noah were having a night out and decided to order a pizza for $10. It turned out …Read More »
Which letter replaces the question mark
Which letter replaces the question markRead More »
Which room is safest puzzle
A murderer is condemned to death. He has to choose between three rooms. The first is full of raging fires, …Read More »
Richie’s Number System
Richie established a very strange number system. According to her claim for different combination of 0 and 2 you will …Read More »
Srabon wanted to pass
The result of math class test came out. Fariha’s mark was an even number. Srabon got a prime!! Nabila got …Read More »
Become Normal!!
Robi is a very serious student. On the first day of this year his seriousness for study was 1 hour. …Read More »
Sakib Knows The Number!
Ragib: I got digits of a 2 digit number Sakib: Is it an odd? Ragib: Yes. Moreover, the sum of …Read More »