Excel for Microsoft 365 Excel for Microsoft 365 for Mac Excel for the web Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 for Mac Excel 2016 Excel 2016 for Mac Excel 2013 Excel 2010 Excel for Mac 2011 Excel Starter 2010 More…Less
Returns the probability associated with a Student’s t-Test. Use T.TEST to determine whether two samples are likely to have come from the same two underlying populations that have the same mean.
Syntax
T.TEST(array1,array2,tails,type)
The T.TEST function syntax has the following arguments:
-
Array1 Required. The first data set.
-
Array2 Required. The second data set.
-
Tails Required. Specifies the number of distribution tails. If tails = 1, T.TEST uses the one-tailed distribution. If tails = 2, T.TEST uses the two-tailed distribution.
-
Type Required. The kind of t-Test to perform.
Parameters
|
If type equals |
This test is performed |
|
1 |
Paired |
|
2 |
Two-sample equal variance (homoscedastic) |
|
3 |
Two-sample unequal variance (heteroscedastic) |
Remarks
-
If array1 and array2 have a different number of data points, and type = 1 (paired), T.TEST returns the #N/A error value.
-
The tails and type arguments are truncated to integers.
-
If tails or type is nonnumeric, T.TEST returns the #VALUE! error value.
-
If tails is any value other than 1 or 2, T.TEST returns the #NUM! error value.
-
T.TEST uses the data in array1 and array2 to compute a non-negative t-statistic. If tails=1, T.TEST returns the probability of a higher value of the t-statistic under the assumption that array1 and array2 are samples from populations with the same mean. The value returned by T.TEST when tails=2 is double that returned when tails=1 and corresponds to the probability of a higher absolute value of the t-statistic under the “same population means” assumption.
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data 1 |
Data 2 |
|
|
3 |
6 |
|
|
4 |
19 |
|
|
5 |
3 |
|
|
8 |
2 |
|
|
9 |
14 |
|
|
1 |
4 |
|
|
2 |
5 |
|
|
4 |
17 |
|
|
5 |
1 |
|
|
Formula |
Description |
Result |
|
=T.TEST(A2:A10,B2:B10,2,1) |
Probability associated with a Student’s paired t-Test, with a two-tailed distribution. |
0.196016 |
Need more help?
The t-Test is used to test the null hypothesis that the means of two populations are equal. Below you can find the study hours of 6 female students and 5 male students. H0: μ1 – μ2 = 0.
Contents
- 1 What does the t-test in excel tell you?
- 2 What is t-test used for?
- 3 What are the 3 types of t tests?
- 4 How do you find t Stat?
- 5 How do you find the T score?
- 6 What is the T score in statistics?
- 7 What is the T-value and p value?
- 8 How do you do a t-test in data analysis?
- 9 What is t-test and types?
- 10 What is T and Z score?
- 11 What is the T table?
- 12 What is the t-value of a 95 confidence interval?
- 13 How do you find the t critical value?
- 14 What does T ratio mean?
- 15 Is a high T-value good or bad?
- 16 Does t-test in Excel give you ap value?
- 17 How do you interpret T stat in regression?
- 18 Which t-test should I use?
- 19 What are the 4 types of t-tests?
What does the t-test in excel tell you?
TEST in Excel. T-Test function in excel is used for calculating the probability of significant difference between two data sets whether any or both of them are under the same population with the same mean.
What is t-test used for?
A t-test is a type of inferential statistic used to determine if there is a significant difference between the means of two groups, which may be related in certain features.
What are the 3 types of t tests?
There are three main types of t-test:
- An Independent Samples t-test compares the means for two groups.
- A Paired sample t-test compares means from the same group at different times (say, one year apart).
- A One sample t-test tests the mean of a single group against a known mean.
How do you find t Stat?
Calculate the T-statistic
Subtract the population mean from the sample mean: x-bar – μ. Divide s by the square root of n, the number of units in the sample: s ÷ √(n).
How do you find the T score?
The formula for the t score is the sample mean minus the population mean, all over the sample standard deviation divided by the square root of the number of observations. The sample mean, sample standard deviation and number of observations are all available in the data from your sample.
What is the T score in statistics?
A t-score (a.k.a. a t-value) is equivalent to the number of standard deviations away from the mean of the t-distribution. The t-score is the test statistic used in t-tests and regression tests. It can also be used to describe how far from the mean an observation is when the data follow a t-distribution.
What is the T-value and p value?
T-Test vs P-Value
The difference between T-test and P-Value is that a T-Test is used to analyze the rate of difference between the means of the samples, while p-value is performed to gain proof that can be used to negate the indifference between the averages of two samples.
How do you do a t-test in data analysis?
There are 4 steps to conducting a two-sample t-test:
- Calculate the t-statistic. As could be seen above, each of the 3 types of t-test has a different equation for calculating the t-statistic value.
- Calculate the degrees of freedom.
- Determine the critical value.
- Compare the t-statistic value to critical value.
What is t-test and types?
Types of t-tests
| Test | Purpose |
|---|---|
| 1-Sample t | Tests whether the mean of a single population is equal to a target value |
| 2-Sample t | Tests whether the difference between the means of two independent populations is equal to a target value |
What is T and Z score?
The T-score is a comparison of a person’s bone density with that of a healthy 30-year-old of the same sex. The Z-score is a comparison of a person’s bone density with that of an average person of the same age and sex.
What is the T table?
A t table is a table showing probabilities (areas) under the probability density function of the t distribution for different degrees of freedom. Table of Upper-Tail and Two-Tail t Critical Values. one-tail p. 0.001. 0.0025.
What is the t-value of a 95 confidence interval?
The t value for 95% confidence with df = 9 is t = 2.262.
How do you find the t critical value?
To find a critical value, look up your confidence level in the bottom row of the table; this tells you which column of the t-table you need. Intersect this column with the row for your df (degrees of freedom). The number you see is the critical value (or the t-value) for your confidence interval.
What does T ratio mean?
The t-ratio is the estimate divided by the standard error. With a large enough sample, t-ratios greater than 1.96 (in absolute value) suggest that your coefficient is statistically significantly different from 0 at the 95% confidence level. A threshold of 1.645 is used for 90% confidence.
Is a high T-value good or bad?
The greater the magnitude of T (it can be either positive or negative), the greater the evidence against the null hypothesis that there is no significant difference. The closer T is to zero, the more likely there isn’t a significant difference.
Does t-test in Excel give you ap value?
When you run the t-test, EXCEL will provide a printout that contains the mean values and other information. The most important part of these results is the p-value. The p-value tells you in an unbiased manner whether you must accept or reject the null hypothesis.
How do you interpret T stat in regression?
The t statistic is the coefficient divided by its standard error. The standard error is an estimate of the standard deviation of the coefficient, the amount it varies across cases. It can be thought of as a measure of the precision with which the regression coefficient is measured.
Which t-test should I use?
If you are studying one group, use a paired t-test to compare the group mean over time or after an intervention, or use a one-sample t-test to compare the group mean to a standard value. If you are studying two groups, use a two-sample t-test. If you want to know only whether a difference exists, use a two-tailed test.
What are the 4 types of t-tests?
Types of t-tests (with Solved Examples in R)
- One sample t-test.
- Independent two-sample t-test.
- Paired sample t-test.
A T-test in excel helps compare the means (average) of two samples and make inferences for the entire populations. By performing a t-test, one can say whether the difference between the two means is statistically significant or by chance alone. An outcome (result) is said to be statistically significant if the reason behind its occurrence can be attributed to a specific cause rather than to coincidence (or chance). Such results are reliable and provide confidence in decision-making.
For example, an organization launches a new policy for the employees (customer service associates or CSA) of its marketing department. According to this policy, if the number of customer complaints resolved in a day crosses 50, two additional leaves (in a month) will be granted to an employee.
Further, the organization performs the following tasks:
- Collects the data of complaints addressed and resolved (before and after the policy) by a sample of CSAs.
- Conducts a paired t-test in excel (refer to the heading “types of t-tests” of this article) to determine whether there is any difference in the productivity of the CSAs before and after the introduction of the policy.
- Interprets and analyzes the findings of the excel t-test to determine whether the results are statistically significantStatistical significance is the probability of an observation not being caused by a sampling error.read more or caused by chance.
The aim of conducting this paired t-test is to assess whether the productivity of employees is impacted positively or negatively by the introduction of the new policy. Moreover, if the productivity increases, similar policies can be launched for the employees of other departments as well.
T-tests are used for testing a hypothesisHypothesis Testing is the statistical tool that helps measure the probability of the correctness of the hypothesis result derived after performing the hypothesis on the sample data. It confirms whether the primary hypothesis results derived were correct.read more. A hypothesis is an assumption that is tested to check whether it holds true or false. The null and alternative hypotheses are two opposing statements.
A null hypothesis is created using the operators, “equal to,” “greater than or equal to” or “less than or equal to.” In contrast, an alternative hypothesis uses the operators, “not equal to,” “greater than,” or “less than.”
A t-test in excel can be conducted by using the Data Analysis ToolPakExcel’s data analysis toolpak can be used by users to perform data analysis and other important calculations. It can be manually enabled from the addins section of the files tab by clicking on manage addins, and then checking analysis toolpak.read more or the TTEST function of Excel. The TTEST function was replaced by the T.TEST function in Excel 2010. However, in this article, we use the TTEST function of Excel for performing the t-test.
The TTEST or the T.TEST functions are categorized under the Statistical functions of Excel.
Table of contents
- T-test in Excel
- Syntax of the TTEST Function of Excel
- Types of T-tests
- How to use the TTEST Function in Excel?
- Example #1–Paired Sample T-test Using One-tail Distribution
- Example #2–Two-sample Equal Variance T-test Using One-tail Distribution
- Example #3–Two-sample Unequal Variance T-test Using One-tail Distribution
- Example #4–Paired Excel T-test Using One-tail Distribution in VBA
- The Errors Returned by the TTEST Function of Excel
- T-TEST in Excel Video
- Frequently Asked Questions
- Recommended Articles
Syntax of the TTEST Function of Excel
The syntax of the TTEST function is shown in the following image:
The TTEST function accepts the following arguments:
- Array1: This is the first dataset on which the excel t-test is to be performed.
- Array2: This is the second dataset on which the excel t-test is to be performed.
- Tails: This specifies the kind of distribution to be used. This argument can take either of the following values:
- 1–This implies a one-tailed distribution. A one-tailed t-test is performed when one wants to study the specific direction (only positive direction or only negative direction) of difference between the two means.
- 2–This implies a two-tailed distribution. A two-tailed t-test is performed when one wants to find out whether the two population means are different from one another or not.
- Type: This is the kind of t-testA T-test is a method to identify whether the means of two groups differ from one another significantly. It is an inferential statistics approach that facilitates the hypothesis testing.read more to be performed. This argument can take any of the following values:
- 1–This implies that a paired samples t-test is to be performed.
- 2–This implies that a two-sample equal variance t-test is to be performed. One must perform this test when there are two independent samples having the same (equal) population variances. The feature of the same variance is known as homoscedasticity.
- 3–This implies that a two-sample unequal variance t-test (or the Welch t-test) is to be performed. One must perform this test when there are two independent samples having unequal or unknown variances. The feature of unequal variances is known as heteroscedasticity.
All the preceding arguments are mandatorily required when conducting a t-test in Excel.
Note: For information about the kind of t-tests, refer to the next heading, “types of t-tests.”
Types of T-tests
A t-test can be of the following types:
- Independent samples t-test–It compares the means of two independent or unrelated samples or groups. It is also called an unpaired t-test or a two-sample t-test. It is used when the population mean or standard deviation is unknown.
- Paired samples t-test–It compares the means of the same group at different time periods. In other words, the t-test is conducted on dependent or related samples. The paired samples t-test is also conducted when the samples are different but subjected to the same conditions. For instance, one may want to measure the effectiveness (using the same technique) of the same product manufactured by two different manufacturers. The paired samples t-test is also called the dependent samples t-test.
- One-sample t-test–It compares the mean of a single sample with the known mean (target value or hypothetical value) of a population (from which this sample is drawn).
Note 1: Select the type of t-test to be conducted by taking into account the kind of data and the kind of analysis required. For instance, if the two sample sets are related, use the paired t-test. Further, the paired samples t-test must be performed when both the sample sets are of the same size. This implies that the number of data points of both samples is the same.
If the samples are independent, use the two-sample equal variance or two-sample unequal variance t-tests depending on whether the variances are equal or unequal respectively.
Note 2: For more information on the type of t-test to be performed, refer to the heading “frequently asked questions” at the end of this article.
How to use the TTEST Function in Excel?
The TTEST function of Excel is simple and easy to use. Let us consider some examples to understand the working of the TTEST function in Excel.
You can download this TTEST Function Excel Template here – TTEST Function Excel Template
Example #1–Paired Sample T-test Using One-tail Distribution
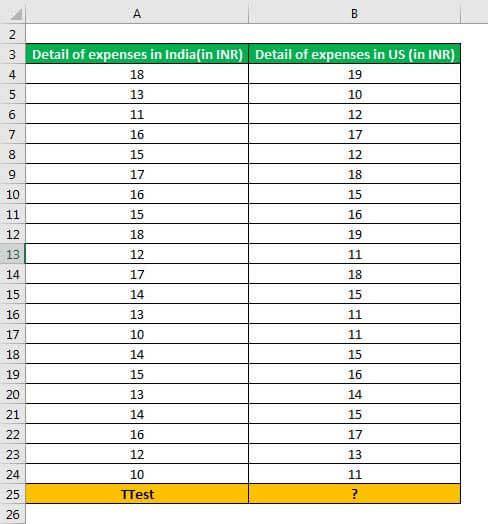
The following image shows the expenses incurred (in INR) by an organization in two countries, India and USA. Perform a paired sample t-test in excel using a one-tail distribution.
The steps to perform a paired t-test with one-tail distribution are listed as follows:
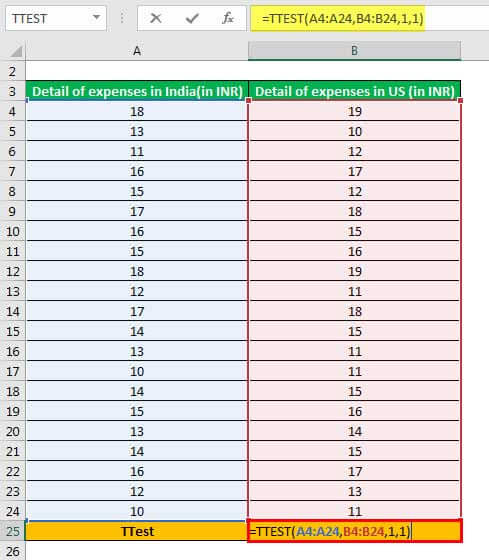
Step 1: Enter the following formula in cell B25.
“=TTEST(A4:A24,B4:B24,1,1)”
The same is shown in the following image.
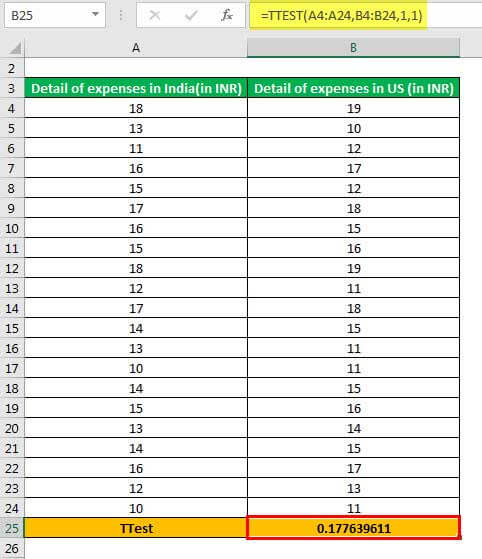
Step 2: Press the “Enter” key. The output in cell B25 is 0.177639611, as shown in the following image.
Explanation: The range A4:A24 (entered in step 1 of the formula) is the first array on which the excel t-test is to be performed. Likewise, the range B4:B24 is the second array on which the t-test is to be performed.
Further, we have entered the “tails” and “type” arguments as 1. This is because a one-tailed, paired t-test needs to be performed.
Interpretation: To accept or reject the null hypothesisNull hypothesis presumes that the sampled data and the population data have no difference or in simple words, it presumes that the claim made by the person on the data or population is the absolute truth and is always right. So, even if a sample is taken from the population, the result received from the study of the sample will come the same as the assumption.read more, perform the following tasks:
- Calculate the t-table value by referring to the one-tail t-distribution table, at a certain significance level (alpha) with the specific degrees of freedomDegrees of freedom (df) refers to the number of independent values (variable) in a data sample used to find the missing piece of information (fixed) without violating any constraints imposed in a dynamic system. These nominal values have the freedom to vary, making it easier for users to find the unknown or missing value in a dataset.read more (df). Compare the t-table value with the calculated t-value (0.177639611). If the calculated t-value is greater than the t-table value, reject the null hypothesis.
- Calculate the p-value based on the t-table value. Compare the p-valueP-Value, or Probability Value, is the deciding factor on the null hypothesis for the probability of an assumed result to be true, being accepted or rejected, & acceptance of an alternative result in case of the assumed results rejection. read more with the significance level. Since the significance level (alpha) is not specified in the question, consider it as 0.05 or 5%. If the p-value is less than the significance level, reject the null hypothesis.
The acceptance or rejection of the null hypothesis should be carried out by using a combination of the p and t values (obtained in the preceding pointers a and b). Further, rejecting a null hypothesis implies accepting the alternative hypothesis.
Note 1: The negative sign (if any) can be ignored when comparing the t-values.
Note 2: The null hypothesis of a paired sample excel t-test assumes that the mean difference of paired observations is zero. In other words, the mean of paired observations is equal.
The alternative hypothesis of a paired sample t-test assumes that the mean difference of paired observations is not equal to zero. For instance, the difference between the paired observations for row 4 is (18-19) or (cell A4-cell B4).
Rejecting the null hypothesis implies that the mean difference of paired observations does exist. In other words, this mean difference is not equal to zero.
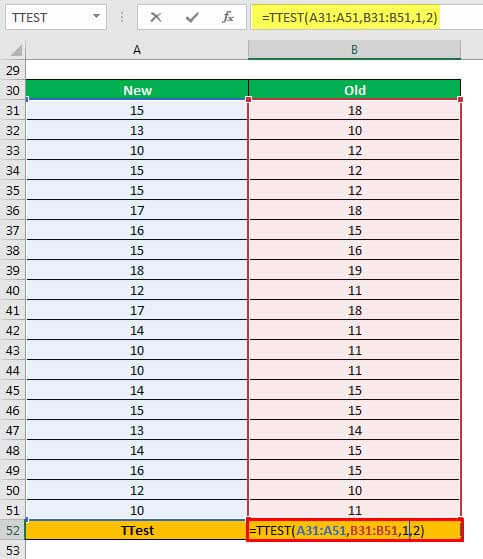
Example #2–Two-sample Equal Variance T-test Using One-tail Distribution
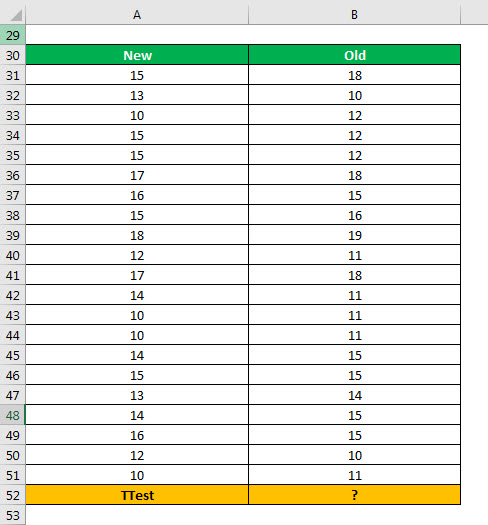
An organization has introduced a new flavor of a beverage in the market. To test the effectiveness of this flavor, two samples (consisting of 21 people in each sample) are created.
The different people who tasted the new flavor are listed in the column “new.” The different people who tasted the old flavor are listed in the column “old.” Consider the groups “new” and “old” as independent samples.
The population variancesPopulation variance can be calculated using this formula: σ2 = ∑ni=1 (xi – μ)2 / N, where, σ2 is population variance, x1, x2, x3,…..xn are the observations, N is the number of observations and µ is the mean of the data set.read more of both samples, “new” and “old,” are equal. Calculate the two-sample equal variance t-test in excel using a one-tail distribution.
The steps to perform the two-sample equal variance t-test using a one-tail distribution are listed as follows:
Step 1: Enter the following formula in cell B52.
“=TTEST(A31:A51,B31:B51,1,2)”
The same is shown in the following image.
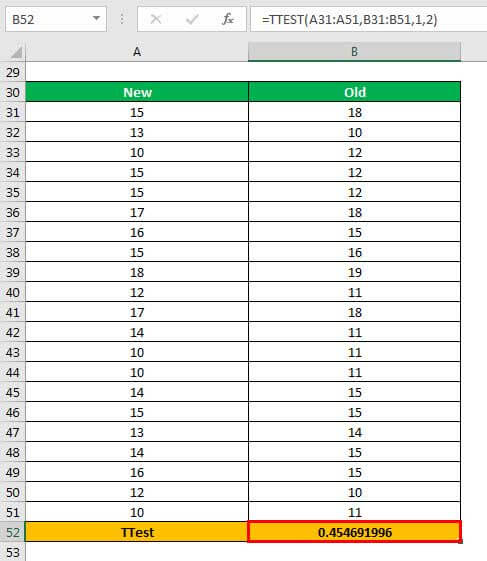
Step 2: Press the “Enter” key. The output in cell B52 is 0.454691996.
Explanation: The first array (in the formula entered in step 1) is A31:A51 and the second array is B31:B51. The argument 1 indicates that a one-tailed test is to be performed. The argument 2 implies that a two-sample equal variance t-test is to be conducted.
Interpretation: To accept or reject the null hypothesis, compare the calculated t-value with the t-table value. At the same time, compare the p-value with the standard significance level (0.05).
Note 1: The null hypothesis of the two-sample equal variance t-test in excel states that the difference between the two sample means is zero. In other words, the two sample means are equal. The alternative hypothesis states that the two sample means are not equal.
Note 2: If one is using the Data Analysis Toolpak, compare the t-statistic of the results obtained with the t-critical one-tail value. If the t-statistic is larger than the t-critical one-tail value, reject the null hypothesis.
Likewise, compare the p one-tail value with the significance level. If the former (p one-tail value) is less than the latter (significance level), reject the null hypothesis.
Rejecting a null hypothesis implies that there is a difference between the two sample means. Moreover, this difference is not explainable by chance alone.
Note 3: While using the Data Analysis Toolpak, if one does not know which t-values (of one-tail or two-tail test) are to be compared, always compare the t-statistic with the t-critical two-tail value.
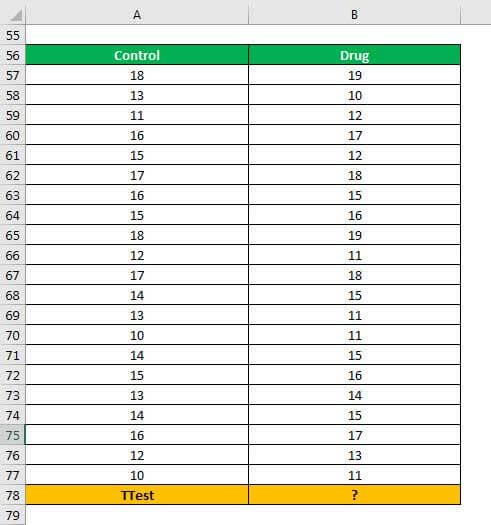
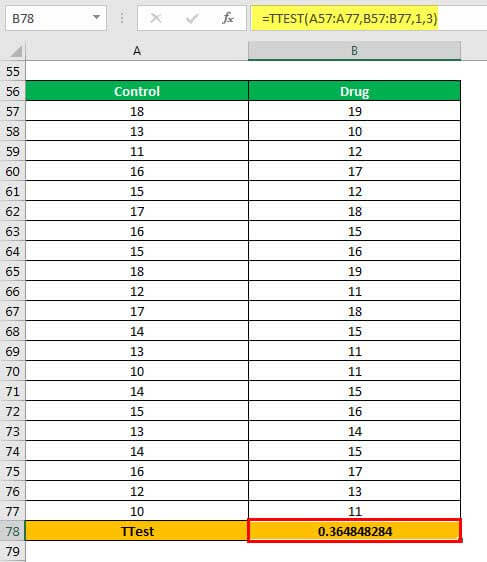
Example #3–Two-sample Unequal Variance T-test Using One-tail Distribution
A researcher wants to study the impact of a new drug on the car driving skills of a person. A total of 21 individuals were administered the drug prior to being given a driving test.
The column A of the following image shows the score assigned to each driver. The column B shows the level of drug (in percentage) given to each driver.
The population variances of both the samples are unequal. Perform the two-sample unequal variance test using a one-tail distribution.
The steps to perform the two-sample unequal variance test using a one-tail distribution are listed as follows:
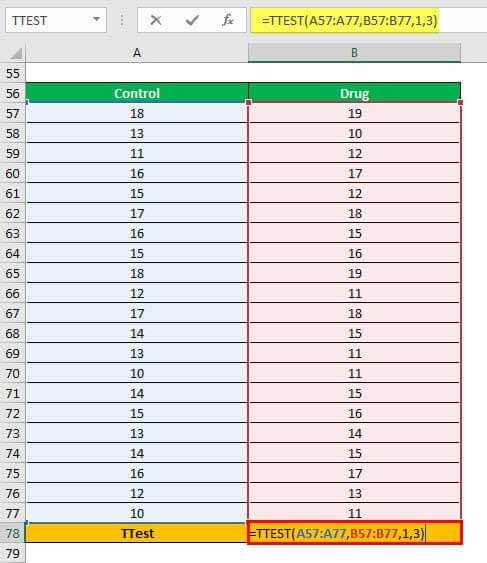
Step 1: Enter the following formula in cell B78.
“=TTEST(A57:A77,B57:B77,1,3)”
The same is shown in the following image.
Step 2: Press the “Enter” key. The output is 0.364848284, as shown in the following image.
Explanation: The range A57:A77 represents the first array (in the formula entered in step 1). The range B57:B77 represents the second array on which the excel t-test is to be performed.
Since a one-tailed test is to be performed, we enter 1 in the “tails” argument. The 3 in the “type” argument implies that the two-sample unequal variance t-test is to be performed.
Interpretation: Compare the t-calculated value with the t-table value. If the former is greater than the latter at the given significance level, reject the null hypothesis. Likewise, if the p-value is smaller than the significance level, reject the null hypothesis and accept the alternative hypothesis.
Note: The null hypothesis for the two-sample unequal variance t-test states that the mean of the two samples is the same (or equal). The alternative hypothesis states that the mean of the two samples is not the same (or unequal).
Example #4–Paired Excel T-test Using One-tail Distribution in VBA
There are two datasets in the ranges A4:A24 and B4:B24 of Excel. Write the VBA codeVBA code refers to a set of instructions written by the user in the Visual Basic Applications programming language on a Visual Basic Editor (VBE) to perform a specific task.read more to conduct a t-test on the given ranges.
The VBA code is written as follows:
Sub TTESTcal() // start the TTEST function scope
Dim TTEST as interger
TTEST = Application.WorksheetFunction.TTest(Range(“A4:A24”),Range(“B4:B24”),1,1)
MsgBox TTEST // print the TTEST value in the message box.
End sub // End the TTEST function
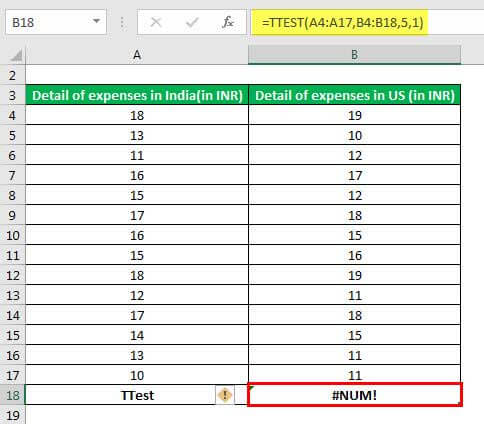
The Errors Returned by the TTEST Function of Excel
The TTEST function can return the following types of errors:
- “#N/A” error: This is displayed if the two arrays supplied are of different lengths and a paired t-test is to be performed.
- “#NAME?” error: This is displayed if either of the arguments “tails” or “type” is provided as a text value.
- “#NUM!” error: This is displayed on account of either of the following reasons:
- If the “tails” argument is other than the numbers 1 or 2
- If the “type” argument is other than the numbers 1, 2 or 3
The “#NUM!” error is shown in the following image. It must be observed that the “tails” argument in the TTEST formula has been entered as 5. Moreover, the two arrays supplied are of different sizes.
Had the arrays been equal in length and the “tails” and “type” arguments had remained 5 and 1 respectively, the “#NUM!” error would still have been displayed.
T-TEST in Excel Video
Frequently Asked Questions
1. Define t-test and state its syntax used in Excel.
A t-test is a hypothesis test that is conducted on random samples drawn from a population. By performing a t-test, the means of two samples are compared. The t-test is a parametric test which assumes that the population data is normally distributed.
A t-test can be performed either by using the Data Analysis ToolPak or the TTEST (or T.TEST) function of Excel. The syntax of the TTEST function of Excel is stated as follows:
“TTEST(array1,array2,tails,type)”
Note 1: A normal distribution is represented by a bell-shaped curve which shows the distribution of the data points.
Note 2: For an explanation related to the arguments of the TTEST function, refer to the heading “syntax of the TTEST function of Excel” of this article.
2. Which t-test should be used in Excel?
One can perform any of the following t-tests on the basis of the given considerations:
a. Independent samples t-test–Perform this test if the two datasets pertain to unrelated or independent samples. In other words, the two datasets come from two different populations. Each population consists of unique data points. Further, the population means and/or the standard deviations are unknown.
b. Paired sample t-test–Perform this test if the two samples are related or dependent on each other. In other words, the two datasets come from the same population and have the same number of data points.
c. One sample t-test–Perform this test if the single sample mean is to be compared with a hypothetical value.
d. Two-sample equal variance t-test–Perform this test if the variances of the two populations are known to be equal.
e. Two-sample unequal variance t-test–Perform this test if the variances of the two populations are unequal. One can also perform this test when he/she does not know whether the variances of the two populations are equal or not.
f. One-tail t-test–Perform this test if one wants to study the specific direction of difference between the two sample means. In other words, the user is interested in one direction of difference (sample A mean is greater than the sample B mean) and not interested in the opposite direction of difference (sample A mean is lesser than the sample B mean). A one-tail t-test can detect differences between the two means in a single direction only.
g. Two-tail t-test–Perform this test if one wants to know whether a difference between the two sample means exists or not. A two-tail t-test can detect both positive and negative differences between the two means. For instance, one may want to find out if sample A mean is greater than or lesser than the sample B mean.
Note: If more than two groups are to be compared, use ANOVA (Analysis of Variance) instead of the t-test.
3. How should the t-test of Excel be interpreted?
Interpreting the results of a t-test helps in accepting or rejecting the null hypothesis. For interpretation, one must perform the following tasks:
a. Compare the calculated t-value or the t-statistic with the t-table value. If the former is more than the latter, reject the null hypothesis.
b. Compare the p-value with the significance level (if not given in the question, assume the standard significance level of 0.05). If the former is less than the latter, reject the null hypothesis.
Prior to carrying out the calculations, it is essential to state the null and alternative hypotheses clearly and precisely. This provides a direction to the process of interpretation of results.
The null and alternative hypotheses are contradictory to each other. To accept or reject either of them, strong evidence is required. So, one must ensure that the sample data supports the acceptance or rejection decision.
Recommended Articles
This has been a guide to t-test in Excel. Here we discuss the t-test formula in Excel and how to use it along with examples and downloadable Excel templates. You may also look at these useful functions in Excel–
- Quartile FormulaQuartile Formula is a statistical tool to calculate the variance from the given data by dividing the same into four defined intervals. First Quartile could be calculated as follows: (Q1) = ((n + 1)/4)th Term.read more
- Mode Formula ExcelThe MODE Function in Excel is a statistical function that returns the most often occurring value in a dataset. In case there are multiple modes, it will return the lowest one. read more
- VBA “MsgBox”VBA MsgBox function is an output function which displays the generalized message provided by the developer. This statement has no arguments and the personalized messages in this function are written under the double quotes while for the values the variable reference is provided.read more
- Not Equal to in Excel“Not Equal to” argument in excel is inserted with the expression <>. The two brackets posing away from each other command excel of the “Not Equal to” argument, and the user then makes excel checks if two values are not equal to each other.read more
17 авг. 2022 г.
читать 3 мин
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
В этом руководстве представлено полное руководство по интерпретации результатов двухвыборочного t-теста в Excel.
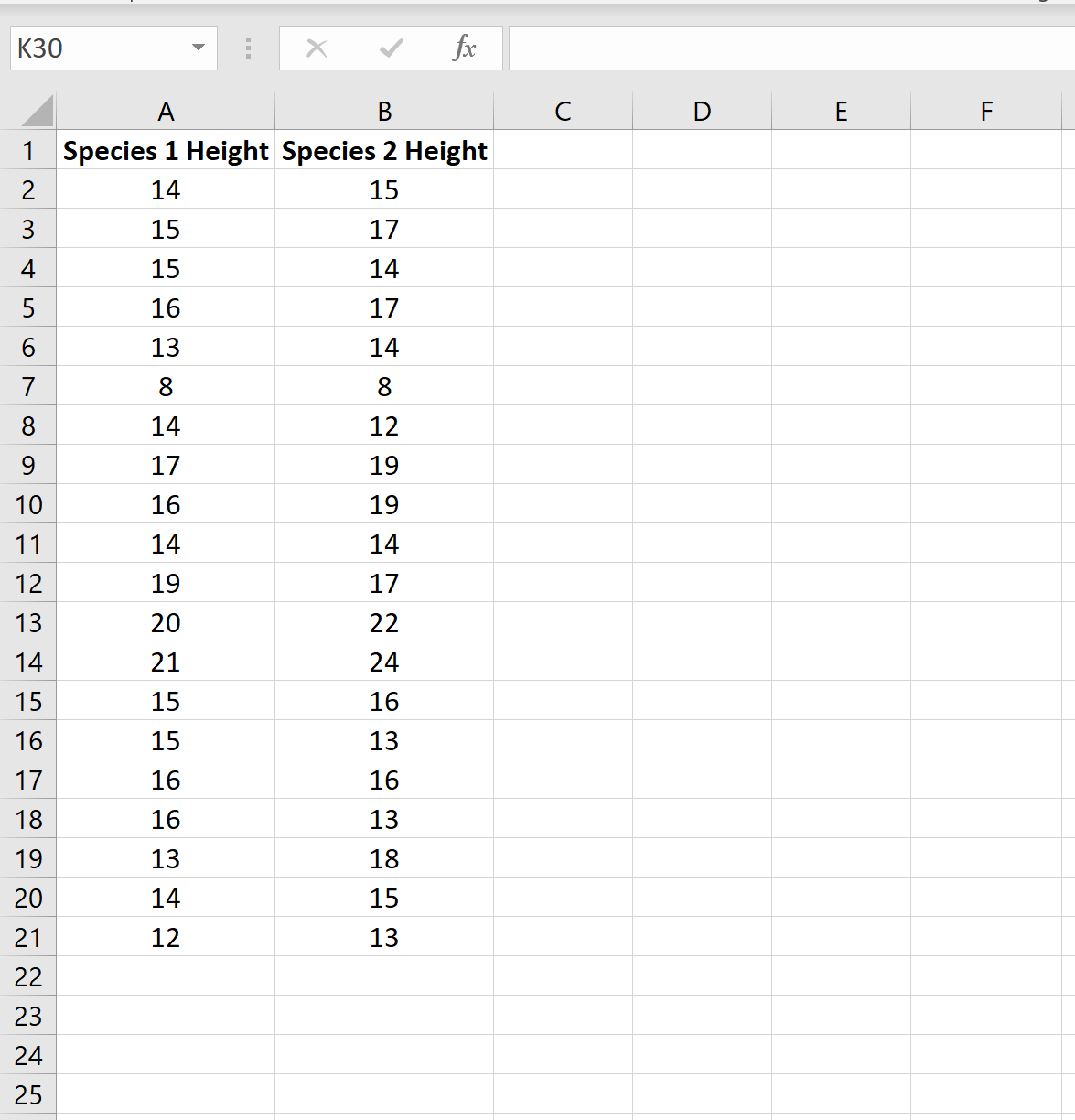
Шаг 1: Создайте данные
Предположим, биолог хочет знать, имеют ли два разных вида растений одинаковую среднюю высоту.
Чтобы проверить это, она собирает простую случайную выборку из 20 растений каждого вида:
Шаг 2. Выполните t-тест для двух выборок.
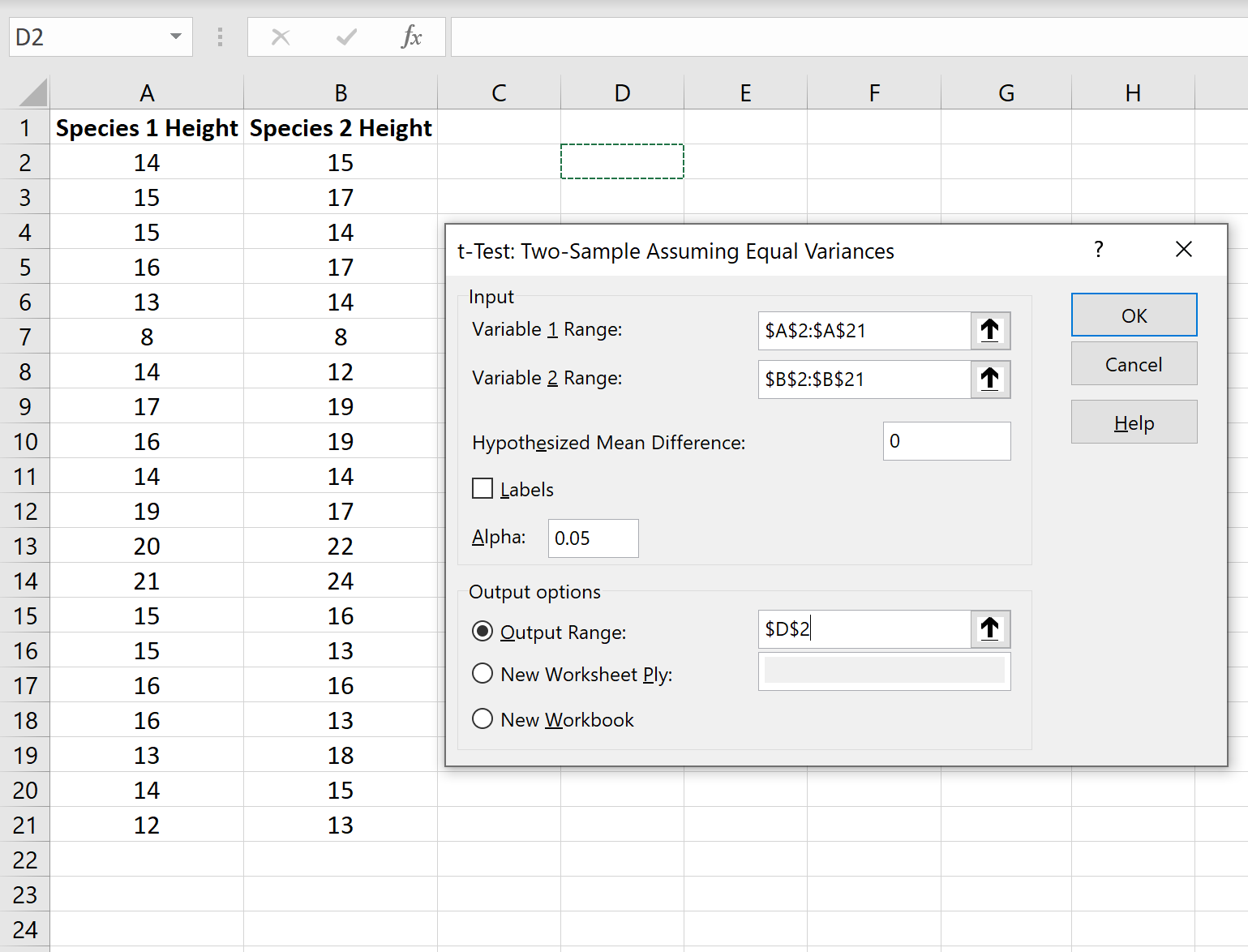
Чтобы выполнить двухвыборочный t-критерий в Excel, щелкните вкладку « Данные » на верхней ленте, а затем щелкните « Анализ данных» :
Если вы не видите эту опцию, вам необходимо сначала загрузить пакет инструментов анализа .
В появившемся окне выберите параметр под названием t-Test: Two-Sample, предполагающий равные отклонения , а затем нажмите OK.Затем введите следующую информацию:
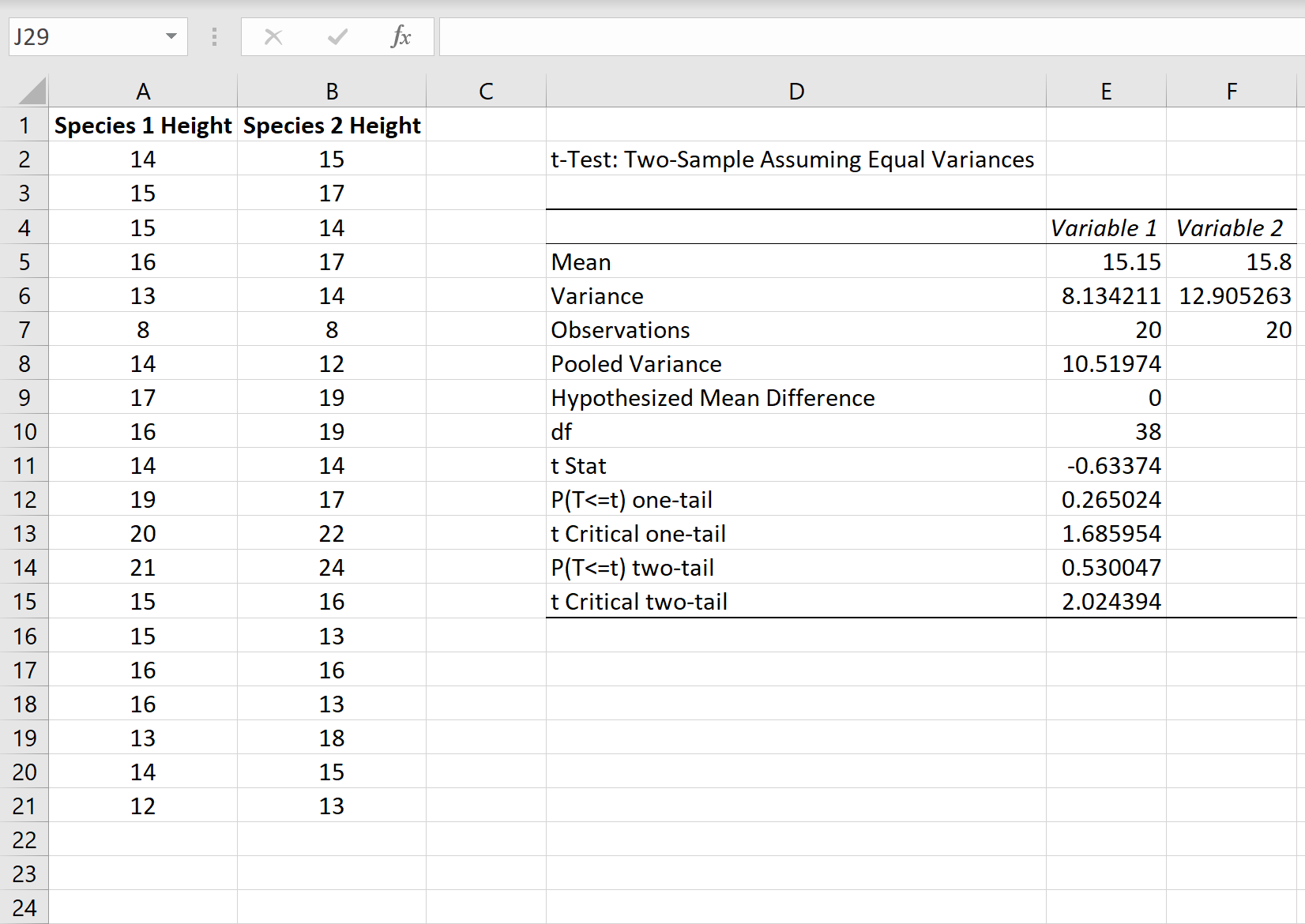
После того, как вы нажмете OK , отобразятся результаты t-теста:
Шаг 3: интерпретируйте результаты
Вот как интерпретировать каждую строку в результатах:
Среднее значение: среднее значение каждого образца.
- Образец 1 Среднее значение: 15,15
- Образец 2 Среднее значение: 15,8
Дисперсия: Дисперсия каждого образца.
- Образец 1 Дисперсия: 8,13
- Образец 2 Дисперсия: 12,9
Наблюдения: количество наблюдений в каждой выборке.
- Образец 1 Наблюдения: 20
- Образец 2 Наблюдения: 20
Объединенная дисперсия: средняя дисперсия выборок, рассчитанная путем «объединения» дисперсий каждой выборки вместе по следующей формуле:
- s 2 p = ((n 1 -1)s 2 1 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- с 2 р = ((20-1)8,13 + (20-1)12,9) / (20+20-2)
- с 2 р = 10,51974
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В этом случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0.
df: Степени свободы для t-критерия, рассчитанные как:
- df = n 1 + n 2 – 2
- df = 20 + 20 – 2
- дф = 38
t Stat: тестовая статистика t , рассчитанная как:
- т знак равно ( Икс 1 — Икс 2 ) / √ с 2 п (1 / п 1 + 1 / п 2 )
- t = (15,15–15,8) / √ 10,51974 (1/20+1/20)
- т = -0,63374
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. Это значение можно найти с помощью любого калькулятора T Score to P Value, используя t = -0,63374 с 38 степенями свободы.
В этом случае р = 0,530047.Это больше, чем 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы сказать, что средние значения двух популяций различны.
t Критический двухсторонний: это критическое значение теста. Это значение можно найти с помощью Калькулятора критического значения t с 38 степенями свободы и уровнем достоверности 95%.
В этом случае критическое значение оказывается равным 2,024394.Поскольку наша тестовая статистика t меньше этого значения, мы не можем отвергнуть нулевую гипотезу. Еще раз, это означает, что у нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
Примечание № 1. Вы придете к одному и тому же выводу независимо от того, используете ли вы метод p-значения или метод критического значения.
Примечание № 2. Если вы выполняете односторонний тест гипотезы , вместо этого вы будете использовать значения для одностороннего P(T<=t) и критического одностороннего t.
Дополнительные ресурсы
В следующих руководствах представлены пошаговые примеры выполнения различных t-тестов в Excel.
Как провести одновыборочный t-тест в Excel
Как провести двухвыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Как выполнить t-критерий Уэлча в Excel
What Is T-Test In Excel?
The T-Test Excel function compares the mean values of samples between two population sets or groups and determines if the two groups are considerably different or not.
The T-Test in Excel helps users perform hypothesis testing. It statistically shows whether we need to go with our null or alternate hypothesis for the population in question.
For example, consider the table with electricity rates in the US (column C) and Australia (column D). We can determine if the mean values of the two data sets have a considerable difference between them using the two sample T-Test in Excel in cell D13.
=T.TEST(C2:C11,D2:D11,1,1)
The T-Test returns the result as 0.017, which is the p-value. The value is below the threshold of 0.05, the default cut-off. It implies that the probability of the two samples’ mean values is the same and less than 5%. It also interprets that the difference in the mean values of the two samples in columns C and D is significant. So, our null hypothesis is false, and we need to reject it.
Table of contents
- What Is T-Test In Excel?
- TTEST() Excel Formula
- How to Use TTEST() Excel Function?
- Examples
- Example #1
- Example #2
- Example #3
- T-Test Excel Errors
- Important Things To Note
- Frequently Asked Questions
- Download Template
- Recommended Articles
- The T-test in Excel compares the mean values of the two population samples to determine the probability of the two data sets being notably different.
- One can decide on the T-test type based on the population samples of interest. The syntax of the T.Test() excel in function is =T.TEST(array1,array2,tails,type)
- We can perform one-tailed or two-tailed T-Tests. And in each category, the T-test type can be:
- Paired
- Two sample equal variance
- Two sample unequal variance
- We can enter the specific T-test formula with the required arguments, or we can install the Analysis ToolPak to get a complete analysis for the needed type of T-test.
TTEST() Excel Formula
Unlike other functions, all the T-Test arguments in Excel are mandatory.
- array1: The first data set.
- array2: The second data set.
- tails: This denotes the distribution tail used in a T-Test in Excel. If the value is 1, it indicates the one-tailed distribution; if the value is 2, it means two-tailed distribution.
- type: It refers to the T-Test type. We can enter the value 1, 2, or 3. While 1 is for Paired T-Test, 2 and 3 denote Two sample equal and unequal variance T-Tests, respectively.
How To Use TTEST() Excel Function?
Following are the steps for the T-test in excel.
- First, ensure you have your data sets in a spreadsheet.
- Then, choose the cell where you want to display the T-Test result, the p-value.
- Enter the T-Test in Excel formula by selecting the Test() function, accessible using Formulas > More Functions > Statistical.
- Enter the first two array arguments by selecting the first and second data sets. Then, provide the tails argument (one or two-tailed T-Test) and decide the type based on the T-Test type (paired T-Test Excel, Two sample equal or unequal variance T-Tests).
- Press Enter to get the output.
- Finally, from the Test() outcome, make the necessary inferences.
Consider the following table that shows the stress levels of a group before (in column A) and after (in column B) attending a therapy. It is a two-tailed T-Test, as we are not making a hypothesis whether the therapy reduced the stress levels. While the null hypothesis is that there is no difference in the mean values of the two samples, the alternate one implies a significant difference.
The second table is where we display the T-Test result.
Since the data set values are before-after measurements, we consider paired T-test.
Here are the steps to use the T-Test in Excel function in this scenario.
Step 1: Choose cell D3 and enter the two sample T-Test in Excel function as:
=T.TEST(A2:A16,B2:B16,2,1)
Please Note: The cell ranges A2:A16 and B2:B16 are the two arrays we need to compare, so they are the first and second arguments. The third argument, 2, denotes a two-tailed T-Test, and the fourth argument, 1, refers to a paired T-Test Excel.
Step 2: Press Enter to view the output.
The function returns the p-value as 0.008. It is less than the standard threshold of significance, 0.05. So, we reject our null hypothesis. It indicates that the mean values of the two samples are notably different. Thus, we have to go with our alternate hypothesis.
Examples
Let us look at the various scenarios where you can use the T-Test in Excel.
Example #1
Below is the table with a list indicating a farm’s height (in feet) of banana trees.
Using this example, we will explain how to calculate using one sample T-Test Excel. We will also determine if a sample mean value differs significantly from a hypothesized mean.
Hypothetically, let us assume that the average height of a banana tree is 11 feet.
We will check whether the heights in the sample differ significantly from the hypothesized average height.
The null and alternative hypotheses will be:
- Null hypothesis: No significant difference between the sample banana tree heights and the average height of the banana tree.
- Alternate hypothesis: Significant difference between the sample banana tree heights and the average height of the banana tree.
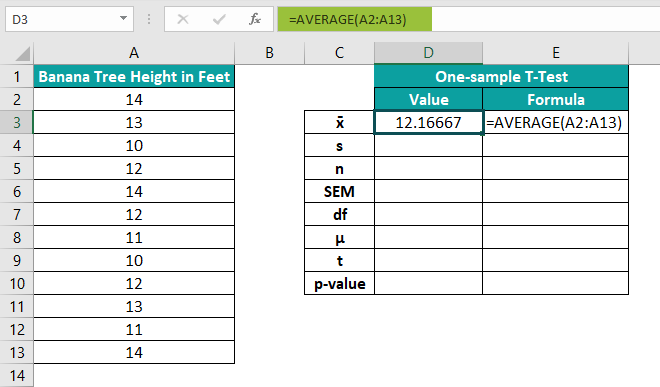
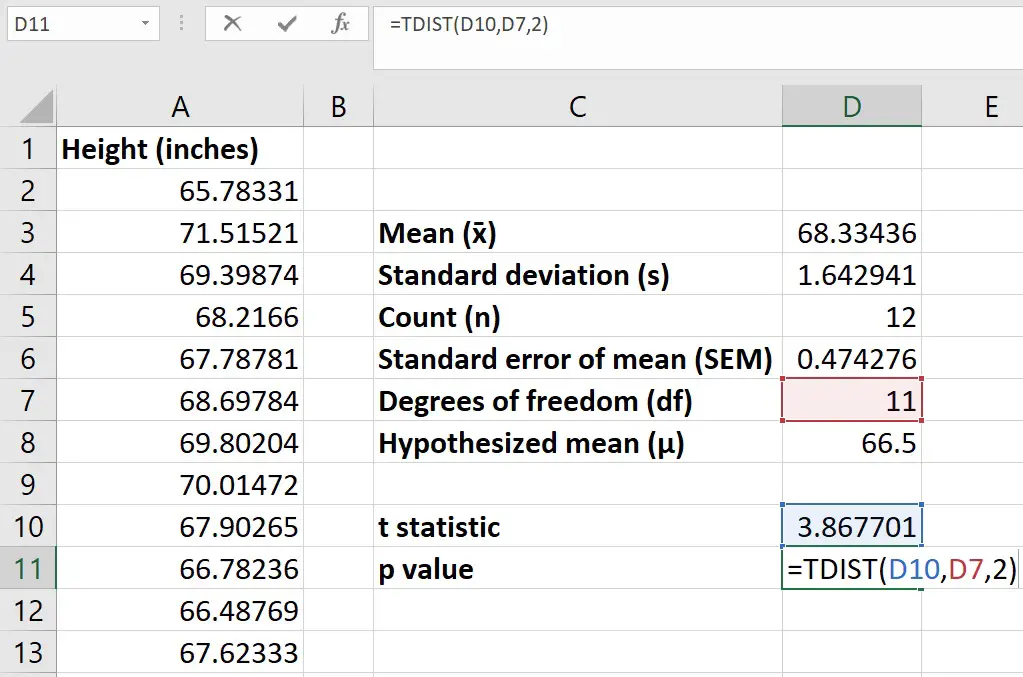
Step 1: Select cell D3 to enter the sample mean (x̄) using the AVERAGE excel formula.
=AVERAGE(A2:A13)
Step 2: Press Enter key to obtain the mean value.
Step 3: Choose cell D4 and enter the sample standard deviation (s) formula.
=STDEV.S(A2:A13)
Step 4: Press Enter key to view the value in cell D4.
Step 5: Count the total data points in the sample (n) using the COUNT() function.
=COUNT(A2:A13)
Step 6: Press Enter key to obtain the results. The COUNT function will return the value as 12.
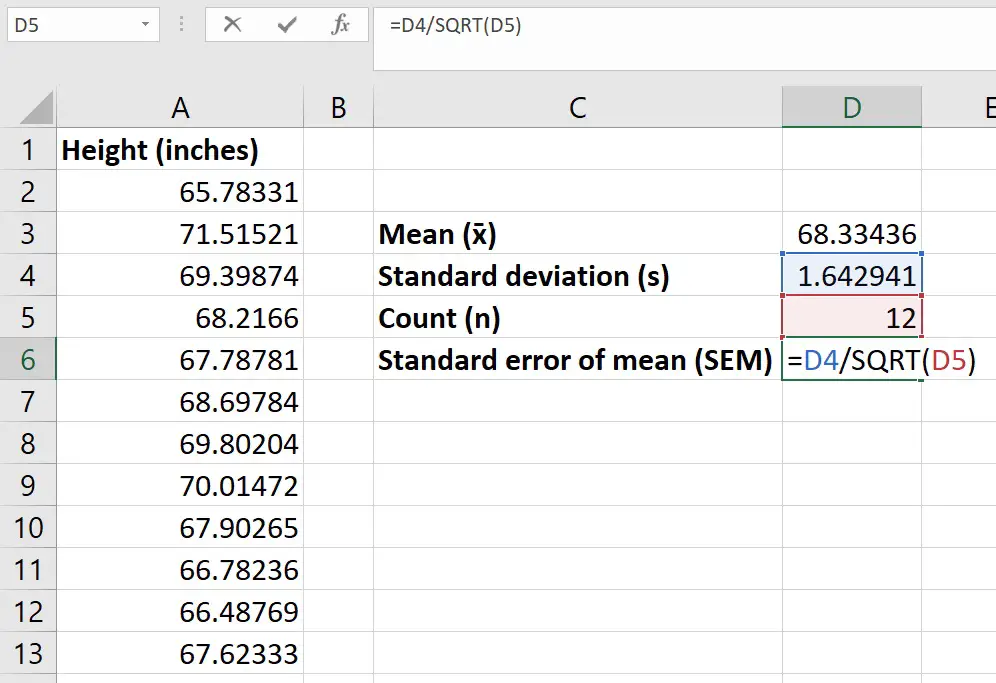
Step 7: Next, determine the standard error in mean (SEM) using the mathematical formula:
SEM = S / √n
Where,
- s: Standard Deviation
- n: Total data points in the sample
Select cell D6 to enter the SEM formula
=D4/SQRT(D5)
Step 8: Press Enter to get the SEM value in cell D6.
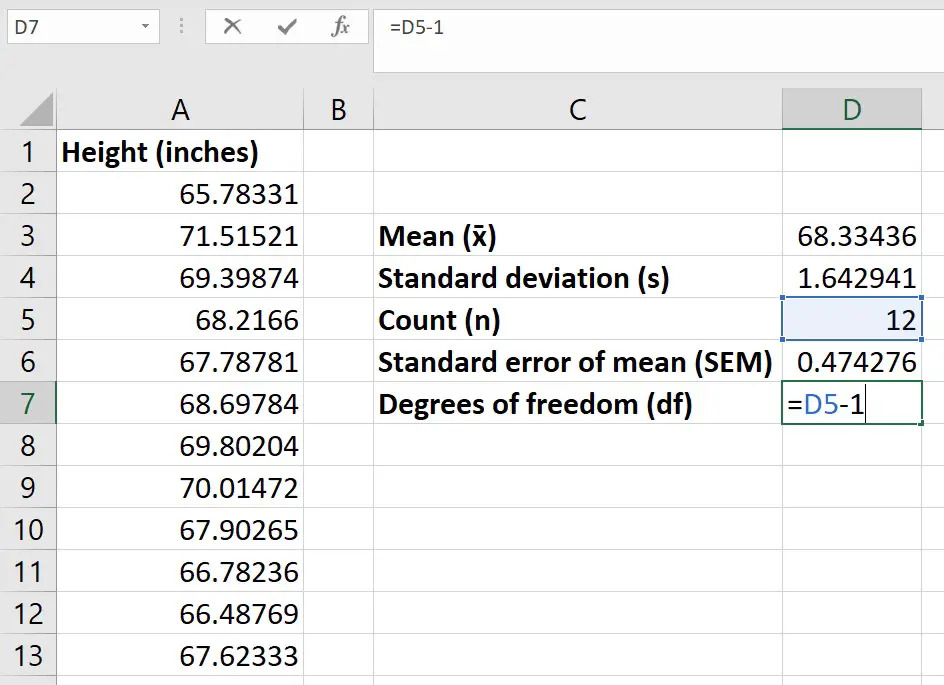
Step 9: Now determine the degree of freedom (df). It is n-1, where n is the total data points in the sample.
Choose cell D7 and enter the df formula:
=D5-1
Step 10: Let us denote the hypothesized mean, 11 feet, as µ. So, enter the µ value in cell D8.
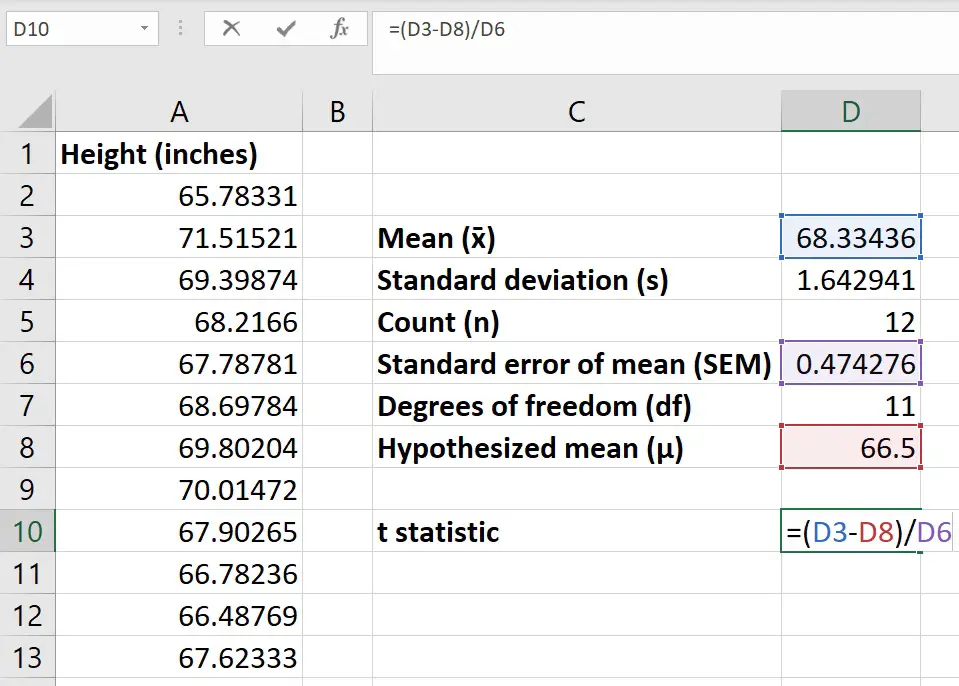
Step 11: Select cell D9 to enter the t-statistic (t) value. The mathematical formula is:
t = (x̄ – µ) / Sx̄
Where,
- x̄: Sample mean
- µ: Hypothesized mean (11 feet in this example)
- Sx̄: SEM
The T-statistic formula for a one-sample T-Test in Excel will be:
=(D3-D8)/D6
Step 12: Press Enter to view the t-statistic value.
Step 13: Choose cell D10 to enter the p-value using the TDIST(). The arguments for the function are t, df, and tails. Next, we will perform a two-tailed T-Test as we have not hypothesized if the sample values are lower or higher than the average. So, the formula in cell D10 will be:
=TDIST(D9,D7,2)
Step 14: Press Enter key to display the p-value.
The p-value is 0.018. It is lower than the default threshold value of 0.05. It interprets that the banana tree heights in the sample differ significantly from the average height of the banana tree. Thus, we reject our null hypothesis and go with the alternate hypothesis.
Example #2
Let us look at the table where the two samples have the same population variance.
The following table shows the number of tasks completed by two teams, Team 1 and Team 2, in columns A and B.
The second table is where you will determine and enter the T-Test result.
The two independent data sets have the same population variation. So, let us calculate the T-Test in Excel function for a one-tailed distribution.
Step 1: Enter the T.Test function in the cell C11.
=T.TEST(A2:A9,B2:B9,1,2)
Please Note: As the population variance is the same for the two data sets, the fourth argument is 2 in the formula, denoting two sample equal variance (homoscedastic).
Step 2: Press Enter to view the T-Test result for the equal variance scenario.
The T.Test() returns the p-value as 0.5. It exceeds the default threshold value, 0.05. So, we need to accept the null hypothesis, implying the two sample data sets have the same mean. Thus, we do not consider the alternate hypothesis, as it may suggest a significant difference in the mean values of the two samples.
Example #3
This example will show how to execute the T-Test in Excel function using the Data Analysis (Analysis ToolPak) in the Data tab.
The below table shows the sample of headcounts in two departments of an IT company.
We can conduct a paired, two sample T-Test using the Analysis ToolPak. But first, we need to install it.
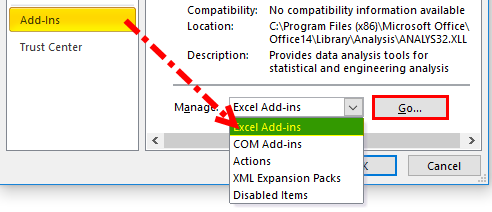
1. Check for the Data Analysis option in the Data. If the option is unavailable in the Data tab, we can install it from File > Options.
2. Choose Add-ins from the menu on the left.
3. Choose Analysis ToolPak from the Inactive Application Add-ins and click on Go.
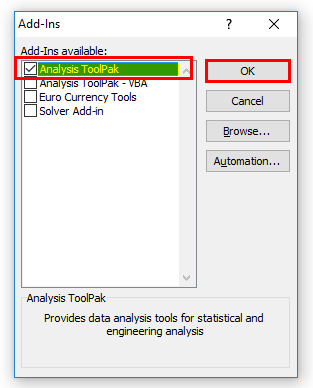
4. Check the Analysis ToolPak box and click OK.
Using the steps mentioned above, we will see the Data Analysis option in the Data tab.
We can proceed with the T-Test using the Analysis ToolPak in the following steps.
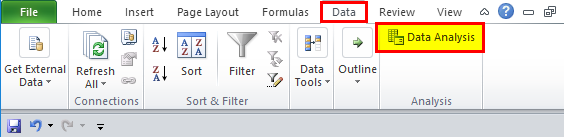
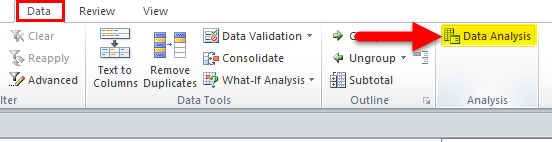
Step 1: Go to Data > Data Analysis.
Step 2: The Data Analysis window pops up. Scroll down to select the t-Test options, choose the Paired Two Sample for Means and click OK.
Step 3: We will see a dialog box where we have to enter the T.Test() arguments.
Please Note: Ensure we select the Labels and Output Range options. Also, the Alpha is 0.05.
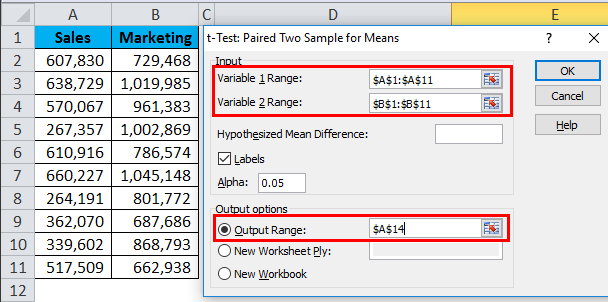
Step 4: With the cursor in the Variable 1 Range, select the cell range A2:A11. Then with the cursor in Variable 2 Range, choose the cell range B2:B11. These will be the absolute cell references for array1 and array2, the first two arguments of the T.Test().
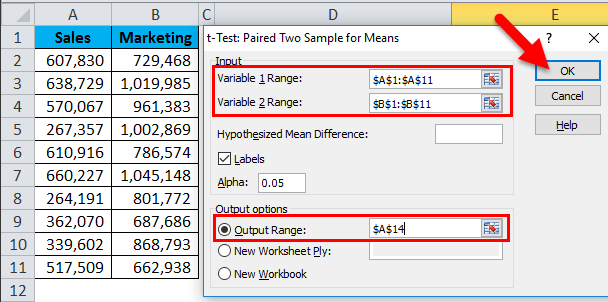
Next, with the cursor in Output Range, select the cell where we want to display the T-Test result. For example, let us choose cell D1.
Step 5: Click OK to view the T-Test result in cell D1. After adjusting the column width, the output will appear as shown below.
The analysis provides the mean, variance, and count of data points (observations) used in the T.Test(). It also shows the correlation, degree of freedom (df), and t-statistic (t Stat) values. And based on all these parameters, we will finally obtain the p-value.
Check the p-value in cell E13. It is 0.000099, a value much lower than the p-value threshold of 0.05. It indicates that our sample data is highly significant, with a considerable difference between the mean values of the two samples.
T-Test Excel Errors
When performing T-Test in Excel, the common possible errors you can get are:
- #N/A: The two arrays you provide have different lengths.
- #NUM!: The argument, tails, is no
- The type argument is not 1, 2, or 3.
- #VALUE!: The argument in the T-Test in Excel function, tails or type, is non-numeric.
Important Things To Note
- The T-test in Excel and hypothesis testing are useful in the business world. You can use them during new product testing and for measuring employee performance.
- You can perform the T-test for dependent and independent data sets.
- The T-test requires the standard deviation of each data set, the total data points in each data set, and the mean difference between the data points.
- The default threshold of significance is 0.05 or 5%. And a p-value below 0.05 makes your data significant.
- The function returns the value that helps users analyze the probability of a significant difference between the mean values of two data sets or groups.
- The Test() is useful for hypothesis testing. It helps determine if we need to accept our null or alternate hypothesis.
Frequently Asked Questions (FAQs)
How to run T-test in Excel?
1. Select the cell where you wish to see the T-test result (return value).
2. Depending on the t-test type you want to perform, enter the required formula and press Enter to get the function return value.
Alternatively, we can:
1. Go to Data > Data Analysis.
2. Select the specific T-test you wish to perform.
3. Enter the two data set ranges, the Alpha value and the cell where you want to display the result.
4. Click on OK to view the complete T-test analysis.
What does the T-test tell you in Excel?
It tells you the probability of two sample data sets being considerably different or belonging to the same population with zero difference in their mean values.
What is the p-value for the t-test in Excel?
Once you run the T-test in Excel, you get the complete analysis, with the most critical information being the p-value. It tells you whether you should accept your null or alternate hypothesis based on the significance threshold (0.05).
What is the difference between a paired (dependent) and unpaired (independent) T-test?
A paired T-test compares the mean value of the sample data sets provided for the same group in two different scenarios. The variance may or may not be equal.
An unpaired T-test compares the mean values of independent populations with the assumption that their variance is equal.
Download Template
This article must be helpful to understand the T-test in Excel, with its formula and examples. You can download the template here to use it instantly.
Recommended Articles
This has been a guide to T-Test in Excel. Here we learn to use one sample, two sample, and paired t-test with formula, examples, and a downloadable template. You can learn more from the following articles –
- Standard Deviation In Excel
- Data Table in Excel
- OFFSET Function In Excel
In this tutorial, I will show you how to perform a one-sample T-test by using Microsoft Excel.
What is a one-sample T-test?
A one-sample T-test is a statistical test to determine if a sample mean is significantly different from a hypothesized mean.
Example data
For this tutorial, I have a sample of 12 young female adults (18 years old). I measured their height in inches and entered the data into a single column in Excel.
Hypotheses
For the purpose of this example, I will pretend the national average height of 18-year-old girls is 66.5 inches.
I want to perform a one-sample T-test in Excel to determine if there is any significant difference between the heights of my sample compared with the national average height (66.5 inches).
The null and alternative hypothesis are:
- Null hypothesis – There is no significant difference between the heights of the sample, compared with the national average
- Alternative hypothesis – There is a significant difference between the heights of the sample, compared with the national average
There is no function in Excel to perform a one-sample T-test. Instead, I will show you a step-by-step process on how to achieve this.
Firstly, calculate the mean, standard deviation (SD) and standard error of the mean (SEM) in Excel. Then, use this information to determine the t-statistic and ultimately the p-value.
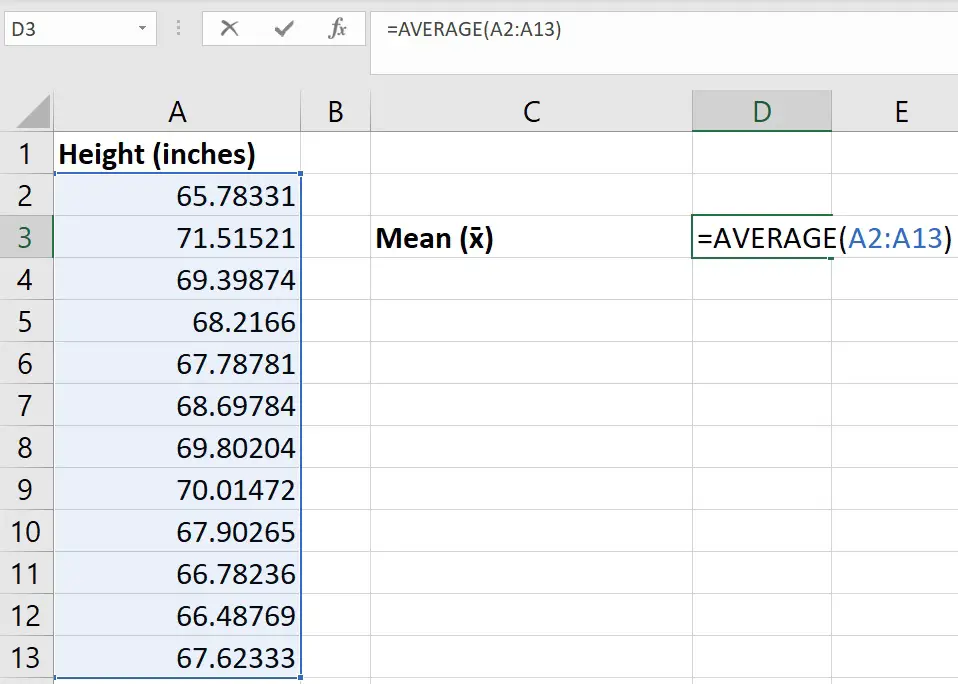
Step 1: Calculate the average
The first thing you should do is to calculate the average value of the sample data.
This can be easily calculated by using the AVERAGE function in Excel.
In Excel, click on an empty cell and enter the following…
=AVERAGE(cell1:cell2)
Replace cell1 in the equation with the cell containing the first data point and replace cell2 with the cell containing the last data point.
Below is a screenshot of what my example looks like.
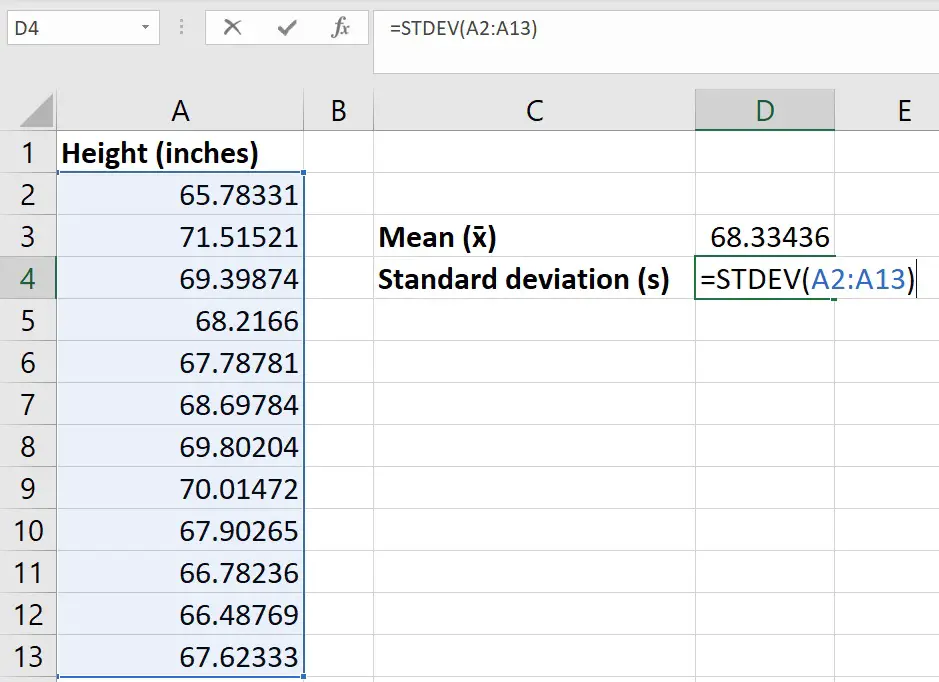
Step 2: Calculate the standard deviation
The next step is the calculate the SD of the sample data.
To do this, use the STDEV function.
In an empty cell, enter the following…
=STDEV(cell1:cell2)
Again, replace cell1 and cell 2 in the equation with the cell containing the first and last data points, respectively.
Note, you can also use the STDEV.S function to achieve the same result.
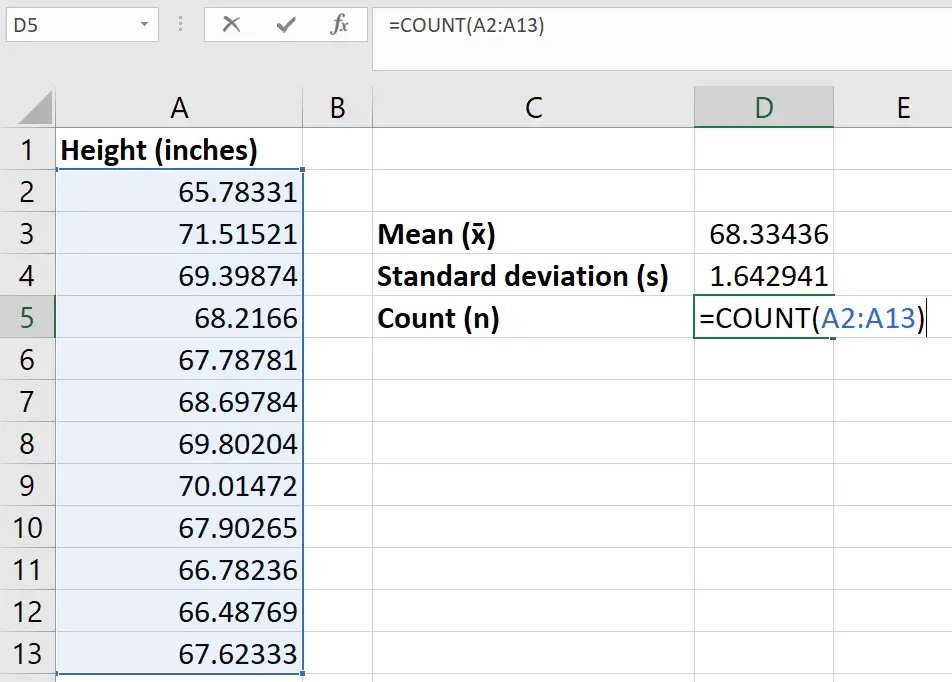
Step 3: Calculate the number of observations
For the next step, simply count the number of observations in the sample.
This can be easily done if you have relatively small numbers. Otherwise, use the COUNT function to get Excel to count them for you.
In an empty cell, enter the following…
=COUNT(cell1:cell2)
As before, replace the cell1 and cell2 with the respected first and last cells.
Step 4: Calculate the standard error of the mean
Now we have the mean and n, we can now work out the standard error of the mean (SEM).
To manually calculate the SEM, simply divide the SD by the square root of n.
In Excel, click on an empty cell and enter the following…
=SD/SQRT(n)
Replace the following:
- SD – With the cell containing the SD
- n – With the cell containing the n
Step 5: Calculate the degrees of freedom
To calculate the degrees of freedom (df) in this case, simply subtract 1 from the n.
In a new cell, enter the following…
=n-1
Replace n with the cell containing the n.
Step 6: Calculate the t-statistic
Before calculating the t-statistic, enter the hypothesized mean into a new cell in Excel.
The hypothesized mean is the value you want to compare your sample data to. So, in my example, this will be the national average height of 18-year-old girls – 66.5.
The formula to calculate the t-statistic for a one-sample T-test is shown below.
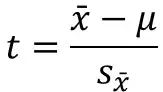
Where:
- x̄ – The sample mean
- μ – The hypothesized mean; in this case, the population mean
- sx̄ – The SEM
So, to work this out in Excel, click on an empty cell and enter the following…
=(x̄ - μ)/sx̄
Replace each component of the formula with the cell containing the corresponding value.
Step 7: Calculate the p-value
The last step is to calculate the p-value by using the t-statistic and the df. This is achieved by using the TDIST function.
In an empty cell, enter the following…
=TDIST(t, df, tails)
Replace the following components of the function with…
- t – The cell containing the t-statistic
- df – The cell containing the df
- tails – Enter 1 if you want to perform a one-tailed analysis, or a 2 if you want to do a two-tailed analysis
For my example, I did not hypothesize if my sample data was greater or lower than the national average. Therefore, I will perform a two-tailed analysis.
If I hypothesized the sample data will be greater than the national average, then I would select to do a one-tailed analysis instead.
So, the p-value for my example is 0.0026.
If my alpha level was set at 0.05, then since the p-value is below the alpha level, I will reject the null hypothesis and accept the alternative hypothesis.
In other words, there is a significant difference between the heights of the sample, compared with the national average.
Wrapping up
In this tutorial, I have shown you how to perform a one-sample T-test in Excel. There is no function to perform a one-sample T-test in Excel. However, you can still perform this by using a stepwise approach.
Microsoft Excel version used: 365 ProPlus
T.TEST in Excel (Table of Contents)
- T.TEST Function in Excel
- T.TEST Formula in Excel
- How to Use T.TEST Function in Excel?
T.TEST in Excel
T-Test function in excel is used for calculating the probability of significant difference between two data sets whether any or both of them are under the same population with the same mean. T-Test, which also includes whether the data sets we are using for calculation is a one-tail distribution or two tail distribution with a kind of variance that may be equal or unequal.
T.TEST Formula in Excel:
The Formula for the T.TEST Function in Excel is as follows:
The Formula of T.TEST includes 4 types of arguments:
Array1: This is the first set of the sample you are testing.
Array2: This is the second set of the sample you are comparing.
Tails: This is the number of tails for the distribution. There are two types of tails are there. 1. One-tailed distribution and 2.Two-tailed distribution
Type: There are 3 types of T.Test available in statistics.
- Paired, this examines whether the mean between paired sets is equal.
- Two-sample equal variance examines whether the variance of means between two sets is equal.
- Two-sample unequal variance examines whether the variance of means between two sets is unequal.
In recent versions, T.TEST is introduced. In earlier versions, TTEST is the formula. Still, it is available in recent versions to support compatibility.
How to Use T.TEST Function in Excel?
T.TEST Function in Excel is very simple and easy to use. Let us understand the working of T.TEST in Excel by Some Examples.
You can download this T.TEST Function Excel Template here – T.TEST Function Excel Template
Example #1
The functionality of the T.TEST can be best explained by using an example dataset to get the logic of the T.TEST.
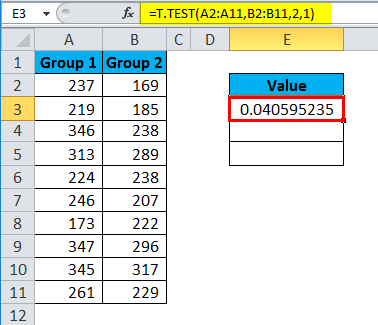
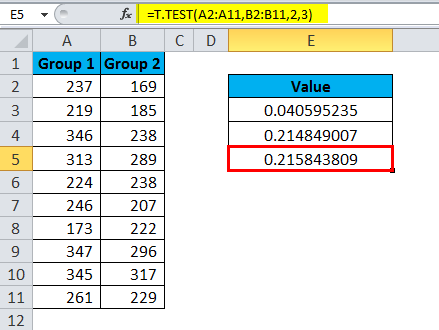
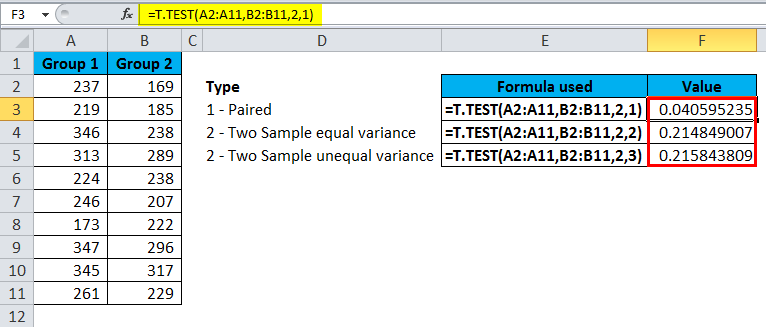
I have Group 1 and Group 2 test scores of a classroom. I need to run T.TEST to find is there a significant difference between these two groups.
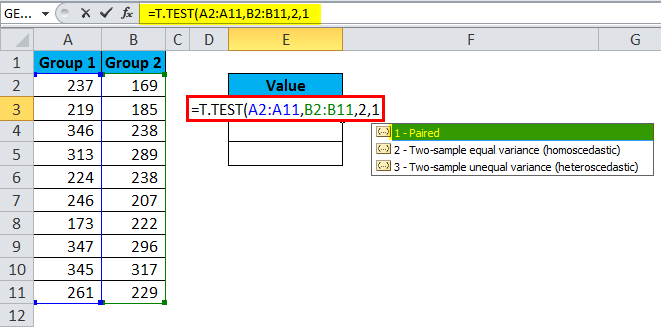
Apply T.TEST to get the difference.
The first test is a type of Paired.
The result is 0.04059.
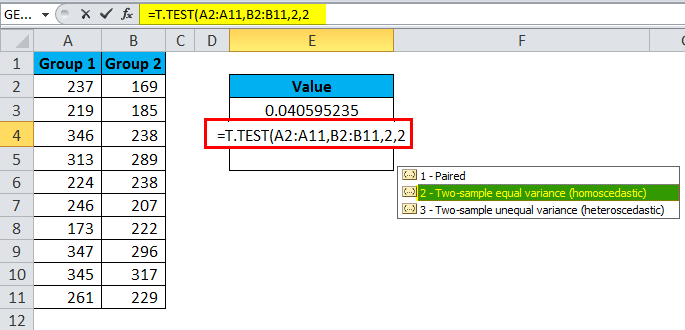
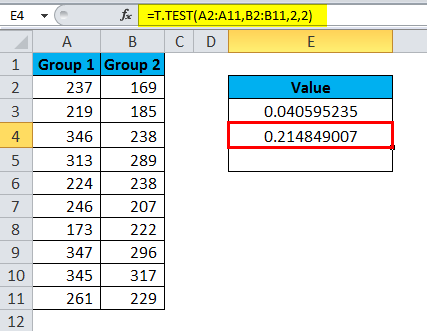
The second test is a type of Two Samples equal variance.
The result is 0.2148.
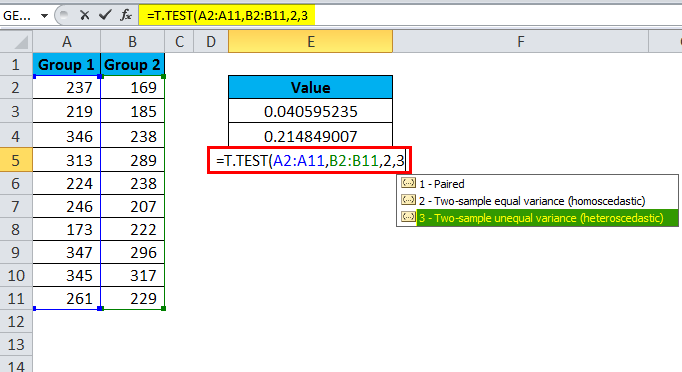
The third test is a type of Two Sample unequal variance.
The result is 0.2158.
The returned value is generally called as the P-value. If the P-value is <0.05, we can come to the conclusion that the two sets of data have a different mean. Otherwise, the two means are not significantly different from each other.
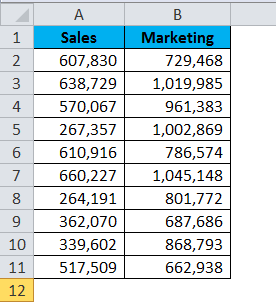
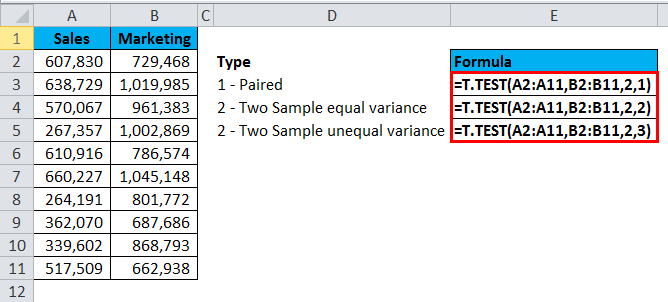
Example #2
I have the salary numbers of two different departments. I want to find if the mean of two department’s salaries is significantly different are not.
Apply the T.TEST function to see the difference.
The above formula returns the result as:
Run T.TEST using Analysis Tool Pack
We can run the T.TEST using the analysis tool pack located under the Data ribbon tab.
If you do not find this option in your excel, follow the below steps to unhide this.
Step 1: Go to File and Options
Step 2: Click on Add-Ins
Step 3: Select Excel Add-ins and click Go
Step 4: Select Analysis ToolPak and click OK.
Step 5: This must have enabled the Data Analysis Option.
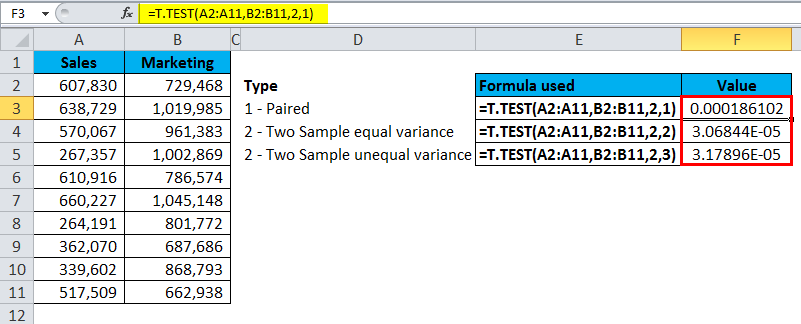
Follow the below Steps to Run T.TEST using Data Analysis ToolPak
Step 1: Click on Data Analysis under the Data tab.
Step 2: Scroll down find the t-Test.
Step 3: Click on the first t-test, and it will open the below dialogue box.
Step 4: Select the Variable 1 range and Variable 2 range.
Step 5: Once all the above boxes filled, click on the OK button.
It will show a detailed report.
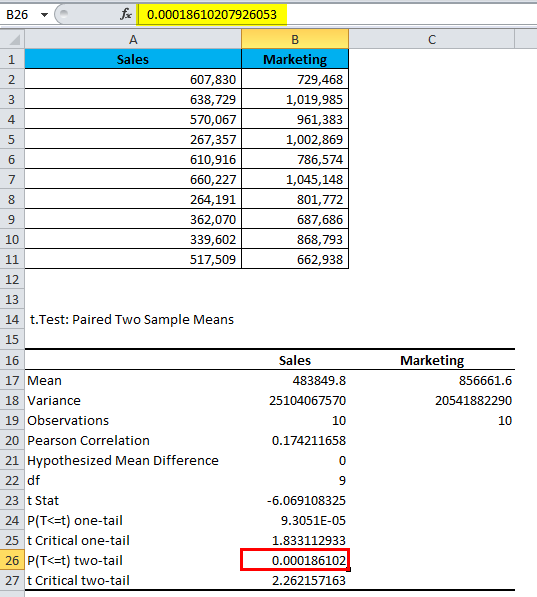
This will show the mean of each data set, their variance, how many observations are taken into consideration, correlation, and P-value.
We need to see the P-value (refer to B26), i.e. 0.000186102 that is way below than the expected P-value of 0.05.
As long as the P-value is less than 0.05, our data is significant.
Things to Remember
- The T.TEST can accept only numerical values, anything other than numerical values; we get the result of #VALUE!
- If the tails value is other than 1 or 2, we will get #NUM! error
- Learn the difference between the One-tailed test and the Two-tailed test to understand it better.
- One of the assumptions is samples have been randomly drawn from the large data.
- Standard P-Value is 0.05 i.e. 5%. If the variance is less than 5%, then your data is significant.
Recommended Articles
This has been a guide to T.TEST in Excel. Here we discuss the T.TEST Formula in Excel and how to use T.TEST Function in Excel along with excel examples and downloadable excel templates. You may also look at these useful functions in excel –
- CEILING Function in Excel
- Examples of COMBIN Function
- SUMPRODUCT Function in Excel
- How to Use LEN Function in Excel?
- Examples of PRODUCT Function in Excel
Calculate the probability that is associated with a Student’s T-Test
What is the T-TEST Function?
The T.TEST Function[1] is categorized under Excel Statistical functions. It will calculate the probability that is associated with a Student’s T-Test. The function is commonly used to test the probability of two samples that have underlying populations with the same mean.
In financial analysis, suppose we wish to understand the amount spent by Europeans and Americans on food. We cannot practically record the spending habits of every European and American, so we would take a sample of each population. In such a scenario, T-test will help us find the answer to the question of whether the difference in food spending of the two groups is representative of a true difference between Europeans and Americans in general or if it is just a meaningless statistical difference.
Formula
=T.TEST(array1,array2,tails,type)
The formula uses the following arguments:
- Array1 (It is a required argument) – The first data set.
- Array2 (It is a required argument) – The second data set.
- Tails (It is a required argument) – Specifies if it is a one-tailed or two-tailed test. If tails = 1, T-TEST uses the one-tailed distribution. If tails = 2, T-TEST uses the two-tailed distribution.
- Type (It is a required argument) – The type of t-test to perform:
- 1 – Performs a paired t-test.
- 2 – Two-sample equal variance t-test.
- 3 – Two-sample unequal variance t-test.
How to Use the T-TEST Function in Excel?
To understand the uses of the T.TEST function, let’s consider a few examples:
Example 1 – Perform a T-Test calculation in Excel
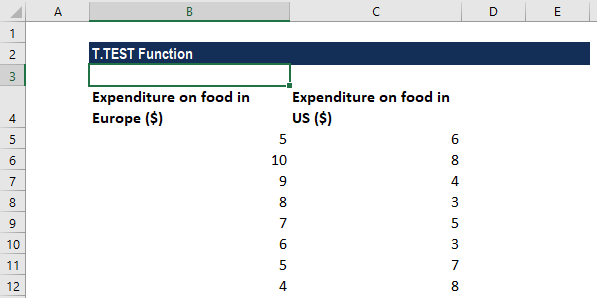
Suppose we are given the following data on the money spent by households in Europe and the US. As the samples are independent of one another, we use the two-sample t-test. Let’s say we want to test if the means between these two data-sets are significantly different, which are Europe $X.XX and US $X.XX. We can use the T-test for that.
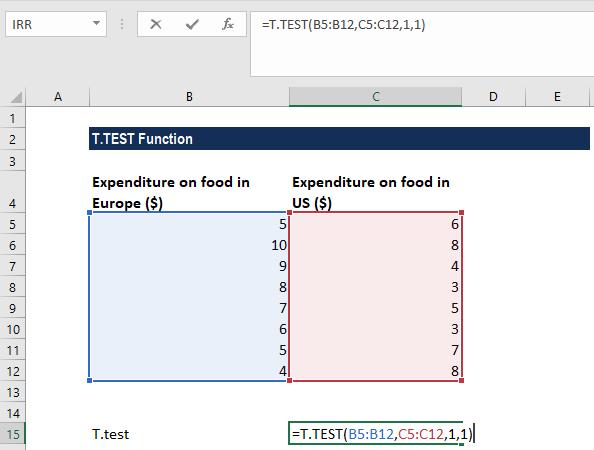
The value associated with the Student’s paired t-test with a one-tailed distribution for the two arrays of data above can be calculated using the Excel function. The formula used is as follows:
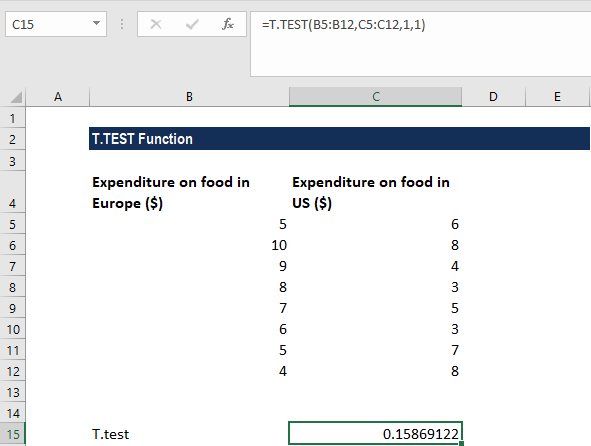
We get the result below:
What Does the Value Mean?
In the example above we have calculated the p-value for the t.test. When conducting hypothesis testing, it is important to set the null and alternative hypothesis.
Things to Remember about the T-TEST Function
- #NUM! error – Occurs when:
- The given tails argument has any value other than 1 or 2.
- The given type argument is not equal to 1,2, or 3.
- #N/A! error – Occurs when the two supplied arrays are of different lengths.
- #VALUE error – Occurs when either the given tails argument or the supplied type argument is non-numeric.
Click here to download the sample Excel file
Additional Resources
Thanks for reading CFI’s guide to the Excel T-test function. By taking the time to learn and master these functions, you’ll significantly speed up your financial analysis. To learn more, check out these additional CFI resources:
- Excel Functions for Finance
- Advanced Excel Formulas Course
- Advanced Excel Formulas You Must Know
- Excel Shortcuts for PC and Mac
- See all Excel resources
Article Sources
- T.TEST Function