| Temperature | |
|---|---|

Thermal vibration of a segment of protein alpha helix. Its amplitude increases with temperature |
|
|
Common symbols |
T |
| SI unit | K |
|
Other units |
°C, °F, °R, °Rø, °Ré, °N, °D, °L, °W |
| Intensive? | Yes |
|
Derivations from |
 , ,  |
| Dimension |  |
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer.
Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called centigrade), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI).
Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature.
Temperature is important in all fields of natural science, including physics, chemistry, Earth science, astronomy, medicine, biology, ecology, material science, metallurgy, mechanical engineering and geography as well as most aspects of daily life.
Effects[edit]
Average daily variation in human body temperature
Many physical processes are related to temperature; some of them are given below:
- the physical properties of materials including the phase (solid, liquid, gaseous or plasma), density, solubility, vapor pressure, electrical conductivity, hardness, wear resistance, thermal conductivity, corrosion resistance, strength
- the rate and extent to which chemical reactions occur[1]
- the amount and properties of thermal radiation emitted from the surface of an object
- air temperature affects all living organisms
- the speed of sound, which in a gas is proportional to the square root of the absolute temperature[2]
Scales[edit]
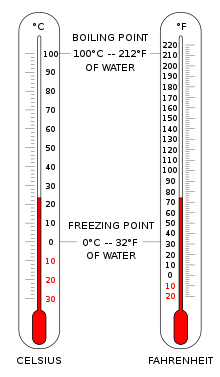
Two thermometers showing temperature in Celsius and Fahrenheit
Temperature scales need two values for definition: the point chosen as zero degrees and the magnitudes of the incremental unit of temperature.
The Celsius scale (°C) is used for common temperature measurements in most of the world. It is an empirical scale that developed historically, which led to its zero point 0 °C being defined as the freezing point of water, and 100 °C as the boiling point of water, both at atmospheric pressure at sea level. It was called a centigrade scale because of the 100-degree interval.[3] Since the standardization of the kelvin in the International System of Units, it has subsequently been redefined in terms of the equivalent fixing points on the Kelvin scale, so that a temperature increment of one degree Celsius is the same as an increment of one kelvin, though numerically the scales differ by an exact offset of 273.15.
The Fahrenheit scale is in common use in the United States. Water freezes at 32 °F and boils at 212 °F at sea-level atmospheric pressure.
Absolute zero[edit]
At the absolute zero of temperature, no energy can be removed from matter as heat, a fact expressed in the third law of thermodynamics. At this temperature, matter contains no macroscopic thermal energy, but still has quantum-mechanical zero-point energy as predicted by the uncertainty principle, although this does not enter into the definition of absolute temperature. Experimentally, absolute zero can be approached only very closely; it can never be reached (the lowest temperature attained by experiment is 100 pK).[citation needed] Theoretically, in a body at a temperature of absolute zero, all classical motion of its particles has ceased and they are at complete rest in this classical sense. The absolute zero, defined as 0 K, is exactly equal to −273.15 °C, or −459.67 °F.
Absolute scales[edit]
Referring to the Boltzmann constant, to the Maxwell–Boltzmann distribution, and to the Boltzmann statistical mechanical definition of entropy, as distinct from the Gibbs definition,[4] for independently moving microscopic particles, disregarding interparticle potential energy, by international agreement, a temperature scale is defined and said to be absolute because it is independent of the characteristics of particular thermometric substances and thermometer mechanisms. Apart from the absolute zero, it does not have a reference temperature. It is known as the Kelvin scale, widely used in science and technology. The kelvin (the unit name is spelled with a lower-case ‘k’) is the unit of temperature in the International System of Units (SI). The temperature of a body in a state of thermodynamic equilibrium is always positive relative to the absolute zero.
Besides the internationally agreed Kelvin scale, there is also a thermodynamic temperature scale, invented by Lord Kelvin, also with its numerical zero at the absolute zero of temperature, but directly relating to purely macroscopic thermodynamic concepts, including the macroscopic entropy, though microscopically referable to the Gibbs statistical mechanical definition of entropy for the canonical ensemble, that takes interparticle potential energy into account, as well as independent particle motion so that it can account for measurements of temperatures near absolute zero.[4] This scale has a reference temperature at the triple point of water, the numerical value of which is defined by measurements using the aforementioned internationally agreed Kelvin scale.
Kelvin scale[edit]
Many scientific measurements use the Kelvin temperature scale (unit symbol: K), named in honor of the physicist who first defined it. It is an absolute scale. Its numerical zero point, 0 K, is at the absolute zero of temperature. Since May, 2019, the kelvin has been defined through particle kinetic theory, and statistical mechanics. In the International System of Units (SI), the magnitude of the kelvin is defined in terms of the Boltzmann constant, the value of which is defined as fixed by international convention.[5][6]
Statistical mechanical versus thermodynamic temperature scales[edit]
Since May 2019, the magnitude of the kelvin is defined in relation to microscopic phenomena, characterized in terms of statistical mechanics. Previously, but since 1954, the International System of Units defined a scale and unit for the kelvin as a thermodynamic temperature, by using the reliably reproducible temperature of the triple point of water as a second reference point, the first reference point being 0 K at absolute zero.[citation needed]
Historically, the temperature of the triple point of water was defined as exactly 273.16 K. Today it is an empirically measured quantity. The freezing point of water at sea-level atmospheric pressure occurs at very close to 273.15 K (0 °C).
Classification of scales[edit]
There are various kinds of temperature scale. It may be convenient to classify them as empirically and theoretically based. Empirical temperature scales are historically older, while theoretically based scales arose in the middle of the nineteenth century.[7][8]
Empirical scales[edit]
Empirically based temperature scales rely directly on measurements of simple macroscopic physical properties of materials. For example, the length of a column of mercury, confined in a glass-walled capillary tube, is dependent largely on temperature and is the basis of the very useful mercury-in-glass thermometer. Such scales are valid only within convenient ranges of temperature. For example, above the boiling point of mercury, a mercury-in-glass thermometer is impracticable. Most materials expand with temperature increase, but some materials, such as water, contract with temperature increase over some specific range, and then they are hardly useful as thermometric materials. A material is of no use as a thermometer near one of its phase-change temperatures, for example, its boiling-point.
In spite of these limitations, most generally used practical thermometers are of the empirically based kind. Especially, it was used for calorimetry, which contributed greatly to the discovery of thermodynamics. Nevertheless, empirical thermometry has serious drawbacks when judged as a basis for theoretical physics. Empirically based thermometers, beyond their base as simple direct measurements of ordinary physical properties of thermometric materials, can be re-calibrated, by use of theoretical physical reasoning, and this can extend their range of adequacy.
Theoretical scales[edit]
Theoretically based temperature scales are based directly on theoretical arguments, especially those of kinetic theory and thermodynamics. They are more or less ideally realized in practically feasible physical devices and materials. Theoretically based temperature scales are used to provide calibrating standards for practical empirically based thermometers.
Microscopic statistical mechanical scale[edit]
In physics, the internationally agreed conventional temperature scale is called the Kelvin scale. It is calibrated through the internationally agreed and prescribed value of the Boltzmann constant,[5][6] referring to motions of microscopic particles, such as atoms, molecules, and electrons, constituent in the body whose temperature is to be measured. In contrast with the thermodynamic temperature scale invented by Kelvin, the presently conventional Kelvin temperature is not defined through comparison with the temperature of a reference state of a standard body, nor in terms of macroscopic thermodynamics.
Apart from the absolute zero of temperature, the Kelvin temperature of a body in a state of internal thermodynamic equilibrium is defined by measurements of suitably chosen of its physical properties, such as have precisely known theoretical explanations in terms of the Boltzmann constant.[citation needed] That constant refers to chosen kinds of motion of microscopic particles in the constitution of the body. In those kinds of motion, the particles move individually, without mutual interaction. Such motions are typically interrupted by inter-particle collisions, but for temperature measurement, the motions are chosen so that, between collisions, the non-interactive segments of their trajectories are known to be accessible to accurate measurement. For this purpose, interparticle potential energy is disregarded.
In an ideal gas, and in other theoretically understood bodies, the Kelvin temperature is defined to be proportional to the average kinetic energy of non-interactively moving microscopic particles, which can be measured by suitable techniques. The proportionality constant is a simple multiple of the Boltzmann constant. If molecules, atoms, or electrons,[9][10] are emitted from material and their velocities are measured, the spectrum of their velocities often nearly obeys a theoretical law called the Maxwell–Boltzmann distribution, which gives a well-founded measurement of temperatures for which the law holds.[11] There have not yet been successful experiments of this same kind that directly use the Fermi–Dirac distribution for thermometry, but perhaps that will be achieved in the future.[12]
The speed of sound in a gas can be calculated theoretically from the molecular character of the gas, from its temperature and pressure, and from the value of the Boltzmann constant. For a gas of known molecular character and pressure, this provides a relation between temperature and the Boltzmann constant. Those quantities can be known or measured more precisely than can the thermodynamic variables that define the state of a sample of water at its triple point. Consequently, taking the value of the Boltzmann constant as a primarily defined reference of exactly defined value, a measurement of the speed of sound can provide a more precise measurement of the temperature of the gas.[13]
Measurement of the spectrum of electromagnetic radiation from an ideal three-dimensional black body can provide an accurate temperature measurement because the frequency of maximum spectral radiance of black-body radiation is directly proportional to the temperature of the black body; this is known as Wien’s displacement law and has a theoretical explanation in Planck’s law and the Bose–Einstein law.
Measurement of the spectrum of noise-power produced by an electrical resistor can also provide accurate temperature measurement. The resistor has two terminals and is in effect a one-dimensional body. The Bose-Einstein law for this case indicates that the noise-power is directly proportional to the temperature of the resistor and to the value of its resistance and to the noise bandwidth. In a given frequency band, the noise-power has equal contributions from every frequency and is called Johnson noise. If the value of the resistance is known then the temperature can be found.[14][15]
Macroscopic thermodynamic scale[edit]
Historically, till May 2019, the definition of the Kelvin scale was that invented by Kelvin, based on a ratio of quantities of energy in processes in an ideal Carnot engine, entirely in terms of macroscopic thermodynamics.[citation needed] That Carnot engine was to work between two temperatures, that of the body whose temperature was to be measured, and a reference, that of a body at the temperature of the triple point of water. Then the reference temperature, that of the triple point, was defined to be exactly 273.16 K. Since May 2019, that value has not been fixed by definition but is to be measured through microscopic phenomena, involving the Boltzmann constant, as described above. The microscopic statistical mechanical definition does not have a reference temperature.
Ideal gas[edit]
A material on which a macroscopically defined temperature scale may be based is the ideal gas. The pressure exerted by a fixed volume and mass of an ideal gas is directly proportional to its temperature. Some natural gases show so nearly ideal properties over suitable temperature range that they can be used for thermometry; this was important during the development of thermodynamics and is still of practical importance today.[16][17] The ideal gas thermometer is, however, not theoretically perfect for thermodynamics. This is because the entropy of an ideal gas at its absolute zero of temperature is not a positive semi-definite quantity, which puts the gas in violation of the third law of thermodynamics. In contrast to real materials, the ideal gas does not liquefy or solidify, no matter how cold it is. Alternatively thinking, the ideal gas law, refers to the limit of infinitely high temperature and zero pressure; these conditions guarantee non-interactive motions of the constituent molecules.[18][19][20]
Kinetic theory approach[edit]
The magnitude of the kelvin is now defined in terms of kinetic theory, derived from the value of the Boltzmann constant.
Kinetic theory provides a microscopic account of temperature for some bodies of material, especially gases, based on macroscopic systems’ being composed of many microscopic particles, such as molecules and ions of various species, the particles of a species being all alike. It explains macroscopic phenomena through the classical mechanics of the microscopic particles. The equipartition theorem of kinetic theory asserts that each classical degree of freedom of a freely moving particle has an average kinetic energy of kBT/2 where kB denotes the Boltzmann constant.[citation needed] The translational motion of the particle has three degrees of freedom, so that, except at very low temperatures where quantum effects predominate, the average translational kinetic energy of a freely moving particle in a system with temperature T will be 3kBT/2.
Molecules, such as oxygen (O2), have more degrees of freedom than single spherical atoms: they undergo rotational and vibrational motions as well as translations. Heating results in an increase of temperature due to an increase in the average translational kinetic energy of the molecules. Heating will also cause, through equipartitioning, the energy associated with vibrational and rotational modes to increase. Thus a diatomic gas will require more energy input to increase its temperature by a certain amount, i.e. it will have a greater heat capacity than a monatomic gas.
As noted above, the speed of sound in a gas can be calculated from the molecular character of the gas, from its temperature and pressure, and from the value of the Boltzmann constant. Taking the value of the Boltzmann constant as a primarily defined reference of exactly defined value, a measurement of the speed of sound can provide a more precise measurement of the temperature of the gas.[13]
It is possible to measure the average kinetic energy of constituent microscopic particles if they are allowed to escape from the bulk of the system, through a small hole in the containing wall. The spectrum of velocities has to be measured, and the average calculated from that. It is not necessarily the case that the particles that escape and are measured have the same velocity distribution as the particles that remain in the bulk of the system, but sometimes a good sample is possible.
Thermodynamic approach[edit]
Temperature is one of the principal quantities in the study of thermodynamics. Formerly, the magnitude of the kelvin was defined in thermodynamic terms, but nowadays, as mentioned above, it is defined in terms of kinetic theory.
The thermodynamic temperature is said to be absolute for two reasons. One is that its formal character is independent of the properties of particular materials. The other reason is that its zero is, in a sense, absolute, in that it indicates absence of microscopic classical motion of the constituent particles of matter, so that they have a limiting specific heat of zero for zero temperature, according to the third law of thermodynamics. Nevertheless, a thermodynamic temperature does in fact have a definite numerical value that has been arbitrarily chosen by tradition and is dependent on the property of particular materials; it is simply less arbitrary than relative «degrees» scales such as Celsius and Fahrenheit. Being an absolute scale with one fixed point (zero), there is only one degree of freedom left to arbitrary choice, rather than two as in relative scales. For the Kelvin scale since May 2019, by international convention, the choice has been made to use knowledge of modes of operation of various thermometric devices, relying on microscopic kinetic theories about molecular motion. The numerical scale is settled by a conventional definition of the value of the Boltzmann constant, which relates macroscopic temperature to average microscopic kinetic energy of particles such as molecules. Its numerical value is arbitrary, and an alternate, less widely used absolute temperature scale exists called the Rankine scale, made to be aligned with the Fahrenheit scale as Kelvin is with Celsius.
The thermodynamic definition of temperature is due to Kelvin. It is framed in terms of an idealized device called a Carnot engine, imagined to run in a fictive continuous cycle of successive processes that traverse a cycle of states of its working body. The engine takes in a quantity of heat Q1 from a hot reservoir and passes out a lesser quantity of waste heat Q2 < 0 to a cold reservoir. The net heat energy absorbed by the working body is passed, as thermodynamic work, to a work reservoir, and is considered to be the output of the engine. The cycle is imagined to run so slowly that at each point of the cycle the working body is in a state of thermodynamic equilibrium. The successive processes of the cycle are thus imagined to run reversibly with no entropy production. Then the quantity of entropy taken in from the hot reservoir when the working body is heated is equal to that passed to the cold reservoir when the working body is cooled. Then the absolute or thermodynamic temperatures, T1 and T2, of the reservoirs are defined such that[21]
-
(1)
The zeroth law of thermodynamics allows this definition to be used to measure the absolute or thermodynamic temperature of an arbitrary body of interest, by making the other heat reservoir have the same temperature as the body of interest.
Kelvin’s original work postulating absolute temperature was published in 1848. It was based on the work of Carnot, before the formulation of the first law of thermodynamics. Carnot had no sound understanding of heat and no specific concept of entropy. He wrote of ‘caloric’ and said that all the caloric that passed from the hot reservoir was passed into the cold reservoir. Kelvin wrote in his 1848 paper that his scale was absolute in the sense that it was defined «independently of the properties of any particular kind of matter». His definitive publication, which sets out the definition just stated, was printed in 1853, a paper read in 1851.[22][23][24][25]
Numerical details were formerly settled by making one of the heat reservoirs a cell at the triple point of water, which was defined to have an absolute temperature of 273.16 K.[26] Nowadays, the numerical value is instead obtained from measurement through the microscopic statistical mechanical international definition, as above.
Intensive variability[edit]
In thermodynamic terms, temperature is an intensive variable because it is equal to a differential coefficient of one extensive variable with respect to another, for a given body. It thus has the dimensions of a ratio of two extensive variables. In thermodynamics, two bodies are often considered as connected by contact with a common wall, which has some specific permeability properties. Such specific permeability can be referred to a specific intensive variable. An example is a diathermic wall that is permeable only to heat; the intensive variable for this case is temperature. When the two bodies have been connected through the specifically permeable wall for a very long time, and have settled to a permanent steady state, the relevant intensive variables are equal in the two bodies; for a diathermal wall, this statement is sometimes called the zeroth law of thermodynamics.[27][28][29]
In particular, when the body is described by stating its internal energy U, an extensive variable, as a function of its entropy S, also an extensive variable, and other state variables V, N, with U = U (S, V, N), then the temperature is equal to the partial derivative of the internal energy with respect to the entropy:[28][29][30]
-
(2)
Likewise, when the body is described by stating its entropy S as a function of its internal energy U, and other state variables V, N, with S = S (U, V, N), then the reciprocal of the temperature is equal to the partial derivative of the entropy with respect to the internal energy:[28][30][31]
-
(3)
The above definition, equation (1), of the absolute temperature, is due to Kelvin. It refers to systems closed to the transfer of matter and has a special emphasis on directly experimental procedures. A presentation of thermodynamics by Gibbs starts at a more abstract level and deals with systems open to the transfer of matter; in this development of thermodynamics, the equations (2) and (3) above are actually alternative definitions of temperature.[32]
Local thermodynamic equilibrium[edit]
Real-world bodies are often not in thermodynamic equilibrium and not homogeneous. For the study by methods of classical irreversible thermodynamics, a body is usually spatially and temporally divided conceptually into ‘cells’ of small size. If classical thermodynamic equilibrium conditions for matter are fulfilled to good approximation in such a ‘cell’, then it is homogeneous and a temperature exists for it. If this is so for every ‘cell’ of the body, then local thermodynamic equilibrium is said to prevail throughout the body.[33][34][35][36][37]
It makes good sense, for example, to say of the extensive variable U, or of the extensive variable S, that it has a density per unit volume or a quantity per unit mass of the system, but it makes no sense to speak of the density of temperature per unit volume or quantity of temperature per unit mass of the system. On the other hand, it makes no sense to speak of the internal energy at a point, while when local thermodynamic equilibrium prevails, it makes good sense to speak of the temperature at a point. Consequently, the temperature can vary from point to point in a medium that is not in global thermodynamic equilibrium, but in which there is local thermodynamic equilibrium.
Thus, when local thermodynamic equilibrium prevails in a body, the temperature can be regarded as a spatially varying local property in that body, and this is because the temperature is an intensive variable.
Basic theory[edit]
Temperature is a measure of a quality of a state of a material.[38] The quality may be regarded as a more abstract entity than any particular temperature scale that measures it, and is called hotness by some writers.[39][40][41] The quality of hotness refers to the state of material only in a particular locality, and in general, apart from bodies held in a steady state of thermodynamic equilibrium, hotness varies from place to place. It is not necessarily the case that a material in a particular place is in a state that is steady and nearly homogeneous enough to allow it to have a well-defined hotness or temperature. Hotness may be represented abstractly as a one-dimensional manifold. Every valid temperature scale has its own one-to-one map into the hotness manifold.[42][43]
When two systems in thermal contact are at the same temperature no heat transfers between them. When a temperature difference does exist heat flows spontaneously from the warmer system to the colder system until they are in thermal equilibrium. Such heat transfer occurs by conduction or by thermal radiation.[44][45][46][47][48][49][50][51]
Experimental physicists, for example Galileo and Newton,[52] found that there are indefinitely many empirical temperature scales. Nevertheless, the zeroth law of thermodynamics says that they all measure the same quality. This means that for a body in its own state of internal thermodynamic equilibrium, every correctly calibrated thermometer, of whatever kind, that measures the temperature of the body, records one and the same temperature. For a body that is not in its own state of internal thermodynamic equilibrium, different thermometers can record different temperatures, depending respectively on the mechanisms of operation of the thermometers.
Bodies in thermodynamic equilibrium[edit]
For experimental physics, hotness means that, when comparing any two given bodies in their respective separate thermodynamic equilibria, any two suitably given empirical thermometers with numerical scale readings will agree as to which is the hotter of the two given bodies, or that they have the same temperature.[53] This does not require the two thermometers to have a linear relation between their numerical scale readings, but it does require that the relation between their numerical readings shall be strictly monotonic.[54][55] A definite sense of greater hotness can be had, independently of calorimetry, of thermodynamics, and of properties of particular materials, from Wien’s displacement law of thermal radiation: the temperature of a bath of thermal radiation is proportional, by a universal constant, to the frequency of the maximum of its frequency spectrum; this frequency is always positive, but can have values that tend to zero. Thermal radiation is initially defined for a cavity in thermodynamic equilibrium. These physical facts justify a mathematical statement that hotness exists on an ordered one-dimensional manifold. This is a fundamental character of temperature and thermometers for bodies in their own thermodynamic equilibrium.[7][42][43][56][57]
Except for a system undergoing a first-order phase change such as the melting of ice, as a closed system receives heat, without a change in its volume and without a change in external force fields acting on it, its temperature rises. For a system undergoing such a phase change so slowly that departure from thermodynamic equilibrium can be neglected, its temperature remains constant as the system is supplied with latent heat. Conversely, a loss of heat from a closed system, without phase change, without change of volume, and without a change in external force fields acting on it, decreases its temperature.[58]
Bodies in a steady state but not in thermodynamic equilibrium[edit]
While for bodies in their own thermodynamic equilibrium states, the notion of temperature requires that all empirical thermometers must agree as to which of two bodies is the hotter or that they are at the same temperature, this requirement is not safe for bodies that are in steady states though not in thermodynamic equilibrium. It can then well be that different empirical thermometers disagree about which is hotter, and if this is so, then at least one of the bodies does not have a well-defined absolute thermodynamic temperature. Nevertheless, anyone has given body and any one suitable empirical thermometer can still support notions of empirical, non-absolute, hotness, and temperature, for a suitable range of processes. This is a matter for study in non-equilibrium thermodynamics.[citation needed]
Bodies not in a steady state[edit]
When a body is not in a steady-state, then the notion of temperature becomes even less safe than for a body in a steady state not in thermodynamic equilibrium. This is also a matter for study in non-equilibrium thermodynamics.
Thermodynamic equilibrium axiomatics[edit]
For the axiomatic treatment of thermodynamic equilibrium, since the 1930s, it has become customary to refer to a zeroth law of thermodynamics. The customarily stated minimalist version of such a law postulates only that all bodies, which when thermally connected would be in thermal equilibrium, should be said to have the same temperature by definition, but by itself does not establish temperature as a quantity expressed as a real number on a scale. A more physically informative version of such a law views empirical temperature as a chart on a hotness manifold.[42][57][59] While the zeroth law permits the definitions of many different empirical scales of temperature, the second law of thermodynamics selects the definition of a single preferred, absolute temperature, unique up to an arbitrary scale factor, whence called the thermodynamic temperature.[7][42][60][61][62][63] If internal energy is considered as a function of the volume and entropy of a homogeneous system in thermodynamic equilibrium, thermodynamic absolute temperature appears as the partial derivative of internal energy with respect the entropy at constant volume. Its natural, intrinsic origin or null point is absolute zero at which the entropy of any system is at a minimum. Although this is the lowest absolute temperature described by the model, the third law of thermodynamics postulates that absolute zero cannot be attained by any physical system.
Heat capacity[edit]
When an energy transfer to or from a body is only as heat, the state of the body changes. Depending on the surroundings and the walls separating them from the body, various changes are possible in the body. They include chemical reactions, increase of pressure, increase of temperature and phase change. For each kind of change under specified conditions, the heat capacity is the ratio of the quantity of heat transferred to the magnitude of the change.[64]
For example, if the change is an increase in temperature at constant volume, with no phase change and no chemical change, then the temperature of the body rises and its pressure increases. The quantity of heat transferred, ΔQ, divided by the observed temperature change, ΔT, is the body’s heat capacity at constant volume:
If heat capacity is measured for a well-defined amount of substance, the specific heat is the measure of the heat required to increase the temperature of such a unit quantity by one unit of temperature. For example, raising the temperature of water by one kelvin (equal to one degree Celsius) requires 4186 joules per kilogram (J/kg).
Measurement[edit]
A typical Celsius thermometer measures a winter day temperature of −17 °C
Temperature measurement using modern scientific thermometers and temperature scales goes back at least as far as the early 18th century, when Daniel Gabriel Fahrenheit adapted a thermometer (switching to mercury) and a scale both developed by Ole Christensen Rømer. Fahrenheit’s scale is still in use in the United States for non-scientific applications.
Temperature is measured with thermometers that may be calibrated to a variety of temperature scales. In most of the world (except for Belize, Myanmar, Liberia and the United States), the Celsius scale is used for most temperature measuring purposes. Most scientists measure temperature using the Celsius scale and thermodynamic temperature using the Kelvin scale, which is the Celsius scale offset so that its null point is 0 K = −273.15 °C, or absolute zero. Many engineering fields in the US, notably high-tech and US federal specifications (civil and military), also use the Kelvin and Celsius scales. Other engineering fields in the US also rely upon the Rankine scale (a shifted Fahrenheit scale) when working in thermodynamic-related disciplines such as combustion.
Units[edit]
The basic unit of temperature in the International System of Units (SI) is the kelvin. It has the symbol K.
For everyday applications, it is often convenient to use the Celsius scale, in which 0 °C corresponds very closely to the freezing point of water and 100 °C is its boiling point at sea level. Because liquid droplets commonly exist in clouds at sub-zero temperatures, 0 °C is better defined as the melting point of ice. In this scale, a temperature difference of 1 degree Celsius is the same as a 1kelvin increment, but the scale is offset by the temperature at which ice melts (273.15 K).
By international agreement,[65] until May 2019, the Kelvin and Celsius scales were defined by two fixing points: absolute zero and the triple point of Vienna Standard Mean Ocean Water, which is water specially prepared with a specified blend of hydrogen and oxygen isotopes. Absolute zero was defined as precisely 0 K and −273.15 °C. It is the temperature at which all classical translational motion of the particles comprising matter ceases and they are at complete rest in the classical model. Quantum-mechanically, however, zero-point motion remains and has an associated energy, the zero-point energy. Matter is in its ground state,[66] and contains no thermal energy. The temperatures 273.16 K and 0.01 °C were defined as those of the triple point of water. This definition served the following purposes: it fixed the magnitude of the kelvin as being precisely 1 part in 273.16 parts of the difference between absolute zero and the triple point of water; it established that one kelvin has precisely the same magnitude as one degree on the Celsius scale; and it established the difference between the null points of these scales as being 273.15 K (0 K = −273.15 °C and 273.16 K = 0.01 °C). Since 2019, there has been a new definition based on the Boltzmann constant,[67] but the scales are scarcely changed.
In the United States, the Fahrenheit scale is the most widely used. On this scale the freezing point of water corresponds to 32 °F and the boiling point to 212 °F. The Rankine scale, still used in fields of chemical engineering in the US, is an absolute scale based on the Fahrenheit increment.
Historical scales[edit]
The following temperature scales are in use or have historically been used for measuring temperature:
- Kelvin scale
- Celsius scale
- Fahrenheit scale
- Rankine scale
- Delisle scale
- Newton scale
- Réaumur scale
- Rømer scale
Plasma physics[edit]
The field of plasma physics deals with phenomena of electromagnetic nature that involve very high temperatures. It is customary to express temperature as energy in a unit related to the electronvolt or kiloelectronvolt (eV/kB or keV/kB). The corresponding energy, which is dimensionally distinct from temperature, is then calculated as the product of the Boltzmann constant and temperature, 
Theoretical foundation[edit]
Historically, there are several scientific approaches to the explanation of temperature: the classical thermodynamic description based on macroscopic empirical variables that can be measured in a laboratory; the kinetic theory of gases which relates the macroscopic description to the probability distribution of the energy of motion of gas particles; and a microscopic explanation based on statistical physics and quantum mechanics. In addition, rigorous and purely mathematical treatments have provided an axiomatic approach to classical thermodynamics and temperature.[68] Statistical physics provides a deeper understanding by describing the atomic behavior of matter and derives macroscopic properties from statistical averages of microscopic states, including both classical and quantum states. In the fundamental physical description, the temperature may be measured directly in units of energy. However, in the practical systems of measurement for science, technology, and commerce, such as the modern metric system of units, the macroscopic and the microscopic descriptions are interrelated by the Boltzmann constant, a proportionality factor that scales temperature to the microscopic mean kinetic energy.
The microscopic description in statistical mechanics is based on a model that analyzes a system into its fundamental particles of matter or into a set of classical or quantum-mechanical oscillators and considers the system as a statistical ensemble of microstates. As a collection of classical material particles, the temperature is a measure of the mean energy of motion, called translational kinetic energy, of the particles, whether in solids, liquids, gases, or plasmas. The kinetic energy, a concept of classical mechanics, is half the mass of a particle times its speed squared. In this mechanical interpretation of thermal motion, the kinetic energies of material particles may reside in the velocity of the particles of their translational or vibrational motion or in the inertia of their rotational modes. In monatomic perfect gases and, approximately, in most gas and in simple metals, the temperature is a measure of the mean particle translational kinetic energy, 3/2 kBT. It also determines the probability distribution function of energy. In condensed matter, and particularly in solids, this purely mechanical description is often less useful and the oscillator model provides a better description to account for quantum mechanical phenomena. Temperature determines the statistical occupation of the microstates of the ensemble. The microscopic definition of temperature is only meaningful in the thermodynamic limit, meaning for large ensembles of states or particles, to fulfill the requirements of the statistical model.
Kinetic energy is also considered as a component of thermal energy. The thermal energy may be partitioned into independent components attributed to the degrees of freedom of the particles or to the modes of oscillators in a thermodynamic system. In general, the number of these degrees of freedom that are available for the equipartitioning of energy depends on the temperature, i.e. the energy region of the interactions under consideration. For solids, the thermal energy is associated primarily with the vibrations of its atoms or molecules about their equilibrium position. In an ideal monatomic gas, the kinetic energy is found exclusively in the purely translational motions of the particles. In other systems, vibrational and rotational motions also contribute degrees of freedom.
Kinetic theory of gases[edit]
A theoretical understanding of temperature in a hard-sphere model of a gas can be obtained from the Kinetic theory.
Maxwell and Boltzmann developed a kinetic theory that yields a fundamental understanding of temperature in gases.[69]
This theory also explains the ideal gas law and the observed heat capacity of monatomic (or ‘noble’) gases.[70][71][72]
Plots of pressure vs temperature for three different gas samples extrapolated to absolute zero
The ideal gas law is based on observed empirical relationships between pressure (p), volume (V), and temperature (T), and was recognized long before the kinetic theory of gases was developed (see Boyle’s and Charles’s laws). The ideal gas law states:[73]
where n is the number of moles of gas and R = 8.314462618… J⋅mol−1⋅K−1[74] is the gas constant.
This relationship gives us our first hint that there is an absolute zero on the temperature scale, because it only holds if the temperature is measured on an absolute scale such as Kelvin’s. The ideal gas law allows one to measure temperature on this absolute scale using the gas thermometer. The temperature in kelvins can be defined as the pressure in pascals of one mole of gas in a container of one cubic meter, divided by the gas constant.
Although it is not a particularly convenient device, the gas thermometer provides an essential theoretical basis by which all thermometers can be calibrated. As a practical matter, it is not possible to use a gas thermometer to measure absolute zero temperature since the gases condense into a liquid long before the temperature reaches zero. It is possible, however, to extrapolate to absolute zero by using the ideal gas law, as shown in the figure.
The kinetic theory assumes that pressure is caused by the force associated with individual atoms striking the walls, and that all energy is translational kinetic energy. Using a sophisticated symmetry argument,[75] Boltzmann deduced what is now called the Maxwell–Boltzmann probability distribution function for the velocity of particles in an ideal gas. From that probability distribution function, the average kinetic energy (per particle) of a monatomic ideal gas is[71][76]
where the Boltzmann constant kB is the ideal gas constant divided by the Avogadro number, and 
Zeroth law of thermodynamics[edit]
When two otherwise isolated bodies are connected together by a rigid physical path impermeable to matter, there is the spontaneous transfer of energy as heat from the hotter to the colder of them. Eventually, they reach a state of mutual thermal equilibrium, in which heat transfer has ceased, and the bodies’ respective state variables have settled to become unchanging.[78][79][80]
One statement of the zeroth law of thermodynamics is that if two systems are each in thermal equilibrium with a third system, then they are also in thermal equilibrium with each other.[81][82][83]
This statement helps to define temperature but it does not, by itself, complete the definition. An empirical temperature is a numerical scale for the hotness of a thermodynamic system. Such hotness may be defined as existing on a one-dimensional manifold, stretching between hot and cold. Sometimes the zeroth law is stated to include the existence of a unique universal hotness manifold, and of numerical scales on it, so as to provide a complete definition of empirical temperature.[59] To be suitable for empirical thermometry, a material must have a monotonic relation between hotness and some easily measured state variable, such as pressure or volume, when all other relevant coordinates are fixed. An exceptionally suitable system is the ideal gas, which can provide a temperature scale that matches the absolute Kelvin scale. The Kelvin scale is defined on the basis of the second law of thermodynamics.
Second law of thermodynamics[edit]
As an alternative to considering or defining the zeroth law of thermodynamics, it was the historical development in thermodynamics to define temperature in terms of the second law of thermodynamics which deals with entropy.[citation needed] The second law states that any process will result in either no change or a net increase in the entropy of the universe. This can be understood in terms of probability.
For example, in a series of coin tosses, a perfectly ordered system would be one in which either every toss comes up heads or every toss comes up tails. This means the outcome is always 100% the same result. In contrast, many mixed (disordered) outcomes are possible, and their number increases with each toss. Eventually, the combinations of ~50% heads and ~50% tails dominate, and obtaining an outcome significantly different from 50/50 becomes increasingly unlikely. Thus the system naturally progresses to a state of maximum disorder or entropy.
As temperature governs the transfer of heat between two systems and the universe tends to progress toward a maximum of entropy, it is expected that there is some relationship between temperature and entropy. A heat engine is a device for converting thermal energy into mechanical energy, resulting in the performance of work. An analysis of the Carnot heat engine provides the necessary relationships. According to energy conservation and energy being a state function that does not change over a full cycle, the work from a heat engine over a full cycle is equal to the net heat, i.e. the sum of the heat put into the system at high temperature, qH > 0, and the waste heat given off at the low temperature, qC < 0.[84]
The efficiency is the work divided by the heat input:
-
(4)
where wcy is the work done per cycle. The efficiency depends only on |qC|/qH. Because qC and qH correspond to heat transfer at the temperatures TC and TH, respectively, |qC|/qH should be some function of these temperatures:
-
(5)
Carnot’s theorem states that all reversible engines operating between the same heat reservoirs are equally efficient.[citation needed] Thus, a heat engine operating between T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and T2, and the second between T2 and T3. This can only be the case if
which implies
Since the first function is independent of T2, this temperature must cancel on the right side, meaning f(T1, T3) is of the form g(T1)/g(T3) (i.e. f(T1, T3) = f(T1, T2)f(T2, T3) = g(T1)/g(T2) · g(T2)/g(T3) = g(T1)/g(T3)), where g is a function of a single temperature. A temperature scale can now be chosen with the property that
-
(6)
Substituting (6) back into (4) gives a relationship for the efficiency in terms of temperature:
-
(7)
For TC = 0 K the efficiency is 100% and that efficiency becomes greater than 100% below 0 K. Since an efficiency greater than 100% violates the first law of thermodynamics, this implies that 0 K is the minimum possible temperature. In fact, the lowest temperature ever obtained in a macroscopic system was 20 nK, which was achieved in 1995 at NIST. Subtracting the right hand side of (5) from the middle portion and rearranging gives[21][84]
where the negative sign indicates heat ejected from the system. This relationship suggests the existence of a state function, S, whose change characteristically vanishes for a complete cycle if it is defined by
-
(8)
where the subscript indicates a reversible process. This function corresponds to the entropy of the system, which was described previously. Rearranging (8) gives a formula for temperature in terms of fictive infinitesimal quasi-reversible elements of entropy and heat:
-
(9)
For a constant-volume system where entropy S(E) is a function of its energy E, dE = dqrev and (9) gives
-
(10)
i.e. the reciprocal of the temperature is the rate of increase of entropy with respect to energy at constant volume.
Definition from statistical mechanics[edit]
Statistical mechanics defines temperature based on a system’s fundamental degrees of freedom. Eq.(10) is the defining relation of temperature, where the entropy 
where 
When two systems with different temperatures are put into purely thermal connection, heat will flow from the higher temperature system to the lower temperature one; thermodynamically this is understood by the second law of thermodynamics: The total change in entropy following a transfer of energy 
and is thus positive if 
From the point of view of statistical mechanics, the total number of microstates in the combined system 1 + system 2 is 
Generalized temperature from single-particle statistics[edit]
It is possible to extend the definition of temperature even to systems of few particles, like in a quantum dot. The generalized temperature is obtained by considering time ensembles instead of configuration-space ensembles given in statistical mechanics in the case of thermal and particle exchange between a small system of fermions (N even less than 10) with a single/double-occupancy system. The finite quantum grand canonical ensemble,[85] obtained under the hypothesis of ergodicity and orthodicity,[86] allows expressing the generalized temperature from the ratio of the average time of occupation 

where EF is the Fermi energy. This generalized temperature tends to the ordinary temperature when N goes to infinity.
Negative temperature[edit]
On the empirical temperature scales that are not referenced to absolute zero, a negative temperature is one below the zero-point of the scale used. For example, dry ice has a sublimation temperature of −78.5 °C which is equivalent to −109.3 °F.[88] On the absolute Kelvin scale this temperature is 194.6 K. No body can be brought to exactly 0 K (the temperature of the ideally coldest possible body) by any finite practicable process; this is a consequence of the third law of thermodynamics.[89][90][91]
The international kinetic theory temperature of a body cannot take negative values. The thermodynamic temperature scale, however, is not so constrained.
For a body of matter, there can sometimes be conceptually defined, in terms of microscopic degrees of freedom, namely particle spins, a subsystem, with a temperature other than that of the whole body. When the body is in its own state of internal thermodynamic equilibrium, the temperatures of the whole body and of the subsystem must be the same. The two temperatures can differ when, by work through externally imposed force fields, energy can be transferred to and from the subsystem, separately from the rest of the body; then the whole body is not in its own state of internal thermodynamic equilibrium. There is an upper limit of energy such a spin subsystem can attain.
Considering the subsystem to be in a temporary state of virtual thermodynamic equilibrium, it is possible to obtain a negative temperature on the thermodynamic scale. Thermodynamic temperature is the inverse of the derivative of the subsystem’s entropy with respect to its internal energy. As the subsystem’s internal energy increases, the entropy increases for some range, but eventually attains a maximum value and then begins to decrease as the highest energy states begin to fill. At the point of maximum entropy, the temperature function shows the behavior of a singularity, because the slope of the entropy as a function of energy decreases to zero and then turns negative. As the subsystem’s entropy reaches its maximum, its thermodynamic temperature goes to positive infinity, switching to negative infinity as the slope turns negative. Such negative temperatures are hotter than any positive temperature. Over time, when the subsystem is exposed to the rest of the body, which has a positive temperature, energy is transferred as heat from the negative temperature subsystem to the positive temperature system.[92] The kinetic theory temperature is not defined for such subsystems.
Examples[edit]
| Temperature | Peak emittance wavelength[a] of black-body radiation |
||
|---|---|---|---|
| Kelvin | Celsius | ||
| Absolute zero (precisely by definition) |
0 K | −273.15 °C | Infinity |
| Blackbody temperature of the black hole at the centre of our galaxy, Sagittarius A*[93] |
15 fK | −273.149999999999985 °C | 2.5×108 km (1.7 AU) |
| Lowest temperature achieved[94] |
100 pK | −273.149999999900 °C | 29000 km |
| Coldest Bose–Einstein condensate[b] |
450 pK | −273.14999999955 °C | 6400 km |
| One millikelvin (precisely by definition) |
0.001 K | −273.149 °C | 2.89777 m (radio, FM band)[c] |
| Cosmic microwave background (2013 measurement) |
2.7260 K | −270.424 °C | 0.00106301 m (millimeter-wavelength microwave) |
| Water triple point (precisely by definition) |
273.16 K | 0.01 °C | 10608.3 nm (long-wavelength IR) |
| Water boiling point[A] | 373.1339 K | 99.9839 °C | 7766.03 nm (mid-wavelength IR) |
| Iron melting point | 1811 K | 1538 °C | 1600 nm (far infrared) |
| Incandescent lamp[B] | 2500 K | ≈2200 °C | 1160 nm (near infrared)[C] |
| Sun’s visible surface[D][d] | 5778 K | 5505 °C | 501.5 nm (green-blue light) |
| Lightning bolt channel[E] |
28 kK | 28000 °C | 100 nm (far ultraviolet light) |
| Sun’s core[E] | 16 MK | 16 million °C | 0.18 nm (X-rays) |
| Thermonuclear weapon (peak temperature)[E][e] |
350 MK | 350 million °C | 8.3×10−3 nm (gamma rays) |
| Sandia National Labs’ Z machine[E][f] |
2 GK | 2 billion °C | 1.4×10−3 nm (gamma rays)[F] |
| Core of a high-mass star on its last day[E][g] |
3 GK | 3 billion °C | 1×10−3 nm (gamma rays) |
| Merging binary neutron star system[E][h] |
350 GK | 350 billion °C | 8×10−6 nm (gamma rays) |
| Relativistic Heavy Ion Collider[E][95] |
1 TK | 1 trillion °C | 3×10−6 nm (gamma rays) |
| CERN’s proton vs nucleus collisions[E][96] |
10 TK | 10 trillion °C | 3×10−7 nm (gamma rays) |
- A For Vienna Standard Mean Ocean Water at one standard atmosphere (101.325 kPa) when calibrated strictly per the two-point definition of thermodynamic temperature.
- B The 2500 K value is approximate. The 273.15 K difference between K and °C is rounded to 300 K to avoid false precision in the Celsius value.
- C For a true black-body (which tungsten filaments are not). Tungsten filament emissivity is greater at shorter wavelengths, which makes them appear whiter.
- D Effective photosphere temperature. The 273.15 K difference between K and °C is rounded to 273 K to avoid false precision in the Celsius value.
- E The 273.15 K difference between K and °C is within the precision of these values.
- F For a true black-body (which the plasma was not). The Z machine’s dominant emission originated from 40 MK electrons (soft x-ray emissions) within the plasma.
See also[edit]
- Atmospheric temperature – Physical quantity that expresses hot and cold in the atmosphere
- Body temperature – Ability of an organism to keep its body temperature within certain boundaries (thermoregulation)
- Color temperature – Property of light sources related to black-body radiation
- Dry-bulb temperature – Temperature of air as measured by a thermometer shielded from radiation and moisture
- Thermal conduction – Process by which heat is transferred within an object
- Convective heat transfer – Heat transfer due to combined effects of advection and diffusion
- Instrumental temperature record – In situ measurements that provide the temperature of Earth’s climate system
- ISO 1 – ISO standard temperature, 20°C
- International Temperature Scale of 1990 (ITS-90) – Practical temperature scale
- Laser schlieren deflectometry
- List of cities by average temperature
- Maxwell’s demon – Thought experiment of 1867
- Orders of magnitude (temperature) – Range of temperatures from absolute zero to very high
- Outside air temperature
- Planck temperature – Units defined only by physical constants
- Rankine scale – Absolute temperature scale using Fahrenheit degrees
- Relativistic heat conduction – Model compatible with special relativity
- Satellite temperature measurements – Measurements of atmospheric, land surface or sea temperature by satellites.
- Scale of temperature – Method to measure temperature quantitatively
- Sea surface temperature – Water temperature close to the ocean’s surface
- Stagnation temperature
- Thermal radiation – Electromagnetic radiation generated by the thermal motion of particles
- Thermoception – Temperature stimulus inferred from a heat flux and converted into a molecular signal
- Thermodynamic (absolute) temperature – Measure of absolute temperature
- Thermography – Use of thermograms to study heat distribution in structures or regions
- Thermometer – Device to measure temperature
- Virtual temperature – temperature of dry air parcels that have a total pressure and density equal to a moist parcel of air
- Wet-bulb globe temperature – Type of apparent temperature used to estimate the effect of temperature and other factors on humans
- Wet-bulb temperature – Temperature read by a thermometer covered in water-soaked cloth
Notes and references[edit]
- Notes
- ^ The cited emission wavelengths are for black bodies in equilibrium. CODATA 2006 recommended value of 2.8977685(51)×10−3 m K used for Wien displacement law constant b.
- ^ A temperature of 450 ±80 pK in a Bose–Einstein condensate (BEC) of sodium atoms was achieved in 2003 by researchers at MIT. Citation: Cooling Bose–Einstein Condensates Below 500 Picokelvin, A.E. Leanhardt et al., Science 301, 12 Sept. 2003, p. 1515. It’s noteworthy that this record’s peak emittance black-body wavelength of 6,400 kilometers is roughly the radius of Earth.
- ^ The peak emittance wavelength of 2.89777 m is a frequency of 103.456 MHz
- ^ Measurement was made in 2002 and has an uncertainty of ±3 kelvins. A 1989 measurement Archived 2010-02-11 at the Wayback Machine produced a value of 5,777.0±2.5 K. Citation: Overview of the Sun (Chapter 1 lecture notes on Solar Physics by Division of Theoretical Physics, Dept. of Physical Sciences, University of Helsinki).
- ^ The 350 MK value is the maximum peak fusion fuel temperature in a thermonuclear weapon of the Teller–Ulam configuration (commonly known as a hydrogen bomb). Peak temperatures in Gadget-style fission bomb cores (commonly known as an atomic bomb) are in the range of 50 to 100 MK. Citation: Nuclear Weapons Frequently Asked Questions, 3.2.5 Matter At High Temperatures. Link to relevant Web page. Archived 2007-05-03 at the Wayback Machine All referenced data was compiled from publicly available sources.
- ^ Peak temperature for a bulk quantity of matter was achieved by a pulsed-power machine used in fusion physics experiments. The term bulk quantity draws a distinction from collisions in particle accelerators wherein high temperature applies only to the debris from two subatomic particles or nuclei at any given instant. The >2 GK temperature was achieved over a period of about ten nanoseconds during shot Z1137. In fact, the iron and manganese ions in the plasma averaged 3.58±0.41 GK (309±35 keV) for 3 ns (ns 112 through 115). Ion Viscous Heating in a Magnetohydrodynamically Unstable Z Pinch at Over 2×109 Kelvin, M.G. Haines et al., Physical Review Letters 96 (2006) 075003. Link to Sandia’s news release. Archived 2010-05-30 at the Wayback Machine
- ^ Core temperature of a high–mass (>8–11 solar masses) star after it leaves the main sequence on the Hertzsprung–Russell diagram and begins the alpha process (which lasts one day) of fusing silicon–28 into heavier elements in the following steps: sulfur–32 → argon–36 → calcium–40 → titanium–44 → chromium–48 → iron–52 → nickel–56. Within minutes of finishing the sequence, the star explodes as a Type II supernova. Citation: Stellar Evolution: The Life and Death of Our Luminous Neighbors (by Arthur Holland and Mark Williams of the University of Michigan). Link to Web site Archived 2009-01-16 at the Wayback Machine. More informative links can be found here «Chapter 21 Stellar Explosions». Archived from the original on 2013-04-11. Retrieved 2016-02-08., and here «Trans». Archived from the original on 2011-08-14. Retrieved 2016-02-08., and a concise treatise on stars by NASA is here «NASA — Star». Archived from the original on 2010-10-24. Retrieved 2010-10-12..
«Stellar». Archived from the original on January 16, 2009. Retrieved 2010-10-12.{{cite web}}: CS1 maint: bot: original URL status unknown (link) - ^ Based on a computer model that predicted a peak internal temperature of 30 MeV (350 GK) during the merger of a binary neutron star system (which produces a gamma–ray burst). The neutron stars in the model were 1.2 and 1.6 solar masses respectively, were roughly 20 km in diameter, and were orbiting around their barycenter (common center of mass) at about 390 Hz during the last several milliseconds before they completely merged. The 350 GK portion was a small volume located at the pair’s developing common core and varied from roughly 1 to 7 km across over a time span of around 5 ms. Imagine two city-sized objects of unimaginable density orbiting each other at the same frequency as the G4 musical note (the 28th white key on a piano). It’s also noteworthy that at 350 GK, the average neutron has a vibrational speed of 30% the speed of light and a relativistic mass (m) 5% greater than its rest mass (m0). Torus Formation in Neutron Star Mergers and Well-Localized Short Gamma-Ray Bursts Archived 2017-11-22 at the Wayback Machine, R. Oechslin et al. of Max Planck Institute for Astrophysics. Archived 2005-04-03 at the Wayback Machine, arXiv:astro-ph/0507099 v2, 22 Feb. 2006. An html summary Archived 2010-11-09 at the Wayback Machine.
- Citations
- ^ Agency, International Atomic Energy (1974). Thermal discharges at nuclear power stations: their management and environmental impacts: a report prepared by a group of experts as the result of a panel meeting held in Vienna, 23–27 October 1972. International Atomic Energy Agency.
- ^ Watkinson, John (2001). The Art of Digital Audio. Taylor & Francis. ISBN 978-0-240-51587-8.
- ^ Middleton, W.E.K. (1966), pp. 89–105.
- ^ a b Jaynes, E.T. (1965), pp. 391–398.
- ^ a b Cryogenic Society (2019).
- ^ a b Draft Resolution A «On the revision of the International System of Units (SI)» to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived from the original (PDF) on 2018-04-29, retrieved 2019-10-20
- ^ a b c Truesdell, C.A. (1980), Sections 11 B, 11H, pp. 306–310, 320–332.
- ^ Quinn, T. J. (1983).
- ^ Germer, L.H. (1925). ‘The distribution of initial velocities among thermionic electrons’, Phys. Rev., 25: 795–807. here
- ^ Turvey, K. (1990). ‘Test of validity of Maxwellian statistics for electrons thermionically emitted from an oxide cathode’, European Journal of Physics, 11(1): 51–59. here
- ^ Zeppenfeld, M., Englert, B.G.U., Glöckner, R., Prehn, A., Mielenz, M., Sommer, C., van Buuren, L.D., Motsch, M., Rempe, G. (2012).
- ^ Miller, J. (2013).
- ^ a b de Podesta, M., Underwood, R., Sutton, G., Morantz, P, Harris, P, Mark, D.F., Stuart, F.M., Vargha, G., Machin, M. (2013). A low-uncertainty measurement of the Boltzmann constant, Metrologia, 50 (4): S213–S216, BIPM & IOP Publishing Ltd
- ^ Quinn, T.J. (1983), pp. 98–107.
- ^ Schooley, J.F. (1986), pp. 138–143.
- ^ Quinn, T.J. (1983), pp. 61–83.
- ^ Schooley, J.F. (1986), pp. 115–138.
- ^ Adkins, C.J. (1968/1983), pp. 119–120.
- ^ Buchdahl, H.A. (1966), pp. 137–138.
- ^ Tschoegl, N.W. (2000), p. 88.
- ^ a b Fermi, E. (1956). Thermodynamics. Dover Publications (still in print). p. 48.
eq.(64)
. - ^ Thomson, W. (Lord Kelvin) (1848).
- ^ Thomson, W. (Lord Kelvin) (1851).
- ^ Partington, J.R. (1949), pp. 175–177.
- ^ Roberts, J.K., Miller, A.R. (1928/1960), pp. 321–322.
- ^ Quinn, T.J. (1983). Temperature, Academic Press, London, ISBN 0-12-569680-9, pp. 160–162.
- ^ Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, pp. 47, 57.
- ^ a b c Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, pp. 49, 69.
- ^ a b Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 14–15, 214.
- ^ a b Callen, H.B. (1960/1985), Thermodynamics and an Introduction to Thermostatistics, (first edition 1960), second edition 1985, John Wiley & Sons, New York, ISBN 0-471-86256-8, pp. 146–148.
- ^ Kondepudi, D., Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures, John Wiley, Chichester, ISBN 0-471-97394-7, pp. 115–116.
- ^ Tisza, L. (1966). Generalized Thermodynamics, M.I.T. Press, Cambridge MA, p. 58.
- ^ Milne, E.A. (1929). The effect of collisions on monochromatic radiative equilibrium, Monthly Notices of the Royal Astronomical Society, 88: 493–502.
- ^ Gyarmati, I. (1970). Non-equilibrium Thermodynamics. Field Theory and Variational Principles, translated by E. Gyarmati and W.F. Heinz, Springer, Berlin, pp. 63–66.
- ^ Glansdorff, P., Prigogine, I., (1971). Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley, London, ISBN 0-471-30280-5, pp. 14–16.
- ^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, pp. 133–135.
- ^ Callen, H.B. (1960/1985), Thermodynamics and an Introduction to Thermostatistics, (first edition 1960), second edition 1985, John Wiley & Sons, New York, ISBN 0-471-86256-8, pp. 309–310.
- ^ Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 3. «Thermodynamics by George Hartley Bryan». Archived from the original on 2011-11-18. Retrieved 2011-10-02.
- ^ Pippard, A.B. (1957/1966), p. 18.
- ^ Adkins,C.J. (1968/1983), p. 20.
- ^ Bryan, G.H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications, B.G. Teubner, Leipzig, p. 5: «… when a body is spoken of as growing hotter or colder an increase of temperature is always implied, for the hotness and coldness of a body are qualitative terms which can only refer to temperature.» «Thermodynamics by George Hartley Bryan». Archived from the original on 2011-11-18. Retrieved 2011-10-02.
- ^ a b c d Mach, E. (1900). Die Principien der Wärmelehre. Historisch-kritisch entwickelt, Johann Ambrosius Barth, Leipzig, section 22, pp. 56–57.
- ^ a b Serrin, J. (1986). Chapter 1, ‘An Outline of Thermodynamical Structure’, pp. 3–32, especially p. 6, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.
- ^ Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, p. 32.
- ^ Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 39–40.
- ^ Planck, M. (1897/1903). Treatise on Thermodynamics, translated by A. Ogg, Longmans, Green, London, pp. 1–2.
- ^ Planck, M. (1914), The Theory of Heat Radiation Archived 2011-11-18 at the Wayback Machine, second edition, translated into English by M. Masius, Blakiston’s Son & Co., Philadelphia, reprinted by Kessinger.
- ^ J.S. Dugdale (1996). Entropy and its Physical Interpretation. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5.
- ^ F. Reif (1965). Fundamentals of Statistical and Thermal Physics. McGraw-Hill. p. 102. ISBN 9780070518001.
- ^ M.J. Moran; H.N. Shapiro (2006). «1.6.1». Fundamentals of Engineering Thermodynamics (5 ed.). John Wiley & Sons, Ltd. p. 14. ISBN 978-0-470-03037-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ T.W. Leland, Jr. «Basic Principles of Classical and Statistical Thermodynamics» (PDF). p. 14. Archived (PDF) from the original on 2011-09-28.
Consequently we identify temperature as a driving force which causes something called heat to be transferred.
- ^ Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, pp. 42, 103–117.
- ^ Beattie, J.A., Oppenheim, I. (1979). Principles of Thermodynamics, Elsevier Scientific Publishing Company, Amsterdam, ISBN 978-0-444-41806-7, p. 29.
- ^ Landsberg, P.T. (1961). Thermodynamics with Quantum Statistical Illustrations, Interscience Publishers, New York, p. 17.
- ^ Thomsen, J.S. (1962). «A restatement of the zeroth law of thermodynamics». Am. J. Phys. 30 (4): 294–296. Bibcode:1962AmJPh..30..294T. doi:10.1119/1.1941991.
- ^ Maxwell, J.C. (1872). Theory of Heat, third edition, Longman’s, Green & Co, London, p. 45.
- ^ a b Pitteri, M. (1984). On the axiomatic foundations of temperature, Appendix G6 on pp. 522–544 of Rational Thermodynamics, C. Truesdell, second edition, Springer, New York, ISBN 0-387-90874-9.
- ^ Truesdell, C., Bharatha, S. (1977). The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines, Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer, New York, ISBN 0-387-07971-8, p. 20.
- ^ a b Serrin, J. (1978). The concepts of thermodynamics, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977, edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, ISBN 0-444-85166-6, pp. 411–451.
- ^ Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, London, pp. 155–158.
- ^ Tait, P.G. (1884). Heat, Macmillan, London, Chapter VII, Section 95, pp. 68–69.
- ^ Buchdahl, H.A. (1966), p. 73.
- ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Section 32., pp. 106–108.
- ^ Green, Don; Perry, Robert H. (2008). Perry’s Chemical Engineers’ Handbook, Eighth Edition (8th ed.). McGraw-Hill Education. p. 660. ISBN 978-0071422949.
- ^ The kelvin in the SI Brochure Archived 2007-09-26 at the Wayback Machine
- ^ «Absolute Zero». Calphad.com. Archived from the original on 2011-07-08. Retrieved 2010-09-16.
- ^ Definition agreed by the 26th General Conference on Weights and Measures (CGPM) Archived 2020-10-09 at the Wayback Machine in November 2018, implemented 20 May 2019
- ^ C. Caratheodory (1909). «Untersuchungen über die Grundlagen der Thermodynamik». Mathematische Annalen. 67 (3): 355–386. doi:10.1007/BF01450409. S2CID 118230148.
- ^ Swendsen, Robert (March 2006). «Statistical mechanics of colloids and Boltzmann’s definition of entropy» (PDF). American Journal of Physics. 74 (3): 187–190. Bibcode:2006AmJPh..74..187S. doi:10.1119/1.2174962. S2CID 59471273. Archived from the original (PDF) on 2020-02-28.
- ^ Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley, New York, ISBN 0-471-04600-0, pp. 148–154.
- ^ a b Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. pp. 391–397. ISBN 978-0-7167-1088-2.
- ^ Kondepudi, D.K. (1987). «Microscopic aspects implied by the second law». Foundations of Physics. 17 (7): 713–722. Bibcode:1987FoPh…17..713K. doi:10.1007/BF01889544. S2CID 120576357.
- ^ The Feynman Lectures on Physics. 39–5 The ideal gas law
- ^ «2018 CODATA Value: molar gas constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «Kinetic Theory». galileo.phys.virginia.edu. Archived from the original on 16 July 2017. Retrieved 27 January 2018.
- ^ Tolman, R.C. (1938). The Principles of Statistical Mechanics, Oxford University Press, London, pp. 93, 655.
- ^ Peter Atkins, Julio de Paula (2006). Physical Chemistry (8 ed.). Oxford University Press. p. 9.
- ^ Maxwell, J.C. (1872). Theory of Heat, third edition, Longman’s, Green & Co, London, p. 32.
- ^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 23, «…, if a temperature gradient exists, …, then a flow of heat, …, must occur to achieve a uniform temperature.»
- ^ Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland Publishing Company., Amsterdam, (1st edition 1949) fifth edition 1965, p. 8, «… will gradually adjust themselves until eventually they do reach mutual equilibrium after which there will of course be no further change.»
- ^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 22.
- ^ Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland Publishing Company., Amsterdam, (1st edition 1949) fifth edition 1965, p. 8: «If two systems are both in thermal equilibrium with a third system then they are in thermal equilibrium with each other.»
- ^ Buchdahl, H.A. (1966). The Concepts of Classical Thermodynamics, Cambridge University Press, Cambridge, p. 29: «… if each of two systems is in equilibrium with a third system then they are in equilibrium with each other.»
- ^ a b Planck, M. (1945). Treatise on Thermodynamics. Dover Publications. p. §90 & §137.
eqs.(39), (40), & (65)
. - ^ Prati, E. (2010). «The finite quantum grand canonical ensemble and temperature from single-electron statistics for a mesoscopic device». J. Stat. Mech. 1 (1): P01003. arXiv:1001.2342. Bibcode:2010JSMTE..01..003P. doi:10.1088/1742-5468/2010/01/P01003. S2CID 118339343. arxiv.org Archived 2017-11-22 at the Wayback Machine
- ^ «Archived copy» (PDF). Archived (PDF) from the original on 2014-04-13. Retrieved 2014-04-11.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Prati, E.; et al. (2010). «Measuring the temperature of a mesoscopic electron system by means of single electron statistics». Applied Physics Letters. 96 (11): 113109. arXiv:1002.0037. Bibcode:2010ApPhL..96k3109P. doi:10.1063/1.3365204. S2CID 119209143. Archived from the original on 2016-05-14. Retrieved 2022-03-02. arxiv.org Archived 2017-11-22 at the Wayback Machine
- ^ Water Science School. «Frozen carbon dioxide (dry ice) sublimates directly into a vapor». USGS.
- ^ Guggenheim, E.A. (1967) [1949], Thermodynamics. An Advanced Treatment for Chemists and Physicists (fifth ed.), Amsterdam: North-Holland Publishing Company., p. 157: «It is impossible by any procedure, no matter how idealized, to reduce the temperature of any system to zero temperature in a finite number of finite operations.»
- ^ Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge, page 51: «By no finite series of processes is the absolute zero attainable.«
- ^ Tisza, L. (1966). Generalized Thermodynamics, MIT Press, Cambridge MA, page 96: «It is impossible to reach absolute zero as a result of a finite sequence of operations.»
- ^ Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (2nd ed.). W.H. Freeman Company. p. Appendix E. ISBN 978-0-7167-1088-2.
- ^ This the Hawking Radiation for a Schwarzschild black hole of mass M = 4.145×106 M☉. It is too faint to be observed.
- ^ «World record in low temperatures». Archived from the original on 2009-06-18. Retrieved 2009-05-05.
- ^ Results of research by Stefan Bathe using the PHENIX Archived 2008-11-20 at the Wayback Machine detector on the Relativistic Heavy Ion Collider Archived 2016-03-03 at the Wayback Machine at Brookhaven National Laboratory Archived 2012-06-24 at the Wayback Machine in Upton, New York. Bathe has studied gold-gold, deuteron-gold, and proton-proton collisions to test the theory of quantum chromodynamics, the theory of the strong force that holds atomic nuclei together. Link to news release. Archived 2009-02-11 at the Wayback Machine
- ^ How do physicists study particles? Archived 2007-10-11 at the Wayback Machine by CERN Archived 2012-07-07 at the Wayback Machine.
Bibliography of cited references[edit]
- Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (1st edition 1968), third edition 1983, Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0.
- Buchdahl, H.A. (1966). The Concepts of Classical Thermodynamics, Cambridge University Press, Cambridge.
- Jaynes, E.T. (1965). Gibbs vs Boltzmann entropies, American Journal of Physics, 33(5), 391–398.
- Middleton, W.E.K. (1966). A History of the Thermometer and its Use in Metrology, Johns Hopkins Press, Baltimore.
- Miller, J (2013). «Cooling molecules the optoelectric way». Physics Today. 66 (1): 12–14. Bibcode:2013PhT….66a..12M. doi:10.1063/pt.3.1840. Archived from the original on 2016-05-15. Retrieved 2013-07-25.
- Partington, J.R. (1949). An Advanced Treatise on Physical Chemistry, volume 1, Fundamental Principles. The Properties of Gases, Longmans, Green & Co., London, pp. 175–177.
- Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge UK.
- Quinn, T.J. (1983). Temperature, Academic Press, London, ISBN 0-12-569680-9.
- Schooley, J.F. (1986). Thermometry, CRC Press, Boca Raton, ISBN 0-8493-5833-7.
- Roberts, J.K., Miller, A.R. (1928/1960). Heat and Thermodynamics, (first edition 1928), fifth edition, Blackie & Son Limited, Glasgow.
- Thomson, W. (Lord Kelvin) (1848). On an absolute thermometric scale founded on Carnot’s theory of the motive power of heat, and calculated from Regnault’s observations, Proc. Camb. Phil. Soc. (1843/1863) 1, No. 5: 66–71.
- Thomson, W. (Lord Kelvin) (March 1851). «On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule’s equivalent of a Thermal Unit, and M. Regnault’s Observations on Steam». Transactions of the Royal Society of Edinburgh. XX (part II): 261–268, 289–298.
- Truesdell, C.A. (1980). The Tragicomical History of Thermodynamics, 1822–1854, Springer, New York, ISBN 0-387-90403-4.
- Tschoegl, N.W. (2000). Fundamentals of Equilibrium and Steady-State Thermodynamics, Elsevier, Amsterdam, ISBN 0-444-50426-5.
- Zeppenfeld, M.; Englert, B.G.U.; Glöckner, R.; Prehn, A.; Mielenz, M.; Sommer, C.; van Buuren, L.D.; Motsch, M.; Rempe, G. (2012). «Sysiphus cooling of electrically trapped polyatomic molecules». Nature. 491 (7425): 570–573. arXiv:1208.0046. Bibcode:2012Natur.491..570Z. doi:10.1038/nature11595. PMID 23151480. S2CID 4367940.
Further reading[edit]
- Chang, Hasok (2004). Inventing Temperature: Measurement and Scientific Progress. Oxford: Oxford University Press. ISBN 978-0-19-517127-3.
- Zemansky, Mark Waldo (1964). Temperatures Very Low and Very High. Princeton, NJ: Van Nostrand.
External links[edit]
- Current map of global surface temperatures
Temperature is an objective measurement of how hot or cold an object is. It can be measured with a thermometer or a calorimeter. It is a means of determining the internal energy contained within a given system.
Because humans easily perceive the amount of heat and cold within an area, it is understandable that temperature is a feature of reality that we have a fairly intuitive grasp on. Consider that many of us have our first interaction with a thermometer in the context of medicine, when a doctor (or our parent) uses one to discern our temperature, as part of diagnosing an illness. Indeed, temperature is a critical concept in a wide variety of scientific disciplines, not just medicine.
Heat Versus Temperature
Temperature is different from heat, although the two concepts are linked. Temperature is a measure of the internal energy of a system, while heat is a measure of how energy is transferred from one system (or body) to another, or, how temperatures in one system are raised or lowered by interaction with another. This is roughly described by the kinetic theory, at least for gases and fluids. The kinetic theory explains that the greater the amount of heat is absorbed into a material, the more rapidly the atoms within that material begin to move, and, the faster atoms move, the more the temperature increases. As atoms begin to slow down their movement, the material becomes cooler. Things get a little more complicated for solids, of course, but that’s the basic idea.
Temperature Scales
Several temperature scales exist. In the United States, the Fahrenheit temperature is most commonly used, though the International System of Units (SI unit) Centigrade (or Celsius) is used in most of the rest of the world. The Kelvin scale is used often in physics and is adjusted so that 0 degrees Kelvin is equal to absolute zero, which is, in theory, the coldest possible temperature and at which point all kinetic motion ceases.
Measuring Temperature
A traditional thermometer measures temperature by containing a fluid that expands at a known rate as it gets hotter and contracts as it gets cooler. As the temperature changes, the liquid within a contained tube moves along a scale on the device. As with much of modern science, we can look back to the ancients for the origins of the ideas about how to measure temperature back to the ancients.
In the first century CE, the Greek philosopher and mathematician Hero (or Heron) of Alexandria (10–70 CE) wrote in his work «Pneumatics» about the relationship between temperature and the expansion of air. After the Gutenberg Press was invented, Hero’s book was published in Europe in 1575, its wider availability inspiring the creation of the earliest thermometers throughout the following century.
Inventing the Thermometer
The Italian astronomer Galileo (1564–1642) was one of the first scientists recorded to have actually used a device that measured temperature, though it is unclear whether he actually built it himself or acquired the idea from someone else. He used a device called a thermoscope to measure the amount of heat and cold, at least as early as 1603.
Throughout the 1600s, various scientists tried to create thermometers that measured temperature by a change of pressure within a contained measurement device. English physician Robert Fludd (1574–1637) built a thermoscope in 1638 that had a temperature scale built into the physical structure of the device, resulting in the first thermometer.
Without any centralized system of measurement, each of these scientists developed their own measurement scales, and none of them really caught on until Dutch-German-Polish physicist and inventor Daniel Gabriel Fahrenheit (1686–1736) built his in the early 1700s. He built a thermometer with alcohol in 1709, but it was really his mercury-based thermometer of 1714 that became the gold standard of temperature measurement.
Edited by Anne Marie Helmenstine, Ph.D.
1
a
: degree of hotness or coldness measured on a definite scale
b
: the degree of heat that is natural to the body of a living being
c
: abnormally high body heat
2
a
: relative state of emotional warmth
scandals raised the political temperature
b
: mood
testing the temperature of voters
Example Sentences
Water boils at a temperature of 212°F.
The samples are kept at a constant temperature.
The weatherman predicted unusually low temperatures for the area.
the normal body temperature of 98.6°F
Recent Examples on the Web
But the first-round playing conditions were much nicer than what Thomas and the other competitors will face on Saturday morning, with temperatures in the low 50s and a 60 percent chance of rain.
—
Lithium, or lithium-ion batteries are growing in popularity for their efficiency, high energy storage, and performance in cold and hot temperatures.
—
The pop-up opening is just in time for a potentially sunny Saturday with temperatures in the 50s.
—
Methane alone has caused about 30 percent of the increase in global temperatures since the Industrial Revolution.
—
The weather at the time of the crash was calm, with temperatures near 80 degrees.
—
The summer heat can get intense, with no sea breeze to help cool temperatures.
—
After heavy rain and storms swept through the region Wednesday, the Easter weekend is expected to be calm, sunny and have seasonally cooler temperatures before more warm weather heads in this direction.
—
By measuring how deep the radar penetrates, the team can also learn how salty the ice is, an important factor in its freezing temperature.
—
See More
These examples are programmatically compiled from various online sources to illustrate current usage of the word ‘temperature.’ Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.
Word History
Etymology
borrowed from Latin temperātūra «mixture of substances in proper proportion, adjustment between extremes, mean,» from temperātus, past participle of temperāre «to moderate, bring to a proper strength or consistency by mixing, maintain in a state of balance» + -ūra -ure — more at temper entry 2
First Known Use
1533, in the meaning defined at sense 3
Time Traveler
The first known use of temperature was
in 1533
Dictionary Entries Near temperature
Cite this Entry
“Temperature.” Merriam-Webster.com Dictionary, Merriam-Webster, https://www.merriam-webster.com/dictionary/temperature. Accessed 14 Apr. 2023.
Share
More from Merriam-Webster on temperature
Last Updated:
9 Apr 2023
— Updated example sentences
Subscribe to America’s largest dictionary and get thousands more definitions and advanced search—ad free!
Merriam-Webster unabridged


- Entertainment & Pop Culture
- Geography & Travel
- Health & Medicine
- Lifestyles & Social Issues
- Literature
- Philosophy & Religion
- Politics, Law & Government
- Science
- Sports & Recreation
- Technology
- Visual Arts
- World History
- On This Day in History
- Quizzes
- Podcasts
- Dictionary
- Biographies
- Summaries
- Top Questions
- Infographics
- Demystified
- Lists
- #WTFact
- Companions
- Image Galleries
- Spotlight
- The Forum
- One Good Fact
- Entertainment & Pop Culture
- Geography & Travel
- Health & Medicine
- Lifestyles & Social Issues
- Literature
- Philosophy & Religion
- Politics, Law & Government
- Science
- Sports & Recreation
- Technology
- Visual Arts
- World History
- Britannica Explains
In these videos, Britannica explains a variety of topics and answers frequently asked questions. - Britannica Classics
Check out these retro videos from Encyclopedia Britannica’s archives. - Demystified Videos
In Demystified, Britannica has all the answers to your burning questions. - #WTFact Videos
In #WTFact Britannica shares some of the most bizarre facts we can find. - This Time in History
In these videos, find out what happened this month (or any month!) in history.
- Student Portal
Britannica is the ultimate student resource for key school subjects like history, government, literature, and more. - COVID-19 Portal
While this global health crisis continues to evolve, it can be useful to look to past pandemics to better understand how to respond today. - 100 Women
Britannica celebrates the centennial of the Nineteenth Amendment, highlighting suffragists and history-making politicians. - Saving Earth
Britannica Presents Earth’s To-Do List for the 21st Century. Learn about the major environmental problems facing our planet and what can be done about them! - SpaceNext50
Britannica presents SpaceNext50, From the race to the Moon to space stewardship, we explore a wide range of subjects that feed our curiosity about space!
What is temperature? or How do you measure the temperature? Any idea! In this article, we will learn all about temperature and its measurements along with the definition, meaning, various scales, etc.
Let’s explore!
Temperature Basics
Temperature measurement is significant in food, pharmaceutical, oil, gas, beverage, and power industries. It is critical and needs accuracy to ensure the proper functioning of plants.
Apart from this, temperature measurement is part of almost everything in our everyday lives. From data loggers to probe thermometers and monitoring weather, we cannot neglect its importance.
- It is needed in hospitals as well for calculating body temperatures.
- It is recorded on devices called thermometers.

Temperature Meaning
The term comes from the Greek words “thermos” (meaning hot) and “metron” (meaning measure). There are various types of thermometers constructed uniquely and are based on specific working principles.
Several different temperature measuring methods are devised for recording temperature on devices like thermometers or sensors.
Temperature Definition
Temperature is defined as the extent of hotness or coldness of a body expressed on a definite scale.
- It’s a scalar physical quantity that indicates heat flow from a hotter body to a colder body.
- Temperature is an intensive property (which means not dependent on the quantity of matter in consideration).
Scales of Temperature
If you want temperature measurements, you should know the different scales of temperature. The most popular temperature scales or temperature units are discussed below.
Fahrenheit
It is used in the United States and some other English-speaking countries. It was invented by an 18th-century German Physicist named Daniel Gabriel Fahrenheit in 1724.
- At that time, he selected the values of 30 for the freezing point of water and 90 for normal body temperature.
- They were changed to 32 and 96 later on.
- However, the latter value was revised to 98.6. The interval between two values is divided into 180 equal parts.
- Fahrenheit is represented as °F.
The conversion of temperature in Celsius or centigrade to Fahrenheit needs the following conversion formula:
°F = (9/5 × °C) + 32
Fahrenheit temperature unit was common in all English-speaking countries during the 1970s, but later on, many countries adopted the Celsius scale.
Celsius
Celsius scale, also called the centigrade scale, was invented in 1742 by Anders Celsius, a Swedish Astronomer. Celsius temperature unit is adopted for everyday use in almost all countries and is widely used in sciences also.
- It is a derived unit in the SI.
- The scale is divided into hundred equal parts. It is based on 0° and 100°, the freezing point and boiling point of water, respectively.
- In the beginning, Celsius used 0° to represent boiling point and 100° for representing the freezing point of water, but now it’s reversed.
- Celsius is represented as °C.
The conversion formula for converting temperature in Fahrenheit to Celsius is:
°C = 5/9 (°F − 32)
Kelvin
Kelvin is the base unit of thermodynamics in the International System of Units for the measurements of temperature.
- It is a standard scientific measurement scale.
- The representation for Kelvin is “K.”
- The final zero i-e zero points of the Kelvin scale is equal to −273.15° on the Celsius temperature scale and −459.67°on on the Fahrenheit temperature scale.
- Absolute zero is the theoretical temperature at which the molecules of a substance have the lowest energy; therefore, all the values on this scale are positive.
Kelvin and Celsius degrees have the same magnitudes because the difference between boiling and freezing points of water is 100 degrees on both scales.
Kelvin scale is the international standard scale for the measurement of temperature. It was invented by Lord Kelvin.
Rankine
Rankine is represented as °R or °Ra. William Rankine invented it in 1859. The reference point is 0°R. The size of one Rankine degree is the same as Fahrenheit. The freezing point of water according to this scale is 491.67°R.
This temperature unit was used in some technology fields in the USA, but NIST doesn’t recommend it, so it is not widely used nowadays.
Reaumur
Reaumur is represented as °Ré or °Re. It was first introduced in 1730 by Réne de Réaumur.
- The scale is based on two points, 0°Re and 80°Re, representing freezing and boiling water points, respectively.
- It was used in Europe and Russia during a period, but it lost its importance in the last century.
Measurements of Temperature
There are four major types of temperature measuring devices. They use different temperature measuring methods based on their working principle. The devices are:
- Mechanical devices
- Thermojunctive devices
- Thermoresistive devices
- Radiative devices
We will learn all devices one by one to clear our basic concept on temperature measurements.
Mechanical Devices for Temperature Measurements
They include liquid-in-glass thermometers, bimetallic strips, pressure, sealed bellows, and bulb and capillary sensors.
Working principle
They are based on the principle of mechanical motion. Whenever heat is given to a substance, it expands. The value of temperature is then recorded from the scale on the instrument. Mechanical devices may consist of liquid, solid, or vapors as temperature-sensitive matter.
Liquid-in Glass Thermometers
Construction
It constitutes:
- A bulb acts as the container for the liquid in the thermometer.
- A glass tube with a small capillary connected to the bulb.
- A temperature scale for recording values.
- Point of reference or calibration point present right above the bulb. It represents the ice point.
- A temperature-sensitive liquid, either mercury or any other alcohol substance.
- An inert gas is filled above the mercury. It may be argon or nitrogen.
Working
- The working principle is heat causes expansion.
- An increase in temperature will cause the liquid to rise.
- The liquid, either mercury or any other alcohol substance, moves up the tube.
- Temperature is recorded through the scale present on the instrument.
Advantages
- It is cost-effective.
- It is handy to use.
- They do not need the power supply for charging like the electrical thermometers.
- Their repeatability is good, and the calibration stays unaffected.
Applications
- They are widely used in medicine, metrology, and industry.
- They have oceanographic applications too.
- They are employed in different configurations in the navy and marine corps.
- They are also used in households.
Limitations
- They are not effective in being used at very high and low temperatures.
- They don’t provide highly accurate results.
- They are delicate, so it needs a lot of care to handle them as they may break.
- The results provided are not digital (as in electrical thermometers); therefore, they are limited to households.
- The temperature measured must be recorded right away because it is affected by environmental conditions like temperature.
- Human eyes record readings, so it needs concentration and good eyesight.
- The temperature can only be recorded in Fahrenheit or Celsius. Conversion is needed if the temperature is required in other scales.
- Temperatures ranging between -200 and 600 degrees Celsius can be calculated using liquid-in-glass thermometers.
Bimetallic strip thermometers
Let’s see the construction, working, advantages, applications, limitations of Bimetalluic strip thermometers.

Construction
- It has two metallic strips. Both are made of different metals.
- The working of bimetallic strip thermometers is based upon thermal expansion properties and the coefficient of thermal expansion of metals.
- One metal has a smaller coefficient of thermal expansion than the other.
- Both the strips are fixed at one end and free at the other end.
- Different metals such as steel and invar, steel and copper, steel and brass, etc., are coupled together.
Working
Let’s see the basic working principle,

- It works by converting the temperature change into mechanical displacement.
- The working of bimetallic strip thermometers is based upon thermal expansion properties and the coefficient of thermal expansion of metals.
- When temperature increases, one strip will expand more than the other, causing the pair to bend towards the free end. The strip will bend towards the direction of the metal, having a smaller coefficient of temperature.
- When the temperature decreases, the strip bends in the direction of metal with a high-temperature coefficient.
- The bending motion is connected to a thermometer dial.
Advantages
- They don’t need a power supply.
- They are cheaper.
- They are simple and durable.
- They are based on robust design.
- It is utilized for a wide range of temperatures.
- They give a linear response to a change in temperature.
- Maintenance and installation are quick and easy.
- They don’t need a power source to operate.
Applications
- They are used as wood burner thermometers or oven thermometers.
- They are widely used in thermostats of air conditioners.
- They are used in industrial devices like heaters, hot wires, and refineries.
- They are used in control devices and oil burners also.
Limitations
- They are not suitable for very low and very high-temperature measurements. The temperature range is 40-80 °F.
- They are less accurate.
- Due to manual reading, they are best to be used at homes only.
- They require frequent calibration.
- If they are handled roughly, calibration gets disturbed.
Pressure Thermometers
Let’s see the construction, working, advantages, applications, limitations of pressure thermometers.

Construction
It consists of:
- A bulb (connected to measuring device by a capillary tube)
- A capillary tube
- Bourdon tube (made of a hardened chromium-molybdenum alloyed steel)
- Arrangement for measuring (calibrated scale with a pointer)
- Linking and gearing mechanism
Working
- Pressure thermometers work on the principle of thermal expansion.
- Temperature measurement takes place indirectly by measuring pressure.
- Instead of liquid or solid, it works by the expansion of a gas. However, some use liquid also instead of gas.
- The bulb is introduced into a medium whose temperature needs to be measured.
- Now, The pressure in the bulb increases or decreases due to the difference in medium and environment’s temperature.
- The pressure change is transmitted to the bourdon tube, which happens through the capillary tube.
- The pointer changes position on the calibration scale. This pressure change is used to indicate the temperature change.
Advantages
- They are simple to use, and the readings can be directly recorded.
- They are not costly.
- Capillary tubes up to 60m can be used.
- They operate successfully and have a high accuracy
- They are sensitive and don’t need much maintenance.
Applications
- They are used in industrial equipment, boilers, compressors, piping, etc.
- They are also used in finding the outside temperature from inside of the building.
Limitations
- They have limited linearity, and there are more chances for errors.
- Sometimes the bulb is too large to fit in the space.
- The maximum temperature is way too limited as compared to electrical thermometers.
- Calibration drift and error caused due to filling the tube.
- The temperature range is limited. Usually -80 to 400 °C.
Thermo-Junction Devices or Thermocouples
Construction
- They are constructed by joining two different metals together that produce a voltage with a temperature change.
- Any two dissimilar metals can be used to construct thermocouples.
- While selecting two materials, an important factor is a thermoelectric difference between the two materials.
- The junction of two metals is termed a sensing junction.
Working
- When metals are connected, voltage is generated at the junction. This voltage is called thermos junction voltage. This effect is known as the “Peltier Effect.”
- When the temperature changes at the junction, the voltage also changes. It is measured by the input circuits of the electronic controller in thermocouples.
- The output voltage is proportional to the temperature difference between free terminals and junctions. It is called the “Thompson Effect.”
- The voltage is measured when the reference junction is kept at a known temperature. At this time, the temperature at the sensing junction is deduced.
- The generated voltage is proportional to the difference in temperatures. This combined effect is known as the “Seebeck Effect or Thermo-junction Effect.”
Advantages
- The readings are consistent.
- They are capable of measuring a wide range of temperatures.
- They have linearity.
- They have an accuracy of 0.05%.
- They are inexpensive and constructed easily.
- They function in a broad range of temperatures and can be inserted in difficult points.
Applications
- Kilns and autoclaves use thermocouples.
- They are used for controlling the temperatures of space crafts, airplanes, and satellites.
- Many thermocouples connected create a thermopile. It produces a large amount of voltage as compared to a single thermocouple.
- Thermopiles can be used for the detection of infrared radiations.
- Thermopiles can also generate power for space probes.
Limitations
- They have low sensitivity as compared to RTDs and thermistors.
- At room temperature, the output of thermocouples is as low as 0.001 volts.
- There are different types of thermocouples. Each of them has its formulas for the conversion of voltage into temperature. These equations are quite complex.
- They are subjected to corrosion due to contact of two dissimilar metals, which can affect calibration and accuracy.
- They require maintenance for good long-term performance.
Thermo-Resistance Temperature Measuring Devices
Thermo-resistive temperature measuring devices include RTDs (resistance temperature detectors) and thermistors.
Resistance Temperature Detectors
Let’s see the basics of resistance temperature detectors along with construction, working, application, advantages, limitations.

Construction
- It is made of a small or long diameter wire wound on an etched grid or a coil on a substrate, just like a strain gage.
- The most common type of metals used in RTDs is BALCO wire, copper, or platinum.
- The bridge circuit consists of three known resistances R1, R2, AND R3 (variable), an unknown variable resistor, a voltage source, and an ammeter in RTDs.
- There is another type of construction known as Wheatstone bridge circuit or two-wire RTD bridge circuit. It is a quarter bridge circuit.
Working
- It is based on the principle that electrical resistance changes linearly with a temperature change.
- They have a positive temperature coefficient.
- The element at base temperature has resistance directly proportional to the length of the element and inversely proportional to the cross-section area.
- An electrical circuit is present that calculates the change in RTD resistance, which is used to calculate the temperature change.
- Resistance of RTD rises with a temperature rise.
Advantages
- They have a linear resistance to temperature.
- They are stable.
- They can perform well over a wide range of temperatures.
- Their accuracy and stability are replacing thermocouples.
- They have high repeatability.
- They have high precision and are mostly used instead of thermocouples in a temperature range up to 600 °C.
Applications
- They are widely used for sensing liquid and air temperature in ducts and pipes.
- They are also used in power electronics, consumer electronics, medical electronics, food handling, processing, etc.
- RTD sensors can measure the engine temperature.
- They have applications in the military, aerospace, and computer also.
- They are present in appliances like coffee machines and cell phones.
Limitations
- They are vulnerable to self-heating.
- They are not very responsive.
- An external circuit power is required to operate.
- Lead wires connecting RTD to the controller can add up to the total resistance of connected RTD. It can cause errors and inaccuracy in temperature measurement.
- They can function at a temperature ranging from -200 to 600 °C. Above this range, It is not the best fit.
- Installation of RTDs is complex and requires experience.
- It is costly as compared to thermocouples.
- It’s difficult to insert thin film RTD elements in small diameter MI cables.
Thermistors
Thermistors are semiconductors that undergo a greater change in resistance over a small range of temperature. It has two types; Positive temperature coefficient (PTC) and Negative temperature coefficient (NTC). NTCs are more commonly used for the measurement of temperature. Temperature and resistance are proportional in PTC and inversely proportional in NTC.
Construction
- Thermal resistors or thermistors are similar to RTDs, but instead of metal, a semiconductor is used.
- They are made up of oxides like manganese oxide, nickel oxide, cobalt oxide, copper oxide, titanium oxide, lithium oxide, etc.
- These oxides are combined in specific proportions.
- They are compressed into required shapes. They are recrystallized by treating them with heat. They are formed into dense ceramic bodies with specific resistance temperature characteristics.
- They come in several sizes and shapes like bead type, disc type, and rod type.
- When greater power dissipation is required, the best options are rod type and disc type.
- Bead type is the smallest in configuration among all. It has a diameter of 0.15mm.
Working
- It is based on the principle of varying resistance due to temperature.
- An ohmmeter calculates the resistance. It is linked in series with the battery and the meter.
- The change in resistance is dependent upon the material used in the construction of the thermistor.
- Thermistors are known to be resistors that limit the amount of current in the circuit. But since it’s a thermal resistor, the change in resistance depends on the temperature change.
- Its temperature rises, the resistance of these resistors decreases in the circuit, which is dependent on the coefficient of temperature.
Advantages
- They are more sensitive than RTDs.
- They have high stability and are responsive.
- They are compact and cheap.
- Its main purpose is to maintain the amount of resistance in the circuit to minimize the effects of temperature.
- They can function over a small range of temperatures.
- They are smaller in size and fit in even the small areas.
- They are compatible with many devices because of the two-wired connection.
- They are easy to use and can be customized.
Limitations
- They cannot be used for high-temperature measurement. The maximum range is 100 or 200 °C sometimes.
- The excitation current is low to avoid self-heating.
- Shielded power lines are filters that will be needed due to high resistance.
- Resistance vs. temperature characteristics has non-linearity.
Applications
- In digital thermometers, they can be used as temperature sensors.
- They are used in automotive industries to check the temperature of coolant and oil in vehicles and trucks.
- It is used in household appliances.
- They are circuit protection devices.
- Thermistors are utilized in circuits of Wheatstone bridge, rechargeable batteries, and electrical devices, etc.
Radiative Temperature Measuring Devices
They include two types of devices; infrared pyrometers and optical pyrometers.
Infrared Pyrometers
If I ask you, what kind of instrument is widely used for temperature measurements of objects? Simple! Infrared pyrometers!
They are non-contact temperature sensors that are used to measure the temperature of objects.
Working principle
It is based on the principle that the amount of energy emitted by objects is the function of their temperature. It measures the temperature by determining the intensity of energy given off by the body.
Advantages
- They don’t make contact with the measuring body, unlike other devices.
- They are useful when the target is inaccessible or too hot that it can damage the instruments.
- They are a good option for surface measurements.
- They are compact and lightweight.
- There is no need to shut down systems for performing diagnoses.
- They are suitable for industry or regulatory requirements.
Applications
- They are suitable for measuring the high temperature inside combustion chambers of gas turbines.
- They are used in salt bath furnaces.
- A hot air balloon has an infrared pyrometer inserted at the top to avoid overheating of fabric.
- They are also present in steam boilers.
Limitations
- They are only used for solid objects, not gas or liquid.
- They are quite expensive.
- Accuracy also varies, depending on the model.
Optical Pyrometers
If I ask you, what kind of instrument is widely used for high temperature measurements? Simple! Optical pyrometers!
They are beneficial in measuring very high temperatures (even flames).
Working principle
They use infrared radiation-sensitive sensors like photoresistors or photodiodes to compare the unknown radiation with the radiation from an internal incandescent source.
Advantages
- They are sensitive to infrared radiation.
- It has higher accuracy.
- Quite useful in high temperatures
- They measure temperature without contact with the object.
- They are used for measuring the temperature of moving and distant bodies.
- It has good accuracy and is lightweight.
Applications
- They are utilized in the smelter industry and metallurgical furnace operations.
- The combustion temperature can be measured in a blast furnace by optical pyrometers.
- They are fitted in gas turbine engines to measure the temperature of turbine blades.
Limitations
- Smoke and dust can affect accuracy.
- It is costly.
- There are more chances of human errors.
- They are not fit for measuring the temperature of clean gases burning and do not radiate visible energy.
High Rated Course
Fundamentals of Heat Transfer Part 1
Fundamentals of Heat Transfer Part 2
Advanced Heat Transfer: Heat Exchangers
Advanced Heat Transfer: Thermal Radiation
Heat Exchangers: Principles, Operation and Design
Conclusion
Hence, we have got a detailed understanding of what is temperature, its measurements, types, various measuring scales, etc.
Any questions, please let us know!
Refer to our most viewed articles,
What is thermodynamics
Intensitve & Extensive Properties
What is Pressure
Bernoulli’s theorem
Venturi meter
Pump basics
Globe valve
Siphon
Reference Articles
Meaning temperature
What does temperature mean? Here you find 137 meanings of the word temperature. You can also add a definition of temperature yourself
1 |
2 The temperature is the specific degree of hotness or coldness of the body. It is usually measured with a thermometer.
|
2 |
1 temperatureTemperature is defined as the measure of the average speed of atoms and molecules. The higher the temperature the faster they move.
|
3 |
1 temperatureTemperature is an intensive property associated with the hotness or coldness of an object. It determines the direction of spontaneous heat flow (always from hot to cold).
|
4 |
1 temperature(Abbrev. TEMP)- The temperature is a measure of the internal energy that a substance contains. This is the most measured quantity in the atmosphere.
|
5 |
1 temperatureDegree of hotness or coldness measured on one of several arbitrary scales based on some observable phenomenon (such as the expansion).
|
6 |
1 temperaturea measurement of how hot or cold something is. • temperature is measured with a thermometer. • temperature is measured in degrees. • two common temperature scales are the Celsius scale (ºC) and [..]
|
7 |
1 temperatureThe degree of hotness or coldness of a substance as measured by a thermometer. It is also a measure of the average speed or kinetic energy of the atoms and molecules in a substance.
|
8 |
1 temperaturedegree of hotness or coldness measured by a thermometer with a numerical scale. Read more in the NG Education Encyclopedia
|
9 |
1 temperatureA physical quantity characterising the mean random motion of molecules in a physical body.
|
10 |
1 temperatureA measure of the amount of heat energy in a substance, such as air, a star, or the human body. Because heat energy corresponds to motions and vibrations of molecules, temperature provides information [..]
|
11 |
1 temperatureforecasted average temperature for each player’s Thursday/Friday tee time
|
12 |
0 temperatureThe degree of hotness or coldness on a definite scale by means of a thermometer.
|
13 |
0 temperaturehow hot or cold something is. It is measured in degrees
|
14 |
0 temperatureA measure of the amount of heat energy in a substance, such as air, a star, or the human body. Because heat energy corresponds to motions and vibrations of molecules, temperature provides information [..]
|
15 |
0 temperatureThis refers to the intensity of heat occurring in a baked product, mixture, or oven. In the United States, temperature is measured in degrees Fahrenheit, although the Celsius scale is used in much of [..]
|
16 |
0 temperaturePhysical parameter characterising the thermal state of a body. Measured in units of degrees Celsius (oC), Fahrenheit (oF) or Kelvin (K).
|
17 |
0 temperatureUse Celsius: 37°C
|
18 |
0 temperaturetemperatur
|
19 |
0 temperatureAn important environmental factor affecting the condition of library collections. Paper and other materials used in the production of books expand and contract with changes in temperature, sometimes a [..]
|
20 |
0 temperatureThe temperature is the specific degree of hotness or coldness of the body. It is usually measured with a thermometer.
|
21 |
0 temperatureHow hot one body is when compared to another.
|
22 |
0 temperatureDegree of warmth or coldness in relation to an arbitrary zero measured on one or more of accepted scales, as Centigrade, Fahrenheit, etc.
|
23 |
0 temperature1) Temperature above the critical phase transformation range at which castings are held as a part of the heat treatment cycle, 2) The temperature maintained when metal is held in a furnace, usually pr [..]
|
24 |
0 temperatureThe temperature of the metal as it is poured into the mold.
|
25 |
0 temperatureTemperature is the measure of the average kinetic energy of the particles in a substance, which is related to how hot or cold that substance is.
|
26 |
0 temperatureThe measure of the average energy of motion of the particles of a substance.
|
27 |
0 temperatureA measure of the average kinetic energy of the molecules in a sample.
|
28 |
0 temperatureThe measure of the intensity of heat that a substance possesses.
|
29 |
0 temperatureWhat a thermometer measures. Temperature is the average kinetic energy per molecule.
|
30 |
0 temperatureWatch Here for definition or Call The BaggingGuys today!
|
31 |
0 temperaturemeasure of how hot or cold something is; measure of the average kinetic energy of the particles in an object. temperature inversion —
|
32 |
0 temperatureA degree of hotness or coldness that can be measured using a thermometer. Also a measure of how fast the atoms and molecules of a substance are moving (see Kinetic energy). Temperature is measured in [..]
|
33 |
0 temperatureA measure of how fast the particles of a substance are moving (fast movement has higher temperatures, slow movement has lower temperatures).
|
34 |
0 temperatureThe physical quantity that is proportional to the average kinetic energy of translation of particles in matter.
|
35 |
0 temperatureIt is a numerical measure of hotness or coldness of a body. According to the molecular model, it is a measure of the average kinetic energy of the molecules of the body. Heat flows from a body at high [..]
|
36 |
0 temperatureamount of heat measured in a body; higher than normal temperature
|
37 |
0 temperatureA SI quantity, measured in kelvin (K).
|
38 |
0 temperaturea critical measurement for ensuring the safety and quality of many food products.
|
39 |
0 temperature(n) the degree of hotness or coldness of a body or environment (corresponding to its molecular activity)(n) the somatic sensation of cold or heat
|
40 |
0 temperatureA measure of how hot or cold something is when it is compared to a reference point (Lesson 19)
|
41 |
0 temperatureThe degree of hotness or coldness of a body or an environment.
|
42 |
0 temperaturea measure of the atomic and molecular vibration in a substance, in degrees. The response of a solid, liquid, or gas to the input or removal of heat energy.
|
43 |
0 temperatureA measure of the warmth or coldness of an object or substance with reference to a standard value.
|
44 |
0 temperatureis the fundamental thermodynamical quantity that is a measure of thermal energy such as the average kinetic energy of molecular vibrations. There are three temperature scales-Celsuis/Centigrade, Farenheit, and Kelvin-all defined in this glossary that are used to measure the coldness/hotness of water.
|
45 |
0 temperatureMeasure of how hot or cold it is in an area.
|
46 |
0 temperatureA measurement of heat intensity.
|
47 |
0 temperatureThe sea surface temperature at the wave monitoring buoy, in degrees Celsius.
|
48 |
0 temperatureA measurement of heat intensity.
|
49 |
0 temperatureDegree of hotness or coldness of an object or location measured on a definite scale.
|
50 |
0 temperatureThe temperature of the medium, such as air,water or earth, into which the heat of the equipment is dissipated. For self ventilated equipment, the ambient temperature is the average temperature of the air in the immediate neighborhood of the equipment. For the air or gas cooled equipment with forced ventilation or secondary water cooling, the am [..]
|
51 |
0 temperaturea measurement of heat intensity.
|
52 |
0 temperaturetemperature of the air surrounding the object under construction or test.
|
53 |
0 temperaturethe temperature to which an adhesive or an assembly is subjected to cure the adhesive (See also temperature, drying and temperature, setting) Note: The temperature attained by the adhesive in the proc [..]
|
54 |
0 temperaturethe temperature to which an adhesive on an adherend or in an assembly or the assembly itself is subjected to dry the adhesive. (See also temperature, curing, and temperature, drying)
|
55 |
0 temperaturethe temperature to which an adhesive or an assembly is subjected to set the adhesive (See also temperature, curing and temperature, drying)
|
56 |
0 temperatureA measure of thermal energy.*
|
57 |
0 temperatureThe measure of intensity and quality of heat.
|
58 |
0 temperatureThe measurement of heat.
|
59 |
0 temperatureIn meteorological terms, temperature refers to the degree of heat or cold of the air as measured by a thermometer.
|
60 |
0 temperatureThe measure of the kinetic energy present in a system.
|
61 |
0 temperaturemeasure of the hotness or coldness of a body.
|
62 |
0 temperatureThe measure of the intensity of heat that a substance possesses.
|
63 |
0 temperatureThe measure of heat matter contains.
|
64 |
0 temperatureThe measure of the intensity of heat that a substance possesses.
|
65 |
0 temperatureThe temperature as read on a standard thermometer.
|
66 |
0 temperatureWet-bulb temperature is the temperature indicated by a wet-bulb thermometer constructed and used according to specification. Wet-bulb temperature will always be less than dry-bulb temperature, except [..]
|
67 |
0 temperatureThe temperature at which the condensation of water vapor in space begins for a given state of humidity and pressure as the temperature of the vapor is reduced. Simply stated, it is the temperature at [..]
|
68 |
0 temperatureThe measurement of heat energy within a body or substance. There are two common scales used to measure temperature, Centigrade & Fahrenheit. The Centigrade scale (also commonly referred to as Celsius) is widely used internationally while the Fahrenheit scale is commonly used in the United States.
|
69 |
0 temperatureA physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as war [..]
|
70 |
0 temperatureA variable indicating the energy which is present inside a body.
|
71 |
0 temperatureThe property of objects that determines the direction of Heat flow when they are placed in direct thermal contact. The temperature is the energy of microscopic Motions (vibrational and translational) [..]
|
72 |
0 temperatureThe measure of the level of Heat of a Human or Animal.
|
73 |
0 temperatureAn absence of warmth or Heat or a Temperature notably below an accustomed norm.
|
74 |
0 temperaturePresence of warmth or Heat or a Temperature notably higher than an accustomed norm.
|
75 |
0 temperatureThe Temperature at the outer surface of the body.
|
76 |
0 temperatureThe Temperature at which a substance changes from one state or conformation of matter to another.
|
77 |
0 temperatureA measure of the energy in a substance. The more heat energy in the substance, the higher the temperature. The Earth receives only one two-billionth of the energy the sun produces. Much of the energy [..]
|
78 |
0 temperatureLevel of done-ness a protein should be cooked to, e.g. medium rare.
|
79 |
0 temperatureof water will affect the efficiency of water treatment processes. Low temperature decreases efficiency of treatment processes and high temperatures enhance the growth of nuisance organisms. This makes [..]
|
80 |
0 temperaturea critical measurement for ensuring the safety and quality of many food products.
|
81 |
0 temperatureTemperature is defined as the measure of the average speed of atoms and molecules. The higher the temperature the faster they move.
|
82 |
0 temperatureThe temperature of air or gas measured from absolute zero. It is the Fahrenheit temperature plus 459.6 and is known as the Rankine temperature. In the metric system, the absolute temperature is the Ce [..]
|
83 |
0 temperatureSee Critical Temperature.
|
84 |
0 temperatureThe total temperature at the discharge connection of the compressor.
|
85 |
0 temperatureThe total temperature at the inlet connection of the compressor.
|
86 |
0 temperatureThe actual temperature of a moving gas stream. It is the temperature indicated by a thermometer moving in the stream and at the same velocity.
|
87 |
0 temperatureThe temperature which would be measured at the stagnation point if a gas stream were stopped, with adiabatic compression from the flow condition to the stagnation pressure.
|
88 |
0 temperatureDegree of hotness or coldness as measured by a thermometer; measurement of speed of motion of molecules.
|
89 |
0 temperatureA measure of the warmth of the ambient air measured by a suitable instrument such as a thermometer.
|
90 |
0 temperatureThe measure of the intensity of heat that a substance possesses.
|
91 |
0 temperatureThe measure of the intensity of heat that a substance possesses.
|
92 |
0 temperatureA measure of heat intensity. The most common scales to measure heat intensity are Fahrenheit and Centigrade. Two scientific scales are Rankine and Kelvin.
|
93 |
0 temperatureThe degree of hotness or coldness as measured on some definite temperature scale.
|
94 |
0 temperatureIn general, the degree of hotness or coldness as measured on some definite temperature scale by means of any of various types of thermometers.
|
95 |
0 temperatureA measurement of the average kinetic energy in a sample (how fast molecules are vibrating).
|
96 |
0 temperature(Abbrev. TEMP)- The temperature is a measure of the internal energy that a substance contains. This is the most measured quantity in the atmosphere.
|
97 |
0 temperatureEquilibrium temperature of water evaporating into air when the latent heat of vaporization is supplied by the sensible heat of air.
|
98 |
0 temperatureDegree of hotness or coldness as measured by a thermometer; measurement of speed of motion of molecules.
|
99 |
0 temperatureTemperature is a measure of the warmth or coldness of an object or substance with reference to a standard value. It can be measured in Kelvin (K), Fahrenheit (F), or Celsius (C).
|
100 |
0 temperatureA measurement related to the amount of kinetic energy within a material or substance. The greater the kinetic energy, the higher the temperature.
|
101 |
0 temperatureThe temperature is a measure of the internal energy that a substance contains. This measure of the internal energy that a substance contains. This is the most measured quantity in the atmosphere. Dewpoint
|
102 |
0 temperatureA measure of the amount of heat energy in a substance, such as air, a star, or the human body. Because heat energy corresponds to motions and vibrations of molecules, temperature provides information about the amount of molecular motion occurring in a substance.
|
103 |
0 temperatureThe intensity of heat in a mixture, baked product, or oven; measured in degrees Fahrenheit (°F) in home baking in the United States.
|
104 |
0 temperatureA measure of heat in an object. It is a physical quantity characterising the random motion of molecules within a body. The most common scale is the Celsius scale with 0°C the freezing point of water at sea level. This corresponds to 273.15 K in the Kelvin scale which has its zero at absolute zero, the lowest physically possible temperature.
|
105 |
0 temperatureDegree of the warmth or coolness of the air.
|
106 |
0 temperatureTemperature is a measure of the heat content of a body (the atmosphere in the case of weather). The molecular motion of a substance creates energy, which can be measured in terms of the heat it generates. Air, water, and soil can all be measured for temperature.
|
107 |
0 temperatureThe heat content of the air.
|
108 |
0 temperatureA measure of the degree of heat in a substance.
|
109 |
0 temperatureA measure of the average kinetic energy of the individual atoms or molecules composing a substance.
|
110 |
0 temperatureThe measure of molecular motion or the degree of heat of a substance. It is measured on an arbitrary scale from absolute zero, where the molecules theoretically stop moving. It is also the degree of h [..]
|
111 |
0 temperaturea measure of the warmth or coldness of an object or substance with reference to a standard value.
|
112 |
0 temperatureThe degree of hotness or coldness in the environment.
|
113 |
0 temperatureThe measure of molecular motion or the degree of heat of a substance. It is measured on an arbitrary scale from absolute zero, where the molecules theoretically stop moving. It is also the degree of h [..]
|
114 |
0 temperatureThe measure of molecular motion or the degree of heat
|
115 |
0 temperature(Abbrev. TEMP)- The temperature is a measure of the internal energy that a substance contains. This is the most measured quantity in the atmosphere.
|
116 |
0 temperatureThe measure of molecular motion or the degree of heat of a substance. It is measured on an arbitrary scale from absolute zero, where the molecules theoretically stop moving. It is also the degree of hotness or coldness. In surface observations, it refers primarily to the free air or ambient temperature close to the surface of the earth.
|
117 |
0 temperatureA characteristic of a color to be warm or cool.
|
118 |
0 temperaturethe warmness or coolness of a color, depending on where the color is situated on the color wheel
|
119 |
0 temperature55 to 125 degrees Celsius. The operational temperature range components or equipment is designed for to meet full military operation. [Military Temperature Range]
|
120 |
0 temperatureDegree of hotness or coldness as measured by a thermometer.
|
121 |
0 temperatureThe temperature at which the condensation of water vapor in a space begins for a given state of humidity and pressure as the temperature of the vapor is reduced. The temperature corresponding to satur [..]
|
122 |
0 temperatureThe temperature of a gas or mixture of gases indicated by an accurate thermometer after correction for radiation.
|
123 |
0 temperatureAn arbitrary index which combines into a single value the effect of temperature, humidity, and air movement on the sensation of warmth or cold felt by the human body. The numerical value is that of th [..]
|
124 |
0 temperatureThe temperature at which no further moisture can be added to the air water vapor mixture. Equals dew point temperature.
|
125 |
0 temperatureThermodynamic wet bulb temperature is the temperature at which liquid or solid water, by evaporating into air, can bring the air to saturation adiabatically at the same temperature. Wet bulb temperatu [..]
|
126 |
0 temperatureHUMIDITY INDEX — Actual temperature and humidity of air sample compared to air at standard conditions.
|
127 |
0 temperature(obsolete) The state or condition of being tempered or moderated. (now,_|rare|archaic) The balance of humours in the body, or one’s character or outlook as considered determined from this; tempera [..]
|
128 |
0 temperaturelang=en 1800s=1843 * »’1843»’ — . »».
|
129 |
0 temperatureTemperature is a physical quantity expressing hot and cold. Temperature is measured with a thermometer, historically calibrated in various temperature scales and units of measurement. The most commonl [..]
|
130 |
0 temperature«Temperature» is the third worldwide and the second American single from Jamaican DJ Sean Paul’s album The Trinity (2005). The song was produced by Rohan «Snowcone» Fuller and rece [..]
|
131 |
0 temperatureTemperature is a physical quantity expressing hot and cold. Temperature is measured with a thermometer, historically calibrated in various temperature scales and units of measurement. The most commonl [..]
|
132 |
0 temperatureTemperature is a physical property of a system that underlies the common notions of hot and cold.
|
133 |
0 temperatureTemperature is a physical quantity expressing hot and cold. Temperature is measured with a thermometer, historically calibrated in various temperature scales and units of measurement. The most commonl [..]
|
134 |
0 temperatureA measure of the intensity of heat in degrees, reflecting the average kinetic energy of the molecules.
|
135 |
0 temperaturemid-15c., «fact of being tempered, proper proportion;» 1530s, «character or nature of a substance,» from Latin temperatura «a tempering, moderation,» from temperatus, pas [..]
|
136 |
0 temperatureThe quantity measured by a thermometer. Bodies in thermal equilibrium with each other have the same temperature. In gaseous fluid dynamics, temperature represents molecular kinetic energy, which is th [..]
|
137 |
0 temperaturethe degree of hotness or coldness of a body or environment (corresponding to its molecular activity) the somatic sensation of cold or heat Temperature is a physical property that quantitatively expres [..]
|
Dictionary.university is a dictionary written by people like you and me.
Please help and add a word. All sort of words are welcome!
Add meaning
tem·per·a·ture
(tĕm′pər-ə-cho͝or′, -chər, tĕm′prə-)
n.
1.
a. The degree of hotness or coldness of a body or environment.
b. A measure of the average kinetic energy of the particles in a sample of matter, expressed in terms of units or degrees designated on a standard scale.
2.
a. The degree of heat in the body of a living organism, usually about 37.0°C (98.6°F) in humans.
b. An abnormally high condition of body heat caused by illness; a fever.
[Middle English, temperate weather, Latin temperātūra, due measure, from temperātus, past participle of temperāre, to mix; see temper.]
American Heritage® Dictionary of the English Language, Fifth Edition. Copyright © 2016 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
temperature
(ˈtɛmprɪtʃə)
n
1. (General Physics) the degree of hotness of a body, substance, or medium; a physical property related to the average kinetic energy of the atoms or molecules of a substance
2. (General Physics) a measure of this degree of hotness, indicated on a scale that has one or more fixed reference points
3. (Pathology) informal a body temperature in excess of the normal
4. archaic
a. compromise
b. temperament
c. temperance
[C16 (originally: a mingling): from Latin temperātūra proportion, from temperāre to temper]
Collins English Dictionary – Complete and Unabridged, 12th Edition 2014 © HarperCollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014
tem•per•a•ture
(ˈtɛm pər ə tʃər, -ˌtʃʊər, -prə-, -pər tʃər, -ˌtʃʊər)
n.
1. a measure of the warmth or coldness of an object or substance with reference to some standard value.
2.
a. the degree of heat in a living body, normally about 98.6°F (37°C) in humans.
b. a level of such heat above the normal; fever: running a temperature.
3. Obs. mildness, as of the weather.
4. Obs. temperament.
[1525–35; < Latin temperātūra blending, tempering. See temperate, -ure]
Random House Kernerman Webster’s College Dictionary, © 2010 K Dictionaries Ltd. Copyright 2005, 1997, 1991 by Random House, Inc. All rights reserved.
tem·per·a·ture
(tĕm′pər-ə-cho͝or′)
1. A measure of the average kinetic energy of atoms or molecules in a system.
2. A numerical measure of hotness or coldness on a standard scale, such as the Kelvin scale. See Note at Celsius.
3. An abnormally high body temperature; a fever.
Usage The molecules of all substances are in motion, and the energy associated with this motion is called kinetic energy. Temperature and heat are both ways of measuring this energy, but they do not mean the same thing. A substance’s temperature is the average kinetic energy of the substance’s molecules. By contrast, a substance’s heat is the total amount of energy contained in the substance. Thus, the water in two different pots, one four times as large as the other, might be at the same temperature, but the water in the larger pot would contain four times as much heat, since it requires four times as much energy to raise the temperature to the temperature of the water in the smaller pot.
The American Heritage® Student Science Dictionary, Second Edition. Copyright © 2014 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.
temperature
1. Degree of “hotness” measured in Celsius, Fahrenheit, etc.
2. A measure of temperature difference representing a single division on a temperature scale.
Dictionary of Unfamiliar Words by Diagram Group Copyright © 2008 by Diagram Visual Information Limited
Translations
teplota
temperaturfeber
lämpötilakuume
temperatura
hõmérséklethőmérsékletláz
hitihiti, hitastig
温度
온도
matuoti kam temperatūrą
temperatūra
febrătemperatură
temperaturavročina
temperaturfeber
อุณหภูมิ
nhiệt độ
temperature
[ˈtemprɪtʃəʳ]
Collins Spanish Dictionary — Complete and Unabridged 8th Edition 2005 © William Collins Sons & Co. Ltd. 1971, 1988 © HarperCollins Publishers 1992, 1993, 1996, 1997, 2000, 2003, 2005
temperature
[ˈtɛmpərətʃər]
n
[air, water, place, room, oven] → température f
The temperature was 30 degrees
BUT Il faisait trente degrés.
Collins English/French Electronic Resource. © HarperCollins Publishers 2005
temperature
temperature
:
temperature chart
n (Med) → Fiebertabelle f; (= curve of graph) → Fieberkurve f
temperature gauge
n → Temperaturanzeiger m
temperature-sensitive
adj → temperaturempfindlich
Collins German Dictionary – Complete and Unabridged 7th Edition 2005. © William Collins Sons & Co. Ltd. 1980 © HarperCollins Publishers 1991, 1997, 1999, 2004, 2005, 2007
temperature
[ˈtɛmprɪtʃəʳ] n → temperatura
to have or run a temperature → avere la febbre
Collins Italian Dictionary 1st Edition © HarperCollins Publishers 1995
temperature
(ˈtemprətʃə) noun
1. the amount or degree of cold or heat. The food must be kept at a low temperature.
2. a level of body heat that is higher than normal. She had a temperature and wasn’t feeling well.
take someone’s temperature
to measure a person’s body heat, using a thermometer.
Kernerman English Multilingual Dictionary © 2006-2013 K Dictionaries Ltd.
temperature
→ دَرَجَةُ الـحَرَارَة teplota temperatur Temperatur θερμοκρασία temperatura lämpötila température temperatura temperatura 温度 온도 temperatuur temperatur temperatura temperatura температура temperatur อุณหภูมิ ısı nhiệt độ 温度
Multilingual Translator © HarperCollins Publishers 2009
tem·per·a·ture
1. n. temperatura, grado de calor o frío de un cuerpo o masa.
2. Condición anormal de frío o calor de un organismo.
high ___ → ___ alta;
[fiebre] calentura → ;
low ___ → ___ baja.
English-Spanish Medical Dictionary © Farlex 2012
- What’s the temperature? (US)
What is the temperature? (UK) - I’d like something for a temperature
- She has a temperature
Collins Multilingual Translator © HarperCollins Publishers 2009
temperature
n temperatura; (fam, fever) fiebre f, calentura; axillary — temperatura axilar; oral — temperatura oral; rectal — temperatura rectal; room — temperatura ambiente; to take (someone’s) — tomar(le) la temperatura (a alguien); to take one’s (own) — tomarse la temperatura; Did you take your temperature at home?..¿Se tomó la temperatura en casa?
English-Spanish/Spanish-English Medical Dictionary Copyright © 2006 by The McGraw-Hill Companies, Inc. All rights reserved.
What do we mean by temperature?
The degree of hotness or coldness of a body or environment. noun
A measure of the average kinetic energy of the particles in a sample of matter, expressed in terms of units or degrees designated on a standard scale. noun
The degree of heat in the body of a living organism, usually about 37.0°C (98.6°F) in humans. noun
An abnormally high condition of body heat caused by illness; a fever. noun
In phenology, the temperature below which the germination of the seed and the growth of the plant do not take place. noun
Mixture, or that which is produced by mixture; a compound. noun
Constitution; state; temperament. noun
Moderation; freedom from passions or excesses. noun
Temper, as of metals. noun
Temperateness; mildness. noun
The state of a substance with regard to sensible heat; the degree or intensity of the sensible heat of a body. noun
Specifically, the thermal element of weather or climate. noun
In physiology and pathology, the degree of heat of a living body, especially of the human body. It is usually taken, clinically, in the axilla, under the tongue, or in the rectum. noun
Constitution; state; degree of any quality. noun
Freedom from passion; moderation. noun
Condition with respect to heat or cold, especially as indicated by the sensation produced, or by the thermometer or pyrometer; degree of heat or cold noun
Mixture; compound. noun
The degree of heat of the body of a living being, esp. of the human body; also (Colloq.), loosely, the excess of this over the normal (of the human body 98°-99.5° F., in the mouth of an adult about 98.4°). noun
A measure of cold or heat, often measurable with a thermometer.
An elevated body temperature, as present in fever and many illnesses.
A property of macroscopic amounts of matter that serves to gauge the average intensity of the random actual motions of the individually mobile particulate constituents. http//arxiv.org/pdf/physics/0004055
The state or condition of being tempered or moderated.
The balance of humours in the body, or one’s character or outlook as considered determined from this; temperament.
The only word spoken by Sean Paul that can be understood Urban Dictionary
If someone is feeling feverish. They may ask someone to check if he /she has a temperature. Urban Dictionary
A plan . Urban Dictionary
Having fever… body temperature goin above 98 degree…. body going warm…. Urban Dictionary
Feeling the perfect temperature in a room. Urban Dictionary
The opposite of using temperature words to describe looks. Temperatureness is often used to distinguish between being hot or cool in a temperature, instead of physical appearance. Urban Dictionary
The art of keeping a comfortable temperature in a public place such as a restaurant or store. Urban Dictionary
You take a girls temperature by slipping a surprise thumb up her butt, while she’s giving you a blow job. Urban Dictionary
When something is really really good!
Refering to something being hot!
WARNING!
Only to be used to describe the VERY best i.e. something that cannot be topped by anything else. Urban Dictionary
When the water in your swimming pool is so damn hot it is no longer refreshing.
Falls Between Comfortable & Piss Warm Urban Dictionary
English[edit]
Etymology[edit]
Borrowed from Latin temperatura[1] (cf. also French température), from the past participle stem of tempero (“I temper”).
Pronunciation[edit]
- (Received Pronunciation) IPA(key): /ˈtɛm.pɹə.t͡ʃə/, /ˈtɛm.pə.ɹə.t͡ʃə/, /ˈtɛm.pə.t͡ʃə/
- (General American) IPA(key): /ˈtɛm.pəɹ.əˌt͡ʃɚ/, /ˈtɛm.pəɹˌt͡ʃɚ/, /ˈtɛm.pɹəˌt͡ʃɚ/, [ˈtʰɛm.pʰəɹˌt͡ʃɚ], [ˈtʰɛm.pʰɹəˌt͡ʃɚ]
Noun[edit]
temperature (countable and uncountable, plural temperatures)
- A measure of cold or heat, often measurable with a thermometer.
- Synonyms: see Thesaurus:temperature
-
The boiling temperature of pure water is 100 degrees Celsius.
-
The temperature in the room dropped nearly 20 degrees; it went from hot to cold.
-
The most accurate way to take your temperature is by sticking a thermometer up your butt.
-
2013 May 11, “The climate of Tibet: Pole-land”, in The Economist, volume 407, number 8835, page 80:
-
Of all the transitions brought about on the Earth’s surface by temperature change, the melting of ice into water is the starkest. It is binary. And for the land beneath, the air above and the life around, it changes everything.
-
- An elevated body temperature, as present in fever and many illnesses.
-
You have a temperature. I think you should stay home today. You’re sick.
-
1951, Josephine Tey, The Daughter of Time:
-
«Aren’t you feeling so well this morning?» she asked him anxiously. «Do you think you’ve got a temperature?»
-
-
- (thermodynamics) A property of macroscopic amounts of matter that serves to gauge the average intensity of the random actual motions of the individually mobile particulate constituents. [1]
- (obsolete) The state or condition of being tempered or moderated.
- (now rare, archaic) The balance of humours in the body, or one’s character or outlook as considered determined from this; temperament.
- , Bk.I, New York 2001, p.136:
- Our intemperence it is that pulls so many several incurable diseases on our heads, that hastens old age, perverts our temperature, and brings upon us sudden death.
- 1759, Laurence Sterne, The Life and Opinions of Tristram Shandy, Gentleman, Penguin 2003, p.5:
- […] that not only the production of a rational Being was concern’d in it, but that possibly the happy foundation and temperature of his body, perhaps his genius and the very cast of his mind […]
- 1993, James Michie, trans. Ovid, The Art of Love, Book II:
- Only a strong dose of love will cure / A woman with an angry temperature.
- , Bk.I, New York 2001, p.136:
Quotations[edit]
- 2007, James Shipman, Jerry Wilson, Aaron Todd, An Introduction to Physical Science: Twelfth Edition, pages 106–108:
- Heat and temperature, although different, are intimately related. […] For example, suppose you added equal amounts of heat to equal masses of iron and aluminum. How do you think their temperatures would change? […] if the temperature of the iron increased by 100 C°, the corresponding temperature change in the aluminum would be only 48 C°.
Hyponyms[edit]
- apparent temperature
- color temperature
- Hagedorn temperature
- Planck temperature
- planetary equilibrium temperature
Derived terms[edit]
- land skin temperature
- temperaturewise
[edit]
- temperature inversion
Translations[edit]
a measure of cold or heat
- Albanian: temperaturë (sq) f
- Arabic: دَرَجَةْ الْحَرَارَة f (darajat al-ḥarāra)
- Armenian: ջերմաստիճան (hy) (ǰermastičan)
- Assamese: ঊষ্ণতা (usnota)
- Asturian: temperatura (ast) f
- Atayal: kinmkilux
- Azerbaijani: hərarət, istilik (az), temperatur
- Basque: tenperatura
- Belarusian: тэмперату́ра (be) f (tempjeratúra), тэмпэрату́ра f (temperatúra)
- Bengali: তাপমাত্রা (bn) (tapomatra)
- Bulgarian: температу́ра (bg) f (temperatúra)
- Burmese: ပြဒါးချိန် (my) (pra.da:hkyin)
- Catalan: temperatura (ca) f
- Chinese:
- Mandarin: 溫度/温度 (zh) (wēndù)
- Czech: teplota (cs) f
- Danish: temperatur (da) c
- Dutch: temperatuur (nl) f
- Esperanto: temperaturo (eo)
- Estonian: temperatuur
- Faroese: hitastig n
- Finnish: lämpötila (fi)
- French: température (fr)
- Galician: temperatura (gl) f
- Georgian: ტემპერატურა (ṭemṗeraṭura)
- German: Temperatur (de) f
- Greek: θερμοκρασία (el) f (thermokrasía)
- Gujarati: તાપમાન (tāpmān)
- Haitian Creole: tanperati
- Hebrew: טֶמְפֶּרָטוּרָה (he) f (temperatúra)
- Hindi: तापमान (hi) m (tāpmān), टेम्परेचर (hi) m (ṭemparecar), टेंपरेचर (hi) m (ṭemprecar)
- Hungarian: hőmérséklet (hu), hőfok (hu)
- Icelandic: hitastig n
- Indonesian: suhu (id), temperatur (id)
- Interlingua: temperatura
- Irish: teocht f
- Italian: temperatura (it) f
- Japanese: 温度 (ja) (おんど, ondo)
- Kannada: ತಾಪಮಾನ (kn) (tāpamāna)
- Kazakh: температура (kk) (temperatura)
- Khmer: កំដៅ (kɑmdaw)
- Korean: 온도(溫度) (ko) (ondo)
- Kyrgyz: температура (ky) (temperatura)
- Lao: ອຸນະພູມ (lo) (ʼu na phūm), ອຸນຫະພູມ (ʼun ha phūm), ອຸນນະພູມ (ʼun na phūm)
- Latvian: temperatūra f
- Lithuanian: temperatūra f
- Macedonian: температу́ра f (temperatúra)
- Malay: suhu (ms)
- Malayalam: ഊഷ്മാവ് (ml) (ūṣmāvŭ), താപനില (ml) (tāpanila)
- Maltese: temperatura f
- Maori: pāmahana
- Marathi: तापमान (tāpmān)
- Mongolian:
- Cyrillic: халуун (mn) (xaluun), температур (temperatur)
- Navajo: naʼalkid
- Nepali: तापक्रम (tāpakram)
- Norman: tempéthatuthe f
- Norwegian:
- Bokmål: temperatur (no) m
- Nynorsk: temperatur m
- Occitan: temperatura (oc) f
- Oriya: ତାପମାତ୍ରା (tapômatra)
- Pali: tejopamāṇa n, uṇhabhūmi f
- Pashto: تودښت (ps) m (tawdǝӽt), تودوخه (ps) f (tawdóxa)
- Persian: درجهٔ حرارت (fa) (dareje-ye harârat), دما (fa) (damâ)
- Polish: temperatura (pl) f
- Portuguese: temperatura (pt) f
- Punjabi: ਤਾਪਮਾਨ (tāpmān)
- Romanian: temperatură (ro) f
- Russian: температу́ра (ru) f (temperatúra)
- Serbo-Croatian:
- Cyrillic: температу́ра f
- Roman: temperatúra (sh) f
- Sinhalese: උෂ්ණත්වය (si) (uṣṇatwaya)
- Slovak: teplota f
- Slovene: temperatura (sl) f
- Spanish: temperatura (es) f
- Sundanese: ᮞᮥᮠᮥ (suhu)
- Swahili: halijoto
- Swedish: temperatur (sv) c
- Tagalog: temperatura (tl), kaintan
- Tajik: дараҷаи харорат (darajayi xarorat), дамо (damo)
- Tamil: வெப்பநிலை (ta) (veppanilai)
- Telugu: ఉష్ణోగ్రత (te) (uṣṇōgrata)
- Thai: อุณหภูมิ (th) (un-hà-puum)
- Tibetan: དྲོ་ཚད (dro tshad), དྲོ་གྲང (dro grang), ཚ་གྲང (tsha grang)
- Turkish: sıcaklık (tr)
- Turkmen: temperatura
- Ukrainian: температу́ра f (temperatúra)
- Urdu: درجہ حرارت (daraja harāra)
- Uyghur: تېمپېراتۇرا (tëmpëratura)
- Uzbek: temperatura (uz)
- Venetian: tenperadura f
- Vietnamese: nhiệt độ (vi)
- Welsh: tymheredd (cy)
- Yiddish: טעמפּעראַטור (temperatur)
elevated body temperature
- Armenian: ջերմություն (hy) (ǰermutʿyun), տաքություն (hy) (takʿutʿyun)
- Azerbaijani: qızdırma
- Belarusian: тэмперату́ра (be) f (tempjeratúra), тэмпэрату́ра f (temperatúra), гара́чка f (haráčka), жар m (žar)
- Bulgarian: температу́ра (bg) (temperatúra), тре́ска (bg) f (tréska)
- Catalan: febre (ca) f
- Chinese:
- Mandarin: 發燒/发烧 (zh) (fāshāo), 熱/热 (zh) (rè)
- Czech: teplota (cs) f
- Dutch: verhoging (nl) f
- Finnish: kuume (fi), lämpö (fi)
- German: (please verify) erhöhte Temperatur f
- Greek: θερμοκρασία (el) f (thermokrasía), πυρετός (el) m (pyretós)
- Guaraní: akãnundu
- Hindi: ताप (hi) m (tāp)
- Hungarian: (chiefly above 37.5—38°C / 99.5—100.4°F) láz (hu), (mild, lower than that) hőemelkedés (hu)
- Interlingua: febre
- Italian: febbre (it) f
- Japanese: 熱 (ja) (ねつ, netsu), 発熱 (ja) (はつねつ, hatsunetsu)
- Korean: 열(熱) (ko) (yeol), 발열(發熱) (ko) (baryeol)
- Latin: febris (la) f
- Macedonian: температу́ра f (temperatúra)
- Middle English: hete
- Polish: gorączka (pl) f
- Portuguese: febre (pt) f
- Romanian: temperatură (ro) f, febră (ro) f
- Russian: температу́ра (ru) f (temperatúra), жар (ru) m (žar), горя́чка (ru) (gorjáčka)
- Sanskrit: ताप (sa) m (tāpa)
- Serbo-Croatian:
- Cyrillic: температу́ра f, вру̀ћица f
- Roman: temperatúra (sh) f, vrùćica f
- Spanish: fiebre (es) f
- Swedish: feber (sv)
- Tajik: харорат (xarorat)
- Tamil: காய்ச்சல் (ta) (kāyccal)
- Turkish: ateş (tr)
- Ukrainian: температу́ра f (temperatúra), гаря́чка f (harjáčka), жар m (žar)
- Uzbek: harorat (uz)
in thermodynamics
- Bengali: তাপমাত্রা (bn) (tapomatra)
- Finnish: lämpötila (fi)
- German: Temperatur (de) f
- Greek: θερμοκρασία (el) f (thermokrasía)
- Japanese: 熱 (ja) (ねつ, netsu)
- Korean: 열(熱) (ko) (yeol)
- Macedonian: температу́ра f (temperatúra)
- Navajo: naʼalkid
- Portuguese: temperatura (pt) f
- Russian: температу́ра (ru) f (temperatúra)
- Serbo-Croatian:
- Cyrillic: температу́ра f
- Roman: temperatúra (sh) f
- Tamil: வெப்பநிலை (ta) (veppanilai)
- Turkish: sıcaklık (tr)
- Ukrainian: температу́ра f (temperatúra)
See also[edit]
- Customary: degrees Fahrenheit (°F), degrees Rankine (°R, measures absolute temperature)
- Metric: degrees Celsius/centigrade (°C), kelvins (K, measures absolute temperature)
- Thesaurus:temperature
- cool
- cold
- fresh
- fever
- hot
- lukewarm
- warm
References[edit]
temperature on Wikipedia.Wikipedia
- ^ http://www.dictionary.com/browse/temperature?s=t
Italian[edit]
Pronunciation[edit]
- IPA(key): /tem.pe.raˈtu.re/
- Rhymes: -ure
- Hyphenation: tem‧pe‧ra‧tù‧re
Noun[edit]
temperature f pl
- plural of temperatura
Latin[edit]
Participle[edit]
temperātūre
- vocative masculine singular of temperātūrus
Middle French[edit]
Etymology[edit]
Borrowed from Latin temperatura.
Noun[edit]
temperature f (plural temperatures)
- disposition; habitual state; temperament