What is fourier analysis in excel

1. Click the File tab, click Options, and then click the Add-Ins category.

2. In the Manage box, select Excel Add-ins and then click Go.

   If you’re using Excel for Mac, in the file menu go to Tools > Excel Add-ins.

3. In the Add-Ins box, check the Analysis ToolPak check box, and then click OK.

   • If Analysis ToolPak is not listed in the Add-Ins available box, click Browse to locate it.

   • If you are prompted that the Analysis ToolPak is not currently installed on your computer, click Yes to install it.

Note: To include Visual Basic for Application (VBA) functions for the Analysis ToolPak, you can load the Analysis ToolPak — VBA Add-in the same way that you load the Analysis ToolPak. In the Add-ins available box, select the Analysis ToolPak — VBA check box.

The Anova analysis tools provide different types of variance analysis. The tool that you should use depends on the number of factors and the number of samples that you have from the populations that you want to test.

Anova: Single Factor

This tool performs a simple analysis of variance on data for two or more samples. The analysis provides a test of the hypothesis that each sample is drawn from the same underlying probability distribution against the alternative hypothesis that underlying probability distributions are not the same for all samples. If there are only two samples, you can use the worksheet function T.TEST. With more than two samples, there is no convenient generalization of T.TEST, and the Single Factor Anova model can be called upon instead.

Anova: Two-Factor with Replication

This analysis tool is useful when data can be classified along two different dimensions. For example, in an experiment to measure the height of plants, the plants may be given different brands of fertilizer (for example, A, B, C) and might also be kept at different temperatures (for example, low, high). For each of the six possible pairs of {fertilizer, temperature}, we have an equal number of observations of plant height. Using this Anova tool, we can test:

• Whether the heights of plants for the different fertilizer brands are drawn from the same underlying population. Temperatures are ignored for this analysis.

• Whether the heights of plants for the different temperature levels are drawn from the same underlying population. Fertilizer brands are ignored for this analysis.

Whether having accounted for the effects of differences between fertilizer brands found in the first bulleted point and differences in temperatures found in the second bulleted point, the six samples representing all pairs of {fertilizer, temperature} values are drawn from the same population. The alternative hypothesis is that there are effects due to specific {fertilizer, temperature} pairs over and above the differences that are based on fertilizer alone or on temperature alone.

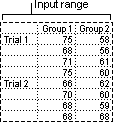
Anova: Two-Factor Without Replication

This analysis tool is useful when data is classified on two different dimensions as in the Two-Factor case With Replication. However, for this tool it is assumed that there is only a single observation for each pair (for example, each {fertilizer, temperature} pair in the preceding example).

The CORREL and PEARSON worksheet functions both calculate the correlation coefficient between two measurement variables when measurements on each variable are observed for each of N subjects. (Any missing observation for any subject causes that subject to be ignored in the analysis.) The Correlation analysis tool is particularly useful when there are more than two measurement variables for each of N subjects. It provides an output table, a correlation matrix, that shows the value of CORREL (or PEARSON) applied to each possible pair of measurement variables.

The correlation coefficient, like the covariance, is a measure of the extent to which two measurement variables «vary together.» Unlike the covariance, the correlation coefficient is scaled so that its value is independent of the units in which the two measurement variables are expressed. (For example, if the two measurement variables are weight and height, the value of the correlation coefficient is unchanged if weight is converted from pounds to kilograms.) The value of any correlation coefficient must be between -1 and +1 inclusive.

You can use the correlation analysis tool to examine each pair of measurement variables to determine whether the two measurement variables tend to move together — that is, whether large values of one variable tend to be associated with large values of the other (positive correlation), whether small values of one variable tend to be associated with large values of the other (negative correlation), or whether values of both variables tend to be unrelated (correlation near 0 (zero)).

The Correlation and Covariance tools can both be used in the same setting, when you have N different measurement variables observed on a set of individuals. The Correlation and Covariance tools each give an output table, a matrix, that shows the correlation coefficient or covariance, respectively, between each pair of measurement variables. The difference is that correlation coefficients are scaled to lie between -1 and +1 inclusive. Corresponding covariances are not scaled. Both the correlation coefficient and the covariance are measures of the extent to which two variables «vary together.»

The Covariance tool computes the value of the worksheet function COVARIANCE.P for each pair of measurement variables. (Direct use of COVARIANCE.P rather than the Covariance tool is a reasonable alternative when there are only two measurement variables, that is, N=2.) The entry on the diagonal of the Covariance tool’s output table in row i, column i is the covariance of the i-th measurement variable with itself. This is just the population variance for that variable, as calculated by the worksheet function VAR.P.

You can use the Covariance tool to examine each pair of measurement variables to determine whether the two measurement variables tend to move together — that is, whether large values of one variable tend to be associated with large values of the other (positive covariance), whether small values of one variable tend to be associated with large values of the other (negative covariance), or whether values of both variables tend to be unrelated (covariance near 0 (zero)).

The Descriptive Statistics analysis tool generates a report of univariate statistics for data in the input range, providing information about the central tendency and variability of your data.

The Exponential Smoothing analysis tool predicts a value that is based on the forecast for the prior period, adjusted for the error in that prior forecast. The tool uses the smoothing constant a, the magnitude of which determines how strongly the forecasts respond to errors in the prior forecast.

Note: Values of 0.2 to 0.3 are reasonable smoothing constants. These values indicate that the current forecast should be adjusted 20 percent to 30 percent for error in the prior forecast. Larger constants yield a faster response but can produce erratic projections. Smaller constants can result in long lags for forecast values.

The F-Test Two-Sample for Variances analysis tool performs a two-sample F-test to compare two population variances.

For example, you can use the F-Test tool on samples of times in a swim meet for each of two teams. The tool provides the result of a test of the null hypothesis that these two samples come from distributions with equal variances, against the alternative that the variances are not equal in the underlying distributions.

The tool calculates the value f of an F-statistic (or F-ratio). A value of f close to 1 provides evidence that the underlying population variances are equal. In the output table, if f < 1 «P(F <= f) one-tail» gives the probability of observing a value of the F-statistic less than f when population variances are equal, and «F Critical one-tail» gives the critical value less than 1 for the chosen significance level, Alpha. If f > 1, «P(F <= f) one-tail» gives the probability of observing a value of the F-statistic greater than f when population variances are equal, and «F Critical one-tail» gives the critical value greater than 1 for Alpha.

The Fourier Analysis tool solves problems in linear systems and analyzes periodic data by using the Fast Fourier Transform (FFT) method to transform data. This tool also supports inverse transformations, in which the inverse of transformed data returns the original data.

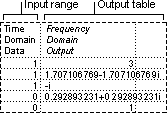
The Histogram analysis tool calculates individual and cumulative frequencies for a cell range of data and data bins. This tool generates data for the number of occurrences of a value in a data set.

For example, in a class of 20 students, you can determine the distribution of scores in letter-grade categories. A histogram table presents the letter-grade boundaries and the number of scores between the lowest bound and the current bound. The single most-frequent score is the mode of the data.

Tip: In Excel 2016, you can now create a histogram or Pareto chart.

The Moving Average analysis tool projects values in the forecast period, based on the average value of the variable over a specific number of preceding periods. A moving average provides trend information that a simple average of all historical data would mask. Use this tool to forecast sales, inventory, or other trends. Each forecast value is based on the following formula.

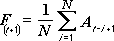
where:

• N is the number of prior periods to include in the moving average

• A
  j is the actual value at time j

• F
  j is the forecasted value at time j

The Random Number Generation analysis tool fills a range with independent random numbers that are drawn from one of several distributions. You can characterize the subjects in a population with a probability distribution. For example, you can use a normal distribution to characterize the population of individuals’ heights, or you can use a Bernoulli distribution of two possible outcomes to characterize the population of coin-flip results.

The Rank and Percentile analysis tool produces a table that contains the ordinal and percentage rank of each value in a data set. You can analyze the relative standing of values in a data set. This tool uses the worksheet functions RANK.EQ andPERCENTRANK.INC. If you want to account for tied values, use the RANK.EQ function, which treats tied values as having the same rank, or use the RANK.AVG function, which returns the average rank for the tied values.

The Regression analysis tool performs linear regression analysis by using the «least squares» method to fit a line through a set of observations. You can analyze how a single dependent variable is affected by the values of one or more independent variables. For example, you can analyze how an athlete’s performance is affected by such factors as age, height, and weight. You can apportion shares in the performance measure to each of these three factors, based on a set of performance data, and then use the results to predict the performance of a new, untested athlete.

The Regression tool uses the worksheet function LINEST.

The Sampling analysis tool creates a sample from a population by treating the input range as a population. When the population is too large to process or chart, you can use a representative sample. You can also create a sample that contains only the values from a particular part of a cycle if you believe that the input data is periodic. For example, if the input range contains quarterly sales figures, sampling with a periodic rate of four places the values from the same quarter in the output range.

The Two-Sample t-Test analysis tools test for equality of the population means that underlie each sample. The three tools employ different assumptions: that the population variances are equal, that the population variances are not equal, and that the two samples represent before-treatment and after-treatment observations on the same subjects.

For all three tools below, a t-Statistic value, t, is computed and shown as «t Stat» in the output tables. Depending on the data, this value, t, can be negative or nonnegative. Under the assumption of equal underlying population means, if t < 0, «P(T <= t) one-tail» gives the probability that a value of the t-Statistic would be observed that is more negative than t. If t >=0, «P(T <= t) one-tail» gives the probability that a value of the t-Statistic would be observed that is more positive than t. «t Critical one-tail» gives the cutoff value, so that the probability of observing a value of the t-Statistic greater than or equal to «t Critical one-tail» is Alpha.

«P(T <= t) two-tail» gives the probability that a value of the t-Statistic would be observed that is larger in absolute value than t. «P Critical two-tail» gives the cutoff value, so that the probability of an observed t-Statistic larger in absolute value than «P Critical two-tail» is Alpha.

t-Test: Paired Two Sample For Means

You can use a paired test when there is a natural pairing of observations in the samples, such as when a sample group is tested twice — before and after an experiment. This analysis tool and its formula perform a paired two-sample Student’s t-Test to determine whether observations that are taken before a treatment and observations taken after a treatment are likely to have come from distributions with equal population means. This t-Test form does not assume that the variances of both populations are equal.

Note: Among the results that are generated by this tool is pooled variance, an accumulated measure of the spread of data about the mean, which is derived from the following formula.

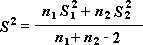
t-Test: Two-Sample Assuming Equal Variances

This analysis tool performs a two-sample student’s t-Test. This t-Test form assumes that the two data sets came from distributions with the same variances. It is referred to as a homoscedastic t-Test. You can use this t-Test to determine whether the two samples are likely to have come from distributions with equal population means.

t-Test: Two-Sample Assuming Unequal Variances

This analysis tool performs a two-sample student’s t-Test. This t-Test form assumes that the two data sets came from distributions with unequal variances. It is referred to as a heteroscedastic t-Test. As with the preceding Equal Variances case, you can use this t-Test to determine whether the two samples are likely to have come from distributions with equal population means. Use this test when there are distinct subjects in the two samples. Use the Paired test, described in the follow example, when there is a single set of subjects and the two samples represent measurements for each subject before and after a treatment.

The following formula is used to determine the statistic value t.

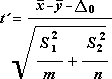
The following formula is used to calculate the degrees of freedom, df. Because the result of the calculation is usually not an integer, the value of df is rounded to the nearest integer to obtain a critical value from the t table. The Excel worksheet function T.TEST uses the calculated df value without rounding, because it is possible to compute a value for T.TEST with a noninteger df. Because of these different approaches to determining the degrees of freedom, the results of T.TEST and this t-Test tool will differ in the Unequal Variances case.

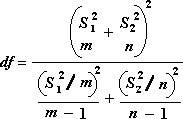
The z-Test: Two Sample for Means analysis tool performs a two sample z-Test for means with known variances. This tool is used to test the null hypothesis that there is no difference between two population means against either one-sided or two-sided alternative hypotheses. If variances are not known, the worksheet function Z.TEST should be used instead.

When you use the z-Test tool, be careful to understand the output. «P(Z <= z) one-tail» is really P(Z >= ABS(z)), the probability of a z-value further from 0 in the same direction as the observed z value when there is no difference between the population means. «P(Z <= z) two-tail» is really P(Z >= ABS(z) or Z <= -ABS(z)), the probability of a z-value further from 0 in either direction than the observed z-value when there is no difference between the population means. The two-tailed result is just the one-tailed result multiplied by 2. The z-Test tool can also be used for the case where the null hypothesis is that there is a specific nonzero value for the difference between the two population means. For example, you can use this test to determine differences between the performances of two car models.