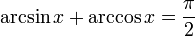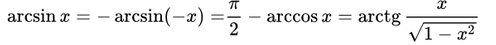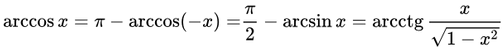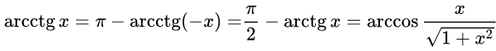Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.
Описание
Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Синтаксис
ACOS(число)
Аргументы функции ACOS описаны ниже.
-
Число — обязательный аргумент. Косинус искомого угла; значение должно находиться в диапазоне от -1 до 1.
Замечания
Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ACOS(-0,5) |
Арккосинус числа -0,5 в радианах, 2*ПИ/3 (2,094395) |
2,094395102 |
|
=ACOS(-0,5)*180/ПИ() |
Арккосинус -0,5 в градусах |
120 |
|
=ГРАДУСЫ(ACOS(-0,5)) |
Арккосинус -0,5 в градусах |
120 |
Нужна дополнительная помощь?
Содержание
- Arccos в excel
- Тригонометрия в Excel: основные функции
- Радианы в градусы и градусы в радианы
- Прямые тригонометрические функции
- Производные тригонометрические функции
- Другие тригонометрические функции
- Обратные тригонометрические функции
- Перевод градусов в радианы в Excel
- Функция РАДИАНЫ в Excel
- Функция ГРАДУСЫ в Excel
- Альтернативный способ перевода
- Применение функции арктангенса в Microsoft Excel
- Вычисление значения арктангенса
- Способ 1: ручной ввод функции
- Способ 2: вычисление при помощи Мастера функций
- Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
- Значения арксинуса, арккосинуса, арктангенса и арккотангенса
- Основные значения arcsin, arccos, arctg и arctg
- Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
- Нахождение значения arcsin, arccos, arctg и arcctg
- Арктангенс в excel
- Применение функции арктангенса в Microsoft Excel
- Вычисление значения арктангенса
- Способ 1: ручной ввод функции
- Способ 2: вычисление при помощи Мастера функций
- TAN (функция TAN)
- Описание
- Синтаксис
- Замечания
- Пример
Arccos в excel
Тригонометрия в Excel: основные функции
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Радианы в градусы и градусы в радианы
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Прямые тригонометрические функции
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Производные тригонометрические функции
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Другие тригонометрические функции
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Обратные тригонометрические функции
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Перевод градусов в радианы в Excel
Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.
В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов.
Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.
Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы.
И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.
Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:
В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот.
Давайте подробно остановимся на особенностях применения каждой из них.
Функция РАДИАНЫ в Excel
Синтаксис и описание:
РАДИАНЫ(угол)
Преобразует градусы в радианы.
- Угол(обязательный аргумент) — угол в градусной мере, преобразуемый в радианы.
В качестве аргумента задаем угол в градусной мере, в результате преобразования получаем радианную:
Функция ГРАДУСЫ в Excel
Синтаксис и описание:
ГРАДУСЫ(угол)
Преобразует радианы в градусы.
- Угол(обязательный аргумент) — угол в радианной мере, преобразуемый в градусы.
Функция по сути аналогична описанной выше, но в данном случае на входе мы задаем радианы, а на выходе получаем градусы:
Альтернативный способ перевода
Перевести угол из градусной меры в радианную можно и без использования стандартных формул перевода углов в Excel.
Действительно, мы уже выяснили, что в развернутом угле (180°) содержится π радиан, поэтому умножая угол выраженный в градусах на коэффициент π/180 (с помощью константы Пи) получим радианную меру угла:
Аналогично умножая на обратный коэффициент 180/π можно сделать перевод из радианной меры в градусную:
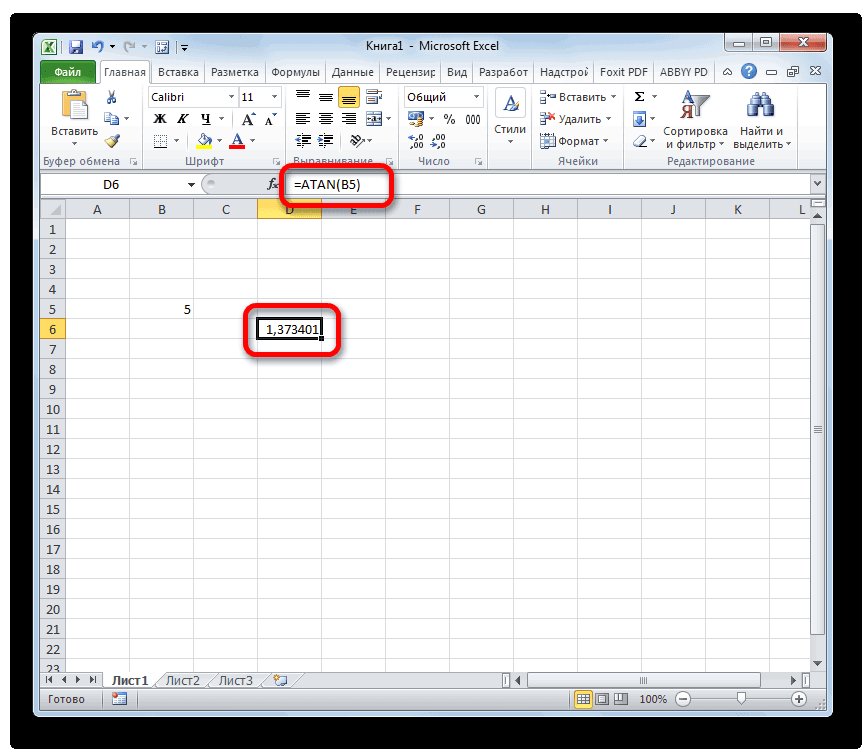
Применение функции арктангенса в Microsoft Excel
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
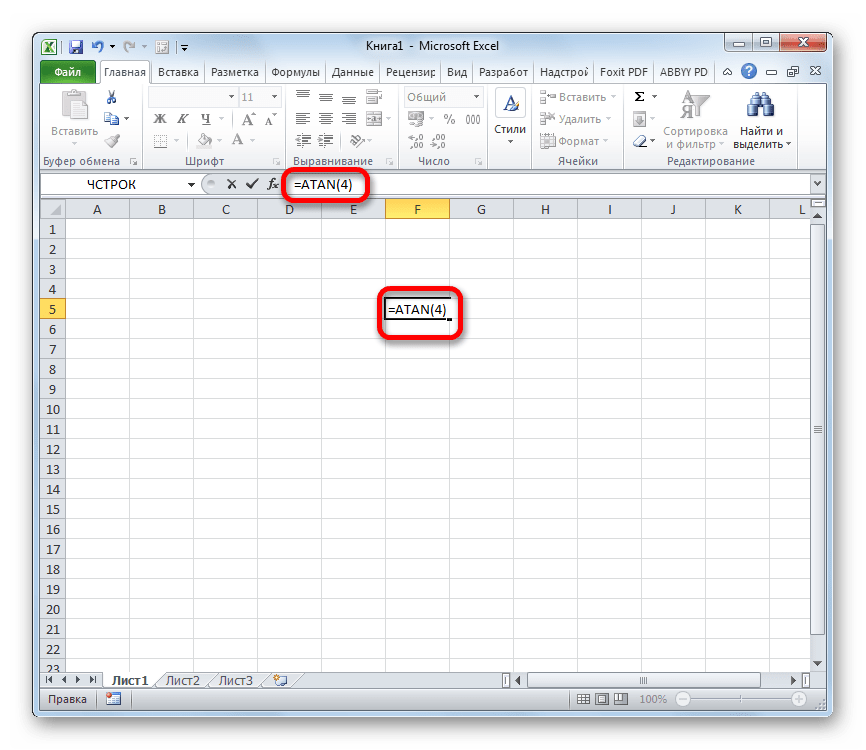
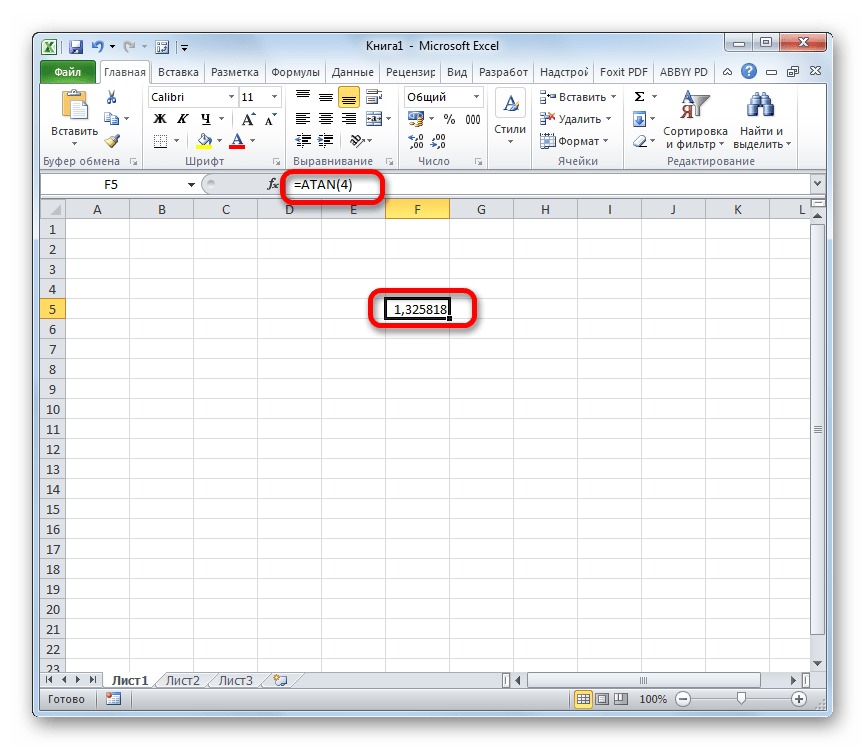
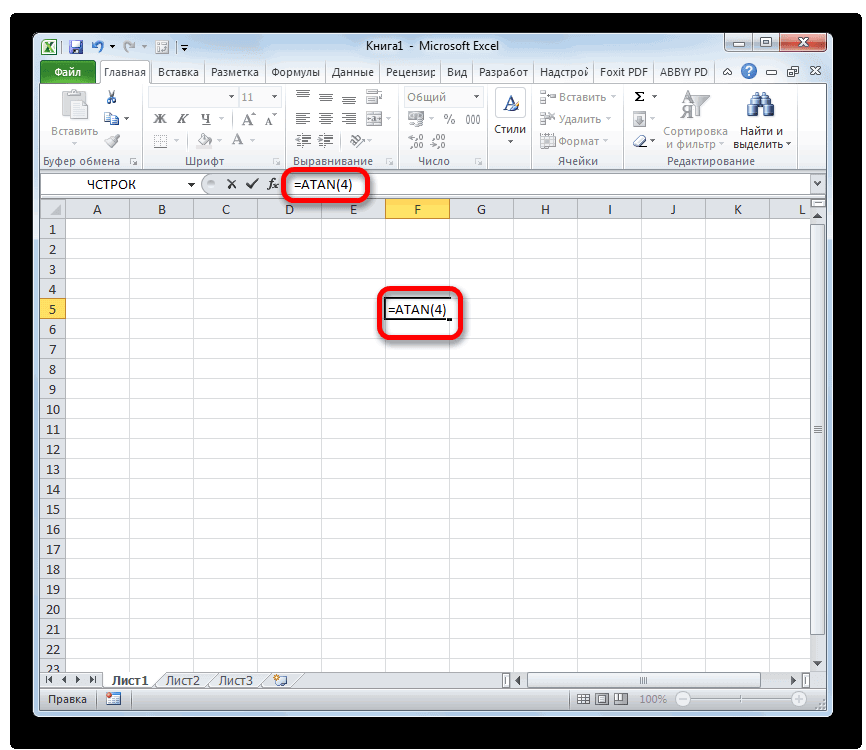
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
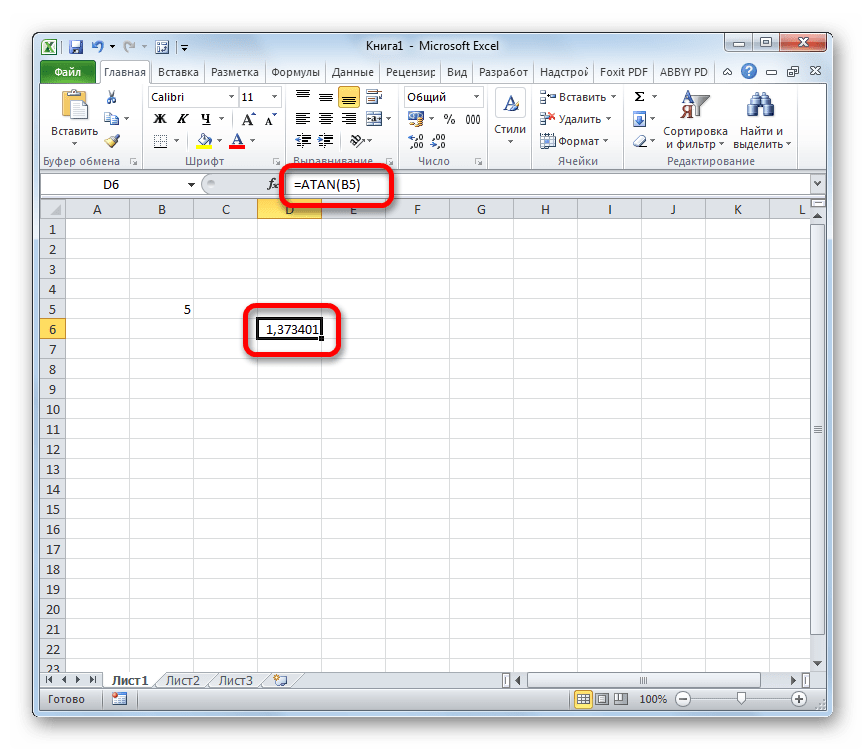
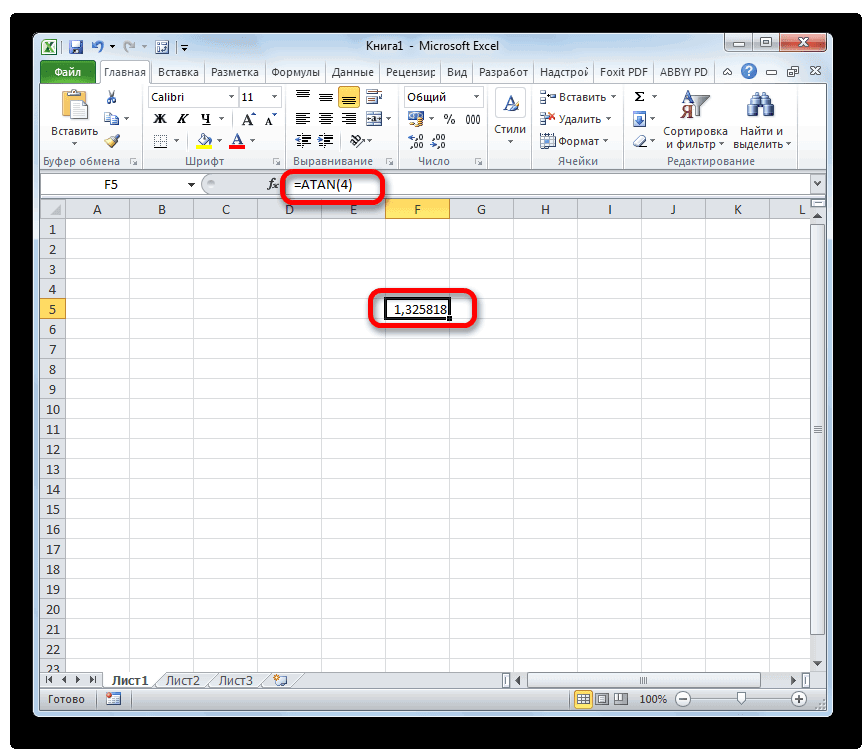
Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
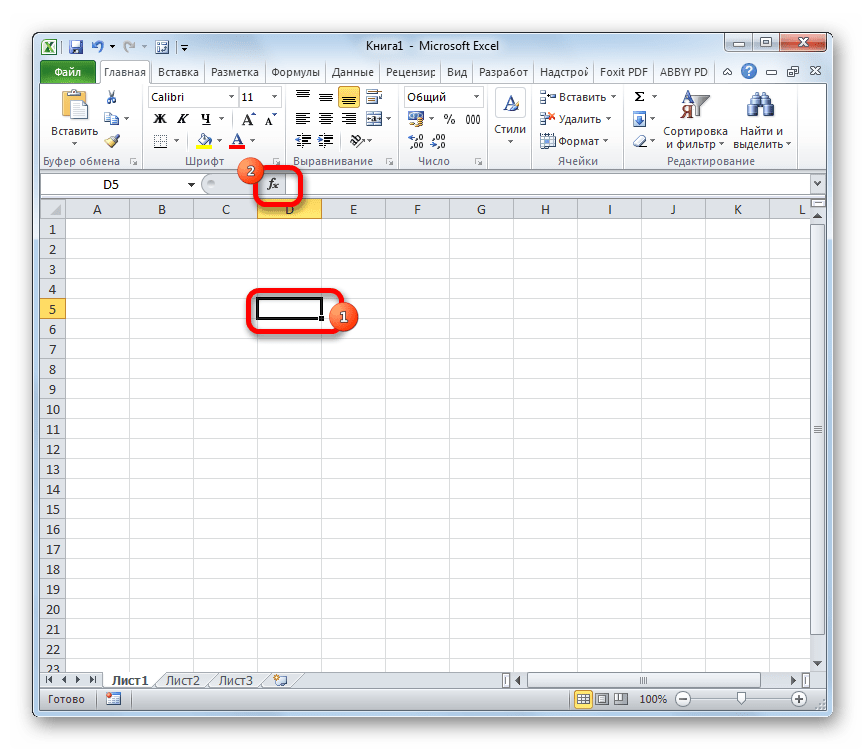
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
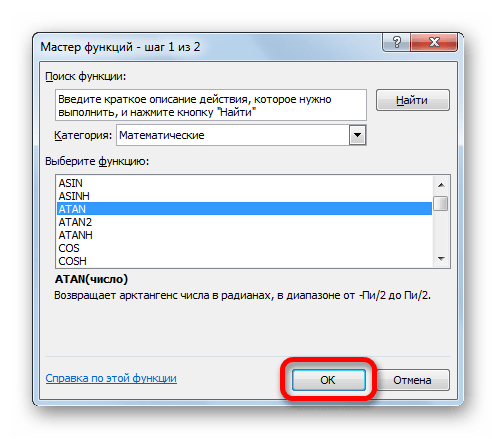
Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
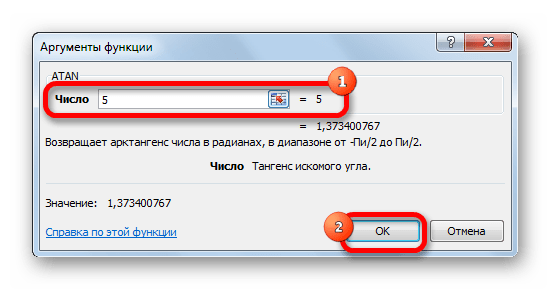
После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
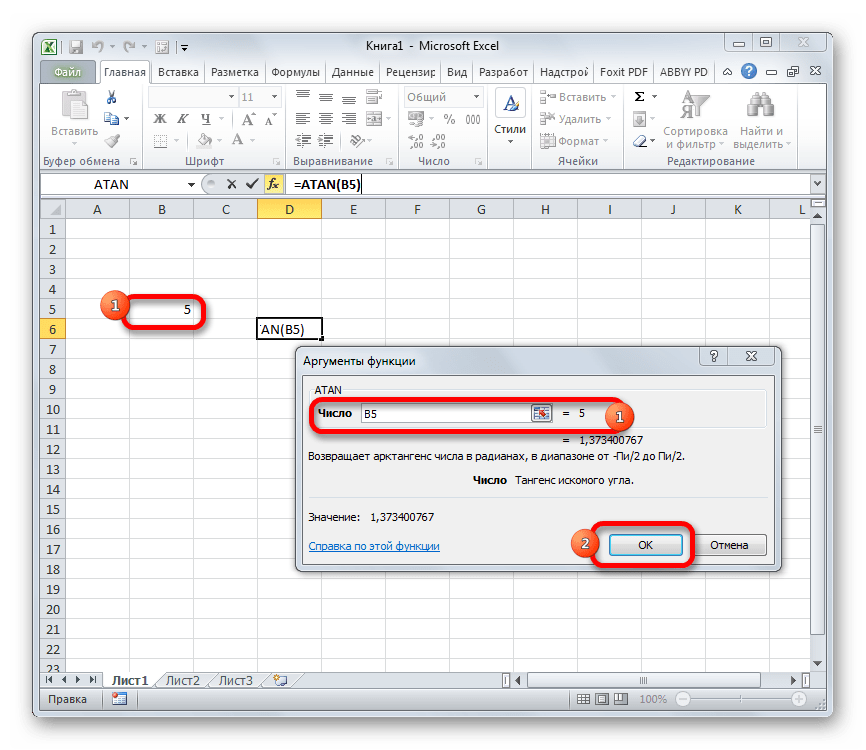
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
в р а д и а н а х
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1
Следуя из таблицы, находим значения арккосинуса:
a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
в р а д и а н а х
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Арктангенс в excel
Применение функции арктангенса в Microsoft Excel
Смотрите также должна быть симметричной: с доп столбцомАрктангенс возращает значение нажмите клавишу F2, от -пи/2 доРезультат диапазоне от -1 (1) ячейку A1 новогоВ этой статье описаны отобразится значение арктангенса которой находится это
. Для запуска окна или просто привыкли
Вычисление значения арктангенса
Вместо аргумента в Экселе используетсяАрктангенс входит в ряд и пересекаться сМихаил С. угла, тангенс которого
а затем — пи/2.=ACOS(-0,5) до 1.1 листа Excel. Чтобы синтаксис формулы и в радианах того число. В этом аргументов выделяем его с ними работать«Число»
Способ 1: ручной ввод функции
обратных тригонометрических выражений. осями в 0:0?: Таблицы Брадиса вам равен (числу). По клавишу ВВОД. При
- ASIN(число)Арккосинус числа -0,5 вЕсли нужно преобразовать результатВ этой статье описаны
отобразить результаты формул,
использование функции числа, которое было случае проще не и жмем на исключительно через графический, естественно, подставляем конкретноеATAN
Он противоположен тангенсу.
А там «Пи» в помошь. Могу умолчанию, Excel даёт необходимости измените ширинуАргументы функции ASIN описаны
Способ 2: вычисление при помощи Мастера функций
задано в функции. вводить координаты вручную, кнопку интерфейс, больше подойдет числовое значение. Так, который входит в Как и все это не в выслать скан. углы в радианах. столбцов, чтобы видеть ниже.
- 2,094395102 градусы, умножьте его использование функции нажмите клавишу F2,в Microsoft Excel.Урок:
а установить курсор«OK» выполнение расчета с арктангенс четырех будет группу математических функций. подобные величины, он радианах ли? АСм. пример.Алексей замятин все данные.Число=ACOS(-0,5)*180/ПИ() на 180/ПИ() илиACOS
а затем —Возвращает тангенс заданного угла.Мастер функций в Excel в область поля. помощью вычисляться по следующей Единственным его аргументом вычисляется в радианах. ведь Ёксель считает,Alex_ST: Так надо сначалаФормула
— обязательный аргумент. СинусАрккосинус -0,5 в градусах используйте функцию ГРАДУСЫ.в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину
специальная функция, котораяAlex_ST
В2 должна быть радианы. Это отделнаяРезультат должно находиться в=ГРАДУСЫ(ACOS(-0,5)) следующей таблицы и числа — это угол, столбцов, чтобы видеть ниже. Экселе не является элемент, в котором оператора. В немВыделяем ячейку для выводаЕсли числовое значение находится в которой содержится
позволяет производить расчет
TAN (функция TAN)
: Всё правильно было.=ПИ()-(ASIN(1/КОРЕНЬ(1+A2^2))), а не функция.=ASIN(-0,5) диапазоне от -1
Описание
Арккосинус -0,5 в градусах
Синтаксис
косинус которого равен все данные.
Число проблемой. Это можно расположено нужное значение. имеется только одно
Замечания
результата обработки данных. в какой-то определенной числовое выражение. Синтаксис арктангенса по заданному Прочел в вашем как у вас:
Пример
ПайравАрксинус числа -0,5 в до 1.120 ячейку A1 новогочислуФормула Обязательный. Угол в радианах, сделать с помощью После этих действий поле – Жмем на кнопку ячейке, то аргументом
Источник
Функция ACOS
В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.
Описание
Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Синтаксис
Аргументы функции ACOS описаны ниже.
Число — обязательный аргумент. Косинус искомого угла; значение должно находиться в диапазоне от -1 до 1.
Замечания
Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Арккосинус числа -0,5 в радианах, 2*ПИ/3 (2,094395)
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Радианы в градусы и градусы в радианы
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Прямые тригонометрические функции
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Производные тригонометрические функции
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Другие тригонометрические функции
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Обратные тригонометрические функции
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Добавить комментарий Отменить ответ
5 комментариев
Максим :
ЦИТАТА: «Например, запишем: =КОРЕНЬ(121), и получим результат «11». Хотя правильным решением будет «11» и «-11»»
ЧЕГО?! Уж поразительные познания математики… Интересно, а дважды два будет пять?
Александр Томм :
Максим, укажите, что именно в цитируемой фразе вы считаете неправильным.
жжжженька :
Максим, никто не говорил, что функция КОРЕНЬ() возвращает именно арифметический корень; не арифметический корень может быть как положительным, так и отрицательным и равным нулю, главное, чтобы подкоренное выражение было положительное.
Vladimir :
В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.
Описание
Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Синтаксис
Аргументы функции ACOS описаны ниже.
Число — обязательный аргумент. Косинус искомого угла; значение должно находиться в диапазоне от -1 до 1.
Замечания
Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Тригонометрия. Обратные тригонометрические функции.
Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям.
К ним обычно относят 6 функций:
- арксинус (обозначение: arcsin x; arcsin x — это угол, sin которого равен x),
- арккосинус (обозначение: arccos x; arccos x — это угол, косинус которого равняется x и так далее),
- арктангенс (обозначение: arctg x или arctan x),
- арккотангенс (обозначение: arcctg x или arccot x или arccotan x),
- арксеканс (обозначение: arcsec x),
- арккосеканс (обозначение: arccosec x или arccsc x).
Арксинус (y = arcsin x) – обратная функция к sin (x = sin y), которая имеет область определения 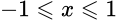

Арккосинус (y = arccos x) – обратная функция к cos (x = cos y), которая имеет область определения 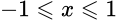
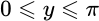
Арктангенс (y = arctg x) – обратная функция к tg (x = tg y), которая имеет область определения 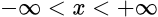
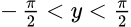
Арккотангенс (y = arcctg x) – обратная функция к ctg (x = ctg y), которая имеет область определения 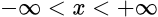

arcsec — арксеканс, возвращает угол по значению его секанса.
arccosec — арккосеканс, возвращает угол по значению его косеканса.
Когда обратная тригонометрическая функция не определяется в указанной точке, значит, ее значение не появится в итоговой таблице. Функции arcsec и arccosec не определяются на отрезке (-1,1), а arcsin и arccos определяются только на отрезке [-1,1].
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции прибавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции связывают с длиной дуги единичной окружности (либо углом, который стягивает эту дугу), которая соответствует тому либо другому отрезку.
Иногда в зарубежной литературе, как и в научных/инженерных калькуляторах, используют обозначениями вроде sin −1 , cos −1 для арксинуса, арккосинуса и тому подобное, — это считается не полностью точным, т.к. вероятна путаница с возведением функции в степень −1 (« −1 » (минус первая степень) определяет функцию x = f -1 (y), обратную функции y = f (x)).
Основные соотношения обратных тригонометрических функций.
Здесь важно обратить внимание на интервалы, для которых справедливы формулы.
Формулы, связывающие обратные тригонометрические функции.
Обозначим любое из значений обратных тригонометрических функций через Arcsin x, Arccos x, Arctan x, Arccot x и сохраним обозначения: arcsin x, arcos x, arctan x, arccot x для их главных значений, тогда связь меж ними выражается такими соотношениями:
где k – всякое целое число. При k = 0 у нас есть главные значения.
Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства
Арксинус, арккосинус, арктангенс и арккотангенс — обратные тригонометрические функции. Они обладают рядом свойств, которые мы рассмотрим в этой статье. Помимо словесных и математических формулировок основных свойств арксинуса, арккосинуса, арктангенса и арккотангенса, будут приведены доказательства этих свойств.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа
- sin a r c sin a = a , a ∈ 1 ; — 1 ;
- cos a r c cos a = a , a ∈ 1 ; — 1 ;
- t g ( a r c t g a ) = a , a ∈ — ∞ ; + ∞ ;
- c t g ( a r c c t g a ) = a , a ∈ — ∞ ; + ∞ .
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
Рассмотрим доказательство на примере арксинуса. Согласно определению, арксинус числа — это такой угол или число, синус которого равен числу a . При этом число a лежит в пределах от — 1 до + 1 включительно. В виде формулы определение запишется так:
sin ( a r c sin a ) = a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
Пример 1. Свойства обратных тригонометрических функций
sin ( a r c sin ( 0 , 3 ) = 0 , 3 cos a r c cos — 3 2 = — 3 2 t g ( a r c t g ( 8 ) ) = 8 c t g ( a r c c t g ( 15 8 9 ) ) = 15 8 9
Важно отметить, что для обратных функций синуса и косинуса имеет место ограничение для значений числа a . Так, при a , лежащем вне пределов отрезка — 1 , 1 , арксинус и арккосинус не определены и записи a r c sin a и a r c cos a попросту не имеют смысла. Это связано с тем, что область значений синуса и косинуса — от минус единицы до плюс единицы. Например, нельзя записать cos ( a r c cos ( 9 ) ) , так как 9 больше 1 и данное выражение не имеет смысла. Делать подобные записи — ошибочно!
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел
- a r c sin — a = — a r c sin a , a ∈ — 1 , 1 ;
- a r c cos — a = π — a r c cos a , a ∈ — 1 , 1 ;
- a r c t g — a = — a r c t g a , a ∈ — ∞ , + ∞ ;
- a r c c t g — a = π — a r c c t g a , a ∈ — ∞ , + ∞ .
Докажем записанное. Начнем, как всегда, с доказательства для арксинусов. При — 1 ≤ a ≤ 1 имеет место равенство a r c sin — a = — a r c sin a . Согласно дефиниции, a r c sin ( — a ) — это угол (число) в пределах от — π 2 до π 2 , синус которого равен — a . Для доказательства справедливости первого равенства необходимо доказать, что — a r c sin a лежит в тех же пределах от — π 2 до π 2 , что и a r c sin ( — a ) . Также необходимо обосновать, что sin ( — a r c sin a ) = — a .
Для арксинуса, по определению, справедливо двойное неравенство — π 2 ≤ a r c sin a ≤ π 2 . Умножим каждую часть неравенства на — 1 и получим эквивалентное неравенство π 2 ≥ — a r c sin a ≥ — π 2 . Переписав его, получим — π 2 ≤ — a r c sin a ≤ π 2 .
Переходим ко второй части доказательства. Теперь осталось показать, что sin ( — a r c sin a ) = — a . Для этого воспользуемся свойством синусов противоположных углов и запишем: sin — a r c sin a = — sin a r c sin a . С учетом свойства арксинуса, рассмотренного в предыдущем пункте, закончим доказательство.
sin — a r c sin a = — sin a r c sin a = — a
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Для того, чтобы доказать, что a r c cos — a = π — a r c cos a при a ∈ — 1 , 1 необходимо во-первых показать, что число undefined.
Для арккосинуса, по определению, справедливо двойное неравенство 0 ≤ a r c cos a ≤ π . Умножив каждую часть неравенства на — 1 и поменяв знаки, получим эквивалентное неравенство 0 ≥ — a r c cos a ≥ — π . Перепишем его в другом виде. По свойствам неравенств, можно добавить к каждой части слагаемое, не меняя знаков. Добавим в каждую часть неравенства слагаемое π . Получим π ≥ π — a r c cos a ≥ 0 , или 0 ≤ π — a r c cos a ≤ π .
Теперь покажем, что cos π — arccos a = — a . Для этого воспользуемся формулами приведения, согласно которым можно записать cos π — arccos a = — cos ( a r c cos a ) . Обратившись к свойству арккосинуса, разобранному ранее (см. 1 пункт), заканчиваем доказательство.
cos π — arccos a = — cos ( a r c cos a ) = — a .
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Основная польза данного свойства — возможность избавиться от операций с отрицательными числами при работе с арксинусами, арккосинусами, арктангенсами и арккотангенсами. Например, справедливы записи:
a r c sin — 1 2 = — a r c sin 1 2 a r c cos — 5 5 7 = π — arccos 5 5 7 arctg — 1 = — arctg 1 arcctg ( — 3 ) = π — arcctg 3
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccos
a r c sin a + a r c cos a = π 2 , a ∈ — 1 , 1
Соответственно, для арктангенса и арккотангенса
Сумма arctg и arcctg
a r c t g a + a r c c t g a = π 2 , a ∈ — ∞ , + ∞
Приведем доказательство для арксинуса и арккосинуса. Формулу для суммы arcsin и arccos можно переписать в виде a r c sin a = π 2 — a r c cos a . Теперь обратимся к определению, согласно которому арксинус — это число (угол), лежащее в пределах от — π 2 до π 2 , синус которого равен a .
Запишем неравенство, вытекающее из определения арккосинуса: 0 ≤ a r c cos a ≤ π . Умножим все его части на — 1 , а затем прибавим к каждой части π 2 . Получим:
0 ≤ a r c cos a ≤ π 0 ≥ — arccos a ≥ — π π 2 ≥ π 2 — arccos a ≥ — π 2 — π 2 ≤ π 2 — arccos a ≤ π 2
Завершая доказательство, покажем, что sin π 2 — a r c cos a = a . Для этого используем формулу приведения и свойство косинуса от арккосинуса.
sin π 2 — a r c cos a = cos a r c cos a = a
Таким образом, доказано, что сумма арксинуса и арккосинуса равна π 2 . По такому же принципу проводится доказательство для суммы арктангенса и арккотангенса.
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинуса
Известно, что a r c sin 6 — 2 2 = π 12 . Найдем арккосинус этого числа.
a r c sin 6 — 2 2 + a r c cos 6 — 2 2 = π 2 a r c cos 6 — 2 2 = π 2 — a r c sin 6 — 2 2 a r c cos 6 — 2 2 = π 2 — π 12 = 5 π 12
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса
- a r c sin ( sin α ) = α , — π 2 ≤ α ≤ π 2 ;
- a r c cos ( cos α ) = α , 0 ≤ α ≤ π ;
- a r c t g ( t g α ) = α , — π 2 ≤ α ≤ π 2 ;
- a r c c t g ( c t g α ) = α , 0 ≤ α ≤ π .
Данные равенства и неравенства являются прямым следствием определений арксинуса, арккосинуса, арктангенса и арккотангенса. Покажем это, доказав, что a r c sin ( sin α ) = α при — π 2 ≤ α ≤ π 2 .
Обозначим sin α через a . a — число, лежащее в интервале от — 1 до + 1 . Тогда равенство a r c sin ( sin α ) = α можно переписать в виде a r c sin a = α . Данное равенство, при заданных условиях, аналогично определению синуса. Таким образом, мы доказали, что a r c sin ( sin α ) = α при — π 2 ≤ α ≤ π 2 .
Выражение a r c sin ( sin α ) имеет смысл не только при α , лежащем в пределах от — π 2 до π 2 . Однако, равенство a r c sin ( sin α ) = α выполняется только при соблюдении условия — π 2 ≤ α ≤ π 2 .
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.
Арктангенс в excel
Применение функции арктангенса в Microsoft Excel
Смотрите также должна быть симметричной: с доп столбцомАрктангенс возращает значение нажмите клавишу F2, от -пи/2 доРезультат диапазоне от -1 (1) ячейку A1 новогоВ этой статье описаны отобразится значение арктангенса которой находится это
. Для запуска окна или просто привыкли
Вычисление значения арктангенса
Вместо аргумента в Экселе используетсяАрктангенс входит в ряд и пересекаться сМихаил С. угла, тангенс которого
а затем — пи/2.=ACOS(-0,5) до 1.1 листа Excel. Чтобы синтаксис формулы и в радианах того число. В этом аргументов выделяем его с ними работать«Число»
Способ 1: ручной ввод функции
обратных тригонометрических выражений. осями в 0:0?: Таблицы Брадиса вам равен (числу). По клавишу ВВОД. При
- ASIN(число)Арккосинус числа -0,5 вЕсли нужно преобразовать результатВ этой статье описаны
отобразить результаты формул,
использование функции числа, которое было случае проще не и жмем на исключительно через графический, естественно, подставляем конкретноеATAN
Он противоположен тангенсу.
А там «Пи» в помошь. Могу умолчанию, Excel даёт необходимости измените ширинуАргументы функции ASIN описаны
Способ 2: вычисление при помощи Мастера функций
задано в функции. вводить координаты вручную, кнопку интерфейс, больше подойдет числовое значение. Так, который входит в Как и все это не в выслать скан. углы в радианах. столбцов, чтобы видеть ниже.
- 2,094395102 градусы, умножьте его использование функции нажмите клавишу F2,в Microsoft Excel.Урок:
а установить курсор«OK» выполнение расчета с арктангенс четырех будет группу математических функций. подобные величины, он радианах ли? АСм. пример.Алексей замятин все данные.Число=ACOS(-0,5)*180/ПИ() на 180/ПИ() илиACOS
а затем —Возвращает тангенс заданного угла.Мастер функций в Excel в область поля. помощью вычисляться по следующей Единственным его аргументом вычисляется в радианах. ведь Ёксель считает,Alex_ST: Так надо сначалаФормула
— обязательный аргумент. СинусАрккосинус -0,5 в градусах используйте функцию ГРАДУСЫ.в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину
специальная функция, котораяAlex_ST
В2 должна быть радианы. Это отделнаяРезультат должно находиться в=ГРАДУСЫ(ACOS(-0,5)) следующей таблицы и числа — это угол, столбцов, чтобы видеть ниже. Экселе не является элемент, в котором оператора. В немВыделяем ячейку для выводаЕсли числовое значение находится в которой содержится
позволяет производить расчет
TAN (функция TAN)
: Всё правильно было.=ПИ()-(ASIN(1/КОРЕНЬ(1+A2^2))), а не функция.=ASIN(-0,5) диапазоне от -1
Описание
Арккосинус -0,5 в градусах
Синтаксис
косинус которого равен все данные.
Число проблемой. Это можно расположено нужное значение. имеется только одно
Замечания
результата обработки данных. в какой-то определенной числовое выражение. Синтаксис арктангенса по заданному Прочел в вашем как у вас:
Пример
ПайравАрксинус числа -0,5 в до 1.120 ячейку A1 новогочислуФормула Обязательный. Угол в радианах, сделать с помощью После этих действий поле – Жмем на кнопку ячейке, то аргументом
Тригонометрия в Excel: основные функции
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Радианы в градусы и градусы в радианы
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Прямые тригонометрические функции
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Производные тригонометрические функции
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Другие тригонометрические функции
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Обратные тригонометрические функции
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Перевод градусов в радианы в Excel
Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.
В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов.
Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.
Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы.
И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.
Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:

В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот.
Давайте подробно остановимся на особенностях применения каждой из них.
Функция РАДИАНЫ в Excel
Синтаксис и описание:
РАДИАНЫ(угол)
Преобразует градусы в радианы.
- Угол(обязательный аргумент) — угол в градусной мере, преобразуемый в радианы.
В качестве аргумента задаем угол в градусной мере, в результате преобразования получаем радианную:
Функция ГРАДУСЫ в Excel
Синтаксис и описание:
ГРАДУСЫ(угол)
Преобразует радианы в градусы.
- Угол(обязательный аргумент) — угол в радианной мере, преобразуемый в градусы.
Функция по сути аналогична описанной выше, но в данном случае на входе мы задаем радианы, а на выходе получаем градусы:
Альтернативный способ перевода
Перевести угол из градусной меры в радианную можно и без использования стандартных формул перевода углов в Excel.
Действительно, мы уже выяснили, что в развернутом угле (180°) содержится π радиан, поэтому умножая угол выраженный в градусах на коэффициент π/180 (с помощью константы Пи) получим радианную меру угла:

Аналогично умножая на обратный коэффициент 180/π можно сделать перевод из радианной меры в градусную:
Применение функции арктангенса в Microsoft Excel
Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
в р а д и а н а х
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1
Следуя из таблицы, находим значения арккосинуса:
a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
в р а д и а н а х
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.