In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y.[1] The set X is called the domain of the function[2] and the set Y is called the codomain of the function.[3][better source needed]
Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly enlarged the domains of application of the concept.
A function is most often denoted by letters such as f, g and h, and the value of a function f at an element x of its domain is denoted by f(x); the numerical value resulting from the function evaluation at a particular input value is denoted by replacing x with this value; for example, the value of f at x = 4 is denoted by f(4). When the function is not named and is represented by an expression E, the value of the function at, say, x = 4 may be denoted by E|x=4. For example, the value at 4 of the function that maps x to 

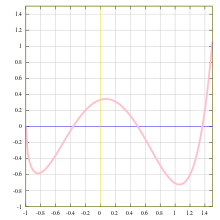
A function is uniquely represented by the set of all pairs (x, f (x)), called the graph of the function, a popular means of illustrating the function.[note 1][4] When the domain and the codomain are sets of real numbers, each such pair may be thought of as the Cartesian coordinates of a point in the plane.
Functions are widely used in science, engineering, and in most fields of mathematics. It has been said that functions are «the central objects of investigation» in most fields of mathematics.[5]
Schematic depiction of a function described metaphorically as a «machine» or «black box» that for each input yields a corresponding output
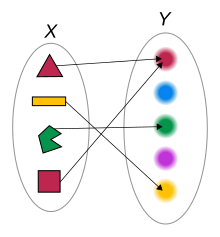
A function that associates any of the four colored shapes to its color.
Definition[edit]
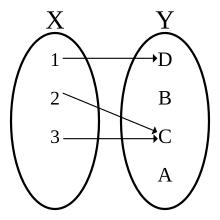
Diagram of a function, with domain X = {1, 2, 3} and codomain Y = {A, B, C, D}, which is defined by the set of ordered pairs {(1, D), (2, C), (3, C)} . The image/range is the set {C, D} .
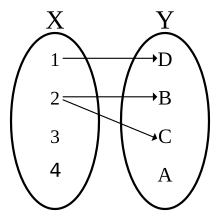
This diagram, representing the set of pairs {(1,D), (2,B), (2,C)} , does not define a function. One reason is that 2 is the first element in more than one ordered pair, (2, B) and (2, C), of this set. Two other reasons, also sufficient by themselves, is that neither 3 nor 4 are first elements (input) of any ordered pair therein.
A function from a set X to a set Y is an assignment of an element of Y to each element of X. The set X is called the domain of the function and the set Y is called the codomain of the function.
A function, its domain, and its codomain, are declared by the notation f: X→Y, and the value of a function f at an element x of X, denoted by f(x), is called the image of x under f, or the value of f applied to the argument x.
Functions are also called maps or mappings, though some authors make some distinction between «maps» and «functions» (see § Other terms).
Two functions f and g are equal if their domain and codomain sets are the same and their output values agree on the whole domain. More formally, given f: X → Y and g: X → Y, we have f = g if and only if f(x) = g(x) for all x ∈ X.[citation needed][note 2]
The domain and codomain are not always explicitly given when a function is defined, and, without some (possibly difficult) computation, one might only know that the domain is contained in a larger set. Typically, this occurs in mathematical analysis, where «a function from X to Y « often refers to a function that may have a proper subset[note 3] of X as domain. For example, a «function from the reals to the reals» may refer to a real-valued function of a real variable. However, a «function from the reals to the reals» does not mean that the domain of the function is the whole set of the real numbers, but only that the domain is a set of real numbers that contains a non-empty open interval. Such a function is then called a partial function. For example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1/f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0.
The range or image of a function is the set of the images of all elements in the domain.[6][7][8][9]
Total, univalent relation[edit]
Any subset of the Cartesian product of two sets X and Y defines a binary relation R ⊆ X × Y between these two sets. It is immediate that an arbitrary relation may contain pairs that violate the necessary conditions for a function given above.
A binary relation is univalent (also called right-unique) if
A binary relation is total if
A partial function is a binary relation that is univalent, and a function is a binary relation that is univalent and total.
Various properties of functions and function composition may be reformulated in the language of relations.[10] For example, a function is injective if the converse relation RT ⊆ Y × X is univalent, where the converse relation is defined as RT = {(y, x) | (x, y) ∈ R}.
Set exponentiation[edit]
The set of all functions from a set 

which is read as 

This notation is the same as the notation for the Cartesian product of a family of copies of 

The identity of these two notations is motivated by the fact that a function 


When 








Notation[edit]
There are various standard ways for denoting functions. The most commonly used notation is functional notation, which is the first notation described below.
Functional notation[edit]
In functional notation, the function is immediately given a name, such as f, and its definition is given by what f does to the explicit argument x, using a formula in terms of x. For example, the function which takes a real number as input and outputs that number plus 1 is denoted by
.
If a function is defined in this notation, its domain and codomain are implicitly taken to both be 

A more complicated example is the function
.
In this example, the function f takes a real number as input, squares it, then adds 1 to the result, then takes the sine of the result, and returns the final result as the output.
When the symbol denoting the function consists of several characters and no ambiguity may arise, the parentheses of functional notation might be omitted. For example, it is common to write sin x instead of sin(x).
Functional notation was first used by Leonhard Euler in 1734.[11] Some widely used functions are represented by a symbol consisting of several letters (usually two or three, generally an abbreviation of their name). In this case, a roman type is customarily used instead, such as «sin» for the sine function, in contrast to italic font for single-letter symbols.
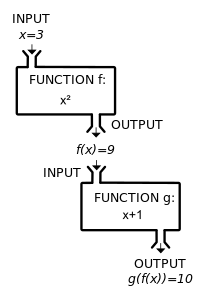
When using this notation, one often encounters the abuse of notation whereby the notation f(x) can refer to the value of f at x, or to the function itself. If the variable x was previously declared, then the notation f(x) unambiguously means the value of f at x. Otherwise, it is useful to understand the notation as being both simultaneously; this allows one to denote composition of two functions f and g in a succinct manner by the notation f(g(x)).
However, distinguishing f and f(x) can become important in cases where functions themselves serve as inputs for other functions. (A function taking another function as an input is termed a functional.) Other approaches of notating functions, detailed below, avoid this problem but are less commonly used.
Arrow notation[edit]
Arrow notation defines the rule of a function inline, without requiring a name to be given to the function. For example, 

The domain and codomain can also be explicitly stated, for example:
This defines a function sqr from the integers to the integers that returns the square of its input.
As a common application of the arrow notation, suppose 



Index notation[edit]
Index notation is often used instead of functional notation. That is, instead of writing f (x), one writes 
This is typically the case for functions whose domain is the set of the natural numbers. Such a function is called a sequence, and, in this case the element 
The index notation is also often used for distinguishing some variables called parameters from the «true variables». In fact, parameters are specific variables that are considered as being fixed during the study of a problem. For example, the map 




Dot notation[edit]
In the notation
the symbol x does not represent any value, it is simply a placeholder meaning that, if x is replaced by any value on the left of the arrow, it should be replaced by the same value on the right of the arrow. Therefore, x may be replaced by any symbol, often an interpunct « ⋅ «. This may be useful for distinguishing the function f (⋅) from its value f (x) at x.
For example, 



Specialized notations[edit]
There are other, specialized notations for functions in sub-disciplines of mathematics. For example, in linear algebra and functional analysis, linear forms and the vectors they act upon are denoted using a dual pair to show the underlying duality. This is similar to the use of bra–ket notation in quantum mechanics. In logic and the theory of computation, the function notation of lambda calculus is used to explicitly express the basic notions of function abstraction and application. In category theory and homological algebra, networks of functions are described in terms of how they and their compositions commute with each other using commutative diagrams that extend and generalize the arrow notation for functions described above.
Other terms[edit]
| Term | Distinction from «function» |
|---|---|
| Map/Mapping | None; the terms are synonymous.[12] |
| A map can have any set as its codomain, while, in some contexts, typically in older books, the codomain of a function is specifically the set of real or complex numbers.[13] | |
| Alternatively, a map is associated with a special structure (e.g. by explicitly specifying a structured codomain in its definition). For example, a linear map.[14] | |
| Homomorphism | A function between two structures of the same type that preserves the operations of the structure (e.g. a group homomorphism).[15] |
| Morphism | A generalisation of homomorphisms to any category, even when the objects of the category are not sets (for example, a group defines a category with only one object, which has the elements of the group as morphisms; see Category (mathematics) § Examples for this example and other similar ones).[16] |
A function is often also called a map or a mapping, but some authors make a distinction between the term «map» and «function». For example, the term «map» is often reserved for a «function» with some sort of special structure (e.g. maps of manifolds). In particular map is often used in place of homomorphism for the sake of succinctness (e.g., linear map or map from G to H instead of group homomorphism from G to H). Some authors[14] reserve the word mapping for the case where the structure of the codomain belongs explicitly to the definition of the function.
Some authors, such as Serge Lang,[13] use «function» only to refer to maps for which the codomain is a subset of the real or complex numbers, and use the term mapping for more general functions.
In the theory of dynamical systems, a map denotes an evolution function used to create discrete dynamical systems. See also Poincaré map.
Whichever definition of map is used, related terms like domain, codomain, injective, continuous have the same meaning as for a function.
Specifying a function[edit]
Given a function 








By listing function values[edit]
On a finite set, a function may be defined by listing the elements of the codomain that are associated to the elements of the domain. For example, if 


By a formula[edit]
Functions are often defined by a formula that describes a combination of arithmetic operations and previously defined functions; such a formula allows computing the value of the function from the value of any element of the domain.
For example, in the above example, 


When a function is defined this way, the determination of its domain is sometimes difficult. If the formula that defines the function contains divisions, the values of the variable for which a denominator is zero must be excluded from the domain; thus, for a complicated function, the determination of the domain passes through the computation of the zeros of auxiliary functions. Similarly, if square roots occur in the definition of a function from 

For example, 




Functions are often classified by the nature of formulas that define them:
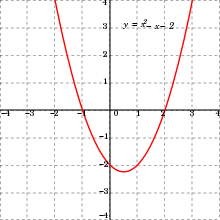
- A quadratic function is a function that may be written
where a, b, c are constants.
- More generally, a polynomial function is a function that can be defined by a formula involving only additions, subtractions, multiplications, and exponentiation to nonnegative integers. For example,
and
- A rational function is the same, with divisions also allowed, such as
and
- An algebraic function is the same, with nth roots and roots of polynomials also allowed.
- An elementary function[note 4] is the same, with logarithms and exponential functions allowed.
Inverse and implicit functions[edit]
A function 



If a function 


More generally, given a binary relation R between two sets X and Y, let E be a subset of X such that, for every 



For example, the equation of the unit circle 
In this example, the equation can be solved in y, giving 


The implicit function theorem provides mild differentiability conditions for existence and uniqueness of an implicit function in the neighborhood of a point.
Using differential calculus[edit]
Many functions can be defined as the antiderivative of another function. This is the case of the natural logarithm, which is the antiderivative of 1/x that is 0 for x = 1. Another common example is the error function.
More generally, many functions, including most special functions, can be defined as solutions of differential equations. The simplest example is probably the exponential function, which can be defined as the unique function that is equal to its derivative and takes the value 1 for x = 0.
Power series can be used to define functions on the domain in which they converge. For example, the exponential function is given by 
By recurrence[edit]
Functions whose domain are the nonnegative integers, known as sequences, are often defined by recurrence relations.
The factorial function on the nonnegative integers (
and the initial condition
Representing a function[edit]
A graph is commonly used to give an intuitive picture of a function. As an example of how a graph helps to understand a function, it is easy to see from its graph whether a function is increasing or decreasing. Some functions may also be represented by bar charts.
Graphs and plots[edit]
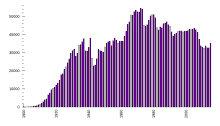
The function mapping each year to its US motor vehicle death count, shown as a line chart
The same function, shown as a bar chart
Given a function 
In the frequent case where X and Y are subsets of the real numbers (or may be identified with such subsets, e.g. intervals), an element 
consisting of all points with coordinates 



Tables[edit]
A function can be represented as a table of values. If the domain of a function is finite, then the function can be completely specified in this way. For example, the multiplication function 

|
y x |
1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 6 | 8 | 10 |
| 3 | 3 | 6 | 9 | 12 | 15 |
| 4 | 4 | 8 | 12 | 16 | 20 |
| 5 | 5 | 10 | 15 | 20 | 25 |
On the other hand, if a function’s domain is continuous, a table can give the values of the function at specific values of the domain. If an intermediate value is needed, interpolation can be used to estimate the value of the function. For example, a portion of a table for the sine function might be given as follows, with values rounded to 6 decimal places:
| x | sin x |
|---|---|
| 1.289 | 0.960557 |
| 1.290 | 0.960835 |
| 1.291 | 0.961112 |
| 1.292 | 0.961387 |
| 1.293 | 0.961662 |
Before the advent of handheld calculators and personal computers, such tables were often compiled and published for functions such as logarithms and trigonometric functions.
Bar chart[edit]
Bar charts are often used for representing functions whose domain is a finite set, the natural numbers, or the integers. In this case, an element x of the domain is represented by an interval of the x-axis, and the corresponding value of the function, f(x), is represented by a rectangle whose base is the interval corresponding to x and whose height is f(x) (possibly negative, in which case the bar extends below the x-axis).
General properties[edit]
This section describes general properties of functions, that are independent of specific properties of the domain and the codomain.
Standard functions[edit]
There are a number of standard functions that occur frequently:
- For every set X, there is a unique function, called the empty function, or empty map, from the empty set to X. The graph of an empty function is the empty set.[note 5] The existence of empty functions is needed both for the coherency of the theory and for avoiding exceptions concerning the empty set in many statements. Under the usual set-theoretic definition of a function as an ordered triplet (or equivalent ones), there is exactly one empty function for each set, thus the empty function
is not equal to
if and only if
, although their graph are both the empty set.
- For every set X and every singleton set {s}, there is a unique function from X to {s}, which maps every element of X to s. This is a surjection (see below) unless X is the empty set.
- Given a function
the canonical surjection of f onto its image
is the function from X to f(X) that maps x to f(x).
- For every subset A of a set X, the inclusion map of A into X is the injective (see below) function that maps every element of A to itself.
- The identity function on a set X, often denoted by idX, is the inclusion of X into itself.
Function composition[edit]
Given two functions 


That is, the value of 
The composition 







The function composition is associative in the sense that, if one of 

The identity functions 


-
A composite function g(f(x)) can be visualized as the combination of two «machines».
-
A simple example of a function composition
-
Another composition. In this example, (g ∘ f )(c) = #.
Image and preimage[edit]
Let 
The image of f is the image of the whole domain, that is, f(X).[17] It is also called the range of f,[6][7][8][9] although the term range may also refer to the codomain.[9][17][18]
On the other hand, the inverse image or preimage under f of an element y of the codomain Y is the set of all elements of the domain X whose images under f equal y.[6] In symbols, the preimage of y is denoted by 
Likewise, the preimage of a subset B of the codomain Y is the set of the preimages of the elements of B, that is, it is the subset of the domain X consisting of all elements of X whose images belong to B.[6] It is denoted by 
For example, the preimage of 

By definition of a function, the image of an element x of the domain is always a single element of the codomain. However, the preimage 

If 
The preimage by f of an element y of the codomain is sometimes called, in some contexts, the fiber of y under f.
If a function f has an inverse (see below), this inverse is denoted 





![{displaystyle f[A],f^{-1}[C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d728b72b3681c1a33529ac867bc49952dc812a4)
Injective, surjective and bijective functions[edit]
Let 
The function f is injective (or one-to-one, or is an injection) if f(a) ≠ f(b) for any two different elements a and b of X.[17][19] Equivalently, f is injective if and only if, for any 












The function f is surjective (or onto, or is a surjection) if its range 











The function f is bijective (or is a bijection or a one-to-one correspondence) if it is both injective and surjective.[17][21] That is, f is bijective if, for any 




Every function 

«One-to-one» and «onto» are terms that were more common in the older English language literature; «injective», «surjective», and «bijective» were originally coined as French words in the second quarter of the 20th century by the Bourbaki group and imported into English.[citation needed] As a word of caution, «a one-to-one function» is one that is injective, while a «one-to-one correspondence» refers to a bijective function. Also, the statement «f maps X onto Y» differs from «f maps X into B«, in that the former implies that f is surjective, while the latter makes no assertion about the nature of f. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage of being more symmetrical.
Restriction and extension[edit]
If 


for all x in S. Restrictions can be used to define partial inverse functions: if there is a subset S of the domain of a function 




Function restriction may also be used for «gluing» functions together. Let 








An extension of a function f is a function g such that f is a restriction of g. A typical use of this concept is the process of analytic continuation, that allows extending functions whose domain is a small part of the complex plane to functions whose domain is almost the whole complex plane.
Here is another classical example of a function extension that is encountered when studying homographies of the real line. A homography is a function 




Multivariate function [edit]
A binary operation is a typical example of a bivariate function which assigns to each pair 

A multivariate function, or function of several variables is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time travelled and its average speed.
More formally, a function of n variables is a function whose domain is a set of n-tuples.
For example, multiplication of integers is a function of two variables, or bivariate function, whose domain is the set of all pairs (2-tuples) of integers, and whose codomain is the set of integers. The same is true for every binary operation. More generally, every mathematical operation is defined as a multivariate function.
The Cartesian product 




where the domain U has the form
When using function notation, one usually omits the parentheses surrounding tuples, writing 

In the case where all the 



It is common to also consider functions whose codomain is a product of sets. For example, Euclidean division maps every pair (a, b) of integers with b ≠ 0 to a pair of integers called the quotient and the remainder:
The codomain may also be a vector space. In this case, one talks of a vector-valued function. If the domain is contained in a Euclidean space, or more generally a manifold, a vector-valued function is often called a vector field.
In calculus[edit]
The idea of function, starting in the 17th century, was fundamental to the new infinitesimal calculus. At that time, only real-valued functions of a real variable were considered, and all functions were assumed to be smooth. But the definition was soon extended to functions of several variables and to functions of a complex variable. In the second half of the 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined.
Functions are now used throughout all areas of mathematics. In introductory calculus, when the word function is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with STEM majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as real analysis and complex analysis.
Real function[edit]
Graph of a linear function
Graph of a polynomial function, here a quadratic function.
Graph of two trigonometric functions: sine and cosine.
A real function is a real-valued function of a real variable, that is, a function whose codomain is the field of real numbers and whose domain is a set of real numbers that contains an interval. In this section, these functions are simply called functions.
The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are continuous, differentiable, and even analytic. This regularity insures that these functions can be visualized by their graphs. In this section, all functions are differentiable in some interval.
Functions enjoy pointwise operations, that is, if f and g are functions, their sum, difference and product are functions defined by
The domains of the resulting functions are the intersection of the domains of f and g. The quotient of two functions is defined similarly by
but the domain of the resulting function is obtained by removing the zeros of g from the intersection of the domains of f and g.
The polynomial functions are defined by polynomials, and their domain is the whole set of real numbers. They include constant functions, linear functions and quadratic functions. Rational functions are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid division by zero. The simplest rational function is the function 
The derivative of a real differentiable function is a real function. An antiderivative of a continuous real function is a real function that has the original function as a derivative. For example, the function 
A real function f is monotonic in an interval if the sign of 
Many other real functions are defined either by the implicit function theorem (the inverse function is a particular instance) or as solutions of differential equations. For example, the sine and the cosine functions are the solutions of the linear differential equation
such that
Vector-valued function[edit]
When the elements of the codomain of a function are vectors, the function is said to be a vector-valued function. These functions are particularly useful in applications, for example modeling physical properties. For example, the function that associates to each point of a fluid its velocity vector is a vector-valued function.
Some vector-valued functions are defined on a subset of 

Function space[edit]
In mathematical analysis, and more specifically in functional analysis, a function space is a set of scalar-valued or vector-valued functions, which share a specific property and form a topological vector space. For example, the real smooth functions with a compact support (that is, they are zero outside some compact set) form a function space that is at the basis of the theory of distributions.
Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and topological properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of ordinary or partial differential equations result of the study of function spaces.
Multi-valued functions[edit]
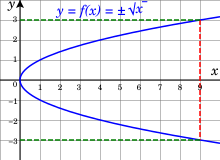
Together, the two square roots of all nonnegative real numbers form a single smooth curve.
Several methods for specifying functions of real or complex variables start from a local definition of the function at a point or on a neighbourhood of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point 
For example, in defining the square root as the inverse function of the square function, for any positive real number 


In the preceding example, one choice, the positive square root, is more natural than the other. This is not the case in general. For example, let consider the implicit function that maps y to a root x of 

Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically analytic functions. The domain to which a complex function may be extended by analytic continuation generally consists of almost the whole complex plane. However, when extending the domain through two different paths, one often gets different values. For example, when extending the domain of the square root function, along a path of complex numbers with positive imaginary parts, one gets i for the square root of −1; while, when extending through complex numbers with negative imaginary parts, one gets −i. There are generally two ways of solving the problem. One may define a function that is not continuous along some curve, called a branch cut. Such a function is called the principal value of the function. The other way is to consider that one has a multi-valued function, which is analytic everywhere except for isolated singularities, but whose value may «jump» if one follows a closed loop around a singularity. This jump is called the monodromy.
In the foundations of mathematics and set theory[edit]
The definition of a function that is given in this article requires the concept of set, since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is generally not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions.
For example, the singleton set may be considered as a function 
These generalized functions may be critical in the development of a formalization of the foundations of mathematics. For example, Von Neumann–Bernays–Gödel set theory, is an extension of the set theory in which the collection of all sets is a class. This theory includes the replacement axiom, which may be stated as: If X is a set and F is a function, then F[X] is a set.
In computer science[edit]
In computer programming, a function is, in general, a piece of a computer program, which implements the abstract concept of function. That is, it is a program unit that produces an output for each input. However, in many programming languages every subroutine is called a function, even when there is no output, and when the functionality consists simply of modifying some data in the computer memory.
Functional programming is the programming paradigm consisting of building programs by using only subroutines that behave like mathematical functions. For example, if_then_else is a function that takes three functions as arguments, and, depending on the result of the first function (true or false), returns the result of either the second or the third function. An important advantage of functional programming is that it makes easier program proofs, as being based on a well founded theory, the lambda calculus (see below).
Except for computer-language terminology, «function» has the usual mathematical meaning in computer science. In this area, a property of major interest is the computability of a function. For giving a precise meaning to this concept, and to the related concept of algorithm, several models of computation have been introduced, the old ones being general recursive functions, lambda calculus and Turing machine. The fundamental theorem of computability theory is that these three models of computation define the same set of computable functions, and that all the other models of computation that have ever been proposed define the same set of computable functions or a smaller one. The Church–Turing thesis is the claim that every philosophically acceptable definition of a computable function defines also the same functions.
General recursive functions are partial functions from integers to integers that can be defined from
- constant functions,
- successor, and
- projection functions
via the operators
- composition,
- primitive recursion, and
- minimization.
Although defined only for functions from integers to integers, they can model any computable function as a consequence of the following properties:
- a computation is the manipulation of finite sequences of symbols (digits of numbers, formulas, …),
- every sequence of symbols may be coded as a sequence of bits,
- a bit sequence can be interpreted as the binary representation of an integer.
Lambda calculus is a theory that defines computable functions without using set theory, and is the theoretical background of functional programming. It consists of terms that are either variables, function definitions (𝜆-terms), or applications of functions to terms. Terms are manipulated through some rules, (the α-equivalence, the β-reduction, and the η-conversion), which are the axioms of the theory and may be interpreted as rules of computation.
In its original form, lambda calculus does not include the concepts of domain and codomain of a function. Roughly speaking, they have been introduced in the theory under the name of type in typed lambda calculus. Most kinds of typed lambda calculi can define fewer functions than untyped lambda calculus.
See also[edit]
Subpages[edit]
- List of types of functions
- List of functions
- Function fitting
- Implicit function
Generalizations[edit]
- Higher-order function
- Homomorphism
- Morphism
- Microfunction
- Distribution
- Functor
[edit]
- Associative array
- Closed-form expression
- Elementary function
- Functional
- Functional decomposition
- Functional predicate
- Functional programming
- Parametric equation
- Set function
- Simple function
Notes[edit]
- ^ This definition of «graph» refers to a set of pairs of objects. Graphs, in the sense of diagrams, are most applicable to functions from the real numbers to themselves. All functions can be described by sets of pairs but it may not be practical to construct a diagram for functions between other sets (such as sets of matrices).
- ^ This follows from the axiom of extensionality, which says two sets are the same if and only if they have the same members. Some authors drop codomain from a definition of a function, and in that definition, the notion of equality has to be handled with care; see, for example, «When do two functions become equal?». Stack Exchange. August 19, 2015.
- ^ called the domain of definition by some authors, notably computer science
- ^ Here «elementary» has not exactly its common sense: although most functions that are encountered in elementary courses of mathematics are elementary in this sense, some elementary functions are not elementary for the common sense, for example, those that involve roots of polynomials of high degree.
- ^ By definition, the graph of the empty function to X is a subset of the Cartesian product ∅ × X, and this product is empty.
- ^ The axiom of choice is not needed here, as the choice is done in a single set.
References[edit]
- ^ Halmos 1970, p. 30; the words map, mapping, transformation, correspondence, and operator are often used synonymously.
- ^ Halmos 1970
- ^ «Mapping», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ^ «function | Definition, Types, Examples, & Facts». Encyclopedia Britannica. Retrieved 2020-08-17.
- ^ Spivak 2008, p. 39.
- ^ a b c d e f Kudryavtsev, L.D. (2001) [1994], «Function», Encyclopedia of Mathematics, EMS Press
- ^ a b Taalman, Laura; Kohn, Peter (2014). Calculus. New York City: W. H. Freeman and Company. p. 3. ISBN 978-1-4292-4186-1. LCCN 2012947365. OCLC 856545590. OL 27544563M.
- ^ a b Trench, William F. (2013) [2003]. Introduction to Real Analysis (2.04th ed.). Pearson Education (originally; self-republished by the author). pp. 30–32. ISBN 0-13-045786-8. LCCN 2002032369. OCLC 953799815. Zbl 1204.00023.
- ^ a b c Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Elementary Real Analysis (PDF) (2nd ed.). Prentice Hall (originally; 2nd ed. self-republished by the authors). pp. A-4–A-5. ISBN 978-1-4348-4367-8. OCLC 1105855173. OL 31844948M. Zbl 0872.26001.
- ^ Schmidt, Gunther (2011). «§5.1 Functions». Relational Mathematics. Encyclopedia of Mathematics and its Applications. Vol. 132. Cambridge University Press. pp. 49–60. ISBN 978-0-521-76268-7.
- ^ Ron Larson, Bruce H. Edwards (2010), Calculus of a Single Variable, Cengage Learning, p. 19, ISBN 978-0-538-73552-0
- ^ Weisstein, Eric W. «Map». mathworld.wolfram.com. Retrieved 2019-06-12.
- ^ a b Lang, Serge (1987). «III §1. Mappings». Linear Algebra (3rd ed.). Springer. p. 43. ISBN 978-0-387-96412-6.
A function is a special type of mapping, namely it is a mapping from a set into the set of numbers, i.e. into, R, or C or into a field K.
- ^ a b Apostol, T.M. (1981). Mathematical Analysis (2nd ed.). Addison-Wesley. p. 35. ISBN 978-0-201-00288-1. OCLC 928947543.
- ^ James, Robert C.; James, Glenn (1992). Mathematics dictionary (5th ed.). Van Nostrand Reinhold. p. 202. ISBN 0-442-00741-8. OCLC 25409557.
- ^ James & James 1992, p. 48
- ^ a b c d e Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2008). The Princeton Companion to Mathematics. Princeton, New Jersey: Princeton University Press. p. 11. doi:10.1515/9781400830398. ISBN 978-0-691-11880-2. JSTOR j.ctt7sd01. LCCN 2008020450. MR 2467561. OCLC 227205932. OL 19327100M. Zbl 1242.00016.
- ^ Quantities and Units — Part 2: Mathematical signs and symbols to be used in the natural sciences and technology, p. 15. ISO 80000-2 (ISO/IEC 2009-12-01)
- ^ a b Ivanova, O.A. (2001) [1994], «Injection», Encyclopedia of Mathematics, EMS Press
- ^ a b Ivanova, O.A. (2001) [1994], «Surjection», Encyclopedia of Mathematics, EMS Press
- ^ a b Ivanova, O.A. (2001) [1994], «Bijection», Encyclopedia of Mathematics, EMS Press
- ^ Gödel 1940, p. 16; Jech 2003, p. 11; Cunningham 2016, p. 57
Sources[edit]
- Bartle, Robert (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05465-8. OCLC 465115030.
- Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. ISBN 978-1-4419-7126-5.
- Cunningham, Daniel W. (2016). Set theory: A First Course. Cambridge University Press. ISBN 978-1-107-12032-7.
- Gödel, Kurt (1940). The Consistency of the Continuum Hypothesis. Princeton University Press. ISBN 978-0-691-07927-1.
- Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 978-0-387-90092-6.
- Jech, Thomas (2003). Set theory (3rd ed.). Springer-Verlag. ISBN 978-3-540-44085-7.
- Spivak, Michael (2008). Calculus (4th ed.). Publish or Perish. ISBN 978-0-914098-91-1.
Further reading[edit]
- Anton, Howard (1980). Calculus with Analytical Geometry. Wiley. ISBN 978-0-471-03248-9.
- Bartle, Robert G. (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05464-1.
- Dubinsky, Ed; Harel, Guershon (1992). The Concept of Function: Aspects of Epistemology and Pedagogy. Mathematical Association of America. ISBN 978-0-88385-081-7.
- Hammack, Richard (2009). «12. Functions» (PDF). Book of Proof. Virginia Commonwealth University. Retrieved 2012-08-01.
- Husch, Lawrence S. (2001). Visual Calculus. University of Tennessee. Retrieved 2007-09-27.
- Katz, Robert (1964). Axiomatic Analysis. D. C. Heath and Company.
- Kleiner, Israel (1989). «Evolution of the Function Concept: A Brief Survey». The College Mathematics Journal. 20 (4): 282–300. CiteSeerX 10.1.1.113.6352. doi:10.2307/2686848. JSTOR 2686848.
- Lützen, Jesper (2003). «Between rigor and applications: Developments in the concept of function in mathematical analysis». In Porter, Roy (ed.). The Cambridge History of Science: The modern physical and mathematical sciences. Cambridge University Press. ISBN 978-0-521-57199-9. An approachable and diverting historical presentation.
- Malik, M. A. (1980). «Historical and pedagogical aspects of the definition of function». International Journal of Mathematical Education in Science and Technology. 11 (4): 489–492. doi:10.1080/0020739800110404.
- Reichenbach, Hans (1947). Elements of Symbolic Logic. Dover. ISBN 0-486-24004-5.
- Ruthing, D. (1984). «Old Intelligencer: Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N.». Mathematical Intelligencer. 6 (4): 71–78. doi:10.1007/BF03026743. S2CID 189883712.
- Thomas, George B.; Finney, Ross L. (1995). Calculus and Analytic Geometry (9th ed.). Addison-Wesley. ISBN 978-0-201-53174-9.
External links[edit]
- «Function», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- NIST Digital Library of Mathematical Functions

Do you follow your instinct when choosing a verb in your function?
Do you use a number of synonyms for the same purpose inconsistently?
If the answer is yes, you are not the only one.
In order to write a clean code, or at least to attempt it, we need to know what words are commonly used so that we can use them, and people can understand easier what we are trying to do.
At the same time, we need to stick with one word for one concept rather than using synonyms inconsistently.
In this post, I’ll summarise commonly used verbs found in programming books and Github regardless of the type of programming language, so we can find the best-suited verbs for our own needs.
On the tables below, we’ll see 5 rows:
- The verb
- The number of times the verb is written on Github to give us some ideas on how commonly it’s used
- Its general definition
- Examples
- Synonyms to avoid using to express the same concept
Just bear with me, this is not a complete list of common words, so please do let me know in the comment if you find some of the definition is too biased on certain programming languages. I’ll also be grateful if you could teach me any other verbs that you think it’s common!
I hope this post helps us, newbies choose a suitable verb and stick to it.
Table of Contents
1️⃣ Alteration
2️⃣ Creation
3️⃣ Establishment
4️⃣ Obtainment
5️⃣ True or False Statement
6️⃣ Conclusion
1. Alteration
| Verb | Written on Github |
Definition | Examples | Synonyms to avoid |
|---|---|---|---|---|
| set | 2B | Often used to put data in an existing resource such as an attribute of an object. | set_name(), set_store_id() | |
| change | 668M | Often used when a whole thing, such as image, is replaced by something else | change_image(), change_colour() | edit |
| edit | 325M | Often used same as change. It could be used especially when action is responsible for rendering the view. | edit_title(), edit_record() | change |
| update | 739M | Often used when one or more of the components is updated as a result, and something new could also be added. | update_file() | |
| add | 1B | Often used to add something into a group of the things. | add_item(), add_member() | append |
| append | 287M | Often used same as add. It could be used when it does not modify the original group of things but produce the new group. | append_item(), append_element() | add |
| remove | 824M | Often used when a given thing is removed from a group of the things. | remove_record(), remove_item() | delete |
| delete | 455M | Often used same as remove, but it could also render nonrecoverable. | delete_record(), delete_item() | remove |
| save | 478M | Often used when preserving data to avoid loss. | save_json(), save_order() | store |
| store | 396M | Often used the same way as save. | store_json(), store_order() | save |
| disable | 586M | Often used to configure a resource an unavailable or inactive state. | disable_user() | hide |
| hide | 237M | Often has the same intention as disable, by hiding it. | hide_field() | disable |
| split | 276M | Used when separating parts of a resource. | split_table(), split_group() | separate |
| separate | 151M | Often used the same way as the verb split. | separate_table(), separate_group() | split |
| merge | 312M | Often used when creating a single resource from multiple resource. | merge_records(), merge_tables() | join |
| join | 220M | It can be used in a same way as merge. | join_records(), join_tables() | merge |
2. Creation
| Verb | Written on Github |
Definition | Examples | Confusing synonyms |
|---|---|---|---|---|
| create | 1B | Used when creating a resource. | create_package(), create_directory() | make, generate |
| make | 797M | Often used in a same way as create. | make_package(), make_statement() | create, generate |
| generate | 286M | Often used in a same way as create. | generate_directory(), generate_statement() | create, make |
| copy | 1B | Used when creating a resource with the same structure and data as the original one. | copy_file(), copy_graph() | clone |
| clone | 147M | Could be used in a same way as copy. | clone_file(), clone_graph() | copy |
3. Establishment
| Verb | Written on Github |
Definition | Examples | Confusing synonyms |
|---|---|---|---|---|
| start | 1B | Generally used when initiating an operation. | start_listening() | begin |
| begin | 342M | Often used in a same way as start. | begin_listening() | start |
| open | 854M | Used when changing state of a resource to make it accessible or usable. | open_file() |
4. Obtainment
| Verb | Written on Github |
Definition | Examples | Confusing synonyms |
|---|---|---|---|---|
| get | 2B | Generally used to obtain a resource. | get_data(), get_store_id() | fetch, retrieve |
| fetch | 146M | Can be used in a same way as get. | fetch_data(), fetch_store_id() | get, retrieve |
| retrieve | 116M | Can be used in a same way as get or fetch | retrieve_data(), retrieve_store_id() | get, fetch |
| read | 1B | Used when acquiring data from a source. | read_file() | |
| find | 672M | Used when looking for an unknown data in a container. | find_element(), find_keyword() | search |
| search | 438M | Generally used in a same way as find. It may refer to look for an unknown data from multiple containers. | search_element(), search_keyword() | find |
| close | 492M | Used when changing state of a resource to make it inaccessible or unusable. | close_file() |
5. True or False Statement
| Verb | Written on Github |
Definition | Examples |
|---|---|---|---|
| is | 3B | Used when defining state of a resource. | Method: is_available(), is_correct() Variables: name_is_available, date_is_correct |
| has | 1B | Used to define whether a resource contains a certain data. | Method: has_name(), has_date() Variables: person_has_name, course_has_date |
| can | 2B | Used to define a certain ability of a resource. | can_load(), can_create() |
| should | 1B | Used to define a certain obligation of a resource. | should_render(), should_print_message() |
6. Conclusion
Writing clean code is not a skill that we can obtain overnight. But at the same time, I believe that we can improve the quality of code significantly and constantly by learning the wisdom of other people’s clean code. To write this bost, I gained so many ideas from the book Clean Code written by Robert C. Martin and many codes on Github. I especially recommend the book for anyone who is just started coding. Many of the contents might seem going too far for newbies, but I am certain that this book will be my forever reference for my career as a developer.
Thanks to these people who share their own hard work!
Thanks for reading. If you have any opinion or question, please leave a comment below! In the meantime, please follow me on Linkedin @Maiko Miyazaki or Twitter @Maiko Miyazaki
A function declaration may be unintentionally turned into a function expression when it appears in an expression context. The function declaration creates functions that are hoisted. Other syntaxes do not hoist the function and the function value is only visible after the definition. A function declaration also creates a variable with the same name as the function name. Thus, unlike those defined by function expressions, functions defined by function declarations can be accessed by their name in the scope they were defined in, as well as in their own body.
This is our Splunktool team suggestion ✌, we tried and its working fine
Get code examples instantly right from your google search results with the Grepper Chrome Extension.
2._
function formatNumber(num) { return num.toFixed(2); } formatNumber(2);
3._
function updateBrand(obj) { obj.brand = "Toyota"; obj = null; } const car = { brand: "Honda", model: "Accord", year: 1998, }; console.log(car.brand); updateBrand(car); console.log(car.brand);
5._
const y = function x() {}; console.log(x);
Suggestion : 2
This is declaring an object property called functionName with a value that’s an anonymous (unnamed) function. This would only occur within curly braces defining an object literal. It’s different from the following, which declares a named function in the current scope, but isn’t a property of any object: Connect and share knowledge within a single location that is structured and easy to search.
A paid website subscription subscribed me on two additional paid websites without my consent. Do I need to do more than cancel on those websites?
1._
functionName: function() { }
2._
function functionName() { }
Suggestion : 3
Now that we know how to access a letter from a word, let’s capitalize it. In JavaScript, we have a method called toUpperCase(), which we can call on strings, or words. As we can imply from the name, you call it on a string/word, and it is going to return the same thing but as an uppercase. In JavaScript, we have a method called join, which we can use to return an array as a string. The method takes a separator as an argument. That is, we specify what to add between words, for example a space.
First of all, let’s start with capitalizing the first letter of a single word. After you learn how to do this, we’ll proceed to the next level – doing it on every word from a sentence. Here is an example:
const publication = "freeCodeCamp";
For instance:
const publication = "freeCodeCamp"; publication[0].toUpperCase();
Running the above code, you are going to get a capital F instead of f. To get the whole word back, we can do this:
const publication = "freeCodeCamp"; publication[0].toUpperCase() + publication.substring(1);
We have to capitalize the first letter from each word from the sentence freeCodeCamp is an awesome resource.
The first step we take is to split the sentence into an array of words. Why? So we can manipulate each word individually. We can do that as follows:
const mySentence = "freeCodeCamp is an awesome resource"; const words = mySentence.split(" ");
After we run the above code, the variable words is assigned an array with each word from the sentence. The array is as follows ["freeCodeCamp", "is", "an", "awesome", "resource"].
const mySentence = "freeCodeCamp is an awesome resource"; const words = mySentence.split(" "); for (let i = 0; i < words.length; i++) { words[i] = words[i][0].toUpperCase() + words[i].substr(1); }
Suggestion : 4
To work around this, we can add backslashes before any character that has a special meaning. If, on the other hand, we just want to make sure the date starts and ends on a word boundary, we can use the marker b. A word boundary can be the start or end of the string or any point in the string that has a word character (as in w) on one side and a nonword character on the other. String values have a replace method that can be used to replace part of the string with another string.
A regular expression is a type of object. It can be either constructed with the RegExp constructor or written as a literal value by enclosing a pattern in forward slash (/) characters.
let re1 = new RegExp("abc"); let re2 = /abc/;
When using the RegExp constructor, the pattern is written as a normal string, so the usual rules apply for backslashes.
The second notation, where the pattern appears between slash characters, treats backslashes somewhat differently. First, since a forward slash ends the pattern, we need to put a backslash before any forward slash that we want to be part of the pattern. In addition, backslashes that aren’t part of special character codes (like n) will be preserved, rather than ignored as they are in strings, and change the meaning of the pattern. Some characters, such as question marks and plus signs, have special meanings in regular expressions and must be preceded by a backslash if they are meant to represent the character itself.
let eighteenPlus = /eighteen+/;
Regular expression objects have a number of methods. The simplest one is test. If you pass it a string, it will return a Boolean telling you whether the string contains a match of the pattern in the expression.
console.log(/abc/.test("abcde")); console.log(/abc/.test("abxde"));
So you could match a date and time format like 01-30-2003 15:20 with the following expression:
let dateTime = /dd-dd-dddd dd:dd/; console.log(dateTime.test("01-30-2003 15:20")); console.log(dateTime.test("30-jan-2003 15:20"));
These backslash codes can also be used inside square brackets. For example, [d.] means any digit or a period character. But the period itself, between square brackets, loses its special meaning. The same goes for other special characters, such as +.
To invert a set of characters—that is, to express that you want to match any character except the ones in the set—you can write a caret (^) character after the opening bracket.
let notBinary = /[^01]/; console.log(notBinary.test("1100100010100110")); console.log(notBinary.test("1100100010200110"));
Suggestion : 5
A closely related and often conflated notion is a keyword, which is a word with special meaning in a particular context. This is a semantic definition. By contrast, names in a standard library but not built into the language are not considered reserved words or keywords. The terms «reserved word» and «keyword» are often used interchangeably – one may say that a reserved word is «reserved for use as a keyword» – and formal use varies from language to language; for this article we distinguish as above.
The sets of reserved words and keywords in a language often coincide or are almost equal, and the distinction is subtle, so the terms are often used interchangeably. However, in careful usage they are distinguished.
In a computer language, a reserved word (also known as a reserved identifier) is a word that cannot be used as an identifier, such as the name of a variable, function, or label – it is «reserved from use». This is a syntactic definition, and a reserved word may have no user-defined meaning.
1._
' Class Definition of This in Visual Basic.NET: Public Class this ' This class does something... End Class
Suggestion : 6
This document serves as the complete definition of Google’s coding standards
for source code in the JavaScript programming language. A JavaScript source file
is described as being in Google Style if and only if it adheres to the rules
herein. Recommended: if any word already has a conventional camel case
appearance in common usage, split this into its constituent parts (e.g.,
AdWords becomes ad words). Note that a word such as iOS is not
really in camel case per se; it defies any convention, so this
recommendation does not apply. Do not use eval or the Function(…string) constructor (except for code
loaders). These features are potentially dangerous and simply do not work in
CSP environments.
For the remaining non-ASCII characters, either the actual Unicode character
(e.g. ∞) or the equivalent hex or Unicode escape (e.g. u221e) is used,
depending only on which makes the code easier to read and understand.
Tip: In the Unicode escape case, and occasionally even when actual Unicode
characters are used, an explanatory comment can be very helpful.
const units = 'μs'; const units = 'u03bcs'; return 'ufeff' + content;
Tip: In the Unicode escape case, and occasionally even when actual Unicode
characters are used, an explanatory comment can be very helpful.
The entire argument to goog.module is what defines a namespace. It is the
package name (an identifier that reflects the fragment of the directory
structure where the code lives) plus, optionally, the main class/enum/interface
that it defines concatenated to the end.
Example
goog.module('search.urlHistory.UrlHistoryService');
The single goog.module statement may optionally be followed by a call to
goog.module.declareLegacyNamespace();. Avoid
goog.module.declareLegacyNamespace() when possible.
Example:
goog.module('my.test.helpers'); goog.module.declareLegacyNamespace(); goog.setTestOnly();
Classes, enums, functions, constants, and other symbols are exported using the
exports object. Exported symbols may be defined directly on the exports
object, or else declared locally and exported separately. Symbols are only
exported if they are meant to be used outside the module. Non-exported
module-local symbols are not declared @private nor do their names end with an
underscore. There is no prescribed ordering for exported and module-local
symbols.
Examples:
const exportedArray = [1, 2, 3]; const moduleLocalArray = [4, 5, 6]; function moduleLocalFunction() { return moduleLocalArray.length; } function exportedFunction() { return moduleLocalFunction() * 2; } exports = {exportedArray, exportedFunction};
Suggestion : 7
A function is a section of code that, once defined, can be reused. Functions are used to make your code easier to understand by breaking it into small, understandable tasks that can be used more than once throughout your program. Let’s create a program that repeats a word a specified number of times. It will take a string parameter called word and an int parameter called reps for the number of times to repeat the word. A parameter is a named entity in a function definition, specifying an argument that the function can accept. In Go, you must specify the data type for each parameter.
In this case, we’ll define a function named hello():
From here, we’ll add a second line to provide the instructions for what the function does. In this case, we’ll be printing Hello, World! to the console:
func hello() { fmt.Println("Hello, World!") }
So, inside of our main() function block, let’s call the function with hello():
package main import "fmt" func main() { hello() } func hello() { fmt.Println("Hello, World!") }
You’ll receive the following output:
Notice that we also introduced a function called main(). The main() function is a special function that tells the compiler that this is where the program should start. For any program that you want to be executable (a program that can be run from the command line), you will need a main() function. The main() function must appear only once, be in the main() package, and receive and return no arguments. This allows for program execution in any Go program. As per the following example:
package main import "fmt" func main() { fmt.Println("this is the main section of the program") }
For nearly a quarter of a century, one of the responsibilities that I’ve taken most seriously is the shepherding of the design of Mathematica. Partly that has involved establishing foundational principles, and maintaining unity and consistency across the system. But at some point all the capabilities of Mathematica must get expressed in the individual built-in functions—like Table or NestList—that ultimately make up the system.
Each one of those functions encapsulates some piece of repeated computational work—often implemented by some deep tower of algorithms. And each one of those now 3000 or so functions requires a name.
We’re currently in the closing weeks of a (spectacular!) new version of Mathematica, and I spent part of last week doing final design reviews for some fascinating new areas of the system. And as part of those design reviews, we were confirming and tweaking some of the names we’re going to use for new functions.
The naming of functions is a strange and difficult art—a bit like an ultimately abstracted form of poetry. The goal is to take the concept and functionality of a function, and capture the essence of it in one, or two, or perhaps three, words (like Riffle, or DeleteCases, or FixedPointList)—chosen so that when someone sees those words, they immediately get the right idea about the function. In even the most succinct forms of ordinary poetry, you get at least a handful of words to communicate with. In function names, you typically get at most perhaps three.
With enough experience, it can sometimes be pretty easy to come up with that little gem of a name for a function. Sometimes it can even seem quite obvious as soon as one thinks about the function. But sometimes it can take immense amounts of time—wrestling with what can seem like an insoluble problem of packing everything one needs to say about a function into that one little name.
It’s an unforgiving and humbling activity. And the issue is almost always the same. The reason you can’t find a good name is because you don’t really understand with complete and ultimate clarity what the function does.
And sometimes that’s because the function really isn’t designed quite right. There’s something muddled about it, that has to be unmuddled before you’ll ever be able to find a good name.
It’s very satisfying, though, when you finally crack it. These days I’m usually working on design reviews with teams of people. And when we finally get the right name, everyone on the call (yes, it’s essentially always a phone call) immediately says “Oh yes, that’s it”. And we all feel a little stupid that we just spent an hour, or however long, just coming up with one or two words.
In ordinary human languages, new words typically develop by some form of natural selection. Usually a word will be introduced—perhaps at first as a phrase—by one person. And then it spreads, sometimes changing a bit, and either becomes popular enough to be widely understood and useful for general communication, or disappears.
But for a computer language the pattern is necessarily different. For once a function name—that corresponds to a “word” in the language—has been introduced, it must immediately be a full, permanent, element of the language. For programs will be written that contain that name, and they would all have to be found and updated if that name was changed. And indeed, in Mathematica, I am proud to say that in nearly a quarter of a century, very very few names have ever had to be changed—so that a program written for Mathematica 1.0 in 1988 can still be understood and executed today by the very latest version of Mathematica.
There is also another difference between words in human languages and function names in a computer language. In a human language, there is no ultimate, absolute, meaning defined for most words. Instead, the best we can do is—like in a dictionary—to define words by relating them to other words.
But in a computer language, each function name ultimately refers to a particular piece of functionality that is defined in an absolute way, and can be implemented by a specific precise program.
This doesn’t usually make it any easier to come up with function names, though. It just means that there’s a clearer notion of the “right name”: the name where a human has the best chance of correctly figuring out from it what the function does.
Function names are in a sense ultimate points of human-machine communication. They’re the places where all that internal computational activity has to be connected with something that humans can understand. When the functionality is simple there are pictorial and other alternatives. But when the functionality is diverse or sophisticated we don’t know any possibility other than to use language—and the linguistic construct of names for things.
The function names in Mathematica are ultimately based on English, and for the most part, they consist of ordinary English words. In ordinary natural human languages, it is possible to introduce a completely new word, and have it gradually gain popularity and understanding. But in the dynamics of computer languages—with their necessarily sudden introduction of new names—one has no choice but to leverage on people’s existing understanding of a human language, like English.
Still, when we come up with function names in Mathematica today, they are in a sense not based just on “raw English”. They also rely on the web of meaning that has developed through the several thousand other functions that already exist in Mathematica.
There are definite conventions about what particular kinds of names mean. (Functions that end in List generate lists; functions that begin with Image operate on images; functions that begin with Find involve some kind of searching; and so on.) There are ways that names tend to appear together in typical usage of the language. And there are definite conceptual frameworks—and metaphors—that have developed in the language and the system. (Nest refers to repeated function application; Flat refers to flattening of nested structures; Dynamic refers to dynamic interactivity; and so on.)
In ordinary human language, natural selection no doubt often favors words that follow certain patterns. Sometimes for example consistency may make words easier to remember; sometimes inconsistency makes them stand out more, and thereby easier to remember. But there is no grand plan to organize the words in a particular way: say to avoid having obscure meanings “take up” short words, or to make words easier to sort in a particular way.
But when we introduce function names in Mathematica we have both the ability—and, I think, the responsibility—to design everything. Of course, the development of Mathematica is incremental, and at any given time we can only foresee a certain amount of what will follow. But still, I take great pains to name every new function in the best possible way.
What are some of the criteria?
First, one must leverage on peoples’ existing knowledge and understanding. If there is a familiar name that’s already widely used, then if at all possible one must use it.
Of course, sometimes that name may only be familiar in some particular area. And it may be very short—perhaps a single letter—and incomprehensible without further context. And in that case, what we typically do in Mathematica is to burn into the name some kind of stylized context. (So, for example, the Fresnel integral S(x) has the name FresnelS in Mathematica.)
In building Mathematica, we’ve had the longstanding principle of always trying to make every function as general as possible—so that it is applicable to as wide a range of situations as possible. Sometimes, though, a function will have one particular, familiar, use. But if the name of the function reflects only that use, one is shortchanging the function. For without a more general name, people will never think to apply it in other cases. (So, for example, it’s List, not “vector”, and it’s Outer, not “outer product”.)
And indeed, one of the responsibilities of function naming is that it is the names of functions that to a large extent directly determine how people will think about a function. If they are led in a particular direction by the name, that will be the direction in which they will go in using the function.
And even the very “texture” of the name is important in getting people to think correctly about functions. A sophisticated function should have a sophisticated name (like DynamicModule or EventHandler). A straightforward, common, function should have a simple name (like Length or Total). A function that does a clear but unusual thing should have an unexpected name (like Thread or Through).
By now in Mathematica there are a great many precedents for how functions should be named. And we always try to follow these precedents whenever possible. First, because they often represent good solutions to the naming problems we’re now trying to solve. And second, because by following them one is maintaining a certain consistency that makes it easier for the system to grow, and for people to learn the system—and to guess about functionality they do not already know.
When one finds a good name for a function, one of the things that happens is that when people hear the name, they can successfully “unpack” it into a one-sentence description of what the function must do—often in effect just by using the name of the function as the main part of a sentence. And indeed, when we’re stuck in trying to find a good name for a function, I’ll often suggest that we try to write a sentence that describes what the function does—that we can perhaps use in the Documentation Center for the function, but then condense down into the nugget we need for the name itself.
One of the painful aspects of function naming is that however clever you are about it, it can never be perfect. I often claim that the only language that is perfectly consistent is the one that does nothing. As soon as there is actual functionality to represent, there are inevitably awkward cases and corners. For example, one wants to maintain consistent simplicity in naming in each area of the system. But then at the overlaps between these areas there are inconsistencies.
And sometimes one runs into limitations of English: there just isn’t any familiar word or phrase for a concept, perhaps because that concept is somehow new to our experience. And in such cases what one typically has to do—just like in natural language—is to come up with an analogy.
Some of the analogies and metaphors we consider start quite wild and outlandish. But eventually they become tamer—like Sow and Reap or Throw and Catch—and an important way to extend the linguistic base for names in Mathematica.
It might be nice if English—like Mathematica—had the feature that a particular word meant only a particular thing, or at least a class of things. But that is not how it works. A single word can act as different parts of speech, and can have wildly different meanings. Usually in actual English usage, one can disambiguate by context.
But in the tiny length of a single function name, one does not have that option. And quite often that means one has to reject some wonderful word just in order to avoid a possible misunderstanding from a different way it can be used in English. (So, for example, “Live” or “Active” can’t be candidates for Dynamic—they’re just too easy to misunderstand.)
If one is lucky, a thesaurus (these days in Wolfram|Alpha) will give one a word that captures the same concept but avoids the potential misunderstanding. But sometimes one has to rearrange the whole structure of the name to avoid the possibility of misunderstanding.
And yet, after all those judgment calls, after all that drilling to clarify precisely what a function does, one has to come to a conclusion: one has to settle on a definite name. That will represent the function—and all the work done to implement it—well. And that will serve as a permanent handle by which people can access some piece of functionality in Mathematica.
I have no idea now how much time I have spent over the past quarter century coming up with names in Mathematica. Each one encapsulates some idea, some creative concept—frozen in a tiny clump of words. Like little poems. Thousands of them.
Pro get/set
When a class has many methods, it is better to use verb prefixes, such as get/set, to distinguish methods from each other.
PHP example:
$foo->setText('Hello world!');
$foo->prependText('So. ');
$foo->appendText(' And welcome');
$x = $foo->getText();
By the way, in Hungarian notation prefixes go with a small letter and will not detract from keyword.
Counter get/set
When you need only two methods, it is easier to use the same noun in the context of using parameters.
jQuery example:
$('.foo').html(); //get
$('.foo').html('Hello world!'); //set
Examples
For functions and static methods with arrays as parameters I use the following rule:
If changes should occur only at run time:
setFoo($arr); // Replace/delete all properties, i.e. if some elements are not passed, the corresponding properties will get empty values.
setFoo([]); // Delete all properties
setFoo(); // Set all properties by default
delFoo($arr); // Delete specified properties
addFoo($arr); // Add/replace specified properties
If changes will be made forever (in DB or files):
deleteFoo(...); // Delete specified properties
insertFoo(...); // Add specified properties
replaceFoo(...); // Add or replace specified properties
updateFoo(...); // Update specified properties
For both cases:
$arr = getFoo(); // Get all properties
$val = getFoo($level1, $level2, ...); // You can obtain the value of the given level, placing the list of arguments
or
$val=getFoo()[$level1][$level2];