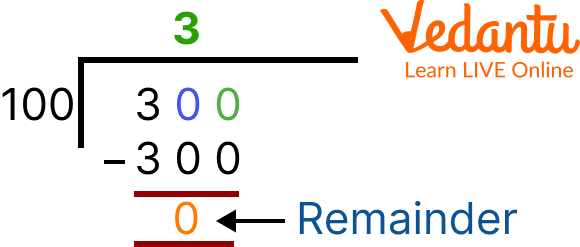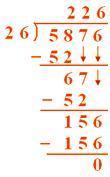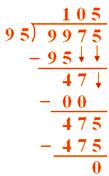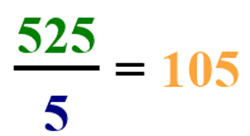Division word problems are important in building proficiency in division. Division is one of the bedrocks of mathematics alongside addition, subtraction and multiplication. Therefore, it is vital that pupils have a deep understanding of division, its function within arithmetic and word problems, and how to apply both short division and long division with success.
Division itself is the mathematical process of breaking a number up into equal parts and then finding out how many equal parts you can have. It may be that you have a remainder following this division or you may have no remainder and so a whole number as your answer.

All Kinds of Word Problems Division
Download this free pack of division word problems to develop your class’ word problem solving skills
What are division word problems?
Division word problems are an extension of the arithmetic method whereby they are word problems with division at the heart.Pupils will be expected to use the process of division to find a solution to the word problem.
Typically, word problems use a story as a scenario and are based on a real life situation where pupils are expected to interpret what the word problem is asking and then apply their division knowledge to find the answer. Division can also be introduced early through the idea of grouping before advancing to the formal method of short division and long division.
To help you with the division journey, we have put together a collection of division word problems which can be used for children between Year 2 to Year 6 – also aimed at both 3rd grade and 4th grade pupils in America.
Division word problems in the national curriculum.
Division word problems in KS1
The national curriculum states that division and word problems should be encountered from Key Stage 1 and throughout our pupils’ primary school journey. Practical resources such as counters, dienes cubes and base ten can be used to supplement the teaching of division.
In Key Stage 1 the focus is on simple addition and subtraction word problems, however, it is standard practice to introduce the concept of grouping and sharing small quantities and to calculate the answer using concrete objects and pictorial representations. It is at this point that the idea of finding fractions of objects can also be introduced and that whilst multiplication of two numbers can be done in any order (the commutative theory), the division of one number by another cannot.
Division word problems in KS2
As children enter Lower Key Stage 2 they begin to develop their mental and written strategies for division. Pupils will begin to use their multiplication knowledge and times tables to assist in their solving of division problems and how they can use the corresponding division facts and multiplication facts to answer questions.
By the end of Year 4, pupils are expected to recall their multiplication and division facts for multiplication times tables up to 12 x 12. They should also use their knowledge of place value, and known and derived facts to assist with simple division such as dividing by 1 and halving.
Introducing short division
Short division is the next step in Lower Key Stage 2. Pupils practise their fluency of short division, also known as ‘the bus stop method’, in order to answer division word problems that have a whole number answer, and those with a remainder.
Before entering Upper Key Stage 2, pupils encounter division word problems and multi step problems with increasingly harder numbers going from a simple short division problem, such as, ‘If we have 30 pupils in our class and we are divided into groups of 5, how many pupils will be in each group?’ to ‘If there are 56 books in our library and they are shared amongst 7 children, how many books would each child get?’
Introducing long division
As our pupils enter Upper Key Stage 2, long division is introduced. By the end of KS2 pupils should be fluent in both multiplication and division and the written strategies, and be able to apply knowledge in fraction word problems and percentage word problems.
Year 5 pupils work towards being able to divide up to 4 digit numbers by a one digit number using short division and being able to interpret remainders in the correct context – even presenting the remainder as a decimal or fraction. Pupils should also be able to divide mentally and know how to divide by 10, 100 and 1000 and how place value works alongside dividing a number so it is 10, 100 or 1000 times smaller.
Year 6 pupils are expected to consolidate on the above formal methods of short division before being able to divide a four digit number by a two digit number using the formal method of long division and to again be able to understand remainders within this and present them in the correct context.
This also flows into division word problems as children should be able to read a multi step problem and know how to correctly interpret it, apply their divisional knowledge and solve the problem successfully. The concept of multi step problems is built upon at each stage of the national curriculum.
Why are word problems important for childrens’ understanding of division?
Word problems, alongside the use of concrete objects and pictorial representations, are important in helping children understand the complexities and possible abstract nature of division.
Whilst children may understand that when we divide our answer will be smaller, before providing a child with word problem worksheets, just like with exploring arrays to support multiplication word problems, it is important to visually explore how division looks – from grouping and beyond.
Applying maths to real life situations
Word problems are important because they provide a real life context for children to understand division and how we encounter it in real life. By allowing children to see how division is used in everyday situations, children will find it more meaningful and relevant which in turn develops a deeper understanding of the four operations as a whole.
Building problem solving skills
Word problems are also vital to developing problem solving skills. Firstly, they must read and understand the problem before being able to identify the relevant information within the contextual problem and apply their knowledge to find a solution. This naturally builds critical thinking and a child’s ability to reason, which is an important skill for any mathematician.
Developing mathematical language skills
Finally, the importance of moving from simple division word problems to more challenging ones enhances pupils’ vocabulary and language skills. For children to develop an understanding of vocabulary such as divisors, quotient and remainders means they must first understand these key words and apply it to the process of division and be able to communicate clearly what they are aiming to do.
Deepening understanding of the inverse relationship between division and multiplication
Division word problems also solidify the connection between multiplication and division. Understanding these inverse operations and being able to interchange the skills of multiplication and division will help make connections between different mathematical concepts and deepen pupils’ learning.
How to teach division word problem solving in primary school.
Having taught the concept of division to pupils using concrete examples, for example how to group or share counters and cubes, the next step is to advance to division word problems.
As with all word problems, it is important that pupils are able to read the question carefully and interpret it so they know what they are being asked. Do they need to add, subtract, multiply or divide? Do they need to solve a multi step problem and so need to do more than one step? They may decide what operation to do, in this blogs’ case – division, and then choose to represent it pictorially.
Example of a division word problem
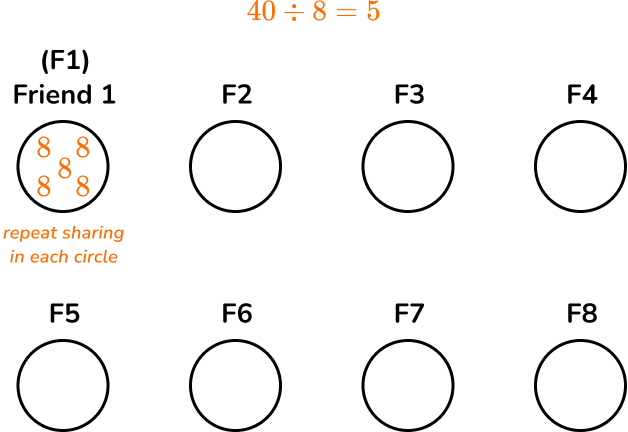
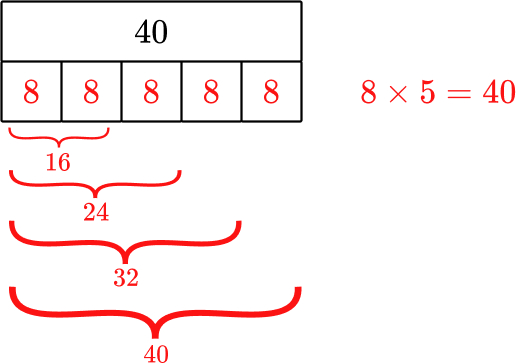
There are 40 sweets ready to go in the party bags for Laura’s birthday. They are to be shared between 8 friends. How many sweets will each child get?
How to solve this:
Firstly we need to interpret the question. Laura has invited 8 friends to her party and she has 40 sweets to share equally between her friends. So we know:
- There are 40 sweets in total
- They are to be divided amongst 8 friends in total
- We therefore need to divide the total number of sweets (40) by the number of friends (8). So to solve this problem we could put the total number of sweets (the dividend – 40 ) in the ‘bus stop’ for short division and divide by the total number of friends (the divisor – 8). If we do this, we would get the answer of 5 – the quotient. Each friend would get 5 sweets each as 40 divided by 8 is 5.
- Alternatively, we could use the inverse – multiplication – to solve this problem. We may not know the division fact that 40 divided by 8 = 5 but if we look to the inverse we may know what numeral multiplied by 8 equals 40. If we did our 8 times table we would get the answer of 5 – the correct answer.
How can we show this pictorially?
We could show 8 circles – each circle to represent a child – and place a sweet in each circle until we have placed all 40 sweets. This would mean we have shared the sweets equally between the friends and would result in each child having 5 sweets.
We could represent the division word problem as a bar model. We could split the bar model into 8 sections. There are 40 sweets and so we share them between the 8 sections. We will again see each section gets 5 sweets.
The below visuals show how this would look:
Or:
Word problems are an important aspect of our learning at Third Space Learning’s one-to-one tuition programme. Tutors will work with our tutees to break down the word problems and identify the correct operation needed to solve the word problem.
Examples of division word problems in the primary setting
Below are examples of what can be expected at each year group from Years 2 to 6. Through our tutoring programme at Third Space Learning, our tutees will become familiar with word problems throughout their learning. They will encounter word problems on a regular basis with each lesson personalised to develop the learning our tutees need. The word problems will increase their confidence, familiarity with vocabulary and mathematical understanding.
Division word problems are essential to developing problem solving skills and mathematical reasoning.
Year 2 division word problems
In Year 2 pupils use division facts for the 2, 5 and 120 times table and solve problems using concrete materials, arrays and see word problems in context.
Question 1:
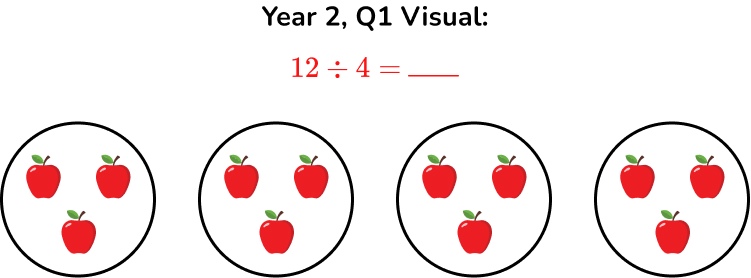
Rosie picks 12 apples on a summer walk and wants to share them equally into 4 baskets. How many apples will be in each basket?
Answer: 3
12 divided by 4 = 3
Pictorially this would look like:
Question 2:
Amy loves baking and has baked 20 cup cakes. She wants to divide them between ten friends. How many cupcakes does each friend get?
Answer: 2
20 divided by 10 = 2
Question 3:
If I have a pizza and it is cut into 16 slices, and I share it amongst 4 people. How many slices will each person get?
Answer: 4
16 divided by 4 = 4
A multiplication fact that would help with this question would be to know 4 x 4 = 16
Question 4:
Rhys says, ‘I have 36 football trading cards and I am going to share them between my 2 friends. Each of my friends will get 14 cards.’ Is Rhys correct?
Answer: he is incorrect
Rhys is incorrect. If he correctly shares 36 cards between his 2 friends, each friend will get 18 cards because 36 divided by 2 = 18.
Question 5:
If a picnic bench can fit 8 children on it, and there are 24 children in our class, how many picnic benches will we need for our class to all have a seat?
Answer: We will need 3 benches.
24 divided by 3 = 8
Year 3 division word problems
With word problems for Year 3, pupils should begin using their recall of the 3, 4 and 8 times table to help with division word problems and be able to divide two digit numbers by one digit numbers using mental and short division.
Question 1:
if a school has 90 pupils in Year 3 and there are 3 classes in Year 3, how many pupils are in each class?
Answer: 30
90 shared equally into 3 classes = 30 children per class
Question 2:
Every day a school gets a delivery of milk in a crate. There are 96 cartons of milk in the crate. If there are 8 milk cartons in a pack, how many packs will be in the crate?
Answer: 8
96 divided by 12 = 8.
There are 8 cartons of milk in a pack.
Question 3:
A delivery of 124 footballs arrives at school for sports day. They are to be shared equally between 4 classes. How many footballs does each class get?
Answer: 31
124 divided by 4 = 31 footballs per class
Question 4:
Year 3 is going to the beach on a school trip. If there are 150 children in Year 3 and only 10 children can go on one mini bus, how many mini buses does Mr. Pearson need to book?
Answer: 15
150 children divided 10 = 15 mini buses.
Question 5:
Everly has a bag of 66 marbles. She says ‘If I share these marbles equally between 8 people, I will have 2 left over.’ Is Everly correct?
Answer: Yes, Everly is correct.
If we divide 66 into 8 groups we will have 2 marbles left.
This is because 66 divided 8 is 8 equal groups with 2 left over, because 8 x 8 is 64 and so there will be 2 marbles left.
Year 4 division word problems
With word problems for year 4, pupils should be using their full knowledge and recall of times tables to 12 x 12 to help with short division of 2 digit and 3 digit numbers by a 1 digit number. Word problems may also involve multi step problems. Remainders may also be within the answer.
Question 1:
If you have 61 flowers and divide them into four flower pots, how many flowers are in each pot? Are there any left over?
Answer: 15 flowers in each pot with 1 flower left over
If we divide 61 into 4 equal groups then we can use the short division method.
We put 61 into the ‘bus stop’ and divide it by 4.
We ask ourselves, how many 4’s go into the first number ‘6’ – and we know 4 x 1 = 4, so only one 4 goes into 6 but we have 2 remaining. We put that 2 next to the 1 in 61 and we now have the number ‘21’. How many 4’s go into 21? 4 x 5 is 20. Therefore, 5 lots of 4 go into 20. We now have the answer 15 flowers….but we would have 1 left over as we had to divide 21 by 4.
So the answer to 61 divided by 4 = 15 remainder 1.
This would look like:
Question 2:
A plate can hold 9 cereal bars. There are 180 cereal bars to put out. How many plates do we need?
Answer: 20 with no remainder.
180 divided by 9 = 20 with no remainder.
We may also know that 9 x 2 = 18 and so can use our place value knowledge to know that 9 x 20 = 180 as the answer would be ten times bigger than 9 x 2.
Questions 3:
Amy is calculating 188 divided by 11 and thinks that as the number 188 ends in an 88, that there will be no remainder. Is she correct?
Answer: Amy is incorrect.
If we do 188 divided by 11 we will get 17 remainder 1.
Question 4:
There are 216 animals in a zoo and they are spread out across 8 different zones. How many animals are in each zone?
Answer: 27
216 divided by 8 = 27
Question 5:
At a sports tournament there are 6 players in each team. There are 132 players altogether.
How many teams are there?
Answer: 22
132 divided by 6 = 22
Year 5 division word problems
Word problems for Year 5 centre around dividing a 4 digit number by a 1 digit number using the formal method of short division. They will also interpret remainders correctly depending on the context. Division and remainders is often demonstrated through money word problems.
Question 1:
Ronan has a ball of string that is 819cm long. He cuts it into 7 equal pieces. How long is 1 piece of string?
Answer: 117cm
819 divided by 7 = 117
Question 2:
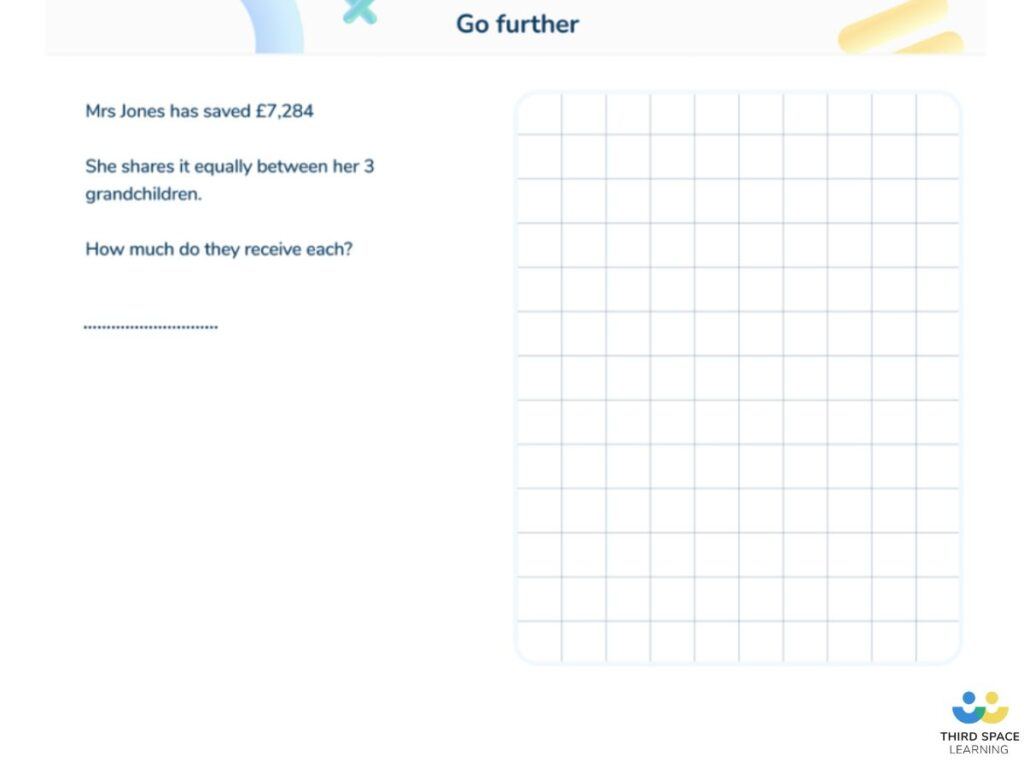
In Key Stage 2 there are 1,248 coloured pencils. If there are 6 classes in Key Stage 2, how many pencils would each class receive?
Answer: 208cm
We use the short division method to divide 1,248 by 6 and we get 208 as the result.
Question 3:
Mia buys three computer games for £84.99. How much is one computer game?
Answer: £28.33
Whilst this involves decimal division due to it being monetary with pounds and pence, the process of short division is the same.
We divide £84.99 by 3 and we get £28.33.
Question 4:
The area of the school hall is 1,704m and needs to be split into four quadrants. What would be the area of each quadrant?
Answer: 426m
We take the total area of the school and divide it by 4 to represent each quadrant. In doing so, we would have 426m for each quadrant.
To check this is the correct answer, we could do the inverse and multiply 426 by 4 and we would get 1,704m.
Question 5:
Packets of sweets are put into multi packs of 8. The multi packs are then placed into boxes of 6. Today, 7800 packets of sweets were packed. How many boxes of sweets were packed?
Answer: 163 boxes
This is a two step problem. First we need to multiply the number of packets in a multi pack – 8 – by the number of boxes of multi packs – 6. We would get the answer 48.
We then have to take the total packets of sweets – 7800 – and divide this by 48. This would be our introduction to long division. If we do this we will get the answer 162.5.
Now we cannot have 162 and a half boxes and so we would round this up to 163 boxes – but the 163rd box would only be half full.
Year 6 division word problems
Word problems for year 6 will be preparing for their SATs exams in May. They would be familiar with the concept of long division and needing to divide a 4 digit number by a 2 digit number using the formal methods of both short and long division.
Question 1:
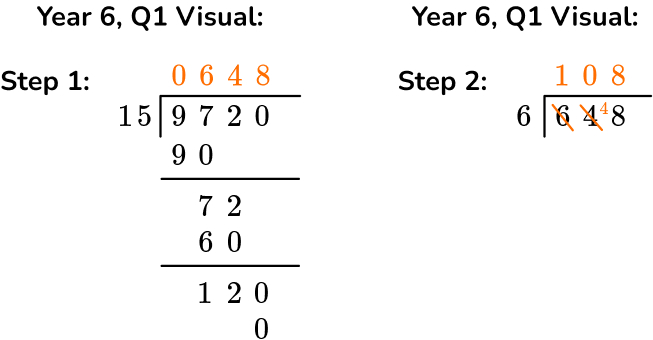
A school is selling tickets at £6 each to attend the Big Christmas Fair. Over 15 weeks it has earned an amazing £9,720! On average, how many tickets were sold each week?
Answer: 108 tickets per week
First, we need to use the formal method of long division to divide the grand total – £9720 by 15. If we do this correctly we will have the answer 648.
Then, we need to take this answer of 648, which is how much is earned each week, and then divide this by £6, the amount each ticket is.
This will result in the number of tickets sold each week – 108 tickets.
Question 2:
A square sports field has a perimeter of 2.696km. How long is each side of the field?
Answer: 674m
To answer this we need to be able to convert the 2.696km into metres. There are 1000 metres in a kilometre so that would be 2,696m. Then we divide this by 4 and get 674m for one side.
Question 3:
Keira is given a toy blocks kit containing 2,208 individual blocks. She wants to split the toy blocks evenly between 15 friends and herself to work on making a toy block city together. How many blocks should she give each of her friends?
Answer: 138 blocks
We need to use the formal method of long division to solve this. We also need to ensure we include Keira and her 15 friends so we have the number 16 as the divisor.
When we divide 2,208 by 16 using long division we get the answer 138.
Question 4:
Wesleigh was running in the cross country race. He ran for a distance of 3,569m and it took him 11 minutes to complete the race. How many metres did he run per minute? Give your answer to the nearest whole metre.
Answer: 324 metres
We need to use long division to divide 3,569 by 11. That will give us an answer of 324.45. As the decimal can be rounded down, the answer is 324 metres.
Question 5:
Sophia is preparing her sweet stall for the fair. She can fit 18 tins of sweets into one crate. How many crates will be needed to153 tins of sweets?
Answer: 9 cratesWe divide 153 by 18 using long division and we have an answer of 8 remainder 5. Therefore, having 8 crates would not be enough as we would have 85 tins left over and so we need a further tin to house the 5 tins left over. So, 9 crates are needed.
More word problems resource
Are you looking for more word problems resources? Take a look at our library of word problems practice questions including: time word problems, ratio word problems, addition word problems and subtraction word problems.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Small numbers can be divided into groups and pieces using the simple division method in mathematics. Divide easy and simple division problems into terms that can be divided using simple division sums.
One of the four fundamental mathematical operations, along with addition, subtraction, and multiplication, is division. Division is the process of dividing a larger group into smaller groups so that each group contains an equal number of things. In this article, you will get some maths word problems, especially division problems and you will also learn how to solve these division problems.
Division Problem
A division problem has three primary components: the dividend, the divisor, and the quotient. The amount that will be divided is the dividend. The quantity of «people» among whom the number is divided is referred to as the divisor. The answer is the quotient.
Other than these 3 components, the remainder is also one component of division. In the case when a dividend is completely divided by the divisor, the remainder will be zero and in other cases, it will be more than zero.
For example, if we divide 100 by 8, we get a remainder greater than 0 i.e., 4.
Dividing 100 by 8
If we divide 300 by 100 then the remainder is zero.
Dividing 300 by 100
How to Write Division in Word
A division symbol (÷) is used to show division. You must have seen this symbol in your maths book, otherwise, if you don’t insert a dividing symbol then the whole division problem can easily be written in words. Like dividing 50 by 5, in this way division is written in words without inserting symbols.
Now, we will see the steps of division. These steps will help you to understand how division is performed.
Steps of Division
Step 1: The Problem should be written out using a Long Division Bar.
The division bar ( 厂 ) resembles a pair of closing parenthesis joined to a horizontal line that crosses the row of numbers directly below the bar. Put the dividend, which is the number you’ll be dividing into, inside the long division bar and the divisor, which is the number you’ll be dividing into, outside.
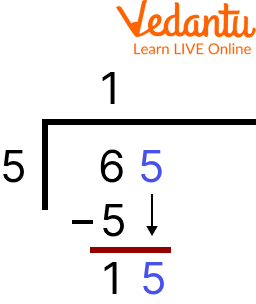
For example, divide 65 by 5
Step 1
Step 2: Divide the Divisor by the Dividend’s Leading Digit.
Calculate how many times the divisor (the number outside the division bar) enters the dividend’s first digit. Put the entire number result directly over the first digit of the divisor, above the division line.
Step 2
Step 3: Divide the Divisor by the Number above the Division Bar.
Multiply the amount you just put above the division bar by the denominator (the number to the left of the division bar). Under the dividend, in a new row, align the result with the dividend’s first digit.
Step 3
Step 4: Subtract the Multiplication Outcome from the Dividend’s First Digit.
Alternatively stated, divide the sum you just entered into the new row beneath the dividend by the digit in the dividend immediately above it. The digits from the subtraction issue should be aligned with the result in a new row.
Step 4
Step 5: Bring the Dividend’s Second Digit Down.
Just to the right of the result of your recent subtraction, move the second digit of the dividend down to the new bottom row.
Step 5
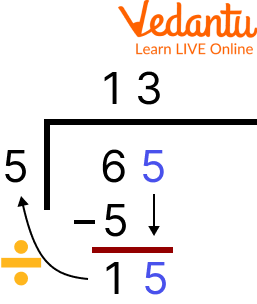
Step 6: The Long Division Procedure should be Repeated.
Use the dividend (the number in the division bar to the left) and the new number in the bottom row this time (the result of your first round of calculations and the digit you carried down). As previously, divide, multiply, and then subtract to determine your outcome.
Step 6
Step 7: Carry out Long Division once more.
As previously, you begin by dividing, move on to multiplying, and end by subtracting. Do another round of division and get the remainder.
Division Problems With Answers
Here are some division word problems that are shared. These are solved examples.
1. Rs. 670 are distributed equally among 7 men. How much money will each person get?
Ans: Money received by 7 men = 670
So, money received by one man = 670 ÷ 7
Dividing 670 by 7
670 ÷ 7 = 95
Therefore, each person gets Rs. 95
2. An active dolphin needs to breathe 7 times a minute. How long would it take them to breathe 49 times?
Ans: Dolphin needs to breathe 7 times a minute.
Time is taken by a dolphin to breathe 49 times = 49 ÷ 7
Dividing 49 by 7
So, 49 ÷ 7 = 7, It would take 7 minutes.
3. Jason has 406 socks in total in his shop which he puts into pairs. How many pairs of socks does he have?
Ans: Total number of socks Jason has in pairs = 406
Number of paired socks = 406 ÷ 7
Dividing 406 by 7
So, 406 ÷ 7 = 58, She owns 58 pairs of socks.
Practise Questions
Q 1. Jasmine runs 3 metres in a minute. How long will it take for her to run 27 metres at the same speed?
Ans: It would take her 9 minutes.
Q 2. An episode of Sally’s favourite cartoon runs for 10 minutes. How many episodes can she watch in 1 hour?
Ans: She can watch 6 episodes.
Summary
In this article, firstly division and important parts of division i.e., divisor, dividend, quotient, and the remainder are discussed. Steps of division for kids are discussed by using examples and pictures of the same. There are 7 main steps present in this division part. Steps of division are applied in a division word problem. Some maths word problems of division are mentioned with proper explanation. Daily life examples are shared in the division word problem.
Table of Contents
- What is a division problem?
- How do you teach division?
- What are 2 ways to solve a division problem?
- How do you set up a division problem?
- What is a division word problem?
- What is an example of a multiplication problem?
Division word problems. Division word problems arise in situations where we are trying to find out how many times a number go into another.In general, Division is the inverse operation of multiplication.
How do you teach division?
Before your child can begin to practice division problems, they first need to understand the concept of division. Explain it to them by relating the idea of division to the idea of sharing. Help them conceptualize it by explaining how a number of items can be shared equally between groups, and give them examples.
What are 2 ways to solve a division problem?
To solve division problems you can make equal groups, create equal groups with place value, and use multiplication.
How do you set up a division problem?
Dividing. Set up the equation. On a piece of paper, write the dividend (number being divided) on the right, under the division symbol, and the divisor (number doing the division) to the left on the outside. The quotient (answer) will eventually go on top, right above the dividend.
Division Word Problems (1-step word problems) Dan went to the market on Friday. He bought two tomatoes. In July, a construction company built 360 miles of road. In February, the company laid down 60 miles of road. Linh ran 21 miles. Linh ran three times as far as Sophie. Molly’s bedroom is 220 square feet. Molly’s dining room is five times the size of her bedroom.
What is a division word problem?
Division Problems Leftover. Is the party over? Long Division. ‘Long Division’ is a division worksheet for primary school kids that will help them practice their understanding of Shorter Division. The Long Division. Santa’s Gifts. Calculator Match. Hot Potato. Sapphires and Rubies. Divide and Conquer. Dividend Challenge.
What is an example of a multiplication problem?
A multiplication problem may be written horizontally such as 2 x 7 = 14. In this example 2 and 7 are the factors and 14 is the product of the multiplication. A multiplication problem may be written vertically. 2 x 7 14.
Word problems on division for fourth grade students are solved here step by step.
Consider the following examples on word problems involving division:
1. $5,876 are distributed equally among 26 men. How much money will each person get?
Solution:
Money received by 26 men = 5876 So, money received by one man = 5876 ÷ 26
= 226
Each man will get $226.
2. If 9975 kg of wheat is packed in 95 bags, how much wheat will each bag contain?
Solution:
Since 95 bags contain wheat 9975 kg
Therefore, 1 bag contains wheat (9975 ÷ 95) kg
= 105 kg
Each bag contains wheat = 105 kg
In a problem sum involving division, we have to be careful about using the remainder.
3. 89
people have been invited to a banquet. The caterer is arranging tables.
Each table can seat 12 people. How many tables are needed?
Solution:
To answer this question, we need to divide 89 by 12
89 ÷ 12
Quotient — 7
Remainder — 5
If the caterer arranges 7 tables, then 5 people will have no place to sit.
So he needs to arrange 7 + 1 = 8 tables.
4. How many hours are there in 1200 minutes?
Solution:
We know that there are 60 minutes in 1 hour.Divide the number of minutes by the number of minutes in 1 hour. We get, divide 1200 by 601200 ÷ 60 = 20
So there are 20 hours in 1200 minutes.
Answer: 20 hours.
5. A bus can hold 108 passengers. If there are 12 rows of seats on the bus, how many seats are in each row?
Solution:
Total number of passengers = 108
There are 12 rows of seats on the bus.
To find how many seats are there in each row, divide the total number of passengers by the number of rows of seats on the bus.
We get, divide 108 by 12
108 ÷ 12 = 9
Therefore, there are 9 seats in each row.
Answer: 9 seats.
6. Tom had 63 apples. He divides all apples evenly among 9 friends. How many apples did Tom give to each of his friends?
Solution:
Total number of apples = 63
There are 9 friends of seats on the bus.
To find how many apples Tom gave to each of his friends, divide the total number of apples by the number of friends.
We get, divide 63 by 9
63 ÷ 9 = 7
Therefore, Tom gives 7 apples to each of his friends.
Answer: 7 Apples
7. Mark baked 195 cookies and divided them equally into 13 packs. How many cookies did Mark put in each packet?
Solution:
Total number of cookies = 195
There are 13 packs.
To find how many cookies did Mark put in each packet, divide the total number of cookies by the number of packs.
We get, divide 195 by 13
195 ÷ 13 = 15
Therefore, Mark put 15 cookies in each pack.
Answer: 15 cookies.
9.
Nancy needs 5 lemons to make a glass of orange juice. If Nancy has 250
oranges, how many glasses of orange juice can she make?
Solution:
Total number of oranges = 250
She needs 5 lemons to make a glass of orange juice.
To
find how many glasses of orange juice can Nancy make, divide the total
number of oranges by the number of oranges needed for each glass of
orange juice.
We get, divide 250 by 5
250 ÷ 5 = 50
Therefore, Nancy can make 50 glasses of orange juice.
Answer: 50 glasses of orange juice.
10. In your classes you counted 120 hands. How many students were at the class?
Solution:
Total number of hands = 120
We have 2 hands.
To find how many students were at the class, divide the total number of hands by the number of hands we have.
We get, divide 120 by 2
220 ÷ 2 = 60
Therefore, there were 60 students at the class.
Answer: 60 students.
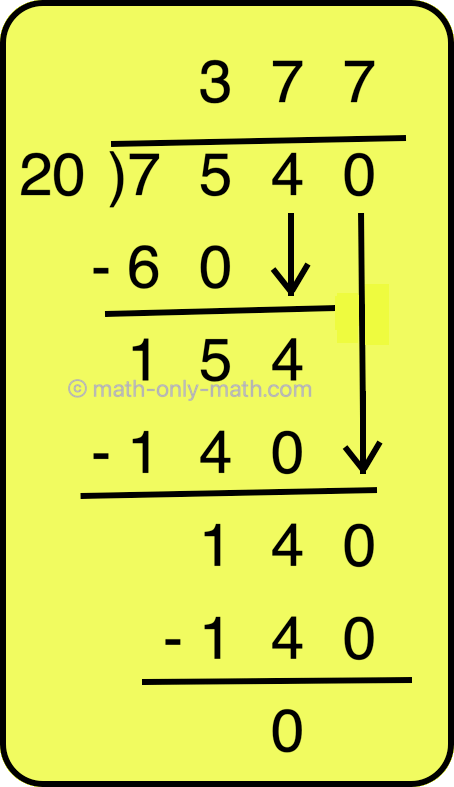
11. The total train fare for 20 persons is 7540 rupees. What is the fare for 1 person.
|
Solution: The total train fare = 7540 rupees Number of persons = 20 Train fare for 1 person = 7540 ÷ 20 = 377 |
|
These are the basic word problems on division.
Questions and Answers on Word Problems on Division:
1. 92 bags of cement can be
loaded in a truck. How many such trucks will be needed to load 2208 bags?
Answer: 24 trucks
2. The total train fare for 11
persons was $3850. What was the fare for one person?
Answer: $350
Related Concept
● Addition
● Word
Problems on Addition
● Subtraction
● Check
for Subtraction and Addition
● Word
Problems Involving Addition and Subtraction
● Estimating
Sums and Differences
● Find the
Missing Digits
● Multiplication
● Multiply
a Number by a 2-Digit Number
● Multiplication
of a Number by a 3-Digit Number
● Multiply a Number
● Estimating Products
● Word
Problems on Multiplication
● Multiplication
and Division
● Terms Used in
Division
● Division
of Two-Digit by a One-Digit Numbers
● Division
of Four-Digit by a One-Digit Numbers
● Division
by 10 and 100 and 1000
● Dividing Numbers
● Estimating
the Quotient
● Division
by Two-Digit Numbers
● Word
Problems on Division
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Word problems are fun and challenging to solve because they represent actual situations that happen in our world. As students, we are always wondering why we should learn one skill or another, and word problems help us see the practical value of what we are learning.
Read the tips and guidance and then work through the multiplication and division word problems in this lesson with your children. Try the three worksheets that are listed within the lesson (you will also find them at the bottom of the page.)
What is multiplication?
The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product. Suppose, you bought 6 pens on one day and 6 pens on the next day. Total pens you bought are now 2 times 6 or 6 + 6 = 12.
This can also be written as 2 x 6 = 12
Not the symbol used for multiplication. The symbol (x) is generally used to represent multiplication. Other common symbols that are used for multiplication are the asterisk (*) and dot (.)
Important terms in the multiplication
Some important terms used in multiplication are –
Multiplicand – The number to be multiplied is called the multiplicand.
Multiplier – The number with which we multiply is called the multiplier.
Product – The result obtained after multiplying the multiplier and the multiplicand is called the product.
The relation between the multiplier, multiplicand and the product can be expressed as –
Multiplier × Multiplicand = Product
Let us understand this using an example.
Suppose we have two numbers 9 and 5. We wish to multiply 9 by 5.
So, we express it as 9 x 5 which gives us 45.
Therefore, 9 x 5 = 45
Here, 9 is the multiplicand, 5 is the multiplier and 45 is the product.
What is division?
Division is the equal sharing of a given quantity.
For example, Alice wants to share 6 bananas equally with her friend Rose. So, she gives 3 of her bananas to Rose and she is also left with 3 bananas. This means that when we divide 6 by 2 we get 3.
Mathematically, we can write this as
6 ÷ 2 = 3
Symbol for Division
In mathematics, there is a symbol for every operation. The symbol for division is (÷). Other than the forward-slash (/) is also used to denote the division of two numbers, where, the dividend comes before the slash and the divisor after it. For instance, if we wish to write 15 is being divided by 3, we can write it as 15 ÷ 3 or 15 / 3. Both mean the same.
Important terms in Division
The number that is to be divided is called the Dividend. Here, 6 is the dividend.
The number by which the dividend is being divided is called the Divisor.
The result obtained by the process of division is called the Quotient.
The number that is left over after finding the quotient is called the Remainder.
Let us understand these by an example.
Suppose, we have a pack of 65 chocolates and we want to divide them equally among 7 children while keeping the remaining chocolates with us. How many chocolates does each child get and how many chocolates are we left with after dividing these chocolates?
Using multiplication tables, we have 7 x 9 = 63
Therefore, 7 x 9 + 2 = 65
This means that the quotient when 65 is divided by 7 will be 9 and the remainder will be 2.
As per the definition of the four terms of division, we have
Divisor = 7
Dividend = 65
Quotient = 9
Remainder = 2
Remember: The remainder is always smaller than the divisor.
Formula for Division
There are four important terms in the division, namely, divisor, dividend, quotient, and the remainder. The formula for divisor constitutes all of these four terms. In fact, it is the relationship of these four terms among each that defines the formula for division. If we multiply the divisor with the quotient and add the result to the remainder, the result that we get is the dividend. This means,
Dividend = Divisor x Quotient + Remainder
What are word problems?
A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation. In other words, word problems describe a realistic problem and ask you to imagine how you would solve it using math. Word problems are fun and challenging to solve because they represent actual situations that happen in our world.
How to Solve Word Problems involving multiplication and division?
The following steps are involved in the process of solving word problems involving multiplication and division of numbers –
- Read through the problem carefully, and figure out what it is about. This is the most important step as it helps to understand two things – what is given in the question and what is required to be found out.
- The next step is to represent unknown numbers using variables. Usually, these unknown numbers are the values that are required to be solved for.
- Once the numbers have been represented as variables, the next step is to translate the rest of the problem in the form of a mathematical expression.
- Once this expression has been formed, the last step is to solve this expression for the variable and obtain the desired result.
Let us understand it through an example.
Example
A hawker delivers 148 newspapers every day. How many newspapers will he deliver in a non-leap year?
Solution
We have been given that a hawker delivers 148 newspapers every day. We need to find out the total number of newspapers that he will deliver in a non-leap year. Let us summarise the given information as
Number of newspapers delivered by the hawker in a day = 148
Number of newspapers that he will deliver in a non-leap year = ?
Now, we know that a non-leap year consists of 365 days. This means that we need to find out the total number of newspapers that the hawker will deliver in 365 days. Therefore,
Total number of days on which hawker delivers the newspapers = 365
Now, to find the total number of newspapers delivered by the hawker in 365 days we will have to multiply the Number of newspapers delivered by the hawker in a day by the total number of days in a year. So, we have,
Number of newspapers that he will deliver in a non-leap year = (Number of newspapers delivered by the hawker in a day ) x (total number of days in a year ) ……….. ( 1 )
Substituting the given values in the above equation, we have
Number of newspapers that he will deliver in a non-leap year = 148 x 365
Now, 148 x 365 = 54020
Hence, the number of newspapers that he will deliver in a non-leap year = 54020
Let us consider another example.
Example
In a school, a fee of £ 345 is collected per student. If there are 240 students in the school, how much fee is collected by the school?
Solution
We have been given that in a school a fee of £ 345 is collected per student. Also, there are 240 students in the school. We need to find out the total fee collected by the school from all students. Let us first summarise this information
Amount of fee collected by the school from each student = £ 345
Number of students in the school = 240
Total amount of fee collected by the school = ?
This can be calculated by multiplying the fee collected for each student by the number of students in the school. Therefore we have,
Total amount of fee collected by the school = (Amount of fee collected by the school from each student ) x (Number of students in the school ) …….. ( 1 )
Substituting the given information in the above equation, we get
Total amount of fee collected by the school = £ ( 345 x 240 )
Now, 345 x 240 = 82800
Hence, Total amount of fee collected by the school = £ 82800
Solving Multiplicative Comparison Word Problems
Multiplication as Comparing
In multiplicative comparison problems, there are two different sets being compared. The first set contains a certain number of items. The second set contains multiple copies of the first set.
Any two factors and their product can be read as a comparison. Let’s look at a basic multiplication equation: 4 x 2 = 8.
8 is the same as 4 sets of 2 or 2 sets of 4.
8 is 4 times as many as 2, and 2 times as many as 4.
What Operation to Use: Multiply? Divide? Add? Subtract?
The hardest part of any word problem is deciding which operation to use. There can be so many details included in a word problem that the question being asked gets lost in the whole situation. Taking time to identify what is important, and what is not, is essential.
Use a highlighter on written problems to identify words that tell you what you are solving, and give you clues about which operations to choose. Make notes in the margins by these words to help you clarify your understanding of the problem.
Remember: If you don’t know what’s being asked, it will be very difficult to know if you have a reasonable answer.
Different Types of Problem
There are three kinds of multiplicative comparison word problems (see list below). Knowing which kind of problem you have in front of you will help you know how to solve it.
- Product Unknown Comparisons
- Set Size Unknown Comparisons
- Multiplier Unknown Comparisons
The rest of this lesson will show how these three types of math problems can be solved.
Multiplication Problems: Product Unknown
In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the “multiplier” amount. The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed.
These problems in which you know both the number in one set, and the multiplier are called “Product Unknown” comparisons, because the total is the part that is unknown.
In order to answer the question you are being asked, you need to multiply the number in the set by the multiplier to find the product.
Product Unknown Comparisons
In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the “multiplier” amount. The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed. These problems in which you know both the number in one set, and the multiplier are called “Product Unknown” comparisons, because the total is the part that is unknown.
Let us understand it through an example.
Example
Mary is saving up money to go on a trip. This month, she saved three times as much as money as she saved last month. Last month, she saved £ 24.00. How much money did Mary save this month?
Solution
We have been given that Mary is saving up money to go on a trip. This month, she saved three times as much as money as she saved last month. Last month, she saved £24.00. we need to find out how much money did Mary save this month?
Now, as much as tells you that you have a comparison. Three times is the multiplier. 24 is the amount in the first set. The question being asked is how much money did Mary save this month? To find the answer, we multiply 24 by 3. Therefore, we have 24.00 x 3 = 72.
It is important to clearly show that you understand what your answer means. Instead of writing just 72, we will write it as Mary saved £ 72 this month.
Note that whenever we finish a math problem of any kind, we always go back to the original problem. Think: “What is the question we are being asked?”
Make sure that our final answer is a reasonable answer for the question we are being asked.
We were asked, “How much money did Mary save this month?”
Our answer is: Mary saved $72.00 this month. Our answer is reasonable because it tells how much money Mary saved this month. We multiplied a whole number by a whole number, so the amount of money Mary saved this month should be more than she saved last month. Seventy-Two is more than 24 . Our answer makes sense.
Multiplication Problems: Set Size Unknown
In some multiplicative comparison word problems, the part that is unknown is the number of items in one set. You are given the amount of the second set, which is a multiple of the unknown first set, and the “multiplier” amount, which tells you how many times bigger (or more) the second set is than the first. Remember, “bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed.
These problems in which you know both the number in the second set, and the multiplier are called “Set Size Unknown” comparisons, because the number in one set is the part that is unknown.
In order to answer the question you are being asked, you need to use the inverse operation of multiplication: division. This kind of division is “partition” or “sharing” division. Dividing the number in the second set by the multiplier will tell you the number in one set, which is the question you are being asked in this kind of problem.
Set Size Unknown Comparisons
In some multiplicative comparison word problems, the part that is unknown is the number of items in one set. You are given the amount of the second set, which is a multiple of the unknown first set, and the “multiplier” amount, which tells you how many times bigger (or more) the second set is than the first. Remember, “bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed. These problems in which you know both the number in the second set and the multiplier are called “Set Size Unknown” comparisons because the number in one set is the part that is unknown.
Let us understand it through an example.
Example
Jeff read 12 books during the month of August. He read four times as many books as Paul. How many books did Paul read?
Solution
We have been given that Jeff read 12 books during the month of August. He read four times as many books as Paul. We need to find out how many books did Paul read?
“As many as “ tells you that we have a comparison. Four times is the multiplier. 12 books is the amount in the second set. How many books did Paul read? This is the question we are being asked. To solve, divide 12 by 4. Now 12 ÷ 4 = 3. It is important to clearly show that we understand what our answer means. Instead of just writing 3, we write complete sentence that Paul read three books.
Note that whenever we finish a math word problem, always go back to the original problem. Think: “What is the question we are being asked?” Make sure that our final answer is a reasonable answer for the question you are being asked. We were asked, “How many books did Paul read?” Our answer is: Paul read three books. Our answer is reasonable because it tells how many books Paul read. We divided a whole number by a whole number, so the number of Paul’s books should be less than the number of Jeff’s books. Three is smaller than 12. My answer makes sense.
Multiplicative Comparison Problems: Multiplier Unknown
In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the number of items in the second set, which is a multiple of the first set. The “multiplier” amount is the part that is unknown.
The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed.
These problems in which you know both the number in one set, and the number in the second set are called “Multiplier Unknown” comparisons, because the multiplier is the part that is unknown.
In order to answer the question you are being asked, you need to use the inverse operation of multiplication: division. This kind of division is called “measurement” division.
Multiplier Unknown Comparisons
In some multiplicative comparison word problems, you are given the number of items in one set, and you are given the number of items in the second set, which is a multiple of the first set. The “multiplier” amount is the part that is unknown. The multiplier amount tells you how many times bigger (or more) the second set is than the first. “Bigger” can also mean “longer,” or “wider,” or “taller” in problems involving measurement, or “faster” in problems involving a rate of speed. These problems in which you know both the number in one set and the number in the second set are called “Multiplier Unknown” comparisons because the multiplier is the part that is unknown. In order to answer the question you are being asked, you need to use the inverse operation of multiplication: division. This kind of division is called “measurement” division.
Let us understand it through an example.
Example
The gorilla in the Los Angeles Zoo is six feet tall. The giraffe is 18 feet tall. How many times taller than the gorilla is the giraffe?
Solution
We have been given that the gorilla in the Los Angeles Zoo is six feet tall. The giraffe is 18 feet tall. We need to find out how many times taller than the gorilla is the giraffe?
Taller than tells us that we have a comparison. Six feet is the amount in the first set. 18 feet is the amount in the second set. How many times taller than the gorilla is the giraffe? This is the question we are being asked. To solve this we divide18 feet by six feet. Now, 18 ÷ 6 = 3. It is important to clearly show that we understand what our answer means. Instead of just writing 3, we write the complete sentence that the giraffe is three times taller than the gorilla.
Note that whenever we finish a math word problem, always go back to the original problem. Think: “What is the question we are being asked?” Make sure that your final answer is a reasonable answer for the question you are being asked. We were asked, “How much taller than the gorilla is the giraffe?” Our answer is: The giraffe is three times taller than the gorilla. Our answer is reasonable because it tells how much taller the giraffe is, compared to the gorilla. We divided a whole number by a whole number, so our quotient should be less than my dividend. Three is less than 18, so our answer makes sense.
Solved Examples
Example 1 There are 287 rows in a stadium. How many students can be seated in this stadium if each row has 165 seats to be occupied?
Solution We are given that,
Number of rows in a stadium = 287
Number of seats in each row = 165
Total number of students that can be seated in the stadium = 287 x 165 = 47335.
Example 2 Henry bought 15 packets of cookies. Each packet contains 35 cookies. How many cookies in all does Henry have?
Solution We are given that
Number of packets of cookies bought by Henry = 15
Number of cookies in each packet = 35
Total number of cookies that Henry has = 15 x 35 = 525
Key Facts and Summary
- The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product.
- Division is the equal sharing of a given quantity.
- A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation.
Recommended Worksheets
Fact Families for Multiplication and Division (Summer Themed) Math Worksheets
Multiplication and Division of Fractions (Veterans’ Day Themed) Math Worksheets
Multiplication and Division Problem Solving (Halloween Themed) Math Worksheets
We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!
Word problems can be such a struggle. Especially in grades 3rd and up when students have to work through all of the operations and multi-step word problems. Students often struggle to identify the operation presented, or miss part of the steps needed to solve. Explicitly teaching word problem types can help our students recognize the operations in context. The Common Core State Standards lay out the different multiplication & division word problem types that students should know. By teaching them explicitly, we help students understand multiplication and division in context to help them truly understand the operations. We connect how the math they’re learning is relevant to their real life. By focusing on the word problems and their types, we’re focusing on what makes multiplication and division what they are.
This post takes an in-depth look at each of the multiplication & division word problem types. I also give some helpful links at the bottom that discuss Cognitively Guided Instruction, or CGI problem types. They use slightly different vocabulary than the CCSS but are the same set of skills. An important note- when I talk about teaching the multiplication & division word problem types explicitly, I don’t mean that they’re only practiced during a specific unit, or that we teach specific keywords for each problem type. Students need to read the problem and understand the context. Recognizing the problem type can support that work, but it’s not focused on keywords. I also do a daily word problem outside of our focused unit work. I firmly believe in spiraling the standards in word problems so students have to focus on context to solve. For more support with problem solving, check out my Why Your Students Struggle with Word Problems, and What You Can Do About It post.
An important note before we begin-throughout our exploration of both operations, we often return back to the total. We identify in our first lesson that multiplication allows us to find the total number of objects arranged in equal groups. When we begin exploring division, we know the total number of objects we have and have to find the unknown in connection with groups. Throughout our work, with arrays, area, and equal groups, we continue to come back to the concept of total to help students identify the operation needed. It is through identifying the total as known or unknown that students will truly understand the multiplication and division operations. As you will see, that’s a focus with each of the multiplication and division word problem types.
Equal Groups as Multiplication & Division
In my Introducing Multiplication and an Working with Division posts I walk through my hands-on, engaging lessons I use to introduce each operation. When introducing both operations, we focus on equal group arrangements. It’s crucial for students to understand that multiplication and division works with equal groups so it makes sense to begin here. When we first start working with multiplication and division word problems, I ask students to identify the items that are arranged in groups, and identify what that group looks like. For example, the group might be a box or a bag. Those objects could also just be objects in other scenarios. So, identifying that an object is grouped within something helps students to understand the word problem and that an equal group scenario is present.
| MULTIPLICATION | QUOTATIVE DIVISION | PARTITIVE DIVISION | |
| TOTAL UNKNOWN | # of GROUPS UNKNOWN | # in each GROUP UNKNOWN | |
|
4 x 6 = ? ? ÷ 4 = 6 |
? X 6 = 24
24 ÷ ? = 6 |
4 x ? = 24 24 ÷ 4 = ? |
|
| Equal Groups | There were 4 bags on the counter. Each bag had 6 apples in it. How many apples were there in all? | There are 24 apples split equally into bags. Each bag has 6 apples in it. How many bags of apples are there? | There are 24 apples split equally into 4 bags. How many apples are in each bag? |
MULTIPLICATION – Total Unknown
These are the word problems we typically think of with multiplication. It’s an arrangement of items into equal groups to find the total number of items. Identifying that the number of groups and the number of items into each group are known, while the total is unknown, helps students solve these word problems.
QUOTATIVE DIVISION – # of Groups Unknown
When the number of groups are unknown, it is a quotative division problem. Let me clear, I don’t teach my students the term quotative. Rather, I teach them that there are two types of division. When students are able to identify that the total number of objects is known, but the number of groups is unknown, they then know that they are dividing. It’s important that students have lots of practice with both types of division.
PARTITIVE DIVISION – # in each Group Unknown
When a word problem identifies the total number of items and how the items are arranged, but doesn’t give the number in each group, these are partitive division. Think of it as partitioning. The number of groups is known so the partitions are known. Again, I don’t teach this term with my students, but it’s important that students know that division is presented in two ways.
Once both operations have been introduced and practiced separately, I like to use my Multiplication & Division Scenario Tables Task Cards to practice writing equations and understanding group arrangements in context. I find that removing all of the components of the word problem, and working through just the total and group information, helps students truly understand the operations in connection with equal groups. This helps them then apply their learning within word problems. Students get practice with different ways items can be grouped, which helps them look for and identify grouping relationships in word problems later.
Arrays as Multiplication & Division
In conjunction with teaching equal group arrangements described above, arrays should also be included. Arrays are how students are first introduced to multiplication in 2nd grade. Students should have background knowledge with rows and columns vocabulary. Arrays are how I connect what we’re learning now, with what they learned before. Therefore, I teach arrays at the same time that I teach equal group arrangements. I correlate rows and the number of groups. I always emphasize that the columns are the same as the number in each row (or the group).
| MULTIPLICATION | QUOTATIVE DIVISION | PARTITIVE DIVISION | |
| TOTAL UNKNOWN | # of GROUPS UNKNOWN | # in each GROUP UNKNOWN | |
| 4 x 6 = ?
? ÷ 4 = 6 |
? X 6 = 24
24 ÷ ? = 6 |
4 x ? = 24 24 ÷ 4 = ? |
|
| Arrays | There are 4 rows of bags with 6 bags in each row. How many bags are there?
The bags are arranged in 4 rows and 6 columns. How many bags are there? |
There are 24 bags arranged in rows of 6. How many rows of bags are there?
There are 24 bags arranged in 6 columns. How many rows of bags are there? |
There are 24 bags arranged evenly in 4 rows. How many bags are in each row? There are 24 bags arranged evenly in 4 rows. How many columns of bags are there? |
It’s important to note that the CCSS lay out two rigors of array word problems: ones where the items in rows are presented, and those that give the word problem in rows and columns. Through continued exposure and practice, students understand that these are interchangeable. Array word problems are not very common, but are definitely a problem type that students should have exposure and practice with. They also lay the foundation for students to work with our next word problem type: area
Area as Multiplication and Division
Area is a critical component of our multiplication and division work. It’s a major part of 3rd grade math instruction and it’s important that students work with many word problems where they have to recognize area in context and solve. This is especially important to learn how to differentiate between area and perimeter by making connections between arrays and what is known about multiplication and division. Area should be introduced with arrays and connected to an area model. This concrete, visual example helps students connect what they already know (arrays) with their new learning (area). Unit squares are written in the standards to be this bridge. Area models continue on as you work with more the more complex rectilinear figures, and to help students understand the distributive property of multiplication. The CCSS don’t list area problems as their own line, rather, they’re included with arrays. While this certainly makes sense since arrays can be created inside the rectangle, and that’s how area should be introduced, most area word problems don’t use rows or columns when providing side lengths. I think it’s an important distinction to look at area word problems separate from arrays.
| SIDE LENGTH UNKNOWN | SIDE LENGTH UNKNOWN | ||
| Area | A rectangle has one side measuring 6 feet and another measuring 4 feet. What is the area of the rectangle? | A rectangle has an area of 24 square feet. If one side is 6 feet long, how long must the perpendicular side be? | A rectangle has an area of 24 square feet. If one side is 6 feet long, how long must the perpendicular side be? |
MULTIPLICATION
Solving area problems again connects back to total and known/unknown values. When students are trying to identify the total area of the shape, and are given both side lengths, students need to multiply to find the area.
DIVISION
When students are given the total area of the shape, but need to find a missing side length, they must divide.
Ultimately, if students have a solid understanding of multiplication and division word problems and their connection to total, they will likely be successful with area word problems.
Comparison Word Problems
The most complex multiplication and division word problem types are comparison word problems, in my opinion. Just as they are in addition & subtraction, the way these problems are structured, cause them to be more complex than the others. For these, it’s important to look at each of the different problem types and digest what’s being given. I use a 3 Reads Routine when working through word problems, and these problems always bring the greatest discussion as students grapple with the information that’s presented.
| COMPARISON UNKNOWN | CONSTANT UNKNOWN | ||
| Compare | The small bag of apples costs $4. The box of apples costs 6 times as much. How much does the box of apples cost? | The small bag of apples costs $4. The box of apples costs $24. How many times as much does the box cost compared to the bag of apples? |
A box of apples costs $24 and is 6 times as much as the cost of the small bag of apples. How much does the small bag cost? |
The multiplication and partitive division (constant unknown) examples have very similar wording since they both have the comparison statement: “6 times as much”. This is a description of the relationship between two groups-the total, and the comparison group. The quotative (comparison) example is worded differently since the unknown is the comparison relationship: “How many times as much does”
The key to understanding multiplicative comparison problems is that the comparison is the repeating groups, whereas the constant is the group size.
In a multiplication word problem, you are told the amount in the comparison group, 6, and the constant, 4. Each bag of apples is $4, so if it’s 6 times as much, it’s the same as having 6 of the bags. Thus, 4 x 6.
In a (partitive) division word problem, you are given the total number (the cost of the box of apples). Once you partition, or divide, that cost into 6 equal groups, you are able to identify the cost of one of those groups, which is the same as the cost of the small bag of apples, and that is the same as the number of ducks.
In a (quotative) division word problem, you are given the constant, the cost of the small bag, along with the cost of the box of apples. The unknown is the relationship between them. With these word problems, the wording of the question can often throw students off.
Once students are able to decompose the word problem to identify the total, and the comparison, they’re able to connect that to what they already know about multiplication and division to help them when solving. Teaching students to closely read the word problem is key. To read more about my 3 Reads Routine you can click the image below.
Looking for additional resources? You can download my Multiplication & Division Word Problem Types reference sheet and use it to help identify and write the different word problem types for classroom practice.
Want additional multiplication & division word problem practice? I have a FREE Multiplication & Division Word Problem Task Cards set. Each of the multiplication & division word problem types discussed here are practiced during the 24 task card set. This is great practice for later in the year to ensure students have ample practice with each type. It would even be a great tool to help students discuss the different problem types and how they’re presented. To download the Multiplication & Division Word Problem Type Task Cards, just fill out the form below and they’ll be sent straight to your email.
>
Newsletter
Sign up to receive your free Multiplication & Division Word Problem Types Task Cards! After confirming your email, you’ll receive the file and be signed up for my weekly newsletter.
You might also find the following links helpful.
Partitive & Quotative Division from SFUSD
CGI Resources from LAUSD
Multiplication & Division Word Problems from ND Counts
Two Ways of Thinking of Division from Langford Math
In grade 3 students move onto more complex word problems using multiplication and division. Below we’ll take you through a step-by-step guide on how to solve a simple division word problem.
Turn the English into Algebra
The first rule of any word problem is to think in math terms. To do that, you’ll need to:
- Read the whole word problem.
- Write down what is asked for. (As students work through the word problem, they can get lost and start to work in a different direction. Having the actual request written down, will help to keep them focus on the goal.)
- Sketch out the word problem, if possible.
- the signs where you see key words. For example, write + where you see add, increase, combine, or – where you see less, difference, reduce.
- Find or work out any formulas.
Division word problem example
Let’s work through a division word problem:
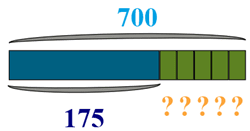
Katie has 700 candies. She gave away 175 candies to her classmates. She put the remaining candies in five separate bags. How may candies are there in each bag?
First, read through the whole word problem once more.
Now, what is being asked? We want to know how many candies are in each of the 5 bags.
Let’s sketch it out:
Write down the math signs where you see key words in the text:
In the above, we can see there are two calculations to be completed.
First, we need to find out how many candies there are left after Katie hands out 175 candies to her classmates:
Now we know there are 525 candies remaining. Next, we need to work out how many candies she put in each of the 5 bags:
We need to divide the 525 candies by 5 bags:
The answer is there are 105 candies in each bag.
For practice, we have division word problems worksheets in our grade 3 word problems section.

Become a Member
This content is available to members only.
Join K5 to save time, skip ads and access more content.
Learn More
1. Dividing Bags of Candy. This is a real-world example of a 3rd grade division word problem that most kids can relate to. Now, obviously a teacher is going to give equal numbers, so the student has to divide.
What is a division story problem?
Create division problems by performing the opposite operations of multiplication problems. For example, instead of creating a problem that asks how many times a factor increases, ask how many times one number divides into another number.
How do you show division?
To show division with a division bar, we write the dividend on top. To show division with a division box, we write the dividend inside the box. The division bar is a way to show division. This means “five times what number is 15?” The answer is 3.
How do you describe division?
The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic, which gives a fair result of sharing. If 3 groups of 4 make 12 in multiplication; 12 divided into 3 equal groups give 4 in each group in division.
What are some words for division?
Some common synonyms of division are fragment, member, part, piece, portion, section, and segment. While all these words mean “something less than the whole,” division applies to a large or diversified part.
What is another word for division?
What is another word for division?
| separation | dividing |
|---|---|
| rift | divergence |
| disseverment | disjunction |
| subdivision | fork |
| breakdown | isolation |
What is a division sentence?
A division sentence is a number sentence that uses the operation of division. Division has an opposite operation, which is multiplication, where multiplication and division undo or reverse each other. We can use the opposite operation of multiplication, or we can use repeated addition, to complete a division sentence.
What is the parts of division?
Each part of a division equation has a name. The three main names are the dividend, the divisor, and the quotient.
What is a division essay?
The purpose of the division essay, also known as the classification essay or the division and classification essay, is to separate things into categories. For example, you might write about diseases that have similar symptoms, or about categories of comedy, or about the causes behind social unrest.
What is a solution sentence?
Introduction Math Solution Sentence Thus the expression means equation where the left side is equal to right side or vice versa. Example: (5+5=10). LHS is the sum of 5 and 5 which is equal to RHS. Math solution for sentence is to find the unknown term by using known term from the expression.
How do you write a subtraction sentence?
Subtraction Sentences The number sentence would be written as 9 – 7 = 2. Subtract the second number from the first number to complete the number sentence. A subtraction number sentence is an equation that shows a number being subtracted from another number with a final answer like the example above.
How do you write a number range in a sentence?
When writing about a number range do you:
- use the word ‘to’ as in 10 to 20.
- use a hyphen separated by spaces as in 10 – 20.
- use a hyphen not separated by spaces as in 10-20?
How do you write a range?
The Range is the difference between the lowest and highest values. Example: In {4, 6, 9, 3, 7} the lowest value is 3, and the highest is 9. So the range is 9 − 3 = 6.
How do you use first and second in a sentence?
First, I prefer the train because I can see the landscape. Second, I have control over my luggage, and third, it is better for the environment. The important thing is not to mix them, as in the following sentence: First, I prefer the train because I can see the landscape.
Is first and foremost correct?
For example, First and foremost, I want to thank our sponsors, or What we need, first and foremost, is a new secretary, or We have to deal, first of all, with the early history. The first term, dating from the late 1300s, is redundant, since first and foremost mean virtually the same thing.
What type of word is first and second?
“First,” “second,” “third,” “fourth” and so on are called “ordinal numbers,” terms defining a thing’s place in a series (as opposed to “cardinal numbers,” such as “one,” “two,” “three,” etc.).