You will encounter these area word problems often in math. Many of
them will require familiarity with basic math, algebra skills, or a
combination of both to solve the problems.
As I solve these area word problems, I will make an attempt to
give you some problems
solving skills
Word problem #1:
The area of a square is 4 inches. What is the length of a side?
Important concept: Square. It
means 4 equal
sides.
Area = s × s= 4 × 4 = 16 inches2
Word problem #2:
A small square is located inside a bigger square. The length of one side of the small square is 3 inches and the length of one side of the big square is 7 inches
What is the area of the region located outside the small square, but inside the big square?
Important concept: Draw a picture and see the problem with your eyes. This is done below:
The area that you are looking for is everything is red. So you need to remove the area of the small square from the area of the big square
Area of big square = s × s = 7 × 7 = 49 inches2
Area of small square = s × s = 3 × 3 = 9 inches2
Area of the region in red = 49 — 9 = 40 inches2
Word problem #3:
A classroom has a length of 20 feet and a width of 30 feet. The headmaster decided that tiles will look good in that class.
If each tile has a length of 24 inches and a width of 36 inches, how many tiles are needed to fill the classroom?
Important concept:
Find area occupied by entire classroom
Find area for one tile
Decide which unit to use. In this case, we could use feet
Area of classroom = length × width = 20 × 30 = 600 ft2
Before we get the area of each tile, convert the dimensions to feet as already stated
Since 1 foot = 12 inches, 36 inches = 3 feet and 24 inches = 2 feet
Area of each tile = length × width = 2 × 3 = 6 ft2
If one tile takes 6 ft2, it takes 100 tiles to cover 600 ft2 (6 × 100 = 600)
Word problem #4:
Sometimes area word problems may require skills in algebra, such as factoring and solving quadratic equations
A room whose area is 24 ft2 has a length that is 2 feet longer than the width. What are the dimensions of the room?
Solution #1 Use of basic math skills and trial and error
Pretend width = 1, then length = 3 ( 1 + 2)
1 × 3 is not equal to 24 and 3 is not close at all to 24. Try bigger numbers
let width = 3, then length = 5 ( 3 + 2)
3 × 5 = 15. It is still not equal to 24
let width = 4, then length = 4 ( 4 + 2)
4 × 6 = 24. We are done!
Solution #2 Use of algebra
Let width = x, so length = x + 2
Area = length × width
24 = x × ( x + 2)
24 = x2 + 2x
x2 + 2x = 24 (swap the left side with the right side)
x2 + 2x — 24 = 0
( x + 6) × ( x — 4 ) = 0
x = -6 and x = 4
So width = 4 and length = 4 + 2 = 6
As you can see area word problems can become very complicated as
shows in the last problem. And the use of basic math skills may not be
the best way to go to solve area word problems. Sometimes algebra
is better because trial and error can take a long time!
Have a question about these area word problems? send me a note.
Recent Articles
-
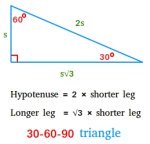
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
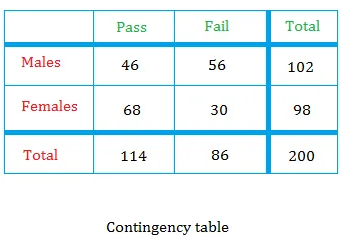
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Related Topics:
More Lessons for Grade 9 Math
Math Worksheets
Examples, videos, worksheets, solutions, and activities to help Algebra students learn how to solve word problems that involve area of shapes.
Learn to write and solve polynomial equations for area of a rectangle
Example: The length of a rectangle is 8 more than the width. Its area is 240 sq. ft. Write an equation for its area letting w be the width. Then solve the equation for w and also find the length.
How to solve word problems involving area, area, perimeter, and quadratic equations?
Examples:
(1) The perimeter of a rectangular concrete slab is 82 feet and its area is 364 square feet. What is the length of the longer side of the slab?
(2) The width of a rectangle is 2 inches less than its length. If the area of the rectangle is 99 square inches, what is its width?
(3) Two of the local ranches are bragging about their ability to use fencing sparingly. Bob says that he was once able to fence in a rectangular pasture of 12,400 square feet with only 440 feet of fencing. Susan says that she was once able to fence in a rectangular pasture of 16,700 square feet with only 520 feet of fencing. Which one is lying?
- Show Step-by-step Solutions
Word Problems on Area
Examples:
(1) The length of a page of a book is 2 cm greater than the width of the page. A book designer finds that the length is increased by 2 cm and the width is increased by 1 cm, the area of the page is increased by 19 cm2 What are the dimensions of the original page?
(2) A rectangular picture is 2 cm longer than it is wide. It is mounted in a frame 3 cm wide, The area of the frame is 168 sq. cm, Find the dimensions of the picture.
(3) A rectangular swimming pool is 4 m longer than it is wide. If a sidewalk 2 m wide is placed around the pool, the area covered by the pool and sidewalk is 192 sq. m greater than the area covered by the pool alone. Find the dimensions of the pool.
Area Word Problems — Geometry Help
How to solve word problems using the formulas for the area and perimeter of rectangles and squares?
Example: A rectangle is twice as long as it is wide. If the area of a rectangle is 98 cm2, find its dimensions.
- Show Step-by-step Solutions
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Teaching your pupils to solve 2-step word problems and multi-step word problems at KS2 is one of hardest parts of a mastery led approach in maths. There are several cognitive functions at play, as children have to wrestle with their knowledge of maths vocabulary, maths operations, and often basic comprehension skills.
In this article we set out some of the sorts of maths word problems pupils can expect from the KS2 maths national curriculum and look at strategies for solving them. In total we’ve provided 30 KS2 word problems to work through, showing the variety of 2-step word problems and multi-step word problems pupils are likely to encounter.
What are word problems
Word problems in maths are sentences describing a real life scenario where children must apply their maths knowledge to reach a solution or unpick the maths problem.
To solve maths word problems children must be familiar with the maths language associated with the mathematical symbols they are used to in order to make sense of the word problem; for example: plus, more, total = add; difference, less, minus = subtract, etc.
What are two-step word problems?
Two-step word problems are problems in which two separate calculations (usually different operations) are required to reach the answer. By different operations we mean addition, subtraction, multiplication or division.
What are multi-step word problems?
Multi-step word problems are maths problems that require multiple calculations to solve them. They will usually will involve more than one operation and often more than one strand from the curriculum. For example a multi-step word problem on area and perimeter may also involve ratio and multiplication.
In KS2 SATs multi-step word problems can be awarded up to 3 marks for a correct answer, but 1 or 2 marks can be achieved by solving some of the steps in the problem correctly.
Two-step word problems and multi-step word problems pupils will encounter in KS2
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”.
The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
| Number and place value | 6 | 9 | 5 | 7 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |
As well as varying in content (sometimes by using a combination of strands in one problem, e.g. shape and calculations), word problems will also vary in complexity, from one-step to multi-step problems.
Different word problems will provide a different level of cognitive demand as an alternative method of adapting the level of difficulty. The STA mathematics test framework (2015) sets these out.
| Strand | 1 | 2 | 3 | 4 |
| Depth of understanding | recall of facts or application of procedures | use facts and procedures to solve simple problems | use facts and procedures to solve more complex problems | understand and use facts and procedures creatively to solve complex or unfamiliar problems |
| Computational complexity | no numeric steps | one, or a small number of numeric steps | a larger number of numeric steps all steps are simple | a larger number of numeric steps, at least one of which is more complex |
| Spatial reasoning | no spatial reasoning required | manipulation of the geometric information is required | complex manipulation of the geometric information is required | interpret, infer or generate new geometric information |
| Data interpretation | no data interpretation required | select and retrieve information | select and interpret information | generate or infer new information from data |
| Response strategy | select one or more responses or construct a simple response | construct a small set of responses | construct a straightforward explanation shows evidence of a method | construct a complex explanation |
Skills required for multi-step word problems
There is a high level of cognitive demand on children when they are faced with multi-step word problems: interpreting the question to find the arithmetic behind it and then calculating the arithmetic itself.
Therefore, a secure knowledge of times tables and a confident understanding of arithmetic are essential skills for being able to successfully solve word problems.

Year 3 to 6 Rapid Reasoning (Weeks 1-6)
Download 480 two-step and multi-step word problems for Years 3 to Year 6 (4 a day x 6 weeks for each year group)
Arithmetic within multi-step word problems
A useful strategy to use in class is to provide children with a list of arithmetic questions you have previously ‘extracted’ from some word problems.
Generally, children are much more confident with arithmetic than word problems, so they should be able to answer these with relative ease.
In the next lesson, give the children the word problems – after a while, ask them which they found easier and why.
Then show the children the arithmetic from the previous day and ask if they can see the similarities. They could then try to ‘extract’ the arithmetic from word problems themselves.
How to teach multi-step word problems
Here are two simple strategies that can be applied to most two-step word problems and multi-step word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
How to solve a year 6 multi-step word problem
Here’s an example.
There are 29 pupils in a class. The teacher has 7 litres of apple juice. She pours 215 millilitres of apple juice for every pupil. How much apple juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
Bar modelling is always a brilliant way of representing even multi step word problems in year 6, but there are always other ways of drawing it out. For example, for this question, you could draw 29 pupils (or stick man x 29) with ‘215 ml’ above each one and then a half-empty bottle with ‘7 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
3. How to answer step by step
- There are 29 pupils in a class.
- The teacher has 7 litres of apple juice. 1) 7 litres = 7,000ml
- She pours 215 millilitres of apple juice for every pupil. 2) 215ml x 29 = 6,235ml
- How much apple juice is left over? 3) 7,000ml – 6,235ml = 765ml
How to solve a year 5 multi-step word problem
A similar approach can be used for this one.
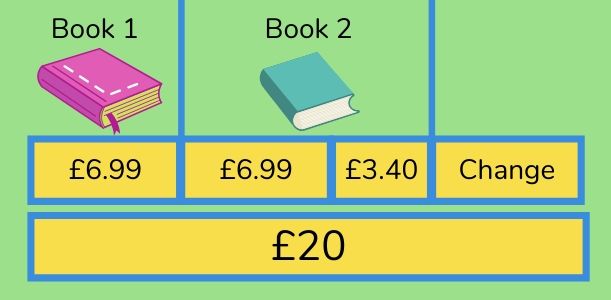
- Mara is in a bookshop. She buys one book for £6.99 and another that costs £3.40 more than the first book. She pays using a £20 notes. What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
3. How to answer step by step
- Mara is in a bookshop.
- She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
- She pays using a £20 note.
- What change does Mara get?
- £20 – £17.38 = £2.62
There are plenty more teacher guides and resources available from Third Space for problem solving in KS2. Find out how to develop maths reasoning skills in KS2, how to balance fluency, reasoning and problem solving in your maths lessons, and get ideas for developing and running maths investigations at KS2.
2-step word problems Year 3
With word problems for Year 3, children will move away from solely using concrete resources when solving word problems and start using written methods. This is also the year in which two-step problems will be introduced.
As some children may not be confident readers, it is important that word problems are explored in a variety of contexts: as a class, in groups, in partners, with an adult, with a list of ‘mathematical vocabulary’ accessible, etc. It is important that children’s literacy skills don’t hinder their progress or in maths.
Example Year 3 word problems
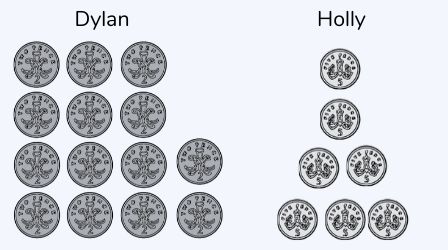
- Dylan and Holly have different amounts of money. Dylan has fifteen 2p coins. Holly has seven 5p coins. Who has the most money, and by how much? Answer: Holly by 5p.
- It takes Jamie 10 minutes to read 3 pages of his book. He reads 18 pages of his book before bed. How long does Jamie spend reading? Answer: 60 minutes.
2-step word problems Year 4
With word problems year 4, children should feel confident using the written method for each of the four operations. This year children will be presented with a variety of problems, including two-step problems, and be expected to work out the appropriate method required to solve each one.
While children should be focusing on formal written methods, it is important that concrete resources and pictorial representations are still used to consolidate their understanding.
Example Year 4 word problem
- Lily, Simon and Rose are each thinking of a number. The sum of their numbers is 9,989. Lily’s number is 1,832. Simon’s number is three thousand more than Lily’s. What is Rose’s number? Answer: 3,325

- Mia has a jug with 2.5 litres of water in it. She pours two glasses of 300ml and three glasses of 500ml. How much water is left in the jug? Give your answer in millilitres. Answer: 400ml
Multi-step word problems: Year 5
Although one and two-step word problems are the mainstay of Year 5 reasoning and problem solving, word problems for year 5 are also when children may start to extend their range to include multi-step problems;
In Upper Key Stage 2, word problems become more complex not only in the calculations (higher numbers, decimals etc.) but also the vocabulary – a subtlety of maths language may mean it is less obvious as to which operation is required.
In the first example below, the children are essentially being asked to add and divide by 7 – or find the ‘mean’ – but the word problem doesn’t use the vocabulary children usually associate with addition or division, such as total, sum, share, split, etc. To reduce the cognitive demand of questions such as these, the numbers could be altered so that children are still required to extract the calculations from the word problems but can then complete those calculations with simpler numbers.
Example Year 5 multi-step word problems
- A writer is working on two projects. She has one week to write 518 maths questions for one project and 476 questions for another project. If she completes the same number of questions every day, how many should she aim to complete each day? Answer: 142
- Walton Wanderers’ new shirt costs £29. In the first month after it was launched, the club shop sold 1,573 shirts. 54 shirts were returned because they did not fit. How much money did the club shop receive by selling the shirts? Answer: £44,051
Multi-step word problems Year 6
With word problems for year 6, children move on from 2-step word problems to multi-step word problems. These could include fractions, decimals and percentages. Some of the most complex problems in KS2 SATS papers are worth 3 marks – these are intended to challenge more able mathematicians.
As previously mentioned, one or two marks can be achieved for correctly solving different ‘steps’ of the problem even without arriving at the correct final answer.
Example Year 6 multi-step word problem
- Sarah makes jewellery with beads. Bracelets have 37 beads. Necklaces have 74 beads. Sarah makes 28 bracelets and 81 necklaces. How many beads does she use altogether? Answer: 7,030
- A field measures 15m by 20m. The field next to it is 300cm longer and 2.5m narrower. What is the difference in area between the two fields? Answer: 15m
For more like this, please refer to this collection of 35 year 6 maths reasoning questions to support teaching in the run up to SATs or if you want to focus specifically on using the bar model as a problem solving tool, try these Year 6 multi-step word problems.
2-step and multi-step word problems by topic
What follows are a series of 2-step word problems and multi-step worded problems based around the national curriculum objectives for each topic in maths. These show you a full range of question and problem types and the type of skills and knowledge your pupils will need to develop. We’ve also added some links to relevant word problems worksheets.

Year 3 to 6 Rapid Reasoning (Weeks 1-6)
Download 480 two-step and multi-step word problems for Years 3 to Year 6 (4 a day x 6 weeks for each year group)
Place value word problems
Place value problems appear throughout KS2. In Year 3, they will be based on five objectives:
- count from 0 in multiples of 4, 8, 50 and 100 (find 10 or 100 more or less than a given number)
- recognise the place value of each digit in a three-digit number
- compare and order numbers up to 1000
- identify, represent and estimate numbers using different representations
- read and write numbers up to 1000 in numerals and in words.
The progression in place value through KS2 ends in Year 6 with problems being based on three objectives:
- read, write, order and compare numbers up to 10 000 000 and determine the value of each digit
- round any whole number to a required degree of accuracy
- use negative numbers in context, and calculate intervals across zero.
Place value multi-step word problem: Year 6
- Mo uses four-digit cards and some zeros to make a seven-digit number on a place-value grid. Mo places the digit with the lowest value in the place with the highest value. He then places the 6 so that it has a value of 60,000. Finally, he places the digit with the highest value in the place with the lowest value. What could Mo’s number be? Write your answer in words.
- Answer: any of the following numbers: one million two hundred and sixty thousand and nine, one million sixty-two thousand and nine, one million sixty thousand two hundred and nine, one million sixty thousand and twenty-nine
For free multi-step word problems worksheets download these free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction problems appear throughout KS2. In Year 3, they will be based on three objectives:
- add and subtract numbers mentally
- add and subtract numbers with up to three digits, using formal written methods of columnar addition and subtraction estimate the answer to a calculation and use inverse operations to check answers
- solve problems, including missing number problems, using number facts, place value, and more complex addition and subtraction.
The progression in addition and subtraction through KS2 ends in Year 6 with problems being based on three objectives:
- perform mental calculations, including with mixed operations and large numbers
- solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why
- use estimation to check answers to calculations and determine, in the context of a problem, an appropriate degree of accuracy.
Addition and subtraction multi-step word problem: Year 6
- Buzzard Sky Diving Company have taken individual bookings worth £12,584 and group bookings worth £15,992. Some people have cancelled at the last minute. £1,629 has had to be returned to them. How much money has the sky diving company taken altogether? Answer: £26,947
For free multi-step and two-step word problems worksheets download these free addition and subtraction word problems for Years 3, 4, 5 and 6 and take a look at our collection of addition and subtraction word problems for Year 3- Year 6.
Tips for solving addition multi-step word problems
Children should be taught to recognise the vocabulary used in addition word problems to signify that the addition operation is required, for example, altogether, combined, total, sum etc. Be mindful that although more can be used for addition (e.g. What is 7 more than 9?), it can also be used for subtraction (e.g. How many more is 9 than 7?).
Addition multi-step word problem: Year 6
- Two different numbers add together to make an even total less than 20. Both numbers are greater than 6 and less than 12. What could the numbers be? Answer: 7 and 9, 7 and 11, 8 and 10
Tips for solving subtraction multi-step word problems
Children should be taught to recognise the vocabulary used in subtraction word problems to signify that the subtraction operation is required, for example, change (money), difference, fewer than, minus etc. They should also by now know their subtraction facts.
Subtraction two-step word problem: Year 5
- Carlos Varqueri – United’s star striker – has asked for a pay rise. He would like another £154,875 a year, so that his wage becomes £800,000 per year. How much money does Carlos earn at the moment? Answer: £645,125
Multiplication and division word problems
Multiplication and division problems appear throughout KS2. In Year 3, they will be based on three objectives:
- recall and use multiplication and division facts for the 3, 4 and 8 multiplication tables
- write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for two-digit numbers times one-digit numbers, using mental and progressing to formal written methods
- solve problems, including missing number problems, involving multiplication and division, including positive integer scaling problems and correspondence problems in which n objects are connected to m objects.
The progression in multiplication and division through KS2 ends in Year 6 with problems being based on six objectives:
- multiply multi-digit numbers up to 4 digits by a two-digit whole number using the formal written method of long multiplication
- divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context
- divide numbers up to 4 digits by a two-digit number using the formal written method of short division where appropriate, interpreting remainders according to the context
- perform mental calculations, including with mixed operations and large numbers
- identify common factors, common multiples and prime numbers
- use estimation to check answers to calculations and determine, in the context of a problem, an appropriate degree of accuracy.
Multiplication and division multi-step word problem: Year 6 (crossover with decimals)
- Lottie is playing a computer game. She has scored 67 points so far. She defeats a giant, which means that her score becomes ten times greater. However, she then gets lots in a maze, which means that her score becomes 1,000 times smaller. What is Lottie’s new score? Answer: 0.67
Tips for solving multiplication multi-step word problems
Children should be taught to recognise the vocabulary used in word problems to signify that the multiplication operation is required, for example, product, double, triple, groups etc. Be mindful that groups can be used in both multiplication and division problems, e.g. ‘What are 7 groups of 5?’ (multiplication) or ‘How many groups of 4 fit into 28?’ (division).
Multiplication multi-step word problem: Year 6
- There are 32 levels in a computer game. The maximum number of points that can be achieved for each level is 1,450. Hauwa completes the game and scores maximum points. How many points does Hauwa score altogether? Answer: 46,400
For free multi-step and two-step word problems worksheets download free multiplication word problems worksheets for Years 3, 4, 5 and 6
Children can practice can practice multiplication word problems in Third Space Learning’s online tuition programmes.
Tips for solving division multi-step word problems
Children should be taught to recognise the vocabulary used in division word problems to signify that the division operation is required, for example, halve, share, groups, split etc.
Division two-step word problem: Year 4
- A group of friends earn £120 by mowing lawns. They share the money equally. They get £15 each. How many friends are there in the group? Answer: 8
For free multi-step and two-step word problems worksheets download this free division word problems worksheet for Years 3, 4, 5 and 6
Mixed operations word problems
In the Year 3 non-statutory notes and guidance of the National Curriculum, it is recommended that pupils practise solving varied addition and subtraction questions and simple multiplication and division problems in contexts, deciding which of the four operations to use and why. These include measuring and scaling contexts, and correspondence problems in which m objects are connected to n objects.
At the end of KS2, the guidance states that pupils could practise addition, subtraction, multiplication and division for larger numbers, using the formal written methods of columnar addition and subtraction, short and long multiplication, and short and long division.
Mixed operations two-step word problem: Year 6 (crossover with money)

- A customer visits Dave’s DIY and buys 18 packs of screws, 18 packs of washers and a screwdriver. How much change is given from £20? Answer: £1.67
Four operations multi-step word problem: Year 5
- Oakthorpe Academy have been given a donation of £5,460 by the PTA. The School Council decide to use £1,755 on buying some new computer equipment. The rest is split equally between five year groups so they can decide for themselves how to spend the money. How much money will each year group have? Answer: £741
Read more
- 33 mental maths strategies you should be teaching in KS1 and KS2
- What are number facts? Activities to support memorisation.
- How primary schools develop fluency in maths
Fraction word problems
Fraction word problems require a good understanding of division and multiplication. Bar models or other pictorial representations are useful strategies in helping children solve problems like these.
Fraction problems appear throughout KS2. In Year 3, they will be based on seven objectives:
- count up and down in tenths
- recognise that tenths arise from dividing an object into 10 equal parts and in dividing one-digit numbers or quantities by 10
- recognise, find and write fractions of a discrete set of objects: unit fractions and non-unit fractions with small denominators
- recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators
- recognise and show, using diagrams, equivalent fractions with small denominators
- add and subtract fractions with the same denominator within one whole
- compare and order unit fractions, and fractions with the same denominators.
The progression in fractions through KS2 ends in Year 6 with problems being based on seven objectives:
- use common factors to simplify fractions and use common multiples to express fractions in the same denomination
- compare and order fractions, including fractions > 1
- add and subtract fractions with different denominators and mixed numbers, using the concept of equivalent fractions
- multiply simple pairs of proper fractions, writing the answer in its simplest form
- divide proper fractions by whole numbers
- associate a fraction with division and calculate decimal fraction equivalents
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
Fraction multi-step word problem: Year 6
- A bakery has 2 and 1/3 rhubarb pies left for sale. A customer buys 3/12 of a pie. What fraction of the pies is left? Write your answer as a mixed number. Answer: 2 and 1/12
For free multi-step and two-step word problems worksheets download fractions and decimals word problems for Years 3, 4, 5 and 6
Decimals word problems
Decimal word problems are commonly used in questions involving money, although they also often appear alongside fractions and/or percentages, requiring children to calculate their equivalences.
Decimal problems begin in Year 4 and will be based on six objectives:
- recognise and write decimal equivalents of any number of tenths or hundredths
- recognise and write decimal equivalents to ¼, ½, ¾
- find the effect of dividing a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths
- round decimals with one decimal place to the nearest whole number
- compare numbers with the same number of decimal places up to two decimal places; solve simple measure and money problems involving fractions and decimals to two decimal places.
The progression in decimals from Year 4 ends in Year 6 with problems being based on six objectives
- associate a fraction with division and calculate decimal fraction equivalents for a simple fraction
- identify the value of each digit in numbers given to three decimal places and multiply and divide numbers by 10, 100 and 1000 giving answers up to three decimal places
- multiply one-digit numbers with up to two decimal places by whole numbers
- use written division methods in cases where the answer has up to two decimal places; solve problems which require answers to be rounded to specified degrees of accuracy
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
Decimals two-step word problem: Year 6 (crossover with multiplication)
- A teaspoon contains 5.26ml of cough medicine. Amber takes 5 teaspoons full every day. How many millilitres of cough medicine does Amber take each day? Answer: 26.3ml
Percentage word problems
Children need a secure understanding in fractions before attempting percentage problems; they are therefore not introduced until Upper Key Stage 2. Percentage word problems begin in Year 5 and will be based on two objectives:
- recognise the per cent symbol (%) and understand that per cent relates to ‘number of parts per hundred’, and write percentages as a fraction with denominator 100, and as a decimal
- solve problems which require knowing percentage and decimal equivalents of ½, ¼, 1/5, 2/5, 4/5 and those fractions with a denominator of a multiple of 10 or 25.
The progression in percentage continues into Year 6 with problems being based on two objectives:
- recall and use equivalences between simple fractions, decimals and percentages, including in different contexts
- solve problems involving the calculation of percentages and the use of percentages for comparison.
Percentage multi-step word problem: Year 6
- Rachel and Max are playing a computer game. The game has 160 levels. Rachel’s counter says she has completed 60% of the game. Max’s counter says that he has completed 45% of the game. What levels are they each on? Answer: Rachel = Level 96, Max = Level 72
For free multi-step and two-step word problems worksheets download decimals and percentages word problems for Years 3, 4, 5 and 6
Measurement word problems
Many measurement word problems require children to convert between metric measures, thus children should be confident in multiplying and dividing by powers of 10. More complex measurement word problems (such as those involving imperial measures) may require children to have an understanding of ratio and proportion.
Word problems involving measures begin in Year 3 and will be based on six objectives:
- measure, compare, add and subtract: lengths (m/cm/mm); mass (kg/g), volume/capacity (l/ml)
- time word problems where children tell and write the time from an analogue clock, including using Roman numerals from I to XII, and 12-hour and 24-hour clocks
- estimate and read time with increasing accuracy to the nearest minute
- record and compare time in terms of seconds, minutes and hours
- use vocabulary such as o’clock, a.m./p.m., morning, afternoon, noon and midnight
- know the number of seconds in a minute and the number of days in each month, year and leap year; compare durations of events
The progression continues into Year 6 with problems being based on three objectives:
- solve problems involving the calculation and conversion of units of measure, using decimal notation up to three decimal places where appropriate
- use, read, write and convert between standard units, converting measurements of length, mass, volume and time from a smaller unit of measure to a larger unit, and vice versa, using decimal notation to up to three decimal places
- convert between miles and kilometres.
Measurement multi-step word problem: Year 6 (crossover with ratio)
- 5 miles are approximately equivalent to 8 km. Mr Norton’s car speedometer shows that he is travelling at 104 km/h. About how many miles per hour (mph) is the car travelling? Answer: 65 mph
Money word problems
Problems involving money link with decimals (money notation) and measures (converting between £ and p). Where possible, especially until their understanding is secure, children should be handling real money to help them solve problems.
Money word problems begin in Year 3 and will be based on one objective: add and subtract amounts of money to give change, using both £ and p in practical contexts. The non-statutory guidance in the curriculum recommends that pupils continue to become fluent in recognising the value of coins, by adding and subtracting amounts, including mixed units, and giving change using manageable amounts.
The decimal recording of money is introduced formally in year 4, where word problems will be based on one objective: solve simple measure and money problems involving fractions and decimals to two decimal places.
Money problems continue throughout KS2 but are not specifically mentioned in the National Curriculum beyond Year 4.
Two-step money word problem: Year 6 (crossover with mixed operations)
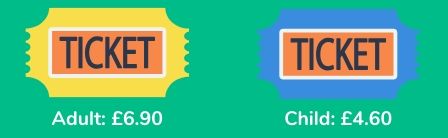
These are the different prices of tickets at a cinema.
- Jamaal’s dad buys two adults’ tickets and four children’s tickets. How much money do the tickets cost altogether? Answer: £32.20
Area word problems
Mathematical questions related to area require a secure understanding of arrays, times tables, multiplication, division and factors. Concrete resources such as Numicon and multilink can be used to support children to solve these problems.
Word problems involving area begin in Year 4 and will be based on one objective: find the area of rectilinear shapes by counting squares. The progression continues into Year 6 with problems being based on three objectives:
- recognise that shapes with the same areas can have different perimeters and vice versa
- recognise when it is possible to use formulae for area and volume of shapes
- calculate the area of parallelograms and triangles
Area multi-step word problem: Year 6
- A square has a side length of 6cm. A triangle has a base of 8cm and a perpendicular height of 7cm. What is the difference in their areas? Answer: 8cm2
Perimeter word problems
As well as being an important life skill, it is important for children to be able to measure accurately with a ruler for some aspects of this mathematical strand. As above, Numicon and multilink are extremely useful resources in supporting children in their calculation of perimeter word problems.
These problems begin in Year 3 and will be based on one objective: measure the perimeter of simple 2-D shapes. The progression continues into Year 6 with problems being based on one objective: recognise that shapes with the same areas can have different perimeters and vice versa.
Perimeter word problem: Year 6 (crossover with decimals and multiplication)
- Josh has drawn a square. Each side is 7.5cm. What is the perimeter of the square? Answer: 30cm
Ratio word problems
In my experience, ratio is most successful when taught with concrete resources such as multilink, Cuisenaire rods or beads. Once children are taught how to represent ratio word problems using equipment (and eventually transferring to a pictorial representation, such as a bar model), the process is a lot easier.
Children won’t encounter ratio word problems until Year 6, where they will be based on three objectives:
- solve problems involving the relative sizes of two quantities where missing values can be found by using integer multiplication and division facts
- solve problems involving similar shapes where the scale factor is known or can be found
- solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
Ratio word problem: Year 6 (crossover with measurement)
- A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
Order of operations word problems
Children won’t encounter word problems about the order of operations until Year 6, where they will be based on one objective: use knowledge of the order of operations to carry out calculations involving the four operations. The non-statutory guidance in the National Curriculum also recommends that children explore the order of operations using brackets (otherwise known as BODMAS or BIDMAS); for example, 2 + 1 x 3 = 5 and (2 + 1) x 3 = 9.
Bodmas word problem: Year 6
- Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
- 50 – 10 × 5 =
- 50 – 10 × 5 =
Volume word problems
Children won’t encounter volume-related word problems until Year 6, where they will be based on two objectives:
- recognise when it is possible to use formulae for area and volume of shapes
- calculate, estimate and compare volume of cubes and cuboids using standard units, including cubic centimetres and cubic metres, and extending to other units
Volume word problem: Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
Algebra word problems
Again algebra word problems only really come up in Year 6; the objectives they will be based on are:
- use simple formulae
- generate and describe linear number sequences
- express missing number problems algebraically
- find pairs of numbers that satisfy an equation with 2 unknowns
- enumerate possibilities of combinations of 2 variables
Algebra word problem: Year 6
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
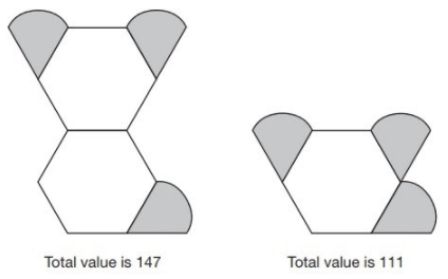
Amina is making designs with two different shapes. She gives each shape a value. Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
More support with KS2 word problems
For more multi-step and 2-step word problems register for free on the Third Space Learning Maths Hub which includes lots more printable word problems worksheets including as part of the free resources on offer a complete set of place value word problems with answer sheets for Year 3 to Year 6: All Kinds of Word Problems on Number and Place Value
If you have any pupils who are struggling to master word problems they may need a more intensive personalised intervention. Third Space Learning’s tuition follows a rigorous step by step process to teaching problem solving with excellent success – pupils make on average double their expected progress with us.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
In word problems on area of a square we will find the area
whose side is given. For finding the area of a given square, we should make
sure that the sides are in the same unit of length. If they are given in
different units, change them to the same unit.
10 mm = 1 cm
100 cm = 1 m
1000 m = 1 km
Word problems on area of a square:
1. Find the area of a square of side 27 cm.
Area of a square = length × length
= 27 × 27 sq. cm.
= 729 sq. cm.
2. Find the area of a square of side 35 m.
Area of a square = length × length
= 35 × 35 sq. m.
= 1225 sq. m.
3. The length of the side of a square is 25 cm. Find the
area.
Length of the side of a square = 25 cm
Are of the square =
Side × Side
=
25 cm × 25 cm
=
625 cm2
4. Length of a side of a square field is 275 m. What will be
cost of levelling the field at a rate of 10 cent per square metre?
Length of the square field = 275 m
Are of the square field = side × side
=
275 m × 275 m
=
75625 m2
Cost of levelling the field = 75625 × 10 cent
=
756250 cent
=
$ 7562.50
● Area.
Area of a Rectangle.
Area of a Square.
To find Area of a Rectangle when Length and Breadth are of Different
Units.
To find Length or Breadth when Area of a Rectangle is given.
Areas of Irregular Figures.
To find Cost of Painting or Tilling when Area and Cost per Unit
is given.
To find the Number of Bricks or Tiles when Area of Path and Brick
is given.
Worksheet on Area.
Worksheet on Area of a Square and Rectangle
Worksheet on Area of Regular Figures
Practice Test on Area.
5th Grade Geometry
5th Grade Math Problems
From Word Problems on Area of a Square to HOME PAGE
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
|
Share this page: |
FacebookTwitterPinterestWhatsAppMessenger |
In this lesson we solve problems involving the areas of squares and rectangles.
Formula for finding the area of a square
The area of a square of side length ‘a’ is given by
Area A = a × a = a2 square units
Formula for finding the area of a rectangle
The area of a rectangle of length l and width w is given by
Area A = l × w square units
An envelope is 9 inches long and 6 inches wide. What is the area of the envelope surface?
Solution
Step 1:
Area of a rectangle = l × w; l = length = 9 in; w = width = 6 in
Step 2:
Area of given envelope = 9 × 6 = 54 square in
A rectangular pool is 5 meters wide and 9 meters long. What is the area of the pool?
Solution
Step 1:
Area of a rectangle = l × w; l = length = 9; w = width = 5
Step 2:
Area of given rectangle = 9 × 5 = 45 square m
What our Area and Perimeter Word Problems lesson plan includes
Lesson Objectives and Overview: Area and Perimeter Word Problems teaches students strategies for solving word problems that include area and perimeter. At the end of the lesson, students will be able to solve real-world and mathematical problems involving perimeters of polygons, find unknown sides, and recognize rectangles with different perimeters/areas. This lesson is for students in 3rd grade and 4th grade.
Classroom Procedure
Every lesson plan provides you with a classroom procedure page that outlines a step-by-step guide to follow. You do not have to follow the guide exactly. The guide helps you organize the lesson and details when to hand out worksheets. It also lists information in the blue box that you might find useful. You will find the lesson objectives, state standards, and number of class sessions the lesson should take to complete in this area. In addition, it describes the supplies you will need as well as what and how you need to prepare beforehand. The supplies you will need for this lesson are scissors and the handouts. To prepare for this lesson ahead of time, you can gather the supplies and copy the handouts.
Options for Lesson
Included with this lesson is an “Options for Lesson” section that lists a number of suggestions for activities to add to the lesson or substitutions for the ones already in the lesson. An optional addition to the lesson activity is to have students write down the sizes of the rectangles and squares. Another addition to the lesson is to have students use your classroom or school to create real-world word problems. You could also invite a carpenter or other professional to come speak to your class about how they use area and perimeter in their jobs. Finally, you could have students design their perfect bedroom, complete with measurements!
Teacher Notes
The teacher notes page includes a paragraph with additional guidelines and things to think about as you begin to plan your lesson. This page also includes lines that you can use to add your own notes as you’re preparing for this lesson.
AREA AND PERIMETER WORD PROBLEMS LESSON PLAN CONTENT PAGES
Area and Perimeter
The Area and Perimeter lesson plan includes three content pages. The lesson begins by reminding students what the differences between area and perimeter are. Perimeter is the continuous line around the boundary of closed geometric figures like rectangles, squares, triangles, and other polygons. We can determine perimeter by using the standard or metric systems of measurement. On the other hand, area is the inside measurement of a surface or shape (the amount of space inside the perimeter). It’s the number of square units that can fit inside a contained space. Like perimeter, we can also measure it using the standard or metric systems of measurement.
Previously, students have likely learned how to find area and perimeter by simply adding or multiplying the lengths and widths of shapes like squares and rectangles. The lesson includes a few examples of this, with solutions. In the example, the square has the same area and perimeter. This is not always true! Also, two rectangles that have the same area can have different perimeters and vice versa. A square can also have the same perimeter as a rectangle, though their areas will be different. The lesson shows examples of both of these scenarios.
Understanding the difference between area and perimeter, as well as how to find them, will help you solve real-world area and perimeter problems!
Real-World Problems
Many people work with area and perimeter every day! Homeowners, construction workers, architects, artists, and more need to know how to find area and perimeter to do their jobs. They must deal with real-world problems that require them to find the area and perimeter of rectangles, squares, and other shapes. Carpenters, for example, might need to measure a space to find out how much wood they’ll need for a project. A painter needs to know how large the walls in a room are so they know how much paint they’ll need.
The lesson then includes a real-world problem as an example. The problem states that a photographer has 15 photos of a certain size and that he needs to make one frame for a collage. Students will determine what size frame he will need to make and how much wood will be needed for the frame. The lesson breaks this down into three steps. The first step is to find the area of each picture to find the total area needed for the frame. The second step is to determine the different perimeter sizes that he could use for the frame. Finally, the third step is to find the area and perimeter of the frame (which is the same measurement as the inches of wood needed for the frame). The lesson then shows students how to solve the problem.
AREA AND PERIMETER WORD PROBLEMS LESSON PLAN WORKSHEETS
The Area and Perimeter lesson plan includes three worksheets: an activity worksheet, a practice worksheet, and a homework assignment. You can refer to the guide on the classroom procedure page to determine when to hand out each worksheet.
CREATE A REAL-WORLD PROBLEM ACTIVITY WORKSHEET
Students will work with a partner to complete this activity. They will begin by cutting out the provided squares. They’ll use these squares to create rectangles with different perimeters but the same areas, squares and rectangles with the same or different areas and perimeters, and rectangles with the same perimeters but different areas.
They will then create a Real-World Word Problem for another pair of students to solve. They’ll write their problem in the space provided on the worksheet, and the answer to the problem in the second empty space on the worksheet. They will then cut both the question and answer key out and will write their names on the backs of each.
Students can work either alone or in groups for this activity if you’d prefer.
ANSWER THE QUESTIONS PRACTICE WORKSHEET
For the practice worksheet, students are asked to answer ten questions related to the lesson material. Questions include “What is the perimeter of a square that measures 5 feet by 5 feet?” and “True or False: Two rectangles can have the same area but different perimeters.”
AREA AND PERIMETER WORD PROBLEMS HOMEWORK ASSIGNMENT
The homework assignment asks students to solve five word problems, drawing pictures if necessary.
Worksheet Answer Keys
This lesson plan includes answer keys for the practice worksheet and the homework assignment. If you choose to administer the lesson pages to your students via PDF, you will need to save a new file that omits these pages. Otherwise, you can simply print out the applicable pages and keep these as reference for yourself when grading assignments.
Additional information
| grade-level |
3rd Grade, 4th Grade |
|---|---|
| subject |
Math, Video |
| State Educational Standards |
LB.MATH.CONTENT.3.MD.D.8, LB.MATH.CONTENT.4.MD.A.3 Lessons are aligned to meet the education objectives and goals of most states. For more information on your state objectives, contact your local Board of Education or Department of Education in your state. |

Ask a Question
Search
LogIn
cancel
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
Search instead for
Did you mean:
cancel
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
Search instead for
Did you mean:
Close X
- Community
- Archived
This Content was Archived
Try searching for related content
About
PTC.com
Products & Solutions
Contact
Resources
My PTC — Support
PTC University
Help Center — Product Guides
Product Documentation
Success Paths — Planning &
Implementation Guides
Other PTC Communities
On Shape
Reality Lab
Vuforia Engine
PTC user
Terms of Service
Legal Policies
youtube

To find the area of a rectangle, multiply its length by its width. The area is measured in units squared. For example, for a rectangle of length 8 cm and width 5 cm, the area is 8 cm × 5 cm = 40 cm2.

The length of a rectangle is the longest side and the width is the shortest side.
In this example, the length is 8 cm and the width is 5 cm.
8 × 5 = 40 and the units for the area of this rectangle are cm2. The area of this rectangle is 40 cm2.
We multiply 8 cm by 5 cm. Multiplying cm × cm gives us cm2.
The formula for the area of a rectangle is Area = Length × Width. This formula can be written as A = L × W or as A = LW.
Here is an example of using the formula to calculate the area of a rectangle.

Area = Length × Width.
Length = 9 cm and Width = 4.
A = 9 × 4 = 36. The units for the area are cm2 since we measured the sides in centimetres.
The area of this rectangle is 36 cm2.
Here is a word problem for finding the area of a rectangle.

The area is found by multiplying the length and the width. In this worded problem, we just need to find the two numbers that show the length and width.
L = 7 and W = 5.
Area = 7 × 5 = 35. The units are cm2. The area of the rectangle is 35 cm2.
How to Find the Area of a Square
To find the area of a square, multiply the length of one side by itself. The units for area are units squared. For example, if a square has a side length of 3 m, then its area is 3 m × 3m = 9 m2.
Here is a square with a side length of 3 m.

A square is a special type of rectangle that has all of its sides the same length.
Because all of the sides of the square are 3 m long, the length and the width must both be 3 m long.

Multiplying the length by the width, the area is 3 m × 3m = 9 m2.
Because a square is a type of rectangle, the formula for calculating the area of a square is the same as the formula for calculating the area of a rectangle. We can use length × width. However, the length and the width are both the same on a square, which makes it even easier to find the area.
The formula for the area of a square is Area = Side Length × Side Length. This formula can be written more simply as Area = L2, where L is the length of one side of the square.
Here is an example of using the formula for the area of a square with a worded problem.

The area of a square is found by Area = Side Length × Side Length. The side length = 6 cm. We simply multiply 6 by 6.
6 cm × 6 cm = 36 cm2 and so, the area of this square is 36 cm2.
Using the alternative form of the formula, we have Area = L2.
L2 means to multiply the value of L by itself.
L = 6 cm and so, L2 = 6 × 6 = 36.
The area is 36 cm2.
Why is the Area of a Rectangle Length Times Width?
The area of a rectangle is the number of unit squares that fit inside it. The length is the number of unit squares that fit in each row and the width is the number of rows of squares. Multiplying the length by the width gives the total number of unit squares inside a rectangle and hence, the area.
Measuring the length or width in a given unit of measurement tells us how many of these units can fit in this direction.
In this example we will use centimetre squares.

Inside the rectangle we can look at individual squares. These squares measure 1 cm by 1 cm. Their area is 1 cm2.
To find the total area of the rectangle, we simply need to count the number of 1 cm2 squares that fit inside it.
Here is a rectangle that is 10 cm long and 6 cm wide.
We can see that there are 10 of the unit squares that can fit in each row because the side length is 10 cm long.

We can see that there are 6 rows because the width is 6 cm long.

We have 6 rows of 10 or 6 lots of 10.

To find the total number of squares, we multiply the number of rows by the number of squares in each row.
6 lots of 10 is written as 6 × 10, which equals 60 squares.
Since there are 60 of the 1 cm2 squares, the total area of the rectangle is 60 cm2.
- 33,092 Visits
This worksheet contains 6 area and perimeter word problems for kids to solve. Kids are instructed to read the questions and write their answers in the space provided showing their work. An example question from this worksheet is “Peter’s desk is 48 inches long and 36 inches wide. What is the perimeter of his desk?”
Subject
- Math
(1,488)- Area and Perimeter
(19)- Area and Perimeter Word Problems
(5)
- Area and Perimeter Word Problems
- Area and Perimeter