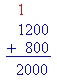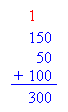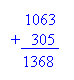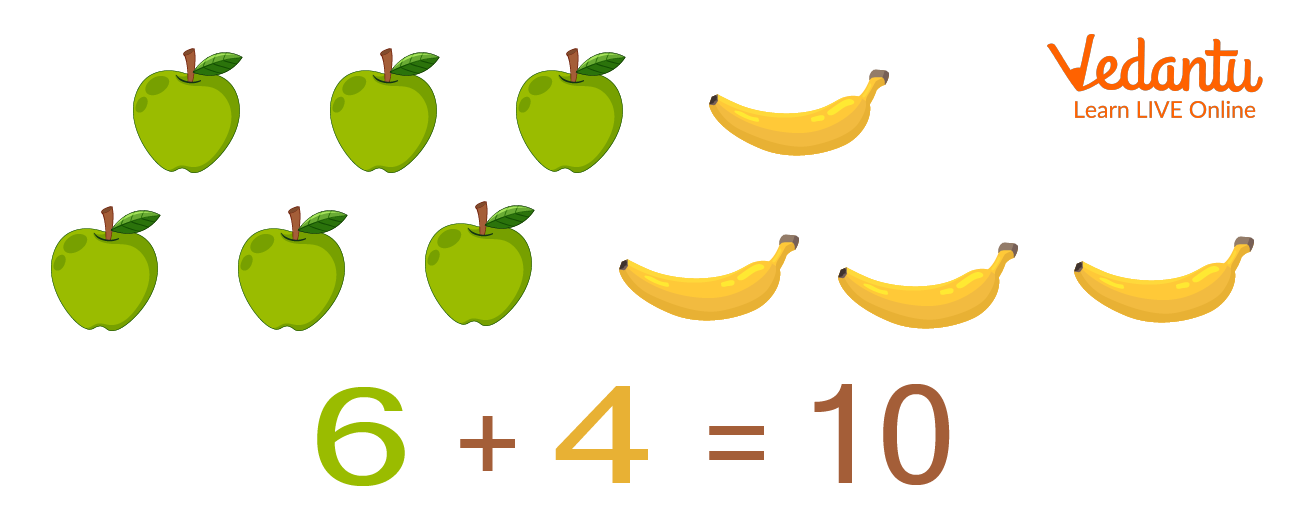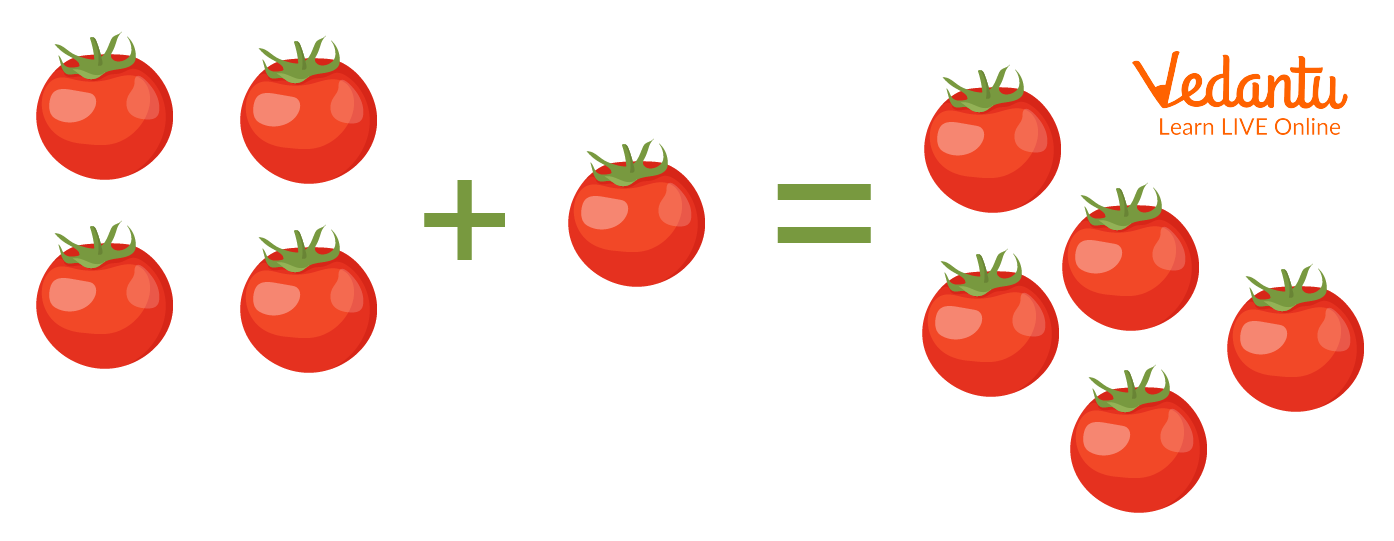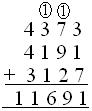Addition word problems arise in any situations where there is a gain or an increase of something as a result of combining one or more numbers. Think of addition as combining parts to form a whole.
Consider the following situations.
Problem #1:
John has 800 dollars in his checking account. He received from his job a check for 1,200 dollars and deposit the amount in his checking account. How much money does he have in his checking after the deposit?
Solution
The fact of receiving money from his job is a gain. Therefore, we need to perform addition.
Total amount in checking account = 800 + 1200 = 2000 dollars
Problem #2:
Peter sells ice cream for a living. On Monday his revenue was 150 dollars. On Tuesday, his revenue was 100 dollars. Finally, on Wednesday, his revenue was 50 dollars. How much is Peter’s revenue so far?
Solution
Peter is experiencing a gain in revenue. Therefore, we use addition.
Peter’s revenue = 150 + 50 + 100 = 300 dollars
Problem #3:
Eiffel Tower is about 1063 feet high. The Statue of Liberty along with its foundation and pedestal is about 305 feet. If you could put the Statue of Liberty on top of the Eiffel Tower, how high up in heaven will the two monuments reach?
Solution
The situation above is a combination of parts to form a whole. Therefore, we use addition.
Problem #4:
Ana found a 15 dollar bill on the floor on Saturday.
Then on Sunday her parents gave her 155 dollars.
How much does Ana have all together?
CLUE:
Saturday~15 dollars
Sunday~155 dollars
Solution:
15+155 = 170 dollars all together
Have A Great Basic Math Word Problem?
Share it here with a very detailed solution!
What Other Visitors Have Said
Click below to see contributions from other visitors to this page…
Mom. How many pens and pencils?
Mr. Bower has 3 times as many pens as pencils. He has 20 pens and pencils altogether. How many pens does he have?
Solve by trial and error:
Say …
Number trick that always equals 5
1. Think of any positive whole number. No fractions, no decimals, and no percents.
2. Double that number.
3. Add 10 to that result in step 2. …
How to Find the Cost to Rent Bikes Not rated yet
The cost to rent a bike for 1 person under age five is 3£ and 5.50£ for anybody over age five. Calculate the cost to rent 7 bikes if 4 people are under …
Max and Mary’s Picnic Not rated yet
Max and Mary are going on a picnic. Mary packs 4 apples, 3 oranges and 2 bananas. Max packs 2 more apples than marry and 8 more oranges than Mary. If Max …
Click here to write your own.
Recent Articles
-
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
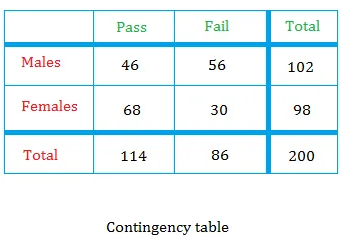
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Addition word problems appear throughout KS1 and KS2. Children are introduced to simple addition and subtraction word problems in the early years. This knowledge is then built upon throughout primary school, right up to Year 6, when pupils work with complex multi-step word problems involving large whole numbers and decimal numbers.
In the early stages, in Key Stage one and lower Key Stage two, addition word problems are taught through the use of concrete resources and visual images. As pupils become more confident with the formal written methods, children progress to use these to help solve more complex addition and subtraction word problems.

All Kinds of Word Problems Addition and Subtraction
Download this free, printable pack of addition word problems worksheets to help your class to develop their addition and problem solving skills.
Children benefit from regular exposure to word problems, alongside any fluency work they are doing. To help you with this, we have put together a collection of 25 addition word problems with answer keys, which can be used with pupils from Year 2 to Year 6.
Addition word problems in the National Curriculum
Addition word problems in Year 1
Pupils in Year 1 are introduced to simple one-step problems involving place value addition and subtraction word problems, through the use of concrete objects, pictorial representations and missing number problems. At this stage, children should be memorising and reasoning with number bonds to 10 and 20. They also need to understand the effect of adding zero.
Addition word problems in Year 2
In Year 2, pupils continue to use concrete objects and pictorial representations to solve addition problems, including those involving numbers, quantities, measures and simple money word problems. They are also expected to apply their increasing knowledge of mental and written methods, using one and two-digit numbers. Pupils start working on basic written addition and are introduced to the concept of regrouping.
Addition word problems in Year 3
By Year 3, pupils are starting to tackle more complex addition word problems. They begin to use written methods to add 3-digit numbers, using formal column method for addition. Pupils also begin solving addition problems involving fractions, in addition to building on their mental addition skills to add a three-digit number and ones, tens and hundreds.
Addition word problems in Year 4
Pupils in Year 4 progress to solving two-step problems in contexts, deciding which operations and methods to use and why. They are also beginning to work with larger numbers, adding up to four digits using the formal written method of column addition.
Addition word problems in Year 5
By Year 5, pupils are solving multi-step word problems in contexts. They add whole numbers with more than four digits and decimal numbers, using formal written methods. Children are also adding increasingly larger numbers mentally.
Third Space Learning’s online one-to-one tutoring programmes work with students to fill their learning gaps and build confidence in maths. Tailored to the needs of each student, Third Space Learning’s tutoring programmes offer students more opportunities to practice their maths skills and reach their year group standard.
covering multi-step addition and subtraction word problems
Addition word problems in Year 6
Pupils in Year 6 continue to work with larger numbers and decimals, solving increasingly complex multi-step problems, deciding which operations to use and why. By this stage students should have a solid grasp of the written methods for all four operations.
Why are word problems important for children’s understanding of addition
Word problems help children to make sense of addition. In the Early Years, simple story problems aid understanding of what is being asked, alongside the use of concrete resources and visual images. Real-life word problems are an important element of the maths curriculum for children throughout the school, giving them the opportunity to put the addition skills they have learnt into context, to understand how they can be used in the outside world.
How to teach addition word problem solving in primary school
Pupils need to be taught how to approach word problems, beginning by reading the questions carefully and making sure they fully understand what is being asked. The next step is to determine what calculation is needed and whether there are concrete resources or pictorial representations they can use to help solve it, or if
Here is an example:
There were 3,756 people on a cruise ship.
456 people get on after the first week, whilst 623 get off.
How many passengers are on board the ship now after the first week?
How to solve:
What do you already know?
- There are 3,756 on the cruise ship at the start of the journey.
- 456 people get on after the first week, therefore we need to add 456 to 3,746. This gives us a total of 4,212 people
- 623 people get off, so we need to subtract 623 from the total number of passengers now on the boat. When we subtract 623 from 4,212, we get a total of 3,589.
How can this be represented pictorially?
- We can draw 2 bar models to represent this problem.
- The number of passengers who got on the ship after the first week is added to the total number of people on the boat at the start of the trip.
- We then draw a second bar model to show how many passengers were left on the ship once the 623 passengers got off after the first week.
Addition word problems for year 2
Addition word problems in Year 2 require pupils to work with 1 and 2-digit numbers. At this stage it is important children are working with concrete resources to support their understanding. Children also begin to learn how to check their answers by finding the inverse of calculations.
Year 2 addition question 1
Maise has 14 crayons. Her friend gives her 8 more.
How many crayons does Maisie have now?
Answer: 22 crayons
14 + 8 = 22
Year 2 addition question 2
Hamza buys a large pack of biscuits, whilst his sister buys a small pack.
The large pack contains 18 biscuits, whilst the small pack contains 8.
How many biscuits does Hamza and his sister have altogether?
Answer: 26 biscuits
18 + 8 = 26
Year 2 addition question 3
13 children sign up for the after school football club and 11 sign up for the netball club.
How many children sign up altogether?
Answer: 24 children
13 + 11 = 24
Year 2 addition question 4
Amal collects 34 conkers. Her brother finds 7 more and adds them to her collection.
How many conkers does Amal have now?
Answer: 41 conkers
34 + 7 = 41
Year 2 addition question 5
38 children were on the bus going to the zoo.
The bus stopped to pick up 12 children from another school.
How many children were on the bus now?
Answer: 50 children
38 + 12 = 50
Addition word problems for year 3
Word problems for Year 3 require pupils to work with larger numbers. By this stage, children are becoming more confident with the formal written column method and are able to use this to solve 2 and 3 digit addition word problems. Addition word problems can be incorporated into other areas of the maths curriculum, for example, through time word problems.
Year 3 addition question 1
Mason has collected 256 stickers. Rory has collected 352 stickers.
How many stickers have the two boys collected between them?
Answer: 608 stickers
256 + 352 = 608
Year 3 addition question 2
A train driver drove 234 miles on Monday and a further 186 miles on Tuesday.
How many miles did he drive in total over the 2 days?
Answer: 420 miles
(Show as column method; 234 + 186 = 420)
Year 3 addition question 3
Sam spent £1.25 on a bar of chocolate in the shop. He then spent 60p on a packet of sweets. How much did he spend all together
Answer: £1.85
1.25 + 85 = 1.85
Year 3 addition question 4
A climber has climbed 238m up the mountain. He has another 174m to go to reach the top. How high is the mountain?
Answer: 412m
(Show has column method: 238 + 174 = 412)
Year 3 addition question 5
A family was travelling to their holiday home.
They set off at 9am and travelled for an hour and a half.
They then had a 20 minute break and travelled for another hour.
What time did they reach their holiday home?
Answer: 11:50am
1 ½ hours + 20 minutes + 1 hours = 2 hours 50
Or
Start at 9am, count on an hour, then another 20 minutes, followed by another hour = 11:50am
Addition word problems for year 4
With word problems for Year 4, pupils progress onto 4 digit addition word problems. They are also beginning to solve more complex, two-step word problems. Children should be encouraged to estimate and find the inverse, to check the accuracy of their calculations. In Year 4, pupils also solve addition word problems involving fractions and decimals.
Year 4 addition question 1
A builder is building a wall around the school playing field.
He has used 4865 bricks so far and has another 1135 bricks to finish the wall.
How many bricks will he use to build the wall?
Answer: 6000 bricks
4865 + 1135 = 6000
Year 4 addition question 2
Hot dogs: £1.60
Burgers: £1.40
Pizza: £1.99
Fries: £1.25
Soft drinks: £1.15
Chloe is buying some food from a cafe.
She buys 2 hot dogs, a pizza, 2 portions of fries and 2 drinks.
How much does she spend altogether?
Answer: £9.99
Hot dogs: £1.60 + £1.60 = £3.20
Pizza: £1.99
Fries: £1.25 + £1.25 = £2.50
Drinks: £1.15 + £1.15 = £2.30
Total= £3.20 + £1.99 + £2.50 + £2.30 = £9.99
Year 4 addition question 3
A runner is completing a 10,000m race.
He has already run 4560m. How much further does he have to run?
Answer: 5440m
Solved mentally by calculating how many more metres to 5000m – 440m, then adding on a further 5000m = 5440m
This can also be solved as a missing number column addition, or as a subtraction calculation.
Year 4 addition question 4
Ben has £50. He buys a t-shirt for £15.50 and a hoodie for £25.50.
How much change does he have left?
Answer: £9 change
£15.50 + £25.50 = £41
£50 – £41 = 9
Year 4 addition question 5
A flight from London to Doha is a distance of 6731 miles. It is then another 12,375km to Sydney.
How far is the journey from London to Sydney, via Doha?
Answer: 19,106 miles
12,375 + 6731 = 19,106
Addition word problems for year 5
Word problems for Year 5 require pupils to solve addition word problems with larger numbers (more than 4 digits), using formal written methods and mentally. Word problems become more complex multi-step problems, involving other operations. Pupils at this stage should continue to be encouraged to check their answers by finding the inverse.
Year 5 addition question 1
Three towns have populations of 14,768, 17,956 and 13,858.
What is the total population of the three towns combined?
Answer: 46,582
(Show as column method 14,768 + 17,956 + 13,858 = 46,582)
Year 5 addition question 2
A car can hold 60 litres of fuel when the tank is full.
If 17.98 litres of fuel has been used, how much fuel does the tank hold now?
Answer: 42.02L
This can be solved mentally, by counting on from 17.98, as a missing number addition question, using column addition, or as a subtraction question.
Year 5 addition question 3
A man weighing 85.23kg gets into a lift. On the next floor, another man gets in, weighing 79.4kg.
If the lift can hold a maximum weight of 500kg, how much more weight can the lift carry?
Answer: 335.37kg
(show as column method)
85.23 + 79.4 = 164.63
500 – 164.63 = 335.37
Or
Count up from 164.63 or solve as a missing number addition.
Year 5 addition question 4
The temperature in Toronto was -27 degrees celsius one January evening. On the same day, the temperature in Doha went up to 29 degrees.
What was the difference between the temperature in Toronto and the temperature in Doha?
Answer: 56 degrees celsius
29 + 27 = 56
Year 5 addition question 5
Large packet of biscuits – £1.75
Small packet of biscuits – 98p
Lucy buys 2 large packets of biscuits and 4 small packets. How much change will she get from a £10 note?
Answer: £2.58
2 large packets = £1.75 + £1.75 = £3.50
4 small packets = 98p x 4 = £3.92
Total = £3.92 + £3.50 = £7.42
£10 – 7.42 = £2.58 or count on from £7.42 to £10
Addition word problems for year 6
With word problems for Year 6, pupils need to be able to solve word problems using larger whole numbers of up to 6 or 7 digits, problems involving fraction word problems and problems involving decimals. Addition word problems in SATs include one-step, two-step and more complex multi-step problems.
Year 6 addition question 1
Mr Jones spent £24,799 on a new car and £8,750 on a caravan.
He has £15,074 left in his bank account.
How much did he have to start with?
Answer: £48,623
24,799 + 8,750 = 33,549
33,549 + 15,074 = 48,623
Year 6 addition question 2
17,523 more people visited a theme park this year than last year.
If 315,736 people visited last year. How many visited this year?
Answer: 333,259 people
315,736 + 17,523 = 333,259
Year 6 addition question 3
A zoo buys 53.7kg of animal feed. Each day, 7.34kg is used for the camels, 2356g for the meerkats and 4.49kg for the zebras.
After 2 days, how much will the zoo have left?
Answer: 25.328kg left
7.34 + 2.356 + 4.49 = 14,186
14,186 + 14,186 = 28.372
53.7 – 28.372 = 25.328
Year 6 addition question 4
A company sent out 1,417,806 flyers in April and 931,368 in May.
- Estimate how many flyers the company sent out in April and May combined.
- What is the actual number of flyers sent out?
Answer
- 2,300,000
1,400,000 + 900,000 = 2,300,00
- 1,417,806 + 931,368 = 2,349,174
Year 6 addition question 5
The Brown family are going on a road trip. They plan to drive 274.3 miles to a hotel. They then have another 276.9 miles to drive to reach their final destination.
If they have travelled 197.8 miles so far, how much further do they have to travel before they reach their final destination?
Answer: 353.4 miles
274.3 + 276.9 = 551.2
551.2 – 197.8 = 353.4
Looking for more word problems resources?
Take a look at our comprehensive collection of word problems practice questions covering a wide range of topics such as ratio word problems, percentages word problems, multiplication word problems, division word problems and more.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Addition is the most basic mathematical operation that we can use for calculations. We need to practice using real-life situations and for that word problems are the best. Addition is based on certain properties, i.e. closure, commutative, and associative. Closure property is when two or more whole numbers are added to get a whole number. Commutative property is when two or more whole numbers are added but the result is not dependent on the order of addends. Associative property is when we add three or more numbers and the result obtained is the same and does not depend on the grouping of the addends.
Addition of Two Types of Fruits
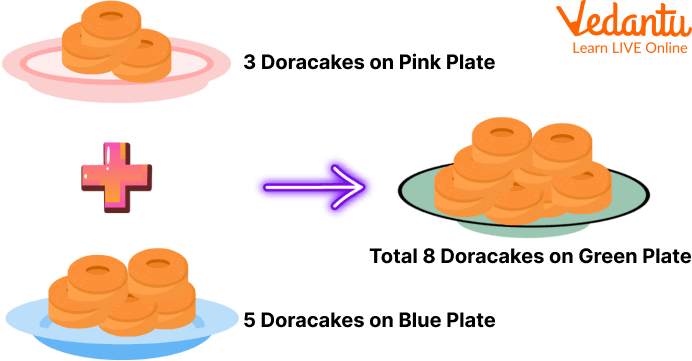
Adding Dora Cakes
In the below examples, we will see some word problems for Class 2 with solutions.
Example 1. Let us take two numbers 30 and 68. What is the sum of those two numbers?
Ans: One number = 30
Other number = 68
Therefore, sum of those two numbers = 30 + 68 = 98
Example 2. If there are 45 boys and 34 girls. What is the total number of students present in the classroom?
Ans: Number of boys in the classroom = 45
Number of girls in the classroom = 34
Therefore, total number of students in the classroom = 45 + 34 = 79
Example 3. Prithvi scored a brave 88 runs in the first match of the Ranji Trophy and scored 62 runs in the second match of the Ranji Trophy group stage. Find the total number of runs scored by him in the two matches.
Ans: Runs scored in first match= 88
Runs scored in the second match= 62
Total runs scored in those two matches = 88 + 62 = 150
2 + 8 = 10 so we carry 1
Now, 8 + 6 = 14 and we add that carried 1 here making it 15
So, the total is 150.
Example 4. There are 58 books on a bookshelf in the central library. 18 more books are kept on the same bookshelf later on. What is the total number of books on that shelf now?
Ans: Books on the bookshelf before = 58
Books on the bookshelf after the addition of new books= 18
Total number of books within the bookshelf = 58 + 18 = 76
8 + 8 = 16 so we carry 1
Now, 5 + 1 = 6 and we add that carried 1 here making it 7
So, the total is 76.
Practice Problem Sums for Class 2
Q1. Shankar went to the local sweet shop and bought 31 Gulab Jamun. Her sister came home for Bhai Duj and brought 23 more Gulab jamun. How many Gulab jamun did Shankar have now altogether?
Ans: 54
Q2. Hema scored 43 marks out of 50 in a summative assessment. She scored 35 in marks on the final exam. How many marks does he get in all?
Ans: 78
Q3. Soham bought 31 pencils. His brother Ram has 46 pencils. How many pencils do they have altogether?
Ans: 77
The Sum of 4 Tomatoes with 1
Summary
In conclusion, we have learnt that addition is the most basic tool of calculation. This tool is the key to every other form of calculation. It is also a real-life skill that comes into use almost every day. Additional word problems are effective in making students understand the application of addition and clarify the concept by actual problems that they would face in life. These problems have everyday incidents regarding addition of objects such as clothes, food items, or toys. It can also relate to money where they calculate the total payable amount for the goods and items they purchase from a shop.
Addition and subtraction are the basic operations of Mathematics taught to primary school children as a fundamental part of their syllabus. These basic operations also help us in building a great base for higher-level maths. We start learning the process of addition and subtraction using an abacus at the initial level and move towards complicated world problems. As your academic level increases, you will understand the relevance and importance of addition and subtraction word problems in the world of Mathematics. Here is an exclusive blog discussing different methods of solving these questions!
This Blog Includes:
- What are Word Problems?
- Single Operation Word Problems
- Multiple Operation Word Problems
- Word Problems for Grade 2
- Word Problems for Grade 3
- Word Problems for Grade 4
- Common Errors
- Tips for Solving Addition and Subtraction Word Problems
- Practice Questions
- FAQs
What are Word Problems?
As the name suggests, word problems are comprehensive questions that are designed to give a real-life simulation of mathematical problems. In the case of addition and subtraction word problems, the question generally revolves around some quantity of an object, which increases and decreases as the question progresses. These questions are pretty direct and easy to solve, even without the use of paper and pen. These word problems can be of the following types, Single and Multiple operations.
Before we move on to the Addition and Subtraction Word Problems,
here is a list of Seating Arrangement Questions for you!
Single Operation Word Problems
This type of word problem deals with a single operation per question. Here are some examples of single-operation addition and subtraction word problems:-
Q1: Mohit has 12 marbles. He buys 5 more. How many does he have now?
For this question, we will follow these simple steps:
Note the number of marbles Mohit has in the beginning(12)
As he buys more marbles, the total number of marbles will increase, so add the number of marbles he purchased(5) to the number of marbles he originally had(12)
The sum of both numbers(12+5) is the total number of marbles Mohit has now, i.e. 17 marbles.
The answer is 17 Marbles
Did you get these Addition and Subtraction word problems?
Great, try out some Algebra Questions as well!
Q2: Joe has 23 oranges. He eats 2 of them. How many does he have now?
For this question, we will follow these steps:
Note the number of oranges he has in the beginning(23)
As he eats the oranges, the number of oranges he has will reduce. To get the new number of oranges he has now, we will subtract the number of oranges he ate(2) from the total number of oranges(23)
The difference between the two numbers(23-2) is the number of oranges he has now, i.e. 21 oranges
The answer is 21 Oranges
Multiple Operation Word Problems
Multiple operation word problems include more than one operation in a single addition and subtraction word problem. They are the most common type of addition and subtraction word problems as they include both operations in a single question. We just follow a step-wise approach to solve these word problems. Here’s an example-
Q1: Aman owns 24 pens. He decides to buy 5 more. When he comes home he loses 3 pens. How many pens does he have now?
For this question, we take the following steps:
Note the original number of pens Aman has (24)
Add the number of pens he buys(24+5=29)
Subtract the number of pens he loses(29-3=26)
The number of pens he has in the end = 26
The answer is 26 Pens
Try out these BODMAS Questions to improve your Mathematics!
Word Problems for Grade 2
Q1. 114 birds were sitting on a tree. 21 more birds flew up to the tree. How many birds were there altogether in the tree?
No. of birds initially = 114
Birds flew up to the tree = 21
Total no. of birds = 114 + 21 = 135
Hence, There were 135 birds in the tree
Q2. 29 birds were sitting in a tree. Some more fly up to the tree. Then there would be 142 birds in the tree. How many flew up to the tree?
No. of birds sitting in a tree = 29
Total no. of birds = 142
Birds flew up to the tree = 142 – 29 = 113
Hence, 113 birds flew up to the tree
Q3. Beth has 74 crayons. She gives 25 of them away to Jen. How many crayons does beth have left.
Total no. of crayons of Beth = 74
Beth gives = 25
No. of crayons left = 74 – 25 = 49
Hence, Beth has 49 crayons left
Q4. Cindy’s mom baked 41 cookies. Paul’s dad baked 38 cookies. Cindy and Paul ate 6 cookies each and then brought them to school for a party. How many cookies did they bring to school altogether?
Cindy’s baked cookies = 41
Paul’s dad baked cookies = 38
Cindy and Paul ate cookies = 6 each
Total no. of cookies baked = 41 + 38 = 79
Total cookies they bring to school = 79 – 12 = 67
Hence, 67 total cookies they bring to the school
Word Problems for Grade 3
Janina owns a catering service company. She was hired to cater for the mayor’s 50th birthday.
Q1. For the appetizers, she needs to make 750 mini meat pies. She divided her crew into 3 teams. If the first team made 235, and the second made 275, how many pies should the third team make?
Total Meat Pies needed = 750
Meat pies made by first-team = 235
Meat pies made by the second team = 275
235 + 275 = 510
Then, Meat Pies made by third-team = 750 – 510 = 240
Hence, meat pies made by third-team = 240
Q2. She needs 280 cups of mushroom soup. If the first team made 90 cups in 60 mins, and the third team made 70 cups in 90 mins, how many cups should the second team prepare in order to meet the required amount of soup?
Total soup cups needed = 280
Cups made by first-team = 90
Cups made by third-team = 70
90+70 = 160
Then, cups made by second-team = 280 – 160 = 120
Hence, the second team should prepare 120 soup cups.
Q3. For the first main dish, they were asked to cook steak. If the third and second-team cooked 240 plates of steak, and the first team cooked 75 plates less than what the second and third-team made, how many steaks did they cook altogether?
Steak cooked by third and second-team = 240
Steak cooked by first-team cooked = 75
Steak cooked by second and third-team = 240 – 75 = 165
Total steaks cooked = 240 + 165 = 405
Hence, they cooked a total of 40 steaks.
Q4. For the second main course, they made fish fillets for the 320 people at the party. The first team made 189 pieces, the second team made 131 pieces and the third team made 180 pieces, how many pieces were made altogether?
Pieces made by first-team = 189
Pieces made by second-team = 131
Pieces made by third-team = 180
Total pieces = 189 + 131 + 180 = 500
Hence, 500 pieces were made altogether.
Word Problems for Grade 4
The table shows the number of people visiting an art museum over 3 months.
| January | February | March | |
| Child | 28 | 34 | 56 |
| Adult | 59 | ? | 55 |
| Senior | 15 | 22 | ? |
| Total | ? | 139 | ? |
Q1. What is the total number of people that visited the art museum in January?
In Jan,
Child = 28
Adult = 59
Senior = 15
Total = 102
Hence, the total number visited the art museum in January = 102
Q2. Compared to January, how many more children go to the museum in February?
Children in January = 28
Children in February = 34
34-28 = 6
Hence, 6 more children go to the museum in February.
Q3. How many adults visited the museum in February?
In February,
Total People = 139
Children = 34
Senior = 22
No. of Adults = 139 – 34 – 22 = 83
Hence, 83 adults visited the museum in February.
Q4. 16 more seniors visited in March. Tell the total no. of seniors who visited the museum in March?
Seniors in Jan and Feb = 15 + 22 = 37
Seniors in March = 37 + 16 = 53
Also, here we can calculate the total no. of visitors = 55 + 56 + 53 = 164
Hence, March has a total no. of 164 visitors in the three months.
Common Errors
When attempting to solve addition and subtraction word problems, there are a few frequent errors. Some of these include:
- Calculation mistakes – You must be very careful when adding or subtracting numbers because it is frequently observed that students make errors when working carelessly.
- Right explanation – When working on word problems, it’s crucial to use correct statements in order to properly explain the actions conducted. Mentioning what is given, what needs to be calculated, and the formula envisioned for usage in this regard are among them.
- Understanding of the Problem – One of the most frequent mistakes is when a student is unable to determine if the issue requires an addition or a subtraction solution.
Tips for Solving Addition and Subtraction Word Problems
Here’s a little helpful tip to get through addition and subtraction word problems:
- Words like purchasing, winning, making, buying or getting something from someone are related to addition problems. If you spot such sentences, you should apply addition operations.
- Words like losing, eating, selling, and giving to someone are related to subtraction problems. If you spot such sentences, you should apply subtraction operations.
Now that you know how to solve addition and subtraction word problems,
you must try these simplification questions as well!
Practice Questions
Having explained the types of questions which can come for addition and subtraction word problems, here are some practice questions for you to sharpen your skills-
Q1: if Kishan has 2 balls and Shyam gives him 9 balls, how many balls does Kishan have now?
Q2: If Seeta has 4 apples and Geeta takes away 3 apples from her, how many apples does Seeta have now?
Q3: Matt has 10 watches. He sells 6 of them. How many watches are left with Matt?
Q4: Joseph has 20 cars. If his friends take away 12 of them, then how many cars are left with Joseph?
Q5: Raman has 25 shirts.12 got dirty and 3 are torn. How many good shirts does Raman have?
Q6: Fred has 50 Rupees as his pocket money. He spends 12 on a burger and 17 on a cold drink. How much money does he have now?
Q7: Bruce has 6 gold medals. He wins 3 more at racing. How many gold medals does he have now?
Q8: ABC company has 250 bikes in their store. They sell 153 of them. Then they make 46 new bikes. How many bikes do they have now?
Q9: Varun has 30 fans. Sonam sold him 40 more and Raju bought 22 fans from him. How many fans does Varun have now?
Q10: Radhika has 45 lipsticks. She bought 25 more and gave 17 to Rama. How many lipsticks does Radhika have now?
Q11: A company has 345 workers. They hire 123 more. 12 people leave the company. 23 workers are absent on Monday. How many workers are there in the company on Monday?
Q12: A person takes 14 minutes for a bath. He further takes 20 minutes to get ready and 20 minutes to drive to his office. How much time does it take to reach the office?
FAQs
What are the most basic parts of mathematics?
Addition, Subtraction, Divide, and Multiply are the four most basic parts of mathematics.
Why learning basic maths is basic important?
The basic parts of maths will be applicable to different course materials as well as different aspects of life.
What problems students should learn first?
Students should learn addition first.
We hope these questions helped you understand addition and subtraction word problems in a better way. Connect with us at Leverage Edu to browse through more such educational and informative blogs.
Different Types of Addition and Subtraction Situations
In our day to day situations, we come across different problems that relate to addition and subtraction in mathematics. For instance, if you buy a few items from a grocery store, you will need to check the bill raised by the store by adding the costs of the items purchased. Similarly, there might be a situation when you need to find the difference between the original and the discounted price of an item. Such situations make it necessary for students to have a strong grasp of the understanding of the concepts of addition and subtraction. However, this cannot be achieved without enough practice.
Important Terms and Keywords in addition and subtraction
Below are some important terms and keywords that are associated with addition and subtraction –
| how many | how much | leftover | still to go |
| additional | together | combined | add |
| both | sum | increase | difference |
| total | change | more | decrease |
| fewer | spent | reduce | remaining |
| less |
Let us discuss some such situations which can be useful in the understanding of these terms.
Situations where we use the term “Add To”
Below are some situational problems where we make use of the term “ Add To ”–
- There are three fishes in a pond. Four more fish are added to the pond. How many fishes are there in the pond now?
We have been given –
Number of fishes in the pond = 3
Number of more fishes added to the pond = 4
For obtaining the total number of fishes in the pond now, we will have to add the number of fishes added to the pond to the number of fishes that were present in the pond earlier. Therefore,
3 + 4 = 7 this is the total number of fishes in the pond now
- There are 2 tigers in a forest. Five more tigers are brought from the nearby forest. How many tigers are there in the forest now?
We have been given –
Number of tigers in the forest = 2
Number of more tigers brought in from nearby forest = 5
For obtaining the total number of tigers in the forest now, we will have to add the number of tigers brought in from the nearby forest to the number of tigers that were present in the forest earlier. Therefore,
2 + 5 = 7 this is the total number of tigers in the forest now
Situations where we use the term “Put Together”
We could have used the term put together as well in the above questions. For instance, the question in the example above could be rephrased as –
- There are three fishes in a pond. Four more fish are added to the pond. How many fishes are there in the pond put together?
Similarly, the second question could also be rephrased as –
- There are 2 tigers in a forest. Five more tigers are brought from the nearby forest. How many tigers are there in the forest put together?
Situations where we use the term “Take From”
Below are some situational problems where we make use of the term “Take From”–
- On his birthday, James placed 12 burning candles on the cake. He blew nine of them. How many of the candles were burning on the cake now?
We have been given –
Number of candles burning on the cake = 12
Number of candles blown by James = 9
For obtaining the total number of candles burning on the cake now, we will have to take the number of candles left burning on the cake from the number of candles that were burning on the cake earlier. Therefore,
12 – 9 = 3 this is the total number of candles left burning on the cake
- There were 16 mangoes on a tree. Samuel plucked 9 of them. How many mangoes were left on the tree?
We have been given –
Number of mangoes on a tree = 15
Number of mangoes plucked by Samuel = 9
For obtaining the total number of mangoes left on the tree now, we will have to take the number of mangoes plucked by Samuel from the number of mangoes on a tree earlier. Therefore,
15 – 9 = 6 this is the total number of mangoes left on the tree now
Situations where we use the term “Compare”
Below are some situational problems where we make use of the term “Compare”–
- Jack scored 25 marks in a test while Peter scored 38 marks in the same test. How many more marks did Peter score as compared to Jack?
We have been given –
Marks scored by Jack in a test= 25
Marks scored by Peter in the same test = 38
For obtaining additional marks scored by Peter, we shall compare his marks with that of Jack. We will have,
25 + ________ = 38
= 13
Hence, Peter scored 13 more marks as compared to Jack.
- Michael has 13 playing cards while Alice has 22 playing cards. How many more playing cards does Alice have as compared to Michael?
We have been given –
Number of cards that Michael has = 13
Number of cards that Alice has = 22
For obtaining additional cards that Alice has as compared to Michael, we shall compare the number of cards that Alice has with that of Michael. We will have,
13 + ________ = 22
= 9
Hence, Alice has 9 more cards as compared to Michael.
Does more always mean to add?
It is usually assumed that the term “ more “ means to add. However, that is not the case. At times, when we ask questions such as “ How much more is A than B “, this means that we need to find the difference between A and B or in other words subtract them.
Common Errors
There are some common mistakes when it comes to solving word problems on addition and subtraction. Some of these are –
- Calculation errors – You need to be extremely careful when adding or subtracting numbers as often it is seen that students make mistakes when working in a careless manner.
- Proper explanation – When it comes to working on word problems, it is important to mention proper statements so as to explain the steps undertaken correctly. These include mentioning what is given, what needs to be calculated and the formula intended to be used for this purpose.
- Understanding of the Problem – One of the most common errors is when a student fails to identify whether the problem needs a solution through addition or subtraction.
Addition and Subtraction Word problems Involving Money
We know that money is available in different forms at different places. For buying things we use coins and notes which are issued by the respective governments of the country we live in. These are called currency. Let us discuss some money-related situations where we make use of addition or subtraction
Example
Suppose, Gracia purchased two items, one at the cost of £ 2.05 while another at the cost of £ 4.20. What is the total cost she needs to pay altogether?
Solution
We have been that given that Gracia purchased two items, one at the cost of £ 2.05 while another at the cost of £ 4.20. We need to find out how much Gracia needs to pay altogether. There are two ways of doing it. Either we add the money directly or first convert the given amounts in pence. We know that
£ 1 = 100 p
Therefore, we have,
£ 2.05 = 2.05 x 100 = 205 p
£ 4.20 = 4.20 x 100 = 420 p
Now we have two values 205 p and 420 p. we can add these values, in the same manner, we add two whole numbers. We will get,
205 p + 420 p = 625 p
Now we have obtained our result in pence. To convert it back into pounds, we will have to divide the result by 100. We will now have,
625 p = £ $frac{625}{100}$ = £ 6.25
Hence, we can say that the sum of £ 2.05 and £ 4.20 = £ 6.25
A direct way of solving this problem would have been to add the two amounts directly. We would then have,
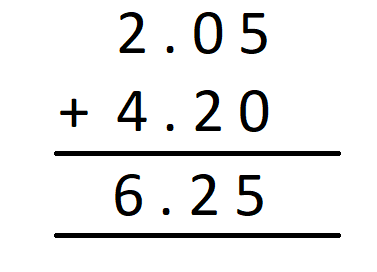
It is important to note here that irrespective of the method we use, we shall get the same result.
Let us consider another example.
Example
Maria purchased a syrup for £ 36.00, a cookies box for £ 29.50 and a hair oil bottle for £ 32.50. If she gave the shopkeeper £ 100, how much money did the shopkeeper return as balance?
Solution
We have been given that Maria purchased a syrup for £ 36.00, a cookies box for £ 29.50 and a hair oil bottle for £ 32.50. She gave the shopkeeper £ 100. We are required to find the money returned by the shopkeeper as a balance. In order to do so, first, let us summarise the items purchased by Maria.
Cost of syrup purchased by Maria = £ 36.00
Cost of cookies box purchased by Maria = £ 29.50
Cost of hair oil bottle purchased by Maria = £ 32.50
Total shopping by Maria = £ 36.00 + £ 29.50 + £ 32.50 = £ 98
Now, Maria gave £ 100 to the shopkeeper. Therefore
Change returned by the shopkeeper = £ 100 – £ 98 = £ 2.00 Change returned by the shopkeeper = £ 100 – £ 98 = £ 2.00
Hence, Maria got £ 2.00 from the shopkeeper as a change.
Addition and Subtraction Word problems Involving Decimals
We perform addition and subtraction of decimals in many situations in our day-to-day lives. For example, you may need to add up your grocery bill before paying at the counter. Have you ever noticed that most of the prices are in decimals? Let us discuss through an example where we use addition or subtraction of decimals in our daily life.
Example
Sophie had £ 305.80 in her bank account. She deposited £ 250.25 more and then withdrew £ 317.50 from her account. What is the balance now in her account?
Solution
Let us first define what is given and what needs to be calculated. We have been given that Sophie had £ 305.80 in her bank account. She deposited £ 250.25 more and then withdrew £ 317.50 from her account. We are required to find the balance in her account now. Therefore,
Initial amount in Sophie’s account = £ 305.80 …………………. ( 1 )
The amount deposited by Sophie = £ 250.25 …………………. ( 2 )
Both the decimal numbers are like terms; hence we can go ahead with the calculations.
Total amount in Sophie’s account = ( 1 ) + ( 2 )
= £ 305.80 + £ 250.25
= £ 556.05 …………………………… ( 3 )
Now, from this total amount, Sophie had withdrawn £ 317.50
Therefore, money left in her account = ( 3 ) – £ 317.50
Again, both the decimal numbers are like terms; hence we can go ahead with the calculations.
= £ 556.05 – £ 317.50
= £ 238.55
Hence, money left in Sophie’s account = £ 238.55
Let us take another example.
Example
Sam, Peter and Henry bought 8.5 litres, 7.25 litres and 9.4 litres of milk respectively from a milk booth. How much milk did they buy in all? If there were 30 litres of milk in both, find the quantity of milk left.
Solution
Let us first define what is given and what needs to be calculated. We have been given that Sam, Peter and Henry bought 8.5 litres, 7.25 litres and 9.4 litres milk respectively from a milk booth. We need to find out –
a) How much milk did they buy in all?
b) If there were 30 litres of milk in both, find the quantity of milk left.
Let us find the answers to the above problems one by one.
Amount of milk bought by Sam = 8.5 litres
Amount of milk bought by Peter = 7.25 litres
Amount of milk bought by Henry = 9.4 litres
The total amount of milk bought by them = 8.5 litres + 7.25 litres + 9.4 litres
Note here that the given decimals are not like terms. Hence, we will first need them to be converted into like terms. Therefore, we now have,
Amount of milk bought by Sam = 8.5 litres = 8.50 litres
Amount of milk bought by Peter = 7.25 litres = 7.25 litres
Amount of milk bought by Henry = 9.4 litres = 9.40 litres
Now that the terms are like terms, we can go ahead with the calculations.
Total milk bought by Sam, Peter and Henry = 8.50 litres + 7.25 litres + 9.40 litres = 25.15 litres
Hence, the total milk bought by Sam, Peter and Henry =25.15 litres
Now, let us solve the second part of the question. We have been given that there were 30 litres of milk in the booth. How much milk is left after Sam, Peter and Henry bought the milk?
Therefore,
Total milk in booth = 30 litres
Milk bought by Sam, Peter and Henry = 25.15 litres
Again, we can see here that the given decimals are not like terms. Hence, we will first need them to be converted into like terms. Therefore, we now have,
Total milk in booth = 30 litres = 30.00 litres
Milk bought by Sam, Peter and Henry = 25.15 litres
Now that the terms are like terms, we can go ahead with the calculations.
Milk left in the booth = 30.00 litres – 25.15 litres
= 4.85 litres
Hence, after Sam, Peter and Henry, 4.85 litres of milk was left in the booth.
Addition and Subtraction Word problems Involving Fractions
It is not just money or decimals, we find everyday situations where we need to solve word problems involving addition and subtraction. We are required to do so in the case of fractions as well. Let us look at some situations where we encounter addition and subtraction word problems involving fractions –
Example
A recipe needs 3/7 teaspoon black pepper and 1/4 teaspoon red pepper. How much more black pepper does the recipe need?
Solution
We have been given that a recipe needs 3/7 teaspoon black pepper and 1/4 teaspoon red pepper. We need to find out how much more black pepper is required in the recipe as compared to red pepper.
First of all, we will summarise the fractions given to us. We have,
Fraction of black pepper needed in the recipe = $frac{3}{7}$
Fraction of red pepper needed in the recipe = $frac{1}{4}$
In order to find out how much more black pepper is required in the recipe as compared to red pepper, we will need to find the difference between the black pepper and the red pepper used.
Therefore, we need to find out the value of $frac{3}{7} – frac{1}{4}$
The denominators of the above fractions are different; therefore, we will find their L.C.M first.
L.C.M of 7 and 4 = 28
Now, we will convert the given fractions into equivalent fractions with denominator 28.
$frac{3}{7} = frac{3 x 4}{7 x 4} = frac{12}{28}$
$frac{1}{4} = frac{1 x 7}{4 x 7} = frac{7}{28}$
Now, that the denominator of both the fractions is the same we will find the difference in their numerators. We have,
$frac{3}{7} – frac{1}{4} = frac{12}{28} – frac{7}{28} = frac{12- 7}{28} = frac{5}{28}$
Hence, the amount of more black pepper required in the recipe as compared to red pepper = $frac{5}{28}$
Recommended Worksheets
Fact Families for Addition and Subtraction (Christmas Themed) Math Worksheets
Problem Solving – Addition and Subtraction (World Teachers’ Day Themed) Math Worksheets
Solving Word Problems involving Addition and Subtraction of numbers within 120 1st Grade Math Worksheets
We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!
Word problems involving addition and subtraction are discussed here step by step.
There are no magic rules to make problem solving easy, but a systematic approach can help to the problems easily.
Word problems based on addition are broadly of two types:
(a) When objects of two or more collections are put together.
For example:
Amy has 20 lemon sweets and 14 orange sweets. What is the total number of sweets Amy has?
(b) When an increase in number takes place.
For example:
Victor has 14 stamps. His friend gave him 23 stamps. How many stamps does Victor have in all?
The key words used in problems involving addition are:
sum; total; in all; all together.
Word problems based on subtraction are of several types:
(a) Partitioning : Take away, remove, given away.
(b) Reducing : Find out how much has been given away or how much remains.
(c) Comparison : More than / less than.
(d) Inverse of addition : How much more to be added.
The key words to look out for in a problem sum involving subtraction are:
take away; how many more ; how many less ; how many left ; greater ; smaller.
1. The girls had 3 weeks to sell tickets for their play. In the first
week, they sold 75 tickets. In the second week they sold 108 tickets and
in the third week they sold 210 tickets. How may tickets did they sell
in all?
Tickets sold in the first week = 75
Tickets sold in the second week = 108
Tickets sold in the third week = 210
Total number of tickets sold = 75 + 108 + 210 = 393
Answer: 393 tickets were sold in all.
2. Mr. Bose spent $450 for petrol on Wednesday. He spent $125 more than
that on Thursday. How much did he spend on petrol on those two days.
This problem has to be solved in two steps.
Step 1: Money spent for petrol on Thursday
450 + 125 = $575
Step 2: Money spent for petrol on both days
450 + 575 = $1025
Examples on word problems on addition and subtraction:
1. What is the sum of 4373, 4191 and 3127?
Solution:
The numbers are arranged in columns and added.
|
|
(i) Ones are added: 3 + 1 + 7 = 11 = 1 Ten + 1 one (ii) Tens are added: 1 + 7 + 9 + 2 = 19 tens = 1 hundred + 9 ten (iii) Hundreds are added: 1 + 3 + 1 + 1 = 6 Hundred (iv) Thousands are added: 4 + 4 + 3 = 11 Thousand |
Therefore, sum =11,691
2. What is the difference of 3867 and 1298?
Solution:
The numbers are arranged in columns and subtracted:
|
|
(i) Ones are subtracted: 7 < 8 1 is borrowed from 6 ten. So, 1 T or 10 + 7 = 17, 17 — 8 = 9 (ii) Tens are subtracted; 5 T < 9 T, So, 1 H or 10 T is borrowed from 8 H, 1 H = 10 T + 5 T = 15T 15T — 9T = 6 (iii) Hundreds are subtracted 7 H – 2 H = 5 H (iv) Thousands are subtracted 3 Th – 1 Th = 2 Th |
Therefore, difference = 2569
3. Subtract 4358 from the sum of 5632 and 1324.
Solution:
Sum of 5632 and 1324
|
|
Difference of 6956 and 4358
|
|
(i) 6 < 8, 1 T or 10 ones are borrowed 1 T or 10+ 6 =16, 16 — 8 = 8 (ii) 4 T < 5 T, 1 H or 10 T is borrowed 10 T + 4 T = 14 T, 14 T – 5 T = 9 T (iii) 8 H – 3 H = 5 H (iv) 6 Th – 4 Th = 2 Th |
Therefore, 2598 is the answer.
4. Find the number, which is
(i) 1240 greater than 3267.
(ii) 1353 smaller than 5292.
Solution:
(i) The number is 1240 more than 3267
Therefore, the number = 3267 + 1240 or = 4507
(ii) The number is 1353 less than 5292
Therefore, the number
= 5292 – 1353 or
= 3939
5. The population of a town is 16732. If there are 9569 males then find the number of females in the town.
Solution:
|
Population of the town Number of males Therefore, number of females |
= 1 6 7 3 2 = — 9 5 6 9 = 7 1 6 3 |
6. In a factory there are 35,675 workers. 10,750 workers come in
the first shift, 12,650 workers in the second shift and the rest come in
the third shift. How many workers come in the third shift?
Solution:
Number of workers coming in the first and second shift
= 10750 + 12650 = 23400
Therefore, number of workers coming in the third shift = 35675 — 23400 = 12275
Related Concept
● Addition
● Word
Problems on Addition
● Subtraction
● Check
for Subtraction and Addition
● Word
Problems Involving Addition and Subtraction
● Estimating
Sums and Differences
● Find the
Missing Digits
● Multiplication
● Multiply
a Number by a 2-Digit Number
● Multiplication
of a Number by a 3-Digit Number
● Multiply a Number
● Estimating Products
● Word
Problems on Multiplication
● Multiplication
and Division
● Terms Used in
Division
● Division
of Two-Digit by a One-Digit Numbers
● Division
of Four-Digit by a One-Digit Numbers
● Division
by 10 and 100 and 1000
● Dividing Numbers
● Estimating
the Quotient
● Division
by Two-Digit Numbers
● Word
Problems on Division
HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Addition and subtraction word problems are commonly taught in Year 2 (Key Stage 1 in the UK) or second grade (in the USA).
The strategy to solve word problems is to firstly, write out the numbers involved and secondly, to decide which operation to use by reading the keywords in the question.
To solve addition and subtraction word problems, we try to read the question and look for keywords. The keyword list below will help to identify whether we have an addition or subtraction word problem.

Some common addition keywords are:
- Add
- Plus
- More
- Total
- Increase
- Together / Altogether
- Combined
- Sum
- Grow
If we see these words, we likely have an addition word problem.
Some common subtraction keywords are:
- Subtract
- Minus
- Take away
- Less / Fewer than
- Difference
- Decrease
- How many are left / remain?
- Change – in money questions
- Words ending in ‘er’, such as shorter, longer, faster.
Here is our first example of a word problem.
William has 20 counters and is given 7 more.
How many does he have in total?
We can see that we have the two addition keywords which are: ‘more‘ and ‘total‘.

When teaching word problems, it is useful to first write out the numbers that are in the text of the question.
We have 20 and 7.
The words ‘more‘ and ‘total‘ tell us that this is an addition word problem. We start with 20 counters and add 7 more.
Once we know that we have an addition word problem, then we can add the numbers.
20 + 7 = 27

William has 27 counters in total.
Here is another word problem example.
Phoebe has 12 cm of ribbon and Jack has 23 cm.
How much do they have altogether?
Our strategy is to first write out the numbers involved in the question.
We write down 12 and then 23. We can write the numbers above each other and line up the digits in each number.

There is only one keyword in this question which is altogether.
This in an addition keyword which tells us that we want to combine the two amounts to make a total.
We want to add the numbers 12 and 23.
It is common for children to write down the units involved in the question at this stage. However, it is easiest to just write down the numbers themselves and then to put the units in at the end of the question as part of checking the working out.

Adding the units column, 2 + 3 = 5.
Adding the digits in the tens column, 1 + 2 = 3.
Therefore 12 + 23 = 35 and so, we have 35 cm of ribbon in total.
We are measuring the length of ribbon in cm and so, we write ‘cm’ at the end of our answer.
Here is another word problem example.
I buy 2 sweets that cost 43 pence each.
How much do they cost in total?
Each sweet costs 43 pence and there are two of them.
We write down 43 twice in this question.

The keyword ‘total‘ tells us that this is an addition word problem.
We will add the two 43 amounts by writing their digits directly above each other without writing ‘pence’ at the end.

Adding the units, 3 + 3 = 6.
Adding the tens, 4 + 4 = 8.
The two sweets cost 86 pence in total.
We can write the pence or ‘p’ on the final answer now that the calculation has been done.
In this worded question, we have only one number in the text itself. There is only one ’43’ written.
It can help to draw a diagram when teaching word problems to children to help picture the situation.
Here is another word problem involving money.
Matthew has 35 pence.
He spends 13 pence.
How much does he have left?
We write down the numbers involved, which are 35 and 13.
In this word problem, the keyword is left.
Finding how much is left is a keyword for a subtraction word problem.
This means that we subtract the smaller number from the larger number.

To subtract 13 from 35, we write the larger number above the smaller number and line up the digits.
Subtracting the units column, 5 – 3 = 2.
Subtracting the tens column, 3 – 1 = 2.
35 – 13 = 22

This was a problem involving finding change with money.
Spending money and then receiving change is also very likely to indicate that a word problem is a subtraction one.
In this next worded problem, Adam has 59 grams of chocolate.
He eats 49 grams.
How much does he have left?
The first step of the word problem strategy is to write out both of the numbers involved in the question.
We have 59 and 49.
The second step is to identify keywords. The word left is a subtraction keyword.
We want to see how much is left after 49 grams have been subtracted.

We write the subtraction with the larger number above the smaller number.
Subtracting the units column digits, 9 – 9 = 0.
Subtracting the tens column digits, 5 – 4 = 1.
59 – 49 = 10.

There are 10 grams of chocolate remaining.
Here is another word problem example.
I have a candle that is 38 cm long.
After I light it, 11 cm melts away.
How long is the candle now?
This word problem is trickier in that there are not any direct keywords in the question.
However the phrase ‘melts away tells us that we are removing, or subtracting.
Again, when teaching word problems, drawing a diagram is a useful technique.
If no diagram or picture is given, it helps to draw the situation at the start and also the situation at the end.

Subtracting the digits in the units column, 8 – 1 = 7.
Subtracting the digits in the tens column, 3 – 1 = 2.
38 – 11 = 27
27 cm of the candle remains.

In this example, the candle reduced in size because we were removing length as it melted.
The candle has become shorter. Shorter is a word which ends in ‘er’, which can also indicate that we have a subtraction word problem.
‘er’ words often look for a difference between two values and finding a difference is a subtraction.
Again, it can help to draw the situation with a diagram to help understand what type of word problem we have.

Word Problems: Word Problems are an important aspect of the primary curriculum because they require students to apply their understanding of various topics to “real-life” circumstances. They also assist students in becoming acquainted with mathematical terminology like more, fewer, subtract, difference, altogether, equal, share, multiply, reduced, etc.
A word problem consists of a description of a real-life scenario where a mathematical calculation is required to solve a problem. Students need to learn how to solve word problems as it enables them to apply mathematical concepts to various real-life scenarios. This means that to understand the word problem, students must be familiar with the terminology linked with the mathematical symbols they are used to. Let us learn in detail about Word Problems in this article.
What is a Word Problem?
In real life, mathematical problems do not usually present themselves as (2+3) or (6-4.) Instead, they are a bit more complex than we think. Authors of mathematical curriculum sometimes implement word problems to help students understand how they are related to the real world.
Learn 10th CBSE Exam Concepts
Word problems often show mathematics happening more naturally in the real world. Word problems can vary from simple to complex.
Examples:
Here are a few examples to get you some ideas:
1. Keerthi had (5) apples. Her mother gave her (7) more apples. Now, how many apples does Keerthi have altogether?
2. There were (18) pencils and (9) pens. How many more pencils than pens are there?
3. Spurti has one dozen eggs. Her friends ate (4) for breakfast. Now, how many eggs are left with Spurti?
4. There are (18) apples. Swetha, Priya, and Rachana want to eat them in equal share. How many apples will each of the friends get?
As you can notice, word problems involve addition, subtraction, multiplication, division, or even multiple operations.
Word Problems on Quadratic Equation
Handling Maths Word Problems in General
Steps for Solving a Word Problem:
To work out any word problem, follow the steps given below:
1. Read the Problem: First, read through the problem once.
2. Highlight Facts: Then, read through the problem again and underline or highlight important facts such as numbers or words that indicate an operation.
3. Draw a Picture: Drawing a picture sometimes help visualise the problem more clearly. It can also help understand clearly the algebraic operations that need to be carried out.
4. Determine the Operation(s): Next, determine the operation or operations that need to be performed. Is it addition, subtraction, multiplication, division? What needs to be done? Drawing the picture should be a big help in figuring this out. However, look for clues in words such as:
(i) Addition: add, total, brought, plus, altogether, and, combine, more, in all
(ii) Subtraction: subtract, fewer, take away, than, left
(iii) Multiplication: total, times, triple, twice, in all
(iv) Division: each, per, out of, equal pieces, split, average
Practice 10th CBSE Exam Questions
5. Make a Math Sentence: Next, translate the word problem and drawings into a math or number sentence. This means write a sentence such as (18+3=)
6. Solve the Problem: Then, solve the number sentence and find the solution—for example, (3+8=11.)
7. Check Your Answer: Finally, check the result obtained to ensure the correct answer.
With the above (7) steps, solving word problems in mathematics becomes easy.
Addition Word Problems
Addition word problems arise in situations where there is an increase of something or gain as a result of combining one or more numbers. Think of addition as combining parts to form a whole.
Example: Teena has (6) chocolates, her brother gives her (4) chocolates. How many chocolates in total does Teena have?
To find the total chocolates, we add the number of chocolates Teena has and the number of chocolates her brother gave her.

Thus, Teena has (10) chocolates now.
Attempt 10th CBSE Exam Mock Tests
Subtraction Word Problems
Subtraction word problems arise in situations where there is a decrease of something or loss as a result of deducting a number from another.
Example: Arya plucked (10) cherries from the tree, and her friend asked her to give (4) cherries to her. How many cherries are left with Arya?
Here we subtract the number of cherries given to Arya’s friend from the total cherries plucked by Arya.

Thus, the number of cherries left with Arya is (6.)
Multiplication Word Problems
Multiplication word problems are helpful for students to develop their multiplication knowledge by applying it to real-life situations. In this kind of multiplication word problem, one quantity is compared with another quantity, larger or smaller. Work out the multiplication problem using the clues provided.
Example: Ajay has two bunch of tomatoes. Each bunch has (4) tomatoes. What is the total number of tomatoes does Ajay have?
Here, we multiply the number of the bunch by the number of tomatoes in each bunch

Thus, Ajay has (8) tomatoes in total.
Division Word Problems
Division word problems are more confusing for students to understand. The words generally used in division word problems are “shared among” or “given to each” or similar phrases that imply total quantity to be split evenly into groups. We use division or multiplication when the problem involves equal parts of a whole.
Example: He divides (12) apples evenly among (4) friends. How many apples did John give to each of his friends?
To find how many apples John gave to each of his friends, we divide the total number of apples by the number of friends.

Hence, each of John’s friends gets (3) apples.
Fraction Word Problems
Fraction word problems look more complex, but in reality, fraction word problems are just as easy as those involving whole numbers. Here, one extra step of simplification may be needed in some cases. Students should know the operations with fractions to solve word problems on fractions.
Example: Swaroop had half an apple, and his mother gave him another quarter of an apple. What portion of apple does Swaroop have?
The given example is the addition word problem that involves fractions.
Here, we add the portion of apple Swaroop initially had with the portion his mother gives. i.e., (frac{1}{2} + frac{1}{4} = frac{{2 + 1}}{4} = frac{3}{4}.)

Thus, Swaroop has (frac{3}{4})th of apple.
Solved Examples
Q.1. The male population of a village is (76138,) and the female population is (13776.) What is the total population of the village?
Ans: Male population (=76138)
Female population (=13776)
Total population of the village (=) male population (+) female population (=76138+13776 )
(=89914 )

Thus, the total population of the village is (89914.)
Q.2. Likith had collected (208) coins. He lost of (52) coins. How many coins are left with Likith?
Ans: Total coins Likith collected (=208)
The number of coins lost (=52)
Number of coins left (=208 – 52=156)

Thus, the number of coins left is (156.)
Q.3. The cost of one shirt is (₹206.) A retailer wants to buy (68) such shirts. How much should he pay?
Ans: Given that the cost of one shirt (=₹206)
Number of shirts a retailer wants to buy (=68)
Total amount to be paid (=₹206×68)

Therefore, the total amount to be paid is (₹14008.)
Q.4 If (4472,{rm{kg}}) of rice is packed in (52) bags, how much rice will each bag contain?
Ans: Since (52) bags contain rice of (4472,{rm{kg}})
Therefore, (1) bag contains rice ( = left( {frac{{4472}}{{52}}} right){rm{kg}})
( = 86,{rm{kg}})

Thus, each bag of rice contains ( = 86,{rm{kg}}.)
Q.5. One-half of the students in a school are boys, (frac{4}{5}) of these boys are studying in lower classes. What fraction of boys are studying in lower classes?
Ans: Fraction of boys studying in school ( = frac{1}{2})
Fraction of boys studying in lower classes ( = frac{4}{5}) of (frac{1}{2})
( = frac{4}{5} times frac{1}{2})
( = frac{2}{5})
Therefore, (frac{2}{5}) of boys studying in lower classes.
Q.6. Celena planned to interview some candidates for a position in her office. If she scheduled half an hour to meet each of them, how much time did she schedule for all (6) candidates?
Ans: Time spent to meet each candidate ( = frac{1}{2}) hour
Number of applicants (=6)
Time scheduled for all (6) candidates ( = frac{1}{2} times 6 = 3) hours
Thus, Celena scheduled (3) hours for the interview.
Summary
In this article, we studied the meaning and steps to solve word problems. Then we have discussed in detail taking an example of how to do the addition word problem, subtraction, multiplication, division and fraction word problem.
We have solved word problem examples for students to understand the concept clearly.
Learn the Concepts on Unitary Method
Frequently Asked Questions on Word Problems
We have provided some frequently asked questions on Word Problems here:
Q.1. What are word problems in maths?
Ans: A word problem is a few sentences describing a real-life scenario where a problem needs to be solved by a mathematical calculation.
Q.2. What are numberless word problems?
Ans: Numberless word problems are designed to provide scaffolding that allows students to understand the underlying structure of word problems.
Q.3. What is addition word problems?
Ans: Addition word problems appear when there is a gain or an increase of something due to combining one or more numbers. Think of addition as combining parts to form a whole.
Q.4. What are the steps in solving word problems?
Ans: Solving word problem requires the following steps:
1. Read the problem
2. Highlight facts
3. Draw a picture
4. Determine the operation/s.
(i) Addition
(ii) Subtraction
(iii) Multiplication
(iv) Division
5. Make a mathematical sentence
6. Solve the problem
7. Verify your answer
Q.5. What is an example of a word problem?
Ans: The typical examples of word problems in algebra are distance problems, age problems, percentage problems, work problems, mixtures problems and number problems.
Now you are provided with all the necessary information on Maths word problems and we hope this detailed article is helpful to you. If you have any queries regarding this article, please ping us through the comment section below and we will get back to you as soon as possible.
Related Pages
Addition & Subtraction Word
2-Step Word Problems and Bar Models
More Word Problems
More Singapore Math Lessons
Example:
There are 1030 books in the library. We bought 67 more books for the library. How many books are
there in the library now?
Solution:
1030 + 67 = 1097
There are 1097 books in the library now.
Example:
1085 girls and 531 boys took part in an art competition. How many students took part in the
competition altogether?
Solution:
1085 + 531 = 1616
1616 students took part in the competition altogether.
Example:
After giving $1085 to his wife, Simon had $746 left. How money had he at first?
Solution:
1085 + 746 = 1831
Simon had $1831 at first.
Example:
Margret sold 1392 meatballs on Friday. She sold 1940 more meatballs on Saturday than on Friday.
How many meatballs did she sell on Saturday?
Solution:
1392 + 1940 = 3332
She sold 3332 meatballs on Saturday.
A visual way to solve world problems using bar modeling
This type of word problem uses the part-whole model. Because the whole is missing, this is an addition problem.
Example:
Mr. Gray sold 64 drinks in the morning. Mr. Frank sold 25 drinks at night. How many drinks did they
sell altogether?
- Show Video Lesson
How to solve addition problem using part-whole model?
Example:
Maya had some stamps. She gave 7 stamps to her younger brothers. Maya then had 14 stamps. How many
stamps did Maya have at first?
- Show Video Lesson
Examples of 4th Grade word problems and bar models
Example:
Dad bought two hammers. One cost $18 and the other costs $28 more. What was his total bill?
- Show Video Lesson
Model Drawing — addition word problems
Example:
A girl jumps 42cm for her first jump in a high jump competition. Her second jump is 46cm.
How high did she jump in total?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
My students had been struggling with how to solve addition and subtraction word problems for what seemed like forever. They could underline the question and they could find the numbers. Most of the time, my students just added the two numbers together without making sense of the problem.
Ugh.
Can you relate?
Below are five math problem-solving strategies to use when teaching word problems on addition and subtraction using any resource.

So, how do I teach word problems? It’s quite complex, but so much fun, once you get into it.
How to teach addition and subtraction word problems
The main components of teaching addition and subtraction word problems include:
- Teaching the Relationship of the Numbers – As a teacher, know the problem type and help students solve for the action in the problem
- Differentiate the Numbers – Give students just the right numbers so that they can read the problem without getting bogged down with the computation
- Use Academic Vocabulary – And be consistent in what you use.
- Stop Searching for the “Answer” – it’s not about the answer; it’s about the process
- Differentiate between the Models and the Strategies – one has to do with the relationship between the numbers and the other has to do with how students “solve” or compute the problem.
I am a big proponent of NOT teaching keyword lists. It just doesn’t work consistently across all problems. It’s a shortcut that leads to breakdowns in mathematical thinking. Nor should you just give students word problem worksheets and have them look for word problem keywords. I talk more in-depth about why it doesn’t work in The Problem with Using Keywords to Solve Word Problems.
Teach the Relationship of the Numbers in Math Word Problems
One way to help your students solve word problems is to teach them the relationship of the numbers. In other words, help them understand that the numbers in the problem are related to each other in some way.
I teach word problems by removing the numbers. Sounds strange right?
Removing the distraction of the numbers helps students focus on the situation of the problem and understand the action or relationship of the numbers. It also keeps students from solving the problem before we talk about the relationship of the numbers.
When I teach word problems, I give students problems with blank spaces and no numbers. We first talk about the action in the problem. We identify whether something is being added to or taken from something else. That becomes our equation. We identify what we have to solve and set up the equation with blank spaces and a square for the unknown number
___ + ___ = unknown
Do you want a free sample of the word problems I use in my classroom? Click the link or the image below. FREE Sample of Word Problems by Problem Type
Differentiate the numbers in the Word Problems
Only after we have discussed the problem do I give students numbers. I differentiate numbers based on student needs. At the beginning of the year, we all do the same numbers, so that I can make sure students understand the process.

After students are familiar with the process, I start to give different students different numbers, based on their level of mathematical thinking.
I also change numbers throughout the year, from one-digit to two-digit numbers. The beauty of the blank spaces is that I can put any numbers I want into the problem, to practice the strategies we have been working on in class.
At some point, we do create a list of words, but not a keyword list. We create a list of actions or verbs and determine whether those actions are joining or separating something. How many can you think of?
Here are a few ideas:
Join: put, got, picked up, bought, made
Separate: ate, lost, put down, dropped, used

Don’t be afraid to use academic vocabulary when teaching word problems
I teach my students to identify the start of the problem, the change in the problem, and the result of the problem. I teach them to look for the unknown.
These are all words we use when solving problems and we learn the structure of a word problem through the vocabulary and relationship of the numbers.
In fact, using the same vocabulary across problem types helps students see the relationship of the numbers at a deeper level.
Take these examples, can you identify the start, change and result in each problem? Hint: Look at the code used for the problem type in the lower right corner.
For compare problems, we use the terms, larger, smaller, more and less. Try out these problems and see if you can identify the components of the word problems.

Stop searching for “the answer” when solving word problems
This is the most difficult misconception to break.
Students are not solving a word problem to find “the answer”. Although the answer helps me, the teacher, understand whether or not the student understood the relationship of the numbers, I want students to be able to explain their process and understand the depth of word problems.
Okay, they’re first and second-graders. I know.
My students can still explain, after instruction, that they started with one number. The problem resulted in other another number. Students then know that they are searching for the change between those two numbers.
It’s all about the relationship.

Differentiate between the models and the strategies
A couple of years ago, I came across this article about the need to help students develop adequate models to understand the relationship of the numbers within the problem.
A light bulb went off in my head. I needed to make a distinction between the models students use to understand the relationship of the numbers in the problem and the strategies to solve the computation in the problem. Models and strategies work in tandem but are very different.
Models are the visual ways problems are represented. Strategies are the ways a student solves a problem, putting together and taking apart the numbers.
The most important thing about models is to move away from them. I know that sounds odd.
You spend so long teaching students how to use models and then you don’t want them to use a model. Well, actually, you want students to move toward efficiency.
Younger students will act out problems, draw out problems with representations, and draw out problems with circles or lines. Move students toward efficiency. As the numbers get larger, the model needs to represent the relationship of the numbers
This is a prime example of moving from an inverted-v model to a bar model.
Here is a student moving from drawing circles to using an inverted-v.
Students should be solidly using one model before transitioning to another. They may even use two at the same time while they work out the similarities between the models.
Students should also be able to create their own models. You’ll see how I sometimes gave students copies of the model that they could glue into their notebooks and sometimes students drew their own model. They need to be responsible for choosing what works best for them. Start your instruction with specific models and then allow students to choose one to use. Always move students toward more efficient models.
The same goes for strategies for computation. Teach the strategies first through the use of math fact practice, before applying it to word problems so that students understand the strategies and can quickly choose one to use. When teaching, focus on one or two strategies. Once students have some fluency in a few strategies, have them choose strategies that work for different problems.
Which numbers do you put in the blank spaces?
Be purposeful in the numbers that you choose for your word problems. Different number sets will lend themselves to different strategies and different models. Use number sets that students have already practiced computationally.
If you’ve been taught to make 10, use numbers that make 10. If you’re working on addition without regrouping, use those number sets. The more connections you can make between the computation and the problem-solving the better.
The examples above are mainly for join and separate problems. It’s no wonder our students have so much difficulty with compare problems since we don’t teach them to the same degree as join and separate problems.
Our students need even more practice with those types of problems because the relationship of the numbers is more abstract. I’m going to leave that for another blog post, though.
Do you want a FREE sample of the resource that I use to teach Addition & Subtraction Word Problems by Problem Type? Click this link or the image below.
How to Purchase the Addition & Subtraction Word Problems
The full resource is also available in my store for purchase and on Teachers Pay Teachers.

More Ideas for Teaching Word Problems
44 Responses
-
-
This is great! I teach high school math, and always ask them to “Tell me the story” before we start looking at the numbers. If, in telling the story, they tell me a number, I stop them, and remind them that we’re just looking at what is happening, and ignore the numbers. They look at me like I am crazy, “Ignore the numbers?” Yes, I tell them. The numbers are not important until you understand the story, and even then, meh. I am thinking about giving them word problems without numbers, and use some of your suggestions. Maybe even let them put in numbers and solve their own problems. I’ve seen the word lists like you mentioned, and they’re ok, but they are not always true. Like, “how many all together?” usually means add, but in higher math, it could be addition in the form of repeated addition, aka, multiplication. Those little phrases are usually true for the early word problem problems, but as the students get older, they will need to be able to think about what the problem means, rather than just hunting for words and numbers. LOVE this approach!
-
I love the perspective of a high school math teacher! This is why I want to emphasize teaching about the situation and action of a word problem. I know it can be so simple when students are young, but once they hit third grade and are doing both multiplication and addition within the same problem, boy, does it get complicated! Students really need to understand the problem. Using blank spaces has helped most of my students focus on what is happening in the problem. If you try it, I’d love to hear how it goes!
-
-
Thank you for presenting your work in such an organized fashion. Your thought process is so clear a beginning teacher will be able to instruct children brilliantly! I appreciated the work samples you included. Hope you continue this blog, you’re very talented.
-
Wow! Thank you for posting such an in-depth, organized lesson! My students, as well, struggle with the concept of word problems. This is wonderful!
-
You did a great job presenting this information. I absolutely love your way of teaching students how to think about word problems. Superior work!
-
Thank you so much! I have a lot of fun teaching word problems in the classroom, too.
-
-
Hi Jessica,
I work with Deaf and Hard of Hearing students at the elementary level. The overall and profound struggle of the deaf child is that of access to language(written). For those children not born into Deaf, ASL, 1st language household, we, in many cases, consider these children to be language deprived. Math is typically the stronger subject for my students as it has been, up until recently, the most visual subject, one which requires less reading and more computation and visual or spacial awareness. When the Common Core rolled out, I looked at the Math, more specifically, the word problems with the addition of explaining ones answer, I thought…”if it isn’t already so difficult for my students to navigate the written language presented to them but to now need to explain themselves mathematically” I figured I would go on just blocking out the story and focus on numbers and key words/indicators…. After reading your blog on the topic of word problems and looking at your products I have decided to start a new!!! Knowing the story, for some of my students, might better help them visualize the WHY and the reality of the numbers and their relationships. Knowing the story will also provide context to real life scenarios, which will translate to them being able to better explain their result, outcome or answer. An ah-ha moment for me! Cheers!!!-
I am in my senior year @ UNCG for Deaf Education k-12 and we JUST discussed this today! Things like ‘CUBES’ and other key word memorization methods take away from the importance of understanding the story/situation. Being able to use these real life situations to make connections to the concept helps tremendously, even with large gaps in background knowledge/language. ASL provides the ability to SHOW the story problem, so I hope to take advantage of that when I teach math lessons. I love finding deaf educators!
-
-
Hello Jessica,
I think your strategy is interesting.
I already subsribe, but how to get your free sample of addition word problems.
Thank you-
Hi, Kadek,
It looks like you’ve already downloaded the free sample. Let me know if you’re not able to access it.
Jessica
-
Hi, Jessica,
I already got it yesterday.
Thank you so much for your free sample.
Kadek
-
-
-
I purchased your word problems pack and LOVE it! My 2nd graders are forced to slow down and analyze the story. We’ve had some GREAT discussions in math lately. Another strategy I like to do in problem solving is show the word problem but leave the question out. Kids brainstorm what questions could we ask to go with the problem. Fun stuff happening in math!
-
— so do you wait on teaching compare until they are a little good at joining and separating?
“The examples above are mainly for join and separate problems. It’s no wonder out students have so much difficulty with compare problems, since we don’t teaching them to the same degree as join and separate problems. Our students need even more practice with those types of problems because the relationship of the numbers is more abstract. I’m going to leave that for another blog post, though”-
I totally forgot that I was going to do a follow-up post on compare problems! Thank you for reminding me!
I do introduce join and separate problems first, but I don’t necessarily wait on teaching compare problems until students are proficient solving join/separate problems. Students will progress at different rates and I don’t want to wait to teach something that others’ might be ready to learn. I teach compare problems with a lot of physical modeling first and then we move into using a bar-model as the written model. The other thing I do with these types of problems is use concrete sentence frames. Sometimes, especially my English learners, need some of the vocabulary and sentence structure to better understand the relationship of the numbers.
I vary when I teach them every year. I often do it around Halloween, when we talk about pumpkins and who had a larger pumpkin or more seeds. I also do it when we measure our feet and we discuss the size of feet. It’s a great problem type for measurement, although you can compare any two quantities. Although I have taught a problem type, we continue to use it all year long as we relate to the math around us.
-
Hi. Just wondering if you did have a follow up post on compare problems. Thank you!
-
Not yet, but it’s on the plan for this month. I took a (long) break from doing FB lives and am starting back up again. That is one that I’ll do this month. I don’t have an exact date yet – kinda depends on when I can get my kids out of the house! 🙂
-
-
-
-
I cannot wait to try this with my students! We are getting their baseline today and then we are going to start on Thursday. I wish I could pick your brain about this and how you teach this beginning to end. Do you start by teaching them the vocabulary and just labeling the parts (start, change, result)?
-
I love how you teach student to label parts of the word problem while trying to solve it (S for Start, C for Change, etc.) You seem to have easily clarified the steps of solving problems in very clear (and cute) kid friendly language. Nice job. Thank you for sharing.
-
I love this idea of having the students organize the information. My question is how do you teach them when to add or multiply or subtract/divide? At that point do they look for works like equal groups?
-
I’m sorry…I have one more question. Can you apply this method to multi-step word problems?
-
Yes! Each “step” in the word problem would have its own equation, which may be dependent on the first equation. You’re using the same process, reading the problem for a context, setting up an equation, then giving students the numbers. With second graders, I do a lot of acting out for multistep problems, as it’s generally a new concept for them.
-
-
We don’t look for keywords but set up an equation based on the situation or context of the word problem. The situation in the word problem will illustrate the operation, like someone dropping papers, adding items to their cart, sharing something with friends, etc. The situation will tell the operation.
-
-
I love , love , love this concept my year 1 pupils easily grasps the lesson. Thanks a bunch! Do you have strategies like this for multiplication and division?
-
-
Hi Jessica, this is simply great. My 7 year old struggles with worded problems and I’ll try to method with him and hopefully it’ll help him grasp the methodology better. On w different note, I’ve been trying teach him how to solve simple addition and subtraction in the form of an equation. For example 15+—= 43 or 113- = 34. But despite multiple attempts of explaining the logic using beans and smaller numbers, he is struggling to understand. Would you have any tips on those.
Many thanks,
Varsha
-
Thank you so much! This is super helpful for me. I’m currently student teaching in a 2nd grade class. My cooperating teach is EXTREMELY uncooperative and hasn’t/won’t help me in planning lessons. She told me to teach word problems and despite my follow up questions I don’t know what exactly they’ve done already this year or where to start. This post gave me lots of ideas and helped me prepare for last minute shifts as I teach without a plan (unfortunately). If I wasn’t a poor college student I would definitely buy the pack, especially after getting the free samples! These samples are so helpful!
-
Thanks! It is very interesting! Good!
-
Hey! You’re amazing! I’ve heard that this really help kids comprehend better & I want to try it! I sent my info but haven’t received the freebie.
-
Hi, Gisel,
You need to confirm your email address before I can send you any emails. The confirmation may have gone to your spam folder. I also have a different email address than the one for this comment. Feel free to fill out the contact form if you need me to switch the email address. For now, I’ll assume that this comment is a confirmation and manually approve it.
-
-
This worked amazingly well! My second graders were having such a tough time understanding how to do word problems. This strategy helped most of them with the ability to understand how to do word problems and demonstrate their knowledge on testing. Most importantly, after learning this strategy, the students kept asking for more problems to solve.
-
What pacing do you suggest for introducing the different types of problems? Should students master one type before moving on to another?
-
Great question! I would consider your students, grade level, and curriculum. I generally spend more time at the beginning of the year, with easier problem types to establish routines. Some problem types are complementary and easier to teach and practice after students learn one. I also cycle back through problem types as we learn new computation strategies. For instance, in second grade, we do single-digit addition at the beginning of the year, mid-year we move onto two-digit addition and mid- to end-of-the-year we do three-digit addition. We will cycle through problem types we’re already learned but increase the complexity of the numbers.
I would make sure a majority of your class has mastered the process of reading a word problem and identifying the parts. Also, be sure you’re separating student mistakes between computational or mathematical errors and problem-solving errors. As I said in the beginning, I’d take the cues based on your students, grade level, and curriculum. Some years I have spent more time because my students needed more time. Other years I was able to move quicker.
-
Makes sense! Thanks so much!
-
-
-
I absolutely LOVE this post. Thank you for sharing it! I teach third grade and my babies are struggling with what to actually DO in a word problem. I’m going to be trying this with them immediately. Do you have any suggestions for how to incorporate it with multiplication and division problems?
-
-
Thank you for sharing this wonderful resource! Could you explain how you teach your students to use the inverted V model? I noticed the 3 points are labelled as start, change, and result differently for each problem. I am very interested in teaching my students this model!
-
-
Can you go over for me about “start, change and results”? Thanks.
-
-
My 9yr old struggles with word problems to. He’s good in performing the calculations but struggles with tracking and comprehension of word problems. I look forward to giving your tips a try.
Thank you for sharing!!
-
Really its fantastic strategy. Great ideas!
-
Thank you for sharing this great resource. Teaching math word problems to students with disabilities is never easy. I have to come up with a variety of different ways to teach my students on how to make word problem with connections to the real world.
-
First of all ,thanks for sharing this article. you explained it very well and my children learn so many things from this article. i wish you will post more article just like this one