Table of Contents
- What does the key word each mean in math?
- What is the meaning of a word or phrase?
- What are all the math words?
- What is a math word that starts with R?
- What is a number that starts with R?
- What is a math word that starts with S?
- What does V mean in math?
- What is S in calculus?
- What does 12 mean in math?
- What does 5 mean in the Bible?
- What does 444 symbolize in the Bible?
- What does the Bible say about number 444?
- Why do I keep seeing 444 and 222?
A mathematical phrase is a verbal phrase that contains words and/or numbers that can be translated into a mathematical expression, where a…
What does the key word each mean in math?
Division-quotient, dividend, divide, divided by, each, per, average, divided equally. Equal-the same, equals, the same as, equivalent, is equal to. *Remember these words when working on word problems to help set up.
What is the meaning of a word or phrase?
A phrase is a group of words that express a concept and is used as a unit within a sentence. Eight common types of phrases are: noun, verb, gerund, infinitive, appositive, participial, prepositional, and absolute.
What are all the math words?
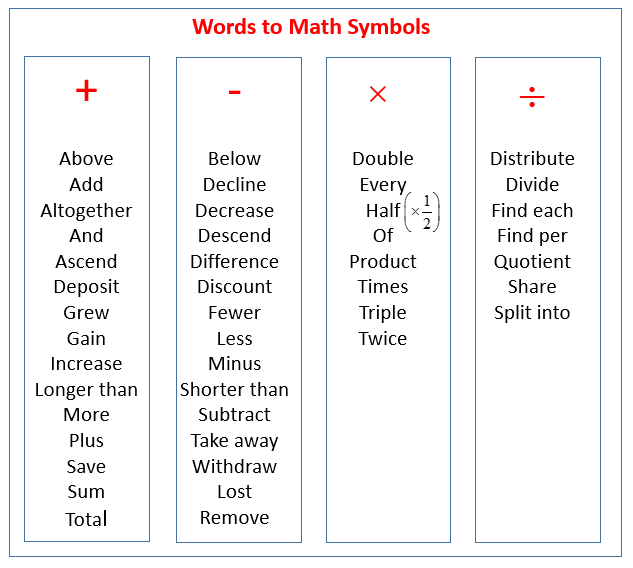
The Basic Operations
| Symbol | Words Used |
|---|---|
| + | Addition, Add, Sum, Plus, Increase, Total |
| − | Subtraction, Subtract, Minus, Less, Difference, Decrease, Take Away, Deduct |
| × | Multiplication, Multiply, Product, By, Times, Lots Of |
| ÷ | Division, Divide, Quotient, Goes Into, How Many Times |
What is a math word that starts with R?
Math Terms from Letter R
- Ray.
- Reasonableness.
- Rectangle.
- Rectangular prism.
- Rectilinear figure.
- Regroup.
- Regular polygon.
- Related facts.
What is a number that starts with R?
Zero
What is a math word that starts with S?
Math Terms from Letter S
- Same.
- Same height.
- Same length.
- Same number.
- Same weight.
- Scale.
- Scale (on a graph)
- Scalene triangle.
What does V mean in math?
Value Variable Variance
What is S in calculus?
The “s” shape is supposed to be an abbreviation for summa, much like the capital sigma, is an symbolic abbreviation for sum. Formally, is called an “integral sign”, and is used in calculus to indicate an integral. You can get a sense of how an integral is defined by looking at .
What does 12 mean in math?
In mathematics, the number 12 represents a quantity or value of 12. The whole number between 11 and 13 is 12. The number name of 12 is twelve. 12 is 2 more than 10.
What does 5 mean in the Bible?
The Biblical and the Prophetic Meaning of Number 5. According to the Bible, there are 5 big mysteries in this world, which are represented as the Father, the Son, the Holy Spirit, the Creation and the Redemption. Number 5 is usually considered to be a symbol of goodness and grace of God.
What does 444 symbolize in the Bible?
444 Meaning in the Bible According to the Bible, seeing 444 is symbolic of change, truth, and personal character. If you have been seeing 444, your guardian angel is alerting you to significant changes that are happening or soon to happen in your life and relationships.
What does the Bible say about number 444?
According to the Bible, number 444 is also associated with the ministry of Christ. People who have used the Hebrew Lexicon of the Old Testament have found that number 444 has the meaning of becoming corrupt. This number means that the sin will enter a family and it will make all of them corrupt.
Why do I keep seeing 444 and 222?
The Meaning Of 111, 222, 333, 444, 555. For example, on a number on a piece of paper, on a book cover, on a billboard, as part of an address or zip code, in your phone and so on. These repeating numbers are a reminder that something very magical and Divine is happening in your life!
A mathematical phrase is a set of words or a combination of words and numbers that can be written as a mathematical expression. An expression is a mathematical phrase that combines numbers and/or variables using mathematical operations. Expressions represent a value. Examples include variables and/or numerals appearing alone or in combination with operators.
Mathematical expressions or phrases may contain variables. Variables are symbols used to represent numbers. Values of the number can change depending on other numbers and variables in the expression. Expressions may be numerical or algebraic. Numerical expressions contain only numbers. An example of such an expression is 9 + 8, and is represented by a single number, 17. Algebraic expressions consist of numbers and variables. An example of an algebraic expression is 9 + x.
When working with math expressions, it is sometimes necessary to simplify the expression. This involves combining similar terms and removing parenthesis by using the distributive property. There are four basic steps involved when solving mathematical problems involving expressions. To do this, group terms carrying the same variable in the math expression, and then simplify the variable by doing the mathematical operations in brackets. Perform multiplication and division operations, starting from left to right. Finally, perform the addition and subtraction operations starting from left to right.
MORE FROM REFERENCE.COM
An expression is a term in mathematics that describes a group of variables, numbers and operators. Operators include division, multiplication, addition and subtraction. Variables in expression are usually denoted as x and y, but it can be and other symbol.
The expressions can be written as verbal phrase or algebraic expression. Here are some examples of algebraic expressions:
1. $ x + 3$
2. $frac{y}{4}$
3. $ 21 − x$
4. $ 8 – 2$
This algebraic expressions can be also written in verbal phrase:
1. A number x increased by 3.
2. A fourth of a number y.
3. 21 decreased by a number x.
4. 8 decreased by 2.
Note that an expression doesn’t need to include a variable to be an expression. Expressions are used to define equations. Two expressions that are equal represent an equation. Try to solve some examples.
Verbal phrases in algebraic expressions worksheets
Verbal expressions — sum (146.5 KiB, 6,639 hits)
Verbal expressions — difference (155.5 KiB, 3,273 hits)
Verbal expressions — product (145.3 KiB, 2,947 hits)
Verbal expressions — quotient (159.0 KiB, 3,566 hits)
Verbal expressions — square and cube (96.3 KiB, 3,342 hits)
Verbal expressions — equations (116.1 KiB, 3,256 hits)
Algebraic expressions — sum (161.8 KiB, 2,048 hits)
Algebraic expressions — difference (175.9 KiB, 1,753 hits)
Algebraic expressions — product (160.1 KiB, 1,916 hits)
Algebraic expressions — quotient (182.9 KiB, 2,698 hits)
Algebraic expressions — square and cube (151.5 KiB, 2,256 hits)
Related Pages
Writing Expressions (Lesson 16)
Writing Expressions (Lesson 17)
Algebraic Expressions
The following table gives some common words or phrases that are usually imply one of the four operations:
add, subtract, multiply, divide. However, depending on the word problem, there are exceptions.
Scroll down the page for more examples and explanations.
Phrase To Algebraic Expression
To write an expression, we often have to interpret a written phrase.
For example, the phrase “6 added to some number” can be written as the expression
x + 6, where the variable x represents the unknown number.
Some examples of common phrases and corresponding expressions that involve
addition are:
| Phrase | Expression |
| 4 more than some number | x + 4 |
| a number increased by 10 | y + 10 |
| 8 plus some number | t + 8 |
| the sum of a number and 12 | w + 12 |
Some examples of common phrases and corresponding expressions that involve
subtraction are:
| Phrase | Expression |
| 4 less than some number | x – 4 |
| a number decreased by 10 | y – 10 |
| 8 minus some number | 8 – t |
| the difference between a number and 12 | w – 12 |
Some examples of common phrases and corresponding expressions that involve
multiplication are:
| Phrase | Expression |
| 4 times some number | 4x |
| twice a number | 2y |
| one-third of some number | |
| the product of a number and 12 | 12w |
Some examples of common phrases and corresponding expressions that involve
division are:
Some examples of common phrases and corresponding expressions that involve
two operations are:
| Phrase | Expression |
| 6 more than 5 times a number | 5x + 6 |
| 4 times the sum of a number and 7 | 4(y + 7) |
| 5 less than the product of 3 and a number | 3w – 5 |
| twice the difference between a number and 9 | 2(z – 9) |
How Do You Write Mathematical Expressions From Word Problems?
There are so many words that you come across when you’re working on algebra problems,
and these words are really code for very specific mathematical symbols.
- Show Video Lesson
How To Write Algebraic Expressions For Word Phrases, By Analyzing The Language Used?
An algebraic expression is a mathematical phrase that contains a combination of numbers,
variables and operational symbols.
A variable is a letter that can represent one or more numbers.
How to write expressions with variables?
Examples:
Write the algebraic expressions to represent the statements.
a) The sum of -7 and the quantity 8 times x
b) Take the quantity -3 times x and then add 1.
c) -6 plus the product of -1 and x.
- Show Video Lesson
How to write algebraic expressions with parentheses?
Examples:
-
First consider the expression for
-5 plus the quantity of 4 times x
Now take the product of -8 and that expression and then add 6. -
First consider the expression for
the sum of 7 and the product of -2 and x
What expression would be:
4 plus the quantity of 2 times that expression.
- Show Video Lesson
How to Write Equations from Word Problems?
This video teaches how to dissect a word problem in order to define a variable and write an equation.
Examples:
-
Half of a number is 16. Write an equation to represent the situation. Define your variable and solve.
-
Mrs. Gaddie has two dogs. Her friend Anna-Marie has three less than twice as many as Mtr. Gaddie.
How many dogs does Anna-Marie have? -
A recycling plant recycles 2 tons of cans yesterday. This is a third of their usual amount.
How much does the plant usually recycle?
- Show Video Lesson
How to Write Algebraic Expressions for Situations?
Example:
Translate the following phrases into algebraic or numeric expressions.
a) 173 less than a number ‘b’
b) Quotient of 173 and ‘b’
c) ‘b’ times 173
d) 173 more than ‘b’
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Algebraic expressions are the phrases used in algebra to combine one or more variables (represented by letters), constants, and the operational (+ — x / ) symbols. Algebraic expressions, however, don’t have an equals (=) sign.
When working in algebra, you will need to change words and phrases into some form of mathematical language. For instance, think about the word sum. What comes to your mind? Usually, when we hear the word sum, we think of addition or the total of adding numbers.
When you have gone grocery shopping, you get a receipt with the sum of your grocery bill. The prices have been added together to give you the sum. In algebra, when you hear «the sum of 35 and n» we know it refers to addition and we think 35 + n. Let’s try a few phrases and turn them into algebraic expressions for addition.
Testing Knowledge of Mathematical Phrasing for Addition
Use the following questions and answers to help your student learn the correct way to formulate Algebraic expressions based on mathematical phrasing:
- Question: Write seven plus n as an Algebraic expression.
- Answer: 7 + n
- Question: What Algebraic expression is used to mean «add seven and n.»
- Answer: 7 + n
- Question: What expression is used to mean «a number increased by eight.»
- Answer: n + 8 or 8 + n
- Question: Write an expression for «the sum of a number and 22.»
- Answer: n + 22 or 22 + n
As you can tell, all of the questions above deal with Algebraic expressions that deal with the addition of numbers — remember to think «addition» when you hear or read the words add, plus, increase or sum, as the resulting Algebraic expression will require the addition sign (+).
Understanding Algebraic Expressions with Subtraction
Unlike with addition expressions, when we hear words that refer to subtraction, the order of numbers cannot be changed. Remember 4+7 and 7+4 will result in the same answer but 4-7 and 7-4 in subtraction do not have the same results. Let’s try a few phrases and turn them into algebraic expressions for subtraction:
- Question: Write seven less n as an Algebraic expression.
- Answer: 7 — n
- Question: What expression can be used to represent «eight minus n?»
- Answer: 8 — n
- Question: Write «a number decreased by 11» as an Algebraic expression.
- Answer: n — 11 (You can’t change the order.)
- Question: How can you express the expression «two times the difference between n and five?»
- Answer: 2 (n-5)
Remember to think subtraction when you hear or read the following: minus, less, decrease, diminished by or difference. Subtraction tends to cause students greater difficulty than addition, so it’s important to be sure to refer these terms of subtraction to ensure students understand.
Other Forms of Algebraic Expressions
Multiplication, division, exponentials, and parentheticals are all part of the ways in which Algebraic expressions function, all of which follow an order of operations when presented together. This order then defines the manner in which students solve the equation to get variables to one side of the equals sign and only real numbers on the other side.
Like with addition and subtraction, each of these other forms of value manipulation come with their own terms that help identify which type of operation their Algebraic expression is performing — words like times and multiplied by trigger multiplication while words like over, divided by, and split into equal groups denote division expressions.
Once students learn these four basic forms of Algebraic expressions, they can then begin to form expressions that contain exponentials (a number multiplied by itself a designated number of times) and parentheticals (Algebraic phrases which must be solved before performing the next function in the phrase). An example of an exponential expression with parentheticals would be 2x2 + 2(x-2).
Writing the phrase as an algebraic expression
Example
Write the phrase as an algebraic expression.
“Four less than twice ???x???”
The phrase “twice ???x???” means “???2??? times ???x???” which we know means to multiply, and so we can write it as ???2x???. Now we have
“Four less than ???2x???”
Less means subtraction, so we’ll subtract ???4??? from ???2x???.
???2x-4???
It may be tempting to write the ???4??? first and subtract ???2x???. Let’s use numbers to help us visualize this. When we say ???4??? less than ???10??? you know that you’d have to subtract ???4??? from ???10???, written out as ???10-4???. So ???4??? less than ???2x??? will be ???2x-4???.
Example
Find the value of the expression.
???frac{1}{4}??? of ???120???
In math, the word “of” (immediately after a proper or improper fraction) tells us to multiply. Therefore, the mathematical expression of the phrase will be
???frac{1}{4} cdot 120???
Because we were asked to actually find the value of the expression, we’ll perform the multiplication to get the simplified value.
???30???
Not only can we translate phrases into expressions, but we can write equations from some phrases as well.
For instance, suppose you wanted to use algebra to solve the following word problem:
John’s age is four less than twice Mary’s age. If Mary is ???18???, how old is John?
The first step in solving a word problem like this is to define the variables. What that means is to state the particular quantity that each variable stands for.
In this problem, we have two quantities: Mary’s age and John’s age. So we’ll define the variables by saying “Let ???x??? be Mary’s age, and let ???y??? be John’s age.” (We could use any letters of the alphabet for the variables, but people often use ???x??? for one of the variables, and if there are one or two additional variables, they tend to use ???y??? and ???z???, in that order.)
The next step in solving a word problem is to “translate” each word or phrase into mathematical symbols. Here, “John’s age” is translated as “???2x-4???.”
How about the word “is” (in “John’s age is four less than twice Mary’s age”)? Well, “is” is translated as an equals sign. To see this, it may help to think of the word “is” as having the same meaning (in math) as “is equal to.”
Combining all of these, we get the equation
???y=2x-4???
The third step in solving a word problem is to use the given data and solve the equation. Here, we’re given Mary’s age as ???18???, so we substitute ???18??? for ???x??? and then solve for ???y???.
???y=2(18)-4???
???y=36-4???
???y=32???
The final step is to answer the question that was asked. Here, we’re asked for John’s age. Since we defined ???y??? as John’s age, the answer is ???32???.
Suppose we’d been given the following word problem instead:
Currently, John’s age is four less than twice Mary’s age. If Mary is now ???18???, how old will John be seven years from now?
To solve this problem, it would be convenient to define ???x??? as Mary’s age now, and ???y??? as John’s age now, because we’re given a relationship between Mary’s age (now) and John’s age (now). Then in the last step (answering the question that was asked), we’d have to evaluate ???y+7??? (to get John’s age seven years from now), and our answer would be ???32+7=39???.