What is a word name for numbers - Word и Excel - помощь в работе с программами

List of Numbers in Words (1 to 100)

1	One	Forty-one
2	Two	Forty-two
3	Three	Forty-three
4	Four	Forty-four
5	Five	Forty-five

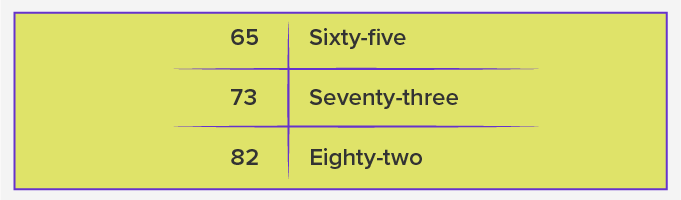
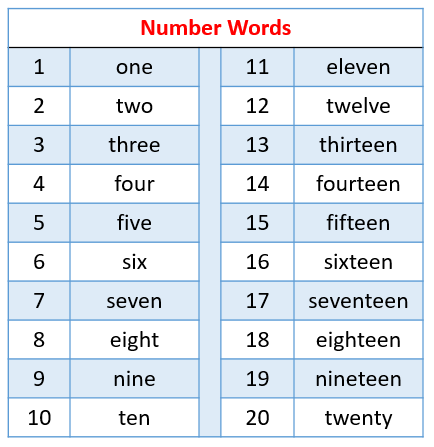
What are number names in maths?

Number Name 1 to 50 in English

1 = One	11 = Eleven	21 = Twenty-one
7 = Seven	17 = Seventeen	27 = Twenty-seven
8 = Eight	18 = Eighteen	28 = Twenty-eight
9 = Nine	19 = Nineteen	29 = Twenty-nine
10 = Ten	20 = Twenty	30 = Thirty

What is an example of number names?

Number Names

128 = 100 + 20 + 8. = One Hundred + Twenty + Eight. So the number-name of 128 is one hundred twenty eight.
412 = 400 + 10 + 2. = Four Hundred + Ten + two. So the number-name of 128 is Four hundred twelve .
685 = 600 + 80 + 5. = Six Hundred + Eighty + Five. So the number-name of 128 is Six hundred eighty five .

How do you write 17 in words?

17 in words is written as Seventeen.

How do you name a number?

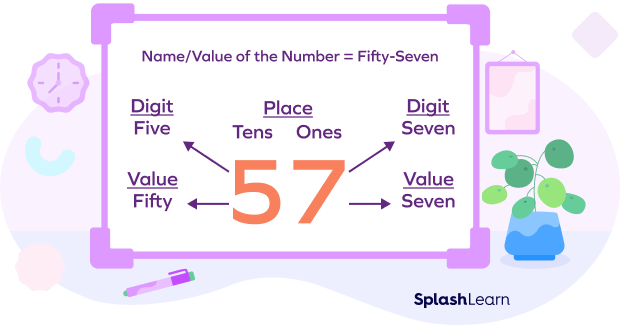
The number is named on the basis of the place values of the concerned digits. The name is taken according to place values of the digits, starting from highest place value to lowest place value. As: (i) 56 = 50 + 6 = fifty six. (ii) 93 is named as ninety three (place value of 9 = 90, of 3 is 3).

How do I teach my child his name number?

Ask the child to start with numbers, it’s name and then the quantity it represents. Number Names Word Puzzles – These are word puzzles just like the classic game of scrabble. The puzzle pieces are to be sorted into the correct Number Names, i.e. the correct spelling for each Number.

How do you number a name?

The name is taken according to place values of the digits, starting from highest place value to lowest place value. As: (i) 56 = 50 + 6 = fifty six. (ii) 93 is named as ninety three (place value of 9 = 90, of 3 is 3). We can expand the number and then it is named as.

How do you write names in numbers?

101: one hundred and one (NOT: one hundred one)
102: one hundred and two (NOT: one hundred two)
175: one hundred and seventy-five (NOT: one hundred seventy-five)
200: two hundred.
300: three hundred.
512: five hundred and twelve (NOT: five hundred twelve)

Источник

Number words are the alphabetical form of numbers. As the name suggests, these are numbers written in words. Word form is writing the numerical/number as you would say it in words.

‘Number words’ or ‘number names’ are simply the names assigned to numbers so that we can identify each number uniquely. When we talk about “math,” what is the first thing that comes to your mind? Numbers! Are you aware that numbers also have names called number names? Yes, like everything else in the world, numbers have names. Let us know the number name definition and the rules to write them.

Related Games

Number Words: Definition

A number word or number name is a way to express numbers in their word form. We can express numbers using their number name form. The spelling of numbers in English is something we should focus on while writing the numbers in word form.

For example, we can write 1 as “one.” So, the number name for 1 is “one.”

Similarly, we can express the number 2 as “two” in its word form.

The number 3 as “three” in its word form, and so on.

For example:

With the help of the number words from one to ten, we can make number words of higher value.

It is important to learn every number word from One to Twenty to learn other number words. Also, the number words from eleven to twenty are very different from other number words.

After learning the number words up to twenty, it is important to learn the number words such as thirty, forty, fifty, sixty until hundred.

Once you know these number words, it is easy to make number words for higher value numbers.

For example:

The above two number words are made from learning the basic number words from one to ten, and the number words for tens value, like sixty, seventy and eighty.

As the numbers increase in value and become larger with three, four, five, six, seven and more digits, the names start to change.

Related Worksheets

Rules to Write Numbers in Word Form

While writing numbers in their number words form, we have to follow certain rules. These rules are as follows:

Rule 1

Always consider place values while writing numbers in the word form.

For example, the digit 2 at the ones place is read as 2. The same digit at the tens place has the value “twenty.” So, 22 can be written as “twenty-two.”

Rule 2

To write numbers between 1–20, refer to the number names chart.

To express numbers beyond 20 in words, you must follow a certain pattern. As per this pattern, the multiples of 10 up to 90 are written as thirty, forty, fifty, sixty, seventy, eighty, and ninety.

Rule 3

For writing multiples of 100 in word form, you can write the digit in the word form and add the word hundred after it.

For example, you can express 200 as two hundred in the word form, 600 as six hundred, and so on.

You can follow the same rule while writing multiples of 1000 in word form. The only difference is that you have to add the word thousand instead of hundred. For example, you can write 3000 as three thousand in the word form.

Rule 4

For writing two-digit or three-digit numbers in word form, you have to write them in their expanded form. Ensure that you take the position of 0 in account.

For example, you can write 107 (expanded into $100 + 0 + 7$) as one hundred seven.

The word form of 125 (expanded into $100 + 20 + 5$) is one hundred twenty-five.

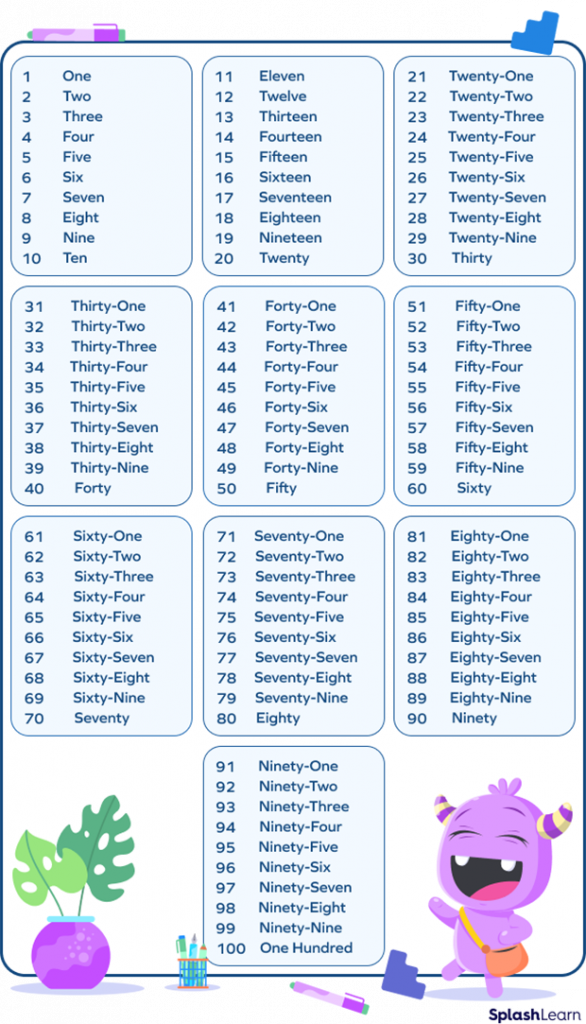
Number Words or Number Names from 1 to 100

Here’s a table containing numbers 1 to 100 and their corresponding word forms:

The Number Words for Higher Values

It becomes easy to convert numbers to number words and number words to number if we know the number words.

For example:

Write the given numbers in words.

Write the given numbers in numerals.

Number Names as per the International Number System

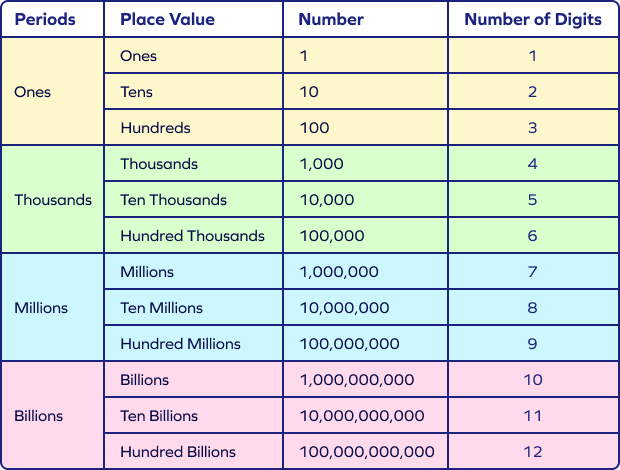
In the international system, the numbers are organized into periods and groups. The periods are categorized as ones, thousands, millions, etc. Each period is grouped into three place values. While writing numbers in this system, we insert a comma or separator after every three digits from the right.

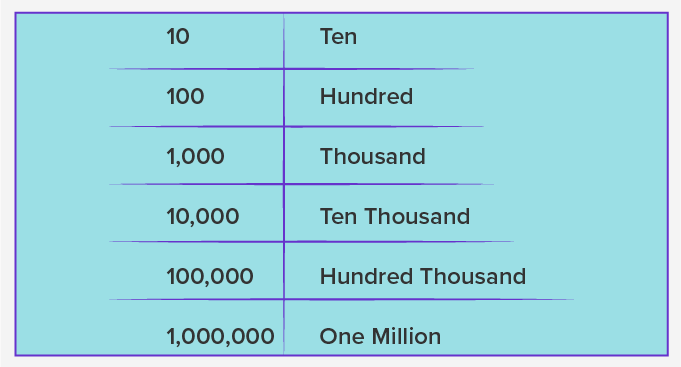
The place value names in the international system are as follows:

Ones
Tens
Hundreds
Thousands
Ten Thousands
Hundred Thousands
Millions
Ten Millions
Hundred Millions
Billions
Ten Billions
Hundred Billions
Trillions, and so on

Example: Suppose you have to write the word form of the number 6,342,715 in the international system.

6,342,715 is Six Million Three Hundred Forty-two Thousand Seven Hundred Fifteen.

Place Value Chart for International System

Here is the place value chart for the international system:

From this place value chart, we understand:

1 million $= 1000$ thousand
1 billion $= 1000$ million

Tips and Tricks to Learn Numbers Names

Here are a few tips to help you learn and write numbers in their word forms:

Write down 1 to 20 as numbers and their spellings.

Write down the multiples of 10 up to 90 and their spellings.

For example, 10: Ten, 20: Twenty, 30: Thirty, and so on.

Write down the multiples of 100 and their spellings.

For example, 100: Three hundred, 200: Two hundred, and so on.

For two-digit numbers beyond 20, expand them and write them in words in their expanded form. For example, you can expand 32 as $30 + 2$ and write “thirty-two.”

Follow the same technique for large numbers.

For example, you can expand 471 as “$400 + 70 + 1$” and write “four hundred seventy-one” or “four hundred and seventy-one.”

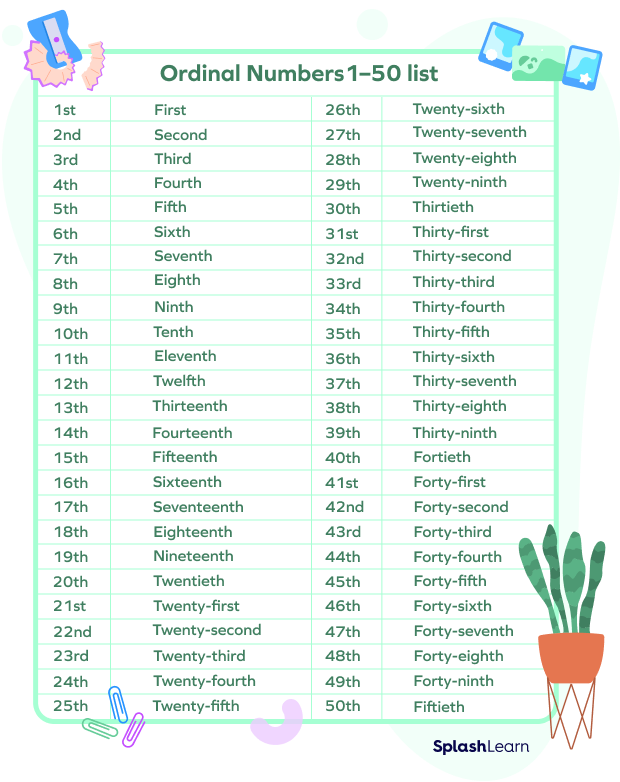
Number Names as per the Ordinal System

An ordinal number expresses the rank or position of something. That is why they are also known as ranking or positioning numbers.

Ordinal numbers are written as 1^st, 2^nd, 3^rd, 4^th, and so on.

Here is a chart of the first 50 ordinal numbers and their number names:

Fun Facts

When writing ordinal numbers in their word form, we use the suffix -th for the numbers 11, 12, and 13; but for all other numbers ending with 1, 2, or 3, we use the suffixes -st, -nd, and -rd, respectively. For example, we express 51 as fifty-first, 52 as fifty-second, and 53 as fifty-third.

The word form of the number 40 is forty and not fourty.

When writing numbers between 21 and 99, we use a hyphen $(-)$ in between.
To write number words, we can write the word form of the numbers as we say them.

Conclusion

Number names offer an easy way to identify and learn numbers. They can help us to understand how the number system functions. Knowing to read and write numbers in words can enable us to identify how numbers relate to one another.

Solved Examples

Write the number 7575 in words.

Solution:

We can expand 7575 as $7000 + 500 + 70 + 5$.

7575 in word form is “seven thousand five hundred seventy-five.”

What comes after the given number name: twenty-nine?

Solution:

Twenty-nine $= 29$

The number after 29 is $29 + 1 = 30$

30 in the word form is Thirty.

So, thirty comes after twenty-nine.

Count the emojis in the given image and write the number in words.

Solution:

$5 + 4 + 3 + 2 + 1 = 15$

The given image has fifteen or 15 smileys.

Express 2022 in words and also in the ordinal system.

Solution:

$2022 = 2000 + 0 + 20 + 2$

In words, we write it as “two thousand twenty-two.”

Also, 2022 is written as “two thousand twenty-second” in the ordinal system.

Write the word form of 404.

Solution:

$404 = 400 + 0 + 4$

404 is four hundred four.

Practice Problmes

Fifty-seven

Five & seven

Seventy five

None of the above

Correct answer is: Fifty-seven
We expand 57 as $50 + 7$. So, it would be written as “fifty-seven.”

Sixty-tenth

Seventieth

Seventy

None of the above

Correct answer is: Seventieth
As per the ordinal system, “seventieth” comes after “sixty-ninth.”

4040 is four thousand forty

4004 is four thousand four

4400 is four thousand four hundred

4440 is four thousand forty-four

Correct answer is: 4440 is four thousand forty-four
4440 is four thousand four hundred forty.

$gt$

$=$

$lt$

None of the above

Correct answer is: $lt$
Four hundred sixty-three is 463. Thus, $436 lt 463$.

Fifth and eighth

Fifth and seventh

Fourth and seventh

Sixth and eighth

Correct answer is: Fifth and seventh
By counting the letters in the word “PLACEMENT,” we can see that the letter E appears in the fifth and seventh positions.

Frequently Asked Questions

Do we have to use commas when writing a number in its word form?

No, we don’t use commas when writing a number in its word form.

Does the word zero appear in any number name?

No, we don’t use the word “zero” when writing a number in words.

Can we write decimal numbers in words?

Yes, we can write decimal numbers in words. For example, we can write 42.35 as forty-two point three five.

Are there any real-life applications of writing numbers in words?

Yes, there are real-life applications of writing numbers in words. For example, it is mandatory to write the amount in both figures and words in a bank cheque.

Why is place value important for writing numbers in words?

The place value helps to determine the place of a digit in a number. This is important for reading a number and writing it in words.

Word Form
Natural Number
Number Words

Источник

In mathematics, Numbers are usually used for counting, measuring, and checking quantities. Just like everything in the world numbers also have their respective words. Here, on this page, you will find the complete information about the Names of the Numbers. Students will already know some number names like from 1 – 20 but, here you can learn from 1 to n-digit number names. In preschool children are taught by number names which are fundamentals of maths.

These Names of the Numbers are helpful to students not only in primary but also in high school too. Many of the problems are related to these Number Names. Teaching the Names of the Numerics will help the students to write them correctly. All students should be known by Number Names of counting numbers. Names of Numbers are represented in alphabetical form. Each Number Name refers to a specific word. Furthermore, check the below sections to know in detail about the Names of the Numbers like Objectives of teaching Number names, etc.

Also, Read: Formation of Numbers

What are Number Names? | Numbers in Words

A number is a series of symbols that have a special significance in themselves. In maths, a Number name is a process of describing numbers in words.

How to Write Number Names in Words?

To write Number Names in words you should know the place value of a digit. Based on the position of numbers we expand the numbers first and write their names of the number and combine those Number Names.

This is the easiest way to write down the Name of the Numbers. With the help of given examples, you can remind them how to expand and spell the words promptly. Let’s dive into the below sections for more details like importance, number names 1-50, etc.

Importance of Number Names in Words

Numbers play a main role in mathematics similarly, Number Names are fundamental for students to know.
These Names help the students when they are ready to solve any problem in classes.
Also, It is the basic rule in maths.
In our real-life situations, we can relate numbers to quantities.

Number Names 1 – 50

Now, let us practice the numbers from 1 – 20 with their Number Names and memorize them easily. Number Name is the method of representing the numbers in words. Have a glance at the below table:

Number Names 1 to 20

Now, learn the Number Names for 30, 40, 50, 60, 70, 80, 90, and 100.

30 – Thirty 70 – Seventy
40 – Forty 80 – Eighty
50 – Fifty 90 – Ninety
60 – Sixty 100 – One Hundred

Number Names 21 to 30

21	22	23	24	25	26	27	28	29	30
Twenty-one	Twenty-Two	Twenty Three	Twenty Four	Twenty Five	Twenty Six	Twenty Seven	Twenty Eight	Twenty Nine	Thirty

31	32	33	34	35	36	37	38	39	40
Thirty-One	Thirty-Two	Thirty-Three	Thirty-Four	Thirty-Five	Thirty-Six	Thirty-Seven	Thirty-Eight	Thirty-Nine	Forty

41	42	43	44	45	46	47	48	49	50
Forty-One	Forty-Two	Forty-Three	Forty-Four	Forty-Five	Forty-Six	Forty-Seven	Forty-Eight	Forty-Nine	Fifty

Examples of Names of Numbers

Example 1:

Write 75 in words?

Solution:

Now, write the place values i.e., 7 = seventy and, 5 = five. Let us expand the numbers
75 = 70 + 5 = seventy-five.

Example 2:

Write 479 in words.

Solution:

Expand the numbers, 479 = 400 + 70 + 9. The Number Name is Four hundred seventy-nine.

Example 3:
Write 862 in words.

Solution:

First, write the given number in expanded form and write the Number Names and then merge that name.
862 = 800 + 60 + 2 i.e., eight hundred + sixty + two.
Now, we’ll merge the Number names. The Name of the Number is Eight Hundred Sixty-Two.

Example 4:

Write 7569 in words?

Solution:
Given number is 7569
First expand the given number into place value
Ie., 7569 = 7000 + 500 + 60 + 9
Now, write in words for each place value
Ie., Seventy thousand + five hundred + sixty + nine

Hence, The Number Name for 7569 is Seventy Thousand Five Hundred Sixty-Nine.

FAQs on Number Names

1. Why is it important to know Number Names for Numbers?

It helps the children how numbers are connected to each other. They understand the Number words and use them in different circumstances.

2. What do Names of the Numbers mean?

Numbers with words are the alphabetical form of numbers in mathematics. With the help of number words, we could make the higher value of the number in words easily.

3. How do you get the Number Name of the highest number?

You should expand the given highest number with the place values and write the names for the respective place values then combine those expanded Number Names. For instance, if the number is 2336. Now, expand the number i.e., 2000 + 300 + 30 + 6 (in words two thousand + three hundred + thirty + six), then merge the number words i.e., 2336 = two thousand three hundred thirty-six.

Источник

Numbers in words means expressing the given numerals in words or spellings. For example, the number 1000 in words is written as one thousand. We can represent all natural numbers in words on the basis of the place value of their digits, such as ones, tens, hundreds, thousands, and so on.

1.	What are Number Names?
2.	Number Names 1 to 100
3.	Numbers in Words in International System
4.	Rules to Write Number Names
5.	Tips to Learn Numbers in Words
6.	FAQs on Numbers in Words

What are Number Names?

When numbers are expressed in words, we call them number names. Number names help us to learn and identify numbers easily.

For example, 1 can be written and read in words as one, therefore, the number name for 1 is one.
2 is written and read in words as two.
3 is written in words as three.
4 is written and read in words as four.
5 is written and read in words as five.
6 is written and read in words as six.
7 is written and read in words as seven.
8 is written and read in words as eight.
9 is written and read in words as nine.
10 is written and read in words as ten.

With the help of number names from one to ten, we can write and read higher-value numbers in words.

Numbers in Words in English

To write numbers in words in English we use the place values (ones, tens, hundreds, thousands, lakhs, crores, and so on…) of each digit in the number. With the help of the Indian place value chart, it is easy to find the place value of each digit based on its position and the number can be written in words. Let us understand this with the help of an example.

Example: Write the given number in words: 23456789 according to the Indian place value chart and according to the International place value chart.

Solution:

According to the Indian place value system, 2,34,56,789 is written and read in words as two crores, thirty-four lakh, fifty-six thousand, seven hundred eighty-nine.

According to the International place value chart, 23,456,789 is written and read in words as twenty-three million, four hundred fifty-six thousand, seven hundred eighty-nine.

Number Names 1 to 100

Number names 1 to 100 can be read and understood using the pattern explained below. Observe the pattern to learn numbers in words from 1 to 100 along with their spellings. First let us start with number names from 1 to 20, followed by number names from 21 to 100.

Number Names 1 to 20

Given below is a chart showing number names from 1 to 20.

1 to 20 Spelling

‘1 to 20 spellings’ means that we need to write the number names from 1 to 20. So, whether we need to write ‘1 to 20 spellings’ or we are asked for ’11 to 20 spellings’, it means that we need to write their number names. The following chart shows the number names from 1 to 20.

Number Names 21 to 100

Observe the chart given below with number names from number 21 to 100 and learn the counting in words.

Numbers in Words in International System

The international system has different place value names for a certain position of a digit in a number. For example, the number 1,000,000 is read as 1 million in words in the international system, whereas, it is read as 10 lakhs in the Indian place value system. In the international system, different periods are formed to read and write large numbers easily. As per the International numeration system, the comma is placed in a number after the hundreds place and then placed after every three digits. The place values in the international system are Ones, Tens, Hundreds, Thousands, Ten Thousand, Hundred Thousands, Millions, and so on.

1 million = 1000 thousands
1 billion = 1000 millions

For example, the number 7,456,123 is written or read in words as seven million four hundred fifty-six thousand one hundred twenty-three in the international number system.

Rules to Write Number Names

There are certain rules that can be followed while writing the numbers in words. These rules are listed below in detail.

Rule 1: Understanding the place value system: The position of a number plays a very crucial role in writing a number in words. Let us understand how to differentiate between the place values based on the position of 1:

1 = ones place
10 = tens place
100 = hundreds place
1000 = thousands place

Rule 2: For numbers between 1-20 we can directly refer to the number names 1 to 20 chart to write their spellings. For example, the number name of 7 is seven, the number name of 15 is fifteen, and so on. After number 20 a generic series or pattern is followed.

Rule 3: The number names for multiples of 100 can be simply written by adding the word ‘hundred’ after the initial word. For example, the number name of 400 is four hundred, the number name for 500 is five hundred, and so on.

Rule 4: To write the number names of more than 2 digit numbers, we write the number in its expanded form. For example, 112 = 100 + 12, and 112 in words is written as one hundred twelve. The expanded form of 153 = 100 + 50 + 3 and 153 in words is written as One hundred fifty-three.

Tips to Learn Number Names

The following tips can be kept in mind to write numbers in words:

The number names from 1 to 10 can be written directly because each number name is unique, as 1- one, 2-two, 3-three, and so on.
The number names from 11 to 20 can also be written directly because each number name is unique, as 11 — eleven, 12-twelve, and so on.
The numbers and spellings of the multiples of 10 can be written as 20- twenty, 30- thirty, 40- forty, 50- fifty, 60- sixty, 70- seventy, 80- eighty, 90- ninety.
Now, after 20, starting from 21, we follow a different rule. The word form of 20 and 1 can be combined to write 21 as twenty-one, 22 as twenty-two, and so on. Similarly, we can write number names for 31, 41, 51, and so on.
For large numbers write the number and their word form, like 100 — hundred, 1000 — thousand, and so on.
The number 101 in words is written as one hundred one and 1001 is written as one thousand one and so on.

Observe the pattern which will help to write and read higher value numbers in words.

100 — Hundred
200 — Two-Hundred
300 — Three-Hundred
400 — Four-Hundred
500 — Five-Hundred
600 — Six-Hundred
700 — Seven-Hundred
800 — Eight-Hundred
900 — Nine-Hundred
1000 — One-Thousand or Thousand

Similarly,

2000 — Two thousand
5000 — Five thousand
10,000 — Ten Thousand
15,000 — Fifteen Thousand
16,000 — Sixteen thousand
20,000 — Twenty Thousand
25,000 — Twenty-Five Thousand
30,000 — Thirty Thousand
35,000 — Thirty-Five Thousand
40, 000 — Forty Thousand
45,000 — Forty-Five Thousand
100,000 — One hundred thousand (One Lakh)
200, 000 — Two hundred thousand (Two Lakhs)
300, 000 — Three hundred thousand (Three Lakhs)
400, 000 — Four hundred thousand (Four Lakhs)
500, 000 — Five hundred thousand (Five Lakhs)

Important Notes on Number Names

Read the number from left to right.
The number 40 in words is written as forty, not fourty.
To write a number in words, first read the number and write the number name as you say it.

☛Related Articles

Check out these interesting articles to know more about Number Names and their related topics.

Number names 1 to 10
Number names 1 to 30
Number names 1 to 40
Number names 41 to 50

FAQs on Numbers in Words

What are Number Names in Math?

Number names in math are the infinite cardinal numbers starting from 1 to n written in their word form. To write number names we use the Indian place value system and the International place value system. For example, 798 is written as ‘seven hundred ninety-eight’.

How to Write Numbers in Words in International System?

In the International system of numeration, we use the place values as ones, tens, hundreds, thousands, ten thousand, hundred thousand, one million, ten million, hundred million, and so on, to write number names for large numbers. For example, 567,898 is written as ‘five hundred sixty-seven thousand eight hundred ninety-eight’.

☛ Check:

Numbers in Words 51 to 60
Numbers in Words 51 to 100
Numbers in Words 91 to 100

How to Write 1100 in Words?

The number 1100 in words is written as One thousand one hundred.

☛ Number Names 1 to 50

How to Write Decimal Number Names?

Decimal number names can be written using the following steps. Let us write the number name for 25.578

First, write the number name for the whole number part. Here, it will be Twenty-five
Then, write the word ‘and’ for the decimal point. Here, it will be Twenty-five and.
Now, write the number name for the decimal part, that is, the number to the right side of the decimal point. Here, it will be rewritten as twenty-five and five hundred seventy-eight thousandths. It should be noted that the decimal part is written using the decimal place value chart in which we use the place values like hundredths, thousandths and so on.

How to Write Number Names in International System?

In the international place-value system, we insert commas after every three digits from the right of the number. So while writing numbers in words we can check the place values and write numbers in words. For example, 37,824,500 is written in words as thirty-seven million eight hundred twenty-four thousand five hundred.

How to Write Numbers in Words?

To write a number in words, start from the left-most digit and write it according to its place value For example, 133 is read or written in words as one hundred thirty-three. By knowing the word form of numbers from 1 to 10 we can read and write the numbers easily. The word form of the first ten natural numbers is 1-one, 2-two, 3-three, 4-four, 5-five, 6-six, 7-seven, 8-eight, 9-nine, 10-ten.

☛ Also Read:

Numbers in Words 100 to 200
Numbers in Words 1 to 1000

How are Numbers in Words Useful in Real Life?

Numbers in words are useful in reading large numbers. If any document contains large numbers, the numbers in words help readers to read numbers correctly and quickly. While doing cheque payments, it is compulsory to write the numbers in figures as well as in words.

The number name of 40 is forty. It should be noted that 40 is often wrongly spelled as Fourty. However, the correct spelling is forty.

When we are asked to write the spellings from 11 to 20, we need to write the number names from 11 to 20 and we write it in the following way. 11 — Eleven, 12 — Twelve, 13 — Thirteen, 14 — Fourteen, 15 — Fifteen, 16 — Sixteen, 17 — Seventeen, 18 — Eighteen, 19 — Nineteen, 20 — Twenty

Источник

This article is about number words. For the mathematical notation of numbers, see numeral system.

In linguistics, a numeral in the broadest sense is a word or phrase that describes a numerical quantity. Some theories of grammar use the word «numeral» to refer to cardinal numbers that act as a determiner that specify the quantity of a noun, for example the «two» in «two hats». Some theories of grammar do not include determiners as a part of speech and consider «two» in this example to be an adjective. Some theories consider «numeral» to be a synonym for «number» and assign all numbers (including ordinal numbers like the compound word «seventy-fifth») to a part of speech called «numerals».^[1]^[2] Numerals in the broad sense can also be analyzed as a noun («three is a small number»), as a pronoun («the two went to town»), or for a small number of words as an adverb («I rode the slide twice»).

Numerals can express relationships like quantity (cardinal numbers), sequence (ordinal numbers), frequency (once, twice), and part (fraction).^[3]

Identifying numerals[edit]

Numerals may be attributive, as in two dogs, or pronominal, as in I saw two (of them).

Many words of different parts of speech indicate number or quantity. Such words are called quantifiers. Examples are words such as every, most, least, some, etc. Numerals are distinguished from other quantifiers by the fact that they designate a specific number.^[3] Examples are words such as five, ten, fifty, one hundred, etc. They may or may not be treated as a distinct part of speech; this may vary, not only with the language, but with the choice of word. For example, «dozen» serves the function of a noun, «first» serves the function of an adjective, and «twice» serves the function of an adverb. In Old Church Slavonic, the cardinal numbers 5 to 10 were feminine nouns; when quantifying a noun, that noun was declined in the genitive plural like other nouns that followed a noun of quantity (one would say the equivalent of «five of people»). In English grammar, the classification «numeral» (viewed as a part of speech) is reserved for those words which have distinct grammatical behavior: when a numeral modifies a noun, it may replace the article: the/some dogs played in the park → twelve dogs played in the park. (Note that *dozen dogs played in the park is not grammatical, so «dozen» is not a numeral in this sense.) English numerals indicate cardinal numbers. However, not all words for cardinal numbers are necessarily numerals. For example, million is grammatically a noun, and must be preceded by an article or numeral itself.

Numerals may be simple, such as ‘eleven’, or compound, such as ‘twenty-three’.

In linguistics, however, numerals are classified according to purpose: examples are ordinal numbers (first, second, third, etc.; from ‘third’ up, these are also used for fractions), multiplicative (adverbial) numbers (once, twice, and thrice), multipliers (single, double, and triple), and distributive numbers (singly, doubly, and triply). Georgian,^[4] Latin, and Romanian (see Romanian distributive numbers) have regular distributive numbers, such as Latin singuli «one-by-one», bini «in pairs, two-by-two», terni «three each», etc. In languages other than English, there may be other kinds of number words. For example, in Slavic languages there are collective numbers (monad, pair/dyad, triad) which describe sets, such as pair or dozen in English (see Russian numerals, Polish numerals).

Some languages have a very limited set of numerals, and in some cases they arguably do not have any numerals at all, but instead use more generic quantifiers, such as ‘pair’ or ‘many’. However, by now most such languages have borrowed the numeral system or part of the numeral system of a national or colonial language, though in a few cases (such as Guarani^[5]), a numeral system has been invented internally rather than borrowed. Other languages had an indigenous system but borrowed a second set of numerals anyway. An example is Japanese, which uses either native or Chinese-derived numerals depending on what is being counted.

In many languages, such as Chinese, numerals require the use of numeral classifiers. Many sign languages, such as ASL, incorporate numerals.

Larger numerals[edit]

English has derived numerals for multiples of its base (fifty, sixty, etc.), and some languages have simplex numerals for these, or even for numbers between the multiples of its base. Balinese, for example, currently has a decimal system, with words for 10, 100, and 1000, but has additional simplex numerals for 25 (with a second word for 25 only found in a compound for 75), 35, 45, 50, 150, 175, 200 (with a second found in a compound for 1200), 400, 900, and 1600. In Hindustani, the numerals between 10 and 100 have developed to the extent that they need to be learned independently.

In many languages, numerals up to the base are a distinct part of speech, while the words for powers of the base belong to one of the other word classes. In English, these higher words are hundred 10², thousand 10³, million 10⁶, and higher powers of a thousand (short scale) or of a million (long scale—see names of large numbers). These words cannot modify a noun without being preceded by an article or numeral (*hundred dogs played in the park), and so are nouns.

In East Asia, the higher units are hundred, thousand, myriad 10⁴, and powers of myriad. In the Indian subcontinent, they are hundred, thousand, lakh 10⁵, crore 10⁷, and so on. The Mesoamerican system, still used to some extent in Mayan languages, was based on powers of 20: bak’ 400 (20²), pik 8000 (20³), kalab 160,000 (20⁴), etc.

Numerals of cardinal numbers[edit]

The cardinal numbers have numerals. In the following tables, [and] indicates that the word and is used in some dialects (such as British English), and omitted in other dialects (such as American English).

This table demonstrates the standard English construction of some cardinal numbers. (See next table for names of larger cardinals.)

Value	Name	Alternate names, and names for sets of the given size
0	Zero	aught, cipher, cypher, donut, dot, duck, goose egg, love, nada, naught, nil, none, nought, nowt, null, ought, oh, squat, zed, zilch, zip, zippo, Sunya (Sanskrit)
1	One	ace, individual, single, singleton, unary, unit, unity, Pratham (Sanskrit)
2	Two	binary, brace, couple, couplet, distich, deuce, double, doubleton, duad, duality, duet, duo, dyad, pair, span, twain, twin, twosome, yoke
3	Three	deuce-ace, leash, set, tercet, ternary, ternion, terzetto, threesome, tierce, trey, triad, trine, trinity, trio, triplet, troika, hat-trick
4	Four	foursome, quadruplet, quatern, quaternary, quaternity, quartet, tetrad
5	Five	cinque, fin, fivesome, pentad, quint, quintet, quintuplet
6	Six	half dozen, hexad, sestet, sextet, sextuplet, sise
7	Seven	heptad, septet, septuple, walking stick
8	Eight	octad, octave, octet, octonary, octuplet, ogdoad
9	Nine	ennead
10	Ten	deca, decade, das (India)
11	Eleven	onze, ounze, ounce, banker’s dozen
12	Twelve	dozen
13	Thirteen	baker’s dozen, long dozen^[6]
20	Twenty	score,
21	Twenty-one	long score,^[6] blackjack
22	Twenty-two	Deuce-deuce
24	Twenty-four	two dozen
40	Forty	two-score
50	Fifty	half-century
55	Fifty-five	double nickel
60	Sixty	three-score
70	Seventy	three-score and ten
80	Eighty	four-score
87	Eighty-seven	four-score and seven
90	Ninety	four-score and ten
100	One hundred	centred, century, ton, short hundred
111	One hundred [and] eleven	eleventy-one^[7]
120	One hundred [and] twenty	long hundred,^[6] great hundred, (obsolete) hundred
144	One hundred [and] forty-four	gross, dozen dozen, small gross
1000	One thousand	chiliad, grand, G, thou, yard, kilo, k, millennium, Hajaar (India)
1024	One thousand [and] twenty-four	kibi or kilo in computing, see binary prefix (kilo is shortened to K, Kibi to Ki)
1100	One thousand one hundred	Eleven hundred
1728	One thousand seven hundred [and] twenty-eight	great gross, long gross, dozen gross
10000	Ten thousand	myriad, wan (China)
100000	One hundred thousand	lakh
500000	Five hundred thousand	crore (Iranian)
1000000	One million	Mega, meg, mil, (often shortened to M)
1048576	One million forty-eight thousand five hundred [and] seventy-six	Mibi or Mega in computing, see binary prefix (Mega is shortened to M, Mibi to Mi)
10000000	Ten million	crore (Indian)(Pakistan)
100000000	One hundred million	yi (China)

English names for powers of 10[edit]

This table compares the English names of cardinal numbers according to various American, British, and Continental European conventions. See English numerals or names of large numbers for more information on naming numbers.

	Short scale	Long scale
Value	American	British (Nicolas Chuquet)	Continental European (Jacques Peletier du Mans)
10⁰	One
10¹	Ten
10²	Hundred
10³	Thousand
10⁶	Million
10⁹	Billion	Thousand million	Milliard
10¹²	Trillion	Billion
10¹⁵	Quadrillion	Thousand billion	Billiard
10¹⁸	Quintillion	Trillion
10²¹	Sextillion	Thousand trillion	Trilliard
10²⁴	Septillion	Quadrillion
10²⁷	Octillion	Thousand quadrillion	Quadrilliard
10³⁰	Nonillion	Quintillion
10³³	Decillion	Thousand quintillion	Quintilliard
10³⁶	Undecillion	Sextillion
10³⁹	Duodecillion	Thousand sextillion	Sextilliard
10⁴²	Tredecillion	Septillion
10⁴⁵	Quattuordecillion	Thousand septillion	Septilliard
10⁴⁸	Quindecillion	Octillion
10⁵¹	Sexdecillion	Thousand octillion	Octilliard
10⁵⁴	Septendecillion	Nonillion
10⁵⁷	Octodecillion	Thousand nonillion	Nonilliard
10⁶⁰	Novemdecillion	Decillion
10⁶³	Vigintillion	Thousand decillion	Decilliard
10⁶⁶	Unvigintillion	Undecillion
10⁶⁹	Duovigintillion	Thousand undecillion	Undecilliard
10⁷²	Trevigintillion	Duodecillion
10⁷⁵	Quattuorvigintillion	Thousand duodecillion	Duodecilliard
10⁷⁸	Quinvigintillion	Tredecillion
10⁸¹	Sexvigintillion	Thousand tredecillion	Tredecilliard
10⁸⁴	Septenvigintillion	Quattuordecillion
10⁸⁷	Octovigintillion	Thousand quattuordecillion	Quattuordecilliard
10⁹⁰	Novemvigintillion	Quindecillion
10⁹³	Trigintillion	Thousand quindecillion	Quindecilliard
10⁹⁶	Untrigintillion	Sexdecillion
10⁹⁹	Duotrigintillion	Thousand sexdecillion	Sexdecilliard
10¹²⁰	Novemtrigintillion	Vigintillion
10¹²³	Quadragintillion	Thousand vigintillion	Vigintilliard
10¹⁵³	Quinquagintillion	Thousand quinvigintillion	Quinvigintilliard
10¹⁸⁰	Novemquinquagintillion	Trigintillion
10¹⁸³	Sexagintillion	Thousand trigintillion	Trigintilliard
10²¹³	Septuagintillion	Thousand quintrigintillion	Quintrigintilliard
10²⁴⁰	Novemseptuagintillion	Quadragintillion
10²⁴³	Octogintillion	Thousand quadragintillion	Quadragintilliard
10²⁷³	Nonagintillion	Thousand quinquadragintillion	Quinquadragintilliard
10³⁰⁰	Novemnonagintillion	Quinquagintillion
10³⁰³	Centillion	Thousand quinquagintillion	Quinquagintilliard
10³⁶⁰	Cennovemdecillion	Sexagintillion
10⁴²⁰	Cennovemtrigintillion	Septuagintillion
10⁴⁸⁰	Cennovemquinquagintillion	Octogintillion
10⁵⁴⁰	Cennovemseptuagintillion	Nonagintillion
10⁶⁰⁰	Cennovemnonagintillion	Centillion
10⁶⁰³	Ducentillion	Thousand centillion	Centilliard

There is no consistent and widely accepted way to extend cardinals beyond centillion (centilliard).

Myriad, Octad, and -yllion systems[edit]

The following table details the myriad, octad, Chinese myriad, Chinese long and -yllion names for powers of 10.

There is also a Knuth-proposed system notation of numbers, named the -yllion system.^[8] In this system, a new word is invented for every 2ⁿ-th power of ten.

Value	Myriad System Name	Octad System Name	Chinese Myriad Scale	Chinese Long Scale	Knuth-proposed System Name
10⁰	One	One	一	一	One
10¹	Ten	Ten	十	十	Ten
10²	Hundred	Hundred	百	百	Hundred
10³	Thousand	Thousand	千	千	Ten hundred
10⁴	Myriad	Myriad	萬 (万)	萬 (万)	Myriad
10⁵	Ten myriad	Ten myriad	十萬 (十万)	十萬 (十万)	Ten myriad
10⁶	Hundred myriad	Hundred myriad	百萬 (百万)	百萬 (百万)	Hundred myriad
10⁷	Thousand myriad	Thousand myriad	千萬 (千万)	千萬 (千万)	Ten hundred myriad
10⁸	Second Myriad	Octad	億 (亿)	億 (亿)	Myllion
10¹²	Third myriad	Myriad Octad	兆	萬億	Myriad myllion
10¹⁶	Fourth myriad	Second octad	京	兆	Byllion
10²⁰	Fifth myriad	Myriad second octad	垓	萬兆
10²⁴	Sixth myriad	Third octad	秭	億兆	Myllion byllion
10²⁸	Seventh myriad	Myriad third octad	穰	萬億兆
10³²	Eighth myriad	Fourth octad	溝 (沟)	京	Tryllion
10³⁶	Ninth myriad	Myriad fourth octad	澗 (涧)	萬京
10⁴⁰	Tenth myriad	Fifth octad	正	億京
10⁴⁴	Eleventh myriad	Myriad fifth octad	載 (载)	萬億京
10⁴⁸	Twelfth myriad	Sixth octad	極 (极) (in China and in Japan)	兆京
10⁵²	Thirteenth myriad	Myriad sixth octad	恆河沙 (恒河沙) (in China)	萬兆京
10⁵⁶	Fourteenth myriad	Seventh octad	阿僧祇 (in China); 恆河沙 (恒河沙) (in Japan)	億兆京
10⁶⁰	Fifteenth myriad	Myriad seventh octad	那由他, 那由多 (in China)	萬億兆京
10⁶⁴	Sixteenth myriad	Eighth octad	不可思議 (不可思议) (in China), 阿僧祇 (in Japan)	垓	Quadyllion
10⁶⁸	Seventeenth myriad	Myriad eighth octad	無量大数 (in China)	萬垓
10⁷²	Eighteenth myriad	Ninth octad	那由他, 那由多 (in Japan)	億垓
10⁸⁰	Twentieth myriad	Tenth octad	不可思議 (in Japan)	兆垓
10⁸⁸	Twenty-second myriad	Eleventh Octad	無量大数 (in Japan)	億兆垓
10¹²⁸				秭	Quinyllion
10²⁵⁶				穰	Sexyllion
10⁵¹²				溝 (沟)	Septyllion
10^1,024				澗 (涧)	Octyllion
10^2,048				正	Nonyllion
10^4,096				載 (载)	Decyllion
10^8,192				極 (极)	Undecyllion
10^16,384					Duodecyllion
10^32,768					Tredecyllion
10^65,536					Quattuordecyllion
10^131,072					Quindecyllion
10^262,144					Sexdecyllion
10^524,288					Septendecyllion
10^1,048,576					Octodecyllion
10^2,097,152					Novemdecyllion
10^4,194,304					Vigintyllion
10^2³²					Trigintyllion
10^2⁴²					Quadragintyllion
10^2⁵²					Quinquagintyllion
10^2⁶²					Sexagintyllion
10^2⁷²					Septuagintyllion
10^2⁸²					Octogintyllion
10^2⁹²					Nonagintyllion
10^2¹⁰²					Centyllion
10^{2^1,002}					Millyllion
10^{2^10,002}					Myryllion

Fractional numerals[edit]

This is a table of English names for non-negative rational numbers less than or equal to 1. It also lists alternative names, but there is no widespread convention for the names of extremely small positive numbers.

Keep in mind that rational numbers like 0.12 can be represented in infinitely many ways, e.g. zero-point-one-two (0.12), twelve percent (12%), three twenty-fifths (3/25), nine seventy-fifths (9/75), six fiftieths (6/50), twelve hundredths (12/100), twenty-four two-hundredths (24/200), etc.

Value	Fraction	Common names
1	1/1	One, Unity, Whole
0.9	9/10	Nine tenths, [zero] point nine
0.833333…	5/6	Five sixths
0.8	4/5	Four fifths, eight tenths, [zero] point eight
0.75	3/4	three quarters, three fourths, seventy-five hundredths, [zero] point seven five
0.7	7/10	Seven tenths, [zero] point seven
0.666666…	2/3	Two thirds
0.6	3/5	Three fifths, six tenths, [zero] point six
0.5	1/2	One half, five tenths, [zero] point five
0.4	2/5	Two fifths, four tenths, [zero] point four
0.333333…	1/3	One third
0.3	3/10	Three tenths, [zero] point three
0.25	1/4	One quarter, one fourth, twenty-five hundredths, [zero] point two five
0.2	1/5	One fifth, two tenths, [zero] point two
0.166666…	1/6	One sixth
0.142857142857…	1/7	One seventh
0.125	1/8	One eighth, one-hundred-[and-]twenty-five thousandths, [zero] point one two five
0.111111…	1/9	One ninth
0.1	1/10	One tenth, [zero] point one, One perdecime, one perdime
0.090909…	1/11	One eleventh
0.09	9/100	Nine hundredths, [zero] point zero nine
0.083333…	1/12	One twelfth
0.08	2/25	Two twenty-fifths, eight hundredths, [zero] point zero eight
0.076923076923…	1/13	One thirteenth
0.071428571428…	1/14	One fourteenth
0.066666…	1/15	One fifteenth
0.0625	1/16	One sixteenth, six-hundred-[and-]twenty-five ten-thousandths, [zero] point zero six two five
0.055555…	1/18	One eighteenth
0.05	1/20	One twentieth, five hundredths, [zero] point zero five
0.047619047619…	1/21	One twenty-first
0.045454545…	1/22	One twenty-second
0.043478260869565217391304347…	1/23	One twenty-third
0.041666…	1/24	One twenty-fourth
0.04	1/25	One twenty-fifth, four hundredths, [zero] point zero four
0.033333…	1/30	One thirtieth
0.03125	1/32	One thirty-second, thirty one-hundred [and] twenty five hundred-thousandths, [zero] point zero three one two five
0.03	3/100	Three hundredths, [zero] point zero three
0.025	1/40	One fortieth, twenty-five thousandths, [zero] point zero two five
0.02	1/50	One fiftieth, two hundredths, [zero] point zero two
0.016666…	1/60	One sixtieth
0.015625	1/64	One sixty-fourth, ten thousand fifty six-hundred [and] twenty-five millionths, [zero] point zero one five six two five
0.012345679012345679…	1/81	One eighty-first
0.010101…	1/99	One ninety-ninth
0.01	1/100	One hundredth, [zero] point zero one, One percent
0.009900990099…	1/101	One hundred-first
0.008264462809917355371900…	1/121	One over one hundred twenty-one
0.001	1/1000	One thousandth, [zero] point zero zero one, One permille
0.000277777…	1/3600	One thirty-six hundredth
0.0001	1/10000	One ten-thousandth, [zero] point zero zero zero one, One myriadth, one permyria, one permyriad, one basis point
0.00001	1/100000	One hundred-thousandth, [zero] point zero zero zero zero one, One lakhth, one perlakh
0.000001	1/1000000	One millionth, [zero] point zero zero zero zero zero one, One ppm
0.0000001	1/10000000	One ten-millionth, One crorth, one percrore
0.00000001	1/100000000	One hundred-millionth
0.000000001	1/1000000000	One billionth (in some dialects), One ppb
0.000000000001	1/1000000000000	One trillionth, One ppt
0	0/1	Zero, Nil

Other specific quantity terms[edit]

Various terms have arisen to describe commonly used measured quantities.

Unit: 1
Pair: 2 (the base of the binary numeral system)
Leash: 3 (the base of the trinary numeral system)
Dozen: 12 (the base of the duodecimal numeral system)
Baker’s dozen: 13
Score: 20 (the base of the vigesimal numeral system)
Shock: 60 (the base of the sexagesimal numeral system)^[9]
Gross: 144 (= 12²)
Great gross: 1728 (= 12³)

Basis of counting system[edit]

Not all peoples count, at least not verbally. Specifically, there is not much need for counting among hunter-gatherers who do not engage in commerce. Many languages around the world have no numerals above two to four (if they’re actually numerals at all, and not some other part of speech)—or at least did not before contact with the colonial societies—and speakers of these languages may have no tradition of using the numerals they did have for counting. Indeed, several languages from the Amazon have been independently reported to have no specific number words other than ‘one’. These include Nadëb, pre-contact Mocoví and Pilagá, Culina and pre-contact Jarawara, Jabutí, Canela-Krahô, Botocudo (Krenák), Chiquitano, the Campa languages, Arabela, and Achuar.^[10] Some languages of Australia, such as Warlpiri, do not have words for quantities above two,^[11]^[12]^[13] and neither did many Khoisan languages at the time of European contact. Such languages do not have a word class of ‘numeral’.

Most languages with both numerals and counting use base 8, 10, 12, or 20. Base 10 appears to come from counting one’s fingers, base 20 from the fingers and toes, base 8 from counting the spaces between the fingers (attested in California), and base 12 from counting the knuckles (3 each for the four fingers).^[14]

No base[edit]

Many languages of Melanesia have (or once had) counting systems based on parts of the body which do not have a numeric base; there are (or were) no numerals, but rather nouns for relevant parts of the body—or simply pointing to the relevant spots—were used for quantities. For example, 1–4 may be the fingers, 5 ‘thumb’, 6 ‘wrist’, 7 ‘elbow’, 8 ‘shoulder’, etc., across the body and down the other arm, so that the opposite little finger represents a number between 17 (Torres Islands) to 23 (Eleman). For numbers beyond this, the torso, legs and toes may be used, or one might count back up the other arm and back down the first, depending on the people.

2: binary[edit]

Binary systems are base 2, using zeros and ones. With only two symbols binary is used for things with coding like computers.

3: ternary[edit]

Base 3 counting has practical usage in some analog logic, in baseball scoring and in self–similar mathematical structures.

4: quaternary[edit]

Some Austronesian and Melanesian ethnic groups, some Sulawesi and some Papua New Guineans, count with the base number four, using the term asu or aso, the word for dog, as the ubiquitous village dog has four legs.^[15] This is argued by anthropologists to be also based on early humans noting the human and animal shared body feature of two arms and two legs as well as its ease in simple arithmetic and counting. As an example of the system’s ease a realistic scenario could include a farmer returning from the market with fifty asu heads of pig (200), less 30 asu (120) of pig bartered for 10 asu (40) of goats noting his new pig count total as twenty asu: 80 pigs remaining. The system has a correlation to the dozen counting system and is still in common use in these areas as a natural and easy method of simple arithmetic.^[15]^[16]

5: quinary[edit]

Quinary systems are based on the number 5. It is almost certain the quinary system developed from counting by fingers (five fingers per hand).^[17] An example are the Epi languages of Vanuatu, where 5 is luna ‘hand’, 10 lua-luna ‘two hand’, 15 tolu-luna ‘three hand’, etc. 11 is then lua-luna tai ‘two-hand one’, and 17 tolu-luna lua ‘three-hand two’.

5 is a common auxiliary base, or sub-base, where 6 is ‘five and one’, 7 ‘five and two’, etc. Aztec was a vigesimal (base-20) system with sub-base 5.

6: senary[edit]

The Morehead-Maro languages of Southern New Guinea are examples of the rare base 6 system with monomorphemic words running up to 6⁶. Examples are Kanum and Kómnzo. The Sko languages on the North Coast of New Guinea follow a base-24 system with a sub-base of 6.

7: septenary[edit]

Septenary systems are very rare, as few natural objects consistently have seven distinctive features. Traditionally, it occurs in week-related timing. It has been suggested that the Palikúr language has a base-seven system, but this is dubious.^[18]

8: octal[edit]

Octal counting systems are based on the number 8. Examples can be found in the Yuki language of California and in the Pamean languages of Mexico, because the Yuki and Pame keep count by using the four spaces between their fingers rather than the fingers themselves.^[19]

9: nonary[edit]

It has been suggested that Nenets has a base-nine system.^[18]

10: decimal[edit]

A majority of traditional number systems are decimal. This dates back at least to the ancient Egyptians, who used a wholly decimal system. Anthropologists hypothesize this may be due to humans having five digits per hand, ten in total.^[17]^[20] There are many regional variations including:

Western system: based on thousands, with variants (see English numerals)
Indian system: crore, lakh (see Indian numbering system. Indian numerals)
East Asian system: based on ten-thousands (see below)

12: duodecimal[edit]

Duodecimal systems are based on 12.

These include:

Chepang language of Nepal,
Mahl language of Minicoy Island in India
Nigerian Middle Belt areas such as Janji, Kahugu and the Nimbia dialect of Gwandara.
Melanesia^{[citation needed]}
reconstructed proto-Benue–Congo

Duodecimal numeric systems have some practical advantages over decimal. It is much easier to divide the base digit twelve (which is a highly composite number) by many important divisors in market and trade settings, such as the numbers 2, 3, 4 and 6.

Because of several measurements based on twelve,^[21] many Western languages have words for base-twelve units such as dozen, gross and great gross, which allow for rudimentary duodecimal nomenclature, such as «two gross six dozen» for 360. Ancient Romans used a decimal system for integers, but switched to duodecimal for fractions, and correspondingly Latin developed a rich vocabulary for duodecimal-based fractions (see Roman numerals). A notable fictional duodecimal system was that of J. R. R. Tolkien’s Elvish languages, which used duodecimal as well as decimal.

16: hexadecimal[edit]

Hexadecimal systems are based on 16.

The traditional Chinese units of measurement were base-16. For example, one jīn (斤) in the old system equals sixteen taels. The suanpan (Chinese abacus) can be used to perform hexadecimal calculations such as additions and subtractions.^[22]

South Asian monetary systems were base-16. One rupee in Pakistan and India was divided into 16 annay. A single anna was subdivided into four paisa or twelve pies (thus there were 64 paise or 192 pies in a rupee). The anna was demonetised as a currency unit when India decimalised its currency in 1957, followed by Pakistan in 1961.

20: vigesimal[edit]

Vigesimal numbers use the number 20 as the base number for counting. Anthropologists are convinced the system originated from digit counting, as did bases five and ten, twenty being the number of human fingers and toes combined.^[17]^[23]
The system is in widespread use across the world. Some include the classical Mesoamerican cultures, still in use today in the modern indigenous languages of their descendants, namely the Nahuatl and Mayan languages (see Maya numerals). A modern national language which uses a full vigesimal system is Dzongkha in Bhutan.

Partial vigesimal systems are found in some European languages: Basque, Celtic languages, French (from Celtic), Danish, and Georgian. In these languages the systems are vigesimal up to 99, then decimal from 100 up. That is, 140 is ‘one hundred two score’, not *seven score, and there is no numeral for 400 (great score).

The term score originates from tally sticks, and is perhaps a remnant of Celtic vigesimal counting. It was widely used to learn the pre-decimal British currency in this idiom: «a dozen pence and a score of bob», referring to the 20 shillings in a pound. For Americans the term is most known from the opening of the Gettysburg Address: «Four score and seven years ago our fathers…».

24: quadrovigesimal[edit]

The Sko languages have a base-24 system with a sub-base of 6.

32: duotrigesimal[edit]

Ngiti has base 32.

60: sexagesimal[edit]

Ekari has a base-60 system. Sumeria had a base-60 system with a decimal sub-base (with alternating cycles of 10 and 6), which was the origin of the numbering of modern degrees, minutes, and seconds.

80: octogesimal[edit]

Supyire is said to have a base-80 system; it counts in twenties (with 5 and 10 as sub-bases) up to 80, then by eighties up to 400, and then by 400s (great scores).

799 [i.e. 400 + (4 x 80) + (3 x 20) + {10 + (5 + 4)}]’

Notes[edit]

^ Charles Follen: A Practical Grammar of the German Language. Boston, 1828, p. 9, p. 44 and 48. Quote: «PARTS OF SPEECH. There are ten parts of speech, viz. Article, Substantive or Noun, Adjective, Numeral, Pronoun, Verb, Adverb, Preposition, Conjunction, and Interjection.», «NUMERALS. The numbers are divided into cardinal, ordinal, proportional, distributive, and collective. […] Numerals of proportion and distribution are […] &c. Observation. The above numerals, in fach or fäl´tig, are regularly declined, like other adjectives.»
^ Horace Dalmolin: The New English Grammar: With Phonetics, Morphology and Syntax, Tate Publishing & Enterprises, 2009, p. 175 & p. 177. Quote: «76. The different types of words used to compose a sentence, in order to relate an idea or to convey a thought, are known as parts of speech. […] The parts of speech, with a brief definition, will follow. […] 87. Numeral: Numerals are words that express the idea of number. There are two types of numerals: cardinal and ordinal. The cardinal numbers (one, two, three…) are used for counting people, objects, etc. Ordinal numbers (first, second, third…) can indicate order, placement in rank, etc.»
^ ^a ^b «What is a numeral?».
^ «Walsinfo.com».
^ «Numbers in Guaraní (Papapy Avañe’ême)». omniglot.com. Retrieved 2021-06-11.
^ ^a ^b ^c Blunt, Joseph (1 January 1837). «The Shipmaster’s Assistant, and Commercial Digest: Containing Information Useful to Merchants, Owners, and Masters of Ships». E. & G.W. Blunt – via Google Books.
^ Ezard, John (2 Jan 2003). «Tolkien catches up with his hobbit». The Guardian. Retrieved 6 Apr 2018.
^ «Large Numbers (page 2) at MROB». mrob.com. Retrieved 2020-12-23.
^ Cardarelli, François (2012). Encyclopaedia of Scientific Units, Weights and Measures: Their SI Equivalences and Origins (Second ed.). Springer. p. 585. ISBN 978-1447100034.
^ «Hammarström (2009, page 197) «Rarities in numeral systems»» (PDF). Archived from the original (PDF) on 2012-03-08. Retrieved 2010-06-16.
^ UCL Media Relations, «Aboriginal kids can count without numbers» Archived 2018-06-20 at the Wayback Machine
^ Butterworth, Brian; Reeve, Robert; Reynolds, Fiona; Lloyd, Delyth (2 September 2008). «Numerical thought with and without words: Evidence from indigenous Australian children». PNAS. 105 (35): 13179–13184. Bibcode:2008PNAS..10513179B. doi:10.1073/pnas.0806045105. PMC 2527348. PMID 18757729. [Warlpiri] has three generic types of number words: singular, dual plural, and greater than dual plural.
^ The Science Show, Genetic anomaly could explain severe difficulty with arithmetic, Australian Broadcasting Corporation
^ Bernard Comrie, «The Typology of Numeral Systems Archived 2011-05-14 at the Wayback Machine», p. 3
^ ^a ^b Ryan, Peter. Encyclopaedia of Papua and New Guinea. Melbourne University Press & University of Papua and New Guinea,:1972 ISBN 0-522-84025-6.: 3 pages p 219.
^ Aleksandr Romanovich Luriicac, Lev Semenovich Vygotskiĭ, Evelyn Rossiter. Ape, primitive man, and child: essays in the history of behavior. CRC Press: 1992: ISBN 1-878205-43-9.
^ ^a ^b ^c Heath, Thomas, A Manual of Greek Mathematics, Courier Dover: 2003. ISBN 978-0-486-43231-1 page, p:11
^ ^a ^b Parkvall, M. Limits of Language, 1st edn. 2008. p.291. ISBN 978-1-59028-210-6
^ Ascher, Marcia (1994), Ethnomathematics: A Multicultural View of Mathematical Ideas, Chapman & Hall, ISBN 0-412-98941-7
^ Scientific American Munn& Co: 1968, vol 219: 219
^ such as twelve months in a year, the twelve-hour clock, twelve inches to the foot, twelve pence to the shilling
^ «算盤 Hexadecimal Addition & Subtraction on a Chinese Abacus». totton.idirect.com. Retrieved 2019-06-26.
^ Georges Ifrah, The Universal History of Numbers: The Modern Number System, Random House, 2000: ISBN 1-86046-791-1. 1262 pages

Number Name 1 to 50 in English

The names of the numbers from 1 to 50 are given in the below table. Students can learn these numbers with their respective names and practice questions based on them.

1 = One	11 = Eleven	21 = Twenty-one	31 = Thirty-one	41 = Forty-one
2 = Two	12 = Twelve	22 = Twenty-two	32 = Thirty-two	42 = Forty-two
3 = Three	13 = Thirteen	23 = Twenty-three	33 = Thirty-three	43 = Forty-three
4 = Four	14 = Fourteen	24 = Twenty-four	34 = Thirty-four	44 = Forty-four
5 = Five	15 = Fifteen	25 = Twenty-five	35 = Thirty-five	45 = Forty-five
6 = Six	16 = Sixteen	26 = Twenty-six	36 = Thirty-six	46 = Forty-six
7 = Seven	17 = Seventeen	27 = Twenty-seven	37 = Thirty-seven	47 = Forty-seven
8 = Eight	18 = Eighteen	28 = Twenty-eight	38 = Thirty-eight	48 = Forty-eight
9 = Nine	19 = Nineteen	29 = Twenty-nine	39 = Thirty-nine	49 = Forty-nine
10 = Ten	20 = Twenty	30 = Thirty	40 = Forty	50 = Fifty

Also read:

Natural Numbers And Whole Numbers
Numbers
Even And Odd Numbers

Rules to Write Numbers from One to Fifty (1 to 50) Spelling

While writing the spelling of the digits from one to fifty (1 to 50), some rules have to be followed.

Rule 1: Grasping on place values: The positional value of the digits in a number can be expressed depending on where they are put. The first four place values depending on the position of the number 1 can be written as

1 – one’s place
10 – tens place
100 – hundreds
1000 – thousands place

Rule 2: The numbers from one to 20, 30…. 100 and 1000 can be referred to through the number names from one to fifty chart along with the spellings. For instance, the number name of 5 is five, the number name of 30 is thirty, and so on.

Rule 3: To write the number names of multiples of the number 100 and thousand, the number name of the digit in the 100’s place and the term “hundred” is written. For example, the number name of 400 is four hundred.

Rule 4: To author the number names of the rest of the other two or three-digit numbers, the expanded form is written. For the numbers (eleven – nineteen) as the final 2 digits, the ones and tens place is taken as one unit. The addends are spelt out and merged with their respective names. For instance, 54 = 50 + 4 and 54 in words is termed as fifty-four.

Strategy To Grasp Number Names Till 50

Number one to number ten number names: No trick as such exists. Memorise the numerals.

Number eleven to twenty number names: The numbers eleven and twelve are different cases. From the number thirteen onwards till nineteen a pattern exists that is the number + teen. Thirteen, fourteen, fifteen, sixteen, seventeen, eighteen, nineteen and the number twenty is varied.

Number twenty one to thirty number names: A pattern exists and it is written as twenty + one, twenty + two, twenty + three…… thirty is different.

Number thirty-one to forty number names: thirty + one, thirty + two…… forty is different.

Number forty-one to fifty number names: forty + one, forty + two…… fifty is different.

Importance of Names of Numbers

The names of the numbers are essential for each student to know. These are basic maths that will help students to spell the numbers correctly. Also, when they attend the classes and their teachers spell such numbers, then they can easily write them.

Numbers play a key role in Mathematics. All the mathematical or arithmetical operations are based on these numbers, not only in primary classes but in higher-level courses too.

Solved Problems on Number Name 1 to 50

Problem 1:

Solve and put down the given expression in words. 320 + 97 – (120 + 260)

Answer:

Now, we have to simplify the expression: 320 + 97 – (120 + 260)

First, simplify the expression inside the bracket

320 + 97 – (120 + 260) = 320 + 97 – 380

320 + 97 – (120 + 260) = 37 = Thirty-seven.

Hence, the simplified expression of 320 + 97 – (120 + 260) is 37.

Thus, the number 37 in words is thirty-seven.

Problem 2:

Find the answer of (one hundred and twenty-one) – (seventy-eight).

Answer:

In the form of numbers, one hundred and twenty-one is expressed as 121, and seventy-eight is expressed as 78.

The given problem is (one hundred and twenty-one) – (seventy-eight).

= (121 – 78)

= 43

On utilising the number name chart from 1 to 50, 43 can be expressed as follows.

43 = 40 + 3 = Forty + Three = Forty Three

Practice Questions

Here are a few problems for primary school students to practice names of all the numbers from 1 to 50.

What is the name of 45? Write in words.
Write the name of 33.
What do we call the number 25?
How do we spell the number 17?
What is the spelling of 40?
Fill in the blocks in the given table:
1. 1 2 4
  
  6 8
  
  9 11
  
  13 14
2. Also, write the names of the numbers in the block.

How to spell 23 in English?

Frequently Asked Questions on Number Names 1 to 50

What are number names?

In Mathematics, the number name is a way of expressing the number in the word form. For example, 10 is written or read as ten.

Write number names from 1 to 10.

The name of the numbers from 1 to 10 are:
1 – One, 2 – Two, 3 – Three, 4 – Four, 5 – Five, 6 – Six, 7 – Seven, 8 – Eight, 9 – Nine, 10 – Ten.

Write 11 to 20 number names.

The number names from 11 to 20 are:
11 – Eleven, 12 – Twelve, 13 – Thirteen, 14 – Fourteen, 15 – Fifteen, 16 – Sixteen, 17 – Seventeen, 18 – Eighteen, 19 – Nineteen, 20 -Twenty.

Write the number 40 in words.

The number 40 is written and read as forty.

How to write the numbers in words?

To write numbers in words, read the number from left to right and write the number according to the place value.

Источник

From Simple English Wikipedia, the free encyclopedia

A Sudoku puzzle is a grid of 81 numbers

A number is a concept from mathematics, used to count or measure. Depending on the field of mathematics, where numbers are used, there are different definitions:

People use symbols to represent numbers; they call them numerals. Common places where numerals are used are for labeling, as in telephone numbers, for ordering, as in serial numbers, or to put a unique identifier, as in an ISBN, a unique number that can identify a book.
Cardinal numbers are used to measure how many items are in a set. For example, {A,B,C} has size «3».
Ordinal numbers are used to specify a certain element in a set or sequence (first, second, third).

Numbers are also used for other things like counting. Numbers are used when things are measured. Numbers are used to study how the world works. Mathematics is a way to use numbers to learn about the world and make things. The study of the rules of the natural world is called science. The work that uses numbers to make things is called engineering.

Numbering methods[change | change source]

Numbers for people[change | change source]

There are different ways of giving symbols to numbers. These methods are called number systems. The most common number system that people use is the base ten number system. The base ten number system is also called the decimal number system. The base ten number system is common because people have ten fingers and ten toes. There are 10 different symbols {0, 1, 2, 3, 4, 5, 6, 7, 8, and 9} used in the base ten number system. These ten symbols are called digits.^[1]

A symbol for a number is made up of these ten digits. The position of the digits shows how big the number is. For example, the number 23 in the decimal number system really means (2 times 10) plus 3. Similarly, 101 means 1 times a hundred (=100) plus 0 times 10 (=0) plus 1 times 1 (=1).

Numbers for machines[change | change source]

Another number system is more common for machines. The machine number system is called the binary number system. The binary number system is also called the base two number system. There are two different symbols (0 and 1) used in the base two number system. These two symbols are called bits.^[2]

A symbol for a binary number is made up of these two bit symbols. The position of the bit symbols shows how big the number is. For example, the number 10 in the binary number system really means 1 times 2 plus 0, and 101 means 1 times four (=4) plus 0 times two (=0) plus 1 times 1 (=1). The binary number 10 is the same as the decimal number 2. The binary number 101 is the same as the decimal number 5.

Names of numbers[change | change source]

English has special names for some of the numbers in the decimal number system that are «powers of ten». All of these power of ten numbers in the decimal number system use just the symbol «1» and the symbol «0». For example, ten tens is the same as ten times ten, or one hundred. In symbols, this is «10 × 10 = 100». Also, ten hundreds is the same as ten times one hundred, or one thousand. In symbols, this is «10 × 100 = 10 × 10 × 10 = 1000». Some other powers of ten also have special names:

1 – one
10 – ten
100 – one hundred
1,000 – one thousand
1,000,000 – one million

When dealing with larger numbers than this, there are two different ways of naming the numbers in English. Under the «long scale», a new name is given every time the number is a million times larger than the last named number. It is also called the «British Standard». This scale used to be common in Britain, but is not often used in English-speaking countries today. It is still used in some other European nations.

Another scale is the «short scale», under which a new name is given every time a number is a thousand times larger than the last named number. This scale is a lot more common in most English-speaking nations today.

1,000,000,000 – one billion (short scale), one milliard (long scale)
1,000,000,000,000 – one trillion (short scale), one billion (long scale)
1,000,000,000,000,000 – one quadrillion (short scale), one billiard (long scale)

Types of numbers[change | change source]

Natural numbers[change | change source]

Natural numbers are the numbers which we normally use for counting: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, etc. Some people say that 0 is a natural number, too. The set of all natural numbers is written as .^[3]

Another name for these numbers is positive numbers. These numbers are sometimes written as +1 to show that they are different from the negative numbers. But not all positive numbers are natural (for example, ${displaystyle {tfrac {1}{2}}}$ is positive, but not natural).

If 0 is called a natural number, then the natural numbers are the same as the whole numbers. If 0 is not called a natural number, then the natural numbers are the same as the counting numbers. So if the words «natural numbers» are not used, then there will be less confusion about whether zero is included or not. But unfortunately, some say that zero is not a whole number, while others say that whole numbers can be negative. «Positive integers» and «non-negative integers» are another way to include zero or exclude zero, but only if people know those words.

Negative numbers[change | change source]

Negative numbers are numbers less than zero.

One way to think of negative numbers is to use a number line. We call one point on this line zero. Then we will label (write the name of) every position on the line by how far to the right of the zero point is. For example, the point one is one centimeter to the right, and the point two is two centimeters to the right.

However, the point one centimeter to the left of the zero point cannot be point one, since there is already a point called one. We therefore call this point minus one (−1, as it is one centimeter away but in the opposite direction).

A drawing of a number line is below.

All the normal operations of mathematics can be done with negative numbers:

Adding a negative number to another is the same as taking away the positive number with the same numerals. For example, 5 + (−3) is the same as 5 − 3, and equals 2.
Taking away a negative number from another is the same as adding the positive number with the same numerals. For example, 5 − (−3) is the same as 5 + 3, and equals 8.
Multiplying two negative numbers together produces a positive number. For example, −5 times −3 is 15.
Multiplying a negative number by a positive number, or multiply a positive number by a negative number, produces a negative result. For example, 5 times −3 is −15.

Since finding the square root of a negative number is impossible for real numbers (as negative times negative equals positive for real numbers), the square root of -1 is given a special name: i. This is also called the imaginary unit.^[3]

Integers[change | change source]

Integers are all the natural numbers, all their opposites, and the number zero.^[4] Decimal numbers and fractions are not integers.

Rational numbers[change | change source]

Rational numbers are numbers which can be written as fractions. This means that they can be written as a divided by b, where the numbers a and b are integers, and b is not zero.

Some rational numbers, such as 1/10, need a finite number of digits after the decimal point to write them in decimal form. The number one tenth is written in decimal form as 0.1. Numbers written with a finite decimal form are rational. Some rational numbers, such as 1/11, need an infinite number of digits after the decimal point to write them in decimal form. There is a repeating pattern to the digits following the decimal point. The number one eleventh is written in decimal form as 0.0909090909 … .

A percentage could be called a rational number, because a percentage like 7% can be written as the fraction 7/100. It can also be written as the decimal 0.07. Sometimes, a ratio is considered as a rational number.

Irrational numbers[change | change source]

Irrational numbers are numbers which cannot be written as a fraction, but do not have imaginary parts (explained later).

Irrational numbers often occur in geometry. For example, if we have a square which has sides of 1 meter, the distance between opposite corners is the square root of two, which equals 1.414213 … . This is an irrational number. Mathematicians have proved that the square root of every natural number is either an integer or an irrational number.

One well-known irrational number is pi. This is the circumference (distance around) of a circle divided by its diameter (distance across). This number is the same for every circle. The number pi is approximately 3.1415926535 … .

An irrational number cannot be fully written down in decimal form. It would have an infinite number of digits after the decimal point, and unlike 0.333333 …, these digits would not repeat forever.

Real numbers[change | change source]

Real numbers is a name for all the sets of numbers listed above:

The rational numbers, including integers
The irrational numbers

The real numbers form the real line. This is all the numbers that do not involve imaginary numbers.

Imaginary numbers[change | change source]

Imaginary numbers are formed by real numbers multiplied by the number i. This number is the square root of minus one (−1).

There is no number in the real numbers which when squared, makes the number −1. Therefore, mathematicians invented a number. They called this number i, or the imaginary unit.^[3]

Imaginary numbers operate under the same rules as real numbers:

The sum of two imaginary numbers is found by pulling out (factoring out) the i. For example, 2i + 3i = (2 + 3)i = 5i.
The difference of two imaginary numbers is found similarly. For example, 5i − 3i = (5 − 3)i = 2i.
When multiplying two imaginary numbers, remember that i × i (i²) is −1. For example, 5i × 3i = ( 5 × 3 ) × ( i × i ) = 15 × (−1) = −15.

Imaginary numbers were called imaginary because when they were first found, many mathematicians did not think they existed.^[5] The person who discovered imaginary numbers was Gerolamo Cardano in the 1500s. The first to use the words imaginary number was René Descartes. The first people to use these numbers were Leonard Euler and Carl Friedrich Gauss. Both lived in the 18th century.

Complex numbers[change | change source]

Complex numbers are numbers which have two parts; a real part and an imaginary part. Every type of number written above is also a complex number.

Complex numbers are a more general form of numbers. The complex numbers can be drawn on a number plane. This is composed of a real number line, and an imaginary number line.

           3i|_
             |
             |
           2i|_          . 2+2i
             |
             |
            i|_
             |
             |
 |_____|_____|_____|_____|_____|_____|_____|_____|
−2    −1     0     1     2     3     4     5     6
             |
           −i|_                .3−i
             |
             |
 .−2−2i   −2i|_
             |
             |
          −3i|_
             |

All of normal mathematics can be done with complex numbers:

To add two complex numbers, add the real and imaginary parts separately. For example, (2 + 3i) + (3 + 2i) = (2 + 3) + (3 + 2)i= 5 + 5i.
To subtract one complex number from another, subtract the real and imaginary parts separately. For example, (7 + 5i) − (3 + 3i) = (7 − 3) + (5 − 3)i = 4 + 2i.

To multiply two complex numbers is more complicated. It is easiest to describe in general terms, with two complex numbers a + bi and c + di.

For example, (4 + 5i) × (3 + 2i) = (4 × 3 − 5 × 2) + (4 × 2 + 5 × 3)i = (12 − 10) + (8 + 15)i = 2 + 23i.

Transcendental numbers[change | change source]

A real or complex number is called a transcendental number if it can not be obtained as a result of an algebraic equation with integer coefficients.

${displaystyle a_{n}x^{n}+dots +a_{2}x^{2}+a_{1}x+a_{0}=0}$

Proving that a certain number is transcendental can be extremely difficult. Each transcendental number is also an irrational number. The first people to see that there were transcendental numbers were Gottfried Wilhelm Leibniz and Leonhard Euler. The first to actually prove there were transcendental numbers was Joseph Liouville. He did this in 1844.

Some well-known transcendental numbers include:

e
π
e^a for algebraic a ≠ 0
${displaystyle 2^{sqrt {2}}}$

[change | change source]

Names of numbers in English

Notes[change | change source]

↑ A finger or a toe is also called a digit.
↑ A bit is a short form of the words «binary digit».
↑ ^3.0 ^3.1 ^3.2 «Compendium of Mathematical Symbols». Math Vault. 2020-03-01. Retrieved 2020-10-12.
↑ «Definition of INTEGER». www.merriam-webster.com. Retrieved 2020-10-12.
↑ «History of Complex Numbers (also known as History of Imaginary Numbers or the History of i)». rossroessler.tripod.com. Retrieved 2020-10-12.

Источник

Numbers in Words is writing the numbers in alphabetical form instead of digits. There are various systems to write numbers in words. After reading this article, you can write whole numbers in words, and write numbers in word form in standard form. We will primarily focus on the Indian & International number system of writing numbers in words in English, with their Rules, Tricks to remember and write spellings. You can learn to spell numbers in words 1 to 100 with Solved Examples and FAQs.

What is Number in Words?

Alphabetical form of numbers is called writing numbers in words. These are numbers written in words as the name implies. In the English language, the number 100, for example, is written as one hundred. All natural numbers, such as ones, tens, hundreds, thousands, and so on, can be represented in words based on the place value of their digits.

What is a Number Name?

Number name is the method of representing numbers in words. The alphabetical form of numbers is called number words. These are numbers written in words as the name implies. In language, the number 100, for example, is written as one hundred. All natural numbers, such as ones, tens, hundreds, thousands, and so on, can be represented as number names based on the place value of their digits.

Examples: 128 = 100 + 20 + 8. One hundred and twenty-eight is the number name of 128.

412 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 12. As a result, the number 412’s name is Four Hundred and Twelve.

685 = 600 + 80 + 5. = 685 = 600 + 80 + 5. Six hundred eighty-five is the number name for 685.

List of Number Names from 1 to 20

Here is a list of Numbers in Words from 1 – 20. A 1-20 number chart is a great way to teach your youngster numbers and practise one-to-one correspondence. The numbers 1 through 20 are represented in the graphic. Each number has a term for it, as well as a number of visuals that correspond to it.

List of Numbers in Words from 1 to 20
1 – One	2 – Two	3 – Three	4 – Four	5 – Five
6 – Six	7 – Seven	8 – Eight	9 – Nine	10 – Ten
11 – Eleven	12 – Twelve	13 – Thirteen	14 – Fourteen	15 – Fifteen
16 – Sixteen	17 – Seventeen	18 – Eighteen	19 – Nineteen	20 – Twenty

List of Number Names from 1 to 50

Here’s a list of Numbers in Words from 1 to 50. 1-50 number chart is a great way to teach and learn number names.

Number In Words 1 – 50
1 One	2 Two	3 Three	4 Four	5 Five
6 Six	7 Seven	8 Eight	9 Nine	10 Ten
11 Eleven	12 Twelve	13 Thirteen	14 Fourteen	15 Fifteen
16 Sixteen	17 Seventeen	18 Eighteen	19 Nineteen	20 Twenty
21 Twenty-one	22 Twenty-two	23 Twenty-three	24 Twenty-four	25 Twenty-five
26 Twenty-six	27 Twenty-seven	28 Twenty-eight	29 Twenty-nine	30 Thirty
31 Thirty-one	32 Thirty-two	33 Thirty-three	34 Thirty-four	35 Thirty-five
36 Thirty-six	37 Thirty-seven	38 Thirty-eight	39 Thirty-nine	40 Forty
41 Forty-one	42 Forty-two	43 Forty-three	44 Forty-four	45 Forty-five
46 Forty-six	47 Forty-seven	48 Forty-eight	49 Forty-nine	50 Fifty

List of Number Names from 1 to 100

Here’s a list of Numbers in Words from 1 – 100. A 1-100 number chart is a great way to teach and learn number names.

List of Number Names from 1 to 100
1 one	2 two	3 three	4 four	5 five
6 six	7 seven	8 eight	9 nine	10 ten
11 eleven	12 twelve	13 thirteen	14 fourteen	15 fifteen
16 sixteen	17 seventeen	18 eighteen	19 nineteen	20 twenty
21 twenty- one	22 twenty- two	23 twenty- three	24 twenty- four	25 twenty- five
26 twenty- six	27 twenty- seven	28 twenty- eight	29 twenty- nine	30 thirty
31 thirty- one	32 thirty- two	33 thirty- three	34 thirty- four	35 thirty- five
36 thirty- six	37 thirty- seven	38 thirty- eight	39 thirty- nine	40 forty
41 forty- one	42 forty- two	43 forty- three	44 forty- four	45 forty- five
46 forty- six	47 forty- seven	48 forty- eight	49 forty- nine	50 fifty
51 fifty- one	52 fifty- two	53 fifty- three	54 fifty- four	55 fifty- five
56 fifty- six	57 fifty- seven	58 fifty- eight	59 fifty- nine	60 sixty
61 sixty- one	62 sixty- two	63 sixty- three	64 sixty- four	65 sixty- five
66 sixty- six	67 sixty- seven	68 sixty- eight	69 sixty- nine	70 seventy
71 seventy- one	72 seventy- two	73 seventy- three	74 seventy- four	75 seventy- five
76 seventy- six	77 seventy- seven	78 seventy- eight	79 seventy- nine	80 eighty
81 eighty- one	82 eighty- two	83 eighty- three	84 eighty- four	85 eighty- five
86 eighty- six	87 eighty- seven	88 eighty- eight	89 eighty- nine	90 ninety
91 ninety- one	92 ninety- two	93 ninety- three	94 ninety- four	95 ninety- five
96 ninety- six	97 ninety- seven	98 ninety- eight	99 ninety- nine	100 one hundred

How to write a Number in Words using International System?

It is based on the International Place Value Chart. The steps to write numbers in International System are as follows.

Step 1: First, we begin from the right side and insert commas after every three digits.

Step 2: Each group is assigned a period starting from the right-hand side as ones, thousands, and millions, followed by billions and so on. This becomes the place value of the digits.

Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.

Step 4: We add up the amounts in the same period. For example, in 27,000 we have a place value of 2 as twenty thousand and 7 as seven thousand. Together it becomes 20 + 7 i.e. twenty-seven thousand.

Step 5: Now write down the face value of each number starting from the left-hand side.

How to write a Number in Words using Indian System?

It is based on the Indian Place Value Chart. The Indian System is a little different from the International system. But it can be easily learnt below and you can convert numbers to words in Indian rupees.

Step 1: First, we begin from the right side and insert commas. The first group is after three-digit and after that every two digits.

Step 2: Each group is assigned a period starting from the right hand side as ones, thousands, lakhs, crores and so on. This becomes the place value of the digits.

Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.

Step 5: Now write down the face value of each number starting from the left-hand side.

Rules of Writing Numbers in Words

In any Numbering System, we always start on the right side. The number is divided into periods, each of which is read separately.
Small numbers ranging from one to ten (or one to nine, depending on the style guide) should normally be spelt out in writing.
Numbers greater than 10 are written as numerals.
All compound numerals from twenty-one to ninety-nine should be hyphenated.

Tips to Write Numbers in Words

Using simple Number/Rhyme pictures associated with a storey is the easiest, but the least reliable, approach to recalling numbers.
A preferable method is to employ a simple peg system, in which you can correlate numerals from the Number/Rhyme System with positions structured using the Alphabet System.

Solved Examples of Numbers in Words

Example 1: Write the numbers in the International and Indian place-value system place commas and the name of the following numbers.

Solution: 721336598 in the Indian system:

Let’s interpret the number by arranging the digits in the Indian place value system from left to right according to their locations as ones, tens, hundreds, thousands, and so on.

The number is written as 72,13,36,598 and read as

Seventy-two crores thirteen lakh thirty-six thousand five hundred and ninety-eight.

721336598 in the International System:

Now, in the international place value system, arrange the digits from left to right according to their locations as ones, tens, hundreds, thousands, and so on, and read and write the number.

The number is written as 721,336,598

Let’s read the number by arranging the digits from left to right.

Seven hundred and twenty-one million, three and thirty-six, hundred thousand five hundred and ninety-eight.

Example 2: Using the International system, write the number; Six million, four hundred and eleven thousand, two hundred and sixty.

Solution: 6,411,260.

Example 3: Using the international system, read the number 7456123.

Solution: 7456123- Seven million Four Hundred Fifty-six thousand one hundred twenty-three.

Example 4: Write the number in words: 12,367,169.

Solution: Twelve million, three hundred and sixty-seven thousand, one hundred and sixty-nine.

Example 5: Write seven hundred forty-three million eight hundred thirteen thousand two hundred fifty-six in the numeral form using the international system.

Solution: 743,813,256.

Hope this article on Number in Words was informative. Get some practice of the same on our free Testbook App. Download Now!

FAQs on Number in Words

Q.1 How do you write numbers in words using the International System?

Ans.1

Step 1: First, we begin from the right side and insert commas after every three digits.
Step 2: Each group is assigned a period starting from the right hand side as ones, thousands, and millions, followed by billions and so on. This becomes the place value of the digits.
Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.
Step 4: We add up the amounts in the same period.
Step 5: Now write down the face value of each number starting from the left hand side.

Q.2 How do you write numbers in words using the Indian System?

Ans.2

Step 1: First, we begin from the right side and insert commas. The first group is after three-digit and after that every two digits.
Step 2: Each group is assigned a period starting from the right-hand side as ones, thousands, lakhs, crores and so on. This becomes the place value of the digits.
Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.
Step 4: We add up the amounts in the same period.
Step 5: Now write down the face value of each number starting from the left-hand side.

For example, in 27,000 we have a place value of 2 as twenty thousand and 7 as seven thousand. Together it becomes 20 + 7 i.e. twenty-seven thousand.

Q.3 What is called 10000000000?

Ans.3 The number: 10000000000 is (10^{13}). I would call it ten million million. You could call it ten trillion. A trillion is a thousand billion.

Q.4 What is number in words?

Ans.4 Alphabetical form of numbers is called writing numbers in words. These are numbers written in words as the name implies.

Q.5 What is a number name?

Ans.5 Number name is the method of representing numbers in words. The alphabetical form of numbers is called number words. These are numbers written in words as the name implies.

Q.6 What are the rules of writing numbers in words?

Ans.6 The rules of writing numbers in words are:

In any Numbering System, we always start on the right side. The number is divided into periods, each of which is read separately.
Small numbers ranging from one to ten (or one to nine, depending on the style guide) should normally be spelt out in writing.
Numbers greater than 10 are written as numerals.
All compound numerals from twenty-one to ninety-nine should be hyphenated.

Источник

How do you write 17 in words?

How do you number a name?

Related Games

Number Words: Definition

Related Worksheets

Rules to Write Numbers in Word Form

Number Words or Number Names from 1 to 100

The Number Words for Higher Values

Number Names as per the International Number System

Place Value Chart for International System

Tips and Tricks to Learn Numbers Names

Number Names as per the Ordinal System

Fun Facts

Conclusion

Solved Examples

Practice Problmes

Frequently Asked Questions

Related Articles

What are Number Names? | Numbers in Words

How to Write Number Names in Words?

Importance of Number Names in Words

Number Names 1 – 50

Examples of Names of Numbers

FAQs on Number Names

What are Number Names?

Numbers in Words in English

Number Names 1 to 100

Number Names 1 to 20

1 to 20 Spelling

Number Names 21 to 100

Numbers in Words in International System

Rules to Write Number Names

Tips to Learn Number Names

FAQs on Numbers in Words

What are Number Names in Math?

How to Write Numbers in Words in International System?

How to Write 1100 in Words?

How to Write Decimal Number Names?

How to Write Number Names in International System?

How to Write Numbers in Words?

How are Numbers in Words Useful in Real Life?

Identifying numerals[edit]

Larger numerals[edit]

Numerals of cardinal numbers[edit]

English names for powers of 10[edit]

Myriad, Octad, and -yllion systems[edit]

Fractional numerals[edit]

Other specific quantity terms[edit]

Basis of counting system[edit]

No base[edit]

2: binary[edit]

3: ternary[edit]

4: quaternary[edit]

5: quinary[edit]

6: senary[edit]

7: septenary[edit]

8: octal[edit]

9: nonary[edit]

10: decimal[edit]

12: duodecimal[edit]

16: hexadecimal[edit]

20: vigesimal[edit]

24: quadrovigesimal[edit]

32: duotrigesimal[edit]

60: sexagesimal[edit]

80: octogesimal[edit]

See also[edit]

Numerals in various languages[edit]

[edit]

Notes[edit]

Further reading[edit]

Number Name 1 to 50 in English

Rules to Write Numbers from One to Fifty (1 to 50) Spelling

Strategy To Grasp Number Names Till 50

Importance of Names of Numbers

Solved Problems on Number Name 1 to 50

Practice Questions

Frequently Asked Questions on Number Names 1 to 50

What are number names?

Write number names from 1 to 10.