What is a word phrase in math?
A mathematical phrase is a verbal phrase that contains words and/or numbers that can be translated into a mathematical expression, where a…
How do you write an expression?
To write an expression, we often have to interpret a written phrase. For example, the phrase “6 added to some number” can be written as the expression x + 6, where the variable x represents the unknown number.
What is expression example?
The definition of an example of expression is a frequently used word or phrase or it is a way to convey your thoughts, feelings or emotions. An example of an expression is the phrase “a penny saved is a penny earned.” An example of an expression is a smile. noun. 67.
What are some good expressions?
Common English idioms & expressions
| Idiom | Meaning | Usage |
|---|---|---|
| It’s a piece of cake | It’s easy | by itself |
| It’s raining cats and dogs | It’s raining hard | by itself |
| Kill two birds with one stone | Get two things done with a single action | by itself |
| Let the cat out of the bag | Give away a secret | as part of a sentence |
What are the expressions explain?
Expression: An expression is a combination of operators, constants and variables. An expression may consist of one or more operands, and zero or more operators to produce a value.
What is C expression write an example?
An expression is a formula in which operands are linked to each other by the use of operators to compute a value. An operand can be a function reference, a variable, an array element or a constant.
What are the two types of expression?
In this article
- Primary expressions.
- Postfix expressions.
- Expressions formed with unary operators.
- Expressions formed with binary operators.
- Expressions with the conditional operator.
- Constant expressions.
- Expressions with explicit type conversions.
- Expressions with pointer-to-member operators.
What are different types of expressions?
There are three kinds of expressions: An arithmetic expression evaluates to a single arithmetic value. A character expression evaluates to a single value of type character. A logical or relational expression evaluates to a single logical value.
What are the 5 types of expression?
Types of Expressions
- Numeric. Use a numeric expression to perform calculations that use numeric constants (integer or decimal) and variables.
- Date. Use date expressions to perform numeric calculations on dates.
- Character.
- Logical.
- Conditional.
Which code example is an expression?
Examples. For example, 2 + 3 is both an arithmetic and programming expression, which evaluates to 5 . A variable is an expression because it denotes a value in memory, so y + 6 is also an expression. An example of a relational expression is 4 ≠ 4 , which evaluates to false .
What are the different types of algebraic expressions?
There are 3 main types of algebraic expressions which include:
- Monomial Expression.
- Binomial Expression.
- Polynomial Expression.
What is algebra example?
Algebra helps in the representation of problems or situations as mathematical expressions. It involves variables like x, y, z, and mathematical operations like addition, subtraction, multiplication, and division to form a meaningful mathematical expression. One simple example of algebra is 2x + 4 = 8. …
Is 2x YZ a Monomial?
2x yz D. 2 + xyz. 2xyz2 is a monomial.
Is 10x a polynomial?
10x is a polynomial. In particular, for an expression to be a polynomial term, it must contain no square roots of variables, no fractional or negative powers on the variables, and no variables in the denominators of any fractions. That’s why 10x is a polynomial because it obeys all the rules.
Is 5x 3 a Monomial?
Step-by-step explanation: A monomial refers to an expression that involves one term, like 5xy. Monomials include variables, numbers, and whole numbers whose multiplication takes place together. Any number, all by itself, can be a monomial, like the number 5 or the number 2,700.
What is Monomial example?
A monomial is an expression in algebra that contains one term, like 3xy. Any number all by itself is a monomial, like 5 or 2,700. A monomial can also be a variable, like “b” or “y.” It can also be a combination of these, like 98b or xy.
Which is called Monomial?
A monomial, also called power product, is a product of powers of variables with nonnegative integer exponents, or, in other words, a product of variables, possibly with repetitions. For example, is a monomial. The constant 1 is a monomial, being equal to the empty product and to x0 for any variable x.
How do you identify a Monomial?
A monomial is an expression in algebra that contains one term, like 3xy. Monomials include numbers, whole numbers and variables that are multiplied together, and variables that are multiplied together. A polynomial is a sum of monomials where each monomial is called a term.
Is 2x one or two terms?
Even though 2x has two parts (2 and x), since they are being multiplied together, 2x is considered a single term (a monomial expression). In expressions containing more than one term, terms are generally separated by addition, subtraction, or division.
Is 2x a coefficient?
In 2x, the coefficient of 2x is 2, and 3 is a constant. Therefore, the coefficients are 1 and 2.
Is 2B a term?
2B is defined as a cyber term because some of its characters are used as substitutes for letters.
What is the constant of 2x?
the 3 is a constant term. where x is the variable, and has a constant term of c. If c = 0, then the constant term will not actually appear when the quadratic is written. when x is multiplied by 2, the result, 2x, is not constant; while 1 * -2 is -2 and still a constant.
What is constant give example?
In Algebra, a constant is a number on its own, or sometimes a letter such as a, b or c to stand for a fixed number. Example: in “x + 5 = 9”, 5 and 9 are constants.
What is constant term example?
A constant term is a term that contains only a number. In other words, there is no variable in a constant term. Examples of constant terms are 4, 100, and -5.
What is the constant of y =- 2x?
Answer. Answer: 2 is the constant of proportionality in the equation y = 2x .
What is the constant of proportionality in an equation?
When two variables are directly or indirectly proportional to each other, then their relationship can be described as y = kx or y = k/x, where k determines how the two variables are related to one another. This k is known as the constant of proportionality.
Is Y 2x a constant variation?
It is a direct variation and the constant of variation is the slope of the line, which is 2. Alan P. y=2x+1 is not a direct variation.
Is Y 2x a linear function?
the equation y = 2x represents a linear or non linear function. y/x = 2, which is a constant. So, the slope is constant, meaning the graph is a straight line. So, it is linear.
Any real-life scenario containing unknown quantities can be modelled into mathematical statements. For instance, say you wanted to model the population of eagles and frogs in a particular habitat. Each year, the population of frogs double while the population of eagles halves. By creating a suitable expression that describes the decrease of eagles and the increase of frogs in this ecosystem, we can make predictions and identify trends in their population.
In this article, we will discuss expressions, what they look like, and how to factorise and simplify them.
Defining an Expression
An expression can be used to describe a scenario when an unknown number is present or when a variable value exists. It helps solve real-world problems in a more simplified and explicit manner.
A variable value is a value that changes over time.
To construct an expression of this kind, you would need to determine which quantity is unknown in the circumstance, and then define a variable to represent it. Before we dive into this topic further, let us first define expressions.
Expressions are mathematical statements that have two terms at least that contain variables, numbers, or both. Expressions are such that they contain also at least, one mathematical operation; addition, subtraction, multiplication, and division.
Let’s see an example of an expression.
The following is a mathematical expression,
[2x+1]
because it contains one variable, (x), two numbers, (2) and (1), and one mathematical operation, (+).
Expressions are very organised, in a way that a statement that has an operator come right after another one is not a valid expression. For example,
[2x+times 1.]
They are also organised in the sense that when a parenthesis opens, there needs to be a close. For example,
[3(4x+2)-6]
is a valid expression. However,
[6-4(18x]
is not a valid expression.
Components of an Expression
Expressions in algebra contain at least a variable, numbers, and an arithmetic operation. However, there are quite a number of terms related to the parts of an expression. These elements are described below.
-
Variables: Variables are the letters that represent an unknown value in a mathematical statement.
-
Terms: Terms are either numbers or variables (or numbers and variables) multiplying and dividing each other and are separated by either the addition (+) or subtraction sign (-).
-
Coefficient: Coefficients are the numbers that multiply variables.
-
Constant: Constants are the numbers in expressions that do not change.
Components of an expression
Examples of Expressions
Here are some examples of mathematical expressions.
1) ((x+1)(x+3))
2) (6a+3)
3) (6x-15y+12)
4) (y^2+4xy)
5) (frac{x}{4}+frac{x}{5})
Notice that all of them contain the necessary components to be considered expressions. They all have variables, numbers, and at least one mathematical operation composing them.
In particular, in the first example, you will find a multiplication implicit in the parenthesis that connects the two terms (x+1) and (x+3); so it is a valid expression. In the fourth example, in the second term, variables (x) and (y) are multiplying and it’s written as (xy). So, that one is also a valid expression.
Writing Expressions
In this segment of our discussion, we will be introduced to writing expressions, particularly translating word problems into mathematical ones. Such skill is important when solving a given question. By doing so, we can visualise anything in terms of numbers and arithmetic operations!
Translating Word Problems into Expressions
Given a sentence that illustrates a mathematical statement, we can translate them into expressions that involve the appropriate components of expressions we had mentioned before and mathematical symbols. The table below demonstrates several examples of word problems that have been translated into expressions.
|
Phrase |
Expression |
|
Five more than a number |
[x+5] |
|
Three-fourths of a number |
[frac{3y}{4}] |
|
Eight larger than a number |
[a+8] |
|
The product of a number with twelve |
[12z] |
|
The quotient of a number and nine |
[frac{x}{9}] |
Types of Maths Expressions
Numerical Expressions
In comparison to what expressions are, there are expressions that do not contain variables. These are called numerical expressions.
Numerical expressions are a combination of numbers with mathematical operators separating them.
They could be as long as possible, containing as many mathematical operators as possible also.
Here are a few examples of numerical expressions.
1) (13-3)
2) (3-7+14-9)
3) (12+frac{4}{17}-2times 11+1)
4) (4-2-1)
Algebraic Expressions
Algebraic expressions are expressions that contain unknowns. Unknowns are variables that are often represented by letters. In most cases throughout our syllabus, these letters are (x), (y) and (z).
However, we may sometimes get expressions that comprise Greek letters as well. For instance, (alpha), (beta) and (gamma). Below are several examples of algebraic expressions.
1) (frac{2x}{7}+3y^2)
2) (4alpha-3beta + 15)
3) (x^2+3y-4z)
Evaluating Maths Expressions
In this section, we will be introduced to evaluating math expression. Here, we would essentially solve a given expression based on the arithmetic operations between the numbers or variables. These basic arithmetic operations (or mathematical symbols) include addition, subtraction, multiplication and division. We will also see how these operations can help us factorise and simplify such expressions.
Addition and Subtraction of Expressions
Addition and subtraction are the primary actions done when adding and subtracting fractions. These are performed on like terms. There are two steps to consider here, namely
-
Step 1: Identify and rearrange like terms to be grouped.
-
Step 2: Add and subtract like terms.
Below is a worked example.
Add the expressions (5a-7b+3c) and (-4a-2b+3c).
Solution
Step 1: We will first put the two expressions together so we can rearrange them.
[5a-7b+3c+(-4a-2b+3c)]
Then,
[5a-7b+3c-4a-2b+3c]
Next,
[5a-4a-7b-2b+3c+3c]
Step 2: We can now successfully add all the like terms.
[a-9b+6c]
Here is another worked example for you.
Add the expressions
(7x^2+8y-9y), (3y+2-3x^2) and (3-y+3x^2).
Solution
Step 1: We will note them down so that they can be rearranged
[7x^2+8y-9+3y+2-3x^2+3-y+3x^2]
Then,
[7x^2+3x^2-3x^2+8y-y+3y-9+2+3]
Step 2: Add the like terms
[7x^2+10y-4]
Factorising Expressions
This is an important element when it comes to dealing with expressions. It helps us group like terms in order for us to perform arithmetic operations more structured manner.
Factorising is the process of reversing the expansion of brackets.
The factorised form of expressions is always in brackets. The process involves taking out the highest common factors (HCF) from all the terms such that when the factors are taken out and multiplied by the values in the brackets, we will arrive at the same expression we had in the first place.
For example, say you had the expression below.
[4x^2+6x]
Notice here that the coefficients of (x^2) and (x) both have a factor of 2 since 4 and 6 are divisible by 2. Furthermore, (x^2) and (x) have a common factor of (x). Thus, you can take these two factors out of this expression, making the factories form equivalent to
[2x(2x+3)]
Let’s explain this again with another example.
Factorise the expression
[6x+9]
Solution
To factorise this we need to find the HCF of (6x) and 9. That value happens to be 3. Therefore, we will note down the value and account for the bracket.
[3(?+?)]
The sign in the bracket above is gotten from the sign in the initial expression. To find out what values must be in the brackets, we will divide the terms in the expressions that we factorised the 3 from by the 3.
[frac{6x}{3}=2x]
and
[frac{9}{3}=3]
Then, we will arrive at
[3(2x+3)]
We can evaluate to see if the answer we have is right by expanding the brackets.
[(3times 2x)+(3times 3)=6x+9]
as we had before!
Let’s go through one more example.
Simplify the expression
[3y^2+12y]
Solution
We will need to find the HCF. Usually, these can be broken down just if they are a bit too complex at first. Looking at the coefficients, we realise that 3 is the HCF. That will be taken outside the bracket.
[3(?+?)]
We can now divide the expression from which the 3 was factored by the 3.
[frac{3y^2}{3}=y^2]
and
[frac{12y}{3}=4y]
This leaves us with the expression;
[3(y^2+4y)]
However, carefully looking at the expression, we will notice that this can be factored further. (y) can be factored out of the expression in the bracket.
[3y(?+?)]
We will go over the process again by dividing the values that y has been factored from by (y).
[frac{y^2}{y}=y]
and
[frac{4y}{y}=4]
This leaves us with the final expression in its factored form;
[3y(y+4)]
We can evaluate this by expanding the brackets.
[(3ytimes y)+(3ytimes 4)=3y^2+12y]
which again, is what we had at the beginning.
Simplifying Expressions
The term simplifying stems from the root word «simple». As the word suggests, simplifying a given expression allows us to solve them more efficiently. When we simplify an expression, we are reducing it into a simpler form by cancelling common factors and regrouping terms that share the same variable.
Simplifying expressions is the process of writing expressions in their most compact and simplest forms such that the value of the original expression is maintained.
This avoids all the lengthy working you might have to perform that may result in unwanted careless mistakes. Surely, you wouldn’t want to have any arithmetic errors now, would you?
There are three steps to follow when simplifying expressions.
-
Eliminate the brackets by multiplying out the factors (if any are present);
-
Remove exponents by using the exponent rules;
-
Add and subtract like terms.
Let’s go through some worked examples.
Simplify the expression
[3x+2(x-4).]
Solution
Here, we will first operate on the brackets by multiplying the factor (outside the bracket) by what is in the brackets.
[3x+2x-8]
We will add like terms, which will give us our simplified form as
[5x-8]
which indeed holds the same value as the expression we had in the beginning.
Here is another example.
Simplify the expression
[x(4-x)-x(3-x).]
Solution
With this problem, we will deal with the brackets first. We will multiply the factors by elements of the brackets.
[x(4-x)-x(3-x)]
This yields,
[4x-x^2-3x+x^2]
We can go ahead here to rearrange them such that like terms are grouped close together.
[4x-3x-x^2+x^2]
Let us now do the additions and subtractions, which will in turn leave us with:
[4x-3x-x^2+x^2=x]
Expressions — Key takeaways
- Expressions are mathematical statements that have two terms at least that contain variables, numbers, or both.
- Terms are either numbers or variables or numbers and variables multiplying each other.
- Numerical expressions are a combination of numbers with mathematical operators separating them.
- Factorising is the process of reversing the expansion of brackets.
- The factorising process involves taking out the highest common factors (HCF) from all the terms such that when the factors are taken out and multiplied by the values in the brackets, we will arrive at the same expression we had in the first place.
- Simplifying expressions is the process of writing expressions in their most compact and simplest forms such that the value of the original expression is maintained.
From Wikipedia, the free encyclopedia
In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.
Many authors distinguish an expression from a formula, the former denoting a mathematical object, and the latter denoting a statement about mathematical objects.[citation needed] For example, 


Examples[edit]
The use of expressions ranges from the simple:
-
(linear polynomial)
-
(quadratic polynomial)
-
(rational fraction)
to the complex:
Syntax versus semantics[edit]
Syntax[edit]
An expression is a syntactic construct. It must be well-formed: the allowed operators must have the correct number of inputs in the correct places, the characters that make up these inputs must be valid, have a clear order of operations, etc. Strings of symbols that violate the rules of syntax are not well-formed and are not valid mathematical expressions.
For example, in the usual notation of arithmetic, the expression 1 + 2 × 3 is well-formed, but the following expression is not:
.
Semantics[edit]
Semantics is the study of meaning. Formal semantics is about attaching meaning to expressions.
In algebra, an expression may be used to designate a value, which might depend on values assigned to variables occurring in the expression. The determination of this value depends on the semantics attached to the symbols of the expression. The choice of semantics depends on the context of the expression. The same syntactic expression 1 + 2 × 3 can have different values (mathematically 7, but also 9), depending on the order of operations implied by the context (See also Operations § Calculators).
The semantic rules may declare that certain expressions do not designate any value (for instance when they involve division by 0); such expressions are said to have an undefined value, but they are well-formed expressions nonetheless. In general the meaning of expressions is not limited to designating values; for instance, an expression might designate a condition, or an equation that is to be solved, or it can be viewed as an object in its own right that can be manipulated according to certain rules. Certain expressions that designate a value simultaneously express a condition that is assumed to hold, for instance those involving the operator 
Formal languages and lambda calculus[edit]
Formal languages allow formalizing the concept of well-formed expressions.
In the 1930s, a new type of expressions, called lambda expressions, were introduced by Alonzo Church and Stephen Kleene for formalizing functions and their evaluation. They form the basis for lambda calculus, a formal system used in mathematical logic and the theory of programming languages.
The equivalence of two lambda expressions is undecidable. This is also the case for the expressions representing real numbers, which are built from the integers by using the arithmetical operations, the logarithm and the exponential (Richardson’s theorem).
Variables[edit]
Many mathematical expressions include variables. Any variable can be classified as being either a free variable or a bound variable.
For a given combination of values for the free variables, an expression may be evaluated, although for some combinations of values of the free variables, the value of the expression may be undefined. Thus an expression represents a function whose inputs are the values assigned to the free variables and whose output is the resulting value of the expression.[citation needed]
For example, the expression
evaluated for x = 10, y = 5, will give 2; but it is undefined for y = 0.
The evaluation of an expression is dependent on the definition of the mathematical operators and on the system of values that is its context.
Two expressions are said to be equivalent if, for each combination of values for the free variables, they have the same output, i.e., they represent the same function. Example:
The expression
has free variable x, bound variable n, constants 1, 2, and 3, two occurrences of an implicit multiplication operator, and a summation operator. The expression is equivalent to the simpler expression 12x. The value for x = 3 is 36.
See also[edit]
- Algebraic closure
- Algebraic expression
- Analytic expression
- Closed-form expression
- Combinator
- Computer algebra expression
- Defined and undefined
- Equation
- Expression (programming)
- Formal grammar
- Formula
- Functional programming
- Logical expression
- Term (logic)
- Well-defined expression
Notes[edit]
References[edit]
- Redden, John (2011). «Elementary Algebra». Flat World Knowledge. Archived from the original on 2014-11-15. Retrieved 2012-03-18.
An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation. This math operation can be addition, subtraction, multiplication, or division. The structure of an expression is:
Expression is (Number/variable, Math Operator, Number/variable)
Expression Examples:
| Example 1: | $7 + 9$ |
| Example 2: | $23.5 times 4$ |
| Example 3: | $37text{s}$ $–$ $6text{t}$ |
| Example 4: | $25text{a}^4 + 9$ $–$ $4 ÷ 15$ |
In all the given expressions, a math operator is used between the two numbers.
Non Examples of Expressions:
Example 1: a
Example 2: $4$
Example 3: $7.89$
Related Games
Parts of an Expression in Math
An expression in Math is made up of the following:
a) Constant: it is a fixed numerical value.
Example: $7, 45, 4frac{1}{3}, −18, sqrt{5}, 7 + sqrt{11}$
b) Variables: they do not take any fixed values. Values are assigned according to the requirement.
Example: a, p, z
c) Terms: can be constants, variables or constants multiplied by variable/(s). Each term in an expression is separated by ‘+’ sign or ‘−’ sign
Example: In $5text{a} + 2text{b}$ $-$ $7$ the terms are: $5text{a}, 2text{b}$, and $7$.
d) Operators: The four operations of addition (+) , subtraction (−),multiplication (×), division (÷) are used to combine the terms of an expression and are called operators.
Related Worksheets
Types of Expression in Math
Numerical Expression
Numerical expression in Math consists of numbers and arithmetic operators. It does not contain any unknown variables, equality or inequality symbols.
Examples:
$65 + 9$ $–$ $4$
$frac{25}{4}+frac{36}{5}$
$42 div 7 times 4$ $–$ $9 + 7$
$14.5 + 9$
Algebraic Expression
An algebraic expression consists of unknown variables, numbers and arithmetic operators. It does not contain any equality or inequality symbols.
Examples:
$5z$
$3text{x}^2 + 5$
$frac{2}{5}text{a}$ $-$ $frac{7}{11}text{b} + 4.5text{c}$
$0.2text{p}^3$ $text{q}^2 + frac{2}{5}$ $text{p}^2$ $text{q}$
Types of Algebraic Expressions
Algebraic expressions are classified on the basis of the number of terms in the expression. The various types of algebraic expressions are:
- Monomial expressions contain only one term. E.g. $4text{x}$
- Binomial expressions contain two unlike terms. E.g. $2text{xy} +x$
- Trinomial expressions contain only three unlike terms. E.g. $3text{t}2$ $-$ $4text{t} + 9$
- Polynomial expressions have two or more terms. This includes binomials and trinomials too and all other expressions with four or more terms. E.g. $2text{x} + 3text{y} + 5text{z}; 4text{t} + 5$ $−$ $4text{u} + text{z}$
Expression vs Equation
A math expression is different from a math equation.
The difference between expressions and equations is that an expression signifies a combination of numbers, variables, and operation symbols whereas an equation will always use an equal (=) operator between two math expressions. Also both sides of the “equal to” sign have the same value.
For example,
| Expression | Equation |
| $22 + 5$ | $22 + 5 = 29$ $–$ $2$ |
| $9 times 5$ | $9 times 5 = 45$ |
| $50 div 10$ | $45 div 9 = 50 div 10$ |
| $15 + 7$ $–$ $6$ | $15 + 7$ $–$ $6 = 16$ |
| $25 + 7$ | $25 + 7 = 64 div 2$ |
| $20 times 5$ | $20 times 5 = 100$ |
Where are expressions used?
Expressions help us in solving word problems. Math expressions are formed using the words of a problem.
Let’s consider the following problem as an example:
Let’s consider a word problem and learn how to write expressions in math
1. Tom has to fill a box with oranges and apples. The number of apples should be 5 more than oranges. Tom picks 3 oranges each time and repeats it 5 times. Count the total number of oranges and apples.
To solve this, formulate the math expressions as follows:
Number of oranges = $3 times 5$
Number of oranges = $15$
Number of apples = Number of oranges $ + 5$
Number of apples = $15 + 5$
Number of apples = $20$
Total number of fruits = Number of oranges + Number of apples
Third math expression will be:
Total number of fruits = $15 + 20$ (Substituting the value of number of oranges and apples)
$= 35$
2. A class of students are going on a trip. Each student has to pay an individual fee of $$$8 and a group fee of $$$30. Write an algebraic expression for the total cost of the trip. Find the total cost of the trip if there are 56 students going on the trip.
Let n represent the number of students.
Algebraic expression will be:
$$$8n + $$$30
To find the total cost of the trip, when n = 56.
$$$8n + $$$30
$$$8(56) + $$$30 (Substituting n with 56)
$$$448 + $$$30
$$$478
PEDMAS
PEDMAS is an acronym where P stands for parenthesis, E for exponents, D for division, M for multiplication, A for addition, and S stands for subtraction.
The order of the letters indicate the order in which the operation must be performed.
The operations of multiplication and division have the same level of priority. Always perform the operation which appears first from left to right.
Similarly addition and subtraction have the same level of priority. Here also perform the one that appears first from left to right.
Example:
$(15 div 3 times 4$ $−$ $7) + (19$ $−$ $4^2)$
$= (5 × 4 − 7) + × (19 − 16)$
$= (20 − 7) + 3$
$= 13 + 3$
$= 16$
Application:
The knowledge of applying math operations on numbers is the first step towards building basic arithmetic reasoning and logic in children. Formulation of math expressions using the respective skill lays a strong foundation to learn algebra and translate real-life problems in suitable mathematical models.
Solved Examples on Expression:
Example 1: Write whether each is an expression or an equation.
| (a) $4 + 8$ | (b) $4 + 12 = 16$ | (c) $5 times 35$ |
| (d) $16 div 4 + 9$ $–$ $2$ | (e) $8 times 4 div 2 = 16$ | (f) $72+94$ |
Solution:
| Expression | Equation |
| $4 + 8$ | $4 + 12 = 16$ |
| $5 times 35$ | $8 times 4 div 2 = 16$ |
| $16 div 4 + 9$ $–$ $2$ | |
| $72+94$ |
Example 2: Write each word phrase as an expression.
- The sum of $10$ and $14$
- 3 more than a number $7$
- Two times $11$, increased by $1$
- 19 less than the product of $15$ and $4$
- The quotient of $33$ and $3$
Solution:
- $10 + 14$
- $7 + 3$
- $2 times 11 + 1$
- $15 times 4$ $–$ $19$
- $33 div 3$
Example 3: Classify the following expression as arithmetic or algebraic.
- $4text{a}$ $–$ $7text{b}$
- $23 + 42$ $–$ $6$
- $715$ $-$ $911$
- $2$ $-$ $5text{x}9text{y}$
- $22$ $–$ $5 + 8$
- $7text{y} + 19text{x}$ $–$ $4text{z}$
Solution:
| Arithmetic | Algebraic |
| $23 + 42$ $–$ $6$ | $4text{a}$ $–$ $7text{b}$ |
| $22$ $–$ $5 + 8$ | $7text{y} + 19text{x}$ $–$ $4text{z}$ |
| $715$ $-$ $911$ | $2$ $-$ $5x9y$ |
Example 4: Write the terms of the given expression $4uv + 7u − 9z + 6z$.
Solution:
$4text{uv}, 7text{u}$, $−$ $9text{z}$ and $6text{z}$ are terms of the given expression.
Example 5: A book has $250$ pages. Ron has $62$ pages left to read. Write an expression to find the number of pages he has read.
Solution:
$250$ $–$ $62$
Example 6: $X$, $Y$, and $Z$ have a few hairbands. $Y$ has $20$ more hairbands than $X$. $Z$ says that she has five more hairbands than the number of headbands that $X$ and $Y$ together have. Express this in the form of an expression?
Solution: Let the number of hair bands with $X$ be$ = text{x}$.
Then, $Y$ has $(text{x}+20)$ hairbands.
$Z$ has $text{x} + (text{x}+20) + 5=2text{x}+25$ hairbands.
Therefore, $Z$ has $(2text{x}+25)$ hairbands.
Practice Problem
$6 + 8 = 14$
$0$ $–$ $16 =$ $–$ $16$
$frac{4}{7}+ frac{4}{7}$ $-$ $frac{1}{7}$
$5text{x}$ $-$ $7text{y}=15$
Correct answer is: $frac{4}{7}+ frac{4}{7}$ $-$ $frac{1}{7}$
As it has numbers (fraction) and mathematical operators, other options are equations as it has equal $(=)$ operator between two math expressions.
$3text{a}+7text{b}$ $-$ $6text{c}=5text{x}$
$9$ $-$ $5text{w}$
$frac{1}{2}+frac{3}{4}$
$44 + 55$
Correct answer is: $9$ $-$ $5text{w}$
It contains variables, numbers, and mathematical operator.Option (a) is an equation, option (c) and option (d) are arithmetic expressions not algebraic as no variables are involved.
Monomial
Binomial
Trinomial
None of these
Correct answer is: Trinomial
If there are three terms in an expression, we call it trinomial expression.
Variable
Constant
Term
Coefficient
Correct answer is: Constant
The term that does not change its value is called a constant.
$3times14$
$10$ $−$ $3 times 14$
$3 times 10$ $−$ $14$
$3 times 14$ $−$ $10$
Correct answer is: $3 times 14$ $−$ $10$
Three times a number 14 is $3 times 14$.
This decreased by 10 equals $3 times 14$ $−$ $10$
$$$$(9.75 + 40)$
$$$$(40 $–$ 9.75)$
$$$$(9.75 times 40)$
$$$$(9.75 $–$ 40)$
Correct answer is: $$$$(9.75 times 40)$
Amount earned in an hour $=$ $$$9.75
Amount earned in 40 hours $=$ $$$$(9.75 times 40)$
Frequently Asked Questions
What is an expression in maths?
An expression is a set of numbers or variables combined using the operations $+$, $–$, $times$ or $div$.
What are types of expression?
Arithmetic expression that contains only numbers and mathematical operators and algebraic expression that contains variables, numbers and mathematical operators.
Can we solve a math expression?
No, we cannot solve a math expression as it does not have an ‘equal to’ sign $( = )$ but we can simplify expressions.
What is the difference between arithmetic expression and algebraic expression?
Mathematical expressions have only numbers and operators, while algebraic expressions have both numbers and variables in terms, separated by operators in between.
Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division. For example, x + y is an expression, where x and y are terms having an addition operator in between. In math, there are two types of expressions, numerical expressions — that contain only numbers; and algebraic expressions- that contain both numbers and variables.
In this article, we will discuss the concept of expressions in math and their different types. We will also understand the difference between an expression and an equation in a tabular way and different types of expressions with the help of examples for a better understanding.
| 1. | |
| 2. | Types of Expressions in Math |
| 3. | Expression vs Equation |
| 4. | Simplifying Expression in Math |
| 5. | FAQs on Expressions in Math |
What is an Expression in Math?
An expression in math is a sentence with a minimum of two numbers/variables and at least one math operation in it. Let us understand how to write expressions. A number is 6 more than half the other number, and the other number is x. This statement is written as x/2 + 6 in a mathematical expression. Mathematical expressions are used to solve complicated puzzles.
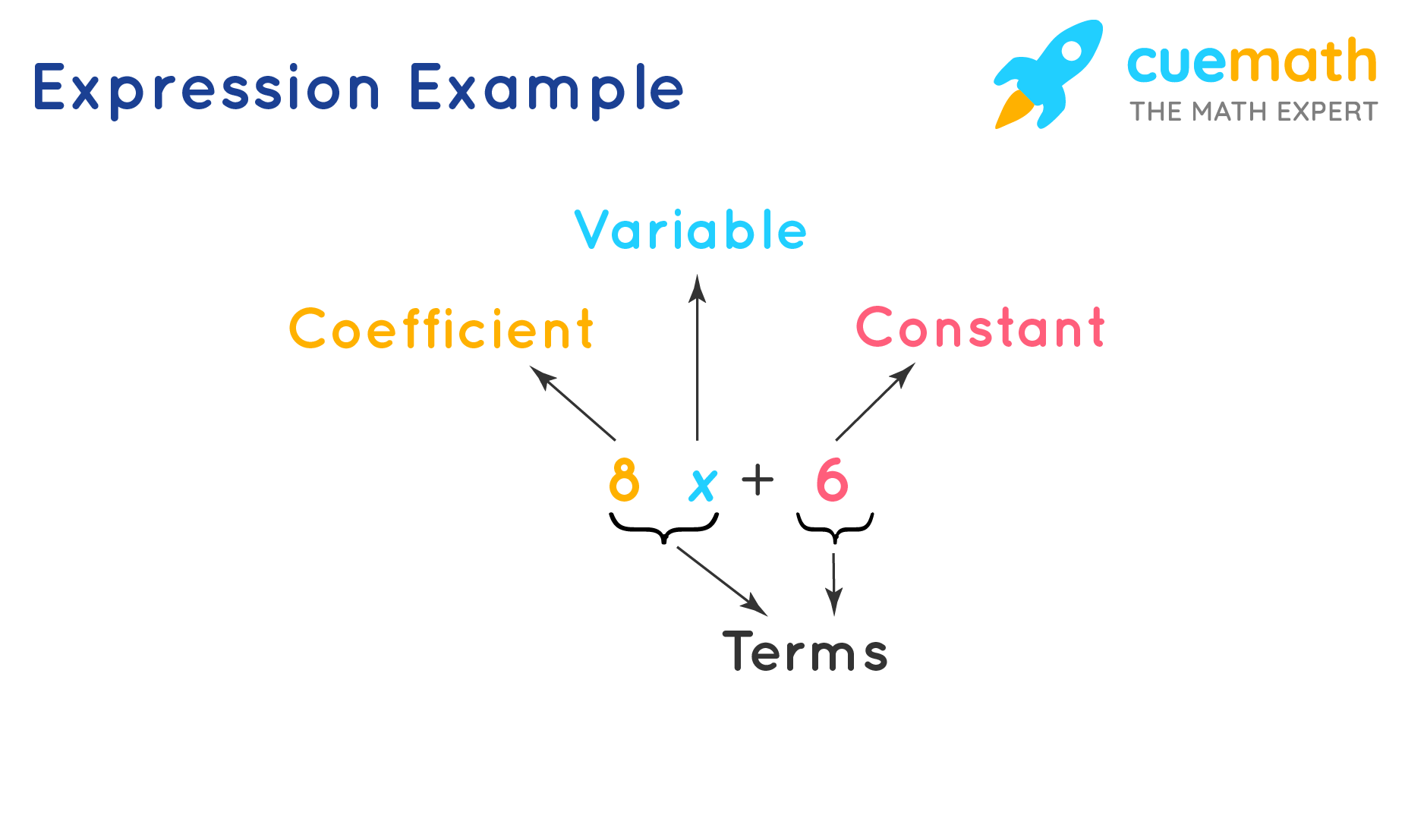
Expression Definition in Math
An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division. The terms involved in an expression in math are:
- Constant: A constant is a fixed numerical value.
- Variable: A variable is a symbol that doesn’t have a fixed value.
- Term: A term can be a single constant, a single variable, or a combination of a variable and a constant combined with multiplication or division.
- Coefficient: A coefficient is a number that is multiplied by a variable in an expression.
Expression in Math Example
There are infinite examples of an expression. For example, 2y-9, 3a×2, -7+6÷3, etc. Let us also look at a real-life example. Sarah told her younger brother Daniel that her age is 3 more than twice his age. She asked him to calculate her age if his age is x years. Let’s help him write an expression. Twice the age of Daniel can be written as 2x. Now Sarah’s age is 3 more than 2x. Therefore, Sarah’s age will be written as 2x+3.
Types of Expressions in Math
There are three basic types of mathematical expressions. Based on the terms that they have, they can be classified as arithmetic/numerical expressions, fractional expressions, and algebraic expressions. Let us learn more about each of them with the help of the table given below:
| Types of Mathematical Expressions | Definition of Expression | List of Mathematical Expressions |
|---|---|---|
| Numerical Expression | Contains only numbers and mathematical operators | 40-5+2 |
| Fractional Expression | Contains fractional numbers and mathematical operators | 5/3 — 7/6 |
| Algebraic Expression | Contains variables, numbers, and mathematical operators | 3x+2y |
Now, algebraic expressions are further classified into monomials, binomials, trinomials, etc. They are also termed as polynomials. Let us look at the types of algebraic expressions in the table given below:
| Category | Definition of Expression | Examples |
|---|---|---|
| Monomial | An expression having a single term with non-negative exponential integers. | 2x2 |
| Binomial | An expression formed by the addition or subtraction of two monomials. | 2x2+5xy |
| Trinomial | An expression formed by the addition or subtraction of three monomials. | 2x2+5xy+4yz |
| Polynomial | An expression formed by one or more monomials. | 2x2+5xy+4yz+2y+3 |
Expression vs Equation
In math, expressions and equations are two different concepts. Let us try to understand the difference between the two. An expression can be a number, a variable, or a combination of numbers and variables connected by mathematical operators, i.e., addition, subtraction, multiplication, and division. On the other hand, an equation is the equality relation between two expressions. Look at the table given below to understand it better:
| Expression | Equation |
|---|---|
| Expressions are only one-sided. | Equations are two-sided (left side and right side) |
| Expressions can be simplified to have a numerical answer. | Equations can be solved to verify the equality or to find the missing values. |
| Expression is the combination of terms having operators in between. |
Equation is the combination of two expressions having an ‘equal to’ (=) in between. |
| Example: 3x-8 | Example: 3x-8=16 |
Look at a few more examples of expressions and equations through the figure given below:
Simplifying Expression in Math
Expressions can be simplified to form an answer. For example, 3+6-2 is an expression that can be simplified to 7. There are two different ways to simplify arithmetic expressions and algebraic expressions. We use the BODMAS rule (PEMDAS rule) to simplify them. In case of algebraic expressions, like terms can be added or subtracted for simplification. Like terms are those that have the same variable raised to the same power. So, we can easily add or subtract two or more like terms by adding their coefficients. For example, 2x+5x results in 7x, whereas 7ab-b is an expression that has two unlike terms, which cannot be added.
In the case of expressions having multiple terms and operators, we apply the PEMDAS rule (BODMAS rule). For example, let us simplify 23 — 6 + 7 × 3. Here, as there are no brackets and exponents, we will first evaluate 7 × 3 which is 21. Now, the expression is 23-6+21. Now, there are two operators, addition and subtraction. Since both are same level operations and subtraction is first from the left side, we will subtract 6 from 23, i.e., 17. Now our expression has become 17+21, which results in 38 and 38 is the simplified value of the expression 23 — 6 + 7 × 3.
Important Notes on Expressions in Math:
- An expression has 3 parts: constant, variable, and term.
- There are 3 types of expressions: arithmetic/numerical, fractional, and algebraic.
- Polynomial is a type of variable expression.
Related Articles
- Division of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Addition of Algebraic Expressions
- Simplifying Rational Expressions
FAQs on Expressions in Math
What is Expression in Math?
Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. We have different types of expressions in math such as numerical expressions, algebraic expressions, fractional expressions, etc.
How do you Identify Like Terms in Mathematical Expressions?
Like terms, in an expression have the same variables raised to the same power. For example, 5x, −x, and −3x are all like terms.
How do you Write an Expression in Math?
We write an expression in math by using numbers or variables and mathematical operators which are addition, subtraction, multiplication, and division. For example, the expression of the mathematical statement «4 added to 2», will be 2+4.
What is a Numerical Expression?
A numerical expression consists of numbers and operators. Numerical expressions are also called number expressions. Examples of number expressions are 8 — 7, 3 + 6 × 7 — 3, etc.
How Many Terms are there in an Expression?
There can be any number of terms in an expression. Expression is a mathematical phrase that consists of terms separated by operators in between. So, we can have an expression with 1 term, 2 terms, 3 terms, or n number of terms.
What is the Difference Between Mathematical Expression and Algebraic Expression?
Generally, mathematical expressions or numerical expressions have only numbers and operators, while algebraic expressions have both numbers and variables in terms, separated by operators in between.
Can you Solve an Expression in Math?
Since expressions do not have an ‘equal to’ sign (=) we cannot solve them. We can only simplify expressions and find their reduced form using the given mathematical operators.
How to Simplify Expressions in Math?
We can simplify expressions in math by reducing the given expression in the simplest form. If it is a numerical expression, then it can be simplified by finding the value of the expression. If it is an algebraic expression, then it can be simplified by reducing it to the simplest form such that it cannot further be reduced.