In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.[2][3] The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.[4]
Solving an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables.[5][6]
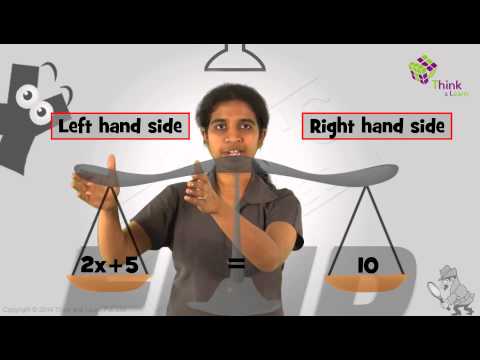
An equation is written as two expressions, connected by an equals sign («=»).[2] The expressions on the two sides of the equals sign are called the «left-hand side» and «right-hand side» of the equation. Very often the right-hand side of an equation is assumed to be zero. This does not reduce the generality, as this can be realized by subtracting the right-hand side from both sides.
The most common type of equation is a polynomial equation (commonly called also an algebraic equation) in which the two sides are polynomials.
The sides of a polynomial equation contain one or more terms. For example, the equation
has left-hand side 

An equation is analogous to a scale into which weights are placed. When equal weights of something (e.g., grain) are placed into the two pans, the two weights cause the scale to be in balance and are said to be equal. If a quantity of grain is removed from one pan of the balance, an equal amount of grain must be removed from the other pan to keep the scale in balance. More generally, an equation remains in balance if the same operation is performed on its both sides.
In Cartesian geometry, equations are used to describe geometric figures. As the equations that are considered, such as implicit equations or parametric equations, have infinitely many solutions, the objective is now different: instead of giving the solutions explicitly or counting them, which is impossible, one uses equations for studying properties of figures. This is the starting idea of algebraic geometry, an important area of mathematics.
Algebra studies two main families of equations: polynomial equations and, among them, the special case of linear equations. When there is only one variable, polynomial equations have the form P(x) = 0, where P is a polynomial, and linear equations have the form ax + b = 0, where a and b are parameters. To solve equations from either family, one uses algorithmic or geometric techniques that originate from linear algebra or mathematical analysis. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.
Differential equations are equations that involve one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model processes that involve the rates of change of the variable, and are used in areas such as physics, chemistry, biology, and economics.
The «=» symbol, which appears in every equation, was invented in 1557 by Robert Recorde, who considered that nothing could be more equal than parallel straight lines with the same length.[1]
Introduction[edit]
Analogous illustration[edit]
Illustration of a simple equation; x, y, z are real numbers, analogous to weights.
An equation is analogous to a weighing scale, balance, or seesaw.
Each side of the equation corresponds to one side of the balance. Different quantities can be placed on each side: if the weights on the two sides are equal, the scale balances, and in analogy, the equality that represents the balance is also balanced (if not, then the lack of balance corresponds to an inequality represented by an inequation).
In the illustration, x, y and z are all different quantities (in this case real numbers) represented as circular weights, and each of x, y, and z has a different weight. Addition corresponds to adding weight, while subtraction corresponds to removing weight from what is already there. When equality holds, the total weight on each side is the same.
Parameters and unknowns[edit]
Equations often contain terms other than the unknowns. These other terms, which are assumed to be known, are usually called constants, coefficients or parameters.
An example of an equation involving x and y as unknowns and the parameter R is
When R is chosen to have the value of 2 (R = 2), this equation would be recognized in Cartesian coordinates as the equation for the circle of radius of 2 around the origin. Hence, the equation with R unspecified is the general equation for the circle.
Usually, the unknowns are denoted by letters at the end of the alphabet, x, y, z, w, …, while coefficients (parameters) are denoted by letters at the beginning, a, b, c, d, … . For example, the general quadratic equation is usually written ax2 + bx + c = 0.
The process of finding the solutions, or, in case of parameters, expressing the unknowns in terms of the parameters, is called solving the equation. Such expressions of the solutions in terms of the parameters are also called solutions.
A system of equations is a set of simultaneous equations, usually in several unknowns for which the common solutions are sought. Thus, a solution to the system is a set of values for each of the unknowns, which together form a solution to each equation in the system. For example, the system
has the unique solution x = −1, y = 1.
Identities[edit]
An identity is an equation that is true for all possible values of the variable(s) it contains. Many identities are known in algebra and calculus. In the process of solving an equation, an identity is often used to simplify an equation, making it more easily solvable.
In algebra, an example of an identity is the difference of two squares:
which is true for all x and y.
Trigonometry is an area where many identities exist; these are useful in manipulating or solving trigonometric equations. Two of many that involve the sine and cosine functions are:
and
which are both true for all values of θ.
For example, to solve for the value of θ that satisfies the equation:
where θ is limited to between 0 and 45 degrees, one may use the above identity for the product to give:
yielding the following solution for θ:
Since the sine function is a periodic function, there are infinitely many solutions if there are no restrictions on θ. In this example, restricting θ to be between 0 and 45 degrees would restrict the solution to only one number.
Properties[edit]
Two equations or two systems of equations are equivalent, if they have the same set of solutions. The following operations transform an equation or a system of equations into an equivalent one – provided that the operations are meaningful for the expressions they are applied to:
- Adding or subtracting the same quantity to both sides of an equation. This shows that every equation is equivalent to an equation in which the right-hand side is zero.
- Multiplying or dividing both sides of an equation by a non-zero quantity.
- Applying an identity to transform one side of the equation. For example, expanding a product or factoring a sum.
- For a system: adding to both sides of an equation the corresponding side of another equation, multiplied by the same quantity.
If some function is applied to both sides of an equation, the resulting equation has the solutions of the initial equation among its solutions, but may have further solutions called extraneous solutions. For example, the equation 




The above transformations are the basis of most elementary methods for equation solving, as well as some less elementary ones, like Gaussian elimination.
Algebra[edit]
Polynomial equations[edit]
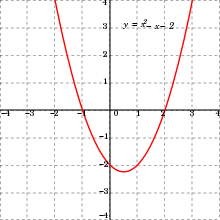
The solutions –1 and 2 of the polynomial equation x2 – x + 2 = 0 are the points where the graph of the quadratic function y = x2 – x + 2 cuts the x-axis.
In general, an algebraic equation or polynomial equation is an equation of the form
, or
[a]
where P and Q are polynomials with coefficients in some field (e.g., rational numbers, real numbers, complex numbers). An algebraic equation is univariate if it involves only one variable. On the other hand, a polynomial equation may involve several variables, in which case it is called multivariate (multiple variables, x, y, z, etc.).
For example,
is a univariate algebraic (polynomial) equation with integer coefficients and
is a multivariate polynomial equation over the rational numbers.
Some polynomial equations with rational coefficients have a solution that is an algebraic expression, with a finite number of operations involving just those coefficients (i.e., can be solved algebraically). This can be done for all such equations of degree one, two, three, or four; but equations of degree five or more cannot always be solved in this way, as the Abel–Ruffini theorem demonstrates.
A large amount of research has been devoted to compute efficiently accurate approximations of the real or complex solutions of a univariate algebraic equation (see Root finding of polynomials) and of the common solutions of several multivariate polynomial equations (see System of polynomial equations).
Systems of linear equations[edit]
A system of linear equations (or linear system) is a collection of linear equations involving one or more variables.[b] For example,
is a system of three equations in the three variables x, y, z. A solution to a linear system is an assignment of numbers to the variables such that all the equations are simultaneously satisfied. A solution to the system above is given by
since it makes all three equations valid. The word «system» indicates that the equations are to be considered collectively, rather than individually.
In mathematics, the theory of linear systems is a fundamental part of linear algebra, a subject which is used in many parts of modern mathematics. Computational algorithms for finding the solutions are an important part of numerical linear algebra, and play a prominent role in physics, engineering, chemistry, computer science, and economics. A system of non-linear equations can often be approximated by a linear system (see linearization), a helpful technique when making a mathematical model or computer simulation of a relatively complex system.
Geometry[edit]
Analytic geometry[edit]
The blue and red line is the set of all points (x,y) such that x+y=5 and —x+2y=4, respectively. Their intersection point, (2,3), satisfies both equations.
A conic section is the intersection of a plane and a cone of revolution.
In Euclidean geometry, it is possible to associate a set of coordinates to each point in space, for example by an orthogonal grid. This method allows one to characterize geometric figures by equations. A plane in three-dimensional space can be expressed as the solution set of an equation of the form 






A conic section is the intersection of a cone with equation 
The use of equations allows one to call on a large area of mathematics to solve geometric questions. The Cartesian coordinate system transforms a geometric problem into an analysis problem, once the figures are transformed into equations; thus the name analytic geometry. This point of view, outlined by Descartes, enriches and modifies the type of geometry conceived of by the ancient Greek mathematicians.
Currently, analytic geometry designates an active branch of mathematics. Although it still uses equations to characterize figures, it also uses other sophisticated techniques such as functional analysis and linear algebra.
Cartesian equations[edit]
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, that are marked using the same unit of length.
One can use the same principle to specify the position of any point in three-dimensional space by the use of three Cartesian coordinates, which are the signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines).
Cartesian coordinate system with a circle of radius 2 centered at the origin marked in red. The equation of a circle is (x − a)2 + (y − b)2 = r2 where a and b are the coordinates of the center (a, b) and r is the radius.
The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane, centered on a particular point called the origin, may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.
Parametric equations[edit]
A parametric equation for a curve expresses the coordinates of the points of the curve as functions of a variable, called a parameter.[7][8] For example,
are parametric equations for the unit circle, where t is the parameter. Together, these equations are called a parametric representation of the curve.
The notion of parametric equation has been generalized to surfaces, manifolds and algebraic varieties of higher dimension, with the number of parameters being equal to the dimension of the manifold or variety, and the number of equations being equal to the dimension of the space in which the manifold or variety is considered (for curves the dimension is one and one parameter is used, for surfaces dimension two and two parameters, etc.).
Number theory[edit]
Diophantine equations[edit]
A Diophantine equation is a polynomial equation in two or more unknowns for which only the integer solutions are sought (an integer solution is a solution such that all the unknowns take integer values). A linear Diophantine equation is an equation between two sums of monomials of degree zero or one. An example of linear Diophantine equation is ax + by = c where a, b, and c are constants. An exponential Diophantine equation is one for which exponents of the terms of the equation can be unknowns.
Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations. In more technical language, they define an algebraic curve, algebraic surface, or more general object, and ask about the lattice points on it.
The word Diophantine refers to the Hellenistic mathematician of the 3rd century, Diophantus of Alexandria, who made a study of such equations and was one of the first mathematicians to introduce symbolism into algebra. The mathematical study of Diophantine problems that Diophantus initiated is now called Diophantine analysis.
Algebraic and transcendental numbers[edit]
An algebraic number is a number that is a solution of a non-zero polynomial equation in one variable with rational coefficients (or equivalently — by clearing denominators — with integer coefficients). Numbers such as π that are not algebraic are said to be transcendental. Almost all real and complex numbers are transcendental.
Algebraic geometry[edit]
Algebraic geometry is a branch of mathematics, classically studying solutions of polynomial equations. Modern algebraic geometry is based on more abstract techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry.
The fundamental objects of study in algebraic geometry are algebraic varieties, which are geometric manifestations of solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are: plane algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves and quartic curves like lemniscates, and Cassini ovals. A point of the plane belongs to an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of the points of special interest like the singular points, the inflection points and the points at infinity. More advanced questions involve the topology of the curve and relations between the curves given by different equations.
Differential equations[edit]
A differential equation is a mathematical equation that relates some function with its derivatives. In applications, the functions usually represent physical quantities, the derivatives represent their rates of change, and the equation defines a relationship between the two. Because such relations are extremely common, differential equations play a prominent role in many disciplines including physics, engineering, economics, and biology.
In pure mathematics, differential equations are studied from several different perspectives, mostly concerned with their solutions — the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form.
If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have been developed to determine solutions with a given degree of accuracy.
Ordinary differential equations[edit]
An ordinary differential equation or ODE is an equation containing a function of one independent variable and its derivatives. The term «ordinary» is used in contrast with the term partial differential equation, which may be with respect to more than one independent variable.
Linear differential equations, which have solutions that can be added and multiplied by coefficients, are well-defined and understood, and exact closed-form solutions are obtained. By contrast, ODEs that lack additive solutions are nonlinear, and solving them is far more intricate, as one can rarely represent them by elementary functions in closed form: Instead, exact and analytic solutions of ODEs are in series or integral form. Graphical and numerical methods, applied by hand or by computer, may approximate solutions of ODEs and perhaps yield useful information, often sufficing in the absence of exact, analytic solutions.
Partial differential equations[edit]
A partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (This is in contrast to ordinary differential equations, which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.
PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.
Types of equations[edit]
Equations can be classified according to the types of operations and quantities involved. Important types include:
- An algebraic equation or polynomial equation is an equation in which both sides are polynomials (see also system of polynomial equations). These are further classified by degree:
- linear equation for degree one
- quadratic equation for degree two
- cubic equation for degree three
- quartic equation for degree four
- quintic equation for degree five
- sextic equation for degree six
- septic equation for degree seven
- octic equation for degree eight
- A Diophantine equation is an equation where the unknowns are required to be integers
- A transcendental equation is an equation involving a transcendental function of its unknowns
- A parametric equation is an equation in which the solutions for the variables are expressed as functions of some other variables, called parameters appearing in the equations
- A functional equation is an equation in which the unknowns are functions rather than simple quantities
- Equations involving derivatives, integrals and finite differences:
- A differential equation is a functional equation involving derivatives of the unknown functions, where the function and its derivatives are evaluated at the same point, such as
. Differential equations are subdivided into ordinary differential equations for functions of a single variable and partial differential equations for functions of multiple variables
- An integral equation is a functional equation involving the antiderivatives of the unknown functions. For functions of one variable, such an equation differs from a differential equation primarily through a change of variable substituting the function by its derivative, however this is not the case when the integral is taken over an open surface
- An integro-differential equation is a functional equation involving both the derivatives and the antiderivatives of the unknown functions. For functions of one variable, such an equation differs from integral and differential equations through a similar change of variable.
- A functional differential equation of delay differential equation is a function equation involving derivatives of the unknown functions, evaluated at multiple points, such as
- A difference equation is an equation where the unknown is a function f that occurs in the equation through f(x), f(x−1), …, f(x−k), for some whole integer k called the order of the equation. If x is restricted to be an integer, a difference equation is the same as a recurrence relation
- A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process
- A differential equation is a functional equation involving derivatives of the unknown functions, where the function and its derivatives are evaluated at the same point, such as
See also[edit]
- Formula
- History of algebra
- Indeterminate equation
- List of equations
- List of scientific equations named after people
- Term (logic)
- Theory of equations
- Cancelling out
Notes[edit]
- ^ As such an equation can be rewritten P – Q = 0, many authors do not consider this case explicitly.
- ^ The subject of this article is basic in mathematics, and is treated in a lot of textbooks. Among them, Lay 2005, Meyer 2001, and Strang 2005 contain the material of this article.
References[edit]
- ^ a b Recorde, Robert, The Whetstone of Witte … (London, England: Jhon Kyngstone, 1557), the third page of the chapter «The rule of equation, commonly called Algebers Rule.»
- ^ a b «Equation — Math Open Reference». www.mathopenref.com. Retrieved 2020-09-01.
- ^ «Equations and Formulas». www.mathsisfun.com. Retrieved 2020-09-01.
- ^ Marcus, Solomon; Watt, Stephen M. «What is an Equation?». Retrieved 2019-02-27.
- ^ Lachaud, Gilles. «Équation, mathématique». Encyclopædia Universalis (in French).
- ^ «A statement of equality between two expressions. Equations are of two types, identities and conditional equations (or usually simply «equations»)». « Equation », in Mathematics Dictionary, Glenn James [de] et Robert C. James (éd.), Van Nostrand, 1968, 3 ed. 1st ed. 1948, p. 131.
- ^ Thomas, George B., and Finney, Ross L., Calculus and Analytic Geometry, Addison Wesley Publishing Co., fifth edition, 1979, p. 91.
- ^ Weisstein, Eric W. «Parametric Equations.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/ParametricEquations.html
External links[edit]
- Winplot: General Purpose plotter that can draw and animate 2D and 3D mathematical equations.
- Equation plotter: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (x and y).
An equation is a mathematical statement with an ‘equal to’ symbol between two expressions that have equal values. For example, 3x + 5 = 15. There are different types of equations like linear, quadratic, cubic, etc. Let us learn more about equations in math in this article.
| 1. | What are Equations? |
| 2. | Parts of an Equation |
| 3. | How to Solve an Equation? |
| 4. | Types of Equations |
| 5. | Equation vs Expression |
| 6. | FAQs on Equations |
What are Equations?
Equations are mathematical statements containing two algebraic expressions on both sides of an ‘equal to (=)’ sign. It shows the relationship of equality between the expression written on the left side with the expression written on the right side. In every equation in math, we have, L.H.S = R.H.S (left hand side = right hand side). Equations can be solved to find the value of an unknown variable representing an unknown quantity. If there is no ‘equal to’ symbol in the statement, it means it is not an equation. It will be considered as an expression. You will learn the difference between equation and expression in the later section of this article.
Look at the following examples. These will give you an idea of the meaning of an equation in math.
| Equations | Is it an equation? | |
|---|---|---|
| 1. | y = 8x — 9 | Yes |
| 2. | y + x2 — 7 | No, because there is no ‘equal to’ symbol. |
| 3. | 7 + 2 = 10 — 1 | Yes |
Now, let us move forward and learn about parts of an equation in math.
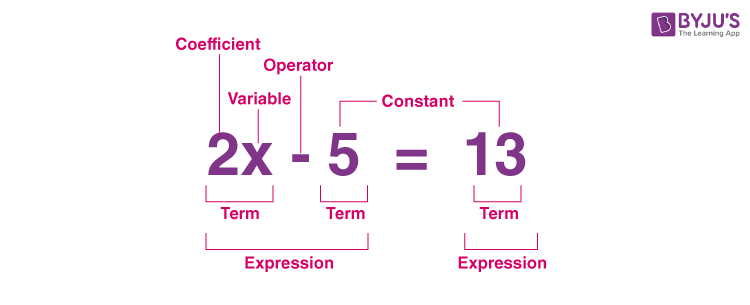
Parts of an Equation
There are different parts of an equation which include coefficients, variables, operators, constants, terms, expressions, and an equal to sign. When we write an equation, it is mandatory to have an «=» sign, and terms on both sides. Both sides should be equal to each other. An equation doesn’t need to have multiple terms on either of the sides, having variables, and operators. An equation can be formed without these as well, for example, 5 + 10 = 15. This is an arithmetic equation with no variables. As opposed to this, an equation with variables is an algebraic equation. Look at the image below to understand the parts of an equation.
How to Solve an Equation?
An equation is like a weighing balance with equal weights on both sides. If we add or subtract the same number from both sides of an equation, it still holds. Similarly, if we multiply or divide the same number into both sides of an equation, it still holds. Consider the equation of a line, 3x − 2 = 4. We will perform mathematical operations on the LHS and the RHS so that the balance is not disturbed. Let’s add 2 on both sides to reduce the LHS to 3x. This will not disturb the balance. The new LHS is 3x − 2 + 2 = 3x and the new RHS is 4 + 2 = 6. So, the equation becomes 3x = 6. Now, let’s divide both sides by 3 to reduce the LHS to x. Thus, the solution of the given equation of a line is x = 2.
The steps to solve a basic equation with one variable (linear) are given below:
- Step 1: Bring all the terms with variables on one side and all the constants on the other side of the equation by applying arithmetic operations on both sides.
- Step 2: Combine all like terms (terms containing the same variable with the same exponent) by adding/subtracting them.
- Step 3: Simplify it and get the answer.
Let us take one more example of a basic equation: 3x — 20 = 7. To bring all the constants on RHS, we have to add 20 to both sides. This implies, 3x — 20 + 20 = 7 + 20, which can be simplified as 3x = 27. Now, divide both sides by 3. This will get you x = 9 which is the required solution of the equation.
Types of Equations
Based on the degree, equations can be classified into three types. Following are the three types of equations in math:
- Linear Equations
- Quadratic Equations
- Cubic Equations
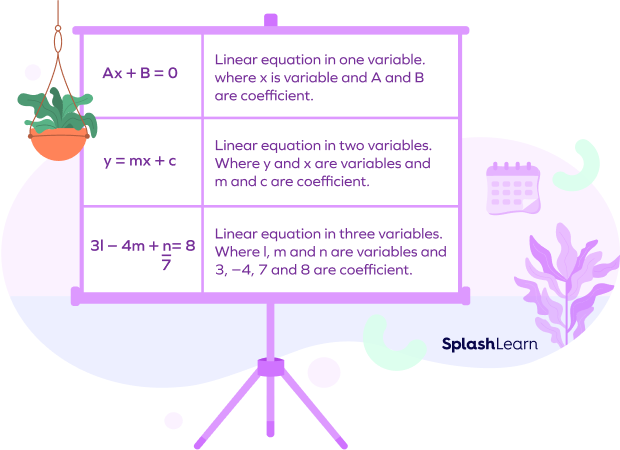
Linear Equation
Equations with 1 as the degree are known as linear equations in math. In such equations, 1 is the highest exponent of terms. These can be further classified into linear equations in one variable, two-variable linear equations, with three variables, etc. The standard form of a linear equation with variables X and Y are aX + bY — c = 0, where a and b are the coefficients of X and Y respectively and c is the constant.
Quadratic Equation
Equations with degree 2 are known as quadratic equations. The standard form of a quadratic equation with variable x is ax2 + bx + c = 0, where a ≠ 0. These equations can be solved by splitting the middle term, completing the square, or by the discriminant method.
Cubic Equations
Equations with degree 3 are known as cubic equations. Here, 3 is the highest exponent of at least one of the terms. The standard form of a cubic equation with variable x is ax3 + bx2 + cx + d = 0, where a ≠ 0.
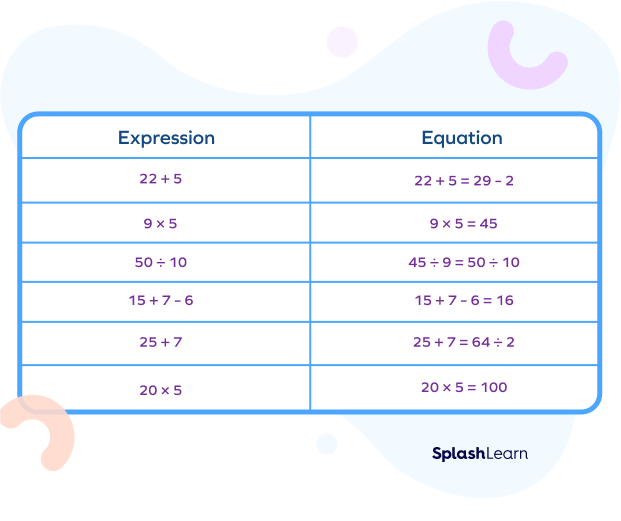
Equation vs Expression
Expressions and equations in math are used simultaneously in algebra, but there is a major difference between the two terms. When 2x + 4 is an expression, 2x + 4 = 0 is considered an equation. Let us understand the basic difference between equation and expression through the table given below:
| Equation | Expression |
|---|---|
| When two expressions are equal in value and written together with an ‘equal to’ sign in between, it is known as an equation in math. | It is a mathematical statement having at least one term or multiple terms connected through operators in between. |
| It has an equal to «=» sign. | An expression does not contain an equal to «=» sign. |
| It can be solved to find the value of the unknown quantity. | It can be simplified to the lowest form. |
| Example: x — 8 = 16, 6y = 33, 3z — 7y = 9, etc. | Example: x — 8, 6y, 3z — 7y — 9, etc. |
Important Notes on Equations in Math:
- The values of the variable that makes an equation true are called the solution or root of the equation.
- The solution of an equation is unaffected if the same number is added, subtracted, multiplied, or divided into both sides of the equation.
- The graph of a linear equation in one or two variables is a straight line.
- The curve of the quadratic equation is in the form of a parabola.
☛ Related Topics:
Check these interesting articles related to the concept of equations in math.
- System of Equations
- Simple Equations and Its Applications
- Solve for x
FAQs on Equation
What is an Equation in Math?
An equation in math is an equality relationship between two expressions written on both sides of the equal to sign. For example, 3y = 16 is an equation.
What is a Linear Equation?
A linear equation is an equation with degree 1. It means the highest exponent of any term could be 1. An example of a linear equation in math is x + y = 24.
What is a Quadratic Equation?
A quadratic equation is an equation with degree 2. It can have any number of variables but the highest power of terms could be only 2. The standard form of a quadratic equation with variable y is ay2 + by + c = 0, where a ≠ 0.
How Equations are Used in Real Life?
In real life, there are many situations in which equations can be used. Whenever an unknown quantity has to be found, an equation can be formed and solved. For example, if the cost of 1 pencil is $1.2, and the total money spent by you on pencils is $9.6, the number of pencils bought can be found by forming an equation based on the given information. Let the number of pencils bought be x. Then, the equation will be 1.2x = 9.6, which can be solved as x = 8.
How to Solve Quadratic Equations?
Quadratic equations in one variable can be solved using the following methods:
- Factorization method
- Completing the square method
- Discriminant method
What are the 3 Types of Equation?
Based on the degree, equations can be classified into the following three types:
- Linear equation
- Quadratic equation
- Cubic equation
What Equation Has No Solution?
Equations of two parallel lines have no solutions as they do not intersect at any point. To identify the equations of parallel lines, we have to compare the coefficients of both the variables in the given two linear equations in two variables. If the ratio of coefficients is the same and unequal to the ratio of constants, it means those equations have no solution. For two equations ax + by + c = 0 and px + qy + r = 0, it will have no solution when a/p = b/q ≠ c/r.
What is the Equation of a Circle?
The equation of a circle with radius r and center (x1, y1) is (x − x1)2 + (y − y1)2 = r2.
equals symbol.
An equation is a mathematical expression that contains an equals symbol. Equations often contain algebra. Algebra is used in maths when you do not know the exact number in a calculation.
Contents
- 1 What is an equation in math example?
- 2 What is equation in simple way?
- 3 What is an equation Class 7?
- 4 How do you explain an equation to a child?
- 5 Where do you write equations?
- 6 What is equation and expression?
- 7 What do we use equations for?
- 8 What are the steps to solving an equation?
- 9 Is it an equation or expression?
- 10 What is an equation in maths ks2?
- 11 What is the symbol for equation?
- 12 How do you write a balanced equation?
- 13 Can Word solve equations?
- 14 How do you write equations in docs?
- 15 How do you write an equation in one variable?
- 16 How do you write an equation given two points?
What is an equation in math example?
An equation is a mathematical sentence that has two equal sides separated by an equal sign. 4 + 6 = 10 is an example of an equation. We can see on the left side of the equal sign, 4 + 6, and on the right hand side of the equal sign, 10.
What is equation in simple way?
A simple equation refers to a mathematical equation that expresses the relationship between two expressions on both sides of the ‘equal to’ sign. This category of an equation consists of a variable, usually in the form of x or y. Solving simple equations often require rearranging it.
What is an equation Class 7?
An equation is a statement of equality between two mathematical expressions containing one or more variables.Now this is called a simple equation. This equation can simplify problems and help us finding the age of Rahul’s father by just substituting Rahul’s age in place of x.
How do you explain an equation to a child?
An equation is a number sentence where one side equals the other, for example: In this case, we know that 4 + 4 = 8 and 10 – 2 = 8, so both sides of this equation are equal, which means it is correct.
Where do you write equations?
Write an equation or formula
- Choose Insert > Equation and choose the equation you want from the gallery.
- After you insert the equation the Equation Tools Design tab opens with symbols and structures that can be added to your equation.
What is equation and expression?
An expression is a number, a variable, or a combination of numbers and variables and operation symbols. An equation is made up of two expressions connected by an equal sign.
What do we use equations for?
An equation is the mathematical representation of those two things which are equal, one on each side of an ‘equals’ sign. Equations are useful to solve our daily life problem. Most of the times we take pre algebra help to resolve real life problems.This is a part of the math equation.
What are the steps to solving an equation?
A General Rule for Solving Equations
- Simplify each side of the equation by removing parentheses and combining like terms.
- Use addition or subtraction to isolate the variable term on one side of the equation.
- Use multiplication or division to solve for the variable.
Is it an equation or expression?
The best way, to identify, whether a given problem is an expression or equation is that if it contains an equal to sign (=) it is an equation. However, if it does not contain an equal to (=) sign, then it is just an expression. It carries numbers, variables and operators, that are used to show the value of something.
What is an equation in maths ks2?
An equation is a sum with an unknown value. Solving an equation means undoing a process to find the unknown value.
What is the symbol for equation?
Basic math symbols
| Symbol | Symbol Name | Example |
|---|---|---|
| ≠ | not equal sign | 5 ≠ 4 5 is not equal to 4 |
| ≈ | approximately equal | sin(0.01) ≈ 0.01, x ≈ y means x is approximately equal to y |
| > | strict inequality | 5 > 4 5 is greater than 4 |
| < | strict inequality | 4 < 5 4 is less than 5 |
How do you write a balanced equation?
Count the numbers of atoms of each kind on both sides of the equation to be sure that the chemical equation is balanced.
Adjust the coefficients.
- 1 Pb atom on both reactant and product sides.
- 2 Na atoms on reactant side, 1 Na atom on product side.
- 2 Cl atoms on both reactant and product sides.
Can Word solve equations?
Yes, Word can do this (the Equation Editor is built in; the computation and graphing stuff is part of a free add-in from Microsoft).
How do you write equations in docs?
Insert an equation
- Open a document in Google Docs.
- Click where you want to put the equation.
- Click Insert. Equation.
- Select the symbols you want to add from one of these menus: Greek letters. Miscellaneous operations. Relations. Math operators. Arrows.
- Add numbers or substitute variables in the box.
How do you write an equation in one variable?
The linear equations in one variable is an equation which is expressed in the form of ax+b = 0, where a and b are two integers, and x is a variable and has only one solution. For example, 2x+3=8 is a linear equation having a single variable in it.
How do you write an equation given two points?
Steps to find the equation of a line from two points:
- Find the slope using the slope formula.
- Use the slope and one of the points to solve for the y-intercept (b).
- Once you know the value for m and the value for b, you can plug these into the slope-intercept form of a line (y = mx + b) to get the equation for the line.
There are numerous ways in which one may define an equation. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an ‘equal’ sign. The most basic and simple algebraic equations consist of one or more variables in math.
Example of an Equation:
4y + 2 = 18
4×2 + 3x − 28 = 0
9m = 49.5
$frac{u}{6}$ = 8
Non examples of an Equation:
k + 7
u + w
x$^{3}$ + 5x
9t
Related Games
Different Types of Equations:
Some of the math equations used in algebra are:
- Linear Equation
A linear equation may have more than one variable. A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation.
- Quadratic Equation
This is a second-order equation. In quadratic equations, at least one of the variables should be raised to exponent 2.
Example:
ax$^{2}$ + bx + c = 0
$frac{p^{2}}{9}$ − 1 = 0
- Cubic Equation
This is a third-order equation. In cubic equations, at least one of the variables should be raised to exponent 3.
Example:
ax$^{3}$ + bx$^{2}$ + cx + d = 0
a$^{3}$ – 27 = 0
- Rational Equation
A rational equation is an equation that contains fractions with a variable in the numerator, denominator, or both.
Example: $frac{x}{2} = frac{x + c}{4}$.
Related Worksheets
Expression vs Equation
A math expression is different from a math equation. An equation will always use an equal (=) operator between two math expressions.
For example,
What is a Solution of an Equation?
The value of the variable which makes the equation a true statement is the solution of the equation.
Example 1:
Verify that x = 3 is the solution of an equation 4x − 8 = − 5 + 3x
Substitute x = 3 in the given equation
LHS
4x − 8 = 4(3) − 8 = 12 − 8 = 4
RHS
−5 + 3x = −5 + 3(3) = −5 + 9 = 4
LHS = RHS
So, x = 3 is the solution of an equation 4x − 8 = −5 + 3x.
Example 2:
Verify that y = −2 is the solution of an equation 2m – 4 = 1
Substitute y = −2 in the given equation.
LHS
2m – 4 = 2(−2) − 4 = − 4 − 4 = − 8
RHS
1
− 8 ≠ 1
LHS ≠ RHS
So, y = −2 is not the solution of given equation 2m – 4 = 1.
How to Solve Linear Equations with One Variable?
- Simplify the expressions inside parentheses, brackets, braces and fractions bars.
- The same quantity can be added, subtracted, multiplied or divided from both sides of an equation without changing the equality.
Or
Any term of an equation may be taken from one side to the other with the change in its sign. This process is called transposition.
Example:
4a – 9 = 13 – 7a
4a + 7a = 13 + 9 [transpose −7a to LHS and − 9 to RHS]
11a = 22 [add like terms]
a = $frac{22}{11}$ [transpose 11 to RHS]
a = 2
Example:
$frac{1}{5} + 3w = frac{2}{5}$
3w = $frac{2}{5} – frac{1}{5}$ [transpose 15 to RHS]
3w = $frac{1}{5}$
w = $frac{1}{5times 3}$ [transpose 3 to RHS]
w = $frac{1}{15}$
Solved Examples:
Example 1: Solve for x.
x + 8 = 12
Solution:
Here is the equation to solve: x + 8 = 12
We need to leave x alone on one side of the equation. For this, we must take 8 out of both sides.
So, x + 8 – 8 = 12 – 8
or, x = 4
Example 2: Determine if the value 3 is a solution of the equation:
4x – 2 = 3x + 1
Solution:
We will substitute the value of 3 in this equation and will check if the left-side equation is equal to the right-hand side.
So,
4(3) – 2 = 3(3) + 1
or, 12 – 2 = 9 + 1
or, 10 = 10
Yes, 3 is a solution to the given equation.
Example 3: Solve the equation: 6(2x + 3) + x – 7 = 3(5x + 7) + 2x
Solution:
6(2x + 3) + x – 7 = 3(5x + 7) + 2x
Expanding the terms we get,
12x + 18 + x – 7 = 15x + 21 + 2x
or, 13x + 11 = 17x + 21
On further simplification,
13x – 17x = 21 – 11
−4x = 10
x = -$frac{10}{4}$
x = -$frac{5}{2}$
Practice Problems
7x + 5y = 19
5 — 2
$frac{4}{7} — frac{2}{7}$
3a + 9b
Correct answer is: 7x + 5y = 19
As option a has an equal sign (=) between two math expressions its an equation. The other options are expressions.
n + 2 = 9
7 — g = 0
x — 4 = 3
h$times$ 1 = 8
Correct answer is: h$times$ 1 = 8
7$times$ 1 = 7 and 7 ≠ 8. So 7 is not the solution for the given equation.
3
2
−3
−1
Correct answer is: −3
9k = −27
k = -$frac{27}{9}$
k = -3
Conclusion
We have thus learned the definition of the equation and its different types. Moreover, a few questions have also been solved here to give a clear idea to the students about solving an equation. A student can have a strong grip on this concept by practising such problems.Teaching maths concepts can be challenging, especially when the students are young kids. So, to make parents’ and teachers’ lives easy, SplashLearn has brought some courses specifically designed for students from K-8. After all, it should be fun to learn!
Frequently Asked Questions
What are the types of Equation?
There are three types of equations based on the degree. Linear equation, quadratic equation, and cubic equation.
How are linear equations used in daily life?
Linear equations are used to find the wages based on hourly pay rate, speed, and medicine dosage based on the patient’s weight.
What must an equation have?
An equation in algebra is a statement of equality that contains one or more unknown quantities or variables.
How do you solve equations?
Solving Equations – A General Rule
- Remove parentheses and combine like terms on each side of the equation.
- To isolate the variable term, you can use addition or subtraction.
- To solve for a variable, use multiplication or division.
Algebraically equality of two objects is often defined if they are «the same». We define this in different contexts, but mostly we define it together with the concept of an order relation. Some examples:
In set theory:
$$ A subseteq B land B subseteq A implies A=B$$
Since a set is defined by the elements it contains, if one set is contained in the other and vice versa, clearly they must contain the same elements. Here we see equality because a set is uniquely determined by its elements.
In ordered fields, using the trichotomy axiom ($mathbb{Q}$ is an ordered field, not completely ordered though, $mathbb{R}$ is):
$$ aleq b land bleq a implies a=b$$
In group theory: let $e$ be the identity element and $a$ an arbitray element in the group:
$$ e cdot a = a cdot e=a$$
This statements tells us that applying the identity elements does not do anything, it also does not matter from which side we apply it. All these examples only further support the idea we see equality as two things being «the same». We can even define the relation «=» for any two numbers, clearly:
$$ a=a$$
$$ a=b implies b=a$$
$$ a=b land b=c implies a=c $$
So equality is an equivalence relation.
Another fun example there are equally as much even-sized subsets as odd-sized of a given set:
$$ 0=(1-1)^n = sum_{k=0} ^n binom{n}{k} (-1)^n $$
Here the binomial tells us how many $k-sized$ subsets there are of a set $n$, we notice that all possible subsets are either even or odd by a partition of the natural numbers into these two sets. We can show there exists a bijection between the two so they have the same cardinality. We can split the sum up over odd and over even $k$ and notice that these two terms cancel, there must be the same amount of terms and thus there must be the same amount of subsets for all $n$. So there are equally as much off-subsets as even -subsets.
Surprisingly when two objects are «the same» in algebra, but have a different representation, we speak of the idea of an «isomorphism», which is also an interesting concept. This means we can identify both the structure and the elements uniquely. All very interesting ideas, definitely a nice question to think about, thank you!
You have probably come across many equations by now. However, what do we actually mean by the term ‘equation’? You may have also heard of an identity. Sometimes it can be difficult to distinguish between equations and identities. In this article, we will be looking at equations, identities as well as their differences. However, we will first outline what we mean when talking about equations and identities. We will do so in the below section, and then discuss the differences between them.
Expressions, equations, identities, and formulae
This section will consist of lots of definitions and examples. However, it is important that you understand each of the key terms as you may be given a particular example in your GCSE exam and asked to determine whether it is an expression, equation, identity, or formula. Here we go…
Definition of expressions
An expression is a collection of mathematical terms, related by mathematical operations. A mathematical term is a single mathematical number or letter, for example, x or 3. We could also have 3x2, where 3 is known as the coefficient of x.
The following are examples of mathematical expressions:
- 5x+1
- 3×2-9x+1
- 7x+2y+z
- ax2+1
- 6×8+7y5+2z3-1
- 7k
Definition of equations
Once we have a firm grasp on what mathematical expressions are we can start to build connections between them, in order to compare them.
If we break down the word equation we get ‘equa-tion’. Now ’equa’ sounds very similar to ‘equal’, which is no coincidence: an equation is a statement that two mathematical expressions shall be the same.
An equation is a statement that two mathematical expressions shall be the same.
An equation is expressed with an equal sign = between two mathematical expressions. The fancy word for the equal sign is the equality symbol.
In a few words, anything with an equal sign is an equation. Sounds simple, right? Here are some examples of equations:
- x=2
- a+b=c
- x2+y=2
- y-2=5y+1
- a2-5a-2=0
- eπi+1=0
Solution of an equation
It is important to note here that two expressions may only be equal under specific conditions. For example, if we are told x-2=0 , we know this is an equation because there is an equality symbol. However, using the basic rules of addition, we know that the equation can only be true if x=2. This is called the solution of the equation.
The solution of an equation is the set of all values that, when substituted for the variables in the equation, make the equation true.
Definition of identities
Some expressions are always equal to each other, regardless of the values of the variables they contain. In this case one speaks of a mathematical identity:
A mathematical identity is where two mathematical expressions are always identical. An identity is expressed using the identity symbol ≡, which looks a bit like an equals sign with an extra line.
- 2x+4x≡6x
- 2a2+3a2≡5a2
- 11x-3x≡8x
- 2y+3y≡5y
- 9p+p≡10p
Differences between identities and equations
Often, one of the biggest challenges is determining whether something is an equation or identity. In this section, we will discuss how to establish whether something is an equation or an identity and note the key difference between them.
As established, an equation shows that two expressions are equal. However, they may only be equal for a specific value. For example, if we have2x+1=5, this equation is only true when x=2. Identities on the other hand show that two expressions are always identical. For example, we could say that 6×2+2×2≡8×2, since, no matter what the value of x is, the two expressions are always the same.
If we asserted the identity ax2+bx≡2×2+3x, we know that the left-hand side is equal to the right-hand side for all values of x because we have an identity symbol. However, the only way for this to be possible is if a=2 and b=3. In this case, we would have2x2+3x≡2×2+3x which we know is true for all values of x.
We could say that since identities show equality between expressions, all identities are equations. However, not all equations are identities so it is important that you are aware of the key difference between the two.
Here is again the main point: Equations show equality under at least one condition, identities show equality under all conditions.
Definition of formulae
We have a fourth thing to consider, and that is a formula. While we are here, it is worth mentioning that the plural of formula is formulae. Now, onto some more definitions and examples…
A formula is a special type of equation representing a general fact or rule one can work with.
A mathematical formula is a type of equation as all formulae have an equal sign. However, they are equations with a specific purpose. They give us a way of working something out. For example, if we wanted to convert degrees Fahrenheit to degrees Celsius, we could use a formula. There are many formulae that are specifically useful for GCSE mathematics, including the quadratic formula, the trigonometric formulae, and also the speed, distance, and time formula. In the example below we will look at some specific formulae.
- x=-b±b2-4ac2a
This is quite possibly one of the most iconic formulae in GCSE mathematics – the quadratic formula. This article is not about the quadratic formula specifically, so we will not talk about it in too much depth. However, this is just a friendly reminder that you probably should learn it.
- mass=volume × density
Again, this article is not specifically about volume, mass, and density so we do not need to talk about it in too much depth. However, you do need to learn this formula at some point! It means that if you have the density of an object and volume, you can work out the mass. It is very handy.
- speed=distancetime
This is another classic. Speed, distance, and time. You do need to know this formula, not just for GCSE mathematics, but for physics too. But once you know it, you can work out the speed of any moving object given the distance and time.
- a2+b2=c2
This is Pythagoras’s Theorem. However, by definition, it is also a formula, as it enables us to work out an unknown quantity which in this case, is the missing side of a right-angled triangle. You need to know this for your GCSE exams.
- v=u+at
This is a formula that relates the final velocity of a moving object, with the initial velocity, time, and acceleration. It is one of the SUVAT formulae which you may come across if you study A-level Mathematics. You don’t specifically need to know this formula, you just need to be able to know that it is a formula, as it enables us to work out something specific (eg, the initial velocity, final velocity, acceleration, or time)
- E=mc2
You may have seen this formula before. It is one of Einstein’s most famous formulae relating mass to energy and the speed of light. It is quite famous, but you do not need to know this formula for GCSE mathematics. You simply need to know that it is a formula as it enables us to work something out.
Above are just a few examples of some formulae that you may or may not need to know for your GCSE maths exams. There are others, however, this article is not about going over every single one. Instead, it is about being able to see a formula, and subsequently being able to state that it is a formula, as opposed to an equation, identity, or expression.
Below we will cover some relevant examples to this topic. You will need to know the differences between an expression, identity, equation, and formula so let’s just quickly recap the differences between these four things.
- An expression is a collection of mathematical terms.
- An equation is anything with an equal sign, hence ‘equa’ ‘tion’.
- An identity is where two mathematical expressions are identical, denoted with an identity symbol, ≡.
- A formula is a type of equation where we are working out something specific, for example, the mass of an object.
Examples of identities and equations
Now that we have thoroughly defined some mathematical terms, we will go through some questions that you may come across in your GCSE exam.
Label the following either an identity, equation, expression, or formula:
- A=πr2
- 9x+8
- x2+4x+3=0
- 4x+x=5x
Solution:
1. is the formula for the area of a circle. It enables us to work out the area given the radius. Thus the first one is a formula.
2. has no equality sign, and is simply a collection of mathematical terms connected with an addition symbol. Thus it is an expression.
3. has an equals sign, and thus it is an equation. It is only true for specific values of x, (x=-3, x=-1), thus it is not an identity.
4. has an equals sign and thus is an equation. However, this equation is true for all values of x and so it is an identity and can be expressed using the identity symbol ≡.
For the below identity, work out the values of a and b:
ax2+bx2+ax≡5×2+3x
Solution:
We know that it is an identity, and so the left-hand side must be equal to the right-hand side. The coefficient of x on the right-hand side is 3 and so the coefficient on the left-hand side must also be 3. Thus, a=3.
On the left-hand side, we could group up the coefficients of x2 as follows:
(a+b)x2+3x≡5×2+3x. Therefore, we could say that a+b=5 since the coefficient of x2 on both sides must be the same. Since we already know that a=3, we can say that 3+b=5 and so b=2. Thus, a=3 and b=2.
Equations and Identities — Key takeaways
- An expression is a collection of mathematical terms, related by mathematical operations.
- An equation is any mathematical relation expressed with an equal sign.
- An identity is where two mathematical expressions are always identical.
- A formula is an equation that enables us to work out something specific.
- Identities are expressed using the symbol ≡which is like an equal sign with an extra line.
- The difference between an equation and an identity is that equations state equality under a specific condition, identities show that two expressions are always equal.
Asked by: Emely Stanton
Score: 4.8/5
(41 votes)
An equation is simply a statement in math in which two things on equal. There are two expressions, one on each side of an equals sign. For example: X = 7. In this case, another way to write the equation would be 7 = 7.
What is an example of an equation in math?
An equation is a mathematical sentence that has two equal sides separated by an equal sign. 4 + 6 = 10 is an example of an equation. We can see on the left side of the equal sign, 4 + 6, and on the right hand side of the equal sign, 10.
What is equation and examples?
In algebra, an equation can be defined as a mathematical statement consisting of an equal symbol between two algebraic expressions that have the same value. … For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an ‘equal’ sign.
What is a number equation?
An equation is simply a number sentence with a variable in the place of an unknown value. A variable is a letter that is substituted in place of the unknown value. It can be any letter you want, although x is most commonly used.
What is a simple equation?
What is a Simple Equation? In the simplest of terms, a variable and an ‘equal to’ sign make up a simple equation. Therefore, a simple equation is a mathematical representation of two expressions on either side of an ‘equal to’ sign. It mostly consists of a variable, frequently accompanied by a numerical constant.
45 related questions found
What are the 3 types of equations?
There are three major forms of linear equations: point-slope form, standard form, and slope-intercept form. We review all three in this article.
Is an equation a formula?
First, an equation is a way to say that one thing is equal to, or the same value as, another. A formula is a special equation that expresses an important relationship between variables expressing commonly-used ideas, like speed, temperature, etc.
Which equation is true?
To make a true equation, check your math to make sure that the values on each side of the equals sign are the same. Ensure that the numerical values on both sides of the «=» sign are the same to make a true equation. For example, 9 = 9 is a true equation. 5 + 4 = 9 is a true equation.
What are the types of equation?
Types of equations
- linear equation for degree one.
- quadratic equation for degree two.
- cubic equation for degree three.
- quartic equation for degree four.
- quintic equation for degree five.
- sextic equation for degree six.
- septic equation for degree seven.
- octic equation for degree eight.
What is an equation Class 7?
An equation is a statement of equality between two mathematical expressions containing one or more variables. … Now this is called a simple equation. This equation can simplify problems and help us finding the age of Rahul’s father by just substituting Rahul’s age in place of x.
What is the most famous math equation?
Think of Pythagoras’ Theorem for example. It features in every elementary child’s school now. When it was first discovered, it was groundbreaking. Einstein’s E=mc² is the world’s most famous equation.
Which equation is not true?
An equation that is never true is called a contradiction. For example, the equation X = x + 1 is a contradiction. There is no value of x that will make the equation true.
What equation is an identity?
An identity is an equation which is always true, no matter what values are substituted. 2 x + 3 x = 5 x is an identity because 2 x + 3 x will always equal regardless of the value of . Identities can be written with the sign ≡, so the example could be written as.
What makes an equation sometimes true?
Also, some equations are true for a range of values: k < 15, p either greater than 2 or less than -2, and x greater than 1 or less than 0. A final one, that is more subtle because it involves two variables, is that p + 12 = f + 12 is true only when p = f. All these equations are sometimes true.
What is area formula?
The most basic area formula is the formula for the area of a rectangle. Given a rectangle with length l and width w, the formula for the area is: A = lw (rectangle). That is, the area of the rectangle is the length multiplied by the width.
How do you write a math equation?
Write an equation to represent this.
- Step 1: Identify the unknowns. There are two unknowns: …
- Step 2: Make the one unknown x. …
- Step 3: Write an expression or value for one part of the equation. …
- Step 4: Write an expression or value for the other part of the equation. …
- Step 5: Remember than an equation has an equals sign.
How do you study equations?
Practice, practice and practice: Practice makes you perfect! When you practice using the formulas you want to learn, your brain understands the application of the formula and remembers it. Try solving and practicing problems using the formula and you will see results! Repetition leads to memorization.
What does an equation show?
Answer: An equation is basically a way to show a relationship of variables (x,y,a,b, etc) and numbers. The relationship between these numbers and variables is a lot like a laundry bag. The amount of shirts and pants in each of those laundry bags could be counted separately, or if you combine them, counted together.
What is standard form in math?
Standard form is a way of writing down very large or very small numbers easily. … The rules when writing a number in standard form is that first you write down a number between 1 and 10, then you write × 10(to the power of a number).
What is the longest math equation?
According to Sciencealert, the longest math equation contains around 200 terabytes of text. Called the Boolean Pythagorean Triples problem, it was first proposed by California-based mathematician Ronald Graham, back in the 1980s.
Who invented math?
Archimedes is known as the Father of Mathematics. Mathematics is one of the ancient sciences developed in time immemorial.
Before going to the definition of an equation, let’s understand how an equation works and how to identify the pattern that makes an equation. This can be understood with the help of the below scenario. Consider the pattern of triangles formed by matchsticks in the figure given below:
Using the above pattern, find the general rule that gives the number of triangles formed by 95 matchsticks.
We may observe that the number of matchsticks in the given matchstick pattern is 3, 5, 7, 9 and so on.
That means the 1st triangle is formed by 3 matchsticks, and the 2nd triangle is formed by adding 2 more sticks to the first one.
Similarly, the third triangle is formed by adding another 2 matchsticks to the previous pattern.
Thus,
| Number of triangles | Number of matchsticks |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
From this, we can say that there is 1 more than twice the number of triangles in the pattern.
Let us take “x” as a variable to form the equation.
Here, the pattern is 2x + 1, where x is the number of triangles.
Now, we can find the number of triangles formed by 95 matchsticks as:
2x + 1 = 95
2x = 94
x = 94/2
x = 47
Hence, we can form 47 triangles using 95 matchsticks in the given pattern.
In the above example, 2x + 1 = 95 represents the equation.
- Algebra
- Linear equations
- Algebraic expressions and Equations
- Math equations
- Expression term factor coefficient
Equation meaning
Mathematically, an equation can be defined as a statement that supports the equality of two expressions, which are connected by the equals sign “=”. For example, 2x – 5 = 13.
Here,
2x – 5 and 13 are expressions
The sign that connects these two expressions is “=”.
Parts of Equation
The parts of the equation 2x – 5 = 13 are explained below.
An equation combines two expressions connected by an equal sign (“=”). These two expressions on either side of the equals sign are called the “left-hand side” and “right-hand side” of the equation. We generally assume the right-hand side of an equation is zero. This will not reduce the generality since we can balance this by subtracting the right-hand side expression from both sides’ expressions.
Equation algebra
In algebra, an equation is a condition on a variable. It is satisfied only for a definite value of the variable. That means, the equation 2x – 5 = 13 is satisfied only for x = 9.
The below figure shows the difference between expression and equation in algebra.
Equation Types
Algebra considers two prominent families of equations, namely polynomial equations and linear equations. Polynomial equations with one variable can be written in P(x) = 0, where P is a polynomial, and ax + b = 0 is the general form of linear equations. Here, a and b are parameters. We can practice geometric or algorithmic methods from linear algebra or mathematical analysis to solve these equations. Also, there are different types of equations, such as:
- Linear equations
- Quadratic equations
- Cubic equations
- Quartic equations
- Differential equations
- Parametric equations
Equation of a line
The standard form of the equation of a line is Ax + By + C = 0. The slope-intercept form of an equation is y = mx + b, where m is the slope of the line and b is the y-intercept. However, there are various types of equations to represent lines.
Click here to know more about the different types of equations of lines.
Equation of x-axis
Generally, we say that the equation of the x-axis equation is of the form y = 0. However, we can also write the x-axis equation as x = c where c is constant.
The x-axis comprises all the real values of x, although the value of y is equal to 0 on the complete x-axis.
Thus, x can be recognised as constant and y as 0.
In the coordinate system representation, we can represent any point on the x-axis as (c, 0), where c is any real number.
Therefore, the x-axis formula will be x= c + y
Here,
c = constant
y = 0
The x-axis formula is x = c, where c is constant.
Equation in One Variable
The equation in one variable means the equation containing only one variable. Let’s have a look at the below equations.
17 – 9 = 8
x + 4 = 4y + 22z
4x2 + 3x – 7 = 0
The three examples above represent equations that propose equality (could be true or not) between two expressions.
The first equation does not contain any variable.
The second equation has three different variables, such as x, y and z. Thus, it is a multivariate equation.
The third equation contains only one variable, i.e. x. Thus, this is an equation in one variable.
Watch the Below Video Lesson to Know how to Solve an Equation
Go through the examples of equations and their solutions given below.
Example 1:
Identify the variable and the value of the variable that satisfy the given equation for the following:
(a) 5b = 60
(b) x + 12 = 20
(c) m – 5 = 5
(d) p/2 = 7
Solution:
(a) 5b = 60
b = 60/5
b = 12
Therefore, the variable is “b” and the solution is b = 12.
Alternative method:
5b = 60
Dividing both sides of the equation by 5,
5b/5 = 60/5
b = 12
(b) x + 12 = 20
x = 20 – 12
x = 8
Here, the variable is “x” and the solution is x = 8.
Alternatively,
x + 12 = 20
Subtracting 12 from both sides of the equation,
x + 12 – 12 = 20 – 12
x = 8
(c) m – 15 = 25
m = 25 + 15
m = 40
Here, the variable is “m” and the solution is m = 40.
Alternative method:
m – 15 = 25
Adding 15 on both sides,
m -15 + 15 = 25+ 15
m = 40
(d) p/2 = 7
p = 2 × 7
p = 14
Here, the variable is “p” and the solution is p = 14.
Alternative method:
p/2 = 7
Multiplying 2 on both sides of the equation,
(p/2) × 2 = 7 × 2
p = 14
Example 2:
Solve the equation: 6(2x + 3) + x – 7 = 3(5x + 7) + 2x
Solution:
6(2x + 3) + x – 7 = 3(5x + 7) + 2x
Expanding the terms we get,
12x + 18 + x – 7 = 15x + 21 + 2x
13x + 11 = 17x + 21
On further simplification,
13x – 17x = 21 – 11
-4x = 10
x = -10/4
x = -5/2
Frequently Asked Questions on Equation
Q1
Define an equation with an example.
An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
For example, 3x – 5 = 16 is an equation. Solving this equation, we get the value of the variable x as x = 7.
Q2
What are the types of equations?
Some of the important types of equations are:
Linear equations
Quadratic equations
Cubic equation
Quartic equations
Differential equations
Parametric equations
Q3
What is the equation of the y-axis?
The equation of the y-axis is x = 0 since the y-axis is parallel to itself at a distance of 0 from it.
Q4
What are the parts of an equation?
An equation contains several parts such as terms, coefficients, exponent, arithmetic operator, equal sign and constants.
Q5
Is the LHS and RHS of an equation must be equal?
Yes, the LHS (left-hand side) and RHS (right-hand side) of an equation must be equal.
In mathematics, you must have come across the word ‘equations’. You must have read questions like, ‘Solve the equation 2x + 12 = 33 to find the value of x’. But, what is the meaning of the term equation? Equations, in math, are statements. These statements often have two linked expressions with an ‘equal to sign. Equations can even have more than two expressions. Mathematicians have solved some equations having more than two expressions up to a certain level. Beyond that, even they are rendered helpless. But, we don’t have to worry about those difficult equations. In this article, we will learn the fundamental concepts of every equation known to humanity. We will study what an equation is and how many types of equations are there in this world.
What are Equations?
A mathematical statement made up of an equal sign between two algebraic expressions with the same value is known as an equation. One or more variables are present in even the basic and most common algebraic equations in mathematics.
Equations Definition
Equations are very easy to identify. Wherever you see two algebraic expressions on the left and right-hand sides of the equal ‘=’ sign, you have found an equation. So we can say that statements with the ‘equal to’ sign in between them are known as equations. If the equal to symbol is not present between the expressions, they are not considered an equation. In the next section of this article, we will see the difference between equations and expressions. For now, look at the examples given below:
Example 1: Is x + y = 13 an equation?
Solution: Yes, x + y = 13 is an equation because it has an ‘equal to’ sign between x + y and 13.
Example 2: Is a – 24 + 13y an equation?
Solution: No! a – 24 + 13y is not an equation because it doesn’t have an equal sign.
Example 3: Is 66 – 12 = 34 – 3 an equation?
Solution: Indeed, this is an equation because 66 – 12 and 34 – 3 have the ‘equal to’ sign between them.
Equations are used in mathematics to solve the values of unknown quantities. They are used in solving word problems and many daily life problems involving time and distance, work, profit and loss, and many more. Let us now learn the basic difference between an equation and an expression.
Equation Vs. Expression
Equations and Expressions are two different things. Students often confuse the two and make a lot of mistakes. See the table mentioned below to clarify the difference between an equation and an expression.
| Equation | Expression |
| In math, an equation is formed when two expressions have the same value and are put together with an ‘equal to’ symbol in the middle. | It’s a mathematical statement with at least one word and several terms linked by operators. |
| It has a “=” symbol next to it. | An equal to “=” symbol does not appear in an expression. |
| It can be solved to determine the unknown quantity’s value. | Maximum it can be reduced to its most basic form. |
| For example: 7x – 2a = 34, 4a + 22 = 3c + b, etc. | For example: 34x – 3z + 2y, a + 3k, etc. |
Parts of an Equation
In every equation, the left-hand side should be equal to the right-hand side. Both sides must be equal. Coefficients, variables, operators, constants, terms, expressions, and an ‘=’ sign are all essential components of an equation. An equation may have any one or all of these terms revolving around the ‘=’ sign. Let us learn these terms individually:
- Term: Any numeric or algebraic entity present around the operators is known as a term.
- Variables: All the alphabetic terms present in an equation whose value is unknown are known as variables.
- Constants: All the numeric terms of an equation are known as constants.
- Coefficients: The constant terms present just before the variables are coefficients.
- Operators: The arithmetic operators like the addition sign, subtraction sign, equal sign, etc., are known as operators.
An equation may have only numeric terms, algebraic terms, or both. We shall learn the steps to solve an equation in the next module.
How to Solve Equation?
You can imagine an equation as a weighing scale. Both sides of an equation result in the same value, hence keeping the weighing scale in balance. It still holds whether we add or remove the same amount from both sides of an equation. The same remains true whether we multiply or divide the same integer into both sides of an equation.
Whatever operation you perform on the left side must also be implemented on the right side of an equation. This is done to maintain the balance of the equation. Let us take an example to understand this concept.
Consider an equation x + 3y = 2a + b. This is a balanced equation. Let us say that we want to add 20 to the left-hand side. The left-hand changes to x + 3y + 20. But now, the equation has been disturbed. We need to add 20 to the right side to balance it. Therefore the new equation will be x + 3y + 20 = 2a + b + 20.
Let us now learn how to solve an equation:
- Step 1: Always keep the variables to one side of the ‘=’ symbol and constants to the other side of the ‘=’ symbol. Normally, the variables are kept to the left-hand side and constants on the right-hand side of the ‘=’ sign.
- Step 2: Do the necessary operations on the like terms like addition or subtraction. Do not operate like terms with unlike terms. You will be following the wrong approach if you do so.
- Step 3: Simplify the equation and get the desired answer.
Look at the example given below:
Example 1: Solve the equation a + 34b – 22 = b + 18
Solution:
From step 1: a + 34b – b = 18 + 22
From step 2: a + 33b = 40
From step 3: This equation cannot be further simplified hence a + 33b = 40, is the solution of this equation.
Example 2: Solve the equation 4x + 3 = x + 27
Solution:
From step 1: 4x – x = 27 – 3
From step 2: 3x = 24
From step 3: x = 24/3, therefore the value of x and the solution to this equation is 8.
Types of Equation
The equations are classified based on the degree of variables. A degree means the power assigned to any variable. Variables having a degree of 1 are known as linear variables. Similarly, the variables having a degree of two are known as quadratic variables, and a degree of three are known as cubic variables, and so on. The equations are classified as linear equations, quadratic equations, cubic equations, etc. Let us study them in detail.
Linear equations: The equations having all the variables of degree as one are known as linear equations. For example, x + 2y = 11, x + 5 = 0, etc. These are further classified as linear equations in one variable, linear equations in two variables, and so on. The standard form of a linear equation is kx + ly – m = 0, where x and y are variables and k, l, and m are constants.
Quadratic equations: The equations having at least one variable of degree two are known as quadratic equations. For instance, x2 + a = 22, k2 – m2 – n = 0, etc. kx2 + lx + m = 0 is the standard form of a quadratic equation.
Cubic equations: The equations having at least one variable having a degree of 3 are known as cubic equations. For example, x3 – x2 + 2 = 31y , k3 – m2 + n3 = 19, etc. The standard form to write a cubic equation is kx3 + lx2 + mx + n = 0.
In all the above cases k, the coefficients of x, x2, and x3 can never be zero. If k = 0, then the terms containing the degree will be eradicated, making the equation invalid.
For instance if in the equation kx2 + lx + m = 0, if k = 0, then the equation becomes lx +m = 0, which is not a quadratic but a linear equation.
Key Notes on Equations
The solution or root of the equation refers to the values of the variable that make an equation true.
When the same number is summed, subtracted, multiplied, or divided into both sides of an equation, the solution remains unaltered.
A straight line graphs a linear equation in one or two variables, while a parabola graphs a quadratic equation.
Practice Questions
Which is a solution of the equation x + 4 = 6?
(1) x = 2
(2) x = 3
(3) x = 4
(4) x = 6
2. The answer to the equation 3n – 2 = 46 is n:
(1) 12
(2) 11
(3) 16
(4) none of these
3. The solution to the equation 3p + 4 = 25 is p =
(1) 5
(2) 6
(3) 4
(4) 7
Frequently Asked Question?
1. How do you write a complete Equation?
You can write a complete equation by adding the equal sign to the beginning of an equation and then writing all of the variables, numbers, or symbols that appear on either side of it.
For example, x + 2 = 5 In this example, “x” is on one side of the equal sign and “2” is on the other side.
2. How do you write a complete Equation?
In order to write a complete equation, you need to know how to solve for one variable at a time.
Let’s say we have the equation:
x + y = 12
To solve for x, we need to isolate it by subtracting y from both sides of the equation:
x + y – y = 12 – y
x = 12 – y
Now, if we want to solve for y, then we just do the same thing: subtract x from both sides and then divide by 2.
3. How does one solve the Equation?
Let’s start with a simple equation:
x² + 3x + 2 = 0
To solve this equation, we’re going to need to isolate the x term. We can do that by adding or subtracting multiples of the same number to both sides of the equation. We will make our life easier by adding 6 to both sides of the equation. This gives us:
x² + 3x + 2 = 0 + 6 (add 6)
x² + 3x + 8 = 6 (subtract 6)
We now have an equation where we can isolate our x term:
(x² + 3x) – 8 = 0 (subtract 8 from both sides)
We can now solve for x: divide both sides by (x² + 3x):
1/2(x² + 3x) – 8/2 = 0 => 1/2(1+3*(-8)) -8/2 => 1/2(-11) -8/2 => 1/2(-11) – (-8/2) => 1/2(-11 – 16) => 1/2(-17)=> x=-17
4. What are the steps in an Equation?
An equation is a mathematical statement that two things are equal. There are four steps to solve an equation:
1. Find the value of one side of the equation by itself. For example, if you have 3+2=5, then 5=3+2.
2. Solve the variable in terms of other variables in the equation by subtracting or dividing both sides of the equation by something. For example, if you have 3x+2=5, then 3x-5/3=0 or -5/3 x = 0, so x = -1/3 or 1/3.
3. Substitute your answer back into the original equation and solve for another variable in terms of all others; this will give you another solution to check against. For example, if x = 1/3 and y = -1/3 (from step 2), then 3(-1/3)+2(-1/3)=5(-1/3). If you add these together, you get -4/9 = 5(-1/9) and -4 + 9 = 5, so -4 + 9 = 5; therefore x may be 1/3 but not necessarily 1/9! So we’re done here!
5. What are the types of Equations?
There are several different types of equations:
* Linear equations are equations that can be written in the form y = mx + b, where m is the slope and b is the y-intercept.
* Quadratic equations have the form ax^2 + bx + c = 0.
* Absolute value equations are of the form |x|.
* Rational expressions are of the form p/q, where p and q are polynomials with no common factors and q ≠ 0.