Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/
From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
In this post, we are going to look at a selection of 3rd grade math word problems in Smartick.
We’ll begin by explaining what a word problem is.
What is a Word Problem?
A word problem is a question or approach, that cannot be answered using one specific operation, but rather a combination of previous knowledge whether mathematical or not.
Solving a math problem is cognitively complex since it involves understanding the situation presented in the word problem, as well as comprehending the message and words used in the word problem. Therefore, at first, to face a math problem is to face a problem of linguistic understanding. Once the word problem is understood, you must choose which, or what, procedures you are going to use to reach a solution (mathematical understanding).
This type of activity helps a child to connect mathematics to the world around them and by doing this, they are able to apply what they have learned to everyday life. To solve a problem, it is not only necessary to master the specific knowledge related to the problem, but also plan and perform some procedures to reach the solution.
3rd Grade Math Word Problems
To assess mathematical competence in 3rd grade math word problems, there are some cognitive processes to keep in mind that fall into these three groups:
- Know and produce. It refers to the knowledge of the basic mathematical language, essential mathematical properties and facts, and the repetition of calculation algorithms practiced, linking them to familiar math processes and problems that include basic operations. This is required for even the most basic exercises.
- Apply and analyze. Involves knowing how to use different mathematical tools and establishing relationships between diverse situations in relatively well-known contexts, selecting problem-solving strategies, performing calculations, and obtaining solutions. This is necessary for exercises that are slightly more difficult.
- Reason and reflect. It requires the ability to think logically and systematically, and involves analyzing the results obtained in solving a problem and reflecting upon the process used. It refers to the interpretation of the results according to the context, communication of the method used, and the result obtained appropriately. It implies a higher degree of competitive acquisition.
Before starting practicing, I would recommend that you try to solve the 3rd grade math word problems on your own, without looking at the solutions. Give it a try!
Word Problem 1
Solution 1
After reading the word problem we need to make sure that we understand the information given.
- The lasagna will be cut into equally sized pieces.
- Catherine and Noah will eat different sized portions.
- Noah will eat 1/4 more than Catherine.
Since we know that Catherine will eat a portion of 1 1/2 (1 full piece and one 1/2 piece) we just need to find out how large Noah’s portion will be. Let’s look at the fraction, how many times can 1/4 go into 1/2? Two times because there are 2 halves to a whole and 4 quarters to a whole, therefore 1/2 = 2/4. Now that we know Catherine will eat 1 2/4 and Noah will eat 1/4 more, 2/4 + 1/4 = 3/4.
Noah will eat 1 3/4 pieces of lasagna.
Word Problem 2
Solution 2
We have been asked to change only one number in the word problem so that the number of cards that Alexander has at the end of the first part of the game is 6. We are told that he has won 17 cards during the second half and finishes the game with 28 cards. In order to know how many cards he had in the first part we should subtract what he has won during the second part from the total number of cards he ended the game with, in other words, 28 – 17 = 11. Since we have been asked to make sure the answer is 6 and can only change one data, we have two valid options.
- Change the number of cards he won during the second part, if he won 17 and we add 5, 17 +5 = 22. Then when we subtract that number from the total, 28 – 22 = 6, it gives us the number we need to solve the word problem. Alexander had 6 cards at the end of the first part of the game.
- Change the number of cards that he had at the end of the game, subtracting 5 from the 28 cards, 28 – 5 = 23. Then subtract the number of cards he won during the second part, 17, from the total, 23 – 17 = 6. Alexander had 6 cards at the end of the first part of the game.
Sometimes math problems have more than one solution.
Word Problem 3
Solution 3
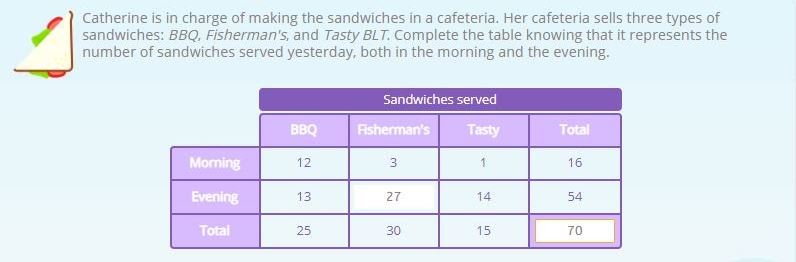
This problem is very easy because the table shown has all of the information.
- The first thing we need to know is the total amount of sandwiches, of all varieties, served yesterday, both day and night. Put simply, we need to add 16 + 54 = 70 sandwiches.
- Next, we need to fill in the empty space for the Fisherman’s sandwich. In order to know how many were served in the evening, we need to subtract the number of sandwiches served during the day from the total.
- 54 – 27 = 27 Fisherman’s sandwiches we served yesterday evening in the cafeteria where Catherine works.
Word Problem 4
Solution 4
First of all, we want to find out the total number of children that are on the bus. To do this, we just need to complete a very simple operation. We know that there are 6 children on the bus and the bus makes 4 trips, so we can do 6 x 4 = 24. Now we know that there are a total of 24 children on the bus during the day. Next, we need to determine how many children are dropped off at each school. The word problem tells us that the same number of children are dropped off at each school, there are two schools, so let’s divide by 2!
24 / 2 = 12, the bus takes 12 children to each school.
If you would like to continue practicing more 3rd grade math word problems and other topics from primary mathematics, adapted to your level, register with Smartick and try it free!
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
| English to Math Translation | Rate/Distance Word Problem |
| Unit Rate Problem | Profit Word Problem |
| “Find the Numbers” Word Problem | Converting Repeating Decimal to Fraction Word Problem |
| Simple Interest Rate Problem | Inequality Word Problems |
| Percent Word Problem | Integer Function Problem |
| Percent Increase Word Problem | Direct, Inverse, Joint and Combined Variation Word Problems (in that section) |
| Ratio/Proportion Word Problems | Work Word Problems (in Rational Functions and Equations) |
| Weighted Average Word Problem | Systems of Equations Word Problems (in that section) |
| Consecutive Integer Word Problem | More Word Problems using Rational Functions (in Rational Functions section) |
| Age Word Problem | Absolute Value Word Problem (in Absolute Values section) |
| Money (Coins) Word Problem | Composition of Functions Word Problems (in Advanced Functions section) |
| Mixture Word Problem, Percent Mixture Word Problem |
The algebra word problems here only involve one variable; later we’ll work on some that involve more than one, such as here in the Systems of Linear Equations and Word Problems section.
English to Math Translation for Word Problems
Doing word problems is almost like learning a new language like Spanish or French; you can basically translate word-for-word from English to Math, and here are some translations:
| English | Math | English | Math | |
| is, yields, will be | (=) | (p) percent | (displaystyle frac{p}{{100}}), or move decimal left 2 places | |
| what number, how much (look at question) | “(x)” (or any variable) | half, twice | (displaystyle frac{n}{2},,,,2n) | |
| in addition to, added to, increased by | (+) | consecutive numbers | Let (n=) first number, (n+1=) second number, (n+2=) third number… | |
| sum of (x) and (y) | (x+y) | odd/even consecutive numbers | Let (n=) first number, (n+2=) second number, (n+4=) third number…
Note: Even if you are looking for odd consecutive numbers, use (n, n+2, n+4, …). |
|
| difference of (x) and (y) | (x-y) | average of (x,y) and (z) (and so on) | (displaystyle frac{{x+y+z+…}}{{text{(how many},,text{numbers},,text{on},,text{top)}}}) | |
| product of (x) and (y) | (xtimes y) | (x) per (y), (x) to (y), (x) over (y), (x) part of (y) | (xdiv y) or (displaystyle frac{x}{y})
Example: number of girls to total people can be represented by (displaystyle frac{{text{girls}}}{{text{total}}}). |
|
| quotient of (x) and (y) | (displaystyle xdiv y,,,,,text{or },,,frac{x}{y}) | (x) per (y), as in (x) “for every” (y)
Other examples of multiplication: each hour, every hour, an hour |
Multiplication, or (xtimes y).
Example: if you drive 50 miles per hour, how many miles will you drive in 5 hours: 250 miles. |
|
| opposite of (x) | (-x) | (y) increased by (x%) | (displaystyle y+left( {ytimes frac{x}{{100}}} right)) | |
| ratio of (x) to (y) | (displaystyle xdiv y,,,,,text{or},,,,frac{x}{y}) | (y) decreased by (x%) | (displaystyle y-left( {ytimes frac{x}{{100}}} right)) | |
| a number (n) less 3 | (n-3) | (y) is at least (or no less than) (x) | (yge x) | |
| a number (n) less than 3 | (3-n) | (y) is at most (or no more than) (x) | (yle x) | |
| a number (n) reduced by 3 | (n-3) | (y) is between (x) and (z) | (xle yle z) (inclusive) (x<y<z) (exclusive) | |
| of | times |
Remember these important things:
- If you’re wondering what the variable (or unknown) should be when working on a word problem, look at what the problem is asking. This is usually what your variable is!
- If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!
- If the problem asks for a Unit Rate, you want the ratio of the (y)-value (typically the dollar amount) to the (x)-value, when the (x)-value is 1.This is basically the slope of the linear functions. You may see feet per second, miles per hour, or amount per unit; these are all unit rates.
Here are problems that use some of the translations above. We’ll get to more difficult algebra word problems later.
Unit Rate Problem:
Problem: You buy 5 pounds of apples for $3.75. What is the unit rate of a pound of apples?
Solution: To get the unit rate, we want the amount for one pound of apples; this is when “(x)” (apples) is 1. We can set up a ratio: (displaystyle frac{{3.75}}{5}=frac{x}{1};,,,x=$.75). We also could have just divided the amount spent by the number of pounds, which makes sense.
(Another cool way to figure out what to do is to think of a simpler problem. If we buy 20 pounds of apples for $10, we “feel” the unit rate is $.50 per pound. And the math agrees with us!)
“Find the Numbers” Word Problems:
Problem: The sum of two numbers is 18. Twice the smaller number decreased by 3 equals the larger number. What are the two numbers?
Solution: We always have to define a variable, and we can look at what they are asking. The problem is asking for both the numbers, so we can make “(n)” the smaller number, and “(18-n)” the larger.
Do you see why we did this? The way I figured this out is to pretend the smaller is 10. (This isn’t necessarily the answer to the problem!) I knew the sum of the two numbers had to be 18, so I knew to take 10 and subtract it from 18 to get the other number. It is easier to think of real numbers, instead of variables when you’re coming up with the expressions.
Translate the English into math and solve:
| Problem/Math | Notes |
| The sum of two numbers is 18. Twice the smaller number decreased by 3 equals the larger number. What are the two numbers?
(displaystyle begin{align}2n-3&=18-n\2n-3,,(+n)&=18-n,,(+n)\3n,-3&=18\,,3n&=21\,frac{{3n}}{3}&=frac{{21}}{3}\n&=7,,,,,,text{(smaller number)}\18-7&=11,,,,text{(larger number)}end{align}) |
Let (n=) the smaller number, and (18-n=) the larger number.
The translation is pretty straight forward; note that we didn’t have distribute the 2 since the problem only calls for twice the smaller number, and then we subtract 3. Check our work: The sum of 7 and 11 is 18. √ Twice the smaller ((2times 7)) decreased by 3 would be (14-3=11). √ |
Another Problem:
Problem: If the product of a number and –7 is reduced by 3, the resulting number is 33 less than twice the opposite of that number. What is the number?
Solution: Define a variable, and look at what they are asking. The problem is asking for a number, so make that (n). Translate word-for-word, and remember that the “opposite” of a number just means to make it negative if it’s positive or positive if it’s negative. Thus, we can just put a negative sign in front of the variable.
If you’re not sure if you should multiply, add, or subtract, try “real numbers” to see what you should do. For example, “8 reduced by 3” is 5, so for the “reduce by 3” part, we subtract 3. Also, “33 less than 133” is 100, so for the “33 less than”, we subtract 33 at the end:
|
Problem/Math |
Notes |
| If the product of a number and –7 is reduced by 3, the resulting number is 33 less than twice the opposite of that number. What is the number?
(displaystyle begin{align}left( {-7} right)n-3&=2left( {-n} right)-33\,,,,,-7n-3&=-2n-33\-7n-3,,left( {+7n+33} right)&=-2n-33,,left( {+7n+33} right)\30&=5n\,frac{{30}}{5}&=frac{{5n}}{5}\n&=6end{align}) |
The opposite of a number means we basically just multiply the number by –1 (in our case, put a negative in front of it). Translate English to math, and, after solving, get 6 as our answer.
Check our work: If we take the product of 6 and –7 (–42) and reduce it by 3, we get –45. Is this number 33 less than twice the opposite of 6? Twice the opposite of 6 is –12, and 33 less than –12 is (-12-33=-45). We got it! √ |
Simple Interest Rate Problem:
Problem: How much money would need to be invested at 2% annual simple interest for 10 years to earn $1200? Use the formula (text{Interest}=text{Principle }times ,text{Rate},times ,text{Time}).
Solution: Using the formula (I=Prt), solve for (displaystyle P:,P=frac{I}{{rt}}=frac{{1200}}{{left( {.02} right)10}};,,,P=$6000). Note that we had to turn (2%) into a decimal: we need to get rid of the % (pretend we’re afraid of it), so we move the decimal 2 places away from it.
Note: Compound Interest problems can be found here in the Exponential Functions section.
Percent Word Problem:
(We saw similar problems in the Percentages, Ratios, and Proportions section!)
|
Percent Problem/Math |
Notes |
| 60 is 20% of what number?
(displaystyle begin{align}60&=.20times n\frac{{60}}{{.2}}&=frac{{.2n}}{{.2}}\300&=,n\n&=300end{align}) |
Translate word-for-word, and remember again that of = times, and (20%=.20=.2).
Check our work: (20%,,,text{of},,,300=.2times 300=60) √ |
Percent Increase Word Problem:
| Percent Increase Problem/Math | Notes |
| The price of a pair of shoes has increased by 15%. The original price of the shoes was $20. What is the new price? (displaystyle begin{array}{l}x=$20+left( {15%,times 20} right)\x=$20+left( {.15times 20} right)\x=$20+$3=$23\x=$23,end{array}) or (displaystyle begin{array}{l}x=$20times left( {1+15%} right)\x=$20times left( {1+.15} right)\x=$20times left( {1.15} right)\x=$23,end{array}) |
15% of the original amount (=15%times 20), since of = times. Turn the 15% into a decimal and add the product to the original amount.
The second way to do it is to multiply the original amount ($20) by (1.15,,(100%+15%)), which adds (displaystyle 15%) to the original amount before multiplying. |
Ratio/Proportion Word Problems
Relating Two Things Together: a Rate
Problem: It takes 2 minutes to print out 3 color photos on Erin’s printer. Write an equation relating the number of color photos (p) to the number of minutes (m).
Solution: This problem seems easy, but you have to think about what the problem is asking. When we are asked to relate something to something else, typically we use the last thing (the “to the” part) as the (y), or the dependent variable. I like to set up these types of problems as proportions, but what we’re looking for is actually a rate of minutes to photos, or how many minutes to print 1 photo. Remember that rate is “how many (y)” to “one (x)”, or in our case, how many “(m)” to one “(p)”. We will see later that this is like a Slope from the Coordinate System and Graphing Lines including Inequalities section. Here’s the math:
| Ratio Problem/Math | Notes |
| It takes 2 minutes to print out 3 color photos on Erin’s printer. Write an equation relating the number of color photos (p) to the number of minutes (m).
(displaystyle begin{align}frac{{text{2 minutes}}}{{text{3 color photos}}}&=frac{{text{how many minutes}}}{{text{1 color photo}}}\frac{text{2}}{text{3}}&=frac{m}{{1p}}\3m&=2p\m&=frac{2}{3}pend{align}) |
To get the rate of minutes to photos, we can set up a proportion with the minutes on the top and the photos on the bottom, and then cross-multiply.
The equation relating the number of color photos (p) to the number of minutes (m) is (displaystyle m=frac{2}{3}p). √ |
Ratio/Proportion Problem:
Problem: The ratio of boys to girls in your new class is 5 : 2. The sum of the kids in the class is 28. How many boys are in the class?
Solution: This is a rati0 problem; we learned about ratios in the Percentages, Ratios, and Proportions section. A ratio is a comparison of two numbers; a ratio of 5 to 2 (also written 5:2 or (displaystyle frac{5}{2})) means you have 5 boys for every 2 girls in your class. For example, if you had only 7 in your class, you’d have 5 boys and 2 girls. But what if you had 14? You’d have 10 boys and 4 girls, since 10 is 5 times 2, and 4 is 2 times 2. Let’s set this up in an equation, though, so we can do the algebra!
There are actually a couple of different ways to do this type of problem. Probably the most common is to set up a proportion like we did in the Percents, Ratios, and Proportions section. Let (x=) the number of boys in the class.
| Ratio Problem/Math | Notes |
| The ratio of boys to girls in your new class is 5:2. The sum of the kids in the class is 28. How many boys are in the class?
(require{cancel} displaystyle begin{align}frac{{text{boys}}}{{text{total in class}}}&=frac{x}{{28}}=frac{5}{7}\\7x&=5times 28=140\frac{{cancel{7}x}}{{cancel{7}}}&=frac{{140}}{7}\x&=20text{ boys}end{align}) |
We know that the sum of the numbers in the ratio is 7 (boys and girls: 5 + 2), and the sum of the kids in the class is 28. We also know the “boys” part of the ratio is 5.
We can set up a proportion with the same things on top or on bottom; our ratios will have “boys” on top and “total in class” on bottom. In other words, we need to see how many boys out of 28 will keep a ratio of 5 boys to 7 total in the class. Cross-multiply to get (x=20). There are 20 boys and 8 girls (28 – 20) in the new class. Check our answer: the ratio of 20 to 8 is the same as the ratio of 5 to 2. And the number of boys and girls add up to 28! √ |
There’s another common way to handle these types of problems, but this way can be a little trickier since the variable in the equation is not what the problem is asking for; we will make the variable a “multiplier” for the ratio. The advantage to this way is we don’t have to use fractions.
| Ratio Word Problem/Math | Notes |
|
The ratio of boys to girls in your new class is 5:2. The sum of the kids in the class is 28. How many boys are in the class? (begin{align}5x+2x&=28\7x=28\frac{{7x}}{7}&=frac{{28}}{7}\x&=4\\5times 4&=20,,,,text{boys}\2times 4&=8,,,,text{girls}end{align}) |
We can multiply both numbers by the same thing to keep the ratio the same – try this with some numbers to see this.
5 times a number, and 2 times that same number must equal 28. Let (x) be the multiplier – not the number of boys or girls. We get 4 as the multiplier, but we’re looking for the number of boys in the class (5 times 4 = 20) and the number of girls in the class (2 times 4 = 8). There are 20 boys and 8 girls. Check our answer: the ratio of 20 to 8 is the same as the ratio of 5 to 2 (each is divided by 4 – the multiplier!) And the number of boys and girls add up to 28! √ |
Here’s a ratio problem that’s pretty tricky; we have to do it in a lot of steps:
| Ratio Problem/Math | Notes |
| One ounce of solution X contains ingredients a and b in a ratio of 2:3. One ounce of solution Y contains ingredients a and b in a ratio of 1:2.
If solution Z is made by mixing solutions X and Y in a ratio of 3:11, then 1260 ounces of solution Z contains how many ounces of ingredient a? Solution Z: (begin{array}{c}3u+11u=1260;,,,,,u=90\3times 90=270,,,text{oz}text{. solution X}\11times 90=990,,,text{oz}text{. solution Y}end{array}) |
Work backwards on this problem, and first work with solution Z, since there are 1260 ounces of it. It’s good to start with the parts of the problems with numbers first!
Since the ratio of X and Y is 3:11 in solution Z, we can find the ratio multiplier ((u)), and find how much of solutions X and Y are in Z. There are 270 ounces of X and 990 of Y in solution Z. |
|
Solution X: (begin{array}{c}2v+3v=270;,,,,v=54\2times 54=108,,,text{oz}text{. ingredient a}\3times 54=162,,,,text{oz}text{. ingredient b}end{array}) Solution Y: (begin{array}{c}1w+2w=990;,,,,w=330\1times 330=330,,,text{oz}text{. ingredient a}\,2times 330=660,,,text{oz}text{. ingredient b}end{array}) |
From above, there are 270 ounces of solution X in solution Z. We can find out how much of ingredients a and b are in solution X by using a ratio multiplier again ((v)), since one ounce of solution X contains ingredients a and b in a ratio of 2:3. There are 108 ounces of ingredient a in solution X.
Do the same for solution Y (using ratio multiplier (w)), which contains ingredients a and b in a ratio of 1:2. There are 330 ounces of ingredient a in solution Y. |
| (108+330=438) | The problem asks for the amount of ingredient a in solution Z, so add the amounts of ingredient a in Solutions X and Y to get 438. 1260 ounces of solution Z contains 438 ounces of ingredient a. √ |
Weighted Average Word Problem:
Weighted average problems have to do with taking averages, but assigning different weights to the elements (for example, counting them more than once).
Problem: You’ve taken four tests in your Algebra II class and made an 89, 92, 78, and 83. The final is worth two test grades. What do you need to make on the final to make an A (a 90) in the class for the semester?
Solution: Define a variable, and look at what is being asked. Let (x=) what you need to make on the final. Now we have 6 test grades that will count towards our semester grade: 4 regular tests and 2 test grades that will be what you get on the final (since it counts twice, we need to add it 2 times). This is called a weighted average, since we “weighted” the final test grade twice. Use the equation for an average:
| Weighted Average Problem/Math | Notes |
| You’ve taken four tests in your Algebra II class and made an 89, 92, 78, and 83. The final is worth two test grades. What do you need to make on the final to make an A (a 90) in the class for the semester?
(require{cancel} displaystyle begin{align}frac{{89+92+78+83+x+x}}{6}&=90\frac{{89+92+78+83+2x}}{{cancel{6}}}times frac{{cancel{6}}}{1}&=90times frac{6}{1}\342+2x&=540\2x&=198\frac{{2x}}{2}&=frac{{198}}{2}\x&=99end{align}) |
The average or mean equation is just adding up all the values, and then dividing by the number of values that we just added up. For this example, divide by 6, since we have 4 tests given, and the final is worth 2 test grades.
You have to make a 99 on the final to make an A in the class! Yikes! Good luck – you can do it! Let’s see if it works: (displaystyle frac{{86+92+78+83+99+99}}{6}=frac{{540}}{6},=90,,,,,surd ) |
HINT: For any problem with weighted averages, you can multiply each value by the weight in the numerator, and then divide by the sum of all the weights that you’ve used. For example, if you had test 1 (say, an 89) counting 20% of your grade, test 2 (80) counting 40% of your grade, and test 3 (78) counting 40% of your grade, take the weighted average as in the formula below. Don’t forget to turn percentages into decimals and make sure that all the percentages that you use (the “weights”) add up to 100 (all the decimals you use as weights should add up to 1). When using decimals, your denominator should be 1:
(displaystyle frac{{left( {89times .2} right),+,left( {80times .4} right),+,left( {78times .4} right)}}{{.2+.4+.4}}=frac{{17.8+32+31.2}}{1}=81)
Consecutive Integer Word Problem:
Problem: The sum of the least and greatest of 3 consecutive integers (numbers in a row) is 60. What are the values of the 3 integers?
Solution: You’ll see these “consecutive integer” problems a lot in algebra. When you see these, you always have to assign “(n)” to the first number, “(n+1)” to the second, “(n+2)” to the third, and so on. This makes sense, since consecutive means “in a row” and we’re always adding 1 to get to the next number.
Note: If the problem asks for even or odd consecutive numbers, use “(n)”, “(n+2)”, “(n+4)”, and so on – for both even and odd numbers! It will work; trust me!
| Consecutive Integer Problem/Math | Notes |
| The sum of the least and greatest of three consecutive integers (numbers in a row) is 60. What are the values of the three integers?
(displaystyle begin{align}n+n+2&=60\2n+2&=60\2n&=58\frac{{2n}}{2}&=frac{{58}}{2}end{align}) (displaystyle n=29,,,,,,n+1=30,,,,,,n+2=31) |
Assign “(n)” to the first number, “(n+1)” to the second, and “(n+2)” to the third, since they are consecutive numbers.
Translate the English into math. The least of the three consecutive numbers is “(n)“, and the greatest is “(n+2)”. Add the least number and the greatest to get 60. The three consecutive numbers are 29, 30, and 31. Check our answer: (29+31=60,,,, surd ) |
Age Word Problem:
Problem: Your little sister Molly is one third the age of your mom. In 12 years, Molly will be half the age of your mom. How old is Molly and your mom now?
Solution: Doesn’t this one sound complicated? It’s a great one to try on your friends! It’s not that bad though – first define a variable by looking at what the problem is asking.
| Age Word Problem/Math | Notes |
| Your little sister Molly is one third the age of your mom. In 12 years, Molly will be half the age of your mom. How old is Molly and your mom now?
(begin{align}M+12&=frac{1}{2}left( {3M+12} right)\2times left( {M+12} right)&=3M+12\2M+24&=3M+12\\24-12&=3M-2M\12&=Mend{align}) (M=12,,,,,,,,,3M=36) |
Let (M=) the age of sister Molly now. From this, we know that your mom is (3M) (make it into an easier problem – if Molly is 10, your mom is 30).
Turn English into math (second sentence). Remember that we have to add 12 years to both ages ((M+12) for Molly and (3M+12) for your mom), since we’re talking about 12 years from now (unfortunately, moms have to age, too). Multiply both sides by 2 to get rid of the fraction, and then “push” the 2 through the parentheses. Get the variables to one side, and the constants to the other. Molly is 12, and your mother is 36. Let’s see if it works: In 12 years, Molly will be 24, and her mom will be 48. Aha! Molly will be half of her mom’s age in 12 years. (surd ) |
Money (Coins) Word Problem:
Note that problems like this with two variables to solve for are more easily solved with a System of Equations, which we will cover in the next section.
| Money Word Problem/Math | Notes |
| Suppose Briley has 10 coins in quarters and dimes and has a total of $1.45. How many of each coin does she have?
(displaystyle begin{align}.25Q+.10(10-Q)&=1.45\.25Q+1-.1Q&=1.45\.15Q+1&=1.45\.15Q&=.45\frac{{.15Q}}{{.15}}&=frac{{.45}}{{.15}}\Q&=3\D&=10-3=7end{align}) |
Let (Q=) the number of quarters that Briley has. Then we know that she has (10-Q) dimes (turn into easier problem – if she has 2 quarters, she has 10 minus 2, or 8 dimes).
Each quarter is worth $.25 and each dime is worth $.10; thus, the number of quarters times .25 plus the number of dimes times .10 must equal her total, or $1.45. (Again, turn into easier problem: if you have 4 quarters, you have .25 times 4 = $1.00 total). Briley has 3 quarters, and 7 dimes. Let’s see if it works: 3 quarters is $.75 and 7 dimes is $.70. If we add $.75 and $.70, we get $1.45. (surd ) |
We could have also done this problem (and many problems like these) with a table:
| Amount | Price | Total | ||
| Quarters | Q | .25 | .25 Q | Multiply across |
| Dimes | 10 – Q | .10 | .10 (10 – Q) | Multiply across |
| Total | 10 | 1.45 | Do Nothing Here | |
| Add Down | Do Nothing Here | Add Down: (.25Q+.10left( {10-Q} right)=1.45); then solve to get (Q=3,,,10-Q=7). |
Mixture Word Problem:
Mixture Word Problems are where different quantities are mixed together, and you are asked to find certain quantities. (They are also solved with multiple variables with Systems of Equations). Here is an example using one variable:
Problem: One kind of candy (jelly) sells for $5 a pound and another (chocolate) for $10 a pound. How many pounds of each should be used to make a mixture of 12 pounds of candy (both kinds) that sells for $80?
Solution: First define a variable, and it helps to use a table. Let (J=) the number of pounds of jelly candy that is used in the mixture. Then (12-J) equals the number of pounds of the chocolate candy.
| Amount | Price | Total | ||
| Jelly Candy | J | 5 | 5J | Multiply across |
| Chocolate Candy | 12 – J | 10 | 10 (12 – J) | Multiply across |
| Total | 12 | 80 | Do Nothing Here | |
| Add Down | Do Nothing Here | Add Down: (5J+10left( {12-J} right)=80); then solve to get (J=8). |
Here’s whole problem:
| Mixture Word Problem | Notes |
| One kind of candy (jelly) sells for $5 a pound and another (chocolate) for $10 a pound. How many pounds of each should be used to make a mixture of 12 pounds of candy (both kinds) that sells for $80? | From the table above:
(begin{align}5J+10(12-J)&=80\5J+120-10J&=80\-5J&=-40\J&=8end{align}) We would need 8 pounds of the jelly candy and (10-8=2) pounds of the chocolate candy. |
Percent Mixture Word Problem:
Problem: A 20% concentrate is to be mixed with a mixture having a concentration of 60% to obtain 80 liters of a mixture with a concentration of 30%. How much of the 20% concentrate and the 60% concentrate will be needed?
Solution: First define a variable, and it helps to use a table. Let (T=) the number of liters we need from the 20% concentrate, and then (80-T) will be the number of liters from the 60% concentrate. (Put in real numbers to check this).
Put this in a chart again – it’s not too bad. This one is a little more difficult since we have to multiply across for the Total row, too, since we want a 30% solution of the total.
| Amount | % Concentrate | Total | ||
| 20% Concentrate | T | .20 | .2T | Multiply across |
| 60% Concentrate | 80 – T | .60 | .60 (80 – T) | Multiply across |
|
Total (What we want) |
80 | .30 | 24 | Multiply across |
| Add Down | Do Nothing Here | Add Down: (.2T+.6left( {80-T} right)=24); then solve to get (t=60). |
Here’s the whole problem:
| Percent Mixture Word Problem | Notes |
| A 20% concentrate is to be mixed with a mixture having a concentration of 60% to obtain 80 liters of a mixture with a concentration of 30%. How much of the 20% concentrate and the 60% concentrate will be needed? | From the table above:
(begin{align}.2T+.6left( {80-T} right)&=24\.2T+48-.6T&=24\-.4T&=-24\T&=60end{align}) We would need 60 liters of the 20% solutions and (80-60=20) liters of the 60% solution. |
Remember that if the problem calls for a pure solution or concentrate, use 100% (if the percentage is that solution) or 0% (if the percentage is another solution). Here’s an example:
Problem: How many ounces of pure water must be added to 100 ounces of a 30% saline solution to make it a 10% saline solution?
Solution:
| Amount | % Saline | Total | ||
| Pure Water | W | 0% = 0 | 0W = 0 | Multiply across |
| 30% Saline (Salt) Solution | 100 | .30 | 30 | Multiply across |
|
10% Saline Solution (What we want) |
W + 100 | .10 | .1(W + 100) | Multiply across |
| Add Down | Do Nothing Here | Add Down: (0+30=.1left( {W+100} right);,,W=200). |
Don’t worry if you don’t totally get these; as you do more, they’ll get easier. We’ll do more of these when we get to the Systems of Linear Equations and Word Problems topics.
Rate/Distance Word Problem:
Distance problems have to do with how far, how fast and how long objects have travelled. Here is an example:
| Distance Word Problem/Math | Notes |
|
A train and a car start at the same place. The train is going 40 miles per hour and a car is going in the opposite direction at 60 miles per hour. How long will it be until they are 100 miles apart? (text{Distance},,=,,text{Rate},,times ,,text{Time}) Total Distance: (100=60t+40t) Solve: (begin{array}{l}100=60t+40t\100=100t;,,,,t=1end{array}) |
Always draw pictures! Remember always that (text{Distance}=text{Rate},times ,text{Time}). The rates of the train and car are 40 and 60, respectively. Usually a rate is “something per something”.
Let (t) equal the how long (in hours) it will be until the train and the car are 100 miles apart. We must figure the distance of the train and car separately, and then we can add distances together to get 100. Again, you can always add distances; look at them separately first, and then you can put them together to equal the total distance (100). The math was pretty easy on this one! In one hour, the train and the car will be 100 miles apart. |
Note that there’s an example of a System Equations Distance Problem here, and a Parametric Distance Problem here in the Parametric Equations section.
Profit Word Problem
Profit word problems have to do with the amount of money made for products or services in business. Here is an example:
Problem: Hannah paid $1.50 each for programs to her play. She sold all but 20 of them for $3 each and made a profit of $15 total. How many programs did Hannah buy? How many did she sell? Hint: Profit = Selling Price – Purchase Price
Solution: It’s easiest to a table to store the information. Let (x=) the number of programs that Hannah bought. Put in real numbers to see how we’d get the number that she sold: if she bought 100 programs and sold all but 20 of them, she would have sold 80 of them. We can see that (80=100-20), so the number sold would be (x-20).
| Number of Programs | Price | Total | ||
| Sold | x – 20 | 3.00 | 3(x – 20) | Multiply across |
| Bought | x | 1.50 | 1.5x | Multiply across |
| Profit | 15 | Total Profit Given | ||
| Do Nothing Here | Do Nothing Here | Subtract Down: To get profit, subtract Total Bought from Total Sold, and set to Profit (15): (3left( {x-20} right)-1.5x=15); solve to get (x=50). |
Here’s the whole problem:
| Profit Word Problem | Notes |
| Hannah paid $1.50 each for programs to her play. She sold all but 20 of them for $3 each and made a profit of $15 total. How many programs did Hannah buy? How many did she sell? | From the table above:
(begin{align}3left( {x-20} right)-1.5x&=15\3x-60-1.5x&=15\1.5x&=75\x&=50end{align}) Hannah bought 50 programs to make a total profit of $15. Since she sold 20 less than she bought, she sold 50 – 20 = 30 programs. |
Converting Repeating Decimal to Fraction Word Problem:
Problem: Convert (.4overline{{25}},,,(.4252525…)) to a fraction.
Solution: Converting repeating decimal to fraction problems can be easily solved with a little trick; we have to set it up as a subtraction, so the repeating part of the decimal is gone. To do this, let (x=) the repeating fraction, and then figure out ways to multiply (x) by 10, 100, and so on (multiples of 10) so we can subtract two numbers and eliminate the repeating part.
The rule of thumb is to multiply the repeating decimal by a multiple of 10 so we get the repeating digit(s) just to the left of the decimal point, and then multiply the repeating digit again by a multiple of 10 so we get repeating digit(s) just to the right of the decimal. Then subtract the two equations that we just created, and solve for (x):
| Repeating Decimal Problem/Math | Notes |
|
Convert (.4overline{{25}},,,(.4252525…)) to a fraction. (begin{array}{l},,,,,,,,,,,x=4.2525252…\text{(original repeating decimal)}\\,,,,,,,1000x=425.252525…\,,,,,,,,underline{{,,,,10x=,,,,,,4.252525…}}\,,,,,,,,,990x=421.0\,,,,,,,,,,,,,,,,,x=frac{{421}}{{990}}end{array}) |
First, let (x=.4overline{{25}}). Since (.4overline{{25}}) has repeating digits 25, we first have to figure out how to multiply (.4overline{{25}}) to get the repeating digits just to the left of the decimal place.
We can do this by multiplying (.4overline{{25}}) by 1000; we get (1000x=4underline{{25}}.252525…) Also, if we multiply (x) by 10, we get the repeating part (25) just to the right of the decimal point; we get (10x=4.underline{{25}}2525…). Now line up and subtract the two equations on the left and solve for (x); we get (displaystyle x=frac{{421}}{{990}}). Pretty cool! Let’s see if it works: Put (displaystyle frac{{421}}{{990}}) in your graphing calculator, and then hit Enter; you should something like .4252525253. √ |
Inequality Word Problems
Note that inequalities are very common in real-world situation, since we commonly hear expressions like “is less than” ((<)), “is more than” ((>)),“is no more than” ((le )), “is at least” ((ge )), and “is at most” ((le )). There are several inequality word problems the Solving Inequalities sections; here’s an example:
Problem: Erica must tutor at least 12 hour per week in order to be eligible for her work-study program at her university. She must also study 10 more hours than the time she’s tutoring, so she can keep up her grades in the program. What is the minimum number of hours Erica must study in order to be eligible for her work-study program?
Solution: First, define a variable (h), which is the number of hours that Erica must study (look at what the problem is asking). We know from above that “at least” can be translated to “(ge)”.
If Erica works, let’s say, 30 hours in her work study program, she’d have to study 40 hours (it’s easier to put in real numbers). So, the amount of time she works in her work study program would be “(h-10)”, and this number must be at least 12. Let’s set up the equation and solve:
| Inequality Word Problem/Math | Notes |
|
Erica must tutor at least 12 hour per week in order to be eligible for her work-study program at her university. She must also study 10 more hours than the time she’s tutoring, so she can keep up her grades in the program. What is the minimum number of hours Erica must study in order to be eligible for her work-study program? (begin{array}{l}h-10ge 12\underline{{,,,,,,+10ge ,,,+10}}\h,,,,,,,,,,,,ge 22end{array}) |
The algebra is simple, and we don’t have to worry about changing the sign, since we’re not multiplying or dividing by a negative number.
Erica would have to tutor at least 22 hours. Notice that 22 hours works, since the problems asked for “at least”. To check your answer, try numbers right around the answer, like 21 hours (which wouldn’t be enough), and 22 hours (which would work!) |
This inequality word problem is a little more advanced:
Problem: (displaystyle frac{4}{5}) of a number is less than 2 less than the same number. Solve the inequality and graph the results.
Solution: This is a little tricky since we have two different meanings of the words “less than”. The words “is less than” means we should use “(<)” in the problem; it’s an inequality. The words “2 less than the same number” means “(x-2)” (try it with “real” numbers).
| Inequality Word Problem/Math | Notes |
|
(displaystyle frac{4}{5}) of a number is less than 2 less than the same number. Solve the inequality and graph the results. (displaystyle begin{array}{l},,,,,,,,,,,,,,frac{4}{5}x,,,,,,,,<,,,,,,,x-2\,,,,,,,,,,,,,,,,underline{{,,,,,,-x<-x,,,,}}\,,,,,,,,,,frac{4}{5}x-x,,<,,,,,,,,-2\,,,,,,,,,,,,,,,,-frac{1}{5}x,,<,,-2\left( {-frac{1}{5}x} right)left( {-5} right),>left( {-2} right)left( {-5} right)\,,,,,,,,,,,,,,,,,,,,,,,,,,x>10,,,,,text{(watch sign!)}end{array}) |
Set up and solve inequalities like we do regular equations. Let “(x)” be the number, and translate the problem word-for-word: (displaystyle frac{4}{5}x<x-2).
Get all the “(x)”s to one side and all the “numbers” to the other sign. (We could have also multiplied both sides by 5 earlier to get rid of the fraction.) Remember to change the sign when we multiply both sides by –5, since we’re multiplying by a negative number. Once we get the answer, we can also graph the solution. Try numbers close to 10, like 9 and 11, to make sure it works. |
Rational Inequality Word Problem
Technically, this next problem contains a rational function, but it’s relatively easy to solve.
| Inequality Word Problem | Math/Notes |
| A school group wants to rent part of a bowling alley to have a party. The bowling alley costs $500 to rent, plus an additional charge of $5 per student to bowl. The group doesn’t want any student to pay more than $15 total to attend this party.
What is an inequality that could represent this situation? How many students would need to attend so each student would pay at most $15? |
Since there is a one-time cost in addition to a per-person cost, the cost per person will depend on the number of students attending the party: the more students, the lower the cost.
For (x) students attending, each would have to pay (displaystyle frac{{500}}{x}) for the bowling alley rent; try it with real numbers! In addition, each student needs to pay their $5 to bowl. Therefore, each student will need to pay (displaystyle frac{{500}}{x}+5), and since we don’t want any student to pay more than $15, the inequality that represents this situation is (displaystyle frac{{500}}{x}+5le 15). To see how many students would have to attend to keep the cost at $15 per person, solve for (x). In this example, we can multiply both sides by (x) without worrying about reversing the inequality sign, since (x) can only be positive: (displaystyle frac{{500}}{x}+5le 15;,,,frac{{500}}{x}le 10;,,,500le 10x;,,,xge 50). At least 50 students would have to attend so that each student pays no more than $15. |
Integer Function Problem (a little bit more advanced…)
Problem: The fee for hiring a tour guide to explore Italy is $1000. One guide can only take 10 tourists and additional tour guides may be hired if needed. What is the cost of hiring tour guides, as a function of the number of tourists who go on the tour? If there are 72 tourists, what is the cost of hiring guides?
Solution: Let’s think about this by using some real numbers. From 1–10 tourists the fee is (1times 1000=$1000), for 11–20 tourists, the fee is (2times 2000=$2000), and so on. Do you see how if we divide the number of tourists by 10, and go up to the next integer, we’ll get the number of tour guides we need? This is because any fraction of a set of ten tourists requires another tour guide.
To get the function we need, we can use the Least Integer Function, or Ceiling Function, which gives the least integer greater than or equal to a number (think of this as rounding up to the closest integer). The integer function is designated by (y=leftlceil x rightrceil ). (We saw a graph of a similar function, the Greatest Integer Function, in the Parent Functions and Transformations section.)
Thus, the cost of hiring tour guides is (displaystyle 1000times leftlceil {frac{x}{{10}}} rightrceil ). For 72 tourists, the cost is (displaystyle 1000times leftlceil {frac{{72}}{{10}}} rightrceil =1000times leftlceil {7.2} rightrceil =1000times 8=$8000). Makes sense!
Now, all these types of problems can get much more difficult (and we will see later how to use two variables with some of them), but it’s important to take baby steps with them. Don’t worry if they seem difficult at this time, but as long as you get the general idea of how we’re doing the translations, you’re in great shape! And don’t forget:
- When assigning variables (letters), look at what the problem is asking. You’ll typically find what the variables should be there.
- If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!
Solving Word Problems in Mathematics
What Is a Word Problem? (And How to Solve It!)
Learn what word problems are and how to solve them in 7 easy steps.
Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances.
As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem.
As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.
If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?
Steps of Solving a Word Problem
To work through any word problem, students should do the following:
1. Read the problem: first, students should read through the problem once.
2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
3. Visualize the problem: drawing a picture or creating a diagram can be helpful.
Students can start visualizing simple or more complex problems by creating relevant images, from concrete (like drawings of putting away cookies from a jar) to more abstract (like tape diagrams). It can also help students clarify the operations they need to carry out. (next step!)
4. Determine the operation(s): next, students should determine the operation or operations they need to perform. Is it addition, subtraction, multiplication, division? What needs to be done?
Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:
– Addition: add, more, total, altogether, and, plus, combine, in all;
– Subtraction: fewer, than, take away, subtract, left, difference;
– Multiplication: times, twice, triple, in all, total, groups;
– Division: each, equal pieces, split, share, per, out of, average.
These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems.
Another way to determine the operation is to search for certain situations, Jennifer Findley suggests. She has a great resource that lists various situations you might find in the most common word problems and the explanation of which operation applies to each situation.
5. Make a math sentence: next, students should try to translate the word problem and drawings into a math or number sentence. This means students might write a sentence such as 3 + 8 =.
Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence.
6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
7. Check the answer: finally, students should check their work to make sure that the answer is correct.
These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that!
At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises!
Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience.
Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.
For example, during the first steps, simple wording and animation help students realize what action the problem represents and find the connection between these actions and key words like “take away” and “left” that may signal them.
From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes.
Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.
Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations.
Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams!
To see the full exercise, follow this link.
The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task.
Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language.
These are the common steps that may help students overcome initial feelings of anxiety and fear of difficulty of the task they are given. Together with a teacher, they can master these foundational skills and build their confidence toward solving word problems. And Happy Numbers can facilitate this growth, providing varieties of engaging exercises and challenging word problems!