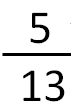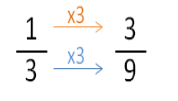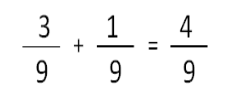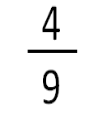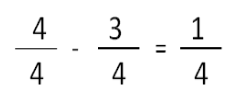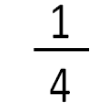Here are some examples and solutions of fraction word problems.
The first example is a one-step word problem.
The second example shows how blocks can be used to help illustrate the problem.
The third example is a two-step word problem.
More examples and solutions using the bar modeling method to solve fraction word problems are shown in
the videos. The bar modeling method, also called tape diagrams, are used in Singapore Math and the Common
Core.
Example:
Martha spent
of her allowance on food and shopping. What fraction of her allowance had she left?
Solution:
She had
of her allowance left.
Example:
of a group of children were girls. If there were 24 girls, how many children were there in the group?
Solution:
3 units = 24
1 unit = 24 ÷ 3 = 8
5 units = 5 × 8 = 40
There were 40 children in the group.
Example:
Sam had 120 teddy bears in his toy store. He sold
of them at $12 each. How much did he receive?
Solution:
Step 1: Find the number of teddy bears sold.
He sold 80 teddy bears.
Step 2: Find how much money he received.
80 × 12 = 960
He received $960.
Bar Modeling With Fractions
Examples:
- Grace thought that a plane journey would take 7/10 hr but the actual journey took 1/5 hr longer.
How long did the actual journey take? - Timothy took 2/3 hr to paint a portrait. This was 1/3 hr shorter than the time he took to paint
scenery. How long did he take to paint scenery?
- Show Video Lesson
How To Solve Real World Problems Involving Multiplication Of Fractions By Using Visual Fraction Models Or Equations To Represent The Problem?
Examples:
- At the animal shelter 4/6 of the animals are cats. Of the cats 1/2 are male. What fraction of the
animals at the shelter are male cats? - A taco recipe called for 2/3 cup of cheese per taco. If Andrew wanted to make 3 tacos, how much
cheese would he need?
- Show Video Lesson
How To Solve Word Problems Using Tape Diagrams And Fraction-By-Fraction Multiplication?
Examples:
- Ethan is icing 30 cupcakes. He spreads mint icing on 1/5 of the cupcakes and chocolate on 1/2 of the
remaining cupcakes. The rest will get vanilla frosting. How many cupcakes have vanilla frosting? - Maddox puts 1/4 of her lawn-mowing money in savings and uses 1/2 of the remaining money to pay back
her sister. If she has $15 left, how much did she have at first?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Fraction word problems are an important piece in teaching fractions. Fractions are a key component of the National Curriculum throughout primary, with children introduced to the concept in Year 1 and continuously building upon their knowledge and understanding, through to Year 6 and beyond.
The abstract nature of fractions makes them one of the more difficult areas of maths for children to understand. It is essential that they are taught through the use of concrete resources and visual images, but also through a link to the real world. Word problems are a great way to help children develop this understanding and should be used alongside any fluency work the children do.
To help you with this, we have put together a collection of 20 word problems which can be used with children from Year 2 to Year 6.
Fraction Lessons Resource Pack
Download this free pack of fraction lessons to support your students and help them to practice fractions problems.
Fraction word problems in the national curriculum
Fractions in KS1
Pupils are first introduced to fractions in Year 1, where they begin to recognise a half and quarter of a shape or quantity. As they progress through Key Stage 1, they are introduced to a wider range of fractions.
In Year 2 pupils need to be able to recognise, find, name and write fractions frac{1}{3}, frac{1}{4}, frac{2}{4} and frac{3}{4} of lengths, shape, a set of objects or quantity.
Fractions in lower KS2
Once pupils move into Key Stage 2, there is an increased focus on fractions, with a significant period of time dedicated to developing students’ knowledge and building on previous learning from Year 3 through to Year 6.
In Year 3, pupils are taught to count in tenths; recognise, find and write fractions of a discrete set of objects; understand the term ‘unit’ and ‘non-unit’ fractions; recognise equivalent fractions, compare and order fractions and add/subtract fractions with the same denominator. At this stage, pupils also begin to solve simple problems involving fractions.
As pupils progress into Year 4, they are also introduced to the concept of decimals alongside the work on fractions. They build upon their understanding of equivalent fractions and adding/subtracting fractions (still with the same denominator.
They also learn to count up and down in hundredths, recognise and write decimals equivalent to frac{1}{4}, frac{1}{2} and frac{3}{4} and begin to solve problems with increasingly harder fractions.
Fractions in upper KS2
As pupils continue through the school, into upper Key Stage 2, they continue to build on their learning. They are introduced to mixed numbers and improper fractions. They are also introduced to the concept of percentages alongside fractions and decimals.
In Year 5, children build on the knowledge gained in Year 4, comparing and ordering fractions; recognising equivalent fractions; addition and subtraction of fractions (with different denominators, but multiples of the same number). Fractions appear in addition and subtraction word problems.
They are also introduced to the multiplication of fractions; converting between improper fractions and mixed numbers and the link between fractions, decimals and percentages. By Year 5 pupils will be completing more complex problems, including multi-step word problems and multiplication word problems.
In Year 6, pupils consolidate and build upon the knowledge of fractions they have gained so far. Pupils continue to add and subtract fractions (with different denominators and mixed numbers). They also develop their understanding of how to multiply fractions and begin to divide fractions by whole numbers, combining fraction and division word problems.
Pupils also continue to build upon their understanding of the equivalences between fractions, decimals and percentages and solve increasingly complex one-step, two-step and multi-step percentage word problems.
Why are word problems important for children’s understanding of fractions?
Word problems, alongside the use of concrete resources and visual images, help children to make sense of the abstract nature of fractions.
For example, if children were presented with the question frac{6}{8} ÷ 3, some might find this difficult to access. If children are given it as a word problem, alongside a visual image, it becomes much more accessible.
The above calculation as a word problem:
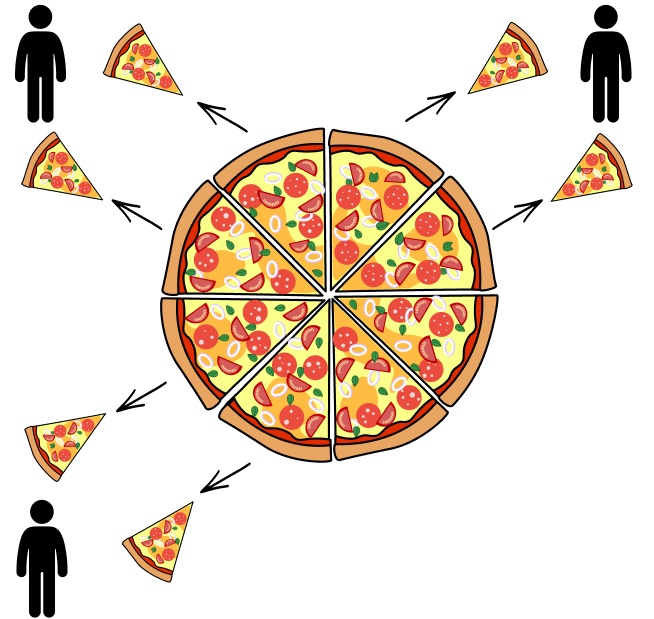
‘3 children shared it{frac{6}{8}} of a pizza, how much did each child get?’
Children can see and understand the concept of 3 children sharing 6 slices of pizza, compared to just seeing the written calculation.
How to teach fraction word problem solving in primary school
As with all word problems, the first thing children need to do is read the question carefully and make sure they understand what is being asked. They then have to decide what calculation is needed and whether they can represent it pictorially.
Here is an example:
Ben has a bag of 48 sweets.
He gives frac{3}{8} of his bag to his brother
How many sweets does he have left?
How to solve:
What do you already know?
- There are 48 sweets altogether.
- The denominator is 8, so we know we need to divide the 48 by 8. This will tell us how many sweets in frac{1}{8} .
- The numerator is 3, therefore we need to multiply the answer by 3, to tell us how many sweets are frac{3}{8} .
- The last step of the problem is to find out how many sweets Ben has left.
- We can either calculate frac{5}{8} , as we know Ben must have frac{5}{8} left, or we subtract the number of sweets in frac{3}{8} from the total of 48.
How can this be drawn/represented pictorially?
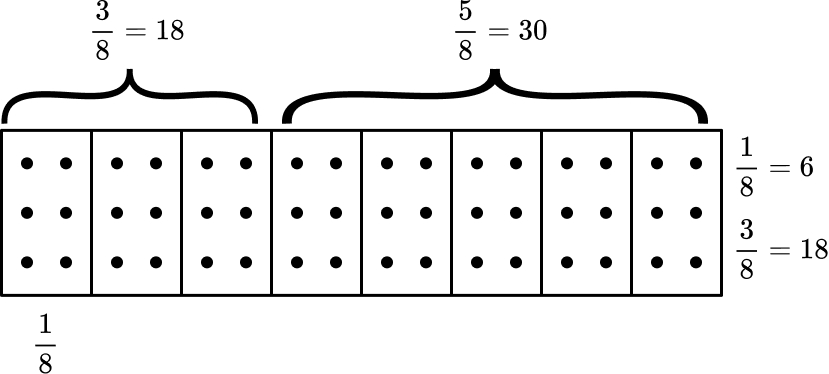
- We can draw a bar model, split into 8 sections.
- The 48 sweets are then shared between the 8 sections (each worth frac{1}{8} ).
- We can see that frac{3}{8} of the 48 sweets equals 18 sweets.
- We can then either subtract 18 from 48, to work out how many sweets were left. 48 – 18 = 30
- Alternatively, we can calculate how many sweets are in frac{5}{8} , which is 30.
Word problems are tied in throughout Third Space Learning’s online one-to-one tuition programmes. Tutors work with students to break down word problems and identify the operations needed to solve problems.
Fraction word problems for primary
The following section lays out the types of fraction word problems that you can expect to see by year group in primary school.
At Third Space Learning we incorporate word problems into our one-to-one online tutoring. With each lesson designed to suit the needs of each individual student, our tutoring programme aims to deepen mathematical understanding and confidence in maths.
Fraction word problems are a great way to strengthen students’ conceptual understanding of fractions and grow their problem solving skills.
Fraction word problems for Year 2
Word problems in Year 2 involve recognising and naming simple fractions and beginning to understand the concept of equivalence.
Question 1
Maisie was having a birthday party.
She invited 16 friends. Half of her friends were from her class and a half were from the other Year 2 class.
How many friends did she invite from each class?
Answer: 8 friends
frac{1}{2} of 16 = 8
Question 2
Ahmed baked 12 cookies.
He ate frac{1}{4} of them.
How many cookies did Ahmed eat?
Answer: 3
frac{1}{4} of 12 = 3
Question 3
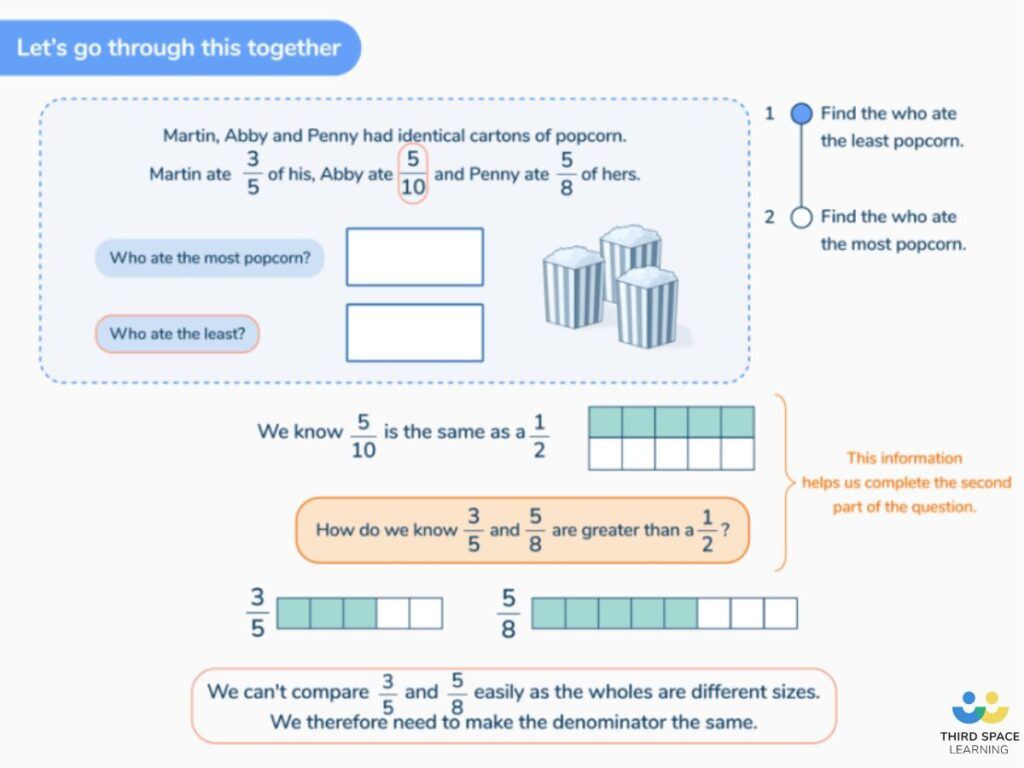
Sara says ‘I ate frac{1}{2} a pizza and my friend ate frac{2}{4} . My friend had more than me, as she had 2 pieces’.
Is she correct? Explain why you have chosen your answer.
Answer: Sara is not correct
frac{1}{2} is the same as frac{2}{4}
Question 4
Tom and Zeyn shared a chocolate bar.
They both had a quarter of the chocolate bar.
How much was left?
Answer: frac{1}{2} of the chocolate bar
frac{2}{4} are equivalent to frac{1}{2}
Fraction word problems for Year 3
Word problems for Year 3 include proper fractions, fractions of amounts, simple equivalent fractions and adding and subtracting fractions with the same denominator.
Question 1
Sophie ate frac{1}{4} of her chocolate bar.
If the bar had 20 squares, how many squares did Sophie eat?
Answer: 5 squares
frac{1}{4} of 20 = 20 ÷ 4 = 5
Question 2
Hamza and Khalifa shared a pizza.
Hamza ate two fourths of the pizza and Khalifa ate one fourth.
How much pizza was left?
Answer: frac{1}{4}
frac{2}{4}+frac{1}{4}=frac{3}{4}
1-frac{3}{4}=frac{1}{4}
Question 3
There are 24 hours in a day.
Maise worked out that she spends frac{1}{8} of her day on Saturday, doing exercise.
How long does she spend exercising on a Saturday?
Answer: 3 hours
frac{1}{8} of 24 hours = 24 ÷ 8 = 3
Question 4
There are 30 children in the class.
frac{2}{5} of the children are wearing jumpers.
How many children are wearing jumpers?
Answer: 12 children
frac{1}{5} of 30 = 30 ÷ 5 = 6
frac{2}{5} of 20 = 12
Fraction word problems for Year 4
Word problems for year 4 include equivalent fractions, fractions of quantities (including non-unit fractions and adding/subtracting fractions with the same denominator. Money word problems often appear in Year 4.
Question 1
Abdullah spent frac{1}{3} of his pocket money for the month on a new game.
He receives £18 per month.
How much did he spend on the game?
Answer: £6
frac{1}{3} of 18 = £6
Question 2
Bethan had a bag of sweets.
She gave frac{2}{7} of the bag to her mum and ate frac{3}{7} of herself.
What fraction of the bag was left?
Answer: frac{2}{7}
frac{2}{7} + frac{3}{7} = frac{5}{7}
frac{7}{7}-frac{5}{7}=frac{2}{7}
Question 3
Jamal ate frac{6}{18} of a chocolate bar.
Mason ate frac{1}{3}
Mason said that Jamal ate more than him. Do you agree? Explain your answer.
Answer: No – they both ate the same.
frac{1}{3} is equivalent to frac{6}{18}
Question 4
frac{2}{7} of a piece of ribbon is 10cm.
How long is the whole piece of ribbon?
Answer: 35cm
frac{2}{7} = 10
frac{1}{7} = 5
frac{7}{7} = 5 x 7 = 35
Fraction word problems for Year 5
Word problems for Year 5 include more complex equivalent fractions, problems involving mixed numbers and improper fractions, adding and subtracting fractions (with different denominators) and multiplying fractions.
Question 1
There are 60 pupils in Year 5.
Eden carried out a survey on favourite foods.
frac{1}{5} of the children said pizza, frac{2}{6} said burgers and frac{3}{10} said hot dogs.
How many pupils did she survey altogether?
Answer: 50 pupils
frac{1}{5} of 60 = 12
frac{2}{6} 0f 60 = 20
frac{3}{10} = 18
Question 2
The Johnson family are driving to the zoo.
They have driven frac{5}{9} of their journey, which is 45 miles.
How much further do they have to drive, to reach their holiday home?
Answer: 20 miles left to drive
frac{5}{9} = 45, therefore frac{1}{9} = 45 ÷ 9 = 5.
frac{5}{9} = 5 x 5 = 25 miles
frac{9}{9} = 9 x 5 = 45 miles
45 – 25 = 20
Question 3
Macy is taking part in the school maths challenge.
She is given a word problems worksheet containing 36 questions.
Macy gets frac{7}{9} of the questions correct.
How many does she get wrong?
Answer: 8 questions wrong
frac{1}{9} of 36 = 4
frac{7}{9} = 28
frac{2}{9} = 8
Question 4
Oliver and Zac are making smoothies.
They make 800 ml of smoothies.
frac{2}{5} is made from apples, frac{3}{7} from strawberries and the rest from orange juice.
How many ml of orange juice do they add to the apples and strawberries?
Answer: 180ml orange juice
frac{2}{5} of 800: frac{1}{5} = 160ml, frac{2}{5} = 320 ml apple juice
frac{3}{8} of 800: frac{1}{8} = 100, frac{3}{8} = 300 ml strawberry juice
800 – 620 = 180ml
Fraction word problems for Year 6
Word problems for year 6 include adding and subtracting fractions with different denominators and mixed numbers, multiplying fractions, dividing fractions by whole numbers and finding equivalent fractions, decimals and percentages.
Question 1
Children in a Year 6 Class at Oak Tree Middle School are answering a set of ratio questions.
There are 10 questions and 28 children completing the activity.
If the children got frac{6}{7} of the total number of questions correct between them.
How many did they get wrong?
Answer: 40 questions wrong
28 x 10 = 280 questions
frac{1}{7} of 280 = 40
frac{6}{7} = 40 x 6 = 240
Question 2
Amber and her 5 friends are sharing 4 pizzas for her birthday party.
The pizzas are split into sixths.
If they each eat the same amount of pizza, how many slices does each person at the party get?
Answer: 4 slices
This is a dividing fractions word problem
frac{24}{6} ÷ 6 = frac{4}{6}
Question 3
A group of friends win a quarter of the total lottery prize for the week.
There are 4 friends and each friend shares an equal fraction of the quarter.
What fraction of the total lottery prize does each friend get?
Answer: frac{1}{16} of the prize fund
Each friend gets frac{1}{4} of the frac{1}{4} prize fund
frac{1}{4} times frac{1}{4} = frac{1}{16}
Question 4
There are 30 children in the class
frac{7}{10} of the pupils in the class are girls.
frac{3}{7} of the girls have their ears pierced.
How many girls have their ears pierced?
Answer: 9 girls have their ears pierced
frac{1}{10} = 3, frac{7}{10} = 21 girls
frac{1}{7} of 21 = 3. frac{3}{7} = 3 x 3 = 9
More word problems resources
Third Space Learning offers a wide range of practice word problems for all primary year groups and covering a large number of topics, including; time word problems, ratio word problems, addition word problems and subtraction word problems.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Today we are going to look at some examples of word problems with fractions.
Although they may seem more difficult, in reality, word problems involving fractions are just as easy as those involving whole numbers. The only thing we have to do is:
- Read the problem carefully.
- Think about what it is asking us to do.
- Think about the information we need.
- Solve it.
- Simplify, if necessary.
- Think about whether our solution makes sense (in order to check it).
As you can see, the only difference in fraction word problems is step 5 (simplify).
There are some word problems which, depending on the information provided, we should express as a fraction. For example:
In my fruit basket, there are 13 pieces of fruit, 5 of which are apples.
How can we express the number of apples as a fraction?
5 – The number of apples (5) corresponds to the numerator (the number which expresses the number of parts that we wish to represent).
13 – The total number of fruits (13) corresponds to the denominator (the number which expresses the number of total possible parts).
The solution to this problem is an irreducible fraction (a fraction which cannot be simplified). Therefore, there is nothing left to do.
Word problems with fractions: involving two fractions
In these problems, we should remember how to carry out operations with fractions.
Carefully read the following problem and the steps we have taken to solve it:
Maria spent of the money her grandparents gave her on an adventure book. She also spent
of the money on a bag of candy.
What fraction of the payment has Maria spent?
We find the common denominator:
We calculate:
Answer:
Word problems with fractions: involving a fraction and a whole number
Finally, we are going to look at an example of a word problem with a fraction and a whole number. Now we will have to convert all the information into a fraction with the same denominator (as we did in the example above) in order to calculate
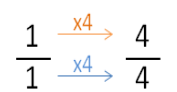
This morning Miguel bought 1 pound of anchovies. In order to eat with his family, he used of a pound. How much does he have left in the refrigerator?
We convert 1 into a fraction with the same denominator:
We calculate:
Answer:
What do you think of this post? Do you see how easy it is to solve word problems with fractions?
To keep learning, try Smartick’s free trial.
Learn More:
- Author
- Recent Posts
Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.

Word Problems on Fractions: A fraction is a mathematical expression for a portion of a whole. Each portion acquired when we divide the entire whole into parts is referred to as a fraction. When we divide a pizza into parts, for example, each slice represents a fraction of the whole pizza. Fractions are subjected to a variety of operations, including addition, subtraction, multiplication, and division. Fractions are used in many real-life situations.
This article will outline how to construct and solve fraction word problems. Students will come across fraction word problems with answers, fraction problem solving and dividing fractions word problems. It is advisable to practice all the problems thoroughly before attempting the exam. Keep reading to know more about word problems on fractions,, definition, types, solved examples and many more
Definition of Fractions
A fraction is a number that is used to expresses a part per whole. Each part obtained when we divide the whole into several parts is called the fraction.
Example: When we cut an apple into two-part, then each part represents the fraction (left(frac{1}{2}right)) of the apple.

A fraction consists mainly of two parts, one is the numerator, and the other one is the denominator. The upper part or topmost part of the fraction is called the numerator, and the bottom part or below part is called the denominator.
Example:

We have mainly three types of fractions: proper fractions, improper fractions, and mixed fractions. They are categorised by the relationship between the numerator and denominator of the fractions.

Word Problems on Fractions
The fraction problem solving consist of a few sentences describing a real-life scenario where a mathematical calculation of fraction formulas are used to solve a problem.
Example: Keerthi took one piece of pizza, which is cut into a total of four pieces. Find the fraction of the pizza taken by Keerthi?
The fraction of pizza taken by Keerthi (=frac{1}{4})
Some of the word problems on fractions that uses fraction formula are listed below:
- Word problems on simplification of fractions
- Word problems on addition and subtraction of fractions
- Word problems on multiplication of fractions
- Word problems on dividing fractions
- Word problems on fractions, percentages, decimals.
Word Problems on Simplifications of Fractions
A fraction in which the numerator and the denominator have no common factor other than “one” is said to be the simplest form of fractions.
Example: Divya took (8) apples from the bucket of (24) apples. Find the fraction of apples taken by the Divya?
The fraction of apples taken by Divya (=frac{8}{24}) and its simplest form is (frac{1}{3})
Word Problems on Addition of Fractions
To add the like fractions (Fractions with the same denominators), keep the denominator the same and add the numerator values of the given fractions.
To add the unlike fractions (fractions with different denominators), convert the denominators of the given fractions equal to L.C.M of their denominators. Now add the numerator value and take the denominator of the resultant as L.C.M.
Example: Sahana bought (frac{1}{4} mathrm{~kg}) of apples and (frac{1}{2} mathrm{~kg}) of oranges from the shop. Total how many fruits she bought?
The total fruits bought by Sahana (=frac{1}{2}+frac{1}{4}=frac{1 times 2+1}{4}=frac{3}{4} mathrm{~kg})
Word Problems on Subtraction of Fractions
To subtract the like fractions (Fractions with the same denominators), keep the denominator the same and find the difference of the numerator values of the given fractions.
To subtract the unlike fractions (fractions with different denominators), convert the denominators of the given fractions equal to L.C.M of their denominators. Now find the difference of the numerator value and take the denominator of the resultant as L.C.M.
Example: Keerthi travelled (frac{2}{5} mathrm{~km}) to school. While returning home, she stopped at her friend’s house at a distance of (frac{1}{3} mathrm{~km}). Find the remaining distance?
The remaining distance needs to be travelled (=frac{2}{5}-frac{1}{3}=frac{(2 times 3)-(1 times 5)}{5 times 3}=frac{6-5}{15}=frac{1}{15} mathrm{~km})
Word Problems on Multiplication of Fractions
To multiply the two or more fractions, find the product of numerators of the given fractions and the product of the denominators of the given fractions separately.
Example: Keerthi had (Rs.10000), and she had donated (frac{1}{10}) of the money to the Oldage home. How much amount did she donate?
The amount Keerthi donated (=frac{1}{10} times Rs.10000= Rs. 1000)
Word Problems on Division of Fractions
The division of fractions is nothing but multiplying the first fraction with the reciprocal of the second fraction. The reciprocal of the fraction is a fraction obtained by interchanging the numerator and denominator.
Example: The area of the rectangle is (frac{15}{4} mathrm{~cm}^{2}), whose length is (frac{5}{2} mathrm{~cm}). Find the width of the rectangle?
We know that area of rectangle (= text {length} times text {bredath})
And, breadth (=frac{text { area }}{text { length }}=frac{15}{frac{4}{2}}=frac{15}{4} times frac{2}{5}=frac{3}{2} mathrm{~cm}).
Word Problems on Conversion of Fractions to Percentage
We know that percentages are also fractions with the denominator equals to hundred. To convert the given fraction to a percentage, multiply it with hundred and to convert any percentage value to a fraction, divide with hundred.
Example: Keerthi ate (frac{2}{5}) of the pizza. How much percentage of pizza is eaten by Keerthi?
The percentage of pizza ate by Keerthi (=frac{2}{5} times 100 %=40 %).
Word Problems on Conversion of Fractions to Decimals
Decimal numbers are the numbers (quotient) obtained by dividing the fraction’s numerator with the given fraction’s denominator. To convert the given decimal to the fractional value by writing the given number without decimals and making the denominator equal to (1) followed by the zeroes and number of zeroes equal to the number of decimal places.
Example: Keerthi got (frac{1}{10}) of the price of a T.V. as a discount. Find the discount in decimal.
The part of the discount received by a Keerthi as a discount (=frac{1}{10}=0.1)
Solved Examples – Word Problems on Fractions
Q.1. In February (2021), a school was working only three-fourths of the total number of days in the month and the remaining number of days given as holidays. How many days did the school work in the month of February?
Ans:
The year (2021) is a non-leap year. We know that a non-leap has (28) days in February month.
So, the total number of days (=28).
Given, the school was working only three-fourths of the total number of days in the month.
The number of days school working in February month (=frac{3}{4}) of (28).
(=frac{3}{4} times 28=21) days
Hence, the school working for (21) days in the month of February for the year (2021).
Q.2. Keerthi needs (1 frac{1}{2}) cups of sugar for baking a cake. She decided to make (6) cakes for her friends. How many cups of sugar did she need for making the (6) cakes?
Ans:
Given, Keerthi needs (1 frac{1}{2}) cup of sugar to make a cake.
The total cups of sugar required to make 6 cakes is calculated by multiplying the sugar needed for one cake with the number of cakes that needs to be prepared by Keerthi and is given by (1 frac{1}{2} times 6)
Convert the above-mixed fraction to an improper fraction by multiplying the denominator with the whole and add to the numerator keeping the same denominator as
(1 frac{1}{2}=frac{(text { whole×denominator })+text { numerator })}{text { denominator }}=frac{(1 times 2)+1}{2}=frac{3}{2})
The total cups of sugar needed for making (6) cakes (=frac{3}{2} times 6=9)
Hence, Keerthi needs (9) cups of sugar to make (6) cakes.
Q.3. An oil container contains (7 frac{1}{2}) litres of oil which are poured into (2 frac{1}{2}) litres bottles. How many bottles are needed to fill (7 frac{1}{2}) litres of oil?
Ans:
Given, a container holds total oil of (7 frac{1}{2}) litres, and the total amount held by each bottle is (2 frac{1}{2}) litres.
Consider the number of bottles required is (x).
From the given question, the total oil in the container is equal to the product of oil in each bottle and the number of bottles required.
(Rightarrow 7 frac{1}{2}=x times 2 frac{1}{2})
(Rightarrow frac{15}{2}=x times frac{5}{2})
(Rightarrow 15=5 x)
(Rightarrow x=frac{15}{5}=3)
Therefore, (3) bottles are required to fill the total oil in the container.
Q.4. A square garden has the area (frac{36}{25} ,text {sq.ft}). Find the side of the square garden.
Ans:
Given the area of the square garden is (frac{36}{25} ,text {sq.ft}).
Let the length of the side of the square garden is (a) fts.
We know that area of the square ( = {rm{side}} times {rm{side}} = {a^2})
Thus, (a^{2}=frac{36}{25})
(Rightarrow a=sqrt{frac{36}{25}}=frac{sqrt{36}}{sqrt{25}}=frac{6}{5}) feet.
Hence, the length of the side of the square garden is (frac{6}{5}) feet.
Q.5. At a party, total (280) ice-creams are prepared. Four-seventh of them is eaten by the children. Find the ice-creams eaten by the children.
Ans:
Total ice-creams prepared (=280)
Number of ice-creams eaten by children (=frac{4}{7}) of (280=frac{4}{7} times 280=160)
Hence, children ate (160) ice-creams.
Summary
In mathematics, a fraction is used to represent a piece of something larger. It depicts the whole’s equal pieces. The numerator and denominator are the two elements of a fraction. The numerator is the number at the top, while the denominator is the number at the bottom. The numerator specifies the number of equal parts taken, whereas the denominator specifies the total number of equal parts in the total.
In this article, we have studied the definitions of fractions, different types of fractions. We also studied the word problems on fractions and their operations. This article gives the word problems on fractions, addition and subtraction of fractions, multiplication of fractions, division of fractions, the simplest form of fractions, conversion of fractions to percentage, decimals etc., with the help of solved examples.
FAQs on Word Problems on Fractions
Here are some of most commonly asked questions on word problems on fractions.
Q.1: How do you solve word problems with fractions?
Ans: To solve word problems with fractions, first, read and write the given data. Write the mathematical form by given data and perform the operations on fractions according to the data.
Q.2: How do you write a fraction division in word problems?
Ans: The fraction division can be written as keeping the first fraction as it is and multiplying it with the reciprocal of the second fraction.
Q.3: How do you know when to divide or multiply fractions in a word problem?
Ans: To find the product, we need to multiply and to find any one of the quantities, we need to divide.
Q.4: What is an example of a fraction word problem?
Ans: Keerthi ate 40% of the pizza. How much is part of the pizza eaten by Keerthi.
Q.5: What is a fraction?
Ans: A fraction is a number that is used to express a part per whole.
Learn About Conversion Of Fractions
We hope this detailed article on Word Problem on Fractions helps you in your preparation. If you get stuck do let us know in the comments section below and we will get back to you at the earliest.
Stay tuned to Embibe to learn more important concepts
What is an example of a fraction word problem?
Example 1: Rachel rode her bike for one-fifth of a mile on Monday and two-fifths of a mile on Tuesday. How many miles did she ride altogether? Analysis: To solve this problem, we will add two fractions with like denominators. Answer: Rachel rode her bike for three-fifths of a mile altogether.
How do you solve word problems with fractions?
Word Problems with Fractions
- Read the problem carefully.
- Think about what it is asking us to do.
- Think about the information we need.
- Solve it.
- Simplify, if necessary.
- Think about whether our solution makes sense (in order to check it).
How do you solve fraction problems?
Use the order of operations to work down multiple fractions, starting with two at a time. To multiply fractions, simply multiply the numerator by the numerator and the denominator by the denominator. The results that you get from multiplying these two numbers is the answer to the multiplication problem.
How do I type fractions into Microsoft Word?
Place the cursor on the document where you would like to insert a fraction. Select “Insert” from the menu. Click on Equation in the upper right. Select fraction under the Equation Tools option. Choose which style fraction you want. Insert the numbers into the fraction boxes.
How do you solve fractions in math?
To solve equations involving fractions, the main step is to isolate the variable, convert the fractions into whole numbers, and then solve the equations as normal. When solving algebraic equations, treat both sides equally.
What is a multiplication problem?
The basic parts of a multiplication problem consist of at least two factors that are multiplied together to result in one product. More than two factors can be involved in a multiplication problem, but the answer always consists of only one product. For example, in the equation 2 x 3 = 6, 2 and 3 are factors, while 6 is the product.
Word problems + fractions = a lot of struggle for many students. Especially when you throw in new concepts like multiplying and dividing fractions. Those fraction word problems are always pretty tricky for my students. The first year that I taught multiplying and dividing fractions, I really had to spend some time breaking down the concepts myself in order to best help my students. On this post, I will share an anchor chart and a free word problem sort that helps my students solve these types of fraction word problems and see the difference/connection between the two.
Note: This is based on 5th grade standards and focuses only on multiplying fractions less than 1 and dividing with unit fractions and whole numbers. Click here to grab some free printables to help your students with solving word problems involving multiplying mixed numbers.
Teach Multiplying and Dividing Fractions with Models and a Context
Before even beginning with word problems, I always introduce multiplying and dividing fractions (separately) with a context/situation. And then we work through the situation and solve the problem/ answer the question using models. This really helps the students conceptually understand the operations. When students are only exposed to algorithms, they may not fully understand the operation. As a result, they will struggle with choosing the correct operations when solving word problems.
Here are my go-to introductory word problems for when I first introduce multiplying and dividing fractions (again I introduce each one separately). I prefer to use fudge for all of my introductory word problems because I love fudge, my students love it, the contexts make sense and are relatable, and it is almost an inside joke between us by the middle of the year. I also use student names or teacher names in the problems whenever possible and friendly fractions for easy modeling and visualizing.
Multiplying Fractions Introductory Word Problem: While shopping at a bakery, Ms. Findley purchased 1/2 of a pound of chocolate fudge. After dinner that night, she ate 1/4 of the chocolate fudge that she bought. How much of a pound of fudge did Ms. Findley eat?
Dividing Fractions Introductory Word Problem: Jamal’s mother made 1/3 of a pound of his favorite fudge, peanut butter caramel fudge. She divided the fudge into 4 equal containers. How much fudge did she put in each container?
How I Use the Introductory Word Problems: I write the problem on an anchor chart, gather my students at our mini-lesson area (around a large rug) and follow these steps:
- Read the word problem once (myself or a student).
- Read it again, if needed (based on the level of my students)
- Have the students retell the problem with partners in their own words.
- Have a few students share their retellings with the class.
- Focus on what the question is asking by writing the question in a sentence.
- Use models to demonstrate the situation in the problem (since these are new concepts for them, this part is heavily teacher driven, but typically I prefer student driven). The students practice with models as well. This can be paper folding models, visual representation drawings, or both — my favorite is both in the beginning.
- Translate the visual into a labeled equation (read more about labeled equations here) and answer the question.
- Discuss the answer and determine if it makes sense.
- Practice similar/same situations but with different numbers.
Reminder: I teach both of these concepts separately for about a week each.
Fraction Word Problems: Do I Divide or Multiply?
Once my students have “mastered” multiplying and dividing fractions and have seen each in a variety of contexts (through the word problems I use), they are ready to tackle both and see the connections and differences between the two. To do this, I use this anchor chart to show some of the situations and contexts that require multiplication and division of fractions. We discuss each one and how it relates back to multiplication and division.

Since it is impossible to expose students to every type of situation and context, the blurb at the end of the chart is key. The students really need to make a habit of checking to see if their answers make sense. This will help them if they choose the wrong operation.
FREE Multiplying and Dividing Fractions Word Problem Sort
In addition to the above anchor chart, we also do a word problem sort. The word problems were specifically written to match the contexts from the chart so this is a great extension of the lesson involving the anchor chart. The students read the word problems, check the chart, and then sort them accordingly. I do this activity with partners or small groups (pulling a group to work with me that may struggle based on previous assessments using exit slips), but this could also be done as a math center activity.
Click here or on the image above to download the multiplying and dividing fractions word problem sort and a printable version of the anchor chart.
My Go-To Resource for Teaching Multiplying and Dividing Fractions
The anchor chart and the sort are used after I have introduced and we have practiced both operations in isolation. I do this by using resources from my Multiplying and Dividing Fractions resource.

- Teaching Posters
- Practice Printables
- Constructed Response Tasks
- and more!
Click here to purchase the Multiplying and Dividing Fractions Resource from my TPT store.
Want More Hands-On Math Activities and Centers?
More Helpful Word Problem Posts, Freebies, and Resources
Teaching Word Problems without Key Words (And What to Teach Instead)
Word Problem of the Day : FREE Starter Packs
8 Ways to Help Students Be Successful with Word Problems
Show the LOVE with Word Problems: Helping Students Answer Word Problems
Teaching Students How To Justify Answers in Math
Solving Multi-Part Word Problems
FREE Word Problem Graphic Organizers/Mats
5th Grade Word Problem of the Day TpT Resource
More Fraction Resources, Freebies, and Blog Posts:
Free Fraction Mats: I use these free downloadable fraction mats to support my students further as they add and subtract fractions with unlike denominators.
Free Fraction Pacing Guide: This blog post shares an “I Can” checklist for students and shares how I pace my 5th grade fraction skills.
Free Fraction Fun with Snacks Printables: If you can use food in your instruction, your students will love reviewing fraction operations (multiplication and division) using Twizzlers, skittles, and brownies.
4 Ways to Teach Students to Make Common Denominators: Read about the four ways I teach my students to find common denominators and grab a free printable.
Free Fraction Activities: Grab some super easy to prep fraction activities on this post.
These Fraction of a Group Word Problems are a great way for children to analyze and understand fractions when they are presented as parts of a set.

The free printable can be found at the END of this post. Click on the blue “get your free printable here” button.
It doesn’t happen very often, but periodically I find a math concept that stumps my seven-year-old. For the most part, he just flies through math, whipping out answers, and surprising his mom with his number sense.
This fraction concept puzzled him. I could see the frustration in his eyes, that normally only appears during writing.
What was causing him such anguish? A fraction of set word problems.
A fraction of a Set
So often most of our fractional instruction revolves around fractions being apart of a whole. We focus on pies, pizza, and visual models. But, we leave out the fact that fractions can be used to be part of a set….such as 2/9 of the M&M’s in the pack are red.
We had played games with this concept, done the clip cards from this fraction set, and had worked on it in through some worksheets in our math curriculum. But now that it was time for some word problems….we were stuck.
parts-of-a-set-word-problems
What is Fraction of a Set Word Problems
There are two main types of fractions of set word problems. The first type gives children information about the part, and then the children have to figure out what the whole is. The other one will tell you information about the whole, and the children will have to figure out about the part.
What is the Whole?
An example of this type of problem might be…..
2/3 are blue, and there are 10 blue shirts.
The children begin by taking the number and dividing it up by the numerator. 10 ÷2 = 5
Now they know that there are 5 shirts in each group. By looking at the denominator they know that there are 3 groups. Soooo, they multiply 5 x 3 which equals 15. There are 15 shirts!!!
What is the Part?
When solving a problem like this, you might see…..
2/5 of the shirts are blue. If there are 15 shirts, how many are blue?
First, children should figure out how many shirts are in each group. So they would take the 15 shirts and divide them into 5 (denominator) equal groups. 15 ÷ 5 = 3
They now know that there are 3 shirts in each group. Since two of the groups (numerator) have blue shirts, the children multiply 3 x 2 to find out that 6 of the shirts are blue.
Prep – Work
There is very little prep work for these printables.
- First, print off the sheets.
- Next, provide counting bears, colored pencils, and a pencil.
- Finally, gather up your 3rd through fifth-graders and you are ready to go.
Don’t want to print them off? Grab this activity in DIGITAL FORM

How to Use
First, have the children read the problem, and underline important information.
In the example above, the student would want to know that 3/5 of the bears are blue, the rest are green, and that there are 15 altogether.
Next, the students use colored bears to work out the problem.
Using the problem above, the children would count out 15 blue bears. Next, they would divide them into five equal groups since the denominator tells us there are five groups.
15 ÷ 5 = 3 so we know that there are three bears in each group.
Using the bears in front of them, they write the answer to the problem in the answer box.
Three of the groups are blue so 3 x 3 = 9. Nine of the shirts are blue.
Two groups are green, so 3 x 2 = 6. Nine of the shirts are green.
Finally, the children write out an equation for what they did.
The children started off taking the 15 bears and dividing them into three groups. They then skip counted or multiplied to figure out how many bears there were altogether.
15 ÷ 5 = 3
2 x 3 = 6 or 3 x 3 = 9.
As we worked through these problems, I began to see the frustration begin to dissolve. So we get to move to our next topic. Two-Digit multiplication!!!!
Parts-of-a-Set-Christmas-Tree-Clip-Cards
You’ve Got This
Part-Of-A-Set-Word-Problems
Rachel
You may also be interested in:
A review on denominators and numerators.

More fraction of a Group Word Problems using Gum Drops. This packet also has multiplying fractions, measuring, line graphs, STEAM and more.


A great variety of fraction word problems with solutions. These word problems will help you find out when you need to add, subtract, multiply or divide fractions.
1. Sarah knows 8 of the 25 students in her class. Write a fraction showing the number of students Sarah knows.
2. Peter correctly solved 18 out of the 20 math problems the teacher gave him. Write a fraction showing the number of math problems Peter solved correctly.
Solution
18/20
3. Darlene ate 3/5 of her pizza. How much pizza can Darlene share with her sister?
Solution
1 represents the entire pizza. To find how much pizza is left, just do 1 — 3/5
1 — 3/5 = 1/1 — 3/5 = 5/5 — 3/5 = 2/5
Darlene can share 2/5 of the pizza.
4. Last week, Steve spent 3 1/2 hours playing soccer and 4 1/2 hours playing table tennis. How much time did Steve spend playing both sports?
Solution
Just add 3 1/2 and 4 1/2 together.
3 1/2 + 4 1/2 = (3 + 4) + 1/2 + 1/2 = 7 + 1 = 8
Steve spent 8 hours playing both sports.
5. John jogged 1 3/4 miles yesterday and 2 1/2 miles today. How many miles did John spend jogging for the past two days?
Solution
Just add 1 3/4 and 2 1/2 together.
1 + 2 = 3
3/4 + 1/2 = 3/4 + 2/4 = 5/4
John jogged 3 5/4 miles for the past two days.
6. Maria bought a pizza and ate half of it. Then, she gave the leftover to his brother and his brother ate half of it. How much of the pizza did his brother eat?
Solution
The brother ate half of half the pizza.
Half of half = 1/2 of 1/2 = 1/2 × 1/2 = 1/4
7. Anthony caught some fish that weighted 6 1/2 pounds. If he gave 4 1/4 pounds of fish to some friends, how much fish does he have for himself?
Solution
Subtract 4 1/4 from 6 1/2.
6 — 4 = 2
1/2 — 1/4 = 2/4 — 1/4 = 1/4
Anthony has 2 1/4 pounds of fish for himself.
8. 1/4 of a tablespoon of baking soda is needed to make a loaf of bread. How many loaves of bread can be made with 5 tablespoons of baking soda?
Solution
Divide 5 by 1/4
5 ÷ 1/4 = 5/1 ÷ 1/4 = 5/1 × 4/1 = 20/1 = 20
20 loaves of bread can be made.
9. A recipe calls for 2 1/8 cups of butter for a casserole. How much butter is needed to make 6 1/2 casseroles?
Solution
Just multiply 2 1/8 by 6 1/2
2 1/8 × 6 1/2 = (2 × 8 + 1)/8 × (6 × 2 + 1)/2
2 1/8 × 6 1/2 = 17/8 × 13/2 = (17 × 13)/(8 × 2)
2 1/8 × 6 1/2 = 221/16 = 13.8125
To make 6 1/2 casseroles, the recipe will need 13.8125 cups of butter.
10. Kevin cooked 8 1/4 pounds of meat for a dinner. If each serving is 3/4 pound, how many servings did he prepare?
Solution
Just divide 8 1/4 by 3/4
8 1/4 ÷ 3/4 = (8 × 4 + 1)/4 ÷ 3/4 = 33/4 ÷ 3/4 = 33/4 × 4/3 = 132/12 = 11
Kevin prepared 11 servings.
Recent Articles
-
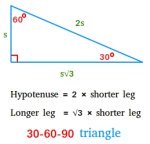
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
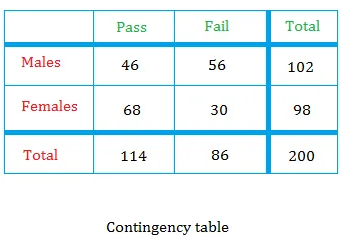
-
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Sometime soon I will do a series of posts on word problems, which are a common point of difficulty with students. But here is one recent example from a high school student, where language was the main difficulty, but the algebra is worth discussing as well. We’ll look a little more deeply into the problem itself, and think about its implications.
Writing and solving an equation
Here is the initial question:
1/2 of a number is 2 more than 1/3 of the number. What is 1/3 of the number?
a. 2
b. 4
c. 8
d. 12
Doctor Rick took the question, and first, as we usually do, pointed out that in order to help, we need some information about the student’s knowledge and needs. When we are just given a problem, we can’t tell what kind of help is needed; the best thing is for the student to show his work so we can see where, if at all, they made a mistake. Sometimes they turn out to be entirely correct, and it was the book that was wrong — so it would be a waste of time to write out a full explanation. Other times, the student is not learning algebra at all, so again, an algebraic solution would be wasted.
But, as we often do, he gave a suggestion to get started, in case that was all that was needed:
One way this problem might be solved is to “translate” the statement into an algebraic equation. Is that something you’ve been learning to do? For instance, give “the number” the name “x”. You’re asked to find “1/3 of the number”, which you can write as (1/3)x or x/3. How would you write “1/2 of the number”? How would you write “2 more than 1/3 of the number”?
In this case (as often happens), the student is not fluent in English, which could be the reason for not giving a full explanation. We find that in such a case, it is better to say more rather than less — the more a student says about his thinking, the more likely we will understand it, even if he doesn’t express it clearly. Here is the response (a little cleaned up):
Not good in English sorry. But I’ll try.
To be honest, I don’t know where to start because I don’t know how to approach this problem. It says “more than” so I think it’s an addition so:
x/2(2) + x/3
…
Then… I’ll need to find 1/3 of that number? I can’t understand it.
Seeing this work gave Doctor Rick a good idea of what was needed. He replied,
Thanks for the additional information about how you’re thinking. That’s the sort of thing I needed.
The problem was:
1/2 of a number is 2 more than 1/3 of the number. What is 1/3 of the number?
You said:
It says that “more than” so I think it’s an addition so:
x/2(2) + x/3
OK, I see some good things here. You translated “1/2 of a number” as x/2, and “1/3 of the number” as x/3. You’re correct that “more than” in this sentence refers to addition (sometimes, as you’ll see later, it can mean other things.)
There are two main difficulties with what you wrote. One is that it isn’t an equation — you didn’t get an equal sign (=) into it. That’s how I’d translate the word “is”. The other problem is that you are not taking the grammar of the sentence into account.
Let’s work step by step, translating one part at a time rather than trying to write the equation all at once. Here’s what I mean:
1/2 of a number is 2 more than 1/3 of the number. _____________/ / _______/ _______________/ x/2 = 2 + x/3Wow, I’m done — I’ve written an equation! It won’t always work this neatly — in this case, the sentence is in nearly mathematical language right from the start. The same thing wouldn’t work for other problems you have sent!
OK, now you have an equation to solve. Can you find the value of x that makes the equation true? And then can you figure out what “1/3 of the number” is?
Doctor Rick has done two things here: one is to look at the whole sentence and translate it into an equation, rather than a mere expression; and the other is to not look at the whole sentence at once, but to break it into parts (according to its grammar) in order to build up the equation part by part. In this case, it was easy to do both things at once; more complicated sentences often require working on each piece separately to avoid confusion, and changing the order of parts. For example, if it had said “2 less than …”, we couldn’t just write “2 – …”, because the order would be wrong. We’d have to say x/3 – 2 instead. So matching up phrase after phrase in order is not always appropriate, but it was convenient here.
This appeared to be the hard part for this student. We like to leave as much as possible for them to solve themselves, so that they get practice doing the work themselves; here it would have been hard to explain the ideas without doing the whole translation, but we can at least leave the solving to the student, who can probably manage that. And Doctor Rick was right about that:
OMG!!! Yah, the ‘is’ is =. Here’s my solution:
x/2 = 2 + x/3
x/2 – x/3 = 2
(3x – 2x)/6 = 2
x = 12
Since the question is what is the 1/3 of the number
x/3 = 12
3(x/3 = 12)
x = 4
Aaaaaaahhhh!!! And guess what! I got it right!!!!!
Well, there are some things to clean up here, but encouragement was appropriate, and Doctor Rick responded encouragingly,
You got it correct, and you are justified in feeling good about yourself! Keep it up!
A closer look
But let’s go back and look at a few details in the solution.
First, the student used a good method, and show work quite well — not too much detail, but including the important steps. His approach was to subtract x/3 from both sides, then combine the left side into a single fraction, which reduces to x/6; then, multiplying both sides by 6, the result is x = 12.
Another approach, often taught in books and saving some work (or at least some writing, or some opportunities to make mistakes in using fractions, is to “clear fractions” before solving. The LCD of all the fractions in x/2 = 2 + x/3 is 6, so we multiply each term by 6 in order to cancel with each denominator:
x/2 = 2 + x/3
6*x/2 = 6*2 + 6*x/3
3x = 12 + 2x
Now, with no fractions to trip over, we can just subtract x from each side and solve:
3x – 2x = 12
x = 12
Second, the student was wise enough not to stop there, but to see that the question was not to give the number, but rather 1/3 of the number. So the answer is 1/3 of 12, which is 4.
But the work he wrote was wrong! It is not uncommon for a student to think correctly, but not yet be skilled in writing what he is thinking. Here, he changed x = 12 to x/3 = 12, replacing x with the x/3 that is desired; what he should have done is to divide both sides by 3, x/3 = 12/3 = 4. I can only guess that, as he approached the finish line, he started thinking and writing too fast, and stumbled. We’ll give him credit.
Let’s take one more step, and check the answer. Recall again that the problem was, “1/2 of a number is 2 more than 1/3 of the number. What is 1/3 of the number?” We found that the number is 12. What is 1/2 of the number? 6. What is 1/3 of the number? 4. Is 6 2 more than 4? Yes. If we had misinterpreted “2 more than” in translating the equation, we probably would interpret it correctly in this more familiar process, so we would have a chance to discover our error.
And, again, part of checking is seeing whether we answered the question that was asked. What is 1/3 of 12? 4. We got it.
What if he didn’t know algebra?
Let’s take this in yet another direction. I mentioned at the start that this problem might have been given to a student who is not learning algebra, though that tends to be our first assumption. How might we solve it then?
The problem, once again, was, “1/2 of a number is 2 more than 1/3 of the number. What is 1/3 of the number?” The question might lead me to focus my attention not on the number itself, but on 1/3 of the number; I may never need to know what the number itself is! Here is a bar representing the number, with 1/3 of it shaded:
+-----------+-----------+-----------+ |XXXXXXXXXXX| | | +-----------+-----------+-----------+
Here I’ve split each third in halves, so I can mark 1/2 of the number:
+-----+-----+-----+-----+-----+-----+ |XXXXX|XXXXX| | | | | +-----+-----+-----+-----+-----+-----+ _________________/
Since the 1/2 is 2 more than 1/3, that difference must be 2:
+-----+-----+-----+-----+-----+-----+ |XXXXX|XXXXX| 2 | | | | +-----+-----+-----+-----+-----+-----+ _________________/
So each piece is 2, and the shaded region (two pieces) is 4. That’s the answer.
This sort of visual thinking is taught commonly today, and is a precursor to algebra. It requires more creativity than algebra, which is just a way to turn any problem into the same kind of symbolic problem, so that you don’t need any special thinking for each problem, but can follow a nearly mindless routine. The thinking I did here involved focusing deeply on the fractions (using a common denominator, for example, without actually saying so) and on relationships. That makes it a very useful experience. Don’t rush to learn (or teach) algebra — being easier (though students are surprised to realize that), it takes away the chance to learn to think deeply!