From Wikipedia, the free encyclopedia
First World problem is an informal term for the issues in First World nations that are complained about in response to the perceived absence of more pressing concerns.[1] Although it has been described as «a subset of the fallacy of relative privation», the term is also used by many people to acknowledge their gratefulness for not having worse problems, and recognise their problems in a global context.[2] The term has been used to minimize complaints about trivial issues and shame the complainer, to generate humour at the expense of first world culture,[3] and as good-humored self-deprecation.[4]
History[edit]
The term First World problem first appeared in 1979 in G. K. Payne’s work Built Environment,[4] but gained recognition as an Internet meme beginning in 2005, particularly on social networking sites like Twitter (where it became a popular hashtag).[5][6] In 2012, UNICEF NZ conducted a survey of First World problems in New Zealand, finding «slow web access» to be the most common.[7] The phrase was added to the Oxford Dictionary Online in November 2012,[8] and to the online Macquarie Dictionary in December 2012.[9]
Examples[edit]
Things that have been cited as being First World problems include:
- Slow Internet access[7]
- Poor mobile-phone coverage[7]
- Phone battery dying (low battery anxiety)[10]
- Television remote not working[7]
- Misplacing AirPods (the most frequent complaint about AirPods). Apple Inc. attempted to alleviate this problem by introducing a «Find My AirPods» application in 2017.[11]
- Not being able to find items in a shop[7]
- Getting a bad haircut[7]
- Bad-tasting fruit[7]
See also[edit]
- Embarrassment of riches
- First World privilege
- Maslow’s hierarchy of needs
- Whataboutism
References[edit]
- ^ Hardy, Quentin (18 May 2012). «Eduardo Saverin’s Billionaire Blues». The New York Times. Retrieved 25 January 2013.
- ^ Turkel, Bruce (6 September 2016). All about Them: Grow Your Business by Focusing on Others. Da Capo Press. ISBN 9780738219202 – via Google Books.
- ^ Glover, Richard (24 November 2012). «As the First World turns». Sydney Morning Herald. Retrieved 25 January 2013.
- ^ a b «First World (Special uses)». Oxford English Dictionary Online. Oxford University Press. Retrieved 18 November 2014.
- ^ López, Tracy (11 July 2012). «How acknowledging your «First World problems» can make you happier». Voxxi. Archived from the original on 17 February 2013. Retrieved 25 January 2013.
- ^ Steinmetz, Katy (20 November 2012). «Oxford Dictionaries adds ‘deets’, ‘4G’ and ‘First World problems’«. Time. Retrieved 25 January 2013.
- ^ a b c d e f g Harper, Paul (8 October 2012). «Kiwis complain about ‘First World problems’«. New Zealand Herald. Archived from the original on 22 February 2013. Retrieved 25 January 2013.
- ^ «First World problem definition». Oxford Dictionaries Online. Oxford University Press. Archived from the original on November 29, 2014. Retrieved 18 November 2014.
- ^ «Word of the Year 2012». Macquarie Dictionary Online. Macquarie Dictionary.
- ^ Sum, Eliza (28 July 2016). ««Battery anxiety» making smartphone users miss meetings, dates and jeopardize relationships». Geelong Advertiser. Retrieved 3 October 2016.
- ^ Stampher, Jillian (January 24, 2017). «Solving First World Problems: Apple To Release ‘Find My AirPods’ Feature With Latest iOS Update». GeekWire.
External links[edit]
The dictionary definition of first world problem at Wiktionary
- First World Problems Anthem
The term First World problem was first coined in the late 1970s, but it was popularized by an internet meme in the early 2000s. We will examine the meaning of the phrase First World problem, where it came from and some examples of its use in sentences.
A First World problem is an inconsequential frustration, an unimportant annoyance that is blown out of proportion due to the sufferer’s lack of real and important problems. An example of a First World problem is a smart phone that only receives wi-fi on the first floor of one’s home and not in the basement. When compared to the desperate problems of war and hunger in poorer nations, a First World problem is very trivial indeed. While the term First World problem was first used in the book Built Environment by G.K. Payne, published in 1979, the term came into popular usage with an internet meme created in 2005, which spread through Tumblr posts and Twitter posts. Today, the term First World problem is used when chastising someone complaining about a trivial problem, or often, when the complainer uses it to acknowledge that triviality of his problem. Note that the Oxford English Dictionary capitalizes the first two words of the phrase, as in First World problem, it is often seen hyphenated and using lowercase letters, as in first-world problem.
Examples
She also acknowledges that she is privileged to have access to a breast pump in the first place, calling her frustrations with pumping a “first world problem.” (The Huffington Post)
First world problem: Ricki-Lee Coulter was recently the victim of a wayward champagne cork that hit her in the right eye. (The Sydney Morning Herald)
I understand that this is a very first-world problem, one that’s wedged somewhere between “I’m too pretty” and “I have a gift card and can’t decide where to spend it,” and I’m sorry about that. (Glamour Magazine)
So there I was, bashing out a hot take on my MacBook Air on a sunny terrace, when I took a sip of my takeaway coffee and my heart sank. The barista had put milk in it. That ruined my whole morning. What a terrible world. But I know, right? First world problem!
The phrase “first world problem” is these days used as a comical apology for moaning about trivia. It is also an enjoyable internet meme, with a dedicated subreddit. (I particularly liked “The Wi-Fi at the luxury Greek villa my wife and I are staying at only supports 4 devices at a time”, and the rather subtle: “I want to order pizza, but it is too early and I don’t want to be judged by my doorman.”) But why do we speak of “first world problems”, exactly, and what might we unintentionally mean when we do?
For a start, the phrase is an anachronism, since we no longer talk about the “third world”. (The usual phrase is the optimistic “developing world”.) The Oxford English Dictionary’s first citation for “first world problem” is from 1979, though it was then meant seriously, to denote housing problems that were specific to the “first” world. The modern, exclusively ironic usage of “first world problems” did not get going until the mid-1990s. And yet search analytics show a big uptake only since 2011, long after we all learned to stop talking about the “third world”. That implies there might be something smug in the modern usage, as well as a hint of enjoyable transgression in using language that is not “politically correct”.
Like many things, “first world problems” has a different force depending on whether you are applying it to yourself or throwing it in someone else’s face. If, at the end of an irate tirade about how my Kenyan coffee beans were over-roasted by the artisanal torréfacteur, I append the phrase “first world problem” with some wry rearrangement of my face muscles, I signal that I know this is just one of the minor frustrations of a very fortunate life. To pre-emptively concede that my problem is just a first world one is to ostentatiously check my privilege before anyone else tells me to do so. At the same time, I remind myself and everyone in earshot that we are indeed living in the “first world”. So it is also a humblebrag.
Such privilege-checking becomes a more violent intervention when demanded by someone else. If, after listening to your pathetic account of how your Uber cab took a whole 10 minutes to arrive, I respond “first world problem”, then I am aggressively staking out the moral high ground and portraying myself (almost certainly dishonestly) as someone who only ever worries about the plight of starving children. Naturally, our powers of sympathy are limited and we all conduct psychic triage on the sufferings of others. But when “first world problem” is just a mealy mouthed way of saying “shut up”, it sounds distinctly compassion-free.
Whoever uses it, though, it’s arguable that the phrase “first world problems” is condescending and dehumanising to literally everyone on the planet. For a start, it patronises those outside the “first world” by implying that hunger, disease and war are not only prevalent among the global poor but in some way the sole conditions of their lives. It implicitly characterises the less fortunate majority of the world’s population as saintly idiots who would never dream of complaining about anything more trivial. In the guise of right-on sympathy, we condescendingly picture others as living lives of homogeneous horror while rhetorically rendering them invisible as people, denying the individuality of everyone’s various joys and sorrows.
At the same time, the phrase declares inadmissible the perfectly real suffering that can be endured by the globally well-off. As is well known, we all compare ourselves to others close by, and feel bad if we are relatively less fortunate. Of course, many problems faced by residents of the EU right now pale in comparison with those experienced by people fleeing Syria. But to conclude that Europeans therefore do not even have the right to complain about their own frustrations is inhumane.
Some may wish to retort that worrying about the political implications of the phrase “first world problem” when used by rich people is itself a first world problem. But repetition of language that implies an unspoken attitude to others will often help that attitude to harden within us. And that’s everyone’s problem.
Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/
The lesser known working title to Canadian singer/songwriter Alanis Morissette’s hit song «Ironic».
Many have been confused as to the choice of ironic as the songs title when the lyrics are more unfortunate than ironic.
In fact there in lies the only thing ironic, it was written by someone who didn’t know the definition of irony.
If you read through the lyrics you can clearly see where she was coming from with «First World Problems» as the working title as seen below;
1)It’s like rain on your wedding day
2)A traffic jam when you’re already late
3)It’s a free ride when you’ve already paid
4)It’s like ten thousand spoons when all you need is a knife
5)A no-smoking sign on your cigarette break
That being said, having the song contain a verse about a husband «kiss(ed) his kids goodbye» get on a plane and have it crash is neither a First World Problems, unfortunate or ironic. It’s just messed up.
Get the First World Problems mug.
A more politically correct term for a «White Whine.» However, both terms remain misleading: White Whines/First World Problems are not exclusive to whites or those in the First World, and there are many whites and people in the First World who do not suffer from being over-privileged.
Person 1: I wanna call this guy out on a white whine, but I don’t want to be offensive.
Person 2: Why not say he’s got First World Problems?
Person 1: Don’t you mean Developed World Problems?
Person 3: whitewhine.com
Get the First World Problems mug.
Problems almost unique to or prevalent in the first world, which actually refers to the US. These problems include:
— medical debt
— extreme poverty
— identity theft
— credit card fraud
— fake news
— queueing forever in cars for “fast food” and coffee
— conspiracy theories
— gun violence
— normalised bigotry and misogyny
— institutionalised corruption
— extreme bureaucracy
Get the First World Problems mug.

3-Step System
1. Read: Read the problem and decide what the question is asking.
- Read the problem 2 times or more.
- Underline or circle key words, phrases, and numbers. Draw a line through irrelevant information.
2. Plan: Think about what the story is asking you to do. What information are you given, and what do you need to find out?
- Draw a picture.
- Circle or underline key words. (Use highlighters or crayons to color-code key numbers and phrases.)
- Write out the question in your own words.
3. Solve: What strategy could you use to find the missing information: addition, subtraction, multiplication, or division?
- Write a number sentence and solve.
- Use counters.
- Create charts.
Check your work by explaining your reasoning. Does your answer make sense?
Download this free strategy checklist from Math Fundamentals to help your child solve word problems.
Different Strategies to Solve Word Problems
Everyone learns in a different way. What makes sense to one individual often isn’t the easiest option for another. Incorporating different strategies to solve word problems can help your child discover what strategy works best for him or her. A few tips to use are:
1. Circle numbers in a story and underline key phrases.
Color coding is a fun method to incorporate to help children decide what operation the question is asking for. Assign a color to each operation and highlight the phrase that identifies it. For example, red links to addition and blue links to subtraction.
2. Incorporate a key word list.
Key word lists are best used for teaching younger children how to solve word problems. As math curriculum advances, children should not be dependent on a key word list to solve a problem. The questions get trickier.
Addition
In all
Together
Total
Altogether
Combine
Sum
Join
Subtraction
Difference
Fewer
How many more
How much more
Left
Remain
Less
3. Visuals
If your child is a visual learner, drawing a picture or using counters can help him or her understand what the problem is asking. Use number lines, charts, or counters or draw a picture.
4. Write your own word problem.
Knowing what is needed to write a word problem is the first step in identifying key words to solve a story. Take turns writing your own word problems with your child and exchange them to solve.
5. Stay organized.
It is important to write clearly and keep work space neat so children can read and follow their own computations. Many children need a separate piece of paper to allow them enough space to solve and understand their answer. Graphing paper is a great option to help students record neat work.
Download this free sample word problem from Math Fundamentals, grade 1.
How to solve a two-step word problem
In a two-step word problem children are being asking to solve two related equations. These can get tricky for children to understand when they transition from one-step to two-step problems. Help your child understand his or her relationships within two-step word problems with these strategies:
1. Circle important information.
Circle numbers and important phrases that ask questions. The number sentences needed to solve these equations are hidden in those asking questions. Identify the first and second questions needed to solve.
2. Distinguish the two parts of the problem.
First identify the first step of the first part of the word problem. Write a number sentence and solve.
3. Use the answer from the first-step solution to the whole problem.
Use the answer from the first question to help you solve the next equation. What operation does the second question require?
Check your work by explaining your reasoning. What was the question answered? Is the answer reasonable for the question being asked?
Download this free sample two-strategy word problem from Math Fundamentals, grade 2
Download this free sample multi-strategy word problem from Math Fundamentals, grade 4
Evan-Moor’s Math Fundamentals is a great resource for training students how to solve word problems in 3 simple steps. It provides step-by-step directions for solving questions and guides children with helpful visuals and key phrases.
Check out Daily Word Problems for consistent practice solving word problems.
For more fun math tips and strategies check out our Math- Ideas, Activities and Lessons Pinterest Board.
Save these tips and Pin It now!

We explain what a word problem is and give examples of the types of word problems your child might be challenged with in each primary-school maths year group, from Year 1 to Year 6.
What is a word problem?
A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation.
Word problems are seen as a crucial part of learning in the primary curriculum, because they require children to apply their knowledge of various different concepts to ‘real-life’ scenarios.
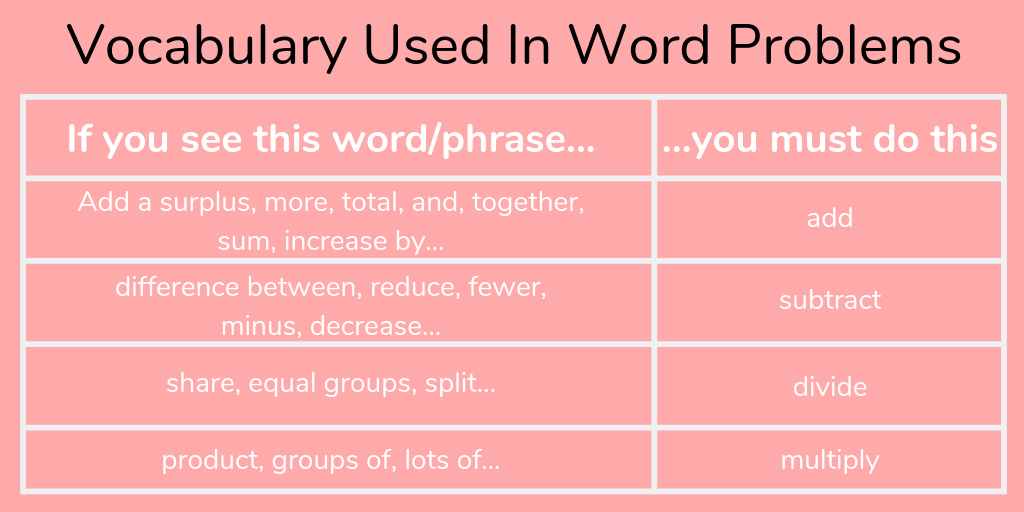
Word problems also help children to familiarise themselves with mathematical language (vocabulary like fewer, altogether, difference, more, share, multiply, subtract, equal, reduced, etc.).
Teachers tend to try and include word problems in their maths lessons at least twice a week.
What is RUCSAC?
In the classroom children might be taught the acronym RUCSAC (Read, Understand, Choose, Solve, Answer, Check) to help them complete word problems.
By following the acronym step by step children learn to apply a structured, analytical strategy to their calculations. They will need to understand what the problem is asking them to find out by reading the question carefully, choosing the correct mathematical operation to help them solve the query and finally checking their answer by using the inverse operation.
Word problem examples for Years 1 to 6
The following are example word problems that apply to each primary year group.
Year 1
In Year 1 a child would usually been given apparatus to help them with a problem (counters, plastic coins, number cards, number lines or picture cards).
Sarah wants to buy a teddy bear costing 30p. How many 10p coins will she need?
Brian has 3 sweets. Tom has double this number of sweets. How many sweets does Tom have?
Year 2
In Year 2, children continue to use apparatus to help them with problem-solving.
Faye has 12 marbles. Her friend Louise has 9 marbles. How many marbles do they both have altogether?
Three children are each given 5 teddy bears. How many teddy bears do they have altogether?
Year 3
In Year 3, some children may use apparatus, but on the whole children will tend to work out word problems without physical aids. Teachers will usually demonstrate written methods for the four operations (addition, subtraction, multiplication and division) to support children in their working out of the problems.
A jumper costs £23. How much will 4 jumpers cost?
Sarah has 24 balloons. She gives a quarter of them away to her friend. How many balloons does she give away?
Children will also start to do two-step problems in Year 3. This is a problem where finding the answer requires two separate calculations, for example:
I have £34. I am given another £26. I divide this money equally into four different bank accounts. How much money do I put in each bank account?
- In this case, the first step would be to add £34 and £26 to make £60.
- The second step would be to divide £60 by 4 to make £15.
Year 4
Children should feel confident in an efficient written method for each operation at this stage. They will continue to be given a variety of problems and have to work out which operation and method is appropriate for each. They will also be given two-step problems.
I have 98 marbles. I share them equally between 6 friends. How many marbles does each friend get? How many marbles are left over?
Year 5
Children will continue to do one-step and two-step problems. They will start to carry out problem-solving involving decimals.
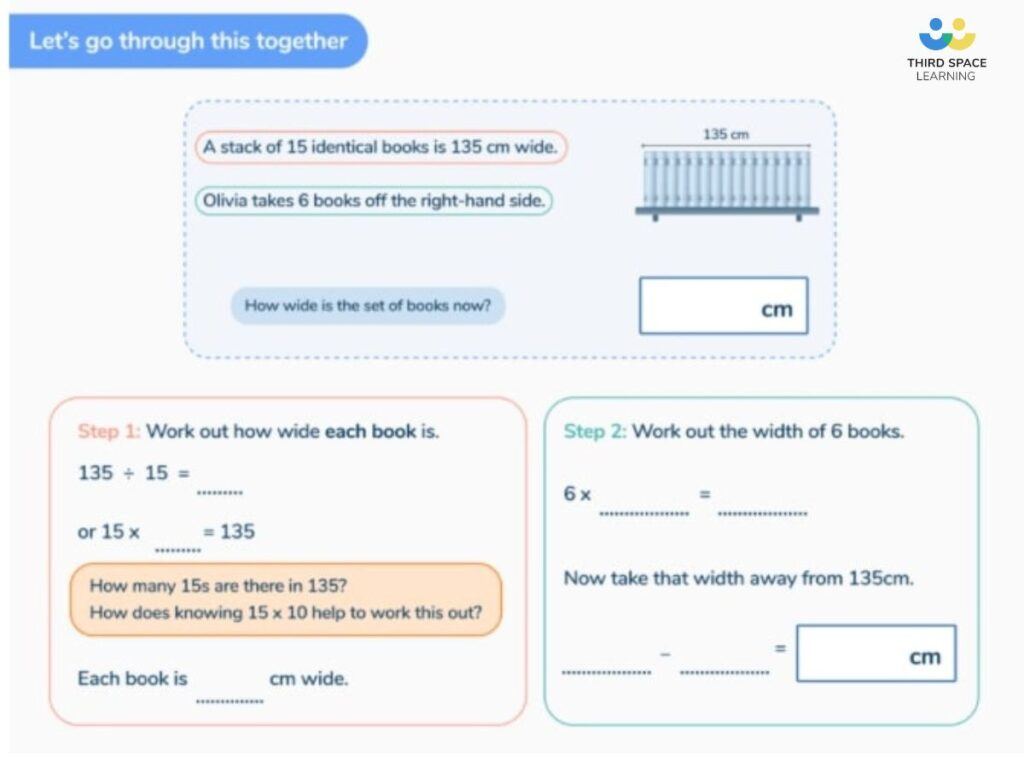
My chest of drawers is 80cm wide and my table is 1.3m wide. How much wall space do they take up when put side by side?
There are 24 floors of a car park. Each floor has room for 45 cars. How many cars can the car park fit altogether?
Year 6
In Year 6 children solve ‘multi-step problems’ and problems involving fractions, decimals and percentages.
Sarah sees the same jumper in two different sales:
In the first sale, the original price of the jumper is £36.15, but has been reduced by a third.
In the second sale, the jumper was priced at £45, but now has 40% off.
How much does each jumper cost and which one is the cheapest?
In the past, calculators were sometimes used for solving two-step problems like the one above, but the new curriculum does not include the use of calculators at any time during primary school.
Solving word problems at KS1 and KS2 is an essential part of the new maths curriculum. Here you can find expert guidance on how to solve maths word problems as well as examples of the many different types of word problems primary school children will encounter with links to hundreds more.
What is a word problem?
A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem.
For example:
Importance of word problems within the national curriculum
The National Curriculum states that its mathematics curriculum “aims to ensure that all pupils:
- become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately;
- reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
- can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.”
To support this schools are adopting a ‘mastery’ approach to maths
The National Centre for Excellence in the Teaching of Mathematics (NCETM) have defined “teaching for mastery”, with some aspects of this definition being:
- Maths teaching for mastery rejects the idea that a large proportion of people ‘just can’t do maths’.
- All pupils are encouraged by the belief that by working hard at maths they can succeed.
- Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other.
- Significant time is spent developing deep knowledge of the key ideas that are needed to underpin future learning. The structure and connections within the mathematics are emphasised, so that pupils develop deep learning that can be sustained.
(The Essence of Maths Teaching for Mastery, 2016)

Year 3 to 6 Rapid Reasoning Worksheet for Weeks 1-6
Download for FREE 6 weeks of Rapid Reasoning worksheets. That include six weeks of daily reasoning and problem-solving questions for years 3, 4, 5 and 6!
Mastery helps children to explore maths in greater depth
One of NCETM’s Five Big Ideas in Teaching for Mastery (2017) is “Mathematical Thinking: if taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others”.
In other words – yes, fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learnt the number skills appropriate to their level/age, they should be progressed to the next level/age of number skills.
The mastery approach encourages exploring the breadth and depth of these concepts (once fluency is secure) through reasoning and problem solving.
See the following example:
| Year 6 objective | Fluency | Reasoning | Problem solving |
|---|---|---|---|
| Solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why. | 7,208 females attended a concert as well as 8,963 males. There were originally 20,000 seats on sale. How many empty seats were there at the concert? | Abdul says, “If I add any two 4-digit numbers together, it will make a 5-digit number.” Do you agree? Explain why. | Three pandas are eating bamboo sticks. There are 51 altogether. They all eat an odd number of sticks. How many bamboo sticks did they each eat? How many different ways can you do it? |
What sort of word problems might my child encounter at school?
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”. The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
|---|---|---|---|---|---|
| Number and place value | 6 | 9 | 7 | 5 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |
How to teach children to solve word problems?
Here are two simple strategies that can be applied to many word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
Let’s see how this can be applied to a word problem to help achieve the answer.
Solving a simple word problem
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
The bar model is always a brilliant way of representing problems, but if you are not familiar with this, there are always other ways of drawing it out.
Read more: What is a bar model
For example, for this question, you could draw 28 pupils (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
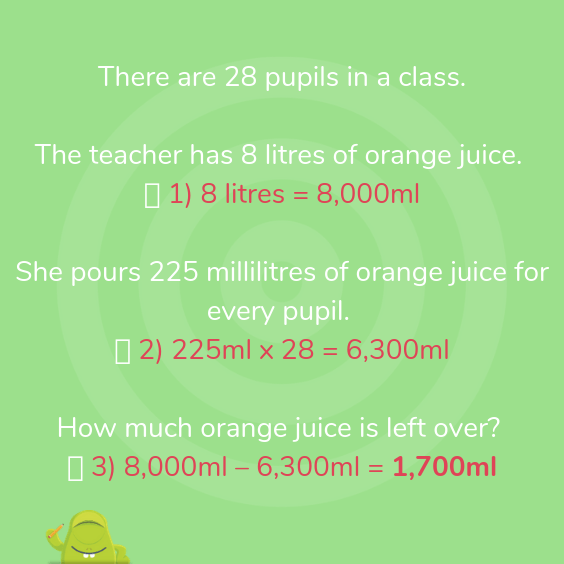
Solving a more complex word problem
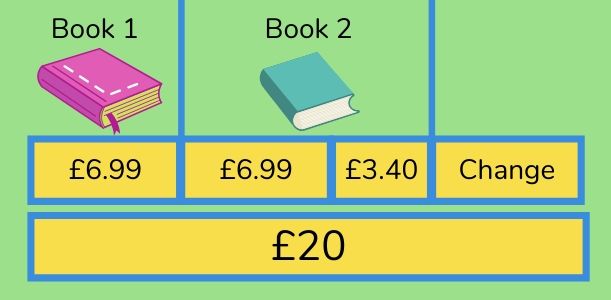
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book.
She pays using a £20 notes.
What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
She pays using a £20 note.
What change does Mara get? 2) £20 – £17.38 = £2.62
Maths word problems for years 1 to 6
The more children learn about maths as the go through primary school, the trickier the word problems they face will become.
Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each primary year group
Word problems in Year 1
Throughout Year 1 a child is likely to be introduced to word problems with the help of concrete resources (pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.
An example of a word problem for Year 1 would be:
Chris is going to buy a cake for his mum which costs 80p. How many 20p coins would he need to do this?
Word problems in Year 2
Year 2 is a continuation of Year 1 when it comes to word problems, with children still using concrete maths resources to help them understand and visualise the problems they are working on
An example of a word problem for Year 2 would be:
A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?
Word problems in Year 3
With word problems for year 3, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the four operations such as addition and subtraction word problems, multiplication and division problems too.
This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.
Year 3 word problem: Geometry properties of shape
Shaun is making 3-D shapes out of plastic straws.
At the vertices where the straws meet, he uses blobs of modelling clay to fix them together
Here are some of the shapes he makes:
| Shape | Number of straws | Number of blobs of modelling clay |
|---|---|---|
| A | 8 | 5 |
| B | 12 | 8 |
| C | 6 | 4 |
One of Sean’s shapes is a cuboid. Which is it? Explain your answer.
Answer: shape B as a cuboid has 12 edges (straws) and 8 vertices (clay)
Year 3 word problem: Statistics
Year 3 are collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.

Answer: a) 9 b) 3 pebbles drawn
Top tip
By the time children are in Year 3 many of the word problems, even one-step story problems tend to be a variation on a multiplication problem. For this reason learning times tables becomes increasingly essential at this stage. One of the best things you can do to help with Year 3 maths at home is support your child to do this.
Word problems in Year 4
At this stage of their primary school career, children should feel confident using the written method for each of the four operations.
Word problems for year 4 will include a variety of problems, including 2-step problems and be children will be expected to work out the appropriate method required to solve each one.
Year 4 word problem: Number and place value
My number has four digits and has a 7 in the hundreds place.
The digit which has the highest value in my number is 2.
The digit which has the lowest value in my number is 6.
My number has 3 fewer tens than hundreds.
What is my number?
Answer: 2,746
Word problems in Year 5
One and 2-step word problems continue with word problems for year 5, but this is also the year that children will be introduced to word problems containing decimals.
These are some examples of Year 5 maths word problems.
Year 5 word problem: Fractions, decimals and percentages
Stan, Frank and Norm are washing their cars outside their houses.
Stan has washed 0.5 of his car.
Frank has washed 1/5 of his car.
Norm has washed 5% of his car.
Who has washed the most?
Explain your answer.
Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.05)
Word problems in Year 6
Word problems for year 6 shift from 2-step word problems to multi-step word problems. These will include fractions, decimals, percentages and time word problems.
Here are some examples of the types of maths word problems Year 6 will have to solve.
Year 6 word problem – Ratio and proportion
This question is from the 2018 key stage 2 SATs paper. It is worth 1 mark.
The Angel of the North is a large statue in England. It is 20 metres tall and 54 metres wide.
Ally makes a scale model of the Angel of the North. Her model is 40 centimetres tall. How wide is her model?
Answer: 108cm
Year 6 word problem – Algebra
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
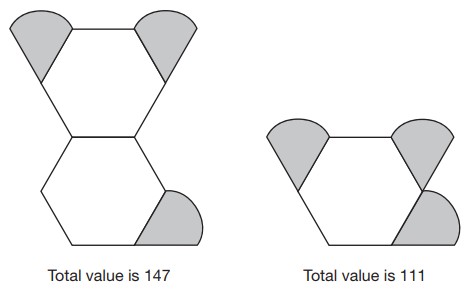
Amina is making designs with two different shapes.
She gives each shape a value.
Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
Year 6 word problem: Measurement
This question is from the 2018 KS2 SATs paper. It is worth 3 marks as it is a multi-step problem.
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
Answer: 1.7 litres or 1,700ml
Topic based word problems
The following examples give you an idea of the kinds of maths word problems your child will encounter for each of the 9 strands of maths in KS2.
Place value word problems
Place value word problem Year 5
This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37
Download free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction word problem Year 3
In Year 3 pupils will solve addition word problems and subtraction word problems with 2 and 3 digits.
Sam has 364 sweets. He gets given 142 more. He then gives 277 away. How many sweets is he left with? Answer: 229
Download free addition and subtraction word problems for Years 3, 4, 5 and 6
Addition word problem Year 3
Alfie thinks of a number. He subtracts 70. His new number is 12. What was the number Alfie thought of? Answer: 82
Subtraction word problem Year 6
The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC
More here: 25 addition and subtraction word problems
Multiplication and division word problems
Multiplication and division word problem Year 3
A baker is baking chocolate cupcakes. She melts 16 chocolate buttons to make the icing for 9 cakes. How many chocolate buttons will she need to melt to make the icing for 18 cakes? Answer: 32
Multiplication word problem Year 4
Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108
Download free multiplication word problems for Years 3, 4, 5 and 6
Division word problem Year 6
A factory produces 1,692 paintbrushes every day. They are packaged into boxes of 9. How many boxes does the factory produce every day? Answer: 188
Download our free division word problems worksheets for Years 3, 4, 5 and 6.
More here: 20 multiplication word problems
More here: 25 division word problems
Free resource: Use these four operations word problems to practise addition, subtraction, multiplication and division all together.
Fraction word problems
Fraction word problem Year 5
At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3
Download free fractions and decimals word problems worksheets for Years 3, 4, 5 and 6
More here: 28 fraction word problems
Decimals word problem Year 4 (crossover with subtraction)
Which two decimals that have a difference of 0.5? 0.2, 0.25, 0.4, 0.45, 0.6, 0.75. Answer: 0.25 and 0.75
Download free decimals and percentages word problems resources for Years 3, 4, 5 and 6
Percentage word problem Year 5
There are 350 children in a school. 50% are boys. How many boys are there? Answer: 175
Measurement word problem Year 3 (crossover with subtraction)
Lucy and Ffion both have bottles of strawberry smoothie. Each bottle contains 1 litre. Lucy drinks ½ of her bottle. Ffion drinks 300ml of her bottle. How much does each person have left in both bottles? Answer: Lucy = 500ml, Ffion = 300ml
More here: 25 percentage word problems
Money word problem Year 3
James and Lauren have different amounts of money. James has twelve 2p coins. Lauren has seven 5p coins. Who has the most money and by how much? Answer: Lauren by 11p.
More here: 25 money word problems
Area word problem Year 4
A rectangle measures 6cm by 5cm.
What is its area? Answer: 30cm2
Perimeter word problem Year 4
The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many metres has she swum? Answer: 108m
Ratio word problem Year 6 (crossover with measurement)
A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
More here: 24 ratio word problems
Bodmas word problem Year 6
Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
50 – 10 × 5 =
50 – 10 × 5 =
Volume word problem Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
How important are word problems when it comes to the SATs?
In the KS1 SATs, 58% (35/60 marks) of the test is comprised of maths ‘reasoning’ (word problems).
In KS2, this increases to 64% (70/110 marks) spread over two reasoning papers, each worth 35 marks. Considering children have, in the past, needed approximately 55-60% to reach the ‘expected standard’, it’s clear that children need regular exposure to and a solid understanding of how to solve a variety of word problems.
Children have the opportunity to practice SATs style word problems in Third Space Learning’s online one-to-one SATs revision programme. Personalised to meet the needs of each student, our programme helps to fill gaps and give students more confidence going in to the SATs exams.
Remember: The word problems can change but the maths won’t
It can be easy for children to get overwhelmed when they first come across word problems in KS2, but it is important that you remind them that whilst the context of the problem may be presented in a different way, the maths behind it remains the same.
Word problems are a good way to bring maths into the real world and make maths more relevant for your child, so help them practise, or even ask them to turn the tables and make up some word problems for you to solve.
This article while written by a teacher for teachers is also suitable for those at home supporting children with home learning. More free home learning resources are also available.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Solving Word Problems in Mathematics
What Is a Word Problem? (And How to Solve It!)
Learn what word problems are and how to solve them in 7 easy steps.
Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances.
As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem.
As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.
If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?
Steps of Solving a Word Problem
To work through any word problem, students should do the following:
1. Read the problem: first, students should read through the problem once.
2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
3. Visualize the problem: drawing a picture or creating a diagram can be helpful.
Students can start visualizing simple or more complex problems by creating relevant images, from concrete (like drawings of putting away cookies from a jar) to more abstract (like tape diagrams). It can also help students clarify the operations they need to carry out. (next step!)
4. Determine the operation(s): next, students should determine the operation or operations they need to perform. Is it addition, subtraction, multiplication, division? What needs to be done?
Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:
– Addition: add, more, total, altogether, and, plus, combine, in all;
– Subtraction: fewer, than, take away, subtract, left, difference;
– Multiplication: times, twice, triple, in all, total, groups;
– Division: each, equal pieces, split, share, per, out of, average.
These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems.
Another way to determine the operation is to search for certain situations, Jennifer Findley suggests. She has a great resource that lists various situations you might find in the most common word problems and the explanation of which operation applies to each situation.
5. Make a math sentence: next, students should try to translate the word problem and drawings into a math or number sentence. This means students might write a sentence such as 3 + 8 =.
Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence.
6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
7. Check the answer: finally, students should check their work to make sure that the answer is correct.
These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that!
At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises!
Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience.
Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.
For example, during the first steps, simple wording and animation help students realize what action the problem represents and find the connection between these actions and key words like “take away” and “left” that may signal them.
From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes.
Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.
Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations.
Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams!
To see the full exercise, follow this link.
The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task.
Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language.
These are the common steps that may help students overcome initial feelings of anxiety and fear of difficulty of the task they are given. Together with a teacher, they can master these foundational skills and build their confidence toward solving word problems. And Happy Numbers can facilitate this growth, providing varieties of engaging exercises and challenging word problems!
Though the majority of ACT math problems use diagrams or simply ask you to solve given mathematical equations, you will also see approximately 15-18 word problems on any given ACT (between 25% and 30% of the total math section). This means that knowing how best to deal with word problems will help you significantly when taking the test. Though there are many different types of ACT word problems, most of them are not nearly as difficult or cumbersome as they may appear.
This post will be your complete guide to ACT word problems: how to translate your word problems into equations and diagrams, the different types of word problems you’ll see on the test, and how best to go about solving your word problems for test day.
What Are Word Problems?
A word problem is any problem that is based mostly or entirely on written description and does not provide you with an equation, diagram, or graph. You must use your reading skills to translate the words of the question into a workable math problem and then solve for your information.
Word problems will show up on the test for a variety of reasons. Most of the time, these types of questions act to test your reading and visualization skills, as well act as a medium to deliver questions that would otherwise be untestable. For instance, if you must determine the number of sides of an unknown polygon based on given information, a diagram would certainly give the game away!
Translating Word Problems Into Equations or Drawings
In order to translate your word problems into actionable math equations that you can solve, you’ll need to know and utilize some key math terms. Whenever you see these words, you can translate them into the proper action. For instance, the word “product” means “the value of two or more values that have been multiplied together,” so if you need to find “the product of a and b,” you’ll need to set up your equation with $a * b$.
|
Key Terms |
Mathematical Action |
|
Sum, increased by, added to, total of |
+ |
|
Difference, decreased by, subtracted from |
— |
|
Product, times |
* or x |
|
Divided by |
/ or ÷ |
|
Equals, is, are, equivalent, same |
= |
|
Is less than |
< |
|
Is greater than |
> |
|
Is less than or equal to |
≤ |
|
Is greater than or equal to |
≥ |
Let’s take a look at this in action with an example problem:
We have two different cable companies that each have different rates for installation and different monthly fees. We are asked to find out how many months it will take for the cost for each company to be the «same,» which means we must set the two rates equal.
Uptown Cable charges 120 dollars for installation plus 25 dollars a month. We do not know how many months we’re working with, so we will have:
$120 + 25x$
Downtown Cable charges 60 dollars for installation and 35 dollars per month. Again, we don’t know how many months we’re working with, but we know they will be the same, so we will have:
$60 + 35x$
And, again, because we are finding the amount of months when the cost is the «same,» we must set our rates equal.
$120 + 25x = 60 + 35x$
From here, we can solve for $x$, since it is a single variable equation.
[Note: the final answer is G, 6 months]
Learning the language of ACT word problems will help you to unravel much of the mystery of these types of questions.
Typical ACT Word Problems
ACT word problems can be grouped into two major categories: word problems where you must simply set up an equation and word problems in which you must solve for a specific piece of information.
Word Problem Type 1: Setting Up an Equation
This is the less common type of word problem on the test, but you’ll generally see it at least once or twice. You’ll also usually see this type of word problem first. For this type of question, you must use the given information to set up the equation, even though you don’t need to solve for the missing variable.
Almost always, you’ll see this type of question in the first ten questions on the test, meaning that the ACT test-makers consider them fairly “easy.” This is due to the fact that you only have to provide the set-up and not the execution.
We consider a “profit” to be any money that is gained, so we must always subtract our costs from our earnings. We know that Jones had to invest 10 million starting capital, so he is only making a profit if he has earned more than 10 million dollars. This means we can eliminate answer choices C, D, and E, as they do not account for this 10 million.
Now each boat costs Jones 7,000 dollars to make and he sells them for 20,000. This means that he earns a profit of:
$20,000 — 7,000$
$13,000$ per boat.
If $x$ represents our number of boats, then our final equation will be:
$13,000x — 10,000,000$
Our final answer is A, $13,000x — 10,000,000$
Word Problem Type 2: Solving for Your Information
Other than the few set-up word questions you’ll see, the rest of your ACT word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of ACT math topics, including averages, single variable equations, and probabilities, among others. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
This question is a rare example of a time in which not every piece of given information is needed to solve the problem. For most ACT word questions, all your given information will come into play at some point, but this is not the case here (though you can use all of your information, should you so choose).
For example, we are told that 25% of a given set of jelly beans are red. 25% translates to $1/4$ because 25% is the same as $25/100$ (or $1/4$). If we are being asked to find how many jelly beans are NOT red, then we know it would be $3/4$ because 100% is the same as 1, and 1 — $1/4$ = $3/4$.
So we didn’t need to know that there were 400 jellybeans to know that our final answer is H, $3/4$.
Alternatively, we could use all of our given information and find 25% of 400 in order to find the remaining jelly beans.
$400 * {1/4}$ or $400/4$
$100$
If 100 jellybeans are red, then 400 — 100 = 300 jelly beans are NOT red. This means that the not-red jelly beans make up,
$300/400$
$3/4$ of the total number of jelly beans.
Again, our final answer is H, $3/4$
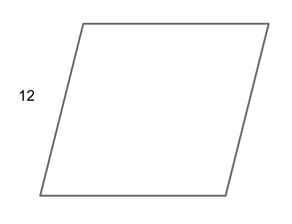
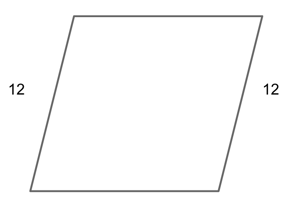
You might also be given a geometry problem as a word problem, which may or may not be set up with a scenario as well.
Geometry questions will be presented as word problems typically because the test-makers felt the problem would be too easy to solve had you been given a diagram.
The test-makers didn’t give us a diagram, so let’s make ourselves one and fill it in with what we know so far.
We know from our studies of parallelograms that opposite side pairs will be equal, so we know that the opposite side of our given will also be 12.
Now we can use this information to subtract from our total perimeter.
$72 — 12 — 12$
$48$
Again, opposite sides will be equal and we know that the sum of the two remaining sides will be 48. This means that each remaining side will be:
$48/2$
$24$
Now we have four sides in the pairings of 12 and 24.
Our final answer is C, 12, 12, 24, 24.
Now, how do we put our knowledge to its best effect? Let’s take a look.
ACT Math Strategies for Your Word Problems
Though you’ll see word problems on a myriad of different types of ACT math topics, there are still a few techniques you can apply to solve your word problems as a whole.
#1: Draw It Out
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what, exactly, you’re working with. For instance, let’s look at how a picture can help you solve a ratio/division problem:
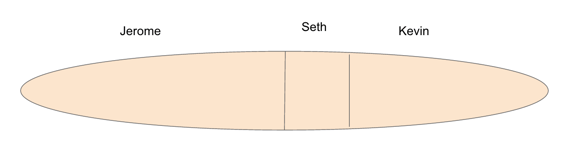
Let’s start by first drawing our sandwich and Jerome’s portion of it.
Now let’s divvy off Kevin’s portion and, by the remainder, Seth’s as well.
By seeing the problem visually, we can see that the ratio of Jerome’s share, to Kevin’s, to Seth’s will go in descending order of size. This let’s us eliminate answer choices A, B, and C, and leaves us with answer choices D and E.
Just by drawing it out and using process of elimination, and without knowing anything else about ratios, we have a 50-50 shot of guessing the right answer. And, again, without knowing anything else about fractions or ratios, we can make an educated guess between the two options. Since Jerome’s share doesn’t look twice as large as Kevin’s, our answer is probably not E.
This leaves us with our final answer D, 3:2:1.
[Note: for a breakdown on how to solve this problem using fractions and ratios instead of using a diagram and educated guessing, check out our guide to ACT fractions and ratios.]
As for geometry problems, remember—you’re often given a word problem as a word problem because it would be too simple to solve had you had a diagram to work with from the get-go. So take back the advantage and draw the picture yourself. Even a quick and dirty sketch can help you visualize the problem much easier than you can in your head and help keep all your information clear.
#2: Memorize Important Terms
If you’re not used to translating English words into mathematical equations, then ACT word problems can sound like so much nonsense and leave you floundering to set up the proper equation. Look to the chart and learn how to translate your keywords into their math equivalents. Doing so will help you to understand exactly what the problem is asking you to find.
There are free ACT math questions available online, so memorize your terms and then practice on real ACT word problems to make sure you’ve got your definitions down and can apply them to real problems.
#3: Underline and Write Out the Key Information
The key to solving a word problem is bringing together all the relevant pieces of given information and putting them in the right places. Make sure you write out all your givens on the diagram you’ve drawn (if the problem calls for a diagram) and that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline them in the problem and then write them out yourself before you set up your equation, so take a moment to perform this step.
#4: Pay Close Attention to Exactly What Is Being Asked of You
Little is more frustrating than solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of $x$ or $x + y$? Better to make sure before you start what you’re supposed to find than realize two minutes down the line that you have to solve the problem all over again.
#5: Brush Up on Any Specific Math Topic in Which You Feel Weak
You are likely to see both diagram/equation problems and word problems for any given ACT math topic on the test. Many of the topics can swing either way, which is why there are so many different types of word problems and why you’ll need to know the ins and outs of any particular math topic in order to solve its corresponding word problem. For example, if you don’t know how to properly set up a system of equations problem, you will have a difficult time of it when presented with a word problem on the topic.
So understand that solving a word problem is a two-step process: it requires you to both understand how word problems themselves work and to understand the math topic in question. If you have any areas of mathematical weakness, now is a good time to brush up on them, or else the word problem might be trickier than you were expecting.
All set? Time to shine!
Test Your Knowledge
Now to put your word problem know-how to the test with real ACT math problems.
Answers: K, C, A, E
Answer Explanations:
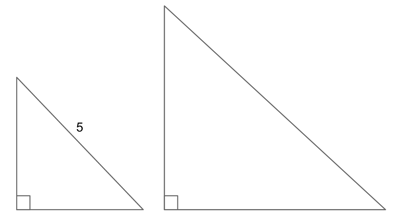
1) First, let us make a sketch of what we have, just so we can keep our measurements straight. We know we have two triangles, one smaller than the other, and the hypotenuse of the smaller triangle is 5.
Now our triangles are in a ratio of 2:5, so if the hypotenuse of the smaller triangle is 5, we can find the hypotenuse of the larger triangle by setting them up in a proportion.
$2/5 = 5/x$
$2x = 25$
$x = 12.5$
Our final answer is K, 12.5.
2) Because we are dealing with a hypothetical number that is increasing and decreasing based on percentage, we can solve this problem in one of two ways—by using algebra or by plugging in our own numbers.
Solving Method 1: Algebra
If we assign our hypothetical number as $x$, we can say that $x$ is increased by 25% by saying:
$x + 0.25x$
Which gives us:
$1.25x$
Now, we can decrease this value by 20% by saying:
$1.25x — (1.25x * 0.2)$
$1.25x — 0.25x$
This leaves us with:
$1x$ or 100% of our original number.
Our final answer is C, 100%.
Solving Method 2: Plugging in Numbers
Alternatively, we can use the same basic process, but make it a little simpler by using numbers instead of variables.
Let’s say our original number is 100. (Why 100? Why not! Our number can literally be anything and 100 is an easy number to work with.)
So if we need to increase 100 by 25%, we first need to find 25% of 100 and then add that to 100.
$100 + (0.25)100$
$100 + 25$
$125$
Now we need to decrease this value by 20%, so we would say:
$125 — (0.2)125$
$125 — 25$
$100$
We are left with the same number we started with, which means we are left with 100% of the number we started with.
Again, our final answer is C, 100%.
3) Let’s first begin by drawing a picture of our scene. We know that one vertex of the square is at (3, 0), so we can mark it on a coordinate plane.
Now, we are told that each side of the square is 3 cm long. To make life simple, we can start by marking all the possible vertexes attached to our known vertex at (3, 0) straight up, down, and side to side. If no answers match, we can then look to vertexes at different angles.
Our possible vertexes are:
(0, 0), (6, 0), 3, 3) and (3, -3)
One of our possible vertexes is at (6, 0 and this matches one of our answer choices, so we can stop here.
Our final answer is A, (6, 0).
4) We are told that Ms. Lopez throws out the lowest test score and then averages the remaining scores. Because Victor’s scores are already in ascending order, we can throw out the first score of 62.
Now to find the average of the remaining 4 scores, let us add them together and then divide by the number of scores.
$(78 + 83 + 84 + 93)/4$
$338/4$
$84.5$
Our final answer is E, 84.5.

Picture: John Morris/Flickr
The Take-Aways
Word problems comprise a significant portion of the ACT, so it’s a good idea to understand how they work and how to translate the words into a proper equation. But remember that translating your word problems is still only half the battle.
You must also supplement this knowledge of how to solve word problems with a solid understanding of the math topic in question. For example, it won’t do a lot of good if you can translate a probability word problem if you don’t understand exactly how probabilities work. So be sure to not only learn how to approach your word problems, but also hone your focus on any math topics you feel you need to improve upon. You can find links to all of our ACT math topic guides here to help your studies.
What’s Next?
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.