English[edit]
Etymology[edit]
From Middle French function, from Old French fonction, from Latin functiō (“performance, execution”), from functus, perfect participle of fungor (“to perform, execute, discharge”), from Proto-Indo-European *bʰewg- (“to enjoy”).
Pronunciation[edit]
- (UK) IPA(key): /ˈfʌŋ(k)ʃən/, /ˈfʌŋkʃn̩/
- (US) IPA(key): /ˈfʌŋkʃən/, [ˈfʌŋkʃɪ̈n], [ˈfʌŋkʃn̩]
- Hyphenation: func‧tion
- Rhymes: -ʌŋkʃən
Noun[edit]
function (plural functions)
- What something does or is used for.
- Synonyms: aim, intention, purpose, role, use
- A professional or official position.
- Synonyms: occupation, office, part, role
- Something which is dependent on or stems from another thing; a result or concomitant.
-
2008 June 1, A. Dirk Moses, “Preface”, in Empire, Colony, Genocide: Conquest, Occupation, and Subaltern Resistance in World History, Berghahn Books, →ISBN, page x:
-
Though most of the cases here cover European encounters with non-Europeans, it is not the intention of the book to give the impression that genocide is a function of European colonialism and imperialism alone.
-
-
- A relation where one thing is dependent on another for its existence, value, or significance.
- (mathematics) A relation in which each element of the domain is associated with exactly one element of the codomain.
- Synonyms: map, mapping, mathematical function, operator, transformation
- Hypernym: relation
- (computing) A routine that receives zero or more arguments and may return a result.
- Synonyms: procedure, routine, subprogram, subroutine, func, funct
- (biology) The physiological activity of an organ or body part.
- (chemistry) The characteristic behavior of a chemical compound.
- (anthropology) The role of a social practice in the continued existence of the group.
- (slang) A party.
Hyponyms[edit]
- The terms below need to be checked and allocated to the definitions (senses) of the headword above. Each term should appear in the sense for which it is appropriate. For synonyms and antonyms you may use the templates
{{syn|en|...}}or{{ant|en|...}}.
- subfunction
- luminosity function
- mass function
- phase function
- source function
- anonymous function
- Boolean function
- built-in function
- computable function
- concave function
- constructor function
- convex function
- error function
- first-class function
- predefined function
- recursive function
- restricted function
- second-class function
- set function
- switch function
- third-class function
- transition function
- user-defined function
- AND function
- Boolean function
- NOR function
- NOT function
- OR function
- propositional function
- switching function
- truth function
- line function
- staff function
- additive function
- aggregate function
- algebraic function
- alternating function
- analytic function
- anonymous function
- Baire function
- bei function
- ber function
- Bessel function
- beta function
- Bloch function
- bounded function
- boxcar function
- Brillouin function
- Cantor function
- characteristic function
- Chebyshev function
- circular function
- comparable function
- complementary function
- composite function
- connect function
- constant function
- constraint function
- contiguous function
- continuous function
- correlation function
- cost function
- critical function
- cylinder function
- decreasing function
- delta function
- density function
- describing function
- differentiable function
- discriminant function
- dissipation function
- distance function
- distribution function
- driving-point function
- eigenfunction
- elementary function
- Emden function
- entire function
- Euler’s phi function
- even function
- explicit function
- exponential function
- first-class function
- form function
- Fowler function
- frontogenetic function
- gamma function
- generating function
- Green’s function
- Hamiltonian function
- Hankel function
- harmonic function
- hei function
- her function
- Hildebrand function
- homogeneous function
- Hugoniot function
- hyperbolic function
- hypergeometric function
- identity function
- implicit function
- impulse function
- incidence function
- increasing function
- independent function
- influence function
- inner function
- integrable function
- integral function
- invariant function
- inverse function
- inverting function
- J function
- jump function
- kei function
- ker function
- Koebe function
- Lagrangian function
- Lamé function
- Legendre function
- Leverett function
- linear function
- Liouville function
- loss function
- Lyapunov function
- mass function
- Massieu function
- Mathieu function
- measurable function
- membership function
- meromorphic function
- microspec function
- Möbius function
- monotone function
- multilinear function
- natural function
- Neumann function
- normalized function
- normalized support function
- number-theoretic function
- objective function
- odd function
- one-way function
- orthogonal function
- orthonormal function
- partial function
- partition function
- Patterson function
- penalty function
- periodic function
- Planck function
- point function
- polynomial function
- power function
- principal function
- psi function
- quadratic function
- Rademacher function
- random function
- rational function
- real function
- recursive function
- regular function
- Riemann function
- Riemann P function
- sample function
- scalar function
- self-organizing function
- sensitivity function
- shear-viscosity function
- sigma function
- signum function
- simple function
- single-valued function
- sinusoidal function
- Smarandache function
- special function
- step function
- stream function
- stress function
- summable function
- support function
- symmetric function
- test function
- theta function
- torsion function
- transcendental function
- transfer function
- transmission function
- trigonometric cofunction
- trigonometric function
- truth function
- unit function
- universal wavelength function
- variadic function
- vector function
- Wannier function
- Weierstrass function
- weight function
- zeta function
- Airy function
- excitation function
- information function of a partition
- Langevin function
- luminosity function
- nuclear response function
- partition function
- psi function
- scattering function
- spectral function
- wave function
- work function
Derived terms[edit]
- analytical function generator
- anatomy of function
- bifunctional
- cofunction
- difunctional
- diode function generator
- dysfunction
- eigenfunction expansion
- function code
- function failure safety
- function generator
- function key
- function multiplier
- function object
- function pointer
- function space
- function switch
- function table
- function unit
- function-evaluation routine
- functional
- functionalism
- functionality
- functionhood
- general-purpose function generator
- implicit function theorem
- inverse function theorem
- malfunction
- malfunction routine
- mathematical function program
- minimal brain dysfunction syndrome
- monofunctional compound
- multifunction array radar
- nonfunctional packages software
- positive linear functional
- programmed function key
- radicofunctional name
- second-class function
- separated-function synchrotron
- sharpness function technique
- step-function generator
- subfunctional
- tapped-potentiometer function generator
- thermodynamic function of state
- tool-function controller
- variable diode function generator
- Ackermann function
- activation function
- adaptive-control function
- antihyperbolic function
- antitrigonometric function
- arc-hyperbolic function
- arithmetic function
- bent function
- binary function
- black-box function
- bodily function
- Borel function
- busy beaver function
- ceil function
- ceiling function
- choice function
- complex function
- consumption function
- cubic function
- cumulative distribution function
- derived function
- Dickman function
- digamma function
- Dirac delta function
- Dirichlet eta function
- divisor function
- electron wave function
- elliptic function
- empty function
- Euler’s totient function
- executive function
- exponential generating function
- feedback transfer function
- floor function
- forcing function
- forward transfer function
- function overloading
- function value
- function word
- Gabor function
- gain of function
- gain-of-function
- gain-of-function research
- Gaussian function
- generic function
- Hammett acidity function
- Hann function
- hash function
- Heaviside unit function
- Helmholtz function
- Herbrand function
- higher-order function
- homogenous function
- hybrid wave function
- inclusion function
- indicator function
- initial mass function
- inverse hyperbolic function
- inverse trigonometric function
- iterated function system
- K-function
- Kelvin function
- lambda function
- liver function test
- logarithmic function
- logarithmic trigonometric function
- logistic function
- loop transfer function
- member function
- mimic function
- Mittag-Leffler function
- moment-generating function
- monotonic function
- Morse function
- onto function
- pairing function
- partial function application
- payoff function
- physical unclonable function
- physically unclonable function
- platelet function test
- polygamma function
- Prandtl-Meyer function
- probability density function
- probability mass function
- pulmonary function test
- quartic function
- quintic function
- radial distribution function
- Riemann zeta function
- Riemann zeta-function
- Schrödinger wave function
- Schur function
- sigmoid function
- sign function
- sink function
- Skolem function
- smooth function
- spatial wave function
- strictly decreasing function
- strictly increasing function
- surjective function
- total function
- trapdoor function
- trigamma function
- Turing computable function
- utility function
- valuation function
- virtual function
- vital function
- von Mangoldt function
- Walsh function
- window function
- Zarankiewicz function
[edit]
- functor
- fungible
Translations[edit]
what something does or is used for
- Afrikaans: funksie (af)
- Albanian: funksion (sq)
- Arabic: وَظِيفَة (ar) f (waẓīfa)
- Armenian: ֆունկցիա (hy) (funkcʿia), գործառույթ (hy) (gorcaṙuytʿ)
- Azerbaijani: funksiya (az)
- Belarusian: фу́нкцыя f (fúnkcyja)
- Bulgarian: фу́нкция (bg) f (fúnkcija)
- Catalan: funció (ca) f
- Chinese:
- Mandarin: 功能 (zh) (gōngnéng), 機能/机能 (zh) (jīnéng)
- Czech: funkce (cs) f, účel (cs) m
- Danish: funktion c
- Dutch: functie (nl) f
- Esperanto: funkcio
- Estonian: funktsioon
- Finnish: tehtävä (fi), tarkoitus (fi), toiminto (fi)
- French: fonction (fr) f
- Galician: función (gl) f
- Georgian: ფუნქცია (ka) (punkcia)
- German: Funktion (de) f, Funktionalität (de) f
- Greek: λειτουργία (el) f (leitourgía)
- Hebrew: תַּפְקִיד (he) m (tafkíd)
- Hungarian: funkció (hu), rendeltetés (hu), szerep (hu), cél (hu)
- Indonesian: fungsi (id)
- Irish: feidhm f, feidhmeannas m
- Italian: funzione (it) f
- Japanese: 機能 (ja) (きのう, kinō)
- Kazakh: функция (funksiä)
- Khmer: មុខងារ (muk ngiə)
- Korean: 기능(機能) (ko) (gineung)
- Kurdish:
- Central Kurdish: کار (ckb) (kar), کاروبار (ckb) (karubar)
- Kyrgyz: функция (ky) (funktsiya)
- Latin: pars (la)
- Latvian: funkcija f
- Lithuanian: funkcija (lt) f
- Macedonian: функција f (funkcija)
- Malay: fungsi (ms)
- Maori: taumahi
- Norwegian:
- Bokmål: funksjon (no) m
- Persian: تابع (fa) (tâbe’)
- Polish: funkcja (pl) f
- Portuguese: função (pt) f
- Punjabi: ਕਾਜ m (kāj)
- Romanian: funcție (ro) f
- Russian: фу́нкция (ru) f (fúnkcija)
- Serbo-Croatian:
- Cyrillic: фу̀нкција f, свр̀ха f
- Roman: fùnkcija (sh) f, svrha (sh) f
- Slovak: funkcia f
- Slovene: funkcija f
- Spanish: función (es) f
- Swedish: funktion (sv) c, uppgift (sv) c
- Tagalog: taan, laan
- Tajik: функсия (tg) (funksiya)
- Turkish: fonksiyon (tr), işlev (tr)
- Turkmen: funksiýa
- Ukrainian: фу́нкція f (fúnkcija)
- Uzbek: funksiya (uz)
- Vietnamese: chức năng (vi), vai trò (vi)
- Welsh: gweithrediad m
professional or official position
- Arabic: مَهَمَّة f (mahamma)
- Belarusian: фу́нкцыя f (fúnkcyja), паса́да f (pasáda)
- Bulgarian: слу́жба (bg) f (slúžba), длъ́жност (bg) f (dlǎ́žnost)
- Catalan: funció (ca) f
- Chinese:
- Mandarin: 職務/职务 (zh) (zhíwù), 職位/职位 (zh) (zhíwèi)
- Czech: funkce (cs) f
- Danish: funktion c
- Dutch: functie (nl) f
- Finnish: tehtävä (fi), toimi (fi)
- French: fonction (fr)
- German: Funktion (de) f, Aufgabe (de) f
- Greek: λειτούργημα (el) n (leitoúrgima), αποστολή (el) f (apostolí), καθήκον (el) n (kathíkon)
- Hebrew: תַּפְקִיד (he) m (tafkíd)
- Hungarian: funkció (hu), feladat (hu)
- Irish: feidhm f
- Japanese: 職務 (ja) (しょくむ, shokumu), 職位 (ja) (しょくい, shokui)
- Khmer: មុខងារ (muk ngiə)
- Korean: 직무(職務) (ko) (jingmu), 직분(職分) (jikbun), 지위(地位) (ko) (jiwi), 직위(職位) (ko) (jigwi)
- Norwegian:
- Bokmål: post (no) m, stilling (no) m
- Polish: funkcja (pl) f, stanowisko (pl) n, posada (pl) f
- Portuguese: função (pt) f
- Romanian: funcție (ro) f
- Russian: фу́нкция (ru) f (fúnkcija), до́лжность (ru) f (dólžnostʹ)
- Serbo-Croatian:
- Cyrillic: фу̀нкција f, слу̀жба f
- Roman: fùnkcija (sh) f, služba (sh) f
- Spanish: cargo (es) m
- Swedish: förrättning (sv) c, kall (sv) n, syssla (sv) c, åliggande (sv) n,
- Ukrainian: фу́нкція f (fúnkcija), поса́да f (posáda)
relation where one thing is dependent on another
- Bulgarian: фу́нкция (bg) f (fúnkcija)
- Czech: funkce (cs) f
- Danish: funktion c
- Dutch: functie (nl) f
- Finnish: funktio (fi), riippuvuus (fi), riippuvuussuhde
- French: en fonction de (fr)
- German: Abhängigkeitsverhältnis n
- Hebrew: פוּנְקְצִיָּה (he) f (funktsiá)
- Hungarian: függvény (hu)
- Italian: funzione (it) f
- Korean: 상관관계 (相關關係) (sanggwan’gwan’gye)
- Norwegian:
- Bokmål: funksjon (no) m
- Portuguese: função (pt) f
- Russian: фу́нкция (ru) f (fúnkcija)
- Serbo-Croatian:
- Cyrillic: фу̀нкција f
- Roman: fùnkcija (sh) f
- Swedish: funktion (sv) c
- Tajik: тобеъ (tg) (tobeʾ)
mathematics: a relation between a set of inputs and a set of permissible outputs
- Arabic: وَظِيفَة (ar) f (waẓīfa), تَابِع m (tābiʕ), دَالَّة f (dālla)
- Armenian: ֆունկցիա (hy) (funkcʿia)
- Azerbaijani: funksiya (az)
- Belarusian: фу́нкцыя f (fúnkcyja)
- Bulgarian: фу́нкция (bg) f (fúnkcija)
- Burmese: ဖန်ရှင် (hpanhrang)
- Catalan: funció (ca) f
- Chinese:
- Mandarin: 函數/函数 (zh) (hánshù)
- Czech: funkce (cs) f
- Danish: funktion c
- Dutch: functie (nl) f, functie (nl) f
- Esperanto: funkcio
- Estonian: funktsioon
- Finnish: funktio (fi), kuvaus (fi)
- French: fonction (fr) f
- German: Funktion (de) f
- Greek: συνάρτηση (el) f (synártisi)
- Hebrew: פוּנְקְצִיָּה (he) f (funktsiá)
- Hindi: फलन (hi) m (phalan)
- Hungarian: függvény (hu)
- Icelandic: fall (is) n
- Ido: funciono (io)
- Indonesian: fungsi (id)
- Irish: feidhm f
- Italian: funzione (it) f
- Japanese: 関数 (ja) (かんすう, kansū), 函数 (ja) (かんすう, kansū)
- Kazakh: функция (funksiä)
- Khmer: អនុគមន៍ (km) (ʼaʼnukum)
- Korean: 함수(函數) (ko) (hamsu)
- Kyrgyz: функция (ky) (funktsiya)
- Lao: ຕຳລາ (tam lā)
- Latin: fūnctiō f
- Malay: fungsi (ms)
- Malayalam: ഫലനം (ml) (falanaṃ), ഏകദം (ēkadaṃ)
- Maori: pānga
- Middle French: fonction
- Macedonian: функција f (funkcija)
- Mongolian:
- Cyrillic: функц (mn) (funkc)
- Norwegian:
- Bokmål: funksjon (no) m
- Old French: function
- Persian: تابع (fa) (tâbe’)
- Polish: funkcja (pl) f
- Portuguese: função (pt) f
- Romanian: funcție (ro) f
- Russian: фу́нкция (ru) f (fúnkcija)
- Serbo-Croatian:
- Cyrillic: фу̀нкција f
- Roman: fùnkcija (sh) f
- Slovak: funkcia f
- Slovene: funkcija f
- Spanish: función (es) f
- Swedish: funktion (sv)
- Tagalog: kabisa
- Tajik: функсия (tg) (funksiya), тобеъ (tg) (tobeʾ)
- Thai: ฟังก์ชัน (th) (fang-chân)
- Turkish: fonksiyon (tr)
- Turkmen: funksiýa
- Ukrainian: фу́нкція f (fúnkcija)
- Uzbek: funksiya (uz)
- Yiddish: פֿונקציע f (funktsye)
computing: routine that returns a result
- Arabic: وَظِيفَة (ar) f (waẓīfa), دَالَّة f (dālla)
- Armenian: ֆունկցիա (hy) (funkcʿia)
- Azerbaijani: funksiya (az)
- Belarusian: фу́нкцыя f (fúnkcyja)
- Bulgarian: фу́нкция (bg) f (fúnkcija)
- Burmese: ဖန်ရှင် (hpanhrang)
- Catalan: funció (ca) f
- Chinese:
- Mandarin: 函數/函数 (zh) (hánshù), 函式 (hánshì)
- Czech: funkce (cs) f
- Danish: funktion c
- Dutch: functie (nl) f
- Esperanto: funkcio
- Estonian: funktsioon
- Finnish: funktio (fi), aliohjelma (fi)
- French: fonction (fr) f
- Georgian: ფუნქცია (ka) (punkcia)
- German: Funktion (de) f
- Greek: συνάρτηση (el) f (synártisi)
- Hebrew: פוּנְקְצִיָּה (he) f (funktsiá)
- Hungarian: függvény (hu)
- Icelandic: fall (is) n
- Irish: feidhm f
- Italian: funzione (it) f
- Japanese: 関数 (ja) (かんすう, kansū)
- Kazakh: функция (funksiä)
- Korean: 함수(函數) (ko) (hamsu)
- Kyrgyz: функция (ky) (funktsiya)
- Lao: ຕຳລາ (tam lā)
- Latvian: funkcija f
- Lithuanian: funkcija (lt) f
- Macedonian: функција f (funkcija)
- Maori: taumahi
- Mongolian:
- Cyrillic: функц (mn) (funkc)
- Norwegian:
- Bokmål: funksjon (no) m
- Persian: تابع (fa) (tâbe’)
- Polish: funkcja (pl) f
- Portuguese: função (pt) f
- Romanian: funcție (ro) f
- Russian: фу́нкция (ru) f (fúnkcija)
- Serbo-Croatian:
- Cyrillic: фу̀нкција f
- Roman: fùnkcija (sh) f
- Slovak: funkcia f
- Slovene: funkcija f
- Spanish: función (es) f
- Swedish: funktion (sv) c, subrutin c
- Tajik: функсия (tg) (funksiya)
- Thai: ฟังก์ชัน (th) (fang-chân)
- Turkish: işlev (tr), fonksiyon (tr)
- Turkmen: funksiýa
- Ukrainian: фу́нкція f (fúnkcija)
- Uzbek: funksiya (uz)
- Vietnamese: hàm (vi), hàm số (vi)
biology: physiological activity of an organ or body part
- Belarusian: фу́нкцыя f (fúnkcyja)
- Bulgarian: фу́нкция (bg) f (fúnkcija)
- Catalan: funció (ca) f
- Chinese:
- Mandarin: 功能 (zh) (gōngnéng)
- Czech: funkce (cs) f
- Dutch: functie (nl) f
- Finnish: toiminta (fi)
- French: fonction (fr) f
- German: Funktion (de) f, Zweck (de) m
- Greek: λειτουργία (el) f (leitourgía)
- Hungarian: működés (hu), funkció (hu)
- Indonesian: fungsi (id), faal (id)
- Irish: feidhm f
- Italian: funzione (it) f
- Japanese: 機能 (ja) (きのう, kinō)
- Korean: 기능(機能) (ko) (gineung)
- Latvian: funkcija f
- Lithuanian: funkcija (lt) f
- Macedonian: функција f (funkcija)
- Norwegian:
- Bokmål: funksjon (no) m
- Portuguese: função (pt) f
- Russian: фу́нкция (ru) f (fúnkcija)
- Serbo-Croatian:
- Cyrillic: фу̀нкција f
- Roman: fùnkcija (sh) f
- Slovak: funkcia f
- Slovene: funkcija f
- Spanish: función (es) f
- Swedish: funktion (sv) c
- Tagalog: taan
- Turkish: fonksiyon (tr), işlev (tr)
- Ukrainian: фу́нкція f (fúnkcija)
References[edit]
function on Wikipedia.Wikipedia
Verb[edit]
function (third-person singular simple present functions, present participle functioning, simple past and past participle functioned)
- (intransitive) To have a function.
- Synonyms: officiate, serve
- (intransitive) To carry out a function; to be in action.
- Synonyms: go, operate, run, work
- Antonym: malfunction
[edit]
- functional
- dysfunction, dysfunctional
Translations[edit]
to have a function
- Czech: fungovat (cs) impf
- Danish: fungere
- Dutch: fungeren (nl), dienen (nl)
- Finnish: toimia (fi)
- Galician: funcionar (gl)
- German: fungieren (de)
- Greek: λειτουργώ ως (leitourgó os)
- Hebrew: תפקד (tifkéd)
- Hungarian: -ra/-re való, -ra/-re szolgál
- Irish: feidhmigh
- Italian: funzionare (it), fungere
- Japanese: 作用する (ja) (さよする, sadō suru), 動く (ja) (うごく, ugoku)
- Portuguese: funcionar (pt)
- Russian: функциони́ровать (ru) impf (funkcionírovatʹ)
- Spanish: fungir (es), servir (es)
- Swedish: fungera (sv), tjänstgöra (sv), verka (sv)
to carry on a function
- Armenian: գործել (hy) (gorcel), աշխատել (hy) (ašxatel), բանել (hy) (banel)
- Belarusian: функцыянава́ць impf (funkcyjanavácʹ), функцыяні́раваць impf (funkcyjaníravacʹ)
- Bulgarian: функциони́рам (bg) impf or pf (funkcioníram)
- Chinese:
- Mandarin: 工作 (zh) (gōngzuò), 運行/运行 (zh) (yùnxíng), 運轉/运转 (zh) (yùnzhuǎn)
- Catalan: funcionar (ca)
- Czech: fungovat (cs) impf
- Danish: fungere, virke
- Dutch: functioneren (nl)
- Esperanto: funkcii
- Finnish: käydä (fi), olla käynnissä, toimia (fi)
- French: fonctionner (fr), marcher (fr)
- Galician: funcionar (gl)
- Georgian: მოქმედებს (mokmedebs), მუშაობს (ka) (mušaobs), ფუნქციონირებს (punkcionirebs)
- German: funktionieren (de), arbeiten (de), wirken (de), (slang) funzen (de)
- Greek: λειτουργώ (el) (leitourgó), εργάζομαι (el) (ergázomai)
- Hebrew: תפקד (tifkéd), פעל (he) (pa’ál)
- Hungarian: működik (hu)
- Irish: feidhmigh
- Italian: funzionare (it)
- Japanese: 作動する (ja) (さどうする, sadō suru), 機能する (ja) (きのうする, kinō suru), 作用する (ja) (さようする, sayō suru), 動く (ja) (うごく, ugoku)
- Korean: 작동하다 (ko) (jakdonghada), 작용하다 (ko) (jagyonghada)
- Macedonian: функциони́ра impf or pf (funkcioníra)
- Malay: berfungsi
- Nepali: चल्नु (ne) (calnu)
- Norman: marchi
- Polish: działać (pl) impf, funkcjonować (pl) impf
- Portuguese: funcionar (pt)
- Quechua: llamk’ay
- Romanian: funcționa (ro)
- Russian: функциони́ровать (ru) impf (funkcionírovatʹ), рабо́тать (ru) impf (rabótatʹ), идти́ (ru) impf (idtí) (clock, watch)
- Slovak: fungovať impf
- Slovene: delovati impf
- Spanish: funcionar (es), fungir (es), marchar (es)
- Swedish: fungera (sv), tjänstgöra (sv)
- Ukrainian: функціонува́ти impf (funkcionuváty)
- Vietnamese: please add this translation if you can
Middle French[edit]
Noun[edit]
function f (plural functions)
- function (what something’s intended use is)
Descendants[edit]
- → English: function
- French: fonction
Thus, in Church’s proposal, the words ˜recursive function of positive integers™ can be replaced by the words ˜function of positive integers computable by Turing machine™. ❋ Copeland, B. Jack (2002)
My thesis now is this: that, when we think of the law that thought is a function of the brain, we are not required to think of productive function only; _we are entitled also to consider permissive or transmissive function_. ❋ J. H. Gardiner (N/A)
The last function A, called the _altitude function_, will be explained when high angle fire is considered. ❋ Various (N/A)
Symbols are used to mark locations of addresses, such as addresses of data or addresses of function pointers .. globl tells the assembler that it shouldnt get rid of the symbol after assembly because the linker needs it. main is the symbol where the program starts.. type main, @function main’s type is a function. main: ❋ Unknown (2009)
For example is there such a thing as a destructor [function () ~function ()] in PHP5 and is it needed? ❋ Unknown (2009)
Face Recognition AF&AE function that improves portrait photography The Optio A40 is equipped with a Face Recognition AF&AE function* that automatically detects and focuses on faces. ❋ Unknown (2008)
as children with ADD get older the pediatric reversal effect fades and instead of finding it easier to function the same drug which worked as a child will have a reverse effect ‘normal’ effect as an adult making it harder for them to function* ❋ Unknown (2010)
$expected must be a well-formed block of HTML. capture (&function, …) — > ($text, $result) Invokes a function while grabbing stdout, so the «http response» doesn’t flood the console that you’re running the unit test from, and you can analyse the result in your test function. ❋ Unknown (2009)
There is also a function called config () for accessing our main config. php file. class Loader function controller ($controller, $function = NULL) if (! file_exists (APPPATH. ‘controllers / ‘. $controller. ❋ Unknown (2009)
AskApache_Net:: _build_sock () * / function _build_sock ($url) {$this — > msg (__function__. ❋ Unknown (2009)
AskApache_Net:: _build_auth_header () * / function _build_auth_header () {$this — > msg (__function__. ❋ Unknown (2009)
The Alliance main function is the hatered of America and the desturction of America along with the extermination of Jews here in America and around the World. ❋ Unknown (2010)
Irony, like all higher brain function, is just far too complex for your worthless substandard brains ❋ Unknown (2010)
You are so stupid higher brain function is something that will never happen for you. ❋ Unknown (2010)
Any form or higher brain function is just too much for poor Timmehs limited faculties ❋ Unknown (2010)
I hate the idea of having shoes whose main function is to look decorative or uniform. ❋ Unknown (2010)
As brain function is altered, the mind will not necessarily be altered ❋ Unknown (2008)
Functional sweets: main function is keeping taste buds occupied ❋ Unknown (2008)
Moreover protein function is not analogous to the coding function of nucleic acids except by grotesque distortion of reality. ❋ Unknown (2006)
Protein function is too sequence dependent to toss off with meteor references. ❋ Unknown (2006)
Me and da [niggas] [goin] to a function over on [Northgate]. ❋ Nutty NIGGA FRom Da NORF (2006)
that function [last night] was [crazy]! ❋ Brackinkidd (2009)
1. [The programmer] made a function to [display] [text]. ❋ Master Quark (2005)
[Julie] is a [TKE] function — she [slept] with both Joe and Steve. ❋ Lauren/tree (2005)
[OMfg] he is a function [with that] [thing] ❋ John (2003)
Did you see him at [the function] last night? [The boy] was [giggin’]. ❋ Grace M For Composition Class (2019)
Huge party last night girl! I did not think you would be in to work today. Say, why is your underwear overtop of your [coat]? And are those [cereal boxes] [on your feet]? You sure you are functional? ❋ Gnostic3 (2018)
Person 1: You going to the [function] tomorrow?
Person 2: [Nawh], my girl don’t like it when I go to functions, she [don’t trust me]. ❋ SExSD (2011)
This functionality will help you [overcome] the opportunity presented by your [synergistic] [paradigm]. ❋ Teej (2003)
[Wow] that [purse] is very functionable ❋ CJOII (2010)
From Simple English Wikipedia, the free encyclopedia
Function may mean:
- professional or official position: Official
- Function (mathematics), the relationship between two or more amounts using algebra
- Computable function in software programming languages
- Function (biology) explains the way a part works in an organism
- Function (philosophy), in philosophy, a relation of objects or events to their use or consequences
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y.[1] The set X is called the domain of the function[2] and the set Y is called the codomain of the function.[3][better source needed]
Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly enlarged the domains of application of the concept.
A function is most often denoted by letters such as f, g and h, and the value of a function f at an element x of its domain is denoted by f(x); the numerical value resulting from the function evaluation at a particular input value is denoted by replacing x with this value; for example, the value of f at x = 4 is denoted by f(4). When the function is not named and is represented by an expression E, the value of the function at, say, x = 4 may be denoted by E|x=4. For example, the value at 4 of the function that maps x to 

A function is uniquely represented by the set of all pairs (x, f (x)), called the graph of the function, a popular means of illustrating the function.[note 1][4] When the domain and the codomain are sets of real numbers, each such pair may be thought of as the Cartesian coordinates of a point in the plane.
Functions are widely used in science, engineering, and in most fields of mathematics. It has been said that functions are «the central objects of investigation» in most fields of mathematics.[5]
Schematic depiction of a function described metaphorically as a «machine» or «black box» that for each input yields a corresponding output
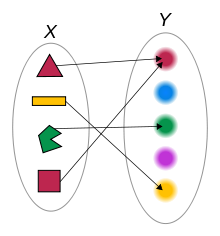
A function that associates any of the four colored shapes to its color.
Definition[edit]
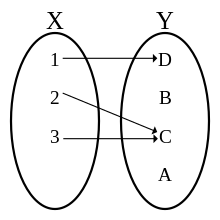
Diagram of a function, with domain X = {1, 2, 3} and codomain Y = {A, B, C, D}, which is defined by the set of ordered pairs {(1, D), (2, C), (3, C)} . The image/range is the set {C, D} .
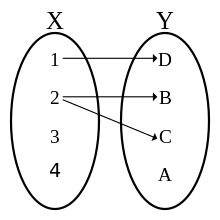
This diagram, representing the set of pairs {(1,D), (2,B), (2,C)} , does not define a function. One reason is that 2 is the first element in more than one ordered pair, (2, B) and (2, C), of this set. Two other reasons, also sufficient by themselves, is that neither 3 nor 4 are first elements (input) of any ordered pair therein.
A function from a set X to a set Y is an assignment of an element of Y to each element of X. The set X is called the domain of the function and the set Y is called the codomain of the function.
A function, its domain, and its codomain, are declared by the notation f: X→Y, and the value of a function f at an element x of X, denoted by f(x), is called the image of x under f, or the value of f applied to the argument x.
Functions are also called maps or mappings, though some authors make some distinction between «maps» and «functions» (see § Other terms).
Two functions f and g are equal if their domain and codomain sets are the same and their output values agree on the whole domain. More formally, given f: X → Y and g: X → Y, we have f = g if and only if f(x) = g(x) for all x ∈ X.[citation needed][note 2]
The domain and codomain are not always explicitly given when a function is defined, and, without some (possibly difficult) computation, one might only know that the domain is contained in a larger set. Typically, this occurs in mathematical analysis, where «a function from X to Y « often refers to a function that may have a proper subset[note 3] of X as domain. For example, a «function from the reals to the reals» may refer to a real-valued function of a real variable. However, a «function from the reals to the reals» does not mean that the domain of the function is the whole set of the real numbers, but only that the domain is a set of real numbers that contains a non-empty open interval. Such a function is then called a partial function. For example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1/f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0.
The range or image of a function is the set of the images of all elements in the domain.[6][7][8][9]
Total, univalent relation[edit]
Any subset of the Cartesian product of two sets X and Y defines a binary relation R ⊆ X × Y between these two sets. It is immediate that an arbitrary relation may contain pairs that violate the necessary conditions for a function given above.
A binary relation is univalent (also called right-unique) if
A binary relation is total if
A partial function is a binary relation that is univalent, and a function is a binary relation that is univalent and total.
Various properties of functions and function composition may be reformulated in the language of relations.[10] For example, a function is injective if the converse relation RT ⊆ Y × X is univalent, where the converse relation is defined as RT = {(y, x) | (x, y) ∈ R}.
Set exponentiation[edit]
The set of all functions from a set 

which is read as 

This notation is the same as the notation for the Cartesian product of a family of copies of 

The identity of these two notations is motivated by the fact that a function 


When 








Notation[edit]
There are various standard ways for denoting functions. The most commonly used notation is functional notation, which is the first notation described below.
Functional notation[edit]
In functional notation, the function is immediately given a name, such as f, and its definition is given by what f does to the explicit argument x, using a formula in terms of x. For example, the function which takes a real number as input and outputs that number plus 1 is denoted by
.
If a function is defined in this notation, its domain and codomain are implicitly taken to both be 

A more complicated example is the function
.
In this example, the function f takes a real number as input, squares it, then adds 1 to the result, then takes the sine of the result, and returns the final result as the output.
When the symbol denoting the function consists of several characters and no ambiguity may arise, the parentheses of functional notation might be omitted. For example, it is common to write sin x instead of sin(x).
Functional notation was first used by Leonhard Euler in 1734.[11] Some widely used functions are represented by a symbol consisting of several letters (usually two or three, generally an abbreviation of their name). In this case, a roman type is customarily used instead, such as «sin» for the sine function, in contrast to italic font for single-letter symbols.
When using this notation, one often encounters the abuse of notation whereby the notation f(x) can refer to the value of f at x, or to the function itself. If the variable x was previously declared, then the notation f(x) unambiguously means the value of f at x. Otherwise, it is useful to understand the notation as being both simultaneously; this allows one to denote composition of two functions f and g in a succinct manner by the notation f(g(x)).
However, distinguishing f and f(x) can become important in cases where functions themselves serve as inputs for other functions. (A function taking another function as an input is termed a functional.) Other approaches of notating functions, detailed below, avoid this problem but are less commonly used.
Arrow notation[edit]
Arrow notation defines the rule of a function inline, without requiring a name to be given to the function. For example, 

The domain and codomain can also be explicitly stated, for example:
This defines a function sqr from the integers to the integers that returns the square of its input.
As a common application of the arrow notation, suppose 



Index notation[edit]
Index notation is often used instead of functional notation. That is, instead of writing f (x), one writes 
This is typically the case for functions whose domain is the set of the natural numbers. Such a function is called a sequence, and, in this case the element 
The index notation is also often used for distinguishing some variables called parameters from the «true variables». In fact, parameters are specific variables that are considered as being fixed during the study of a problem. For example, the map 




Dot notation[edit]
In the notation
the symbol x does not represent any value, it is simply a placeholder meaning that, if x is replaced by any value on the left of the arrow, it should be replaced by the same value on the right of the arrow. Therefore, x may be replaced by any symbol, often an interpunct « ⋅ «. This may be useful for distinguishing the function f (⋅) from its value f (x) at x.
For example, 



Specialized notations[edit]
There are other, specialized notations for functions in sub-disciplines of mathematics. For example, in linear algebra and functional analysis, linear forms and the vectors they act upon are denoted using a dual pair to show the underlying duality. This is similar to the use of bra–ket notation in quantum mechanics. In logic and the theory of computation, the function notation of lambda calculus is used to explicitly express the basic notions of function abstraction and application. In category theory and homological algebra, networks of functions are described in terms of how they and their compositions commute with each other using commutative diagrams that extend and generalize the arrow notation for functions described above.
Other terms[edit]
| Term | Distinction from «function» |
|---|---|
| Map/Mapping | None; the terms are synonymous.[12] |
| A map can have any set as its codomain, while, in some contexts, typically in older books, the codomain of a function is specifically the set of real or complex numbers.[13] | |
| Alternatively, a map is associated with a special structure (e.g. by explicitly specifying a structured codomain in its definition). For example, a linear map.[14] | |
| Homomorphism | A function between two structures of the same type that preserves the operations of the structure (e.g. a group homomorphism).[15] |
| Morphism | A generalisation of homomorphisms to any category, even when the objects of the category are not sets (for example, a group defines a category with only one object, which has the elements of the group as morphisms; see Category (mathematics) § Examples for this example and other similar ones).[16] |
A function is often also called a map or a mapping, but some authors make a distinction between the term «map» and «function». For example, the term «map» is often reserved for a «function» with some sort of special structure (e.g. maps of manifolds). In particular map is often used in place of homomorphism for the sake of succinctness (e.g., linear map or map from G to H instead of group homomorphism from G to H). Some authors[14] reserve the word mapping for the case where the structure of the codomain belongs explicitly to the definition of the function.
Some authors, such as Serge Lang,[13] use «function» only to refer to maps for which the codomain is a subset of the real or complex numbers, and use the term mapping for more general functions.
In the theory of dynamical systems, a map denotes an evolution function used to create discrete dynamical systems. See also Poincaré map.
Whichever definition of map is used, related terms like domain, codomain, injective, continuous have the same meaning as for a function.
Specifying a function[edit]
Given a function 








By listing function values[edit]
On a finite set, a function may be defined by listing the elements of the codomain that are associated to the elements of the domain. For example, if 


By a formula[edit]
Functions are often defined by a formula that describes a combination of arithmetic operations and previously defined functions; such a formula allows computing the value of the function from the value of any element of the domain.
For example, in the above example, 


When a function is defined this way, the determination of its domain is sometimes difficult. If the formula that defines the function contains divisions, the values of the variable for which a denominator is zero must be excluded from the domain; thus, for a complicated function, the determination of the domain passes through the computation of the zeros of auxiliary functions. Similarly, if square roots occur in the definition of a function from 

For example, 




Functions are often classified by the nature of formulas that define them:
- A quadratic function is a function that may be written
where a, b, c are constants.
- More generally, a polynomial function is a function that can be defined by a formula involving only additions, subtractions, multiplications, and exponentiation to nonnegative integers. For example,
and
- A rational function is the same, with divisions also allowed, such as
and
- An algebraic function is the same, with nth roots and roots of polynomials also allowed.
- An elementary function[note 4] is the same, with logarithms and exponential functions allowed.
Inverse and implicit functions[edit]
A function 



If a function 


More generally, given a binary relation R between two sets X and Y, let E be a subset of X such that, for every 



For example, the equation of the unit circle 
In this example, the equation can be solved in y, giving 


The implicit function theorem provides mild differentiability conditions for existence and uniqueness of an implicit function in the neighborhood of a point.
Using differential calculus[edit]
Many functions can be defined as the antiderivative of another function. This is the case of the natural logarithm, which is the antiderivative of 1/x that is 0 for x = 1. Another common example is the error function.
More generally, many functions, including most special functions, can be defined as solutions of differential equations. The simplest example is probably the exponential function, which can be defined as the unique function that is equal to its derivative and takes the value 1 for x = 0.
Power series can be used to define functions on the domain in which they converge. For example, the exponential function is given by 
By recurrence[edit]
Functions whose domain are the nonnegative integers, known as sequences, are often defined by recurrence relations.
The factorial function on the nonnegative integers (
and the initial condition
Representing a function[edit]
A graph is commonly used to give an intuitive picture of a function. As an example of how a graph helps to understand a function, it is easy to see from its graph whether a function is increasing or decreasing. Some functions may also be represented by bar charts.
Graphs and plots[edit]
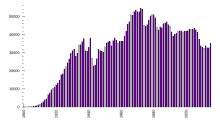
The function mapping each year to its US motor vehicle death count, shown as a line chart
The same function, shown as a bar chart
Given a function 
In the frequent case where X and Y are subsets of the real numbers (or may be identified with such subsets, e.g. intervals), an element 
consisting of all points with coordinates 



Tables[edit]
A function can be represented as a table of values. If the domain of a function is finite, then the function can be completely specified in this way. For example, the multiplication function 

|
y x |
1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 6 | 8 | 10 |
| 3 | 3 | 6 | 9 | 12 | 15 |
| 4 | 4 | 8 | 12 | 16 | 20 |
| 5 | 5 | 10 | 15 | 20 | 25 |
On the other hand, if a function’s domain is continuous, a table can give the values of the function at specific values of the domain. If an intermediate value is needed, interpolation can be used to estimate the value of the function. For example, a portion of a table for the sine function might be given as follows, with values rounded to 6 decimal places:
| x | sin x |
|---|---|
| 1.289 | 0.960557 |
| 1.290 | 0.960835 |
| 1.291 | 0.961112 |
| 1.292 | 0.961387 |
| 1.293 | 0.961662 |
Before the advent of handheld calculators and personal computers, such tables were often compiled and published for functions such as logarithms and trigonometric functions.
Bar chart[edit]
Bar charts are often used for representing functions whose domain is a finite set, the natural numbers, or the integers. In this case, an element x of the domain is represented by an interval of the x-axis, and the corresponding value of the function, f(x), is represented by a rectangle whose base is the interval corresponding to x and whose height is f(x) (possibly negative, in which case the bar extends below the x-axis).
General properties[edit]
This section describes general properties of functions, that are independent of specific properties of the domain and the codomain.
Standard functions[edit]
There are a number of standard functions that occur frequently:
- For every set X, there is a unique function, called the empty function, or empty map, from the empty set to X. The graph of an empty function is the empty set.[note 5] The existence of empty functions is needed both for the coherency of the theory and for avoiding exceptions concerning the empty set in many statements. Under the usual set-theoretic definition of a function as an ordered triplet (or equivalent ones), there is exactly one empty function for each set, thus the empty function
is not equal to
if and only if
, although their graph are both the empty set.
- For every set X and every singleton set {s}, there is a unique function from X to {s}, which maps every element of X to s. This is a surjection (see below) unless X is the empty set.
- Given a function
the canonical surjection of f onto its image
is the function from X to f(X) that maps x to f(x).
- For every subset A of a set X, the inclusion map of A into X is the injective (see below) function that maps every element of A to itself.
- The identity function on a set X, often denoted by idX, is the inclusion of X into itself.
Function composition[edit]
Given two functions 


That is, the value of 
The composition 







The function composition is associative in the sense that, if one of 

The identity functions 


-
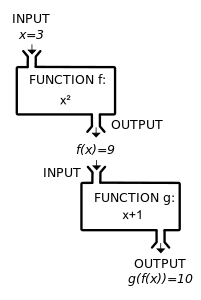
A composite function g(f(x)) can be visualized as the combination of two «machines».
-
A simple example of a function composition
-
Another composition. In this example, (g ∘ f )(c) = #.
Image and preimage[edit]
Let 
The image of f is the image of the whole domain, that is, f(X).[17] It is also called the range of f,[6][7][8][9] although the term range may also refer to the codomain.[9][17][18]
On the other hand, the inverse image or preimage under f of an element y of the codomain Y is the set of all elements of the domain X whose images under f equal y.[6] In symbols, the preimage of y is denoted by 
Likewise, the preimage of a subset B of the codomain Y is the set of the preimages of the elements of B, that is, it is the subset of the domain X consisting of all elements of X whose images belong to B.[6] It is denoted by 
For example, the preimage of 

By definition of a function, the image of an element x of the domain is always a single element of the codomain. However, the preimage 

If 
The preimage by f of an element y of the codomain is sometimes called, in some contexts, the fiber of y under f.
If a function f has an inverse (see below), this inverse is denoted 





![{displaystyle f[A],f^{-1}[C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d728b72b3681c1a33529ac867bc49952dc812a4)
Injective, surjective and bijective functions[edit]
Let 
The function f is injective (or one-to-one, or is an injection) if f(a) ≠ f(b) for any two different elements a and b of X.[17][19] Equivalently, f is injective if and only if, for any 












The function f is surjective (or onto, or is a surjection) if its range 











The function f is bijective (or is a bijection or a one-to-one correspondence) if it is both injective and surjective.[17][21] That is, f is bijective if, for any 




Every function 

«One-to-one» and «onto» are terms that were more common in the older English language literature; «injective», «surjective», and «bijective» were originally coined as French words in the second quarter of the 20th century by the Bourbaki group and imported into English.[citation needed] As a word of caution, «a one-to-one function» is one that is injective, while a «one-to-one correspondence» refers to a bijective function. Also, the statement «f maps X onto Y» differs from «f maps X into B«, in that the former implies that f is surjective, while the latter makes no assertion about the nature of f. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage of being more symmetrical.
Restriction and extension[edit]
If 


for all x in S. Restrictions can be used to define partial inverse functions: if there is a subset S of the domain of a function 




Function restriction may also be used for «gluing» functions together. Let 








An extension of a function f is a function g such that f is a restriction of g. A typical use of this concept is the process of analytic continuation, that allows extending functions whose domain is a small part of the complex plane to functions whose domain is almost the whole complex plane.
Here is another classical example of a function extension that is encountered when studying homographies of the real line. A homography is a function 




Multivariate function [edit]
A binary operation is a typical example of a bivariate function which assigns to each pair 

A multivariate function, or function of several variables is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time travelled and its average speed.
More formally, a function of n variables is a function whose domain is a set of n-tuples.
For example, multiplication of integers is a function of two variables, or bivariate function, whose domain is the set of all pairs (2-tuples) of integers, and whose codomain is the set of integers. The same is true for every binary operation. More generally, every mathematical operation is defined as a multivariate function.
The Cartesian product 




where the domain U has the form
When using function notation, one usually omits the parentheses surrounding tuples, writing 

In the case where all the 



It is common to also consider functions whose codomain is a product of sets. For example, Euclidean division maps every pair (a, b) of integers with b ≠ 0 to a pair of integers called the quotient and the remainder:
The codomain may also be a vector space. In this case, one talks of a vector-valued function. If the domain is contained in a Euclidean space, or more generally a manifold, a vector-valued function is often called a vector field.
In calculus[edit]
The idea of function, starting in the 17th century, was fundamental to the new infinitesimal calculus. At that time, only real-valued functions of a real variable were considered, and all functions were assumed to be smooth. But the definition was soon extended to functions of several variables and to functions of a complex variable. In the second half of the 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined.
Functions are now used throughout all areas of mathematics. In introductory calculus, when the word function is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with STEM majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as real analysis and complex analysis.
Real function[edit]
Graph of a linear function
Graph of a polynomial function, here a quadratic function.
Graph of two trigonometric functions: sine and cosine.
A real function is a real-valued function of a real variable, that is, a function whose codomain is the field of real numbers and whose domain is a set of real numbers that contains an interval. In this section, these functions are simply called functions.
The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are continuous, differentiable, and even analytic. This regularity insures that these functions can be visualized by their graphs. In this section, all functions are differentiable in some interval.
Functions enjoy pointwise operations, that is, if f and g are functions, their sum, difference and product are functions defined by
The domains of the resulting functions are the intersection of the domains of f and g. The quotient of two functions is defined similarly by
but the domain of the resulting function is obtained by removing the zeros of g from the intersection of the domains of f and g.
The polynomial functions are defined by polynomials, and their domain is the whole set of real numbers. They include constant functions, linear functions and quadratic functions. Rational functions are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid division by zero. The simplest rational function is the function 
The derivative of a real differentiable function is a real function. An antiderivative of a continuous real function is a real function that has the original function as a derivative. For example, the function 
A real function f is monotonic in an interval if the sign of 
Many other real functions are defined either by the implicit function theorem (the inverse function is a particular instance) or as solutions of differential equations. For example, the sine and the cosine functions are the solutions of the linear differential equation
such that
Vector-valued function[edit]
When the elements of the codomain of a function are vectors, the function is said to be a vector-valued function. These functions are particularly useful in applications, for example modeling physical properties. For example, the function that associates to each point of a fluid its velocity vector is a vector-valued function.
Some vector-valued functions are defined on a subset of 

Function space[edit]
In mathematical analysis, and more specifically in functional analysis, a function space is a set of scalar-valued or vector-valued functions, which share a specific property and form a topological vector space. For example, the real smooth functions with a compact support (that is, they are zero outside some compact set) form a function space that is at the basis of the theory of distributions.
Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and topological properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of ordinary or partial differential equations result of the study of function spaces.
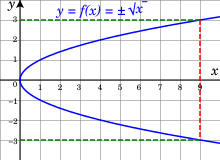
Multi-valued functions[edit]
Together, the two square roots of all nonnegative real numbers form a single smooth curve.
Several methods for specifying functions of real or complex variables start from a local definition of the function at a point or on a neighbourhood of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point 
For example, in defining the square root as the inverse function of the square function, for any positive real number 


In the preceding example, one choice, the positive square root, is more natural than the other. This is not the case in general. For example, let consider the implicit function that maps y to a root x of 

Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically analytic functions. The domain to which a complex function may be extended by analytic continuation generally consists of almost the whole complex plane. However, when extending the domain through two different paths, one often gets different values. For example, when extending the domain of the square root function, along a path of complex numbers with positive imaginary parts, one gets i for the square root of −1; while, when extending through complex numbers with negative imaginary parts, one gets −i. There are generally two ways of solving the problem. One may define a function that is not continuous along some curve, called a branch cut. Such a function is called the principal value of the function. The other way is to consider that one has a multi-valued function, which is analytic everywhere except for isolated singularities, but whose value may «jump» if one follows a closed loop around a singularity. This jump is called the monodromy.
In the foundations of mathematics and set theory[edit]
The definition of a function that is given in this article requires the concept of set, since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is generally not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions.
For example, the singleton set may be considered as a function 
These generalized functions may be critical in the development of a formalization of the foundations of mathematics. For example, Von Neumann–Bernays–Gödel set theory, is an extension of the set theory in which the collection of all sets is a class. This theory includes the replacement axiom, which may be stated as: If X is a set and F is a function, then F[X] is a set.
In computer science[edit]
In computer programming, a function is, in general, a piece of a computer program, which implements the abstract concept of function. That is, it is a program unit that produces an output for each input. However, in many programming languages every subroutine is called a function, even when there is no output, and when the functionality consists simply of modifying some data in the computer memory.
Functional programming is the programming paradigm consisting of building programs by using only subroutines that behave like mathematical functions. For example, if_then_else is a function that takes three functions as arguments, and, depending on the result of the first function (true or false), returns the result of either the second or the third function. An important advantage of functional programming is that it makes easier program proofs, as being based on a well founded theory, the lambda calculus (see below).
Except for computer-language terminology, «function» has the usual mathematical meaning in computer science. In this area, a property of major interest is the computability of a function. For giving a precise meaning to this concept, and to the related concept of algorithm, several models of computation have been introduced, the old ones being general recursive functions, lambda calculus and Turing machine. The fundamental theorem of computability theory is that these three models of computation define the same set of computable functions, and that all the other models of computation that have ever been proposed define the same set of computable functions or a smaller one. The Church–Turing thesis is the claim that every philosophically acceptable definition of a computable function defines also the same functions.
General recursive functions are partial functions from integers to integers that can be defined from
- constant functions,
- successor, and
- projection functions
via the operators
- composition,
- primitive recursion, and
- minimization.
Although defined only for functions from integers to integers, they can model any computable function as a consequence of the following properties:
- a computation is the manipulation of finite sequences of symbols (digits of numbers, formulas, …),
- every sequence of symbols may be coded as a sequence of bits,
- a bit sequence can be interpreted as the binary representation of an integer.
Lambda calculus is a theory that defines computable functions without using set theory, and is the theoretical background of functional programming. It consists of terms that are either variables, function definitions (𝜆-terms), or applications of functions to terms. Terms are manipulated through some rules, (the α-equivalence, the β-reduction, and the η-conversion), which are the axioms of the theory and may be interpreted as rules of computation.
In its original form, lambda calculus does not include the concepts of domain and codomain of a function. Roughly speaking, they have been introduced in the theory under the name of type in typed lambda calculus. Most kinds of typed lambda calculi can define fewer functions than untyped lambda calculus.
See also[edit]
Subpages[edit]
- List of types of functions
- List of functions
- Function fitting
- Implicit function
Generalizations[edit]
- Higher-order function
- Homomorphism
- Morphism
- Microfunction
- Distribution
- Functor
[edit]
- Associative array
- Closed-form expression
- Elementary function
- Functional
- Functional decomposition
- Functional predicate
- Functional programming
- Parametric equation
- Set function
- Simple function
Notes[edit]
- ^ This definition of «graph» refers to a set of pairs of objects. Graphs, in the sense of diagrams, are most applicable to functions from the real numbers to themselves. All functions can be described by sets of pairs but it may not be practical to construct a diagram for functions between other sets (such as sets of matrices).
- ^ This follows from the axiom of extensionality, which says two sets are the same if and only if they have the same members. Some authors drop codomain from a definition of a function, and in that definition, the notion of equality has to be handled with care; see, for example, «When do two functions become equal?». Stack Exchange. August 19, 2015.
- ^ called the domain of definition by some authors, notably computer science
- ^ Here «elementary» has not exactly its common sense: although most functions that are encountered in elementary courses of mathematics are elementary in this sense, some elementary functions are not elementary for the common sense, for example, those that involve roots of polynomials of high degree.
- ^ By definition, the graph of the empty function to X is a subset of the Cartesian product ∅ × X, and this product is empty.
- ^ The axiom of choice is not needed here, as the choice is done in a single set.
References[edit]
- ^ Halmos 1970, p. 30; the words map, mapping, transformation, correspondence, and operator are often used synonymously.
- ^ Halmos 1970
- ^ «Mapping», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ^ «function | Definition, Types, Examples, & Facts». Encyclopedia Britannica. Retrieved 2020-08-17.
- ^ Spivak 2008, p. 39.
- ^ a b c d e f Kudryavtsev, L.D. (2001) [1994], «Function», Encyclopedia of Mathematics, EMS Press
- ^ a b Taalman, Laura; Kohn, Peter (2014). Calculus. New York City: W. H. Freeman and Company. p. 3. ISBN 978-1-4292-4186-1. LCCN 2012947365. OCLC 856545590. OL 27544563M.
- ^ a b Trench, William F. (2013) [2003]. Introduction to Real Analysis (2.04th ed.). Pearson Education (originally; self-republished by the author). pp. 30–32. ISBN 0-13-045786-8. LCCN 2002032369. OCLC 953799815. Zbl 1204.00023.
- ^ a b c Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Elementary Real Analysis (PDF) (2nd ed.). Prentice Hall (originally; 2nd ed. self-republished by the authors). pp. A-4–A-5. ISBN 978-1-4348-4367-8. OCLC 1105855173. OL 31844948M. Zbl 0872.26001.
- ^ Schmidt, Gunther (2011). «§5.1 Functions». Relational Mathematics. Encyclopedia of Mathematics and its Applications. Vol. 132. Cambridge University Press. pp. 49–60. ISBN 978-0-521-76268-7.
- ^ Ron Larson, Bruce H. Edwards (2010), Calculus of a Single Variable, Cengage Learning, p. 19, ISBN 978-0-538-73552-0
- ^ Weisstein, Eric W. «Map». mathworld.wolfram.com. Retrieved 2019-06-12.
- ^ a b Lang, Serge (1987). «III §1. Mappings». Linear Algebra (3rd ed.). Springer. p. 43. ISBN 978-0-387-96412-6.
A function is a special type of mapping, namely it is a mapping from a set into the set of numbers, i.e. into, R, or C or into a field K.
- ^ a b Apostol, T.M. (1981). Mathematical Analysis (2nd ed.). Addison-Wesley. p. 35. ISBN 978-0-201-00288-1. OCLC 928947543.
- ^ James, Robert C.; James, Glenn (1992). Mathematics dictionary (5th ed.). Van Nostrand Reinhold. p. 202. ISBN 0-442-00741-8. OCLC 25409557.
- ^ James & James 1992, p. 48
- ^ a b c d e Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2008). The Princeton Companion to Mathematics. Princeton, New Jersey: Princeton University Press. p. 11. doi:10.1515/9781400830398. ISBN 978-0-691-11880-2. JSTOR j.ctt7sd01. LCCN 2008020450. MR 2467561. OCLC 227205932. OL 19327100M. Zbl 1242.00016.
- ^ Quantities and Units — Part 2: Mathematical signs and symbols to be used in the natural sciences and technology, p. 15. ISO 80000-2 (ISO/IEC 2009-12-01)
- ^ a b Ivanova, O.A. (2001) [1994], «Injection», Encyclopedia of Mathematics, EMS Press
- ^ a b Ivanova, O.A. (2001) [1994], «Surjection», Encyclopedia of Mathematics, EMS Press
- ^ a b Ivanova, O.A. (2001) [1994], «Bijection», Encyclopedia of Mathematics, EMS Press
- ^ Gödel 1940, p. 16; Jech 2003, p. 11; Cunningham 2016, p. 57
Sources[edit]
- Bartle, Robert (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05465-8. OCLC 465115030.
- Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. ISBN 978-1-4419-7126-5.
- Cunningham, Daniel W. (2016). Set theory: A First Course. Cambridge University Press. ISBN 978-1-107-12032-7.
- Gödel, Kurt (1940). The Consistency of the Continuum Hypothesis. Princeton University Press. ISBN 978-0-691-07927-1.
- Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 978-0-387-90092-6.
- Jech, Thomas (2003). Set theory (3rd ed.). Springer-Verlag. ISBN 978-3-540-44085-7.
- Spivak, Michael (2008). Calculus (4th ed.). Publish or Perish. ISBN 978-0-914098-91-1.
Further reading[edit]
- Anton, Howard (1980). Calculus with Analytical Geometry. Wiley. ISBN 978-0-471-03248-9.
- Bartle, Robert G. (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05464-1.
- Dubinsky, Ed; Harel, Guershon (1992). The Concept of Function: Aspects of Epistemology and Pedagogy. Mathematical Association of America. ISBN 978-0-88385-081-7.
- Hammack, Richard (2009). «12. Functions» (PDF). Book of Proof. Virginia Commonwealth University. Retrieved 2012-08-01.
- Husch, Lawrence S. (2001). Visual Calculus. University of Tennessee. Retrieved 2007-09-27.
- Katz, Robert (1964). Axiomatic Analysis. D. C. Heath and Company.
- Kleiner, Israel (1989). «Evolution of the Function Concept: A Brief Survey». The College Mathematics Journal. 20 (4): 282–300. CiteSeerX 10.1.1.113.6352. doi:10.2307/2686848. JSTOR 2686848.
- Lützen, Jesper (2003). «Between rigor and applications: Developments in the concept of function in mathematical analysis». In Porter, Roy (ed.). The Cambridge History of Science: The modern physical and mathematical sciences. Cambridge University Press. ISBN 978-0-521-57199-9. An approachable and diverting historical presentation.
- Malik, M. A. (1980). «Historical and pedagogical aspects of the definition of function». International Journal of Mathematical Education in Science and Technology. 11 (4): 489–492. doi:10.1080/0020739800110404.
- Reichenbach, Hans (1947). Elements of Symbolic Logic. Dover. ISBN 0-486-24004-5.
- Ruthing, D. (1984). «Old Intelligencer: Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N.». Mathematical Intelligencer. 6 (4): 71–78. doi:10.1007/BF03026743. S2CID 189883712.
- Thomas, George B.; Finney, Ross L. (1995). Calculus and Analytic Geometry (9th ed.). Addison-Wesley. ISBN 978-0-201-53174-9.
External links[edit]
- «Function», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- NIST Digital Library of Mathematical Functions
Other forms: functions; functioning; functioned
In the old «Schoolhouse Rock» song, «Conjunction junction, what’s your function?,» the word function means, «What does a conjunction do?» The famous design dictum «form follows function» tells us that an object’s design should reflect what it does.
Function is one of those words that gets used a lot and means lots of different things. It means what something does, but also what a person does, whether something or someone is doing what they should, and crazily enough, a big party. «Your function is to bring the senator coffee at the political function. He cannot function without it.»
Definitions of function
-
noun
what something is used for
“the
function of an auger is to bore holes”-
synonyms:
purpose, role, use
-
noun
the actions and activities assigned to or required or expected of a person or group
“the
function of a teacher”-
synonyms:
office, part, role
-
noun
the normal physiological activity or action of a body part or organ
-
verb
serve a purpose, role, or function
“The table
functions as a desk”-
synonyms:
serve
-
serve, service
be used by; as of a utility
-
serve, service
-
verb
perform as expected when applied
-
synonyms:
go, operate, run, work
-
run
be operating, running or functioning
-
work
operate in or through
-
run
-
verb
perform duties attached to a particular office or place or function
-
noun
a relation such that one thing is dependent on another
“height is a
function of age”“price is a
function of supply and demand” -
noun
(mathematics) a mathematical relation such that each element of a given set (the domain of the function) is associated with an element of another set (the range of the function)
-
synonyms:
map, mapping, mathematical function, single-valued function
see moresee less-
types:
- show 35 types…
- hide 35 types…
-
multinomial, polynomial
a mathematical function that is the sum of a number of terms
-
expansion
a function expressed as a sum or product of terms
-
inverse function
a function obtained by expressing the dependent variable of one function as the independent variable of another; f and g are inverse functions if f(x)=y and g(y)=x
-
Kronecker delta
a function of two variables i and j that equals 1 when i=j and equals 0 otherwise
-
metric, metric function
a function of a topological space that gives, for any two points in the space, a value equal to the distance between them
-
transformation
(mathematics) a function that changes the position or direction of the axes of a coordinate system
-
isometry
a one-to-one mapping of one metric space into another metric space that preserves the distances between each pair of points
-
operator
(mathematics) a symbol or function representing a mathematical operation
-
circular function, trigonometric function
function of an angle expressed as a ratio of the length of the sides of right-angled triangle containing the angle
-
threshold function
a function that takes the value 1 if a specified function of the arguments exceeds a given threshold and 0 otherwise
-
exponential, exponential function
a function in which an independent variable appears as an exponent
-
biquadratic, biquadratic polynomial, quartic polynomial
a polynomial of the fourth degree
-
homogeneous polynomial
a polynomial consisting of terms all of the same degree
-
monic polynomial
a polynomial in one variable
-
quadratic, quadratic polynomial
a polynomial of the second degree
-
series
(mathematics) the sum of a finite or infinite sequence of expressions
-
reflection
(mathematics) a transformation in which the direction of one axis is reversed
-
rotation
(mathematics) a transformation in which the coordinate axes are rotated by a fixed angle about the origin
-
translation
(mathematics) a transformation in which the origin of the coordinate system is moved to another position but the direction of each axis remains the same
-
affine transformation
(mathematics) a transformation that is a combination of single transformations such as translation or rotation or reflection on an axis
-
linear operator
an operator that obeys the distributive law: A(f+g) = Af + Ag (where f and g are functions)
-
identity, identity element, identity operator
an operator that leaves unchanged the element on which it operates
-
sin, sine
ratio of the length of the side opposite the given angle to the length of the hypotenuse of a right-angled triangle
-
arc sine, arcsin, arcsine, inverse sine
the inverse function of the sine; the angle that has a sine equal to a given number
-
cos, cosine
ratio of the adjacent side to the hypotenuse of a right-angled triangle
-
arc cosine, arccos, arccosine, inverse cosine
the inverse function of the cosine; the angle that has a cosine equal to a given number
-
tan, tangent
ratio of the opposite to the adjacent side of a right-angled triangle
-
arc tangent, arctan, arctangent, inverse tangent
the inverse function of the tangent; the angle that has a tangent equal to a given number
-
cotan, cotangent
ratio of the adjacent to the opposite side of a right-angled triangle
-
arc cotangent, arccotangent, inverse cotangent
the inverse function of the cotangent; the angle that has a cotangent equal to a given number
-
sec, secant
ratio of the hypotenuse to the adjacent side of a right-angled triangle
-
arc secant, arcsec, arcsecant, inverse secant
the inverse function of the secant; the angle that has a secant equal to a given number
-
cosec, cosecant
ratio of the hypotenuse to the opposite side of a right-angled triangle
-
arc cosecant, arccosecant, inverse cosecant
the angle that has a cosecant equal to a given number
-
dilation
(mathematics) a transformation that changes the size of a figure but not its shape
-
type of:
-
mathematical relation
a relation between mathematical expressions (such as equality or inequality)
-
noun
a formal or official social gathering or ceremony
“it was a black-tie
function” -
noun
a vaguely specified social event
“a seemingly endless round of social
functions”-
synonyms:
affair, occasion, social function, social occasion
see moresee less-
types:
- show 31 types…
- hide 31 types…
-
party
an occasion on which people can assemble for social interaction and entertainment
-
celebration, jubilation
a joyful occasion for special festivities to mark some happy event
-
ceremonial, ceremonial occasion, ceremony, observance
a formal event performed on a special occasion
-
fundraiser
a social function that is held for the purpose of raising money
-
photo op, photo opportunity
an occasion that lends itself to (or is deliberately arranged for) taking photographs that provide favorable publicity for those who are photographed
-
sleepover
an occasion of spending a night away from home or having a guest spend the night in your home (especially as a party for children)
-
bash, brawl, do
an uproarious party
-
birthday party
a party held on the anniversary of someone’s birth
-
bun-fight, bunfight
(Briticism) a grand formal party on an important occasion
-
ceilidh
an informal social gathering at which there is Scottish or Irish folk music and singing and folk dancing and story telling
-
cocktail party
an afternoon party at which cocktails are served
-
dance
a party for social dancing
-
feast, fete, fiesta
an elaborate party (often outdoors)
-
house party
a party lasting over one or more nights at a large house
-
jolly
a happy party
-
tea party
a party at which tea is served
-
whist drive
a progressive whist party
-
circumstance
formal ceremony about important occasions
-
funeral
a ceremony at which a dead person is buried or cremated
-
hymeneals, nuptials, wedding, wedding ceremony
the social event at which the ceremony of marriage is performed
-
pageant, pageantry
a rich and spectacular ceremony
-
dedication
a ceremony in which something (as a building) is dedicated to some goal or purpose
-
opening
a ceremony accompanying the start of some enterprise
-
commemoration, memorialisation, memorialization
a ceremony to honor the memory of someone or something
-
military ceremony
a formal ceremony performed by military personnel
-
induction, initiation, installation
a formal entry into an organization or position or office
-
exercise
(usually plural) a ceremony that involves processions and speeches
-
fire walking
the ceremony of walking barefoot over hot stones or a bed of embers
-
formalities, formality
a requirement of etiquette or custom
-
Maundy
a public ceremony on Maundy Thursday when the monarch distributes Maundy money
-
potlatch
a ceremonial feast held by some Indians of the northwestern coast of North America (as in celebrating a marriage or a new accession) in which the host gives gifts to tribesmen and others to display his superior wealth (sometimes, formerly, to his own impoverishment)
-
type of:
-
social event
an event characteristic of persons forming groups
-
noun
a set sequence of steps, part of larger computer program
DISCLAIMER: These example sentences appear in various news sources and books to reflect the usage of the word ‘function’.
Views expressed in the examples do not represent the opinion of Vocabulary.com or its editors.
Send us feedback
EDITOR’S CHOICE
Look up function for the last time
Close your vocabulary gaps with personalized learning that focuses on teaching the
words you need to know.
Sign up now (it’s free!)
Whether you’re a teacher or a learner, Vocabulary.com can put you or your class on the path to systematic vocabulary improvement.
Get started