What do word problems teach

If you are looking for tips and ideas for how to teach word problems to your elementary students, then you’ve found the right place! We know that teaching elementary students how to solve word problems is important for math concept and skill application, but it sure can feel like a daunting charge without knowing about the different types, the best practices for teaching them, and common misconceptions to plan in advance for, as well as having the resources you need. All this information will make you feel confident about how to teach addition, subtraction, multiplication, and division word problems! Teaching students how to solve word problems will be so much easier!

This blog post will address the following questions:

• What is a word problem?
• What is a multi-step word problem?
• Why are elementary math word problems important?
• Why are math word problems so hard for elementary students?
• What are the types of word problems?
• How do I teach math word problems in a systematic way?
• What are the best elementary math word problem strategies I can teach my students and what are some tips for how to teach math word problems strategies?
• Do you have any helpful tips for how to teach word problems?
• What are the common mistakes I should look for that my students may make?
• How do I address my students’ common misconceptions surrounding elementary math word problems?

What is a Word Problem?

A word problem is a math situation that calls for an equation to be solved.  Students must apply their critical thinking skills to determine how to solve the problem.  Word problems give students the opportunity to practice turning situations into numbers.  This is critical as students progress in their education, as well as in their day-to-day life.  By teaching students how to solve word problems in a strategic way, you are setting them up for future success!

What is a Multi-Step Word Problem?

A multi-step word problem, also known as a two-step word problem or two-step equation word problem, is a math situation that involves more than one equation having to be answered in order to solve the ultimate question.  This requires students to apply their problem solving skills to determine which operation or operations to use to tackle the problem and find the necessary information.  In some cases, the situation may call for mixed operations, and in others the operations will be the same.  Multi-step word problems offer students the opportunity to practice the skill of applying different math concepts with a given problem.

Why are Word Problems Important in Math?

Word problems are essential in math because they give students the opportunity to apply what they have learned to a real life situation.  In addition, it facilitates students in developing their higher order thinking and critical thinking skills, creativity, positive mindset toward persevering while problem solving, and confidence in their math abilities.  Word problems are an effective tool for teachers to determine whether or not students understand and can apply the concepts and skills they learned to a real life situation.

Why do Students Struggle with Math Word Problems?

Knowing why students have trouble with word problems will help you better understand how to teach them. The reason why math word problems are difficult for your students is because of a few different reasons. First, students need to be able to fluently read and comprehend the text. Second, they need to be able to identify which operations and steps are needed to find the answer. Finally, they need to be able to accurately calculate the answer. If you have students who struggle with reading or English is their second language (ESL), they may not be able to accurately show what they know and can do because of language and literacy barriers. In these cases, it is appropriate to read the text aloud to them or have it translated into their native language for assignments and assessments.

Types of Word Problems

Knowing the different types of word problems will help you better understand how to teach math word problems. Read below to learn about the four types of basic one-step addition and subtraction word problems, the subcategories within each of them, and specific examples for all of them. Two-step equation word problems can encompass two of the same type or two separate types (also known as mixed operation word problems).

1. Join

This type of word problem involves an action that increases the original amount. There are three kinds: Result unknown, change unknown, and initial quantity unknown.

Result Unknown

Example: There were 7 kids swimming in the pool. 3 more kids jumped in. How many kids are in the pool now? (7 + 3 = ?)

Change Unknown

Example: There were 8 kids swimming in the pool. More kids jumped in. Now there are 15 kids in the pool. How many kids jumped in? (8 + ? = 15)

Initial Quantity Unknown

Example: There were kids swimming in the pool. 2 kids jumped in. Now there are 6 kids in the pool. How many kids were swimming in the pool at first? (? + 2 = 6)

2. Separate

This type of word problem involves an action that decreases the original amount. There are three kinds: Result unknown, change unknown, and initial quantity unknown.

Result Unknown

Example: There were 12 kids swimming in the pool. 6 of the kids got out of the pool. How many kids are in the pool now? (12 – 6 = ?)

Change Unknown

Example: There were 9 kids swimming in the pool. Some of the kids got out of the pool. Now there are 4 kids in the pool. How many kids got out of the pool? (9 – ? = 4)

Initial Quantity Unknown

Example: There were kids swimming in the pool. 3 of the kids got out of the pool. Now there are 2 kids in the pool. How many kids were in the pool at first? (? – 3 = 2)

3. Part-Part-Whole

This type of word problem does not involve an action like the join and separate types. Instead, it is about defining relationships among a whole and two parts. There are two kinds: result unknown and part unknown.

Result Unknown

Example: There are 5 boys and 9 girls swimming in the pool. How many kids are in the pool? (5 + 9 = ?)

Part Unknown

Example: There are 12 kids swimming in the pool. 8 of them are girls and the rest of them are boys. How many boys are swimming in the pool? (8 + ? = 12)

4. Compare

This type of word problem does not involve an action or relationship like the three other types. Instead, it is about comparing two different unrelated items. There are two kinds: Difference unknown and quantity unknown.

Difference Unknown

Example: There are 2 kids in the pool. There are 7 kids in the yard. How many more kids are in the yard than in the pool? (2 + ? = 7 or 7 – 2 = ?)

Quantity Unknown

Example 1: There are 5 kids in the pool. There are 3 fewer kids playing in the yard. How many kids are playing in the yard? (5 – 3 = ?)

Example 2: There are 2 kids in the pool. There are 10 more kids playing in the yard than in the pool. How many kids are playing in the yard? (2 + 10 = ?)

How to Solve Word Problems in 5 Easy Steps

Here are 5 steps that will help you teach word problems to your 1st, 2nd, 3rd, 4th or 5th grade students:

1. Read the problem.
2. Read the problem a second time and make meaning of it by visualizing, drawing pictures, and highlighting important information (numbers, phrases, and questions).
3. Plan how you will solve the problem by organizing information in a graphic organizer and writing down equations and formulas that you will need to solve.
4. Implement the plan and determine answer.
5. Reflect on your answer and determine if it is reasonable.  If not, check your work and start back at step one if needed.  If the answer is reasonable, check your answer and be prepared to explain how you solved it and why you chose the strategies you did.

5 Math Word Problem Strategies

Here are 5 strategies for how to teach elementary word problems:

Visualize

Understand the math situation and what the question is asking by picturing what you read in your head while you are reading.

Draw Pictures

Make meaning of what the word problem is asking by drawing a picture of the math situation.

Make Models

Use math tools like base-ten blocks to model what is happening in the math situation.

Highlight Important Information

Underline or highlight important numbers, phrases, and questions.

Engage in Word Study

Look for key words and phrases like “less” or “in all.” Check out this blog post if you are interested in learning more about math word problem keywords and their limitations.

10 Tips for Teaching Students How to Solve Math Word Problems

Here are 10 tips for how to teach math word problems:

1. Model a positive attitude toward word problems and math.
2. Embody a growth mindset.
3. Model! Provide plenty of direct instruction.
4. Give lots of opportunities to practice.
5. Explicitly teach strategies and post anchor charts so students can access them and remember prior learning.
6. Celebrate the strategies and process rather than the correct answer.
7. Encourage students to continue persevering when they get stuck.
8. Invite students to act as peer tutors.
9. Provide opportunities for students to write their own word problems.
10. Engage in whole-group discussions when solving word problems as a class.

Common Misconceptions and Errors When Students Learn How to Solve Math Word Problems

Here are 5 common misconceptions or errors elementary students have or make surrounding math word problems:

1. Use the Incorrect Operation

Elementary students often apply the incorrect operations because they pull the numbers from a word problem and add them without considering what the question is asking them or they misunderstand what the problem is asking.  Early in their experience with word problems, this strategy may work most of the time; however, its effectiveness will cease as the math gets more complex.  It is important to instruct students to develop and apply problem-solving strategies.

Although helpful in determining the meaning, elementary students rely solely on key words and phrases in a word problem to determine what operation is being called for. Again, this may be an effective strategy early on in their math career, but it should not be the only strategy students use to determine what their plan of attack is.

2. Get Stuck in a Fixed Mindset

Some elementary students give up before starting a word problem because they think all word problems are too hard.  It is essential to instill a positive mindset towards math in students. The best way to do that is through modeling. If you portray an excitement for math, many of your students will share that same feeling.

3. Struggle with Reading Skills Component

For first and second graders (as well as struggling readers and ESL students), it is common for students to decode the text incorrectly. Along the same lines, some elementary students think they can’t solve word problems because they do not know how to read yet.  The purpose of word problems is not to assess whether a child can read or not.  Instead, the purpose is to assess their critical thinking and problem-solving skills.  As a result, it is appropriate to read word problems to elementary students.

4. Calculate Incorrectly

You’ll find instances where students will understand what the question is asking, but they will calculate the addends or the subtrahend from the minuend incorrectly. This type of error is important to note when analyzing student responses because it gives you valuable information for when you plan your instruction.

5. Encode Response Incorrectly

Another error that is important to note when analyzing student responses is when you find that they encode their solution in writing incorrectly. This means they understand what the problem is asking, they solve the operations correctly, document their work meticulously, but then write the incorrect answer on the line.

How to Address Common Misconceptions Surrounding Math Word Problems

You might be wondering, “What can I do in response to some of these misconceptions and errors?” After collecting and analyzing the data, forming groups based on the results, and planning differentiated instruction, you may want to consider trying out these prompts:

• Can you reread the question aloud to me?
• What is the question asking us to do?
• How can we represent the information and question?
• Can we represent the information and question with an equation?
• What is our first step?
• What is our next step?
• Can you think of any strategies we use to help us solve?
• How did you find your answer?
• Can you walk me through how you found your answer step by step?
• What do we need to remember when recording our answer?

Now that you have all these tips and ideas for how to teach word problems, we would love for you to try these word problem resources with your students. They offer students opportunities to practice solving word problems after having learned how to solve word problems. You can download word problem worksheets specific to your grade level (along with lots of other math freebies) in our free printable math resources bundle using this link: free printable math activities for elementary teachers.

Check out my monthly word problem resources!

• 1st Grade Word Problems
• 2nd Grade Word Problems
• 3rd Grade Word Problems
• 4th Grade Word Problems
• 5th Grade Word Problems

Solving word problems in elementary school is an essential part of the math curriculum. Here are over 30 math word problems to practice with children, plus expert guidance on how to solve them.

This blog is part of our series of blogs designed for teachers, schools and parents supporting home learning.

What is a word problem?

A word problem in math is a math question written as one sentence or more that requires children to apply their math knowledge to a ‘real-life’ scenario. 

This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem. 

For example:

Isn’t brilliant arithmetic enough?

In short, no. Students need to build good reading comprehension, even in math. Overtime math problems become increasingly complex and require students to possess deep conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. 

As students progress through their mathematical education, they will need to be able to apply mathematical reasoning and develop mathematical arguments and proofs using math language. They will also need to be dynamic, applying their math knowledge to a variety of increasingly sophisticated problems. 

To support this schools are adopting a ‘mastery’ approach to math

“Teaching for mastery”, is defined with theses component: 

• Math teaching for mastery rejects the idea that a large proportion of people ‘just can’t do math’.  
• All students are encouraged by the belief that by working hard at math they can succeed. 
• Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other. 
• Significant time is spent developing deep knowledge of the key ideas that are needed to support future learning. The structure and connections within the mathematics are emphasized, so that students develop deep learning that can be sustained.

(The Essence of Maths Teaching for Mastery, 2016)

Mastery helps children to explore math in greater depth

Fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learned the number skills appropriate to their grade level/age, they should be progressed to the next grade level/age of number skills. 

The mastery approach encourages exploring the breadth and depth of these math concepts (once fluency is secure) through reasoning and problem solving. 

How to teach children to solve word problems? 

Here are two simple strategies that can be applied to many word problems before solving them.

1. What do you already know?
2. How can this problem be drawn/represented pictorially?

Let’s see how this can be applied to word problems to help achieve the answer.

Solving a simple word problem

There are 28 students in a class.

The teacher has 8 liters of orange juice.

She pours 225 milliliters of orange juice for every student.

How much orange juice is left over?

1. What do you already know?

• There are 1,000ml in 1 liter
• Pours = liquid leaving the bottle = subtraction
• For every = multiply
• Left over = requires subtraction at some point

2. How can this problem be drawn/represented pictorially?

The bar model, also known as strip diagram, is always a great way of representing problems. However, if you are not familiar with this, there are always other ways of drawing it out. 

Read more: What is a bar model

For example, for this question, you could draw 28 students (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 liters’ marked at the top.

Now to put the math to work. This is a 5th grade multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.

Solving a more complex, mixed word problem

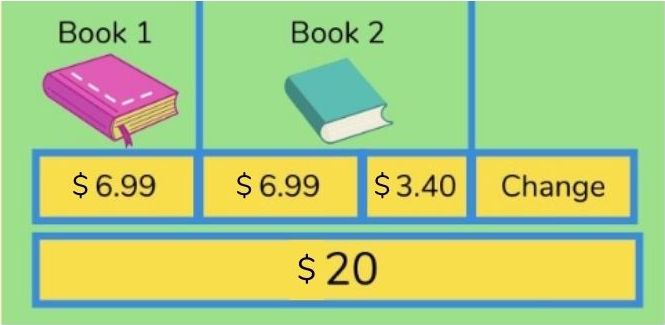
Mara is in a bookshop.

She buys one book for $6.99 and another that costs $3.40 more than the first book.

She pays using a $20 bill.

What change does Mara get? (What is the remainder?)

1. What do you already know?

• More than = add
• Using decimals means I will have to line up the decimal points correctly in calculations
• Change from money = subtract

2. How can this problem be drawn/represented pictorially?

See this example of bar modelling for this question:

Now to put the math to work using what we already know and what we’ve drawn to break down the steps.

Mara is in a bookshop. 

She buys one book for $6.99 and another that costs $3.40 more than the first book. 1) $6.99 + ($6.99 + $3.40) = $17.38

She pays using a $20 bill.

What change does Mara get? 2) $20 – $17.38 = $2.62

Math Word Problems For Kindergarten to Grade 5

The more children learn about math as they go through elementary school, the trickier the word problems they face will become.

Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each elementary grade. 

Word problems in kindergarten

Throughout kindergarten a child is likely to be introduced to word problems with the help of concrete resources (manipulatives, such as pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.

An example of a word problem for kindergarten would be

Chris has 3 red bounce balls and 2 green bounce balls. How many bounce balls does Chris have in all?

Word problems 1st grade

First grade is a continuation of kindergarten when it comes to word problems, with children still using concrete resources to help them understand and visualize the problems they are working on

An example of a word problem for first grade would be:

A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?

Word problems in 2nd grade

In second grade, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the adding and subtracting within 100, adding up to 4- two-digit numbers at a time.

This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.

Second grade word problem: Geometry properties of shape

Shaun is making shapes out of plastic straws.

At the vertices where the straws meet, he uses blobs of modeling clay to fix them together

Here are some of the shapes he makes:

Shape	Number of straws	Number of blobs of modeling clay
A	4	4
B	3	3
C	6	6

One of Sean’s shapes is a triangle. Which is it? Explain your answer.

Answer: shape B as a triangle has 3 sides (straws) and 3 vertices, or angles (clay)

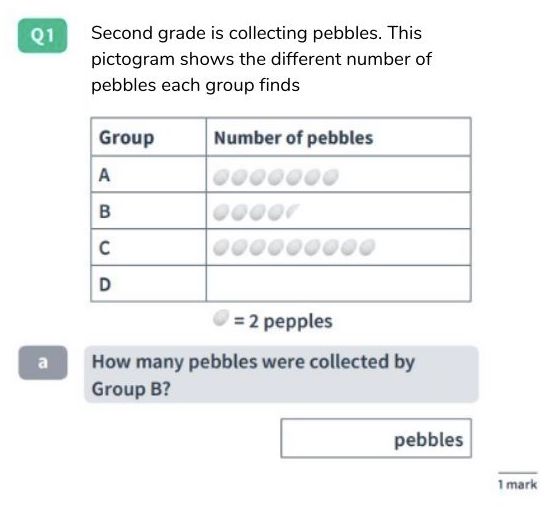
Second grade word problem: Statistics

2nd grade is collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.

Word problems in 3rd grade

At this stage of their elementary school career, children should feel confident using the written method for addition and subtraction. They will begin multiplying and dividing within 100. 

This year children will be presented with a variety of problems, including 2-step problems and be expected to work out the appropriate method required to solve each one. 

3rd grade word problem: Number and place value

My number has four digits and has a 7 in the hundreds place.

The digit which has the highest value in my number is 2.

The digit which has the lowest value in my number is 6.

My number has 3 fewer tens than hundreds.

What is my number?

Answer: 2,746

Word problems in 4th grade

One and two-step word problems continue in fourth grade, but this is also the year that children will be introduced to word problems containing decimals.

Fourth grade word problem: Fractions and decimals

Stan, Frank and John are washing their cars outside their houses.

Stan has washed 0.5 of his car.

Frank has washed 1/5 of his car.

Norm has washed 2/5 of his car.

Who has washed the most?

Explain your answer.

Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.4)

Word problems in 5th grade

In fifth grade children move on from 2-step word problems to multi-step word problems. These will include fractions and decimals.

Here are some examples of the types of math word problems in fifth grade will have to solve.

5th grade word problem – Ratio and proportion

The Angel of the North is a large statue in England. It is 20 meters tall and 54 meters wide. 

Ally makes a scale model of the Angel of the North. Her model is 40 centimeters tall. How wide is her model?

Answer: 108cm

Fifth grade word problem – Algebra

Amina is making designs with two different shapes.

She gives each shape a value.

Calculate the value of each shape.

Answer: 36 (hexagon) and 25. 

Fifth grade word problem: Measurement

There are 28 students in a class.

The teacher has 8 liters of orange juice.

She pours 225 milliliters of orange juice for every student.

How much orange juice is left over?

Answer: 1.7 liters or 1,700ml

Topic based word problems

The following examples give you an idea of the kinds of math word problems your child will encounter in elementary school

Place value word problem fourth grade

This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37

Download free number and place value word problems for grades 2, 3, 4 and 5

Addition and subtraction word problem grade 2

Sam has 64 sweets. He gets given 12 more. He then gives 22 away. How many sweets is he left with? Answer: 54

Download free addition and subtraction word problems for for grades 2, 3, 4 and 5

Addition word problem grade 2

Sammy thinks of a number. He subtracts 70. His new number is 12. What was the number Sammy thought of? Answer: 82

Subtraction word problem fifth grade

The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC

Multiplication word problem third grade

Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108

Download free multiplication word problems for grades 2, 3, 4 and 5. 

Division word problem fifth grade

A factory produces 3,572 paint brushes every day. They are packaged into boxes of 19. How many boxes does the factory produce every day? Answer: 188

Download free division word problems for grades 2, 3, 4 and 5. 

Free resource: Use these four operations word problems to practice addition, subtraction, multiplication and division all together.

Fraction word problem fourth grade

At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3

Download free fractions and decimals word problems for grades 2, 3, 4 and 5. 

Money word problem second grade 

Lucy and Noor found some money on the playground at recess. Lucy found 2 dimes and 1 penny, and Noor found 2 quarters and a dime. How many cents did Lucy and Noor find? Answer: Lucy = $0.21, Noor = $0.60; $0.21 + $0.61 = $0.81

Area word problem 3rd grade

A rectangle measures 6cm by 5cm.

What is its area? Answer: 30cm2

Perimeter word problem 3rd grade

The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many meters has she swum? Answer: 108m

Ratio word problem 5th grade (crossover with measurement)

A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots

PEMDAS word problem fifth grade

Draw a pair of parentheses in one of these calculations so that they make two different answers. What are the answers?

50 – 10 × 5 =

50 – 10 × 5 =

Volume word problem fifth grade

This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3

Remember: The word problems can change but the math won’t 

It can be easy for children to get overwhelmed when they first come across word problems, but it is important that you remind them that while the context of the problem may be presented in a different way, the math behind it remains the same. 

Word problems are a good way to bring math into the real world and make math more relevant for your child. So help them practice, or even ask them to turn the tables and make up some word problems for you to solve. 

Word problems are described as «verbal descriptions of problem situations wherein one or more questions are raised the answer to which can be obtained by the application of mathematical operations to numerical data available in the problem statement» (Verschaffel, Greer, & De Corte, 2000). Solving word problems involves:

• The well-organized and flexible use of both conceptual and procedural knowledge
• Strategies and metacognition
• Positive affect and beliefs (De Corte, Greer, & Verschaffel, 1996; Schoenfeld, 1992)

Is Solving Word Problems the Same as Mathematical Modeling?

Solving word problems is not considered to be the same as mathematical modeling. Mathematical modeling tends to be a more complex process involving identifying questions to answer about the real world, making assumptions, identifying variables, translating a phenomenon into a mathematical model, assessing the solution, and iterating on the process to refine and extend the model (COMAP & SIAM, 2016). The process to solve a word problem isn’t necessarily as complex, as the problem itself usually gives the reader the question to answer and the information necessary to answer it, and doesn’t require modeling’s level of meaning-making and interpretation. These differences are relative, however, depending on the abilities of the student and the nature of the solution required to answer the problem.

Understanding the Challenge

What Makes Word Problems Difficult for Students?

Students’ primary difficulty in solving word problems is attributed to their «suspension of sense-making» (Schoenfeld, 1991; Template:Verschaffel, Greer, & De Corte). Instead of thinking through the context of the word problem to understand it, many students simply seek a simple application of arithmetic needed to produce an answer, whether it makes sense or not. In a video, Kaplinsky (2013) reproduces a result of early 1980s research conducted at the Institut de Recherche sur l’Enseignement des Mathématiques in France.

Math teachers are often concerned about students’ abilities to transfer classroom learning into the world beyond the classroom, but this «suspension of sense-making» shows that the reverse is also difficult – students struggle to apply their knowledge and understanding of the world back into a mathematics classroom. Having been conditioned with years of arithmetic, almost always involving obvious operations and the expectation that each problem has a correct answer, students develop a «compulsion to calculate» (Stacey & MacGregor, 1999) that can interfere with the development of the algebraic thinking that is usually needed to solve word problems. Some (but not all) research findings suggest that «compulsion to calculate» worsens as students age and develop beliefs that math is a collection of rules (Radatz, 1983; Stern, 1992, both as cited in Verschaffel, Greer, & De Corte, 2000, p. 5).

Students can also struggle with word problems because they have difficulty with academic vocabulary, mathematical vocabulary, or both. Due to these difficulties, English language learners and students of low socioeconomic status score lower on standardized assessment items than proficient speakers of English (Abedi & Lord, 2001).

What Makes Word Problems Difficult for Teachers?

Some teachers ignore or struggle to apply their real-world knowledge when solving word problems, just like students (Verschaffel, De Corte, & Borghart, 1997). During instruction, teachers often try to help students «strip away the stuff we don’t really need» (Chapman, 2006, p. 219) and reduce the problem to the numbers and keywords or phrases that indicate operations or relations. This dismissal of the real-world aspects of word problems can contribute to students’ suspension of sense-making and their compulsion to calculate.

Most teachers believe or assume that students will have more difficulty solving a word problem than solving an algebraic equation that represents the same mathematics without the words. Because of this, they believe in teaching word problems only after students master solving similar problems as equations. Traditional math textbooks reinforce this belief by placing word problems at the end of practice sets. This belief or assumption has been shown to be false, at least under some conditions. When tested, students have shown that they can be more successful with word or verbal problems than they are with equivalent problems that are purely symbolic (Nathan & Koedinger, 2000a, 2000b). Other research suggests that skill in algorithmic computation may not correspond to students’ ability to conceptualize the relationship between numbers in word problems (Fuchs et al., 2006).

Recommendations

Use Word Problems to Teach Students Mathematics

Word problems are not just for applications of already-known mathematics. In fact, the most powerful way to use word problems in the classroom is as a means to help students learn math. By situating mathematics in contexts that are understandable for students, word problems encourage students to pursue solution strategies that make sense to them and lead more often to correct answers (Koedinger & Nathan, 2004). These strategies can then be made more formal and symbolic with additional instruction.

This is obvious for teachers of young children. In early mathematics, problems are almost always situated in realistic contexts that children can make sense of. There is no reason that this should end in early childhood. Students at all levels should engage in mathematics in a sensible context before it is made formal and symbolic.

Engage Student Reasoning

Instead of dismissing the context of word problems, teachers should take time with students to make sense of word problems and their supporting context. Teachers should push back against students’ compulsion to calculate by focusing on the relationship between the knowns and unknowns in word problems, and not rush to find an answer (Kieran, 2014). Some types of word problems might be particularly useful for promoting reasoning because they either lack an obvious strategy, don’t have one right answer, or could be «tricky» for students who assume the problem is straightforward. Some examples:

1. Pete organized a birthday party for his tenth birthday. He invited 8 boy friends and 4 girl friends. How many friends did Pete invite for his birthday party?
2. Carl has 5 friends and Georges has 6 friends. Carl and Georges decide to give a party together. They invite all their friends. All friends are present. How many friends are there at the party?
3. Kathy, Ingrid, Hans and Tom got from their grandfather a box with 14 chocolate bars, which they shared equally amongst themselves. How many chocolate bars did each grandchild get?
4. Grandfather gives his 4 grandchildren a box containing 18 balloons, which they share equally. How many balloons does each grandchild get?
5. A shopkeeper has two containers for apples. The first container contains 60 apples and the other 90 apples. He puts all the apples into a new, bigger container. How many apples are there in that new container?
6. What will be the temperature of water in a container if you pour 1 jug of water at 80 degrees F and 1 jug of water at 40 degrees F into it? (Nesher, 1980)

Verschaffel, De Corte, and Lasure (1994) used these word problems to see if students would reason differently with the odd- and even-numbered items. Their research and subsequent studies have shown that the vast majority of students – sometimes more than 90 percent – will calculate and produce answers for the even-numbered items just as they do for the odd-numbered items, without any additional reasoning about real-world considerations. Giving students a general warning, such as «these problems are not as easy as they look,» did not significantly help students. Instead, teachers can promote student reasoning by providing supports specific to each problem, such as encouraging students to explain their answer and why it makes sense, to draw a picture of their solution, or to consider a hypothetical but contrasting solution from another student. While these strategies can increase the number of students who reason with these problems correctly, in multiple studies they rarely produced correct answers for much more than 50 percent of students (see Chapter 3, Verschaffel, Greer, De Corte). In other words, these strategies are helpful but unlikely by themselves to ensure success for all students.

Numberless Word Problems

Perhaps the most direct way of pushing back against students’ compulsion to calculate is to give them word problems without numbers. Brian Bushart, an elementary teacher and mathematics curriculum coordinator from Texas, popularized the idea of «numberless word problems» after a colleague tried the approach with some third-grade students. Numberless word problems aren’t entirely new, as the book Problems Without Figures (Gillan, 1909) presented something vaguely similar in the early 20th century. Bushart’s approach goes much further by focusing on the instructional moves and opportunities for student discourse that century-old approaches did not. Bushart’s blog post (2014) and subsequent collection of resources (n.d.) describe both his process for numberless word problems and numerous examples for a range of content and grade levels.

Example 1: A Single-Step Word Problem

For an example of a numberless word problem, consider this item released from the Grade 4 PARCC test (PARCC, 2016a):

A pitcher contains 2 liters of juice. A glass is filled with 180 milliliters of juice from the pitcher. How many milliliters of juice are left in the pitcher after filling the glass?

Instead of giving students this problem as written, teachers can present a numberless version of this problem on a series of slides:

Slide 1: A pitcher contains some juice.

Slide 2: A pitcher contains some juice. A glass is filled with some of the juice from the pitcher.

Slide 3: A pitcher contains some juice. A glass is filled with some of the juice from the pitcher. How much juice is left in the pitcher after filling the glass?

Slide 4: A pitcher contains 2 liters of juice. A glass is filled with some of the juice from the pitcher. How much juice is left in the pitcher after filling the glass?

Slide 5: A pitcher contains 2 liters of juice. A glass is filled with 180 milliliters of juice from the pitcher. How much juice is left in the pitcher after filling the glass?

Slide 6: A pitcher contains 2 liters of juice. A glass is filled with 180 milliliters of juice from the pitcher. How many milliliters of juice are left in the pitcher after filling the glass?

Teachers can adjust the number of slides depending on student ability, the difficulty of the problem, and the amount of time the teacher wishes to dedicate to building and sharing student sense-making. In this example, a teacher might stop after Slide 1 to make sure students know what a pitcher is and to have students estimate the capacity of a pitcher. After Slide 2, the teacher can ask students to explain what will happen to the amount of juice in the pitcher, and the relationship between the juice in the pitcher and the juice in the glass. With each subsequent slide, the teacher can continue to probe students’ sense-making and understanding of the relationships between the quantities described by the problem.

Example 2: A Multi-Step Word Problem

Teachers can also use numberless word problems with multi-step word problems. Consider this multi-step item released from the Grade 5 PARCC test (PARCC, 2016b):

Dana is making bean soup. The recipe she has makes 10 servings and uses [math]displaystyle{ frac{3}{4} }[/math] of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup? She has [math]displaystyle{ frac{1}{16} }[/math] of a pound of beans in one container and [math]displaystyle{ frac{1}{4} }[/math] of a pound of beans in another container. How many more pounds of beans does Dana need to make 5 servings of soup?

Just as with Example 1, a teacher could present a numberless version of this word problem on a series of slides.

Slide 1: Dana is making bean soup. The recipe she has makes a number of servings and uses an amount beans.

The teacher could use Slide 1 to make sure students understand the basic context. Students may observe that «If she wants to make more soup she’ll need more beans,» or have other insights that help establish the relationship between the amount of soup and the amount of beans.

Slide 2: Dana is making bean soup. The recipe she has makes a number of servings and uses an amount of beans. What amount of beans does she need to make a smaller number of servings of soup?

With Slide 2, students should observe that less soup should need less beans. Students might begin to conjecture with statements like, «If she wants half as much soup, she’ll need half the beans.»

Slide 3: Dana is making bean soup. The recipe she has makes a number of servings and uses an amount of beans. What amount of beans does she need to make a smaller number of servings of soup? She already has a small amount of beans. How much more beans does Dana need to make her soup?

After seeing Slide 3, students should now grapple with an even more complex relationship: Not only does Dana need less beans because she’s making less soup than called for by the recipe, but she already has some of the beans that she’ll need. Student observations and conjectures at this point should suggest two operations, such as a first step involving division to find the amount of beans needed in the reduced recipe, and a second step to subtract the amount of beans Dana already has. With this multi-step complexity, it would be useful for students to draw or otherwise illustrate their thinking.

Slide 4: Dana is making bean soup. The recipe she has makes 10 servings and uses an amount of beans. What amount of beans does she need to make 5 servings of soup? She already has a small amount of beans. How much more beans does Dana need to make 5 servings of soup?

Slide 4 specifies the numbers of servings, but not the beans. With this information, students can revise their observations to make clear that the recipe’s amount of beans needs to be divided by 2, with an additional amount subtracted, to find how many more beans Dana needs.

Slide 5: Dana is making bean soup. The recipe she has makes 10 servings and uses [math]displaystyle{ frac{3}{4} }[/math] of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup? She already has a small amount of beans. How many more pounds of beans does Dana need to make 5 servings of soup?

With Slide 5, students should have already decided that the amount of beans in the recipe needs to be divided by 2, and now they can focus on finding [math]displaystyle{ frac{3}{4} div 2 }[/math]. Students may also notice that the problem now makes clear that all measurements of beans is in pounds.

Slide 6: Dana is making bean soup. The recipe she has makes 10 servings and uses [math]displaystyle{ frac{3}{4} }[/math] of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup? She has [math]displaystyle{ frac{1}{16} }[/math] of a pound of beans in one container and [math]displaystyle{ frac{1}{4} }[/math] of a pound of beans in another container. How many more pounds of beans does Dana need to make 5 servings of soup?

Slide 6 presents the word problem in its original form, and students may be surprised that the small amount of beans Dana already had is represented as two amounts that need to be considered together. Because of the complexity of this problem, there may not be an ideal time to introduce this information, but a 5th grader who has reasoned through the problem and gotten this far should be able to reason with the two small quantities of beans, either by adding them first and then subtracting the sum from [math]displaystyle{ frac{3}{8} }[/math] or by performing two subtractions.

Add Authenticity

Students have shown to be more successful with word problems when they are required to engage with the context in authentic ways. For example, DeFranco and Curcio (1997, as cited by Verschaffel, Greer, De Corte) gave a group of 20 sixth grade students the following word problem: “328 senior citizens are going on a trip. A bus can seat 40 people. How many buses are needed so that all the senior citizens can go on the trip?” Later, the researchers gave the students a similar problem, except they presented it in the form of a fact sheet with the numbers of people and the size of vans, and instructions for making a phone call that simulated placing an actual order for the number of required vehicles. In the first scenario, only 2 of the 20 students answered correctly and properly reasoned with the remainder left by the division. In the second scenario, using a more authentic setting, 16 of the 20 students answered correctly and reasoned appropriately with the remainder, either by rounding up to the next whole van or requesting «like a car or something» to transport the small number of remaining passengers.

Address Language Complexity

Language complexity can be addressed either by reducing the complexity or providing students with additional support. For students who struggle with the language of word problems, it can be helpful to rewrite the problem using simpler, more familiar language, or a student’s native language (Bernardo, 1999). These kinds of modifications tend to help English learners and low-SES students more than their English-proficient and higher-SES counterparts, meaning this strategy could help reduce achievement gaps (Abedi & Lord, 2001).

Teachers can also provide extra support. Recommendations for teaching English language learners include focusing on student reasoning and discourse, rather than correctness of language use, and using language learners’ knowledge and experiences as resources (Moschkovich, 2012). The Understanding Language website (ell.stanford.edu) is a recommended resource for understanding how to support language learners in mathematics.

References

Abedi, J., & Lord, C. (2001). The language factor in mathematics tests. Applied Measurement in Education, 14(3), 219–234. https://doi.org/10.1207/S15324818AME1403_2

Bernardo, A. B. I. (1999). Overcoming obstacles to understanding and solving word problems in mathematics. Educational Psychology, 19(2), 149–163. https://doi.org/10.1080/0144341990190203

Bushart, B. (n.d.). Numberless word problems. Retrieved November 16, 2017, from https://bstockus.wordpress.com/numberless-word-problems/

Bushart, B. (2014, October 6). Numberless word problems [Blog post]. Retrieved November 16, 2017, from https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/

Chapman, O. (2006). Classroom practices for context of mathematics word problems. Educational Studies in Mathematics, 62(2), 211–230. https://doi.org/10.1007/s10649-006-7834-1

COMAP, & SIAM. (2016). GAIMME: Guidelines for assessment & instruction in mathematical modeling education. Bedford, MA. Retrieved from http://www.comap.com/Free/GAIMME/index.html

De Corte, E., Greer, B., & Verschaffel, L. (1996). Mathematics teaching and learning. In D. C. Berliner & R. C. Calfee (Eds.), Handbook of educational psychology (pp. 491–549). New York, NY: Lawrence Erlbaum Associates.

DeFranco, T. C., & Curcio, F. R. (1997). A division problem with a remainder embedded across two contexts: Children’s solutions in restrictive vs. real-world settings. Focus on Learning Problems in Mathematics, 19(2), 58–72.

Fuchs, L. S., Fuchs, D., Compton, D. L., Powell, S. R., Seethaler, P. M., Capizzi, A. M., … Fletcher, J. M. (2006). The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29

Gillan, S. Y. (1909). Problems without figures. Milwaukee, WI: S. Y. Gillan & Company. Retrieved from http://www.schoolinfosystem.org/pdf/2008/10/problemswithoutfigures.pdf

Kaplinsky, R. (2013). How old is the shepard? Retrieved November 3, 2017, from https://www.youtube.com/watch?v=kibaFBgaPx4

Kieran, C. (2014). What does research tell us about fostering algebraic reasoning in school algebra? Reston, VA. Retrieved from http://www.nctm.org/Research-and-Advocacy/Research-Brief-and-Clips/Algebraic-Reasoning-in-School-Algebra/

Koedinger, K. R., & Nathan, M. J. (2004). The real story behind story problems: Effects of representations on quantitative reasoning. Journal of the Learning Sciences, 13(2), 129–164. https://doi.org/10.1207/s15327809jls1302_1

Moschkovich, J. N. (2012). Mathematics, the Common Core, and language. Understanding Language: Language, Literacy, and Learning in the Content Areas. Retrieved from http://ell.stanford.edu/publication/mathematics-common-core-and-language

Nathan, M. J., & Koedinger, K. R. (2000a). An investigation of teachers’ beliefs of students’ algebra development. Cognition and Instruction, 18(2), 209–237. https://doi.org/10.1207/S1532690XCI1802_03

Nathan, M. J., & Koedinger, K. R. (2000b). Teachers’ and researchers’ beliefs about the development of algebraic reasoning. Journal for Research in Mathematics Education, 31(2), 168–190. https://doi.org/10.2307/749750

Nesher, P. (1980). The stereotyped nature of school word problems. For the Learning of Mathematics, 1(1), 41–48. Retrieved from http://flm-journal.org/Articles/flm_1-1_Nesher.pdf

PARCC. (2016a). Math Spring Operational 2016 Grade 4 Released Items. Partnership for Assessment of Readiness for College and Careers. Retrieved from http://parcc-assessment.org/images/releaseditems/Grade_04_Math_Item_Set.pdf

PARCC. (2016b). Math Spring Operational 2016 Grade 5 Released Items. Partnership for Assessment of Readiness for College and Careers. Retrieved from http://parcc-assessment.org/images/releaseditems/Grade_05_Math_Item_Set.pdf

Radatz, H. (1983). Untersuchungen zum Lösen eingekleideter Aufgaben. Zeitschrift Fur Mathematic-Didaktik, 4(2), 205–2017. https://doi.org/10.1007/BF03339231

Schoenfeld, A. H. (1991). On mathematics as sense-making: An informal attack on the unfortunate divorce of formal and informal mathematics. In J. F. Voss, D. N. Perkins, & J. W. Segal (Eds.), Informal reasoning and education (pp. 311–343). Hillsdale, NJ: Lawrence Erlbaum Associates.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). Reston, VA: National Council of Teachers of Mathematics.

Stacey, K., & MacGregor, M. (1999). Learning the algebraic method of solving problems. The Journal of Mathematical Behavior, 18(2), 149–167. https://doi.org/10.1016/S0732-3123(99)00026-7

Stern, E. (1992). Warum werden Kapitänsaufgaben “gelöst”? Dav Verstehen von Textaufgaben aus phychologischer Sicht. Der Mathematikunterricht, 28(5), 7–29.

Verschaffel, L., De Corte, E., & Borghart, I. (1997). Pre-service teachers’ conceptions and beliefs about the role of real-world knowledge in mathematical modelling of school word problems. Learning and Instruction, 7(4), 339–359. https://doi.org/10.1016/S0959-4752(97)00008-X

Verschaffel, L., De Corte, E., & Lasure, S. (1994). Realistic considerations in mathematical modeling of school arithmetic word problems. Learning and Instruction, 4(4), 273–294. https://doi.org/10.1016/0959-4752(94)90002-7

Verschaffel, L., Greer, B., & De Corte, E. (2000). Making sense of word problems. Lisse, The Netherlands: Swets & Zeitlinger.

My students had been struggling with how to solve addition and subtraction word problems for what seemed like forever. They could underline the question and they could find the numbers. Most of the time, my students just added the two numbers together without making sense of the problem.

Ugh.

Can you relate?

Below are five math problem-solving strategies to use when teaching word problems on addition and subtraction using any resource.

So, how do I teach word problems? It’s quite complex, but so much fun, once you get into it.

How to teach addition and subtraction word problems

The main components of teaching addition and subtraction word problems include:

1. Teaching the Relationship of the Numbers – As a teacher, know the problem type and help students solve for the action in the problem
2. Differentiate the Numbers – Give students just the right numbers so that they can read the problem without getting bogged down with the computation
3. Use Academic Vocabulary – And be consistent in what you use.
4. Stop Searching for the “Answer” – it’s not about the answer; it’s about the process
5. Differentiate between the Models and the Strategies – one has to do with the relationship between the numbers and the other has to do with how students “solve” or compute the problem.

I am a big proponent of NOT teaching keyword lists. It just doesn’t work consistently across all problems. It’s a shortcut that leads to breakdowns in mathematical thinking. Nor should you just give students word problem worksheets and have them look for word problem keywords. I talk more in-depth about why it doesn’t work in The Problem with Using Keywords to Solve Word Problems.

Teach the Relationship of the Numbers in Math Word Problems

One way to help your students solve word problems is to teach them the relationship of the numbers. In other words, help them understand that the numbers in the problem are related to each other in some way.

I teach word problems by removing the numbers. Sounds strange right?

Removing the distraction of the numbers helps students focus on the situation of the problem and understand the action or relationship of the numbers. It also keeps students from solving the problem before we talk about the relationship of the numbers.

When I teach word problems, I give students problems with blank spaces and no numbers. We first talk about the action in the problem. We identify whether something is being added to or taken from something else. That becomes our equation. We identify what we have to solve and set up the equation with blank spaces and a square for the unknown number

___ + ___ = unknown

Do you want a free sample of the word problems I use in my classroom?  Click the link or the image below. FREE Sample of Word Problems by Problem Type

Differentiate the numbers in the Word Problems

Only after we have discussed the problem do I give students numbers. I differentiate numbers based on student needs. At the beginning of the year, we all do the same numbers, so that I can make sure students understand the process.

After students are familiar with the process, I start to give different students different numbers, based on their level of mathematical thinking.

I also change numbers throughout the year, from one-digit to two-digit numbers. The beauty of the blank spaces is that I can put any numbers I want into the problem, to practice the strategies we have been working on in class.

At some point, we do create a list of words, but not a keyword list. We create a list of actions or verbs and determine whether those actions are joining or separating something. How many can you think of?

Here are a few ideas:

Join: put, got, picked up, bought, made
Separate: ate, lost, put down, dropped, used

Don’t be afraid to use academic vocabulary when teaching word problems

I teach my students to identify the start of the problem, the change in the problem, and the result of the problem. I teach them to look for the unknown.

These are all words we use when solving problems and we learn the structure of a word problem through the vocabulary and relationship of the numbers.

In fact, using the same vocabulary across problem types helps students see the relationship of the numbers at a deeper level.

Take these examples, can you identify the start, change and result in each problem? Hint: Look at the code used for the problem type in the lower right corner.

For compare problems, we use the terms, larger, smaller, more and less. Try out these problems and see if you can identify the components of the word problems.

Stop searching for “the answer” when solving word problems

This is the most difficult misconception to break.

Students are not solving a word problem to find “the answer”. Although the answer helps me, the teacher, understand whether or not the student understood the relationship of the numbers, I want students to be able to explain their process and understand the depth of word problems.

Okay, they’re first and second-graders. I know.

My students can still explain, after instruction, that they started with one number. The problem resulted in other another number. Students then know that they are searching for the change between those two numbers.

It’s all about the relationship.

Differentiate between the models and the strategies

A couple of years ago, I came across this article about the need to help students develop adequate models to understand the relationship of the numbers within the problem.

A light bulb went off in my head. I needed to make a distinction between the models students use to understand the relationship of the numbers in the problem and the strategies to solve the computation in the problem. Models and strategies work in tandem but are very different.

Models are the visual ways problems are represented. Strategies are the ways a student solves a problem, putting together and taking apart the numbers.

The most important thing about models is to move away from them. I know that sounds odd.

You spend so long teaching students how to use models and then you don’t want them to use a model. Well, actually, you want students to move toward efficiency.

Younger students will act out problems, draw out problems with representations, and draw out problems with circles or lines. Move students toward efficiency. As the numbers get larger, the model needs to represent the relationship of the numbers

This is a prime example of moving from an inverted-v model to a bar model.

Here is a student moving from drawing circles to using an inverted-v.

Students should be solidly using one model before transitioning to another.  They may even use two at the same time while they work out the similarities between the models.

Students should also be able to create their own models. You’ll see how I sometimes gave students copies of the model that they could glue into their notebooks and sometimes students drew their own model.  They need to be responsible for choosing what works best for them. Start your instruction with specific models and then allow students to choose one to use. Always move students toward more efficient models.

The same goes for strategies for computation. Teach the strategies first through the use of math fact practice, before applying it to word problems so that students understand the strategies and can quickly choose one to use. When teaching, focus on one or two strategies. Once students have some fluency in a few strategies, have them choose strategies that work for different problems.

Which numbers do you put in the blank spaces?

Be purposeful in the numbers that you choose for your word problems. Different number sets will lend themselves to different strategies and different models. Use number sets that students have already practiced computationally.

If you’ve been taught to make 10, use numbers that make 10. If you’re working on addition without regrouping, use those number sets. The more connections you can make between the computation and the problem-solving the better.

The examples above are mainly for join and separate problems. It’s no wonder our students have so much difficulty with compare problems since we don’t teach them to the same degree as join and separate problems.

Our students need even more practice with those types of problems because the relationship of the numbers is more abstract. I’m going to leave that for another blog post, though.

Do you want a FREE sample of the resource that I use to teach Addition & Subtraction Word Problems by Problem Type?  Click this link or the image below.

How to Purchase the Addition & Subtraction Word Problems

The full resource is also available in my store for purchase and on Teachers Pay Teachers.

More Ideas for Teaching Word Problems