From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Solving Word Problems in Mathematics
What Is a Word Problem? (And How to Solve It!)
Learn what word problems are and how to solve them in 7 easy steps.
Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances.
As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem.
As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.
If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?
Steps of Solving a Word Problem
To work through any word problem, students should do the following:
1. Read the problem: first, students should read through the problem once.
2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
3. Visualize the problem: drawing a picture or creating a diagram can be helpful.
Students can start visualizing simple or more complex problems by creating relevant images, from concrete (like drawings of putting away cookies from a jar) to more abstract (like tape diagrams). It can also help students clarify the operations they need to carry out. (next step!)
4. Determine the operation(s): next, students should determine the operation or operations they need to perform. Is it addition, subtraction, multiplication, division? What needs to be done?
Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:
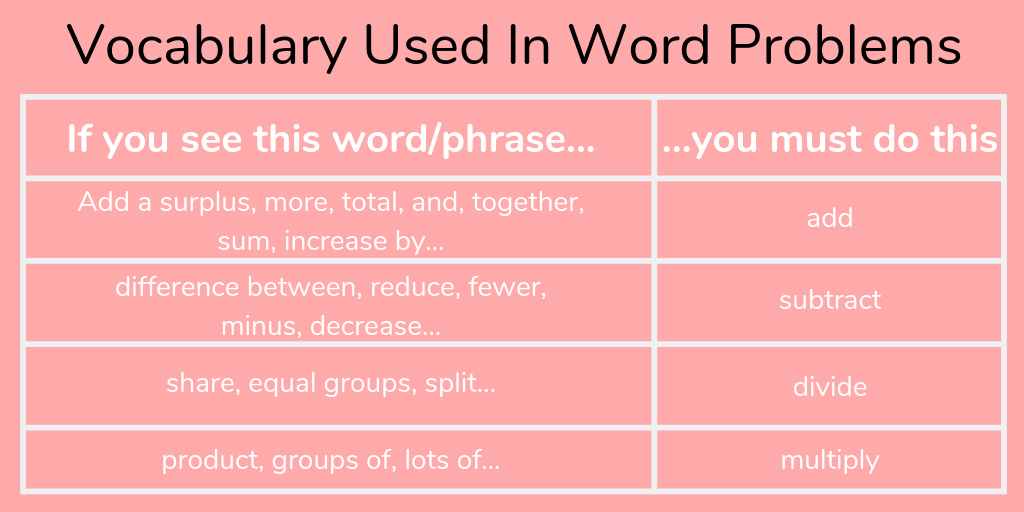
– Addition: add, more, total, altogether, and, plus, combine, in all;
– Subtraction: fewer, than, take away, subtract, left, difference;
– Multiplication: times, twice, triple, in all, total, groups;
– Division: each, equal pieces, split, share, per, out of, average.
These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems.
Another way to determine the operation is to search for certain situations, Jennifer Findley suggests. She has a great resource that lists various situations you might find in the most common word problems and the explanation of which operation applies to each situation.
5. Make a math sentence: next, students should try to translate the word problem and drawings into a math or number sentence. This means students might write a sentence such as 3 + 8 =.
Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence.
6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
7. Check the answer: finally, students should check their work to make sure that the answer is correct.
These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that!
At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises!
Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience.
Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.
For example, during the first steps, simple wording and animation help students realize what action the problem represents and find the connection between these actions and key words like “take away” and “left” that may signal them.
From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes.
Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.
Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations.
Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams!
To see the full exercise, follow this link.
The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task.
Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language.
These are the common steps that may help students overcome initial feelings of anxiety and fear of difficulty of the task they are given. Together with a teacher, they can master these foundational skills and build their confidence toward solving word problems. And Happy Numbers can facilitate this growth, providing varieties of engaging exercises and challenging word problems!
Solving word problems at KS1 and KS2 is an essential part of the new maths curriculum. Here you can find expert guidance on how to solve maths word problems as well as examples of the many different types of word problems primary school children will encounter with links to hundreds more.
What is a word problem?
A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem.
For example:
Importance of word problems within the national curriculum
The National Curriculum states that its mathematics curriculum “aims to ensure that all pupils:
- become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately;
- reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
- can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.”
To support this schools are adopting a ‘mastery’ approach to maths
The National Centre for Excellence in the Teaching of Mathematics (NCETM) have defined “teaching for mastery”, with some aspects of this definition being:
- Maths teaching for mastery rejects the idea that a large proportion of people ‘just can’t do maths’.
- All pupils are encouraged by the belief that by working hard at maths they can succeed.
- Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other.
- Significant time is spent developing deep knowledge of the key ideas that are needed to underpin future learning. The structure and connections within the mathematics are emphasised, so that pupils develop deep learning that can be sustained.
(The Essence of Maths Teaching for Mastery, 2016)

Year 3 to 6 Rapid Reasoning Worksheet for Weeks 1-6
Download for FREE 6 weeks of Rapid Reasoning worksheets. That include six weeks of daily reasoning and problem-solving questions for years 3, 4, 5 and 6!
Mastery helps children to explore maths in greater depth
One of NCETM’s Five Big Ideas in Teaching for Mastery (2017) is “Mathematical Thinking: if taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others”.
In other words – yes, fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learnt the number skills appropriate to their level/age, they should be progressed to the next level/age of number skills.
The mastery approach encourages exploring the breadth and depth of these concepts (once fluency is secure) through reasoning and problem solving.
See the following example:
| Year 6 objective | Fluency | Reasoning | Problem solving |
|---|---|---|---|
| Solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why. | 7,208 females attended a concert as well as 8,963 males. There were originally 20,000 seats on sale. How many empty seats were there at the concert? | Abdul says, “If I add any two 4-digit numbers together, it will make a 5-digit number.” Do you agree? Explain why. | Three pandas are eating bamboo sticks. There are 51 altogether. They all eat an odd number of sticks. How many bamboo sticks did they each eat? How many different ways can you do it? |
What sort of word problems might my child encounter at school?
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”. The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
|---|---|---|---|---|---|
| Number and place value | 6 | 9 | 7 | 5 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |
How to teach children to solve word problems?
Here are two simple strategies that can be applied to many word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
Let’s see how this can be applied to a word problem to help achieve the answer.
Solving a simple word problem
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
The bar model is always a brilliant way of representing problems, but if you are not familiar with this, there are always other ways of drawing it out.
Read more: What is a bar model
For example, for this question, you could draw 28 pupils (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
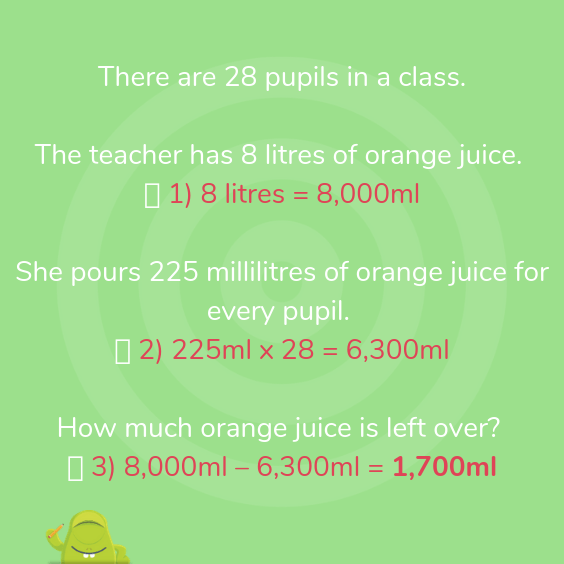
Solving a more complex word problem
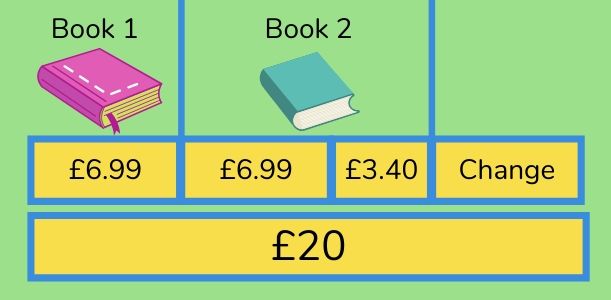
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book.
She pays using a £20 notes.
What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
She pays using a £20 note.
What change does Mara get? 2) £20 – £17.38 = £2.62
Maths word problems for years 1 to 6
The more children learn about maths as the go through primary school, the trickier the word problems they face will become.
Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each primary year group
Word problems in Year 1
Throughout Year 1 a child is likely to be introduced to word problems with the help of concrete resources (pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.
An example of a word problem for Year 1 would be:
Chris is going to buy a cake for his mum which costs 80p. How many 20p coins would he need to do this?
Word problems in Year 2
Year 2 is a continuation of Year 1 when it comes to word problems, with children still using concrete maths resources to help them understand and visualise the problems they are working on
An example of a word problem for Year 2 would be:
A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?
Word problems in Year 3
With word problems for year 3, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the four operations such as addition and subtraction word problems, multiplication and division problems too.
This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.
Year 3 word problem: Geometry properties of shape
Shaun is making 3-D shapes out of plastic straws.
At the vertices where the straws meet, he uses blobs of modelling clay to fix them together
Here are some of the shapes he makes:
| Shape | Number of straws | Number of blobs of modelling clay |
|---|---|---|
| A | 8 | 5 |
| B | 12 | 8 |
| C | 6 | 4 |
One of Sean’s shapes is a cuboid. Which is it? Explain your answer.
Answer: shape B as a cuboid has 12 edges (straws) and 8 vertices (clay)
Year 3 word problem: Statistics
Year 3 are collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.

Answer: a) 9 b) 3 pebbles drawn
Top tip
By the time children are in Year 3 many of the word problems, even one-step story problems tend to be a variation on a multiplication problem. For this reason learning times tables becomes increasingly essential at this stage. One of the best things you can do to help with Year 3 maths at home is support your child to do this.
Word problems in Year 4
At this stage of their primary school career, children should feel confident using the written method for each of the four operations.
Word problems for year 4 will include a variety of problems, including 2-step problems and be children will be expected to work out the appropriate method required to solve each one.
Year 4 word problem: Number and place value
My number has four digits and has a 7 in the hundreds place.
The digit which has the highest value in my number is 2.
The digit which has the lowest value in my number is 6.
My number has 3 fewer tens than hundreds.
What is my number?
Answer: 2,746
Word problems in Year 5
One and 2-step word problems continue with word problems for year 5, but this is also the year that children will be introduced to word problems containing decimals.
These are some examples of Year 5 maths word problems.
Year 5 word problem: Fractions, decimals and percentages
Stan, Frank and Norm are washing their cars outside their houses.
Stan has washed 0.5 of his car.
Frank has washed 1/5 of his car.
Norm has washed 5% of his car.
Who has washed the most?
Explain your answer.
Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.05)
Word problems in Year 6
Word problems for year 6 shift from 2-step word problems to multi-step word problems. These will include fractions, decimals, percentages and time word problems.
Here are some examples of the types of maths word problems Year 6 will have to solve.
Year 6 word problem – Ratio and proportion
This question is from the 2018 key stage 2 SATs paper. It is worth 1 mark.
The Angel of the North is a large statue in England. It is 20 metres tall and 54 metres wide.
Ally makes a scale model of the Angel of the North. Her model is 40 centimetres tall. How wide is her model?
Answer: 108cm
Year 6 word problem – Algebra
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
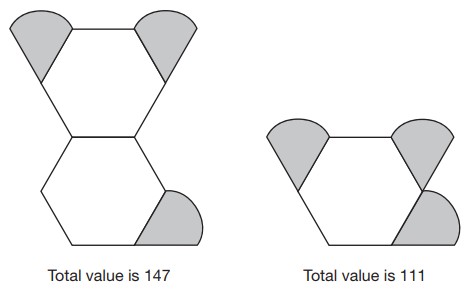
Amina is making designs with two different shapes.
She gives each shape a value.
Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
Year 6 word problem: Measurement
This question is from the 2018 KS2 SATs paper. It is worth 3 marks as it is a multi-step problem.
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
Answer: 1.7 litres or 1,700ml
Topic based word problems
The following examples give you an idea of the kinds of maths word problems your child will encounter for each of the 9 strands of maths in KS2.
Place value word problems
Place value word problem Year 5
This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37
Download free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction word problem Year 3
In Year 3 pupils will solve addition word problems and subtraction word problems with 2 and 3 digits.
Sam has 364 sweets. He gets given 142 more. He then gives 277 away. How many sweets is he left with? Answer: 229
Download free addition and subtraction word problems for Years 3, 4, 5 and 6
Addition word problem Year 3
Alfie thinks of a number. He subtracts 70. His new number is 12. What was the number Alfie thought of? Answer: 82
Subtraction word problem Year 6
The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC
More here: 25 addition and subtraction word problems
Multiplication and division word problems
Multiplication and division word problem Year 3
A baker is baking chocolate cupcakes. She melts 16 chocolate buttons to make the icing for 9 cakes. How many chocolate buttons will she need to melt to make the icing for 18 cakes? Answer: 32
Multiplication word problem Year 4
Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108
Download free multiplication word problems for Years 3, 4, 5 and 6
Division word problem Year 6
A factory produces 1,692 paintbrushes every day. They are packaged into boxes of 9. How many boxes does the factory produce every day? Answer: 188
Download our free division word problems worksheets for Years 3, 4, 5 and 6.
More here: 20 multiplication word problems
More here: 25 division word problems
Free resource: Use these four operations word problems to practise addition, subtraction, multiplication and division all together.
Fraction word problems
Fraction word problem Year 5
At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3
Download free fractions and decimals word problems worksheets for Years 3, 4, 5 and 6
More here: 28 fraction word problems
Decimals word problem Year 4 (crossover with subtraction)
Which two decimals that have a difference of 0.5? 0.2, 0.25, 0.4, 0.45, 0.6, 0.75. Answer: 0.25 and 0.75
Download free decimals and percentages word problems resources for Years 3, 4, 5 and 6
Percentage word problem Year 5
There are 350 children in a school. 50% are boys. How many boys are there? Answer: 175
Measurement word problem Year 3 (crossover with subtraction)
Lucy and Ffion both have bottles of strawberry smoothie. Each bottle contains 1 litre. Lucy drinks ½ of her bottle. Ffion drinks 300ml of her bottle. How much does each person have left in both bottles? Answer: Lucy = 500ml, Ffion = 300ml
More here: 25 percentage word problems
Money word problem Year 3
James and Lauren have different amounts of money. James has twelve 2p coins. Lauren has seven 5p coins. Who has the most money and by how much? Answer: Lauren by 11p.
More here: 25 money word problems
Area word problem Year 4
A rectangle measures 6cm by 5cm.
What is its area? Answer: 30cm2
Perimeter word problem Year 4
The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many metres has she swum? Answer: 108m
Ratio word problem Year 6 (crossover with measurement)
A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
More here: 24 ratio word problems
Bodmas word problem Year 6
Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
50 – 10 × 5 =
50 – 10 × 5 =
Volume word problem Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
How important are word problems when it comes to the SATs?
In the KS1 SATs, 58% (35/60 marks) of the test is comprised of maths ‘reasoning’ (word problems).
In KS2, this increases to 64% (70/110 marks) spread over two reasoning papers, each worth 35 marks. Considering children have, in the past, needed approximately 55-60% to reach the ‘expected standard’, it’s clear that children need regular exposure to and a solid understanding of how to solve a variety of word problems.
Children have the opportunity to practice SATs style word problems in Third Space Learning’s online one-to-one SATs revision programme. Personalised to meet the needs of each student, our programme helps to fill gaps and give students more confidence going in to the SATs exams.
Remember: The word problems can change but the maths won’t
It can be easy for children to get overwhelmed when they first come across word problems in KS2, but it is important that you remind them that whilst the context of the problem may be presented in a different way, the maths behind it remains the same.
Word problems are a good way to bring maths into the real world and make maths more relevant for your child, so help them practise, or even ask them to turn the tables and make up some word problems for you to solve.
This article while written by a teacher for teachers is also suitable for those at home supporting children with home learning. More free home learning resources are also available.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
A word problem is a compilation of several easy-to-understand sentences describing real-life scenarios where a specific problem needs a solution using stepwise mathematical calculation.
Word problems are a crucial part of learning in the curriculum of primary school students because they need children to apply their knowledge about a variety of different concepts to find solutions to a real-life problems.
In classroom settings, children are taught about the acronym RUCSAC which stands for:
i. R- Read
ii. U- Understand
iii. C- Choose
iv. S- Solve
v. A- Answer
vi. C- Check
These values help students to work their minds and apply prior knowledge to yield accurate solutions to problems.
There are four types of operations included in the topic Word Problems. These four operations perform different kinds of functions in different kinds of Word Problems. Students are trained in school to identify the Word Problem and apply the operations required to successfully calculate the result of the Problem.
The Four Operations of Word Problems are explained below in detail.
-
Addition: Addition is the first operation that a Word Problem may contain. Addition, as its name justifies, is about calculating the ‘sum’ of the given numbers. In simple words, it means to add the given numbers together and find a solution.
-
Subtraction: Subtraction is the second operation introduced to students. It is a little more complicated than addition. The subtraction operation is used to calculate ‘take-aways’ from the given numbers. In simple words, it means to subtract one quantity from the larger given quantity and calculate results.
-
Multiplication: Multiplication is the third operation in the list of Word Problems. According to its name, it helps us to calculate the product of two given numbers. In other words, multiplication operates as the process of multiplying the given quantities to yield a result.
-
Division: Lastly, Division is introduced as the fourth operation in the list of operations for Word Problems. Division is a technique through which we can divide the given quantities in a problem. To put it plainly, division operation splits the larger quantity or number into smaller parts.
Word Problems On Four Operations
1. Word Problem Based on Addition: In a class on the day of the examination, the total number of students present in each room was 50. How many students do two examination rooms have?
You need to add the number of students present in both the rooms (50+50) to find the accurate solution to the given problem.
Answer: There are a total of 100 students in 2 examination halls.
2. Word Problem Based on Subtraction: Paul and Amber entered a Card Challenge. They made a huge pyramid from 13687 cards, but Amber accidentally knocked 2956 pieces of cards to the floor before the judges saw their finished work. How many cards were left standing?
The number of cards on the floor (2956) must be subtracted from the total number of cards (13687) to calculate how many cards were still standing.
Answer: There are 10,731(13687-2956) cards standing.
3. Word Problem Based on Multiplication: You are the manager of a furniture company that produces 1350 chairs each month. In a year, how many chairs does the company make?
To calculate this, you need to multiply the number of chairs produced in each month (1350) by the number of months contained in each year (12).
Answer: In a year, a total of 16,200(1350 12) chairs are produced.
4. Word Problem Based on Division: 7000 books need to be arranged equally on a few shelves. If each bookshelf can hold 1000 books, how many bookshelves are required to fit them all?
To answer this problem, you need to divide the number of books one shelf can hold (1000) by the number of total books given (7000).
Answer: 7 bookshelves are required to hold 70000 books.
Mixed Operation Word Problems
Mixed Word Problems consists of the combination of more than one of the Four Operations as mentioned above (addition, subtraction, multiplication, division). They encourage a student to understand and link the various operations needed to solve the problem and build better concentration and think faster.
An Example: If each bottle needs 2 liters of syrup and there are 30 bottles, how much sugar syrup is needed to fill all of them, and how many drinks can be made from one bottle if each glass contains 200 ml syrup? This is a Mixed Word Operation.
Solution: Quantity of syrup each bottle can hold = 2L= 2000mL
Number of bottles = 30
Total quantity of sugar syrup = $30times2$
Ans: i) 60L of syrup can be contained in 30 bottles.
Quantity of syrup in each glass = 200mL
Total number of drinks that can be made with one bottle of syrup = $dfrac{2000}{200}mL$
= 10
Ans: ii) 10 drinks can be made from each bottle.
Solved Examples On Word Problem
An example of a Word Problem is given below:
Example:
Martha bought five apples from the market. She gave one to her mother, one to her brother Jimmy and one to her grandfather. How many apples does she have left?
Solution:
Total number of apples bought by Martha= 5
No. of apples, Martha gave to her mother, her brother, and grandfather= (1+1+1)
Therefore, the no. of remaining apples: 5- (1+1+1)
5- 3 = 2.
Martha has two apples left.
Practice Question MCQs
1. What is the average of: 1,2,3,5,9
-
3
-
4
-
5
-
8
Answer: B)
2. Find the value of: 0.0030.02
-
0.06
-
0.006
-
0.0006
-
0.00006
Answer: D)
Conclusion
The fundamentals of mathematics are arithmetic operations. It contains mostly arithmetic operations like addition, subtraction, multiplication, and division. These are also referred to as mathematical operations. In our daily lives, we employ mathematical operations to calculate overall business income and costs, create a monthly or yearly budget, measure lengths, and so on. We use them virtually every day, for example, while calculating the total number of questions given in homework, time, money, the number of chocolates we ate, the amount of marks gained in all courses, and so on.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
Word problems in math impose a significant challenge on students. Most math students consider word problems hard for two reasons: either they do not understand word problems, or they do not know how to express their answers in words. Advanced-level word problems have more complexity of the statements. Research has shown that metacognitive strategies influence students’ success in solving math word problems. On the contrary, if a good math teacher does not teach students word problems correctly, they approach word problems with confusion.
What Are Word Problems in Math?
Word problems in math are hypothetical or real-life scenarios that need to be solved by a way of a mathematical calculation.
Why Are Word Problems Important in Math?
Math education is not just about asking students simple questions like 2+2 or 4-3. Regular practice of complex word problems makes students understand how math works in real life. It also helps them develop critical thinking skills and become problem solvers of tomorrow.
Solving Math Word Problems Using the GRASS Method (Step by Step Method)
An excellent way to solve math word problems is by using “GRASS”. GRASS is an acronym for Given, Required, Analysis, Solution, and Statement. You can use the GRASS method to break down a word problem and make it easier to solve. Here is a breakdown of the steps you should follow to solve word problems in math.
1. GIVEN: Read the question carefully. Figure out what values are given.
First of all, read the question carefully and understand what the writer is asking. Then underline the values given in the question.
2. REQUIRED: Figure out what is required.
Underline or highlight what the question is asking for. Let’s say you have to solve this word problem: Sara had four apples, and she had given three to her brother. In this problem, you need to underline four, given, and three to get the idea of the most critical parts of the question.
3. ANALYSIS: Analyze the question and use appropriate math operations.
The next step is to analyze the question and determine the operation to be used. To analyze the question, you can draw a picture of the problem to understand the problem quickly. For example, you can illustrate people or objects given in the question to visualize the problem more efficiently.
To determine the operation, identifying some common keywords could be helpful. Below we have shared a table of keywords with you to help you determine the correct mathematical operation.
4. SOLUTION: Solve the question.
Once you have determined the correct mathematical operators for the problem, you can easily perform a mathematical operation to solve the problem. This is where your knowledge of the underlying concept comes into play.
5. STATEMENT: State your answer in simple words.
Congratulations! You have done the hard work in the previous steps. The last step is to state your answer in the simplest words possible. Your answer must be short, clear, and precise.
Some Common Keywords Used in Word Problems
Here is a table showing a list of different keywords used in elementary-level word problems. Note that this is not a comprehensive and definite list. You should practice critical thinking to master word problems rather than memorizing these keywords.
Word Problems in Math – Some Examples
In this section, we have demonstrated how to apply the GRASS method to solve word problems on addition, subtraction, multiplication, and division.
Addition Word Problems
Addition word problems involve situations where there is an increase of something as due to combining one or more quantities.
Example: A truck was driven 932 km in January and 227 km in February. Over how much distance was the truck driven in the two months?
Given:
Distance covered in January = 932 km
Distance covered in February = 227 km
Required:
The distance covered in January and February
Analysis:
Write down how you are going to solve this problem:
Distance covered in 2 months = Distance covered in January + Distance covered in February
Solution:
Distance covered in 2 months = Distance covered in January + Distance covered in February
= 932 km + 227 km
Statement:
The total distance covered by the truck in January and February is 1159 km.
Subtraction Word Problems
Subtraction word problems involve situations where there is a loss of quantity or numbers because of removing a smaller part from a bigger object or a group of objects.
Example: Mathew had $9,800 in his bank account in January 2021. He spent on buying a TV set for $460 in April 2021 and a dishwasher for $340 in October 2021. What was Mathew’s bank balance in August 2021?
Given:
There are three values given in this problem:
Mathew’s bank balance in January 2021: $9,800
Amount spent in April 2021: $460
Amount spent in October 2021: $340
Required:
Mathew’s bank balance in August 2021
Analysis:
In this problem, we are given three quantities, and we need to find out Mathew’s bank balance in August. To better visualize the problem, we can draw a timeline for the events that took place.
Note that we don’t need to consider the amount spent in October 2021 in our calculations because we need to figure out the bank balance in August. Therefore, we need to consider the values for the months of January, April, and August only.
Bank Balance in August 2021 = Bank Balance in January 2021 – Total Spending up to August 2021
Solution:
Bank Balance in August 2021 = Bank Balance in January 2021 – Total Spending up to August 2021
= $9800 – $460
Statement:
Mathew’s bank balance in August 2021 was $9,340.
Multiplication Word Problems
Multiplication word problems involve situations where we have to combine groups of equal sizes repeatedly.
Example: A jacket was priced at $300. Each month for three months, the price was increased by $15. How much was the jacket increased in price?
Given:
Price of jacket: $300
Increase in the price each month: $15 (let’s represent this with the letter K)
Required:
The increase in the price for over three months (let’s represent this with the letter L)
Analysis:
One way to represent this problem is by using a tape diagram.
Since this problem involves repeated addition of the same quantity (that is K in this case), we can multiply the value of K by the number of times it is repeated (that is 3 in this case).
Solution:
Let’s multiply the value of K by 3 to get the value of L.
L = K X 3
Putting the value of K in the equation, we get
L = $15 X 3
Statement:
The total increase in the price of the jacket for three months is $45.
Division Word Problems
Division word problems involve situations where we divide or distribute something into equal parts. The resultant number is a fraction or a whole number.
Example: Olivia prepared food boxes to give away 300 donuts to charity. She put 8 donuts into each box. How many boxes of donuts were there? How many donuts were left over?
Given:
Total number of donuts = 300
The number of donuts in each box = 8
Required:
The number of boxes =?
The number of leftover donuts =?
Analysis:
Let’s visualize this problem using a tape diagram.
To find the number of leftover donuts, we need to find out the number of donuts packed in the boxes first. The problem states that Olivia put 8 donuts in each box, which implies that she distributed the donuts equally. Therefore, to get the total number of boxes, we can divide the total number of donuts by the number of donuts put in each box.
The quotient will indicate the number of boxes.
The remainder will indicate the number of leftover donuts.
If we get zero as the remainder, we can say that no donuts were left over. Otherwise, we can simply state the number of leftover donuts.
Solution:
Statement:
There were 37 boxes of donuts and 4 donuts were left over.
Can Online Word Problem Solver Help Math Students?
Many students rely heavily on online problem-solvers these days. While an online word problem solver can help students finish a math assignment faster, it may cease their ability to give reasons and think critically about math problems.
In the absence of an effective math tutor, students take longer than usual to master math word problems. Math Project is an award-winning after-school math program that focuses on increasing the math knowledge of students and developing their confidence to solve any kind of word problem without any difficulty. Call now at 1-844-628-4243 to book a free assessment.
Book a free assessment
Citations
Language and the Performance of English-Language Learners in Math Word Problems — https://meridian.allenpress.com
The impact of metacognitive strategies and self-regulating processes of solving math word problems — https://iejee.com
Division (mathematics) — https://en.wikipedia.org
: Decision problem pertaining to equivalence of expressions
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that [math]displaystyle{ x,y,z }[/math] are symbols representing real numbers — then a relevant solution to the word problem would, given the input [math]displaystyle{ (x cdot y)/z mathrel{overset{?}{=}} (x/z)cdot y }[/math], produce the output EQUAL, and similarly produce NOT_EQUAL from [math]displaystyle{ (x cdot y)/z mathrel{overset{?}{=}} (x/x)cdot y }[/math].
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in a equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that [math]displaystyle{ x cdot y cdot z^{-1} }[/math] is the normal form of [math]displaystyle{ (x cdot y)/z }[/math], [math]displaystyle{ (x/z)cdot y }[/math], and [math]displaystyle{ (y/z)cdot x }[/math], and devise a transformation system to rewrite those expressions to that form, in the process proving that all equivalent expressions will be rewritten to the same normal form.[2] But not all solutions to the word problem use a normal form theorem — there are algebraic properties which indirectly imply the existence of an algorithm.[1]
While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms [math]displaystyle{ t_1,t_2 }[/math] containing variables have instances that are equal, or in other words whether the equation [math]displaystyle{ t_1 = t_2 }[/math] has any solutions. As a common example, [math]displaystyle{ 2 + 3 stackrel{?}{=} 8 + (-3) }[/math] is a word problem in the integer group ℤ,
while [math]displaystyle{ 2 + x stackrel{?}{=} 8 + (-x) }[/math] is a unification problem in the same group; since the former terms happen to be equal in ℤ, the latter problem has the substitution [math]displaystyle{ {x mapsto 3} }[/math] as a solution.
History
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]:342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]:354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]:355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]:355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system [math]displaystyle{ T:=(Sigma, R) }[/math] and two words (strings) [math]displaystyle{ u, v in Sigma^* }[/math], can [math]displaystyle{ u }[/math] be transformed into [math]displaystyle{ v }[/math] by applying rules from [math]displaystyle{ R }[/math]? Note that the rewriting here is one-way. The word problem is the accessibility problem for symmetric rewrite relations, i.e. Thue systems.[27]
The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finally presented semigroups.[29][30]
The word problem for groups
- Main page: Word problem for groups
Given a presentation [math]displaystyle{ langle Smid mathcal{R} rangle }[/math] for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max Dehn in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable.[31]
The word problem in combinatorial calculus and lambda calculus
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems
Solving the word problem: deciding if [math]displaystyle{ x stackrel{*}{leftrightarrow} y }[/math] usually requires heuristic search (red, green), while deciding [math]displaystyle{ xdownarrow = ydownarrow }[/math] is straightforward (grey).
The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under [math]displaystyle{ stackrel{*}{leftrightarrow} }[/math]?[29] The word problem for an ARS is undecidable in general. However, there is a computable solution for the word problem in the specific case where every object reduces to a unique normal form in a finite number of steps (i.e. the system is convergent): two objects are equivalent under [math]displaystyle{ stackrel{*}{leftrightarrow} }[/math] if and only if they reduce to the same normal form.[33]
The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity (typically binary operations), and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 =a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient space W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
- [math]displaystyle{ ((a^{-1} cdot a) cdot (b cdot b^{-1}))^{-1} stackrel{R2}{rightsquigarrow} (1 cdot (b cdot b^{-1}))^{-1} stackrel{R13}{rightsquigarrow} (1 cdot 1)^{-1} stackrel{R1}{rightsquigarrow} 1 ^{-1} stackrel{R8}{rightsquigarrow} 1 }[/math], and
- [math]displaystyle{ b cdot ((a cdot b)^{-1} cdot a) stackrel{R17}{rightsquigarrow} b cdot ((b^{-1} cdot a^{-1}) cdot a) stackrel{R3}{rightsquigarrow} b cdot (b^{-1} cdot (a^{-1} cdot a)) stackrel{R2}{rightsquigarrow} b cdot (b^{-1} cdot 1) stackrel{R11}{rightsquigarrow} b cdot b^{-1} stackrel{R13}{rightsquigarrow} 1 }[/math]
share the same normal form, viz. [math]displaystyle{ 1 }[/math]; therefore both terms are equal in every group.
As another example, the term [math]displaystyle{ 1 cdot (a cdot b) }[/math] and [math]displaystyle{ b cdot (1 cdot a) }[/math] has the normal form [math]displaystyle{ a cdot b }[/math] and [math]displaystyle{ b cdot a }[/math], respectively. Since the normal forms are literally different, the original terms cannot be equal in every group. In fact, they are usually different in non-abelian groups.
| A1 | [math]displaystyle{ 1 cdot x }[/math] | [math]displaystyle{ = x }[/math] |
| A2 | [math]displaystyle{ x^{-1} cdot x }[/math] | [math]displaystyle{ = 1 }[/math] |
| A3 | [math]displaystyle{ (x cdot y) cdot z }[/math] | [math]displaystyle{ = x cdot (y cdot z) }[/math] |
| R1 | [math]displaystyle{ 1 cdot x }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R2 | [math]displaystyle{ x^{-1} cdot x }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R3 | [math]displaystyle{ (x cdot y) cdot z }[/math] | [math]displaystyle{ rightsquigarrow x cdot (y cdot z) }[/math] |
| R4 | [math]displaystyle{ x^{-1} cdot (x cdot y) }[/math] | [math]displaystyle{ rightsquigarrow y }[/math] |
| R8 | [math]displaystyle{ 1^{-1} }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R11 | [math]displaystyle{ x cdot 1 }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R12 | [math]displaystyle{ (x^{-1})^{-1} }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R13 | [math]displaystyle{ x cdot x^{-1} }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R14 | [math]displaystyle{ x cdot (x^{-1} cdot y) }[/math] | [math]displaystyle{ rightsquigarrow y }[/math] |
| R17 | [math]displaystyle{ (x cdot y)^{-1} }[/math] | [math]displaystyle{ rightsquigarrow y^{-1} cdot x^{-1} }[/math] |
See also
- Conjugacy problem
- Group isomorphism problem
References
- ↑ 1.0 1.1 1.2 1.3 Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ↑ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Miller, Charles F. (2014). Downey, Rod. ed. «Turing machines to word problems». Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. ISBN 9781107338579. http://minerva-access.unimelb.edu.au/bitstream/11343/51723/1/cfm-lnl42-turings-legacy-pp329-385-2014.pdf. Retrieved 6 December 2021.
- ↑ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ↑ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ↑ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue» (in English). Bulletin of the European Association for Theoretical Computer Science 72: 256–269.
- ↑ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0071&DMDID=DMDLOG_0013&L=1.
- ↑ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0072&DMDID=DMDLOG_0039&L=1.
- ↑ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ↑ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen 166 (3): 208–228. doi:10.1007/BF01361168. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002296799&L=1.
- ↑ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen 178 (2): 119–130. doi:10.1007/BF01350654. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002300036&L=1.
- ↑ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ↑ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ↑ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue». Journal of Symbolic Logic 12 (1): 1–11. doi:10.2307/2267170. https://www.wolframscience.com/prizes/tm23/images/Post2.pdf. Retrieved 6 December 2021.
- ↑ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20.». Journal of Symbolic Logic 16 (3): 215. doi:10.2307/2266407.
- ↑ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics 52 (2): 491–505. doi:10.2307/1969481.
- ↑ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory» (in ru). Proceedings of the Steklov Institute of Mathematics 44: 1–143.
- ↑ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings) 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ↑ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings) 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ↑ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ↑ Boone, William W. (1958). «The word problem». Proceedings of the National Academy of Sciences 44 (10): 1061–1065. doi:10.1073/pnas.44.10.1061. PMID 16590307. PMC 528693. Bibcode: 1958PNAS…44.1061B. http://www.pnas.org/cgi/reprint/44/10/1061.pdf.
- ↑ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics 70 (2): 207–265. doi:10.2307/1970103.
- ↑ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 262 (1311): 455–475. doi:10.1098/rspa.1961.0132. Bibcode: 1961RSPSA.262..455H.
- ↑ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics 77 (1): 16–32. doi:10.2307/1970200.
- ↑ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups». http://www.personal.psu.edu/t20/logic/seminar/050517.pdf.
- ↑ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ↑ 27.0 27.1 Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ↑ Davis, Martin (1978). «What is a Computation?». Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. https://www.cs.princeton.edu/courses/archive/spring11/cos116/handouts/daviscomputation.pdf. Retrieved 5 December 2021.
- ↑ 29.0 29.1 Baader, Franz; Nipkow, Tobias (5 August 1999) (in en). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3. https://www.google.com/books/edition/Term_Rewriting_and_All_That/N7BvXVUCQk8C?hl=en&gbpv=1&pg=PA59.
- ↑
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» (in Russian). Doklady Akademii Nauk SSSR 173 (6): 1264–1266. ISSN 0869-5652. http://mi.mathnet.ru/eng/dan/v173/i6/p1264.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics 8 (2): 555–557. ISSN 0197-6788.
- ↑ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory» (in ru). Trudy Mat. Inst. Steklov 44: 1–143.
- ↑ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ↑ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ↑ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ↑ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics 42 (1): 325–329. doi:10.2307/1969001.
- ↑ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics 43 (1): 104–115. doi:10.2307/1968883.
- ↑ K. H. Bläsius and H.-J. Bürckert, ed (1992). Deduktionsssysteme. Oldenbourg. pp. 291.; here: p.126, 134
- ↑ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Lesson 9: Introduction to Word Problems
/en/algebra-topics/solving-equations/content/
What are word problems?
A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you’ve ever taken a math class, you’ve probably solved a word problem. For instance, does this sound familiar?
Johnny has 12 apples. If he gives four to Susie, how many will he have left?
You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you’re supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:
12 — 4
12 — 4 = 8, so you know Johnny has 8 apples left.
Word problems in algebra
If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
We’ll work through an algebra word problem using these steps. Here’s a typical problem:
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?
It might seem complicated at first glance, but we already have all of the information we need to solve it. Let’s go through it step by step.
Step 1: Read through the problem carefully.
With any problem, start by reading through the problem. As you’re reading, consider:
- What question is the problem asking?
- What information do you already have?
Let’s take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
There’s only one question here. We’re trying to find out how many miles Jada drove. Now we need to locate any information that will help us answer this question.
There are a few important things we know that will help us figure out the total mileage Jada drove:
- The van cost $30 per day.
- In addition to paying a daily charge, Jada paid $0.50 per mile.
- Jada had the van for 2 days.
- The total cost was $360.
Step 2: Represent unknown numbers with variables.
In algebra, you represent unknown numbers with letters called variables. (To learn more about variables, see our lesson on reading algebraic expressions.) You can use a variable in the place of any amount you don’t know. Looking at our problem, do you see a quantity we should represent with a variable? It’s often the number we’re trying to find out.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
Since we’re trying to find the total number of miles Jada drove, we’ll represent that amount with a variable—at least until we know it. We’ll use the variable m for miles. Of course, we could use any variable, but m should be easy to remember.
Step 3: Translate the rest of the problem.
Let’s take another look at the problem, with the facts we’ll use to solve it highlighted.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It’s $30 per day, and $0.50 per mile. A simpler way to say this would be:
$30 per day plus $0.50 per mile is $360.
If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360. The shorter version will be easier to translate into a mathematical expression.
Let’s start by translating $30 per day. To calculate the cost of something that costs a certain amount per day, you’d multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅days, or 30 times the number of days. (Not sure why you’d translate it this way? Check out our lesson on writing algebraic expressions.)
$30 per day and $.50 per mile is $360
$30 ⋅ day + $.50 ⋅ mile = $360
As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50, $.50 per mile became $.50 ⋅ mile, and is became =.
Next, we’ll add in the numbers and variables we already know. We already know the number of days Jada drove, 2, so we can replace that. We’ve also already said we’ll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.
$30 ⋅ day + $.50 ⋅ mile = $360
30 ⋅ 2 + .5 ⋅ m = 360
Now we have our expression. All that’s left to do is solve it.
Step 4: Solve the problem.
This problem will take a few steps to solve. (If you’re not sure how to do the math in this section, you might want to review our lesson on simplifying expressions.) First, let’s simplify the expression as much as possible. We can multiply 30 and 2, so let’s go ahead and do that. We can also write .5 ⋅ m as 0.5m.
30 ⋅ 2 + .5 ⋅ m = 360
60 + .5m = 360
Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we’ll know what m is equal to—in other words, it will let us know the number of miles in our word problem.
We can start by getting rid of the 60 on the left side by subtracting it from both sides.
The only thing left to get rid of is .5. Since it’s being multiplied with m, we’ll do the reverse and divide both sides of the equation with it.
.5m / .5 is m and 300 / 0.50 is 600, so m = 600. In other words, the answer to our problem is 600—we now know Jada drove 600 miles.
Step 5: Check the problem.
To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got—600—and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada’s distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let’s take another look at the problem.
The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?
According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:
$30 per day and $0.50 per mile
30 ⋅ day + .5 ⋅ mile
30 ⋅ 2 + .5 ⋅ 600
60 + 300
360
According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We’re done!
While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.
Practice!
Let’s practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.
Problem 1
Try completing this problem on your own. When you’re done, move on to the next page to check your answer and see an explanation of the steps.
A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?
Problem 2
Here’s another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Problem 1 Answer
Here’s Problem 1:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
Answer: $29
Let’s solve this problem step by step. We’ll solve it the same way we solved the problem on page 1.
Step 1: Read through the problem carefully
The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it. Let’s look at the problem again. The question is right there in plain sight:
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So is the information we’ll need to answer the question:
- A single ticket costs $8.
- The family pass costs $25 more than half the price of the single ticket.
Step 2: Represent the unknown numbers with variables
The unknown number in this problem is the cost of the family pass. We’ll represent it with the variable f.
Step 3: Translate the rest of the problem
Let’s look at the problem again. This time, the important facts are highlighted.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
In other words, we could say that the cost of a family pass equals half of $8, plus $25. To turn this into a problem we can solve, we’ll have to translate it into math. Here’s how:
- First, replace the cost of a family pass with our variable f.
- Next, take out the dollar signs and replace words like plus and equals with operators.
- Finally, translate the rest of the problem. Half of can be written as 1/2 times, or 1/2 ⋅ :
f equals half of $8 plus $25
f = half of 8 + 25
f = 1/2 ⋅ 8 + 25
Step 4: Solve the problem
Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.
- f is already alone on the left side of the equation, so all we have to do is calculate the right side.
- First, multiply 1/2 by 8. 1/2 ⋅ 8 is 4.
- Next, add 4 and 25. 4 + 25 equals 29 .
f = 1/2 ⋅ 8 + 25
f = 4 + 25
f = 29
That’s it! f is equal to 29. In other words, the cost of a family pass is $29.
Step 5: Check your work
Finally, let’s check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let’s look at the original problem again.
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.
- We could translate this into this equation, with s standing for the cost of a single ticket.
- Let’s work on the right side first. 29 — 25 is 4.
- To find the value of s, we have to get it alone on the left side of the equation. This means getting rid of 1/2. To do this, we’ll multiply each side by the inverse of 1/2: 2.
1/2s = 29 — 25
1/2s = 4
s = 8
According to our math, s = 8. In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that’s correct!
A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?
So now we’re sure about the answer to our problem: The cost of a family pass is $29.
Problem 2 Answer
Here’s Problem 2:
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
Answer: $70
Let’s go through this problem one step at a time.
Step 1: Read through the problem carefully
Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it. What’s the question here?
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
To solve the problem, you’ll have to find out how much money Mo gave to charity. All the important information you need is in the problem:
- The amount Flor donated is three times as much the amount Mo donated
- Flor and Mo’s donations add up to $280 total
Step 2: Represent the unknown numbers with variables
The unknown number we’re trying to identify in this problem is Mo’s donation. We’ll represent it with the variable m.
Step 3: Translate the rest of the problem
Here’s the problem again. This time, the important facts are highlighted.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
The important facts of the problem could also be expressed this way:
Mo’s donation plus Flor’s donation equals $280
Because we know that Flor’s donation is three times as much as Mo’s donation, we could go even further and say:
Mo’s donation plus three times Mo’s donation equals $280
We can translate this into a math problem in only a few steps. Here’s how:
- Because we’ve already said we’ll represent the amount of Mo’s donation with the variable m, let’s start by replacing Mo’s donation with m.
- Next, we can put in mathematical operators in place of certain words. We’ll also take out the dollar sign.
- Finally, let’s write three times mathematically. Three times m can also be written as 3 ⋅ m, or just 3m.
m plus three times m equals $280
m + three times m = 280
m + 3m = 280
Step 4: Solve the problem
It will only take a few steps to solve this problem.
- To get the correct answer, we’ll have to get m alone on one side of the equation.
- To start, let’s add m and 3m. That’s 4m.
- We can get rid of the 4 next to the m by dividing both sides by 4. 4m / 4 is m, and 280 / 4 is 70.
m + 3m = 280
4m = 280
m = 70.
We’ve got our answer: m = 70. In other words, Mo donated $70.
Step 5: Check your work
The answer to our problem is $70, but we should check just to be sure. Let’s look at our problem again.
Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?
If our answer is correct, $70 and three times $70 should add up to $280.
- We can write our new equation like this:
- The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.
- The last step is to add 70 and 210. 70 plus 210 equals 280.
70 + 3 ⋅ 70 = 280
70 + 210 = 280
280 = 280
280 is the combined cost of the tickets in our original problem. Our answer is correct: Mo gave $70 to charity.
/en/algebra-topics/distance-word-problems/content/
Word problems are described as «verbal descriptions of problem situations wherein one or more questions are raised the answer to which can be obtained by the application of mathematical operations to numerical data available in the problem statement» (Verschaffel, Greer, & De Corte, 2000). Solving word problems involves:
- The well-organized and flexible use of both conceptual and procedural knowledge
- Strategies and metacognition
- Positive affect and beliefs (De Corte, Greer, & Verschaffel, 1996; Schoenfeld, 1992)
Is Solving Word Problems the Same as Mathematical Modeling?
Solving word problems is not considered to be the same as mathematical modeling. Mathematical modeling tends to be a more complex process involving identifying questions to answer about the real world, making assumptions, identifying variables, translating a phenomenon into a mathematical model, assessing the solution, and iterating on the process to refine and extend the model (COMAP & SIAM, 2016). The process to solve a word problem isn’t necessarily as complex, as the problem itself usually gives the reader the question to answer and the information necessary to answer it, and doesn’t require modeling’s level of meaning-making and interpretation. These differences are relative, however, depending on the abilities of the student and the nature of the solution required to answer the problem.
Understanding the Challenge
What Makes Word Problems Difficult for Students?
Students’ primary difficulty in solving word problems is attributed to their «suspension of sense-making» (Schoenfeld, 1991; Template:Verschaffel, Greer, & De Corte). Instead of thinking through the context of the word problem to understand it, many students simply seek a simple application of arithmetic needed to produce an answer, whether it makes sense or not. In a video, Kaplinsky (2013) reproduces a result of early 1980s research conducted at the Institut de Recherche sur l’Enseignement des Mathématiques in France.
Math teachers are often concerned about students’ abilities to transfer classroom learning into the world beyond the classroom, but this «suspension of sense-making» shows that the reverse is also difficult – students struggle to apply their knowledge and understanding of the world back into a mathematics classroom. Having been conditioned with years of arithmetic, almost always involving obvious operations and the expectation that each problem has a correct answer, students develop a «compulsion to calculate» (Stacey & MacGregor, 1999) that can interfere with the development of the algebraic thinking that is usually needed to solve word problems. Some (but not all) research findings suggest that «compulsion to calculate» worsens as students age and develop beliefs that math is a collection of rules (Radatz, 1983; Stern, 1992, both as cited in Verschaffel, Greer, & De Corte, 2000, p. 5).
Students can also struggle with word problems because they have difficulty with academic vocabulary, mathematical vocabulary, or both. Due to these difficulties, English language learners and students of low socioeconomic status score lower on standardized assessment items than proficient speakers of English (Abedi & Lord, 2001).
What Makes Word Problems Difficult for Teachers?
Some teachers ignore or struggle to apply their real-world knowledge when solving word problems, just like students (Verschaffel, De Corte, & Borghart, 1997). During instruction, teachers often try to help students «strip away the stuff we don’t really need» (Chapman, 2006, p. 219) and reduce the problem to the numbers and keywords or phrases that indicate operations or relations. This dismissal of the real-world aspects of word problems can contribute to students’ suspension of sense-making and their compulsion to calculate.
Most teachers believe or assume that students will have more difficulty solving a word problem than solving an algebraic equation that represents the same mathematics without the words. Because of this, they believe in teaching word problems only after students master solving similar problems as equations. Traditional math textbooks reinforce this belief by placing word problems at the end of practice sets. This belief or assumption has been shown to be false, at least under some conditions. When tested, students have shown that they can be more successful with word or verbal problems than they are with equivalent problems that are purely symbolic (Nathan & Koedinger, 2000a, 2000b). Other research suggests that skill in algorithmic computation may not correspond to students’ ability to conceptualize the relationship between numbers in word problems (Fuchs et al., 2006).
Recommendations
Use Word Problems to Teach Students Mathematics
Word problems are not just for applications of already-known mathematics. In fact, the most powerful way to use word problems in the classroom is as a means to help students learn math. By situating mathematics in contexts that are understandable for students, word problems encourage students to pursue solution strategies that make sense to them and lead more often to correct answers (Koedinger & Nathan, 2004). These strategies can then be made more formal and symbolic with additional instruction.
This is obvious for teachers of young children. In early mathematics, problems are almost always situated in realistic contexts that children can make sense of. There is no reason that this should end in early childhood. Students at all levels should engage in mathematics in a sensible context before it is made formal and symbolic.
Engage Student Reasoning
Instead of dismissing the context of word problems, teachers should take time with students to make sense of word problems and their supporting context. Teachers should push back against students’ compulsion to calculate by focusing on the relationship between the knowns and unknowns in word problems, and not rush to find an answer (Kieran, 2014). Some types of word problems might be particularly useful for promoting reasoning because they either lack an obvious strategy, don’t have one right answer, or could be «tricky» for students who assume the problem is straightforward. Some examples:
- Pete organized a birthday party for his tenth birthday. He invited 8 boy friends and 4 girl friends. How many friends did Pete invite for his birthday party?
- Carl has 5 friends and Georges has 6 friends. Carl and Georges decide to give a party together. They invite all their friends. All friends are present. How many friends are there at the party?
- Kathy, Ingrid, Hans and Tom got from their grandfather a box with 14 chocolate bars, which they shared equally amongst themselves. How many chocolate bars did each grandchild get?
- Grandfather gives his 4 grandchildren a box containing 18 balloons, which they share equally. How many balloons does each grandchild get?
- A shopkeeper has two containers for apples. The first container contains 60 apples and the other 90 apples. He puts all the apples into a new, bigger container. How many apples are there in that new container?
- What will be the temperature of water in a container if you pour 1 jug of water at 80 degrees F and 1 jug of water at 40 degrees F into it? (Nesher, 1980)
Verschaffel, De Corte, and Lasure (1994) used these word problems to see if students would reason differently with the odd- and even-numbered items. Their research and subsequent studies have shown that the vast majority of students – sometimes more than 90 percent – will calculate and produce answers for the even-numbered items just as they do for the odd-numbered items, without any additional reasoning about real-world considerations. Giving students a general warning, such as «these problems are not as easy as they look,» did not significantly help students. Instead, teachers can promote student reasoning by providing supports specific to each problem, such as encouraging students to explain their answer and why it makes sense, to draw a picture of their solution, or to consider a hypothetical but contrasting solution from another student. While these strategies can increase the number of students who reason with these problems correctly, in multiple studies they rarely produced correct answers for much more than 50 percent of students (see Chapter 3, Verschaffel, Greer, De Corte). In other words, these strategies are helpful but unlikely by themselves to ensure success for all students.
Numberless Word Problems
Perhaps the most direct way of pushing back against students’ compulsion to calculate is to give them word problems without numbers. Brian Bushart, an elementary teacher and mathematics curriculum coordinator from Texas, popularized the idea of «numberless word problems» after a colleague tried the approach with some third-grade students. Numberless word problems aren’t entirely new, as the book Problems Without Figures (Gillan, 1909) presented something vaguely similar in the early 20th century. Bushart’s approach goes much further by focusing on the instructional moves and opportunities for student discourse that century-old approaches did not. Bushart’s blog post (2014) and subsequent collection of resources (n.d.) describe both his process for numberless word problems and numerous examples for a range of content and grade levels.
Example 1: A Single-Step Word Problem
For an example of a numberless word problem, consider this item released from the Grade 4 PARCC test (PARCC, 2016a):
A pitcher contains 2 liters of juice. A glass is filled with 180 milliliters of juice from the pitcher. How many milliliters of juice are left in the pitcher after filling the glass?
Instead of giving students this problem as written, teachers can present a numberless version of this problem on a series of slides:
Slide 1: A pitcher contains some juice.
Slide 2: A pitcher contains some juice. A glass is filled with some of the juice from the pitcher.
Slide 3: A pitcher contains some juice. A glass is filled with some of the juice from the pitcher. How much juice is left in the pitcher after filling the glass?
Slide 4: A pitcher contains 2 liters of juice. A glass is filled with some of the juice from the pitcher. How much juice is left in the pitcher after filling the glass?
Slide 5: A pitcher contains 2 liters of juice. A glass is filled with 180 milliliters of juice from the pitcher. How much juice is left in the pitcher after filling the glass?
Slide 6: A pitcher contains 2 liters of juice. A glass is filled with 180 milliliters of juice from the pitcher. How many milliliters of juice are left in the pitcher after filling the glass?
Teachers can adjust the number of slides depending on student ability, the difficulty of the problem, and the amount of time the teacher wishes to dedicate to building and sharing student sense-making. In this example, a teacher might stop after Slide 1 to make sure students know what a pitcher is and to have students estimate the capacity of a pitcher. After Slide 2, the teacher can ask students to explain what will happen to the amount of juice in the pitcher, and the relationship between the juice in the pitcher and the juice in the glass. With each subsequent slide, the teacher can continue to probe students’ sense-making and understanding of the relationships between the quantities described by the problem.
Example 2: A Multi-Step Word Problem
Teachers can also use numberless word problems with multi-step word problems. Consider this multi-step item released from the Grade 5 PARCC test (PARCC, 2016b):
Dana is making bean soup. The recipe she has makes 10 servings and uses [math]displaystyle{ frac{3}{4} }[/math] of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup? She has [math]displaystyle{ frac{1}{16} }[/math] of a pound of beans in one container and [math]displaystyle{ frac{1}{4} }[/math] of a pound of beans in another container. How many more pounds of beans does Dana need to make 5 servings of soup?
Just as with Example 1, a teacher could present a numberless version of this word problem on a series of slides.
Slide 1: Dana is making bean soup. The recipe she has makes a number of servings and uses an amount beans.
The teacher could use Slide 1 to make sure students understand the basic context. Students may observe that «If she wants to make more soup she’ll need more beans,» or have other insights that help establish the relationship between the amount of soup and the amount of beans.
Slide 2: Dana is making bean soup. The recipe she has makes a number of servings and uses an amount of beans. What amount of beans does she need to make a smaller number of servings of soup?
With Slide 2, students should observe that less soup should need less beans. Students might begin to conjecture with statements like, «If she wants half as much soup, she’ll need half the beans.»
Slide 3: Dana is making bean soup. The recipe she has makes a number of servings and uses an amount of beans. What amount of beans does she need to make a smaller number of servings of soup? She already has a small amount of beans. How much more beans does Dana need to make her soup?
After seeing Slide 3, students should now grapple with an even more complex relationship: Not only does Dana need less beans because she’s making less soup than called for by the recipe, but she already has some of the beans that she’ll need. Student observations and conjectures at this point should suggest two operations, such as a first step involving division to find the amount of beans needed in the reduced recipe, and a second step to subtract the amount of beans Dana already has. With this multi-step complexity, it would be useful for students to draw or otherwise illustrate their thinking.
Slide 4: Dana is making bean soup. The recipe she has makes 10 servings and uses an amount of beans. What amount of beans does she need to make 5 servings of soup? She already has a small amount of beans. How much more beans does Dana need to make 5 servings of soup?
Slide 4 specifies the numbers of servings, but not the beans. With this information, students can revise their observations to make clear that the recipe’s amount of beans needs to be divided by 2, with an additional amount subtracted, to find how many more beans Dana needs.
Slide 5: Dana is making bean soup. The recipe she has makes 10 servings and uses [math]displaystyle{ frac{3}{4} }[/math] of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup? She already has a small amount of beans. How many more pounds of beans does Dana need to make 5 servings of soup?
With Slide 5, students should have already decided that the amount of beans in the recipe needs to be divided by 2, and now they can focus on finding [math]displaystyle{ frac{3}{4} div 2 }[/math]. Students may also notice that the problem now makes clear that all measurements of beans is in pounds.
Slide 6: Dana is making bean soup. The recipe she has makes 10 servings and uses [math]displaystyle{ frac{3}{4} }[/math] of a pound of beans. How many total pounds of beans does she need to make 5 servings of soup? She has [math]displaystyle{ frac{1}{16} }[/math] of a pound of beans in one container and [math]displaystyle{ frac{1}{4} }[/math] of a pound of beans in another container. How many more pounds of beans does Dana need to make 5 servings of soup?
Slide 6 presents the word problem in its original form, and students may be surprised that the small amount of beans Dana already had is represented as two amounts that need to be considered together. Because of the complexity of this problem, there may not be an ideal time to introduce this information, but a 5th grader who has reasoned through the problem and gotten this far should be able to reason with the two small quantities of beans, either by adding them first and then subtracting the sum from [math]displaystyle{ frac{3}{8} }[/math] or by performing two subtractions.
Add Authenticity
Students have shown to be more successful with word problems when they are required to engage with the context in authentic ways. For example, DeFranco and Curcio (1997, as cited by Verschaffel, Greer, De Corte) gave a group of 20 sixth grade students the following word problem: “328 senior citizens are going on a trip. A bus can seat 40 people. How many buses are needed so that all the senior citizens can go on the trip?” Later, the researchers gave the students a similar problem, except they presented it in the form of a fact sheet with the numbers of people and the size of vans, and instructions for making a phone call that simulated placing an actual order for the number of required vehicles. In the first scenario, only 2 of the 20 students answered correctly and properly reasoned with the remainder left by the division. In the second scenario, using a more authentic setting, 16 of the 20 students answered correctly and reasoned appropriately with the remainder, either by rounding up to the next whole van or requesting «like a car or something» to transport the small number of remaining passengers.
Address Language Complexity
Language complexity can be addressed either by reducing the complexity or providing students with additional support. For students who struggle with the language of word problems, it can be helpful to rewrite the problem using simpler, more familiar language, or a student’s native language (Bernardo, 1999). These kinds of modifications tend to help English learners and low-SES students more than their English-proficient and higher-SES counterparts, meaning this strategy could help reduce achievement gaps (Abedi & Lord, 2001).
Teachers can also provide extra support. Recommendations for teaching English language learners include focusing on student reasoning and discourse, rather than correctness of language use, and using language learners’ knowledge and experiences as resources (Moschkovich, 2012). The Understanding Language website (ell.stanford.edu) is a recommended resource for understanding how to support language learners in mathematics.
References
Abedi, J., & Lord, C. (2001). The language factor in mathematics tests. Applied Measurement in Education, 14(3), 219–234. https://doi.org/10.1207/S15324818AME1403_2
Bernardo, A. B. I. (1999). Overcoming obstacles to understanding and solving word problems in mathematics. Educational Psychology, 19(2), 149–163. https://doi.org/10.1080/0144341990190203
Bushart, B. (n.d.). Numberless word problems. Retrieved November 16, 2017, from https://bstockus.wordpress.com/numberless-word-problems/
Bushart, B. (2014, October 6). Numberless word problems [Blog post]. Retrieved November 16, 2017, from https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/
Chapman, O. (2006). Classroom practices for context of mathematics word problems. Educational Studies in Mathematics, 62(2), 211–230. https://doi.org/10.1007/s10649-006-7834-1
COMAP, & SIAM. (2016). GAIMME: Guidelines for assessment & instruction in mathematical modeling education. Bedford, MA. Retrieved from http://www.comap.com/Free/GAIMME/index.html
De Corte, E., Greer, B., & Verschaffel, L. (1996). Mathematics teaching and learning. In D. C. Berliner & R. C. Calfee (Eds.), Handbook of educational psychology (pp. 491–549). New York, NY: Lawrence Erlbaum Associates.
DeFranco, T. C., & Curcio, F. R. (1997). A division problem with a remainder embedded across two contexts: Children’s solutions in restrictive vs. real-world settings. Focus on Learning Problems in Mathematics, 19(2), 58–72.
Fuchs, L. S., Fuchs, D., Compton, D. L., Powell, S. R., Seethaler, P. M., Capizzi, A. M., … Fletcher, J. M. (2006). The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29
Gillan, S. Y. (1909). Problems without figures. Milwaukee, WI: S. Y. Gillan & Company. Retrieved from http://www.schoolinfosystem.org/pdf/2008/10/problemswithoutfigures.pdf
Kaplinsky, R. (2013). How old is the shepard? Retrieved November 3, 2017, from https://www.youtube.com/watch?v=kibaFBgaPx4
Kieran, C. (2014). What does research tell us about fostering algebraic reasoning in school algebra? Reston, VA. Retrieved from http://www.nctm.org/Research-and-Advocacy/Research-Brief-and-Clips/Algebraic-Reasoning-in-School-Algebra/
Koedinger, K. R., & Nathan, M. J. (2004). The real story behind story problems: Effects of representations on quantitative reasoning. Journal of the Learning Sciences, 13(2), 129–164. https://doi.org/10.1207/s15327809jls1302_1
Moschkovich, J. N. (2012). Mathematics, the Common Core, and language. Understanding Language: Language, Literacy, and Learning in the Content Areas. Retrieved from http://ell.stanford.edu/publication/mathematics-common-core-and-language
Nathan, M. J., & Koedinger, K. R. (2000a). An investigation of teachers’ beliefs of students’ algebra development. Cognition and Instruction, 18(2), 209–237. https://doi.org/10.1207/S1532690XCI1802_03
Nathan, M. J., & Koedinger, K. R. (2000b). Teachers’ and researchers’ beliefs about the development of algebraic reasoning. Journal for Research in Mathematics Education, 31(2), 168–190. https://doi.org/10.2307/749750
Nesher, P. (1980). The stereotyped nature of school word problems. For the Learning of Mathematics, 1(1), 41–48. Retrieved from http://flm-journal.org/Articles/flm_1-1_Nesher.pdf
PARCC. (2016a). Math Spring Operational 2016 Grade 4 Released Items. Partnership for Assessment of Readiness for College and Careers. Retrieved from http://parcc-assessment.org/images/releaseditems/Grade_04_Math_Item_Set.pdf
PARCC. (2016b). Math Spring Operational 2016 Grade 5 Released Items. Partnership for Assessment of Readiness for College and Careers. Retrieved from http://parcc-assessment.org/images/releaseditems/Grade_05_Math_Item_Set.pdf
Radatz, H. (1983). Untersuchungen zum Lösen eingekleideter Aufgaben. Zeitschrift Fur Mathematic-Didaktik, 4(2), 205–2017. https://doi.org/10.1007/BF03339231
Schoenfeld, A. H. (1991). On mathematics as sense-making: An informal attack on the unfortunate divorce of formal and informal mathematics. In J. F. Voss, D. N. Perkins, & J. W. Segal (Eds.), Informal reasoning and education (pp. 311–343). Hillsdale, NJ: Lawrence Erlbaum Associates.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). Reston, VA: National Council of Teachers of Mathematics.
Stacey, K., & MacGregor, M. (1999). Learning the algebraic method of solving problems. The Journal of Mathematical Behavior, 18(2), 149–167. https://doi.org/10.1016/S0732-3123(99)00026-7
Stern, E. (1992). Warum werden Kapitänsaufgaben “gelöst”? Dav Verstehen von Textaufgaben aus phychologischer Sicht. Der Mathematikunterricht, 28(5), 7–29.
Verschaffel, L., De Corte, E., & Borghart, I. (1997). Pre-service teachers’ conceptions and beliefs about the role of real-world knowledge in mathematical modelling of school word problems. Learning and Instruction, 7(4), 339–359. https://doi.org/10.1016/S0959-4752(97)00008-X
Verschaffel, L., De Corte, E., & Lasure, S. (1994). Realistic considerations in mathematical modeling of school arithmetic word problems. Learning and Instruction, 4(4), 273–294. https://doi.org/10.1016/0959-4752(94)90002-7
Verschaffel, L., Greer, B., & De Corte, E. (2000). Making sense of word problems. Lisse, The Netherlands: Swets & Zeitlinger.
This article is for parents who think about how to help with math and support their children. The math word problems below provide a gentle introduction to common math operations for schoolers of different grades.
What are math word problems?
During long-time education, kids face various hurdles that turn into real challenges. Parents shouldn’t leave their youngsters with their problems. They need an adult’s possible help, but what if the parents themselves aren’t good at mathematics? All’s not lost. You can provide your kid with different types of support. Not let a kid burn the midnight oil! Help him/ her to get over the challenges thanks to these captivating math word examples.
Math word problems are short math questions formulated into one or several sentences. They help schoolers to apply their knowledge to real-life scenarios. Besides, this kind of task helps kids to understand this subject better.
Addition for the first and second grades
These math examples are perfect for kids that just stepped into primary school. Here you find six easy math problems with answers:
1. Peter has eight apples. Dennis gives Peter three more. How many apples does Peter have in all?
Show answer
Answer: 8 apples + 3 apples = 11 apples.
2. Ann has seven candies. Lack gives her seven candies more. How many candies does Ann have in all?
Show answer
Answer: 7 candies + 7 candies = 14 candies.
3. Walter has two books. Matt has nine books. If Matt gives all his books to Walter, how many books will Walter have?
Show answer
Answer: 2 books + 9 books = 11 books.
4. There are three crayons on the table. Albert puts five more crayons on the table. How many crayons are on the table?
Show answer
Answer: 3 crayons + 5 crayons = 8 crayons.
5. Bill has nine oranges. His friend has one orange. If his friend gives his orange to Bill, how many oranges will Bill have?
Show answer
Answer: 9 oranges + 1 orange = 10 oranges.
6. Jassie has four leaves. Ben has two leaves. Ben gives her all his leaves. How many leaves does Jessie have in all?
Show answer
Answer: 4 leaves + 2 leaves = 6 leaves.
Subtraction for the first and second grades
1. There were three books in total at the book shop. A customer bought one book. How many books are left?
Show answer
Answer: 3 books – 1 book = 2 books.
2. There are five pizzas in total at the pizza shop. Andy bought one pizza. How many pizzas are left?
Show answer
Answer: 5 pizzas – 1 pizza = 4 pizzas.
3. Liza had eleven stickers. She gave one of her stickers to Sarah. How many stickers does Liza have?
Show answer
Answer: 11 stickers – 1 sticker = 10 stickers.
4. Adrianna had ten stones. But then she left two stones. How many stones does Adrianna have?
Show answer
Answer: 10 stones – 2 stones = 8 stones.
5. Mary bought a big bag of candy to share with her friends. There were 20 candies in the bag. Mary gave three candies to Marissa. She also gave three candies to Kayla. How many candies were left?
Show answer
Answer: 20 candies – 3 candies – 3 candies = 14 candies.
6. Betty had a pack of 25 pencil crayons. She gave five to her friend Theresa. She gave three to her friend Mary. How many pencil crayons does Betty have left?
Show answer
Answer: 25 crayons – 5 crayons – 3 crayons = 17 crayons.
Multiplication for the 2nd grade and 3rd grade
See the simple multiplication word problems. Make sure that the kid has a concrete understanding of the meaning of multiplication before.
Bill is having his friends over for the game night. He decided to prepare snacks and games.
1. He makes mini sandwiches. If he has five friends coming over and he made three sandwiches for each of them, how many sandwiches did he make?
Show answer
Answer: 5 x 3 = 15 sandwiches.
2. He also decided to get some juice from fresh oranges. If he used two oranges per glass of juice and made six glasses of juice, how many oranges did he use?
Show answer
Answer: 2 x 6 = 12 oranges.
3. Then Bill prepared the games for his five friends. If each game takes 7 minutes to prepare and he prepared a total of four games, how many minutes did it take for Bill to prepare all the games?
Show answer
Answer: 7 x 4 = 28 minutes.
4. Bill decided to have takeout food as well. If each friend and Bill eat three slices of pizza, how many slices of pizza do they have in total?
Show answer
Answer: 6 (5 friends and Bill) x 3 slices of pizza = 18 slices of pizza.
Mike is having a party at his house to celebrate his birthday. He invited some friends and family.
1. He and his mother prepared cupcakes for dessert. Each box had 8 cupcakes, and they prepared four boxes. How many cupcakes have they prepared in the total?
Show answer
Answer: 8 x 4 = 32 cupcakes.
2. They also baked some cookies. If they baked 6 pans of cookies, and there were 7 cookies per pan, how many cookies did they bake?
Show answer
Answer: 6 x 7 = 42 cookies.
3. Mike planned to serve some cold drinks as well. If they make 7 pitchers of drinks and each pitcher can fill 5 glasses, how many glasses of drinks are they preparing?
Show answer
Answer: 7 x 5 = 35 glasses.
4. At the end of the party, Mike wants to give away some souvenirs to his 6 closest friends. If he gives 2 souvenir items for each friend, how many souvenirs does Mike prepare?
Show answer
Answer: 6 x 2 = 12 souvenirs.
Division: best for 3rd and 4th grades
1. If you have 10 books split evenly into 2 bags, how many books are in each bag?
Show answer
Answer: 10 : 2 = 5 books.
2. You have 40 tickets for the fair. Each ride costs 2 tickets. How many rides can you go on?
3. The school has $20,000 to buy new equipment. If each piece of equipment costs $100, how many pieces can the school buy in total?
Show answer
Answer: $20,000 : $100= 200.
4. Melissa has 2 packs of tennis balls for $10 in total. How much does 1 pack of tennis balls cost?
5. Jack has 25 books. He has a bookshelf with 5 shelves on it. If Jack puts the same number of books on each shelf, how many books will be on each shelf?
6. Matt is having a picnic for his family. He has 36 cookies. There are 6 people in his family. If each person gets the same number of cookies, how many cookies will each person get?
Division with remainders for fourth and fifth grades
1. Sarah sold 35 boxes of cookies. How many cases of ten boxes, plus extra boxes does Sarah need to deliver?
Show answer
Answer: 35 boxes divided by 10 boxes per case = 3 cases and 5 boxes.
2. Candies come in packages of 16. Mat ate 46 candies. How many whole packages of candies did he eat, and how many candies did he leave? 46 candies divided by 16 candies = 2 packages and 2 candies left over.
3. Mary sold 24 boxes of chocolate biscuits. How many cases of ten boxes, plus extra boxes does she need to deliver?
Show answer
Answer: 24 boxes divided by 10 boxes per case = 2 cases and four boxes.
4. Gummy bears come in packages of 25. Suzie and Tom ate 30 gummy bears. How many whole packages did they eat? How many gummy bears did they leave?
Show answer
Answer: 30 divided by 25 = 1 package they have eaten and 20 gummy bears left over.
5. Darel sold 55 ice-creams. How many cases of ten boxes, plus extra boxes does he need to deliver?
Show answer
Answer: 55 boxes divided by 10 boxes per case = 5 cases and 5 boxes.
6. Crackers come in packages of 8. Mat ate 20 crackers. How many whole packages of crackers did he eat, and how many crackers did he leave?
Show answer
Answer: 20 divided by 8 = 2 packages eaten and 4 crackers are left.
Mixed operations for the fifth grade
These math word problems involve four basic operations: addition, multiplication, subtraction, and division. They suit best for the fifth-grade schoolers.
200 planes are taking off from the airport daily. During the Christmas holidays, the airport is busier — 240 planes are taking off every day from the airport.
1. During the Christmas holidays, how many planes take off from the airport in each hour if the airport opens 12 hours daily?
Show answer
Answer: 240÷12=20 planes take off from this airport each hour during the Christmas holidays.
2. Each plane takes 220 passengers. How many passengers depart from the airport every hour during the Christmas holidays? 20 x 220 = 4400.
Show answer
Answer: 4400 passengers depart from the airport every hour.
3. Compared with a normal day, how many more passengers are departing from the airport in a day during the Christmas holidays?
Show answer
Answer: (240-200) x 220 = 8800 more passengers departing from the airport in a day during the Christmas holidays.
4. During normal days on average 650 passengers are late for their plane daily. During the Christmas holidays, 1300 passengers are late for their plane. That’s why 14 planes couldn’t take off and are delayed. How many more passengers are late for their planes during Christmas week?
Show answer
Answer: 1300 – 650 = 650 more passengers are late for their planes each day during the Christmas holidays.
5. According to the administration’s study, an additional 5 minutes of delay in the overall operation of the airport is caused for every 27 passengers that are late for their flights. What is the delay in the overall operation if there are 732 passengers late for their flights?
Show answer
Answer: 732 ÷ 27 × 5 = 136. There will be a delay of 136 minutes in the overall operation of the airport.
Extra info math problems for the fifth grade
1. Ann has 7 pairs of red socks and 8 pairs of pink socks. Her sister has 12 pairs of white socks. How many pairs of socks does Ann have?
2. Kurt spent 17 minutes doing home tasks. He took a 3-minute snack break. Then he studied for 10 more minutes. How long did Kurt study altogether?
Show answer
Answer: 17 + 10 = 27 minutes.
3. There were 15 spelling words on the test. The first schooler spelled 9 words correctly. Miguel spelled 8 words correctly. How many words did Miguel spell incorrectly?
4. In the morning, Jack gave his friend 2 gummies. His friend ate 1 of them. Later Jack gave his friend 7 more gummies. How many gummies did Jack give his friend in all?
5. Peter wants to buy 2 candy bars. They cost 8 cents, and the gum costs 5 cents. How much will Peter pay?
Finding averages for 5th grade
We need to find averages in many situations in everyday life.
1. The dog slept 8 hours on Monday, 10 hours on Tuesday, and 900 minutes on Wednesday. What was the
average number of hours the dog slept per day?
Show answer
Answer: (8+10+(900:60)) : 3 = 11 hours.
2. Jakarta can get a lot of rain in the rainy season. The rainfall during 6 days was 90 mm, 74 mm, 112 mm, 30 mm, 100 mm, and 44 mm. What was the average daily rainfall during this period?
Show answer
Answer: (90+74+112+30+100+44) : 6 = 75 mm.
3. Mary bought 4 books. The prices of the first 3 books were $30, $15, and $18. The average price she paid for the 4 books was $25 per books. How much did she pay for the 4th books?


Math & logic courses for kids
Times more complex than school, extremely fun, interactive and rewarding to keep 7-13 years old kids engaged. We’re gonna make them love math!
learn more
Ordering and number sense for the 5th grade
1. There are 135 pencils, 200 pens, 167 crayons, and 555 books in the bookshop. How would you write these numbers in ascending order?
Show answer
Answer: 135, 167, 200, 555
2. There are five carrots, one cabbage, eleven eggs, and 15 apples in the fridge. How would you write these numbers in descending order?
3. Peter has completed exercises on pages 279, 256, 264, 259, and 192. How would you write these numbers in ascending order?
Show answer
Answer: 192, 256, 259, 264, 279.
4. Mary picked 32 pants, 15 dresses, 26 pairs of socks, 10 purses. Put all these numbers in order.
5. The family bought 12 cans of tuna, 23 potatoes, 11 onions, and 33 pears. Put all these numbers in order.
Fractions for the 6th-8th grades
1. Jannet cooked 12 lemon biscuits for her daughter, Jill. She ate up 4 biscuits. What fraction of lemon biscuits did Jill eat?
Show answer
Answer: 1/3 of the lemon biscuits.
2. Guinet travels a distance of 7 miles to reach her school. The bus covers only 5 miles. Then she has to walk 2 miles to reach the school. What fraction of the distance does Guinet travel by bus?
Show answer
Answer: 5/7 of the distance
3. Bob has 24 pencils in a box. Eighteen pencils have #2 marked on them, and the 6 are marked #3. What fraction of pencils are marked #3?
Show answer
Answer: 1/4 of the pencils.
4. My mother places 15 tulips in a glass vase. It holds 6 yellow tulips and 9 red tulips. What fraction of tulips are red?
Show answer
Answer: 3/5 of the tulips.
5. Bill owns 14 pairs of socks, of which 7 pairs are white, and the rest are brown. What fraction of pairs of socks are brown?
Show answer
Answer: 1/2 of the pairs of socks.
6. Bred spotted a total of 39 birds in an aviary at the Zoo. He counted 18 macaws and 21 cockatoos. What fraction of macaws did Bred spot at the aviary?
Show answer
Answer: 6/13 of the birds.
Decimals for the 6th grade
Write in words the following decimals:
- 0,004
- 0,07
- 2,1
- 0,725
- 46,36
- 2000,19
Show answer
Answer:
- 0,004 = four thousandths.
- 0,07 = seven hundredths.
- 2,1 = two and one tenth.
- 0,725 = seven hundred twenty five thousandths.
- 46,36 = foury six and thirty six hundredths.
- 2000,19 = two thousand and nineteen hundredths.
Comparing and sequencing for the 6th grade
1. The older brother picked 42 apples at the orchard. The younger brother picked only 22 apples. How many more apples did the older brother pick?
Show answer
Answer: 42 – 22 = 20 apples more.
2. There were 16 oranges in a basket and 66 oranges in a barrel. How many fewer oranges were in the basket than were in the barrel?
Show answer
Answer: 66 – 16 = 50 fewer oranges.
3. There were 40 parrots in the flock. Some of them flew away. Then there were 25 parrots in the flock. How many parrots flew away?
Show answer
Answer: 40 – 25 = 15 parrots flew away.
4. One hundred fifty is how much greater than fifty-three?
5. On Monday, the temperature was 13°C. The next day, the temperature dropped by 8 degrees. What was the temperature on Tuesday?
6. Zoie picked 15 dandelions. Her sister picked 22 ones. How many more dandelions did her sister pick than Zoie?
Show answer
Answer: 22-15 = 7 dandelions more.
Time for the 4th grade
1. The bus was scheduled to arrive at 7:10 p.m. However, it was delayed for 45 minutes. What time was it when the bus arrived?
2. My mother starts her 7-hour work at 9:15 a.m. What time does she get off from work?
3. Jack’s walk started at 6:45 p.m. and ended at 7:25 p.m. How long did his walk last?
4. The school closes at 9:00 p.m. Today, the school’s principal left 15 minutes after the office closed, and his secretary left the office 25 minutes after he left. When did the secretary leave work?
5. Suzie arrives at school at 8:20 a.m. How much time does she need to wait before the school opens? The school opens at 8:35 a.m.
6. The class starts at 9:15 a.m.. The first bell will ring 20 minutes before the class starts. When will the first bell ring?
Money word problems for the fourth grade
1. James had $20. He bought a chocolate bar for $2.30 and a coffee cup for $5.50. How much money did he have left?
Show answer
Answer: $20.00 – $2.30 – $5.50 = $12.20. James had $12.20 left.
2. Coffee mugs cost $1.50 each. How much do 7 coffee mugs cost?
Show answer
Answer: $1.5 x 7 = $10.5.
3. The father gives $32 to his four children to share equally. How much will each of his children get?
4. Each donut costs $1.20. How much do 6 donuts cost?
Show answer
Answer: $1.20 * 6 = $7,2.
5. Bill and Bob went out for takeout food. They bought 4 hamburgers for $10. Fries cost $2 each. How much does one hamburger with fries cost?
Show answer
Answer: $10 ÷ 4 = $2.50. One hamburger costs $2.50. $2.50 + $2.00 = $4.50. One hamburger with fries costs $4.50.
6. A bottle of juice costs $2.80, and a can is $1.50. What would it cost to buy two cans of soft drinks and a bottle of juice?
Show answer
Answer: $1.50 x 2 + $2.80 = $5.80.
Measurement word problems for the 6th grade
The task is to convert the given measures to new units. It best suits the sixth-grade schoolers.
- 55 yd = ____ in.
- 43 ft = ____ yd.
- 31 in = ____ ft.
- 29 ft = ____ in.
- 72 in = ____ ft.
- 13 ft = ____ yd.
- 54 lb = ____ t.
- 26 t = ____ lb.
- 77 t = ____ lb.
- 98 lb = ____ t.
- 25 lb = ____ t.
- 30 t = ____ lb.
Show answer
Answer:
- 55 yd = 1.980 in
- 43 ft = 14 yd 1 ft
- 31 in = 2 ft 7 in
- 29 ft = 348 in
- 72 in = 6 ft
- 13 ft = 4 yd 1 ft.
- 54 lb = 0,027 t
- 26 t = 52.000 lb
- 77 t = 154.000 lb
- 98 lb = 0,049 t
- 25 lb = 0?0125 t
- 30 t = 60.000 lb.
Ratios and percentages for the 6th-8th grades
It is another area that children can find quite difficult. Let’s look at simple examples of how to find percentages and ratios.
1. A chess club has 25 members, of which 13 are males, and the rest are females. What is the ratio of males to all club members?
2. A group has 8 boys and 24 girls. What is the ratio of girls to all children?
3. A pattern has 4 red triangles for every 12 yellow triangles. What is the ratio of red triangles to all triangles?
4. An English club has 21 members, of which 13 are males, and the rest are females. What is the ratio of females to all club members?
5. Dan drew 1 heart, 1 star, and 26 circles. What is the ratio of circles to hearts?
6. Percentages of whole numbers:
- 50% of 60 = …
- 100% of 70 = …
- 90% of 70 = …
- 20% of 30 = …
- 40% of 10 = …
- 70% of 60 = …
- 100% of 20 = …
- 80% of 90 = …
Show answer
Answer:
- 50% of 60 = 30
- 100% of 70 = 70
- 90% of 70 = 63
- 20% of 30 = 6
- 40% of 10 = 4
- 70% of 60 = 42
- 100% of 20 = 20
- 80% of 90 = 72.
Probability and data relationships for the 8th grade
1. John ‘s probability of winning the game is 60%. What is the probability of John not winning the game?
2. The probability that it will rain is 70%. What is the probability that it won’t rain?
3. There is a pack of 13 cards with numbers from 1 to 13. What is the probability of picking a number 9 from the pack?
4. A bag had 4 red toy cars, 6 white cars, and 7 blue cars. When a car is picked from this bag, what is the probability of it being red or blue?
5. In a class, 22 students like orange juice, and 18 students like milk. What is the probability that a schooler likes juice?
Geometry for the 7th grade
The following task is to write out equations and find the angles. Complementary angles are two angles that sum up to 90 degrees, and supplementary angles are two angles that sum up to 180 degrees.
1. The complement of a 32° angle = …
2. The supplement of a 10° angle = …
3. The complement of a 12° angle = …
4. The supplement of a 104° angle = …
Variables/ equation word problems for the 5th grades
1. The park is 𝑥 miles away from Jack’s home. Jack had to drive to and from the beach with a total distance of 36 miles. How many miles is Jack’s home away from the park?
Show answer
Answer: 2𝑥 = 36 → 𝑥 = 18 miles.
2. Larry bought some biscuits which cost $24. He paid $x and got back $6 of change. Find x.
Show answer
Answer: x = 24 + 6 = $30.
3. Mike played with his children on the beach for 90 minutes. After they played for x minutes, he had to remind them that they would be leaving in 15 minutes. Find x.
Show answer
Answer: x = 90 – 15 = 75 minutes.
4. At 8 a.m., there were x people at the orchard. Later at noon, 27 of the people left the orchard, and there were 30 people left in the orchard. Find x.
Show answer
Answer: x = 30 + 27 = 57 people
Travel time word problems for the 5th-7th grades
1. Tony sprinted 22 miles at 4 miles per hour. How long did Tony sprint?
Show answer
Answer: 22 miles divided by 4 miles per hour = 5.5 hours.
2. Danny walked 15 miles at 3 miles per hour. How long did Danny walk?
Show answer
Answer: 15 miles divided by 3 miles per hour = 5 hours.
3. Roy sprinted 30 miles at 6 miles per hour. How long did Roy sprint?
Show answer
Answer: 30 miles divided by 6 miles per hour = 5 hours.
4. Harry wandered 5 hours to get Pam’s house. It is 20 miles from his house to hers. How fast did Harry go?
Show answer
Answer: 20 miles divided by 5 hours = 4 miles per hour.
STEM subjects for kids
STEM courses for kids ages 7-13 in physics, chemistry, math and logic in interactive game format
learn more