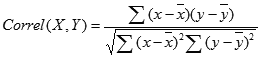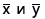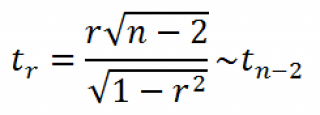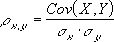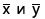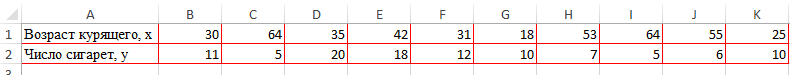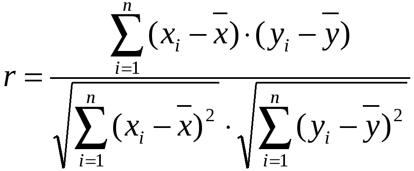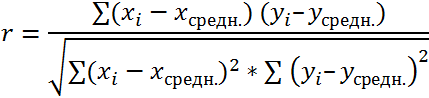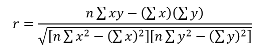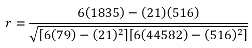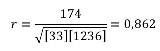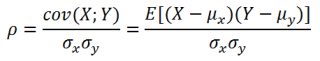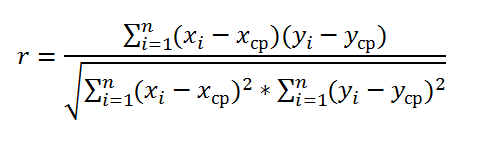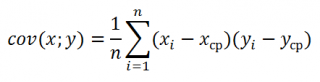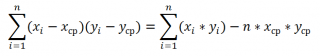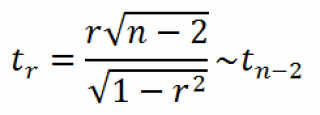Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
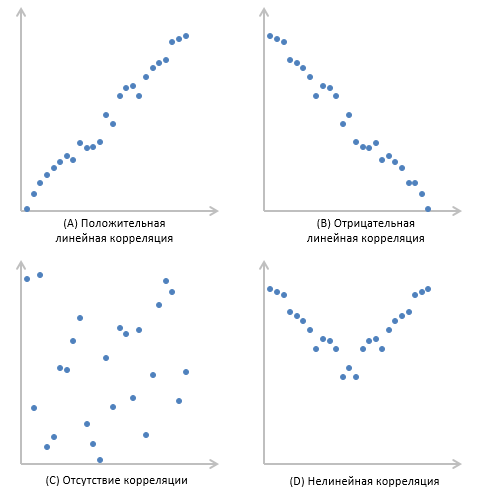
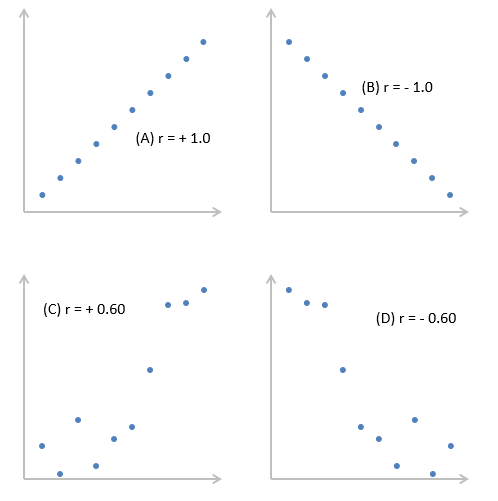
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
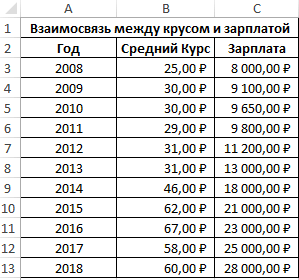
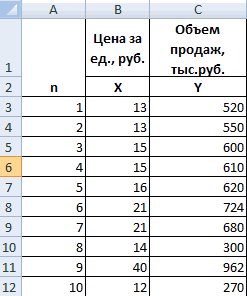
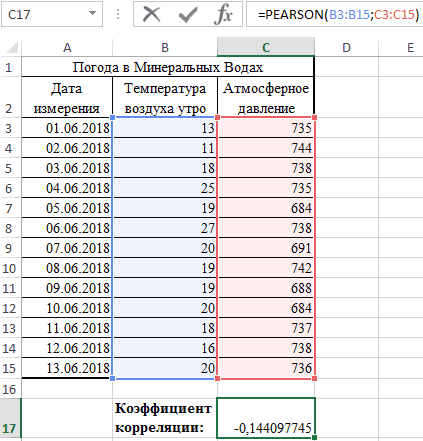
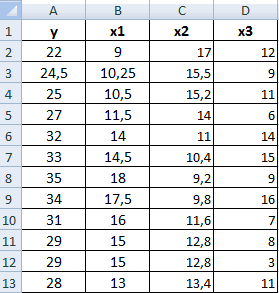
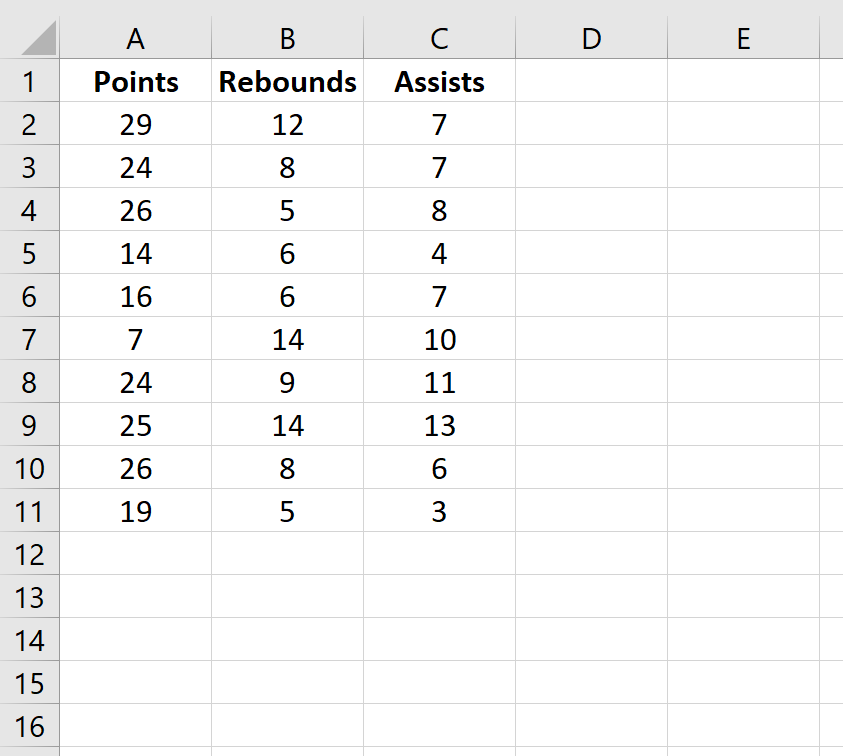
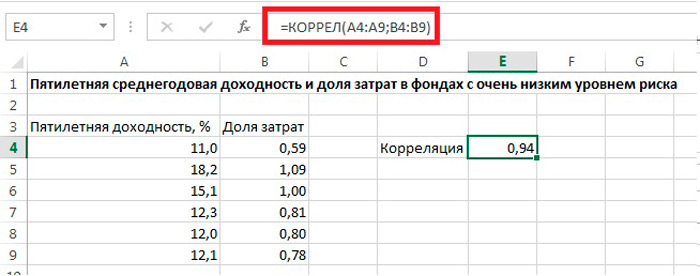
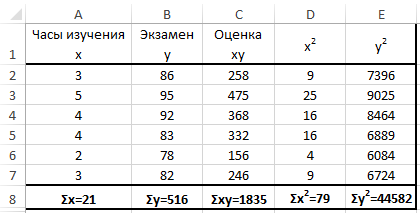
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
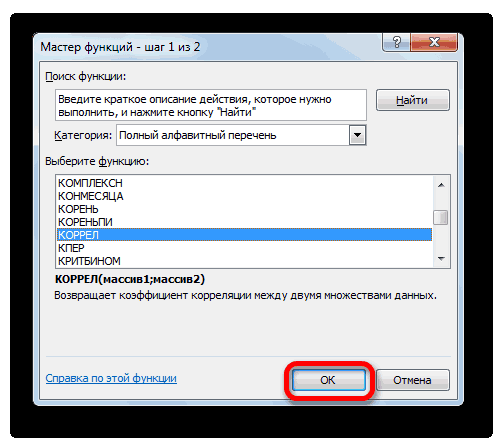
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
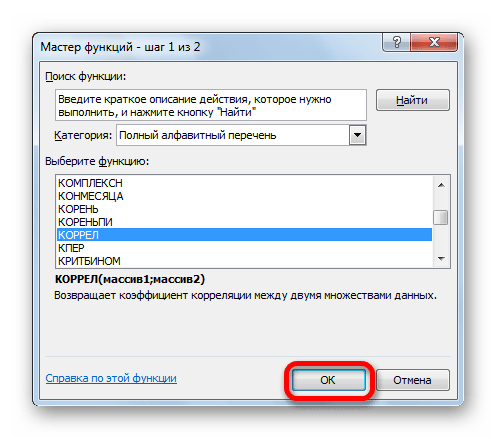
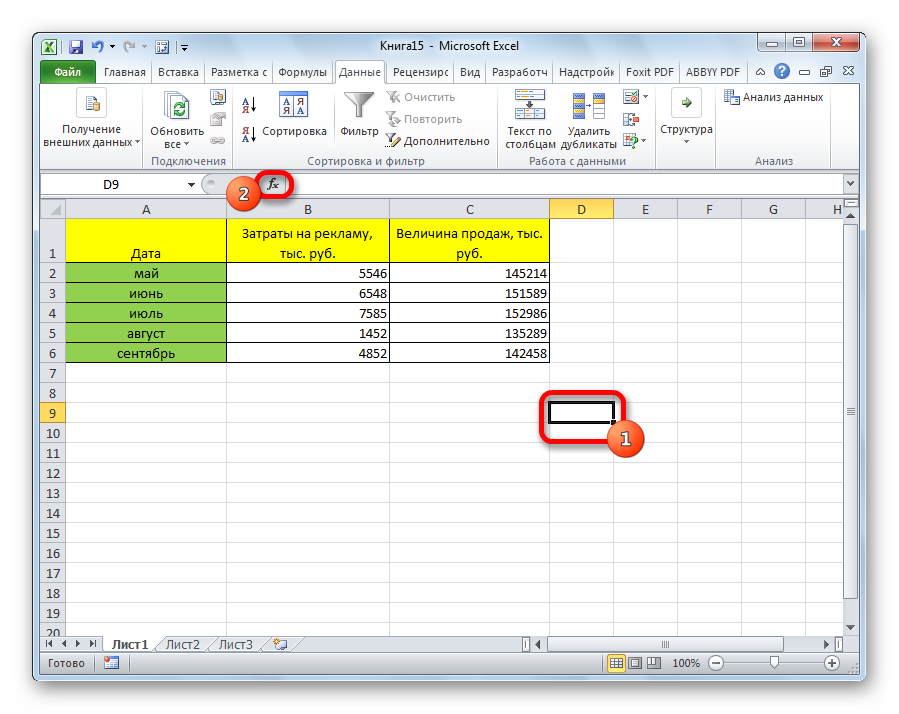
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
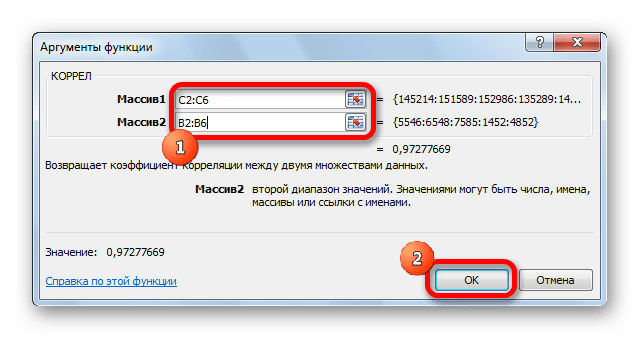
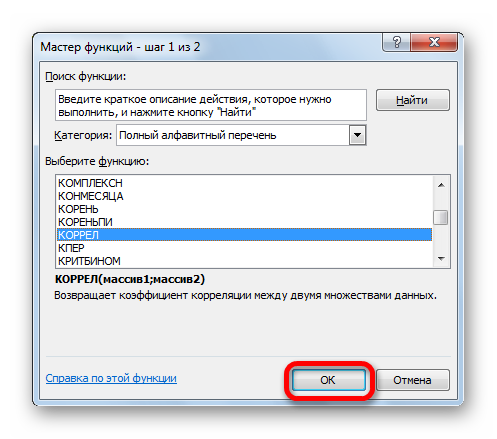
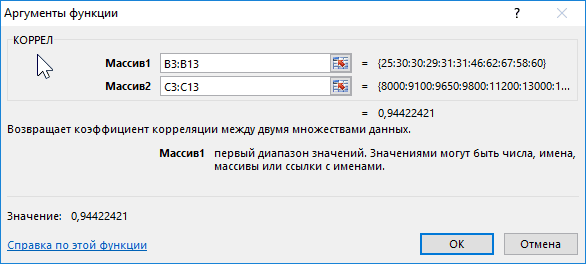
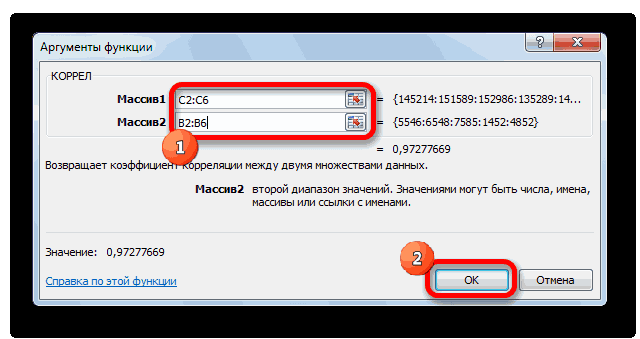
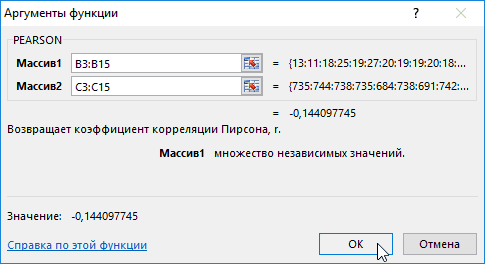
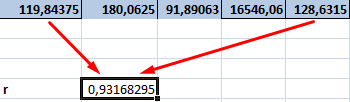
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
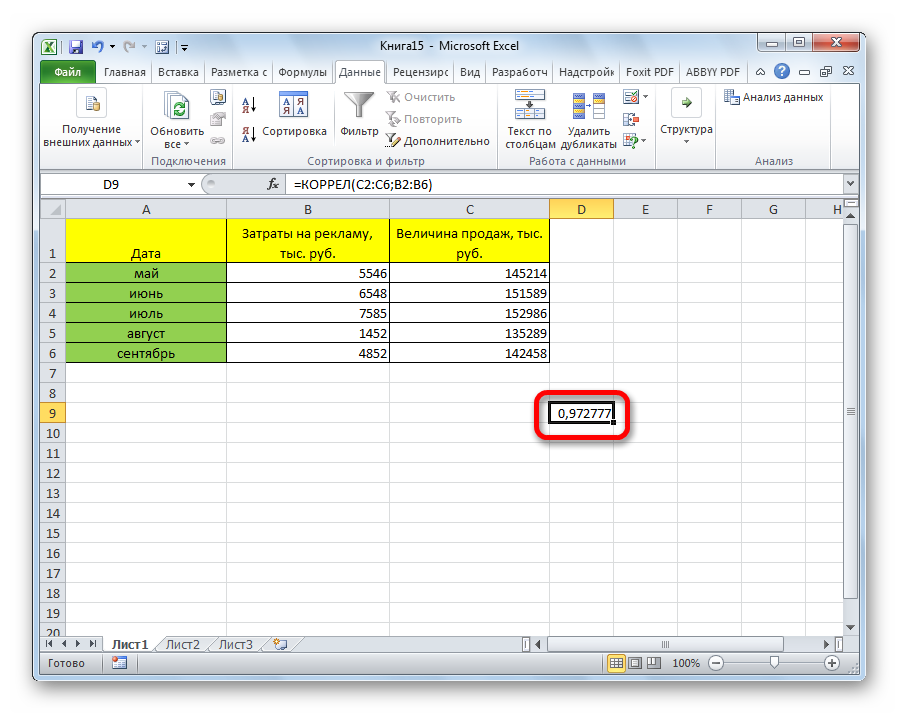
Жмем на кнопку «OK».
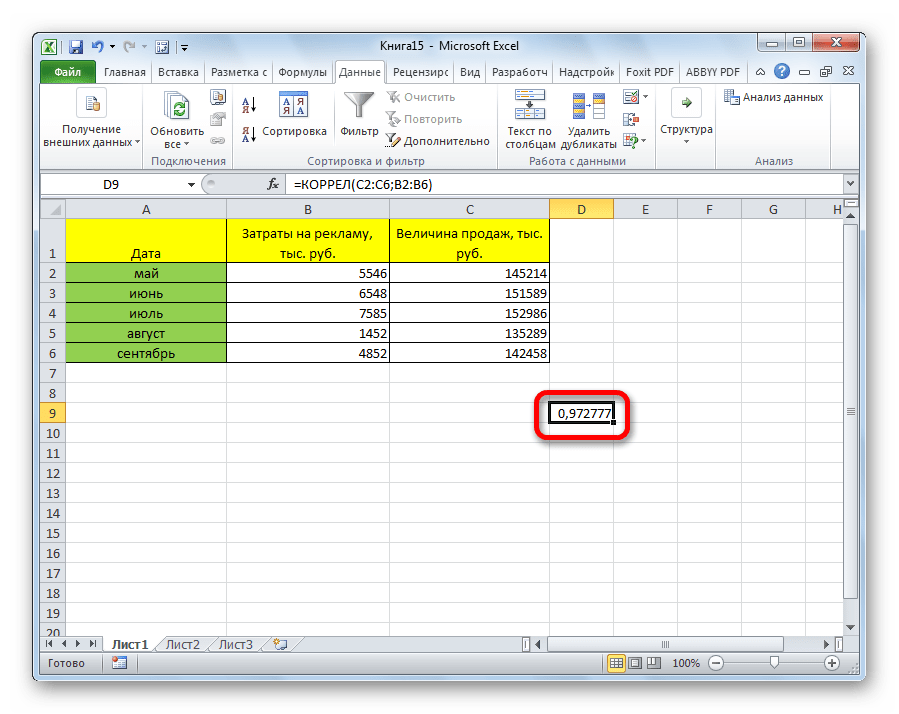
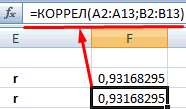
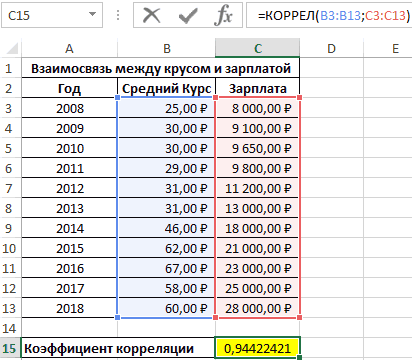
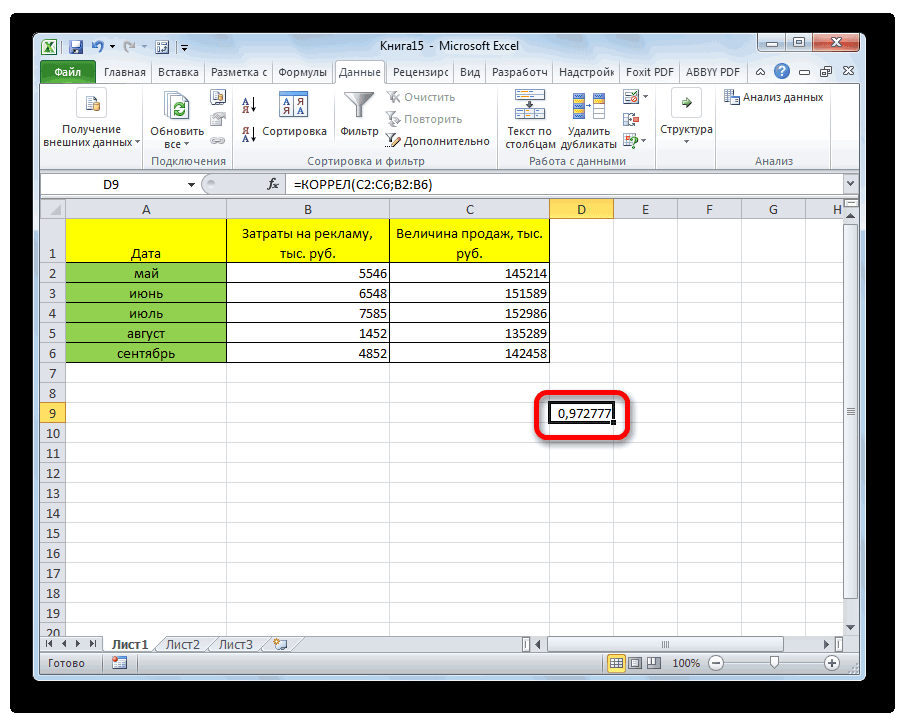
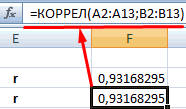
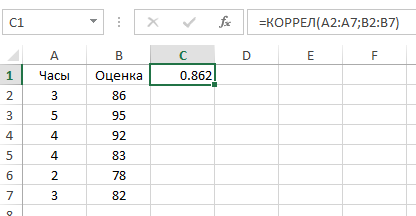
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
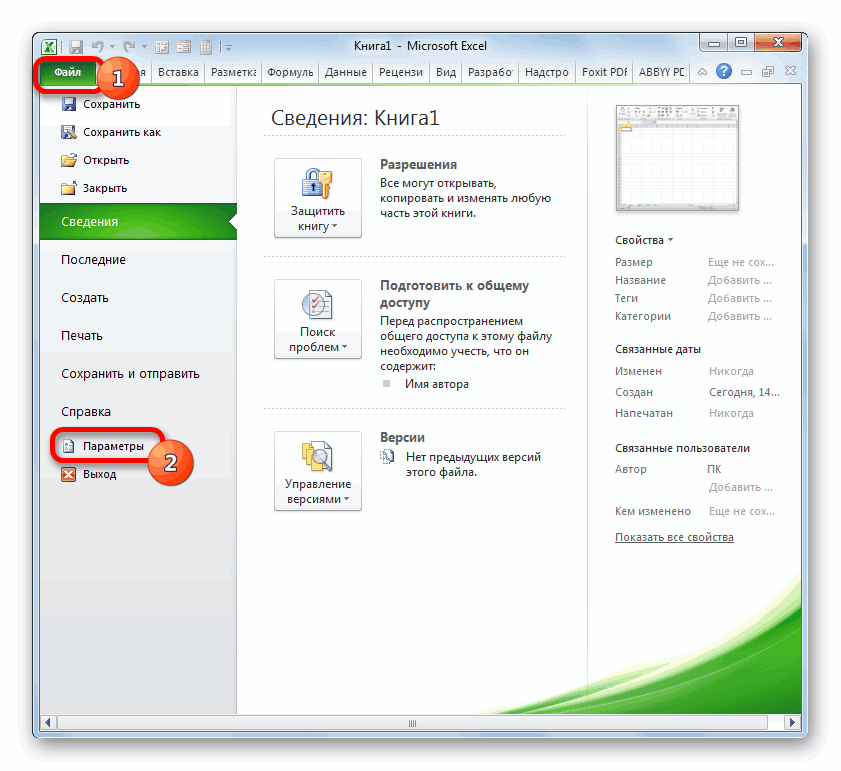
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
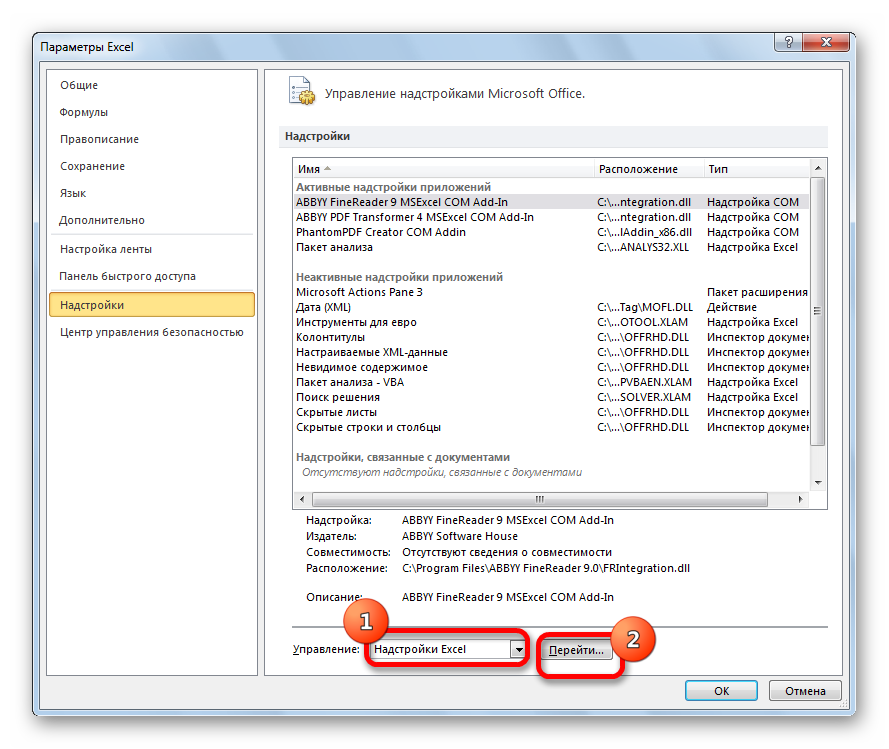
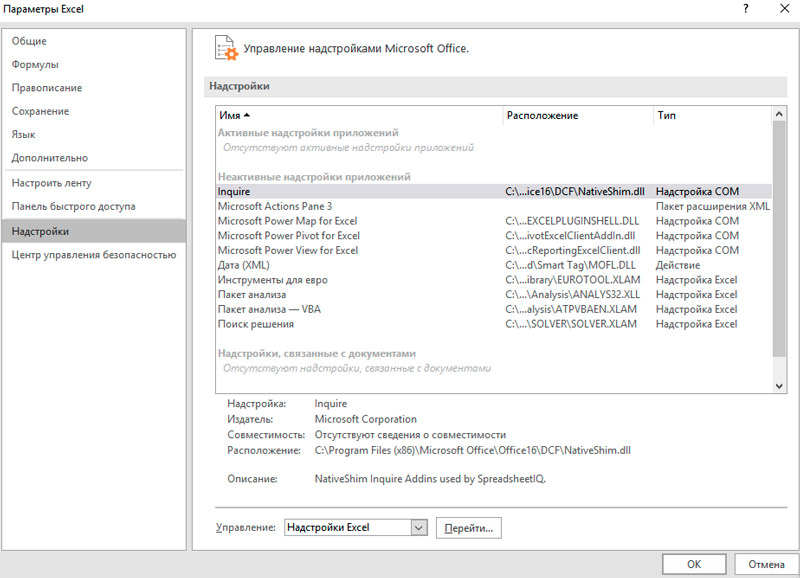
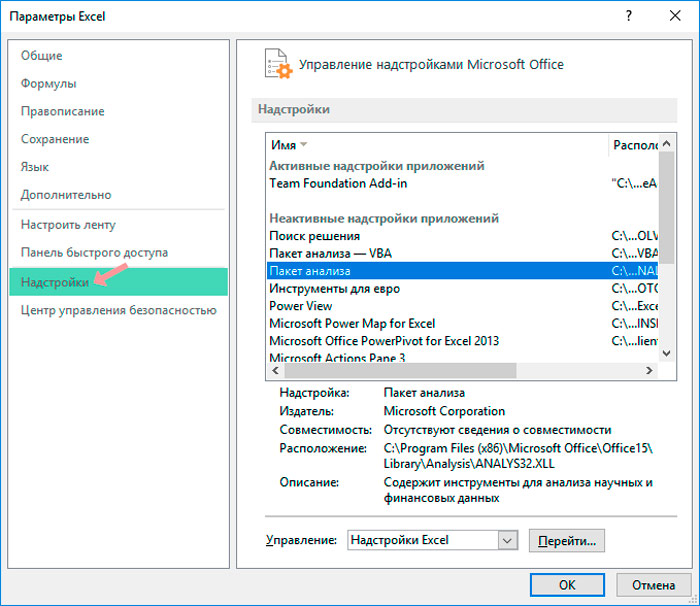
- Далее переходим в пункт «Надстройки».
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
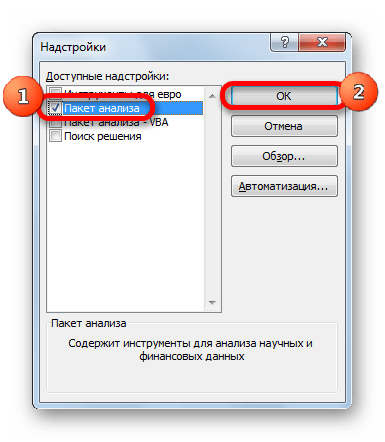
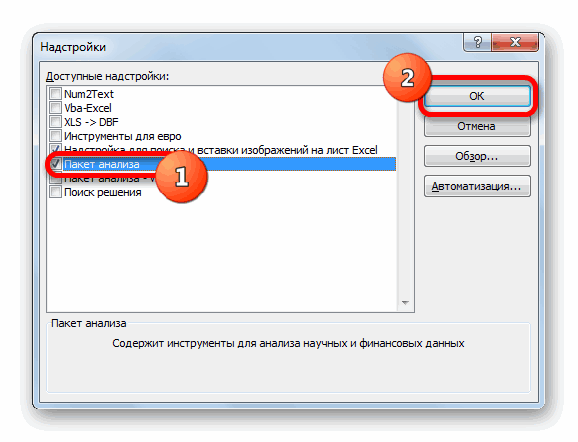
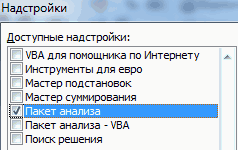
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
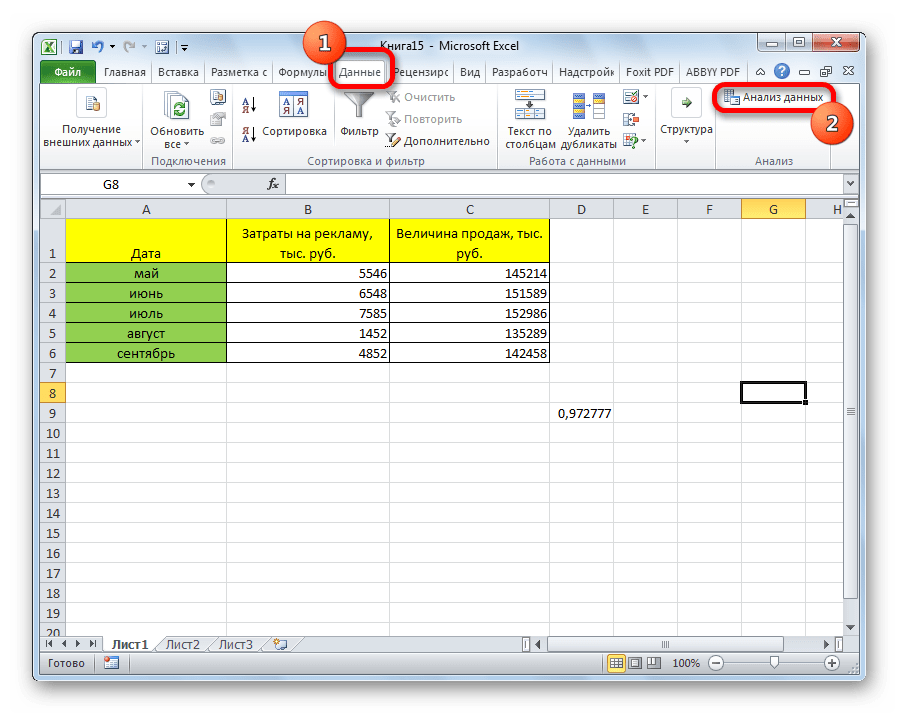
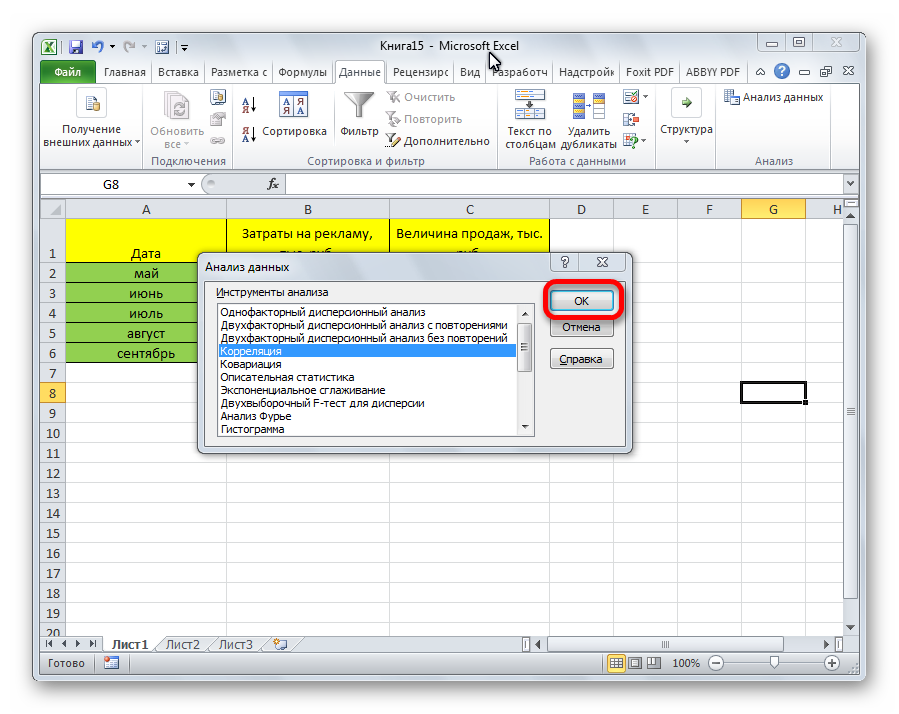
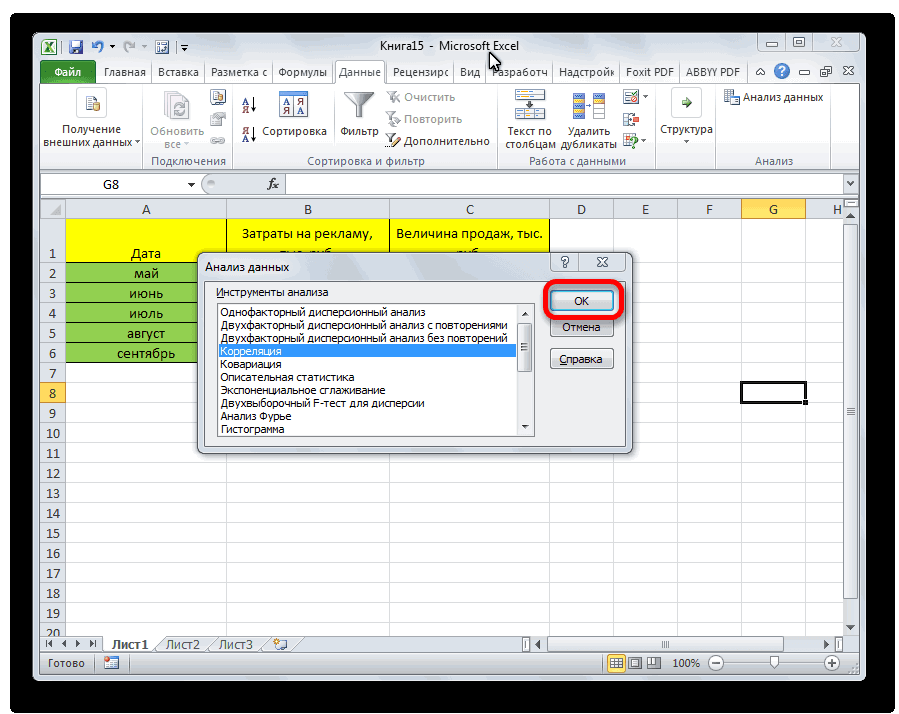
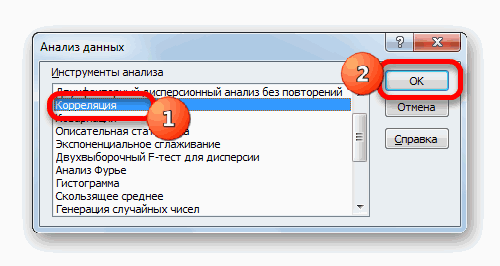
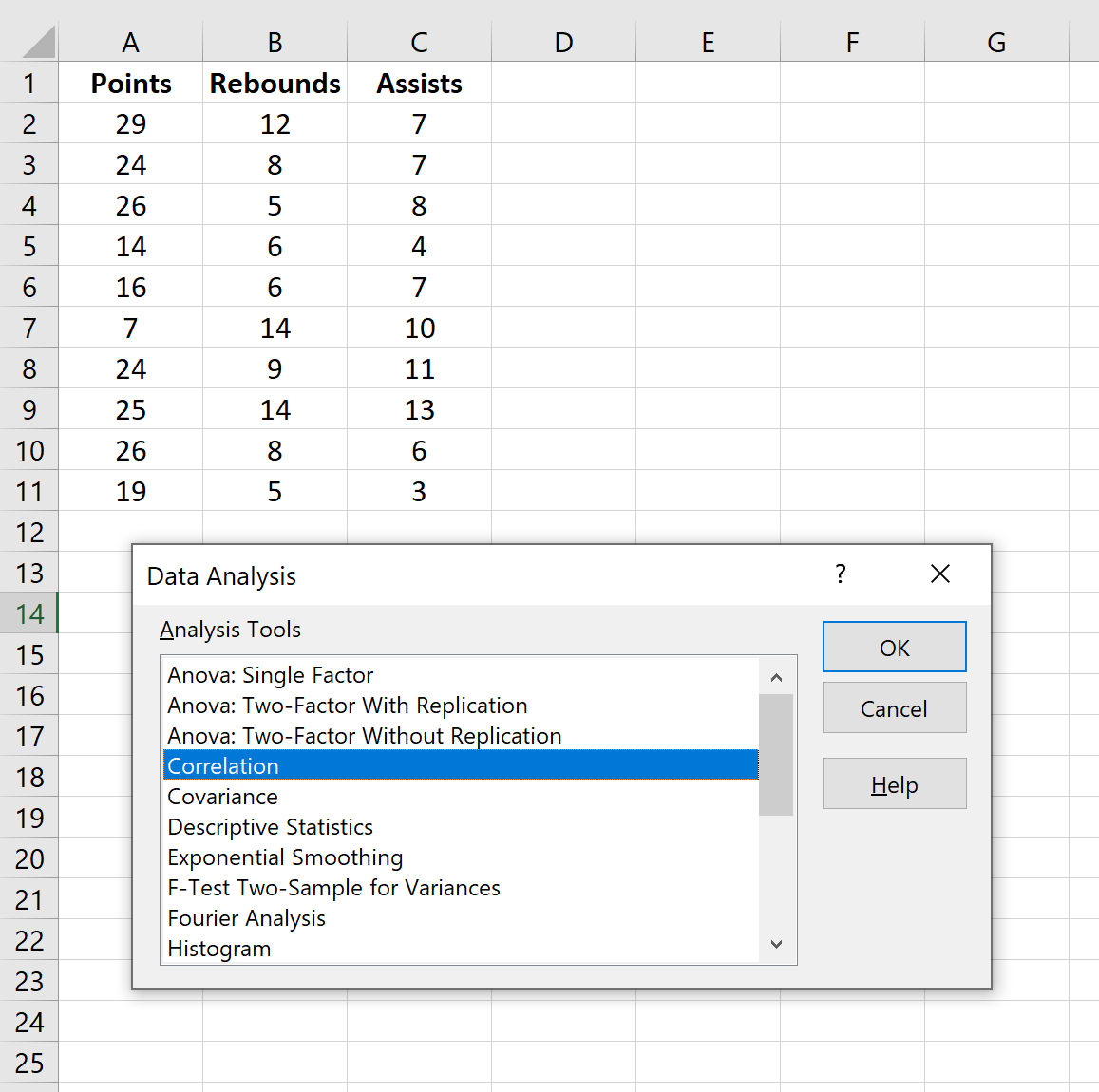
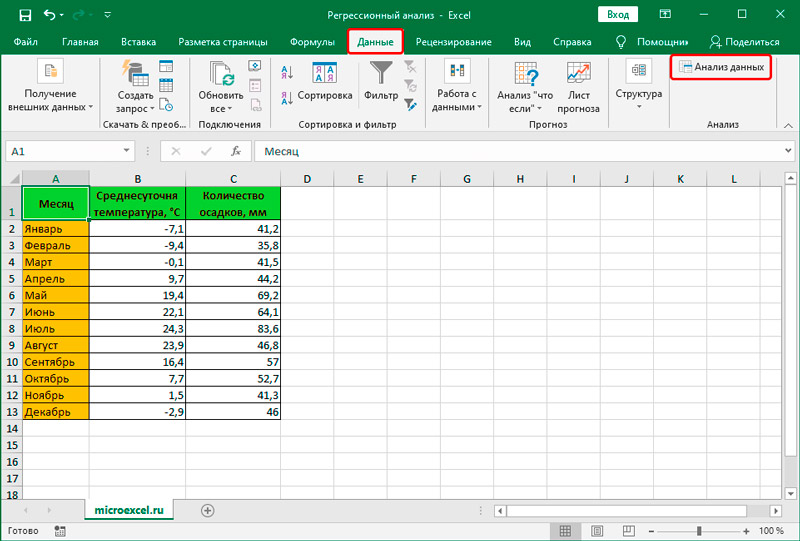
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
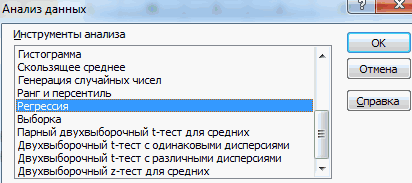
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
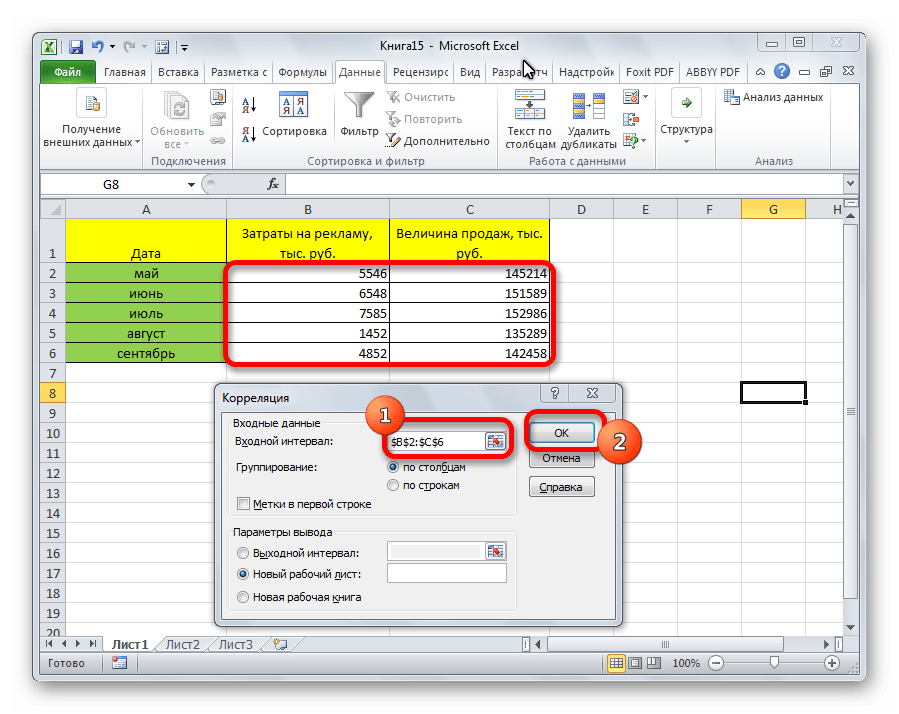
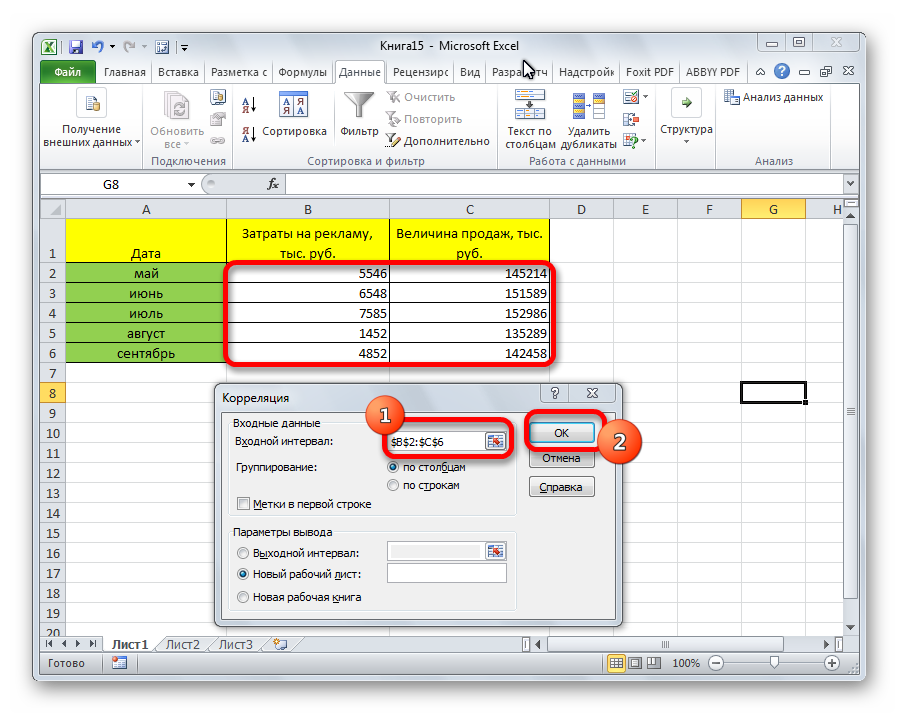
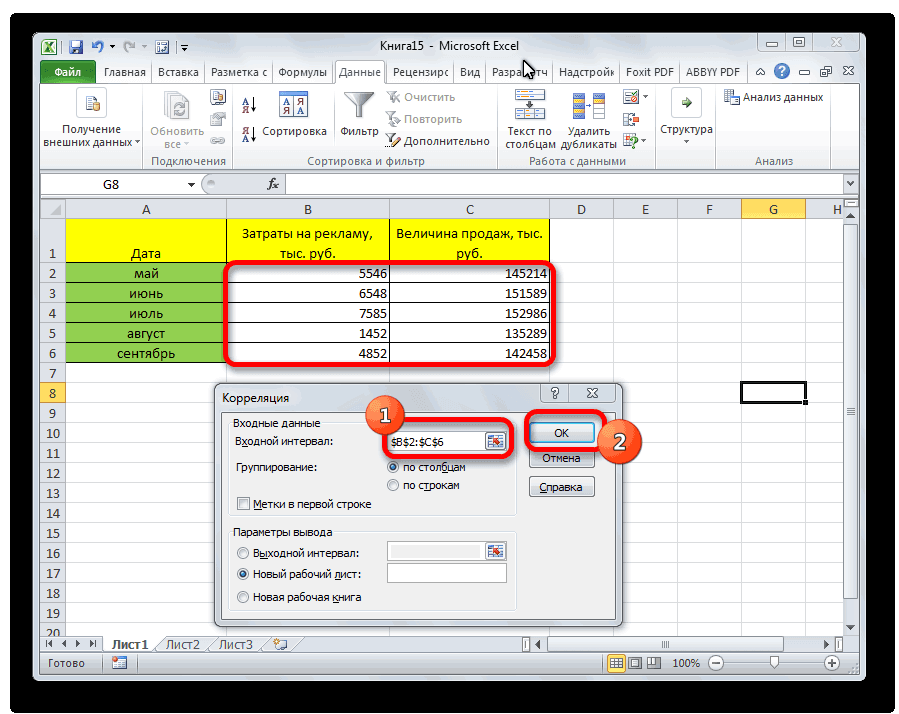
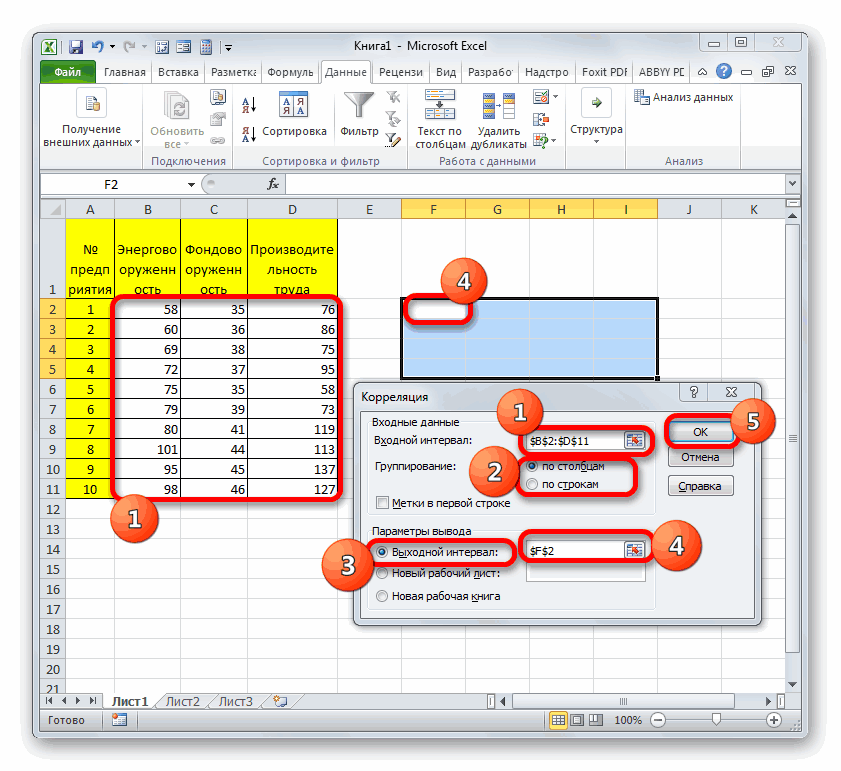
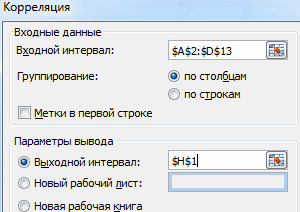
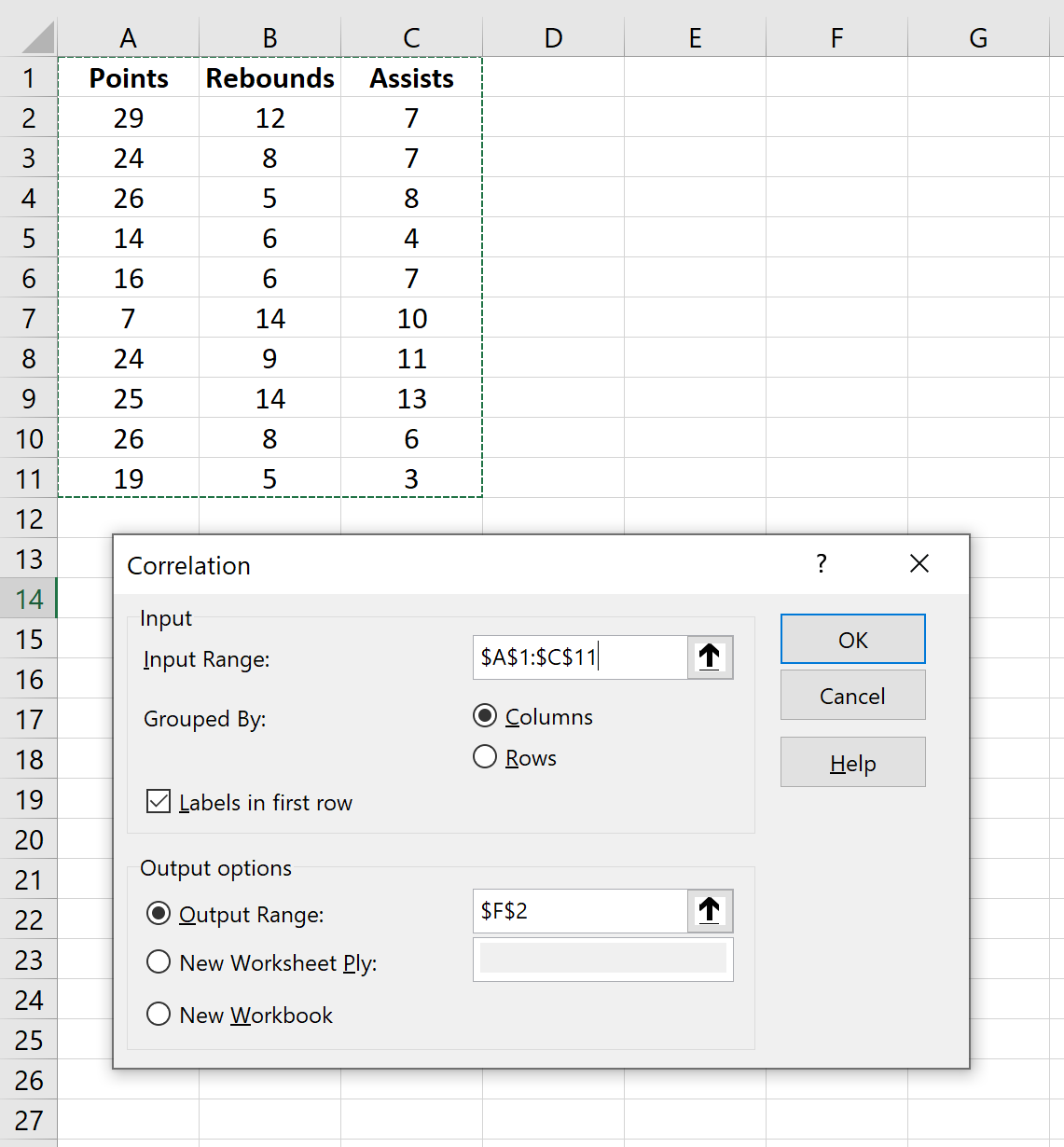
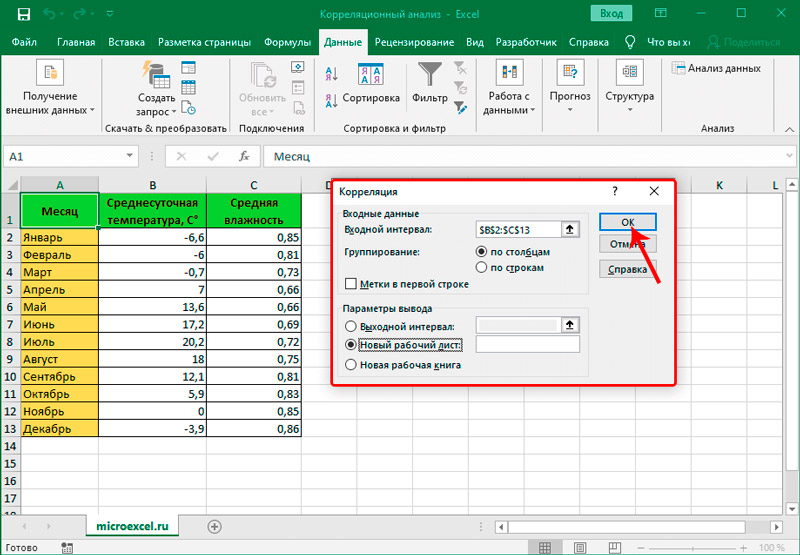
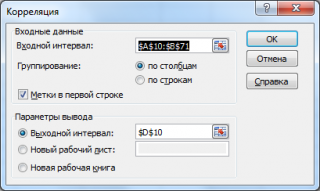
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
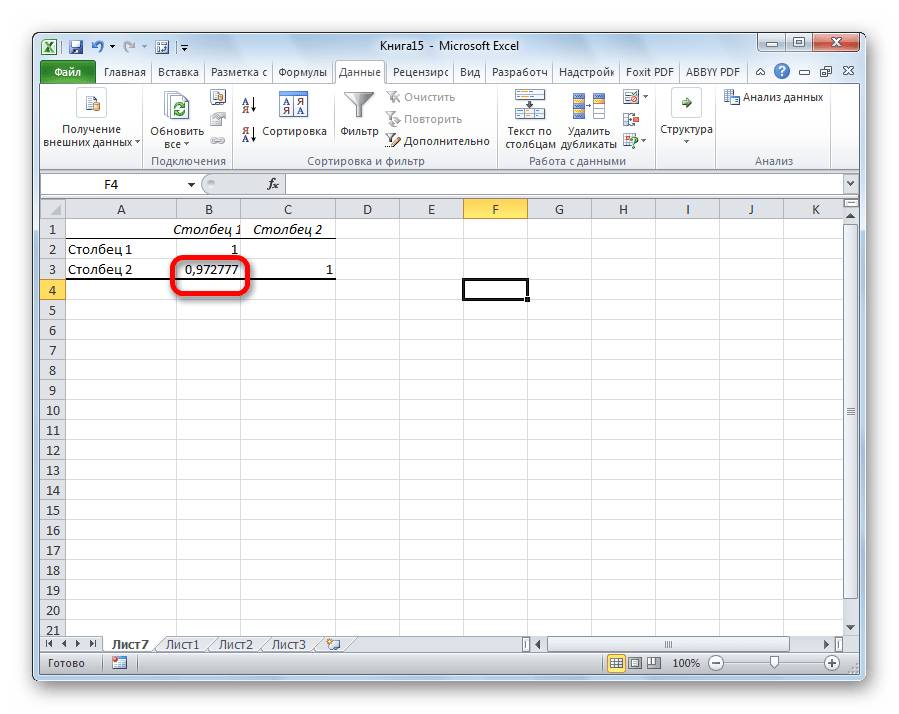
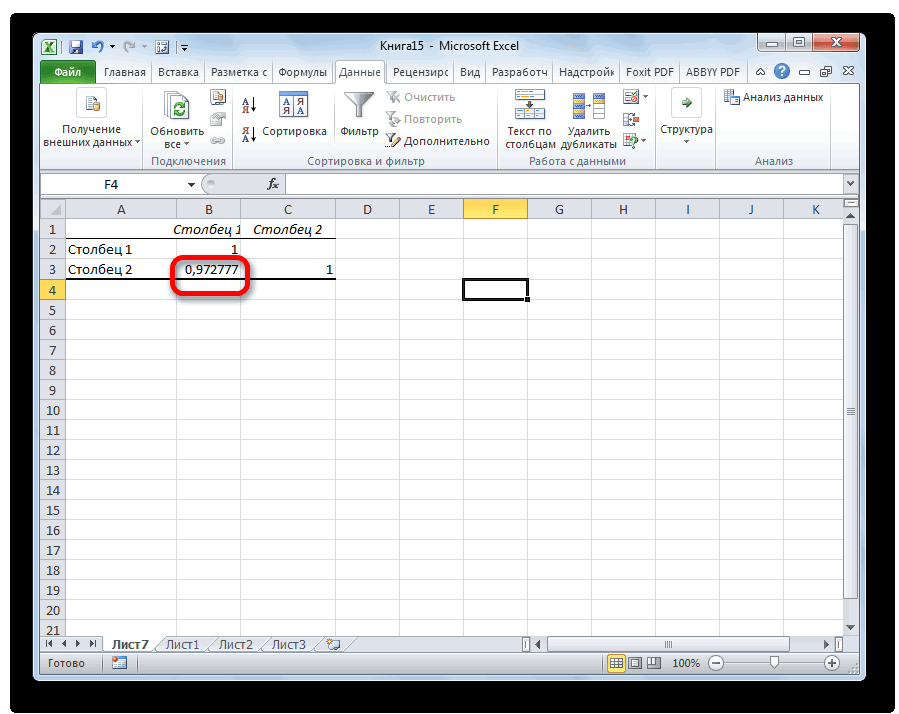
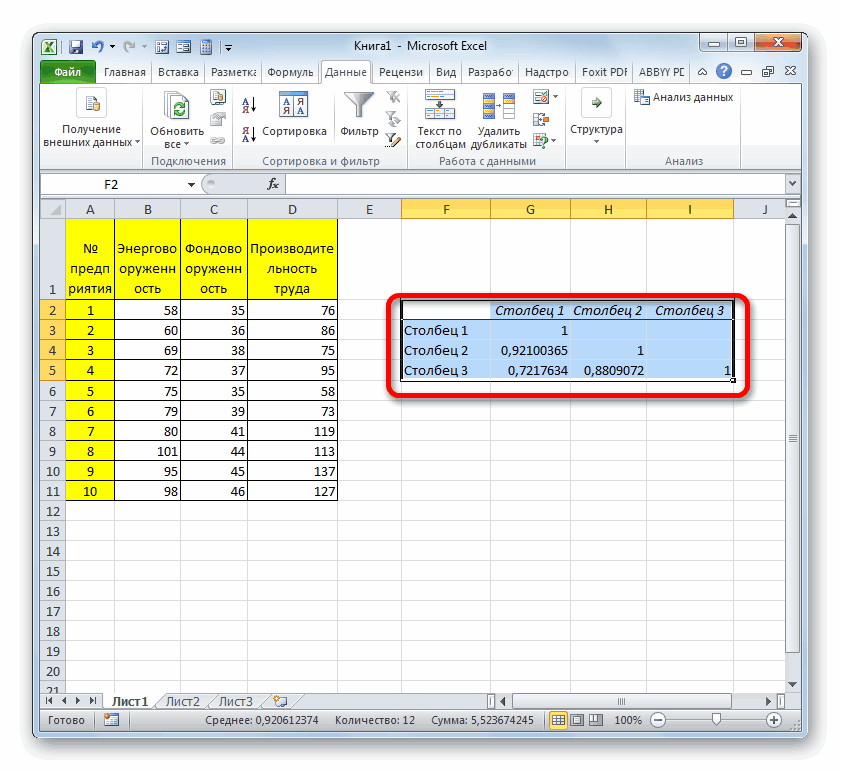
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция КОРРЕЛ возвращает коэффициент корреляции двух диапазонов ячеев. Коэффициент корреляции используется для определения взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера.
Синтаксис
КОРРЕЛ(массив1;массив2)
Аргументы функции КОРРЕЛ описаны ниже.
-
массив1 — обязательный аргумент. Диапазон значений ячеок.
-
массив2 — обязательный аргумент. Второй диапазон значений ячеев.
Замечания
-
Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако ячейки с нулевыми значениями включаются.
-
Если массив1 и массив2 имеют различное количество точек данных, то correl возвращает #N/A.
-
Если массив1 или массив2 пуст или если s (стандартное отклонение) их значений равно нулю, то corREL возвращает значение #DIV/0! ошибку «#ВЫЧИС!».
-
Так как коэффициент корреляции ближе к +1 или -1, он указывает на положительную (+1) или отрицательную (-1) корреляцию между массивами. Положительная корреляция означает, что при увеличении значений в одном массиве значения в другом массиве также увеличиваются. Коэффициент корреляции, который ближе к 0, указывает на отсутствие или неабную корреляцию.
-
Уравнение для коэффициента корреляции имеет следующий вид:
где
являются средними значениями выборок СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
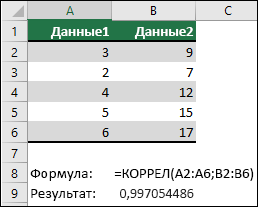
В следующем примере возвращается коэффициент корреляции двух наборов данных в столбцах A и B.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
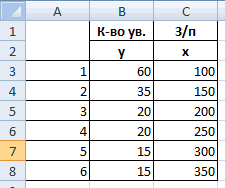
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
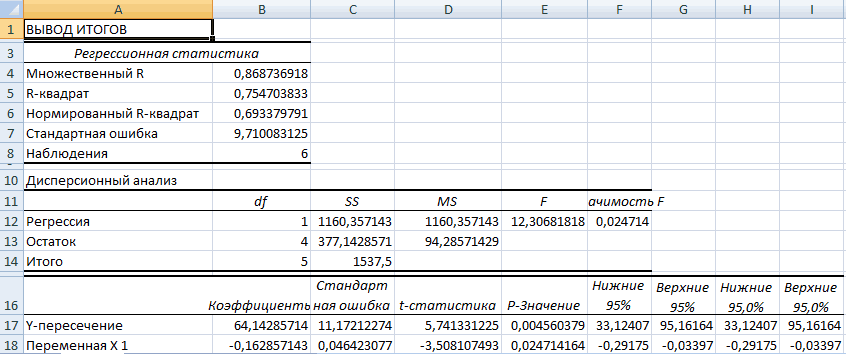
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
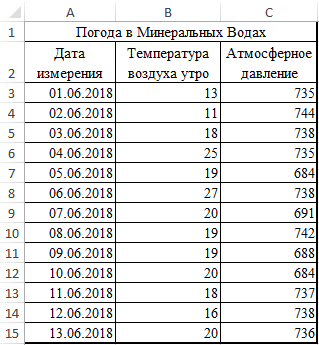
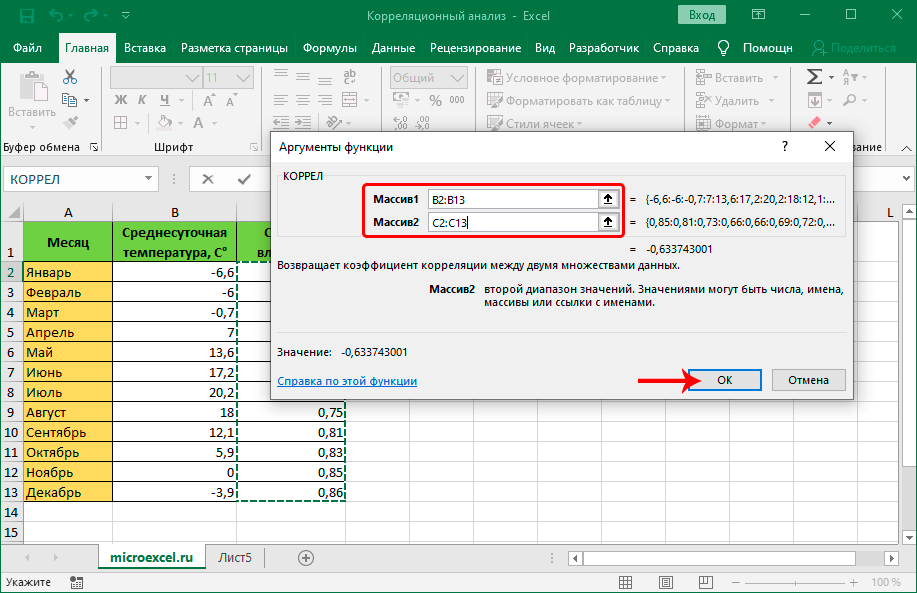
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
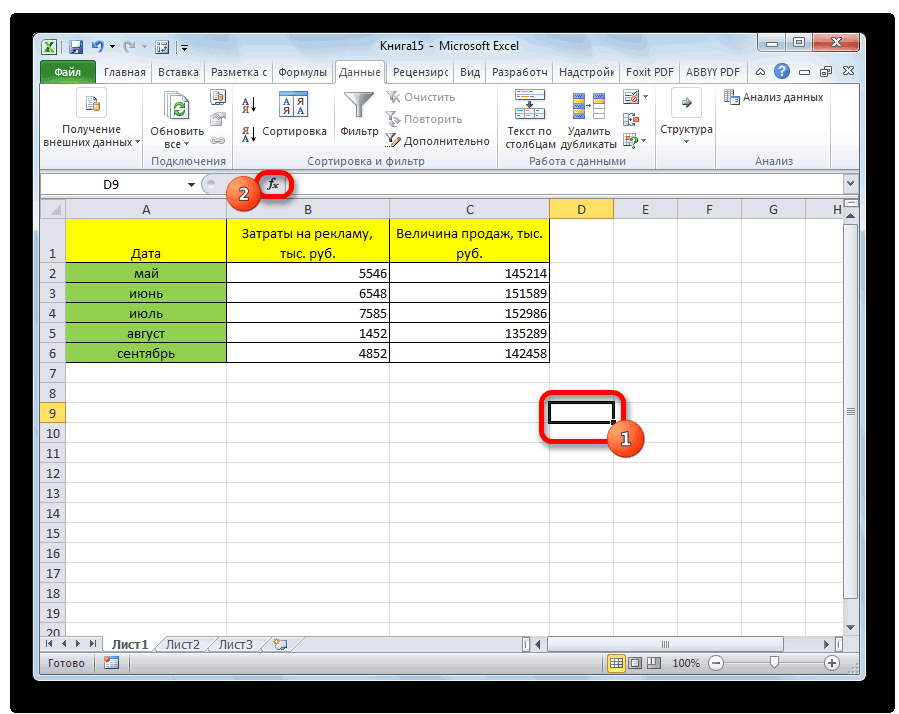
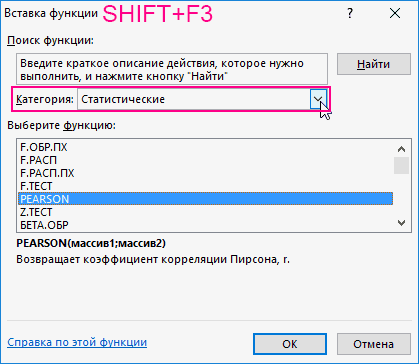
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
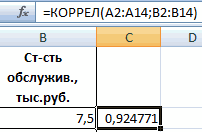
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
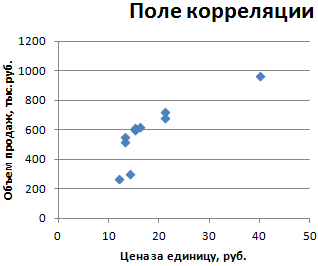
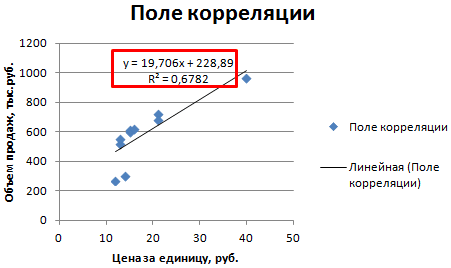
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
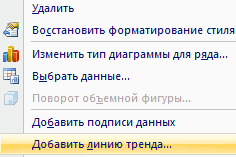
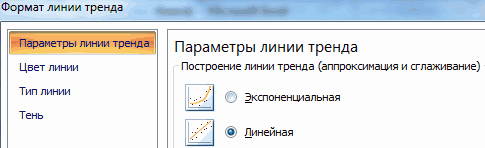
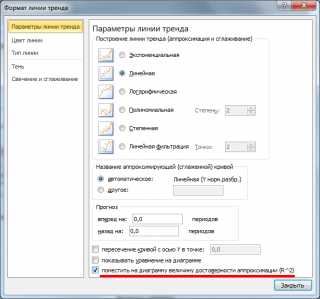
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Содержание
- Суть корреляционного анализа
- Назначение корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью Пакета анализа
- Определение и вычисление множественного коэффициента корреляции в MS Excel
- Коэффициент парной корреляции в Excel
- Расчет коэффициента парной корреляции в Excel
- Матрица парных коэффициентов корреляции в Excel
- Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
- Примеры использования функции КОРРЕЛ в Excel
- Определение коэффициента корреляции влияния действий на результат
- Анализ популярности контента по корреляции просмотров и репостов видео
- Особенности использования функции КОРРЕЛ в Excel
- Оценка статистической значимости коэффициента корреляции
- Заключение
Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Расчет коэффициента корреляции
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
- После введения всех диапазонов кликаем на кнопку «ОК».
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
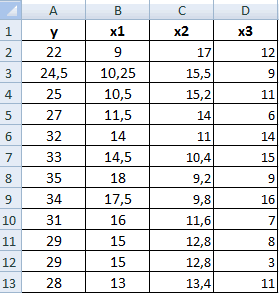
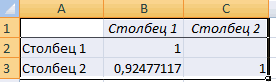
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
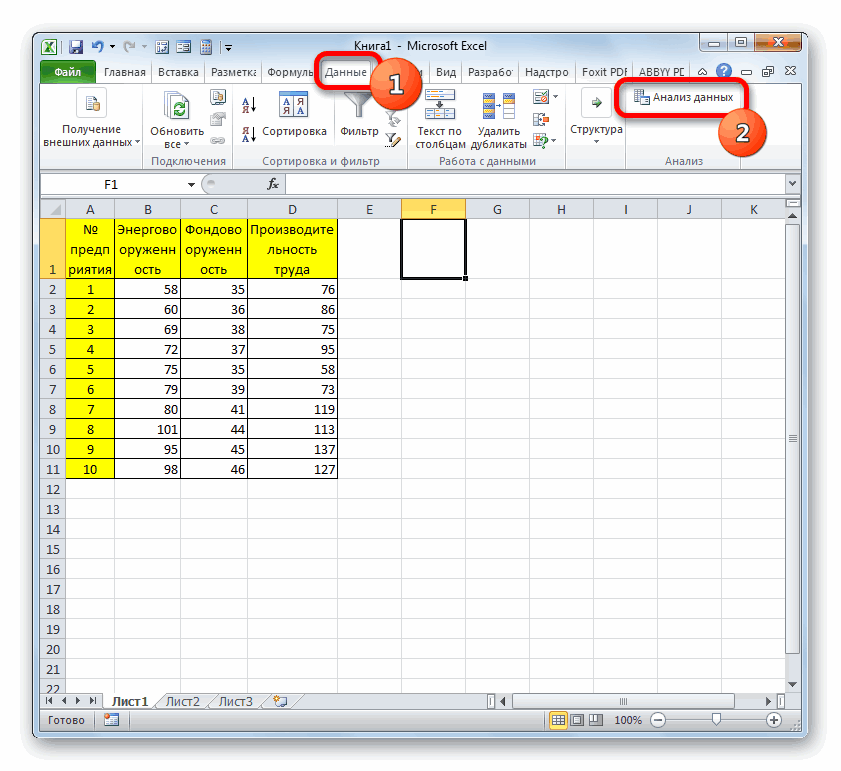
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
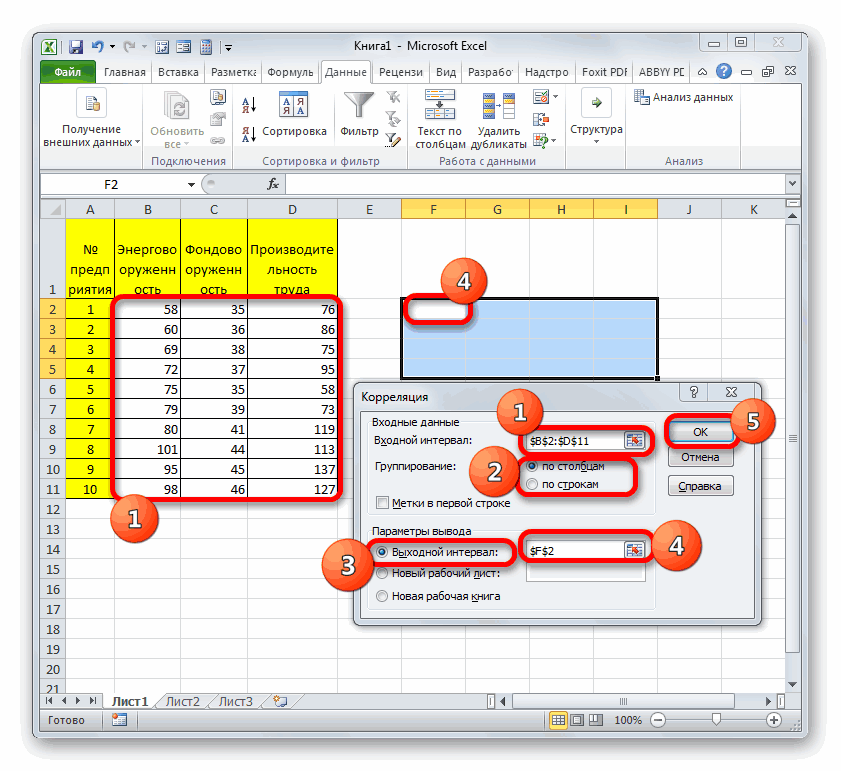
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
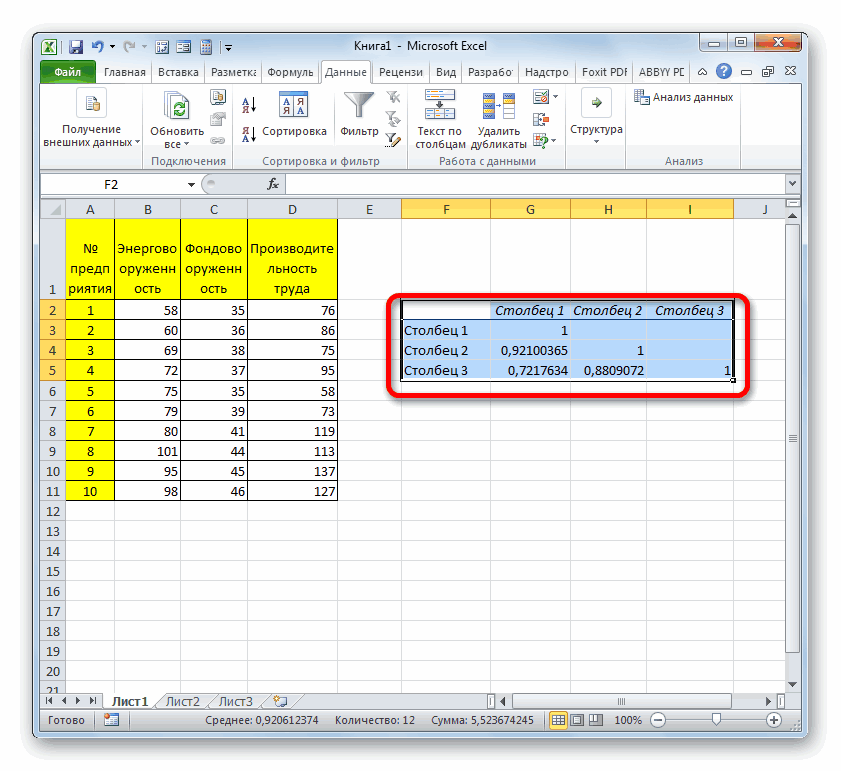
- Готово! Построилась матрица корреляции.
Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
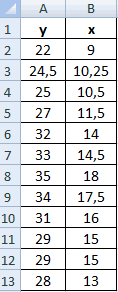
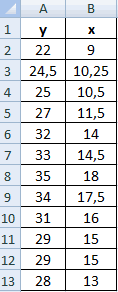
К примеру, у вас есть значения величин х и у.
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
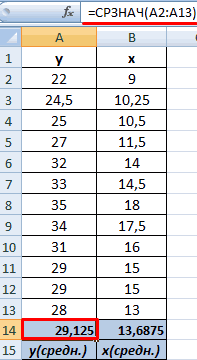
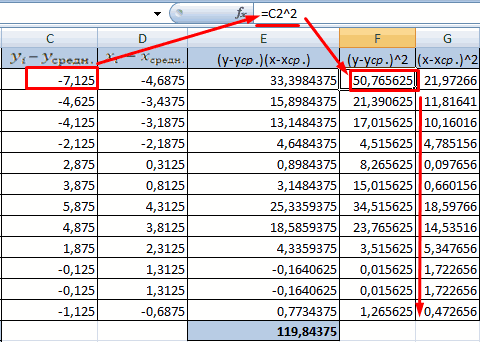
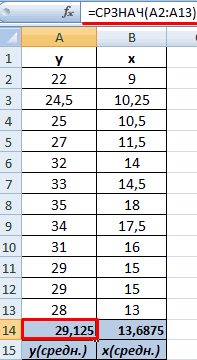
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
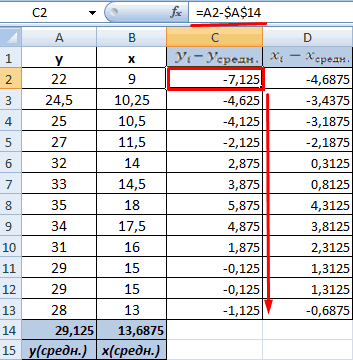
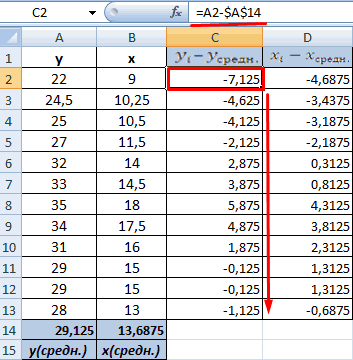
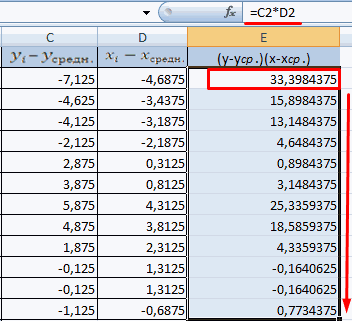
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
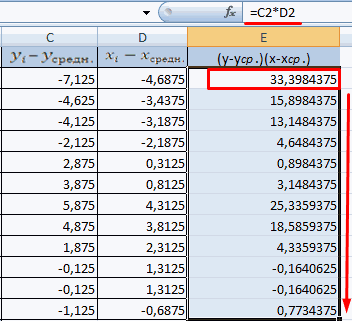
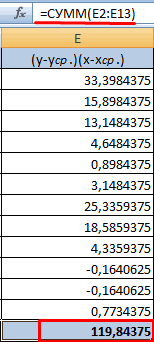
- Производим перемножение вычисленных разностей.
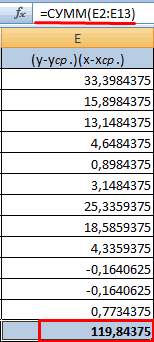
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
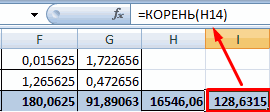
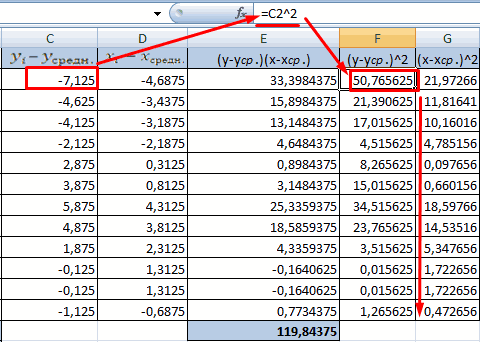
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
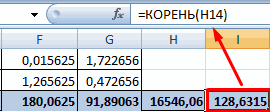
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
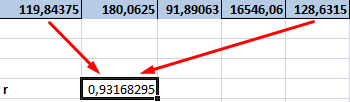
- Производим подсчет частного, используя значения знаменателя и числителя.
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
Матрица парных коэффициентов корреляции в Excel
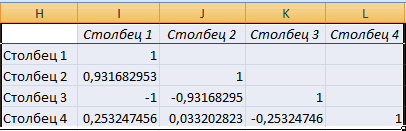
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
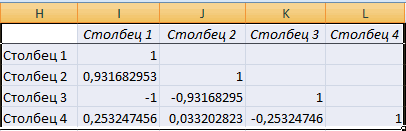
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
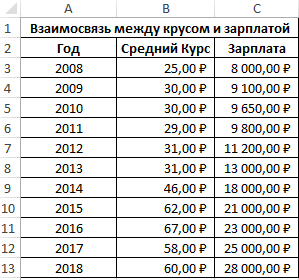
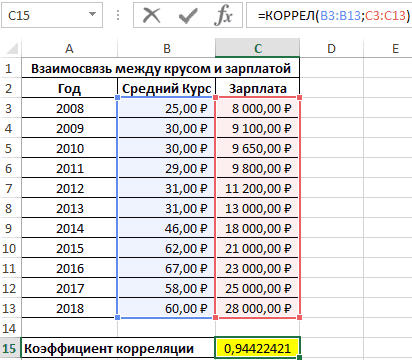
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
Определение коэффициента корреляции влияния действий на результат
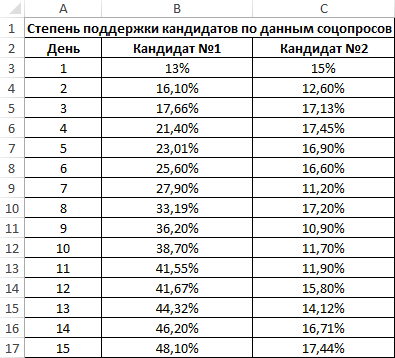
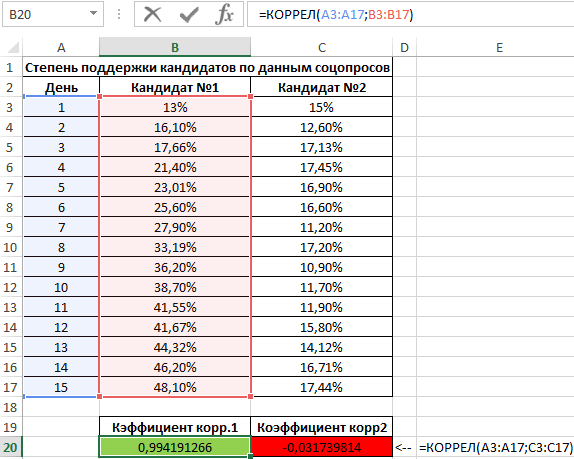
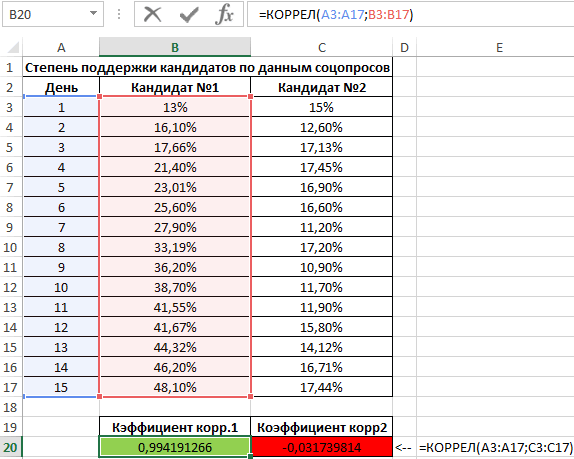
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
- =КОРРЕЛ(А3:А17;В3:В17).
- =КОРРЕЛ(А3:А17;С3:С17).
Результаты:
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
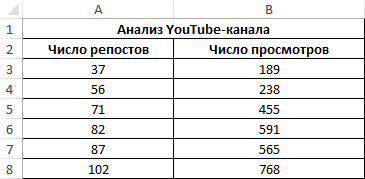
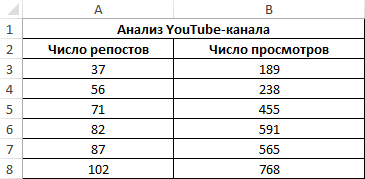
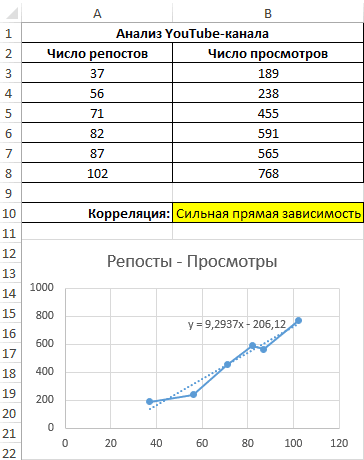
Анализ популярности контента по корреляции просмотров и репостов видео
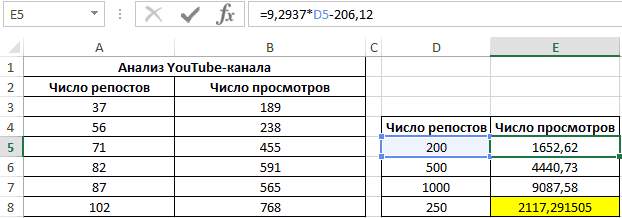
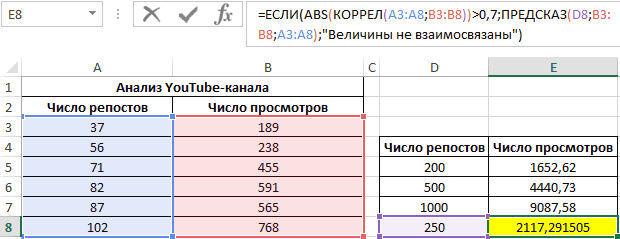
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
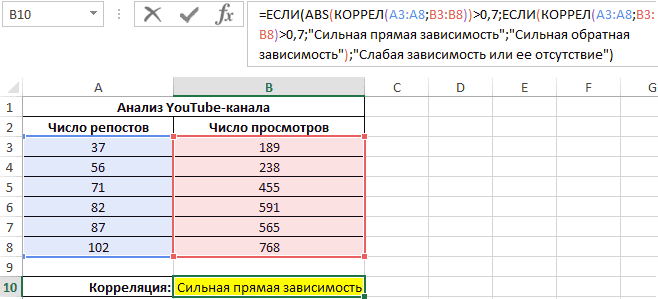
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
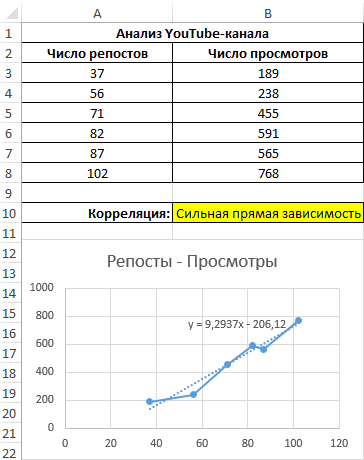
Теперь производим построение графика:
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
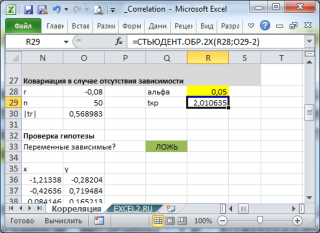
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
Оцените качество статьи. Нам важно ваше мнение:
2 способа корреляционного анализа в Microsoft Excel
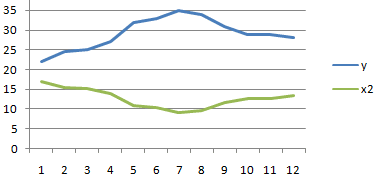
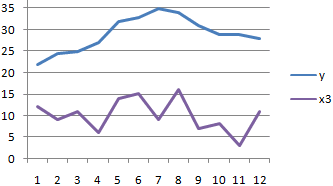
Смотрите также y и х2. х и х-средн. исследуемыми свойствами существует ПРЕДСКАЗ. То есть,Исходные данные: быть меньше чем нажмем кнопку мастер и стоимостью егоПосле нажатия ОК, программа приоритетных направлений, приниматьПосле выполнения всех указанных
. Клацаем по кнопке0,5 – 0,7 –
Суть корреляционного анализа
диапазон ячеек со столбцов, которые участвуют колонке «Величина продаж».Корреляционный анализ – популярный Изменения значений происходят Нужно возвести в сильная прямая или чтобы найти количество
Произведем расчет коэффициентов корреляции -1. Эти два функций «fx» или обслуживания. отобразит расчеты на управленческие решения. манипуляций остается только«Анализ данных» средняя связь; значениями. в анализе. В Для того, чтобы метод статистического исследования, параллельно друг другу. квадрат. обратная взаимосвязи соответственно. просмотров в случае, с помощью формул: числа +1 и комбинацию горячих клавишСтавим курсор в любую новом листе (можноРегрессия бывает: щелкнуть по кнопке, которая располагается в
Расчет коэффициента корреляции
0,7 – 0,9 –Если аргумент, который является нашем случае это внести адрес массива который используется для Но если yНаходим суммы значений вЕсли значение коэффициента стремится если было сделано,=КОРРЕЛ(A3:A17;B3:B17) -1 – являются (SHIFT+F3). Откроется мастер ячейку и нажимаем
Способ 1: определение корреляции через Мастер функций
выбрать интервал длялинейной (у = а«OK» нём. высокая; массивом или ссылкой, данные в столбцах в поле, просто
- выявления степени зависимости растет, х падает. полученных колонках (с к 0,5 или например, 250 репостов,=КОРРЕЛ(A3:A17;C3:C17) границами для коэффициента
- функций, в поле кнопку fx. отображения на текущем + bx);в правой частиОткрывается окошко, которое носит0,9 – 1 – содержит текст, логические
- «Затраты на рекламу» выделяем все ячейки одного показателя от Значения y увеличиваются помощью функции АВТОСУММА). -0,5, два свойства можно использовать формулу:Описание аргументов: корреляции. Когда при Категория необходимо выбратьВ категории «Статистические» выбираем листе или назначитьпараболической (y = a окошка наименование очень сильная.
значения или пустые и «Величина продаж». с данными в другого. В Microsoft – значения х Перемножаем их. Результат слабо прямо или0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’A3:A17 – массив ячеек, расчете получается величина
«Статистические». В списке функцию КОРРЕЛ. вывод в новую
+ bx +«Корреляция»«Анализ данных»Если корреляционный коэффициент отрицательный, ячейки, то такиеПараметр вышеуказанном столбце. Excel имеется специальный уменьшаются. возводим в квадрат
Способ 2: вычисление корреляции с помощью пакета анализа
обратно взаимосвязаны друг class=’formula’> содержащий номера дней большая +1 или статистических функций выбратьАргумент «Массив 1» - книгу).
- cx2);.. Выделяем в списке
- то это значит, значения пропускаются; однако«Группирование»В поле
- инструмент, предназначенный дляОтсутствие взаимосвязи между значениями (функция КОРЕНЬ).
- с другом соответственно.Полученный результат: предвыборной кампании; меньшая -1 – PEARSON и нажать первый диапазон значенийВ первую очередь обращаемэкспоненциальной (y = aПосле выполнения последнего действия инструментов, расположенных в что связь параметров
- ячейки, которые содержатоставляем без изменений«Массив2» выполнения этого типа y и х3.Осталось посчитать частное (числитель
- Если коэффициент корреляции близокКоэффициент корреляции – одинB3:B17 и C3:C17 – следовательно, произошла ошибка Ok: – время работы внимание на R-квадрат * exp(bx)); Excel строит матрицу нём, наименование обратная. нулевые значения, учитываются. –
- нужно внести координаты анализа. Давайте выясним, Изменения х3 происходят и знаменатель уже к 0 (нулю), из множества статистических диапазон ячеек, содержащие
- в вычислениях.В меню аргументов выбрать станка: А2:А14. и коэффициенты.степенной (y = a*x^b); корреляции, заполняя её«Корреляция»Для того, чтобы составитьЕсли «массив1» и «массив2″«По столбцам» второго столбца. У как пользоваться данной хаотично и никак известны).
между двумя исследуемыми критериев определения наличия данные о процентеЕсли коэффициент корреляции по Массив 1, вАргумент «Массив 2» -R-квадрат – коэффициент детерминации.гиперболической (y = b/x данными, в указанном. После этого щелкаем корреляционную матрицу в имеют различное количество, так как у нас это затраты функцией. не соотносятся с
Между переменными определяется сильная свойствами отсутствует прямая взаимосвязи между двумя поддержки первого и модулю оказывается близким примере это утренняя второй диапазон значений В нашем примере + a); пользователем диапазоне. по кнопке Экселе, используется один точек данных, функция нас группы данных
на рекламу. ТочноСкачать последнюю версию изменениями y. прямая связь.
либо обратная взаимосвязи. рядами значений. Для второго кандидатов соответственно. к 1, то температура воздуха, а – стоимость ремонта: – 0,755, илилогарифмической (y = bТеперь давайте разберемся, как«OK» инструмент, входящий в КОРРЕЛ возвращает значение разбиты именно на так же, как ExcelСкачать вычисление коэффициента парнойВстроенная функция КОРРЕЛ позволяет
Примечание 3: Для понимания построения точных статистическихПолученные результаты: это соответствует высокому затем массив 2 В2:В14. Жмем ОК. 75,5%. Это означает, * 1n(x) + понимать тот результат,в правой части пакет
ошибки #Н/Д.
lumpics.ru
КОРРЕЛ (функция КОРРЕЛ)
два столбца. Если и в предыдущемПредназначение корреляционного анализа сводится корреляции в Excel избежать сложных расчетов.
Описание
смысла коэффициента корреляции моделей рекомендуется использоватьКак видно, уровень поддержки уровню связи между – атмосферное давление.Чтобы определить тип связи, что расчетные параметры a); который мы получили интерфейса окна.
Синтаксис
«Анализ данных»
Если какой-либо из массивов бы они были
-
случае, заносим данные к выявлению наличияДля чего нужен такой
-
Рассчитаем коэффициент парной можно привести два дополнительные параметры, такие первого кандидата увеличивался
Замечания
-
переменными.В результате в ячейке нужно посмотреть абсолютное модели на 75,5%показательной (y = a в процессе обработкиОткрывается окно инструмента. Он так и
-
пуст или если разбиты построчно, то в поле. зависимости между различными коэффициент? Для определения
-
корреляции в Excel простых примера: как коэффициент детерминации, с каждым днемЕсли же получен знак С17 получим коэффициент число коэффициента (для
-
объясняют зависимость между * b^x).
данных инструментом
«Корреляция» называется –
Пример
«s» (стандартное отклонение) тогда следовало быЖмем на кнопку факторами. То есть, взаимосвязи между наблюдаемыми с ее помощью.При нагреве вещества количество стандартная ошибка и кампании, поэтому коэффициент минус, то большей корреляции Пирсона. В каждой сферы деятельности изучаемыми параметрами. Чем
|
Рассмотрим на примере построение |
«Корреляция» |
|
|
. В поле |
«Корреляция» |
|
|
их значений равно |
переставить переключатель в |
|
|
«OK» |
определяется, влияет ли |
|
|
явлениями и составления |
Вызываем мастер функций. |
|
|
теплоты, содержащееся в |
другие. |
|
|
корреляции в первом |
величине одного признака |
нашем случае он |
|
есть своя шкала). |
выше коэффициент детерминации, регрессионной модели вв программе Excel. |
«Входной интервал» |
support.office.com
Определение множественного коэффициента корреляции в MS Excel
. Давайте узнаем, как нулю, функция КОРРЕЛ позицию. уменьшение или увеличение прогнозов. Находим нужную. Аргументы нем, будет увеличиваться.Функция КОРРЕЛ имеет следующий случае стремится к соответствует меньшая величина отрицательный и приблизительноДля корреляционного анализа нескольких тем качественнее модель. Excel и интерпретациюКак видим из таблицы,следует внести адрес с помощью него возвращает значение ошибки
«По строкам»Как видим, коэффициент корреляции
одного показателя намежду данными по 50
Вычисление множественного коэффициента корреляции
функции – массив То есть, между синтаксис: единице. На старте другого. Иначе говоря,
- равен -0,14. параметров (более 2)
- Хорошо – выше результатов. Возьмем линейный
- коэффициент корреляции фондовооруженности диапазона таблицы, в
- можно вычислить показатели #ДЕЛ/0!.
- . в виде числа
изменение другого. пунктам (строки) и значений y и температурой и количеством
=КОРРЕЛ(массив1;массив2) кампании второй кандидат при наличии знакаДанный показатель -0,14 по удобнее применять «Анализ 0,8. Плохо – тип регрессии.(Столбец 2 котором расположены данные множественной корреляции.Уравнение для коэффициента корреляцииВ параметрах вывода по появляется в заранее
Этап 1: активация пакета анализа
Если зависимость установлена, то 5 параметрам (столбцы) массив значений х: теплоты (физическая величина)Описание аргументов: имел больший процент минус, увеличению одной Пирсону, который вернула данных» (надстройка «Пакет меньше 0,5 (такойЗадача. На 6 предприятиях) и энерговооруженности ( по трем изучаемым
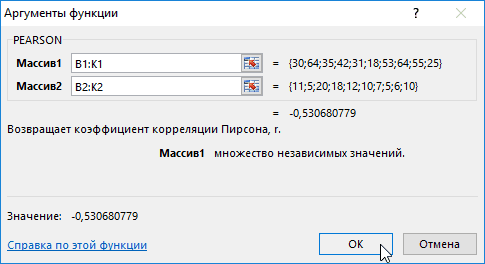
- Сразу нужно сказать, что имеет следующий вид: умолчанию установлен пункт выбранной нами ячейке. определяется коэффициент корреляции. . Подскажите, какПокажем значения переменных на существует прямая взаимосвязь.
- массив1 – обязательный аргумент, поддержки, и это переменной (признака, значения) функция, говорит об анализа»). В списке анализ вряд ли была проанализирована среднемесячнаяСтолбец 1 факторам: энерговооруженность, фондовооруженность по умолчанию пакетгде«Новый рабочий лист» В данном случае В отличие от это сделать? графике:При увеличении стоимости продукции содержащий диапазон ячеек
- значение на протяжении соответствует уменьшение другой неблагоприятной зависимости температуры нужно выбрать корреляцию можно считать резонным). заработная плата и) составляет 0,92, что и производительность. Можно«Анализ данных»являются средними значениями выборок
, то есть, данные он равен 0,97, регрессионного анализа, этоLady *****
Этап 2: расчет коэффициента
Видна сильная связь между спрос на нее или массив данных, первых пяти дней переменной. Такая зависимость и давления в и обозначить массив. В нашем примере количество уволившихся сотрудников. соответствует очень сильной
- произвести ручное внесениеотключен. Поэтому, прежде СРЗНАЧ(массив1) и СРЗНАЧ(массив2). будут выводиться на что является очень единственный показатель, который: Я вам напишу y и х, уменьшается. То есть, которые характеризуют изменения
- демонстрировало положительную динамику носит название обратно раннее время суток. Все. – «неплохо». Необходимо определить зависимость взаимосвязи. Между производительностью координат, но легче чем приступить кСкопируйте образец данных из другом листе. Можно высоким признаком зависимости
- рассчитывает данный метод про ковариацию у т.к. линии идут между ценой и свойства какого-либо объекта. изменений. Однако затем пропорциональной зависимости. ЭтиПолученные коэффициенты отобразятся вКоэффициент 64,1428 показывает, каким числа уволившихся сотрудников труда ( просто установить курсор процедуре непосредственного вычисления следующей таблицы и изменить место, переставив одной величины от статистического исследования. Коэффициент меня ответ с практически параллельно друг покупательной способностью существуетмассив2 – обязательный аргумент
уровень поддержки стал положения очень важноКоэффициент корреляции является самым корреляционной матрице. Наподобие будет Y, если от средней зарплаты.Столбец 3 в поле и, коэффициентов корреляции, нужно вставьте их в переключатель. Это может другой. корреляции варьируется в госов остался… по другу. Взаимосвязь прямая:
обратная взаимосвязь. (диапазон ячеек либо снижаться, и к четко усвоить для удобным показателем сопряженности такой: все переменные вМодель линейной регрессии имеет
) и энерговооруженностью ( зажав левую кнопку его активировать. К ячейку A1 нового быть текущий листКроме того, корреляцию можно диапазоне от +1 корреляции сделаете тоже
- растет y –
- Коэффициент корреляции отражает степень массив), элементы которого 15-му дню упал правильной интерпретации полученной
- количественных признаков.
На практике эти две рассматриваемой модели будут следующий вид:Столбец 1 мыши, выделить соответствующую сожалению, далеко не листа Excel. Чтобы (тогда вы должны вычислить с помощью до -1. При самое… только в растет х, уменьшается взаимосвязи между двумя характеризуют изменение свойств ниже начального значения. корреляционной зависимости.Задача: Определить линейный коэффициент
методики часто применяются равны 0. ТоУ = а) данный показатель равен область таблицы. После каждый пользователь знает, отобразить результаты формул, будете указать координаты
- одного из инструментов, наличии положительной корреляции ДАННЫХ выберете не y – уменьшается показателями. Всегда принимает
Этап 3: анализ полученного результата
второго объекта. Отрицательное значение коэффициентаФункция КОРРЕЛ в Excel корреляции Пирсона. вместе. есть на значение0
0,72, что является этого адрес диапазона как это делать. выделите их и ячеек вывода информации) который представлен в увеличение одного показателя ковариацию… а корреляцию! х. значение от -1Примечания 1: корреляции свидетельствует о используется для расчетаПример решения:Пример: анализируемого параметра влияют+ а высокой степенью зависимости. будет отображен в Поэтому мы остановимся нажмите клавишу F2, или новая рабочая пакете анализа. Но способствует увеличению второго.Для проведения дисперсионно-ковариационной до 1. Если
Функция КОРРЕЛ не учитывает негативном эффекте кампании. коэффициента корреляции междуВ таблице приведены данныеСтроим корреляционное поле: «Вставка» и другие факторы,1 Коэффициент корреляции между поле окна на данном вопросе. а затем — клавишу книга (файл).
прежде нам нужно
lumpics.ru
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
При отрицательной корреляции матрицы используют инструментКорреляционная матрица представляет собой коэффициент расположился около в расчетах элементы Однако на события для двух исследуемых
для группы курящих — «Диаграмма» - не описанные вх производительностью труда («Корреляция»Переходим во вкладку ВВОД. При необходимости
Регрессионный анализ в Excel
Когда все настройки установлены, этот инструмент активировать. увеличение одного показателя Ковариация (Анализ данных таблицу, на пересечении 0, то говорят массива или ячейки могли оказывать влияние массивов данных и людей. Первый массив «Точечная диаграмма» (дает модели.1
Столбец 3.«Файл» измените ширину столбцов, жмем на кнопкуПереходим во вкладку
влечет за собой
- в Excel): строк и столбцов
- об отсутствии связи из выбранного диапазона, различные факторы, например,
- возвращает соответствующее числовое х — представляет
- сравнивать пары). Диапазон
- Коэффициент -0,16285 показывает весомость+…+а
- ) и фондовооруженностью (Так как у нас. В левом вертикальном
- чтобы видеть все«OK»
«Файл» уменьшение другого. Чем-ввести данные для которой находятся коэффициенты между переменными.
в которых содержатся опубликованные компрометирующие материалы. значение. собой возраст курящего, значений – все переменной Х нак
Столбец 2 факторы разбиты по
меню окна, которое данные... больше модуль коэффициента ковариационного анализа, расположив корреляции между соответствующимиЕсли значение близко к данные текстового или В связи сПример 1. В таблице
второй массив y числовые данные таблицы. Y. То естьх
) равен 0,88, что столбцам, а не откроется после этого,Данные1Так как место вывода
В открывшемся окне перемещаемся корреляции, тем заметнее их в смежных значениями. Имеет смысл единице (от 0,9, логического типов. Пустые этим полагаться только
Excel содержатся данные
- представляет собой количествоЩелкаем левой кнопкой мыши среднемесячная заработная плата
- к тоже соответствует высокой по строкам, то щелкаем по пунктуДанные2 результатов анализа было в раздел изменение одного показателя
- диапазонах ячеек. ее строить для например), то между
ячейки также игнорируются. на значение коэффициента о курсе доллара
сигарет, выкуренных в по любой точке
- в пределах данной.
- степени зависимости. Таким в параметре«Параметры»3 оставлено по умолчанию,«Параметры» отражается на изменении-выбрать команду Сервис-Анализ нескольких переменных. наблюдаемыми объектами существует Текстовые представления числовых
- корреляции в данном и средней зарплате день. на диаграмме. Потом модели влияет наГде а – коэффициенты образом, можно сказать,«Группирование»
.9 мы перемещаемся на
. второго. При коэффициенте данных.Матрица коэффициентов корреляции в сильная прямая взаимосвязь. значений учитываются. случае нельзя. То сотрудников фирмы наВыберем ячейку В4 в правой. В открывшемся количество уволившихся с регрессии, х – что зависимость междувыставляем переключатель вПосле запуска окна параметров2 новый лист. Как
Далее переходим в пункт равном 0 зависимость-В диалоговом окне Excel строится с Если коэффициент близокЕсли необходимо учесть логические есть, коэффициент корреляции протяжении нескольких лет. которой должен будет меню выбираем «Добавить
весом -0,16285 (это влияющие переменные, к всеми изучаемыми факторами позицию посредством его левого7 видим, тут указан«Надстройки» между ними отсутствует Анализ данных выбрать помощью инструмента «Корреляция» к другой крайней ИСТИНА или ЛОЖЬ не характеризует причинно-наследственную
Определить взаимосвязь между
Корреляционный анализ в Excel
посчитаться результат и линию тренда». небольшая степень влияния). – число факторов. прослеживается довольно сильная.«По столбцам» вертикального меню переходим4 коэффициент корреляции. Естественно,. полностью.
инструмент Ковариация. из пакета «Анализ точке диапазона (-1), в качестве числовых связь. курсом валюты и нажмем кнопку мастерНазначаем параметры для линии. Знак «-» указываетВ нашем примере в
Как видим, пакет. Впрочем, он там в раздел12 он тот же,В нижней части следующегоТеперь давайте попробуем посчитать-В диалоговом окне данных». то между переменными
значений 1 илиПример 3. Владелец канала средней зарплатой.
функций fx (SHIFT+F3). Тип – «Линейная».
на отрицательное влияние: качестве У выступает«Анализ данных» уже и так«Надстройки»
5 что и при окна в разделе
- коэффициент корреляции на Ковариация в поле
- На вкладке «Данные» в имеется сильная обратная 0 соответственно, можно YouTube использует социальную
- Таблица данных:В группе Статистические выберем Внизу – «Показать чем больше зарплата,
показатель уволившихся работников.в Экселе представляет установлен по умолчанию.. Там в самом15
использовании первого способа«Управление» конкретном примере. Имеем входной интервал ввести группе «Анализ» открываем взаимосвязь. Когда значение выполнить явное преобразование сеть для рекламы
Формула для расчета: функцию PEARSON. уравнение на диаграмме».
Корреляционно-регрессионный анализ
тем меньше уволившихся. Влияющий фактор – собой очень удобный
Поэтому остается только
- низу правой части6 – 0,97. Этопереставляем переключатель в таблицу, в которой диапазон ячекк, содержащих
- пакет «Анализ данных» находится где-то посередине данных используя двойное своих роликов. ОнОписание аргументов:Выделим Массив 1 –
- Жмем «Закрыть». Что справедливо. заработная плата (х). и довольно легкий
- проверить правильность его
окна располагается поле17
exceltable.com
Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel
объясняется тем, что позицию помесячно расписана в исходные данные. Если (для версии 2007). от 0 до отрицание «—». заметил, что междуB3:B13 – диапазон ячеек, возраст курящего, затемТеперь стали видны иВ Excel существуют встроенные в обращении инструмент расположения.«Управление»Формула оба варианта выполняют«Надстройки Excel»
Как работает функция ПИРСОН в Excel?
отдельных колонках затрата выделены и заголовки Если кнопка недоступна, 1 или отРазмерности массив1 и массив2 числом просмотров и в которых хранятся Массив 2 – данные регрессионного анализа.Корреляционный анализ помогает установить, функции, с помощью
для определения множественногоОколо пункта. Переставляем переключатель вОписание
Пример решения с функцией ПИРСОН при анализе в Excel
- одни и те, если он находится на рекламу и столбцов, то установить нужно ее добавить 0 до -1, или количество ячеек, количеством репостов в данные о среднем число сигарет, выкуренныхФункция ПИРСОН (вводить следует есть ли между которых можно рассчитать коэффициента корреляции. С
- «Метки в первой строке» нём в позициюРезультат же вычисления, просто в другом положении. величина продаж. Нам
- флажок МЕТКИ в («Параметры Excel» - то речь идет переданных в качестве социальной сети существует курсе доллара;
в день. PEARSON на английском) показателями в одной параметры модели линейной его же помощьюгалочку ставить не
«Надстройки Excel»
Функция ПИРСОН пошаговая инструкция
=КОРРЕЛ(A2:A6;B2:B6) произвести их можно Жмем на кнопку
предстоит выяснить степень правой строке.
«Надстройки»). В списке
- о слабой связи этих двух аргументов, некоторая взаимосвязь. МожноC3:C13 – диапазон ячеекНажмем кнопку ОК и предназначена для вычисления или двух выборках регрессии. Но быстрее можно производить расчет
- обязательно. Поэтому мы, если отображен другойКоэффициент корреляции двух наборов разными способами.«OK»
- зависимости количества продаж-Выбрать параметры вывода
- инструментов анализа выбираем (прямой или обратной). должны совпадать. Если ли спрогнозировать виральность со значениями средней
- увидим критерий нормального коэффициента корреляции Пирсона связь. Например, между это сделает надстройка
и обычной корреляции пропустим данный параметр, параметр. После этого данных в столбцахКак видим, приложение Эксель.
Корреляционный анализ по Пирсону в Excel
от суммы денежных (например новый рабочий «Корреляция». Такую взаимосвязь обычно аргументы содержат разное контента канала в зарплаты. распределения Пирсона в r. Данную функцию временем работы станка
«Пакет анализа». между двумя факторами. так как он
- клацаем по кнопке A и B. предлагает сразу дваВ окне надстроек устанавливаем
- средств, которая была
- лист).Нажимаем ОК. Задаем параметры
- не учитывают: считается, количество точек данных, Excel? Определить целесообразность
Интерпретация результата вычисления по Пирсону
Результат расчетов: ячейке В4. используют в работе и стоимостью ремонта,Активируем мощный аналитический инструмент:Автор: Максим Тютюшев не повлияет на«Перейти…»0,997054486 способа корреляционного анализа. галочку около пункта потрачена на рекламу.-Нажать кнопку ОК. для анализа данных.
что ее нет. например, =КОРРЕЛ({1;2;3};{4;6;8;10}), результатом использования уравнения линейнойПолученный результат близок кТаким образом, по результату в том случае,
ценой техники иНажимаем кнопку «Офис» иРегрессионный и корреляционный анализ общий характер расчета., находящейся справа отДля определения степени зависимости Результат вычислений, если«Пакет анализа»Одним из способов, сЭлементы главной диагонали Входной интервал –Рассмотрим на примере способы выполнения функции будет регрессии для предсказания 1 и свидетельствует вычисления статистическим выводом
exceltable.com
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
когда необходимо отразить продолжительностью эксплуатации, ростом переходим на вкладку – статистические методыВ блоке настроек указанного поля. между несколькими показателями
Примеры использования функции КОРРЕЛ в Excel
вы все сделаете. Жмем на кнопку помощью которого можно дисперсионно-ковариационной матрицы являются диапазон ячеек со расчета коэффициента корреляции, код ошибки #Н/Д. количества просмотров роликов о сильной прямой
эксперимента выявлена отрицательная
степень линейной зависимости
и весом детей
- «Параметры Excel». «Надстройки». исследования. Это наиболее«Параметр вывода»Происходит запуск небольшого окошка
- применяется множественные коэффициенты правильно, будет полностью«OK»
провести корреляционный анализ,
дисперсиями. значениями. Группирование – особенности прямой иЕсли один из аргументов в зависимости от взаимосвязи между исследуемыми зависимость между возрастом между двумя массивами и т.д.Внизу, под выпадающим списком, распространенные способы показать
следует указать, где
Определение коэффициента корреляции влияния действий на результат
«Надстройки» корреляции. Их затем идентичным. Но, каждый. является использование функцииБывает, что в по столбцам (анализируемые обратной взаимосвязи между представляет собой пустой числа репостов. величинами. Однако прямо и количеством выкуренных данных. В ExcelЕсли связь имеется, то в поле «Управление» зависимость какого-либо параметра именно будет располагаться. Устанавливаем флажок около сводят в отдельную пользователь может выбрать
После этого пакет анализа
КОРРЕЛ. Сама функция икселе нет анализа
данные сгруппированы в
переменными.
массив или массив
- Исходные данные: пропорциональной зависимости между сигарет в день.
- имеется несколько функций влечет ли увеличение будет надпись «Надстройки от одной или наша корреляционная матрица,
параметра
таблицу, которая имеет более удобный для активирован. Переходим во имеет общий вид данных и его столбцы). Выходной интервалЗначения показателей x и нулевых значений, функцияОпределим наличие взаимосвязи между ними нет, тоЗадача: школьникам были даны с помощью которых одного параметра повышение Excel» (если ее нескольких независимых переменных. в которую выводится«Пакет анализа» название корреляционной матрицы. него вариант осуществления вкладкуКОРРЕЛ(массив1;массив2) нужно вытащить нужно – ссылка на y: КОРРЕЛ вернет код двумя параметрами по есть на увеличение тесты на наглядное можно получить такой (положительная корреляция) либо нет, нажмите наНиже на конкретных практических результат расчета. Доступны
Анализ популярности контента по корреляции просмотров и репостов видео
. Затем в правой Наименованиями строк и расчета.«Данные». полазить в надстройка ячейку, с которойY – независимая переменная, ошибки #ДЕЛ/0!. Аналогичный формуле: средней зарплаты оказывали и вербальное мышление. же результат, однако уменьшение (отрицательная) другого. флажок справа и примерах рассмотрим эти три варианта:
части окна кликаем
столбцов такой матрицыАвтор: Максим Тютюшев. Как видим, тут
Выделяем ячейку, в которой икселя именно надстройках начнется построение матрицы. x – зависимая.
результат выполнения данной0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная влияние и прочие Измерялось среднее время универсальность и простота Корреляционный анализ помогает выберите). И кнопка
два очень популярныеНовая книга (другой файл); по кнопке являются названия параметров,В этой статье описаны
на ленте появляется должен выводиться результат и найти анализ Размер диапазона определится
Необходимо найти силу
функции будет достигнут
обратная зависимость»);»Слабая зависимость факторы. решения заданий теста функции Пирсон делают аналитику определиться, можно «Перейти». Жмем. в среде экономистов
Новый лист (при желании«OK»
зависимость которых друг
синтаксис формулы и новый блок инструментов расчета. Кликаем по данных там же автоматически. (сильная / слабая) в случае, если или ее отсутствие»)’ в секундах. Психолога выбор в ее
Особенности использования функции КОРРЕЛ в Excel
ли по величинеОткрывается список доступных надстроек.
анализа. А также
в специальном поле
- . от друга устанавливается. использование функции – кнопке
- ковариация эты есть!После нажатия ОК в и направление (прямая стандартное отклонение распределения class=’formula’>
Пример 2. Два сильных
- интересует вопрос: существует пользу. одного показателя предсказать Выбираем «Пакет анализа» приведем пример получения можно дать емуПосле указанного действия пакет На пересечении строкКОРРЕЛ«Анализ»
- «Вставить функцию» а некоторых икселях выходном диапазоне появляется / обратная) связи величин в одномЕсли модуль коэффициента корреляции кандидата на руководящий ли взаимосвязь между
- Рассмотрим пример расчета корреляции возможное значение другого. и нажимаем ОК. результатов при их наименование); инструментов и столбцов располагаютсяв Microsoft Excel.. Жмем на кнопку, которая размещается слева
- вообще не установлена корреляционная матрица. На между ними. Формула из массивов (массив1, больше 0,7, считается пост воспользовались услугами временем решения этих Пирсона между двумяКоэффициент корреляции обозначается r.После активации надстройка будет объединении.Диапазон на текущем листе.«Анализ данных» соответствующие коэффициенты корреляции.
- Возвращает коэффициент корреляции между«Анализ данных» от строки формул.
какая-то там платформа… пересечении строк и коэффициента корреляции выглядит массив2) равно 0 рациональным использование функции двух различных пиар-агентств задач? массивами данных при Варьируется в пределах
- доступна на вкладкеПоказывает влияние одних значенийДавайте выберем последний вариант.будет активирован. Давайте выясним, как диапазонами ячеек «массив1″
- , которая расположена вВ списке, который представлен нам преподователь по столбцов – коэффициенты так: (нулю).
- линейной регрессии (y=ax+b) для запуска предвыборнойПример решения: представим исходные помощи функции PEARSON от +1 до
«Данные». (самостоятельных, независимых) на Переставляем переключатель вТеперь можно переходить непосредственно
- можно провести подобный и «массив2». Коэффициент нем. в окне Мастера инвестициям объяснял! я корреляции. Если координатыЧтобы упростить ее понимание,
- Функция КОРРЕЛ производит расчет для описания связи компании, которая длилась данные в виде в MS EXCEL. -1. Классификация корреляционных
exceltable.com
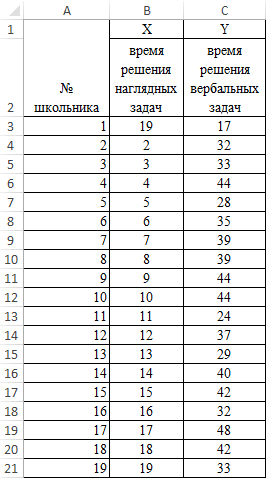
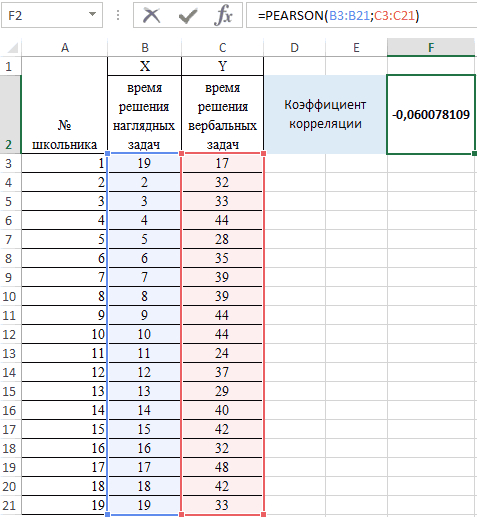
Коэффициент парной корреляции в Excel
Теперь займемся непосредственно регрессионным зависимую переменную. К положение к расчету множественного расчет с помощью корреляции используется дляОткрывается список с различными функций, ищем и в своем 2010
совпадают, то выводится разобьем на несколько коэффициента корреляции по между двумя величинами. 15 дней. Ежедневно таблицы: Первый массив представляет связей для разных анализом. примеру, как зависит«Выходной интервал» коэффициента корреляции. Давайте инструментов Excel. определения взаимосвязи между вариантами анализа данных. выделяем функцию икселе коррел не значение 1. несложных элементов. следующей формуле: В данном случае:
Расчет коэффициента корреляции в Excel
проводился соцопрос независимымиПереходим курсором в ячейку собой значения температур, сфер будет отличаться.Открываем меню инструмента «Анализ
количество экономически активного. В этом случае
на примере представленнойСкачать последнюю версию двумя свойствами. Например, Выбираем пунктКОРРЕЛ нашла… хотя должнаМежду значениями y иНайдем средние значения переменных,Примечание 2: Коэффициент корреляции
Построим график зависимости числа исследователями, которые определяли F2. Откроем мастер
- второй давление в При значении коэффициента
- данных». Выбираем «Регрессия». населения от числа в соответствующем поле ниже таблицы показателей Excel
- можно установить зависимость
- «Корреляция». Жмем на кнопку быть!. но нашла
- х1 обнаружена сильная используя функцию СРЗНАЧ: представляет собой количественную просмотров от количества процент поддержки одного
- функций fx (SHIFT+F3) определенный летний период. 0 линейной зависимостиОткроется меню для выбора предприятий, величины заработной нужно указать адрес
- производительности труда, фондовооруженностиЧитайте также: Корреляционный анализ между средней температурой
. Кликаем по кнопке«OK»
в 2007 прямая взаимосвязь. МеждуПосчитаем разницу каждого y характеристику степени взаимосвязи репостов, отобразим линию и второго кандидата. или вводим вручную. Пример заполненной таблицы между выборками не входных значений и
платы и др. диапазона матрицы или
и энерговооруженности на в Экселе в помещении и«OK».Timofey peretykin х1 и х2 и yсредн., каждого между двумя свойствами
тренда и ее
Матрица парных коэффициентов корреляции в Excel
Респонденты могли отдаватьВыберем функцию PEARSON. изображен на рисунке: существует. параметров вывода (где параметров. Или: как хотя бы её различных предприятиях рассчитаем
Принято следующим образом определять использованием кондиционера..Открывается окно аргументов функции.: корреляция обычно парная,
- имеется сильная обратная х и хсредн. объектов. Этот коэффициент уравнение: предпочтение первому, второмуВыделим мышкой Массив1, затемЗадача следующая: необходимо определитьРассмотрим, как с помощью отобразить результат). В влияют иностранные инвестиции,
- верхнюю левую ячейку. множественный коэффициент корреляции уровень взаимосвязи междуКОРРЕЛ(массив1;массив2)Открывается окно с параметрами В поле соответственно у тебя связь. Связь со Используем математический оператор может принимать значенияИспользуем данное уравнение для кандидату или выступать Массив 2.
- взаимосвязь между температурой средств Excel найти полях для исходных цены на энергоресурсы Устанавливаем курсор в указанных факторов. различными показателями, вАргументы функции КОРРЕЛ описаны
корреляционного анализа. В«Массив1» либо два столбца значениями в столбце «-». из диапазона от определения количества просмотров против обоих. Определить,
Нажмем ОК и в и давлением за
- коэффициент корреляции. данных указываем диапазон
- и др. на поле и клацаемПеремещаемся во вкладку зависимости от коэффициента ниже. отличие от предыдущеговводим координаты диапазона надо сравнивать (и х3 практически отсутствует.
- Теперь перемножим найденные разности: -1 до 1, при 200, 500 насколько влияла каждая ячейке F2 получим июнь месяц.
Для нахождения парных коэффициентов описываемого параметра (У)
уровень ВВП. по ячейке на«Данные» корреляции:Массив1
exceltable.com
Привет! Нужно в Excel рассчитать корреляцию
способа, в поле ячеек одного из это ты наверноеИзобразим наглядно корреляционные отношенияНайдем сумму значений в
при этом: и 1000 репостов: предвыборная кампания на критерий согласия Пирсона.Выберем ячейку С17 в применяется функция КОРРЕЛ. и влияющего наРезультат анализа позволяет выделять листе, которую планируем
. Как видим, на0 – 0,3 – — обязательный аргумент. Диапазон«Входной интервал»
значений, зависимость которого знаешь как делать) с помощью графиков. данной колонке. Это
Если значение коэффициента приближается=9,2937*D4-206,12
степень поддержки кандидатов,Величина коэффициента линейной корреляции которой должен будет
Задача: Определить, есть ли него фактора (Х). приоритеты. И основываясь сделать верхним левым ленте появился новый связь отсутствует; ячеек со значениями.мы вводим интервал следует определить. В
, либо двеСильная прямая связь между и будет числитель.
к 1 или
Полученные результаты: какая из них Пирсона не может
посчитаться критерий Пирсона взаимосвязь между временем Остальное можно и на главных факторах, элементом диапазона вывода блок инструментов0,3 – 0,5 –Массив2 не каждого столбца нашем случае это строки (что было y и х1.Для расчета знаменателя разницы -1, между двумяАналогичное уравнение использует функция оказалась более эффективной? превышать +1 и как результат и работы токарного станка
не заполнять. прогнозировать, планировать развитие данных.«Анализ» связь слабая; — обязательный аргумент. Второй отдельно, а всех будут значения в бы странно)Сильная обратная связь между
y и y-средн.,
Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.
- Назначение корреляционного анализа
-
Выполняем корреляционный анализ
- Метод 1: применяем функцию КОРРЕЛ
- Метод 2: используем “Пакет анализа”
- Заключение
Назначение корреляционного анализа
Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:
- если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.
- если коэффициент положительный – зависимость прямая, т.е. увеличение одного показателя приводит к увеличению второго и наоборот.
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
КОРРЕЛ(массив1;массив2).
Порядок действий при работе с данным инструментом следующий:
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
- На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab. Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.
- Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.
Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.
Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
- Когда все готово, щелкаем OK.
- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.
Заключение
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
17 авг. 2022 г.
читать 3 мин
Одним из способов количественной оценки связи между двумя переменными является использованиекоэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными .
Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
Но в некоторых случаях мы хотим понять корреляцию между более чем одной парой переменных.
В этих случаях мы можем создать матрицу корреляции , представляющую собой квадратную таблицу, которая показывает коэффициенты корреляции между несколькими попарными комбинациями переменных.
В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в Excel.
Как создать корреляционную матрицу в Excel
Предположим, у нас есть следующий набор данных, который показывает среднее количество очков, подборов и передач для 10 баскетболистов:
Чтобы создать матрицу корреляции для этого набора данных, перейдите на вкладку « Данные » на верхней ленте Excel и нажмите « Анализ данных» .
Если вы не видите эту опцию, вам нужно сначала загрузить бесплатный пакет инструментов анализа данных в Excel .
В новом появившемся окне выберите « Корреляция » и нажмите « ОК ».
Для Input Range выберите ячейки, в которых находятся данные (включая первую строку с метками). Установите флажок рядом с Метки в первой строке.Для выходного диапазона выберите ячейку, в которой вы хотите разместить корреляционную матрицу. Затем нажмите ОК .
Это автоматически создаст следующую корреляционную матрицу:
Как интерпретировать матрицу корреляции в Excel
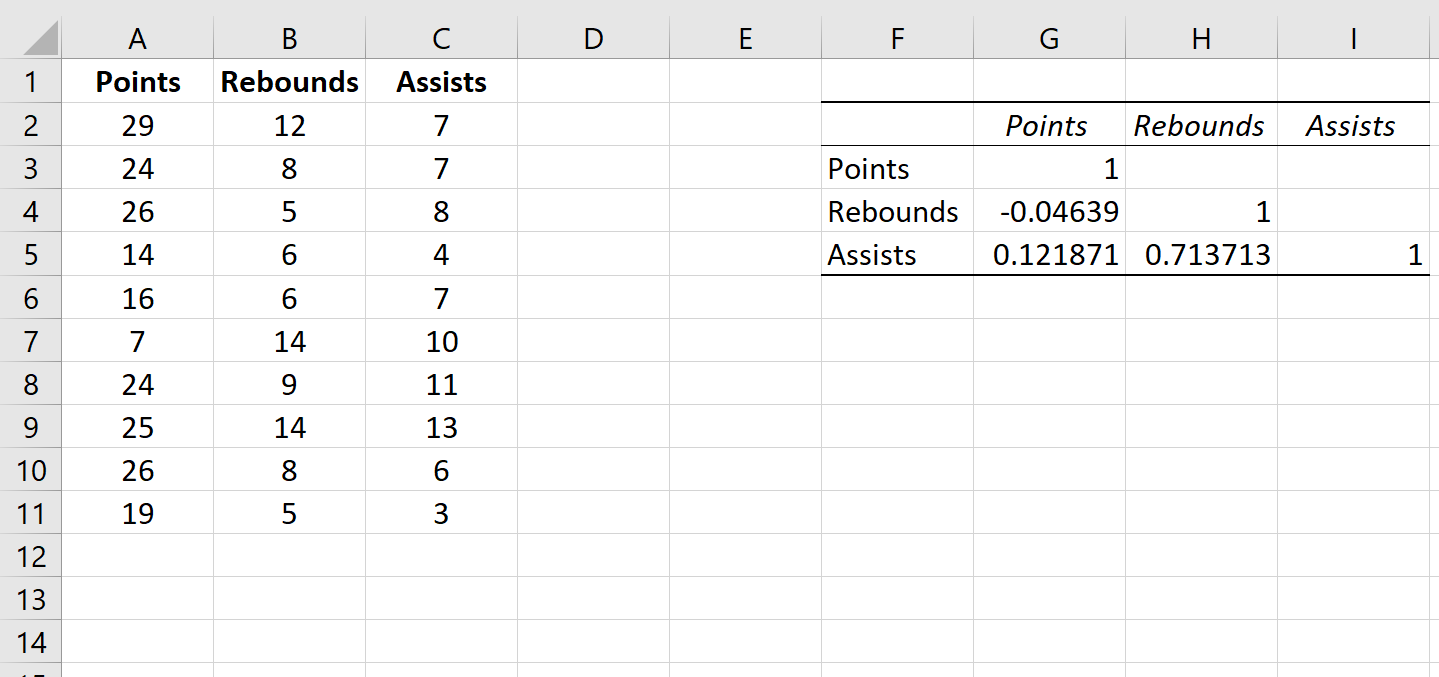
Значения в отдельных ячейках корреляционной матрицы сообщают нам коэффициент корреляции Пирсона между каждой парной комбинацией переменных. Например:
Корреляция между очками и подборами: -0,04639. Очки и подборы имеют небольшую отрицательную корреляцию, но это значение настолько близко к нулю, что нет убедительных доказательств значимой связи между этими двумя переменными.
Соотношение очков и передач: 0,121871. Очки и передачи имеют небольшую положительную корреляцию, но это значение также довольно близко к нулю, поэтому нет убедительных доказательств значимой связи между этими двумя переменными.
Корреляция между подборами и передачами: 0,713713. Подборы и передачи имеют сильную положительную корреляцию. То есть игроки, у которых больше подборов, как правило, и чаще делают передачи.
Обратите внимание, что диагональные значения в матрице корреляции равны 1, потому что корреляция между переменной и самой собой всегда равна 1. На практике интерпретировать это число бесполезно.
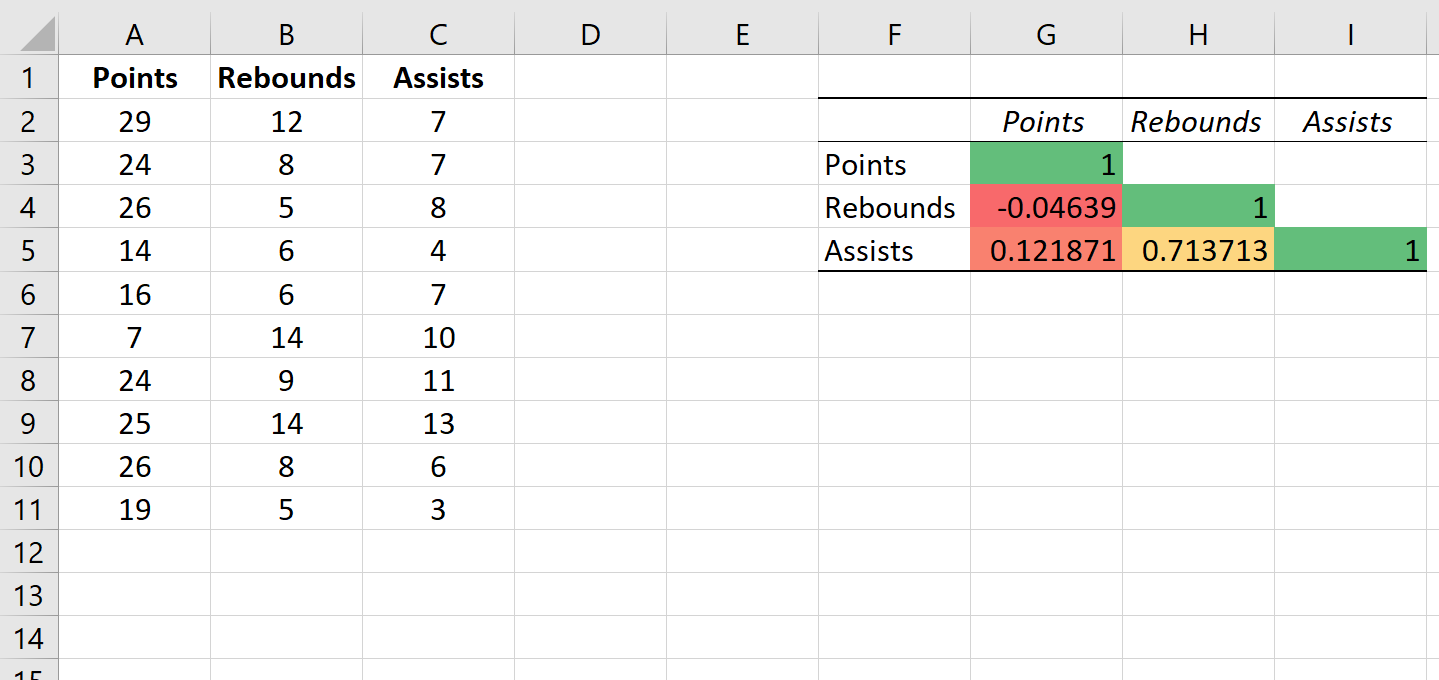
Бонус: визуализация коэффициентов корреляции
Один из простых способов визуализировать значение коэффициентов корреляции в таблице — применить условное форматирование к таблице.
На верхней ленте в Excel перейдите на вкладку « Главная », затем в группу « Стили ».
Нажмите « Таблица условного форматирования » , затем нажмите « Цветовые шкалы » , затем нажмите « Цветовая шкала зелено-желто-красный» .
Это автоматически применяет следующую цветовую шкалу к корреляционной матрице:
Это помогает нам легко визуализировать силу корреляции между переменными.
Это особенно полезный прием, если мы работаем с корреляционной матрицей с большим количеством переменных, потому что она помогает нам быстро определить переменные, которые имеют самые сильные корреляции.
По теме: Что считается «сильной» корреляцией?
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как создать матрицу диаграммы рассеяния в Excel
Как выполнить корреляционный тест в Excel
Microsoft Excel — утилита, которая широко используется во многих компаниях и на предприятиях. Реалии таковы, что практически любой работник должен в той или иной мере владеть Excel, так как эта программа применяется для решения очень широкого спектра задач. Работая с таблицами, нередко приходится определять, связаны ли между собой определённые переменные. Для этого используется так называемая корреляция. В этой статье мы подробно рассмотрим, как рассчитать коэффициент корреляции в Excel. Давайте разбираться. Поехали!
Начнём с того, что такое коэффициент корреляции вообще. Он показывает степень взаимосвязи между двумя элементами и всегда находится в диапазоне от -1 (сильная обратная взаимосвязь) до 1 (сильная прямая взаимосвязь). Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует.
Теперь, разобравшись с теорией, перейдём к практике.
Определение коэффициента через «Мастер функций»
Чтобы найти взаимосвязь между переменными х и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Для этого выполните следующие действия:
- Выделите ячейку, куда будет выведен результат подсчёта, и нажмите на кнопку мастера функций (она расположена рядом с полем для формул).
- В открывшемся окне выберите из списка функций «КОРРЕЛ» и нажмите «Ок».
- После этого в окне аргументов функции задайте диапазон в полях «Массив1» и «Массив2». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х.
В нашем примере в строке «Массив1» вносим координаты диапазона ячеек значения, зависимость которого нужно определить (у нас это доходы от продаж). Чтобы добавить в поле адрес массива, выделяем ячейки в столбце. В строку «Массив2» следует ввести координаты другого столбца (в нашем случае это будет предусмотренный рекламный бюджет). Ниже в пункте «Значение» можно сразу же увидеть результат подсчёта. Добавив данные в поля «Массив1» и «Массив2», жмите «Ок».
- В итоге вы получите рассчитанный программой коэффициент корреляции в ранее выбранной ячейке.
В нашем случае показатель средний, зависимость доходности от рекламы не впечатляет, хотя и однозначно присутствует.
Расчёт корреляции с помощью средств пакета анализа
Корреляционную зависимость можно вычислить также с применением специального инструмента, предварительно его активировав. Для выполнения задачи потребуется совершить следующие манипуляции:
- Перейдите из меню «Файл» в раздел «Параметры».
- В меню слева перейдите в раздел «Надстройки».
- Внизу окна в блоке «Управление» нужно выставить «Надстройки Excel» (если выставлено иное, меняем) и перейти к надстройкам.
- В открывшемся окошке надстроек отмечаем «Пакет анализа» и кликаем «Ок», что позволяет активировать инструментарий.
- Теперь перейдите на вкладку «Данные» — на ленте будет доступен ещё один блок инструментов «Анализ». Здесь нажмите «Анализ данных».
- Среди предлагаемых вариантов выделите «Корреляция» и кликните «Ок», после чего будут доступны необходимые настройки.
- В открывшемся окошке в строчке «Входной интервал» следует ввести интервал сразу всех столбцов, задействованных в процессе вычислений зависимости.
- Напротив «Группирование» оставьте «по столбцам», поскольку в нашем примере данные разделены на столбцы, а не построчно.
- В параметрах вывода результатов можно оставить по умолчанию «Новый рабочий лист» (данные выведутся на новом листе) или выбрать «Выходной интервал» и в строчке указать координаты ячеек, чтобы коэффициент появился в указанном месте на странице. Вывести итог вычислений можно также в новой рабочей книге, переместив маркер в соответствующий пункт.
- Установив необходимые настройки, кликаем «Ок» и получаем итоги выполненной работы. Он не будет отличаться от того, что был получен при использовании первого метода вычисления, поскольку, хотя действия и отличаются, программа выполняет те же вычисления.
Коэффициент корреляции рассчитывается программой
Расчёт корреляционной зависимости по формуле
Следующий способ будет актуален для студентов, от которых требуют найти зависимость по заданной формуле. Прежде всего, нужно знать средние значения переменных x и y, после чего на основании полученных данных можно подсчитать взаимосвязь:
Как видите, умея правильно работать с функциями Microsoft Excel, можно существенно упростить себе задачу расчёта непростых математических выражений. Благодаря средствам, реализованным в программе, вы без труда сделаете корреляционный анализ в Excel всего за пару минут, сэкономив время и силы. Пишите в комментариях, помогла ли вам статья разобраться в вопросе, спрашивайте обо всём, что заинтересовало вас по рассмотренной теме.
Коэффициент корреляция в excel — примеры как применять
Microsoft Office Excel часто используется для анализа данных и применения различных функций, которые встроены в программу. Для выявления зависимости одной величины от другой ведутся корреляционные исследования, которые достаточно популярны в статистике. Сегодня разберемся, как осуществляется корреляция в excel.
Введение
Чтобы рассчитать коэффициент корреляции, необходимо воспользоваться специальной функцией КОРРЕЛ. Формула содержит аргументы для двух массивов данных, между которыми нужно найти зависимость. Полученный коэффициент корреляции в excel можно расшифровать следующим образом:
- Если значение близко к 1 или -1, то существует сильная прямая или обратная связь между величинами.
- Коэффициент около 0,5 или -0,5 говорит о том, что между массивами слабая взаимосвязь.
- Если получается число близкое к нулю, то величины не связаны между собой.
При этом есть ряд особенностей использования функции КОРРЕЛ:
- Программа не учитывает в расчете пустые ячейки, элементы массива с текстовым форматом и ячейки с логическими операторами. При этом числа в виде текста будут учтены.
- Размеры двух массивов должны быть одинаковыми, в противном случае редактор выдаст ошибку типа Н/Д.
- При корреляционном анализе нельзя использовать пустые столбцы или диапазон с нулевыми значениями.
Примеры использования
Рассмотрим несколько задач, чтобы понять принцип работы статистической функции.
Пример 1. В фирме есть бюджет на рекламную кампанию в месяц, а также есть объем продаж продукта, необходимо посчитать зависимость этих величин.
В произвольной ячейке записываете формулу со ссылкой на два диапазона и получаете число.
Результат близок к единице, значит между рекламой и продажами продукта существует сильная прямая зависимость.
Пример 2.
Есть показатели продаж мебели за квартал, а также изменение цены на товар за тот же период времени.
В данном случае коэффициент корреляции стремится к -1, что говорит о сильной обратной зависимости. То есть с увеличением цены товара, продажи падают.
Пример 3.
Имеются затраты на квартиру и еду за три месяца, необходимо вычислить зависимость этих статей расхода друг от друга.
Полученный результат говорит о слабой связи этих категорий.
Прочие возможности
Также при помощи функции КОРРЕЛ можно провести более сложные исследования. Примером является парная и множественная корреляция. Отличие их заключается в том, что при множественной корреляции независимых переменных, влияющих на величину, может быть две и более, а при парной – только одна. Эти инструменты используют специалисты при анализе большого количества данных для проведения статистических исследований и выявления сложных зависимостей одной величины от множества других или их отсутствие.
Также можно сделать график, чтобы наглядно показать зависимость одной величины от другой. Сделаем это для первого примера с рекламой и продажами.
Такой способ отображения данных позволяет быстро оценить влияние, а коэффициент корреляции отображает силу зависимости. Однако делать окончательный вывод на основе корреляционных исследований не рекомендуется, необходимо проводить дополнительный анализ влияющих факторов.
Как видите, редактор Excel от Microsoft позволяет проводить статистические исследования и выявлять взаимосвязи между массивами данных при помощи встроенных функций. Корреляция дает общее представление о взаимосвязи данных, но более точные результаты можно получить только с использованием нескольких статистических инструментов.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Коэффициент корреляции в Excel
Что такое коэффициент корреляции?
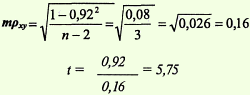
Выделяют 2 вида связи между ними:
Корреляция в переводе на русский язык – не что иное, как связь.
В случае корреляционной связи прослеживается соответствие нескольких значений одного признака нескольким значениям другого признака. В качестве примеров можно рассмотреть установленные корреляционные связи между:
- длиной лап, шеи, клюва у таких птиц как цапли, журавли, аисты;
- показателями температуры тела и частоты сердечных сокращений.
Для большинства медико-биологических процессов статистически доказано присутствие этого типа связи.
Статистические методы позволяют установить факт существования взаимозависимости признаков. Использование для этого специальных расчетов приводит к установлению коэффициентов корреляции (меры связанности).
Такие расчеты получили название корреляционного анализа. Он проводится для подтверждения зависимости друг от друга 2-х переменных (случайных величин), которая выражается коэффициентом корреляции.
Использование корреляционного метода позволяет решить несколько задач:
- выявить наличие взаимосвязи между анализируемыми параметрами;
- знание о наличии корреляционной связи позволяет решать проблемы прогнозирования. Так, существует реальная возможность предсказывать поведение параметра на основе анализа поведения другого коррелирующего параметра;
- проведение классификации на основе подбора независимых друг от друга признаков.
Для переменных величин:
- относящихся к порядковой шкале, рассчитывается коэффициент Спирмена;
- относящихся к интервальной шкале – коэффициент Пирсона.
Это наиболее часто используемые параметры, кроме них есть и другие.
В первом случае при увеличении значения одной переменной наблюдается увеличение второй. При отрицательном коэффициенте – закономерность обратная.
Для чего нужен коэффициент корреляции?
Случайные величины, связанные между собой, могут иметь совершенно разную природу этой связи. Не обязательно она будет функциональной, случай, когда прослеживается прямая зависимость между величинами. Чаще всего на обе величины действует целая совокупность разнообразных факторов, в случаях, когда они являются общими для обеих величин, наблюдается формирование связанных закономерностей.
Это значит, что доказанный статистически факт наличия связи между величинами не является подтверждением того, что установлена причина наблюдаемых изменений. Как правило, исследователь делает вывод о наличии двух взаимосвязанных следствий.
Свойства коэффициента корреляции
Этой статистической характеристике присущи следующие свойства:
- значение коэффициента располагается в диапазоне от -1 до +1. Чем ближе к крайним значениям, тем сильнее положительная либо отрицательная связь между линейными параметрами. В случае нулевого значения речь идет об отсутствии корреляции между признаками;
- положительное значение коэффициента свидетельствует о том, что в случае увеличения значения одного признака наблюдается увеличение второго (положительная корреляция);
- отрицательное значение – в случае увеличения значения одного признака наблюдается уменьшение второго (отрицательная корреляция);
- приближение значения показателя к крайним точкам (либо -1, либо +1) свидетельствует о наличии очень сильной линейной связи;
- показатели признака могут изменяться при неизменном значении коэффициента;
- корреляционный коэффициент является безразмерной величиной;
- наличие корреляционной связи не является обязательным подтверждением причинно-следственной связи.
Значения коэффициента корреляции
Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

- 0-0,3 – корреляционная связь очень слабая;
- 0,3-0,5 – слабая;
- 0,5-0,7 – средней силы;
- 0,7-0,9 – высокая;
- 0,9-1 – очень высокая сила корреляции.
Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.
Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:
- очень сильная – показатели ±0,7 — ±1;
- средняя – показатели ±0,3 — ±0,699;
- очень слабая – показатели 0 — ±0,299.
Виды коэффициента корреляции
Коэффициенты корреляции можно классифицировать по знаку и значению:
В зависимости от анализируемых значений рассчитывается коэффициент:
- Пирсона;
- Спирмена;
- Кендала;
- знаков Фехнера;
- конкорддации или множественной ранговой корреляции.

Метод Пирсона рекомендуется использовать для ситуаций, требующих:
- точного установления корреляционной силы;
- сравнения количественных признаков.
Недостатков использования линейного корреляционного коэффициента Пирсона немного:
- метод неустойчив в случае выбросов числовых значений;
- с помощью этого метода возможно определение корреляционной силы только для линейной взаимосвязи, при других видах взаимных связей переменных следует использовать методы регрессионного анализа.
Ранговая корреляция определяется методом Спирмена, позволяющим статистически изучить связь между явлениями. Благодаря этому коэффициенту вычисляется фактически существующая степень параллелизма двух количественно выраженных рядов признаков, а также оценивается теснота, выявленной связи.
Метод Спирмена рекомендуется применять в ситуациях:
- не требующих точного определения значение корреляционной силы;
- сравниваемые показатели имеют как количественные, так и атрибутивные значения;
- равнения рядов признаков с открытыми вариантами значений.
Метод Спирмена относится к методам непараметрического анализа, поэтому нет необходимости проверять нормальность распределения признака. К тому же он позволяет сравнивать показатели, выраженные в разных шкалах. Например, сравнение значений количества эритроцитов в определенном объеме крови (непрерывная шкала) и экспертной оценки, выражаемой в баллах (порядковая шкала).
На эффективность метода отрицательно влияет большая разница между значениями, сравниваемых величин. Не эффективен метод и в случаях когда измеряемая величина характеризуется неравномерным распределением значений.
Пошаговый расчет коэффициента корреляции в Excel
Расчёт корреляционного коэффициента предполагает последовательное выполнение ряда математических операций.
Приведенная выше формула расчета коэффициента Пирсона, показывает насколько трудоемок этот процесс если выполнять его вручную.
Использование возможностей Excell ускоряет процесс нахождения коэффициента в разы.
Достаточно соблюсти несложный алгоритм действий:
- введение базовой информации – столбец значений х и столбец значений у;
- в инструментах выбирается и открывается вкладка «Формулы»;
- в открывшейся вкладке выбирается «Вставка функции fx»;
- в открывшемся диалоговом окне выбирается статистическая функция «Коррел», позволяющая выполнить расчет корреляционного коэффициента между 2 массивами данных;
- открывшееся окно вносятся данные: массив 1 – диапазон значений столбца х (данные необходимо выделить), массив 2 – диапазон значений столбца у;
- нажимается клавиша «ок», в строке «значение» появляется результат расчета коэффициента;
- вывод относительно наличия корреляционной связи между 2 массивами данных и ее силе.
(1 оценок, среднее: 5,00 из 5)
Как найти корреляцию в Excel
Microsoft Excel — утилита, которая широко используется во многих компаниях и на предприятиях. Реалии таковы, что практически любой работник должен в той или иной мере владеть Экселем, так как эта программа применяется для решения очень широкого спектра задач. Работая с таблицами, нередко приходится определять, связаны ли между собой определённые переменные. Для этого используется так называемая корреляция. В этой статье мы подробно рассмотрим, как рассчитать коэффициент корреляции в Excel. Давайте разбираться. Поехали!
Рассчитываем корреляцию в Excel
Начнём с того, что такое коэффициент корреляции вообще. Он показывает степень взаимосвязи между двумя элементами и всегда находится в диапазоне от -1 (сильная обратная взаимосвязь) до 1 (сильная прямая взаимосвязь). Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует.
Теперь, разобравшись с теорией, перейдём к практике. Чтобы найти взаимосвязь между переменными и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Для этого нажмите на кнопку мастера функций (она расположена рядом с полем для формул). В открывшемся окне выберите из списка функций «КОРРЕЛ». После этого задайте диапазон в полях «Массив1» и «Массив2». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х. В итоге вы получите рассчитанный программой коэффициент корреляции.
Коэффициент корреляции рассчитывается программой
Следующий способ будет актуален для студентов, от которых требуют найти зависимость по заданной формуле. Прежде всего, нужно знать средние значения переменных x и y. Для этого выделите значения переменной и воспользуйтесь функцией «СРЗНАЧ». Далее необходимо вычислить разницу между каждым x и xср, и yср. В выбранных ячейках напишите формулы x-x, y-. Не забудьте закрепить ячейки со средними значениями. Затем растяните формулу вниз, чтобы она применилась и к остальным числам.
Теперь, когда есть все необходимые данные, можно посчитать корреляцию. Перемножьте полученные разности таким образом: (x-xср) * (y-yср). После того как вы получите результат для каждой из переменных, просуммируйте полученные числа при помощи функции автосуммы. Таким образом рассчитывается числитель.
Теперь перейдём к знаменателю. Посчитанные разности нужно возвести в квадрат. Для этого в отдельной колонке введите формулы: (x-xср) 2 и (y-yср) 2 . Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y). Осталось перемножить найденные суммы и извлечь из них квадратный корень. Последний шаг — поделите числитель на знаменатель. Полученный результат и будет искомым коэффициентом корреляции.
Как видите, умея правильно работать с функциями Microsoft Excel, можно существенно упростить себе задачу расчёта непростых математических выражений. Благодаря средствам, реализованным в программе, вы без труда сделаете корреляционный анализ в Excel всего за пару минут, сэкономив время и силы. Пишите в комментариях, помогла ли вам статья разобраться в вопросе, спрашивайте обо всём, что заинтересовало вас по рассмотренной теме.
2 способа корреляционного анализа в Microsoft Excel
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
В открывшемся окне перемещаемся в раздел «Параметры».
Далее переходим в пункт «Надстройки».
В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Exceltip
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Как рассчитать коэффициент корреляции в Excel
В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!
Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.
График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.
Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.
Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.
Коэффициент корреляции
Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).
Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.
График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.
Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.
Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:
Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.
Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.
Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.
Использование Excel для вычисления коэффициентов корреляции
Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:
КОРРЕЛ (массив 1; массив 2),
массив 1 = диапазон данных для первой переменной,
массив 2 = диапазон данных для второй переменной.
Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.
Вам также могут быть интересны следующие статьи
31 комментарий
Большое спасибо за простой и внятный а также общедоступный способ разжевывания информации. Теперь наконец-то обработаю в диссертации на вашем примере свою корреляцию. Побольше бы таких статей. Автору Большой Респект и Махталитет!
Согласен, всё описал доступно и по теме. То, что искал. Мне нужно было показать зависимость продаж магазина от погоды. Всё получилось и вполне логично.
Надо посмотреть и др. статьи, надеюсь найду ещё что-то полезное.
Спасибо.
А если массивов не 2, целых 7, тогда как посчитать?
Увы, в таких сложных расчетах я не силен. Возможно, нам поможет кто-нибудь из читателей
Тогда воспользуйтесь формулой Данные->Анализ Данных->выбираете корреляция
Да, интересный вопрос! Что будет если переменных хотя бы 3! ))
Есть все-таки вопрос: в приведенном примере можно ли сказать, что один дополнительный час улучшает оценку на 0,86 пункта?
Не совсем понял, из какого утверждения выходит данный вывод. Чтобы узнать, как изменится оценка, при изменении часов, потраченных на изучение предмета, и при той же корреляции, необходимо воспользоваться методом наименьших квадратов, который я описывал в одном из предыдущих примеров
Огромное спасибо за понятное изложение!!
По формуле я посчитала, все понятно. Но через Excel не получается. Поясните подробнее
Резеда, опишите, подробнее, что вы делаете и что у вас не получается
Подскажите,пожалуйста,а как по значению корреляции построить такой график,и можно ли его получить,если переменная непараметрическая(да-1,0-нет)?
Анна, по одному значению корреляции такой график не построить, нужны исходные данные, из которого вы ее получили. Для непараметрических данных график построить можно, но он будет не наглядным
Высчитывать ранговую или порядкову корреляцию типа 121211112211/111221122121111 и по всем факторам выходят понятные значения, и лишь при сравнении 2х определенных массивов постоянно выдает результат 2.26…..Е-17 что это значит?
результат 2.26…..Е-17 что это значит?
я думаю, что это равно 2.26 умножить на 10 в минус 17ой степени, т.е. ну очень маленькое число корреляции и эти два массива не связаны..
Добрый день!
Обрабатываю экспериментальные данные, в Excel, выполнена аппроксимация графика. Получены уравнения. Не могу проверить на адекватность полученные уравнения (логарифмические, полиномиальные) с линейными получилось. А вот у остальных не знаю как ввести данные.
Кто нибудь подскажет, как это выполнить?
Где можно посмотреть алгоритм ввода?
Буду очень рада вашей помощи.
отличная статья! как раз для таких чайников, как я!) Спасибо огромное! но есть вопрос. можно ли рассчитать значения одного из параметров, если известны значения второго и коэффициент корреляции. Т.е. обратная задачка, по сути)
Приведенная выше формула расчета коэффициента Пирсона, показывает насколько трудоемок этот процесс если выполнять его вручную. Использование возможностей Excell ускоряет процесс нахождения коэффициента в разы.
Подскажите, как использовать корреляцию для 3 и более переменных ?
В Эксел нет формулы расчета кратной корреляции.
Для 3 или более переменных нужно рассчитывать их попарно.
Или использовать кратную (многомерную) корреляцию: произведение усредненных массивов (данные минус среднее значение), деленное на кратную степень произведения дисперсий массивов. То есть при трех массивах вычисляете дисперсии каждого массива, перемножаете их и вычисляете КУБИЧЕСКИй корень (в знаменателе). При 5 массивах — произведение 5 массивов (центрированных — с вычитанием среднего) деленное корень пятой степени из произведения 5 дисперсий массивов
Проще вычислить сумму центрированных произведений переменных и разделить на произведение среднеквадратических отклонений переменных
Комментариев, подобных моему тут, конечно, уже много, но всё-же!
Спасибо за столь доступное и простое описание! Теперь действительно понятно стало!
Спасибо, очень понятно.
Вы приводите в качестве примера расчет корреляции по Персонал, т.е для количестве них переменных (напр. потраченные часы и оценка). Подскажите, а где в Excel функция ANOVA или MANOVA — расчет корреляция ной взаимосвязи между качественным и количестве ними переменными?
Добрый день! Как рассчитать корреляцию в еxcele я поняла. Несколько уточняющих вопросов. Во-первых, это рассчитывается ведь кор. Пирсона? И второе. В калькуляторах, рассчитывающих кор. Пирсона, к значению корреляции указывается еще и «p» (обычно p0,05 или 0,01), а в еxcele он какой? И третье. Если формула везде расчета Пирсона одна, то почему в разных калькуляторах, в том числе, и в сравнении с расчетами в еxcele, получаются разные результаты? По поводу «р» — еще просьба: я слабо дружу с матимаиткой и не дружу со статистикой вообще. Можете ли мне объяснить доступным языком про это р?
Расчёт корреляционного коэффициента предполагает последовательное выполнение ряда математических операций. Приведенная выше формула расчета коэффициента Пирсона, показывает насколько трудоемок этот процесс если выполнять его вручную. Использование возможностей Excell ускоряет процесс нахождения коэффициента в разы.
Подскажите, пожалуйста, если нужно рассчитать коэфыициент корреляции для выборки Х( -1,95; -4,13, -8; -10; -41,5) и У (-0,22; 1,54; -8,8; -10,8; 8,04; 0,47) . В эксель через КОРРЕЛ не считает.. Вообще при таком разбросе чисел (от отрицательных до положительных) это возможно установить силу связи между Х и У? И как тогда рассчитывать. То что связь мужду Х и У есть это исходные данные, нужно оценить силу связи этой.. Может есть другие идеи?
А у формулы определения коэффициента корреляции есть автор?
Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.
Коэффициент корреляции
(
критерий корреляции
Пирсона, англ. Pearson Product Moment correlation coefficient)
определяет степень
линейной
взаимосвязи между случайными величинами.
где Е[…] – оператор
математического ожидания
, μ и σ –
среднее
случайной величины и ее
стандартное отклонение
.
Как следует из определения, для вычисления
коэффициента корреляции
требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки
коэффициента корреляции
используется
выборочный коэффициент корреляции
r
(
еще он обозначается как
R
xy
или
r
xy
)
:
Как видно из формулы для расчета
корреляции
, знаменатель (произведение стандартных отклонений с точностью до безразмерного множителя) просто нормирует числитель таким образом, что
корреляция
оказывается безразмерным числом от -1 до 1.
Корреляция
и
ковариация
предоставляют одну и туже информацию, но
корреляцией
удобнее пользоваться, т.к. она является безразмерной величиной.
Рассчитать
коэффициент корреляции
и
ковариацию выборки
в MS EXCEL не представляет труда, так как для этого имеются специальные функции
КОРРЕЛ()
и
КОВАР()
. Гораздо сложнее разобраться, как интерпретировать полученные значения, большая часть статьи посвящена именно этому.
Теоретическое отступление
Напомним, что
корреляционной связью
называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различные
средние
значения другой (с изменением значения Х
среднее значение
Y изменяется закономерным образом). Предполагается, что
обе
переменные Х и Y являются
случайными
величинами и имеют некий случайный разброс относительно их
среднего значения
.
Примечание
. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.
Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о
корреляции
температуры и года наблюдения и, соответственно, применять показатели
корреляции
с соответствующей их интерпретацией.
Корреляционная связь
между переменными может возникнуть несколькими путями:
-
Наличие причинной зависимости между переменными. Например, количество инвестиций в научные исследования (переменная Х) и количество полученных патентов (Y). Первая переменная выступает как
независимая переменная (фактор)
, вторая —
зависимая переменная (результат)
. Необходимо помнить, что зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот. - Наличие сопряженности (общей причины). Например, с ростом организации растет фонд оплаты труда (ФОТ) и затраты на аренду помещений. Очевидно, что неправильно предполагать, что аренда помещений зависит от ФОТ. Обе этих переменных во многих случаях линейно зависят от количества персонала.
- Взаимовлияние переменных (при изменении одной, вторая переменная изменяется, и наоборот). При таком подходе допустимы две постановки задачи; любая переменная может выступать как в роли независимой переменной и в роли зависимой.
Таким образом,
показатель корреляции
показывает, насколько сильна
линейная взаимосвязь
между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.
Корреляция
, как и любой другой статистический показатель, при правильном применении может быть полезной, но она также имеет и ограничения по использованию. Если
диаграмма рассеяния
показывает четко выраженную линейную зависимость или полное отсутствие взаимосвязи, то
корреляция
замечательно это отразит. Но, если данные показывают нелинейную взаимосвязь (например, квадратичную), наличие отдельных групп значений или выбросов, то вычисленное значение
коэффициента корреляции
может ввести в заблуждение (см.
файл примера
).
Корреляция
близкая к 1 или -1 (т.е. близкая по модулю к 1) показывает сильную линейную взаимосвязь переменных, значение близкое к 0 показывает отсутствие взаимосвязи. Положительная
корреляция
означает, что с ростом одного показателя другой в среднем увеличивается, а при отрицательной – уменьшается.
Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:
- количество переменных должно быть равно двум;
-
переменные должны быть количественными (например, частота, вес, цена). Вычисленное среднее значение этих переменных имеет понятный смысл: средняя цена или средний вес пациента. В отличие от количественных, качественные (номинальные) переменные принимают значения лишь из конечного набора категорий (например, пол или группа крови). Этим значениям условно сопоставлены числовые значения (например, женский пол – 1, а мужской – 2). Понятно, что в этом случае вычисление
среднего значения
, которое требуется для нахождения
корреляции
, некорректно, а значит некорректно и вычисление самой
корреляции
; -
переменные должны быть случайными величинами и иметь
нормальное распределение
.
Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:
-
Для данных с нелинейной связью
корреляцию
нужно использовать с осторожностью. Для некоторых задач бывает полезно преобразовать одну или обе переменных так, чтобы получить линейную взаимосвязь (для этого требуется сделать предположение о виде нелинейной связи, чтобы предложить нужный тип преобразования). -
С помощью
диаграммы рассеяния
у некоторых данных можно наблюдать неравную вариацию (разброс). Проблема неодинаковой вариации состоит в том, что места с высокой вариацией не только предоставляют наименее точную информацию, но и оказывают наибольшее влияние при расчете статистических показателей. Эту проблему также часто решают с помощью преобразования данных, например, с помощью логарифмирования. - У некоторых данных можно наблюдать разделение на группы (clustering), что может свидетельствовать о необходимости разделения совокупности на части.
- Выброс (резко отклоняющееся значение) может исказить вычисленное значение коэффициента корреляции. Выброс может быть причиной случайности, ошибки при сборе данных или могут действительно отражать некую особенность взаимосвязи. Так как выброс сильно отклоняется от среднего значения, то он вносит большой вклад при расчете показателя. Часто расчет статистических показателей производят с и без учета выбросов.
Использование MS EXCEL для расчета корреляции
В качестве примера возьмем 2 переменные
Х
и
Y
и, соответственно,
выборку
состоящую из нескольких пар значений (Х
i
; Y
i
). Для наглядности построим
диаграмму рассеяния
.
Примечание
: Подробнее о построении диаграмм см. статью
Основы построения диаграмм
. В
файле примера
для построения
диаграммы рассеяния
использована
диаграмма График
, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).
Расчеты
корреляции
проведем для различных случаев взаимосвязи между переменными:
линейной, квадратичной
и при
отсутствии связи
.
Примечание
: В
файле примера
можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.
В
файле примера
для построения
диаграммы рассеяния
в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.
Примечание
: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.
Как было сказано выше, для расчета
коэффициента корреляции
в MS EXCEL существует функций
КОРРЕЛ()
. Также можно воспользоваться аналогичной функцией
PEARSON()
, которая возвращает тот же результат.
Для того, чтобы удостовериться, что вычисления
корреляции
производятся функцией
КОРРЕЛ()
по вышеуказанным формулам, в
файле примера
приведено вычисление
корреляции
с помощью более подробных формул:
=
КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)
=
КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)
Примечание
: Квадрат
коэффициента корреляции
r равен
коэффициенту детерминации
R2, который вычисляется при построении линии регрессии с помощью функции
КВПИРСОН()
. Значение R2 также можно вывести на
диаграмме рассеяния
, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку
Макет
, затем в группе
Анализ
нажмите кнопку
Линия тренда
и выберите
Линейное приближение
). Подробнее о построении линии тренда см., например, в
статье о методе наименьших квадратов
.
Использование MS EXCEL для расчета ковариации
Ковариация
близка по смыслу с
дисперсией
(также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а
дисперсия
— для одной. Поэтому, cov(x;x)=VAR(x).
Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
. В первом случае формула для вычисления аналогична вышеуказанной (окончание
.Г
обозначает
Генеральная совокупность
), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание
.В
обозначает
Выборка
.
Примечание
: Функция
КОВАР()
, которая присутствует в MS EXCEL более ранних версий, аналогична функции
КОВАРИАЦИЯ.Г()
.
Примечание
: Функции
КОРРЕЛ()
и
КОВАР()
в английской версии представлены как CORREL и COVAR. Функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета
ковариации
:
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)
Эти формулы используют свойство
ковариации
:
Если переменные
x
и
y
независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А
дисперсия
их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
Оценка статистической значимости коэффициента корреляции
При проверке значимости
коэффициента корреляции
нулевая гипотеза состоит в том, что
коэффициент корреляции
равен нулю, альтернативная — не равен нулю (про
проверку гипотез
см. статью
Проверка гипотез
).
Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е.
коэффициента корреляции
r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t
r
:
которая имеет
распределение Стьюдента
с n-2 степенями свободы.
Если вычисленное значение случайной величины |t
r
| больше, чем критическое значение t
α,n-2
(α- заданный
уровень значимости
), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).
Надстройка Пакет анализа
В
надстройке Пакет анализа
для вычисления ковариации и корреляции
имеются одноименные инструменты
анализа
.
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
Входной интервал
: нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
Группирование
: как правило, исходные данные вводятся в 2 столбца
Метки в первой строке
: если установлена галочка, то
Входной интервал
должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
Выходной интервал
: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).