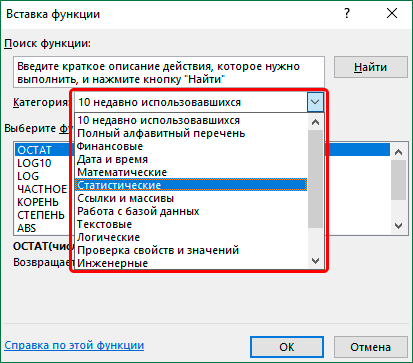
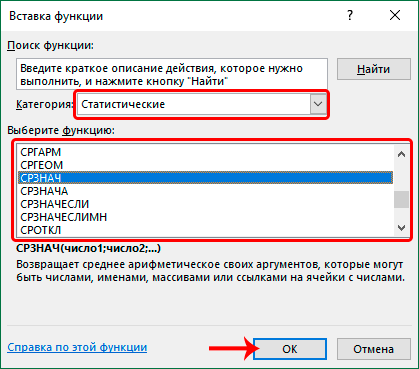
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
СРОТКЛ |
Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего. |
|
СРЗНАЧ |
Возвращает среднее арифметическое аргументов. |
|
СРЗНАЧА |
Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения. |
|
СРЗНАЧЕСЛИ |
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые удовлетворяют заданному условию. |
|
СРЗНАЧЕСЛИМН |
Возвращает среднее значение (среднее арифметическое) всех ячеек, которые удовлетворяют нескольким условиям. |
|
БЕТА.РАСП |
Возвращает интегральную функцию бета-распределения. |
|
БЕТА.ОБР |
Возвращает обратную интегральную функцию указанного бета-распределения. |
|
БИНОМ.РАСП |
Возвращает отдельное значение вероятности биномиального распределения. |
|
БИНОМ.РАСП.ДИАП |
Возвращает вероятность пробного результата с помощью биномиального распределения. |
|
БИНОМ.ОБР |
Возвращает наименьшее значение, для которого интегральное биномиальное распределение меньше заданного значения или равно ему. |
|
ХИ2.РАСП |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.РАСП.ПХ |
Возвращает одностороннюю вероятность распределения хи-квадрат. |
|
ХИ2.ОБР |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.ОБР.ПХ |
Возвращает обратное значение односторонней вероятности распределения хи-квадрат. |
|
ХИ2.ТЕСТ |
Возвращает тест на независимость. |
|
ДОВЕРИТ.НОРМ |
Возвращает доверительный интервал для среднего значения по генеральной совокупности. |
|
ДОВЕРИТ.СТЬЮДЕНТ |
Возвращает доверительный интервал для среднего генеральной совокупности, используя t-распределение Стьюдента. |
|
КОРРЕЛ |
Возвращает коэффициент корреляции между двумя множествами данных. |
|
СЧЁТ |
Подсчитывает количество чисел в списке аргументов. |
|
СЧЁТЗ |
Подсчитывает количество значений в списке аргументов. |
|
СЧИТАТЬПУСТОТЫ |
Подсчитывает количество пустых ячеек в диапазоне. |
|
СЧЁТЕСЛИ |
Подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному условию. |
|
СЧЁТЕСЛИМН |
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих нескольким условиям. |
|
КОВАРИАЦИЯ.Г |
Возвращает ковариацию, среднее произведений парных отклонений. |
|
КОВАРИАЦИЯ.В |
Возвращает ковариацию выборки — среднее попарных произведений отклонений для всех точек данных в двух наборах данных. |
|
КВАДРОТКЛ |
Возвращает сумму квадратов отклонений. |
|
ЭКСП.РАСП |
Возвращает экспоненциальное распределение. |
|
F.РАСП |
Возвращает F-распределение вероятности. |
|
F.РАСП.ПХ |
Возвращает F-распределение вероятности. |
|
F.ОБР |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ОБР.ПХ |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ТЕСТ |
Возвращает результат F-теста. |
|
ФИШЕР |
Возвращает преобразование Фишера. |
|
ФИШЕРОБР |
Возвращает обратное преобразование Фишера. |
|
ПРЕДСКАЗ |
Возвращает значение линейного тренда. Примечание: В Excel 2016 эта функция заменена на ПРЕДСКАЗ.ЛИНЕЙН из нового набора функций прогнозирования. Однако она по-прежнему доступна для совместимости с предыдущими версиями. |
|
ПРЕДСКАЗ.ETS |
Возвращает будущее значение на основе существующих (ретроспективных) данных с использованием версии AAA алгоритма экспоненциального сглаживания (ETS). |
|
ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ |
Возвращает доверительный интервал для прогнозной величины на указанную дату. |
|
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ |
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду. |
|
ПРЕДСКАЗ.ETS.СТАТ |
Возвращает статистическое значение, являющееся результатом прогнозирования временного ряда. |
|
ПРЕДСКАЗ.ЛИНЕЙН |
Возвращает будущее значение на основе существующих значений. |
|
ЧАСТОТА |
Возвращает распределение частот в виде вертикального массива. |
|
ГАММА |
Возвращает значение функции гамма |
|
ГАММА.РАСП |
Возвращает гамма-распределение. |
|
ГАММА.ОБР |
Возвращает обратное значение интегрального гамма-распределения. |
|
ГАММАНЛОГ |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАММАНЛОГ.ТОЧН |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАУСС |
Возвращает значение на 0,5 меньше стандартного нормального распределения. |
|
СРГЕОМ |
Возвращает среднее геометрическое. |
|
РОСТ |
Возвращает значения в соответствии с экспоненциальным трендом. |
|
СРГАРМ |
Возвращает среднее гармоническое. |
|
ГИПЕРГЕОМ.РАСП |
Возвращает гипергеометрическое распределение. |
|
ОТРЕЗОК |
Возвращает отрезок, отсекаемый на оси линией линейной регрессии. |
|
ЭКСЦЕСС |
Возвращает эксцесс множества данных. |
|
НАИБОЛЬШИЙ |
Возвращает k-ое наибольшее значение в множестве данных. |
|
ЛИНЕЙН |
Возвращает параметры линейного тренда. |
|
ЛГРФПРИБЛ |
Возвращает параметры экспоненциального тренда. |
|
ЛОГНОРМ.РАСП |
Возвращает интегральное логарифмическое нормальное распределение. |
|
ЛОГНОРМ.ОБР |
Возвращает обратное значение интегрального логарифмического нормального распределения. |
|
МАКС |
Возвращает наибольшее значение в списке аргументов. |
|
МАКСА |
Возвращает наибольшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МАКСЕСЛИ |
Возвращает максимальное значение из заданных определенными условиями или критериями ячеек. |
|
МЕДИАНА |
Возвращает медиану заданных чисел. |
|
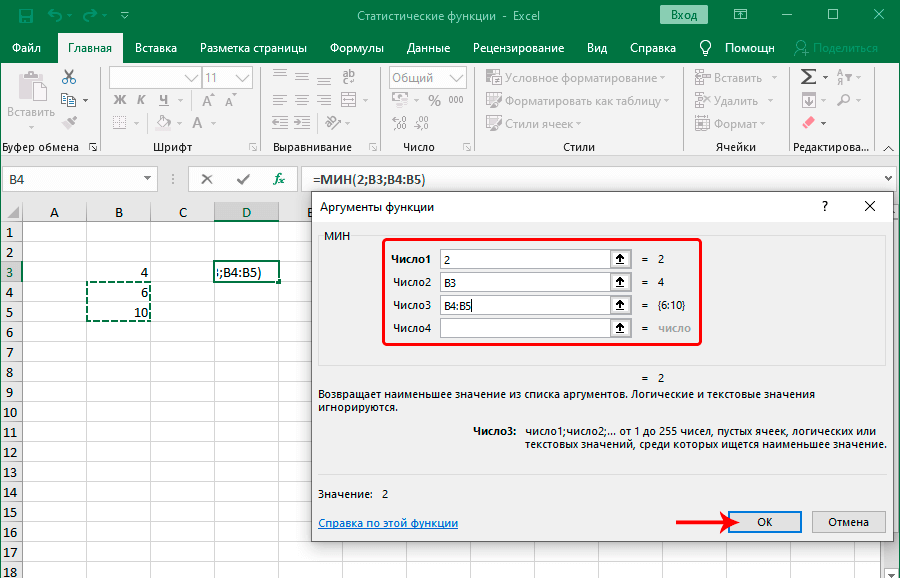
МИН |
Возвращает наименьшее значение в списке аргументов. |
|
МИНЕСЛИ |
Возвращает минимальное значение из заданных определенными условиями или критериями ячеек. |
|
МИНА |
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МОДА.НСК |
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных. |
|
МОДА.ОДН |
Возвращает значение моды набора данных. |
|
ОТРБИНОМ.РАСП |
Возвращает отрицательное биномиальное распределение. |
|
НОРМ.РАСП |
Возвращает нормальное интегральное распределение. |
|
НОРМ.ОБР |
Возвращает обратное значение нормального интегрального распределения. |
|
НОРМ.СТ.РАСП |
Возвращает стандартное нормальное интегральное распределение. |
|
НОРМ.СТ.ОБР |
Возвращает обратное значение стандартного нормального интегрального распределения. |
|
ПИРСОН |
Возвращает коэффициент корреляции Пирсона. |
|
ПРОЦЕНТИЛЬ.ИСКЛ |
Возвращает k-ю процентиль для значений диапазона, где k — число от 0 и 1 (не включая эти числа). |
|
ПРОЦЕНТИЛЬ.ВКЛ |
Возвращает k-ю процентиль для значений диапазона. |
|
ПРОЦЕНТРАНГ.ИСКЛ |
Возвращает ранг значения в наборе данных как процентную долю набора (от 0 до 1, исключая границы). |
|
ПРОЦЕНТРАНГ.ВКЛ |
Возвращает процентную норму значения в наборе данных. |
|
ПЕРЕСТ |
Возвращает количество перестановок для заданного числа объектов. |
|
ПЕРЕСТА |
Возвращает количество перестановок для заданного числа объектов (с повторами), которые можно выбрать из общего числа объектов. |
|
ФИ |
Возвращает значение функции плотности для стандартного нормального распределения. |
|
ПУАССОН.РАСП |
Возвращает распределение Пуассона. |
|
ВЕРОЯТНОСТЬ |
Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов. |
|
КВАРТИЛЬ.ИСКЛ |
Возвращает квартиль набора данных на основе значений процентили из диапазона от 0 до 1, исключая границы. |
|
КВАРТИЛЬ.ВКЛ |
Возвращает квартиль набора данных. |
|
РАНГ.СР |
Возвращает ранг числа в списке чисел. |
|
РАНГ.РВ |
Возвращает ранг числа в списке чисел. |
|
КВПИРСОН |
Возвращает квадрат коэффициента корреляции Пирсона. |
|
СКОС |
Возвращает асимметрию распределения. |
|
СКОС.Г |
Возвращает асимметрию распределения на основе заполнения: характеристика степени асимметрии распределения относительно его среднего. |
|
НАКЛОН |
Возвращает наклон линии линейной регрессии. |
|
НАИМЕНЬШИЙ |
Возвращает k-ое наименьшее значение в множестве данных. |
|
НОРМАЛИЗАЦИЯ |
Возвращает нормализованное значение. |
|
СТАНДОТКЛОН.Г |
Вычисляет стандартное отклонение по генеральной совокупности. |
|
СТАНДОТКЛОН.В |
Оценивает стандартное отклонение по выборке. |
|
СТАНДОТКЛОНА |
Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения. |
|
СТАНДОТКЛОНПА |
Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения. |
|
СТОШYX |
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии. |
|
СТЬЮДРАСП |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.2Х |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.ПХ |
Возвращает t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ОБР |
Возвращает значение t для t-распределения Стьюдента как функцию вероятности и степеней свободы. |
|
СТЬЮДЕНТ.ОБР.2Х |
Возвращает обратное t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ТЕСТ |
Возвращает вероятность, соответствующую проверке по критерию Стьюдента. |
|
ТЕНДЕНЦИЯ |
Возвращает значения в соответствии с линейным трендом. |
|
УРЕЗСРЕДНЕЕ |
Возвращает среднее внутренности множества данных. |
|
ДИСП.Г |
Вычисляет дисперсию по генеральной совокупности. |
|
ДИСП.В |
Оценивает дисперсию по выборке. |
|
ДИСПА |
Оценивает дисперсию по выборке, включая числа, текст и логические значения. |
|
ДИСПРА |
Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения. |
|
ВЕЙБУЛЛ.РАСП |
Возвращает распределение Вейбулла. |
|
Z.ТЕСТ |
Возвращает одностороннее значение вероятности z-теста. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Статьи по теме
Excel (по категориям)
Excel (по алфавиту)
Содержание
- Статистические функции
- МАКС
- МИН
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МОДА.ОДН
- МЕДИАНА
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
- Вопросы и ответы
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.
Запустить Мастер функций можно тремя способами:
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
- Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
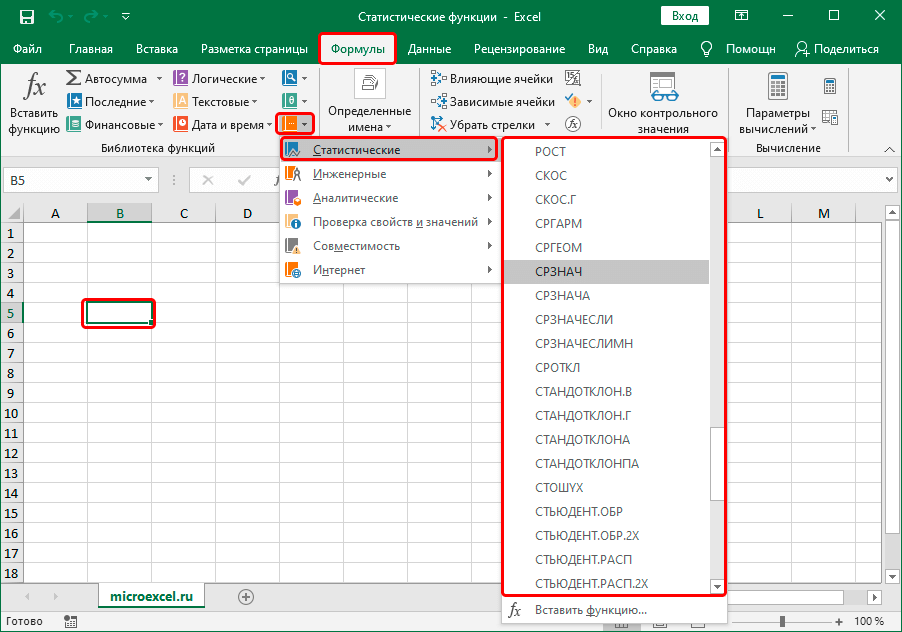
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Урок: Мастер функций в Excel
МАКС
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
=МАКС(число1;число2;…)
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
МИН
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
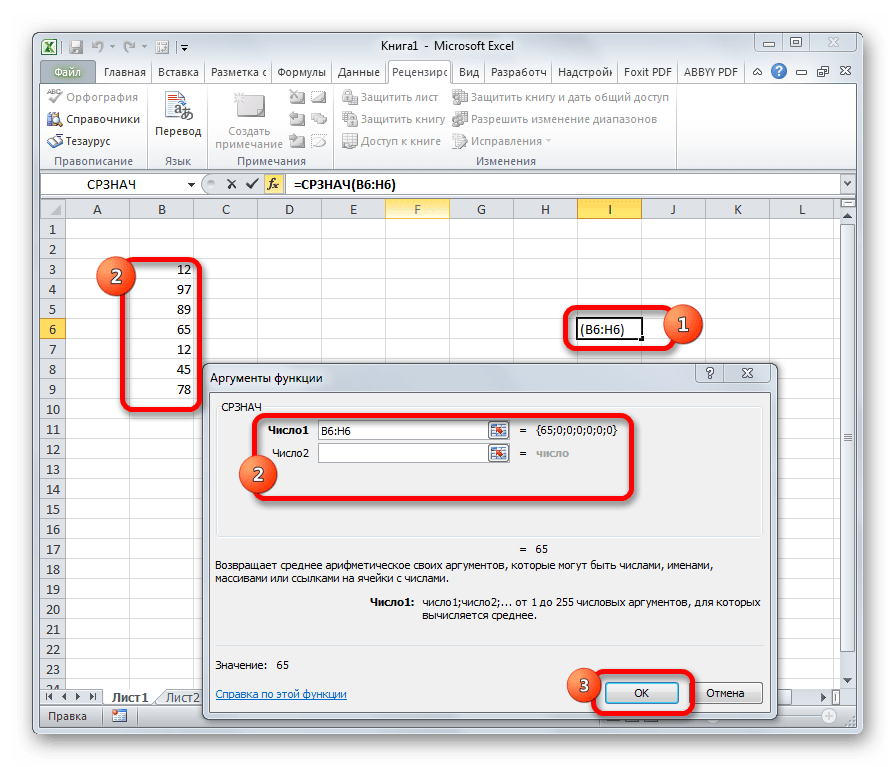
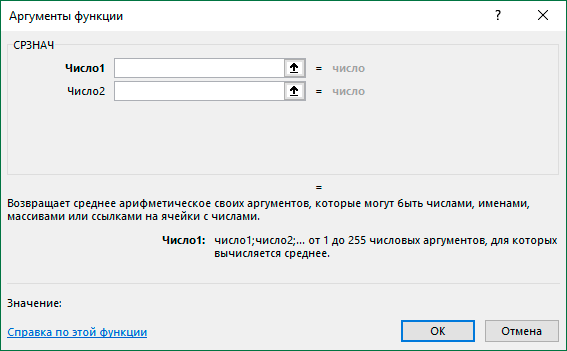
СРЗНАЧ
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
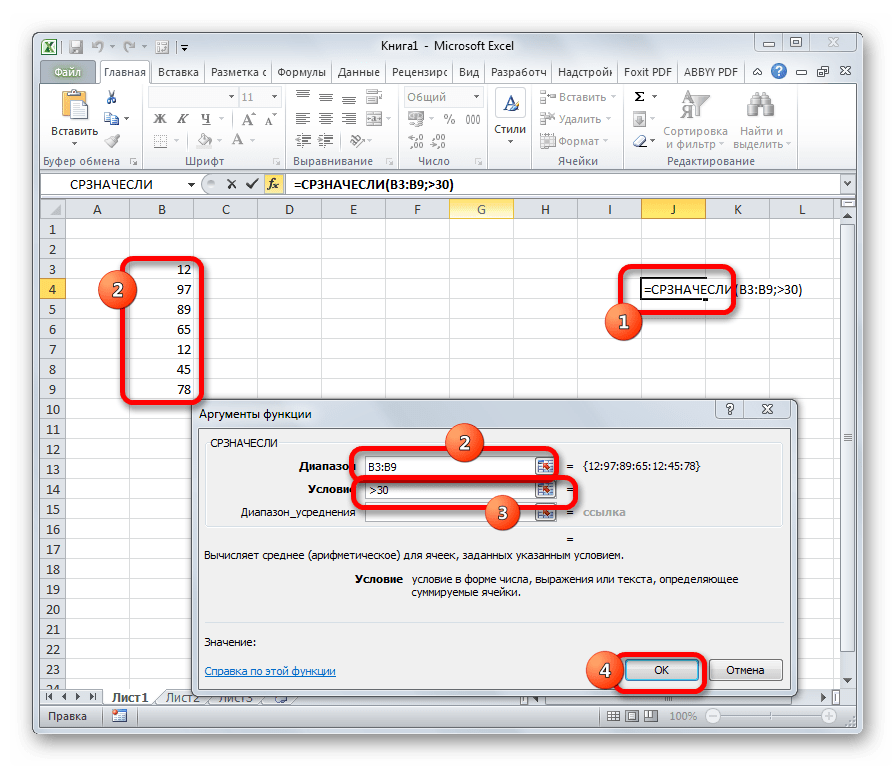
СРЗНАЧЕСЛИ
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])
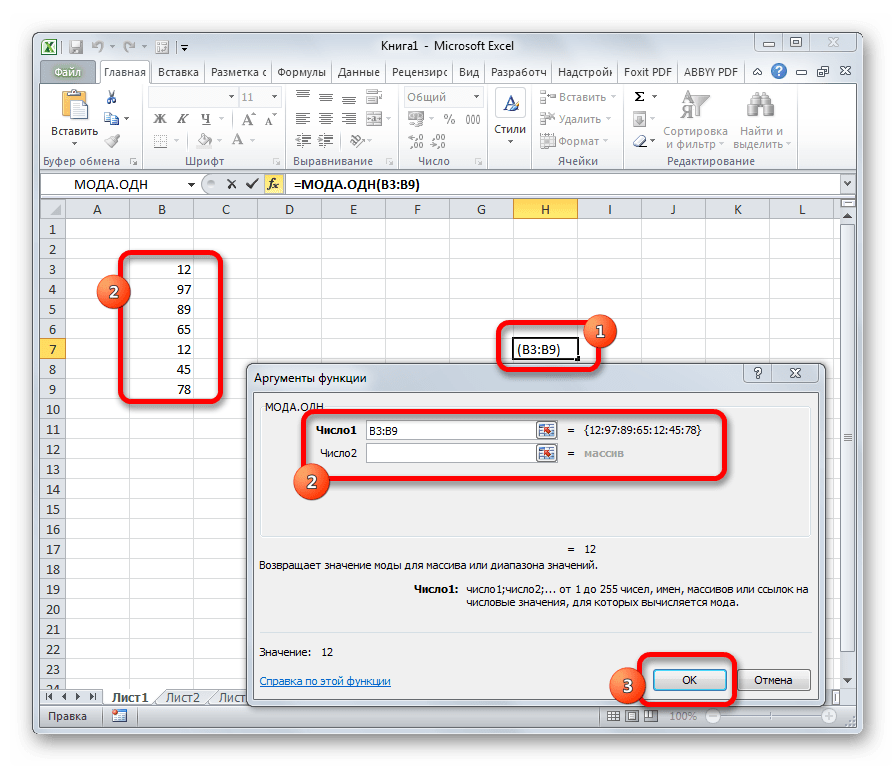
МОДА.ОДН
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
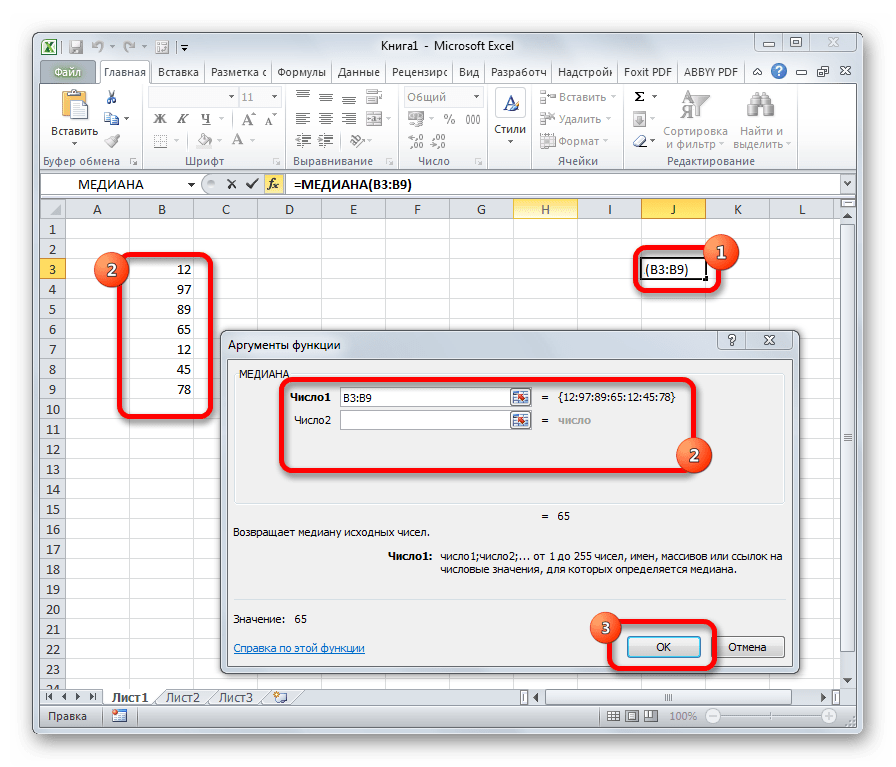
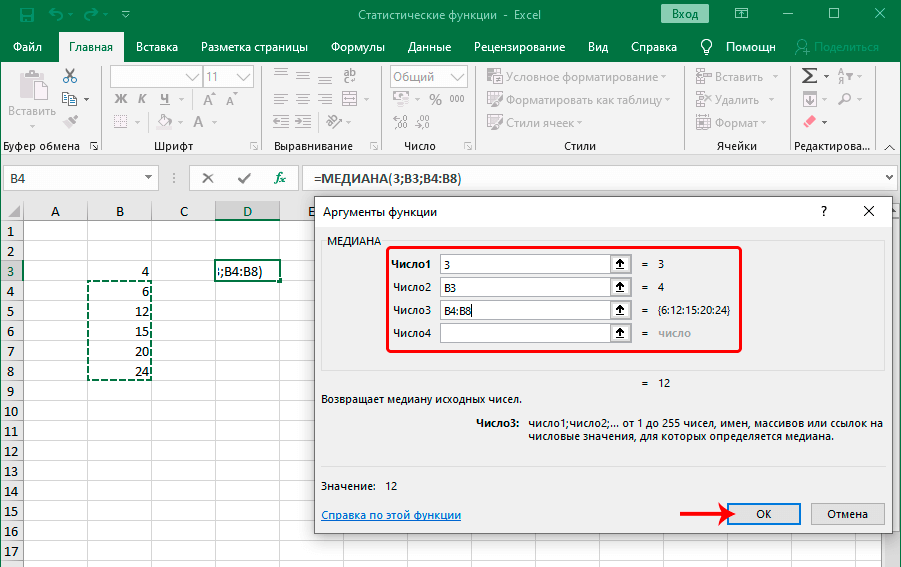
МЕДИАНА
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
СТАНДОТКЛОН
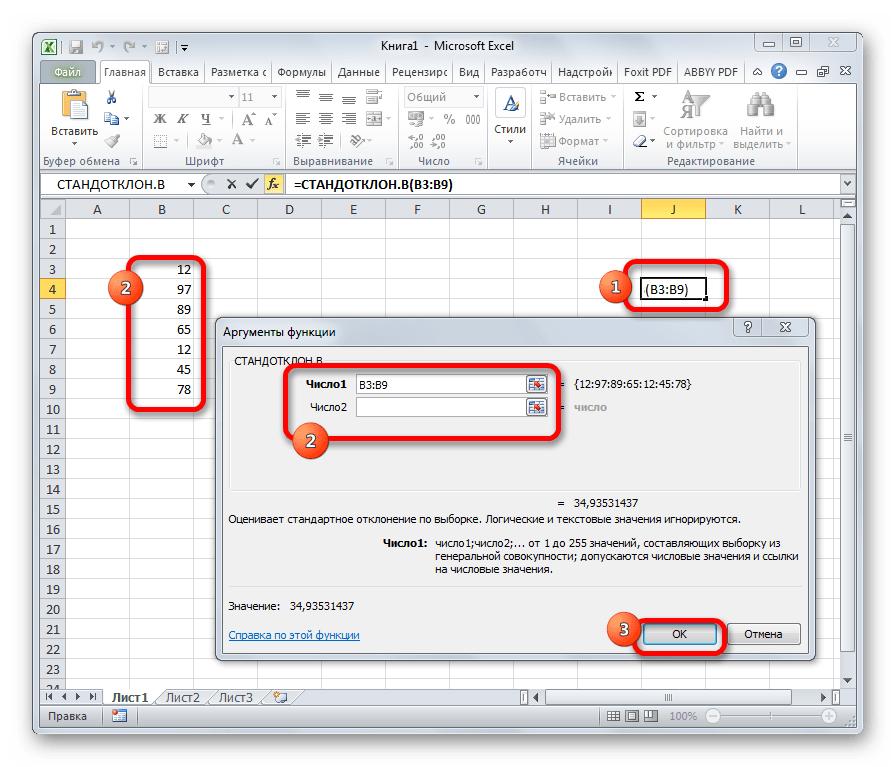
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:
=СТАНДОТКЛОН.В(число1;число2;…)
=СТАНДОТКЛОН.Г(число1;число2;…)
Урок: Формула среднего квадратичного отклонения в Excel
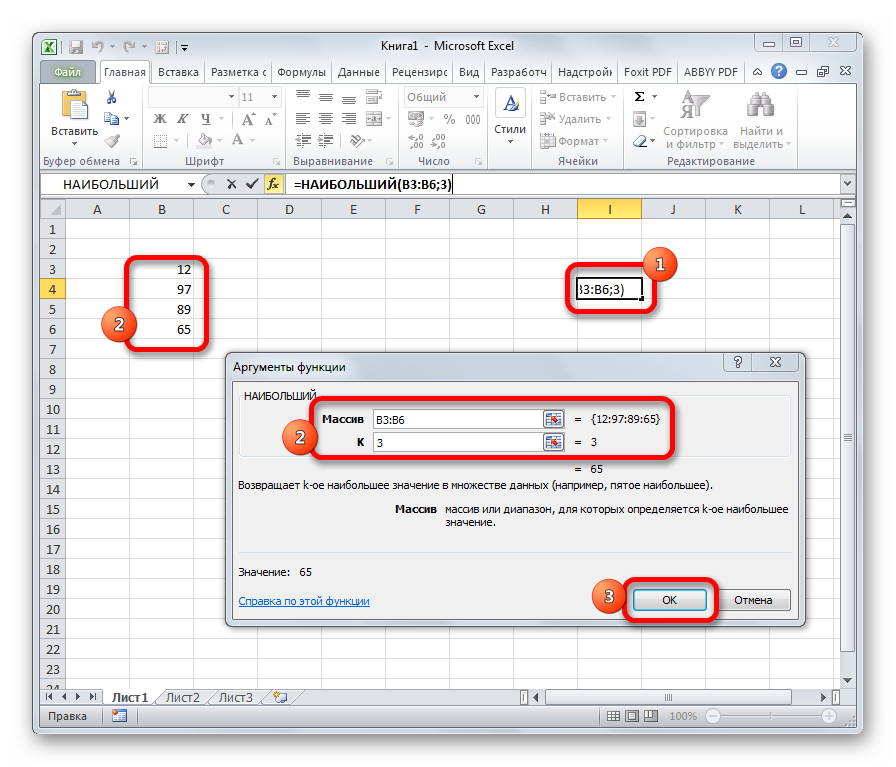
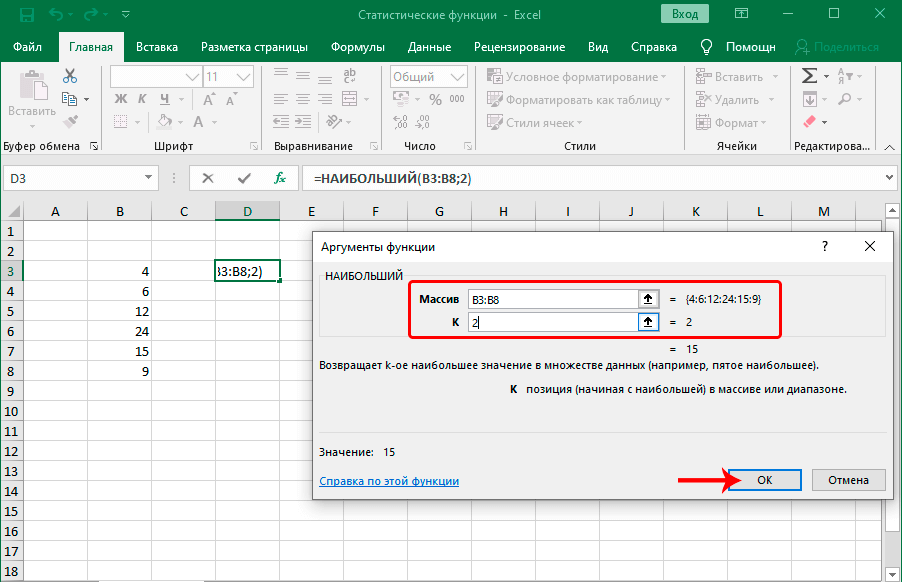
НАИБОЛЬШИЙ
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
=НАИБОЛЬШИЙ(массив;k)
В данном случае, k — это порядковый номер величины.
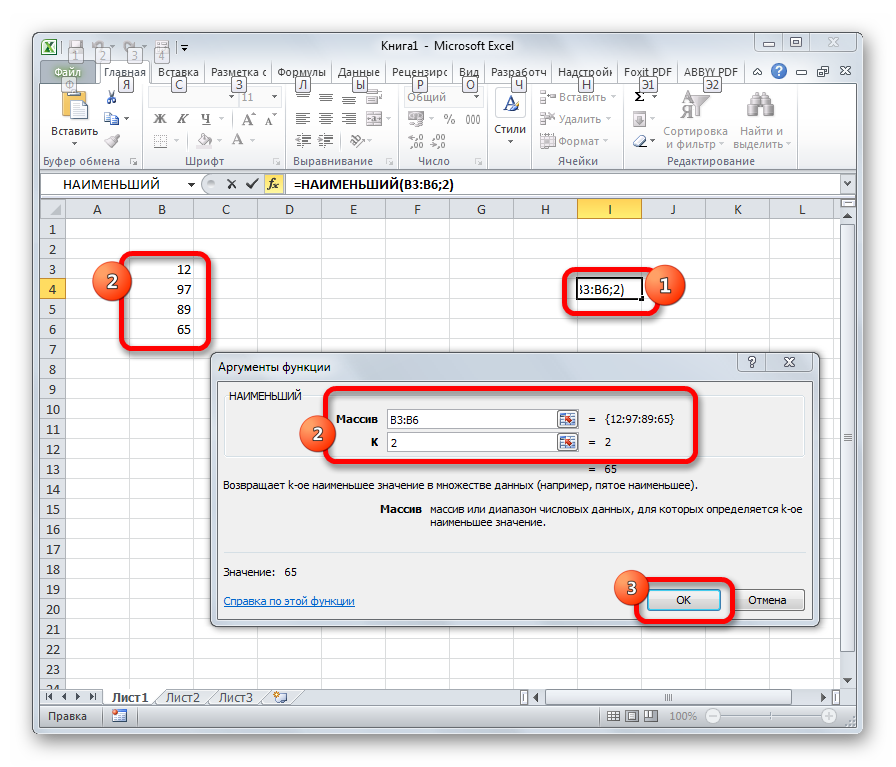
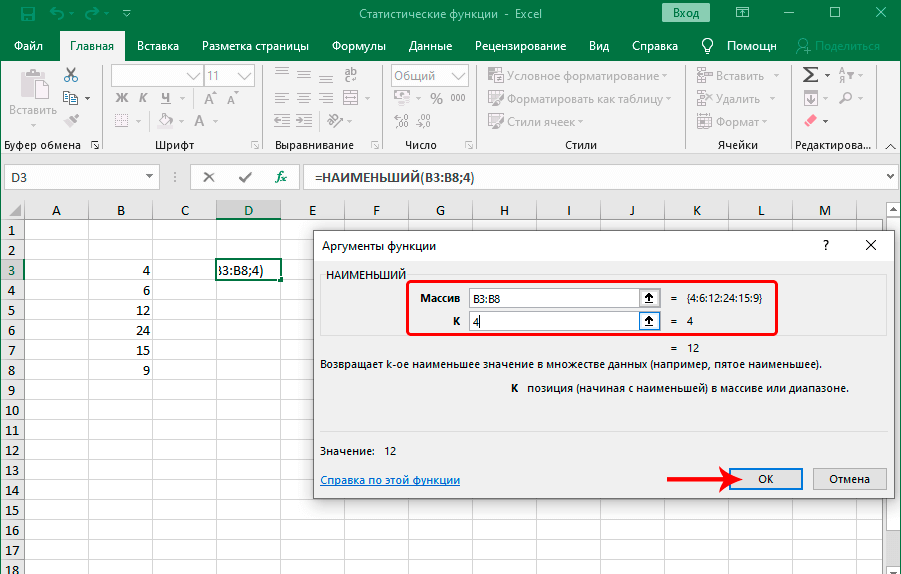
НАИМЕНЬШИЙ
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
=НАИМЕНЬШИЙ(массив;k)
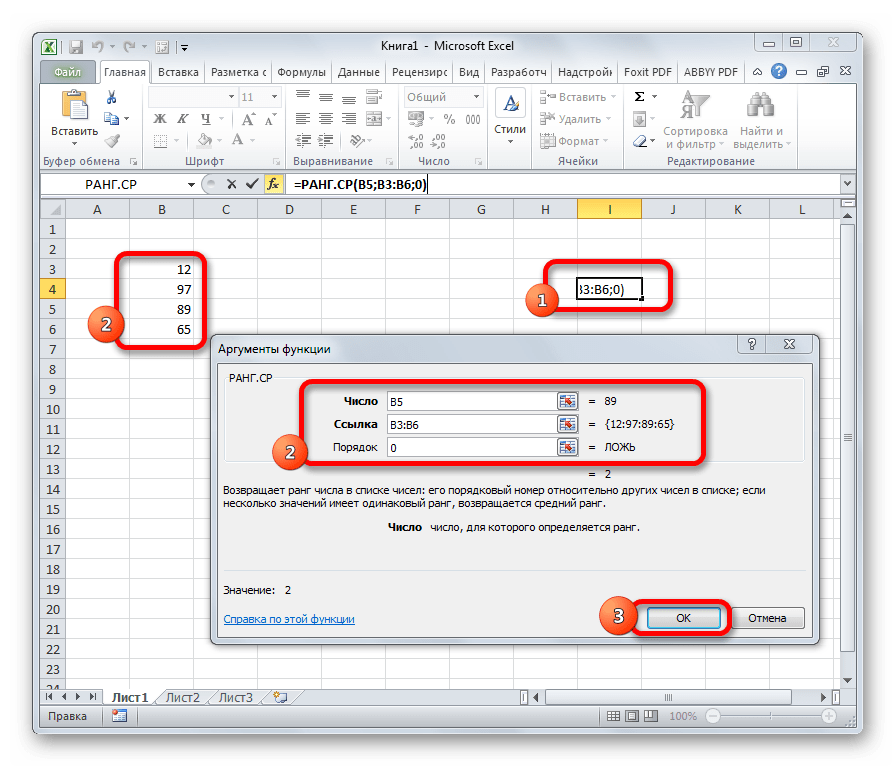
РАНГ.СР
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
=РАНГ.СР(число;массив;порядок)
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.
-
Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
- Заключение
Использование статистических функций
Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.
Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:
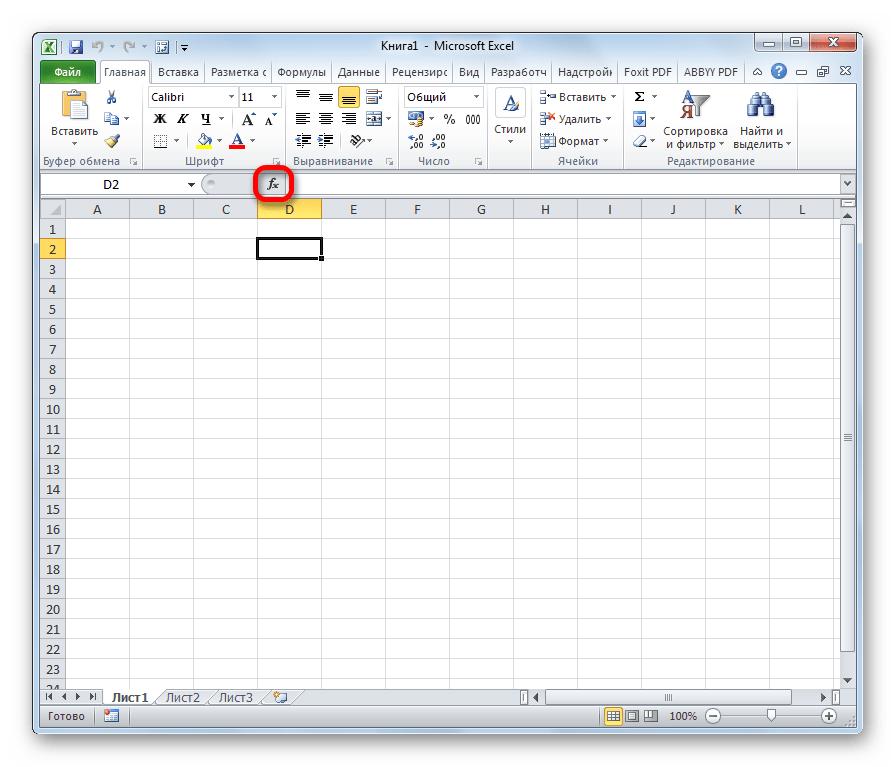
- Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
- Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
- Используем сочетание клавиш Shift+F3.
Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.
Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.
На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.
Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.
Давайте теперь рассмотрим наиболее популярные функции.
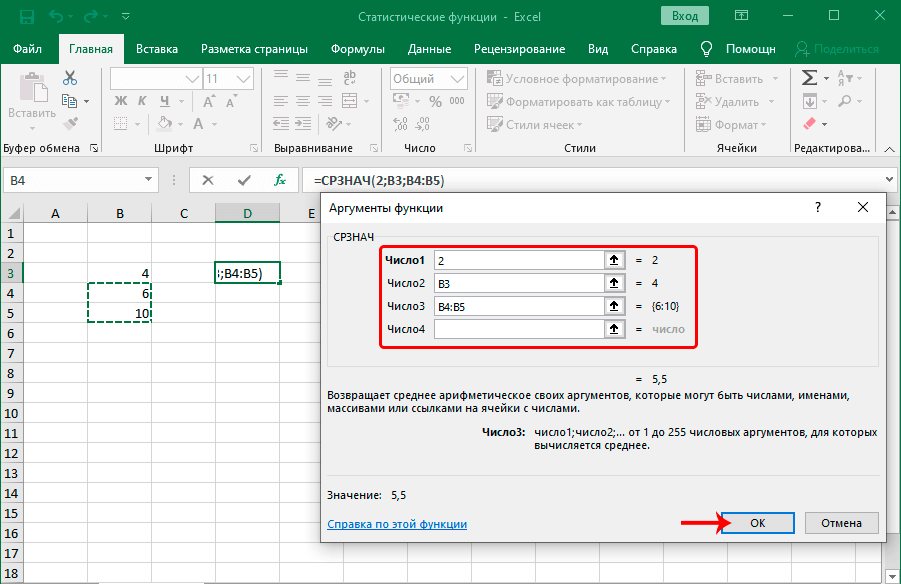
СРЗНАЧ
Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов функции можно указать:
- конкретные числа;
- ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
- диапазон ячеек – указывается вручную или путем выделения в таблице.
- переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.
МАКС
Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:
=МАКС(число1;число2;…)
В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.
МИН
Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:
=МИН(число1;число2;…)
Аргументы функции заполняются так же, как и для оператора МАКС.
СРЗНАЧЕСЛИ
Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:
=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)
В аргументах указываются:
- Диапазон ячеек – вручную или с помощью выделения в таблице;
- Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
- Диапазон_усреднения – не является обязательным аргументом для заполнения.
МЕДИАНА
Оператор находит медиану заданного диапазона значений. Синтаксис функции:
=МЕДИАНА(число1;число2;…)
В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.
НАИБОЛЬШИЙ
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:
=НАИБОЛЬШИЙ(массив;k)
Аргумента функции два: массив и номер позиции – K.
Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.
НАИМЕНЬШИЙ
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:
=НАИМЕНЬШИЙ(массив;k)
МОДА.ОДН
Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:
=МОДА.ОДН(число1;число2;…)
В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.
Для вертикальных массивов, также, используется функция МОДА.НСК.
СТАНДОТКЛОН
Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:
- СТАДНОТКЛОН.В – находит стандартное отклонение выборки
- СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности
Формулы функций выглядят следующим образом:
- =СТАДНОТКЛОН.В(число1;число2;…)
- =СТАДНОТКЛОН.Г(число1;число2;…)
СРГЕОМ
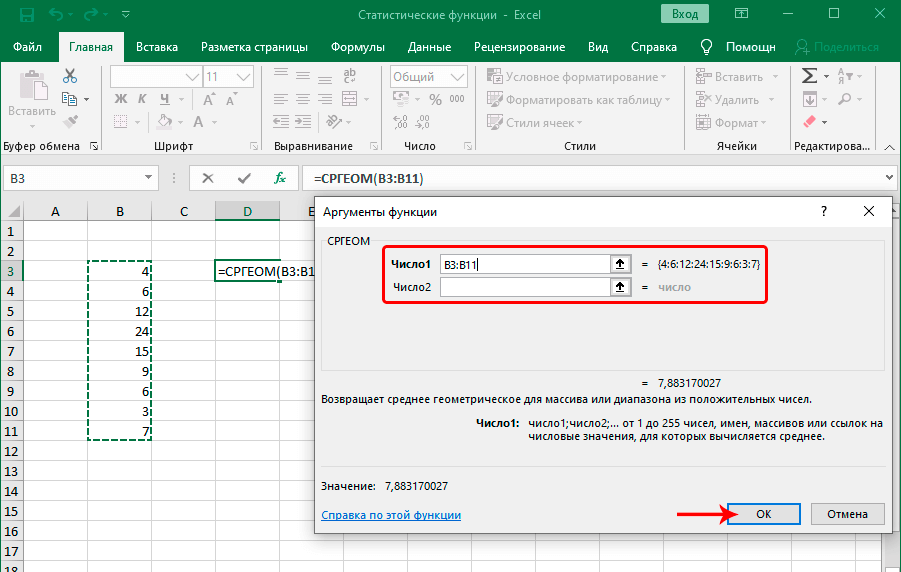
Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:
=СРГЕОМ(число1;число2;…)

Заключение
В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.
Статистика – наука, которая используется для любых других исследований, а также обработки большого количества количественных и даже качественных данных. И что важно, это одно из главных применений электронных таблиц Excel, поэтому давайте более подробно рассмотрим, статистические формулы. Во-первых, что они нам дают? Прежде всего, они позволяют структурировать информацию и осуществить ее анализ. Статистические функции в Excel относятся к совершенно отдельной категории.
Содержание
- Как пользоваться статистическими функциями
- Перечень статистических функций
- Функция СРГЕОМ
- Функция СТАНДОТКЛОН
- Функция МОДА.ОДН
- Функция НАИМЕНЬШИЙ
- Функция НАИБОЛЬШИЙ
- Функция МЕДИАНА
- Функция СРЗНАЧЕСЛИ
- Функция МИН
- Функция МАКС
- Функции СРЗНАЧ и СРЗНАЧА
- Функция РАНГ.СР
Как пользоваться статистическими функциями
Есть несколько способов ввода любой функции, и статистические не являются исключением:
- Ввести непосредственно в ячейке, предварительно нажав клавишу =. Это касается самых простых функций, несложных для запоминания и содержащих один или два аргумента. Например, так можно делать для операции умножения, сложения, вычитания и деления. А вот если функция сложная, то можно воспользоваться помощником. Это уже второй способ.
- Помощник по использованию функций. Он не только подсказывает, какая формула что означает, а и помогает ввести правильные аргументы применительно к конкретной функции.
Вызвать помощник можно несколькими способами:
- Воспользоваться кнопкой «Вставить функцию», расположенной слева от строки формул.
- Вызвать мастер ввода функций через кнопку «Вставить функцию», которая находится в левой части панели, которая открывается по клику на вкладку «Формулы».
- Воспользовавшись горячими клавишами Shift+F3.
Любой из этих методов приводит к одному результату – вызову мастера функций. Можно использовать тот, который больше всего подходит в конкретной ситуации. После того, как окно откроется, нам первым делом нужно выбрать категорию: статистические функции.
После того, как тип функции будет выбран, нам нужно выбрать подходящую формулу из списка. Под перечнем видим, что есть описание, в котором рассказывается, что конкретная функция делает.
Чтобы подтвердить выбор функции, которая будет вводиться, нужно нажать клавишу ОК. После этого появится такое окно, в котором можно ввести параметры функции (или, как их еще называют, аргументы).
Интересный факт. Можно выбрать функцию еще одним способом. Для этого нужно перейти на вкладку «Формулы» и нажать на кнопку «Другие функции», расположенной на ленте.
Далее будет пункт «Другие функции» – «Статистические» и в появившемся списке ищем подходящую функцию и выбираем ее. Этот перечень может прокручиваться.
Перечень статистических функций
А теперь давайте перейдем непосредственно к рассмотрению статистических функций.
Функция СРГЕОМ
Много кто знает о таком параметре, как среднее арифметическое. Вычисляется оно с помощью функции, о которой мы еще сегодня обязательно поговорим. Но есть еще одна функция, которая определяет среднее геометрическое.
Формула очень простая: =СРГЕОМ(число1;число2;…). Кроме чисел также можно указать диапазон значений, которые учитываются этой функцией. Что же такое среднее геометрическое? Это число, которое может заменять любое из чисел в последовательности таким образом, чтобы не менялось произведение этих значений. Еще один часто используемый термин – среднее пропорциональное. Это синоним к среднему геометрическому. Такой второй термин используется, потому что среднее геометрическое пропорционально к первому и второму числам.
Функция СТАНДОТКЛОН
Один из главных статистических параметров, который должен рассчитываться вместо со средним арифметическим – стандартное отклонение. Это мера, демонстрирующая степень разброса значений. Выполняет ту же функцию, что и дисперсия, просто представлена в том же виде, что и среднее значение, в отличие от дисперсии.
Вообще, стандартное отклонение рассчитывается, как квадратный корень из дисперсии. Но в Эксель есть специальная формула, которая сразу вычисляет степень дисперсии, после чего на основе полученного значения получает стандартное (или среднеквадратическое) отклонение.
Сама эта формула довольно старая, но знать о ней надо, потому что время от времени ее можно найти в готовых таблицах. Сейчас уже есть более новые версии этой функции – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Последняя функция находит среднеквадратическое отклонение по генеральной совокупности, в то время как первая ориентируется исключительно на выборку.
В остальном, синтаксис обеих функций такой же, как и для вычисления среднего арифметического (об этом мы поговорим позже) – числа, которые перечислены через скобку.
Функция МОДА.ОДН
Мода выборки абсолютно не связана с одеждой или популярными машинами. Но при этом она связана со словом «популярный». Если говорить о статистике, то это значение в выборке, которое встречается наиболее часто. Соответственно, функция МОДА.ОДН дает возможность определить это значение.
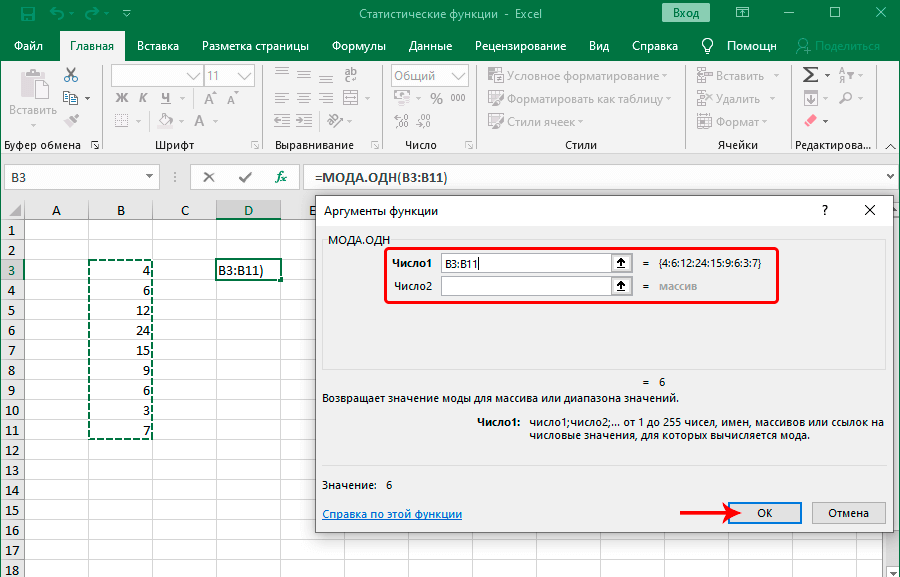
Если говорить о синтаксисе, то он похож на многие другие статистические функции. Сначала пишется оператор, после чего в скобках записываются его аргументы, которые являют собой числа, разделенные запятой. В качестве значения аргумента может выступать не только число, но и отдельные ячейки, диапазоны значений. Это дает возможность более гибко управлять выборкой. На этом скриншоте отчетливо видно, как это работает на практике.
Эта функция подходит для горизонтальных массивов. Если же нужно определить моду выборки для вертикального массива, используется похожая функция МОДА.НСК. Общий внешний вид функции следующий: =МОДА.ОДН(аргумент 1, аргумент 2; аргумент …).
Функция НАИМЕНЬШИЙ
Задача этой функции – выполнение поиска из того набора значений, который был указан пользователем. Принцип ее работы такой же, как и следующий, только поиск осуществляется по направлению снизу вверх, от наименьшего числа к самому большому. Синтаксис этой функции предельно простой: =НАИМЕНЬШИЙ(массив;k).
Функция имеет два основных аргумента: массив данных, по которым будет осуществляться поиск и порядковый номер элемента, который надо найти. Далее функция работает следующим образом: сначала она ищет самое маленькое значение, потом начинает перебирать цифры снизу вверх. Первое значение считается 1. То есть, если использовать число 1 во втором аргументе, то результат будет эквивалентным функции МИН, о которой мы поговорим немного позже.
Функция НАИБОЛЬШИЙ
Функция НАИБОЛЬШИЙ является аналогичной, только отсчет выполняет, начиная с самого большого значения. После того, как передать ей коэффициент, она ищет в порядковом ряду с большего в меньший число, занимающее соответствующее место и возвращает его. Работают обе функции аналогичным образом. Предположим, у нас есть числовой ряд. Если в нем в качестве числа k указать 2, то в результате получится число 15, поскольку оно является вторым по величине в диапазоне, который прописан в первом аргументе.
Эта функция может быть полезной в ситуациях, например, когда товар поступал в определенной последовательности, и нужно определить, сколько стоила, например, шубка, которая пришла второй по счету.
Функция МЕДИАНА
В статистике медиана – это разновидность среднего числа, которое находится ровно посередине числового ряда. Очень часто медиана является лучшим решением, чем стандартное среднее арифметическое, потому что позволяет определить действительно среднестатистическое значение. Синтаксис этой функции аналогичен тому, который имеет любой другой оператор, определяющий среднее значение – перечень цифр, ячеек или диапазонов, из которых данные будут получаться.
На этом примере видно, как на практике осуществляется работа с функцией. В диалоговом окне «Аргументы функции» можно вводить большое количество чисел, ячеек и диапазонов. На картинке мы попробовали ввести число в первую строку, ячейку во вторую и диапазон значений в третью. Получили в результате число 12. Максимальное количество аргументов этой функции – 255, что более, чем достаточно для полноценного использования этой функции.
Функция СРЗНАЧЕСЛИ
Это улучшенная версия функции СРЗНАЧ, задача которой – находить среднее арифметическое, но лишь при условии, что определенное условие выполняется. Эта функция уже несколько сложнее тех, которые приводились выше: =СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения). Давайте рассмотрим каждый аргумент более подробно:
- Диапазон. Это ячейки, которые проверяются на предмет соответствия определенному условию.
- Условие. Это критерий, на предмет соответствия которому проверяется диапазон.
- Диапазон усреднения. Это тот диапазон, из которого будет доставаться среднее арифметическое. Этот аргумент вводить необязательно, поскольку диапазон ячеек и диапазон усреднения могут совпадать.
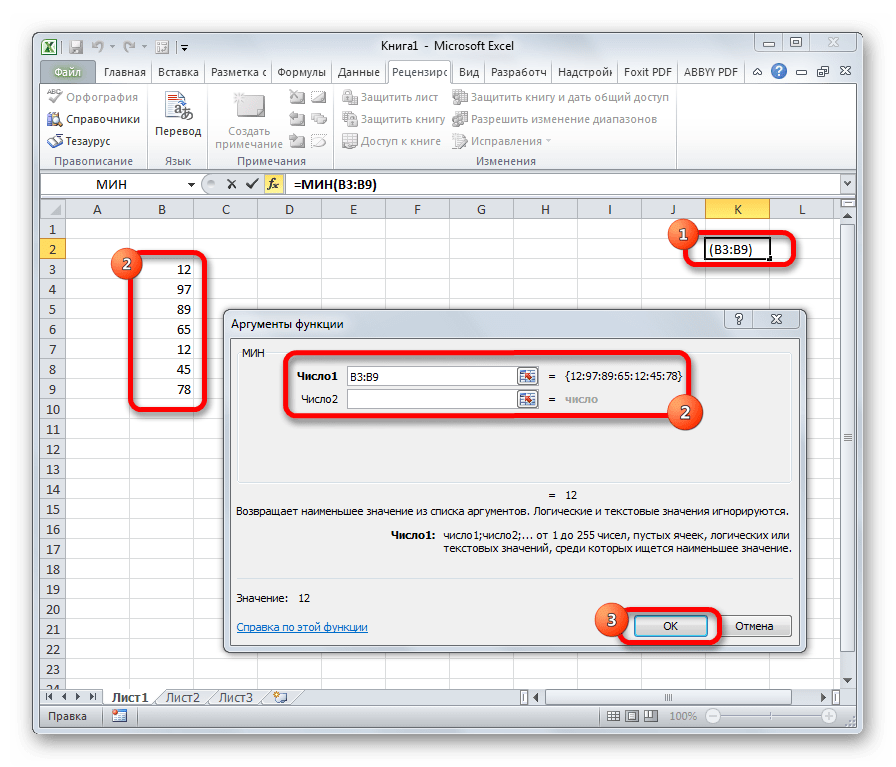
Функция МИН
В статистических подсчетах нередко нужно не только определить среднее значение, среднеквадратическое отклонение и вычислить другие показатели. Также важно значение наименьшего и наибольшего числа, в том числе, для получения указанных показателей. Практическое применение этой функции довольно обширное:
- На рынке акций для определения времени, когда цела была наиболее низкой.
- Для определения слабых мест в годовом бюджете (например, в каком месяце доходы компании были минимальными) с целью их дальнейшего исправления. Например, можно определить наименее доходный месяц и проанализировать факторы, которые этому способствовали.
Существует огромное количество других ситуаций, когда можно использовать функцию МИН. В самом общем виде она выглядит следующим образом: =МИН(число1;число2;…). Принцип заполнения аргументов этой функции аналогичен функции МАКС.
Функция МАКС
Как становится понятно из названия, эта функция ищет максимальное значение в определенной числовой выборке. Ситуации, в которых она может использоваться, в принципе, те же за тем лишь исключением, что все в противоположную сторону. Например, компания может с помощью функции МАКС определить самый доходный месяц и понять, каковы причины этого успеха.
Функции СРЗНАЧ и СРЗНАЧА
Стандартная функция СРЗНАЧ определяет среднее арифметическое в числовой выборке. Общий вид формулы такой же, как и для любой другой выборки значений. Сначала пишется название функции, после чего в скобках приводятся числа и диапазоны, которые необходимо обработать с помощью этой функции. То есть, общий вид формулы следующий: =СРЗНАЧ(число1;число2;…).
Как мы поняли, можно использовать как обычные числа (очень полезно для использования значений, которые не будут меняться в течение ближайшего времени), ссылки на ячейку (они применяются для тех значений, которые в будущем изменятся) и на диапазон (в этом случае будет использоваться целый набор чисел за один раз). Чтобы после ввода одного аргумента начать записывать другой, достаточно нажать на соответствующее поле в мастере функций или просто нажать на клавишу Tab.
Максимальное количество аргументов, которые можно использовать в этой функции – 255. При этом обязательным аргументом является только первое число. В качестве аргументов не могут использоваться текстовые и логические значения. Они просто не учитываются формулой, в которой используется указанный оператор. Основное отличие функции СРЗНАЧА от СРЗНАЧ заключается в том, что текстовые значения и «ЛОЖЬ» считаются нулевыми, а значение «Истина» приравнивается к единице.
Функция РАНГ.СР
С помощью функции РАНГ.СР пользователь может вернуть ранг числа. Если несколько чисел в одном диапазоне относятся к одному рангу, то возвращается среднее. Имеет три аргумента, два из которых – обязательные:
- Число. Это то число, для которого осуществляется определение ранга.
- Ссылка. Это массив чисел, или ссылка на этот массив.
- Порядок. Это число, которое влияет на способ, в который значения будут упорядочиваться.
Таким образом, статистические функции Excel – это превосходный инструмент для обработки больших массивов информации.
Оцените качество статьи. Нам важно ваше мнение:
Содержание
- Статистические функции в Excel. Описание всех функций, как их использовать
- Как пользоваться статистическими функциями
- Перечень статистических функций
- Функция СРГЕОМ
- Функция СТАНДОТКЛОН
- Функция МОДА.ОДН
- Функция НАИМЕНЬШИЙ
- Функция НАИБОЛЬШИЙ
- Функция МЕДИАНА
- Функция СРЗНАЧЕСЛИ
- Функция МИН
- Функция МАКС
- Функции СРЗНАЧ и СРЗНАЧА
- Функция РАНГ.СР
- Лекция 2. Microsoft excel. Средства статистической обработки ms Excel
- Статистические функции в ms Excel
Статистические функции в Excel. Описание всех функций, как их использовать
Статистика – наука, которая используется для любых других исследований, а также обработки большого количества количественных и даже качественных данных. И что важно, это одно из главных применений электронных таблиц Excel, поэтому давайте более подробно рассмотрим, статистические формулы. Во-первых, что они нам дают? Прежде всего, они позволяют структурировать информацию и осуществить ее анализ. Статистические функции в Excel относятся к совершенно отдельной категории.
Как пользоваться статистическими функциями
Есть несколько способов ввода любой функции, и статистические не являются исключением:
- Ввести непосредственно в ячейке, предварительно нажав клавишу =. Это касается самых простых функций, несложных для запоминания и содержащих один или два аргумента. Например, так можно делать для операции умножения, сложения, вычитания и деления. А вот если функция сложная, то можно воспользоваться помощником. Это уже второй способ.
- Помощник по использованию функций. Он не только подсказывает, какая формула что означает, а и помогает ввести правильные аргументы применительно к конкретной функции.
Вызвать помощник можно несколькими способами:
- Воспользоваться кнопкой «Вставить функцию», расположенной слева от строки формул.
- Вызвать мастер ввода функций через кнопку «Вставить функцию», которая находится в левой части панели, которая открывается по клику на вкладку «Формулы».
- Воспользовавшись горячими клавишами Shift+F3.
Любой из этих методов приводит к одному результату – вызову мастера функций. Можно использовать тот, который больше всего подходит в конкретной ситуации. После того, как окно откроется, нам первым делом нужно выбрать категорию: статистические функции.
После того, как тип функции будет выбран, нам нужно выбрать подходящую формулу из списка. Под перечнем видим, что есть описание, в котором рассказывается, что конкретная функция делает.
Чтобы подтвердить выбор функции, которая будет вводиться, нужно нажать клавишу ОК. После этого появится такое окно, в котором можно ввести параметры функции (или, как их еще называют, аргументы).
Интересный факт. Можно выбрать функцию еще одним способом. Для этого нужно перейти на вкладку «Формулы» и нажать на кнопку «Другие функции», расположенной на ленте.
Далее будет пункт «Другие функции» – «Статистические» и в появившемся списке ищем подходящую функцию и выбираем ее. Этот перечень может прокручиваться.
Перечень статистических функций
А теперь давайте перейдем непосредственно к рассмотрению статистических функций.
Функция СРГЕОМ
Много кто знает о таком параметре, как среднее арифметическое. Вычисляется оно с помощью функции, о которой мы еще сегодня обязательно поговорим. Но есть еще одна функция, которая определяет среднее геометрическое.
Формула очень простая: =СРГЕОМ(число1;число2;…). Кроме чисел также можно указать диапазон значений, которые учитываются этой функцией. Что же такое среднее геометрическое? Это число, которое может заменять любое из чисел в последовательности таким образом, чтобы не менялось произведение этих значений. Еще один часто используемый термин – среднее пропорциональное. Это синоним к среднему геометрическому. Такой второй термин используется, потому что среднее геометрическое пропорционально к первому и второму числам.
Функция СТАНДОТКЛОН
Один из главных статистических параметров, который должен рассчитываться вместо со средним арифметическим – стандартное отклонение. Это мера, демонстрирующая степень разброса значений. Выполняет ту же функцию, что и дисперсия, просто представлена в том же виде, что и среднее значение, в отличие от дисперсии.
Вообще, стандартное отклонение рассчитывается, как квадратный корень из дисперсии. Но в Эксель есть специальная формула, которая сразу вычисляет степень дисперсии, после чего на основе полученного значения получает стандартное (или среднеквадратическое) отклонение.
Сама эта формула довольно старая, но знать о ней надо, потому что время от времени ее можно найти в готовых таблицах. Сейчас уже есть более новые версии этой функции – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Последняя функция находит среднеквадратическое отклонение по генеральной совокупности, в то время как первая ориентируется исключительно на выборку.
В остальном, синтаксис обеих функций такой же, как и для вычисления среднего арифметического (об этом мы поговорим позже) – числа, которые перечислены через скобку.
Функция МОДА.ОДН
Мода выборки абсолютно не связана с одеждой или популярными машинами. Но при этом она связана со словом «популярный». Если говорить о статистике, то это значение в выборке, которое встречается наиболее часто. Соответственно, функция МОДА.ОДН дает возможность определить это значение.
Если говорить о синтаксисе, то он похож на многие другие статистические функции. Сначала пишется оператор, после чего в скобках записываются его аргументы, которые являют собой числа, разделенные запятой. В качестве значения аргумента может выступать не только число, но и отдельные ячейки, диапазоны значений. Это дает возможность более гибко управлять выборкой. На этом скриншоте отчетливо видно, как это работает на практике.
Эта функция подходит для горизонтальных массивов. Если же нужно определить моду выборки для вертикального массива, используется похожая функция МОДА.НСК. Общий внешний вид функции следующий: =МОДА.ОДН(аргумент 1, аргумент 2; аргумент …).
Функция НАИМЕНЬШИЙ
Задача этой функции – выполнение поиска из того набора значений, который был указан пользователем. Принцип ее работы такой же, как и следующий, только поиск осуществляется по направлению снизу вверх, от наименьшего числа к самому большому. Синтаксис этой функции предельно простой: =НАИМЕНЬШИЙ(массив;k).
Функция имеет два основных аргумента: массив данных, по которым будет осуществляться поиск и порядковый номер элемента, который надо найти. Далее функция работает следующим образом: сначала она ищет самое маленькое значение, потом начинает перебирать цифры снизу вверх. Первое значение считается 1. То есть, если использовать число 1 во втором аргументе, то результат будет эквивалентным функции МИН, о которой мы поговорим немного позже.
Функция НАИБОЛЬШИЙ
Функция НАИБОЛЬШИЙ является аналогичной, только отсчет выполняет, начиная с самого большого значения. После того, как передать ей коэффициент, она ищет в порядковом ряду с большего в меньший число, занимающее соответствующее место и возвращает его. Работают обе функции аналогичным образом. Предположим, у нас есть числовой ряд. Если в нем в качестве числа k указать 2, то в результате получится число 15, поскольку оно является вторым по величине в диапазоне, который прописан в первом аргументе.
Эта функция может быть полезной в ситуациях, например, когда товар поступал в определенной последовательности, и нужно определить, сколько стоила, например, шубка, которая пришла второй по счету.
Функция МЕДИАНА
В статистике медиана – это разновидность среднего числа, которое находится ровно посередине числового ряда. Очень часто медиана является лучшим решением, чем стандартное среднее арифметическое, потому что позволяет определить действительно среднестатистическое значение. Синтаксис этой функции аналогичен тому, который имеет любой другой оператор, определяющий среднее значение – перечень цифр, ячеек или диапазонов, из которых данные будут получаться.
На этом примере видно, как на практике осуществляется работа с функцией. В диалоговом окне «Аргументы функции» можно вводить большое количество чисел, ячеек и диапазонов. На картинке мы попробовали ввести число в первую строку, ячейку во вторую и диапазон значений в третью. Получили в результате число 12. Максимальное количество аргументов этой функции – 255, что более, чем достаточно для полноценного использования этой функции.
Функция СРЗНАЧЕСЛИ
Это улучшенная версия функции СРЗНАЧ, задача которой – находить среднее арифметическое, но лишь при условии, что определенное условие выполняется. Эта функция уже несколько сложнее тех, которые приводились выше: =СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения). Давайте рассмотрим каждый аргумент более подробно:
- Диапазон. Это ячейки, которые проверяются на предмет соответствия определенному условию.
- Условие. Это критерий, на предмет соответствия которому проверяется диапазон.
- Диапазон усреднения. Это тот диапазон, из которого будет доставаться среднее арифметическое. Этот аргумент вводить необязательно, поскольку диапазон ячеек и диапазон усреднения могут совпадать.
Функция МИН
В статистических подсчетах нередко нужно не только определить среднее значение, среднеквадратическое отклонение и вычислить другие показатели. Также важно значение наименьшего и наибольшего числа, в том числе, для получения указанных показателей. Практическое применение этой функции довольно обширное:
- На рынке акций для определения времени, когда цела была наиболее низкой.
- Для определения слабых мест в годовом бюджете (например, в каком месяце доходы компании были минимальными) с целью их дальнейшего исправления. Например, можно определить наименее доходный месяц и проанализировать факторы, которые этому способствовали.
Существует огромное количество других ситуаций, когда можно использовать функцию МИН. В самом общем виде она выглядит следующим образом: =МИН(число1;число2;…). Принцип заполнения аргументов этой функции аналогичен функции МАКС.
Функция МАКС
Как становится понятно из названия, эта функция ищет максимальное значение в определенной числовой выборке. Ситуации, в которых она может использоваться, в принципе, те же за тем лишь исключением, что все в противоположную сторону. Например, компания может с помощью функции МАКС определить самый доходный месяц и понять, каковы причины этого успеха.
Функции СРЗНАЧ и СРЗНАЧА
Стандартная функция СРЗНАЧ определяет среднее арифметическое в числовой выборке. Общий вид формулы такой же, как и для любой другой выборки значений. Сначала пишется название функции, после чего в скобках приводятся числа и диапазоны, которые необходимо обработать с помощью этой функции. То есть, общий вид формулы следующий: =СРЗНАЧ(число1;число2;…).
Как мы поняли, можно использовать как обычные числа (очень полезно для использования значений, которые не будут меняться в течение ближайшего времени), ссылки на ячейку (они применяются для тех значений, которые в будущем изменятся) и на диапазон (в этом случае будет использоваться целый набор чисел за один раз). Чтобы после ввода одного аргумента начать записывать другой, достаточно нажать на соответствующее поле в мастере функций или просто нажать на клавишу Tab.
Максимальное количество аргументов, которые можно использовать в этой функции – 255. При этом обязательным аргументом является только первое число. В качестве аргументов не могут использоваться текстовые и логические значения. Они просто не учитываются формулой, в которой используется указанный оператор. Основное отличие функции СРЗНАЧА от СРЗНАЧ заключается в том, что текстовые значения и «ЛОЖЬ» считаются нулевыми, а значение «Истина» приравнивается к единице.
Функция РАНГ.СР
С помощью функции РАНГ.СР пользователь может вернуть ранг числа. Если несколько чисел в одном диапазоне относятся к одному рангу, то возвращается среднее. Имеет три аргумента, два из которых – обязательные:
- Число. Это то число, для которого осуществляется определение ранга.
- Ссылка. Это массив чисел, или ссылка на этот массив.
- Порядок. Это число, которое влияет на способ, в который значения будут упорядочиваться.
Таким образом, статистические функции Excel – это превосходный инструмент для обработки больших массивов информации.
Источник
Лекция 2. Microsoft excel. Средства статистической обработки ms Excel
1. Систематизировать знания о статистических функциях в Excel, получить представление о способах обработки статистические данных в табличном процессоре.
2. Ознакомиться с возможностями Пакета анализа в Excel.
3. Привести примеры работы со списками в Excel.
Статистические функции в ms Excel
Пусть представлены следующие статистические данные (см. таб. 1), по которым надо вычислить:
количество опрошенных женщин;
процент женщин среди опрошенных;
процент мужчин среди опрошенных;
средний возраст опрошенных (среднеарифметическое);
средний возраст (медиана);
минимальный и максимальный возраст опрошенных;
количество женщин с высшим образованием;
средний возраст женщин с высшим образованием;
Данные социологического опроса
Для такого рода вычислений будем пользоваться встроенными функциями. Рассмотрим некоторые из них.
1) СЧЕТ(значение1; значение2;…), которая подсчитывает количество чисел в списке аргументов. Функция СЧЁТ используется для получения количества числовых ячеек в интервалах или массивах ячеек.
Аргументы: значение1; значение2; …— это от 1 до 30 аргументов, которые могут содержать или ссылаться на данные различных типов, но в подсчете участвуют только числа.
2) СЧЕТЕСЛИ(диапазон;критерий), где диапазон – диапазон, в котором нужно подсчитать ячейки. Критерий – критерий в форме числа, выражения или текста, который определяет, какие ячейки надо подсчитывать.
3) СРЗНАЧ, которая возвращает среднее (арифметическое) своих аргументов. СРЗНАЧ(число1; число2; . )
Число1, число2, . – это от 1 до 30 аргументов, для которых вычисляется среднее.
4) МЕДИАНА(число1;число2;. ). Число1, число2. – от 1 до 30 чисел, для которых определяется медиана. Медиана – это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана.
5) МОДА(число1;число2;. ). Число1, число2. – от 1 до 30 чисел, для которых определяется мода. МОДА определяет значение, которое чаще других встречается во множестве чисел.
6) МАКС(число1;число2; . ). Число1, число2. – от 1 до 30 чисел, среди которых требуется найти наибольшее.
7) МИН(число1;число2; . ). Число1, число2. – от 1 до 30 чисел, среди которых требуется найти наименьшее.

9) функции ДИСП и СТАНДОТКЛОН используются, если необходимо произвести вычисления дисперсии и стандартного отклонения по выборке.
Источник