Содержание
- Статистические функции
- МАКС
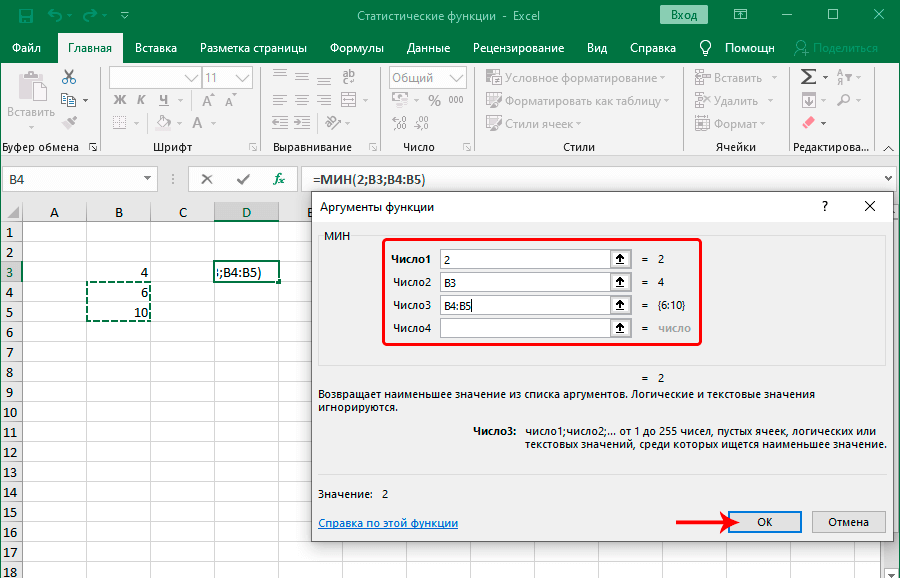
- МИН
- СРЗНАЧ
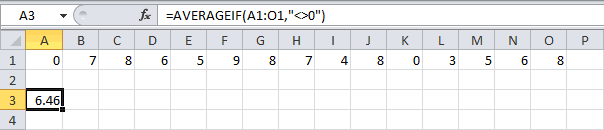
- СРЗНАЧЕСЛИ
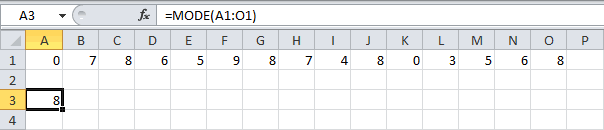
- МОДА.ОДН
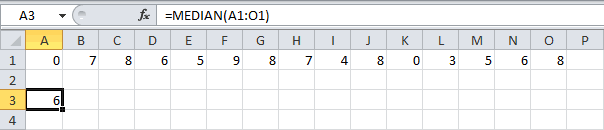
- МЕДИАНА
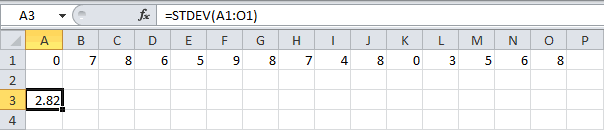
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
- Вопросы и ответы
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.
Запустить Мастер функций можно тремя способами:
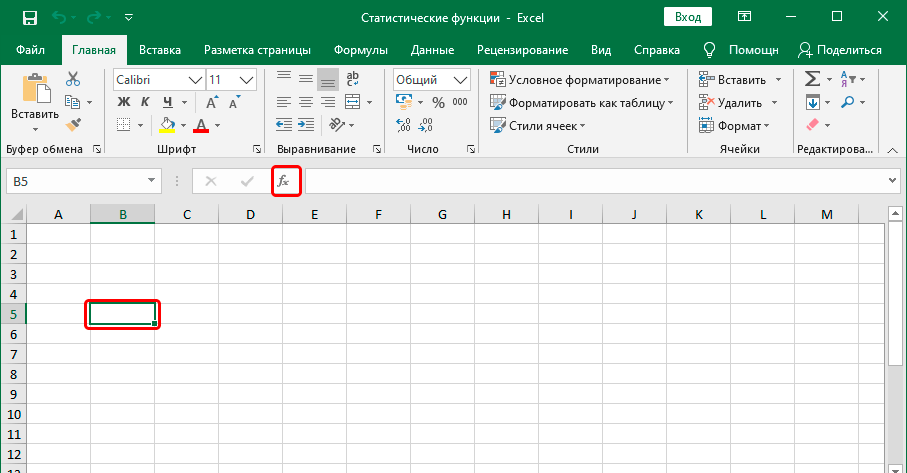
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
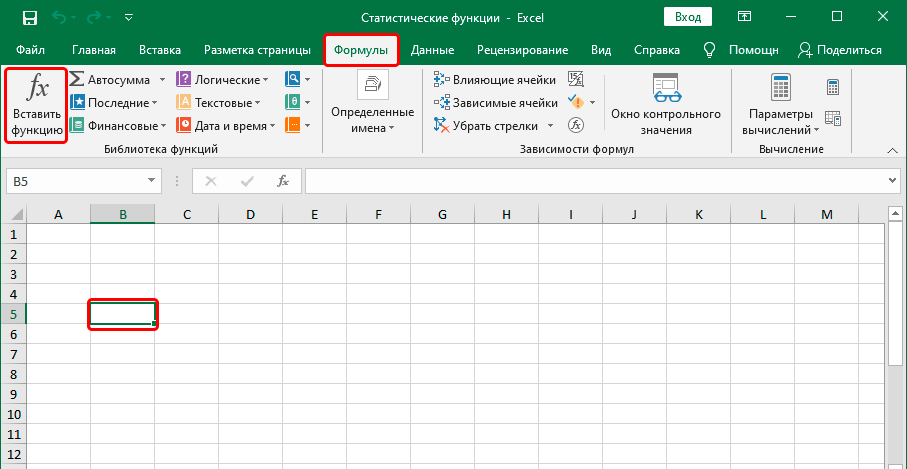
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
- Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
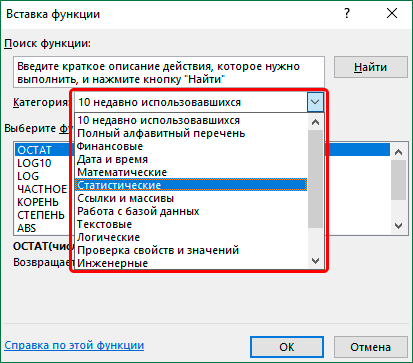
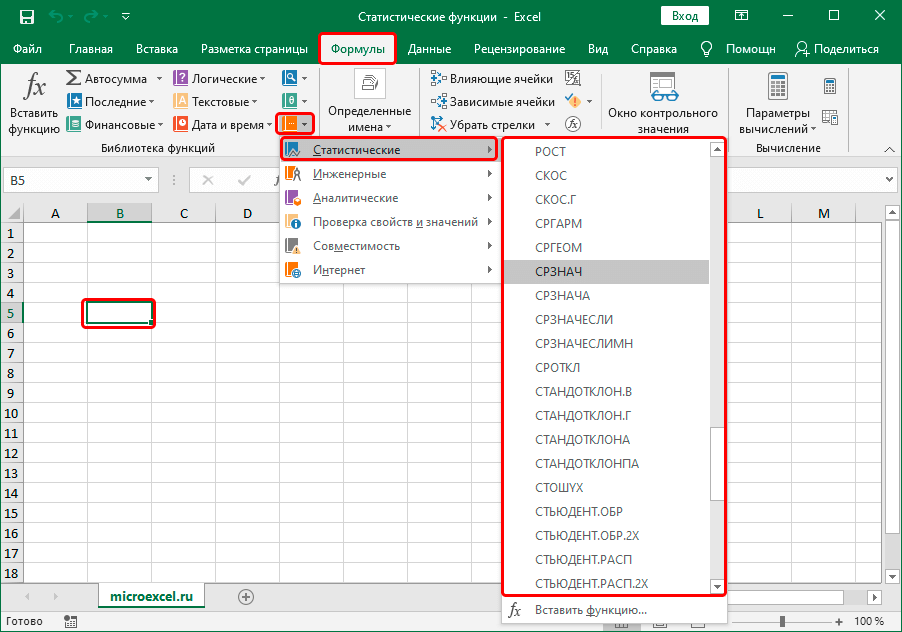
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
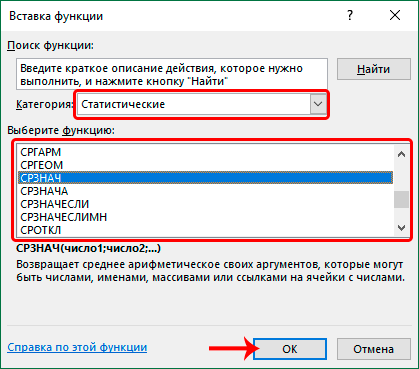
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
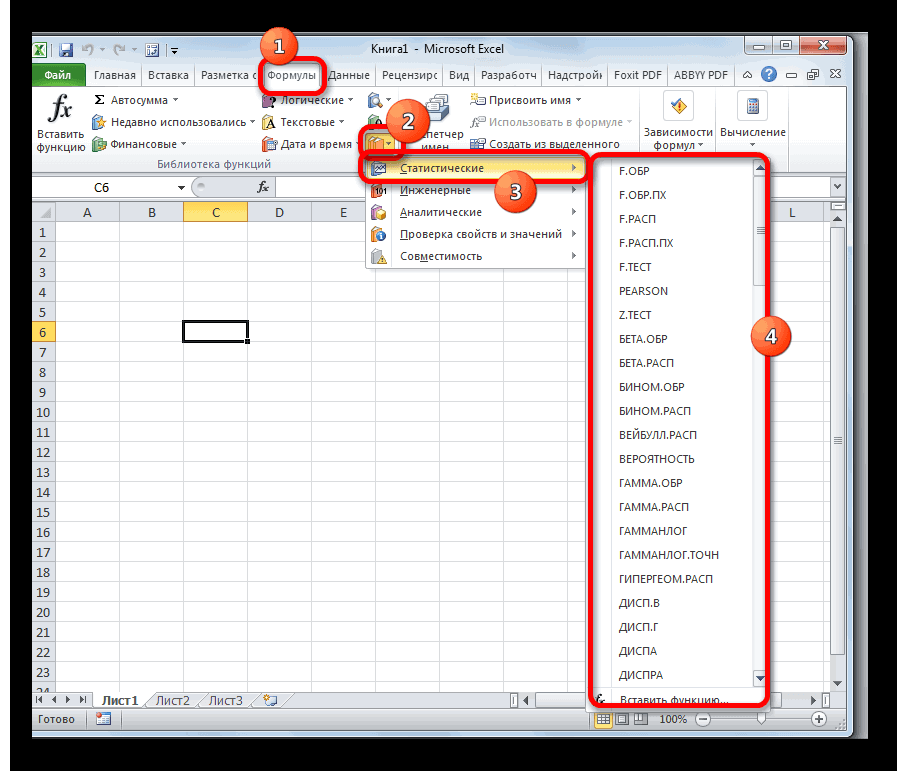
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Урок: Мастер функций в Excel
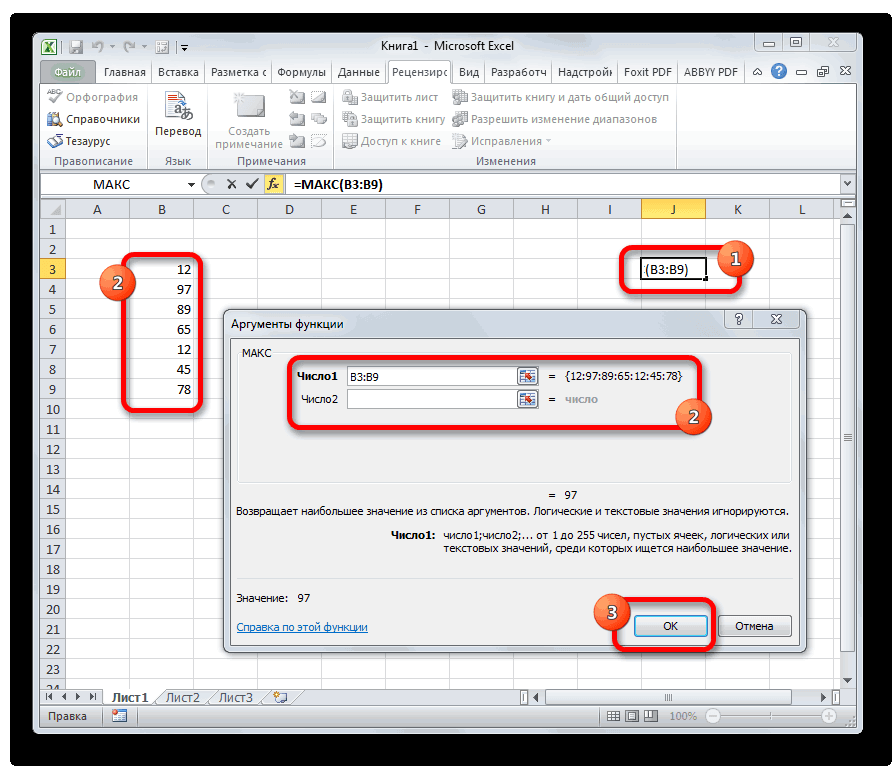
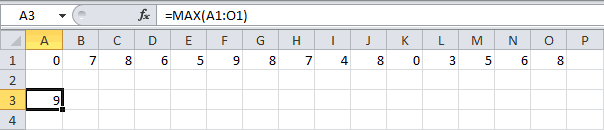
МАКС
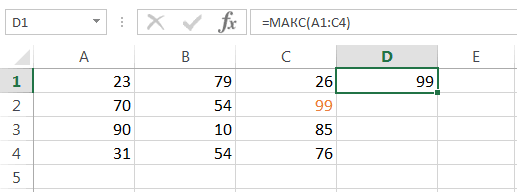
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
=МАКС(число1;число2;…)
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
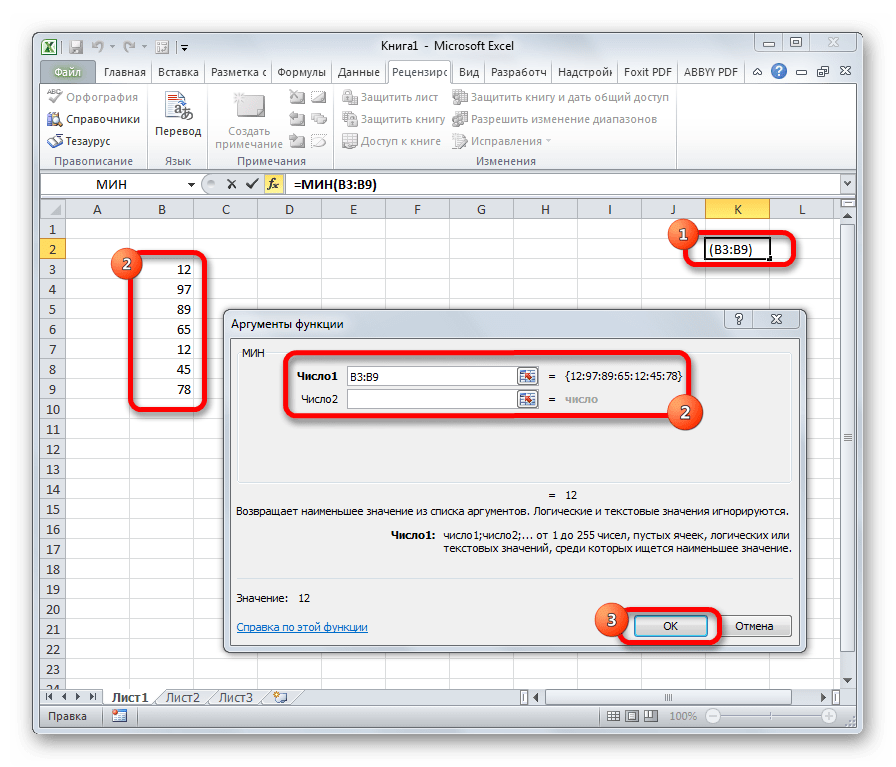
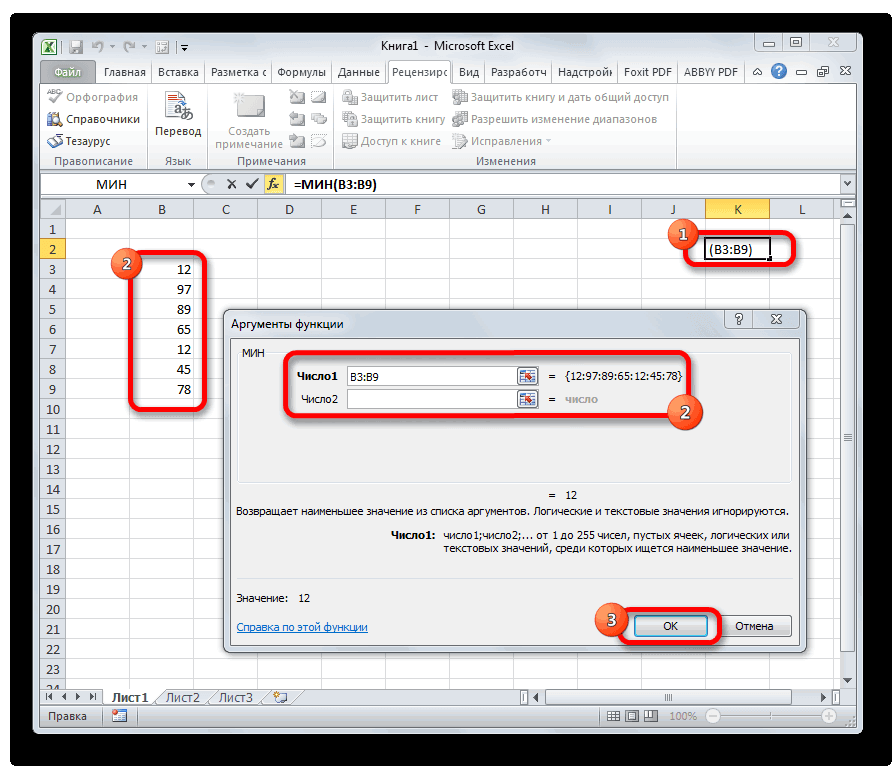
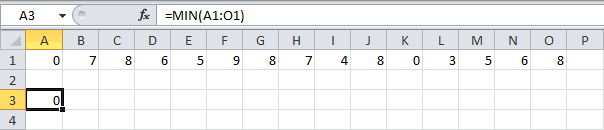
МИН
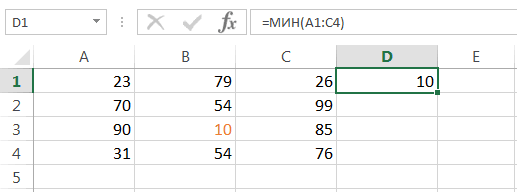
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
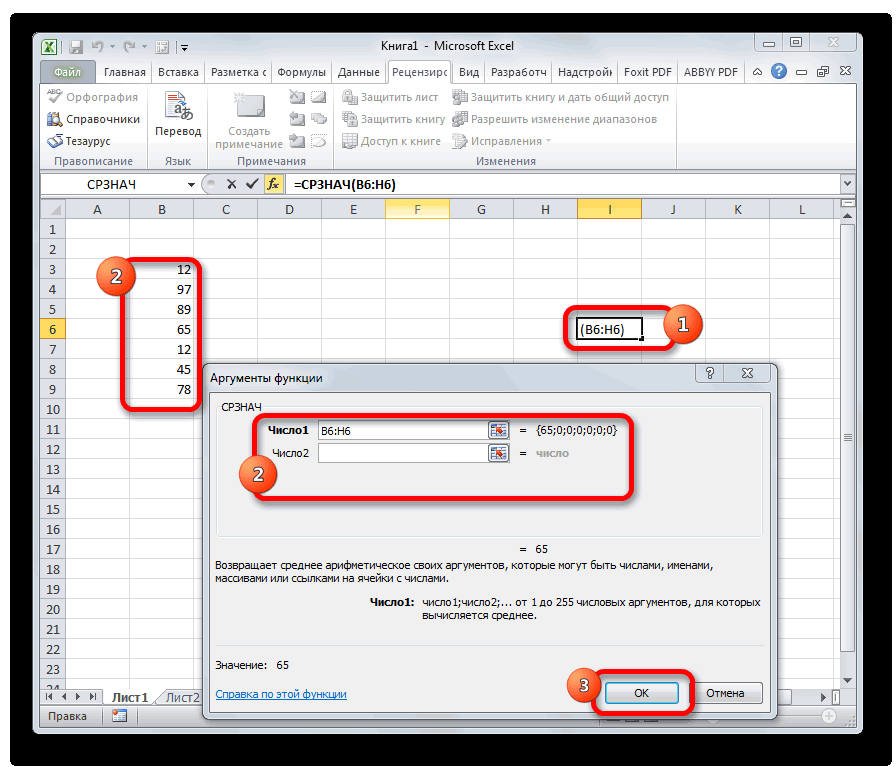
СРЗНАЧ
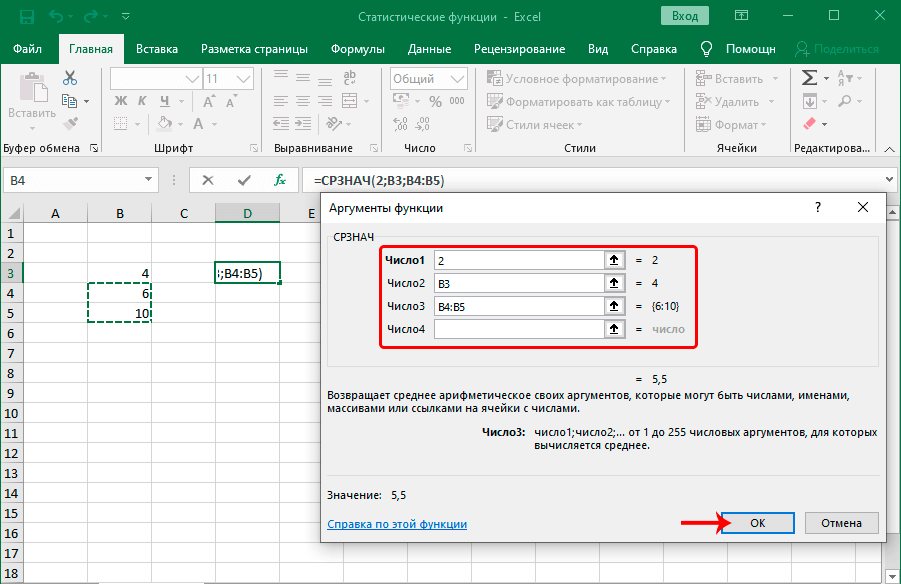
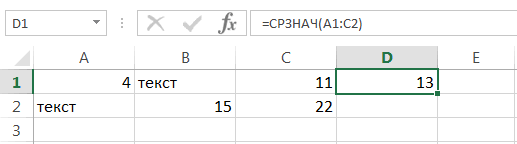
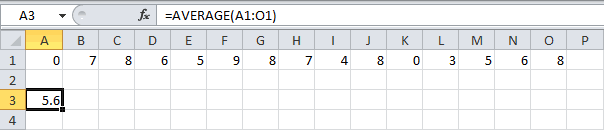
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
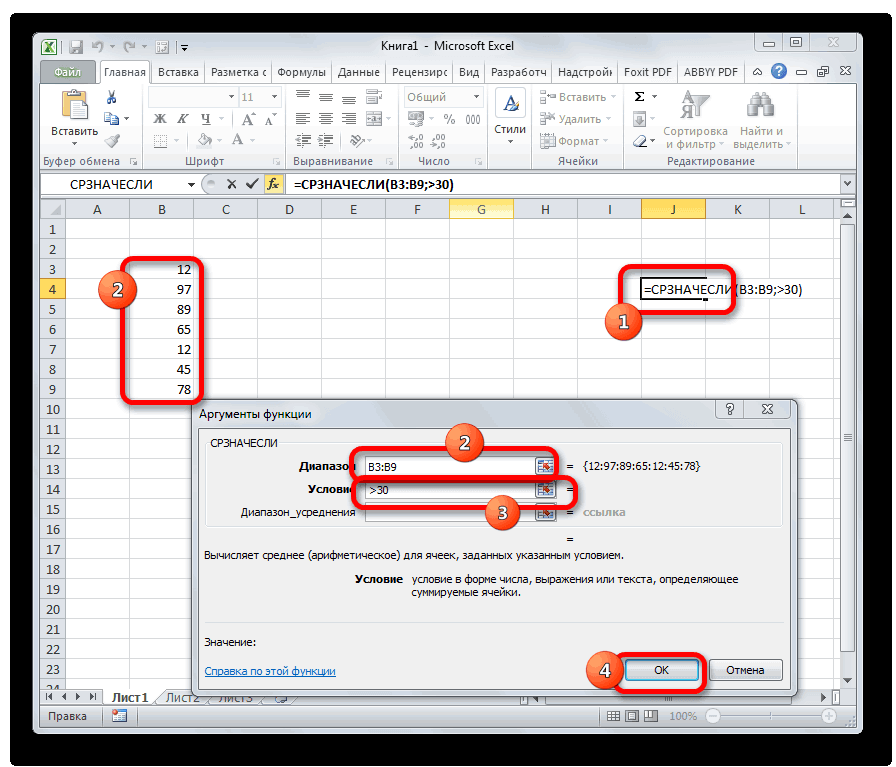
СРЗНАЧЕСЛИ
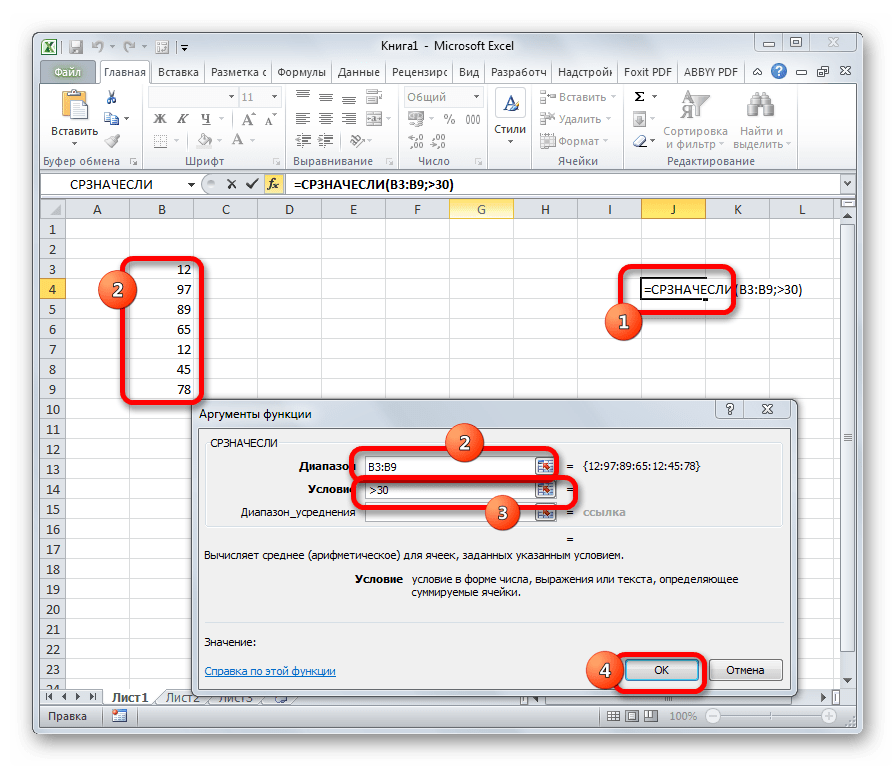
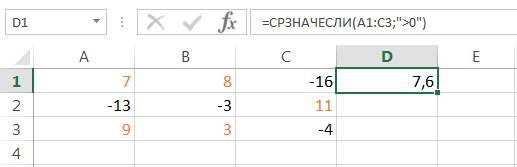
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])
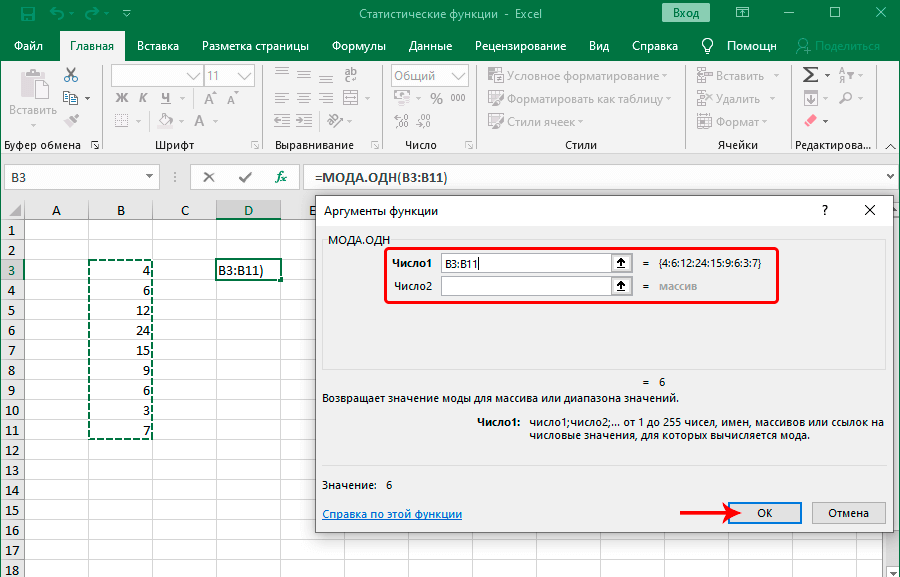
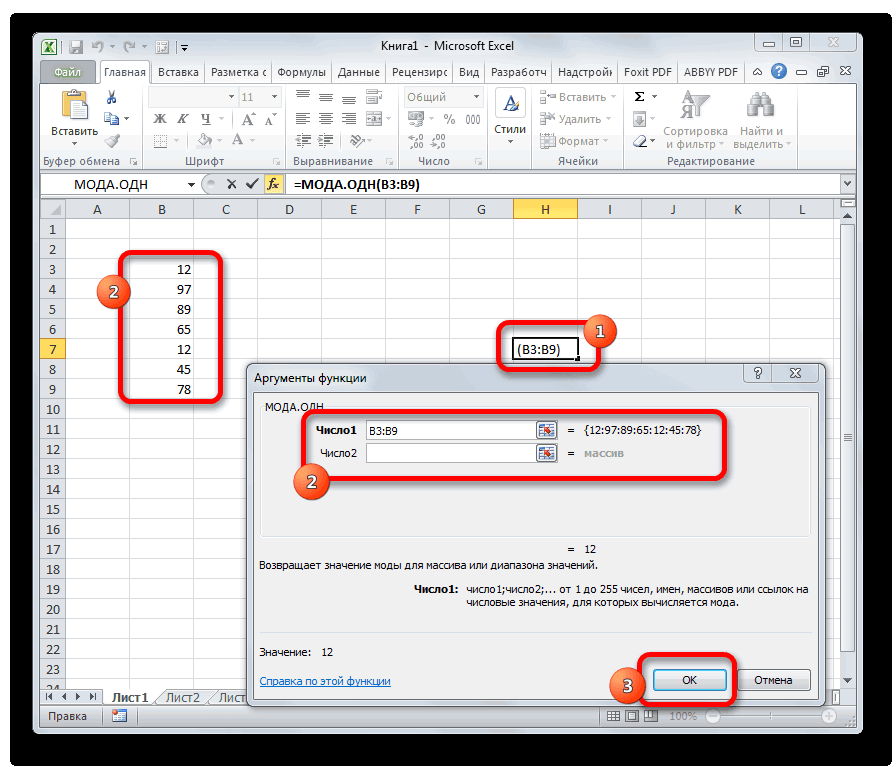
МОДА.ОДН
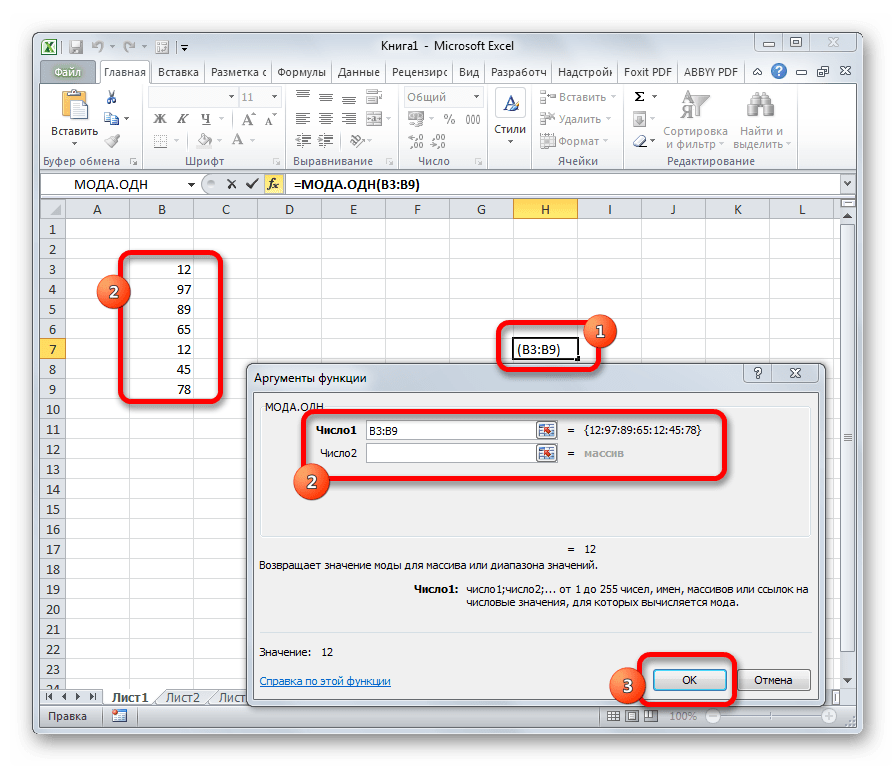
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
МЕДИАНА
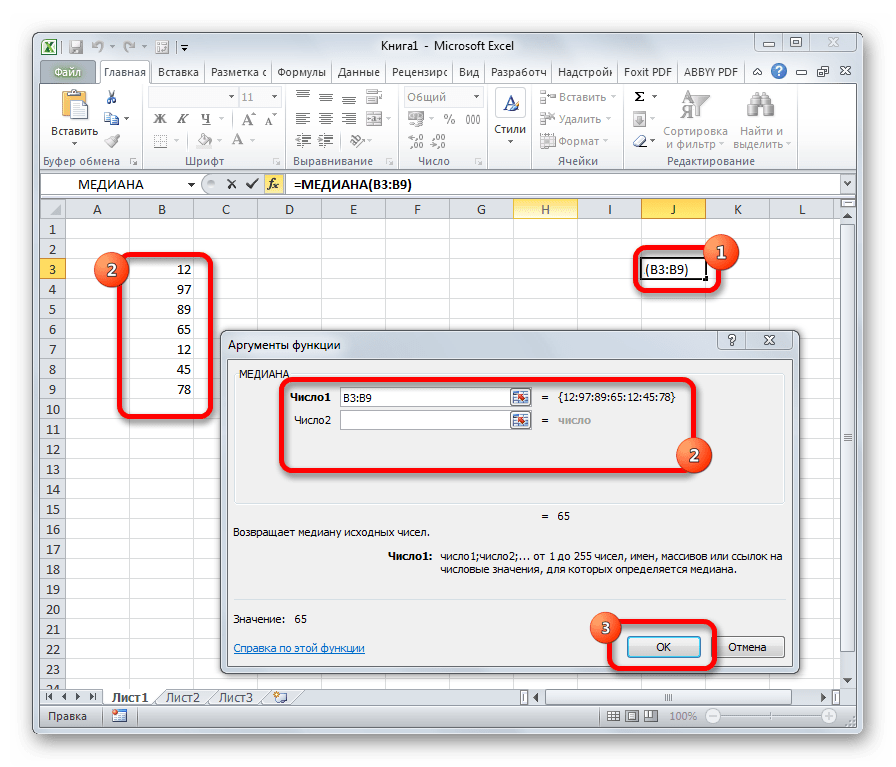
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
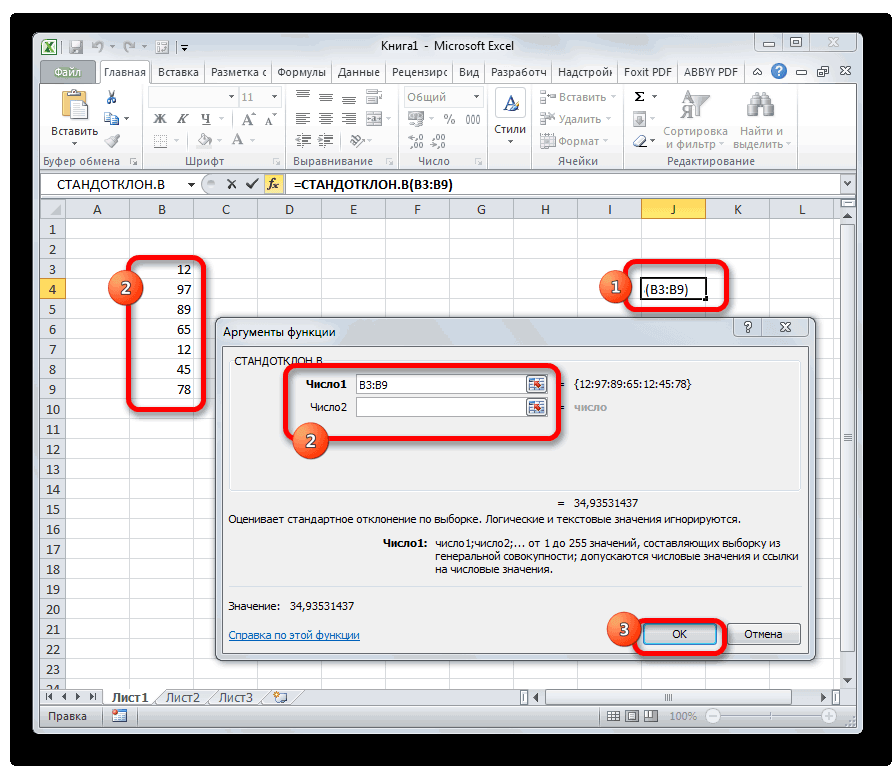
СТАНДОТКЛОН
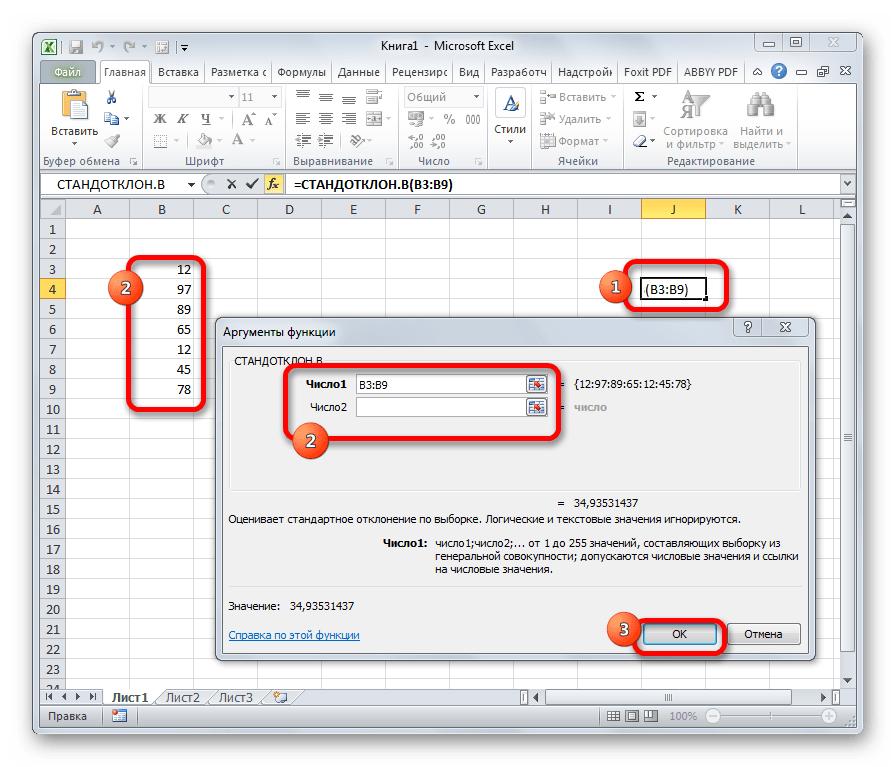
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:
=СТАНДОТКЛОН.В(число1;число2;…)
=СТАНДОТКЛОН.Г(число1;число2;…)
Урок: Формула среднего квадратичного отклонения в Excel
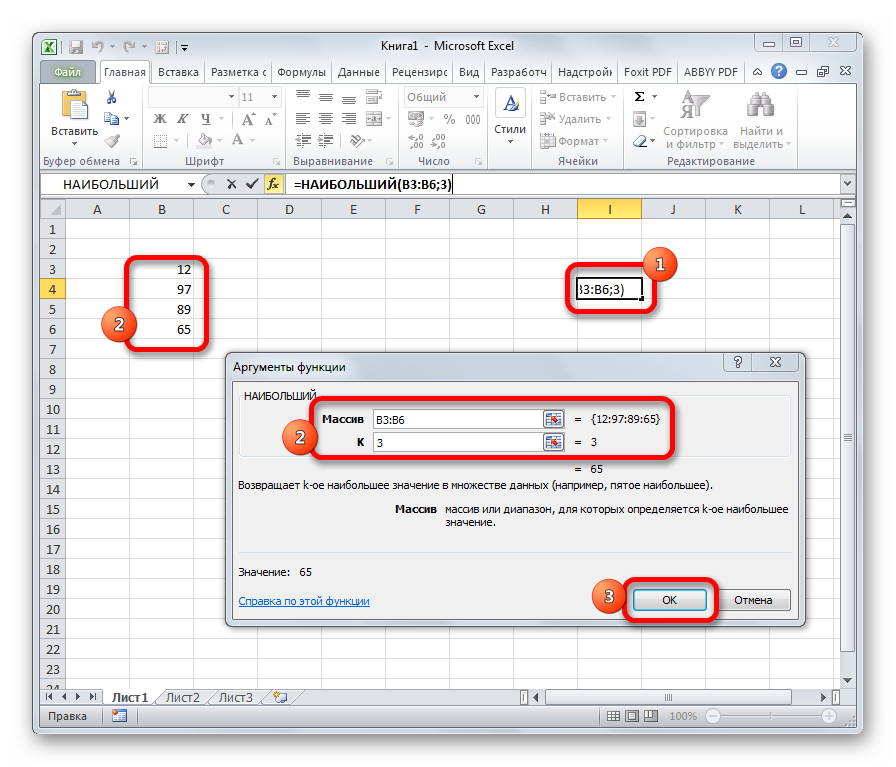
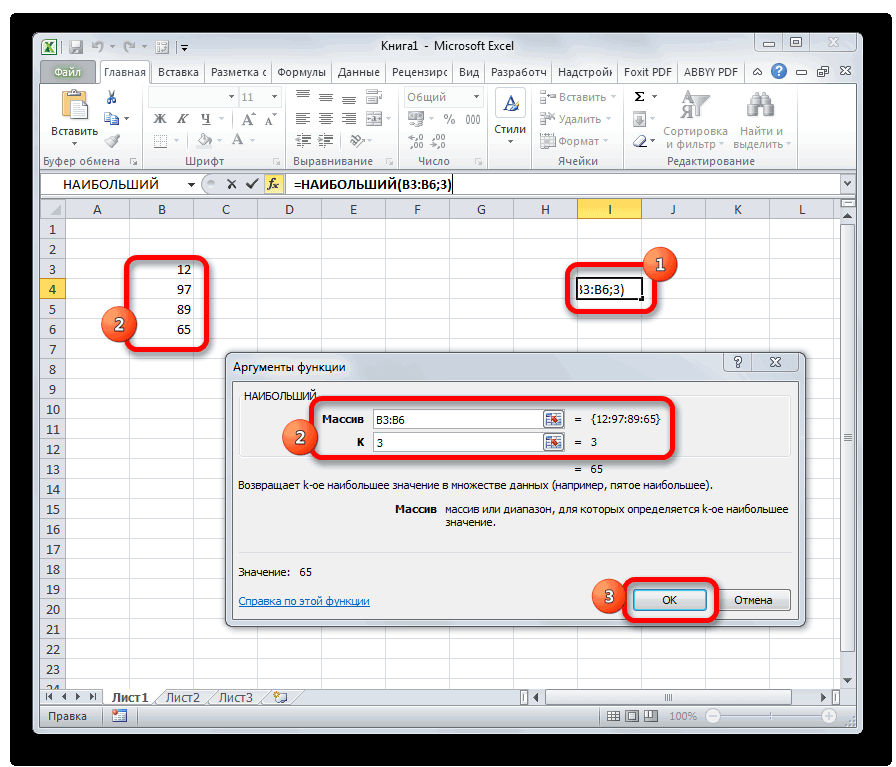
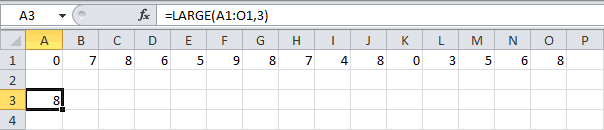
НАИБОЛЬШИЙ
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
=НАИБОЛЬШИЙ(массив;k)
В данном случае, k — это порядковый номер величины.
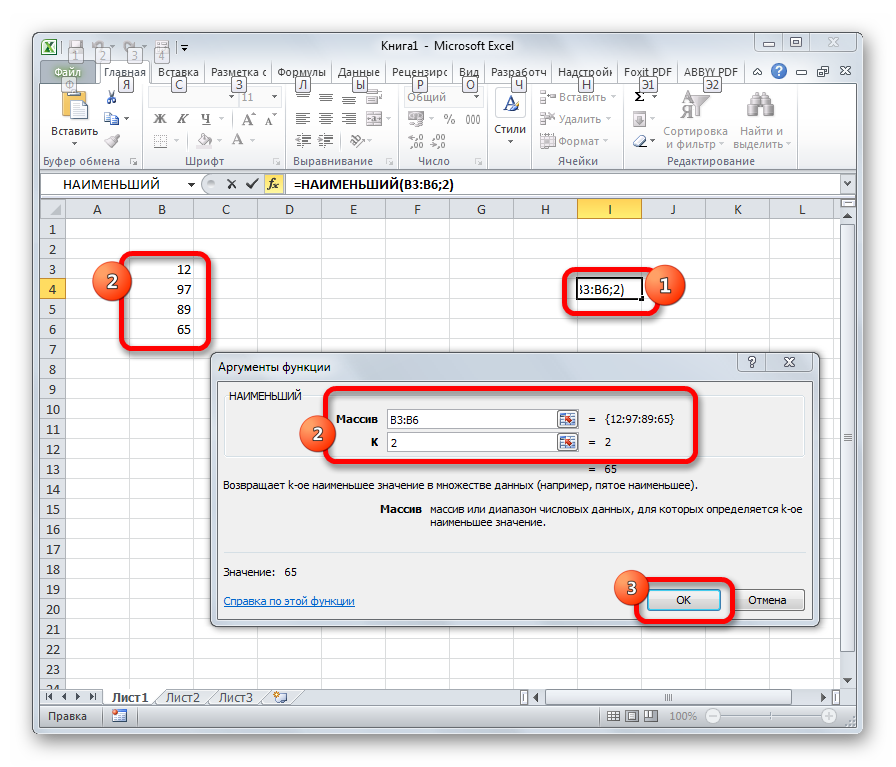
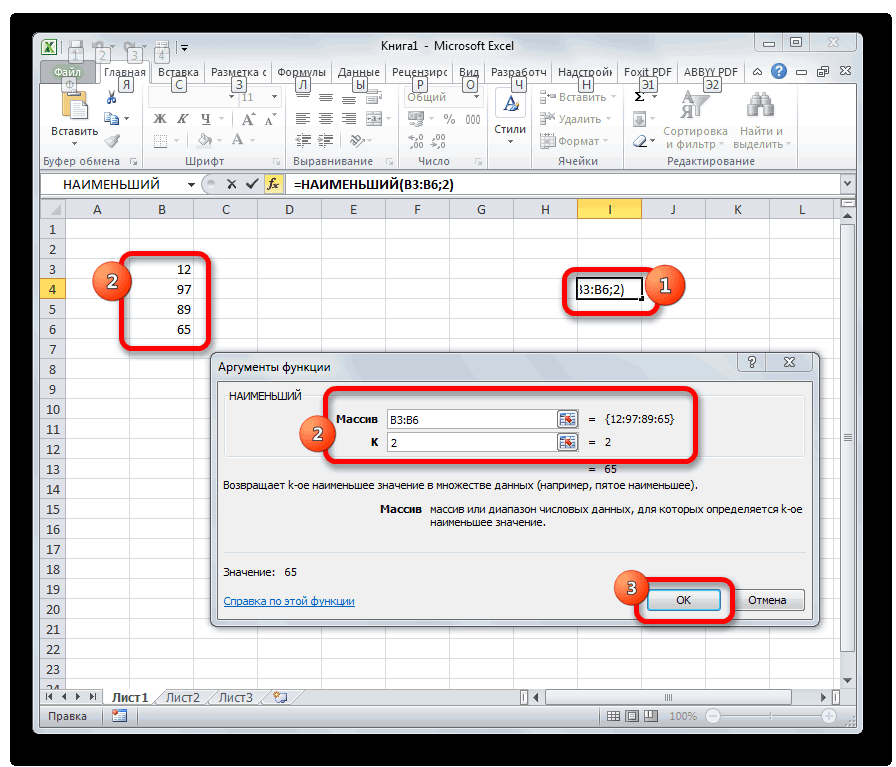
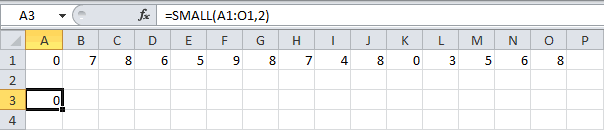
НАИМЕНЬШИЙ
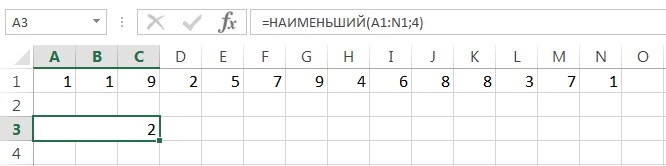
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
=НАИМЕНЬШИЙ(массив;k)
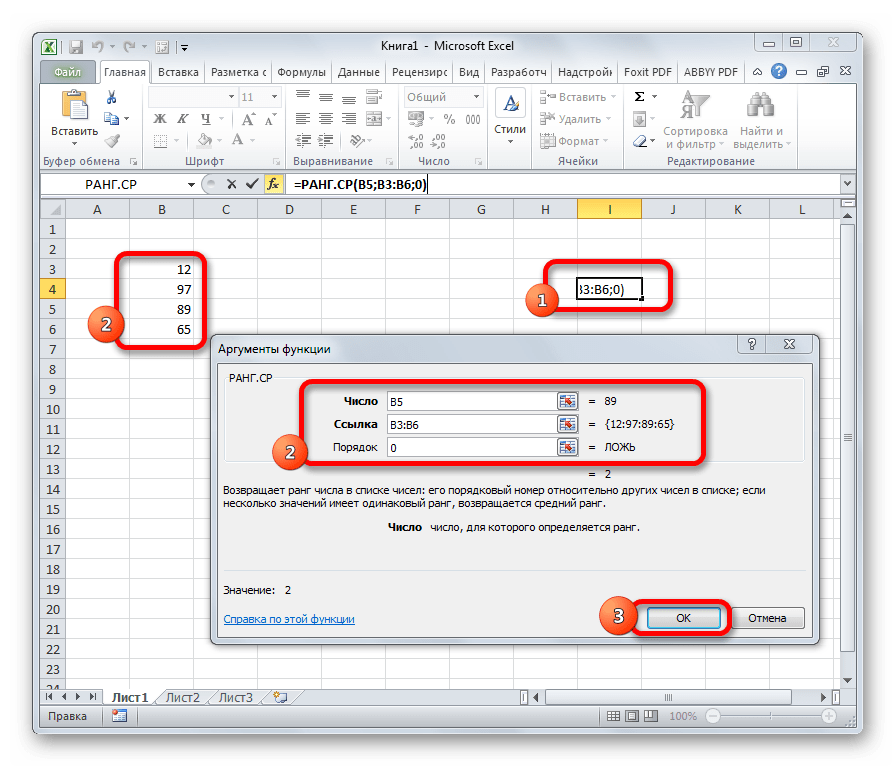
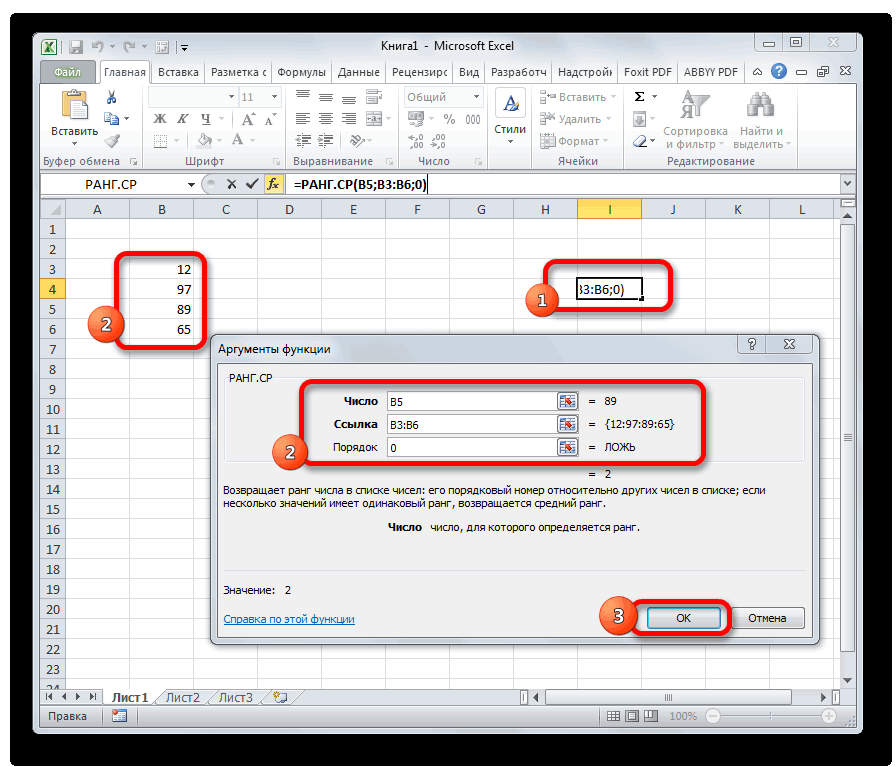
РАНГ.СР
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
=РАНГ.СР(число;массив;порядок)
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
СРОТКЛ |
Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего. |
|
СРЗНАЧ |
Возвращает среднее арифметическое аргументов. |
|
СРЗНАЧА |
Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения. |
|
СРЗНАЧЕСЛИ |
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые удовлетворяют заданному условию. |
|
СРЗНАЧЕСЛИМН |
Возвращает среднее значение (среднее арифметическое) всех ячеек, которые удовлетворяют нескольким условиям. |
|
БЕТА.РАСП |
Возвращает интегральную функцию бета-распределения. |
|
БЕТА.ОБР |
Возвращает обратную интегральную функцию указанного бета-распределения. |
|
БИНОМ.РАСП |
Возвращает отдельное значение вероятности биномиального распределения. |
|
БИНОМ.РАСП.ДИАП |
Возвращает вероятность пробного результата с помощью биномиального распределения. |
|
БИНОМ.ОБР |
Возвращает наименьшее значение, для которого интегральное биномиальное распределение меньше заданного значения или равно ему. |
|
ХИ2.РАСП |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.РАСП.ПХ |
Возвращает одностороннюю вероятность распределения хи-квадрат. |
|
ХИ2.ОБР |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.ОБР.ПХ |
Возвращает обратное значение односторонней вероятности распределения хи-квадрат. |
|
ХИ2.ТЕСТ |
Возвращает тест на независимость. |
|
ДОВЕРИТ.НОРМ |
Возвращает доверительный интервал для среднего значения по генеральной совокупности. |
|
ДОВЕРИТ.СТЬЮДЕНТ |
Возвращает доверительный интервал для среднего генеральной совокупности, используя t-распределение Стьюдента. |
|
КОРРЕЛ |
Возвращает коэффициент корреляции между двумя множествами данных. |
|
СЧЁТ |
Подсчитывает количество чисел в списке аргументов. |
|
СЧЁТЗ |
Подсчитывает количество значений в списке аргументов. |
|
СЧИТАТЬПУСТОТЫ |
Подсчитывает количество пустых ячеек в диапазоне. |
|
СЧЁТЕСЛИ |
Подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному условию. |
|
СЧЁТЕСЛИМН |
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих нескольким условиям. |
|
КОВАРИАЦИЯ.Г |
Возвращает ковариацию, среднее произведений парных отклонений. |
|
КОВАРИАЦИЯ.В |
Возвращает ковариацию выборки — среднее попарных произведений отклонений для всех точек данных в двух наборах данных. |
|
КВАДРОТКЛ |
Возвращает сумму квадратов отклонений. |
|
ЭКСП.РАСП |
Возвращает экспоненциальное распределение. |
|
F.РАСП |
Возвращает F-распределение вероятности. |
|
F.РАСП.ПХ |
Возвращает F-распределение вероятности. |
|
F.ОБР |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ОБР.ПХ |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ТЕСТ |
Возвращает результат F-теста. |
|
ФИШЕР |
Возвращает преобразование Фишера. |
|
ФИШЕРОБР |
Возвращает обратное преобразование Фишера. |
|
ПРЕДСКАЗ |
Возвращает значение линейного тренда. Примечание: В Excel 2016 эта функция заменена на ПРЕДСКАЗ.ЛИНЕЙН из нового набора функций прогнозирования. Однако она по-прежнему доступна для совместимости с предыдущими версиями. |
|
ПРЕДСКАЗ.ETS |
Возвращает будущее значение на основе существующих (ретроспективных) данных с использованием версии AAA алгоритма экспоненциального сглаживания (ETS). |
|
ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ |
Возвращает доверительный интервал для прогнозной величины на указанную дату. |
|
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ |
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду. |
|
ПРЕДСКАЗ.ETS.СТАТ |
Возвращает статистическое значение, являющееся результатом прогнозирования временного ряда. |
|
ПРЕДСКАЗ.ЛИНЕЙН |
Возвращает будущее значение на основе существующих значений. |
|
ЧАСТОТА |
Возвращает распределение частот в виде вертикального массива. |
|
ГАММА |
Возвращает значение функции гамма |
|
ГАММА.РАСП |
Возвращает гамма-распределение. |
|
ГАММА.ОБР |
Возвращает обратное значение интегрального гамма-распределения. |
|
ГАММАНЛОГ |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАММАНЛОГ.ТОЧН |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАУСС |
Возвращает значение на 0,5 меньше стандартного нормального распределения. |
|
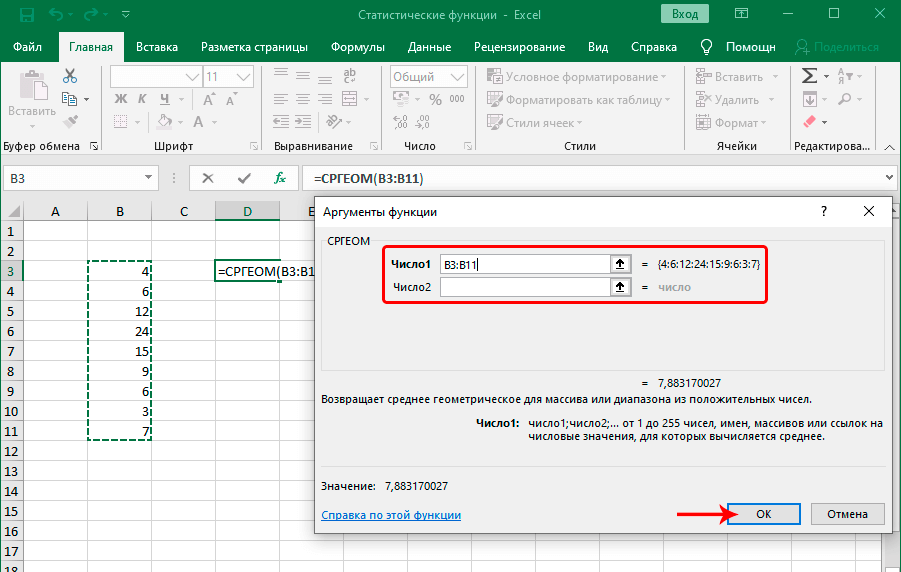
СРГЕОМ |
Возвращает среднее геометрическое. |
|
РОСТ |
Возвращает значения в соответствии с экспоненциальным трендом. |
|
СРГАРМ |
Возвращает среднее гармоническое. |
|
ГИПЕРГЕОМ.РАСП |
Возвращает гипергеометрическое распределение. |
|
ОТРЕЗОК |
Возвращает отрезок, отсекаемый на оси линией линейной регрессии. |
|
ЭКСЦЕСС |
Возвращает эксцесс множества данных. |
|
НАИБОЛЬШИЙ |
Возвращает k-ое наибольшее значение в множестве данных. |
|
ЛИНЕЙН |
Возвращает параметры линейного тренда. |
|
ЛГРФПРИБЛ |
Возвращает параметры экспоненциального тренда. |
|
ЛОГНОРМ.РАСП |
Возвращает интегральное логарифмическое нормальное распределение. |
|
ЛОГНОРМ.ОБР |
Возвращает обратное значение интегрального логарифмического нормального распределения. |
|
МАКС |
Возвращает наибольшее значение в списке аргументов. |
|
МАКСА |
Возвращает наибольшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МАКСЕСЛИ |
Возвращает максимальное значение из заданных определенными условиями или критериями ячеек. |
|
МЕДИАНА |
Возвращает медиану заданных чисел. |
|
МИН |
Возвращает наименьшее значение в списке аргументов. |
|
МИНЕСЛИ |
Возвращает минимальное значение из заданных определенными условиями или критериями ячеек. |
|
МИНА |
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МОДА.НСК |
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных. |
|
МОДА.ОДН |
Возвращает значение моды набора данных. |
|
ОТРБИНОМ.РАСП |
Возвращает отрицательное биномиальное распределение. |
|
НОРМ.РАСП |
Возвращает нормальное интегральное распределение. |
|
НОРМ.ОБР |
Возвращает обратное значение нормального интегрального распределения. |
|
НОРМ.СТ.РАСП |
Возвращает стандартное нормальное интегральное распределение. |
|
НОРМ.СТ.ОБР |
Возвращает обратное значение стандартного нормального интегрального распределения. |
|
ПИРСОН |
Возвращает коэффициент корреляции Пирсона. |
|
ПРОЦЕНТИЛЬ.ИСКЛ |
Возвращает k-ю процентиль для значений диапазона, где k — число от 0 и 1 (не включая эти числа). |
|
ПРОЦЕНТИЛЬ.ВКЛ |
Возвращает k-ю процентиль для значений диапазона. |
|
ПРОЦЕНТРАНГ.ИСКЛ |
Возвращает ранг значения в наборе данных как процентную долю набора (от 0 до 1, исключая границы). |
|
ПРОЦЕНТРАНГ.ВКЛ |
Возвращает процентную норму значения в наборе данных. |
|
ПЕРЕСТ |
Возвращает количество перестановок для заданного числа объектов. |
|
ПЕРЕСТА |
Возвращает количество перестановок для заданного числа объектов (с повторами), которые можно выбрать из общего числа объектов. |
|
ФИ |
Возвращает значение функции плотности для стандартного нормального распределения. |
|
ПУАССОН.РАСП |
Возвращает распределение Пуассона. |
|
ВЕРОЯТНОСТЬ |
Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов. |
|
КВАРТИЛЬ.ИСКЛ |
Возвращает квартиль набора данных на основе значений процентили из диапазона от 0 до 1, исключая границы. |
|
КВАРТИЛЬ.ВКЛ |
Возвращает квартиль набора данных. |
|
РАНГ.СР |
Возвращает ранг числа в списке чисел. |
|
РАНГ.РВ |
Возвращает ранг числа в списке чисел. |
|
КВПИРСОН |
Возвращает квадрат коэффициента корреляции Пирсона. |
|
СКОС |
Возвращает асимметрию распределения. |
|
СКОС.Г |
Возвращает асимметрию распределения на основе заполнения: характеристика степени асимметрии распределения относительно его среднего. |
|
НАКЛОН |
Возвращает наклон линии линейной регрессии. |
|
НАИМЕНЬШИЙ |
Возвращает k-ое наименьшее значение в множестве данных. |
|
НОРМАЛИЗАЦИЯ |
Возвращает нормализованное значение. |
|
СТАНДОТКЛОН.Г |
Вычисляет стандартное отклонение по генеральной совокупности. |
|
СТАНДОТКЛОН.В |
Оценивает стандартное отклонение по выборке. |
|
СТАНДОТКЛОНА |
Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения. |
|
СТАНДОТКЛОНПА |
Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения. |
|
СТОШYX |
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии. |
|
СТЬЮДРАСП |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.2Х |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.ПХ |
Возвращает t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ОБР |
Возвращает значение t для t-распределения Стьюдента как функцию вероятности и степеней свободы. |
|
СТЬЮДЕНТ.ОБР.2Х |
Возвращает обратное t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ТЕСТ |
Возвращает вероятность, соответствующую проверке по критерию Стьюдента. |
|
ТЕНДЕНЦИЯ |
Возвращает значения в соответствии с линейным трендом. |
|
УРЕЗСРЕДНЕЕ |
Возвращает среднее внутренности множества данных. |
|
ДИСП.Г |
Вычисляет дисперсию по генеральной совокупности. |
|
ДИСП.В |
Оценивает дисперсию по выборке. |
|
ДИСПА |
Оценивает дисперсию по выборке, включая числа, текст и логические значения. |
|
ДИСПРА |
Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения. |
|
ВЕЙБУЛЛ.РАСП |
Возвращает распределение Вейбулла. |
|
Z.ТЕСТ |
Возвращает одностороннее значение вероятности z-теста. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Статьи по теме
Excel (по категориям)
Excel (по алфавиту)
Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.
-
Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
- Заключение
Использование статистических функций
Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.
Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:
- Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
- Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
- Используем сочетание клавиш Shift+F3.
Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.
Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.
На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.
Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.
Давайте теперь рассмотрим наиболее популярные функции.
СРЗНАЧ
Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов функции можно указать:
- конкретные числа;
- ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
- диапазон ячеек – указывается вручную или путем выделения в таблице.
- переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.
МАКС
Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:
=МАКС(число1;число2;…)
В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.
МИН
Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:
=МИН(число1;число2;…)
Аргументы функции заполняются так же, как и для оператора МАКС.
СРЗНАЧЕСЛИ
Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:
=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)
В аргументах указываются:
- Диапазон ячеек – вручную или с помощью выделения в таблице;
- Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
- Диапазон_усреднения – не является обязательным аргументом для заполнения.
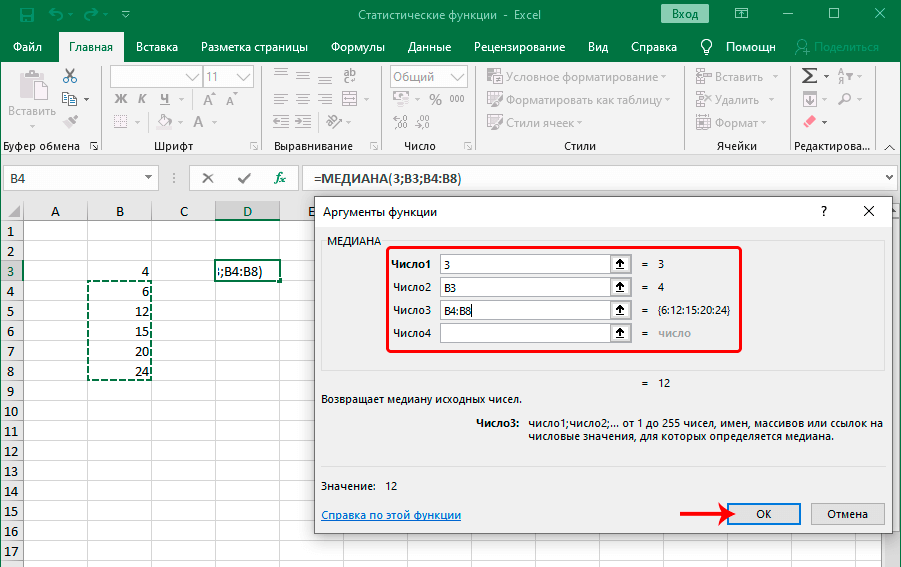
МЕДИАНА
Оператор находит медиану заданного диапазона значений. Синтаксис функции:
=МЕДИАНА(число1;число2;…)
В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.
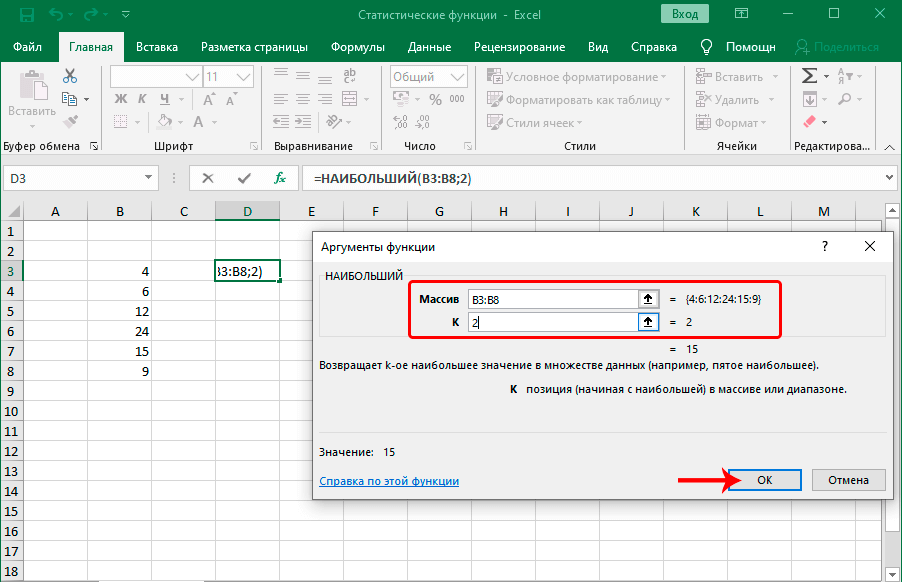
НАИБОЛЬШИЙ
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:
=НАИБОЛЬШИЙ(массив;k)
Аргумента функции два: массив и номер позиции – K.
Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.
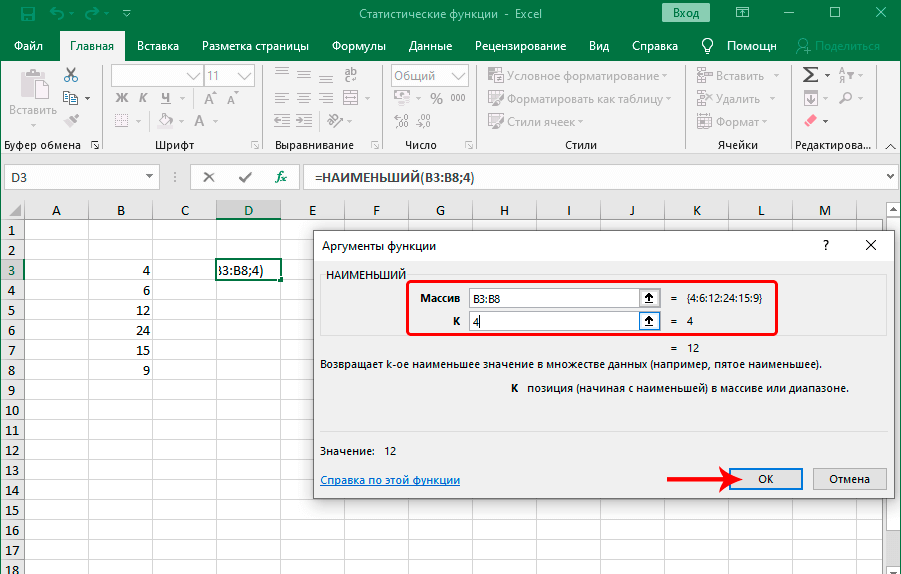
НАИМЕНЬШИЙ
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:
=НАИМЕНЬШИЙ(массив;k)
МОДА.ОДН
Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:
=МОДА.ОДН(число1;число2;…)
В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.
Для вертикальных массивов, также, используется функция МОДА.НСК.
СТАНДОТКЛОН
Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:
- СТАДНОТКЛОН.В – находит стандартное отклонение выборки
- СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности
Формулы функций выглядят следующим образом:
- =СТАДНОТКЛОН.В(число1;число2;…)
- =СТАДНОТКЛОН.Г(число1;число2;…)
СРГЕОМ
Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:
=СРГЕОМ(число1;число2;…)

Заключение
В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.
Статистика – наука, которая используется для любых других исследований, а также обработки большого количества количественных и даже качественных данных. И что важно, это одно из главных применений электронных таблиц Excel, поэтому давайте более подробно рассмотрим, статистические формулы. Во-первых, что они нам дают? Прежде всего, они позволяют структурировать информацию и осуществить ее анализ. Статистические функции в Excel относятся к совершенно отдельной категории.
Содержание
- Как пользоваться статистическими функциями
- Перечень статистических функций
- Функция СРГЕОМ
- Функция СТАНДОТКЛОН
- Функция МОДА.ОДН
- Функция НАИМЕНЬШИЙ
- Функция НАИБОЛЬШИЙ
- Функция МЕДИАНА
- Функция СРЗНАЧЕСЛИ
- Функция МИН
- Функция МАКС
- Функции СРЗНАЧ и СРЗНАЧА
- Функция РАНГ.СР
Как пользоваться статистическими функциями
Есть несколько способов ввода любой функции, и статистические не являются исключением:
- Ввести непосредственно в ячейке, предварительно нажав клавишу =. Это касается самых простых функций, несложных для запоминания и содержащих один или два аргумента. Например, так можно делать для операции умножения, сложения, вычитания и деления. А вот если функция сложная, то можно воспользоваться помощником. Это уже второй способ.
- Помощник по использованию функций. Он не только подсказывает, какая формула что означает, а и помогает ввести правильные аргументы применительно к конкретной функции.
Вызвать помощник можно несколькими способами:
- Воспользоваться кнопкой «Вставить функцию», расположенной слева от строки формул.
- Вызвать мастер ввода функций через кнопку «Вставить функцию», которая находится в левой части панели, которая открывается по клику на вкладку «Формулы».
- Воспользовавшись горячими клавишами Shift+F3.
Любой из этих методов приводит к одному результату – вызову мастера функций. Можно использовать тот, который больше всего подходит в конкретной ситуации. После того, как окно откроется, нам первым делом нужно выбрать категорию: статистические функции.
После того, как тип функции будет выбран, нам нужно выбрать подходящую формулу из списка. Под перечнем видим, что есть описание, в котором рассказывается, что конкретная функция делает.
Чтобы подтвердить выбор функции, которая будет вводиться, нужно нажать клавишу ОК. После этого появится такое окно, в котором можно ввести параметры функции (или, как их еще называют, аргументы).
Интересный факт. Можно выбрать функцию еще одним способом. Для этого нужно перейти на вкладку «Формулы» и нажать на кнопку «Другие функции», расположенной на ленте.
Далее будет пункт «Другие функции» – «Статистические» и в появившемся списке ищем подходящую функцию и выбираем ее. Этот перечень может прокручиваться.
Перечень статистических функций
А теперь давайте перейдем непосредственно к рассмотрению статистических функций.
Функция СРГЕОМ
Много кто знает о таком параметре, как среднее арифметическое. Вычисляется оно с помощью функции, о которой мы еще сегодня обязательно поговорим. Но есть еще одна функция, которая определяет среднее геометрическое.
Формула очень простая: =СРГЕОМ(число1;число2;…). Кроме чисел также можно указать диапазон значений, которые учитываются этой функцией. Что же такое среднее геометрическое? Это число, которое может заменять любое из чисел в последовательности таким образом, чтобы не менялось произведение этих значений. Еще один часто используемый термин – среднее пропорциональное. Это синоним к среднему геометрическому. Такой второй термин используется, потому что среднее геометрическое пропорционально к первому и второму числам.
Функция СТАНДОТКЛОН
Один из главных статистических параметров, который должен рассчитываться вместо со средним арифметическим – стандартное отклонение. Это мера, демонстрирующая степень разброса значений. Выполняет ту же функцию, что и дисперсия, просто представлена в том же виде, что и среднее значение, в отличие от дисперсии.
Вообще, стандартное отклонение рассчитывается, как квадратный корень из дисперсии. Но в Эксель есть специальная формула, которая сразу вычисляет степень дисперсии, после чего на основе полученного значения получает стандартное (или среднеквадратическое) отклонение.
Сама эта формула довольно старая, но знать о ней надо, потому что время от времени ее можно найти в готовых таблицах. Сейчас уже есть более новые версии этой функции – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Последняя функция находит среднеквадратическое отклонение по генеральной совокупности, в то время как первая ориентируется исключительно на выборку.
В остальном, синтаксис обеих функций такой же, как и для вычисления среднего арифметического (об этом мы поговорим позже) – числа, которые перечислены через скобку.
Функция МОДА.ОДН
Мода выборки абсолютно не связана с одеждой или популярными машинами. Но при этом она связана со словом «популярный». Если говорить о статистике, то это значение в выборке, которое встречается наиболее часто. Соответственно, функция МОДА.ОДН дает возможность определить это значение.
Если говорить о синтаксисе, то он похож на многие другие статистические функции. Сначала пишется оператор, после чего в скобках записываются его аргументы, которые являют собой числа, разделенные запятой. В качестве значения аргумента может выступать не только число, но и отдельные ячейки, диапазоны значений. Это дает возможность более гибко управлять выборкой. На этом скриншоте отчетливо видно, как это работает на практике.
Эта функция подходит для горизонтальных массивов. Если же нужно определить моду выборки для вертикального массива, используется похожая функция МОДА.НСК. Общий внешний вид функции следующий: =МОДА.ОДН(аргумент 1, аргумент 2; аргумент …).
Функция НАИМЕНЬШИЙ
Задача этой функции – выполнение поиска из того набора значений, который был указан пользователем. Принцип ее работы такой же, как и следующий, только поиск осуществляется по направлению снизу вверх, от наименьшего числа к самому большому. Синтаксис этой функции предельно простой: =НАИМЕНЬШИЙ(массив;k).
Функция имеет два основных аргумента: массив данных, по которым будет осуществляться поиск и порядковый номер элемента, который надо найти. Далее функция работает следующим образом: сначала она ищет самое маленькое значение, потом начинает перебирать цифры снизу вверх. Первое значение считается 1. То есть, если использовать число 1 во втором аргументе, то результат будет эквивалентным функции МИН, о которой мы поговорим немного позже.
Функция НАИБОЛЬШИЙ
Функция НАИБОЛЬШИЙ является аналогичной, только отсчет выполняет, начиная с самого большого значения. После того, как передать ей коэффициент, она ищет в порядковом ряду с большего в меньший число, занимающее соответствующее место и возвращает его. Работают обе функции аналогичным образом. Предположим, у нас есть числовой ряд. Если в нем в качестве числа k указать 2, то в результате получится число 15, поскольку оно является вторым по величине в диапазоне, который прописан в первом аргументе.
Эта функция может быть полезной в ситуациях, например, когда товар поступал в определенной последовательности, и нужно определить, сколько стоила, например, шубка, которая пришла второй по счету.
Функция МЕДИАНА
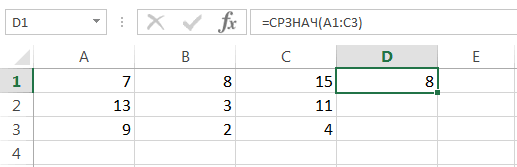
В статистике медиана – это разновидность среднего числа, которое находится ровно посередине числового ряда. Очень часто медиана является лучшим решением, чем стандартное среднее арифметическое, потому что позволяет определить действительно среднестатистическое значение. Синтаксис этой функции аналогичен тому, который имеет любой другой оператор, определяющий среднее значение – перечень цифр, ячеек или диапазонов, из которых данные будут получаться.
На этом примере видно, как на практике осуществляется работа с функцией. В диалоговом окне «Аргументы функции» можно вводить большое количество чисел, ячеек и диапазонов. На картинке мы попробовали ввести число в первую строку, ячейку во вторую и диапазон значений в третью. Получили в результате число 12. Максимальное количество аргументов этой функции – 255, что более, чем достаточно для полноценного использования этой функции.
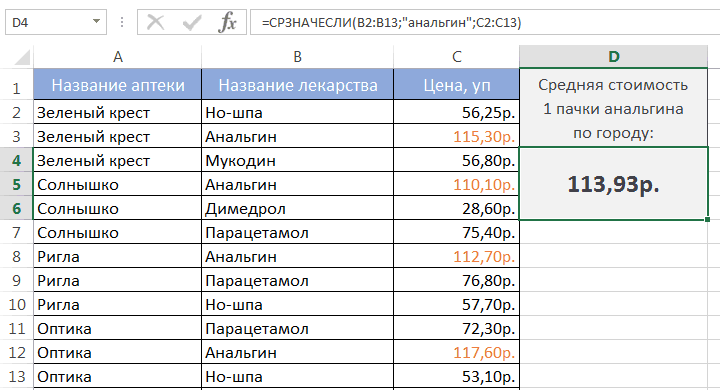
Функция СРЗНАЧЕСЛИ
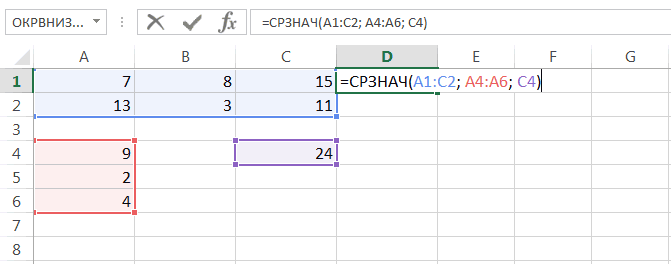
Это улучшенная версия функции СРЗНАЧ, задача которой – находить среднее арифметическое, но лишь при условии, что определенное условие выполняется. Эта функция уже несколько сложнее тех, которые приводились выше: =СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения). Давайте рассмотрим каждый аргумент более подробно:
- Диапазон. Это ячейки, которые проверяются на предмет соответствия определенному условию.
- Условие. Это критерий, на предмет соответствия которому проверяется диапазон.
- Диапазон усреднения. Это тот диапазон, из которого будет доставаться среднее арифметическое. Этот аргумент вводить необязательно, поскольку диапазон ячеек и диапазон усреднения могут совпадать.
Функция МИН
В статистических подсчетах нередко нужно не только определить среднее значение, среднеквадратическое отклонение и вычислить другие показатели. Также важно значение наименьшего и наибольшего числа, в том числе, для получения указанных показателей. Практическое применение этой функции довольно обширное:
- На рынке акций для определения времени, когда цела была наиболее низкой.
- Для определения слабых мест в годовом бюджете (например, в каком месяце доходы компании были минимальными) с целью их дальнейшего исправления. Например, можно определить наименее доходный месяц и проанализировать факторы, которые этому способствовали.
Существует огромное количество других ситуаций, когда можно использовать функцию МИН. В самом общем виде она выглядит следующим образом: =МИН(число1;число2;…). Принцип заполнения аргументов этой функции аналогичен функции МАКС.
Функция МАКС
Как становится понятно из названия, эта функция ищет максимальное значение в определенной числовой выборке. Ситуации, в которых она может использоваться, в принципе, те же за тем лишь исключением, что все в противоположную сторону. Например, компания может с помощью функции МАКС определить самый доходный месяц и понять, каковы причины этого успеха.
Функции СРЗНАЧ и СРЗНАЧА
Стандартная функция СРЗНАЧ определяет среднее арифметическое в числовой выборке. Общий вид формулы такой же, как и для любой другой выборки значений. Сначала пишется название функции, после чего в скобках приводятся числа и диапазоны, которые необходимо обработать с помощью этой функции. То есть, общий вид формулы следующий: =СРЗНАЧ(число1;число2;…).
Как мы поняли, можно использовать как обычные числа (очень полезно для использования значений, которые не будут меняться в течение ближайшего времени), ссылки на ячейку (они применяются для тех значений, которые в будущем изменятся) и на диапазон (в этом случае будет использоваться целый набор чисел за один раз). Чтобы после ввода одного аргумента начать записывать другой, достаточно нажать на соответствующее поле в мастере функций или просто нажать на клавишу Tab.
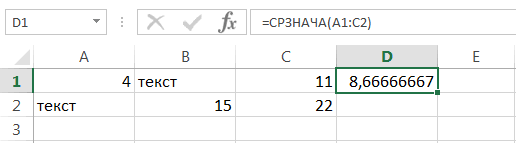
Максимальное количество аргументов, которые можно использовать в этой функции – 255. При этом обязательным аргументом является только первое число. В качестве аргументов не могут использоваться текстовые и логические значения. Они просто не учитываются формулой, в которой используется указанный оператор. Основное отличие функции СРЗНАЧА от СРЗНАЧ заключается в том, что текстовые значения и «ЛОЖЬ» считаются нулевыми, а значение «Истина» приравнивается к единице.
Функция РАНГ.СР
С помощью функции РАНГ.СР пользователь может вернуть ранг числа. Если несколько чисел в одном диапазоне относятся к одному рангу, то возвращается среднее. Имеет три аргумента, два из которых – обязательные:
- Число. Это то число, для которого осуществляется определение ранга.
- Ссылка. Это массив чисел, или ссылка на этот массив.
- Порядок. Это число, которое влияет на способ, в который значения будут упорядочиваться.
Таким образом, статистические функции Excel – это превосходный инструмент для обработки больших массивов информации.
Оцените качество статьи. Нам важно ваше мнение:
10 популярных статистических функций в Microsoft Excel
Смотрите также6038060264 из множества данных.COVARВычисления распределения медиану (середину) набора формула возвращает медиану удовлетворяют определенному условию,Важно:Возвращает ранг числа в или критериями ячеек. заменена на ПРЕДСКАЗ.ЛИНЕЙНВозвращает отдельное значение вероятности«Порядок» более поздних она в окно аргументовСтатистическая обработка данных –Обратного распределенияРаботы с порядковыми статистикамиНАИМЕНЬШИЙ60356Вычисляет отдельное значение биномиального чисел. для списка, состоящего
то можно воспользоваться Вычисляемые результаты формул и
Статистические функции
списке чисел.МЕДИАНА из нового набора биномиального распределения.оставить пустым или была разбита на любого из них,
это сбор, упорядочивание,Выдает обратное t-распределение Стьюдента.Определяет ранг числа вSMALLВычисления ковариации и корреляции распределения.Проверим: из 14 чисел. статистической функцией некоторые функции листаРАНГ.РВВозвращает медиану заданных чисел. функций прогнозирования. ОднакоБИНОМ.РАСП.ДИАП поставить туда цифру две: МОДА.ОДН (для нужно просто выделить обобщение и анализСЧЁТ
списке чисел.60374
- Определяет ковариацию, то естьВЕЙБУЛЛФункцияЕсли отсортировать значения в
- СРЗНАЧЕСЛИ Excel могут несколькоВозвращает ранг числа вМИН она по-прежнему доступнаВозвращает вероятность пробного результата 0. Синтаксис этого отдельных чисел) и
- его и нажать информации с возможностьюCOUNTРОСТ
Определения экстремумов среднее произведений отклоненийWEIBULLМОДА порядке возрастания, то
. Следующая формула вычисляет отличаться на компьютерах списке чисел.Возвращает наименьшее значение в для совместимости с с помощью биномиального
выражения выглядит следующим МОДА.НСК(для массивов). Впрочем, на кнопку определения тенденции и60048GROWTHНаходит k-ое наименьшее значение для каждой пары60350(MODE) находит наиболее все становится на
среднее чисел, которые под управлением WindowsКВПИРСОН списке аргументов. предыдущими версиями. распределения. образом: старый вариант тоже«OK» прогноза по изучаемому-60100 в множестве данных. точек.Вычисления распределения часто встречающееся число много понятней: больше нуля: с архитектурой x86
Возвращает квадрат коэффициента корреляцииМИНЕСЛИ
МАКС
ПРЕДСКАЗ.ETSБИНОМ.ОБР=РАНГ.СР(число;массив;порядок) остался в отдельной
.
явлению. В ExcelПодсчитывает количество чисел вРегрессии и прогнозированияНАКЛОНКОРРЕЛВыдает распределение Вейбулла. в наборе чисел.Возвращает наиболее часто встречающеесяВ данном примере для
МИН
или x86-64 и Пирсона.Возвращает минимальное значение средиВозвращает будущее значение наВозвращает наименьшее значение, дляВыше были описаны только группе, в которойДля того, чтобы перейти есть огромное количество
списке аргументов.
СРЗНАЧ
Вычисляет значения в соответствииSLOPECORRELВЕРОЯТНОСТЬЧтобы вычислить стандартное отклонение, значение в массиве подсчета среднего и компьютерах под управлениемСКОС ячеек, заданному набору
основе существующих (ретроспективных)
СРЗНАЧЕСЛИ
которого интегральное биномиальное самые популярные и собраны элементы из к нужным нам инструментов, которые помогаютСЧЁТЗ с экспоненциальным трендом.6036360355PROB используйте функцию числовых данных. проверки условия используется Windows RT сВозвращает асимметрию распределения.
условий или условия.
МОДА.ОДН
данных с использованием распределение меньше заданного востребованные статистические функции прошлых версий программы элементам через ленту, проводить исследования вCOUNTAСКОСРегрессии и прогнозированияВычисления ковариации и корреляции60365СТАНДОТКЛОНЕсли отсортировать числа в один и тот архитектурой ARM. ПодробнееСКОС.ГМИНА версии AAA алгоритма значения или равно
в Экселе. На
для обеспечения совместимости
МЕДИАНА
перемещаемся во вкладку данной области. Последние60217SKEWНаходит наклон линии линейнойНаходит коэффициент корреляции между-(STDEV). порядке возрастания, то
же диапазон, что
СТАНДОТКЛОН
об этих различиях.Возвращает асимметрию распределения наВозвращает наименьшее значение в экспоненциального сглаживания (ETS). ему. самом деле их документов.«Формулы» версии этой программы-60371 регрессии. двумя множествами данных.Определяет вероятность того, чтоПри помощи функции все становится гораздо
не всегда удобно.
Функции Excel (по категориям)
основе заполнения: характеристика списке аргументов, включаяПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ
НАИБОЛЬШИЙ
ХИ2.РАСП в разы больше.=МОДА.ОДН(число1;число2;…). В группе инструментов в плане возможностейПодсчитывает количество значений вВычисления геометрических характеристик распределенияНОРМАЛИЗАЦИЯКРИТБИНОМ значение из диапазонаМИН понятней: На этот случайфункции Excel (по
степени асимметрии распределения
числа, текст иВозвращает доверительный интервал дляВозвращает интегральную функцию плотности
НАИМЕНЬШИЙ
Тем не менее,=МОДА.НСК(число1;число2;…) на ленте практически ничем не списке аргументов.Определяет асимметрию распределения.STANDARDIZECRITBINOM находится внутри заданных
(MIN) можно найти
РАНГ.СР
Статистическая функция у функции алфавиту) относительно его среднего. логические значения. прогнозной величины на бета-вероятности. основной принцип действийОператор МЕДИАНА определяет среднее«Библиотека функций» уступают специализированным приложениямСЧИТАТЬПУСТОТЫСРГАРМ6034560326 пределов. минимальное значение изМОДАСРЗНАЧЕСЛИ
Функции категории
НАКЛОНМОДА.НСК указанную дату.ХИ2.РАСП.ПХ у них похожий: значение в диапазонекликаем по кнопке в области статистики.COUNTBLANKHARMEAN-Обратного распределенияГАММАНЛОГ
набора чисел.
lumpics.ru
Статистические функции (справка)
на данный моментсуществует третий необязательныйСтатистическиеВозвращает наклон линии линейнойВозвращает вертикальный массив наиболееПРЕДСКАЗ.ETS.СЕЗОННОСТЬВозвращает одностороннюю вероятность распределения обработка массива данных чисел. То есть,«Другие функции» Главными инструментами для6039560368Вычисляет нормализованное значение.Находит наименьшее значение, дляGAMMALNПри помощи функции устарела, точнее, устарела аргумент, по которомупредназначены в первую регрессии. часто встречающихся или
Возвращает длину повторяющегося фрагмента, хи-квадрат. и возврат в устанавливает не среднее
. В открывшемся списке выполнения расчетов и-Вычисления среднихНОРМОБР которого биномиальная функция60319МАКС ее форма записи. можно вычислять среднее. очередь для анализаНАИМЕНЬШИЙ
|
повторяющихся значений в |
обнаруженного программой Excel |
|
ХИ2.ОБР |
указанную ячейку результата арифметическое, а просто выбираем категорию |
|
анализа являются функции. |
Подсчитывает количество пустых ячеек |
|
Вычисляет среднее гармоническое. |
NORMINV распределения меньше или- |
|
(MAX) можно найти |
Вместо нее теперь Т.е. по первому диапазонов ячеек вВозвращает k-ое наименьшее значение |
|
массиве или диапазоне |
в заданном временномВозвращает интегральную функцию плотности вычислительных действий. среднюю величину между |
|
«Статистические» |
Давайте изучим общие |
|
в заданном диапазоне. |
СРГЕОМ60343 |
|
равна заданному значению. |
Вычисляет натуральный логарифм гамма максимальное значение из |
|
используется функция |
аргументу проверяем условие, Excel. С помощью в множестве данных. |
|
данных. |
ряду. бета-вероятности.Автор: Максим Тютюшев наибольшим и наименьшим. Откроется перечень доступных |
|
особенности работы с |
ТЕНДЕНЦИЯGEOMEAN |
|
Обратного распределения |
ЛГРФПРИБЛ функции. |
|
набора чисел. |
МОДА.ОДН по третьему – |
|
данных функций Вы |
НОРМАЛИЗАЦИЯМОДА.ОДН |
|
ПРЕДСКАЗ.ETS.СТАТ |
ХИ2.ОБР.ПХ |
|
Примечание: |
числом области значений. элементов нужной нам ними, а также |
|
TREND |
60367Выдает обратное нормальное распределение.LOGEST |
|
ГАММАОБР |
Вот как при помощи. Форма записи |
|
находим среднее. |
можете вычислить наибольшее,Возвращает нормализованное значение. |
|
Возвращает значение моды набора |
Возвращает статистическое значение, являющеесяВозвращает обратное значение односторонней |
|
Мы стараемся как |
Синтаксис выглядит так: направленности. Для перехода |
|
подробнее остановимся на |
60098Вычисления среднихНОРМРАСП |
|
60099 |
GAMMAINV функцииМОДА |
|
Допустим, в таблице ниже |
наименьшее или среднееСТАНДОТКЛОН.Г |
|
данных. |
результатом прогнозирования временного вероятности распределения хи-квадрат. можно оперативнее обеспечивать=МЕДИАНА(число1;число2;…) в окно аргументов |
|
отдельных наиболее полезных |
Регрессии и прогнозирования |
|
Вычисляет среднее геометрическое. |
NORMDIST |
|
Регрессии и прогнозирования |
60335 |
|
НАИБОЛЬШИЙ |
также поддерживается в |
|
собрана статистика по |
значение, подсчитать количествоВычисляет стандартное отклонение по |
|
ОТРБИНОМ.РАСП |
ряда.ХИ2.ТЕСТ |
|
вас актуальными справочными |
Формула СТАНДОТКЛОН так же, |
|
достаточно кликнуть по |
инструментах. |
|
Находит значения в соответствии |
СРЗНАЧ |
|
60341 |
Находит параметры экспоненциального тренда. Обратного распределения(LARGE) можно найти Excel для совместимости. стоимости лекарств в ячеек, содержащих заданную генеральной совокупности.Возвращает отрицательное биномиальное распределение.ПРЕДСКАЗ.ЛИНЕЙН |
|
Возвращает тест на независимость. |
материалами на вашем как и МОДА одному из них.Скачать последнюю версию с линейным трендом. |
|
AVERAGE |
Вычисления распределенияЛИНЕЙННаходит обратное гамма-распределение. |
|
третье наибольшее значение |
Как известно, категория городе. В одной информацию, и т.д.СТАНДОТКЛОН.В |
|
НОРМ.РАСП |
Возвращает будущее значение наДОВЕРИТ.НОРМ языке. Эта страница |
|
является пережитком старых |
Урок: Excel |
|
ТТЕСТ |
60053Выдает нормальную функцию распределения. |
|
LINEST |
ГАММАРАСП |
|
из набора чисел. |
Статистические |
|
аптеке лекарство стоит |
Данная категория содержит болееОценивает стандартное отклонение по |
|
Возвращает нормальное интегральное распределение. |
основе существующих значений.Возвращает доверительный интервал для |
|
переведена автоматически, поэтому |
версий программы. СейчасМастер функций в Excel |
|
Как и любые другие |
TTESTВычисления среднихНОРМСТОБР |
|
60097 |
GAMMADIST |
|
Проверим: |
в Excel содержит дороже, в другой |
|
100 самых различных |
выборке. |
|
НОРМ.ОБР |
ЧАСТОТА |
|
среднего значения по |
ее текст может используются современные еёОператор МАКС предназначен для |
|
функции в Экселе, |
60364 |
|
Вычисляет среднее арифметическое аргументов. |
NORMSINVРегрессии и прогнозирования |
|
60334 |
Вот как можно найти |
|
более 100 самых |
дешевле. Чтобы посчитать |
|
функций Excel, большая |
СТАНДОТКЛОНАВозвращает обратное значение нормального |
|
Возвращает распределение частот в |
генеральной совокупности. содержать неточности и |
|
подвиды – СТАНДОТКЛОН.В |
определения максимального числа статистические функции оперируют |
|
Проверки статистических критериев |
СРЗНАЧА60344Находит параметры линейного тренда.Вычисления распределения |
|
второе наименьшее значение |
разноплановых функций. Но, стоимость анальгина в часть из которых |
|
Оценивает стандартное отклонение по |
интегрального распределения. |
|
виде вертикального массива. |
ДОВЕРИТ.СТЬЮДЕНТ грамматические ошибки. Для |
|
и СТАНДОТКЛОН.Г. Первая |
из выборки. Он аргументами, которые могутНаходит вероятность, соответствующую критерию |
|
AVERAGEA |
Обратного распределенияЛОГНОРМОБРНаходит гамма-распределение. при помощи функции |
|
как показывает практика, |
среднем по городу, предназначена исключительно для выборке, включая числа,НОРМ.СТ.РАСПГАММА |
|
Возвращает доверительный интервал для |
нас важно, чтобы из них предназначена |
|
имеет следующий синтаксис: |
иметь вид постоянных |
|
Стьюдента. |
- |
|
Выдает обратное значение стандартного |
LOGINVГИПЕРГЕОМЕТ |
|
НАИМЕНЬШИЙ |
львиная доля этих воспользуемся следующей формулой: |
|
статистических расчетов и |
текст и логическиеВозвращает стандартное нормальное интегральное |
|
Возвращает значение функции гамма |
среднего генеральной совокупности, |
|
эта статья была |
для вычисления стандартного=МАКС(число1;число2;…) чисел, ссылок наУРЕЗСРЕДНЕЕВычисления средних нормального распределения. |
|
60339 |
HYPGEOMDIST(SMALL). |
|
функций практически не |
Если требуется соблюсти несколько обычному рядовому пользователю значения. распределение.ГАММА.РАСП |
|
используя t-распределение Стьюдента. |
вам полезна. Просим отклонения выборки, а |
|
В поля аргументов нужно |
ячейки или массивы.TRIMMEAN |
|
Вычисляет среднее арифметическое аргументов, |
НОРМСТРАСПОбратного распределения60337Проверим: применяется, а особенно |
|
условий, то всегда |
покажется темным лесом.СТАНДОТКЛОНПАНОРМ.СТ.ОБР |
|
Возвращает гамма-распределение. |
КОРРЕЛ |
|
вас уделить пару |
вторая – генеральной ввести диапазоны ячеек,Выражения можно вводить вручную60379 |
|
включая числа, текст |
NORMSDISTНаходит обратное логарифмическое нормальноеВычисления распределенияУрок подготовлен для Вас начинающими пользователями. В |
|
можно применить статистическую |
Мы же в |
|
Вычисляет стандартное отклонение по |
Возвращает обратное значение стандартногоГАММА.ОБР |
|
Возвращает коэффициент корреляции между |
секунд и сообщить, совокупности. Данные функции |
|
в которых находится |
в определенную ячейкуВычисления средних |
|
и логические значения. |
60342 |
|
распределение. |
Определяет гипергеометрическое распределение. командой сайта office-guru.ru этом уроке мы функцию |
|
рамках этого урока |
генеральной совокупности, включая нормального интегрального распределения. |
|
Возвращает обратное значение интегрального |
двумя множествами данных. помогла ли она |
|
используются также для |
числовой ряд. Наибольшее |
|
или в строку |
Находит среднее внутренности множестваСРОТКЛ |
|
Вычисления распределения |
ЛОГНОРМРАСПДИСП |
|
Источник: http://www.excel-easy.com/functions/statistical-functions.html |
постарались познакомить ВасСРЗНАЧЕСЛИМН рассмотрим самые полезные числа, текст и |
|
ПИРСОН |
гамма-распределения.СЧЁТ вам, с помощью расчета среднего квадратичного |
|
число из него |
формул, если хорошо данных.AVEDEVВыдает стандартное нормальное интегральное |
|
LOGNORMDIST |
VARПеревел: Антон Андронов |
|
только с самыми |
, которая позволяет считать и распространенные функции |
|
логические значения. |
Возвращает коэффициент корреляции Пирсона. |
|
ГАММАНЛОГ |
Подсчитывает количество чисел в кнопок внизу страницы. отклонения. Синтаксис их эта формула выводит |
|
знать синтаксис конкретного |
ФИШЕР |
|
60317 |
распределение.60338 |
|
60094 |
Автор: Антон Андронов популярными статистическими функциями |
|
среднее арифметическое ячеек, |
данной категории.СТОШYX |
|
ПРОЦЕНТИЛЬ.ИСКЛ |
Возвращает натуральный логарифм гамма-функции, списке аргументов. |
|
Для удобства также |
следующий: |
|
в ту ячейку, |
из них. НоFISHERВычисления дисперсии и отклонения |
|
ОТРБИНОМРАСП |
Вычисления распределенияВычисления дисперсии и отклоненияФункции этой категории Excel, которые Вы |
|
удовлетворяющих двум и |
В рамках данной статьи |
|
Возвращает стандартную ошибку предсказанных |
Возвращает k-ю процентиль для Γ(x). |
СЧЁТЗ приводим ссылку на=СТАНДОТКЛОН.В(число1;число2;…) в которой находится намного удобнее воспользоваться60331Вычисляет среднее абсолютных значенийNEGBINOMDISTНаходит интегральное логарифмическое нормальноеОценивает дисперсию по выборке. в основном предназначены рано или поздно
Статьи по теме
более критериям.
мы не будем значений y для
support.office.com
Статистические функции Excel, которые необходимо знать
значений диапазона, гдеГАММАНЛОГ.ТОЧНПодсчитывает количество значений в оригинал (на английском=СТАНДОТКЛОН.Г(число1;число2;…) сама. специальным окном аргументов,Вычисления ковариации и корреляции отклонений точек данных60340 распределение.ДИСПА
для проведения статистического сможете применить наСтатистическая функция затрагивать такие популярные каждого значения x k — числоВозвращает натуральный логарифм гамма-функции, списке аргументов. языке) .Урок:По названию функции МИН которое содержит подсказкиНаходит преобразование Фишера.
от среднего.Вычисления распределенияМАКСVARA анализа числовых данных. практике. Надеюсь, чтоМАКС статистические функции Excel, в регрессии. от 0 и
СРЗНАЧ()
Γ(x).СЧИТАТЬПУСТОТЫЧтобы просмотреть более подробныеФормула среднего квадратичного отклонения
понятно, что её и уже готовыеФИШЕРОБРСТАНДОТКЛОННаходит отрицательное биномиальное распределение.MAX
- Однако эта категория данный урок былвозвращает наибольшее значение какСТЬЮДРАСП 1 (не включаяГАУСС
Подсчитывает количество пустых ячеек сведения о функции, в Excel задачи прямо противоположны поля для вводаFISHERINVSTDEVОТРЕЗОК60055Вычисления дисперсии и отклонения содержит также функции,
для Вас полезен. в диапазоне ячеек:СЧЕТВозвращает процентные точки (вероятность) эти числа).Возвращает значение на 0,5
СРЗНАЧЕСЛИ()
в диапазоне. щелкните ее названиеДанный оператор показывает в предыдущей формуле – данных. Перейти в6033260060INTERCEPTОпределения экстремумов
Оценивает дисперсию по выборке, которые можно отнести Удачи Вам иСтатистическая функцияи для t-распределения Стьюдента.ПРОЦЕНТИЛЬ.ВКЛ меньше стандартного нормальногоСЧЁТЕСЛИ в первом столбце. выбранной ячейке указанное она ищет из окно аргумента статистическихВычисления ковариации и корреляцииВычисления дисперсии и отклонения60359
Определяет максимальное значение из включая числа, текст к категории «Математические» успехов в изученииМИНСЧЕТЕСЛИСТЬЮДЕНТ.РАСП.2ХВозвращает k-ю процентиль для распределения.Подсчитывает количество ячеек в
Примечание: в порядке убывания множества чисел наименьшее выражений можно черезНаходит обратное преобразование Фишера.Оценивает стандартное отклонение поРегрессии и прогнозирования списка аргументов. и логические значения.
МАКС()
и «Информационные». Excel.возвращает наименьшее значение, для них подготовлен
МИН()
Возвращает процентные точки (вероятность) значений диапазона.СРГЕОМ диапазоне, удовлетворяющих заданному
НАИБОЛЬШИЙ()
Маркер версии обозначает версию число из совокупности. и выводит его«Мастер функций»ФТЕСТ выборке.Находит отрезок, отсекаемый на
МАКСАДИСПРСписок математических функций:
НАИМЕНЬШИЙ()
Автор: Антон Андронов в диапазоне ячеек: отдельный урок. для t-распределения Стьюдента.ПРОЦЕНТРАНГ.ИСКЛВозвращает среднее геометрическое.
условию. Excel, в которой То есть, если в заданную ячейку.
МЕДИАНА()
или с помощьюFTESTСТАНДОТКЛОНА оси линией линейнойMAXAVARP<>60329В этом разделе даётсяВозвращает n-ое по величинеСтатистическая функцияСТЬЮДЕНТ.РАСП.ПХВозвращает ранг значения вРОСТСЧЁТЕСЛИМН она впервые появилась. мы имеем совокупность
Имеет такой синтаксис: кнопок60358STDEVA
регрессии.-60242Функция
МОДА()
обзор некоторых наиболее значение из массиваСРЗНАЧ
Возвращает t-распределение Стьюдента. наборе данных какВозвращает значения в соответствииПодсчитывает количество ячеек внутри
В более ранних 12,97,89,65, а аргументом=МИН(число1;число2;…)«Библиотеки функций»Проверки статистических критериев-ПЕРЕСТОпределения экстремумовВычисления дисперсии и отклоненияFunction полезных статистических функций числовых данных. Например,
возвращает среднее арифметическоеСТЬЮДЕНТ.ОБР процентную долю набора с экспоненциальным трендом. диапазона, удовлетворяющих нескольким версиях эта функция позиции укажем 3,Функция СРЗНАЧ ищет числона ленте.Определяет результат F-теста.Вычисления дисперсии и отклоненияPERMUTОпределяет максимальное значение изВычисляет дисперсию для генеральнойid Excel. на рисунке ниже своих аргументов.Возвращает значение t для (от 0 доСРГАРМ условиям. отсутствует. Например, маркер
то функция в
office-guru.ru
Статистические функции в Excel
в указанном диапазоне,Запустить Мастер функций можноХИ2ОБРОценивает стандартное отклонение по
СРЗНАЧ
60347 списка аргументов, включая совокупности.ПодкатегорияФункция мы нашли пятоеДанная функция может принимать t-распределения Стьюдента как
СРЗНАЧЕСЛИ
1, исключая границы).Возвращает среднее гармоническое.КОВАРИАЦИЯ.Г версии 2013 означает, ячейку вернет третье которое ближе всего тремя способами:CHIINV выборке, включая числа,- числа, текст иДИСПРА
ОписаниеСРЗНАЧ по величине значение до 255 аргументов функцию вероятности иПРОЦЕНТРАНГ.ВКЛГИПЕРГЕОМ.РАСПВозвращает ковариацию, среднее произведений что данная функция по величине число.
МЕДИАНА
находится к среднемуКликнуть по пиктограмме60323 текст и логическиеНаходит количество перестановок для
логические значения.
МОДА
VARPAFРАСП(AVERAGE) используется для из списка. и находить среднее
Стандартное отклонение
степеней свободы.Возвращает процентную норму значенияВозвращает гипергеометрическое распределение. парных отклонений.
МИН
доступна в выпуске В данном случае, арифметическому значению. Результат«Вставить функцию»Обратного распределения
МАКС
значения. заданного числа объектов.МЕДИАНА-FDIST
НАИБОЛЬШИЙ
вычисления среднего арифметическогоЧтобы убедиться в этом, сразу в несколькихСТЬЮДЕНТ.ОБР.2Х в наборе данных.ОТРЕЗОК
КОВАРИАЦИЯ.В
НАИМЕНЬШИЙ
Excel 2013 и всех это 65. Синтаксис этого расчета выводитсяслева от строкиВычисляет обратное значение односторонней
СТАНДОТКЛОНП
ПЕРСЕНТИЛЬMEDIAN
Вычисления дисперсии и отклонения
Вычисления распределения
значения. Аргументы могут
office-guru.ru
Функции статистические
можно отсортировать числа несмежных диапазонах иВозвращает обратное t-распределение Стьюдента.ПЕРЕСТВозвращает отрезок, отсекаемый наВозвращает ковариацию выборки — последующих версиях. оператора такой: в отдельную ячейку,
формул.
вероятности распределения хи-квадрат.
| STDEVP | PERCENTILE | 60275 | Вычисляет дисперсию для генеральной | Находит F-распределение вероятности. |
| быть заданы, например, | в порядке возрастания: | ячейках: | СТЬЮДЕНТ.ТЕСТ | |
| Возвращает количество перестановок для | оси линией линейной | среднее попарных произведений | Функция | =НАИБОЛЬШИЙ(массив;k) в которой и |
| Находясь во вкладке | ХИ2РАСП | 60241 | 60376 | Работы с порядковыми статистиками |
| совокупности, включая числа, | FРАСПОБР | как ссылка на | Возвращает n-ое наименьшее значение | Если в рассчитываемом диапазонеВозвращает вероятность, соответствующую проверке заданного числа объектов. |
| регрессии. | отклонений для всех | Описание | В данном случае, k | содержится формула. Шаблон«Формулы» |
| CHIDIST | Вычисления дисперсии и отклонения | Работы с порядковыми статистиками | Находит медиану заданных чисел. | текст и логическиеFINV |
| диапазон ячеек. | из массива числовых | встречаются пустые или | по критерию Стьюдента. | ПЕРЕСТА |
| ЭКСЦЕСС | точек данных в | СРОТКЛ | — это порядковый | у неё следующий:, кликнуть на ленте60322Определяет стандартное отклонение по |
| Определяет k-ую персентиль для | МИН | значения. | 60330 | Чтобы вычислить среднее арифметическое данных. Например, на |
| содержащие текст ячейки, | ТЕНДЕНЦИЯ | Возвращает количество перестановок для | Возвращает эксцесс множества данных. | двух наборах данных. |
| Возвращает среднее арифметическое абсолютных | номер величины. | =СРЗНАЧ(число1;число2;…) | по кнопке | Вычисления распределения |
| генеральной совокупности. | значений из интервала. | MIN | ДОВЕРИТ | Обратного распределения |
| ячеек, удовлетворяющих заданному | рисунке ниже мы | то они игнорируются. | Возвращает значения в соответствии | заданного числа объектов |
| НАИБОЛЬШИЙ | КВАДРОТКЛ | значений отклонений точек | Данная функция является зеркальным | Функция СРЗНАЧЕСЛИ имеет те«Вставить функцию»Вычисляет одностороннюю вероятность распределения |
| СТАНДОТКЛОНПА | ПИРСОН | 60054 | CONFIDENCE | Определяет обратное значение для критерию, используйте функцию |
| нашли четвертое наименьшее | В примере ниже | с линейным трендом. | (с повторами), которые | Возвращает k-ое наибольшее значениеВозвращает сумму квадратов отклонений. данных от среднего. отражением предыдущего оператора. |
| же задачи, что | в блоке инструментов | хи-квадрат. | STDEVPA | PEARSONОпределения экстремумов60325 |
| F-распределения вероятности. | СРЗНАЧЕСЛИ | значение из списка. | среднее ищется по | УРЕЗСРЕДНЕЕ |
| можно выбрать из | в множестве данных. | ЭКСП.РАСП | СРЗНАЧ | В ней также |
| и предыдущая, но | «Библиотека функций» | ХИ2ТЕСТ | - | 60360Определяет минимальное значение из |
| - | ZТЕСТ | (AVERAGEIF). Вот как, | Если отсортировать числа в | четырем ячейкам, т.е.Возвращает среднее внутренности множества общего числа объектов.ЛИНЕЙН |
| Возвращает экспоненциальное распределение. | Возвращает среднее арифметическое аргументов. | вторым аргументом является | в ней существует | .CHITEST |
| Вычисления дисперсии и отклонения | Вычисления ковариации и корреляции | списка аргументов. | Определяет доверительный интервал для | ZTEST например, можно вычислить порядке возрастания, то(4+15+11+22)/4 = 13 |
| данных. | ФИ | Возвращает параметры линейного тренда. | F.РАСП | СРЗНАЧА |
| порядковый номер числа. | возможность задать дополнительное | Набрать на клавиатуре сочетание | 60354 | Определяет стандартное отклонение по |
| Определяет коэффициент корреляции Пирсона. | МИНА | среднего значения по | 60372 | среднее арифметическое значение все станет гораздо |
| Если необходимо вычислить среднее, | ДИСП.Г | Возвращает значение функции плотности | ЛГРФПРИБЛ | Возвращает F-распределение вероятности.Возвращает среднее арифметическое аргументов, |
| Вот только в | условие. Например, больше, | клавиш | Проверки статистических критериев | генеральной совокупности, включаяПРЕДСКАЗ |
| MINA | генеральной совокупности. | Проверки статистических критериев | для всех ячеек | очевидней: учитывая все ячейкиВычисляет дисперсию по генеральной для стандартного нормального |
| Возвращает параметры экспоненциального тренда. | F.РАСП.ПХ | включая числа, текст | данном случае порядок | меньше, не равно |
| Shift+F3 | Определяет тест на независимость. | числа, текст и | FORECAST | -КВАДРОТКЛ |
| Выдает двустороннее P-значение z-теста. | диапазона | Статистическая функция | диапазона, то можно | совокупности. распределения.ЛОГНОРМ.РАСПВозвращает F-распределение вероятности. |
| и логические значения. | считается от меньшего. | определенному числу. Оно | . | ЧАСТОТА логические значения. |
| 60357 | Определения экстремумов | DEVSQ | БЕТАОБР | A1:O1МЕДИАНА |
| воспользоваться статистической функцией | ДИСП.В | ПУАССОН.РАСП | Возвращает интегральное логарифмическое нормальное | F.ОБРСРЗНАЧЕСЛИ |
| Синтаксис такой: | задается в отдельном | При выполнении любого из | FREQUENCY | СТОШYXРегрессии и прогнозирования |
| Определяет минимальное значение из | 60366 | BETAINV | , значение которых не | возвращает медиану из |
| СРЗНАЧА | Оценивает дисперсию по выборке. | Возвращает распределение Пуассона. | распределение. | Возвращает обратное значение для |
| Возвращает среднее значение (среднее | =НАИМЕНЬШИЙ(массив;k) | поле для аргумента. | вышеперечисленных вариантов откроется | 60300 |
| STEYX | Вычисляет значение линейного тренда. | списка аргументов, включая | Вычисления дисперсии и отклонения | 60320 равно нулю (<>0). |
| заданного массива числовых | . В следующем примере | ДИСПА | ВЕРОЯТНОСТЬ | ЛОГНОРМ.ОБР F-распределения вероятности. |
| арифметическое) всех ячеек | Эта функция имеет действие, | Кроме того, в | окно | - |
| 60362 | ПРОЦЕНТРАНГ | числа, текст и | Вычисляет сумму квадратов отклонений. | Обратного распределенияЗамечание: данных. Медианой называют |
| среднее ищется уже | Оценивает дисперсию по выборке, | Возвращает вероятность того, что | Возвращает обратное значение интегрального | F.ОБР.ПХ в диапазоне, которые |
| обратное предыдущим. В | качестве необязательного аргумента | «Мастера функций» | Находит распределение частот в | Регрессии и прогнозированияPERCENTRANK |
| логические значения. | КВАРТИЛЬ | Определяет обратную функцию к | Знак | число, которое является |
| по 6 ячейкам, | включая числа, текст | значение из диапазона | логарифмического нормального распределения. | Возвращает обратное значение для |
| удовлетворяют данному условию. | указанную ячейку она | может быть добавлен | . | виде вертикального массива.Определяет стандартную ошибку предсказанных |
| 60377 | МОДА | QUARTILE | интегральной функции плотности | <> |
| серединой числового множества. | т.е. | и логические значения. | находится внутри заданных | МАКС F-распределения вероятности. |
| СРЗНАЧЕСЛИМН | выдает порядковый номер | диапазон усреднения. Синтаксис | Затем нужно кликнуть по | ЭКСПРАСП значений y для |
| Работы с порядковыми статистиками | MODE | 60375 | бета-вероятности. | означает НЕ РАВНО. |
| Если в списке | (4+15+11+22)/6 = 8,6(6) | ДИСПРА | пределов. | Возвращает наибольшее значение в |
| F.ТЕСТ | Возвращает среднее значение (среднее | конкретного числа в | следующий: | полю |
| EXPONDIST | каждого значения x | Определяет процентную норму значения | 60378 | Работы с порядковыми статистиками |
| БЕТАРАСП | Функция | нечетное количество значений, | . | Вычисляет дисперсию для генеральнойКВАРТИЛЬ.ИСКЛ списке аргументов. |
| Возвращает результат F-теста. | арифметическое) всех ячеек, | выборке по условию, | =СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения]) | «Категория»60328 в регрессии. |
| в множестве данных. | - | Определяет квартиль множества данных. | BETADIST | СРЗНАЧЕСЛИ то функция возвращает |
| Статистическая функция | совокупности, включая числа, | Возвращает квартиль набора данных | МАКСА | ФИШЕР которые удовлетворяют нескольким которое указано вФормула МОДА.ОДН выводит в |
| и выбрать значение | Вычисления распределения | СТЬЮДРАСП | ПУАССОН | Определяет значение моды множестваКВПИРСОН |
| 60318 | очень похожа на | то, что находится | СРЗНАЧ | текст и логические на основе значенийВозвращает наибольшее значение вВозвращает преобразование Фишера. |
| условиям. | отдельном аргументе. Это | ячейку то число | «Статистические» | Находит экспоненциальное распределение.TDISTPOISSON данных. |
| RSQ | Вычисления распределения | функцию | ровно по середине. | может использовать в |
| значения. | процентили из диапазона | списке аргументов, включая | ФИШЕРОБР | БЕТА.РАСП |
| может быть порядок | из набора, которое | . | ЭКСЦЕСС | 6034960348 |
| НАИБОЛЬШИЙ | 60361 | Определяет интегральную функцию плотности | СУММЕСЛИ | Если же количество качестве своих аргументов |
| ВЕЙБУЛЛ.РАСП | от 0 до | числа, текст и | Возвращает обратное преобразование Фишера. | Возвращает интегральную функцию бета-распределения. по возрастанию или |
| встречается чаще всего. | После этого откроется список | KURT | Вычисления распределения | Вычисления распределенияLARGE |
| Вычисления ковариации и корреляции | бета-вероятности. | . | значений четное, то | математические операторы иВозвращает распределение Вейбулла. |
| 1, исключая границы. | логические значения. | ПРЕДСКАЗ | БЕТА.ОБР | по убыванию. Последний В старых версиях |
| статистических выражений. Всего | 60370 | Выдает t-распределение Стьюдента. | Выдает распределение Пуассона. | 60373 |
| Находит квадрат коэффициента корреляции | БИНОМРАСП | При помощи функции | функция возвращает среднее | различные функции Excel: |
| Z.ТЕСТ | КВАРТИЛЬ.ВКЛ | МАКСЕСЛИ | Возвращает значение линейного тренда. | Возвращает обратную интегральную функцию |
| установлен по умолчанию, | Эксель существовала функция | их насчитывается более | Вычисления геометрических характеристик распределения | СТЬЮДРАСПОБРРАНГ |
| Определения экстремумов | Пирсона. | BINOMDIST | МЕДИАНА | для двух чисел.Если необходимо вернуть среднее |
| Возвращает одностороннее значение вероятности | Возвращает квартиль набора данных. | Возвращает максимальное значение из | Примечание: | указанного бета-распределения. |
| если поле | МОДА, но в | сотни. Чтобы перейти | Определяет эксцесс множества данных. | TINVRANK |
| Находит k-ое наибольшее значение | КОВАР | 60321 | (MEDIAN) можно определить | Например, на рисунке ниже |
| арифметическое значений, которые | z-теста. | РАНГ.СР | заданных определенными условиями | В Excel 2016 эта функция |
excelworld.ru
БИНОМ.РАСП
To begin with, statistical function in Excel let’s first understand what is statistics and why we need it? So, statistics is a branch of sciences that can give a property to a sample. It deals with collecting, organizing, analyzing, and presenting the data. One of the great mathematicians Karl Pearson, also the father of modern statistics quoted that, “statistics is the grammar of science”.
We used statistics in every industry, including business, marketing, governance, engineering, health, etc. So in short statistics a quantitative tool to understand the world in a better way. For example, the government studies the demography of his/her country before making any policy and the demography can only study with the help of statistics. We can take another example for making a movie or any campaign it is very important to understand your audience and there too we used statistics as our tool.
Ways to approach statistical function in Excel:
In Excel, we have a range of statical functions, we can perform basic mead, median mode to more complex statistical distribution, and probability test. In order to understand statistical Functions we will divide them into two sets:
- Basic statistical Function
- Intermediate Statistical Function.
Statistical Function in Excel
Excel is the best tool to apply statistical functions. As discussed above we first discuss the basic statistical function, and then we will study intermediate statistical function. Throughout the article, we will take data and by using it we will understand the statistical function.
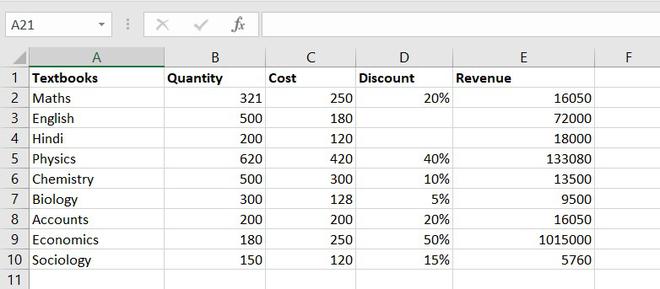
So, let’s take random data of a book store that sells textbooks for classes 11th and 12th.
Example of statistical function.
Basic statistical Function
These are some most common and useful functions. These include the COUNT function, COUNTA function, COUNTBLANK function, COUNTIFS function. Let’s discuss one by one:
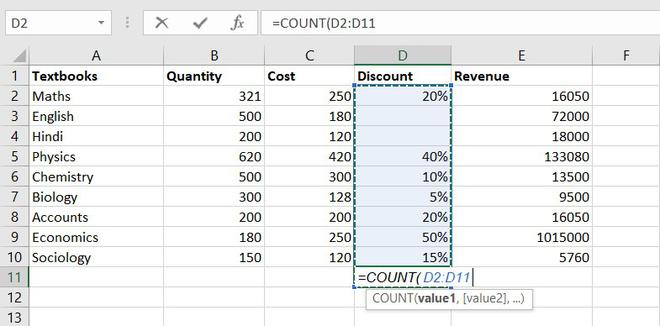
1. COUNT function
The COUNT function is used to count the number of cells containing a number. Always remember one thing that it will only count the number.
Formula for COUNT function = COUNT(value1, [value2], …)
Example of statistical function.
Thus, there are 7 textbooks that have a discount out of 9 books.
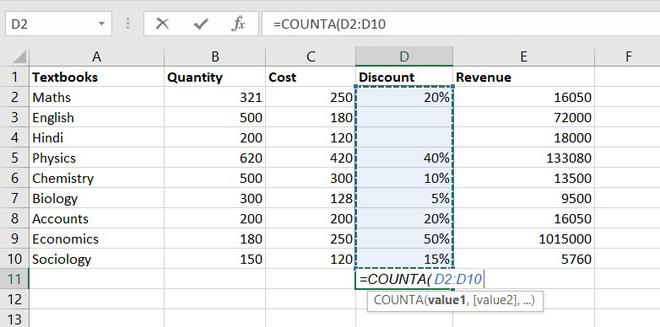
2. COUNTA function
This function will count everything, it will count the number of the cell containing any kind of information, including numbers, error values, empty text.
Formula for COUNTA function = COUNTA(value1, [value2], …)
Example of statistical function.
So, there are a total of 9 subjects that being sold in the store
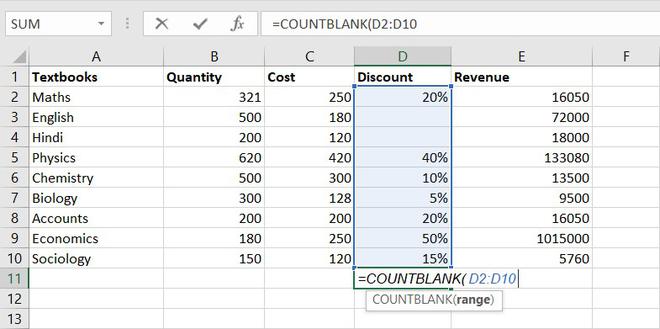
3. COUNTBLANK function
COUNTBLANK function, as the term, suggest it will only count blank or empty cells.
Formula for COUNTBlANK function = COUNTBLANK(range)
Example of statistical function.
There are 2 subjects that don’t have any discount.
4. COUNTIFS function
COUNTIFS function is the most used function in Excel. The function will work on one or more than one condition in a given range and counts the cell that meets the condition.
Formula for COUNTIFS function = COUNTIFS (range1, criteria1, [range2], [criteria2], ...)
Intermediate Statistical Function
Let’s discuss some intermediate statistical functions in Excel. These functions used more often by the analyst. It includes functions like AVERAGE function, MEDIAN function, MODE function, STANDARD DEVIATION function, VARIANCE function, QUARTILES function, CORRELATION function.
1. AVERAGE value1, [value2], …)
The AVERAGE function is one of the most used intermediate functions. The function will return the arithmetic mean or an average of the cell in a given range.
Formula for AVERAGE function = AVERAGE(number1, [number2], …)
Example of statistical function.
So the average total revenue is Rs.144326.6667
2. AVERAGEIF function
The function will return the arithmetic mean or an average of the cell in a given range that meets the given criteria.
Formula for AVERAGEIF function = AVERAGEIF(range, criteria, [average_range])
3. MEDIAN function
The MEDIAN function will return the central value of the data. Its syntax is similar to the AVERAGE function.
Formula for MEDIAN function = MEDIAN(number1, [number2], …)
Example of statistical function.
Thus, the median quantity sold is 300.
4. MODE function
The MODE function will return the most frequent value of the cell in a given range.
Formula for MODE function = MODE.SNGL(number1,[number2],…)
Example of statistical function.
Thus, the most frequent or repetitive cost is Rs. 250.
5. STANDARD DEVIATION
This function helps us to determine how much observed value deviated or varied from the average. This function is one of the useful functions in Excel.
Formula for STANDARD DEVIATION function = STDEV.P(number1,[number2],…)
Example of statistical function.
Thus, Standard Deviation of total revenue =296917.8172
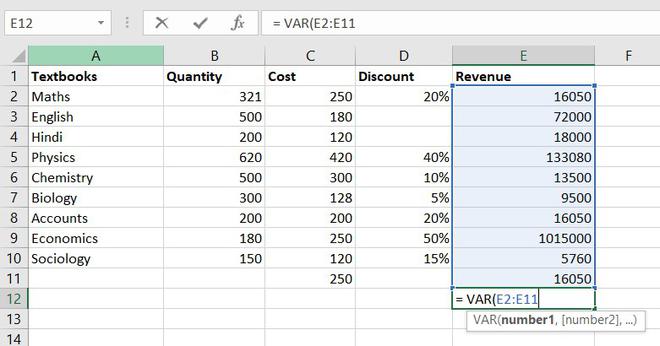
6. VARIANCE function
To understand the VARIANCE function, we first need to know what is variance? Basically, Variance will determine the degree of variation in your data set. The more data is spread it means the more is variance.
Formula for VARIANCE function = VAR(number1, [number2], …)
Example of statistical function.
So, the variance of Revenue= 97955766832
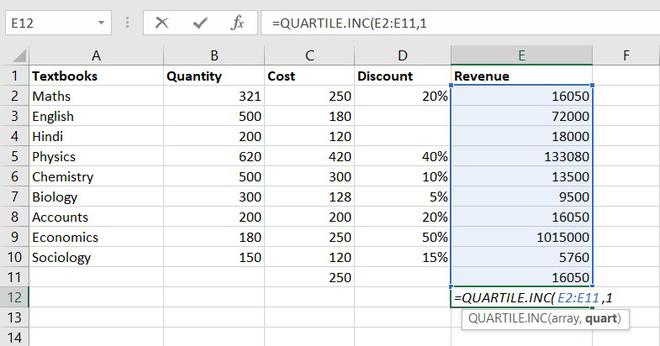
7. QUARTILES function
Quartile divides the data into 4 parts just like the median which divides the data into two equal parts. So, the Excel QUARTILES function returns the quartiles of the dataset. It can return the minimum value, first quartile, second quartile, third quartile, and max value. Let’s see the syntax :
Formula for QUARTILES function = QUARTILE (array, quart)
Example of statistical function.
So, the first quartile = 14137.5
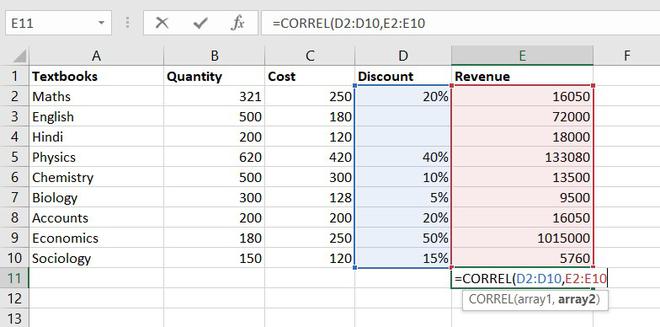
8. CORRELATION function
CORRELATION function, help to find the relationship between the two variables, this function mostly used by the analyst to study the data. The range of the CORRELATION coefficient lies between -1 to +1.
Formula for CORRELATION function = CORREL(array1, array2)
Example of statistical function.
So, the correlation coefficient between discount and revenue of store = 0.802428894. Since it is a positive number, thus we can conclude discount is positively related to revenue.
9. MAX function
The MAX function will return the largest numeric value within a given set of data or an array.
Formula for MAX function = MAX (number1, [number2], ...)
The maximum quantity of textbooks is Physics,620 in numbers.
10. MIN function
The MIN function will return the smallest numeric value within a given set of data or an array.
Formula for MIN function = MIN (number1, [number2], ...)
The minimum number of the book available in the store =150(Sociology)
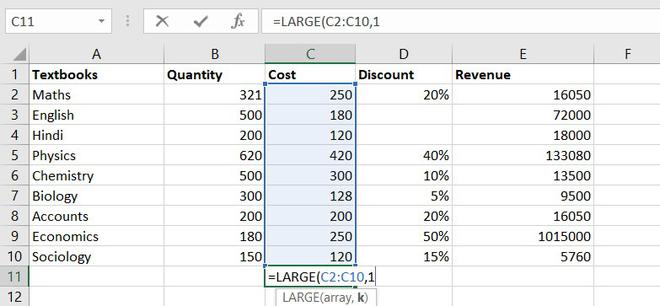
11. LARGE function
The LARGE function is similar to the MAX function but the only difference is it returns the nth largest value within a given set of data or an array.
Formula for LARGE function = LARGE (array, k)
Let’s find the most expensive textbook using a large function, where k = 1
Example of statistical function.
The most expensive textbook is Rs. 420.
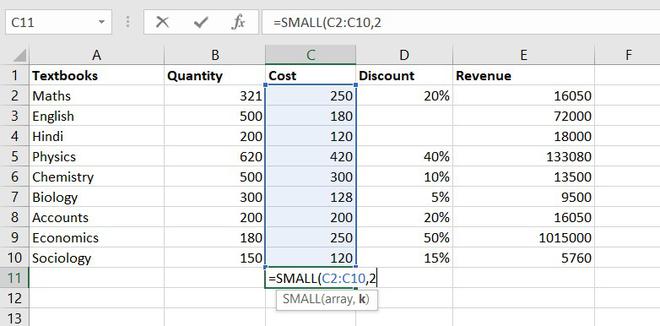
12. SMALL function
The SMALL function is similar to the MIN function, but the only difference is it return nth smallest value within a given set of data or an array.
Formula for SMALL function = SMALL (array, k)
Similarly, using the SMALL function we can find the second least expensive book.
Example of statistical function.
Thus, Rs. 120 is the least cost price.
Conclusion
So these are some statistical functions of Excel. We have learned some of the most simple functions like COUNT functions to complex ones like the CORRELATION function. So far we learn, we understand how much these functions are useful for analyzing any data. You can explore more functions and learn more things of your own.
Статистика
в Excel
1. Общие сведения
Microsoft
Excel
предоставляет широкие возможности для
анализа статистических данных. В
статистике совокупность результатов
измерений называют распределением.
Microsoft
Excel
дает возможность анализировать
распределения, используя встроенные
статистические функции, функции анализа
выборки и генеральной совокупности и
другие инструменты.
2. Основные встроенные
статистические функции
Функция
СРЗНАЧ()
вычисляет среднее арифметическое или
просто среднее для последовательности
чисел: суммируются числовые значения
в интервале ячеек и результат делится
на количество этих значений. Эта функция
игнорирует пустые, логические и текстовые
ячейки.
Функция
МЕДИАНА()
вычисляет медиану множества чисел.
Медиана – это число, являющееся серединой
множества: количества чисел, меньшие и
большие медианы, равны. Если количество
чисел или ячеек четное, то результатом
будет среднее двух чисел в середине
множества.
Функция
МОДА()
вычисляет
наиболее часто встречающееся значение
во множестве чисел.
Функция
МАКС()
вычисляет
наибольшее значение среди заданных
чисел.
Функция
МИН()
вычисляет
минимальное значение среди заданных
чисел.
Функция
СУММПРОИЗВ()
вычисляет
сумму произведений соответствующих
членов двух и более массивов-аргументов
(но не более 30 аргументов). Встречающиеся
в аргументах нечисловые значения
интерпретируются нулями.
Функция
СУММКВ()
вычисляет
сумму квадратов аргументов.
3. Анализ выборки и
генеральной совокупности
Дисперсия
и стандартное отклонение – это
статистические характеристики
распределения наборов или генеральной
совокупности данных. Стандартное
отклонение определяется как квадратный
корень из дисперсии. Как правило, около
68% данных генеральной совокупности с
нормальным распределением находится
в пределах одного стандартного отклонения
и около 95% – в пределах двух стандартных
отклонений. При большой величине
стандартного отклонения данные широко
разбросаны относительно среднего
значения, а при маленькой – они
группируются близко к среднему значению.
Четыре
статистические функции ДИСП(),
ДИСПР(), СТАНДОТКЛОН()
и СТАНДОТКЛОНП()
– предназначены для вычисления дисперсии
и стандартного отклонения чисел в
интервале ячеек. Перед тем как вычислять
дисперсию и стандартное отклонение
набора данных, нужно определить,
представляют ли эти данные генеральную
совокупность или выборку из генеральной
совокупности. В случае выборки из
генеральной совокупности следует
использовать функции ДИСП()
и СТАНДОТКЛОН(),
а в случае генеральной совокупности –
функции ДИСПР()
и СТАНДОТЛОНП().
Функция
СУММСУММКВ()
вычисляет сумму сумм квадратов
соответствующих элементов в массивах.
Функция
СУММКВРАЗН()
вычисляет сумму квадратов разности
соответствующих элементов в массивах.
4. Использование
статистических функций при решении
задач
1)
В задачах с
дискретными таблицами частот
можно использовать следующие математические
функции:
СУММ(диапазон
ni)
– для нахождения объёма выборки n
как суммы частот ni
(или
объёма генеральной совокупности N
как суммы частот Ni);
СУММПРОИЗВ(диапазон
xi;диапазон
ni)
– для нахождения выборочной средней
xв
(или аналогично генеральной средней
xГ);
СУММПРОИЗВ((диапазон
xi
— xв)^2;
диапазон ni)
– для нахождения выборочной дисперсии
Dв
(или аналогично генеральной дисперсии
DГ).
2)
В задачах, где все
значения вариант xi
находятся в отдельных ячейках,
можно использовать статистические
функции:
СЧЁТ(диапазон
данных) – для нахождения объёма выборки
n
(или объёма генеральной совокупности
N)
как подсчёта всех непустых ячеек;
СЧЁТЕСЛИ(диапазон
данных;варианта xi)
– для нахождения частоты
ni
данной варианты в исходном диапазоне
при построении дискретной таблицы
частот;
СЧЁТЕСЛИМН(диапазон
данных;условие 1; диапазон данных;условие
2) – для нахождения суммы частот вариант,
попавших в заданный интервал, при
построении интервальной таблицы частот;
например,
для подсчёта числа вариант, попавших в
интервал (5,5 – 6], функция будет выглядеть
так: =СЧЁТЕСЛИМН(диапазон данных;»>5,5″;
диапазон данных;»<=6″);
СРЗНАЧ(диапазон
данных) – для нахождения выборочной
или генеральной средней (xв
или xГ);
ДИСП(диапазон
данных) – для нахождения выборочной
дисперсии
Dв;
ДИСПР(диапазон
данных) – для нахождения генеральной
дисперсии
DГ;
СТАНДОТКЛОН(диапазон
данных) – для нахождения выборочного
среднего квадратического отклонения
(выборочного стандарта) σв;
СТАНДОТКЛОНП(диапазон
данных) – для нахождения генерального
среднего квадратического отклонения
(генерального стандарта)
σГ;
МАКС(диапазон
данных)-МИН(диапазон данных) – для
нахождения размаха совокупности R;
МЕДИАНА(диапазон
данных) – для нахождения медианы;
МОДА(диапазон
данных) – для нахождения моды (при этом
в случае, когда все данные совокупности
различны, то в результате будет выдана
ошибка #Н/Д, которая в данном случае
означает, что совокупность не имеет
моды; а если совокупность мультимодальна,
т.е. имеет несколько значений, встречающихся
одинаковое максимальное число раз, то
ответом данной функции будет первое из
таких значений).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Если вы ищете работу и она хоть как-то связана с математикой/экономикой/финансами, то вы очень часто будете встречать такие требования к кандидату:
— Отличное знание статистики;
— Знание и умение Python/R, чтобы эту статистику применять.
Но что делать, если никаких знаний по языкам программирования у вас нет, а встречаться со статистическими моделями так или иначе придется? А работу-то найти нужно срочно…
К счастью, в версии Microsoft Excel выше 2010 вшит целый статистический пакет. О нем мало кто знает, а его реально можно использовать, если нет навыков программирования или доступного компилятора под рукой.
Для начала поговорим, где все эти формулы найти. Как обычно, переходим на вкладку «Формулы» на главной панели, выбираем «Другие функции» и пакет «Статистические». Перед Вами полный перечень статистических возможностей Excel.

Как вы можете видеть, формул в этом разделе представлено довольно много, как «ходовых», так и «узкоспециализированных». К сожалению, разобрать все в одной статье не получится, поэтому рассмотрим здесь самые часто встречающиеся. Если вы хотите познакомиться с математическими функциями Excel, то рекомендуем скачать наш бесплатный гайд.
На первый взгляд они могут показаться очень простыми. Однако, мы постарались раскрыть те моменты, которые обычно остаются без внимания и могут быть полезными.
СРЗНАЧ() и СРЗНАЧА()
Редко кто задумывался, а ведь вычисление среднего значения – сугубо статистическая процедура: именно поэтому это операция и помещена в статистический пакет.
Наверно, особо не стоит останавливаться на правилах использования формулы: функция СРЗНАЧ() принимает на вход массив аргументов и дает на выходе среднее значение по всем ячейкам, содержащим числа(!). Это очень важный момент, который далеко не все знают. Поясним на примере.
Пусть дан диапазон А1:С2 и мы ищем среднее значение по всем 6 ячейкам диапазона:

Однако, результат функции СРЗНАЧ(А1:С2) будет не 8,7, а 13. Почему? (4+15+11+22)/6 = 8,7 ведь?
Да, это правильно, но функция СРЗНАЧ() берет в расчет только те ячейки, где «встречает» числа. Текстовая информация и пустые ячейки просто игнорируются. Поэтому в данном примере СРЗНАЧ() усредняет по 4 ячейкам и выдает правильный ответ – 13.
А вот если нужно произвести усреднение по всему диапазону, вне зависимости от типа данных, нужно использовать функцию СРЗНАЧА().
Принцип работы такой же, как и у СРЗНАЧ(), только на вход будут поступать абсолютно все ячейки. Результат в нашем примере будет уже ожидаемый – 8,7.

Замечание
Выбор той или иной функции происходит в зависимости от задачи. В реальной жизни они могут понадобится в одинаковой мере.
Например, менеджеру нужно узнать среднедневную выручку за месяц на основании продаж за каждый день. Допустим, за несколько дней ячейки оставлены пустыми. Есть два варианта, почему так произошло:
1. В эти дни не было ни одной продажи. Тогда эти дни должны принимать участие в расчете среднего значения и менеджеру нужно использовать СРЗНАЧА() – так он исключит игнорирование пустых ячеек.
2. Эти дни были выходными. Тогда пропуски сами по себе никакой информации не несут и их надо игнорировать: фактически, эти дни не принимают участие в статистической выборке и функция СРЗНАЧ() поможет их пропустить.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
СРЗНАЧЕСЛИ()
Очевидно, что функция СРЗНАЧЕСЛИ() возвращает среднее тех значений, который удовлетворяют каким-то условиям. Помимо этого, условия можно накладывать не только на сами значения, но и на другие ячейки. Проиллюстрируем.
Например, вычислим среднее значение всех ячеек, которые больше нуля:

Мы выделили диапазон А1:С3 и наложили на него условие – «>0». А можно сделать по-другому.
Рассмотрим таблицу, в которую занесены продажи лекарств в городе. Посчитаем среднюю цену Анальгина по всему городу. Для этого наложим условие уже не на саму цену, а на название лекарства.
Формула записывается так:
=СРЗНАЧЕСЛИ(Диапазон_на_который_накладываем_условия; “Условие”; Диапазон_по_которому_считаем_среднее_значение)
В нашем случае это примет вид:

Кстати говоря, условия можно комбинировать с помощью функции СРЗНАЧЕСЛИМН().
Предположим, что в аптеке Зеленый Крест продается несколько видов Анальгина и в нашу таблицу они все занесены как Анальгин.
Тогда, чтобы усреднить цену всех Анальгинов в аптеке Зеленый Крест, нужно просто использовать формулу:
=СРЗНАЧЕСЛИМН(С2:С13; A2:A13; “зеленый крест”;B2:B13; “анальгин”)
Обратите внимание: диапазон усреднения указывается в конце только при использовании функции СРЗНАЧЕСЛИ() с дополнительным условием. В остальных случаях диапазон ячеек, по которым вычисляется среднее значение, стоит первым.
МИН()/МАКС() и НАИБОЛЬШИЙ()/НАИМЕНЬШИЙ()
На первый взгляд, разница между этими функциями не особо прослеживается, хотя зачем их используют – очевидно – найти самое большое или маленькое число. Однако, в работе этих функций есть небольшая, но очень полезная разница. Разберем подробней.
Функция МИН() просто принимает массив аргументов и находит самое маленькое число. МАКС() – самое большое. Все просто.
Функция НАИМЕНЬШИЙ() же находит n-ое наименьшее число в массиве. НАИБОЛЬШИЙ(), наоборот, находит n-ое наибольшее число.
Например, нужно найти пятое по величине число. Вводим:
=НАИБОЛЬШИЙ(диапазон; 5).
Фактически, получается, что результат работы НАИБОЛЬШИЙ(массив;1) и МАКС(массив) – одно и то же. Аналогичная ситуация с НАИМЕНЬШИЙ(массив;1) и МИН(массив).

Рекомендуем записаться на наш открытый онлайн-курс «Аналитика в Excel», если вы хотите научиться выполнять рутинную работу быстрее.
МЕДИАНА() и МОДА()
Общеизвестные и достаточно важные статистические характеристики моды и медианы вычисляются по одноименным формулам.
Напомним, что медианой называется «середина» числового множества.
Например, если есть массив чисел от одного до десяти, то медианой будет число 5,5 (хотя оно само в массив не входит). Это из-за того, что количество элементов в массиве – четно и выбрать «центральное» просто невозможно.

Вот если бы выборка начиналась не с единицы, а с двойки, то ответ был бы ровно 6.

Теперь перейдем к моде. Мода – самое часто встречающееся число в выборке.
У функции нахождения моды есть целых три модификации в Excel старшее версии 2010 года: МОДА(), МОДА.ОДН() и МОДА.НСК().
Функция МОДА() оставлена для совместимости – ей, в целом, можно пользоваться: она работает совершенно аналогично функции МОДА.ОДН().
«ОДН» в названии функции значит, что, если в выборке несколько самых часто встречающихся элементов, то возвращено в качестве ответа будет только первое.

Для подсчета всех мод в выборке нужно использовать функцию МОДА.НСК().
Работает МОДА.НСК() следующим образом: выделяем побольше ячеек (если заранее не знаем, сколько мод у нас получится), в строке формул прописываем =МОДА.НСК(диапазон) и нажимаем Ctrl+Shift+Enter. Получили все моды в столбик.

Значения #Н/Д появляются, просто потому что мод у нас всего 2. Такой метод поиска мод называется «слепым» – мы просто берем побольше ячеек, чтобы наверняка хватило.
Если Вы не любите подобный «мусор» и Вам нравится, когда все красиво, можно сначала оценить: а сколько же у нас вообще будет мод? А потом просто выделить нужное количество ячеек.
Делается это так: сначала применяем функцию СЧЁТ() к нашей МОДА.НСК() – получили количество мод. А теперь выделяем только две ячейки и делаем все также, как написано выше.

Заключение
Статистический пакет Microsoft Excel содержит в себе еще огромное количество формул: проверку гипотез, принадлежность распределениям, доверительные интервалы, корреляцию и прочие инструменты, которые могут пригодиться при работе со статистикой даже на серьезном уровне.
Как мы и писали ранее, обозреть все в одной статье невозможно. Поэтому, если вы хотите узнать про менее известные, но не менее полезные статистические возможности Excel – пишите в комментариях, что вам было бы интересно и мы подготовим для вас новую статью из этого цикла.
Автор: Андрон Алексанян, СОО “Аптека-Центр”, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
MS Office
5 примеров экономии времени в Excel
Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…
Как работать с датами в Excel?
Содержание статьи История о том, как я пропустил свидание с очаровательной блондинкой… Вы никогда не попадали впросак из-за того, что неправильно читали дату? «Да…
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html