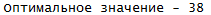Венгерский метод в excel

Для
решения данной задачи используем
программу Excel.
Создаем в Excel
две матрицы рис. 5.1. В первой таблице
введены исходные данные, а также формула
для определения суммарной эффективности.
Во второй таблице создаем матрицу
результатов решения и ограничений
решения транспортной задачи.

Рис. 5.1.Исходные
матрицы для решения транспортной задачи.

Суммарная
эффективность определяется, как
СУММПРОИЗВ(C8:G12;C17:G21).

Для
решения транспортной задачи венгерским
методом в таблице результатов решения
задаются проверки ограничений:

1. Определяются
   суммы по строкам (СУММ С17:G17).

2. Определяются
   суммы по столбцам (СУММ С17:С21).

Для
решения транспортной задачи в Microsoft
Excel
воспользуемся функцией «Поиск решений».
В меню «Сервис», переходим в пункт
«Надстройки», в доступных надстройках
выбираем «Поиск решения».

При
выполнении функции «Поиск решения»
необходимо установить целевую ячейку.

Целевая
ячейка для примера 1 будет равна
максимальному значению, а для примера
2 -минимальному значению. Целевая ячейка
задается в ячейке, где определяется
суммарная эффективность решения задачи.
Далее, указываем диапазон ячеек, где
подбирается возможный вариант решений
($C$176:
$G$21).
Задаем ограничения, согласно условиям
транспортной задачи (рис.5.2.).

Рис. 5.2.Поиск
решения транспортной задачи для примера
1.

Выполнив функцию
«Поиск решения», получаем оптимальное
решение транспортной задачи венгерским
методом. Рисунок 5.3. — для примера 1
(определение максимальной суммарной
эффективности), а рисунок 5.4. – для
примера 2 (определение минимальной
суммарной эффективности).

Рис. 5.3.Результаты
решения транспортной задачи (пример
1).

Рис. 5.4.Результаты
решения транспортной задачи (пример
2).

5.5. Варианты заданий.

Задача:
Имеются
5 лесопунктов и 5 комплектов
лесозаготовительного оборудования (5
технологических линий). Каждая
технологическая линия может дать
производительность С(ij).

Выполнить:
Распределить технологические линии по
лесопунктам, чтобы общая производительность
была максимальной или минимальной.

1. Сформулировать
   задачу. Привести математическую
   постановку задачи.

2. Решить задачу с
   краткими пояснениями.

3. Решить задачу на
   ЭВМ.

4. Сделать выводы
   по полученному результату.

Задание
выбирается по последней и предпоследней
цифре зачетной книжки. Исходные данные
берутся в таблице по последнему номеру
зачетной книжки (таблица 5.1). Если
предпоследняя цифра зачетной книжки
четная- то производительность должна
быть максимальной, если -нечетная, то
производительность должна быть
минимальной.

Таблица 5.1.

Исходные данные для решения транспортной задачи венгерским методом.

6.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1. Выбираем последнюю клетку(1,3)

2. x₁₃=min{10,10} = 10

3.a₁^‘ = b₃ = 0

4.Таблица исчерпана. Конец.

Переходим к описанию следующего шага метода потенциалов.

ШАГ 2. Проверка текущего плана на оптимальность.

Признаком того, что текущий план перевозок является оптимальным, служит условие

(1)u_i +vj -c_ij ≤0

которое выполняется для всех клеток таблицы. Неизвестные здесь величины u_i и vj (называемые потенциалами) определяются из условий

(2)u_i + v_j = c_ij

Условие (1) означает невозможность появления «спекулятивной» цены. Само же название «потенциалы» заимствовано из физического закона о том, что работа по перемещению заряда в электростатическом поле равна разности потенциалов в данных точках поля (У нас: «…цена перевозки единицы продукции по коммуникации равна разности цен в конце и в начале пути»)

Так как заполненных клеток в таблице (m+n-1) штук, а неизвестных и (m+n) штук, то для их определения имеется система из (m+n-1) уравнений относительно (m+n) неизвестных. Чтобы найти решение (хотя бы какое-нибудь) такой системы, достаточно положить одно из неизвестных (произвольное) равным некоторому произвольно выбранному числу. Тогда остальные определяются единственным образом. Можно решать эту систему непосредственно (продолжаем работать с нашим «старым» примером и найдем потенциалы для начального плана, построенного способом МС).

Заполненные клетки Уравнения

(1,1) u₁ + v₁ =5

(1,2) u₁ + v₂ =10

(1,3) u₁ + v₃ =12

(2,3) u₂ +v₃ =4

(3,2) u₃ +v₂ =0

Положим, например, неизвестное u ₁ равным 0 (через него можно из первых трех уравнений найти v₁, v₂ и v₃). Последовательно из них находим u _{2 ,} u _3.

Этот метод можно сформулировать в виде единого правила:

Неизвестный потенциал находится вычитанием известного из цены перевозки в заполненной клетке

Применим это правило для определения u и v в нашем примере и получим:

u₁ =0, u₂ =-8, u₃ =-6

v₁ =5, v₂ =10, v₃ =12

Переходим к проверке условий оптимальности (1). Достаточно проверять их для незаполненных клеток, так как для клеток заполненных эти условия выполняются как равенства. Для проверки берется незаполненная клетка, складываются соответствующие ей потенциалы (первый элемент строки и последний элемент столбца) и из них вычитается цена перевозки в данной клетке. Если полученное число отрицательное (или ноль), то оптимальность в данной клетке не нарушается (в случае выполнения условия (1) для всех незаполненных клеток, имеем оптимальный план перевозок). Если же в таблице встретилась хотя бы одна клетка, для которой это число положительно, тогда решение не является оптимальным и может быть улучшено.

Проверим на оптимальность имеющееся решение

(2,1) u₂+v₁-c₂₁=-8+5-8=-11<0

(2,2) u ₂ +v₂ -c₂₂=-8+10-6=-4<0

(3,1) u ₃ +v₁ -c₃₁=-10+ 5-0=-5<0

(3,3) u ₃ +v₃ -c₃₃=-10+12-0=2>0

Следовательно, условие оптимальности нарушено в клетке (3,3).

Имеющийся план перевозок можно улучшить.

Дадим описание заключительного шага алгоритма метода потенциалов.

ШАГ 3 Улучшение плана перевозок.

Улучшение плана происходит путем назначения перевозки θ>0 в ту клетку (i , j) таблицы, в которой нарушилось условие оптимальности. Но назначение ненулевой перевозки нарушает условия баланса вывоза продукции от поставщика i (вывозит весь запас и еще плюсθ>0 ) и условия баланса привоза продукции к потребителю j (получает все что можно и еще плюс θ > 0). Условия баланса восстанавливают путем уменьшения вывоза от i-поставщика к какому-то другому потребителю j (уменьшают на θ перевозку в какой-то заполненной клетке (i , j) строки i). При этом нарушается баланс привоза продукции к потребителю j (получает на θ меньше, чем ему требуется). Восстанавливают баланс в столбце j, тогда он нарушается в некоторой строке i и т.д. до тех пор, пока цикл перемещения перевозок не замкнется на клетке, в которой нарушалось условие оптимальности. Продемонстрируем эти рассуждения на нашем примере.

1. Оптимальность нарушена в клетке (3,3). Назначим в нее перевозку θ>0 (+θ означает, увеличение на θ).

2.Нарушается баланс вывоза от поставщика 3 (вывозит 50+ θ, а это больше его запаса!). Уменьшаем на θ перевозку в заполненной клетке строки 3 (вне заполненной уменьшать нельзя, так как это приведет к отрицательной перевозке).

Рассмотрим те клетки цикла в которых уменьшаем на θ перевозку и берём минимум из вычетаемых, у нас это min{10- θ ,50- θ }=10.

И данное число надо подставить в цикл

§3. Транспортные задачи по различным критериям

Транспортная задача по критерию времени

Иногда возникает ситуация, когда в условиях (ТЗ) необходимо минимизировать не стоимость перевозок, а время их выполнения (Срочные грузы, перевозки скоропортящихся продуктов, работа «скорой помощи» и т.д.)

Имеется m поставщиков однородного груза и n потребителей груза. Для каждой пары ( , ) известно время , за которое груз перевозится от к . Требуется составить такой план перевозок, при котором все запасы поставщиков будут вывезены, а все запросы потребителей будут полностью удовлетворенны и наибольшее время доставки всех грузов будет минимизирован.

Задача о назначениях (Венгерский метод)

Имеется n видов работ и n рабочих. Каждый рабочий может выполнить любую из n работ за некоторое время (цена рабочего). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий.

§4. Решение транспортной задачи в Excel

В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов.

• В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах.

• В ячейки E5:I5 — заявки на продукцию, поступившие от магазинов.

• В ячейки B8:F9 — матрицу транспортных расходов, задающую расходы на перевозку из I-го склада в J-й магазин единицы продукции.

• В ячейки B13:F14 — план перевозок — матрицу, задающую количество товара, перевезенного из I-го склада в J-й магазин. Начальное распределение плана задано по принципу «каждой сестре по серьге», равномерно распределив всю имеющуюся на складе продукцию по магазинам. Эти ячейки являются регулируемыми и Решатель должен найти более подходящее решение, изменив значения в этих ячейках.

• В ячейку D15 — записал целевую функцию:

{ =СУММ((B8:F8*B13:F13)+(B9:F9*B14:F14))}

• В ячейки D17:H17 записал ограничения, задающие требование о точном выполнении заявки каждого магазина. Как обычно, я записал соответствующую формулу в первую из этих ячеек:

{=СУММ(B13:B14) — E5 }

Затем скопировал ее. При копировании формула автоматически меняется, задавая нужное ограничение. Правда, нужно следить при этом за правильной ориентацией данных. Например, в данном случае формулу нужно копировать в строку, а не в столбец.

• Затем задал следующую группу ограничений. Эти ограничения отвечают тому естественному условию, что со склада нельзя увести больше продукции, чем там имеется. Формула, помещенная в ячейку D18, имеет вид:

{=C4 — СУММ(B13:F13)}

Эта формула скопирована уже по столбцу в ячейку D19. Подготовительный этап завершен — можно вызывать Решатель.

При вызове Решателя и задании параметров в его диалоговом окне выполнялась стандартная работа по указанию ячейки с целевой функцией, диапазоном регулируемых ячеек и заданием ограничений. Заметьте, помимо двух групп ограничений я задал и ограничения целочисленности переменных. Предполагается, что продукция может перевозиться только целыми единицами — бочками, мешками, ящиками. Такие ограничения в Решателе создаются совсем просто, — достаточно среди операторов, связывающих левую и правую части ограничения, выбрать оператор int. Взгляните, как выглядят результаты моей работы:

Рис. 2.21. Окно Решателя при решении транспортной задачи

Прежде чем дать команду на решение задачи, я провел настройку параметров в окне Options. В частности я включил флажки, указывающие на линейность модели и положительность переменных. Кроме того, я увеличил точность решения целочисленной задачи, задав в окне Tolerance значение в 1% вместо 5%, принятых по умолчанию.

Рис. 2.22. Настройка в окне параметров Решателя при решении транспортной задачи

Осталось щелкнуть кнопку «Solve» и получить оптимальный план перевозок. Вы можете проанализировать, насколько оптимальный план отличается от равномерного распределения, предложенного в качестве первоначального варианта, и как уменьшились транспортные расходы:

Рис. 2.23. Решение транспортной задачи

Параметры, управляющие работой Решателя

Рассмотрим возможности управления работой Решателя, задаваемые в окне Параметры (Options):

• Максимальное время (MaxTime) — ограничивает время, отведенное на процесс поиска решения. По умолчанию задано 100 секунд, что обычно достаточно для задач небольшой размерности, имеющих около 10 ограничений. Для задач большой размерности придется это значение увеличивать.

• Предельное число итераций (Iterations) — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, но это число можно увеличивать до 32767. Чаще всего, если решение не получено за 100 итераций, надежд получить его при увеличении этого значения мало. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.

• Относительная погрешность (Precision) — задает точность выполнения ограничений. Иногда проще изменить ограничение, отодвинув границу, чем пытаться выполнить ограничения с высокой точностью.

• Сходимость (Convergence) — задается десятичной дробью, меньшей единицы, позволяя остановить процесс поиска при сходимости решения к неподвижной точке, когда относительные изменения в течение последних 5 итераций не превышают заданную дробь.

• Линейная модель (Assume Linear Model) — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Эта дополнительная информация позволяет Решателю упростить процесс поиска решения.

• Неотрицательные значения (Assume Non-Negative) — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

• Показывать результаты итераций (Show Iteration Results) — флажок, позволяющий включить пошаговый процесс поиска, показывая на экране результаты каждой итерации. В сложных ситуациях, когда Решатель не находит решения автоматически, рекомендуется включать этот флажок, так как иногда можно найти точку, от которой процесс поиска уклонился в сторону.

• Автоматическое масштабирование (Use Automating Scaling) — флажок автоматического изменения масштаба следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, задающая суммарную стоимость, измеряется в миллионах рублей.

• Относительная погрешность (Tolerance) — задается в процентах. Указанное значение имеет смысл только для задач с целочисленными ограничениями. Решатель в таких задачах вначале находит оптимальное не целочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более чем на указанное данным параметром количество процентов. Если такая точка найдена, Решатель сообщает об успехе. При большом допуске (по умолчанию 5%) может быть потеряно лучшее целочисленное решение, правда, отличающееся от найденного Решателем в пределах допуска. Для целочисленных задач допуск имеет смысл уменьшить, что я и сделал при решении транспортной задачи. Хочу еще раз обратить внимание на эту особенность решения задач целочисленного программирования. Если значение параметра Tolerance задать большим, то Решатель может остановиться раньше времени, не найдя лучшего целочисленного решения. Если же его взять малым, то наилучшее целочисленное решение будет отличаться от оптимального нецелочисленного решения на величину большую, чем ту, которая задается параметром Tolerance. В этом случае формально решение заканчивается неуспехом, поскольку найденное решение не удовлетворяет всем требованиям. Конечно, параметр Tolerance играет служебную роль, и «умный» Решатель, найдя наилучшее целочисленное решение, должен был бы уведомлять, что решение найдено, но ограничение по Tolerance не выполнено. Этого, однако, не происходит. Мы еще столкнемся с этой ситуацией при рассмотрении следующей задачи.

• Сохранить модель (Save Model) — командная кнопка; позволяет открыть диалоговое окно, где можно указать имя сохраняемой модели. Имеет смысл использовать эту возможность, когда на рабочем листе несколько моделей, так как единственная модель запоминается автоматически.

• Загрузить модель (Load Model) — позволяет загрузить одну из сохраненных моделей.

• Есть еще несколько более специальных параметров, которыми можно управлять, варьируя процедурами, применяемыми в процессе поиска. К ним следует прибегать в тяжелых ситуациях, когда решение найти не удается.

Венгерский алгоритм, или о том, как математика помогает в распределении назначений

Привет, друзья! В этой статье хотел бы рассказать про интересный алгоритм из дисциплины «Исследование операций» а именно про Венгерский метод и как с его помощью решать задачи о назначениях. Немного затрону теории про то, в каких случаях и для каких задач применим данный алгоритм, поэтапно разберу его на мною выдуманном примере, и поделюсь своим скромным наброском кода его реализации на языке R. Приступим!

Пару слов о методе

Для того чтобы не расписывать много теории с математическими терминами и определениями, предлагаю рассмотреть пару вариантов построения задачи о назначениях, и я думаю Вы сразу поймете в каких случаях применим Венгерский метод:

• Задача о назначении работников на должности. Необходимо распределить работников на должности так, чтобы достигалась максимальная эффективность, или были минимальные затраты на работу.
• Назначение машин на производственные секции. Распределение машин так, чтобы при их работе производство было максимально прибыльным, или затраты на их содержание минимальны.
• Выбор кандидатов на разные вакансии по оценкам. Этот пример разберем ниже.

Как Вы видите, вариантов для которых применим Венгерский метод много, при этом подобные задачи возникают во многих сферах деятельности.

В итоге задача должна быть решена так, чтобы один исполнитель (человек, машина, орудие, …) мог выполнять только одну работу, и каждая работа выполнялась только одним исполнителем.

Необходимое и достаточное условие решения задачи – это ее закрытый тип. Т.е. когда количество исполнителей = количеству работ (N=M). Если же это условие не выполняется, то можно добавить вымышленных исполнителей, или вымышленные работы, для которых значения в матрице будут нулевыми. На решение задачи это никак не повлияет, лишь придаст ей тот необходимый закрытый тип.

Step-by-step алгоритм на примере

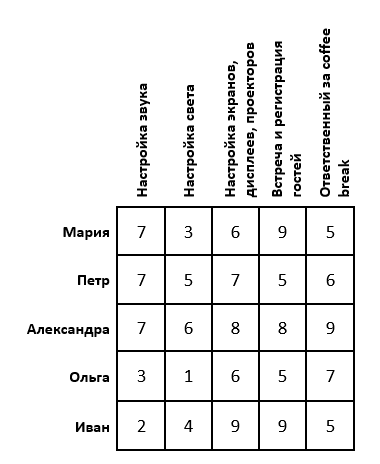
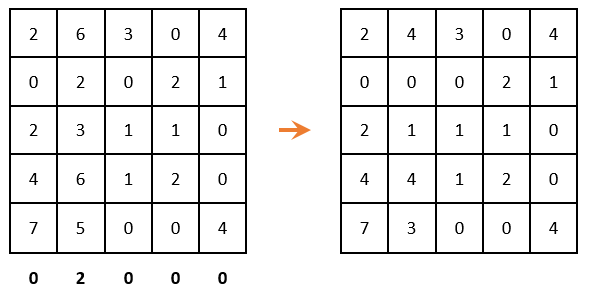
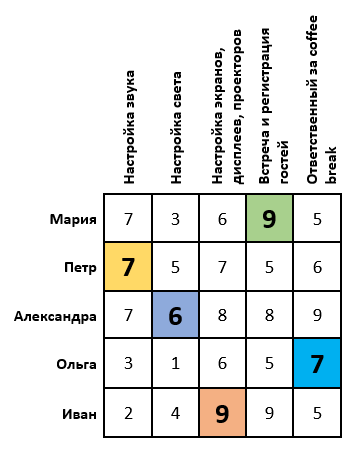
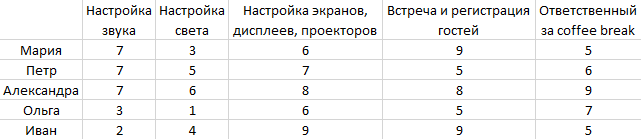
Постановка задачи: Пусть намечается важная научная конференция. Для ее проведения необходимо настроить звук, свет, изображения, зарегистрировать гостей и подготовиться к перерывам между выступлениями. Для этой задачи есть 5 организаторов. Каждый из них имеет определенные оценки выполнения той, или иной работы (предположим, что эти оценки выставлены как среднее арифметическое по отзывам их сотрудников). Необходимо распределить организаторов так, чтобы суммарная их оценка была максимальной. Задача имеет следующий вид:

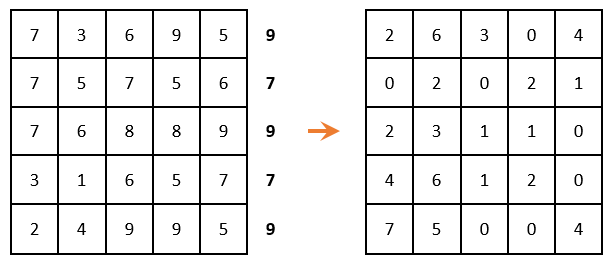
Если задача решается на максимум (как в нашем случае), то в каждой строке матрицы необходимо найти максимальный элемент, его же вычесть из каждого элемента соответствующей строки и умножить всю матрицу на -1. Если задача решается на минимум, то этот шаг необходимо пропустить.

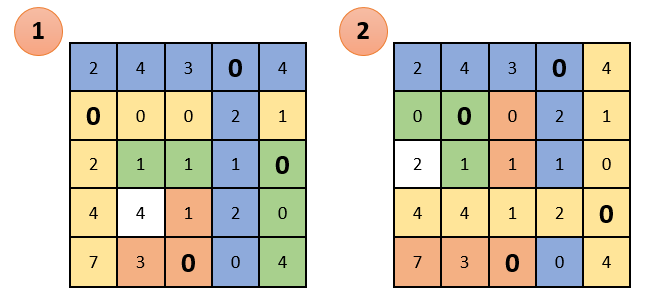
В каждой строке и в каждом столбце должен быть только один выбранный ноль. (т.е. когда выбрали ноль, то остальные нули в этой строке или в этом столбце уже не берем в расчет). В этом случае это сделать невозможно:

(Если задача решается на минимум, то необходимо начинать с этого шага). Продолжаем решение далее. Редукция матрицы по строкам (ищем минимальный элемент в каждой строке и вычитаем его из каждого элемента соответственно):

Т.к. все минимальные элементы – нулевые, то матрица не изменилась. Проводим редукцию по столбцам:

Опять же смотрим чтобы в каждом столбце и в каждой строке был только один выбранный ноль. Как видно ниже, в данном случае это сделать невозможно. Представил два варианта как можно выбрать нули, но ни один из них не дал нужный результат:

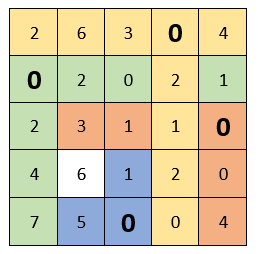
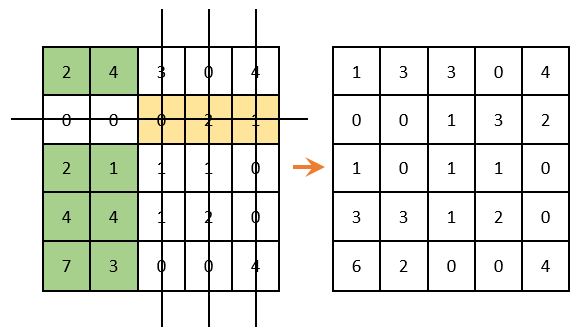
Продолжаем решение дальше. Вычеркиваем строки и столбцы, которые содержат нулевые элементы (ВАЖНО! Количество вычеркиваний должно быть минимальным). Среди оставшихся элементов ищем минимальный, вычитаем его из оставшихся элементов (которые не зачеркнуты) и прибавляем к элементам, которые расположены на пересечении вычеркнутых строк и столбцов (то, что отмечено зеленым – там вычитаем; то, что отмечено золотистым – там суммируем; то, что не закрашено – не трогаем):

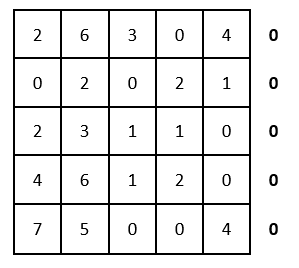
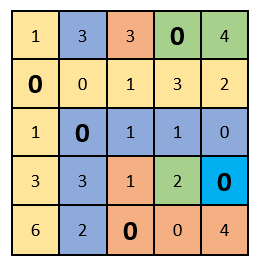
Как теперь видно, в каждом столбце и строке есть только один выбранный ноль. Решение задачи завершаем!

Подставляем в начальную таблицу месторасположения выбранных нулей. Таким образом мы получаем оптимум, или оптимальный план, при котором организаторы распределены по работам и сумма оценок получилась максимальной:

Если же вы решаете задачу и у вас до сих пор невозможно выбрать нули так, чтобы в каждом столбце и строке был только один, тогда повторяем алгоритм с того места где проводилась редукция по строкам (минимальный элемент в каждой строке).

Реализация на языке программирования R

Венгерский алгоритм реализовал с помощью рекурсий. Буду надеяться что мой код не будет вызывать трудностей. Для начала необходимо скомпилировать три функции, а затем начинать расчеты.

Данные для решения задачи берутся из файла example.csv который имеет вид:

#Подключаем библиотеку для удобства расчетов
library(dplyr)

#Считываем csv фаил (первый столбик - названия строк; первая строка - названия столбцов)
table <- read.csv("example.csv",header=TRUE,row.names=1,sep=";")

#Проводим расчеты
unique_index <- hungarian_algorithm(table,T)

#Выводим
cat(paste(row.names(table[as.vector(unique_index$row),])," - ",names(table[as.vector(unique_index$col)])),sep = "n")

#Считаем оптимальный план
cat("Оптимальное значение -",sum(mapply(function(i, j) table[i, j], unique_index$row, unique_index$col, SIMPLIFY = TRUE)))



#____________________Алгоритм венгерского метода__________________________________

hungarian_algorithm <- function(data,optim=F){
  
#Если optim = T, то будет искаться максимальное оптимальное значение
  if(optim==T)
  {
    data <- data %>% 
      apply(1,function(x) (x-max(x))*(-1)) %>% 
      t() %>% 
      as.data.frame()
    optim <- F
  }
  
#Редукция матрицы по строкам
  data <- data %>%
    apply(1,function(x) x-min(x)) %>% 
    t() %>% 
    as.data.frame()
  
#Нахождение индексов всех нулей
  zero_index <- which(data==0, arr.ind = T)
  
#Нахождение всех "неповторяющихся" нулей слева-направо
  unique_index <- from_the_beginning(zero_index)
  
#Если количество "неповторяющихся" нулей не равняется количеству строк в исходной таблице, то..
  if(nrow(unique_index)!=nrow(data))
#..Ищем "неповторяющиеся" нули справа-налево
    unique_index <- from_the_end(zero_index)
  
#Если все еще не равняется, то продолжаем алгоритм дальше
  if(nrow(unique_index)!=nrow(data))
  {
    
#Редукция матрицы по столбцам
    data <- data %>%
      apply(2,function(x) x-min(x)) %>% 
      as.data.frame()
    
    zero_index <- which(data==0, arr.ind = T)
    unique_index <- from_the_beginning(zero_index)
    
    if(nrow(unique_index)!=nrow(data))
      unique_index <- from_the_end(zero_index)
    
    if(nrow(unique_index)!=nrow(data))
    {
      
#"Вычеркиваем" строки и столбцы которые содержат нулевые элементы (ВАЖНО! количество вычеркиваний должно быть минимальным)
      index <- which(apply(data,1,function(x) length(x[x==0])>1))
      index2 <- which(apply(data[-index,],2,function(x) length(x[x==0])>0))
      
#Среди оставшихся элементов ищем минимальный
      min_from_table <- min(data[-index,-index2])
      
#Вычитаем минимальный из оставшихся элементов
      data[-index,-index2] <- data[-index,-index2]-min_from_table
      
#Прибавляем к элементам, расположенным на пересечении вычеркнутых строк и столбцов
      data[index,index2] <- data[index,index2]+min_from_table
      
      zero_index <- which(data==0, arr.ind = T)
      unique_index <- from_the_beginning(zero_index)
      
      if(nrow(unique_index)!=nrow(data))
        unique_index <- from_the_end(zero_index)
      
#Если все еще количество "неповторяющихся" нулей не равняется количеству строк в исходной таблице, то..
      if(nrow(unique_index)!=nrow(data))
#..Повторяем весь алгоритм заново
        hungarian_algorithm(data,optim)
      
      else
#Выводим индексы "неповторяющихся" нулей
        unique_index
    }
    else
#Выводим индексы "неповторяющихся" нулей
      unique_index
  }
  else
#Выводим индексы "неповторяющихся" нулей
    unique_index
}
#_________________________________________________________________________________


#__________Функция для нахождения "неповторяющихся" нулей слева-направо___________

from_the_beginning <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){
  
#Выбор индексов нулей, которые не лежат на строках i, и столбцах j
  find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]
  
  if(length(find_zero)>2){
    
#Записываем индекс строки в вектор
    i <- c(i,as.vector(find_zero[1,1]))
  
#Записываем индекс столбца в вектор
    j <- c(j,as.vector(find_zero[1,2]))
    
#Записываем индексы в data frame (это и есть индексы уникальных нулей)
    index <- rbind(index,setNames(as.list(find_zero[1,]), names(index)))
    
#Повторяем пока не пройдем по всем строкам и столбцам
    from_the_beginning(find_zero,i,j,index)}
  else
    rbind(index,find_zero)
}
#_________________________________________________________________________________

#__________Функция для нахождения "неповторяющихся" нулей справа-налево___________

from_the_end <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){
  find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]
  if(length(find_zero)>2){
    i <- c(i,as.vector(find_zero[nrow(find_zero),1]))
    j <- c(j,as.vector(find_zero[nrow(find_zero),2]))
    index <- rbind(index,setNames(as.list(find_zero[nrow(find_zero),]), names(index)))
    from_the_end(find_zero,i,j,index)}
  else
    rbind(index,find_zero)
}
#_________________________________________________________________________________

Результат выполнения программы:

В завершение

Спасибо большое что потратили время на чтение моей статьи. Все используемые ссылки предоставлю ниже. Надеюсь, Вы узнали что-то для себя новое или обновили старые знания. Всем успехов, добра и удачи!

Используемые ресурсы

1. Штурмовал википедию
2. И другие хорошие сайты
3. Подчеркнул для себя немного информации с этой статьи

Лабораторная
работа №5

Условие задачи

Имеется 6 исполнителей, которые могут
выполнять 6
различных
работ.

Известны затраты, связанные с
назначением i
—
го
исполнителя на j
–
ю работу, задаваемые
матрицей (c
i
j )
размерностью
66 ( i,
j 16 ).

Необходимо произвести назначение
исполнителей на работы таким образом, чтобы общие затраты всех
назначений были бы минимальными, при условии, что каждый исполнитель может
быть назначен только на одну работу и за каждой работой может
быть закреплен только один исполнитель.

Автоматизация
решения задачи о назначениях в MS Excel

Данная задачa, которая является
совершенно полной и может быть решена с использованием модуля «Поиск решения»
электронных таблиц MS Excel. Для этого расположим данные на листе Excel как
показано на рис.1.

рис.1

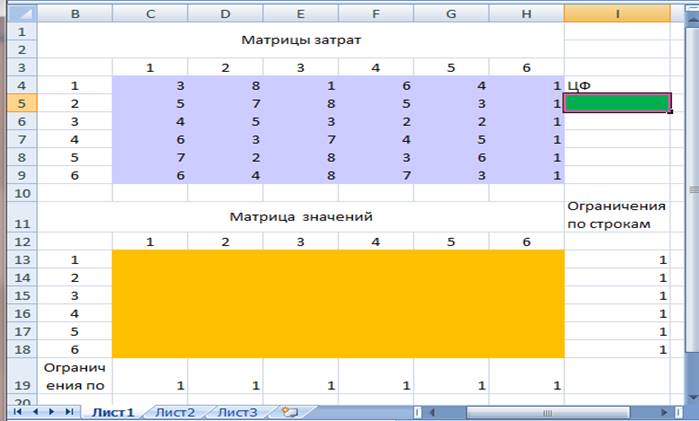
Матрица затрат задана массивом чисел C4:H9, матрица
назначений (переменных) – массивом C13:H18, формулы для
целевой функции и основных ограничений – по строкам и столбцам матрицы
переменных – указаны в соответствующих ячейках на рис.2.

рис.2

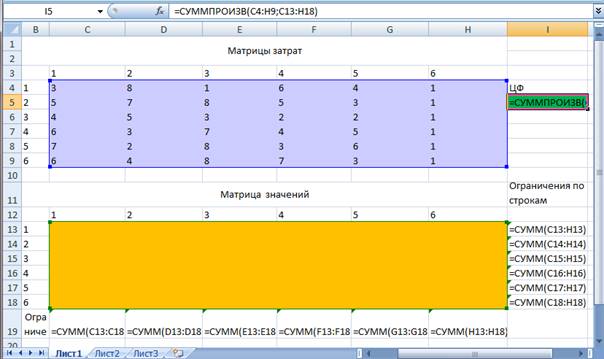
В результате, после ввода всех формул,
массивов и ограничений окно модуля «Поиск решения» выглядит так, как показано
на рис. 3

рис.3

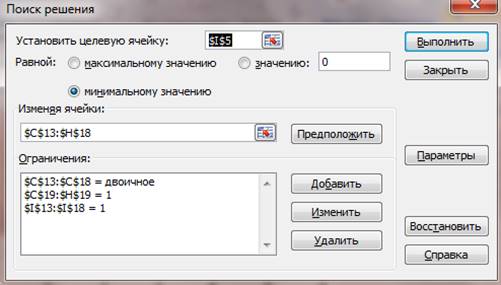
После ввода необходимых параметров
«Линейная модель» модуль «Поиск решения» запускается на решение задачи, а
его результат представлен на рис.4.

рис.4

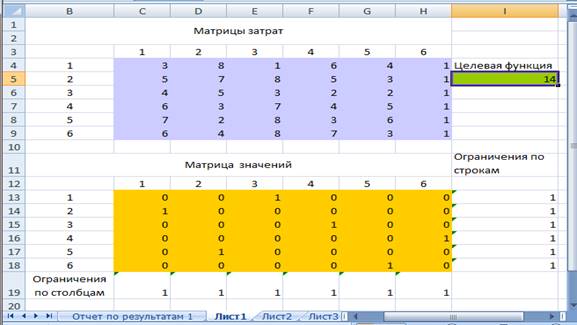
Автоматизация
решения задачи о назначениях в ПЭР

Для решения этой задачи в среде ПЭР необходимо
в главном меню программы выбрать пункт «Задача о назначениях».

Далее в режиме ввода новой задачи ввести
в ПЭР все необходимые параметры задачи.

После чего ввести числовые данные задачи.

После того, как данные задачи будут
сформированы необходимо войти в режим решения задачи о назначениях
функционального меню ПЭР и вывести таблицы всех итераций решения данной
задачи. Начальная таблица приведена на рис.4

рис.4

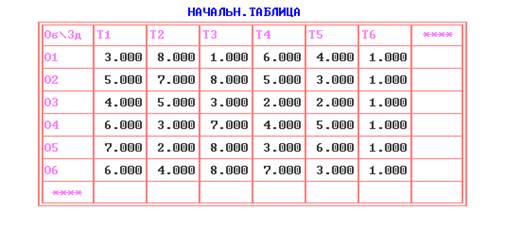
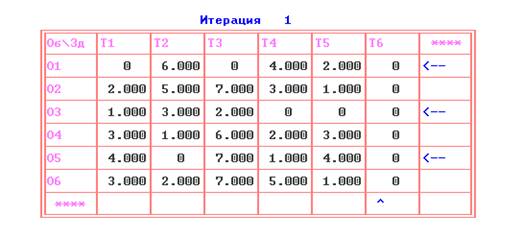
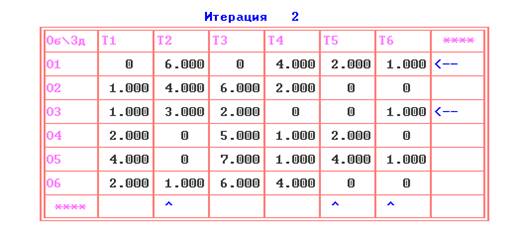
На первой итерации ПЭР «получает»
приведенную матрицу.

Специальными стрелками в последних
строке и столбце таблицы первой итерации обозначены вертикальные и
горизонтальные лини зачеркивания.

рис.5

рис.6

рис.7

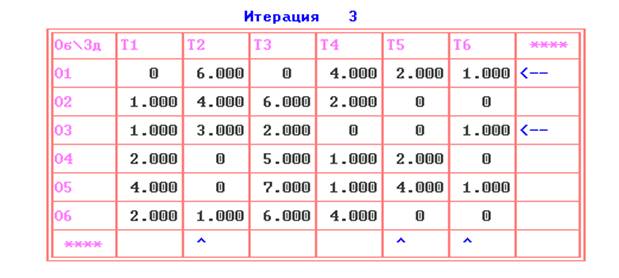
На первой итерации ПЭР «получает»
приведенную матрицу.

Специальными стрелками в последних строке
и столбце таблицы первой итерации обозначены вертикальные и
горизонтальные лини зачеркивания.

рис.8

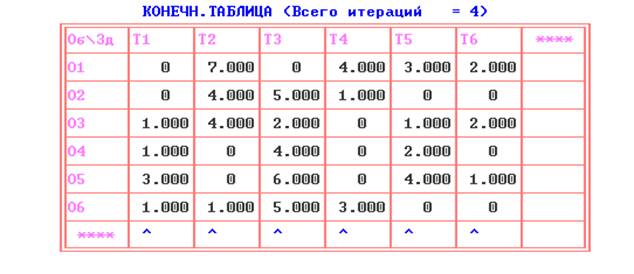
Однако, сам план назначений в табличной
форме выводится отдельно как показано на рис.9

рис.9

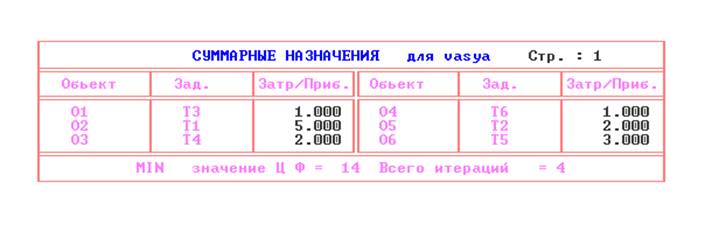
Автоматизация решения задачи о
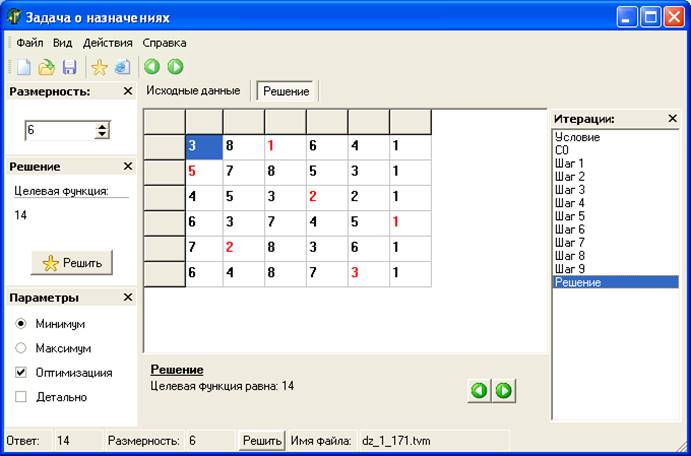
назначениях в программе Venger

Программа Venger разработана специально
для автоматизации процесса решения задачи о назначениях по алгоритму
венгерского метода и предназначена для использования в среде ОС Windows.

На итерации «Решение» отображается
исходная матрица эффективностей назначений, в которой красным цветом
выделены элементы, соответствующие единичным элементам матрицы назначений.

Выделенные элементы являются слагаемыми
оптимального значения целевой функции данной задачи.

рис.10

Вывод:  Я

v Приобретение навыков
построения математической модели задачи о назначениях.

v
Приобретение
навыков автоматизированного решения задачи о назначениях в среде программ Microsoft Excel и ПЭР.

v
Приобретение
навыков автоматизированного решения задачи о назначениях по алгоритму
венгерского метода в среде программы Venger.