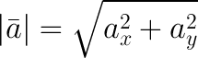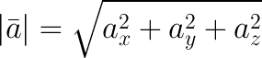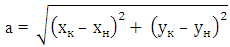Вектор числа в excel - Word и Excel - помощь в работе с программами

Подборка по базе: Учебное пособие по речевой коммуникации в профсфере 2018 (1).doc, Экономическая теория. Часть 2. Макроэкономика — пособие (1) (1)., методическое пособие_наращивание волос.docx, Стандартизация, подтв. соответствия Методич. пособие.docx, Методическое пособие для курсовой работы на конкурс.docx, Методическое пособие к Лабораторной работе №1.pdf, 208101 Учеб. пособие Физико-химические процессы в техносфере 200, Методическое пособие по МДК 02.01 (Заочнаяформа обучения).pdf, Единовременное пособие на рождение ребенка.docx, типология пособие.pdf

6.1. Векторы

Векторы — это наборы чисел, расположенные горизонтально (вектор-строка) или вертикально (вектор-столбец).

сложение — два вектора а и b с одинаковым числом компонент образуют новый вектор с:с_i= a_i+ b_i ;
умножение на число — каждая компонента вектора умножается на число, т.е. b = λа означает b_i= λа_i

здесь i — номер компоненты вектора.

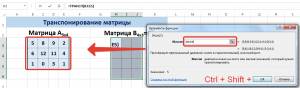
Упражнение 6.1.1. Сложить два вектора:

Ввести в первую строку вектор Х — (А1:Е1)
Ввести во вторую строку вектор Y — (А2:Е2)
Найти сумму векторов –

выделить блок ячеек для результата в третьей строке ( А3:Е3 );
ввести в строке формул =А1:Е1+А2:Е2
нажать Ctrl+Shift+Enter.

Иллюстрация к примеру — рис. 14.

Рис. 14. Иллюстрация к упражнению 6.1.1.

Задача 6.1.1 . Умножить вектор на число.

Умножение вектор-столбца на вектор-строку.

В блоке (вектор-столбце) А2:А5 записаны числа: 1,2,3,4. Требуется получить в блоке B2:D5 три вектор-столбца, каждый из которых представляет собой результат умножения исходного вектор-столбца на вектор-строку: 2, -3, 4 (B1:D1). Рис.15. К упр. 6.1.2.

1-й способ: записать в ячейку В2 формулу =$А2*В$1 и скопировать ее в остальные ячейки диапазона B2:D5.

2 -й способ (более экономный): выделить блок B2:D5. Запишем в него формулу массива <=А2:А5*B1:D1>.

Анализ решения. Табличный массив <2;-3;4>— вектор-строка, а блок А2:А5 — вектор-столбец. Значит, матрица B2:D5 размерностью 4Х3 является результатом умножения вектор-столбца А2:А5 (4Х1) на вектор-строку B1:D1 (1Х3).

Примечание. Если ввести формулу <=B1:D1* А2:А5>, то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомножителе должно равняться числу строк во втором сомножителе).

У
пражнение 6.1.3. Вычислить скалярное произведение двух векторов.

Установить курсор в ячейку, где нужен результат.
Щёлкнуть кнопку автосуммы — .
Выделить массив Х (А5:А12).
Нажать знак умножить —*.
Выделить массив Y (B5:B12).
Нажать Ctrl + Shift + Enter.

Примечание. Тот же результат можно получить с помощью обычной функции: =СУММПРОИЗВ (А5:А12, В5:В12).

6.2. Матричные операции

Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы.

Упражнение 6.2.1. Сложение матриц.

Задание. Сложить матрицы М и N, где

Решение.
M= и N=

1-й способ:

Ввести матрицу М в блок А1:С2, а матрицу N в блок Е1:G2.
В блок А4:С5 ввести табличную формулу <= А1:С2 + E1:G2>.

Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы.

Использование имен делает процедуру ввода табличной формулы намного проще:

Задать диапазонам А1:С2 и E1:G2 имена М и N.
В блок E4:G5 ввести табличную формулу < = М + N >.

Результат, естественно, тот же: M+N =

Упражнение 6.2.2 . Вычислить линейную комбинацию матриц 2*М — N (матрицы М.и N из упражнения 6.2.1.).

Решение. В блок А7:С8 ввести табличную формулу <= 2*М — N >.

Результат: 2*M — N =

Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложении матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сложение.

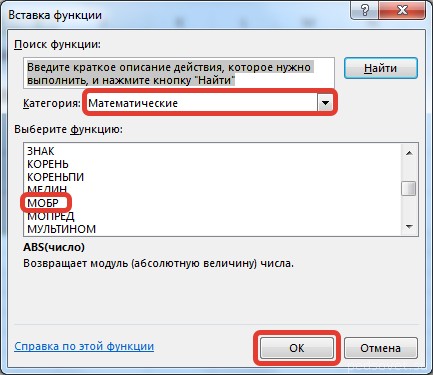
Для матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»:

МОБР — вычисление обратной матрицы;

МУМНОЖ — перемножение матриц;

Примечание. Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.

Упражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы:

Решение. Разместить исходную матрицу в блоке А1 :СЗ.

В ячейке Е2 поместить формулу для вычисления определителя = МОПРЕД (А1:СЗ).
В блок А5:С7 ввести формулу для вычисления обратной матрицы:

выделить блок А5:С7 (он имеет три строки и три столбца, как и исходная матрица).
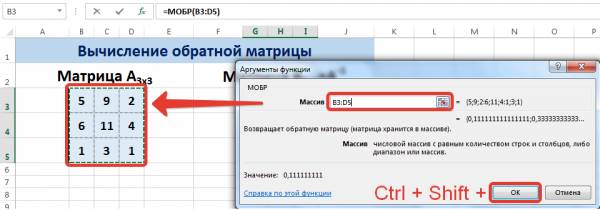
Ввести формулу <=МОБР (А1:СЗ)>.

Примечания:

При использовании Мастера функций нужно завершать ввод нажатием комбинации клавиш Ctrl+Shift+Enter (вместо щелчка по кнопке «ОК»).
Для удобства работы рекомендуется задавать имена исходной матрице и обратной матрице.

Проверить правильность вычисления обратной матрицы умножением ее на исходную:

задать имена исходной матрице — А и обратной матрице — АО;
в блок D5:F7 ввести формулу .
как и следовало ожидать, получилась матрица, близкая к единичной.

Рис. 16. Иллюстрация к упражнению 6.2.3.

У
Решение:
пражнение 6.2.4. Вычислить абсолютные отклонения величин в матрицах.

В блок А9:С11 ввести табличную формулу <= abs (A-AО)>.

Пример вычисления определителя матрицы

А, введенной в формулу как массив констант: =МОПРЕД(<-73; 78; 24:

Задача 6.2.2 . При каком значении элемента а₃₃ определитель матрицы А обратится в нуль.

Задача 6.2.3. Дана матрица S = . Вычислить матрицу 2SS Т — Е, где Т — операция транспонирования,

Е — единичная матрица.

Задача 6.2.4. Вычислить обратную матрицу для

и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы.

 Набор матричных операций в Excel беден.

Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive .

Вычисление длины (модуля) вектора в EXCEL

history 14 декабря 2015 г.

Группы статей

Пользовательский формат

Векторы

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

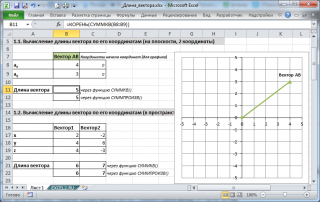
1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a _x и a _y , то длину вектора можно найти по формуле

В случае вектора в пространстве добавляется третья координата

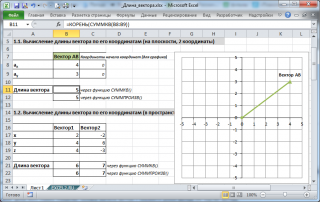
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).

Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .

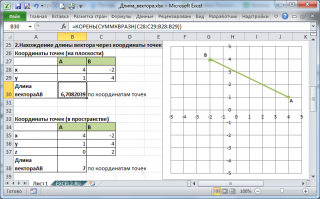
2. Нахождение длины вектора через координаты точек

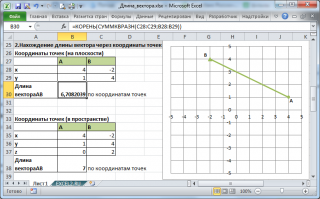
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

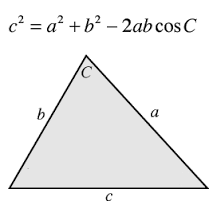
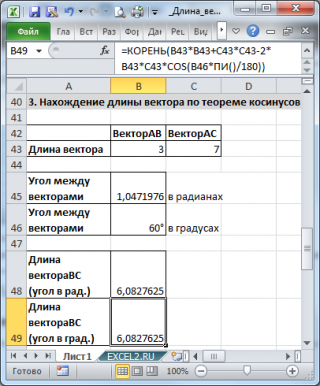
3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

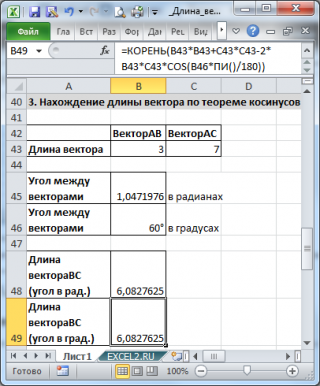
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL

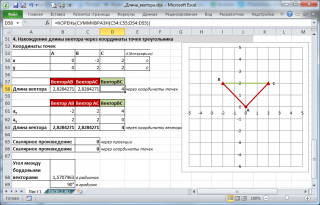
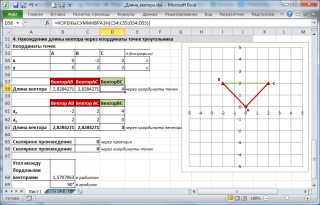
4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.

Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .

Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).

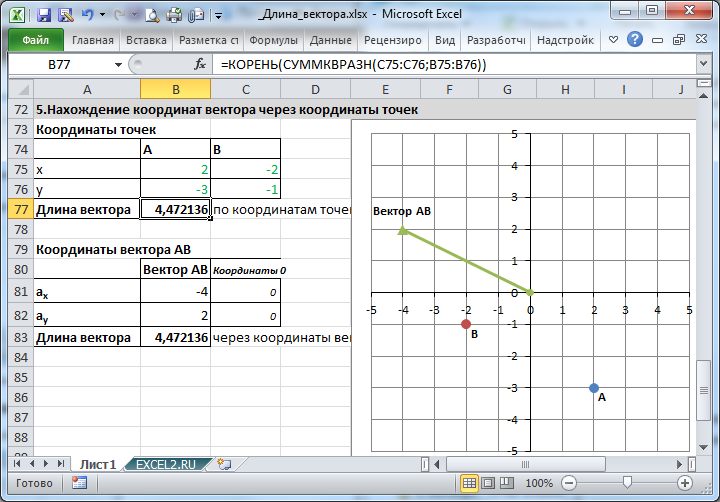
5. Нахождение координат вектора через координаты точек

Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.

Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)

Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:

умножение и деление матрицы на число;
сложение, вычитание и умножение матриц;
транспонирование матрицы;
нахождение обратной матрицы;
вычисление определителя.

Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, а_ij — элемент матрицы.

Умножение и деление матрицы на число в Excel

Способ 1

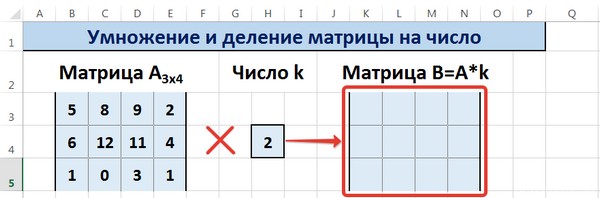
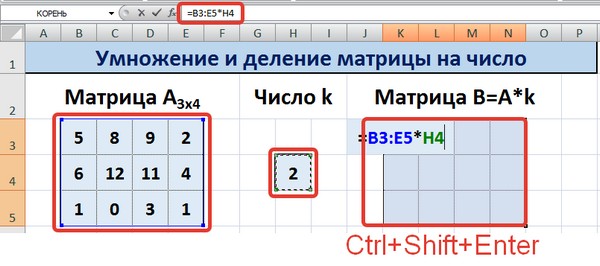
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

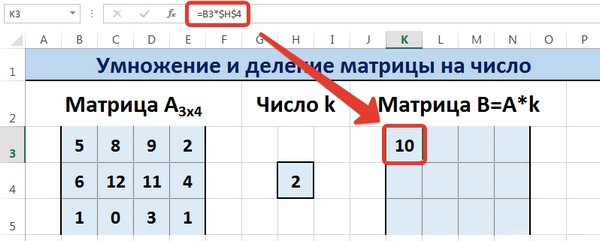
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

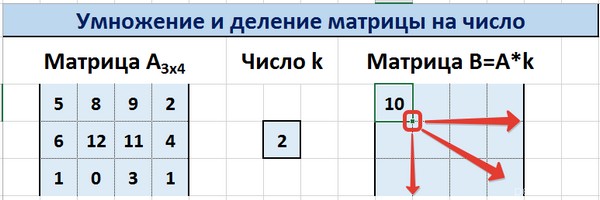
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

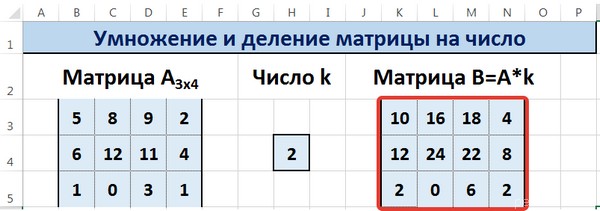
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

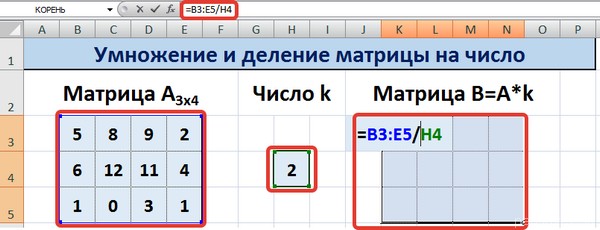
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

Сложение и вычитание матриц в Excel

Способ 1

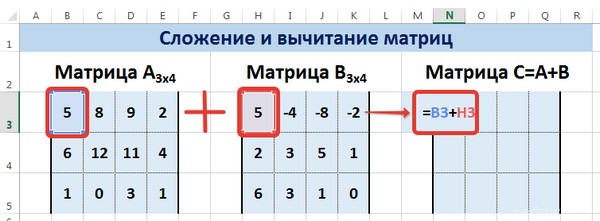
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. с_ij = а_ij + b_ij.

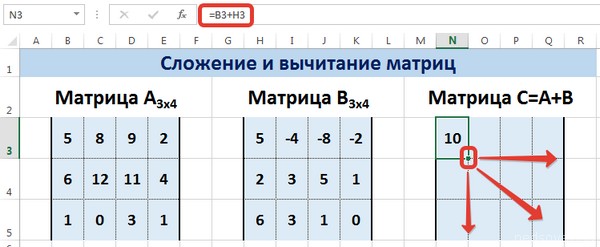
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

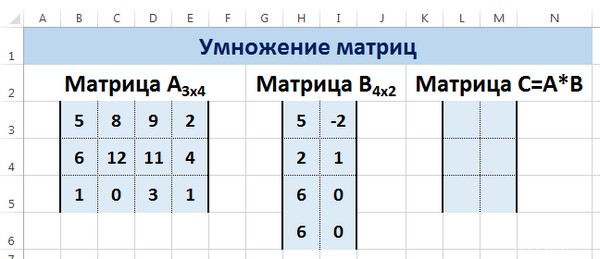
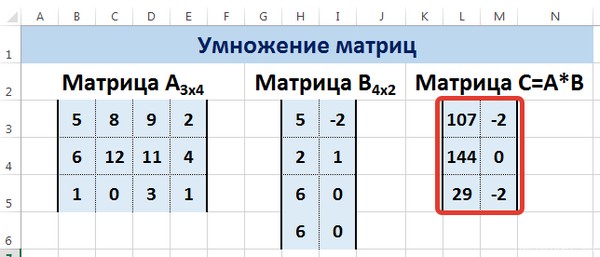
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

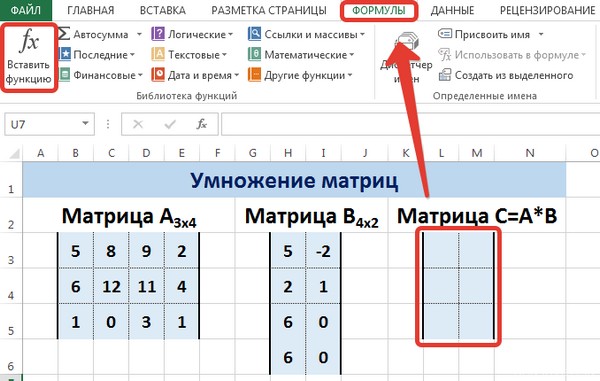
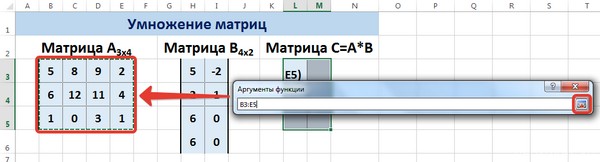
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

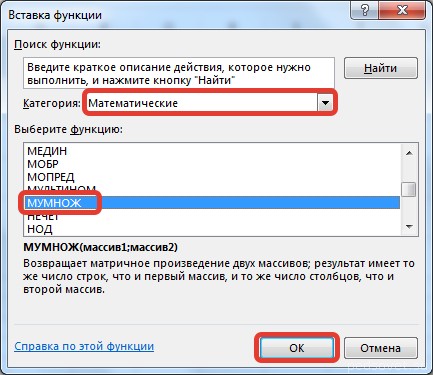
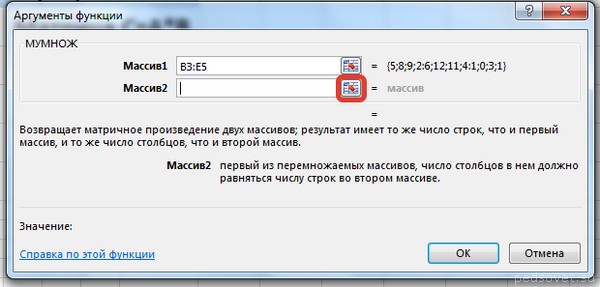
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

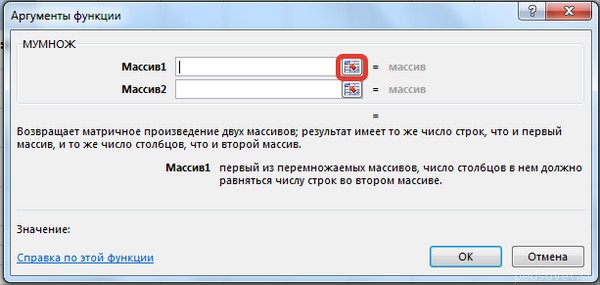
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

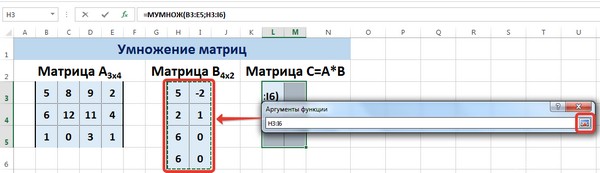
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

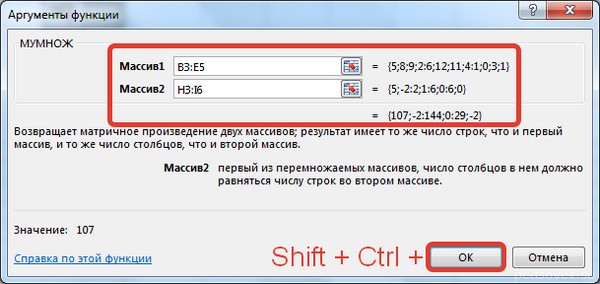
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

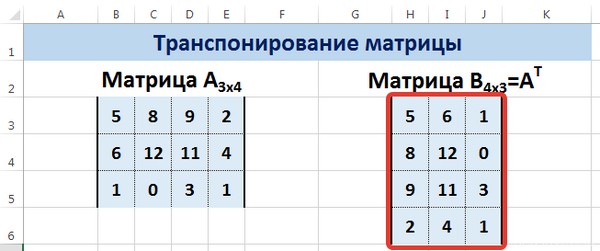
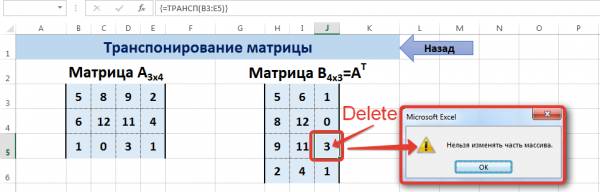
Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .

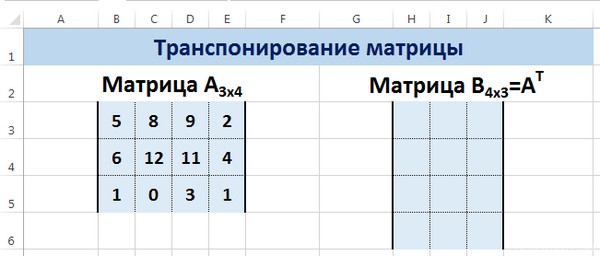
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.

Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.

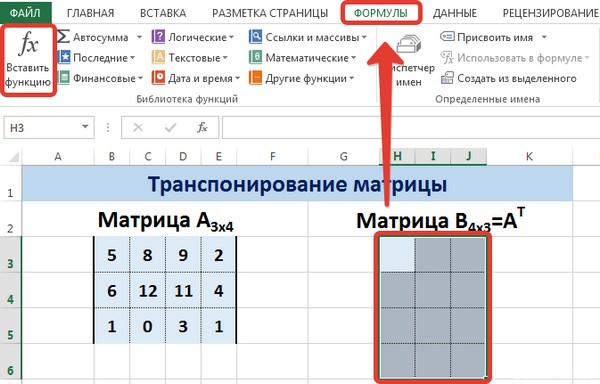
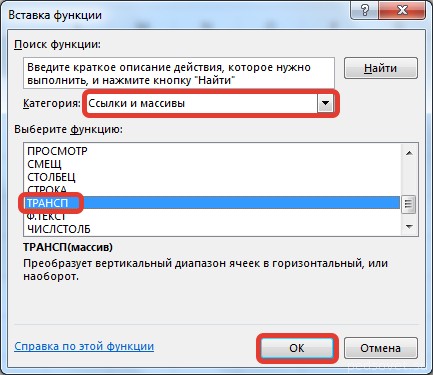
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения

Мы получили транспонированную матрицу.

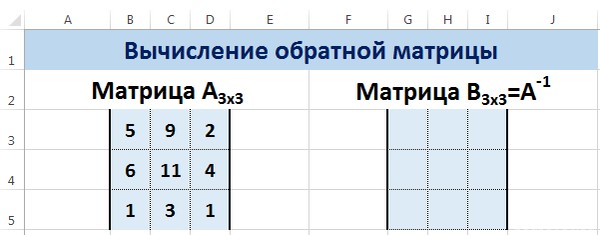
Нахождение обратной матрицы в Excel

Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

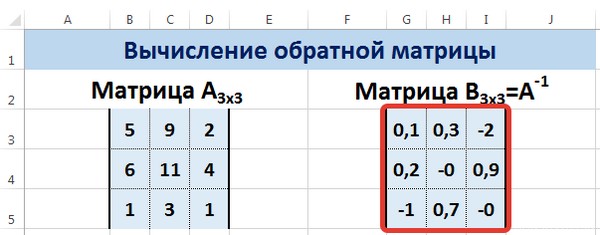
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

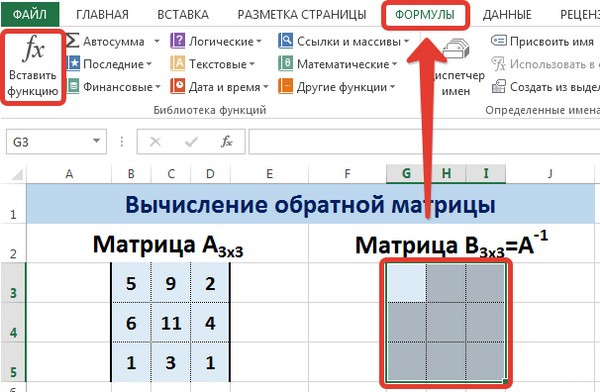
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения

Мы получили обратную матрицу.

Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

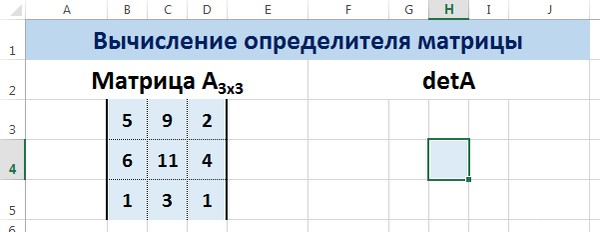
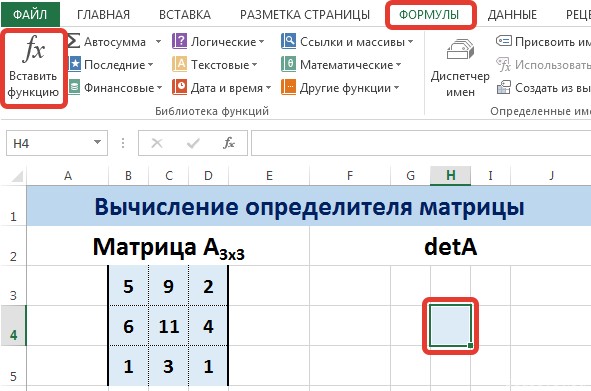
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().

Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.

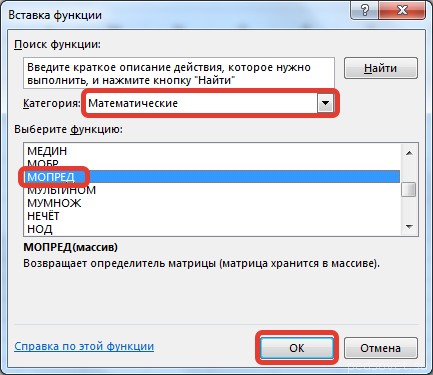
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.

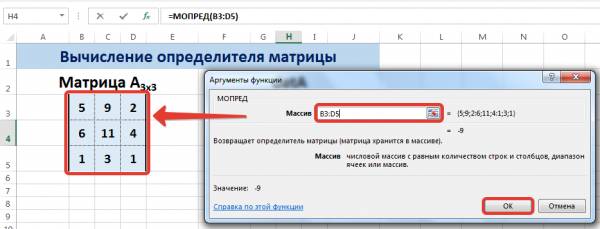
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

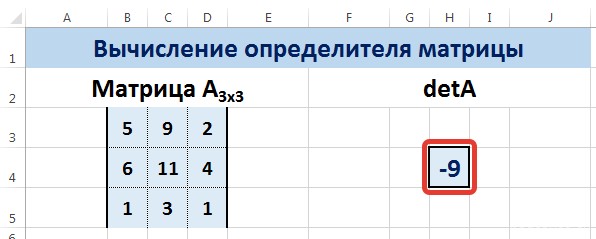
Нажмите для увеличения

Мы вычислили определитель матрицы А.

В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

источники:

http://excel2.ru/articles/vychislenie-dliny-modulya-vektora-v-ms-excel

http://pedsovet.su/excel/6080_operacii_s_matricami

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Еще…Меньше

Windows: 2208 (сборка 15601)
Mac: 16.65 (сборка 220911)
Веб: представлено 15 сентября 2022
г.
iOS: 2.65 (сборка 220905)
Android: 16.0.15629

Переносит предоставленную строку или столбец значений по строкам после указанного количества элементов, чтобы сформировать новый массив.

Синтаксис

=СВЕРНСТРОК(вектор; количество_для_переноса; [заполняющее_значение])

Синтаксис функции WRAPROWS поддерживает следующие аргументы:

вектор Вектор или ссылка для переноса.
количество_для_переноса Максимальное количество значений для каждой строки.
заполняющее_значение Значение, используемое для заполнения. Значение по умолчанию — #Н/Д.

Заметки

Элементы вектора помещаются в двухмерный массив по строкам. Каждая строка содержит количество элементов, равное значению аргумента «количество_для_переноса». Строка заполняется аргументом «заполняющее_значение», если недостаточно элементов для ее заполнения. Если wrap_count больше или равно числу элементов в векторе, то вектор просто возвращается в одной строке.

Ошибки

Excel возвращает #ЗНАЧ, если вектор не является одномерным массивом.
Excel возвращает #ЧИСЛО!, если wrap_count меньше 1.
Excel возвращает ошибку #Н/Д для каждой ячейки в возвращаемом массиве, который не содержит результатов.

Примеры

Скопируйте образец данных из следующей таблицы и вставьте его в ячейку A1 нового листа Excel. При необходимости можно отрегулировать ширину столбцов, чтобы видеть все данные.

Переносит строку в диапазоне A2:G2 в массив в диапазоне A4:C6 из 3 столбцов. Последние два отсутствующих элемента возвращают #N/A.

Данные
A	B	C	D	E	F	G
Формулы
=WRAPROWS(A2:G2,3)

Переносит строку в диапазоне A2:G2 в массив в диапазоне A4:C6 из 3 столбцов. Последние два отсутствующих элемента возвращают символ панели «x».

Данные
A	B	C	D	E	F	G
Формулы
=WRAPROWS(A2:G2,3,»x»)

См. также

Функция CHOOSECOLS

Функция CHOOSEROWS

Функция WRAPCOLS

Нужна дополнительная помощь?

Источник

Вектор

– это направленный отрезок прямой.

Длина этого отрезка определяет числовое значение вектора и называется

длиной вектора или модулем вектора.

1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a
_x
и a
_y
, то длину вектора можно найти по формуле

В случае вектора в пространстве добавляется третья координата

В MS EXCEL выражение

=КОРЕНЬ(СУММКВ(B8:B9))

позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки

B8:B9

, см.

файл примера

).

Функция

СУММКВ()

возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =

B8*B8+B9*B9

.

В

файле примера

также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение

=КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9))

.

2. Нахождение длины вектора через координаты точек

Если вектор

задан через координаты точек его начала и конца, то формула будет другой

=КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны

C28:C29

и

B28:B29

соответственно.

Функция

СУММКВРАЗН()

в

озвращает сумму квадратов разностей соответствующих значений в двух массивах.

3. Нахождение длины вектора по теореме косинусов

Найдем длину вектора с используя формулу

=КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках

B43:B43

содержатся длины векторов а и b, а в ячейке

В45

— угол между ними в радианах (в долях числа

ПИ()

).

Если угол задан в градусах, то формула будет немного отличаться

=КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание

: для наглядности в ячейке со значением угла в градусах можно применить

пользовательский формат

, см. например, статью

Отображение широты и долготы в MS EXCEL

4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.

Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле

=КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55))

.

5. Нахождение координат вектора через координаты точек

Источник

Пример формулы массива

Что такое формула массива в Excel
Массивы в Excel
- Отличие массивов от диапазонов в Excel
- Размерность массивов
- Виды массивов
Методы создания массивов
- Массив констант, созданный вручную
- Именованный массив констант
- С помощью функций
- С помощью математических операторов
- С помощью операторов сравнения
- С помощью других массивов
- С помощью комбинаций указанных методов
Вывод массива на лист
Взаимодействие функций Excel с массивами
Формулы массива – примеры формул

Формулы массива – загадочная и, казалось бы, сложнейшая сущность в Excel. Но на практике все очень просто, нужно только понять принцип их работы и рассмотреть несколько примеров.

Не знаю, новичок вы в Excel или уже опытный пользователь, но коль судьба привела вас на эту страницу, в ходе прочтения вы:

узнаете все о формулах массива;
увидите множество примеров таких формул;
сможете начать активно их применять на практике.

Поехали!

Формула массива (array formula) – это такая формула, в процессе вычисления которой создается один или несколько массивов. При этом не обязательно как результат вычисления, но и как промежуточный этап.

Будьте на 100% уверены: если формула

принимает массив на вход,
создает его как промежуточную сущность
или выводит как результат вычислений

– это формула массива.

Слишком очевидно и все еще непонятно? Не беда – читаем далее.

На деле, прежде, чем говорить о формулах массива, нужно упомянуть сами массивы и их отличие от диапазонов. Т.к. многие не до конца понимают разницу.

Массивы в Excel

Массив (array) – это фиксированный набор элементов с фиксированным порядком. Иными словами, все элементы массива, включая их положение в нем, являются его неотъемлемой частью, их порядок и количество нельзя изменить.

Отличие массивов от диапазонов в Excel

В отличие от массива, диапазон (range) – это просто метод адресации к ячейкам в Excel, никак не связанный с самим их содержимым.

Между ячейками диапазона можно вставить дополнительные столбцы и строки, сделав его длиннее и шире, а ссылка на такой диапазон изменится автоматически.

Содержимое диапазона также можно свободно сортировать, если в нем нет объединенных ячеек.

Если же на лист Excel выведен массив, ни сортировка строк, ни вставка строк и столбцов в середину диапазона, в который он выведен, не возможна – это нарушило бы само его определение.

При попытке изменения порядка элементов массива Excel выдаст ошибку. К сожалению, она не очень информативна и не сообщает, какой массив или массивы имеются в виду. Текст ошибки:

Нельзя изменить часть массива.

Ошибка Excel при попытке нарушить целостность массива

Размерность массивов

Как массивы, так и диапазоны в Excel могут быть одномерными (вектор), двумерными (таблица) и трехмерными (многослойная таблица).

Одномерные массивы (векторы) в свою очередь могут быть вертикальными и горизонтальными.

Одномерные и двумерные массивы в Excel

Трехмерные массивы – довольно редко используемая на практике сущность.

Виды массивов

По типам элементов в них:
По типу данных –

числовой массив (массив чисел)
строковый массив (текстовые значения)
булевый массив (значения ИСТИНА-ЛОЖЬ)
смешанного типа

По изменяемости элементов –

массив констант,
вычисляемый массив

Методы создания массивов

Создать массив в Excel можно множеством способов. Ниже – подробнее с примерами. Все перечисленные выражения в них являются формулами массива, даже если не содержат в себе функций.

Массив констант, созданный вручную

Одномерные и двумерные массивы констант можно создавать вручную и сразу выводить на лист безо всяких дополнительных операций над ними.

При этом разделителем между элементами слева направо является точка с запятой, а разделителем строк – двоеточие.

Двумерные массивы вводятся построчно, т.е. сначала первая строка через точку с запятой, далее двоеточие, вторая строка через точку с запятой, и так далее.

Именованный массив констант

Если приходится один и тот же набор сущностей использовать часто в формулах, его можно сохранить в книге как именованный массив.

Массив цифр как в примере ниже, поможет быстро найти цифры в текстовых ячейках.

создание именованного массива констант на примере цифр

Создаем именованный массив в Excel

Это позволит больше не вводить его вручную, а обращаться к нему по его имени. Более того, Microsoft Excel помогает при их вводе всплывающими подсказками.

Используем именованный массив

С помощью функций

Указанные выше методы создания массивов довольно редки на практике. Чаще всего массивы создаются автоматически при обращении различных функций к диапазонам в Excel.

Единственное условие для создания массива с помощью функции – функция не должна обладать агрегирующим свойством. Например, СУММ, СРЗНАЧ не создадут массив при обращении к диапазону.

На этом сайте есть статья – как дописать символ, слово или текст к нескольким ячейкам. Там рассматриваются несколько способов, в том числе без создания дополнительного столбца. Но вот еще один – с помощью функции СЦЕПИТЬ и формулы массива:

Формула массива с функциями СЦЕПИТЬ и СИМВОЛ

Кавычки-ёлочки в этой формуле нам помогает создать функция СИМВОЛ.

С помощью математических операторов

Достаточно применить любую из математических операций к диапазону – и будет создан массив, аналогичный по размерам.

Массивы в Excel, полученные с помощью математических операторов

С помощью операторов сравнения

Аналогично математическим операторам, массивы создаются при сравнении диапазонов с константой или значением ячейки. Результатом операции сравнения являются значения ИСТИНА или ЛОЖЬ.

Массивы в Excel, полученные с помощью операторов сравнения

С помощью других массивов

В двух предыдущих примерах массивы создавались на основе взаимодействия диапазона ячеек и некой константы.

Но можно создать массив и по принципу наоборот – на основе одной ячейки, произведя ее взаимодействие (операторами или функциями) с массивом констант.

Размер результирующего массива в таком случае будет аналогичен размеру массива констант.

Еще раз обратите внимание на разделители строк и столбцов в массивах. Столбцы разделяются точкой с запятой, строки – двоеточием.

С помощью комбинаций указанных методов

Как вы уже догадались, возможности фантазии безграничны – можно строить какие угодно комбинации перечисленных выше методов, производя операции над массивами и диапазонами.

Вывод массива на лист

Для корректного вывода массива на лист нужно выделить диапазон ячеек эквивалентной размерности и размера, использовать метод создания массива (вручную или формулой), и нажать

Ctrl+Shift+Enter

Если выделить недостаточное количество ячеек – будут выведены не все элементы массива, а только те, что соответствуют по порядку.
Если выделить избыточное количество – лишние ячейки выдадут ошибку #Н/Д.

На примере результирующий массив должен быть размером 5*5, но перед вводом формулы массива был выделен диапазон 6*6.

Ошибка НД при несоответствии размера диапазона и массива

Взаимодействие функций Excel с массивами

Как мы уже выяснили чуть ранее, некоторые функции могут создавать массивы, если их применить к диапазону ячеек. Они обычно обращаются к одной ячейке, и таких функций в Excel большинство.

Однако, есть ряд функций, называемых агрегирующими. Если им на вход подается диапазон или массив, они возвращают единственное результирующее значение. Самая популярная – функция СУММ. Но есть и множество других.

Из раздела математических функций к таковым также относятся ПРОИЗВЕД, СУММПРОИЗВ, СУММЕСЛИ, СУММЕСЛИМН.

Практически все статистические функции по природе берут на вход диапазон или массив и возвращают одно число. Наиболее популярные из них – СРЗНАЧ, МИН, МАКС, СЧЁТ, СЧЁТЗ, СЧЁТЕСЛИ.

Среди логических функций агрегирующим свойством обладают функция И и функция ИЛИ.

Ну и особняком можно выделить функции поиска. Их нельзя в полной мере назвать агрегирующими, но их взаимодействие с массивами весьма похоже. Ведь они тоже:

учитывают весь массив
выводят одно значение

ВЫБОР, ВПР, ГПР, ИНДЕКС, ПОИСКПОЗ – эти функции поиска используются наиболее часто.

Формулы массива – примеры формул

Ну что ж, теперь, когда основной понятийный аппарат рассмотрен, приступим к практическому этапу. Я покажу на нескольких задачках из реальной жизни, как их решать, используя комбинации функций и массивов, которые они создают и обсчитывают.

Приступаем к практическим шагам:

Учимся формулам массива 1/4:

Как создать алфавит в Excel

Источник

Вы когда-нибудь пытались преобразовать матрицу ячеек в одну строку или столбец в Excel? Возможно, вы можете скопировать строку или столбец и вставить их одну за другой в один вектор, но это займет много времени, если есть несколько строк и столбцов. В этой статье я расскажу о некоторых интересных методах и надеюсь, что они помогут вам.

Преобразование матрицы ячеек в одну строку или столбец с помощью формул

Преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel

Преобразование нескольких столбцов или строк в один столбец или строку:

Программа Kutools for Excel Transform Range может помочь вам преобразовать диапазон ячеек только в один столбец или строку, напротив, он также может преобразовывать одну строку или столбец в диапазон ячеек.

Kutools for Excel : с более чем 200 удобными надстройками Excel, которые можно бесплатно попробовать без ограничений в течение 60 дней. Скачать и бесплатную пробную версию сейчас!

Содержание

Преобразование матрицы ячейки в одну строку или столбец с формулами
Преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel
Демо: преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel

Преобразование матрицы ячейки в одну строку или столбец с формулами

Следующие формулы могут помочь вам быстро преобразовать матрицу в одну строку или столбец. Пожалуйста, сделайте следующее:

Преобразуйте матрицу ячеек в один столбец

1 . Прежде всего, вы должны определить имя диапазона для данных матрицы. Выберите диапазон ячеек и введите имя диапазона в поле Имя , которое находится рядом со строкой формул, а затем нажмите клавишу Enter . В этом случае я набираю «Матрица» в качестве определенного имени, см. Снимок экрана:

2 . Затем введите следующие формулы:

(1.) Преобразуйте матрицу в один столбец на основе строки, это означает, что значения берутся из каждой строки, перемещаясь затем вниз: = OFFSET (Matrix, TRUNC ((ROW () – ROW ($ G $ 1))/COLUMNS (матрица)), MOD (ROW () – ROW ($ G $ 1), COLUMNS (Matrix)), 1,1) ( Matrix – это имя диапазона, которое вы определили на шаге 1, а G1 – это ячейка, в которую вы вводите эту формулу). Затем перетащите маркер заполнения к ячейкам, пока не отобразится 0, см. Снимок экрана:

(2.) Преобразуйте матрицу в один столбец на основе столбца, это означает, что значения берутся из столбцов, перемещаясь вниз на один столбец, а затем в правый столбец: = OFFSET (Matrix, MOD (ROW () – ROW ($ G $ 1), ROWS (матрица)), TRUNC ((ROW () – ROW ($ G $ 1))/ROWS (матрица)), 1,1) ( Matrix – это имя диапазона, которое вы определили на шаге 1, а G1 – это ячейка, в которую вы вводите эту формулу). Затем перетащите маркер заполнения в ячейки, пока не отобразится 0, см. Снимок экрана:

Преобразование матрицы ячеек в одну строку

Чтобы преобразовать матрицу ячеек в одну строку, вы можете использовать следующие формулы:

(1.) Преобразуйте матрицу в одну строку на основе строки, это означает, что значения берутся из каждой строки слева направо в одной строке, а затем перемещаются вниз в следующую строку: = OFFSET (Matrix, TRUNC ((COLUMN () – COLUMN ($ A $ 7))/COLUMNS (Matrix)), MOD ((COLUMN () – COLUMN ($ A $ 7)) , COLUMNS (Matrix)), 1,1) ( Matrix – это имя диапазона, которое вы создали для своего диапазона данных, а A7 – это (введите эту формулу). Затем перетащите маркер заполнения вправо в ячейки, пока не отобразится 0, см. снимок экрана:

(2.) Преобразование матрицы в одну строку на основе столбца, это означает, что значения берутся из каждого столбца, перемещаясь на один столбец вниз, а затем в правый столбец: = OFFSET (Matrix, MOD ((COLUMN () – COLUMN ($ A $ 7)), ROWS (Matrix)), TRUNC ((COLUMN () – COLU MN ($ A $ 7))/(ROWS (Matrix))), 1,1) ( Matrix – это имя диапазона, которое вы создали для своего диапазона данных, а A7 – ячейка, в которой вы вводите эту формулу). Затем перетащите маркер заполнения вправо к ячейкам, пока не отобразится 0, см. Снимок экрана:

Преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel

Если приведенные выше формулы слишком длинные напомню, что здесь я могу порекомендовать простой и мощный инструмент – Kutools for Excel , с его утилитой Transform Range , вы можете быстро преобразовать несколько столбцов и строк в один столбец или строку по мере необходимости.

Kutools for Excel : с более чем 300 удобными надстройками Excel, которые можно попробовать бесплатно без ограничений в течение 30 дней .

Перейти к загрузке
Бесплатная пробная версия 30 днейПокупка
PayPal/MyCommerce

После установки Kutools for Excel выполните следующие действия:

1 . Выберите матрицу ячеек, которую вы хотите преобразовать.

2 . Затем нажмите Kutools > Range > Transform Range , см. Снимок экрана:

3 . В диалоговом окне Преобразовать диапазон выберите Диапазон в один столбец , если вы хотите преобразовать матрицу в один столбец, или выберите Диапазон в одна строка , если вы хотите преобразовать матрицу в одну строку, см. снимок экрана:

4 . Затем нажмите кнопку OK и в появившемся поле Transform Range выберите ячейку, в которую вы хотите поместить результат, см. Снимок экрана:

5 . Затем нажмите кнопку OK , выбранная матрица ячеек была преобразована в одну строку или столбец.

Чтобы узнать больше об этом диапазоне преобразования утилита.

Загрузите бесплатную пробную версию Kutools for Excel прямо сейчас!

Демо: преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel

Kutools for Excel : с более чем 300 удобными надстройками Excel, вы можете попробовать бесплатно без ограничений в течение 30 дней. Загрузить и бесплатная пробная версия сейчас!

Источник