Вейвлет анализ в excel

There, I said it, and aloud: ‘EXCEL’!

I got this idea of making a modern (no, I am NOT kidding) educational tool to interactively construct and study Ricker wavelets after reading William Ashcroft’s A Petroleum Geologist’s Guide to Seismic Reflection. The book is a gem, in my opinion (I discovered it thanks to a blog post by Matt Hall a couple of years ago) and comes with some interesting tools on a DVD, which are unfortunately a bit outdated. So I went back to my old Geophysics Bible (Yilmaz’ book Seismic Data Analysis), and mashed a few ideas up; you can Download the Excel file here. Please feel free to use it, peruse it, and abuse it, in your classes, labs, nightmares, etcetera…

The tool is fairly simple. In Sheet 1 the user enters the dominant frequency of the desired Ricker wavelet, as shown in the middle of Figure 1. From that informatin the wavelet is constructed using the equation A = g^2 * 1/exp g^2 where g is the ration between frequency f  (in increments of 5 Hz up to an arbitrary 125 Hz – but this could be easily changed!) and the dominant frequency f1 just entered.  frequencies. The frequency spectrum of the wavelet is shown as a graph.

In Figure 2 I show the same Sheet, but for a wavelet of dominant frequency equal to 50 Hz.

A number of ancillary graphs, shown in Figure 3, display individual building blocks of the formula A = g^2 * 1/exp g^2.

In Sheet 2 the user can view a plot of the wavelet in the time domain,  add Constant phase shifts and Linear phase shifts, and experiment with different combinations of them, as shown in Figures 4-7, below.

Finally, Sheet 3 displays a plot of the wavelet, and of the individual frequency components that make it up. Have fun!!!

References and further playing

A Petroleum Geologist’s Guide to Seismic Reflection, William Ashcroft, 2011, Wiley.

Практика работы с функциями вейвлет-анализа и синтеза сигналов представлена почти во всех системах компьютерной математики (СКМ). В книге [7] дано подробное описание практики вейвлет-анализа в СКМ: Mathcad (Wavelet Extension Pack), MATLAB (Wavelet Toolbox) и Mathematica (Wavelet Explorer). Вопросы теории фильтрации, вейвлет-преобразований, кратно-масштабный анализ (КМА) и его применение в системе MATLAB представлены в [8]. Система Маple версии 15 и более поздних версий имеет систему программирования [9] и реализацию для проведения вейвлет-анализа, такие как дискретное вейвлет-преобразование (ДВП) и другие. Очевидным недостатком СКМ является трудность использования их возможностей в построении автоматизированных КИС. Среда разработки ВП NI LabVIEW [10] имеет возможности не только разработки распределенных КИС, в том числе на базе средств технического зрения (модуль IMAQ Vision) [11, 12] и робототехники [13], но и заданной реализации математической обработки сигналов [14]. Дополнительный модуль Advanced Signal Processing Toolkit фирмы National Instruments (NI) содержит огромный набор функций, реализующих практически все современные математические методы обработки сигналов: частотно-временного анализа (Time Frequency Analysis); функций статистического и корреляционного анализа, оценки спектра и моделирования (Time Series Analysis); функции вейвлет-анализа (Wavelet Analysis). Среда разработки приложений на базе NI LabVIEW позволяет также использовать узлы свойств для обеспечения серверов сценариев, предоставляемых другими производителями ПО, такими, например, как MATLAB [15]. Это расширяет ее функциональные возможности информационного анализа сигналов. Несмотря на широкие возможности модуля Advanced Signal Processing Toolkit, в настоящее время в литературе отсутствует систематическое описание его состава и функциональных возможностей, отсутствует описание практики его применения для анализа сигналов.

Функции вейвлет-анализа входят в дополнительный пакет Advanced Signal Processing Toolkit. Наряду с другими функциями обработки сигналов эти функции представлены в палитре функций (Signal Processing) следующими палитрами виртуальных подприборов (ВПП): Continuous Wavelet, Discrete Wavelet, Wavelet Packet, Feature Extraction, Utilities, Online Wavelet Analysis (рис. 1).

В первой палитре ВПП Continuous Wavelet находится две функции вейвлет-преобразований:

• WA Continuous Wavelet Transform VI;
• WA Analytic Wavelet Transform VI.

Функция WA Continuous Wavelet Transform VI вычисляет непрерывное вейвлет-преобразование (CWT — НВП) входного сигнала, представленного 1D-массивом с различными типами вейвлетов. Вход данных для входного сигнала полиморфный, что обеспечивает возможность работы с разными форматами входных сигналов (массив, волна). ВПП WA Continuous Wavelet Transform VI реализует алгоритм НВП, который определяется следующим уравнением:

где s(t) — входной сигнал, j₀ — функция материнского вейвлета, a, τ — масштаб и сдвиг (a > 0 — вещественное).

Аналитическое вейвлет-преобразование (AWT-АВП) является частным случаем НВП с комплекснозначным вейвлетом Морле, который называется также вейвлетом Габора. Следующее уравнение определяет комплекснозначный вейвлет Морле:

Вторая палитра функций Discrete Wavelet реализует прямое или обратное дискретное вейвлет-преобразование (DWT — ДВП), вычисление недецимированного прямого или обратного вейвлет-преобразования (UWT), вычисление целочисленного прямого или обратного вейвлет-преобразования (IWT — ЦВП), на выходе которого получаются характерные коэффициенты DWT, UWT и IWT, а также позволяет производить вычисление любого пути преобразования или реконструкции. Палитра ВПП Discrete Wavelet (рис. 2) представлена набором из четырех экспресс-функций (табл. 1) и набором ряда простых ВПП (функций), представленных в таблице 2. Палитра содержит еще одну подпалитру четырех функций Filter Banks.

Экспресс-функции — это многофункциональные функции, выбор параметров, работа которых и предварительный просмотр результатов их действия задается в окне конфигуратора.

Пример работы экспресс-функции Multiresolution Analysis 2D Express VI в окне ее конфигуратора представлен на рис. 3. В конфигураторе ВПП выбирается изображение или указывается путь к файлу изображения, устанавливается уровень разложения (Levels), тип вейвлета (Wavelet). Выбранные параметры позволяют сразу увидеть результат в окнах просмотра. Как и для всех экспресс-функций, часть установленных параметров не является впоследствии ее входными данными, то есть после закрытия окна конфигуратора их изменить нельзя.

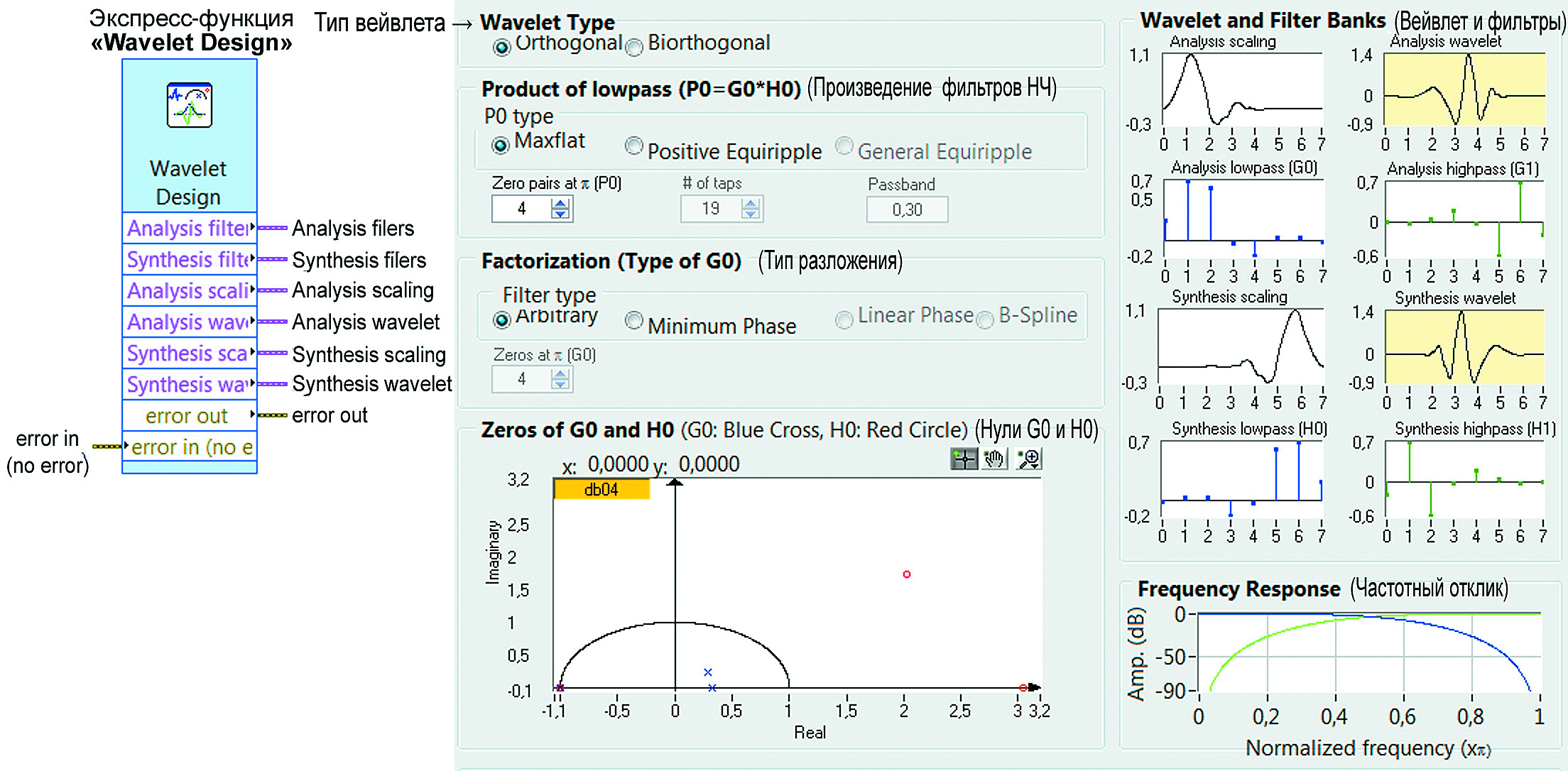
Экспресс ВП Wavelet Design Express VI конструирует заданные фильтры вейвлетов анализа и фильтры синтеза для дискретного вейвлет-анализа и реконструкции (рис. 4). Общее количество синтезируемых фильтрами вейвлетов (табл. 2) превышает количество известных поименованных. В нижнем окне графика (Zeros of G0 and H0) отображается название вейвлета, соответствующего сконструированным фильтрам.

В палитре дискретного вейвлет-преобразования представлена палитра простых (низкоуровневых) функций (ВПП), использующих набор двухканальных (квадратурных) фильтров для вычисления одноуровневого дискретного вейвлет-преобразования или синтеза, используя для вычисления материнской и масштабирующей функций набор фильтров, получение заранее проектируемой функции вейвлета для коэффициентов, заданных фильтрами анализа. Описание и назначение функций ВПП палитры Discrete Wavelet представлены в таблице 3. Вход данных сигнала для ВПП полиморфный относительно типов (форматов) подаваемых сигналов.​

№	Иконка	Название	Описание
1.		WA Discrete Wavelet Transform VI	Вычисляет дискретное многоуровневое вейвлет-преобразование (DWT — ДВП) сигнала. ВПП возвращает коэффициенты аппроксимации на верхнем уровне и коэффициенты детализации на всех нижних уровнях для 1D входного сигнала. Этот ВПП возвращает коэффициенты аппроксимации и коэффициенты детализации на всех уровнях для 2D входного сигнала. Этот ВПП вычисляет ДВП на каждом уровне, используя фильтры НЧ- и фильтры ВЧ-анализа с коэффициентами прореживания 2.
2.		WA Integer Wavelet Transform VI	Вычисляет многоуровневое целочисленное вейвлет-преобразование (IWT — ЦВП) сигнала, используя восходящую схему. Этот ВПП возвращает коэффициенты аппроксимации на верхнем уровне и коэффициенты детализации на всех нижних уровнях для входа 1D-сигнала и возвращает коэффи-циенты аппроксимации и коэффициенты детализации на всех уровнях для 2D входного сигнала.
3.		WA Undecimated Wavelet Transform VI	В отличие от ДВП, которое производит снижение разрешения коэффициентов аппроксимации и коэффициентов детализации на каждом уровне разложения, недецимированное вейвлет-преобразование (UWT) не включает даунсамплинг операции. Таким образом, коэффициенты аппроксимации и коэффициенты детализации на каждом уровне имеют одинаковую длину, как и исходный сигнал. UWT пересчитывает коэффициенты нижних и верхних фильтров на каждом уровне. Операция дискретизации эквивалентна дилатации вейвлетов. Разрешение коэффициентов UWT уменьшается с увеличением уровня разложения.
4.		WA Arbitrary Path Decomposition VI	Выполняет анализ разложением частотного поддиапазона каскадными фильтрами НЧ и фильтрами ВЧ с применением коэффициента прореживания 2 после каждого шага фильтрации. Путь указывает поддиапазон частот и определяет каскад НЧ- и ВЧ-фильтров анализа сигнала.
5.		WA Inverse Discrete Wavelet Transform VI	Вычисляет многоуровневое обратное ДВП (IDWT — ОДВП) и возвращает реконструированный сигнал от коэффициентов аппроксимации и детализации. Интерполятор с коэффициентом 2 синтезирующих фильтров НЧ и ВЧ осуществляет обратное ДВП на каждом уровне.
6.		WA Inverse Integer Wavelet Transform VI	Вычисляет многоуровневое обратное целочисленное вейвлет-преобразование (ОЦВП) и возвращает восстановленный сигнал от коэффициентов аппроксимации и коэффициентов детализации.
7.		WA Inverse Undecimated Wavelet Transform VI	Вычисляет многоуровневое обратное недецимированное вейвлет-преобразование (IUWT) и возвращает реконструированный сигнал от коэффициентов аппроксимации и детализации.
8.		WA Arbitrary Path Reconstruction VI	Восстанавливает сигнал с коэффициентами частотных поддиапазонов.
9.		WA Get Coefficients of Discrete Wavelet Transform VI	Возвращает коэффициенты аппроксимации или детализации на определенном уровне ДВП. Для вычисления ДВП сигнала используется ВПП WA Discrete Wavelet Transform VI.
10.		WA Get Coefficients of Integer Wavelet Transform VI	Возвращает коэффициенты аппроксимации или детализации на определенном уровне ЦВП. Для вычисления ЦВП сигнала используется ВПП WA Integer Wavelet Transform VI.
11.		WA Get Coefficients of Undecimated Wavelet Transform VI	Возвращает коэффициенты аппроксимации или детализации на определенном уровне недецимированного вейвлет-преобразования (UWT). Для вычисления UWT сигнала используется ВПП WA Undecimated Wavelet Transform VI.
12.		WA Set Coefficients of Discrete Wavelet Transform VI	Устанавливает коэффициенты аппроксимации или детализации на определенном уровне ДВП. Для вычисления ДВП сигнала используется ВПП WA Discrete Wavelet Transform VI. Для получения коэффициентов ДВП используется ВПП WA Get Coefficients of Discrete Wavelet Transform VI.
13.		WA Set Coefficients of Integer Wavelet Transform VI	Устанавливает коэффициенты аппроксимации или детализации на определенном уровне ЦВП. Для вычисления ЦВП сигнала используется ВПП WA Integer Wavelet Transform VI. Для получения коэффициентов ЦВП используется ВПП WA Get Coefficients of Integer Wavelet Transform VI.
14.		WA Set Coefficients of Undecimated Wavelet Transform VI	Устанавливает коэффициенты аппроксимации или детализации на определенном уровне недецимированного вейвлет-преобразования (UWT). Для вычисления UWT сигнала используется ВПП WA Undecimated Wavelet Transform VI. Для получения коэффициентов UWT используется ВПП WA Get Coefficients of Undecimated Wavelet Transform VI.

В отличие от дискретного преобразования Фурье (ДПФ), которое представляет собой дискретный вариант преобразования Фурье, дискретное вейвлет-преобразование (DWT — ДВП) на самом деле не является дискретным вариантом непрерывного вейвлет-преобразования (НВП). ДВП функционально отличается от НВП. Для реализации ДВП использует дискретные банки фильтров для вычисления дискретных вейвлет-коэффициентов. Использование банков двухканальных фильтров реконструкции — идеальный и эффективный способ (perfect reconstruction — PR) реализации ДВП. На рис. 5 показана двухканальная система PR-банка фильтров.

Сигнал X(z) сначала фильтруется банком фильтров, состоящих из фильтров G₀(z) и G₁(z). Выходы G₀(z) и G₁(z) затем прореживаются с коэффициентом 2 (децимация). После некоторой обработки модифицированные сигналы повышают дискретизацию с коэффициентом 2 и фильтруются другим банком фильтров, состоящим из H₀(z) и H₁(z). Если нет обработки между двумя банками фильтров, сумма выходов H₀(z) и H₁(z) совпадает с исходным сигналом X(z), с учетом времени задержки. Это система двухканальных PR-фильтров, где G₀(z) и G₁(z) образуют банк фильтров анализа, H₀(z) и H₁(z) образуют банк фильтров синтеза.

Обычно считают G₀(z) и H₀(z) фильтрами НЧ, а G(z) и H₁(z) — фильтрами ВЧ. Индексы 0 и 1 относятся к фильтрам низких и высоких частот соответственно. Операция ↓2 обозначает прореживание сигнала с коэффициентом два (децимация). Применение фактора децимации до сигнала гарантирует, что количество выходных отсчетов двух фильтров нижних частот равно числу исходных входных выборок сигнала X(z). Таким образом, нет избыточной информации, которая добавляется при разложении сигнала. Можно использовать систему PR-банка двухканальных фильтров при последовательном разложении сигнала фильтрами НЧ, как показано на рис. 6.

Фильтры НЧ удаляют высокочастотные колебания из сигнала и сохраняют медленные тренды. Выходы фильтров НЧ обеспечивают аппроксимацию сигнала, фильтры ВЧ — удаляют медленные тренды из сигнала и сохраняют высокочастотные колебания. Выходы фильтров ВЧ обеспечивают подробную информацию о сигнале. Выходы фильтров НЧ и ВЧ определяют коэффициенты аппроксимации и коэффициенты детализации соответственно. Символы «А» и «D» на рис. 6 представляют информацию аппроксимации и детализации соответственно.

В описании ВП вейвлет-анализа используемые LabVIEW индексы «0» и «1» описывают путь разложения, где «0» указывает фильтрацию НЧ, а «1» указывает фильтрацию ВЧ. Например, D₂ на рис. 6 обозначает вывод двухкаскадной фильтрации операции фильтрации НЧ, а затем ВЧ-фильтрации. Таким образом, описывается путь разложения с последовательностью «01». Аналогично, D_L обозначает выход из операций фильтрации «000…1», в котором общее количество разложений: 0…L–1. Импульсный отклик «000…1» асимптотически сходится в материнский вейвлет, и импульсный отклик «000…0» сходится к масштабирующей функции в вейвлет-преобразовании.

Сигнальное 1D-вейвлет-разложение и реконструкцию можно расширить для обработки 2D-сигнала. На каждом уровне этот ВПП реализует ДВП 1D на каждой строке сигнала. Затем данный ВПП применяет ДВП к каждому столбцу 1D-сигнала предыдущего выхода. Этот ВП выполняет обратное преобразование с обратной операцией. Рис. 7 показывает реализацию банка фильтров для 2D ДВП. Выход low_low — это приближение входного 2D-сигнала в большем масштабе, выходы low_high, high_low и high_high соответствуют детальной информации по столбцу, строке и диагональным направлениям.

Функции ВПП банков фильтров (Filter Banks) применяются для вычисления двухканального дискретного вейвлета путем одноуровневого преобразования или синтеза на основе банка фильтров, путем вычисления функции материнского вейвлета и масштабирующей функции из банка фильтров и получения коэффициентов анализирующих и синтезирующих фильтров для заданного вейвлета. Описание и назначение ВПП подпалитры Filter Banks (рис. 2) представлены в таблице 4. Вход данных сигналов ВПП полиморфный для различных типов сигналов.

Пример использования WA Analysis Filter Bank VI для 2D-изображения представлен на рис. 8.

Палитра функций ВПП Wavelet Packet предназначена для вычислений различных видов пакетного вейвлет-анализа, таких как пакетное разложение, реконструкция пакетов и различные операции по дереву вейвлет-разложения пакетов. Состав палитры представлен на рис. 9.

Экспресс-функция (ВПП) Wavelet Packet Analysis Express VI из данной палитры разлагает сигнал в соответствии с указанной
древовидной структурой и восстанавливает сигнал от указанных узлов. Этот ВП возвращает также коэффициенты разложения и энтропию выбранных узлов (рис. 10). Настройки ВПП позволяют выбрать тип вейвлета, уровень декомпозиции, тип энтропии. Узлы в дереве декомпозиции (Decomposition Tree) активны для выбора, два окна предварительного просмотра отображают исходный и выбранный узлы сигналов.

Описание и назначение других функций ВПП палитры Wavelet Packet позволяют реализовать алгоритм пакетной обработки низкоуровневым способом, их описание представлено в таблице 5. Вход данных сигнала ВПП полиморфный для различных типов сигналов.

Палитра функций Feature Extraction используется для оценки плотности вероятности функции, обнаружения пиков, обнаружения границ и гребней функций на основе кратномасштабного вейвлет-анализа (КМА), с целью снижения шума, путем вычитания трендов. Функции палитры Feature Extraction представлены на рис. 11.

Экспресс-функция Wavelet Denoise Express VI выполняет шумоподавление для 1D-сигналов с помощью дискретного вейвлет-преобразования (ДВП) недецимированного вейвлет-преобразования (UWT) заданным типом вейвлета. На рис. 12 показан результат действия функции в окне ее конфигуратора для зашумленного сигнала (Gaussian White Noise, σ = 0,6), сигнала типа меандр (square) частотой 25 Гц, частотой выборки 5000 Гц.

Описание и назначение других ВПП палитры Feature Extraction представлены в таблице 6. Тип входного сигнала полиморфного входа устанавливается автоматически или выбирается вручную.

Палитра утилит функций Utilities содержит ВПП для чтения файлов данных, которые используют как демонстрационные данные и отображают квадрат величины амплитуды или фазы вейвлет-коэффициентов сигнала на графике интенсивности. Палитра содержит три ВПП, показанные на рис. 13а, описание и назначение функций представлено в таблице 7.

Палитра функций Online Wavelet Analysis предназначена для онлайн-вейвлет-анализа путем выполнения онлайн-вычитания тренда и пикового детектирования. Палитра содержит два ВПП, показанных на рис. 13б. Описание функций ВПП палитры Online Wavelet Analysis представлено в таблице 8. Вход данных сигнала полиморфный для различных типов сигналов.

Наряду с NI LabVIEW среда программирования LabWindows/CVI была разработана фирмой National Instruments в середине 1980‑х годов. В отличие от ряда широко известных средств разработки (Borland C++, Delphi, MS Visual Studio и т. д.), LabWindows/CVI ориентирована на разработку ПО, управляющего научным экспериментом, технологическим либо измерительным процессом. Эта направленность и определила содержание и функциональность данного программного продукта. Среда LabWindows/CVI включает интегрированную среду разработки (IDE) на основе языка ANSI C и обширную библиотеку компонентов, которая состоит из следующих составных частей: набор компонентов для создания пользовательского интерфейса; набор библиотек для управления измерительными и управляющими устройствами (VISA Library, VXI Library, RS‑232 Library, GRIB/Grib 488.2 Library); средства для удаленного управления приложениями через локальную сеть или Интернет (Network Variable Library); средства обработки полученных данных — фильтрация, математическая обработка полученных данных, генерация сигналов различной формы (Analysis Library, Advanced Analysis Library); стандартная библиотека ANSI C. Также в библиотеку входят средства для использования технологий DDE, ActiveX, различных сетевых протоколов, технологий .NET, создания многопоточных приложений и др.

Библиотека Signal Processing Toolkit for CVI позволяет реализовать в приложении функции проведения всех видов вейвлет-анализа. Удобный набор приложений, включающий объединенный частотно-временной анализ (JTFA), сверхразрешающий спектральный анализ (Super-Resolution Spectral Analysis) и вейвлет-анализ, представлен приложением с запускающей панелью CVI SPT Start-Up (рис. 14). Этот программный продукт предназначен в первую очередь для демонстрационных целей и оценочного анализа полученных данных.

Анализ представленных средств модуля Advanced Signal Processing Toolkit показывает, что в настоящее время среда разработки NI LabVIEW имеет полный набор функций, реализующих все методы вейвлет-анализа, позволяющие в интерактивном режиме проводить анализ 1D и 2D (изображений) сигналов. Экспресс-функции набора указанных средств дают возможность концептуально оценить эффективность использования вейвлет-анализа с различными параметрами для различных исследуемых сигналов. Методы вейвлет-обработки и анализа сигналов могут выполняться как модельно, так и в реальном времени с использованием аппаратных средств сбора данных, поэтому их можно быстро интегрировать в промышленную платформу КИС. В то же время среда разработки NI LabVIEW позволяет быстро адаптировать ранее созданные готовые решения к различным условиям обработки и сигналам, изменять алгоритм или выбранные параметры, обеспечить быстрое модельное и натурное тестирование независимо от используемой платформы. В отличие от средств математической реализации вейвлет-анализа в СКМ, методы вейвлет-анализа, реализованные в NI LabVIEW, сочетают исследовательский и практический уровень обработки реальных сигналов, расширяя возможности КИС и повышая точность определения параметров исследуемых сигналов.

Reading time
20 min

Views 8.9K

Введение

При проведении CWT анализа средствами библиотеки PyWavelets (бесплатное программное обеспечение с открытым исходным кодом, выпущенное по лицензии MIT) возникают проблемы с визуализацией результата. Предложенная разработчиками тестовая программа по визуализации приведена в следующем листинге:

 import pywt
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(-1, 1, 200, endpoint=False)
sig  = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4)))
widths = np.arange(1, 31)
cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5')
plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto',
             vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max())  # doctest: +SKIP
plt.show() # doctest: +SKIP

При работе с комплексными вейвлетами, например с ‘cmor1-1.5’, программа выдаёт ошибку:

File"C:UsersUserAppDataLocalProgramsPythonPython36libsite-packagesmatplotlibimage.py", line 642, in set_data
    raise TypeError("Image data cannot be converted to float")
TypeError: Image data cannot be converted to float

Указанная ошибка, а так же сложности с выбором масштаба (widths) для обеспечения необходимого временного разрешения, затрудняют, особенно для начинающих пользователей, изучение CWT анализа, что и побудило меня к написанию данной статьи учебного характера.

Целью настоящей публикации является рассмотрение применения нового модуля визуализации scaleogram для анализа простых и специальных сигналов, а так же при использовании методов нормализации, логарифмического масштабирования и синтеза, которые позволяют получить дополнительную информацию при анализе временных рядов.

В статье использована информация из публикации “A gentle introduction to wavelet for data analysis”. В приведенных в указанной публикации листингах примеров исправлены ошибки, и каждый листинг примера приведен к законченному виду, что позволяет его использовать без ознакомления с предыдущими. Для вейвлет – анализа специальных сигналов использованы данные из базы примеров PyWavelets.

Вейвлет-скалограмма — это двумерное представление одномерных данных. На ось X наносится время, а на ось Y — шкала – результат вейвлет — преобразования сигнала соответствующее значению амплитуды сигнала в момент времени X. Аналитическое значение такого графического отображения сигнала состоит в том, что разрешение по времени отображается на оси Y, что даёт дополнительную информацию о динамических свойствах сигнала.

Вейвлет — скалограммы простых сигналов

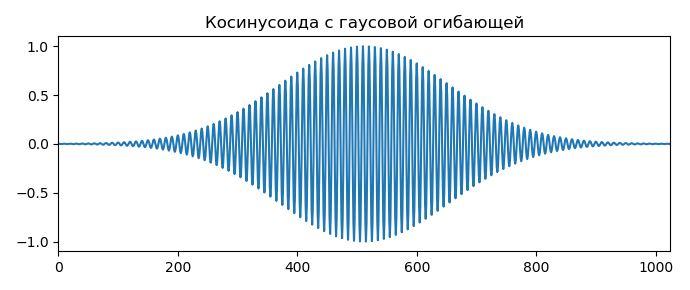
1. Косинусоида с гауссовой огибающей (Заменяя вейвлеты. можно исследовать зависимость временного разрешения от масштаба):

from numpy import* 
from pylab import*
import scaleogram as scg 
import pywt
# Заменяя вейвлеты, можно исследовать зависимость временного разрешения от масштаба
# Без указания вейвлета программа использует вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
#Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time =arange(ns)
scales = scg.periods2scales( arange(1, 40) )
p1=10;
periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2)
fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9));  
lines = ax1.plot(periodic1); 
ax1.set_xlim(0, len(time))
ax1.set_title("Косинусоида с гаусовой огибающей")
fig1.tight_layout()
ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); 
txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w"))
tight_layout()
print("Вейвлет функция для преобразования сигнала:", scg.get_default_wavelet(), "(",
      pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")")
show()

Вейвлет функция для преобразования сигнала: cmor1-1.5 ( Complex Morlet wavelets )

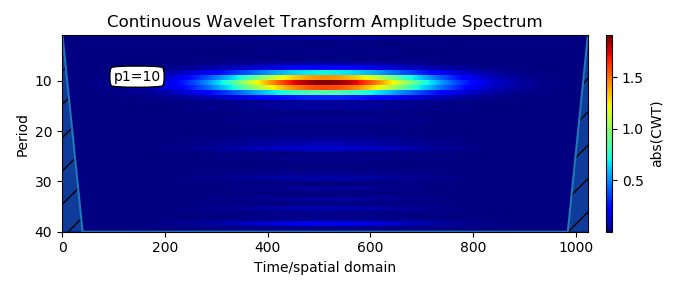
Периодический сигнал теперь появляется в виде горизонтальной непрерывной полосы в точке Y = p1, интенсивность которой изменяется в зависимости от амплитуды периодического сигнала.

Наблюдается некоторая нечеткость в обнаружении, поскольку ширина полосы не равна нулю, это связано с тем, что вейвлеты не обнаруживают одну частоту, а скорее полосу. Данный эффект связан с полосой пропускания вейвлета.

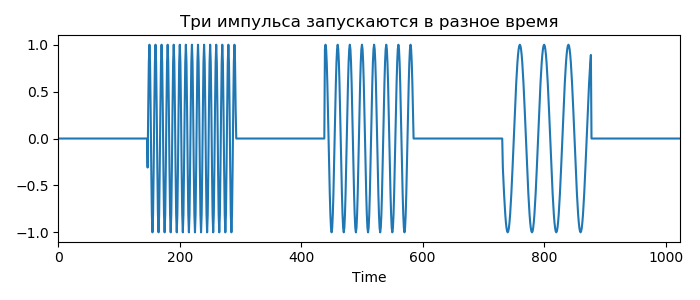
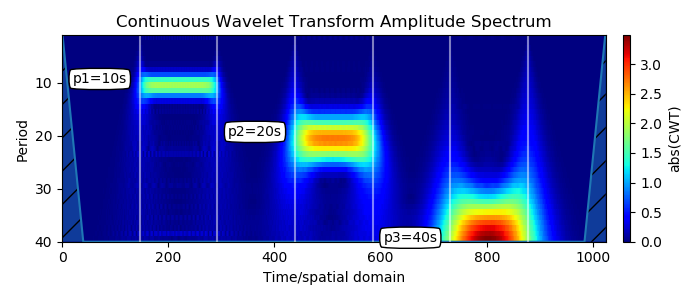
2. Последовательно добавляются три импульса с возрастающим периодом (Для рассмотрения периодических вариации в разных масштабах: анализ мульти разрешения):

from  numpy import* 
import pandas as pd 
from pylab import*
import scaleogram as scg 
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
# Без указания вейвлета программа использует вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
pulses = zeros(ns, dtype=float32)
steps  = linspace(0, ns, 8)
periods = [10, 20, 40]
for i in range(0,3):
    step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2])
    pulses += cos(2*pi/periods[i]*time) * step_mask

fig1, ax1 = subplots(1, 1, figsize=(7,3));  
lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); 
ax1.set_title("Три импульса запускаются в разное время"); ax1.set_xlabel("Time")
fig1.tight_layout()

ax2 = scg.cws(pulses, scales=scales, figsize=(7,3))

for i in range(0, 3):
    txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), 
                       bbox=dict(boxstyle="round4", fc="w"))
    ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5)
    ax2.plot(steps[i*2+2]*np.ones(2),   ax2.get_ylim(), '-w', alpha=0.5)
tight_layout()
show()

Импульсы появляются в ожидаемом месте Y, соответствующем их периодичности, они локализованы по частоте и во времени. Начало полосы и конец соответствуют импульсу.
Ширина полосы масштабируется с длиной периода. Это известное свойство вейвлет-преобразования: когда масштаб увеличивается, разрешение по времени уменьшается. Это также известно как компромисс между временем и частотой. Когда вы смотрите на спектрограмму такого типа, вы проводите много разрешающий анализ.

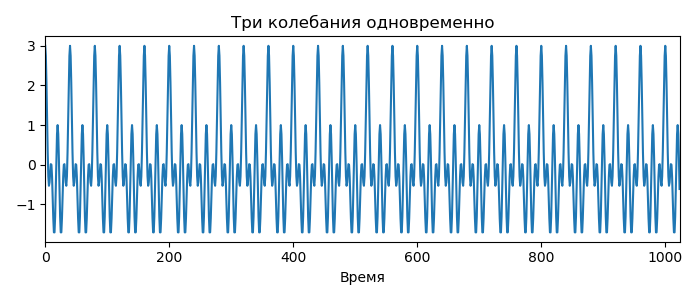
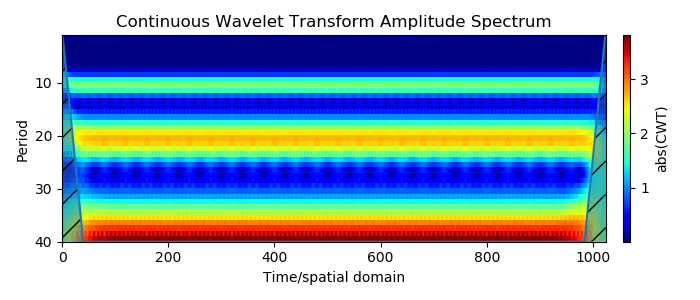
3. Три периодических колебания разной частоты одновременно (Вейвлет — анализ способен различить составляющие сигнала по частотам, если их отличия существенны):

from  numpy import* 
import pandas as pd 
from pylab import*
import scaleogram as scg 
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
allwaves = np.zeros(ns, dtype=np.float32)
periods = [10, 20, 40]
for i in range(0,3):
    allwaves += cos(2*np.pi/periods[i]*time)

fig1, ax1 = subplots(1, 1, figsize=(6.5,2));  
lines = ax1.plot(allwaves); ax1.set_title("Три колебания одновременно") 
ax1.set_xlim(0, len(time)); ax1.set_xlabel("Время")
fig1.tight_layout()

ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2))
tight_layout()
show()

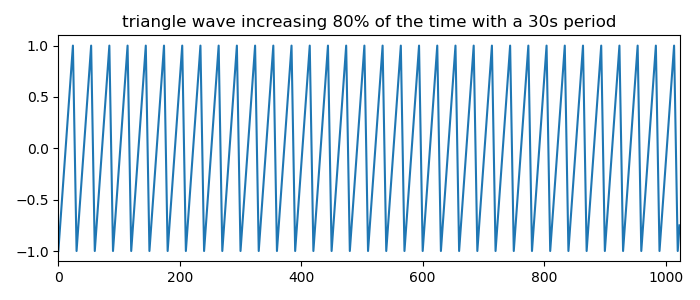
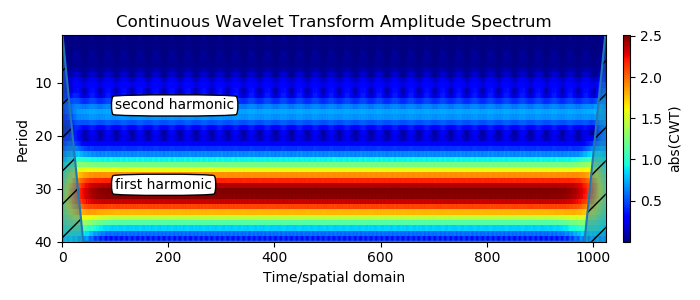
4. Периодический сигнал не синусоидальной формы (Рассматривается отличие в вейвлет — преобразованиях сигнала треугольной формы с периодом 30 секунд от ранее рассмотренных):

from  numpy import* 
from pylab import*
import scipy.signal
import scaleogram as scg 
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунд
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
ptri    = 30.0 # period in samples
raising = 0.8  # fraction of the period raising
triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising)

# plot the signal 
fig1, ax1 = subplots(1, 1, figsize=(7,3));  
lines = ax1.plot(triangle); 
ax1.set_xlim(0, len(time))
ax1.set_title("triangle wave increasing 80% of the time with a 30s period")
fig1.tight_layout()

# and the scaleogram
ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); 
txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w"))
txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w"))
tight_layout()
show()

Большая полоса — это первая гармоника. Вторая гармоника видна ровно в половине значения периода первой гармоники. Это ожидаемый результат для периодических несинусоидальных сигналов. Нечеткие вертикальные элементы появляются вокруг второй гармоники, которая слабее и имеет амплитуду 1/4 от первой для сигнала треугольной формы.

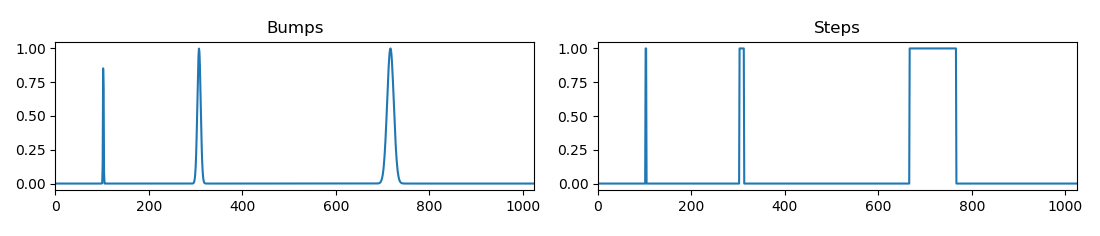
5. Гладкие импульсы (гауссианы) схожи с реальными структурами данных. (В этом примере показано, как использовать вейвлет — анализ для обнаружения локализованных изменений сигнала во времени):

Серия гладких импульсов с различными значениями сигмы:

Ширина импульсов:

from  numpy import* 
from pylab import*
import scaleogram as scg 
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунд
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
# несколько гауссовских импульсов с учетом сигмы
s1=1; s2=5; s3=10
events = [ns*0.1, ns*0.3, ns*0.7]
bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + 
        exp(-((time-events[2])/s3)**2) 

# несколько шагов с учетом полуширины
w1=1; w2=5; w3= 50
steps = ((time > events[0]-w1) & (time < events[0]+w1)) + 
    ((time > events[1]-w2) & (time < events[1]+w2)) + 
    ((time > events[2]-w3) & (time < events[2]+w3))

# график импульсов
fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); 
ax1.set_title("Bumps"); ax2.set_title("Steps")
lines = ax1.plot(bumps); ax1.set_xlim(0, len(time))
lines = ax2.plot(steps); ax2.set_xlim(0, len(time))
fig1.tight_layout()

# и скалограмма
scales_bumps = scg.periods2scales(arange(1, 120, 2) )
fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3));  
ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3)
ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4)
for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]:
    ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5)
    ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5)
fig2.tight_layout()
show()

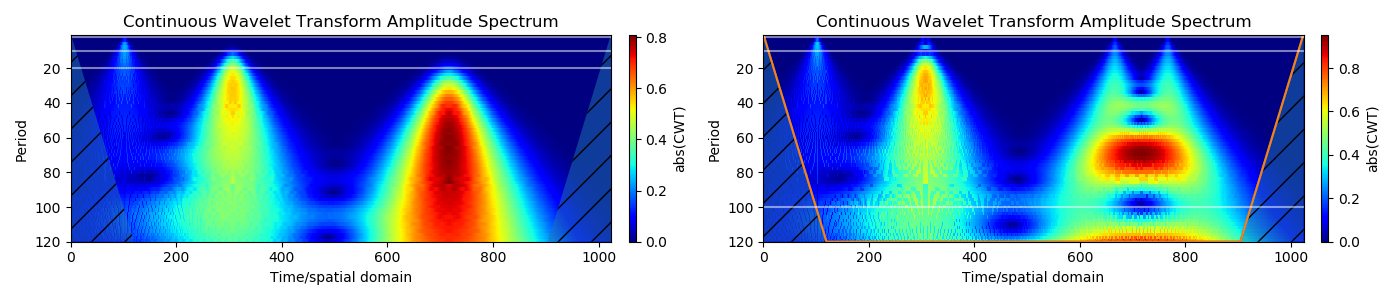
Дискретные импульсы создают конусообразные структуры на сиалограмме, которые также известны как конус влияния. Гладкие импульсы (гауссианы) схожи с реальными структурами данных и создают конусы, расширяющиеся в сторону больших масштабов. Горизонтальные направляющие линии приблизительно соответствуют периодам времени (2 с, 10 с, 20 с). Следовательно, импульс похож на периодический сигнал с одним периодом.

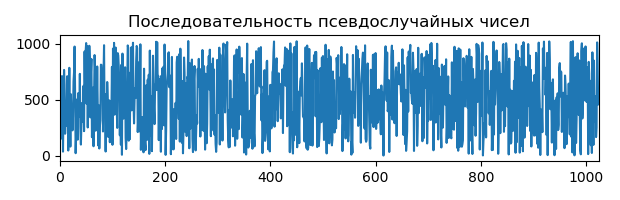
6. Шум (Отображение шума на сиалограмме):

from numpy import* 
from pylab import*
import scaleogram as scg 
import random
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
#Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time =arange(ns)
scales = scg.periods2scales( arange(1, 40) )
noise =random.sample(range(ns), ns)


fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2));  
ax1.set_title("Последовательность псевдослучайных чисел")
lines = ax1.plot(time, noise) 
ax1.set_xlim(0, ns)
fig1.tight_layout()

ax2 = scg.cws(noise, scales=scales, figsize=(7,2))
tight_layout()
show()

Шум обычно отображается в виде набора элементов, а некоторые неровности могут выглядеть как объекты реальных данных, поэтому при использовании реальных данных необходимо соблюдать осторожность, и, при необходимости, проверить уровень шума. Верхний график будет отличатся при каждом запуске программы.

Вейвлет скалограммы специальных сигналов

В базе данных PyWavelets содержаться двадцать специальных сигналов вейвлет преобразования которых будут полезны как для изучения, так и для разработки. Поэтому приведу листинг позволяющий провести вейвлет анализ всех двадцати сигналов:

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
from pylab import*
import scaleogram as scg 
import pywt
signals = pywt.data.demo_signal('list')
signal_length=1024
for signal in signals:
    if signal in ['Gabor', 'sineoneoverx']:
        x = pywt.data.demo_signal(signal)
    else:
        x = pywt.data.demo_signal(signal, signal_length)   
    times=[]
    signals=[]
    for time, sig in enumerate(x.real):
        times.append(time)
        signals.append(sig)
    scg.set_default_wavelet('cmor1-1.5')
    scales = scg.periods2scales( arange(1, 40) )
    fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9));  
    lines = ax1.plot(signals); 
    ax1.set_xlim(0, len(times))
    ax1.set_title("%s"%signal)
    fig1.tight_layout()
    ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); 
    tight_layout()
    show()

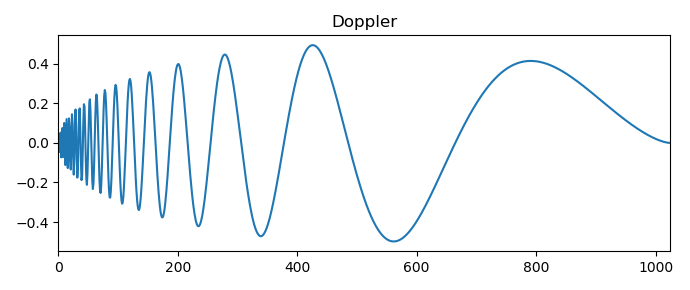
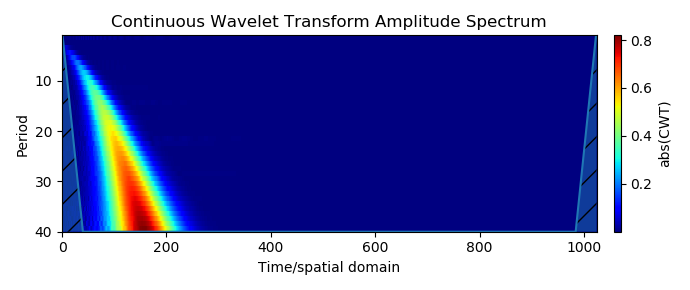
Приведу только один результат вейвлет преобразования Доплеровского сигнала:

Рассмотрены наиболее распространённые разновидности простых и специальных сигналов, что позволяет перейти к использованию скалограммы для решения некоторых задач анализа временных рядов.

Вейвлет скалограммы временных рядов

1. CDC данные о рождаемости в США 1969-2008 (Данные о рождаемости содержат периодические особенности, как в годовом масштабе так и в меньшем):

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)

fig = figure(figsize=(12,2))
lines = plot(births.index, births.values/1000, '-')
xlim(datetime_lim)

ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)");
xlim = xlim()

ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day")
set_x_yearly(ax, len(births))
show()

Горизонтальная линия появляется с периодичностью около 7 дней. Высокие значения появляются вблизи границ шкалы, что является нормальным поведением вейвлет — обработки. Эти эффекты хорошо известны как конус влияния, именно поэтому (необязательная) маска накладывается на эту область.

2. Нормализация (Удаление среднего значения —births_normed = births-births.mean() является обязательным, в противном случае границы данных рассматриваются как этапы, которые создают много ложных конусовидных обнаружений):

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day")
set_x_yearly(ax, len(births))
show()

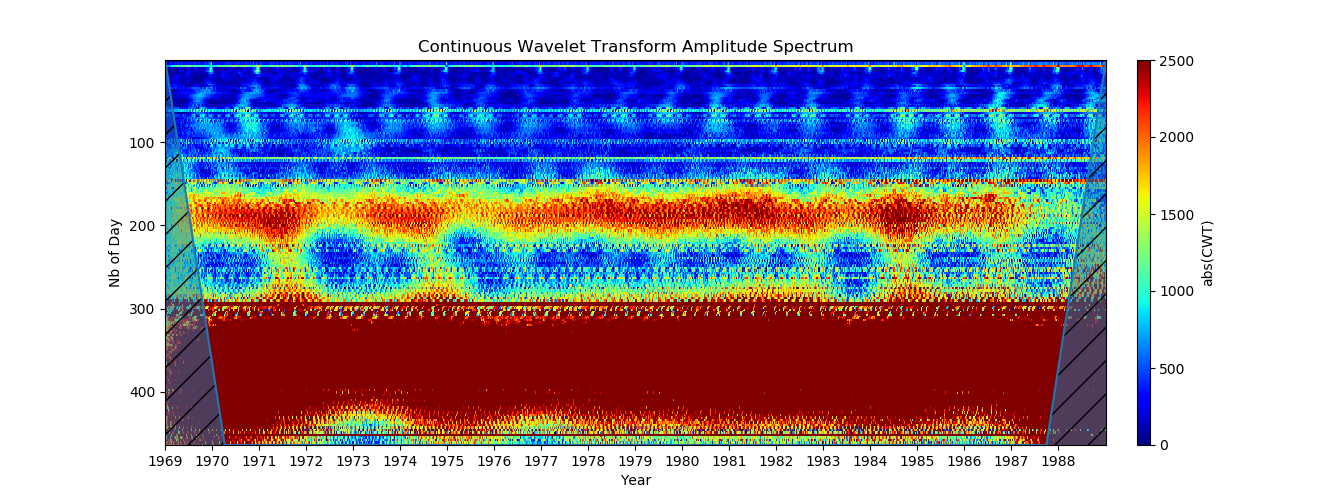
3. Cмена масштаба по амплитуде (Чтобы увидеть годовые объекты, с помощью period2scales () уточняется масштаб по оси Y.):

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
scales = scg.periods2scales(np.arange(1, 365+100, 3))
ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day",
            clim=(0, 2500))
set_x_yearly(ax, len(births))
show()

Диапазон амплитуд цветовой карты (ось Y) теперь задается параметром clim = (0,2500). Точное значение для амплитуды колебаний зависит от вейвлета, но будет оставаться близко к порядку действительного значения. Это намного лучше, теперь мы очень хорошо видим годовую вариацию, а также примерно 6 месяцев!

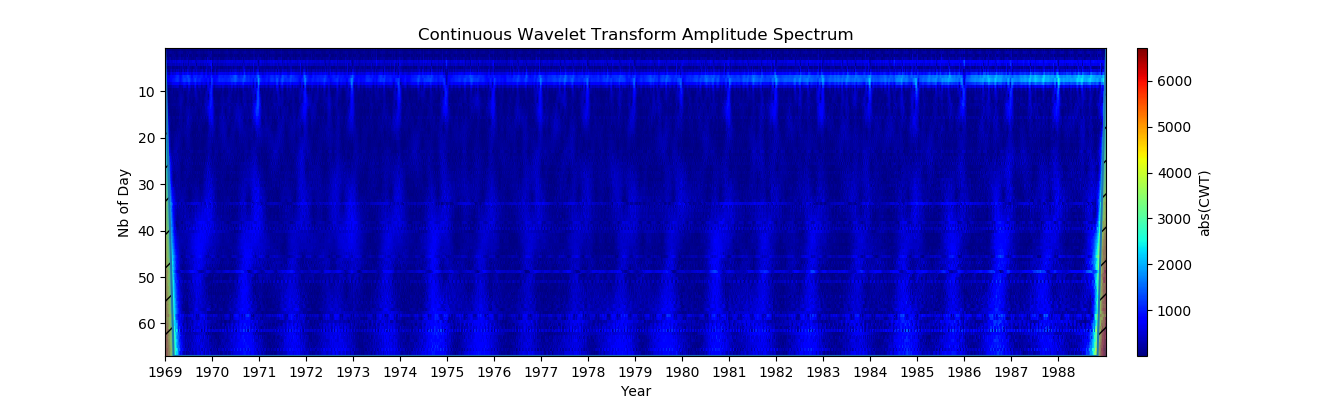
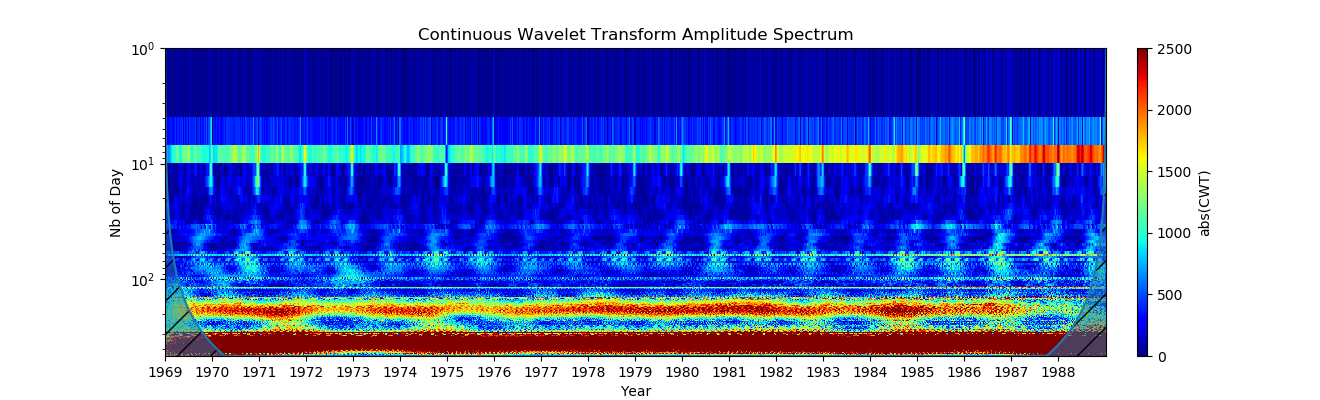
4. Использование логарифмической шкалы (Чтобы можно было видеть маленькие и большие периоды одновременно, лучше использовать логарифмическую шкалу на оси Y. Это достигается с помощью опции xscale = log.)

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
scales = scg.periods2scales(np.arange(1, 365+100, 3))
ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))
print("Number of available days:", len(births_normed))
show()

Результат намного лучше, но теперь пиксели при низких значениях периодов вытянуты вдоль оси Y.

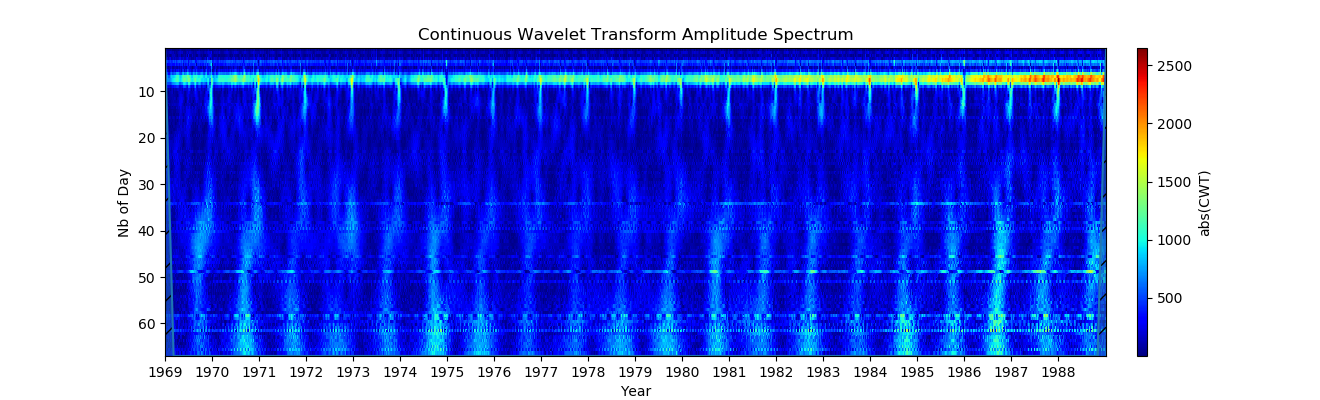
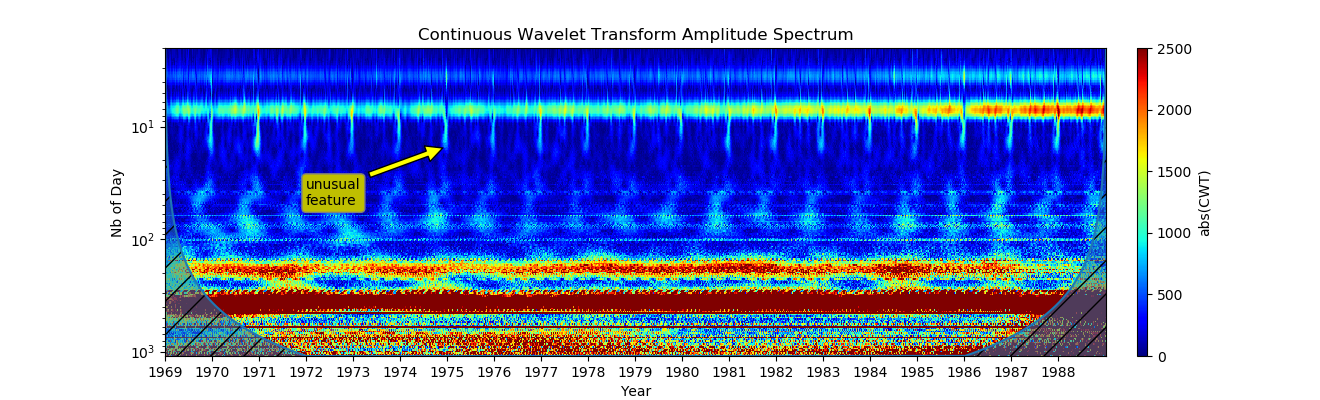
5. Равномерное распределение по логарифмической шкале( Чтобы получить однородное распределение по шкале, значения периода должно быть равномерно распределено, а затем преобразовано в значения шкалы, как показано ниже:):

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))

# сохранить CWT в объекте, чтобы избежать пересчета для следующих участков
cwt = scg.CWT(births_normed, scales=scales) 

ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))

bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5")
arrowpropsf = dict(facecolor='yellow', shrink=0.05)
text = ax.annotate("unusualnfeature", xy=(365*6, 15), xytext=(365*3, 50), 
                   bbox=bboxf, arrowprops=arrowpropsf)
show()

Мы можем видеть изменения сигнала на всех масштабах. Сиалограмма показывает каждый год в одинаковых периодах.

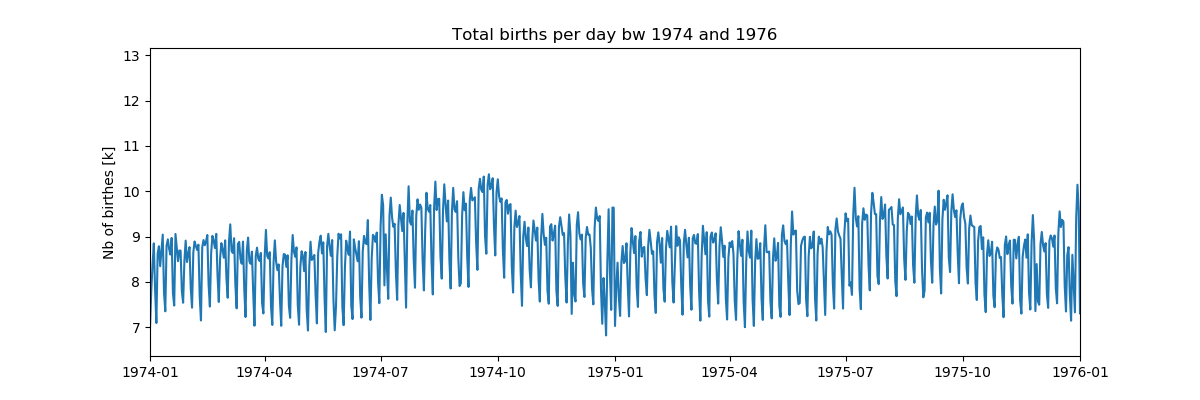
6. Выделение части шкалы времени (Проверка наличия промежуточных данных между отметками шкалы времени в поисках артефактов или отсутствующих данных.):

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg
import pywt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
cwt = scg.CWT(births_normed, scales=scales) 
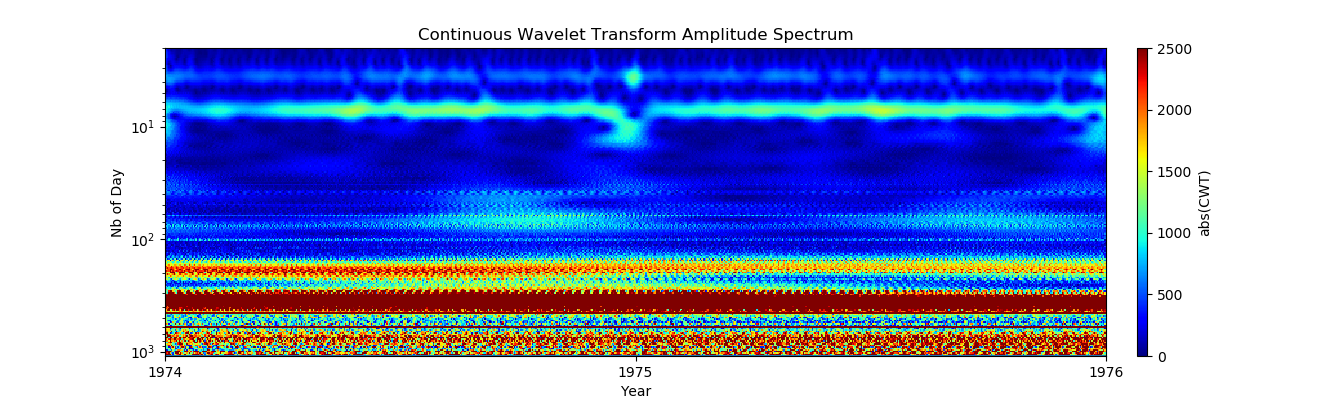
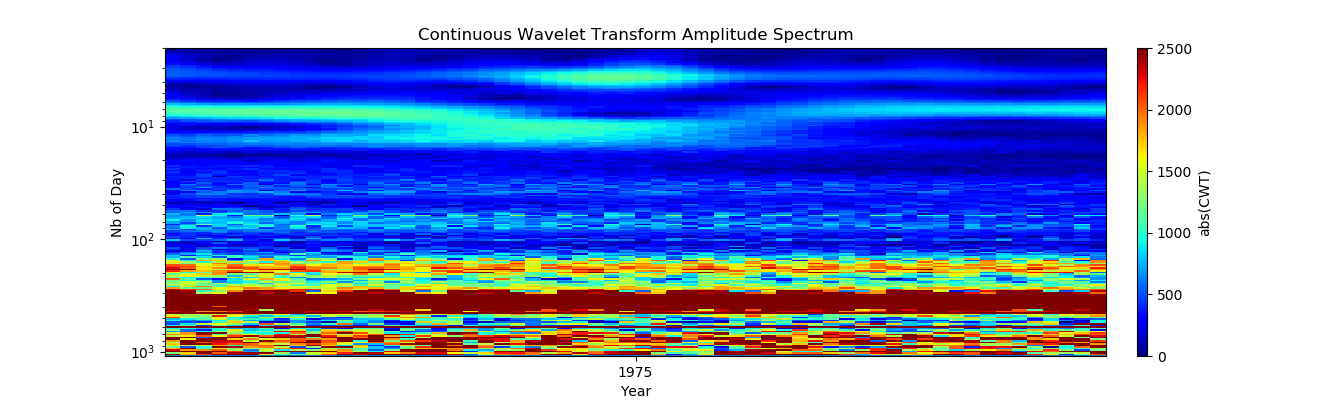
# увеличить на два года: 1974-1976

fig = figure(figsize=(12,4))
lines =plot(births.index, births.values/1000, '-')
xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01"))
ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976");

# перерисовать предыдущую масштабограмму с увеличением
ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))
xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 )
show()

На первый взгляд, еженедельные модели выглядят очень равномерно, но что-то происходит на Рождество, давайте еще раз рассмотрим этот период:

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg
import pywt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
cwt = scg.CWT(births_normed, scales=scales) 
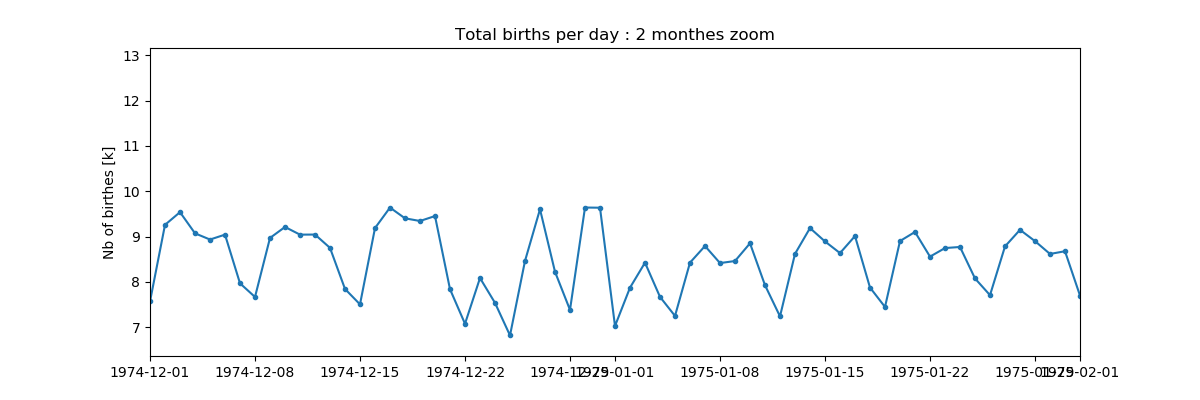
#Изменить масштабы: декабря 1975 года и января 1976 года
fig = figure(figsize=(12,4))
lines = plot(births.index, births.values/1000, '.-')
xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01"))
ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom");

# перерисовать предыдущую масштабограмму с увеличением
ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))
xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 )
show()

Теперь ясно, что это эффект конца года:

• Рождество: 23/24/25 декабря показывает аномально низкое число рождений, и эти дни отклоняются от недельного графика;
• Есть данные за декабрь, что согласуется с наличием некоторого значения для затронутых дат 1-е и 2-е января, в эти даты обычно меньше личных событий

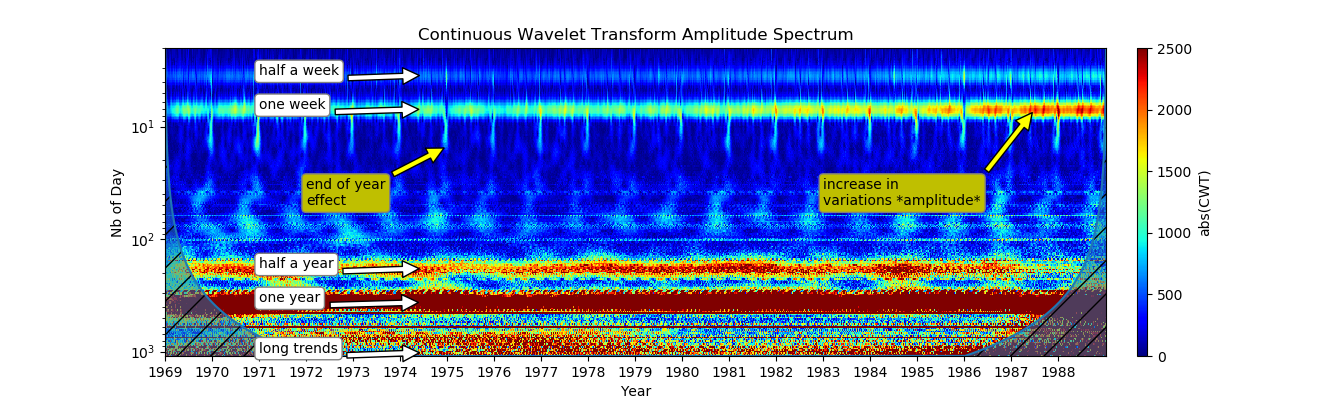
7. Синтез (Сиалограмму строят из нормализованных данных, при лучшей читаемости для всех масштабов):

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg
import pywt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
cwt = scg.CWT(births_normed, scales=scales) 
ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))

bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5")
bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5")
arrowprops = dict(facecolor='white', shrink=0.05)
arrowprops2 = dict(facecolor='yellow', shrink=0.05)
for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), 
                      (365, "one year"), (365*2.8, "long trends")]:
    text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), 
                       bbox=bbox, arrowprops=arrowprops)
text = ax.annotate("end of yearneffect", xy=(365*6, 15), xytext=(365*3, 50), 
                   bbox=bbox2, arrowprops=arrowprops2)
text = ax.annotate("increase innvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), 
                   bbox=bbox2, arrowprops=arrowprops2)
show()

CWT раскрывает много информации за короткий промежуток времени:

Еженедельная вариация, показывающая привычки в больницах, присутствует в течение нескольких десятилетий;

В 80-х годах наблюдается увеличение недельного показателя, который может быть вызван изменением рабочих привычек больниц, изменением рождаемости или простым изменением населения;

Вторая полоса в полугодии — это явно вторая гармоника. Нечеткие модели появляются в зоне от 3 до 1 месяца, что может быть связано с третьей гармоникой, поскольку годовые колебания настолько сильны. Это также может быть вызвано влиянием праздников на рождаемость и может потребовать дальнейшего изучения;

Эффект конца года был отмечен на Рождество и 1 января. Этот, возможно, остался невидимым с другим частотным методом.

Выводы:

В этой публикации мы увидели, как базовый вид вариаций сигнала переводится на скалограмму. Затем был использован пример упорядоченного по времени набора данных, чтобы шаг за шагом продемонстрировать, как CWT применяется к стандартным данным.

Приведенная методика может быть расширена для анализа сетевого трафика и для обнаружения необычного поведения объектов. CWT — это мощный инструмент, который все чаще используется в качестве входных данных для нейронных сетей и может использоваться для создания новых функций с целью классификации или обнаружения аномалий.

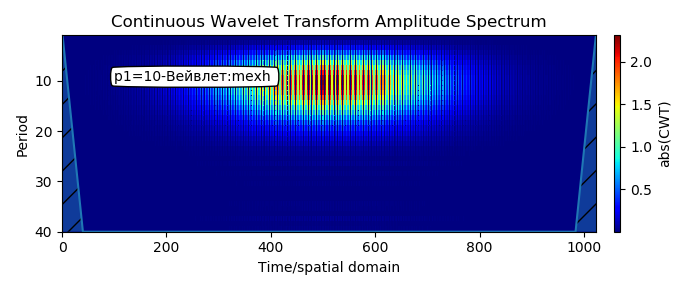
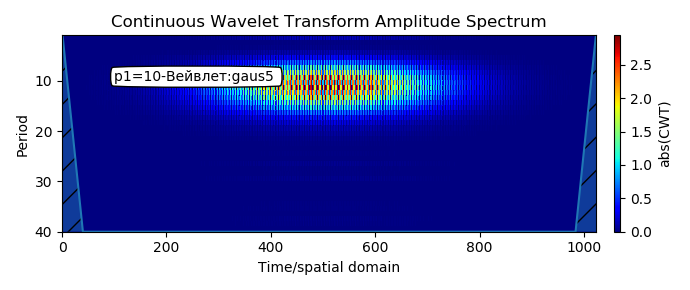
Каждый пример реализован в виде самостоятельной программы, что позволяет выбрать пример под свою задачу, не вникая в предыдущие и последующие примеры. Пользователь может попробовать любые вейвлет – функции из списка приведенного в начале каждой программы, например, такие как mexh или gaus5. Для примера 1 соответственно:

P.S. Для практического использования листингов приведу версии используемых в них модулей:

>>> import scaleogram; print(scaleogram .__version__)
0.9.5
>>> import pandas; print(pandas .__version__)
0.24.1
>>> import numpy; print(numpy .__version__)
1.16.1
>>> import  matplotlib; print(matplotlib .__version__)
3.0.2

Для самостоятельного набора данных в файл *.csv привожу структуру данных(в одном столбце):
year,month,day,gender,births
1969,1,1,F,4046
1969,1,1,M,4440
1969,1,2,F,4454
1969,1,2,M,4548
…
Для версии 0.24.1 pandasс потребуется явно регистрировать конвертеры matplotlib.

Чтобы зарегистрировать конвертеры:

from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()