1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
Option Explicit Public a As Variant Public b As Variant Public x As Variant Sub Main() Dim MyR As Range Dim n As Integer, i As Integer Dim RowB As Integer, ColE As Integer Set MyR = Selection With MyR If .Columns.Count - 1 <> .Rows.Count Then MsgBox "Вы должны были выделить область n строк и n+1 колонку!", vbCritical Exit Sub End If n = .Rows.Count 'Определили число строк матрицы If n < 2 Then MsgBox "Вы должны были выделять область, а не ячейку!", vbCritical Exit Sub End If RowB = .Rows(1).Row ColE = .Columns(1).Column + n End With 'Одна из фишек VBA - одной командой инициализируем массивы a = MyR.Resize(n, n) 'матрица системы b = MyR.Offset(0, n).Resize(n, 1) 'матрица (вектор) свободных членов ReDim x(1 To n) Forwards n 'Прямой ход Backwards n 'Обратный ход For i = 1 To n Cells(RowB + i - 1, ColE + 1).Value = x(i) Next i MsgBox "Решение помещено правее свободных членов", vbInformation Cells(RowB + n, 1).Select End Sub Sub Forwards(n As Integer) Dim c As Double Dim i As Integer, m As Integer, j As Integer, k As Integer, l As Integer For i = 1 To n - 1 l = i For m = i + 1 To n If Abs(a(m, i)) > Abs(a(l, i)) Then l = m Next m If l <> i Then Swap i, l, n End If For k = i + 1 To n c = a(k, i) / a(i, i) a(k, i) = 0 For j = i + 1 To n a(k, j) = a(k, j) - c * a(i, j) Next j b(k, 1) = b(k, 1) - c * b(i, 1) Next k Next i End Sub Sub Swap(i1 As Integer, i2 As Integer, n As Integer) 'Обменивает местами элементы в строках i1 и i2) Dim t As Double Dim j As Integer For j = 1 To n t = a(i1, j) a(i1, j) = a(i2, j) a(i2, j) = t Next j t = b(i1, 1) b(i1, 1) = b(i2, 1) b(i2, 1) = t End Sub Sub Backwards(n As Integer) Dim i As Integer, j As Integer Dim t As Double x(n) = b(n, 1) / a(n, n) For i = n - 1 To 1 Step -1 t = 0 For j = i + 1 To n t = t + a(i, j) * x(j) Next j x(i) = (b(i, 1) - t) / a(i, i) Next i End Sub |
Решение системы линейных алгебраических уравнений методом Гаусса средствами языка программирования Visual Basic
Министерство образования и науки Республики Башкортостан
ГАОУ СПО «Стерлитамакский колледж строительства, экономики и права»
«Программирование в компьютерных системах»
по разделу 1 Объектно-ориентированное программирование
междисциплинарного курса 01.02. Прикладное программирование
Решение системы линейных алгебраических уравнений
методом Гаусса средствами языка программирования Visual Basic
3 курса, группы ПО-31
Системы линейных алгебраических уравнений
Решение систем линейных уравнений графическим способом
Список использованной литературы
Приложение А (программный код)
В курсовом проекте рассмотрена программа, реализующая приближенное решение систем линейных уравнений графическим способом, с подключением модуля “Метод Гаусса”, созданная в среде программирования Visual Basic 2010.
Системы линейных уравнений, описывают экономические процессы в обществе и производстве. Навыки решения таких систем я вляются профессионально необходимыми и демонстрируют готовность студента к профессионльной деятельности. Автоматизировать процесс решения таких систем поможет программный продукт, представленный в данном курсовом проекте. Программа написана средствами языка программирования Visual Basic , обладающего возможностями, которые помогут решить графически систему линейных уравнений, а так же реализовать метод Гаусса. Метод Гаусса выбран ак универсальный для систем линейных уравнений.
Цель курсового проекта:
Разработать код программного продукта, реализующего прибл иженно е решение систем линейных уравнений графическим способом, с подключением модуля, реализующего метод Гаусса решения систем линейных уравнений.
Задачи курсового проекта:
1. Разработать программный код модуля, реализующего прибл иженно е решение систем линейных уравнений графическим способом.
2. Выполнить отладку программного модуля «Метод Гаусса» и приближенного решения с использованием специализированных программных средств.
3. Выполнить тестирование программного модуля «Метод Гаусса» и приближенного решения по составленным тестовым заданиям.
Системы линейных алгебраических уравнений.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Где m -количество линейных уравнений;
n -количество переменных ;
x 1 , x2, …, xn — неизвестные, которые надо определить;
Система называется однородной, если все её свободные члены равны нулю ( b 1 = b2 = … = bm = 0 ), иначе — неоднородной.
Система называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы — совокупность n чисел c 1 , c2, …, cn , таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида может иметь одно или более решений.
Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Система линейных уравнений может быть представлена в матричной форме как:
Где A — это матрица системы,
x — столбец неизвестных,
b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Эквивалентные системы линейных уравнений
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений
,
Где C — невырожденная матрица.
В частности, если сама матрица A — невырожденная, и для неё существует обратная матрица A -1 , то решение системы уравнений можно формально записать в виде
.
Решение систем линейных уравнений графическим способом
Решение систем линейных уравнений графическим способом заключается в построении графика каждого уравнения , входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков . Координаты этой точки ( x; y ) и будут являться решением данной системы уравнений.
Если прямые , являющиеся графиками уравнений системы, пересекаются , то система уравнений имеет единственное р ешение.
Если прямые , являющиеся графиками уравнений системы, параллельны , то система уравнений не имеет решений .
Если прямые , являющиеся графиками уравнений системы, совпадают , то система уравнений имеет бесконечное множество решений.
Примеры
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек . Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5) .
Выражаем у через х из каждого уравнения системы, а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3).
Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В (-2; 5).
Ответ: (-2; 5).
Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
Пусть исходная система выглядит следующим образом
Где A называется основной матрицей системы,
b — столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj 1 ,…, x jr .
Тогда переменные xj 1 ,…, x jr называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число Bi ≠0 , где i > r ,то рассматриваемая система несовместна, т. е. у неё нет ни одного решения.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x :
Если свободным переменным системы придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему, то мы получим все решения этой СЛАУ . Так как эта система получена путём элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях системы эквивалентны, то есть множества их решений совпадают.
Разрешается:
1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений;
2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа;
3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число.
С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы.
Для начала избавимся от переменной x 1 во втором уравнении. Для этого из второго уравнения вычтем первое уравнение, предварительно умноженное на 3:
.
Переменная x 2 найдена. Осталось определить значение переменной x 1 . Для этой цели преобразуем первое уравнение, убрав из него переменную x 2 . Вычтем из первого уравнения второе уравнение, предварительно умноженное на 2. Первое уравнение станет таким:
Ответ найден. Запишем то же решение, но уже без промежуточных пояснений. Римскими цифрами I и II будем обозначать первое и, соответственно, второе уравнения.
означает, что из второго уравнения вычли утроенное первое уравнение
означает, что левую и правую части второго уравнения разделили на (-7).
Итак, решение методом Гаусса заданной СЛАУ будет иметь вид:
Обычно работают с матричной формой записи
В матричной форме записи метод Гаусса станет таким:
Visual Basic
Visual Basic — это простой и быстрый способ создания программ для Microsoft Windows. Даже если вы не знакомы с программированием для Windows, с Visual Basic вы получите полный набор средств для упрощения разработки.
Так что же такое Visual Basic? Слово «Visual» относится к методу, используемому для создания того, что видит пользователь — графического пользовательского интерфейса , или GUI. Слово «Basic» относится к аббревиатуре BASIC (Beginners All-Purpose Symbolic Instruction Code — многоцелевой код символьных инструкций для начинающих) языка программирования, который используется программистами намного чаще, чем любой другой язык в истории вычислений. Для создания различных полезных программ достаточно изучить лишь некоторые из его возможностей.
Окно Form является вашей программы. Его можно двигать по экрану, увеличивать, уменьшать, менять его свойства в окне свойств, упорядочивать на нём объекты и в окне Code писать для него процедуры. Само окно тоже считается как объект, так сказать, «высший объект». Один из объектов всегда является «актуальным объектом», чьи свойства будут перечислены в окне свойств. Объект становится актуальным, когда на него кликнут. Узнают это чаще всего по обрамлению или по какой-нибудь другой маркировке.
Здесь всегда перчислены свойства актуального объекта (см. выше). Свойство, представленное синим, может быть изменено в строке справа. Иногда нужно вносить данные самому, иногда можно выбирать из выпадающего списка, который отображён в строке справа в виде маленькой стрелки вниз. Заметьте, что при изменении свойств окна, изменения происходят синхронно.
Здесь можно выбрать объекты, которые нужно поместить на форме. Например, чтобы нарисовать линию, кликните на символ линии. Теперь кликните на то место на форме, где должна начинаться линия и тяните мышь с нажатой кнопкой туда, где эта линия должна кончаться. Отпустите кнопку мышки. Готово! Отдельные объекты будут описаны позже.
В Basic’e процедуры начинаются с команды Sub, потом идёт имя процедуры и (). Оканчиваются процедуры командой End Sub (англ. subroutine: подпрограмма). Между этим стоят команды, принадлежащие этой процедуре. Они будут, при вызове процедуры, следовать одна за другой.
В большинстве своём процедуры — это процедуры события: для каждого события, на которое должна реагировать программа, нужно писать процедуру. Причём Sub, имя процедуры, () и End Sub будут заданы самим Basic’ом.
Процедура события Form_Load выполняется каждый раз при запуске вашего приложения прежде, чем окно появится на экране. Поэтому бесполезно уже в этой процедуре что-либо писать в окне или рисовать (например Print), т. к. это просто не будет сделанно. Окна-то ещё нет!
Событие Click происходит в том случае, если на объекте кликнуть левой кнопкой мыши. Если, к примеру, пользователь щёлкнет на одном из элементов управления, событие Click этого объекта будет тут же исполнено. Можно кликнуть по форме — для этого имеется событие Form_Click, которое может содержать различные процедуры.
Это событие происходит при двойном клике мышкой на каком-либо объекте. Внимание: ещё при первом нажатии произойдёт событие Click, но при мнгновенном втором уже нет.
Это то свойство имеется у всех объектов. Оно определяет имя объекта, под которым этот объект будет применяться в Basic-содах. Это свойство может быть изменено только в режиме design и не в самой программе. Предустановки для этого свойства — это, например, «Form1» у окна. Если где-нибудь в программе нужно обратиться к этому объекту, к примеру, если надо поменять его свойство, то надо использовать имя этого объекта.
Это свойство имеется у окон, кнопок, «этикеток» и у могих других элемнтов управления. У окон это свойство задаёт текст, который будет отображён в заголовке этого окна. Этот текст отображается также в иконке окна в таскбаре. У элементов управления это свойство определяет текст, который находится на самих элементах управления или в близи них. Это свойство может быть изменено как в режиме design, так и в ходе самой программы.
Это свойство имеется у окон и всех элементов управления, кроме таймера (он всегда «невидим»). Это свойство определяет, видим или скрыт объект, и может быть изменено, как в режиме design, так и в ходе программы. Это свойство может принимать значения только True или False.
Это свойство присутсвует у всех окон и элементов управления. Оно определяет будет ли форма или элемент управления реагировать на события произведённые пользователем. Этим свойством они будут либо включены либо выключены. Если элементы управления будут выключены они станут серыми вместо чёрных и становятся неактивными, «потушенными». Это свойство также, как и свойство Visible принимает значения только True или False
Свойства Left, Top
Эти свойства имеются у окон и почти всех элементов управления. Они определяют координаты левого верхнего угла объекта. У окон это координаты относительно экрана, а у элементов управления относительно к верхнему левому углу «внутренней» площади, т. е. окна, в котором они находятся. В режиме design эти свойства могут быть изменены при перетягивании мышкой и в окне свойств. В ходе программы эти свойства могут быть изменены тоже, но уже путём присвоения.
Свойства Width, Height
Эти свойства определяют ширину и высоту объекта. Также Вы можете изменять их как в режиме design, так и в ходе программы. Размеры объекта изменяются тогда сразу.
Командные кнопки (button) применяются чаще всего и являются простейшими элементами управления: как правило — это такие серые ящички, на которых находится текст, как например, «OK» или «Отмена», и по которым просто кликают.
Таймер назван так правильно: он никакой не настоящий элемент управления и на окне невидим, если программа запущена. Всё, что он делает — это в через определённые отрезки времени выполняет какое-нибудь событие, событие Timer’a. Много таймеров применять не надо, т. к. в Windows’e постоянно имеется максимум 16 таймеров одновременно.
Текстовое поле и поле надписи
В текстовомм поле пользователь должен вводить текст, который потом может быть использован в программе, например его имя или очки игры. На экране видно ящичек, в котором, если на него кликнуть, появится курсор. Поле надписи (этикетка, Label) используется, чтобы показывать текст, который пользователь не может изменить.
Графическое поле отображает графику, которая была сохранена, как. bmp или. ico файл. При этом будет показана только часть картинки. которая, которая поместилась в размеры графического поля. Если написать процедуру для события Click, можно использовать графическое поле, как красивую кнопку.
Программа реализующаяриближенное решение систем линейных уравнений графическим способом, с подключением модуля “Метод Гаусса”.
Программаное обеспечение необходимое для функционирования программы:
Microsoft Visual Studio 2010
Windows Xp , Windows Vista , Windows 7
Visual Basic 2010.
Программа создана для решения систем линейных алгебраических уравнений графическим способом, а так же методом Гаусса.
Программа вычисляет корни одновременно только 2 уравнений, методом Гаусса, а так же графическим способом.
Описание логической структуры:
Технология визуального программирования. Визуальная технология программирования позволяет программисту легко и быстро легко и быстро строить нагшлядный графический интерфейс для своих программ на основе стандартного набора шаблонов, графически отображаемых на экране объектов.
Структура программы с описанием функций составных частей и связи между ними:
Этот блок программы отвечает за построение системы координат на форме. Первые 2 цикла это разметка по оси Х и по оси Y . Следующие 4 строки, это оси X и Y . И наконец оставшиеся 2 цикла это Засечки по осям координат.
Этот блок отвечает за ввод данных.
Решение поставленной задачи. Первые 4 строки нужны для построения прямых на графике. Остальное, это решение методом Гаусса.
Вывод корней, полученных методом Гаусса.
Построение прямых на графике.
Связи программы с другими программами:
Связи программы с другими программами отсутствуют.
Используемые технические характеристики:
Оперативная память: 2Гб;
Процессор: Intel Pentium 4, 3.00 Ггц;
Тип системы: 32 разрядная ОС;
Вызов и загрузка:
Запуск программы происходит через редактор Visual Studio 2010.
В пункте “Файл” нажимаем на “Открыть проект”, далее на жестком диске находим папку с названием SLAU , в ней находим файл SLAU . vbproj . Кликаем на него, после чего запускается программа.
В левом верхнем углу программы, есть несколько текстовых полей, под строкой “Введите коэффициенты при x ”. В эти текстовые поля нужно ввести коэффициенты при переменных, а так же свободные члены.
После нажатия на кнопку “Построить график”, в правом верхнем углу будет построен график. На это графике будут построены 2 прямые, точка пересечения которых и будет являться примерным решением системы линейных алгебраических уравнений, которые вы ввели в правом углу.
Внизу написаны 2 переменные x 1 и x 2, а так же их значения. Эти переменные были найдены с помощью метода Гаусса, и являются точным решением системы линейных алгебраических уравнений.
После нажмите на кнопку “Построить график”.
Рис3. Выполненная программа.
В ходе курсового проекта рассмотрен метод решения систем линейных уравнений графическим способом, а так же метод Гаусса решения систем линейных уравнений. Для достижения этой цели выполнена систематизация знаний и умений по теме «Решение систем линейных уравнений», применение графики в Visual Basic 2010. Язык программирования Visual Basic отлично подошел для выполнения данного проекта, так как среда разработки языка Visual Basic , включает в себя инструменты для визуального построения интерфейса.
Были выполнены все задачи, а именно:
Построение кода модуля с заданной функциональностью; отладка программных модулей с использованием специализированных программных средств; выполнено тестирование готовых программных модулей и составил отчетную документацию с использованием информационно-коммуникационные технологий.
В ходе работы над курсовым проектом я научился работать с графикой в Visual Basic , применил свои знания в области решения систем линейных уравнений графическим способом, а так же с помощью метода Гаусса.
Список использованной литературы
http://ru. wikipedia. org
http://www. /index. php? option=com_content&view=article&id=58:&catid=19&Itemid=50
Public Class Form1
Dim Graph1 As Graphics
Dim Pen1 As New Pen ( Color .Black, 2)
Dim Pen2 As New Pen ( Color .Black, 1)
Dim brush1 As New SolidBrush ( Color .Black)
Dim font1 As New Font ( «times new roman» , 7)
Dim X, Y, a1, a2, b1, b2, c1, c2, k1, k2, m1, m2, d, z1, z2, x1, y1 As Single
Private Sub Form1_Load( ByVal sender As System. Object , ByVal e As System. EventArgs ) Handles MyBase .Load
Label1.Text = «Введите коэфициенты при х»
Button1.Text = » Построить граффик «
Private Sub Button1_Click( ByVal sender As System. Object , ByVal e As System. EventArgs ) Handles Button1.Click
Graph1 = Me .PictureBox1.CreateGraphics()
For X = -15 To 15 Step 3
Graph1.DrawString(X, font1, brush1, X * 10 + 150, 150)
For Y = -15 To 150 Step 3
Graph1.DrawString(Y, font1, brush1, 150, 150 — Y * 10)
Блог инженера-программиста / шапку скоро поменяю /
Решение системы линейных уравнений методом Гаусса в MS Excel
Автор Инженер
На днях понадобилось найти корни системы линейных уравнений методом Гаусса в Microsoft Excel. Готовый алгоритм решения можно найти в книге Гарнаева «Использование Excel и VBA в экономике и финансах», но объяснение там очень скудное и не совсем понятное. Постараюсь описать подробней для тех, кому может понадобиться этот алгоритм.
Лирическое отступление: в тексте будет предлагаться ввести в диапазон ячеек формулу вида: <=A1:B3+$C$2:$C$3>и т.п., это так-называемые «формулы массива» (формула, выполняющая несколько вычислений над одним или несколькими наборами значений, а затем возвращающая один или несколько результатов. Формулы массива заключены в фигурные скобки < >). Microsoft Excel автоматически заключает ее в фигурные скобки ( < >). Для введения такого типа формул необходимо выделить весь диапазон, куда нужно вставить формулу, в первой ячейке ввести формулу без фигурных скобок (для примера выше — =A1:B3+$C$2:$C$3 ) и нажать Ctrl+Shift+Enter .
Пускай имеем систему линейных уравнений: 
1. Запишем коэффициенты системы уравнений в ячейки A1:D4 а столбец свободных членов в ячейки E1:E4 . Если в ячейке A1 находится 0, необходимо поменять строки местами так, чтоб в этой ячейке было отличное от ноля значение. Для большей наглядности можно добавить заливку ячеек, в которых находятся свободные члены. (скриншот)
2. Необходимо коэффициент при x1 во всех уравнениях кроме первого привести к 0. Для начала сделаем это для второго уравнения. Скопируем первую строку в ячейки A6:E6 без изменений, в ячейки A7:E7 необходимо ввести формулу: <=A2:E2-$A$1:$E$1*(A2/$A$1)>. Таким образом мы от второй строки отнимаем первую, умноженную на A2/$A$1, т.е. отношение первых коэффициентов второго и первого уравнения. Для удобства заполнения строк 8 и 9 ссылки на ячейки первой строки необходимо использовать абсолютные (используем символ $). (скриншот)
3. Копируем введенную формулу формулу в строки 8 и 9, таким образом избавляемся от коэффициентов перед x1 во всех уравнениях кроме первого. (скриншот)
4. Теперь приведем коэффициенты перед x2 в третьем и четвертом уравнении к 0. Для этого скопируем полученные 6-ю и 7-ю строки (только значения) в строки 11 и 12, а в ячейки A13:E13 введем формулу <=A8:E8-$A$7:$E$7*(B8/$B$7)>, которую затем скопируем в ячейки A14:E14 . Таким образом реализуется разность строк 8 и 7, умноженных на коэффициент B8/$B$7 . Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби. (скриншот)
5. Осталось привести коэффициент при x3 в четвертом уравнении к 0, для этого вновь проделаем аналогичные действия: скопируем полученные 11, 12 и 13-ю строки (только значения) в строки 16-18, а в ячейки A19:E19 введем формулу <=A14:E14-$A$13:$E$13*(C14/$C$13)>. Таким образом реализуется разность строк 14 и 13, умноженных на коэффициент C14/$C$13 . Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби. (скриншот)
6. Прямая прогонка методом Гаусса завершена. Обратную прогонку начнем с последней строки полученной матрицы. Необходимо все элементы последней строки разделить на коэффициент при x4. Для этого в строку 24 введем формулу <=A19:E19/D19>. (скриншот)
7. Приведем все строки к подобному виду, для этого заполним строки 23, 22, 21 следующими формулами:
23: <=(A18:E18-A24:E24*D18)/C18>— отнимаем от третьей строки четвертую умноженную на коэффициент при x4 третьей строки.
22: <=(A17:E17-A23:E23*C17-A24:E24*D17)/B17>— от второй строки отнимаем третью и четвертую, умноженные на соответствующие коэффициенты.
21: <=(A16:E16-A22:E22*B16-A23:E23*C16-A24:E24*D16)/A16>— от первой строки отнимаем вторую, третью и четвертую, умноженные на соответствующие коэффициенты.
Результат (корни уравнения) вычислены в ячейках E21:E24 . (скриншот)
UPDATE от 25 апреля 2012 г. Выкладываю xls-файл с решением линейных уравнений методом Гаусса в Microsoft Excel: Показать ссылку
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 
графическим способом. Преобразуем данную систему 
. Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу =1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы.
Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
. Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения: 
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения: 
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:
; 
источники:
http://otadmina.ru/reshenie-sistem-uravneniy-metodom-gaussa/
http://urok.1sept.ru/articles/510787
|
Решение уравнении методом гауса |
||||||||
Ответить |
||||||||
Ответить |
При решении задачи A действия выполняются над числовыми коэффициентами, а имена неизвестных не участвуют в вычислениях. Поэтому при решении задачи в Excel будем хранить только коэффициенты и значения правых частей уравнений, записывая их в расширенную (n*(n+1))-матрицу Ab: A x b с расширенной (n (n 1)) -матрицей Ab
|
2 |
1 |
1 x |
7 |
2 |
1 |
1 |
7 |
|||||
|
1 |
Ab Ab1 |
|||||||||||
|
4 |
3 |
0 x2 |
10 , |
4 |
3 |
0 |
10 |
|||||
|
2 2 |
2 2 |
3 |
||||||||||
|
3 x3 |
11 |
11 |
Для изучения в Excel метода Гаусса с выбором главного элемента по столбцу для решения СЛАУ используем следующий алгоритм:
|
a. На k-ом (k=1,…, n-1) шаге среди строк с k-ой |
0 |
1 |
0 |
||||||||
|
по n-ую выбирают ту (допустим l-ую), кото- |
P1 |
||||||||||
|
1 |
0 |
0 |
|||||||||
|
рая в k-ом столбце имеет наибольший по аб- |
0 |
0 |
1 |
||||||||
|
солютной величине элемент – главный эле- |
|||||||||||
|
4 |
3 |
0 |
10 |
||||||||
|
мент. Эту строку (l-ую) матрицы Abk пере- |
|||||||||||
|
Ab1 |
|||||||||||
|
ставляют с k-ой строкой. Перестановку на k— |
P1 |
2 |
1 1 |
7 |
|||||||
|
2 |
2 |
3 |
11 |
||||||||
|
ом шаге при изучении метода в Excel удоб- |
|||||||||||
|
но реализовывать умножением Pk Ab матрицы перестановок Pk |
на |
расширенную матрицу Ab. Матрица перестановок – это единичная матрица, в которой единицы с главной диагонали k-го и l-го столбца переставлены соответственно в l-ый и k-ый столбцы.
|
b. Далее готовится (в Excel) матрица |
Lk , умножая |
||||||||||
|
4 |
0 |
0 |
|||||||||
|
которую на расширенную матрицу |
Abk , произ- |
||||||||||
|
2 |
1 |
0 |
|||||||||
|
водят исключение неизвестных. При подготовке |
2 |
0 |
|||||||||
|
(в Excel) сначала в единичную матрицу E на ме- |
1 |
||||||||||
|
сто элементов k-го столбца, расположенных в |
1 |
0 |
0 |
||||||||
|
строках с k-ой по n-ую, переписывают элементы |
L1 |
— 0,5 |
1 |
0 |
|||||||
|
A с тем же расположением. А затем нормируют |
0,5 |
0 |
|||||||||
|
1 |
|||||||||||
|
их – делят все переписанные эле- |
|||||||||||
|
4 |
3 |
0 |
10 |
||||||||
|
менты на главный элемент. |
Ab2 L1 P1 Ab1 |
||||||||||
|
c. Затем умножением Lk Abk выпол- |
0 |
— 0,5 |
1 |
2 |
|||||||
|
0 |
3,5 |
3 |
|||||||||
|
16 |
|||||||||||
|
няется исключение k-го неизвест- |
|||||||||||
|
11 |
Abk,k Abn,k
ного из строк с (k+1)-ой по n-ую, то есть фактически обнуляются соответствующие элементы расширенной матрицы.
|
d. После (n-1)-го шага матрица системы A |
|||||||
|
4 |
3 |
0 |
10 |
||||
|
становится верхней треугольной, то есть |
|||||||
|
имеет нули ниже главной диагонали. Ре- |
Ab3 |
0 |
3,5 |
3 |
16 |
||
|
0 |
0 |
1,43 |
|||||
|
шается система уравнений с верхней |
4,29 |
||||||
|
x3 |
4,29/1,43 |
3 |
|||||
|
треугольной матрицей просто: из по- |
|||||||
|
(16 3 |
3) / 3,5 2 |
||||||
|
следнего уравнения находится неизвест- |
x2 |
||||||
|
ное xn , которое затем подставляется в |
x1 (10 0 3 3 2) / 4 1 |
||||||
|
предыдущие уравнения. Затем находится |
|||||||
xn 1, и так далее. То есть осуществляется обратная подстановка метода Гаусса.
Отметим особенности реализации алгоритма
Перестановку строк выполняется умножением матрицы перестановок на матрицу Ab. Матрица перестановок k-ой и l-ой строк – это единичная матрица, у которой в k-ой и l-ой строках единицы с главной диагонали смещены соответственно в l-ой и k-ой столбцы.
Для умножения матриц в Excel имеется функция МУМНОЖ, а вот для автоматического создания единичной матрицы E в выделенной квадратной области следует подготовить специальный макрос (который будем вызывать по нажатию клавиш Ctrl+Shift+E или щелчку по связанной с макросом фигуре – кружку E, см. табл. 1.1). Операцию перестройки единичной матрицы в матрицу перестановок будем выполнять вручную.
Исключение неизвестных на k-ом шаге выполняется умножением матрицы исключений на расширенную матрицу. Матрица исключений получается из единичной после замены на сходственных элементов в k-ом столбце и их нормировании – делении на элемент Abk,k . Эту замену можно выполнять вручную (специальной вставкой), а вот для нормирования полезно разработать специальный макрос (его будем вызывать по нажатию клавиш Ctrl+Shift+L или щелчку по L- кружку).
Обратный ход метода Гаусса можно выполнять вручную, но можно подготовить для этого (и с целью контроля) специальный макрос, ко-
12
торый будет решать СЛАУ с верхней треугольной матрицей (его будем вызывать по нажатию клавиш Ctrl+Shift+x или щелчку по x-кружку).
Макрос, используемый на этапах a и b алгоритма:
|
Sub E( ) |
‘ Запускается по Ctrl+Shift+E и создаѐт единичную матрицу E |
|
|
Dim TR As Range |
‘ в выделенной прямоугольной области. |
|
|
Dim n As Integer |
||
|
For Each TR In Selection.Areas |
‘ Цикл по выделенным областям. |
|
|
n = Sqr(TR.Count) |
‘ Определение числа выделенных ячеек. |
|
|
i1 = TR.Row: j1 = TR.Column |
‘ Номера начальных строки и столбца. |
|
|
TR = 0 |
‘ Обнуление диапазона и запись |
|
|
For i = 1 To N: Cells(i1 + i — 1, j1 + i — 1) = 1: Next i ‘ на главную диагональ. |
||
|
Next |
‘ Конец цикла по выделенным областям |
|
|
End Sub |
||
|
Макрос, используемый на этапе b алгоритма: |
||
|
Sub Lk() |
‘ запускается по Ctrl+Shift+L и нормирует главный столбец |
|
|
Dim TR As Range: Dim n As Integer |
||
|
For Each TR In Selection.Areas |
‘ Цикл по выделенным областям. |
n = TR.Count: i1 = TR.Row: j1 = TR.Column ‘ опр. числа эл-тов и индексов For i = i1 + 1 To i1 + n — 1
Cells(i, j1) = — Cells(i, j1) / Cells(i1, j1)
Next i Cells(i1, j1) = 1
Next End Sub
Макрос для этапа d алгоритма:
|
Sub TrSolve( ) |
‘ запускается по Ctrl+Shift+x и решает СЛАУ |
|
|
Dim n As Integer |
‘ с верхней треугольной матрицей |
|
|
Dim TR As Range |
‘ в выделенной прямоугольной области. |
|
|
For Each TR In Selection.Areas |
‘ Цикл по выделенным областям. |
|
|
in = TR.Row: jn = TR.Column |
‘ строка и столбец начала матрицы |
|
|
n = TR.Rows.Count |
‘ число строк матрицы |
If n + 1 <> TR.Columns.Count Then
13
MsgBox «Выделена не подходящий диапазон», , «TrSolve»: Exit Sub
End If
Dim b( ) As Double: ReDim b(n)
For i = 1 To n: b(i) = TR.Cells(i, n + 1): Next ‘готовим массив b правых чаcтей
|
For k = n To 1 Step — 1 |
||
|
Cells(in + n, jn + k — 1) = b(k) / TR.Cells(k, k) |
‘ вычисление и запись Xk |
|
|
For i = 1 To n – 1 |
‘ цикл подстановки в уравнения вычисленного Xk |
b(i) = b(i) — TR.Cells(i, k) * Cells(in + k — 1, jn + n + 1)
Next i Next k
Next End Sub
Описание решения на Excel задачи A
При решении задачи A (на этапе 1 ) расширенную матрицу Ab1 поме-
|
щаем в диапазон G2:J4 (см. таблицу 1.1). |
Таблица 1.1 |
|||||||||||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|||||||||||
|
1 |
Матрица перестановок (шаг k=1) |
2 |
Расширенная матрица СЛАУ |
1 |
||||||||||||||||
|
2 |
0 |
1 |
0 |
2 |
1 |
1 |
7 |
|||||||||||||
|
3 |
P1= |
1 |
0 |
0 |
Ab1= |
4 |
3 |
0 |
10 |
|||||||||||
|
4 |
0 |
0 |
1 |
-2 |
2 |
3 |
11 |
|||||||||||||
|
5 |
Матрица исключений (шаг k=1) |
4 |
Строки переставлены (шаг k=1) |
3 |
||||||||||||||||
|
6 |
1 |
0 |
0 |
4 |
3 |
0 |
10 |
|||||||||||||
|
7 |
L1= |
-0,5 |
1 |
0 |
P1*Ab1= |
2 |
1 |
1 |
7 |
|||||||||||
|
8 |
0,5 |
0 |
1 |
-2 |
2 |
3 |
11 |
|||||||||||||
|
9 |
Матрица перестановок (шаг k=2) |
6 |
Матрица СЛАУ после шага k=1 |
5 |
||||||||||||||||
|
10 |
1 |
0 |
0 |
4 |
3 |
0 |
10 |
|||||||||||||
|
11 |
P2= |
0 |
0 |
1 |
Ab2=L1*(P1*Ab1)= |
0 |
-0,5 |
1 |
2 |
|||||||||||
|
12 |
0 |
1 |
0 |
0 |
3,5 |
3 |
16 |
|||||||||||||
|
13 |
Матрица исключений (шаг k=2) |
8 |
Строки переставлены шаг k=2 |
7 |
||||||||||||||||
|
14 |
1 |
0 |
0 |
4 |
3 |
0 |
10 |
|||||||||||||
|
15 |
L2= |
0 |
1 |
0 |
P2*Ab2= |
0 |
3,5 |
3 |
16 |
|||||||||||
|
16 |
0 |
0,14286 |
1 |
0 |
-0,5 |
1 |
2 |
|||||||||||||
|
17 |
Матрица СЛАУ после шага k=2 |
9 |
||||||||||||||||||
|
18 |
4 |
3 |
0 |
10 |
||||||||||||||||
|
19 |
Ab3=L2*(P2*Ab2)= |
0 |
3,5 |
3 |
16 |
|||||||||||||||
|
20 |
0 |
0 |
1,4286 |
4,2857 |
||||||||||||||||
|
21 |
10 Решение СЛАУ с верхней треугольной матрицей x1,x2, x3= |
1 |
2 |
3 |
||||||||||||||||
В 1-ом столбце Ab1 главный элемент равен 4, он находится во 2-ой строке. В соответствии с этим, (на этапе 2 ) слева в ячейках B2:D4 на-
14
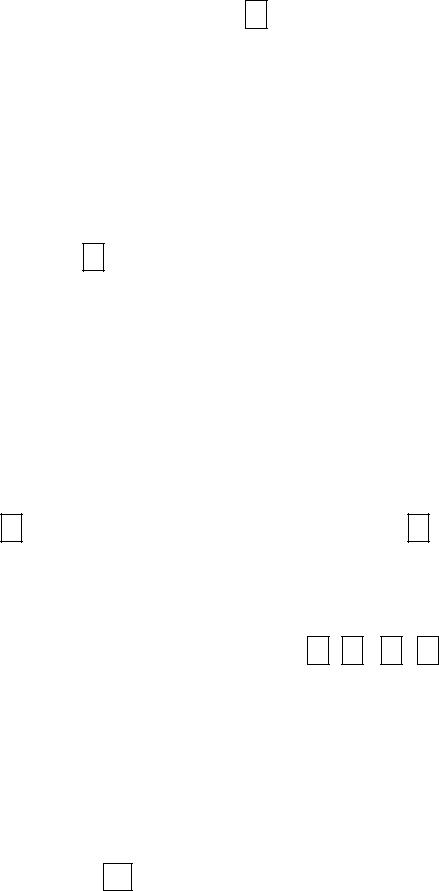
биваем (или переделываем из единичной) матрицу перестановок P1, которая будет задавать перестановки 1-ой и 2-ой строк. Под матрицей Ab1 (в диапазоне G6:J8) разместим (на этапе 3 ) матрицу, которая получится как результат умножения P1 на Ab1.
Напомним, как выполняется в Excel умножение матриц. Для этого: выделяем G6:J8, нажимаем F2, в ячейку G6 вставляем как формулу функцию МУМНОЖ. Вызвав эту функцию, указываем сначала диапазон B2:D4 первой матрицы, а затем – второй G2:J4. Для записи матрицы результата в диапазон, начинающийся в ячейке G6, следует нажать
Ctrl+Shift+Enter.
После получения матрицы P1*Ab1 с переставленными 2-ой и 1-ой строками готовим (на этапе 4 ) слева матрицу L1 для исключения неиз-
вестных из строк со 2-ой по 3-ью (c k+1 по n) первого столбца. Для этого выделяем диапазон B6:D8 (строк c k по n) и запускаем макрос E создания единичной матрицы (по Ctrl+Shift+E или кликнув по кружку E — фигуры, с которой мы связали этот макрос). Затем выделяем в матрице P1*Ab1 1-ый столбец (G6:G8) с главным элементом. Копируем значе-
ния из G6:G8 и, выделив B6:B8, помещаем специальной вставкой (зна-
чения) в столбец единичной матрицы. Не сбрасывая выделение B6:B8, запускаем (по Ctrl+Shift+L или кликнув по L-кружку фигуры) макрос Lk нормирования этого вектора. В результате получим показанную в таблице 1.1 (для этапа 4 ) матрицу L1. После умножения (на этапе 5 ) этой
матрицы на расширенную матрицу P1*Ab1 (диапазон G6:J8) заносим в G10:J12 матрицу произведения Ab2=L1*(P1*Ab1) с исключенным неиз-
вестным x1 из G11:G12.
Аналогичным образом действуем дальше (на этапах 6 , 7 , 8 , 9 ) до получения матрицы Ab3 (G18:J20), у которой все элементы под главной диагональю (левой (3х3)-подматрицы Ab3) равны нулю. Расширенная матрица Ab3 соответствует СЛАУ с верхней треугольной матрицей; она просто решается последовательным вычислением x1, x2 , x3 — обратной подстановкой. Еѐ алгоритм реализован в макросе TrSolve, который запускается по Ctrl+Shift+x (или кликнув по соответствующему x-кружку фигуры) при предварительно выделенной расширенной матрице
(G18:J20) и выводит (на этапе 10 ) вычисленные неизвестные x1, x2 , x3
15
системы в ячейки G21:I21 под соответствующими столбцами верхней треугольной матрицы Ab3.
1.3. Применение в Excel процедуры метода Гаусса
Задача В. Используя обращение к стандартной процедуре решения СЛАУ методом Гаусса, составить в Excel «функцию, определѐнную пользователем» для решения СЛАУ.
Замечание. В Excel есть функция МОБР для обращения матриц, с помощью которой решают СЛАУ, по схеме:
|
Ax b |
x A 1b |
|||||||||||||||||||||
|
Например, матрица A (см. рис. 1.1) записана в ячейки диапазона A1:C3, |
||||||||||||||||||||||
|
а для |
моделиро- |
|||||||||||||||||||||
|
A |
B |
C |
D |
E |
||||||||||||||||||
|
вания |
реальных |
|||||||||||||||||||||
|
1 |
100000 |
200000 |
300000 |
700000 |
733184 |
|||||||||||||||||
|
вычислений |
по- |
|||||||||||||||||||||
|
2 |
400000 |
500000 |
600000 |
1000000 |
1044480 |
|||||||||||||||||
|
следний |
еѐ |
ко- |
||||||||||||||||||||
|
3 |
700000 |
800000 |
900000 |
1100000 |
1155072 |
|||||||||||||||||
|
эффициент |
||||||||||||||||||||||
|
4 |
-4,908E+13 |
9,817E+13 |
-4,908E+13 |
3,534E+15 |
||||||||||||||||||
|
900000 |
в |
ячейке |
||||||||||||||||||||
|
С3 задан с отно- |
Рис. 1.1. |
сительной погрешностью 5×10-15 представления чисел в машине. Определитель матрицы A, вычисленный с помощью функции МОПРЕД, ра-
вен -122,236. Вычисленные через обратную матрицу A 1 и столбец b правых частей (D1:D3) неизвестные x1, x2, x3, помещены в ячейки A4:C4 под соответствующие столбцы матрицы A.
Встречаются руководства, в которых для «проверки» полученные неизвестные умножают на матрицу A, ожидая получить вектор b. В нашем случае после умножения этот вектор (он записан в ячейках E1:E3) с инженерной погрешностью (до 4%) совпадает с исходным. Но оказывается, мы «решили» систему, которая не имеет решения – решили «без проблем» и не почувствовали этого. То есть процедура МОПР не выявляет особенных матриц и спокойно вычисляет обратные матрицы и в случаях, когда этих матриц не существует. Такие случаи возможны, когда СЛАУ составлена не верно, и какие-либо еѐ уравнения является линейной комбинацией других уравнений системы.
16
Кроме того методически не правильно применять для решения СЛАУ более трудоѐмкую процедуру обращения матриц (вычисление A 1 из
AA 1 E равносильно решению стольких СЛАУ, сколько имеется неизвестных). Поэтому целесообразно пополнить арсенал функций Excel процедурой эффективного решения СЛАУ с оценкой близости системы к вырожденной – с оценкой числа обусловленности.
Решение задачи В. Рассмотренный алгоритм решения СЛАУ методом Гаусса удобно записать на Фортране – языке, хорошо подходящем для записи алгоритма. Упрощѐнный (без оценки числа обусловленности), но более наглядный, вариант процедуры представлен ниже:
Subroutine KGAUSS(Ab, N, X, IAI)
|
Real(8) Ab(N,N+1), X(N) |
! Описание массивов |
||
|
IAI=1 |
|||
|
Do k=1, N |
! |
<==> For k=1 To N ! Перебор строк — шаги прямого хода |
|
|
Call CMEHA |
! Выбор и анализ гл. элемента |
||
|
If( IAI == 0 ) Return ! <==> Exit Sub ! Выход, если гл. элемент = 0 |
|||
|
Do i=k+1, N |
! Перебор строк с k+1-ой по N-ую |
||
|
Ab(i,k) = Ab(i,k)/Ab(k,k) |
|||
|
Ab(i,k+1:N+1) = Ab(i,k+1:N+1) — Ab(i,k)*Ab(k,k+1:N+1) |
|||
|
End Do |
|||
|
End Do |
! |
<==> Next k |
|
|
Do k = N, 1,-1 |
! Обратная подстановка (обратный ход) |
X(k)=Ab(k,N+1)/Ab(k,k)
Ab(1:N-1,N+1) = Ab(1:N-1,N+1) — Ab(1:N-1,k)*X(k)
End Do
Contains ! ——- Внутренние подпрограммы: —————————————-
Subroutine CMEHA ! Процедура выбора гл. элемента и перестановки строк
|
Real(8) W(N+1) ; Integer L(1) |
! Описание массивов |
|
L=MaxLoc(abs(Ab(K:N,K))) |
! Опр. номера строки с гл. элементом |
|
W=Ab(K,:); Ab(K,:)=Ab(L(1)+K-1,:); Ab(L(1)+K-1,:)=W ! Перестановки |
|
|
If(abs(Ab(K,K) )== 0D0) IAI=0 ! |
IAI — признак вырожденности системы |
End Subroutine End
Замечание. В Фортране примечания записываются справа от знака «!». Цикл Do – End Do Фортрана соответствует циклу For – Next Бейсика. Запись A(i, j1:j2) указывает на элементы с j1-го по j2-ой в i-ой строке, а запись A(i, : ) — на все элементы i-ой строки матрицы A.
17
Дополнив процедуру KGAUSS оценкой числа обусловленности, оттранслировав и включив дополненную процедуру KFGAUSS (Карл Фридрих Гаусс) в библиотеку (названную нами Math32.dll) динамического вызова, получим возможность обращаться к ней из VBA. Однако при этом следует учесть ряд особенностей. Во-первых, необходимо в VBA декларировать подключаемую процедуру, записав:
Declare Sub KFGAUSS Lib «С:ПутьMath32.dll» (ByRef Ab As Double, _
ByVal N As Long, ByRef X As Double, ByRef CD As Double)
Во-вторых, следует учесть, что в процедуру надо передавать адрес начала массивов, а не весь массив, включая границы индексов, как это делается в Бейсике. То есть обращение из VBA к процедуре KFGAUSS может иметь вид:
Call KFGAUSS(AiB(1, 1), N, X(1), CD)
Отметим ещѐ одну особенность реализации процедуры KFGAUSS, позволяющую вычислять определитель левой квадратной (N×N)-части расширенной матрицы AiB. Этот определитель вычисляется как произведение диагональных элементов матрицы, а знак произведения, который зависит от чѐтного или нечѐтного числа выполненных перестановок, кодируется знаком переменной CD, то есть определитель
det(A)= Aib(1,1)×…×AiB(N,N)×знак(CD).
Число обусловленности матрицы системы положительное и равно абсолютной величине |CD|. Если |CD| порядка десятков (не больше 1000), то система достаточно хорошо обусловлена, и точность еѐ решения высокая. Большая величина |CD|, скажем, 1012, говорит о близости системы к вырожденной, |CD|=1E32 указывает на точную вырожденность системы. Отметим, что для представленной на рис. 1.1 СЛАУ число обусловленности равно 3,534×1015. Оно получено в ячейке D4 с помощью разбираемой ниже функции пользователя для решения СЛАУ и указывает на близость рассмотренной системы к вырожденной.
С учѐтом сделанных замечаний в Excel функция, определённая пользователем, для решения СЛАУ и выдачи числа обусловленности матрицы системы, может иметь следующий вид:
18
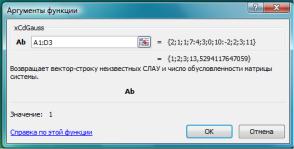
Public Function xCdGauss(Ab As Range) As Variant
Dim N As Long, CD As Double
N = Ab.Rows.Count
ReDim AiB(1 To N, 1 To N + 1) As Double
ReDim X(1 To N + 1) As Double
For i = 1 To N
For j = 1 To N + 1
AiB(i, j) = Ab(i, j)
Next j
Next i
|
Call KFGAUSS(AiB(1, 1), N, X(1), CD) |
Рис. 1.2. |
|||||||||||||||||
|
X(N + 1) = Abs(CD) |
||||||||||||||||||
|
A |
B |
C |
D |
|||||||||||||||
|
xCdGauss = X |
||||||||||||||||||
|
1 |
2 |
1 |
1 |
7 |
||||||||||||||
|
End Function |
2 |
4 |
3 |
0 |
10 |
|||||||||||||
|
Функция |
используется |
следующим |
3 |
-2 |
2 |
3 |
11 |
|||||||||||
|
4 |
1 |
2 |
3 |
13,52941 |
||||||||||||||
|
образом. Для решения СЛАУ с рас- |
||||||||||||||||||
|
Рис. 1.3. |
||||||||||||||||||
|
ширенной |
матрицей A1:D3 коэффи- |
|||||||||||||||||
циентов, например, показанной на рис. 1.3, выделяется горизонтальный диапазон, например, A4:D4 из N+1 ячеек (N=3 – число уравнений). Затем нажимают клавишу F2 и выбирают в ленте: Формулы, Вставить функцию, Категория — Определѐнные пользователем, xCdGauss, OK. В
возникшем окне Аргументы функции (см. рис. 1.2) указывают для аргумента Ab диапазон A1:D3 ячеек с коэффициентами расширенной матрицы СЛАУ, а затем нажимают Ctrl+Shift+Enter. В ячейках A4:C4 появятся вычисленные значения неизвестных СЛАУ, а в ячейке D4 число обусловленности матрицы системы.
Подготовка на листе матриц с вычисляемыми коэффициентами
Часто в математических расчѐтах встречаются СЛАУ, коэффициенты которых могут быть вычислены по сравнительно простым формулам. Как правило, эти СЛАУ имеют большое число уравнений. При необходимости размещения коэффициентов таких систем в ячейках листа Excel целесообразно подготовить формулу, задающую коэффициенты,
19
и использовать вместе с ней заранее составленную (стандартную) процедуру, заполняющую числами ячейки прямоугольного диапазона.
Идею организации подобного заполнения рассмотрим на следующем простом примере
Пример 1.9. Подготовить в выделяемом квадратном диапазоне единичную матрицу E.
Решение примера начнѐм с присвоения имѐн i, j, f соответственно ячейкам I1, J1, F1 рабочего листа. Переменными i и j будем обозначать соответственно строки и столбцы выделенного диапазона, а в ячейку с именем f запишем формулу =ЕСЛИ(i=j; 1; 0) . В процедуре, заполняющей выделяемый диапазон, будем ссылаться на поименованные ячейки:
Sub PutKoeff()
Dim R As Range
Set R = Application.InputBox(prompt:=»Укажите матрицу», Type:=8)
|
i1 = R.Row: j1 = R.Column |
|
|
For i = 0 To R.Rows.Count — 1 |
|
|
For j = 0 To R.Columns.Count — 1 |
|
|
Range(«i») = i + 1 |
‘ запись в ячейку i номера строки |
|
Range(«j») = j + 1 |
‘ запись в ячейку j номера столбца |
|
Cells(i1 + i, j1 + j) = Range(«f») |
‘ перезапись в ячейку диапазона значения из f |
|
Next j |
|
|
Next i |
|
|
End Sub |
Свяжем запуск данного макроса с фигурой (как это упомянуто вскользь в разделе «Описание решения на Excel задачи A»). Для этого вставим на лист (или, как это было сделано ранее, на рисунок SmartArt) какую-либо фигуру, вызвав нажатием правой клавишей мыши контекстное меню, назначим макрос данному объекту. После этого макрос запускается щелчком по фигуре, мы выделяем квадратный диапазон ячеек, в котором затем формируется единичная матрица.
В следующем примере разбирается более сложный случай.
20
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Function det(matrix)
Dim n As Byte, j As Byte
Dim i_ As Byte, j_ As Byte
Dim minor()
n = UBound(matrix)
If n = 1 Then det = matrix(1, 1): Exit Function
ReDim minor(1 To n - 1, 1 To n - 1)
For j = 1 To n 'по первой строке
For i_ = 1 To n - 1
For j_ = 1 To n - 1
If j_ < j Then minor(i_, j_) = matrix(i_ + 1, j_)
If j_ >= j Then minor(i_, j_) = matrix(i_ + 1, j_ + 1)
Next j_
Next i_
det = det + (-1) ^ (1 + j) * matrix(1, j) * det(minor)
Next j
End Function
Private Sub Command1_Click()
Dim i As Integer, j As Integer
n = CInt(InputBox("Число строк")) 'матрица ТОЛЬКО квадратная
ReDim A(1 To n, 1 To n) As Single
For i = 1 To n
For j = 1 To n
A(i, j) = InputBox("a(" & i & " , " & j & " ) ")
Text1.Text = Text1.Text & A(i, j) & ""
Next j
Text1.Text = Text1.Text + vbCrLf
Next i
MsgBox det(A) 'Call det(matrix) - бред {Function det, а не Sub det}
End Sub