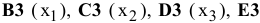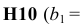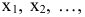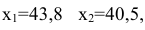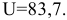БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Энергетический факультет
А.В. Манюкевич
Лабораторный практикум
по курсу «Информатика»
«Программирование на языке VBAдляEXCEL»
для студентов специальности 1 27 01 01
«Экономика и организация производства»
Минск 2007
УДК 620.9
Рецензенты
Манюкевич А.В.
Лабораторный практикум по курсу
«Информатика. Программирование на языке
VBA для EXCEL» для студентов специальности
1 27 01 01 «Экономика и организация
производства»
Лабораторный практикум предназначен
для студентов экономических специальностей.
Рассмотрены принципы автоматизации
проектов в EXCELс использованием
встроенного языка программированияVisualBasicforApplication.
Лабораторная работа №1
Цель:Изучить основные методы
программирования сложных функций на
языкеVBA.
Краткие теоретические сведения
Структурным элементом программы,
написанной на языке VBA, является модуль–
совокупность объявлений и процедур,
объединенных в единое целое. По своему
предназначению модули делятся на два
типа: стандартные модулиимодули
объектов. К стандартным модулям
относятся те, которые содержат макросы.
К модулям объектов относятся модули,
связанные с рабочей книгой, рабочими
листами, формами и модули класса. Мы
будем использовать только стандартные
модули.
Чтобы осуществить вставку модуля
необходимо находясь в среде VBA выполнить
команду Insert (Вcтавить) / Module (Модуль).
Окно редактирования кода служит в
качестве редактора для ввода и изменения
кода внутри модуля. Каждый модуль состоит
из области описанияи одной или
несколькихпроцедур. Процедура
представляет собой последовательностьоператоров, которые часто называютпрограммными кодами. Входящие в
модуль процедуры объединены общейобластью описания. В ней описываются
данные и объекты, которые являются
общепринятыми для процедур модуля.
Иерархия указанных объектов такова:
-
модуль;
-
область описания;
-
процедура;
-
код;
-
оператор.
При создании и редактировании кода
удобно пользоваться командой Insert
(Вcтавить) / Procedure (Процедуру). В
появившемся окне необходимо выбрать
функцию или подпрограмму и задать ее
имя. После этого будут автоматически
сформированы операторы начала и конца
процедуры и можно переходить непосредственно
к набору операторов процедуры. Для
набора следующей процедуры в том же
модуле необходимо повторить командуInsert (Вcтавить) / Procedure (Процедуру).
Если нужно создать новый модуль
повторяется командаInsert (Вcтавить) /
Module (Модуль).
Проверка правописания осуществляется
на этапе компиляции командой Debug
(Отладка) / Compile VBAProject(компилировать).
Для запуска программы требуется выполнить
командуRun (Запуск) / Run Sub/UserForm (Запуск
подпрограммы/UserForm)или нажать клавишу<F5>или соответствующую кнопку
панели инструментов.
В появившемся окне следует выбрать имя
нужной программы и щелкнуть по кнопке
Run (Выполнить).
Для того чтобы сохранить или открыть
созданную ранее программу используют
стандартные средства Excel, например,
соответствующие пункты меню Файл/Сохранить
как… , Открыть.
Запуск или редактирование существующего
программного кода после запуска Excel
может быть осуществлен после
последовательного выполнения команд:
Tool (Сервис) / Macro (Макрос) / Макросы. В
появившемся диалоговом окне следует
указать имя процедуры и нажать кнопку,
отвечающую за выполнение требуемого
действия (выполнить или изменить).
Структура программного кода
В общем виде программа на VBAвыглядит следующим образом:
[Option Explicit]
[Private
| Public] [Static] Function <Имя>
([<Список
аргументов>])
[Dim
<Имя> [As <Тип>]]
[Const
<Имя> [As <Тип>]
= <Выражение>]
[Инструкции]
[Exit Function]
[Инструкции]
End Function
В этой
записи:
Option
Explicit – инструкция, предписывающая
явное описание всех переменных,
встречающихся в программе;
Public –
ключевое слово, которое указывает,
что процедура доступна для всех других
процедур во всех модулях;
Private –ключевое слово, указывающее, что процедура
доступна для других процедур только
того модуля, в котором она описана;
Static –ключевое слово, указывающее, что локальные
переменные процедуры сохраняются в
промежутках времени между вызовами
этой процедуры;
<Имя> –имя процедуры, удовлетворяющее стандартным
правилам именования;
<Список
аргументов> – список переменных,
представляющий аргументы, которые
передаются в процедуру при ее вызове.
Имена переменных разделяются запятой.
Dim
<Имя> [As <Тип>] –блок описания
переменных;
Const
<Имя> [As <Тип>] = <Выражение> –блок
описания констант;
Инструкции –любой набор любых команд VBA;
Exit
Function– инструкция,
выполнение которой приводит к немедленному
выходу из процедуры;
Создадим
пользовательскую функцию F(x) = cos2
(π*x).
Function F(x)
Pi = Atn(l) / 4
F = Cos(Pi * x)^2
End
Function
Поскольку
в VBA
отсутствует стандартное число π, то оно
вычисляется по функции:
Pi
= Atn(l)
/ 4
По
умолчанию функция попадает в раздел
Определенные
пользователем
списка Категория
окна Мастер
функций EXCEL.
Вызов данной функции не отличается от
вызова стандартных функций EXCEL.
При создании функций пользователя
полезно знать, какие встроенные
математические функции имеются в VBA. На
самом деле, таких функций совсем не
много.
Таблица
1- Основные математические функции VBA
|
Функция |
Возвращаемое |
|
Abs(number) |
Абсолютное |
|
Аtn |
Арктангенс |
|
Сos |
Косинус |
|
Exp(number) |
Экспонента, |
|
Log(number) |
Натуральный |
|
Rnd(number) |
Случайное |
|
Sgn |
Знак числа. |
|
Sin |
Синус |
|
Sqr(number) |
Квадратный |
|
Tan(number) |
Тангенс |
|
Fix(number), Int |
Обе функции |
Типы данных
Типы данных являются одним
из важнейших элементов языка VBА.
Подобно всем современным языкам
программирования, VBA
поддерживает несколько типов данных,
которые можно использовать для объявления
типов переменных или создания массивов.
При объявлении переменных
тип данных указывается после ключевого
слова As,
с помощью одного из ключевых слов,
представленных в Таблице 2.
Таблица
2- Типы данных
|
Тип |
Значения |
Размер, |
|
Byte |
От |
1 |
|
Boolean |
True |
2 |
|
Integer |
От |
2 |
|
Long |
От |
4 |
|
Single |
От -3,402823 От |
4 |
|
Double |
От -4,94065645841247 от |
8 |
|
Currency |
От 922 337 203 685 477,5807 |
8 |
|
Decimal |
±79228162514264337 |
14 |
|
Date |
От |
8 |
|
Object |
Любой |
4 |
|
String |
От |
10 + длина |
|
String |
От 1 до приблизительно |
Длина |
|
Variant |
Любое |
16 |
|
Variant |
Как |
22 + длина |
|
Тип |
Диапазон |
Размер |
Переменные типа Byte,
Boolean,
Integer,
Long,
Currency,
Decimal,
Single,
Double
и
Date
в VBA
называются числовыми
переменными. Числовыми
переменными являются
также переменные подтипов Empty,
Integer,
Long,
Single,
Double,
Currency,
Decimal,
Date,
Error,
Boolean
и
Byte
типа
Variant.
Переменные типа String
относят к строковым
переменным. Этот
тип переменных может содержать буквы,
цифры пробелы, знаки пунктуации и
специальные символы.
VBA
не требует обязательного объявления
переменных. В случае если переменная
не была объявлена, ей автоматически
присваивается тип Variant.
Этот тип является универсальным и может
содержать данные различных подтипов:
Integer,
Long,
String
и т. п.
Соглашение об именах констант и переменных
При написании программ на
VBA
принято придерживаться определенных
правил при задании имен констант и
переменных в зависимости от их типа.
Например, при объявлении переменной
типа Integer
вначале имени ставится специальный
префикс int.
Префиксы, используемые в именах переменных
в зависимости от их типа, представлены
в таблице 3.
Таблица
3 — Префиксы, используемые в именах
переменных в зависимости от их типа
|
Тип данных |
Префикс |
|
Boolean |
bin |
|
Byte |
byt |
|
Currency |
cur |
|
Date |
dtm |
|
Double |
dbl |
|
Error |
err |
|
Integer |
int |
|
Long |
lng |
|
Object |
obj |
|
Single |
sng |
|
String |
str |
|
Типы |
udt |
|
Variant |
vnt |
При задании имен переменных не
рекомендуется, как слишком сильно
сокращать слова, так и давать переменным
очень длинные имена, так как это ухудшает
читаемость текста программы, особенно
для больших проектов.
Соседние файлы в папке Лабораторные работы
- #
- #
- #
Содержание
- 4. Использование vba в среде excel. Линейные программы.
- 4.1. Элементы управления
- «Программирование линейных алгоритмов на языке vba»
- Краткие теоретические сведения
- Линейное программирование в Excel
- Линейное программирование
- Решение задач линейного программирования с использованием microsoft excel
- Цель работы
- Порядок выполнения работы
- Инструкция по использованию microsoft excel для решения задач линейного программирования
- Одноиндексные задачи линейного программирования
- Ввод исходных данных
- Целочисленное программирование
- Двухиндексные задачи линейного программирования
- Задачи с булевыми переменными
- Возможные ошибки при вводе условий задач линейного программирования
- Как решить задачу линейного программирования в excel
- Инструкция по использованию microsoft excel для решения задач линейного программирования
- Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
- Технология решения транспортной задачи
4. Использование vba в среде excel. Линейные программы.
VBA (Visual Basic for Application) − это объектно-ориентиро-ванный язык программирования, встроенный во все программы Microsoft Office. Язык VBA использует понятие объектов: (рабочая книга (Workbooks), рабочий лист (Worksheets), ячейки (Cells), область (Range), элементы управления на рабочих листах).
4.1. Элементы управления
Основными компонентами программ на VBA являются процедуры. Процедура – это самостоятельная программа, включающая операторы описания данных и исполняемые операторы. Процедура выполняется тогда, когда происходит то или иное событие, например, щелчок (Click) по командной кнопке, для которой записана конкретная процедура.
Создание проекта программы на VBA состоит из двух взаимосвязанных процессов: размещение элементов управления (кнопки, текстовые окна, списки и др.) на рабочем листе Excel или на форме (формах) пользователя и написание текста процедуры для этих элементов в соответствии с алгоритмом решения задачи.
Для размещения элемента управления на рабочем листе в Excel 2003 надо вызвать панель инструментов Элементы управления (командой Вид/Панели инструментов/Элементы управления), активизировать на панели нужный элемент и поместить его в соответствующем месте рабочего листа (установить указатель мыши в нужное место, нажать левую кнопку мыши и, не отпуская ее, очертить размеры элемента управления движением курсора мыши по диагонали).
Надпись, шрифт и цвет надписи и т. д. можно изменить, открыв окно свойств нажатием на кнопку Свойства на панели инструментов Элементы управления (рис. 4.1). В левом столбце окна свойств написаны названия свойств, в правом – их значения. Для изменения надписи используется свойство Caption, для изменения шрифта надписи – Font, для изменения цвета букв – ForeColor, для изменения цвета кнопки – BackColor и т. д. Значение свойства Name, определяющее имя элемента, задается только латинскими буквами.
– переход в режим Конструктора (редактора VBA)
– активизация окна Свойства
– переход в окно Исходный текст (программы)
Рис. 4.1. Панель Элементы управления
Чтобы разместить элементы управления на рабочем листе в Excel 2007, необходимо придерживаться следующего порядка действия. Вначале надо поместить на ленту вкладку Разработчик. Для этого надо нажать кнопку Оffice 
Для записи процедуры, которая связывается с некоторым элементом управления, необходимо:
перейти в режим конструктора, щелкнув по кнопке Режим конструктора на панели инструментов Элементы управления (если этот режим не установлен первоначально);
активизировать элемент управления, для которого нужно написать программу обработки события, и перейти в окно программного кода, щелкнув по кнопке Исходный текст на панели инструментов Элементы управления (при этом откроется окно редактора VBA). Перейти в окно программ также можно, сделав двойной щелчок по элементу управления;
в окне программного кода выбрать из предлагаемого списка событие, при совершении которого должна выполняться процедура (по умолчанию компьютер выбирает событие Click (щелчок)).
Когда происходит то или иное событие, то выполняется процедура обработки события, которая заключена между ключевыми словами (процедурными скобками) Sub…End Sub.
Пример. Разработать программу, которая будет выводить в окно сообщения слово «Привет» при совершении события «щелчок по командной кнопке».
Для этого на панели Элементы управления надо выбрать элемент Кнопка и поместить его на рабочем листе (появится кнопка с надписью CommandButton1). Затем следует дважды щелкнуть по кнопке и откроется редактор VBA, в котором записать следующую процедуру:
Здесь функция MsgBox() активизирует диалоговое окно с сообщением, записанным в кавычках.
Для запуска процедуры надо перейти на лист рабочей книги Excel, выйти из режима конструирования, отжав кнопку Режим конструктора на панели инструментов Элементы управления, нажать на кнопку, для которой была написана процедура обработки события, и проанализировать результат.
Источник
«Программирование линейных алгоритмов на языке vba»
Цель:Изучить основные методы программирования сложных функций на языкеVBA.
Краткие теоретические сведения
Структурным элементом программы, написанной на языке VBA, является модуль– совокупность объявлений и процедур, объединенных в единое целое. По своему предназначению модули делятся на два типа: стандартные модулиимодули объектов. К стандартным модулям относятся те, которые содержат макросы. К модулям объектов относятся модули, связанные с рабочей книгой, рабочими листами, формами и модули класса. Мы будем использовать только стандартные модули.
Чтобы осуществить вставку модуля необходимо находясь в среде VBA выполнить команду Insert (Вcтавить) / Module (Модуль).
Окно редактирования кода служит в качестве редактора для ввода и изменения кода внутри модуля. Каждый модуль состоит из области описанияи одной или несколькихпроцедур. Процедура представляет собой последовательностьоператоров, которые часто называютпрограммными кодами. Входящие в модуль процедуры объединены общейобластью описания. В ней описываются данные и объекты, которые являются общепринятыми для процедур модуля. Иерархия указанных объектов такова:
При создании и редактировании кода удобно пользоваться командой Insert (Вcтавить) / Procedure (Процедуру). В появившемся окне необходимо выбрать функцию или подпрограмму и задать ее имя. После этого будут автоматически сформированы операторы начала и конца процедуры и можно переходить непосредственно к набору операторов процедуры. Для набора следующей процедуры в том же модуле необходимо повторить командуInsert (Вcтавить) / Procedure (Процедуру). Если нужно создать новый модуль повторяется командаInsert (Вcтавить) / Module (Модуль).
Проверка правописания осуществляется на этапе компиляции командой Debug (Отладка) / Compile VBAProject(компилировать). Для запуска программы требуется выполнить командуRun (Запуск) / Run Sub/UserForm (Запуск подпрограммы/UserForm)или нажать клавишу или соответствующую кнопку панели инструментов.
В появившемся окне следует выбрать имя нужной программы и щелкнуть по кнопке Run (Выполнить).
Для того чтобы сохранить или открыть созданную ранее программу используют стандартные средства Excel, например, соответствующие пункты меню Файл/Сохранить как… , Открыть.
Запуск или редактирование существующего программного кода после запуска Excel может быть осуществлен после последовательного выполнения команд: Tool (Сервис) / Macro (Макрос) / Макросы. В появившемся диалоговом окне следует указать имя процедуры и нажать кнопку, отвечающую за выполнение требуемого действия (выполнить или изменить).
Структура программного кода
В общем виде программа на VBAвыглядит следующим образом:
[Private | Public] [Static] Function ([ ])
Option Explicit – инструкция, предписывающая явное описание всех переменных, встречающихся в программе;
Public – ключевое слово, которое указывает, что процедура доступна для всех других процедур во всех модулях;
Private –ключевое слово, указывающее, что процедура доступна для других процедур только того модуля, в котором она описана;
Static –ключевое слово, указывающее, что локальные переменные процедуры сохраняются в промежутках времени между вызовами этой процедуры;
–имя процедуры, удовлетворяющее стандартным правилам именования;
– список переменных, представляющий аргументы, которые передаются в процедуру при ее вызове. Имена переменных разделяются запятой.
Dim [As ] –блок описания переменных;
Const [As ] = –блок описания констант;
Инструкции –любой набор любых команд VBA;
Exit Function– инструкция, выполнение которой приводит к немедленному выходу из процедуры;
Создадим пользовательскую функцию F(x) = cos 2 (π*x).
Поскольку в VBA отсутствует стандартное число π, то оно вычисляется по функции:
По умолчанию функция попадает в раздел Определенные пользователем списка Категория окна Мастер функций EXCEL. Вызов данной функции не отличается от вызова стандартных функций EXCEL.
При создании функций пользователя полезно знать, какие встроенные математические функции имеются в VBA. На самом деле, таких функций совсем не много.
Таблица 1- Основные математические функции VBA
Источник
Линейное программирование в Excel
Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
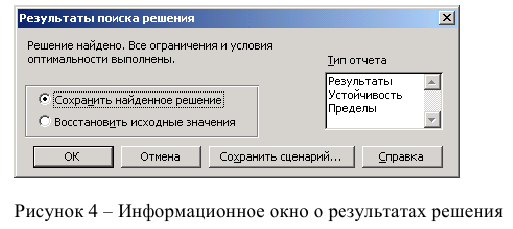
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 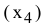
правым частям ограничений соответствуют ячейки
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «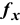
• курсор в поле F6;
• нажав кнопку «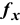
• выберите в окне «Категория» категорию «Математические»;
• в окне «Функция» выберите функцию СУММПРОИЗВ;
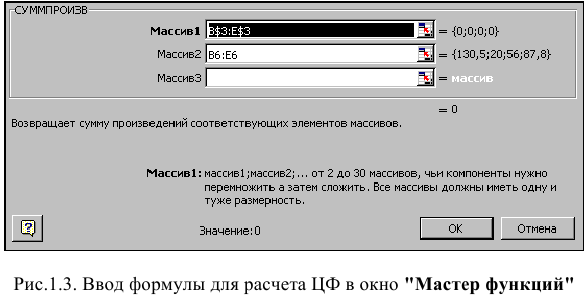
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.
Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
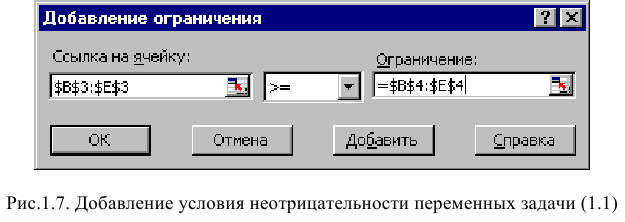
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Задание знаков ограничений , =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12 Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.
Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
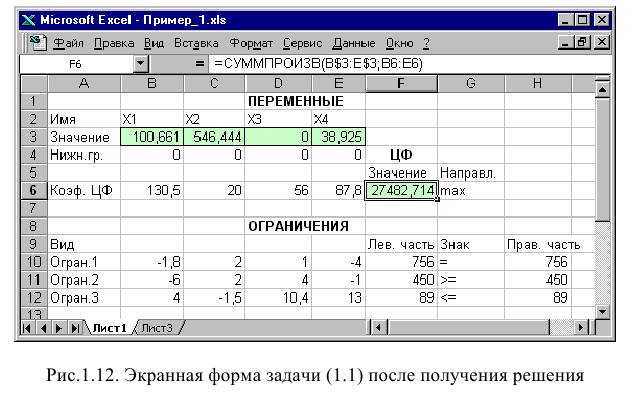
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
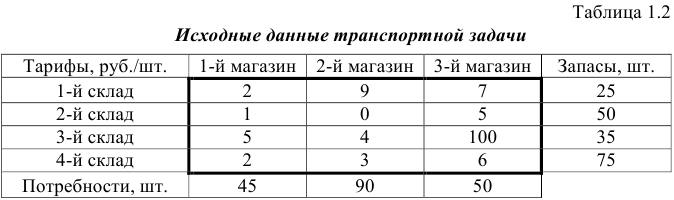
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
Целевая функция и ограничения данной задачи имеют вид
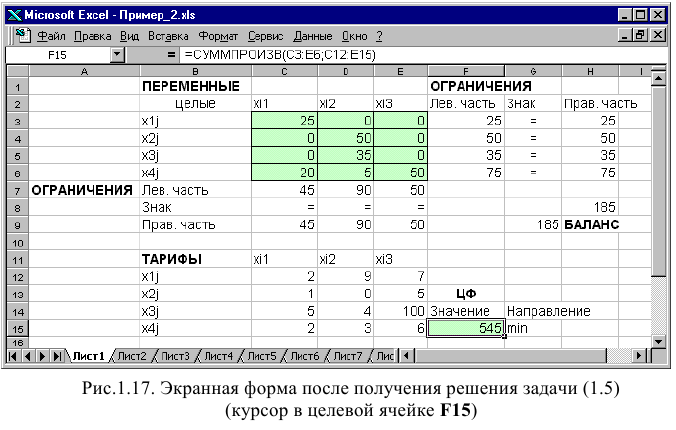
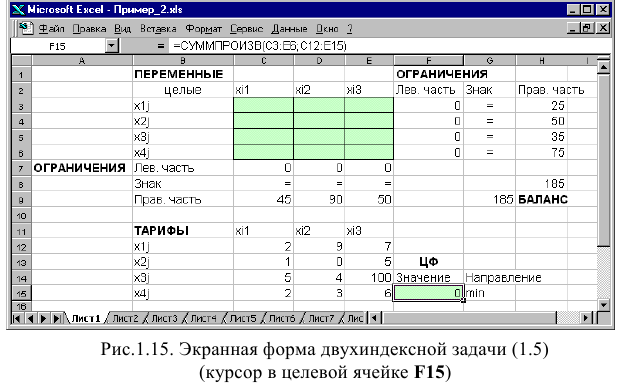
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
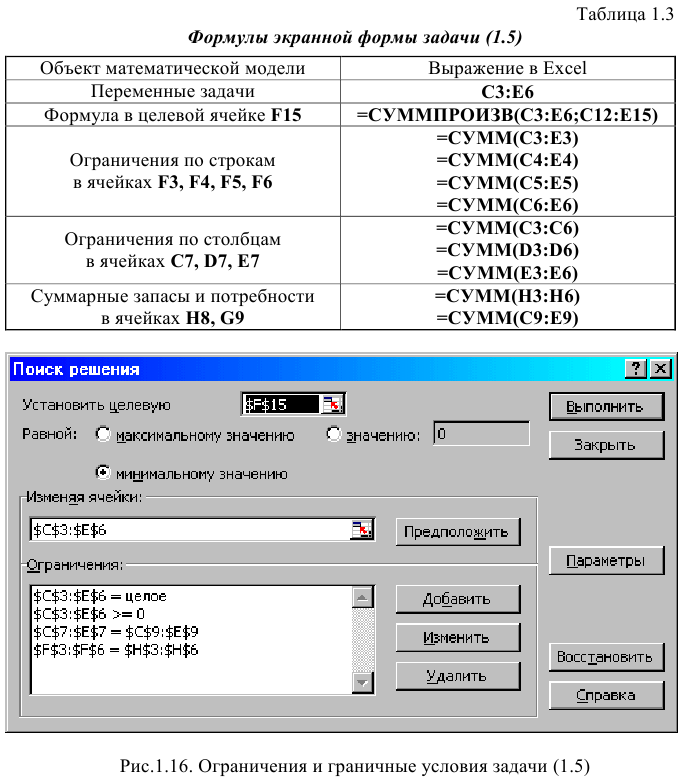
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 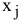
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
Создание экранной формы и ввод в нее условия задачи
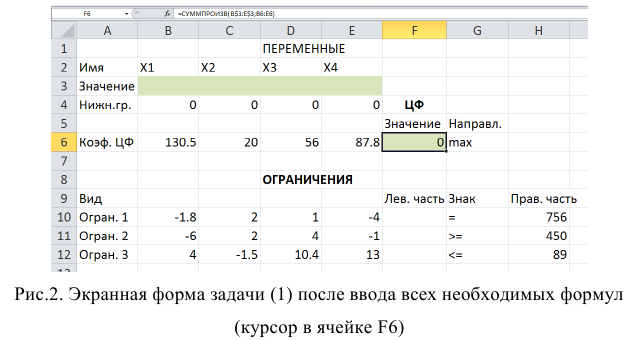
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
коэффициентам ЦФ соответствуют ячейки
правым частям ограничений соответствуют ячейки
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
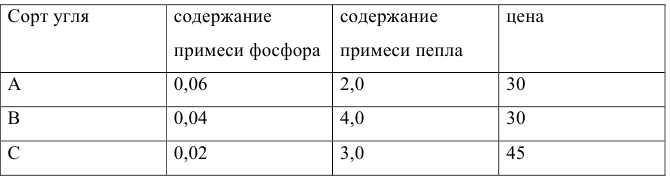
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
Составим математическую модель задачи. Пусть 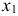
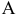
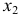
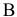
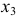
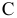
Целевая функция: 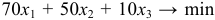
Решение задачи с помощью MS Excel.
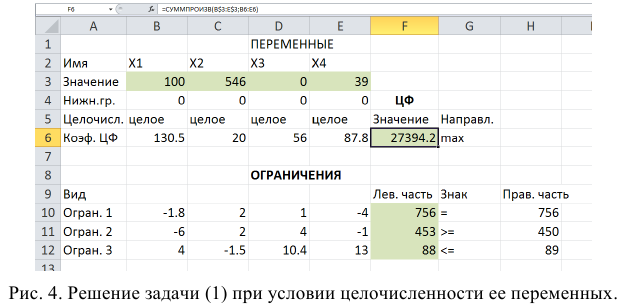
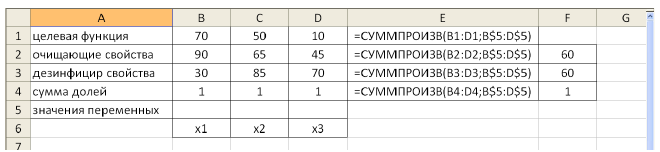
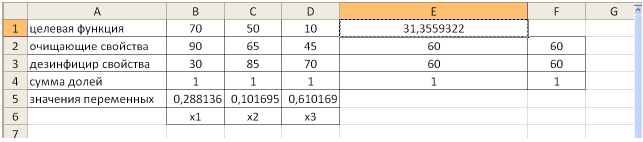
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
(т.е. очистители 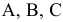
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 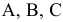
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: 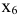
Прибыль, которую получит инвестор, задается целевой функцией:
Ограничения на суммарный объем активов —
Ограничение на размер доли каждого актива
Необходимость долгосрочного инвестирования (например, более 3 лет)
Учет необходимости снижения риска —
Естественное экономическое ограничение — неотрицательность искомых переменных —
Для решения задачи выполним следующие шаги.
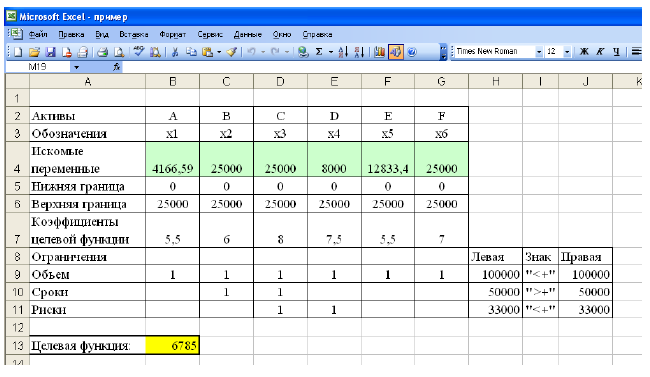
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
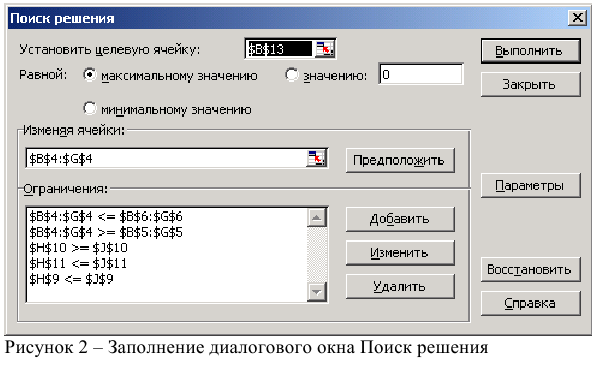
Рисунок 1 — Исходные данные для решения ЗЛП
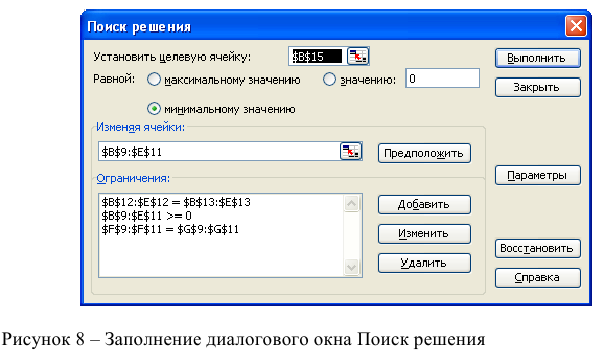
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
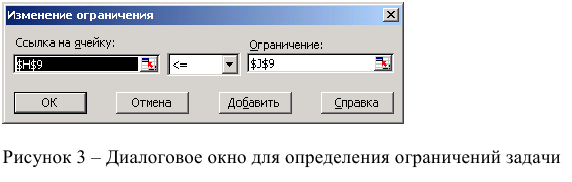
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
Технология решения транспортной задачи
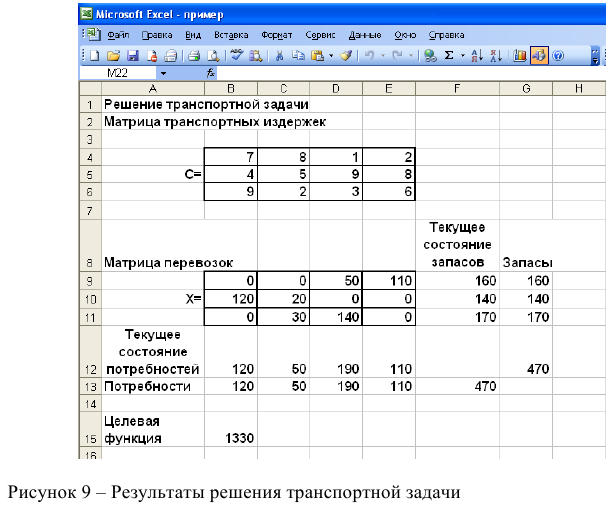
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности 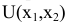
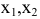
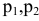
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
где 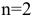
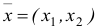
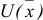
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
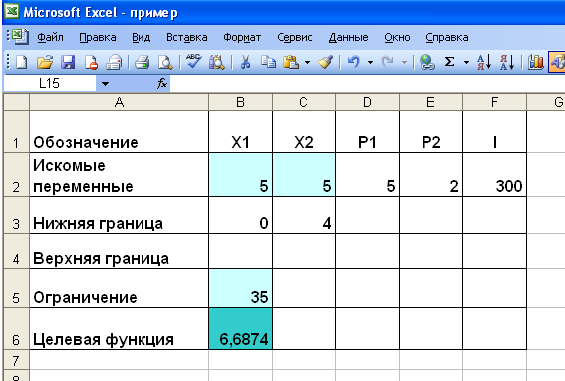
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
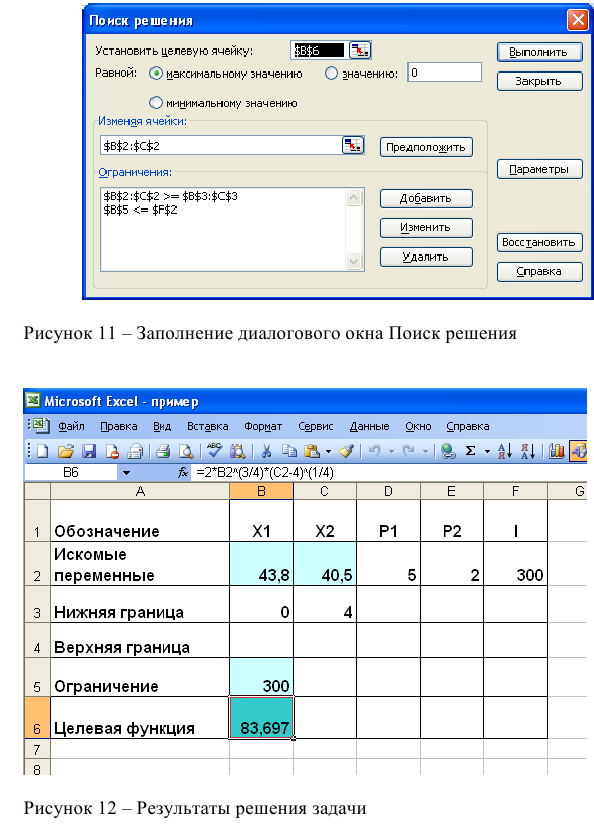
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
Найдем точки экстремума функции Лагранжа.
Приравняем каждое уравнение к 0:
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
Подставим второе уравнение в первое и построим аналитические функции спроса:
Максимальное значение функции полезности-
Решением задачи потребительского выбора будет набор
Возможно эти страницы вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
|
Группа: Проверенные Ранг: Форумчанин Сообщений: 131
Замечаний: |
Добрый вечер.
Помогите с вопросом о линейном программировании (максимизация выпуска продукции).
В таблице записаны названия трех деталей и сколько на них уходит ресурсов, и какова цена единицы каждой продукции.
Как макросом при нажатии на кнопку — решить эту задачу линейного программирования и выписать ответ в ячейки D16, E16, F16 ?
(Вопрос в задаче звучит так: Сколько надо выпустить продукции A, B и C — чтобы получить максимальную прибыль ? )
К сообщению приложен файл:
1_.xlsb
(9.0 Kb)

Цель работы: ознакомиться со средой VBA. Овладеть навыками программирования в VBA.
Задание 1. Программирование линейного алгоритма.
Пример1 : Написать программу вычисления функции f(x)=x2+1 в диалоговом режиме.
В программе нам понадобятся две переменные – x и f. Для ввода значения х будем использовать функцию ввода InputBox, а для вывода значения f – оператор вывода MsgBox. Переменные х и у опишем как переменные вещественного типа, т.е. Single.
Чтобы попасть в VBA необходимо выполнить команду СервизМакросРедактор Visual Basic или нажать клавиши <Alt>+<F11>. Появиться окно VBA. Для вставки модуля выполним команду ВставкаМодуля (рис.7.).
В открывшемся окне модуля наберите следующую строку Sub PR1() и нажмите клавишу <Enter>. Таким образом у вас будет создан каркас процедуры:
Sub Pr1()
End Sub
Теперь необходимо наполнить этот каркас операторами.
Во-первых, опишем наши переменные x и f – Dim x as Single, f as Single
Во-вторых, огранизуем ввод переменной х – x = InputBox(“Введите значение х”)
В-третьих, запишем оператор для вычисления f
f = x^2+1
В-четвертых, выведем значение переменной f – MsgBox «f=» & Format(f, «###.#0»). Функцию Format использовали для того, чтобы вывести значение функции с 2-мя знаками после запятой. Итак, процедура должна иметь следующий вид:
Sub Pr1()
Dim x As Single, f As Single
x = InputBox(«Введите значение х»)
f = x ^ 2 + 1
MsgBox «f=» & Format(f, «###.#0»)
End Sub
Для запуска программы на выполнение нажмите клавишу <F5>. Для запуска программы с листа Excel необходимо выполнить следующие действия:
1. Зайти на лист Excel.
2. Выполнить команду ВидПанели инструментовЭлементы управления (рис.8.).
3. Щелкнуть на элементе управления кнопка и нарисуйте кнопку на листе Excel
4. Вызовите контекстное меню для нарисованной кнопки (щелчок правой кнопкой мыши) и выполните команду Свойства. Откроется окно свойств кнопки (Рис.3.). Используя свойства BackColor, Font, ForeColor выберите закраску фона кнопки и шрифт для надписи на кнопке.
5. В окне свойства Caption введите текст надписи на кнопке – Диалоговый режим.
6. Выполните двойной щелчок на кнопке. Откроется окно процедуры и каркас заготовки процедуры для кнопки
Private Sub CommandButton1_Click()
End Sub
7. Внутри каркаса напишите операторы, которые должны будут выполняться для при щелчке на этой кнопке. В нашем случае щелчок на кнопке, должен вызывать процедуру вычисления функции. Для вызова процедуры достаточно указать её имя. Итак, процедура для кнопки будет иметь следующий вид:
Private Sub CommandButton1_Click()
Pr1
End Sub
8. Зайдите на лист Excel и отключите режим конструктора на панели элементов управления («отожмите» кнопку конструктора)
9. Щелкните на кнопке для запуска процедуры расчета функции.
Пример 2. Написать программу вычисления функции f(x)=x2+1 с использованием ячеек Excel.
Любая ячейка или группа ячеек является объектом Range, который в свою очередь, является производным от объекта Worksheet. Например, для обращения к значению ячейки А1 на втором листе Excel, необходимо использовать следующую конструкцию : Worksheets(2).Range(“A1”)
Итак, оформим программу вычисления функции, причем значение переменной х будем считывать из ячейки листа Excel и значение переменной f, так же будем помещать в ячейку.
1. В ячейку A1 введите – х=, а в ячейку A2 – f(x)=
2. В ячейку B1 введите любое числовое значение переменной х
3. Зайдите в редактор VBA , откройте первый модуль, установите курсор под оператором End Sub
4. Наберите оператор начала процедуры для второго примера – Sub Pr2() и нажмите <Enter>
5. Опишите переменные x и f
6. Переменной х присвоим значение содержимого ячейки B1. Для этого запишите следующую конструкцию – x=Range(“B1”)
7. Напишите оператор вычисления функции (см. пример 1)
8. Поместим значение переменной f в ячейку B2 – Range(“B2”)=f
9. Оформите вызов программы Pr2 c листа Excel (с помощью кнопки, см. пример 1)
Задание 2.
Напишите программу вычисления функции из лабораторной №4 для одного значения х.
А В С
1 Иванов П.С.
2 оклад 500
3 северные 400
4 Итого начислено: 900
5 подоходный налог 65
6 Итого удержано: 65
7 Итого к выплате 835
Задание 3.
Напишите программу вычисления заработной платы для отдельного сотрудника. Исходные данные – ФИО, оклад и северные вводить в диалоговом режиме, а расчетный лист сотрудника оформите на втором листе Excel в виде таблицы
Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
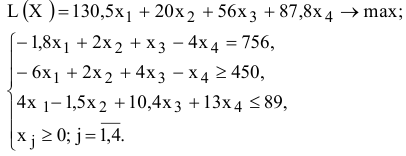
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
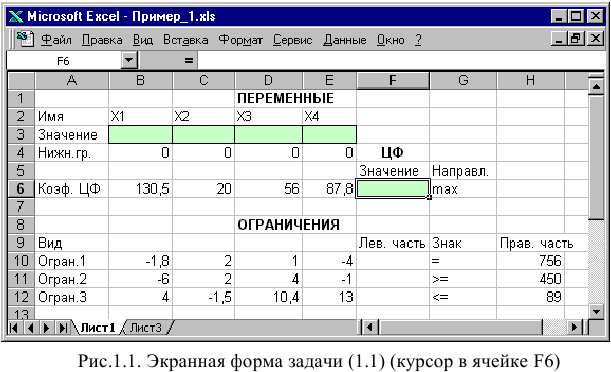
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 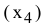
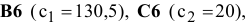
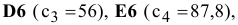
правым частям ограничений соответствуют ячейки
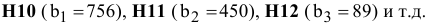
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
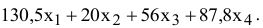
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
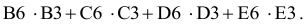
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
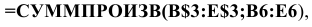
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
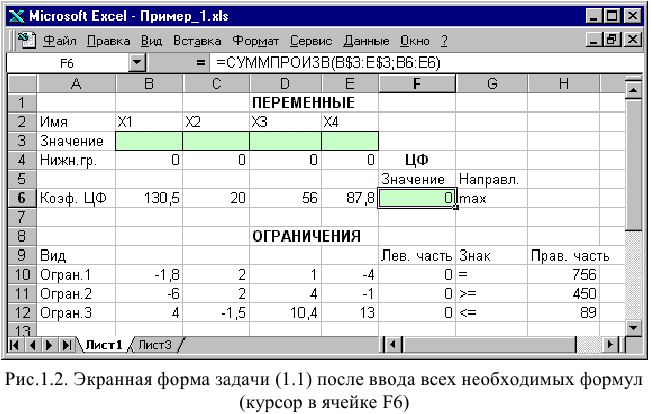
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «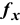
• курсор в поле F6;
• нажав кнопку «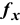
• выберите в окне «Категория» категорию «Математические»;
• в окне «Функция» выберите функцию СУММПРОИЗВ;
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).

Задание ЦФ
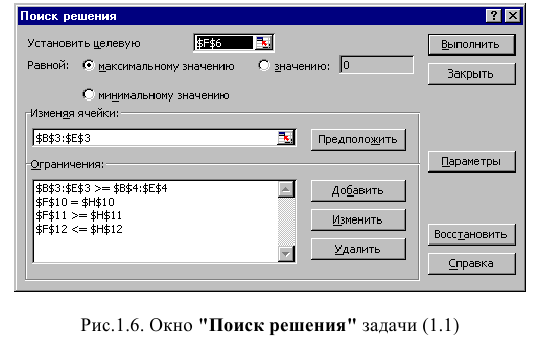
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Задание знаков ограничений <. >, =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
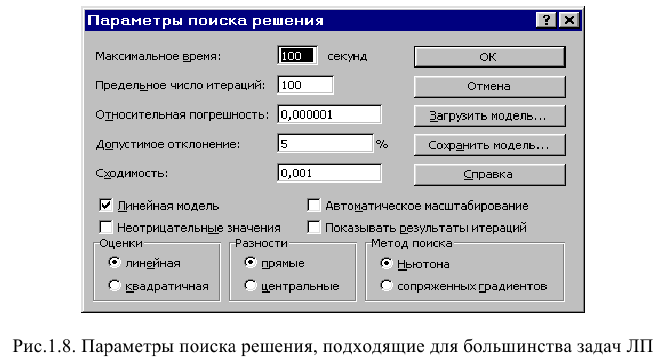
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
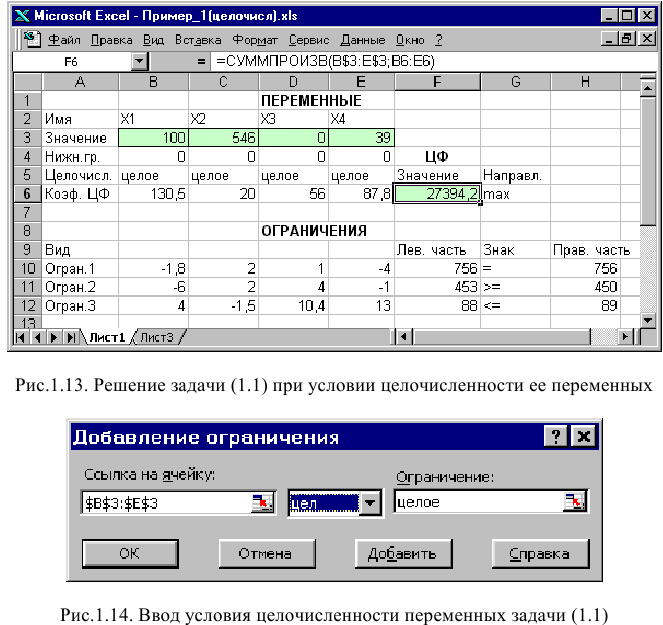
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
Целевая функция и ограничения данной задачи имеют вид
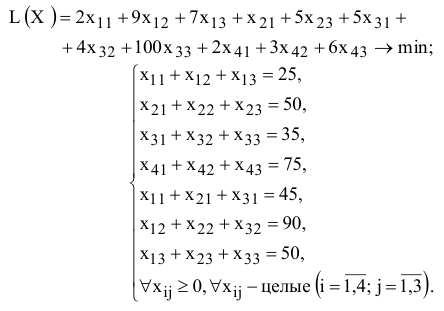
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 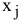
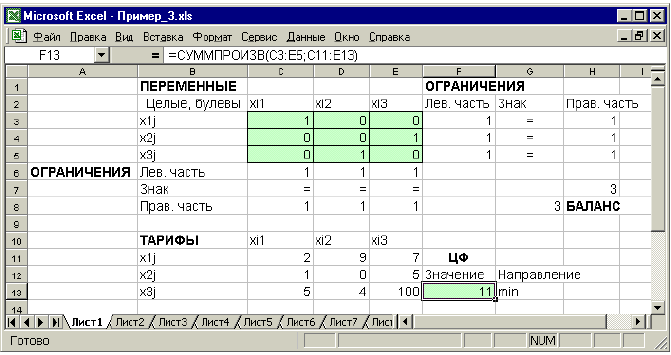
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
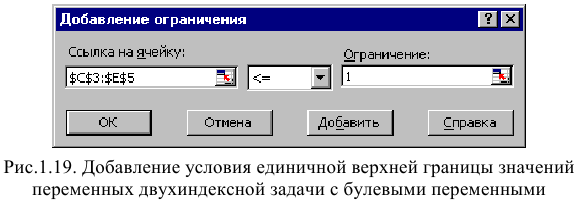
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
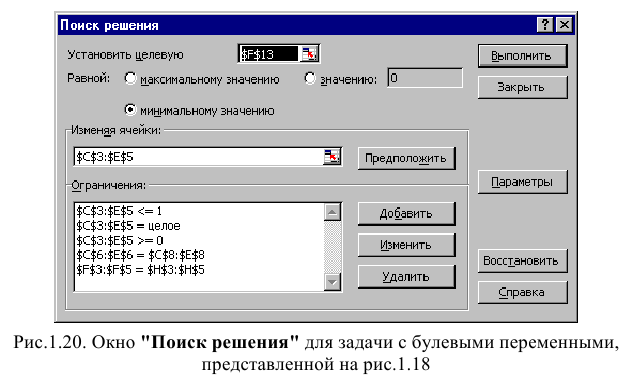
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Одноиндексные ЗЛП
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
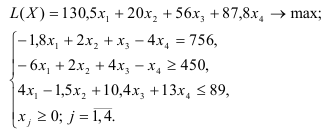
- Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
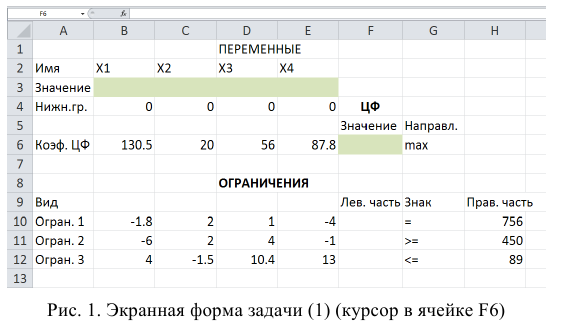
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
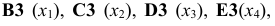
коэффициентам ЦФ соответствуют ячейки
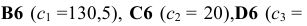
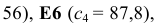
правым частям ограничений соответствуют ячейки
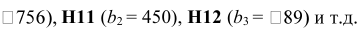
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
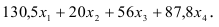
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
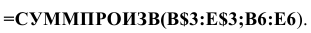
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
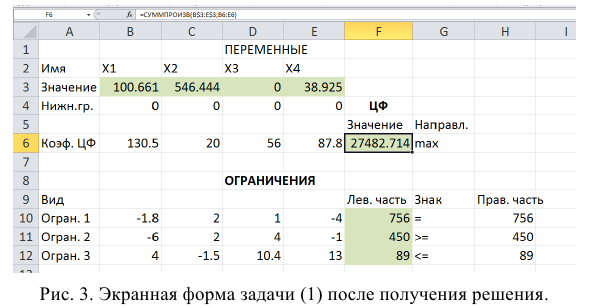
Целочисленное программирование
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
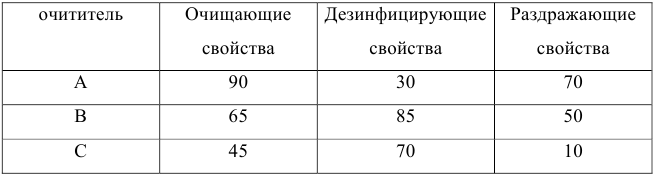
Составим математическую модель задачи. Пусть 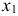
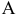
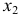
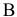
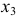
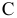
Целевая функция: 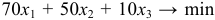
Ограничения:
Решение задачи с помощью MS Excel.
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
«Поиск решения».
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
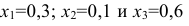
(т.е. очистители 
Задача 2.
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
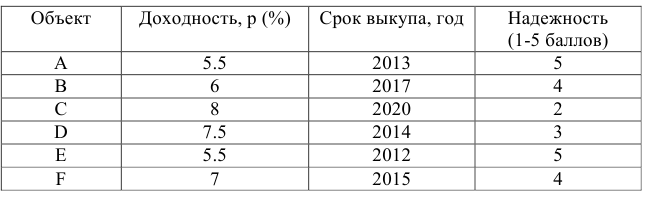
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: 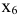
Прибыль, которую получит инвестор, задается целевой функцией:
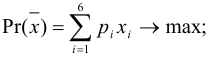
Сформируем ограничения:
Ограничения на суммарный объем активов —
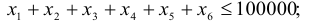
Ограничение на размер доли каждого актива
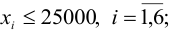
Необходимость долгосрочного инвестирования (например, более 3 лет)
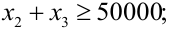
Учет необходимости снижения риска —
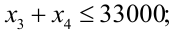
Естественное экономическое ограничение — неотрицательность искомых переменных —
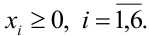
Для решения задачи выполним следующие шаги.
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
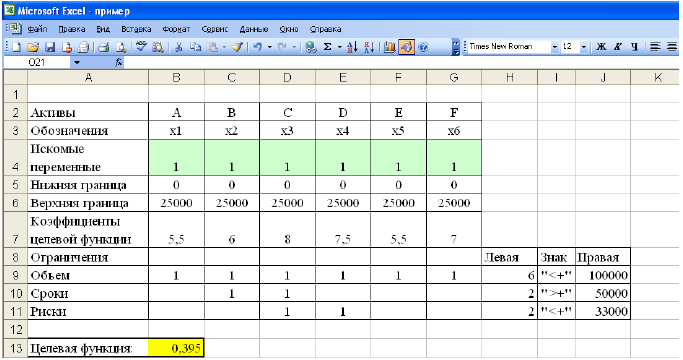
Рисунок 1 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
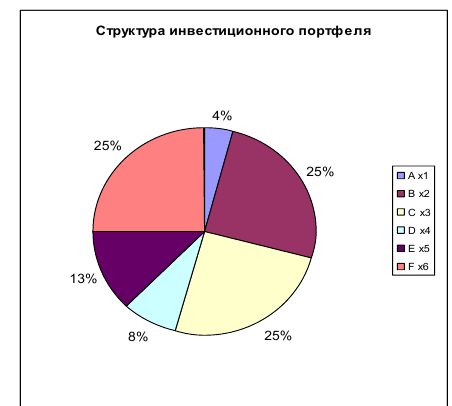
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
Технология решения транспортной задачи
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
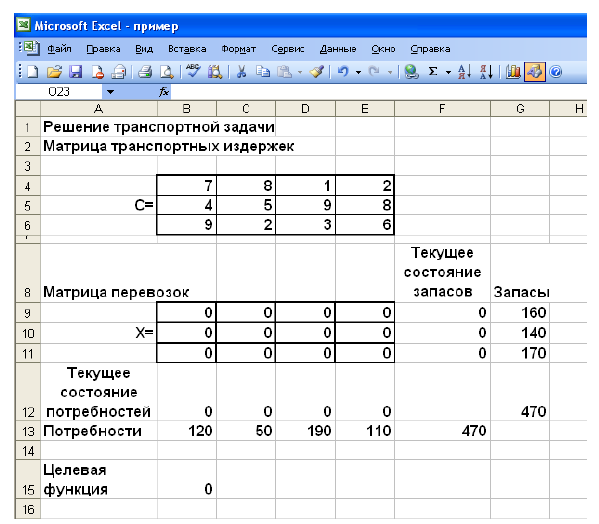
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности 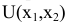
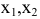
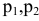
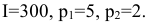
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
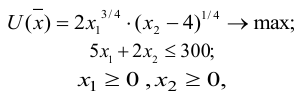
где 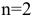
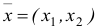
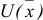
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
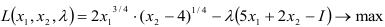
Найдем точки экстремума функции Лагранжа.
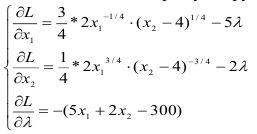
Приравняем каждое уравнение к 0:
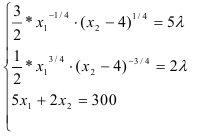
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
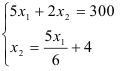
Подставим второе уравнение в первое и построим аналитические функции спроса:
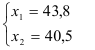
Максимальное значение функции полезности-
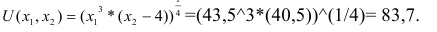
Решением задачи потребительского выбора будет набор
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию