Нужно сделать в Excel
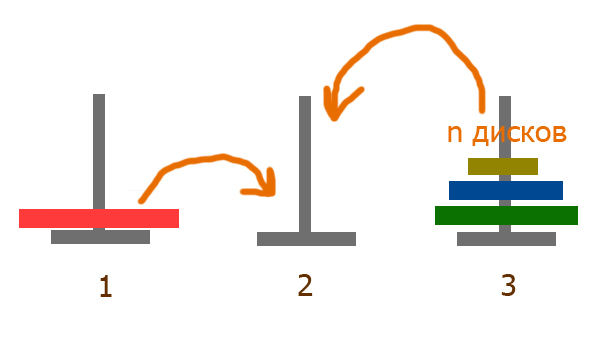
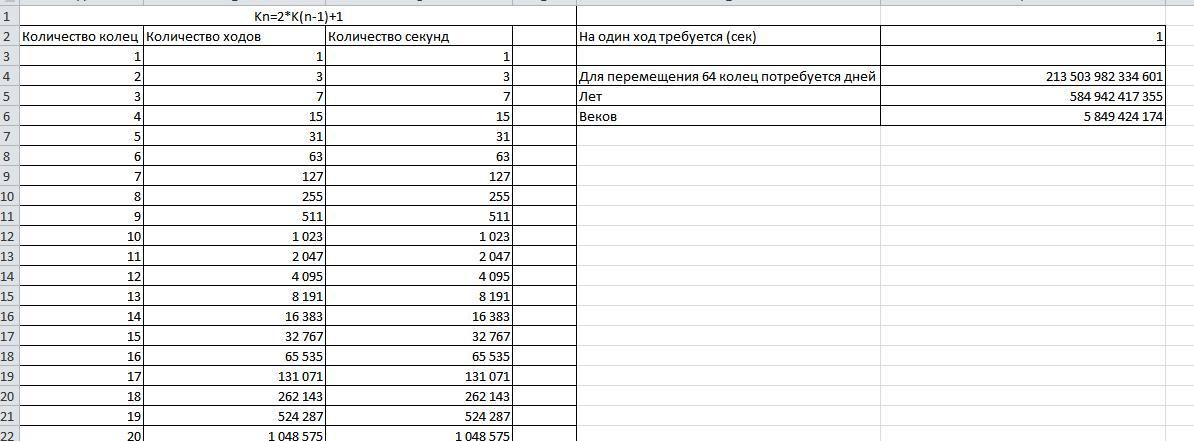
В основу эффективного решения головоломки «Ханойская башня» положен алгоритм, суть которого сводится к следующему: для перемещения башни, состоящей из n колец, с первого стержня на третий мы должны решить чуть более простую задачу переместить на второй стержень башню, состоящую из n-1 кольца. После этого нижний диск с первого стержня перемещается на третий и повторно осуществляется перемещение башни из n-1 кольца, но уже со второго диска на третий. Таким образом, число ходов, необходимых для перемещения башни из n колец, равно удвоенному числу ходов, необходимых для перемещения башни из n-1 кольца, и ещё одному ходу. Используйте эту закономерность для вычисления числа ходов, необходимых для перемещения башни из 64 колец. Вычислите, сколько времени займёт такое перемещение, если считать, что на один ход требуется 1 секунда.
Ответы на вопрос
Ответ:
Объяснение:
В приложенном файле формата Excel
Приложения:
Новые вопросы
Запишите натуральные числа, которые лежат на координатном луче между числами 398 и 403 *
398, 399, 400
398, 399, 400, 401, 402, 403
399, 400, 401, 402…
Содержание
- Задача ханойская башня
- Информатика задача программирование
- Сортировка «Ханойская башня»
- Алгоритм
- Сложность
- Реализация
- Характеристики алгоритма
- Ссылки
- Статьи серии:
- Русские Блоги
- Алгоритм (9) Ханойской башни и его реализация кода
- оглавление
- 1. Что такое Ханойская башня
- 2. Перемещение процесса Ханойской башни
- В-третьих, идея алгоритма Ханоты
- 1. Пример кода
- 2. Расширенные проблемы
Задача ханойская башня
Сегодня разберём известную задачу Ханойская башня. Подобные задачи способствуют повышению уровня грамотности при написании программ, развивают алгоритмические способности и поднимают общий тонус для участия в экзаменах и олимпиадах по информатике.
Задача : Есть три стержня. На одном из которых нанизаны диски. Диски располагаются в виде пирамидки(ханойской башни): в самом низу лежит самый большой диск, затем идёт чуть поменьше диск, затем ещё меньше диск и т. д. Необходимо переместить диски с одного стержня на другой. Можно использовать все три стержня, но при условии: перекладывать можно только по одному диску за ход, складывать диски можно только меньший на больший.
Нам необходимо составить алгоритм для решения данного задания при любом количестве n. Для начала докажем, что задача вообще имеет решение при любом количестве n. Для этого будем использовать метод математической индукции.
В основе метода математической индукции лежит принцип математической индукции.
Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если оно справедливо для n = 1 и из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1.
То есть, доказательство по методу математической индукции проводится в три этапа:
- во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);
- во-вторых, предполагается справедливость утверждения при любом натуральном n=k;
- в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.
Используем метод математической индукции:
- Наша задача точно решается для одного диска. Это очевидно. Просто берём и перемещаем диск с одного стержня на другой.
- Пусть мы умеем перекладывать n дисков. Докажем, что тогда и n+1 мы также можем переложить.
- Пускай нам надо переложить n+1 дисков на второй стержень. Т.к. мы умеем перекладывать n дисков, то мы эту стопку переложим на третий стержень. Затем, положив самый большой диск на второй стержень, мы воспользуемся тем, что умеем перекладывать стопку из n элементов и переложим эту стопку с третьего стержня на второй. Таким образом, мы доказали, что задача решается для любого числа дисков.
Ещё раз о методе математической индукции. Мы доказали, что для одного диска всё работает отлично. Также мы доказали, что если для n дисков задача решается, то для n+1 тоже будет решаться. Но если вместо n подставить нашу 1, то уже для 2 тоже будет выполняться. В свою очередь 2 «тянет» за собой 3 и т.д. Таким образом, у нас задача будет решаться для любого натурального числа.
Сами наши рассуждения по поводу метода математической индукции нам подсказывают, что здесь можно воспользоваться рекурсией
Программу напишем на C#, т.к. этот язык в большинстве случаев принимается на олимпиадах по информатике. n-Количество дисков, i-номер стержня-источника, p-номер стержня-приёмника, v-вспомогательный стержень. Переменные соответственно i,p,v должны принимать значения от 1 до 3. Переменная n>0. Защита от «дурака» в данной функции не реализована. Если понадобится — реализуете сами. Также, здесь приведена сама функция Hanoy, которая и реализует всю работу. Остальные строки кода консольного приложения C# здесь опущены.
Как мы с вами разобрались, когда размышляли о математической индукции, чтобы переложить n дисков на стержень-приёмник, нам необходимо сначала переложить n-1 дисков на вспомогательный стержень, затем переложить самое большое кольцо на стрежень-приёмник, и повторить действия для n-1 дисков, переместив их из вспомогательного стержня, уже на стержень назначения. Таким образом, наша Ханойская башня из n элементов переместится со стержня источника на стержень-приёмник. Обратите внимание, что функция Hanoy вызывает сама себя, т.е. функцию Hanoy (Это и есть рекурсия!). Это происходит из-за того, что для перемещения Ханойской башни из n элементов, ей необходимо воспользоваться результатом своей же работы для n-1 элементов.
Запускаем нашу функцию Hanoy из функции Main (Для языка C# в консольном приложении) для 3х дисков:
Время работы пропорционально 2 n − 1, где n-количество дисков.
На сегодня всё. Надеюсь, Вам понравилась задача Ханойская башня. Давайте изучать классику Информатики вместе! Если у Вас что-то не получилось, пишите в комментариях. До новых встреч!
Источник
Информатика задача программирование
В основу эффективного решения головоломки «Ханойская башня» положен алгоритм, суть которого сводится к следующему: для перемещения башни, состоящей из n колец, с первого стержня на третий мы должны решить чуть более простую задачу переместить на второй стержень башню, состоящую из n-1 кольца. После этого нижний диск с первого стержня перемещается на третий и повторно осуществляется перемещение башни из n-1 кольца, но уже со второго диска на третий. Таким образом, число ходов, необходимых для перемещения башни из n колец, равно удвоенному числу ходов, необходимых для перемещения башни из n-1 кольца, и ещё одному ходу. Используйте эту закономерность для вычисления числа ходов, необходимых для перемещения башни из 64 колец. Вычислите, сколько времени займёт такое перемещение, если считать, что на один ход требуется 1 секунда.
НУЖНО СДЕЛАТЬ В EXCEL
Я вроде нашёл формулу 2 в степени n минус 1, но эта формула нужна для перемещения на третий стержень, а в задаче вроде нужно переместиться на 2
Хелп, я правда не знаю, что делать.
«. решить чуть более простую задачу переместить на второй стержень. «
третий стержкнь от второго отличается только расположением.
Измените первый ход и конечный результат тоже изменится.
«. После этого НИЖНИЙ диск . «
Хочется верить что это опечатка
В смысле? От того, прыгнем ли мы первым ходом на 2 или на 3 стержень, конечный результат — пирамида на 3 стержне, — ну никак не поменяется.
И, таки, да — НИЖНИЙ. Именно так эта головоломка и складывается.
«Используйте эту закономерность для вычисления числа ходов, необходимых для перемещения башни из 64 колец. Вычислите, сколько времени займёт такое перемещение, если считать, что на один ход требуется 1 секунда.»
Ну? И где здесь «нужно найти перемещение на второй» ? ГДЕ ?! С закрытыми глазами условие читаем ?
Ты ж уже формулу нашёл, так в чём проблема ?! Забивай в любую ячейку =СТЕПЕНЬ (2;64)-1 и получай свой результат. Тоже мне, блин, проблема на пустом месте.
Источник
Сортировка «Ханойская башня»
Ханойские башни
Про знаменитую игру Эдуарда Люка́ на Хабре не писа́л только ленивый. Кажется, все покровы сорваны и что-то ещё по поводу алгоритма добавить уже невозможно. Но нет, у данной темы есть ещё скрытые ресурсы. Сегодня, в частности, мы переделаем алгоритм решения этой головоломки в полноценную сортировку. (Зачем? Just for fun. В пятницу можно.)
Данный пост посвящается памяти истинного гуру программирования Андрея Mrrl Астрелина, который когда-то мне просто и доходчиво объяснил этот алгоритм. Псевдокод ниже по тексту — его авторства.
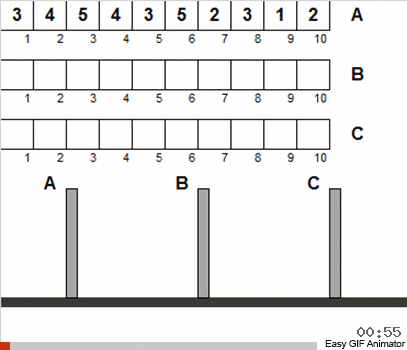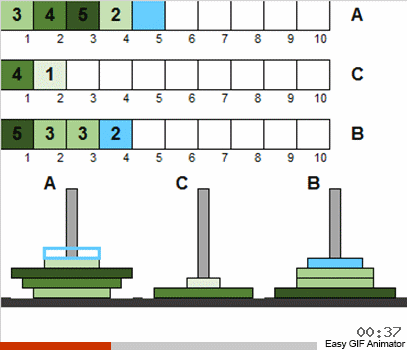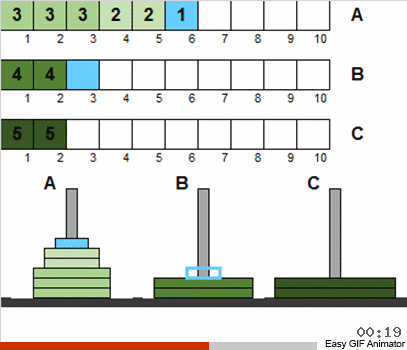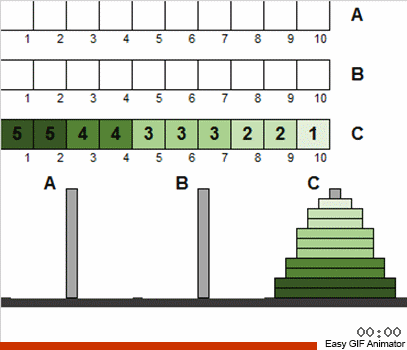
В классической головоломке изначально диски на первом шесте уже упорядочены. Но мы разрешим им быть нанизанными в любом порядке.
Кроме того, размеры дисков предполагаются уникальными. Не будем цепляться за это ограничение и разрешим повторы.
Если позволить себе только эти две вольности, то начальные условия головоломки можно интерпретировать как массив (диски — это числа), а задача сводится к тому, что данный массив требуется отсортировать.
Остальные условия мы (почти) не меняем:
- У нас два вспомогательных шеста (пара пустых массивов).
- Можем переносить диски по одному.
- Класть только меньшие на бо́льшие (раз мы разрешили одинаковые размеры дисков, то также можно класть перемещаемый диск сверху на другие такого же размера).
- Имеем право сравнивать переносимый диск только с самым верхними дисками (то бишь, все 3 массива являются стеками).
Наша задача: взять классический рекурсивный алгоритм головоломки…
… и превратить его в сортировку!
На самом деле, от того что мы разрешили начальную неупорядоченность и повторы для размеров дисков — от этого принципиально не поменялось ничего. По большому счёту задача решаема всё тем же классическим рекурсивным способом. Самое главное что нужно понять — все перемещения дисков разделяются на несколько этапов, каждый из которых — это классичекий «ханой» в миниатюре.
То есть мы на каждом этапе рассматриваем не все имеющиеся диски, а только совокупность тех из них, которые удовлетворяют старым условиям. Отсортировав по классике это небольшое множество мы приблизим общее состояние системы к классической головоломке. Тогда мы опять берём то множество дисков, которое соответствует классике и применяем известный алгоритм вновь. И это множество будет бо́льшим, чем на предыдущем шаге! И так повторяем до тех пор, пока все диски на всех шестах вдруг не станут отличаться от классического состояния.
Нарушенная изначально система (тем, что на входе диски не упорядочены) самовосстанавливается с каждой итерацией.
Что касается разрешения повторов, то это вообще не имеет никакого значения. Потому что подряд идущие одинаковые диски мы просто перемещаем как один диск.
Алгоритм
Назовем столбики A, B, C (A в начале непустой).
А->С() — переложить один диск с А на С.
top(A), top(С) — размер верхнего диска А или С. Если столбик пуст, то этот размер = MaxInt.
В->С(К) — переложить с В на С все диски, размер которых меньше К (мы это можем сделать, если верхние диски А и С не меньше К).
swap() — переставить столбики В и С (или переименовать их — нам ведь все равно, где окажутся диски).
while(A) — цикл пока А не пуст.
Тогда работает такой алгоритм:
Сложность
В худшем случае сортировка стремится к сложности по времени для классического алгоритма, который хоть прост и изящен, но при этом максимально неэффективен. Насчёт лучшей и средней предположить затрудняюсь.
Насчёт памяти можно сказать, что если используется рекурсия, то и затраты будут соответствующие.
Реализация
Свой вариант на Python пока не написал (сделаю это позже). Однако ниже в разделе «Ссылки» накидал несколько ссылок, по которым можно посмотреть имплементации на различных языках. Особенно интересен вариант на Джаве. Автор не стал брать за основу общеизвестный рекурсивный способ для решения головоломки, а построил кратчайшее дерево путей. Предположительно, это является самым эффективным решением, если писать сортировку в стиле «Ханойской башни».
Характеристики алгоритма
| Название | Сортировка «Ханойская башня», Tower of Hanoi sort | |
|---|---|---|
| Автор идеи | Эдуард Люка́ | |
| Класс | Сортировки вставками | |
| Сравнения | Есть | |
| Временна́я сложность | лучшая | ? |
| средняя | ? | |
| худшая | O(2 n ) |
Ссылки

Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировка библиотекаря
- Пасьянсная сортировка
- Сортировка «Ханойская башня»
- Сортировка выворачиванием
- Сортировка таблицей Юнга
- Сортировки выбором
- Сортировки слиянием
- Сортировки распределением
- Гибридные сортировки
В приложении AlgoLab данная сортировка теперь доступна. Хотя она относится к классу сортировок вставками, по причине экстравагантности алгоритма она помещена в раздел «Прочие сортировки». Ещё там есть ограничение — числа в сортируемом массиве могут быть только от 1 до 5 (связано с непростой прорисовкой дисков). Другие числа всё равно будут заменены на эти.
Также есть ограничение на размер массива — не более 20-ти элементов. Сделано это сугубо в Ваших же интересах — если возьмёте слишком большой массив, то, может так статься, что сортировать его придётся до глубокой старости.

Статья написана при поддержке компании EDISON Software, которая профессионально разрабатывает умное городское освещение и поддерживает сайты на питоне
Источник
Русские Блоги
Алгоритм (9) Ханойской башни и его реализация кода
Этот блог использует графическую форму для имитации процесса перемещения диска башни Ханоя и имеет полную реализацию кода. Из-за моих плохих знаний, неизбежно, что будут неправильные вещи. Я действительно надеюсь, что друзья, которые любят программирование и алгоритмы, выскажут ваши ценные мнения.
оглавление
1. Что такое Ханойская башня
Ханойская Башня: проблема Ханойской Башни (также известной как Ханойская Башня) — образовательная игрушка, происходящая из древней легенды в Индии. Когда Брахма сотворил мир, он создал три алмазных столба, на одном из которых были сложены 64 золотых диска по порядку снизу вверх. Брахма приказал Брамину переместить диск на другой столбец в порядке размера снизу. И оговаривают,Невозможно увеличить диск на маленьком диске, только один диск может быть перемещен между тремя опорами одновременно。
2. Перемещение процесса Ханойской башни
Ханойская башня Анимация: демонстрирует процесс движения диска 
(эта анимация поступает из сети)
Ниже показан процесс перемещения каждой пластины в трех случаях (n представляет количество дисков):
В-третьих, идея алгоритма Ханоты
Когда n равно 1, переместите диск из A в C напрямую;
Переместите (n-1) пластины выше столба A от A до B;
Переместите n-ую пластину над колонной A от A до C;
Переместите (n-1) пластин в столбце B первого шага из B в C
В реализации алгоритма мы используем идею рекурсии. Для имитации процесса движения и общего количества движений.
1. Пример кода
Результаты выполнения кода:
2. Расширенные проблемы
Если для перемещения диска требуется 1 секунда, сколько времени займет ожидание восстановления всех 64 дисков?
Когда используется диск, мощность 2 уменьшается на 1.
Когда два диска, мощность 2 уменьшается на 1
При наличии 3 дисков мощность 2 уменьшается на 1
При наличии 4 дисков мощность 2 уменьшается на 1
…
Когда n дисков, мощность 2 уменьшается на 1
Когда n = 64, это (от 2 до 64 степени минус 1) раз.
Результаты выполнения кода:
Для перемещения всех дисков потребуется около 584,9 миллиардов лет. Какое ужасное число!
Источник
Ханойская башня на пальцах
Время на прочтение
6 мин
Количество просмотров 226K
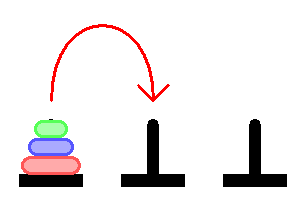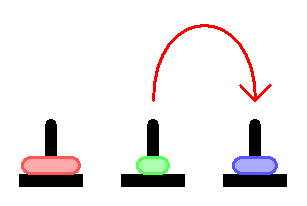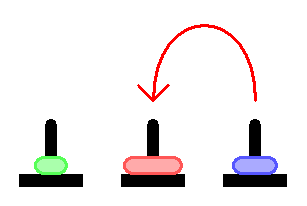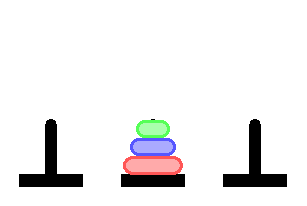
Википедия по этому поводу пишет очень строго, по делу, и ничего не объясняет. Мол принимайте как прописную истину. Поэтому понять как она решается — сходу трудновато. А ведь задача очень простая, и между тем интересная в программировании и математически.
В статье будет много картинок. Объяснение как решать задачу рекурсивно и как она решается бинарным поиском.
В общем статья посвящается тем смелым, кто пока еще боится Ханойской башни, но хочет перестать её бояться.
Правила игры
Они очень просты. Есть 1 пирамидка с дисками разного размера, и еще 2 пустые пирамидки. Надо переместить диски с одной пирамидки на другую. Перекладывать можно только по одному диску за ход. Складывать диски можно только меньший на больший.
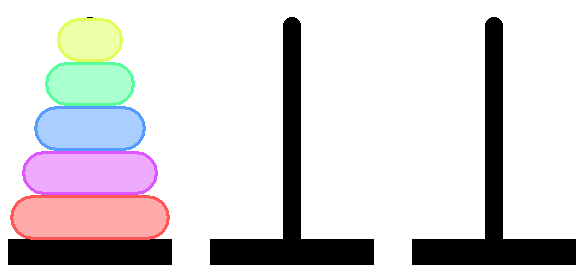
Итак у нас есть вот такая пирамидка:
И нам надо переложить её скажем на среднюю ось.
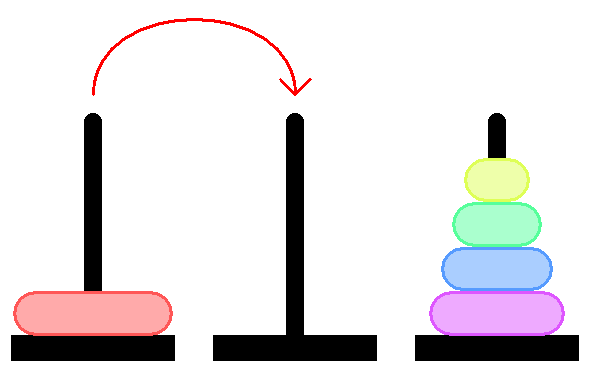
Если начать решать задачу не с начала, а с конца — она оказывается очень простой. Давайте подумаем. Чтобы переложить пирамидку на вторую ось — нам надо переложить самый нижний диск, а сделать это можно только когда 4 верхних диска будут на третьей оси:
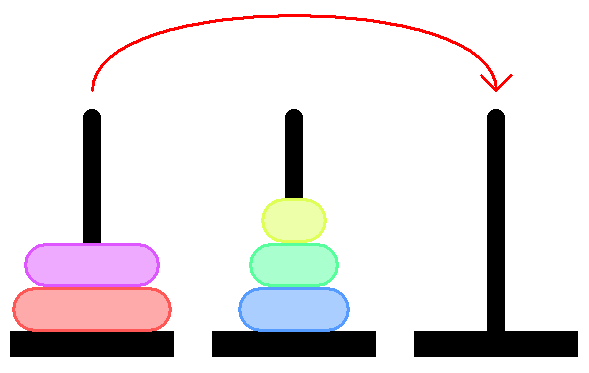
Для того, чтобы переложить 4 диска на третью ось нужно по сути решить ту же задачу, но для 4-х дисков. То есть на третью ось мы можем переложить 4-ый диск только тогда, когда у нас 3 диска на второй оси:
Чувствуете рекурсию?
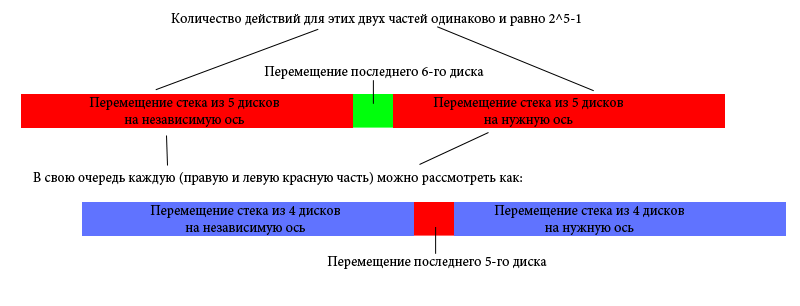
Перекладывание стека из 5 дисков — это:
1. Перекладывание стека из 4х дисков на независимую ось
2. Перекладывание 5-го диска на нужную нам ось
3. Перекладывание стека из 4х дисков на нужную нам ось
В свою очередь перекладывание стека из 4 дисков — это:
1. Перекладывание стека из 3х дисков на независимую ось
2. Перекладывание 4-го диска на нужную нам ось
3. Перекладывание стека из 3х дисков на нужную нам ось
Вот и все.
Рекурсивная реализация
После такого подробного описания не составит сложности реализовать это алгоритмически.
Реализация на Delphi
Итак я описал модуль с типами башенок:
unit untHTypes;
interface
const MaxRingCount = 5;
type
TTower = record
RingCount: Integer;
Rings: array [0..MaxRingCount-1] of Integer;
procedure MoveRing(var AtTower: TTower);
end;
TTowers = array [0..2] of TTower;
procedure InitTowers(var towers: TTowers);
implementation
procedure InitTowers(var towers: TTowers);
var i: Integer;
begin
towers[0].RingCount := MaxRingCount;
towers[1].RingCount := 0;
towers[2].RingCount := 0;
for i := 0 to MaxRingCount - 1 do
begin
towers[0].Rings[i] := MaxRingCount - i;
towers[1].Rings[i] := 0;
towers[2].Rings[i] := 0;
end;
end;
{ TTower }
procedure TTower.MoveRing(var AtTower: TTower);
begin
Assert(RingCount > 0);
Assert(AtTower.RingCount - 1 < MaxRingCount);
if AtTower.RingCount > 0 then
Assert(Rings[RingCount - 1] < AtTower.Rings[AtTower.RingCount - 1]);
Dec(RingCount);
AtTower.Rings[AtTower.RingCount] := Rings[RingCount];
Rings[RingCount] := 0;
Inc(AtTower.RingCount);
end;
end.
TTower — структура описывающая башню. В ней в RingCount хранится количество фактически одетых колец на башне. Размер колец хранится в массиве Rings от 1 и до MaxRingCount. Поскольку у нас 3 башни — то был объявлен тип TTowers = array [0..2] of TTower;
Так же с башни можно переложить верхее кольцо на другую с помощью функции MoveRing. Функция проверяет корректность операции через Assert-ы.
Само же решение башни находится в файле проекта:
program Hanoy;
{$APPTYPE CONSOLE}
uses
SysUtils,
untHTypes in 'untHTypes.pas';
{$R *.res}
procedure SolveHanoy;
var towers: TTowers;
function GetThirdIndex(index1, index2: Integer): Integer; //по двум имеющимся осям возвращает третью независимую ось
begin //на которую временно можно переложить стек
Assert(index1 <> index2);
case index1 of
0: if index2 = 1 then Result := 2 else Result := 1;
1: if index2 = 2 then Result := 0 else Result := 2;
2: if index2 = 0 then Result := 1 else Result := 0;
else
Assert(False,'wrong indeces');
end;
end;
procedure MoveStack(stacksize: Integer; fromindex, atindex: Integer); //перемещает стек из пирамидок с одной оси на другую
var thirdindex: Integer;
begin
if stacksize = 0 then Exit;
thirdindex := GetThirdIndex(fromindex, atindex); //подбираем независимую ось
MoveStack(stacksize - 1, fromindex, thirdindex); //перемещаем подстек (на 1 меньший) на независимую ось
towers[fromindex].MoveRing(towers[atindex]); //перемещаем последнее кольцо на нужную нам ось
WriteLn(fromindex,'-',atindex); // записываем в консоль наше действие
MoveStack(stacksize - 1, thirdindex, atindex); //вовзращаем подстек с независимой на нужную нам ось
end;
begin
InitTowers(towers);
MoveStack(MaxRingCount, 0, 1);
end;
begin
SolveHanoy;
end.
Алгоритмическая сложность
Мы легко можем подсчитать, сколько действий нам понадобится, чтобы переместить пирамидку.
Если мы перемещаем стек из одного диска — то нам нужно 1 действие.
Если стек из двух — то 1 * 2 (переместить дважды стек из одного диска ) + 1 (перемещаем последний диск)
Если из трех ((1 * 2) + 1) * 2 + 1
Из пяти: (((((1 * 2) + 1) * 2 + 1) * 2 + 1) * 2 + 1)
Итак каждая операция увеличивает в 2 раза + 1 кол-во перемещений. Раскрыв скобки для n операций — получаем:
От суммы можно избавиться, ибо она равна:
p.s. я избавился от суммы в голове, вспомнив сумму членов бесконечно убывающей геометрической прогрессии, но я надеюсь математики покажут как правильно записать эти преобразования
Итого у нас после всех преобразований вышло:
То есть если нам захочется странного, например записать решение ханойской башни для 64 дисков, то никаких современных носителей информации нам не хватит. В действительности — нам вообще не надо ничего никуда записывать. Это все равно, что записывать все числа от 0 до +бесконечности, чтобы потом их использовать, потому что решение ханойской башни — это фрактал.
Фрактальная природа
Да да. Решение ханойской башни имеет фрактальную природу. Давайте посмотрим. Допустим у нас каждое действие записывается в строку. Тогда для башни из 6 дисков можно записать это как-то так:
Ну а поскольку это фрактал — то мы можем легко назвать любую операцию зная лишь её порядковый номер. И даже более, мы можем в точности восстановить положение всех дисков на момент любой операции.
Бинарный алгоритм
Итак, мы знаем точное количество операций, а так же знаем индекс операции, для которой мы хотим восстановить состояние.
Допустим у нас башня из 6 дисков (перемещаем как обычно, с 1-ой на среднюю ось), а значит операций у нас 2^6-1 = 63. Допустим нам требуется восстановить состояние для 49-ой операции.
Делим целочисленно 63 на 2. Получается 31. Это индекс операции, на которой будет перемещен 6-ой диск:
У нас 49-ый индекс операции. Это значит что 6-ой диск уже лежит на средней оси. Кроме того, поскольку мы находимся в правой части, то пятый диск у нас лежит либо на 3-ей оси, либо на 2-ой. Для того чтобы мы могли работать с башней по тому же алгоритму — отнимаем от 49-ой операции 32, находим индекс подоперации. Это 17. Для перемещения стека из 5 дисков нужна 31 операция, при этом 5-ый диск перемещается на 16-ю операцию и с 3-ей оси на 2-ую.
Итак число 17 лежит правее:
А это значит что диск 5 уже перемещен на вторую ось.
По аналогии восстанавливаем положение остальных дисков.
Реализация (бинарный способ)
Я добавил красивую отрисовку башенок. Согласитесь, скучно смотреть в консольный лог. Поэтому реализация разрослась, и я прикреплю полный проект (исходник + бинарник) в конце статьи. Здесь же приведу
код рекурсивной функции на Delphi
procedure TfrmView.RestoreDisk(size, actionIndex, actionCount, fromAxe, atAxe: Integer);
var pivot: Integer;
i: Integer;
thirdAxe: Integer;
begin
pivot := actionCount div 2;
thirdAxe := GetThirdIndex(fromAxe, atAxe);
if actionIndex = pivot then //попали в центр, значит знаем какой диск сейчас перекладывается
begin //и можем восстановить весь стек дисков меньшего размера. Конец рекурсии
FTowers[fromAxe].PutRing(size);
for i := size - 1 downto 1 do
FTowers[thirdAxe].PutRing(i);
FAction.FromIndex := fromAxe;
FAction.AtIndex := atAxe;
end
else
if actionIndex < pivot then
begin //значит выполняется стадия перекладывания подстека на независимую ось
FTowers[fromAxe].PutRing(size); //и нижний диск еще не переложен
RestoreDisk(size - 1, actionIndex, actionCount - pivot - 1, fromAxe, thirdAxe);
end
else
begin //значит выполняется стадия перекладывания подстека с независимой на нужную ось
FTowers[atAxe].PutRing(size); //и нижний диск уже переложен
RestoreDisk(size - 1, actionIndex - pivot - 1, actionCount - pivot - 1, thirdAxe, atAxe);
end;
end;
procedure TfrmView.RestoreTowers;
var index: Integer;
begin
ClearTowers(FTowers);
index := tbOperation.Position;
RestoreDisk(MaxRingCount, index, 2 shl (MaxRingCount - 1) - 1, 0, 1);
Invalidate;
end;
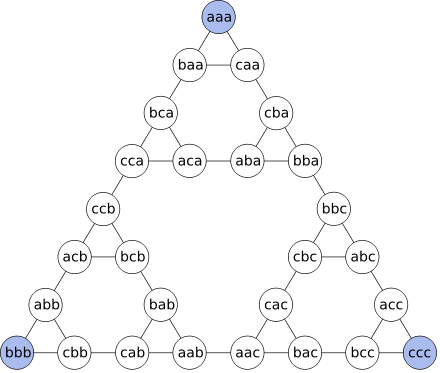
Треугольник Серпинского
Я хотел бы еще вскользь упомянуть интересную особенность. Если все возможные перемещения колец собрать в граф, то для каждого узла будет чаще всего по 3 связи. Все узлы и связи можно красиво расположить в форме треугольника. Треугольника Серпинского:
Подробнее об этом сказано на википедии вот тут. Что в общем не удивительно, потому что мы уже знаем фрактальную природу решения 
Итого
Я постарался показать, насколько иногда просто может решаться казалось бы не совсем очевидная задача. Более того, при внимательном изучении можно
внезапно обнаружить
совершенно другие интересные алгоритмы решения задачи, открывающие новые возможности. Ищите разные подходы, экспериментируйте, анализируйте. Ведь мы на то и программисты.
Спасибо тем кто дочитал, и кому статья понравилась. Прикрепляю демо пример, в котором можно поелозить трекбаром, и посмотреть на то как перекладываются башенки.
Пример бинарного алгоритма (exe + исходный код, Delphi)
Этот блог использует графическую форму для имитации процесса перемещения диска башни Ханоя и имеет полную реализацию кода. Из-за моих плохих знаний, неизбежно, что будут неправильные вещи. Я действительно надеюсь, что друзья, которые любят программирование и алгоритмы, выскажут ваши ценные мнения.
оглавление
- 1. Что такое Ханойская башня
- 2. Перемещение процесса Ханойской башни
- В-третьих, идея алгоритма Ханоты
- 1. Пример кода
- 2. Расширенные проблемы
1. Что такое Ханойская башня
Ханойская Башня: проблема Ханойской Башни (также известной как Ханойская Башня) — образовательная игрушка, происходящая из древней легенды в Индии. Когда Брахма сотворил мир, он создал три алмазных столба, на одном из которых были сложены 64 золотых диска по порядку снизу вверх. Брахма приказал Брамину переместить диск на другой столбец в порядке размера снизу. И оговаривают,Невозможно увеличить диск на маленьком диске, только один диск может быть перемещен между тремя опорами одновременно。
2. Перемещение процесса Ханойской башни
Ханойская башня Анимация: демонстрирует процесс движения диска
(эта анимация поступает из сети)
Ниже показан процесс перемещения каждой пластины в трех случаях (n представляет количество дисков):
1 диск:
Ситуация с 2 дисками:
Ситуация с 3 дисками:
В-третьих, идея алгоритма Ханоты
Когда n равно 1, переместите диск из A в C напрямую;
Когда n> 1:
-
Переместите (n-1) пластины выше столба A от A до B;
-
Переместите n-ую пластину над колонной A от A до C;
-
Переместите (n-1) пластин в столбце B первого шага из B в C
В реализации алгоритма мы используем идею рекурсии. Для имитации процесса движения и общего количества движений.
1. Пример кода
public class Hanoi {
/**
* Количество ходов
*/
static int m = 0;
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print(«Чтобы играть в Ханойскую башню, пожалуйста, введите количество дисков:»);
int n = input.nextInt();
char a = 'A';
char b = 'B';
char c = 'C';
hanoi(n, a, b, c);
System.out.println(«Переместите все диски от А до С, всего». + m + "Время.");
}
/**
* Ханойская башня
*
* @ param n количество тарелок
* @ парам столбца А
* @парам б столб B
* @param c C
*/
public static void hanoi(int n, char a, char b, char c) {
if (n == 1) {
move(1, a, c);
} else {
// Рекурсивно расположите слой n-1 над стойкой A от A, через C, до B
hanoi(n - 1, a, c, b);
move(n, a, c);
// Рекурсивно нанести слой n-1 на столб B из B, через A, в C
hanoi(n - 1, b, a, c);
}
}
/**
* Шаг
*
* @param n количество дисков
* @ param I позиция перед переездом
* @парам j позиция после перемещения
*/
public static void move(int n, char i, char j) {
m++;
System.out.println(" " + m + "Время:" + n + "Номер диска:" + i + " -> " + j);
}
}
Результаты выполнения кода:
Чтобы играть в Ханойскую башню, пожалуйста, введите количество дисков:3
Первый1раз: 1диск: A -> C
Первый2раз: 2диск: A -> B
Первый3раз: 1диск: C -> B
Первый4раз: 3диск: A -> C
Первый5раз: 1диск: B -> A
Первый6раз: 2диск: B -> C
Первый7раз: 1диск: A -> C
Переместил диски от А до С, и в общей сложности переместил7Времена.
2. Расширенные проблемы
Если для перемещения диска требуется 1 секунда, сколько времени займет ожидание восстановления всех 64 дисков?
Когда используется диск, мощность 2 уменьшается на 1.
Когда два диска, мощность 2 уменьшается на 1
При наличии 3 дисков мощность 2 уменьшается на 1
При наличии 4 дисков мощность 2 уменьшается на 1
…
Когда n дисков, мощность 2 уменьшается на 1
Когда n = 64, это (от 2 до 64 степени минус 1) раз.
Пример кода:
public class Test {
public static void main(String[] args) {
double a = Math.pow(2, 64) - 1;
System.out.println(«Значение 2 ^ 64-1:» + a);
// Для перемещения диска требуется 1 секунда, а b дисков можно переместить за один год
double b = 60 * 60 * 24 * 365;
System.out.println(«Количество движущихся дисков за один год:» + b);
// время, необходимое для перемещения 64 дисков
double time = a / b;
System.out.println(«Время, необходимое для перемещения 64 дисков:» + time + "год");
}
}
Результаты выполнения кода:
2^64-1Значение: 1.8446744073709552E19
Количество движущихся дисков за один год: 3.1536E7
мобильный64Необходимое время: 5.84942417355072E11 год
Для перемещения всех дисков потребуется около 584,9 миллиардов лет. Какое ужасное число!
предыдущийАлгоритм (8) использует метод циклического перебора и метод деления, чтобы найти наибольший общий делитель и наименьшее общее кратное
В основу эффективного решения головоломки «Ханойская башня» положен алгоритм, суть которого сводится к следующему : для перемещения башни, состоящей из п колец, спервого стержня на третий мы должны решить чуть более простую задачу переместить на второй стержень башню, состоящую из п — 1 кольца.
После этого нижний диск с первого стержня перемещается на третий и повторно осуществляется перемещение башни из п — 1 кольца, но уже со второго диска на третий.
Таким образом, число ходов, необходимых для перемещения башни из л колец, равно удвоенному числу ходов, необходимых для перемещения башни из и — 1 кольца, и ещё одному ходу.
Используйте эту закономерность для вычисления числа ходов, необходимых для перемещения башни из 64 колец.
Вычислите, сколько времени займёт такое перемещение, если считать, что на один ход требуется 1 секунда.
На этой странице сайта размещен вопрос В основу эффективного решения головоломки «Ханойская башня» положен алгоритм, суть которого сводится к следующему : для перемещения башни, состоящей из п колец, спервого стержня на третий мы должны ? из категории
Информатика с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Before getting started, let’s talk about what the Tower of Hanoi problem is. Well, this is a fun puzzle game where the objective is to move an entire stack of disks from the source position to another position. Three simple rules are followed:
- Only one disk can be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack. In other words, a disk can only be moved if it is the uppermost disk on a stack.
- No larger disk may be placed on top of a smaller disk.
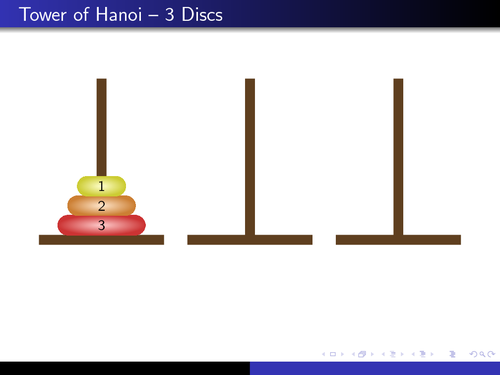
Now, let’s try to imagine a scenario. Suppose we have a stack of three disks. Our job is to move this stack from source A to destination C. How do we do this?
Before we can get there, let’s imagine there is an intermediate point B.
We can use B as a helper to finish this job. We are now ready to move on. Let’s go through each of the steps:
- Move the first disk from A to C
- Move the first disk from A to B
- Move the first disk from C to B
- Move the first disk from A to C
- Move the first disk from B to A
- Move the first disk from B to C
- Move the first disk from A to C
Boom! We have solved our problem.
You can see the animated image above for a better understanding.
Now, let’s try to build the algorithm to solve the problem. Wait, we have a new word here: “Algorithm”. What is that? Any idea? No problem, let’s see.
What is an algorithm?
An algorithm is one of the most important concepts for a software developer. In fact, I think it’s not only important for software development or programming, but for everyone. Algorithms affect us in our everyday life. Let’s see how.
Suppose you work in an office. So every morning you do a series of tasks in a sequence: first you wake up, then you go to the washroom, eat breakfast, get prepared for the office, leave home, then you may take a taxi or bus or start walking towards the office and, after a certain time, you reach your office. You can say all those steps form an algorithm.
In simple terms, an algorithm is a set of tasks. I hope you haven’t forgotten those steps we did to move three disk stack from A to C. You can also say that those steps are the algorithm to solve the Tower of Hanoi problem.
In mathematics and computer science, an algorithm is an unambiguous specification of how to solve a class of problems. Algorithms can perform calculation, data processing and automated reasoning tasks. — Wikipedia
If you take a look at those steps you can see that we were doing the same task multiple times — moving disks from one stack to another. We can call these steps inside steps recursion.
Recursion
Recursion is calling the same action from that action. Just like the above picture.
So there is one rule for doing any recursive work: there must be a condition to stop that action executing. I hope you understand the basics about recursion.
Now, let’s try to build a procedure which helps us to solve the Tower of Hanoi problem. We are trying to build the solution using pseudocode. Pseudocode is a method of writing out computer code using the English language.
tower(disk, source, intermediate, destination)
{
}This is the skeleton of our solution. We take the total disks number as an argument. Then we need to pass source, intermediate place, and the destination so that we can understand the map which we will use to complete the job.
Now we need to find a terminal state. The terminal state is the state where we are not going to call this function anymore.
IF disk is equal 1In our case, this would be our terminal state. Because when there will be one disk in our stack then it is easy to just do that final step and after that our task will be done. Don’t worry if it’s not clear to you. When we reach the end, this concept will be clearer.
Alright, we have found our terminal state point where we move our disk to the destination like this:
move disk from source to destinationNow we call our function again by passing these arguments. In that case, we divide the stack of disks in two parts. The largest disk (nth disk) is in one part and all other (n-1) disks are in the second part. There we call the method two times for -(n-1).
tower(disk - 1, source, destination, intermediate)As we said we pass total_disks_on_stack — 1 as an argument. And then again we move our disk like this:
move disk from source to destinationAfter that we again call our method like this:
tower(disk - 1, intermediate, source, destination)Let’s see our full pseudocode:
tower(disk, source, inter, dest)
IF disk is equal 1, THEN
move disk from source to destination
ELSE
tower(disk - 1, source, destination, intermediate) // Step 1
move disk from source to destination // Step 2
tower(disk - 1, intermediate, source, destination) // Step 3
END IF
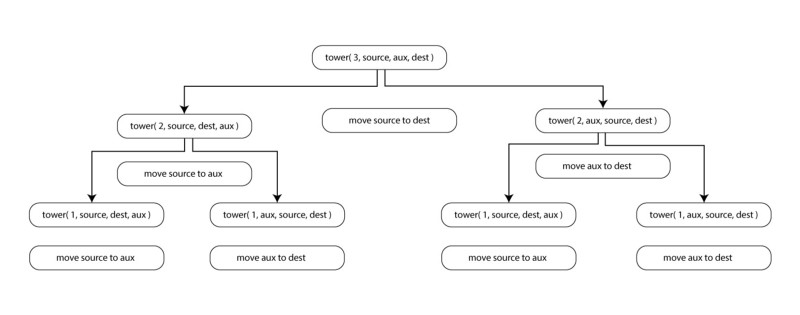
ENDThis is the tree for three disks:
This is the full code in Ruby:
def tower(disk_numbers, source, auxilary, destination)
if disk_numbers == 1
puts "#{source} -> #{destination}"
return
end
tower(disk_numbers - 1, source, destination, auxilary)
puts "#{source} -> #{destination}"
tower(disk_numbers - 1, auxilary, source, destination)
nil
endCall tower(3, 'source','aux','dest')
Output:
source -> dest
source -> aux
dest -> aux
source -> dest
aux -> source
aux -> dest
source -> destIt took seven steps for three disks to reach the destination. We call this a recursive method.
Time complexity and space complexity calculations
Time complexity
When we run code or an application in our machine it takes time — CPU cycles. But it’s not the same for every computer. For example, the processing time for a core i7 and a dual core are not the same. To solve this problem there is a concept used in computer science called time complexity.
Time complexity is a concept in computer science that deals with the quantification of the amount of time taken by a set of code or algorithm to process or run as a function of the amount of input.
In other words, time complexity is essentially efficiency, or how long a program function takes to process a given input. — techopedia
The time complexity of algorithms is most commonly expressed using big O notation. It’s an asymptotic notation to represent the time complexity.
Now, the time required to move n disks is T(n). There are two recursive calls for (n-1). There is one constant time operation to move a disk from source to the destination, let this be m1. Therefore:
T(n) = 2T(n-1) + m1 ..... eq(1)And
T(0) = m2, a constant ...... eq(2)
From eq (1)
T(1) = 2T(1-1) + m1
= 2T(0)+m1
= 2m2 + m1 ..... eq(3) [From eq 2]
T(2) = 2T(2-1) + m1
= 2T(1) + m1
= 4m2 + 2m1 + m1 .... eq(4) [From eq(3)]
T(3) = 2T(3-1) + m1
= 2T(2) + m1
= 8m2 + 4m1 + 2m1 + m1 [From eq(4)]From these patterns — eq(2) to the last one — we can say that the time complexity of this algorithm is O(2^n) or O(a^n) where a is a constant greater than 1. So it has exponential time complexity. For the single increase in problem size, the time required is double the previous one. This is computationally very expensive. Most of the recursive programs take exponential time, and that is why it is very hard to write them iteratively.
Space complexity
After the explanation of time complexity analysis, I think you can guess now what this is…This is the calculation of space required in ram for running a code or application.
In our case, the space for the parameter for each call is independent of n, meaning it is constant. Let it be J. When we do the second recursive call, the first one is over. That means that we can reuse the space after finishing the first one. Hence:
T(n) = T(n-1) + k .... eq(1)
T(0) = k, [constant] .... eq(2)
T(1) = T(1-1) + k
= T(0) + k
= 2K
T(2) = 3k
T(3) = 4kSo the space complexity is O(n).
After these analyses, we can see that time complexity of this algorithm is exponential but space complexity is linear.
Conclusion
From this article, I hope you can now understand the Tower of Hanoi puzzle and how to solve it. Also, I tried to give you some basic understanding about algorithms, their importance, recursion, pseudocode, time complexity, and space complexity. If you want to learn these topics in detail, here are some well-known online courses links:
- Algorithms, Part I
- Algorithms, Part II
- The Google course on Udacity
- Javascript Algorithms And Data Structures Certification (300 hours)
You can visit my data structures and algorithms repo to see my other problems solutions.
I am on GitHub | Twitter | LinkedIn
Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started