2.4.1 Общие рекомендации
В пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:
-
определение
наращенной суммы (будущей стоимости), -
определение
начального значения (текущей стоимости), -
определение срока
платежа и процентной ставки, -
расчет периодических
платежей, связанных с погашением займов.
Для
расчетов Excel
использует приведенную выше формулу
(22)
Эти
формулы используют встроенные функции
БC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.
В
финансовых функциях Excel
необходимо строго учитывать знаки
величин PV,
FV
и С. Когда мы отдаем какую – либо величину,
ставим перед ней знак минус, если получаем
– плюс.
Работать
с финансовыми функциями удобно с помощью
Мастера функций
Когда
появляется окно выбранной функции, в
его поля нужно ввести заданные значения.
Если какое – либо значение равно нулю,
это поле можно не заполнять. Если рента
постнумерандо, поле Тип
тоже можно не заполнять.
Не
забывайте в поле Норма
вводить величину процентной ставки за
период r/m,
а в поле Число
– периодов
– число периодов выплат или начисления
процентов n=k·m.
2.4.2 Вычисление будущего значения
В
Excel
будущему значению FV
соответствует функция БС.
БС
— стоимость
постоянных платежей в определенные
периоды на основе постоянной процентной
ставки.
Позволяет рассчитать
объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.
Синтаксис
БС(ставка;кпер;плт;пс;тип)
ставка
— процентная
ставка за период.
кпер
— количество
периодов, в которые производится выплата
годовых процентов.
плт
-выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.
пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.
тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.
Единицы
измерения для аргументов ставка
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по четырехгодичному
займу из расчета 12% годовых, то норма
должна быть 12%/12, а кпер
должно быть 4*12. Если производятся
ежегодные платежи по тому же займу, то
ставка
должна быть
12%, а кпер
должно быть 4.
Ваш вклад
представляется отрицательным числом,
а деньги, которые вы получите, представляются
положительным числом.
В
принятых в данной работе обозначениях
FV=БС(r/m;
k·m;
С; PV;
тип).
Пример
15 Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.
Через год на счете
будет:
БС
(0,5%;12;-100;-1000;1)=2301,40 р.
Определение будущей
стоимости на основе постоянной процентной
ставки.
Пример
16 Определить
сумму вклада на банковском счете, если
положить 37 тыс. руб. на 3 года под 11,5%
годовых. Проценты начисляются каждые
полгода.
Алгоритм решения
задачи:
Поскольку
необходимо рассчитать единую сумму
вклада на основе постоянной процентной
ставки, то используем функцию БС(). В
связи с тем, что проценты начисляются
каждые полгода, аргумент ставка равен
11,5%/2. Общее число периодов начисления
равно 3*2 (аргумент кпер). По условию
аргумент пс
(начальное значение) равен 37000 руб. и
задается в виде отрицательной величины
(- 37 000), т.к. с точки зрения вкладчика это
отток его денежных средств (вложение
средств). Аргумент платеж отсутствует,
т.к. вклад не пополняется, аргумент тип
равен 0, т.к. в подобных операциях проценты
начисляются в конце каждого периода
(задается по умолчанию). Тогда к концу
3-го года на банковском счете имеем:
= БС(11,5%/2;3*2;;-37000) =
51746,86 руб.
Отметим, что по
условию задачи указаны годовой процент
и число лет. Если процент начисляется
несколько раз в год, то следует рассчитать
общее число периодов начисления процентов
и ставку процента за период начисления.
Для наиболее распространенных методов
внутригодового учета процента можно
привести следующую таблицу расчета
основных величин.
Расчет процентной
ставки для различной периодичности
начислений
|
Метод начисления |
Общее число |
Ставка процента |
|
Ежегодный |
N |
K |
|
Полугодовой |
N*2 |
K/2 |
|
Квартальный |
N*4 |
K/4 |
|
Месячный |
N*12 |
K/12 |
|
Ежедневный |
N*365 |
K/365 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассчитаем в MS EXCEL сколько времени потребуется для погашения кредита в случае равных ежемесячных платежей (по аннуитетной схеме). Процентная ставка и величина платежа — известны, начисление процентов за пользование кредитом – ежемесячное. Также в статье разберем случай накопления вклада.
Аннуитетная схема
предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье
Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)
показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. Расчет количества периодов, необходимых для погашения кредита произведем сначала с помощью финансовой функции MS EXCEL КПЕР(), затем приведем расчет с помощью эквивалентной формулы (см.
файл примера
).
Функция КПЕР(ставка; плт; пс; [бс]; [тип])
позволяет вычислить количество периодов, через которое
текущая сумма вклада
(пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). Бс (
будущая стоимость
) может быть =0 или опущена. Тип – это число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов): 0 – в конце периода, 1 – в начале. Также функцию
КПЕР()
можно использовать для определения количества периодов, необходимых для погашения долга по ссуде.
Примечание
. Обзор всех функций аннуитета
найдете здесь
.
Эквивалентная формула для расчета количества периодов:
Если ставка равна 0, то: Кпер = (Пс + Бс) /ПЛТ
Задача1
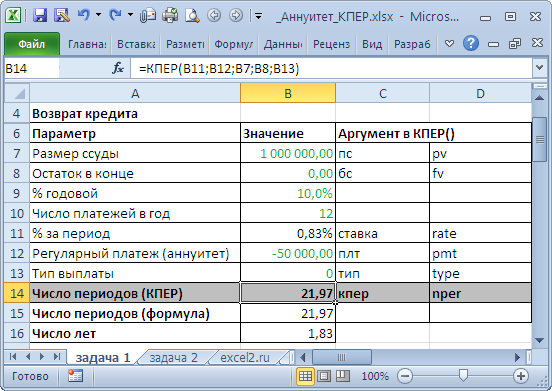
Сколько времени потребуется для погашения кредита 1 млн. рублей в случае равных ежемесячных взносов. Начисление процентов за пользование кредитом – ежемесячное, годовая процентная ставка = 10%. Ежемесячный платеж 50 000р.
Решение
1
Так как погашение кредита производится ежемесячно (12 раз в году), то ставка за период составит 10%/12. Формула
=КПЕР(10%/12;-50000;1000000;0;0)
вернет количество периодов, после которых кредит будет возвращен в полном размере. Знак минус перед 2-м аргументом функции (величина ежемесячного платежа) показывает, что разнонаправленные денежные потоки должны иметь разные знаки (+1000000 – это деньги, которые
банк
дал
нам, -50000 – это деньги, которые мы
возвращаем банку
). Конечно, можно и наоборот: деньги, которые банк дал нам учитывать со знаком минус, а те деньги, которые мы отдаем банку учитывать со знаком +. Формула вернет 21,97, т.е. потребуется 22 месяца, чтобы полностью вернуть 1 млн. руб., возвращая ежемесячно по 50 тыс. руб. (последний платеж будет несколько меньше, о том, как его рассчитать – читайте ниже).
Расчет последнего платежа
При расчете количества периодов погашения ссуды может получиться нецелое количество периодов. В этом случае, последний платеж будет несколько меньше, чем предыдущие. Найдем величину этого платежа. Учтем, что в последнем периоде нам будет необходимо погасить оставшуюся задолженность и заплатить % банку (% от суммы оставшейся задолженности). Найдем сначала количество полных периодов
=ЦЕЛОЕ(КПЕР(10%/12;-50000;1000000;0;0))
и поместим результат в ячейку G21. Чтобы вычислить сколько было погашено основной суммы долга за все целые периоды можно использовать формулу
=СУММПРОИЗВ(ОСПЛТ(10%/12;СТРОКА(ДВССЫЛ(«1:»&G21)); КПЕР(10%/12;-50000;1000000;0;0);1000000;0;0))
(Альтернатива –
используйте функцию
ОБЩДОХОД()
)
Примечание
. Сумму платежа, идущую на оплату основной суммы долга в один определенный период, можно вычислить с помощью функции
ОСПЛТ()
. Складывая результат
ОСПЛТ()
для всех целых периодов с помощью функции
СУММПРОИЗВ()
получим сколько было погашено основной суммы долга.
Далее вычтем из суммы кредита выплаченную сумму за все целые периоды (с учетом знаков). Затем вычислим проценты за последний период = СУММПРОИЗВ(…)*10%/12 Сложим остаток основной суммы долга и проценты за последний (неполный) период (см.
файл примера
). В результате получим -48487,18р. (это несколько меньше регулярного платежа -50000р.)
Если функция КПЕР() возвращает ошибку
В некоторых случаях функция
КПЕР()
возвращает значение ошибки #ЧИСЛО! Разобраться, почему это происходит, можно, вспомнив альтернативную формулу (см. выше). Понятно, что логарифм числа может быть вычислен только для положительного числа, а это означает, что величина платежа ПЛТ должна быть больше величины ежемесячных процентов начисляемых на остаток тела кредита, т.е. больше ПС*СТАВКА (это справедливо только при БС=0 и ТИП=0). Оно и понятно, нам нужно ежемесячно не только оплачивать проценты, но и возвращать основную сумму долга.
Количество периодов, через которое будет погашено 80% кредита
Сколько времени потребуется, чтобы погасить кредит не полностью, а например, на 80%? Записав формулу
=КПЕР(10%/12;-50000;1000000;-1000000*(1-80%);0)
получим, что для этого потребуется 17,88 периодов (месяцев). Величину БС = -1000000*(1-80%) мы нашли пользуясь тождеством для аннуитета (справедливо, если Тип=0): СУММ(ОСПЛТ(за все периоды)) + ПС + БС = 0 Из условий задачи ПС = 1000000 (начальная сумма кредита), выплаченная сумма кредита, т.е. СУММ(ОСПЛТ(за все периоды)) равна -1000000*80%. Решая уравнение, получим, что БС = -1000000*(1-80%). БС в данном случае – это непогашенная сумма кредита (конечно, чтобы найти, что БС=20% от суммы кредита, не требует использования тождества. Но важен знак БС).
Задача2
Рассчитать, через сколько времени вклад размером 200 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 10% годовых, начисление процентов производится ежеквартально, также ежеквартально вклад пополняется на 10 000 руб.
Решение2
Так как взносы и начисление процентов происходит ежеквартально (4 раза в год), то ставка за период составит 10%/4. Формула
=КПЕР(10%/4;-10000;-200000;1000000;0)
вернет количество периодов, после которых вклад достигнет 1 млн. руб., т.е. 34,31 квартал (см.
файл примера, лист Задача2
).
На данном уроке мы научимся практически применять вычислительный инструмент «Подбор параметр» в Excel. Специально для Вас подготовлено 3 практических примера, которые могут пригодиться Вам уже сегодня.
Подбор параметра для банковских депозитов
На протяжении 10-ти лет мы хотим накопить 20 000$. Свои сбережения будем откладывать на банковский депозит по 5% годовых. Деньги будем вносить на банковский депозитный счет ежегодно и одинаковыми частями взносов. Какой должен быть размер ежегодного взноса, чтобы за 10 лет собрать 20 000$ при 5-т и процентах годовых?
Для решения данной задачи в Excel воспользуемся инструментом «Подбор параметра»:
- Составьте таблицу как показано на рисунке:
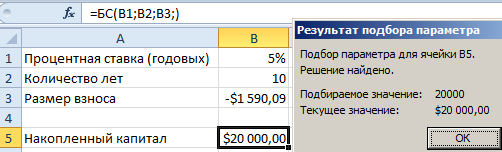
- В ячейку B5 введите функцию: =БС(B1;B2;B3;)
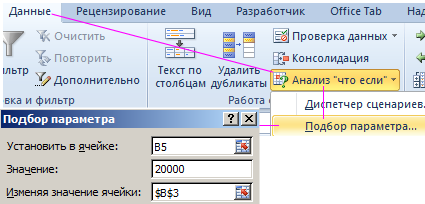
- Оставаясь на ячейке B5, выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра»
- В появившемся окне заполните поля, так как на рисунке и нажмите ОК.
Результат вычисления получился с отрицательным числом – это правильно в соответствии со стандартом финансовых функций Excel. Регулярные взносы должны отображаться отрицательным значением, так как это категория расходных операций. А по истечению 10 лет мы получим на приход +20 000$.
Полезный совет! Если Вы нужно узнать размер ежемесячных взносов, тогда перед использованием инструмента «Подбор параметра» нужно процентную ставку разделить на 12 (чтобы перевести в ежемесячный процент).
А количество лет нужно перевести в количество месяцев умножив на 12. Таким образом, в ячейке B3 мы получим необходимую сумму ежемесячного взноса для достижения цели.
Поиск решений подбором параметра при ценообразовании
Стратегия для построения производственного плана выпуска продукта:
- В текущем году продукт должен быть продан в количестве 10 000шт.
- Производственные расходы 1-ой штуки: 7,5 руб.
- Расходы на реализацию: 450 000 руб.
Какую установить розничную цену, чтобы рентабельность производства сохранялась на уровне 20%?
Рентабельность определяется как соотношение дохода к прибыли (прибыль разделить на доход) и выражается только в процентах!
Снова решим поставленную задачу в Excel с помощью подбора параметра:
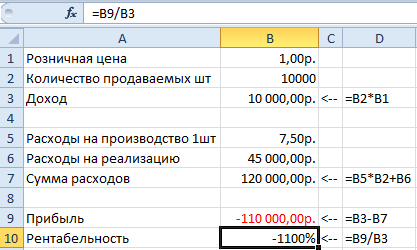
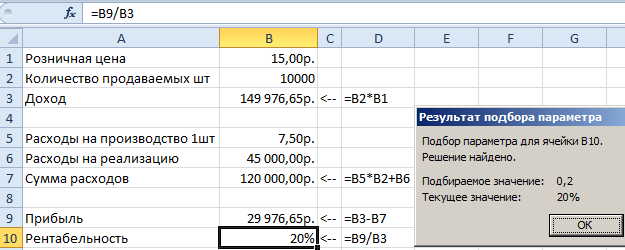
- Составьте таблицу с исходными данными и формулами, так как указано на рисунке ниже. Обратите внимание! В столбце D указаны, какие именно нужно вводить формулы в соответствующие ячейки столбца B. А в ячейке B1 указана цена 1 руб. чтобы избежать ошибок в формуле B3 и B10 (вероятная ошибка деления на 0). Не забудьте отформатировать все ячейки соответствующим форматам: денежный, общий, процентный.
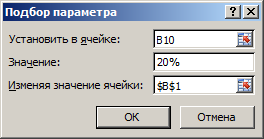
- Перейдите в ячейку B10 и выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра»
- Заполните поля в появившемся диалоговом окне как на рисунке и нажмите ОК.
Как видно розничную цену (B1) нужно устанавливать в 2 раза выше производственных расходов на 1-ну штуку продукции. Только тогда мы сможем удержать рентабельность производства на уровне 20% при таких расходах на реализацию. В реальности бывает и еще хуже.
Подбор параметра для банковских кредитов
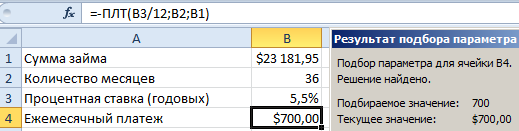
Допустим, Вы хотите приобрести автомобиль в кредит. Максимальная сумма ежемесячного взноса, которую Вы можете себе позволить, составляет 700$. Банк не может выдать Вам кредит сроком более чем на 3 года, с процентной ставкой 5,5% годовых. Можете ли вы себе позволить при таких условиях кредитования приобрести автомобиль стоимостью в 30 000$, а если нет, то на какую сумму можно рассчитывать?
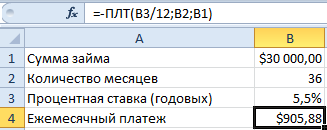
Составьте таблицу условий кредитования в Excel как показано ниже на рисунке. Обратите внимание! Ячейка B4 содержит формулу: =-ПЛТ(B3/12;B2;B1).
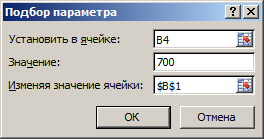
Как видно Вы не можете себе позволить такой дорогой автомобиль. Теперь узнаем, какая максимальная стоимость автомобиля соответствует Вашим финансовым возможностям. Для этого перейдите в ячейку B4 и выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
Заполните поля в появившемся диалоговом окне как показано выше на рисунке и нажмите ОК.
Как видно максимальная стоимость автомобиля, на которую можно рассчитывать составляет при таких финансовых возможностях и условиях кредитования составляет – 23 1812$.
Внимание! Если срок кредитования определяется количеством месяцев, а не лет, то годовую процентную ставку нужно перевести в месячную. Поэтому в первом аргументе функции ПЛТ стоит значение B3/12 (5,5% годовых разделено на 12 месяцев).
Используя финансовые функции, следует помнить об их стандартах. Например, сумма займа всегда отображаются как отрицательное число. Поэтому перед функцией ПЛТ мы использовали знак минус.
На чтение 1 мин Опубликовано 07.06.2015
Форматы Денежный (Currency) и Финансовый (Accounting) в Excel очень похожи. Этот пример продемонстрирует разницу.
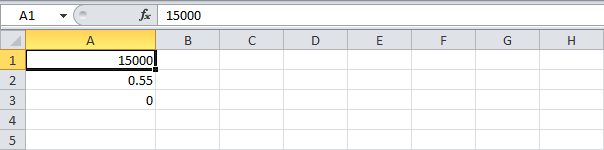
- Введите следующие значения:
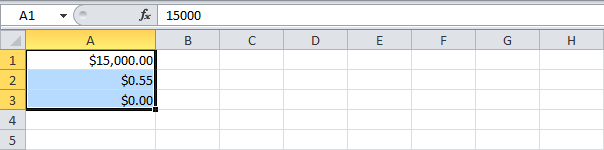
- Денежный формат добавляет знак доллара перед числом.
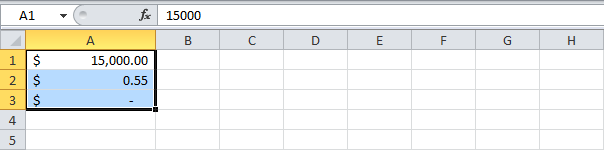
- Финансовый формат выравнивает знаки доллара по левому краю ячейки и отображает тире для нулевых значений.
Примечание: Денежный формат может отображать отрицательные числа со знаком минус, красным цветом, в скобках или красным цветом в скобках. Финансовый формат отображает отрицательные числа в скобках.
Оцените качество статьи. Нам важно ваше мнение:
Для Google Docs эти формулы тоже подходят.
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
Какие данные нужны
Для начала надо правильно написать формулу — в любой свободной ячейке.
=ПЛТ(ставка;кпер;пс)
В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:
- Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
- Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
- Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
Какие данные нужны
Формула расчёта довольно простая:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
В ней всего две переменные:
- Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
- Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).
Как всё посчитать
Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:
Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.
3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.
Как всё посчитать
Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.
Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
Какие данные нужны
Чтобы определить более выгодное предложение, применим формулу:
=ЧИСТВНДОХ(значения;даты)
Достаточно знать всего две переменные:
- Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
- Даты — график платежей, по которым будут выплачивать прибыль.
Как всё посчитать
Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
Какие данные нужны
Полезной будет эта формула:
=СТАВКА(кпер;плт;пс)
Три переменных в ней означают следующее:
- Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
- Плт — размер платежей. Считаются и основной долг, и проценты.
- Пс — общая сумма займа. В нашем примере это 100 000 рублей.
Как всё посчитать
Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.
6. PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
Какие данные нужны
Пригодится формула расчёта текущей стоимости:
=ПС(ставка; кпер; плт)
Для этого потребуется информация, которая есть на сайте любого банка:
- Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
- Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
- Плт — размер комфортного платежа.
Как всё посчитать
Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.
Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.
7. NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Какие данные нужны
Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)
Она состоит из четырёх основных значений и одного дополнительного:
- Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
- Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
- Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
- Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
- Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.
Как всё посчитать
Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.
Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.
Читайте также 🧐
- Как вести бюджет, если у вас непостоянный доход
- 20 полезных шаблонов «Google Таблиц» на все случаи жизни
- 10 крутых приложений, чтобы взять финансы под контроль